A&A 460, 831-842 (2006)
DOI: 10.1051/0004-6361:20065607
O. Kochukhov1 - V. Tsymbal2,3 - T. Ryabchikova4,3 - V. Makaganyk2 - S. Bagnulo5
1 - Department of Astronomy and Space Physics, Uppsala University, 751 20, Uppsala, Sweden
2 - Tavrian National University, Yaltinskaya 4, 95007 Simferopol, Crimea, Ukraine
3 - Department of Astronomy, University of Vienna, Türkenschanzstraße 17, 1180 Vienna, Austria
4 - Institute of Astronomy, Russian Academy of Sciences, Pyatnitskaya 48, 109017 Moscow, Russia
5 - European Southern Observatory, Casilla 19001, Santiago 19, Chile
Received 15 May 2006 / Accepted 27 August 2006
Abstract
Context. High spectral resolution studies of cool Ap stars reveal conspicuous anomalies of the shape and strength of many absorption lines. This is a signature of large atmospheric chemical gradients (chemical stratification) produced by the selective radiative levitation and gravitational settling of chemical species.
Aims. Previous observational studies of the chemical stratification in Ap stars were limited to fitting simple parametrized chemical profiles. Here we present a new approach to mapping the vertical chemical structures in stellar atmospheres.
Methods. We have developed a regularized chemical inversion procedure that uses all information available in high-resolution stellar spectra. The new technique for the first time allowed us to recover chemical profiles without making a priori assumptions about the shape of chemical distributions. We have derived average abundances and applied the vertical inversion procedure to the high-resolution VLT UVES spectra of the weakly magnetic, cool Ap star HD 133792.
Results. Our spectroscopic analysis yielded improved estimates of the atmospheric parameters of HD 133792. We show that this star has negligible
![]() and the mean magnetic field modulus
and the mean magnetic field modulus
![]() = 1.1
= 1.1 ![]() 0.1 kG. We have derived average abundances for 43 ions and obtained vertical distributions of Ca, Si, Mg, Fe, Cr, and Sr. All these elements except Mg show high overabundance in the deep layers and solar or sub-solar composition in the upper atmosphere of HD 133792. In contrast, the Mg abundance increases with height.
0.1 kG. We have derived average abundances for 43 ions and obtained vertical distributions of Ca, Si, Mg, Fe, Cr, and Sr. All these elements except Mg show high overabundance in the deep layers and solar or sub-solar composition in the upper atmosphere of HD 133792. In contrast, the Mg abundance increases with height.
Conclusions. We find that transition from the metal-enhanced to metal-depleted zones typically occurs in a rather narrow range of depths in the atmosphere of HD 133792. Based on the derived photospheric abundances, we conclude that HD 133792 belongs to the rare group of evolved cool Ap stars, which possesses very large Fe-peak enhancement, but lacks a prominent overabundance of the rare-earth elements.
Key words: stars: abundances - stars: atmospheres - stars: chemically peculiar - stars: individual: HD 133792
Michaud (1970) considered in detail a process of element separation in stellar atmospheres under the mutual action of radiative acceleration and gravitational settling. He showed that in atmospheres with suppressed convection and turbulence this process could lead to chemical anomalies in the form of under- or overabundances. This radiative diffusion hypothesis was first applied to interpret the abundance anomalies inferred for the atmospheres of magnetic chemically peculiar Ap stars (Michaud et al. 1974), which were known to be slow rotators and whose atmospheres are stabilized by the strong magnetic field.
Diffusion processes are not only responsible for the observed average atmospheric abundance anomalies but also lead to an inhomogeneous abundance distribution through the stellar atmosphere depending on the balance between radiative
acceleration and surface gravity. Borsenberger et al. (1981) calculated Ca and Sr abundance profiles for atmospheres with
![]()
![]() 10 000 K and demonstrated the influence of chemical stratification on the profile of the
resonance Ca II 3933 Å line. These interesting theoretical predictions notwithstanding, the absence of high-resolution, high signal-to-noise spectroscopic observations at that time did not permit a direct comparison between observations and diffusion calculations. Later Babel (1992) carried out detailed diffusion calculations
for Ca, Ti, Cr, Mn, and Sr in
10 000 K and demonstrated the influence of chemical stratification on the profile of the
resonance Ca II 3933 Å line. These interesting theoretical predictions notwithstanding, the absence of high-resolution, high signal-to-noise spectroscopic observations at that time did not permit a direct comparison between observations and diffusion calculations. Later Babel (1992) carried out detailed diffusion calculations
for Ca, Ti, Cr, Mn, and Sr in
![]() = 8500 K stellar atmosphere and applied his model to explain an unusual shape of the
Ca II 3933 Å line, which often shows extremely wide wings and a very sharp narrow core in the spectra of Ap stars. Babel's calculations inspired the use of a simple approximation of the vertical element distribution in the
stellar atmosphere in the form of a step function. This parametrization is now widely employed in observational stratification studies, for example Mn in HgMn stars (Sigut 2001), Si, Ca, Cr, Fe in Ap stars (Wade et al. 2003; Ryabchikova et al. 2002,2005).
= 8500 K stellar atmosphere and applied his model to explain an unusual shape of the
Ca II 3933 Å line, which often shows extremely wide wings and a very sharp narrow core in the spectra of Ap stars. Babel's calculations inspired the use of a simple approximation of the vertical element distribution in the
stellar atmosphere in the form of a step function. This parametrization is now widely employed in observational stratification studies, for example Mn in HgMn stars (Sigut 2001), Si, Ca, Cr, Fe in Ap stars (Wade et al. 2003; Ryabchikova et al. 2002,2005).
Despite the encouraging success of the previous attempts to model chemical gradients using the prescribed parametrized shape, real element distributions in the atmospheres of peculiar stars may differ considerably from the simple step function, at least for some chemical elements. Some theoretical studies also hinted at the possibility of complex vertical abundance distributions (e.g. Fig. 6 in Borsenberger et al. 1981). Moreover, recent self-consistent model atmosphere calculations including diffusion (LeBlanc & Monin 2004) have identified a number of additional effects, like mass loss and weak turbulent mixing, which may significantly affect the shape of the vertical chemical profiles but are difficult to predict ab initio. These interesting hydrodynamical effects, treated as free parameters in the current theoretical diffusion modelling, could be potentially constrained by comparison with the observed vertical abundance distributions.
Meanwhile modern spectrographs at large telescopes, such UVES at the ESO VLT, have reached remarkable precision and spectral coverage, and now allow us to record very high signal-to-noise ratio data covering the whole optical region spectra of moderately bright Ap stars. This dramatic improvement in the quality and quantity of the available observational material suggests that unprecedented details of the stellar atmospheric properties, and, in particular, the vertical abundance distributions, can be deduced with the help of detailed modelling of the spectral line profiles. These facts stimulated a recent surge of interest in the observational analysis of chemical stratification and emphasized the need to improve stratification modelling techniques.
In this paper we present a new procedure to study vertical chemical inhomogeneities in Ap-star atmospheres. We have chosen HD 133792 (HR 5623, HIP 74181) for our modelling. This star was classified as an A0p Sr-Cr-Eu object by Jaschek & Jaschek (1959). Mathys (1990) noted that HD 133792 exhibits remarkably sharp lines
and no evidence of a strong magnetic field. Martinez & Kurtz (1994) detected no rapid pulsational variability in HD 133792. Despite its brightness and extremely low
![]() ,
facilitating detailed spectroscopic studies,
the star was never analysed with the model atmosphere method.
,
facilitating detailed spectroscopic studies,
the star was never analysed with the model atmosphere method.
The paper is structured as follows. The principles and numerical details of the vertical inversion procedure are given in Sect. 2. Observations of HD 133792 and spectra reduction are described in Sect. 3. Fundamental stellar parameters are determined in Sect. 4 and the abundance analysis is presented in Sect. 5. We derive the vertical distribution of chemical elements in Sect. 6. Section 7 concludes the paper with the summary and discussion.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{5607f1.eps}\end{figure}](/articles/aa/full/2006/48/aa5607-06/Timg10.gif) |
Figure 1:
Depth variation of the iron abundance and opacities for a chemically homogeneous
(left column) and stratified (right column) stellar atmosphere. a) Fe abundance as a function of the optical depth in continuum at |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17.65cm,clip]{5607f2.eps}\end{figure}](/articles/aa/full/2006/48/aa5607-06/Timg11.gif) |
Figure 2: Normalized disk-centre intensity profile of the Fe II 4923.93 Å line computed for the stratified iron abundance distribution shown in Fig. 1 using different radiative transfer algorithms: a) DELOQ, b) DELOB, c) Feautrier, d) MW, e) IS. In each plot the lower panel shows the line profiles computed for the model atmosphere with 49 (dotted line), 118 (dashed line), and 332 (solid line) layers. The upper panels show the difference with respect to the computation for the model atmosphere discretized into 628 layers. |
| Open with DEXTER | |
The stability of the atmosphere of magnetic stars facilitates efficient radiative diffusion and may lead to a buildup of significant chemical abundance gradients in the line-forming regions. Theoretical calculations (Babel 1992; LeBlanc & Monin 2004) and interpretation of the observations of cool Ap stars (e.g., Ryabchikova et al. 2002,2005) point to the presence of steep photospheric abundance gradients: variation by up to 2-3 orders of magnitude may occur for some elements over a small range of optical depths. This extreme vertical chemical non-uniformity has to be carefully accounted for in the solution of the radiative transfer equation. It is not clear to what extent existing numerical radiative transfer schemes are able to cope with a strong depth dependence of the line absorption coefficient and to generate sufficiently accurate theoretical spectra. Since most of the methods rely on discretizing the stellar atmosphere into a number of layers, performance of the numerical radiative transfer techniques is expected to improve with the number of layers. In the context of the vertical inverse problem solution attempted here, the best radiative transfer algorithm is the one achieving acceptable accuracy with the least number of vertical zones in the chemically stratified model atmosphere.
We have evaluated the performance of 8 different radiative transfer algorithms commonly used in simulating stellar spectra: the DELO solution with linear (DELOL, Rees et al. 1989), quadratic (DELOQ, Socas-Navarro et al. 2000) and Bezier spline (DELOB, Piskunov, private communication) interpolation formulae for the source function; the Feautrier method (Rees et al. 1989); Hermitian solution (Ruis-Cobo et al. 1999); stepwise Unno solution (MW, Martin & Wickramasinghe 1979); Discontinuous Finite Element method (DFE, Castor et al. 1992) and the integral solution of the radiative transfer equation as implemented in the ATLAS9 model atmosphere code (IS, Kurucz 1993). The disk-centre intensity across the Fe II 4923.93 Å line was calculated with each of the algorithms assuming an LTE source function and using an identical set of line and continuous opacities. The latter were calculated using the SYNTH3 code
(Kochukhov 2007; Ryabchikova et al. 2005) for the 49-layer
![]() K,
K,
![]() chemically stratified model atmosphere kindly provided by LeBlanc & Monin (2004). In
this theoretical model the Fe distribution changes from
chemically stratified model atmosphere kindly provided by LeBlanc & Monin (2004). In
this theoretical model the Fe distribution changes from
![]() at the bottom of the atmosphere to
at the bottom of the atmosphere to
![]() in the uppermost layers with a large gradient at
in the uppermost layers with a large gradient at
![]() .
For comparison we also evaluated the disk-centre intensity with the same model atmosphere and homogeneous Fe abundance
.
For comparison we also evaluated the disk-centre intensity with the same model atmosphere and homogeneous Fe abundance
![]() .
The depth dependence of the iron concentration and of the line and continuous absorption coefficients are illustrated in Figs. 1a and b, respectively.
.
The depth dependence of the iron concentration and of the line and continuous absorption coefficients are illustrated in Figs. 1a and b, respectively.
Calculation of the Fe II 4923.93 Å line profile was carried out with the original 49-layer
depth grid and for the models interpolated onto a finer grid, containing 118, 332, and 628 layers.
Interpolation employed the adaptive depth grid refinement procedure of the SYNTH3 code,
which subdivides layers where the line
absorption coefficient changes rapidly. The maximum error of each of the resulting Fe II line profiles was recorded relative to the DELOQ solution for the 628-layer grid. The Fe II line shapes corresponding to the stratified case are presented in Fig. 2. As expected, little discrepancy is found between the spectra computed for the model with the maximum number of grid points. This verifies the internal consistency of the radiative transfer schemes. However, as illustrated in Fig. 1c, the algorithms show rather different convergence properties. In the case of the chemically homogeneous atmosphere, most of the methods already provide an accuracy of 1% or better for the original 49-layer model. At the same time, the stratified case turns out to be considerably more challenging: all methods except Kurucz's integral solution require at least 100 layers in the model atmosphere to achieve the necessary accuracy. On the other hand, the former method attains an acceptable
maximum error of ![]() 0.5% for the original 49-layer model atmosphere.
0.5% for the original 49-layer model atmosphere.
The outcome of our numerical tests highlights the stability and efficiency of the IS radiative transfer algorithm. In principle, each of the studied numerical schemes can be successfully used for the forward modelling of the effects of chemical stratification if a sufficiently fine vertical discretization is used. The advantage of the IS method is to provide the required accuracy at the least cost. This is why we consider this algorithm to be the optimum choice for the vertical inversion procedure (VIP) which reconstructs a non-parametrized chemical distribution using a fixed depth grid. Taking these results into account, we have adopted the IS algorithm in our vertical inversion code described below.
Synthetic spectrum calculation for a chemically inhomogeneous stellar atmosphere is based on the SYNTHV code written by Tsymbal (1996). The code accepts an LTE plane-parallel model atmosphere in the ATLAS9 format. In addition, the input of VIP consists of a configuration file that specifies wavelength regions of interest and indicates the respective line lists. Atomic line parameters are extracted from the VALD database (Kupka et al. 1999).
The code calculates new number densities for a given abundance stratification of any number of chemical elements. Partition functions are calculated using the tables given in the PFSAHA subroutine of the ATLAS9 code (Kurucz 1993). For some of the rare-earth elements we have updated these data
following Cowley & Barisciano (1994). For calculations of the ionic populations we take into
account up to 6 ionization states of light elements (atomic number ![]() 28) and up to 4 states for heavy elements. Calculation of the continuum opacity is performed for the blue and red edges of each of the wavelength intervals and is based on the ATLAS9 subroutine KAPP (Kurucz 1993). We include H I, He I, He II, H-, different metallic bound-free and free-free transitions,
Rayleigh scattering for H I, He I and H2+, and electron scattering.
28) and up to 4 states for heavy elements. Calculation of the continuum opacity is performed for the blue and red edges of each of the wavelength intervals and is based on the ATLAS9 subroutine KAPP (Kurucz 1993). We include H I, He I, He II, H-, different metallic bound-free and free-free transitions,
Rayleigh scattering for H I, He I and H2+, and electron scattering.
For each wavelength region the VIP code calculates the line opacity due to all atomic lines included in the input line lists. Radiative damping, Stark broadening and van der Waals broadening are taken into account. For all lines, except the He I and hydrogen lines, we use the Voigt profile to approximate the line opacity and adopt the broadening constants supplied by VALD or calculated according to the classical expressions (see Gray 1992). The Stark broadening of the hydrogen lines is estimated by interpolating in the tables by Lemke (1997). For the He I we use the Stark broadening profiles of Barnard et al. (1974) when available.
The radiative transfer equation is solved with the modified ATLAS9 subroutine JOSH. The specific intensity is calculated for 7 angles between the local outward normal and the line of sight. Each intensity profile is convolved with appropriate functions to model stellar rotation, radial-tangential macroturbulent broadening, and the instrumental profile. The flux spectrum is produced by integrating specific intensities over the stellar disk.
Different spectral intervals are treated independently, which permits us to use different instrumental broadening profiles and radial velocity corrections.
We must solve an inverse problem in order to find the distribution of a chemical element with depth in the stellar atmosphere. We seek the vertical chemical profile that would provide an adequate description of the spectral line intensities and profiles of all spectral features belonging to a given species. This problem is similar to abundance Doppler imaging (Kochukhov et al. 2004), except that the aim is to obtain the best-fit chemical stratification instead of a 2D picture of the horizontal abundance distribution.
Similar to Doppler imaging, the vertical inversion belongs to the class of ill-posed problems
(Tikhonov & Arsenin 1977). A given sample of spectral lines recorded in the optical spectra of A-type stars is characterized by a very uneven sensitivity to the properties of different atmospheric layers. Typically, the chemical composition of the line forming regions (optical depth
![]() )
is very well constrained, whereas very few or no lines sample the uppermost and deepest layers. This presents a formidable difficulty for a vertical inversion algorithm: a multitude of widely different, high-contrast solutions can provide a reasonable description of observations. Furthermore, inversions are unstable with respect to the initial guess, and the properties of
solutions, especially the amplitude of abundance gradients, will strongly depend on the
vertical sampling of the stellar model atmosphere adopted in the inversion.
)
is very well constrained, whereas very few or no lines sample the uppermost and deepest layers. This presents a formidable difficulty for a vertical inversion algorithm: a multitude of widely different, high-contrast solutions can provide a reasonable description of observations. Furthermore, inversions are unstable with respect to the initial guess, and the properties of
solutions, especially the amplitude of abundance gradients, will strongly depend on the
vertical sampling of the stellar model atmosphere adopted in the inversion.
A common procedure to alleviate this non-uniqueness and instability of the ill-posed problem is to introduce a regularization. This brings in additional a priori information that can be used to constrain the problem and decouple solution from the vertical sampling used in the model atmosphere. For instance, one can look for a solution that maximizes the entropy (Vogt et al. 1987) or impose a requirement that the solution must be a smooth function (Goncharskij et al. 1977). The second criterion, also known as the Tikhonov regularization procedure, is appropriate for the vertical inversion problem and is implemented in our code.
Thus, the vertical chemical inversion reduces to the mathematical problem of finding a depth-dependent chemical distribution
![]() that minimizes the function
that minimizes the function
The chemical distribution
![]() is a discrete function that defines the concentration
of a given element in each model atmosphere layer. Its shape is not prescribed in advance
but is constrained entirely by the available observations and by the Tikhonov regularization function. The role of regularization is to ensure the stability of the inversion procedure and to provide the simplest
(smoothest) solution that fits observations.
is a discrete function that defines the concentration
of a given element in each model atmosphere layer. Its shape is not prescribed in advance
but is constrained entirely by the available observations and by the Tikhonov regularization function. The role of regularization is to ensure the stability of the inversion procedure and to provide the simplest
(smoothest) solution that fits observations.
We use the Levenberg-Marquardt method (Press et al. 1986) as the minimization algorithm. It combines the best features of the gradient search with the method of linearizing the fitting function, which ensures rapid convergence close to the minimum. For the VIP code we have adapted the Levenberg-Marquardt routine described by Piskunov & Kochukhov (2002). Trial inversions demonstrate that VIP converges to a stable solution in no more than 10-15 iterations.
Derivatives of the fitting function with respect to the abundance in each layer,
![]() ,
are required by the Levenberg-Marquardt algorithm and
are evaluated analytically for the regularization function. A numerical approximation is used for
the first derivatives of the synthetic line profiles:
,
are required by the Levenberg-Marquardt algorithm and
are evaluated analytically for the regularization function. A numerical approximation is used for
the first derivatives of the synthetic line profiles:
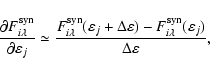 |
(2) |
The regularization parameter ![]() is determined empirically. We adjust regularization in such a way that i) the solution
is determined empirically. We adjust regularization in such a way that i) the solution
![]() is smooth but, at the same time, gives a satisfactory description of the stellar observations and ii) the solution is independent of the initial guess. In practice, these requirements are fulfilled when the contribution of regularization to the total discrepancy function
is smooth but, at the same time, gives a satisfactory description of the stellar observations and ii) the solution is independent of the initial guess. In practice, these requirements are fulfilled when the contribution of regularization to the total discrepancy function ![]() is comparable to, but not larger than the first term of Eq. (1).
is comparable to, but not larger than the first term of Eq. (1).
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{5607f3.eps}\end{figure}](/articles/aa/full/2006/48/aa5607-06/Timg35.gif) |
Figure 3:
a) Dependence of the inferred iron vertical distribution on the
regularization parameter adopted in VIP reconstruction. Solid line: reconstruction with the optimal regularization,
dashed line: inversion with 20 times higher regularization; dashed-dotted line:
distribution obtained using 10 times smaller regularization.
The horizontal dotted line shows homogeneous Fe distribution adopted as the initial guess.
b) Reconstruction of the Fe distribution using optimal regularization and different homogeneous initial guesses (
|
| Open with DEXTER | |
Figure 3 illustrates dependence of the vertical Fe abundance inversion in HD 133792 on the choice of regularization strength. The vertical distributions recovered with widely different ![]() are shown in Fig. 3a. The solid curve corresponds to the results obtained with the optimum regularization.
Regularization that is too weak leads to large abundance gradients (dashed-dotted curve) and cannot
ensure uniqueness of the solution. On the other hand, a much stronger regularization (dashed line)
smoothes the inferred vertical distribution of Fe and does not allow us to achieve a low
are shown in Fig. 3a. The solid curve corresponds to the results obtained with the optimum regularization.
Regularization that is too weak leads to large abundance gradients (dashed-dotted curve) and cannot
ensure uniqueness of the solution. On the other hand, a much stronger regularization (dashed line)
smoothes the inferred vertical distribution of Fe and does not allow us to achieve a low ![]() in the fit to observations.
in the fit to observations.
The stability test of the vertical inversion using the optimum regularization is presented in
Fig. 3b. The thick solid line shows the average of 16 Fe distributions recovered in the
inversions started from constant Fe abundance
![]() in the range from -2.5 to -4.0 dex. The dark area represents the full span of the individual vertical solutions. Its
maximum width is 0.07 dex, and the mean width is 0.03 dex. Thus, despite drastically different initial guesses, regularization has ensured convergence to nearly the same Fe stratification.
in the range from -2.5 to -4.0 dex. The dark area represents the full span of the individual vertical solutions. Its
maximum width is 0.07 dex, and the mean width is 0.03 dex. Thus, despite drastically different initial guesses, regularization has ensured convergence to nearly the same Fe stratification.
In addition to chemical stratification, elements are often distributed inhomogeneously over the surface of magnetic chemically peculiar stars (e.g., Kochukhov et al. 2004). In principle, it is possible to compute a synthetic spectrum taking into account a non-uniform distribution of elements over the stellar surface and chemical stratification at the same time. However, such a 3D abundance mapping procedure requires complete rotational phase coverage and can only be applied to rapidly rotating Ap stars. On the other hand, HD 133792 investigated in our paper is an extremely slow rotator (see Sect. 4) and lacks evidence of spectroscopic variability. Therefore, no information can be derived about possible spotted distribution of elements over the surface of HD 133792, and this effect is disregarded in the present study.
High-resolution, high signal-to-noise ratio spectra of HD 133792 were obtained with the UVES instrument of the ESO VLT on 26 February 2002
in the program 68.D-0254. The UVES spectrometer is
described by Dekker et al. (2000). The observations were carried out
using both available dichroic modes. The detailed log of the
observations is given in Table 1. In both the blue
arm and the red arm the slit width was set to 0.5
![]() ,
for a spectral
resolution of about 80 000. The slit was oriented along the
parallactic angle, in order to minimize losses due to atmospheric
dispersion. Almost the full wavelength interval from 3030 to 10 400 Å was observed, except for a few gaps, the largest of which are at
5760-5835 Å and 8550-8650 Å. In addition, there are several small
gaps, about 1 nm each, due to the lack of overlap between the
échelle orders in the 860U setting.
,
for a spectral
resolution of about 80 000. The slit was oriented along the
parallactic angle, in order to minimize losses due to atmospheric
dispersion. Almost the full wavelength interval from 3030 to 10 400 Å was observed, except for a few gaps, the largest of which are at
5760-5835 Å and 8550-8650 Å. In addition, there are several small
gaps, about 1 nm each, due to the lack of overlap between the
échelle orders in the 860U setting.
The UVES data have been reduced with the automatic pipeline described in Ballester et al. (2000). For all settings, science frames are bias-subtracted and divided by the extracted flat-field, except for the 860 nm setting, where the 2D (pixel-to-pixel) flat-fielding is used, in order to better correct for the fringing. Because of the high flux of the spectra, we used the UVES pipeline average extraction method.
All spectra were normalized to the continuum with an interactive procedure that employed either a low-degree polynomial or a smoothing spline function.
Table 1: Log of UVES observations of HD 133792.
![\begin{figure}
\par\includegraphics[width=17.65cm,clip]{5607f4.eps}\end{figure}](/articles/aa/full/2006/48/aa5607-06/Timg38.gif) |
Figure 4:
Magnetic broadening of lines in the spectrum of HD 133792. In each panel observations
(symbols) are compared with the theoretical spectra computed for
|
| Open with DEXTER | |
We used the Strömgren photometric indices of HD 133792 to obtain an initial estimate of the stellar
model atmosphere parameters. The observed colours, b-y=0.026, c1=0.180, m1=1.110 (Hauck &
Mermilliod 1998), were dereddened adopting
E(B-V)=0.09. This colour excess follows from
the reddening maps by Lucke (1978) and high-resolution dust maps by Schlegel et al.
(1998). Taking into account H
![]() (Hauck & Mermilliod 1998), we have
established
(Hauck & Mermilliod 1998), we have
established
![]() K and
K and
![]() with the calibration by Moon & Dworetsky
(1985) implemented in the TEMPLOGG code (Rogers 1995).
with the calibration by Moon & Dworetsky
(1985) implemented in the TEMPLOGG code (Rogers 1995).
Model atmospheres for HD 133792 were calculated with the ATLAS9 code (Kurucz 1993),
using the ODF with 3 times the solar metallicity and zero microturbulent velocity. With
these metal-enhanced models we further fine-tuned the stellar parameters to fit the
hydrogen H![]() and H
and H![]() lines. This procedure yielded the final parameters
lines. This procedure yielded the final parameters
![]() K and
K and
![]() .
The final model atmosphere of HD 133792 has 72 layers and
covers optical depths from
.
The final model atmosphere of HD 133792 has 72 layers and
covers optical depths from
![]() to
to
![]() .
.
The projected rotational velocity of HD 133792 was established by synthetic spectrum fitting of the
magnetically insensitive Fe I lines. In particular, for the Fe I 5434.52 Å line
(mean Landé factor z=-0.01) no rotational Doppler broadening appears to be necessary after the
instrumental smearing corresponding to the resolution of our UVES observations is accounted for
(see Fig. 4). The respective upper
![]() limit is
limit is ![]() 1.0 km s-1.
1.0 km s-1.
Using the Hipparcos parallax of HD 133792 (![]()
![]() 0.66 mas, Perryman et al. 1997)
and adopting
0.66 mas, Perryman et al. 1997)
and adopting
![]() very close to the value established above, Kochukhov & Bagnulo (2006)
determined
very close to the value established above, Kochukhov & Bagnulo (2006)
determined
![]()
![]() 0.10 and M=2.80
0.10 and M=2.80 ![]()
![]() .
Comparison with the theoretical stellar interior models (Schaller et al. 1992) suggests that HD 133792 is
significantly evolved from the ZAMS and is likely to be close to the end of its main sequence
evolutionary phase.
.
Comparison with the theoretical stellar interior models (Schaller et al. 1992) suggests that HD 133792 is
significantly evolved from the ZAMS and is likely to be close to the end of its main sequence
evolutionary phase.
One derives
![]() from the aforementioned value of the stellar luminosity and
from the aforementioned value of the stellar luminosity and
![]() K. This radius implies a lower limit of about 200 d for the rotation period if the
star is viewed equator-on.
K. This radius implies a lower limit of about 200 d for the rotation period if the
star is viewed equator-on.
No resolved Zeeman split spectral lines are found in the spectra of HD 133792, indicating a mean field strength of ![]() 2 kG (Mathys 1990). Mathys & Lanz (1992) have also failed to detect relative intensification of the Fe II 6147 and 6149 Å lines and, on this basis, have suggested a zero magnetic field for the star. However, detailed magnetic spectrum
synthesis calculations by Takeda (1991) showed this interpretation to be invalid. For magnetic fields weaker than
2 kG (Mathys 1990). Mathys & Lanz (1992) have also failed to detect relative intensification of the Fe II 6147 and 6149 Å lines and, on this basis, have suggested a zero magnetic field for the star. However, detailed magnetic spectrum
synthesis calculations by Takeda (1991) showed this interpretation to be invalid. For magnetic fields weaker than
![]() 2 kG, the diagnostic content of this particular Fe II line pair is highly ambiguous, and, in general, there is no correlation between the difference of the equivalent widths of the two Fe II lines and magnetic field intensity.
2 kG, the diagnostic content of this particular Fe II line pair is highly ambiguous, and, in general, there is no correlation between the difference of the equivalent widths of the two Fe II lines and magnetic field intensity.
With our high-quality spectra we see
clear indication of an extra broadening, invariably correlating with the magnetic sensitivity, for many spectral lines.
Examples of this are illustrated in Fig. 4 for several Fe and Cr lines with large Landé factors. We have carried out polarized radiative transfer calculations with the SYNTHMAG code (Piskunov 1999) to estimate the mean field strength. The best fit is achieved for
![]() = 1.1
= 1.1 ![]() 0.1 kG, confirming our earlier field
strength measurement (Ryabchikova et al. 2004b).
0.1 kG, confirming our earlier field
strength measurement (Ryabchikova et al. 2004b).
Recently Kochukhov & Bagnulo (2006) detected a marginal positive longitudinal field of ![]() 120 G based on the two low-resolution spectropolarimetric observations
of HD 133792 with FORS1 at VLT. The longitudinal field did not change sign nor appreciably vary in strength between the two FORS1
120 G based on the two low-resolution spectropolarimetric observations
of HD 133792 with FORS1 at VLT. The longitudinal field did not change sign nor appreciably vary in strength between the two FORS1
![]() field measurements separated by 9 months. The large
field measurements separated by 9 months. The large
![]() to
to
![]() ratio obtained for HD 133792 hints that currently this star is observed at the crossover phase.
ratio obtained for HD 133792 hints that currently this star is observed at the crossover phase.
Our line identification is based on the theoretical spectrum calculated for the whole spectral region 3050-9000 Å using the line extraction from VALD (Kupka et al. 1999 and references therein) and DREAM (Biémont et al. 1999) databases. Atomic data on the REE elements compiled in the DREAM database were extracted via the VALD interface. Comparison of the synthetic and observed spectra allowed us to choose the least blended lines for the chemical abundance and stratification analysis.
Spectral lines in HD 133792 are very sharp due to a negligible rotation and a rather small magnetic field intensity. Thus, for most elements we have measured equivalent widths and carried out abundance analysis with the Kurucz's WIDTH9 code, modified by one of us (VT) to accept the line lists in the VALD output format. Only in the case of either blended lines or lines affected by hyperfine and/or isotopic splitting did we employ spectral synthesis for abundance determination (Be, Mn I, Mn II, Eu II).
The recent experimental oscillator strengths currently included in the VALD database were used for the following elements: Ti II (Pickering et al. 2001), Mn II (Kling & Griesmann 2000; Kling et al. 2001), Nd II (Den Hartog et al. 2004), Dy II (Wickliffe et al. 2000). For Ce II, Ce III, Nd III oscillator strengths were taken from the DREAM database (Palmeri et al. 2000; Biémont et al. 2002; Zhang et al. 2002), while for Pr III the calculations (Ryabtsev, private communication) based on the extended energy levels analysis (Wyart et al. 2006) were used. For Eu II atomic data are taken from Lawler et al. (2001). Abundances from the Cr II, Fe II, Co II lines were based on the oscillator strengths calculated with the orthogonal operator technique (Raassen & Uylings 1998). Its advantage was discussed by Ryabchikova et al. (2005).
Hyperfine splitting of the Mn I (Blackwell-Whitehead et al. 2005) and Mn II (Holt et al. 1999) lines was taken into account. However, its effect was found to be negligible for Mn I lines (![]() 0.04 dex) and very small for Mn II lines. For the abundance analysis we used only Mn II lines for which experimental oscillator strengths and hfs constants are available. The
Co I lines are too weak in the spectrum of HD 133792 to be influenced by hfs.
0.04 dex) and very small for Mn II lines. For the abundance analysis we used only Mn II lines for which experimental oscillator strengths and hfs constants are available. The
Co I lines are too weak in the spectrum of HD 133792 to be influenced by hfs.
Table 2: Atmospheric abundances in the Ap star HD 133792 with the error estimates based on n measured lines. Abundances in the solar atmosphere and in the evolved Ap star HD 204411 are given for comparison.
The final results of the abundance analysis assuming chemical homogeneity of the HD 133792 atmosphere are presented in Table 2. We have compared them with the atmospheric abundances in another evolved, slightly cooler Ap star with a very weak magnetic field, HD 204411 (Ryabchikova et al. 2005), and in the solar atmosphere (Asplund et al. 2005).
The light elements Be, C, N, and O, are underabundant by an order of magnitude in HD 133792 when compared with the chemical composition of the solar photosphere. The UVES spectra allowed us to investigate the resonance Be II lines, which are only marginally visible in HD 133792, indicating an order of magnitude Be deficiency. Thus, on the basis of much more accurate spectroscopic observations we have confirmed the earlier coarse assessment of
a Be underabundance in the atmospheres of 4 cool magnetic Ap stars (Gerbaldi et al. 1986), which contrasts with the very high Be overabundance derived for non-magnetic hot HgMn stars (Boesgaard et al. 1982). The upper limit for the He abundance, obtained from the He I ![]() 4471 line, is
4471 line, is
![]() = -2.5, which is 1.5 dex lower than the solar value. The large underabundance of light elements is typical of cool Ap stars (Gerbaldi et al. 1989; Roby & Lambert 1990).
= -2.5, which is 1.5 dex lower than the solar value. The large underabundance of light elements is typical of cool Ap stars (Gerbaldi et al. 1989; Roby & Lambert 1990).
Abundances of Mg, Si and Ca derived from the lines of neutrals and first ions differ significantly, which is an indication of chemical stratification (see Ryabchikova et al. 2003).
The Fe-peak elemental abundances are similar in both HD 133792 and HD 204411, with more pronounced Fe and, in particular, Cr anomalies in HD 133792. This is in agreement with the general dependence of the Cr and Fe abundance on the effective temperature in Ap stars (Ryabchikova et al. 2004a; Ryabchikova 2005). We did not notice any significant dependence of the individual line abundances on the wavelength or excitation energy for Cr lines. On the other hand, such a dependence exists for Fe lines: abundances derived from the low excitation lines below the Balmer Jump (BJ) are systematically smaller than those derived from the lines above the BJ. This is another signature of possible stratification of elements.
Special attention was given to the careful study of the rare-earth elements. The evolved Ap star HD 204411 is very Cr-Fe overabundant and REE-poor compared to the majority of magnetic Ap stars, where a large REE overabundance is typical. REE lines are very weak in the spectrum of HD 133792 and reliable abundances can be derived only for the lines of Ce III, Pr III, Nd II, Nd III, and Eu II. We find a REE overabundance of about 1.5 dex relative to the solar composition, with a hint of decreasing overabundance towards the heavier species.
For the stratification analysis we have chosen chemical elements with a large number of unblended spectral lines (Cr and Fe) and elements showing the most conspicuous discrepancies between the line-by-line abundances derived in the approximation of a chemically homogeneous atmosphere (Ca, Mg, Si, Sr).
The lack of the accurate atomic data precludes a stratification analysis for some other elements showing discrepant abundances. For instance, a significantly different abundance is derived from the Co II lines with different excitation energies. However, hyperfine splitting strongly affects these lines, and the hfs parameters are not known for many Co II transitions.
Stratification calculations were performed for 6 elements. Atomic parameters of the spectral lines employed for each of the element are listed in Table 3. The central wavelength, excitation potential, oscillator strength, and the Stark broadening constant are provided. For the Cr II and Sr II lines marked by asterisks in Table 3, experimental Stark broadening data were taken from Rathnore et al. (1984) and Fleurier et al. (1977), respectively. For all other lines the broadening constants were either extracted from the VALD database or calculated using the classical approximation (Gray 1992).
Table 3:
A list of spectral lines used for the stratification calculations. The columns give the ion identification, central wavelength, the excitation potential (in eV) of the lower level, oscillator strength (![]() ), the Stark damping constant ("appr'' marks lines for which the classical approximation was used), and the reference for oscillator strength.
), the Stark damping constant ("appr'' marks lines for which the classical approximation was used), and the reference for oscillator strength.
The final depth-dependent abundances derived for the atmosphere of HD 133792 using the VIP procedure are plotted as a function of
![]() in Fig. 5. A comparison between observations and theoretical
spectra is presented in Figs. 6-9. Each of these plots shows observations and
the best-fit synthetic spectrum computed with the stratified abundance.
For comparison the best-fit calculation assuming a homogeneous chemical distribution is also
given.
in Fig. 5. A comparison between observations and theoretical
spectra is presented in Figs. 6-9. Each of these plots shows observations and
the best-fit synthetic spectrum computed with the stratified abundance.
For comparison the best-fit calculation assuming a homogeneous chemical distribution is also
given.
Magnesium. We have used 4 lines of Mg I, one unblended Mg II line and 3 Mg II doublets to derive the vertical stratification of magnesium in HD 133792. This is the only element for which abundance increases with height in the stellar atmosphere. The concentration of Mg is slightly below solar
in the deep layers and reaches a 1.7 dex overabundance above
![]() .
The transition zone extends over
.
The transition zone extends over ![]() 4 dex in
4 dex in
![]() .
Figure 8 shows that an inhomogeneous Mg distribution substantially improves the fit to the Mg II lines, especially the feature at
.
Figure 8 shows that an inhomogeneous Mg distribution substantially improves the fit to the Mg II lines, especially the feature at
![]() 4481 Å. The mean deviation between observations and spectrum synthesis - a parameter that is used to quantify the
quality of the fit - is lower by a factor of 2 for the model with a stratified Mg distribution.
4481 Å. The mean deviation between observations and spectrum synthesis - a parameter that is used to quantify the
quality of the fit - is lower by a factor of 2 for the model with a stratified Mg distribution.
Silicon. This element shows outstanding stratification signatures in the spectra of HD 133792.
We have employed 7 Si II lines and one neutral Si transition for the reconstruction of the silicon stratification in the atmosphere of HD 133792. We find that below
![]() Si is overabundant by 1.5 dex with respect to the Sun. On the other hand, the upper atmospheric layers are characterized by a 1.7 dex deficiency of Si. The transition zone is extremely narrow and is centred at
Si is overabundant by 1.5 dex with respect to the Sun. On the other hand, the upper atmospheric layers are characterized by a 1.7 dex deficiency of Si. The transition zone is extremely narrow and is centred at
![]() .
A dramatic improvement of the fit quality is evident (see Fig. 8) for the theoretical spectrum which
takes the Si stratification into account. Such calculations allow us to reduce the mean deviation by as much as a factor of 3 in comparison with the best-fit homogeneous model.
.
A dramatic improvement of the fit quality is evident (see Fig. 8) for the theoretical spectrum which
takes the Si stratification into account. Such calculations allow us to reduce the mean deviation by as much as a factor of 3 in comparison with the best-fit homogeneous model.
Calcium. Ca is another element showing very strong vertical inhomogeneity in HD 133792. The Ca distribution inferred for this star is similar to that of Si, but shows a larger change from the lower to upper atmosphere. Ca is overabundant by 1.4 dex in the deep layers, whereas the deficiency with respect to solar composition reaches 2.5 dex in the shallow layers. Thus, the abundance of Ca in the atmosphere of HD 133792 changes by almost 4 orders of magnitude. We obtain a 3.6 times lower mean deviation with the stratified Ca model. These results are based on 4 Ca I and 3 Ca II lines (see Fig. 9). The resonance Ca II K line is especially useful in the chemical inversion.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{5607f5.eps}\end{figure}](/articles/aa/full/2006/48/aa5607-06/Timg65.gif) |
Figure 5: Chemical stratification in the atmosphere of HD 133792. |
| Open with DEXTER | |
Chromium. Many strong unblended spectral lines of neutral and singly ionized Cr are
identified in the spectra of HD 133792. For the VIP inversion we have employed 9 Cr I and 17 Cr II lines. Very high quality of the UV portion of the UVES spectra of HD 133792 permitted analysis of the outstanding Cr II 3180.29, 3421.20 and 3422.73 Å lines (see Fig. 7). We find weak evidence for the
presence of vertical stratification of Cr. This element is strongly enhanced over the whole line-forming region in the photosphere of HD 133792. The Cr overabundance changes from 2.7 dex in the deeper layers to 2.2 dex in the upper atmosphere. The stratified Cr distribution leads to a marginal (![]() 20% of the mean deviation) improvement of the fit to the observed line profiles (Fig. 7).
20% of the mean deviation) improvement of the fit to the observed line profiles (Fig. 7).
Iron. The vertical distribution of Fe was obtained from 11 Fe I and 12 Fe II lines, including the strong line of Fe II at ![]() 5018.44 Å (Fig. 6).
Chemical inversion suggests a 1.9 dex enhancement in the deep layers and
5018.44 Å (Fig. 6).
Chemical inversion suggests a 1.9 dex enhancement in the deep layers and ![]() 1.0 dex overabundance in the upper atmosphere, with the smooth transition at
1.0 dex overabundance in the upper atmosphere, with the smooth transition at
![]() .
Comparison of the observed and
theoretical spectra computed for the homogeneous and stratified Fe distribution is illustrated in
Fig. 6. The case for the Fe stratification in HD 133792 is somewhat stronger than for Cr: the inferred Fe abundance step reaches 0.9 dex and the decrease of the mean deviation is more substantial (
.
Comparison of the observed and
theoretical spectra computed for the homogeneous and stratified Fe distribution is illustrated in
Fig. 6. The case for the Fe stratification in HD 133792 is somewhat stronger than for Cr: the inferred Fe abundance step reaches 0.9 dex and the decrease of the mean deviation is more substantial (![]() 40%).
40%).
Strontium. Our Sr abundance inversion relied on 5 Sr II lines and two weak Sr I features (Fig. 9). The most important information about the vertical distribution of Sr in HD 133792 comes from the shapes of the profiles of strong Sr II lines. Accounting for the stratification of this element noticeably improves the fit to the outer wings of the Sr II 4125.52 and 4305.44 Å lines. A large overabundance of Sr is derived for the whole atmosphere of HD 133792. The Sr enhancement ranges from 5.9 dex deep in the atmosphere to 2.5 dex in the upper layers. Remarkably, the VIP inversion provides a hint that the Sr vertical distribution is more complicated than the step-like profile found for other elements.
Thanks to recent advances in the instrumentation at large telescopes, high-resolution, very high S/N spectra have been obtained for a large number of Ap stars. This dramatic improvement of the data quality stimulated a renewal of interest in the atmospheric properties of magnetic CP stars. Modern investigations of the spectral line intensities and shapes show that many peculiar features in the Ap-star spectra originate from an inhomogeneous vertical distribution of chemical elements in stellar atmospheres. Thus, magnetic chemically peculiar stars represent the only type of non-degenerate stellar objects where direct observations and diagnosis of the chemical diffusion signatures becomes possible. Observational study of the chemical stratification in Ap stars is able to provide crucial and unique constraints for the theoretical modelling of chemical diffusion in stellar atmospheres and also helps to understand the relation between diffusion and hydrodynamic mixing processes.
![\begin{figure}
\par\includegraphics[width=17.65cm,clip]{5607f6.eps}\end{figure}](/articles/aa/full/2006/48/aa5607-06/Timg67.gif) |
Figure 6: Comparison of the observed Fe line profiles (symbols) and calculations for the stratified abundance distribution (full line) and for the best-fit homogeneous abundance (dashed line) of Fe. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17.65cm,clip]{5607f7.eps}\end{figure}](/articles/aa/full/2006/48/aa5607-06/Timg68.gif) |
Figure 7: Same as in Fig. 6 but for Cr. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.15cm,clip]{5607f8a.eps}\includegraphics[width=8.15cm,clip]{5607f8b.eps}\end{figure}](/articles/aa/full/2006/48/aa5607-06/Timg69.gif) |
Figure 8: Same as in Fig. 6 but for Mg (left panel) and Si (right panel). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.15cm,clip]{5607f9a.eps}\includegraphics[width=8.15cm,clip]{5607f9b.eps}\end{figure}](/articles/aa/full/2006/48/aa5607-06/Timg70.gif) |
Figure 9: Same as in Fig. 6 but for Ca (left panel) and Sr (right panel). |
| Open with DEXTER | |
Until now observational analyses of stratification in peculiar stars have been limited to fitting simple parametrized vertical chemical profiles to a small number of diagnostic lines (Wade et al. 2003; Ryabchikova et al. 2002,2005). Most often, chemical distributions were approximated with a step function, whose shape is described by two abundance values and the position of the transition zone.
In the present study we have developed and applied the first assumption-free method of reconstruction of the chemical stratification in stellar atmospheres. In our technique, the individual chemical composition is derived for all atmospheric layers contributing to the line absorption. Uniqueness and stability of the chemical inversion is achieved by applying the Tikhonov regularization function. This means that our code finds the simplest elemental distribution sufficient to fit observations.
The vertical inversion procedure is successfully applied to the weakly magnetic, evolved Ap star HD 133792. We have reconstructed vertical distributions of 6 elements. Magnesium is found to have an abundance close to the solar one in the lower atmosphere and shows an increase of concentration with height. All other elements
have the opposite vertical distribution: high abundance deep in the photosphere and a lower abundance in the upper layers. The transition region is narrow for Si, Ca and Sr, and is located close to
![]() .
Fe and Cr are overabundant over the whole atmosphere of HD 133792, and the respective change of the
concentration of these elements is smaller than for other species and occurs between
.
Fe and Cr are overabundant over the whole atmosphere of HD 133792, and the respective change of the
concentration of these elements is smaller than for other species and occurs between
![]() and -2.
and -2.
Our investigation of the diffusion signatures in HD 133792 confirms the validity of the step-like, parametrized stratification models applied in previous studies of Ap stars. However, we find that for some species the transition region can be rather extended (Mg), or the vertical distribution is more complex than a simple one-step function (Sr). Thus, the applicability of the latter approximation is wide, but not universal. In this context, our automatic regularized inversion approach appears to be more robust and should be preferred whenever possible.
Stratification analysis of HD 133792 is supplemented by a detailed chemical abundance study assuming homogeneous vertical distribution of elements. We have measured the concentration of 43 ions of 32 chemical elements. The outstanding characteristic of the chemical composition of HD 133792 is a very large overabundance of the iron-peak elements in its atmosphere, combined with a fairly small enhancement of heavy elements, in particular REE. Strontium and, possibly, palladium are the only heavy elements in HD 133792 showing a very large overabundance with respect to the solar chemical composition.
HD 133792 is the second star with a detailed abundance analysis, including stratification effects, whose position on the H-R diagram clearly shows that the star is close to finishing its main sequence life. The first such star was HD 204411 (Ryabchikova et al. 2005). Both stars possess weak magnetic fields and have a small overabundance of the REEs compared with many other Ap stars in the 8500-9500 K effective temperature region. The most remarkable abundance characteristic of both stars is an extremely high overabundance of Cr and Fe, in particular in HD 133792.
Cowley & Henry (1979) have defined a group of 5 stars characterized by strong lines of the Fe-peak elements and REE lines weaker than in "normal'' Ap stars. HD 204411 is a member of this group. The H-R diagram position of these objects indicates that all of them are close to the end of their main sequence life (Kochukhov & Bagnulo 2006).
We were able to extract high-resolution spectra from the ELODIE archive![]() for the three other stars of this group: 73 Dra (HD 196502), HD 8441, and HD 216533. Photometric indicators suggest
for the three other stars of this group: 73 Dra (HD 196502), HD 8441, and HD 216533. Photometric indicators suggest
![]() = 8900-9200 K for these three objects. A preliminary determination of the Pr and Nd abundance based on the
strongest lines of the second ions shows that in all three stars abundances of these rare-earth elements are comparable to those found in HD 133792. In contrast, REE abundances in the young star HD 66318 of similar effective temperature, much stronger magnetic field (Bagnulo et al. 2003) and the same large Cr and
Fe anomalies are by an order of magnitude higher. For all stars these abundance estimates were based on the same lines of Pr III and Nd III.
= 8900-9200 K for these three objects. A preliminary determination of the Pr and Nd abundance based on the
strongest lines of the second ions shows that in all three stars abundances of these rare-earth elements are comparable to those found in HD 133792. In contrast, REE abundances in the young star HD 66318 of similar effective temperature, much stronger magnetic field (Bagnulo et al. 2003) and the same large Cr and
Fe anomalies are by an order of magnitude higher. For all stars these abundance estimates were based on the same lines of Pr III and Nd III.
Evidently, on the basis of our detailed abundance analysis we may extend the definition of the group of stars with weak REE lines as a group of evolved Ap stars with small to moderate REE anomalies, and very large Cr and Fe overabundances. All stars of this group lie near maximum in plots of Cr and Fe abundance versus
![]() (Ryabchikova et al. 2004a). Comparison between Cr and Fe abundances in evolved Ap stars with weak magnetic fields and in the young star HD 66318 with an extremely large magnetic field shows
that neither evolutionary status nor magnetic field play an important role in creating the Fe-peak abundance anomalies. On the other hand, the REE overabundance is clearly less pronounced in the group of evolved Ap stars. Further detailed chemical and evolutionary analysis of Ap stars in the effective temperature range
8500-10 000 K is required to understand the role of the magnetic field and/or evolution in creating and maintaining REE atmospheric anomalies in magnetic peculiar stars.
(Ryabchikova et al. 2004a). Comparison between Cr and Fe abundances in evolved Ap stars with weak magnetic fields and in the young star HD 66318 with an extremely large magnetic field shows
that neither evolutionary status nor magnetic field play an important role in creating the Fe-peak abundance anomalies. On the other hand, the REE overabundance is clearly less pronounced in the group of evolved Ap stars. Further detailed chemical and evolutionary analysis of Ap stars in the effective temperature range
8500-10 000 K is required to understand the role of the magnetic field and/or evolution in creating and maintaining REE atmospheric anomalies in magnetic peculiar stars.
Acknowledgements
Resources provided by the electronic databases (VALD, SIMBAD, NASA's ADS) are acknowledged. This work was supported by the grant from the Swedish Kungliga Fysiografiska Sällskapet, by the Austrian Fonds zur Förderung der wissenschaftlichen Forschung (projects P17580N2, P17890) and BM:BWK (project COROT), and by the Presidium of RAS Program "Origin and Evolution of Stars and Galaxies''.