A&A 460, 759-767 (2006)
DOI: 10.1051/0004-6361:20065251
Asteroseismology and evolutionary status of Procyon A
J. Provost1 - G. Berthomieu1 - M. Martic2 -
P. Morel1
1 - Département Cassiopée, UMR CNRS 6202, Observatoire de la Côte
d'Azur, BP 4229, 06304 Nice Cedex 4, France
2 -
Service d'Aéronomie du CNRS, BP 3, 91371 Verrières-le-Buisson Cedex, France
Received 22 March 2006 / Accepted 22 June 2006
Abstract
Models of Procyon A satisfying the actual observational constraints,
particularly the asteroseismic ones, are discussed.
The oscillations of these models were computed and analysed.
We looked for seismic signatures of the evolutionary status of Procyon A.
We show that the behavior of the small frequency spacings,
particularly
 allows us to distinguish
between main sequence and post-main sequence models,
all satisfying the observational
constraints on mass, effective temperature,
radius, and surface metallicity of Procyon A.
We also introduce a new seismic evolution criterion,
allows us to distinguish
between main sequence and post-main sequence models,
all satisfying the observational
constraints on mass, effective temperature,
radius, and surface metallicity of Procyon A.
We also introduce a new seismic evolution criterion,
 ,
based on the comparison of the low and high frequency parts
of the power spectrum.
The comparison of the seismic properties of the models with
the available asteroseismic observations
does not allow us to
definitely decide on the stage of evolution of Procyon A.
Much more accurate frequencies must
be obtained especially in the low-frequency domain to distinguish between the models.
,
based on the comparison of the low and high frequency parts
of the power spectrum.
The comparison of the seismic properties of the models with
the available asteroseismic observations
does not allow us to
definitely decide on the stage of evolution of Procyon A.
Much more accurate frequencies must
be obtained especially in the low-frequency domain to distinguish between the models.
Key words: stars: oscillations - stars: evolution - stars: individual: Procyon A
Many works have been devoted to the study of the structure and
evolutionary status of Procyon A through computation of models
satisfying the observational constraints for mass, effective
temperature, metallicity, and, more recently, radius and asteroseismic
frequencies (Guenther & Demarque 1993; Chaboyer et al. 1999;
Kervella et al. 2004;
Provost et al. 2004; Eggenberger et al. 2005; Straka et al. 2005).
Using seismic measurements in Eggenberger
et al. (2004), Eggenberger et al. (2005)
determine global constraints for the age, initial
helium and metallicity contents, and for the mixing length parameter of Procyon A.
They conclude in favor of a main sequence model with a mass of 1.497  .
Kervella et al. (2004) measured the diameter of Procyon A and
discussed its evolutionary state, and conclude
that Procyon A is ending its life on the main sequence.
Preliminary results of Provost et al. (2004), considering only
the frequency measurements of Martic et al. (2004)
and models with a simplified equation of state, favored more evolved models.
.
Kervella et al. (2004) measured the diameter of Procyon A and
discussed its evolutionary state, and conclude
that Procyon A is ending its life on the main sequence.
Preliminary results of Provost et al. (2004), considering only
the frequency measurements of Martic et al. (2004)
and models with a simplified equation of state, favored more evolved models.
In this paper, we try to determine how the age and
structure of Procyon A can be derived from all the observational
constraints. We do not search for the best model that fits the
observations, but our aim is instead to delimit the range
of models compatible
with the observations within their uncertainties and some uncertainties
of the physics and to point out the observational improvements that
would allow us to select the best model.
First we discuss the observational constraints (Sect. 2).
Then, we proceed in two steps to determine how all these observations
constrain our knowledge of the age, evolutionary status, and structure
of Procyon A.
In the first one, models with different masses, chemical
compositions, and convection parameters, which together
fulfill the constraints
of Table 1, have been computed (Sects. 3 and 4).
In a second step we study their asteroseismic
properties and determine criteria that would help to distinguish between
these models (Sect. 5).
Finally we apply these criteria to the observed frequencies (Sect. 6)
and conclude (Sect. 7).
Table 1:
Adopted constraints for our models of Procyon A:
mass  ,
effective temperature
,
effective temperature
 ,
radius
,
radius  ,
surface metallicity
,
surface metallicity
![${\rm [{Fe/ H}]_s}$](/articles/aa/full/2006/48/aa5251-06/img4.gif) ,
and galactic enhancement
,
and galactic enhancement
 .
.
Different estimates of the mass of Procyon A have been made by
measuring the orbit of the astrometric binary system Procyon A and B. The
estimate of the masses depends on the value of the parallax used.
With the parallax and astrometric data
from HST-WFPC2 observations (Girard et al. 2000),
Allende Prieto et al. (2002) (hereafter
referred to as AP02) estimated the mass of Procyon A in the
range between 1.41  and 1.53
and 1.53  .
Adopting the very
precisely measured parallax by Hipparcos, the same authors
derived a lower mass range (see Table 1)
that we used to constrain our models.
This is in agreement with the recent astrometric study of
Procyon by Gatewood & Han (2000), who give
a mass of 1.43
.
Adopting the very
precisely measured parallax by Hipparcos, the same authors
derived a lower mass range (see Table 1)
that we used to constrain our models.
This is in agreement with the recent astrometric study of
Procyon by Gatewood & Han (2000), who give
a mass of 1.43 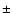 0.034
0.034  for Procyon A.
for Procyon A.
The effective temperature of Procyon A is taken from AP02.
Kervella et al. (2004) measured the angular diameter of Procyon A with
VINCI/VLTI instrument and, using Hipparcos parallax, derived a linear
diameter of
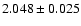 relative to the solar diameter.
The constraints on effective temperature and radius induce two limit
values for the luminosity, namely
relative to the solar diameter.
The constraints on effective temperature and radius induce two limit
values for the luminosity, namely
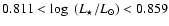 .
This range is included in the range given by Steffen (1985).
All these constraints define an area in the
HR diagram where the models must be located (see Fig. 1).
.
This range is included in the range given by Steffen (1985).
All these constraints define an area in the
HR diagram where the models must be located (see Fig. 1).
The surface metallicity of Procyon A has been estimated by AP02.
The constraint on surface metallicity is related to the
solar metallicity
by
![${\rm\left[{Fe/H}\right]_s} \sim \log~ (Z/X)_{\rm s} -\log~ (Z/X)_\odot$](/articles/aa/full/2006/48/aa5251-06/img44.gif) (Morel et al. 2000), where Z and X are the mass fraction of
heavy elements and hydrogen.
We used the standard solar metallicity of
(Morel et al. 2000), where Z and X are the mass fraction of
heavy elements and hydrogen.
We used the standard solar metallicity of
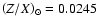 .
.
In order to satisfy the constraint from the chemical evolution
of the galaxies,
the initial values of
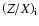 and
and  were chosen according to Chaboyer et al. (1999)
such that
were chosen according to Chaboyer et al. (1999)
such that
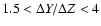 with primordial
helium equal to 0.24 (see Fig. 4).
with primordial
helium equal to 0.24 (see Fig. 4).
A constraint on the age can be deduced from the binarity of Procyon A.
Provencal et al. (2002)
discuss the cooling time of the white dwarf Procyon B
and find that the progenitor ended its lifetime 1.7  0.1 Gyr ago.
If the mass of the progenitor is around 2.5-3
0.1 Gyr ago.
If the mass of the progenitor is around 2.5-3  and has a solar metallicity,
its lifetime on the main sequence (MS) is around 600-400 Myr.
This lifetime is slightly shorter if the progenitor has a sub-solar metallicity
(Bressan et al. 1993).
This would lead to an age of Procyon A on the order of or larger than 2000 Myr.
and has a solar metallicity,
its lifetime on the main sequence (MS) is around 600-400 Myr.
This lifetime is slightly shorter if the progenitor has a sub-solar metallicity
(Bressan et al. 1993).
This would lead to an age of Procyon A on the order of or larger than 2000 Myr.
![\begin{figure}
\par\includegraphics[angle=-90,width=6.7cm,clip]{5251fig1.ps}\end{figure}](/articles/aa/full/2006/48/aa5251-06/Timg48.gif) |
Figure 1:
Examples of main sequence (MS) and post-main sequence (PoMS1 and PoMS2 - see description in text) models satisfying the observational constraints for Procyon A:
its position in the HR diagram constrained by effective temperature and the luminosity from Steffen (1985) (dashed box); the VINCI/VLTI (Kervella et al. 2002) radius measurement
reduces the possible domain (grey area). |
| Open with DEXTER |
Recently, Martic et al. (2004) and Eggenberger et al. (2004)
identified peaks of frequencies of acoustic modes with degrees  = 0, 1, 2 in the power spectrum of Doppler-shift measurements.
This corresponds to acoustic waves stochastically excited by the convective
envelope with frequencies obeying quasi-asymptotic relations.
As in the solar case (Gough 1991),
the set of frequencies is characterized by
the large and small frequency spacings defined by:
= 0, 1, 2 in the power spectrum of Doppler-shift measurements.
This corresponds to acoustic waves stochastically excited by the convective
envelope with frequencies obeying quasi-asymptotic relations.
As in the solar case (Gough 1991),
the set of frequencies is characterized by
the large and small frequency spacings defined by:
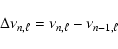 |
(1) |
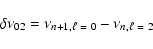 |
(2) |
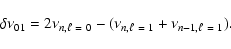 |
(3) |
where n is the radial order of the oscillation.
In the high-frequency range, the large frequency
spacing
 does not vary much with the frequency and is
somewhat independent of the degree of the oscillation modes.
does not vary much with the frequency and is
somewhat independent of the degree of the oscillation modes.
An estimate of the mean of the large frequency spacings
 in the observed spectrum of Procyon A
as made by Martic et al. (2004) using the so-called "comb response method'' gives
in the observed spectrum of Procyon A
as made by Martic et al. (2004) using the so-called "comb response method'' gives
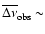 53.5
53.5  0.5
0.5  Hz
in the frequency range of the excess power between 300 to 1400
Hz
in the frequency range of the excess power between 300 to 1400  Hz.
If the frequency range is restricted to the high-frequency
part,
Hz.
If the frequency range is restricted to the high-frequency
part,
 is higher, around 54.5
is higher, around 54.5  Hz.
For about the same high-frequency range, Eggenberger et al.
(2004) estimate this mean value by adjusting an echelle diagram to the
different peaks of the observed spectrum and obtain a higher value
Hz.
For about the same high-frequency range, Eggenberger et al.
(2004) estimate this mean value by adjusting an echelle diagram to the
different peaks of the observed spectrum and obtain a higher value
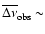 55.5
55.5 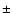 0.5
0.5  Hz
(Fig. 2).
Hz
(Fig. 2).
![\begin{figure}
\par\includegraphics[angle=-90,width=6.85cm,clip]{5251fig2.ps}\end{figure}](/articles/aa/full/2006/48/aa5251-06/Timg53.gif) |
Figure 2:
Large frequency spacings
 for degrees
for degrees
 = 0 and = 0 and  = 1 for frequencies of Martic et al. (2004) (star)
and Eggenberger et al. (2004)(square). The hatched areas
indicate the values of mean large frequency spacing = 1 for frequencies of Martic et al. (2004) (star)
and Eggenberger et al. (2004)(square). The hatched areas
indicate the values of mean large frequency spacing
 for the two sets of observations
(lower for the Martíc's data).
for the two sets of observations
(lower for the Martíc's data). |
| Open with DEXTER |
Eggenberger et al. (2004) mention an error of 0.57  Hz for frequency
determination, corresponding to half of the time resolution, but
they notice that the dispersion of the observed large frequency spacings
around the theoretical curve is higher.
The difference between the estimations of
Hz for frequency
determination, corresponding to half of the time resolution, but
they notice that the dispersion of the observed large frequency spacings
around the theoretical curve is higher.
The difference between the estimations of
 is larger than the errors given by the observers.
The mean spacing is essentially proportional to the characteristic
frequency
is larger than the errors given by the observers.
The mean spacing is essentially proportional to the characteristic
frequency
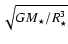 (where
(where  and
and  are the mass and the radius of the star). A difference in
the quantity
are the mass and the radius of the star). A difference in
the quantity
 in the high-frequency range
of 1
in the high-frequency range
of 1  Hz leads to a difference in mass at a constant radius of 3.6% and a difference in radius at a constant mass of 1.2%, which is on the order of
the uncertainty of the observational
determination of the mass and the radius of Procyon A. According to the
adopted value of
Hz leads to a difference in mass at a constant radius of 3.6% and a difference in radius at a constant mass of 1.2%, which is on the order of
the uncertainty of the observational
determination of the mass and the radius of Procyon A. According to the
adopted value of
 ,
it is expected that
different models of Procyon A will be selected. Recently
MOST data on Procyon were obtained (Mathews et al. 2004).
These data are contaminated by scattered Earthlight, modulated
by the 101.413 min orbital period of the satellite,
and their analysis is controversial. However, some estimation of
,
it is expected that
different models of Procyon A will be selected. Recently
MOST data on Procyon were obtained (Mathews et al. 2004).
These data are contaminated by scattered Earthlight, modulated
by the 101.413 min orbital period of the satellite,
and their analysis is controversial. However, some estimation of
 ,
about 54.5
,
about 54.5  Hz, is given by
Regulo & Roca-Cortes (2005) and Garcia et al. (2006).
Hz, is given by
Regulo & Roca-Cortes (2005) and Garcia et al. (2006).
![\begin{figure}
\par\includegraphics[angle=-90,width=6.1cm,clip]{5251fi3a.ps}\par\includegraphics[angle=-90,width=6.1cm,clip]{5251fi3b.ps}\end{figure}](/articles/aa/full/2006/48/aa5251-06/Timg55.gif) |
Figure 3:
Small frequency spacings
 and
and
 for
the frequencies of Martic et al. (2004) and Eggenberger et al. (2004).
The same symbols as in Fig. 2.
for
the frequencies of Martic et al. (2004) and Eggenberger et al. (2004).
The same symbols as in Fig. 2. |
| Open with DEXTER |
The observed small frequency spacings
 and
and
 are given in Fig. 3. Errors on the observed spacings
are not provided by the authors.
Identification of the successive modes is not always available
due to aliases, destructive interferences with noise background, and
the finite lifetime of modes. Martic & Lebrun (2006) use the technique of
2D collapsograms, which allows the exploration for the best signature
of the mean spacings in different frequency regions of the excess power,
independent of the mode degree.
The significant departure of the modes in the region of the maximum
oscillation amplitudes from the asymptotic relation explains the
difficulties in finding the mean main frequency separation.
are given in Fig. 3. Errors on the observed spacings
are not provided by the authors.
Identification of the successive modes is not always available
due to aliases, destructive interferences with noise background, and
the finite lifetime of modes. Martic & Lebrun (2006) use the technique of
2D collapsograms, which allows the exploration for the best signature
of the mean spacings in different frequency regions of the excess power,
independent of the mode degree.
The significant departure of the modes in the region of the maximum
oscillation amplitudes from the asymptotic relation explains the
difficulties in finding the mean main frequency separation.
All the models were computed with the CESAM code (Morel 1997),
with the following physics:
nuclear data from NACRE collaboration (Angulo et al. 1999),
CEFF equation of state, OPAL opacities fitted at low
temperature with Alexander & Ferguson tables,
Eddington law for the atmosphere description (see Morel et al. 1994).
We define the stellar radius of a model as the bolometric one.
The convection is described either with the classical mixing length theory
(hereafter MLT), with a mixing-length parameter 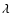 of order 1.9 close to the solar value (Morel et al. 1999) or according to Canuto & Mazitelli (1991) (hereafter CM)
with a mixing-length parameter
of order 1.9 close to the solar value (Morel et al. 1999) or according to Canuto & Mazitelli (1991) (hereafter CM)
with a mixing-length parameter 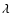 of order 1. For some models, an overshooting of the
convective core over a distance equal to
of order 1. For some models, an overshooting of the
convective core over a distance equal to
 ,
is introduced, where
,
is introduced, where 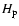 and
and 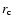 are the pressure height scale and the radius of the convective core. We vary the overshoot parameter
are the pressure height scale and the radius of the convective core. We vary the overshoot parameter 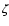 from 0 to 0.2.
This value is recommended by Schaller et al. (1992)
and confirmed by results obtained for the Hyades (Perryman et al. 1998),
contrary to Straka et al. (2005), who give an upper limit on Procyon A's
core overshoot extent of
from 0 to 0.2.
This value is recommended by Schaller et al. (1992)
and confirmed by results obtained for the Hyades (Perryman et al. 1998),
contrary to Straka et al. (2005), who give an upper limit on Procyon A's
core overshoot extent of 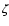 about 0.4.
about 0.4.
The microscopic diffusion of chemical species
is taken into account according to
Burgers (1969), using the resistance coefficients of Paquette et al. (1986).
For stellar models with mass larger than 1.4  ,
the use of microscopic
diffusion alone produces an important depletion of helium
and heavy elements and a concomitant enhancement of the hydrogen content
at the surface. Different
ways have been used to overcome this problem. Eggenberger et al. (2005)
introduce some turbulence due to rotation. Di Mauro (2004) suppresses
diffusion in the outer layers "to be sure that helium and heavy elements
are not totally drained out of the envelope''. Chaboyer et al. (1999) include
a wind mass loss in the diffusion equations that reduces the diffusion
in the outer layers of the star model. According to the prescription
of Morel & Thévenin (2002), we introduce an additional mixing proportional to the radiative viscosity (e.g. Mihalas & Weibel-Mihalas 1984),
parameterized by Re
,
the use of microscopic
diffusion alone produces an important depletion of helium
and heavy elements and a concomitant enhancement of the hydrogen content
at the surface. Different
ways have been used to overcome this problem. Eggenberger et al. (2005)
introduce some turbulence due to rotation. Di Mauro (2004) suppresses
diffusion in the outer layers "to be sure that helium and heavy elements
are not totally drained out of the envelope''. Chaboyer et al. (1999) include
a wind mass loss in the diffusion equations that reduces the diffusion
in the outer layers of the star model. According to the prescription
of Morel & Thévenin (2002), we introduce an additional mixing proportional to the radiative viscosity (e.g. Mihalas & Weibel-Mihalas 1984),
parameterized by Re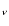 .
The parameter Re
.
The parameter Re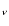 has been calibrated by Morel & Thévenin
to
has been calibrated by Morel & Thévenin
to 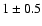 by comparison
of their models to stellar observations of the Hyades, but
the physical meaning of this efficient source of mixing has
been questioned by Alecian & Michaud (2005).
by comparison
of their models to stellar observations of the Hyades, but
the physical meaning of this efficient source of mixing has
been questioned by Alecian & Michaud (2005).
![\begin{figure}
\par\includegraphics[width=6.85cm,clip]{5251fig4.ps}\end{figure}](/articles/aa/full/2006/48/aa5251-06/Timg63.gif) |
Figure 4:
Initial chemical composition of our models for Procyon A
satisfying the constraints of Table 1.
Grey open symbols indicate MS models, dark filled symbols PoMS models.
Diamond 1.36  ,
circle 1.38 ,
circle 1.38  ,
triangle 1.42 ,
triangle 1.42  ,
stars 1.44 ,
stars 1.44  ,
square 1.45 ,
square 1.45  ,
diamond 1.46 ,
diamond 1.46  ,
cross 1.48 ,
cross 1.48  .
The two full lines indicate the minimum and maximum values of .
The two full lines indicate the minimum and maximum values of  resulting from the constraint of the galaxy chemical evolution
given in Table 1. The dotted line corresponds to a stronger constraint resulting from the constraint of the galaxy chemical evolution
given in Table 1. The dotted line corresponds to a stronger constraint
 . . |
| Open with DEXTER |
With fixed values of mixing length and overshoot
parameters, the models depend on the mass, the initial metallicity and
helium contents, and the age, or respectively,  ,
,
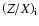
 and t. These unknowns are adjusted to fit the observational
constraints ie.
and t. These unknowns are adjusted to fit the observational
constraints ie.
 ,
,
 ,
,
![$\rm {\left[Fe/ H\right]_s}$](/articles/aa/full/2006/48/aa5251-06/img64.gif) .
Models of mass between 1.36 to 1.48
.
Models of mass between 1.36 to 1.48  were considered. For
each mass, mixing length, overshoot and additional mixing parameters,
different sets of
were considered. For
each mass, mixing length, overshoot and additional mixing parameters,
different sets of
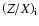 and
and  give models that fit the
observational constraints of Table 1. We found models, either in main sequence
with a small convective core and mass from 1.42 to 1.48
give models that fit the
observational constraints of Table 1. We found models, either in main sequence
with a small convective core and mass from 1.42 to 1.48  or later, in post main sequence (PoMS) with mass from 1.36 to 1.45
or later, in post main sequence (PoMS) with mass from 1.36 to 1.45  .
In the following we differentiate two types of PoMS models: PoMS1 models in the phase of
disappearance of convective core and of increasing effective
temperature and more evolved PoMS2 models after the exhaustion of the central hydrogen
(central hydrogen less than 0.001). The evolutionary tracks of some models
are given in Fig. 1.
.
In the following we differentiate two types of PoMS models: PoMS1 models in the phase of
disappearance of convective core and of increasing effective
temperature and more evolved PoMS2 models after the exhaustion of the central hydrogen
(central hydrogen less than 0.001). The evolutionary tracks of some models
are given in Fig. 1.
The MS models correspond to the higher masses.
When the mass decreases, some core overshoot must be included in
the modeling to obtain more luminous models with evolutionary
tracks crossing the constrained area in the HR diagram.
If we restrict the core overshoot parameter (
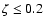 ),
the mass of MS models must be larger than 1.41
),
the mass of MS models must be larger than 1.41  .
The uncertainty on the radius induces
a crossing time of the allowed region in the HR diagram
(Fig. 1) of about 80 Myr.
As seen in Figs. 4 and 5, MS models
have ages below 2000 Myr and high values of
.
The uncertainty on the radius induces
a crossing time of the allowed region in the HR diagram
(Fig. 1) of about 80 Myr.
As seen in Figs. 4 and 5, MS models
have ages below 2000 Myr and high values of  and
and
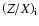 (
(
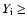 0.3,
0.3,
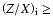 0.030).
We note that the range of
0.030).
We note that the range of
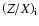 of our models is
wide compared to the range of the surface metallicity
of our models is
wide compared to the range of the surface metallicity
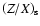 .
Indeed,
.
Indeed,
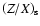 depends not only on
depends not only on
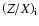 and
and  ,
but also on the mass
(and consequently on the age) and on the description of the diffusion.
If we restrict it to MS or PoMS models, the range of
,
but also on the mass
(and consequently on the age) and on the description of the diffusion.
If we restrict it to MS or PoMS models, the range of
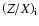 is about
half, from 0.026 to 0.032 for PoMS models and from 0.30 to 0.038
for MS models. The range is slightly wider for MS models because it appears
that their surface metallicity is more sensitive to the description
of the diffusion.
The constraint from the galactic chemical evolution strongly limits the number of MS models with lower masses as seen in Fig. 4.
is about
half, from 0.026 to 0.032 for PoMS models and from 0.30 to 0.038
for MS models. The range is slightly wider for MS models because it appears
that their surface metallicity is more sensitive to the description
of the diffusion.
The constraint from the galactic chemical evolution strongly limits the number of MS models with lower masses as seen in Fig. 4.
The PoMS models can be obtained for mass smaller
than 1.46. The uncertainty on the radius induces a smaller uncertainty on the age of less than 40 Myr. Within the range of MLT parameters we are considering,
a majority of PoMS models do not have core overshoot. However, we find a few models with a very small core overshoot (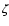 less or equal to 0.05).
The PoMS models have lower values of
less or equal to 0.05).
The PoMS models have lower values of  and
and
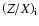 than MS models
and ages greater than 2000 Myr.
than MS models
and ages greater than 2000 Myr.
![\begin{figure}
\par\includegraphics[width=6.85cm,clip]{5251fig5.ps}\end{figure}](/articles/aa/full/2006/48/aa5251-06/Timg69.gif) |
Figure 5:
Initial helium versus age. Same models and symbols as in Fig. 4. |
| Open with DEXTER |
Adiabatic frequencies of all the models were computed
in the observed frequency range
from 300 to 1500  Hz. We note that the upper limit is
close to the acoustic cut-off frequency of the models.
Hz. We note that the upper limit is
close to the acoustic cut-off frequency of the models.
The frequency of acoustic modes and the period of gravity modes
can be respectively approximated by the following first-order asymptotic expressions:
Here c is the sound speed and N the Brunt-Väissälä frequency N (
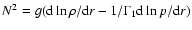 ).
The quantities
).
The quantities
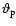 and
and
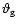 depend
on the stellar atmosphere and on the stratification at the boundaries of the inner
radiative zone (RZ), respectively, and they are of order unity.
The quantity
depend
on the stellar atmosphere and on the stratification at the boundaries of the inner
radiative zone (RZ), respectively, and they are of order unity.
The quantity 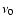 is the inverse of the sound travel time across
a stellar diameter. It varies very little for stars of given mass and radius
and different chemical compositions. It is a theoretical estimate of the
mean large spacing at high frequency.
is the inverse of the sound travel time across
a stellar diameter. It varies very little for stars of given mass and radius
and different chemical compositions. It is a theoretical estimate of the
mean large spacing at high frequency.
The value of the characteristic period of gravity modes P0is given by the inverse of the integration of Brunt-Väissälä frequency
in the inner radiative zone.
The values of P0 range from 10 to 50 min for PoMS models
and from 50 to 80 min for MS models.
For PoMS models P0 corresponds to a frequency higher than 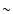 800
800  Hz.
This means that we may expect that
the frequency domains of acoustic and gravity modes,
which are well separated in solar type stars, are overlapping here.
Hz.
This means that we may expect that
the frequency domains of acoustic and gravity modes,
which are well separated in solar type stars, are overlapping here.
For models in the early MS, the frequency range we consider
corresponds to acoustic modes. Here the models are more evolved, and their spectrum
contains some modes that are not pure acoustic modes, but mixed and gravity
modes. Indeed a large peak of the Brunt-Väissälä frequency,
which may be as large as 1500  Hz, appears in the
phase of central hydrogen burning due to the existence of a convective core and increases later on. This is seen in the propagation diagram (Fig. 7,
left panel), where the local Brunt-Väissälä frequency,
Hz, appears in the
phase of central hydrogen burning due to the existence of a convective core and increases later on. This is seen in the propagation diagram (Fig. 7,
left panel), where the local Brunt-Väissälä frequency, 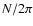 ,
and the local Lamb frequency,
,
and the local Lamb frequency,
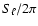 (
(
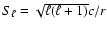 ), are plotted as a function of the radius of the star.
The gravity and acoustic modes are propagating in the regions
of the star where their frequencies are smaller or larger than
both N and
), are plotted as a function of the radius of the star.
The gravity and acoustic modes are propagating in the regions
of the star where their frequencies are smaller or larger than
both N and 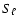 ,
respectively. Thus gravity modes may exist with frequencies as high as the maximum of N. The frequency of the gravity modes of highest
frequency,
,
respectively. Thus gravity modes may exist with frequencies as high as the maximum of N. The frequency of the gravity modes of highest
frequency,
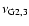 ,
are indicated for
,
are indicated for 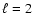 and 3 by
horizontal lines in the propagation diagram (Fig. 7, left panel).
In contrast, for
and 3 by
horizontal lines in the propagation diagram (Fig. 7, left panel).
In contrast, for 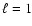 ,
we found
no gravity modes in the considered frequency range, but only
mixed modes.
,
we found
no gravity modes in the considered frequency range, but only
mixed modes.
The gravity modes are characterized by a large amplitude in the core of the star and consequently
a much higher energy than the adjacent acoustic modes
as seen Fig. 7 (right panel).
In Fig. 8 the kinetic energy density is plotted
for some modes: an acoustic mode, a gravity mode, and two mixed modes
with both acoustic and gravity characters.
If one assumes that all the modes in a given frequency
range have the same total energy, the surface amplitude of gravity
modes would be smaller than that of acoustic adjacent modes.
We studied the properties of the gravity modes with the highest
frequency for 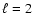 and 3.
We find a strong correlation between their frequencies
and 3.
We find a strong correlation between their frequencies
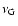 and the characteristic period of gravity modes P0 (Fig. 6).
Such modes are expected
to have a small surface amplitude, but also very small line-width.
They will be difficult to observe, but we hope that the new
methods, which are being developed in the COROT frame for detecting such
long-lived modes embedded in an acoustic spectrum (Moreira et al. 2005),
may help to extract them from future observations.
Knowing the frequency of these high-frequency gravity modes would
give a new constraint on the evolutionary status of Procyon A.
and the characteristic period of gravity modes P0 (Fig. 6).
Such modes are expected
to have a small surface amplitude, but also very small line-width.
They will be difficult to observe, but we hope that the new
methods, which are being developed in the COROT frame for detecting such
long-lived modes embedded in an acoustic spectrum (Moreira et al. 2005),
may help to extract them from future observations.
Knowing the frequency of these high-frequency gravity modes would
give a new constraint on the evolutionary status of Procyon A.
![\begin{figure}
\par\includegraphics[width=6.85cm,clip]{5251fig6.ps}\end{figure}](/articles/aa/full/2006/48/aa5251-06/Timg86.gif) |
Figure 6:
Frequencies
 of the highest-frequency gravity modes
for
of the highest-frequency gravity modes
for  = 2 and 3 versus the characteristic period P0.
The two regions where points are lacking correspond to the turning point
of the evolutionary track in the HR diagram.
There the models stay a very short time. Same models and symbols as in Fig. 4. = 2 and 3 versus the characteristic period P0.
The two regions where points are lacking correspond to the turning point
of the evolutionary track in the HR diagram.
There the models stay a very short time. Same models and symbols as in Fig. 4. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{5251fi7a.ps}\includegraphics[width=7.4cm,clip]{5251fi7b.ps}\end{figure}](/articles/aa/full/2006/48/aa5251-06/Timg87.gif) |
Figure 7:
Left panel: propagation diagram: variation of the Brunt-Väissälä
frequency N (full line) and of the Lamb frequency S (
( = 1, 2, 3
dashed lines) in = 1, 2, 3
dashed lines) in  Hz as a function of the stellar normalized radius rfor a PoMS model with mass 1.38 Hz as a function of the stellar normalized radius rfor a PoMS model with mass 1.38  .
Right panel: frequency versus logarithm of the non-dimensioned kinetic energy E of the mode for consecutive
modes of degree .
Right panel: frequency versus logarithm of the non-dimensioned kinetic energy E of the mode for consecutive
modes of degree  = 0 (dotted), 1 (full), 2 (dashed), 3 (fancy)
of the same model. The values of the highest frequency gravity modes for = 0 (dotted), 1 (full), 2 (dashed), 3 (fancy)
of the same model. The values of the highest frequency gravity modes for  = 2 and = 2 and  = 3
are given by the horizontal lines in the left panel and by the arrows
in the right panel. The heavy lines indicate the regions where these modes are propagative.
Most of their amplitude is located in the core (see also
Fig. 8 (1)). = 3
are given by the horizontal lines in the left panel and by the arrows
in the right panel. The heavy lines indicate the regions where these modes are propagative.
Most of their amplitude is located in the core (see also
Fig. 8 (1)). |
| Open with DEXTER |
Let us now consider the acoustic part of the spectrum.
We define the following seismic quantity:
 ,
mean of the large frequency spacings
,
mean of the large frequency spacings
 computed with those frequencies
higher than 800
computed with those frequencies
higher than 800  Hz and with degrees
Hz and with degrees  = 0 and 1.
Most of our models have a mean large frequency spacing
= 0 and 1.
Most of our models have a mean large frequency spacing
 from 53.5
from 53.5  Hz to 57.5
Hz to 57.5  Hz.
However, the uncertainty on the radius induces an uncertainty on
Hz.
However, the uncertainty on the radius induces an uncertainty on
 of about 1
of about 1  Hz.
If we normalize this quantity to the radius of Procyon A given by
Kervella et al. (2004), we obtain less dispersed values,
which are plotted in Fig. 9 as a function of the mass.
The remaining dispersion is due to the difference in chemical composition.
At any given mass, the normalized large frequency spacing is larger for PoMS models
than for MS models.
Hz.
If we normalize this quantity to the radius of Procyon A given by
Kervella et al. (2004), we obtain less dispersed values,
which are plotted in Fig. 9 as a function of the mass.
The remaining dispersion is due to the difference in chemical composition.
At any given mass, the normalized large frequency spacing is larger for PoMS models
than for MS models.
![\begin{figure}
\par\includegraphics[width=7.65cm,clip]{5251fig8.ps}\end{figure}](/articles/aa/full/2006/48/aa5251-06/Timg90.gif) |
Figure 8:
Kinetic energy density as a function of the radius for
different type of modes  = 2 of the same PoMS model as
in Fig. 7: (1) gravity mode = 2 of the same PoMS model as
in Fig. 7: (1) gravity mode
 Hz,
(2) acoustic mode p20 Hz,
(2) acoustic mode p20
 Hz, (3) and (4) two consecutive
mixed modes Hz, (3) and (4) two consecutive
mixed modes
 and 998
and 998  Hz in between the pure acoustic modes p12 and p14. Hz in between the pure acoustic modes p12 and p14. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{5251fig9.ps}\end{figure}](/articles/aa/full/2006/48/aa5251-06/Timg91.gif) |
Figure 9:
Large frequency spacing normalized to the observed
radius of Procyon A as a function of the mass. Its increase with respect to the mass
is larger for PoMS than for MS models.
Open (filled) symbols for MS (PoMS) models. |
| Open with DEXTER |
Figure 10 shows that the variations with the frequency
in the large frequency spacings
 have a different behavior for degree
have a different behavior for degree 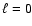 and 1 in the frequency range
below 800
and 1 in the frequency range
below 800  Hz. The few gravity
modes
Hz. The few gravity
modes 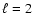 in the high-frequency range,
which do not obey the asymptotic properties
of p-modes, are not included in our computation of the
frequency spacings.
in the high-frequency range,
which do not obey the asymptotic properties
of p-modes, are not included in our computation of the
frequency spacings.
For all the models, the curves representing
 ,
for degree
,
for degree 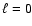 are close within 3
are close within 3  Hz
and compatible with the observations.
They have a different behavior for degree
Hz
and compatible with the observations.
They have a different behavior for degree 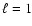 in the lower part of the
frequency domain.
Indeed contrary to the MS models, evolved models have many mixed
modes in the low-frequency range, as seen in Fig. 7.
This induces irregularities in the large frequency spacing for non radial modes.
Thus to measure the degree of evolution, we introduce the following quantity:
in the lower part of the
frequency domain.
Indeed contrary to the MS models, evolved models have many mixed
modes in the low-frequency range, as seen in Fig. 7.
This induces irregularities in the large frequency spacing for non radial modes.
Thus to measure the degree of evolution, we introduce the following quantity:
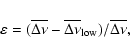 |
(4) |
where
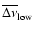 is the mean large frequency spacing at low frequency 500-800
is the mean large frequency spacing at low frequency 500-800  Hz for
Hz for  = 1.
It is expected from Fig. 10 that
= 1.
It is expected from Fig. 10 that
 will
be very low for MS models and significantly high for PoMS models.
Indeed this is seen clearly in Fig. 11, where
will
be very low for MS models and significantly high for PoMS models.
Indeed this is seen clearly in Fig. 11, where
 is plotted as a function of
is plotted as a function of
 .
This
shows that the determination of
.
This
shows that the determination of
 allows us to distinguish between MS and evolved
models. If an observational determination of the mean large spacings
can be obtained separately in the two frequency domains,
allows us to distinguish between MS and evolved
models. If an observational determination of the mean large spacings
can be obtained separately in the two frequency domains,
 and
and
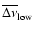 ,
a difference between the two values higher than 3
,
a difference between the two values higher than 3  Hz
(
Hz
(
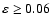 )
would imply that the star is in the PoMS2 evolutionary stage.
)
would imply that the star is in the PoMS2 evolutionary stage.
![\begin{figure}
\par\includegraphics[width=6.55cm,clip]{5251f10a.ps}\vspace*{-0.09cm}
\includegraphics[width=6.55cm,clip]{5251f10b.ps}\end{figure}](/articles/aa/full/2006/48/aa5251-06/Timg96.gif) |
Figure 10:
Large frequency spacings for  = 0 ( up) and 1 ( down) for MS/PoMS models
(full/dashed line)
compared to Martic (stars) and Eggenberger (square) observations. = 0 ( up) and 1 ( down) for MS/PoMS models
(full/dashed line)
compared to Martic (stars) and Eggenberger (square) observations. |
| Open with DEXTER |
The evolutionary stage of a star is strongly related to the structure
of the stellar core, where the nuclear reactions modify
the stellar stratification and density. The periods of the gravity
modes are very dependent on the properties of this inner region.
Figure 12 shows that there is a good correlation
between
 and the quantity P0.
and the quantity P0.
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{5251fi11.ps}\end{figure}](/articles/aa/full/2006/48/aa5251-06/Timg97.gif) |
Figure 11:
Seismic quantity
 characterizing the model
evolutionary stage versus the mean large frequency spacing
characterizing the model
evolutionary stage versus the mean large frequency spacing
 .
Grey open symbols indicate MS models, dark filled symbols PoMS models.
Diamond 1.36 .
Grey open symbols indicate MS models, dark filled symbols PoMS models.
Diamond 1.36  ,
circle 1.38 ,
circle 1.38  ,
triangle 1.42 ,
triangle 1.42  ,
stars 1.44 ,
stars 1.44  ,
square 1.45 ,
square 1.45  ,
diamond 1.46 ,
diamond 1.46  ,
cross 1.48 ,
cross 1.48  . .
|
| Open with DEXTER |
Let us now examine the two small frequency spacings
 and
and
 ,
which are combinations of acoustic modes penetrating differently
towards the center and thus very sensitive to the central part
of the stellar interior.
For MS models, the variation in
,
which are combinations of acoustic modes penetrating differently
towards the center and thus very sensitive to the central part
of the stellar interior.
For MS models, the variation in
 for radial order that is high enough can be roughly approximated as:
for radial order that is high enough can be roughly approximated as:
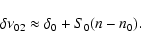 |
(5) |
The variation in
 is better approximated
by a quadratic expression:
is better approximated
by a quadratic expression:
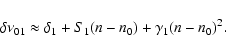 |
(6) |
Although the behavior of these small spacings is more complex for
evolved models,
we characterize the seismic properties of the models
using the above global quantities  ,
S0,
,
S0,  ,
S1,
and
,
S1,
and  .
The fit is made in the frequency range 800-1400
.
The fit is made in the frequency range 800-1400  Hz,
corresponding to a radial order from about 14 to 24 with n0 = 19.
Hz,
corresponding to a radial order from about 14 to 24 with n0 = 19.
Figure 13 shows the slope S0 and  that
characterize the variation with the frequency of the
small spacing
that
characterize the variation with the frequency of the
small spacing
 .
There,
.
There,  is roughly the mean of
is roughly the mean of
 in the considered frequency range.
For MS models,
in the considered frequency range.
For MS models,
 decreases with the frequency and
there is an almost linear relation between
decreases with the frequency and
there is an almost linear relation between  and the negative slope S0. The quantity
and the negative slope S0. The quantity  increases
from 3.5 to 4.3
increases
from 3.5 to 4.3  Hz for masses from 1.42 to 1.48
Hz for masses from 1.42 to 1.48  .
.
![\begin{figure}
\par\includegraphics[width=6.85cm,clip]{5251fi12.ps}\end{figure}](/articles/aa/full/2006/48/aa5251-06/Timg100.gif) |
Figure 12:
Characteristic period P0 of gravity modes as a function
of the seismic quantity
 characterizing the model
evolutionary stage.
characterizing the model
evolutionary stage. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=6.85cm,clip]{5251fi13.ps}\end{figure}](/articles/aa/full/2006/48/aa5251-06/Timg101.gif) |
Figure 13:
Characteristics  and S0of the small frequency spacings
and S0of the small frequency spacings
 .
The dashed box indicates the location of PoMS1 models.
Same models and symbols as in Fig. 11. .
The dashed box indicates the location of PoMS1 models.
Same models and symbols as in Fig. 11. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{5251fi14.ps}\end{figure}](/articles/aa/full/2006/48/aa5251-06/Timg104.gif) |
Figure 14:
Variation in the small frequency spacing
 with the frequency for the same MS/PoMS models
(full/dashed line) as in Fig. 10.
The dashed line with the highest peak in the high-frequency range
(
with the frequency for the same MS/PoMS models
(full/dashed line) as in Fig. 10.
The dashed line with the highest peak in the high-frequency range
(
 Hz) corresponds to the PoMS model
with the lower negative value of the slope S0 (model at the upper left corner
in Fig. 13). If we perform a least-square linear fit removing the point at the peak,
we obtain a slope Hz) corresponds to the PoMS model
with the lower negative value of the slope S0 (model at the upper left corner
in Fig. 13). If we perform a least-square linear fit removing the point at the peak,
we obtain a slope
 
 Hz, instead of -0.125 Hz, instead of -0.125  Hz.
This would move the corresponding point towards a region in continuity
with MS models in Fig. 13. Hz.
This would move the corresponding point towards a region in continuity
with MS models in Fig. 13. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.05cm,clip]{5251fi15.ps}\end{figure}](/articles/aa/full/2006/48/aa5251-06/Timg105.gif) |
Figure 15:
Behavior of the small frequency spacing
 .
Same symbols as in Fig. 13 (grey/dark for MS/PoMS models), but
with different sizes for the PoMS models (dark symbols), the largest
full symbols corresponding to the PoMS2 models (central hydrogen less than 0.001).
Upper panel: .
Same symbols as in Fig. 13 (grey/dark for MS/PoMS models), but
with different sizes for the PoMS models (dark symbols), the largest
full symbols corresponding to the PoMS2 models (central hydrogen less than 0.001).
Upper panel:  versus slope S1.
Lower panel: curvature versus slope S1.
Lower panel: curvature  versus slope S1.
The three groups of points with versus slope S1.
The three groups of points with  correspond to models
with different overshoot parameters,
correspond to models
with different overshoot parameters,
 and 0. from
the left to the right.
and 0. from
the left to the right. |
| Open with DEXTER |
For PoMS models the small spacing
 has higher values,
has higher values,
 higher than 4
higher than 4  Hz. The values of the slope S0 are very dispersed, due to the fact that the quasi-linear variation of
Hz. The values of the slope S0 are very dispersed, due to the fact that the quasi-linear variation of
 with the radial order is perturbed around the frequencies of the mixed modes for
with the radial order is perturbed around the frequencies of the mixed modes for 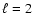 .
An example of this variation is given in Fig. 14,
where a peak due to the presence of two consecutive mixed modes in
.
An example of this variation is given in Fig. 14,
where a peak due to the presence of two consecutive mixed modes in
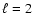 spectrum is clearly visible. Such peaks mainly influence the determination of the slope S0 and explain the dispersion of the points corresponding to PoMS models
in Fig. 13.
However, the value of
spectrum is clearly visible. Such peaks mainly influence the determination of the slope S0 and explain the dispersion of the points corresponding to PoMS models
in Fig. 13.
However, the value of  can be used to distinguish between
MS and PoMS models, except for the MS models of highest masses.
This criteria is less selective in our case than in Straka et al. (2005).
can be used to distinguish between
MS and PoMS models, except for the MS models of highest masses.
This criteria is less selective in our case than in Straka et al. (2005).
Figure 15 shows the quantities  ,
S1, and
,
S1, and  that characterize the variation with the frequency of the
small spacing
that characterize the variation with the frequency of the
small spacing
 (cf. Eq. (6)).
For MS models, the small spacing
(cf. Eq. (6)).
For MS models, the small spacing
 decreases with
the frequency (
decreases with
the frequency ( ).
The three groups of points with
).
The three groups of points with  correspond to models
with different overshoot parameters,
correspond to models
with different overshoot parameters,
 and 0.0 from
the left to the right. The smallest values of
and 0.0 from
the left to the right. The smallest values of  and S1 correspond
to the larger
and S1 correspond
to the larger 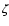 value
(
value
(
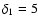
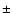
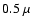 Hz for
Hz for 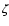 = 0.2,
= 0.2,
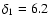
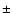
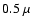 Hz for
Hz for 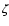 = 0.1,
= 0.1,
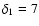
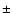
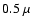 Hz for
Hz for 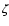 = 0).
= 0).
In contrast, the small spacing
 increases with the frequency (
increases with the frequency (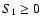 )
for PoMS models. The values of
)
for PoMS models. The values of  range from 6 to 8
range from 6 to 8  Hz.
Figure 15 shows that the highest values of
Hz.
Figure 15 shows that the highest values of
 or
or  occur for the PoMS1 models. They have also the lowest positive
values of S1. The lower panel exhibits a negative
"curvature''
occur for the PoMS1 models. They have also the lowest positive
values of S1. The lower panel exhibits a negative
"curvature''  for all the models of
Fig. 15.
for all the models of
Fig. 15.
In conclusion, determining the sign of S1 is a very good way
to distinguish between MS and PoMS models.
For MS models, its value indicates the amount of
convective core overshoot in the core. In contrast, the quantity  ,
which is close to a mean value of
,
which is close to a mean value of
 ,
cannot be used
to characterize the evolutionary stage of a star such as Procyon A.
,
cannot be used
to characterize the evolutionary stage of a star such as Procyon A.
In this section we present our results on Procyon A
and compare them to previous works. We first consider the
effects of the uncertainties on the global constraints
in the modeling and evolution of Procyon A, and we discuss the
sensitivity of our results upon the various assumptions about the physics
used in this modeling (Sect. 6.1). Second, we try to derive
information on the evolutionary status of Procyon A
from the available seismic observations (Sect. 6.2).
The observations of Procyon A give constraints on the mass,
the effective temperature, the stellar radius and the surface
chemical composition. Our results have shown that they are
compatible with both MS and PoMS models.
The MS models of Procyon A have high initial
helium and heavy element contents.
Their ages range from about 1400 to 2000 Myr.
Their masses range from 1.42  to 1.48
to 1.48  .
For the lowest masses, some core overshoot is needed
to satisfy the observational constraints.
The PoMS models have lower masses, initial
.
For the lowest masses, some core overshoot is needed
to satisfy the observational constraints.
The PoMS models have lower masses, initial  and
and
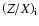 and larger ages. Note that due to the properties of its white dwarf companion,
it is expected that Procyon A has an age of at least
2000 Myr (Kervella et al. 2004; Provost et al. 2004).
and larger ages. Note that due to the properties of its white dwarf companion,
it is expected that Procyon A has an age of at least
2000 Myr (Kervella et al. 2004; Provost et al. 2004).
We used a high limit for the constraint linked to the chemical
evolution of the galaxies
 ,
as in Chaboyer et al. (1999). If we take a lower maximum value of this constraint,
i.e. 3 instead of 4., most of the MS models would be ruled out, unless we accept higher mass
and final surface metallicity.
We have shown (Provost et al. 2005) that if microscopic diffusion
of chemical species is not taken
into account, the models satisfying the same constraints have lower
initial helium content, thus lower
,
as in Chaboyer et al. (1999). If we take a lower maximum value of this constraint,
i.e. 3 instead of 4., most of the MS models would be ruled out, unless we accept higher mass
and final surface metallicity.
We have shown (Provost et al. 2005) that if microscopic diffusion
of chemical species is not taken
into account, the models satisfying the same constraints have lower
initial helium content, thus lower
 .
This may explain why the models of Straka et al. (2005), which have
higher surface metallicity and no envelope element diffusion, are
mostly MS models.
.
This may explain why the models of Straka et al. (2005), which have
higher surface metallicity and no envelope element diffusion, are
mostly MS models.
We looked at the influence of the additional mixing parameter Re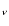 related to radiative viscosity and of the descriptions of the convection on both the global
and asteroseismic properties of the models.
related to radiative viscosity and of the descriptions of the convection on both the global
and asteroseismic properties of the models.
Both MS and PoMS models satisfying the observational constraints for Procyon A and with given mass,
age, and initial chemical composition
have been computed for different values of the additional mixing
parameter Re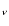 from 0.5 to 1.5.
Their properties are given in Table 2,
and their evolutionary tracks and surface metallicity as a function of
the age are given in Fig. 16.
These different treatments of mixing do not
modify the structure of the models much, which have same limit for the
convection zone and convective core (for MS models),
and thus their seismic properties.
The surface metallicity is strongly modified relative to the uncertainty on the observed metallicity
for MS models, which means that it depends strongly on the way diffusion
is treated in the modeling. As seen in Fig. 16, the situation
is very different for PoMS models, which are older at the end of hydrogen burning.
Their surface chemical composition is almost insensitive to the value of Re
from 0.5 to 1.5.
Their properties are given in Table 2,
and their evolutionary tracks and surface metallicity as a function of
the age are given in Fig. 16.
These different treatments of mixing do not
modify the structure of the models much, which have same limit for the
convection zone and convective core (for MS models),
and thus their seismic properties.
The surface metallicity is strongly modified relative to the uncertainty on the observed metallicity
for MS models, which means that it depends strongly on the way diffusion
is treated in the modeling. As seen in Fig. 16, the situation
is very different for PoMS models, which are older at the end of hydrogen burning.
Their surface chemical composition is almost insensitive to the value of Re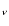 .
These results agree with the discussion by
Provost et al. (2005), who studied the effect of varying the parameter Re
.
These results agree with the discussion by
Provost et al. (2005), who studied the effect of varying the parameter Re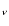 on the stellar modeling and frequencies.
on the stellar modeling and frequencies.
Table 2:
Global parameters of models differing by the way diffusion is treated varying the additional mixing parameter: (a) MS model of mass M = 1.46  ,
(b) PoMS model of mass M = 1.38
,
(b) PoMS model of mass M = 1.38  .
.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{5251f16a.ps}\par\includegraphics[angle=-90,width=7.5cm,clip]{5251f16b.ps}\end{figure}](/articles/aa/full/2006/48/aa5251-06/Timg115.gif) |
Figure 16:
MS and PoMS models computed with different values of the additional mixing parameter (cf. Table 2):
 = 0.5 (dotted line), 1. (dashed line), 1.5 (full line). The evolutionary tracks and final position in the HR diagram are
very close ( higher panel). The variation in surface metallicity
as a function of the age and its final value are very different for MS models
( lower panel). = 0.5 (dotted line), 1. (dashed line), 1.5 (full line). The evolutionary tracks and final position in the HR diagram are
very close ( higher panel). The variation in surface metallicity
as a function of the age and its final value are very different for MS models
( lower panel). |
| Open with DEXTER |
We also considered models with different
treatments of the convection and with different values of the mixing
length parameter 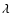 .
Their properties are given in Table 3.
Models with CM with
.
Their properties are given in Table 3.
Models with CM with
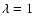 and MLT with
and MLT with
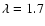 are very close.
One important effect of varying
are very close.
One important effect of varying 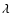 concerns the surface metallicity
of the model. For both MS and PoMS models with MLT,
concerns the surface metallicity
of the model. For both MS and PoMS models with MLT,
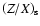 increases when the value of
increases when the value of 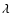 increases. As expected, when
increases. As expected, when 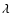 increases by 10%, the depth of the convection
zone decreases by 4%.
increases by 10%, the depth of the convection
zone decreases by 4%.
Table 3:
Global parameters of models differing by the way convection is treated: the Canuto & Mazitelli theory and
 ,
and the classical mixing length theory with
,
and the classical mixing length theory with
 .
(a) MS models
.
(a) MS models
 ,
(b) PoMS models
,
(b) PoMS models
 ).
).
Finally we note that the masses we are looking for are lower than
the mass 1.497  obtained by Eggenberger et al. (2005) in their work.
However, we computed a model with the same stellar parameters
as these authors and obtained too high a luminosity, well beyond
the observational constraints. This result may come from the difference
between the stellar evolutionary codes that are used.
The model comparison, carried on in the COROT context
(Monteiro et al. 2005), shows that the luminosity of models computed
with the evolutionary code GENEC is systematically smaller
than the luminosity obtained with our code.
obtained by Eggenberger et al. (2005) in their work.
However, we computed a model with the same stellar parameters
as these authors and obtained too high a luminosity, well beyond
the observational constraints. This result may come from the difference
between the stellar evolutionary codes that are used.
The model comparison, carried on in the COROT context
(Monteiro et al. 2005), shows that the luminosity of models computed
with the evolutionary code GENEC is systematically smaller
than the luminosity obtained with our code.
All the models of Procyon A that we computed satisfying the
observational constraints of Table 1 have mean large frequency spacing from 53
to 56.5  Hz, compatible
with the range of values given by different observers.
Our results show that a low value of the mean large frequency spacing
Hz, compatible
with the range of values given by different observers.
Our results show that a low value of the mean large frequency spacing
 would favor PoMS and MS models of low mass.
However, we must keep in mind that low-mass MS models
need to be initialized with a large
would favor PoMS and MS models of low mass.
However, we must keep in mind that low-mass MS models
need to be initialized with a large
 close to
the upper limit (close to 4) given by the galactic chemical evolution.
close to
the upper limit (close to 4) given by the galactic chemical evolution.
We have derived several criteria to establish the evolutionary
stage of Procyon A.
First, looking in the low frequency range where mixed modes appear
when the star is evolved, we introduced a parameter
 that characterizes the behavior of the
that characterizes the behavior of the  = 1 large frequency spacing.
It allows us to distinguish between the models, as it
is very small for MS models and increases up to 0.25 for PoMS models.
If we compute
= 1 large frequency spacing.
It allows us to distinguish between the models, as it
is very small for MS models and increases up to 0.25 for PoMS models.
If we compute
 for the available observations
(Martic et al. 2004), we obtain a low value
for the available observations
(Martic et al. 2004), we obtain a low value
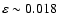 .
If we assume that mixed modes have enough energy to be observed, such a low value of
.
If we assume that mixed modes have enough energy to be observed, such a low value of
 would
indicate that Procyon A is in MS phase.
would
indicate that Procyon A is in MS phase.
In the high-frequency range,
the mean small spacing
 gives a way to establish
the stellar evolutionary stage as in Straka et al. (2005),
but in our case the separation of the two groups of models is not as sharp.
This may be due to the choice of the frequency domain on which the
mean
gives a way to establish
the stellar evolutionary stage as in Straka et al. (2005),
but in our case the separation of the two groups of models is not as sharp.
This may be due to the choice of the frequency domain on which the
mean  is estimated. Straka et al. (2005) consider larger radial orders corresponding to higher frequencies.
For PoMS models, the slope of
is estimated. Straka et al. (2005) consider larger radial orders corresponding to higher frequencies.
For PoMS models, the slope of
 as a function
of the frequency is small, and the mean of
as a function
of the frequency is small, and the mean of
 is not
sensitive to the frequency domain. In contrast, for MS models the
decrease in
is not
sensitive to the frequency domain. In contrast, for MS models the
decrease in
 with the frequency is noticeable
(Fig. 13), and its mean value decreases if we take
a higher-frequency range, leading to a better separation between PoMS and MS models.
If we consider the observations of Eggenberger et al. (2004),
we obtain a value of
with the frequency is noticeable
(Fig. 13), and its mean value decreases if we take
a higher-frequency range, leading to a better separation between PoMS and MS models.
If we consider the observations of Eggenberger et al. (2004),
we obtain a value of  about 5
about 5  Hz or higher, thereby favoring PoMS models.
The slope S0 is positive, but its value is not reliable
because it crucially depends on the choice of the mode
Hz or higher, thereby favoring PoMS models.
The slope S0 is positive, but its value is not reliable
because it crucially depends on the choice of the mode 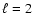 around 800
around 800  Hz and around 1142
Hz and around 1142  Hz.
With Martic et al. (2004) measurements, we obtain
a value
Hz.
With Martic et al. (2004) measurements, we obtain
a value  around 4
around 4  Hz and a negative slope S0 compatible with MS models.
Hz and a negative slope S0 compatible with MS models.
We have shown that the small spacing
 leads
to a better criterion for distinguishing MS and PoMS models,
since
leads
to a better criterion for distinguishing MS and PoMS models,
since
 varies with frequency in opposite way
for these two types of models.
Moreover, it allows us to estimate the amount of convective-core overshoot
for MS models,
within the physical assumptions made to compute the models.
The observational errors in the quantity
varies with frequency in opposite way
for these two types of models.
Moreover, it allows us to estimate the amount of convective-core overshoot
for MS models,
within the physical assumptions made to compute the models.
The observational errors in the quantity
 are larger because
they are combinations of three frequencies. Indeed,
according to the observations of Martic et al. (2004), the estimations of
are larger because
they are combinations of three frequencies. Indeed,
according to the observations of Martic et al. (2004), the estimations of  and S1 crucially depend on the point with the highest frequency.
The results of the quadratic fit are not reliable.
As an example, we obtain a positive slope S1 and positive
curvature
and S1 crucially depend on the point with the highest frequency.
The results of the quadratic fit are not reliable.
As an example, we obtain a positive slope S1 and positive
curvature  ,
and these results do not correspond to any model (cf. Fig. 15).
,
and these results do not correspond to any model (cf. Fig. 15).
Our results show that neither the spectroscopic and interferometric
nor the asteroseismic observational constraints are accurate enough
to distinguish between main sequence and post-main sequence models of
Procyon A.
Particularly the dispersion of 2  Hz given for the mean large frequency spacing is
too high to constrain the models.
Moreover, the small frequency spacings
Hz given for the mean large frequency spacing is
too high to constrain the models.
Moreover, the small frequency spacings
 and
and
 give contradictory indications of the age of Procyon A. They are inconsistent with theoretical properties.
We have also shown that the detection of frequencies of degrees
give contradictory indications of the age of Procyon A. They are inconsistent with theoretical properties.
We have also shown that the detection of frequencies of degrees
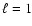 in the low-frequency range (500 to 800
in the low-frequency range (500 to 800  Hz), where mixed
modes may appear, are required
for determining the evolutionary stage of Procyon.
Hz), where mixed
modes may appear, are required
for determining the evolutionary stage of Procyon.
Acknowledgements
We are grateful to F. Thévenin for many valuable discussions
and to P. Eggenberger for his constructive remarks.
This work was done using the computing facilities provided by
the OCA program "Simulations interactives et Visualisation en Astronomie
et Mécanique'' (SIVAM).
- Alecian, G., &
Michaud, G. 2005, A&A, 431, 1 [EDP Sciences] [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Allende Prieto, C.,
Asplund, M., Garcia Lopez, R. J., & Lambert, D. L. 2002, ApJ,
567, 544 [NASA ADS] [CrossRef] (In the text)
- Angulo, C., Arnould,
M., Rayet, M., & the NACRE collaboration 1999, Nucl. Phys. A,
656, and WEB site https://pntpm.ulb.ac.be/Nacre/nacre.html
(In the text)
- Bressan, A., Fagotto,
F., Bertelli, G., & Chiosi, C. 1993, A&AS, 100, 647 [NASA ADS] (In the text)
- Burgers, J. M. 1969,
Flow Equations for Composite Gases (New York Academic Press)
(In the text)
- Canuto, V. M., &
Mazitelli, I. 1991, ApJ, 370, 295 [NASA ADS] [CrossRef] (In the text)
- Chaboyer, B., Demarque,
P., & Guenther, D. B. 1999, ApJ, 525, L41 [NASA ADS] [CrossRef] (In the text)
- Di Mauro, M. P. 2004,
in Helio- and Asteroseismology, Towards a Golden Future SOHO 14 -
GONG 2004 Meeting 12-16 Juillet 2004, New Haven USA, ed. D. Danesy,
ESA SP-559, 186
(In the text)
- Eggenberger, P.,
Carrier, F., Bouchy, F., & Blecha, A. 2004, A&A, 422,
247 [EDP Sciences] [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Eggenberger, P.,
Carrier, F., & Bouchy, F. 2005, New Astron., 10, 195 [NASA ADS] (In the text)
- Garcia, R. A., Lambert,
P., Ballot, J., et al. 2006, A&A, sumitted
(In the text)
- Gatewood, G., &
Han, I. 2006, ApJ, 131, 1015 [NASA ADS] (In the text)
- Girard, T. M., Wu, H.,
Lee, J. T., et al. 2000, AJ, 119, 2428 [NASA ADS] [CrossRef] (In the text)
- Gough, D. O. 1991,
Comments on Helioseismic Inference, in Progress of Seismology of
the Sun and Stars, ed. Y. Osaki, & H. Shibahashi (Springer
Verlag), 283
(In the text)
- Guenther, D. B., &
Demarque, P. 1993, ApJ, 405, 298 [NASA ADS] [CrossRef] (In the text)
- Kervella, P.,
Thévenin, F., Morel, P., et al. 2004, A&A, 413, 251 [EDP Sciences] [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Martic, M., &
Lebrun, J. C. 2006, A&A, in preparation
- Martic, M., Lebrun,
J. C., Appourchaux, T., & Korzennik, S. 2004, A&A, 418,
295 [EDP Sciences] [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Matthews, J., Kushnig,
R., Guenther, D. B., et al. 2004, Nature, 430, 51 [NASA ADS] [CrossRef]
- Mihalas, D., &
Weibel-Mihalas, B. 1984, Foundations of Radiation Hydrodynamics
(Oxford University Press), 461
(In the text)
- Monteiro, M. J. P. F.
G., Castro, M., Christensen-Dalsgaard, J., et al. 2005, COROT Week
9, ESTEC, 5-9 December 2005
http://www.astro.up.pt/corot/welcome/meetings/m5/ESTA_CW9_Monteiro_3.pdf
(In the text)
- Moreira, O.,
Appourchaux, T., Berthomieu, G., & Toutain, T. 2005, MNRAS,
357, 191 [NASA ADS] (In the text)
- Morel, P. 1997,
A&AS, 124, 597 [EDP Sciences] [NASA ADS] (In the text)
- Morel, P., van't Veer,
C., Provost, J., et al. 1994, A&A, 286, 91 [NASA ADS] (In the text)
- Morel, P., Provost, J.,
Lebreton, Y., Thévenin, F., & Berthomieu, G. 2000,
A&A, 363, 675 [NASA ADS] (In the text)
- Morel, P., &
Thévenin, F. 2002, A&A, 390, 611 [EDP Sciences] [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Paquette, C.,
Pelletier, C., Fontaine, G., & Michaud, G. 1986, ApJS, 61,
177 [NASA ADS] [CrossRef] (In the text)
- Perryman, M. A. C.,
Brown, A. G. A., Lebreton, Y., et al. 1998, A&A, 331, 81 [NASA ADS] (In the text)
- Provencal, J. L.,
Shipman, H. L., Koester, D., et al. 2002, ApJ, 568, 324 [NASA ADS] [CrossRef] (In the text)
- Provost, J., Martic,
M., & Berthomieu, G. 2004, in Helio- and Asteroseismology:
Towards a Golden Future SOHO 14 - GONG 2004 Meeting 12-16 July
2004, New Haven USA, ed. D. Danesy, ESA SP-559, 594
(In the text)
- Provost, J.,
Berthomieu, G., Bigot, L., & Morel, P. 2005, A&A, 432,
225 [EDP Sciences] [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Regulo, C., & Roca
Cortés, T. 2005, A&A, 444, L5 [EDP Sciences] [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Schaller, D., Schaerer,
D., Meynet, G., & Maeder, A. 1992, A&AS, 96, 269 [NASA ADS] (In the text)
- Steffen, M. 1985,
A&AS, 59, 403 [NASA ADS] (In the text)
- Straka, C., Demarque,
P., & Guenther, D. B. 2005, ApJ, 629, 1075 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2006
![\begin{figure}
\par\includegraphics[angle=-90,width=6.7cm,clip]{5251fig1.ps}\end{figure}](/articles/aa/full/2006/48/aa5251-06/Timg48.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=6.1cm,clip]{5251fi3a.ps}\par\includegraphics[angle=-90,width=6.1cm,clip]{5251fi3b.ps}\end{figure}](/articles/aa/full/2006/48/aa5251-06/Timg55.gif)
![\begin{figure}
\par\includegraphics[width=6.85cm,clip]{5251fig4.ps}\end{figure}](/articles/aa/full/2006/48/aa5251-06/Timg63.gif)
![\begin{figure}
\par\includegraphics[width=6.85cm,clip]{5251fig5.ps}\end{figure}](/articles/aa/full/2006/48/aa5251-06/Timg69.gif)
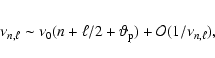
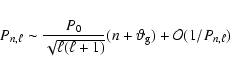
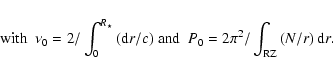
![\begin{figure}
\par\includegraphics[width=6.85cm,clip]{5251fig6.ps}\end{figure}](/articles/aa/full/2006/48/aa5251-06/Timg86.gif)
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{5251fi7a.ps}\includegraphics[width=7.4cm,clip]{5251fi7b.ps}\end{figure}](/articles/aa/full/2006/48/aa5251-06/Timg87.gif)
![\begin{figure}
\par\includegraphics[width=7.65cm,clip]{5251fig8.ps}\end{figure}](/articles/aa/full/2006/48/aa5251-06/Timg90.gif)
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{5251fig9.ps}\end{figure}](/articles/aa/full/2006/48/aa5251-06/Timg91.gif)
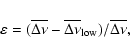
![\begin{figure}
\par\includegraphics[width=6.55cm,clip]{5251f10a.ps}\vspace*{-0.09cm}
\includegraphics[width=6.55cm,clip]{5251f10b.ps}\end{figure}](/articles/aa/full/2006/48/aa5251-06/Timg96.gif)
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{5251fi11.ps}\end{figure}](/articles/aa/full/2006/48/aa5251-06/Timg97.gif)
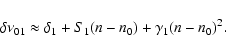
![\begin{figure}
\par\includegraphics[width=6.85cm,clip]{5251fi12.ps}\end{figure}](/articles/aa/full/2006/48/aa5251-06/Timg100.gif)
![\begin{figure}
\par\includegraphics[width=6.85cm,clip]{5251fi13.ps}\end{figure}](/articles/aa/full/2006/48/aa5251-06/Timg101.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{5251fi14.ps}\end{figure}](/articles/aa/full/2006/48/aa5251-06/Timg104.gif)
![\begin{figure}
\par\includegraphics[width=7.05cm,clip]{5251fi15.ps}\end{figure}](/articles/aa/full/2006/48/aa5251-06/Timg105.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{5251f16a.ps}\par\includegraphics[angle=-90,width=7.5cm,clip]{5251f16b.ps}\end{figure}](/articles/aa/full/2006/48/aa5251-06/Timg115.gif)