A&A 460, 653-664 (2006)
DOI: 10.1051/0004-6361:20054501

Properties of X-ray rich gamma ray bursts and X-ray flashes detected with BeppoSAX and Hete-2[*]

V. D'Alessio1 - L. Piro1 - E. M. Rossi2,3,[*]


1 - INAF - Sezione di Roma, via del Fosso del Cavaliere, 100, 00113 Roma, Italy
2 - Max Planck Institute for Astrophysics, Garching Karl-Schwarzschild-Str. 1, Postfach 1317, 85741 Garching, Germany
3 - JILA, University of Colorado, 440 UCB Boulder, CO 80309-0440, USA

Received 9 November 2005 / Accepted 16 June 2006

Abstract
We study the spectrum of the prompt emission and the X-ray and optical afterglow fluxes of 54 X-Ray Rich Gamma Ray Burst (XRRs) and X-Ray Flashes (XRFs), observed by BeppoSAX and HETE-2. A comparison is then performed with classical Gamma Ray Bursts (GRBs). The goal of this paper is to investigate the nature of XRRs/XRFs, as high redshift GRBs or off-axis GRBs, analyzing both their prompt and afterglow properties. We find that the XRR/XRF spectral indexes of the Band function are similar to those of classical GRBs, whereas the peak energy is lower by a factor of 4. We study the optical and X-Ray afterglow properties of the XRRs/XRFs; in particular we analyze the XRR 011030 afterglow. We find that the X-ray and optical flux distributions and the lightcurves of the XRRs/XRFs sample are consistent with those of classical GRBs; in particular, they show evidence of a break and no rising temporal slope. We compare these results with the afterglow predictions of the high redshift scenario, where XRFs are GRBs at higher redshift and of the off-axis scenario, where the observed differences are due to viewing angle effects. In this last framework, we consider jets with a homogeneous, a -2 power-law shaped and a Gaussian luminosity angular distribution. We find that the high redshift scenario can explain some events but not the total sample of XRRs/XRFs. The off-axis model may be consistent with our findings when a homogeneous jet is considered. However, given the uncertainties on the selection effects in our sample, a Gaussian jet viewed at small angles from the Gaussian core and a power-law shaped cannot be ruled out.

Key words: X-rays: general - gamma rays: bursts

1 Introduction

Several satellites have observed Fast X-Ray Transients (Arefiev et al. 2003); the origin of these events was attributed to a mixed contributions from different sources, such as flare stars and RS CVn systems. Gotthelf et al. (1996) first used the alternative term X-Ray Flashes for this phenomenon. The discovery that a large fraction of these events (in particular those with a duration of less than 1000 s) are a class of GRBs was made with the Wide Field Cameras (WFC) on BeppoSAX (Heise et al. 2001).

XRFs are Gamma-Ray Bursts (GRBs) characterized by no or faint signal in the gamma ray energy range. They show an isotropic distribution on the sky and a duration between a few tens and $\sim$103 s, like long GRBs (Heise et al. 2001). An intermediate class of bursts has been observed between the XRF and the GRB classes, the X-Ray Rich Gamma Ray Bursts (XRRs), with an X-Ray emission stronger than gamma-ray one (Barraud et al. 2003; Atteia et al. 2004). We classify bursts according the definition proposed by Lamb & Graziani (2003).

Table 3: Hardness Ratio $H_{\rm h}=S[2,30]/S[30,400]$ and $H_{\rm s}=S[2,10]/S[40,700]$ for 54 XRRs/XRFs.

There are several studies of the spectral properties of the XRRs/XRFs; Kippen et al. (2003) analyzed a sample of 9 XRFs observed by BeppoSAX using untriggered BATSE data and found that the photon indices $\beta _1$ and $\beta _2$ of the Band function of the XRFs are similar to those of the GRBs, instead of  $E_{\rm peak}$, whose value is less than 10 keV for most XRFs. This result has been confirmed by Sakamoto et al. (2005) with the analysis of 42 XRRs/XRFs observed by HETE-2.

Several theories have been proposed to explain the origin of XRFs: high redshift GRBs (Heise et al. 2001), GRBs with a uniform jet viewed off-axis (Yamazaki et al. 2004,2002,2003), GRBs with the Universal Power-law-shaped jet (Lamb et al. 2005), a Gaussian jet (Zhang et al. 2004), a ring shaped jet (Eichler & Levinson 2004) and multi sub-jets (Toma et al. 2005), a variable jet opening-angle (Lamb et al. 2005), dirty fireballs (Dermer 1999), clean fireballs (Barraud et al. 2005), a photosphere dominated emission (Ramirez Ruitz & Lloyd-Ronning 2002) and off-axis cannonballs (Dar & De Rujula 2004).

We focus here on two models: the high redshift and the off-axis scenario. In the former case, XRFs are high-redshift GRBs while in the latter, they are GRBs viewed at a large angle from the jet axis. The main goal of this paper is to investigate the properties of XRRs/XRFs constrain these theories.

The paper is organized as follows. In Sect. 2, we compile a sample of 54 BeppoSAX and HETE-2 events, catalogued as XRRs/XRFs in the literature, and we classify them with the same hardness spectral ratio. This allows us to build a homogeneous sample. In Sect. 3, we study and compare the distributions of the spectral parameters $\beta _1$, $\beta _2$ and  $E_{\rm peak}$ of the prompt emission of XRRs/XRFs and GRBs. In Sect. 4, we describe the observations and the data analysis of the optical and X-ray afterglow flux; in particular we study two Chandra observations of the afterglow of the burst XRR 011030. We present our afterglow results in Sects. 4.3 and 5, we discuss them in the framework of the high redshift and off-axis scenario; in Sect. 6 we present our conclusions.

   
2 Definition of the catalog

We considered all the events observed until 31 December 2003 and classified as XRRs/XRFs, available in the literature and from the web. We compiled a sample of 54 events, 17 observed by BeppoSAX and 37 by HETE-2. We have not considered the BeppoSAX bursts XRF 991217 (Muller et al. 1999) and XRF 000608 (Gandolfi 2000), detected only by the WFCs, due to the lack of spectral information in the literature. Lamb & Graziani (2003) proposed to classify bursts according to their spectral hardness ratio  $(H_{\rm h})$: GRBs have $H_{\rm h}=S(2,30)/S(30,400) \le 0.32$, XRRs have $ 0.32 \le H_{\rm h} \le 1$ and XRFs have $H_{\rm h} \ge 1$ where  S(E1,E2) is the fluence in the energy range E1-E2. We adopted their definition in order to build a homogeneous sample out of a collection of events observed by different satellites. The BeppoSAX instruments have energy ranges compatible with the HETE-2 ones; moreover, the sensitivity of WFC, $\sim$4 $\times $ 10-9 erg cm-2 s-1 (De Pasquale et al. 2006), is comparable to that of WXM, equal to $\sim$9 $\times $ 10-9 erg cm-2 s-1 (Ricker et al. 2002). Thus the combined sample derived from these two satellites is homogeneous. We calculated the hardness ratio ($H_{\rm h}$) for those bursts that do not have this parameter available, using the spectral parameters of the prompt emission. The data are reported in Tables 1-3. For completeness we also report the hardness ratio calculated in the BeppoSAX ranges ( $H_{\rm s}=S(2,10)/S(40,700)$) in Table 3.

All the BeppoSAX bursts include data of the WFCs (2-28 keV). At higher energies they present data or upper limits from BeppoSAX GRBM, BATSE and WIND, except for XRR 011030 and XRF 020427. The HETE-2 bursts include data of WXM (2-25 keV) and FREGATE (8-400 keV); in the cases of XRF 031109 and XRR 031220 only the FREGATE spectral data are available.

Three bursts (XRF 981226, XRF 990704 and XRF 020427) have time resolved spectra: $H_{\rm h}$ and $H_{\rm s}$ have been obtained as the mean weighted by the different integration times. For XRR 991106 we only have a lower limit to the X- to $\gamma$-ray peak flux ratio $\sim$0.75 (Gandolfi et al. 1999) and we classify it as an XRR. The results are reported in Table 3. We estimated typical uncertainties of 50% on the ratio, due to large errors on the spectral parameters.

We find that all the events, including the BeppoSAX ones, are consistent with the XRR/XRF definition ( $H_{\rm h}\ge0.32$) given by Lamb & Graziani (2003).

The resulting total sample is of 54 bursts, 26 XRFs and 28 XRRs. We analyzed XRRs and XRFs as a unique class due to the small number of events with X-ray and optical afterglow detections.

   
3 Prompt emission: spectral parameter distributions

We studied and compared the prompt emission spectral parameters of XRRs/XRFs and GRBs. We considered the events fitted by the Band law: $\beta _1$ ($\beta_2)$ is the low (high) spectral index, $E_{\rm peak}$is the peak energy ( $E_{\rm peak}=(2+\beta _1)\times E_{\rm o}$) and $E_{\rm o}$ is the break energy. In addition, we took into account bursts described by a power law exponential model, following the relation N(E) = $KE^{\beta_1}\times \exp~(-E/E_{\rm o})$. We built up the distributions of $\beta _1$, $\beta _2$ and $E_{\rm peak}$ for XRRs/XRFs (excluding parameters with no errors and upper limits) and for 31 GRBs, 21 reported in Kippen et al. (2003) and 10 in Sakamoto et al. (2005). These distributions are shown in Figs. 1-3.


  \begin{figure} \par\includegraphics[angle=90,width=7cm,clip]{4501fig1.ps} \end{figure} Figure 1: Distribution of spectral slope $\beta _1$ for 38 XRRs/XRFs (red dotted line) and 31 GRBs (black dashed line). (This figure is available in color in electronic form.)
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=90,width=7cm,clip]{4501fig2.ps} \end{figure} Figure 2: Distribution of spectral slope $\beta _2$ for 19 XRRs/XRFs (red dotted line) and 25 GRBs (black dashed line). (This figure is available in color in electronic form.)
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=90,width=7.1cm,clip]{4501fig3.ps}\end{figure} Figure 3: Distribution of the logarithm of $E_{\rm peak}$ for 42 XRRs/XRFs (red dotted line) and 30 GRBs (black dashed line). (This figure is available in color in electronic form.)
Open with DEXTER

The reported values for $\beta _1$, $\beta _2$ and $E_{\rm peak}$ are the result of the convolution of the intrinsic distribution with the measurement error distributions. Assuming that both are Gaussian, it is possible to deconvolve the two distributions: we obtained the best estimate mean value and standard deviation of the parent distribution (see Table 4), following the maximum likelihood method (Maccacaro et al. 1988). We find that the mean XRR/XRF value of $\langle \beta_1 \rangle_i \simeq -1.2$ and of $\langle \beta_2 \rangle_i \simeq -1.7$ are consistent with those of GRBs ( $\langle \beta_1 \rangle_i \simeq -1$ and $\langle \beta_2 \rangle_i \simeq -2.3)$ within two $\sigma$. Instead, the peak energy $\langle E_{{\rm p,xr}} \rangle_i \simeq 36$ keV is significantly smaller by a factor of $\sim$4.5 with respect to that of GRBs ( $\langle E_{{\rm p,grb}} \rangle_i \simeq 162$ keV).

Table 4: Mean values and standard deviation of spectral parameters $\beta _1$, $\beta _2$ and $\log E_{\rm peak}$ for the parent distribution of XRRs/XRFs and GRBs classes, according to the likelihood method. In the last row is the $\log E_{\rm peak}$ instrinsic mean value for the subsample of events used for the X-ray afterglow flux analysis in Sect. 4.3.

We note that 12 XRRs/XRFs have known redshift (see Table 5): the mean value is $\langle z_{{\rm xr}} \rangle=1.7$ $\pm$ 0.3, with a minimum and maximum measured redshift of z=0.17 and of z=3.4, respectively. In order to analyse the intrinsic properties of the prompt emission we compared the rest frame peak energy, $\langle \tilde{E}_{\rm p} \rangle$, of 10 XRRs/XRFs (excluding XRF 020903, having an upper limit on the peak energy and XRR 030323) and 12 GRBs. We find that $\langle \tilde{E}_{\rm p} \rangle_i$ of XRRs/XRFs is smaller by a factor$\sim$ of 4 compared to the GRB one. In both cases, data confirm the soft nature of these events.

Table 5: Intrinsic Peak Energy, Isotropic Energy [1, 1000 keV] and redshift values or constraints for 14 XRRs/XRFs: the Type column indicates if the measure of the redshift is obtained from Host Galaxy spectroscopy (HG), or from Optical afterglow spectroscopy (OT). We report also the pseudo-redshift for 6 possibly high redshift GRBs(16).

   
4 The afterglow properties

We studied the afterglow properties of XRRs/XRFs, analyzing the temporal profile and the distribution of the afterglow flux. We use the X-ray and the optical detections reported in the GRB Coordinates Network (GCN)[*] and in published papers (see Table 6 for references). In the case of XRR 011030 we carried out the analysis of Chandra follow-up observations. In Table 6, we list the general information for the XRR/XRF sample, with possible detections in the X-ray, optical and radio bands and of the host galaxy. In Table 5, we report the redshift for 16 XRRs/XRFs.

Table 6: Afterglow properties of 54 XRRs/XRFS: X-ray ToO observations (AX), time in days of the start of ToO and satellite which performed the observation, optical afterglow detection (OT), time of the OT detection and observed magnitude, Radio afterglow detection (RT) and host galaxy detection.

The events XRR 971024, XRR 980128, XRR 980306 and XRR 000208 have none of this information available in the literature and so we excluded them from our analysis.

For 15 bursts, X-ray afterglow observations have been performed and all of them show an afterglow candidate. 40 bursts present at least an optical observation. 16 of these show an optical transient (OT) candidate, while 11 events present an R magnitude $\le$22 at 1 day and are thus defined as DARK. 10 bursts out of 20 have a radio afterglow candidate detection. The possible host galaxy has been found for 17 bursts.

In the following section, we present the analysis of the two Chandra observations of the XRR 011030 X-ray afterglow. The study of the lightcurves and the flux distributions of the whole sample are reported in Sects. 4.2 and 4.3.

   
4.1 The case of XRR 011030: Chandra observations

XRR 011030 was detected by WFC1 of BeppoSAX on October 2001 (Gandolfi 2001). The duration of this burst is 1200 s in 2-28 keV with a total fluence of $S_{\rm x}$ = 1.2 $\times $ 10-6 erg cm-2 (Galli & Piro 2005). The spectrum is well fitted by a power-law with a photon index $\Gamma=-(1.8\pm0.2)$ (Galli & Piro 2005). Two X-ray observations have been performed for this event, after 11 and 31.2 days, that lasted 46.61 and 20.12 ks respectively; they were made by ACIS-I on CHANDRA. A new X-ray transient was discovered at RA 20:43:32.5 and Dec +77:17:17.4, at 1.2 arcsec from the radio transient position (Harrison et al. 2001). We processed the Chandra data available in the archives of Chandra observations[*] with CIAO version 3.1, using the task acis_process_events. The spectra have been extracted selecting a circular area around the source, which is in the center, to optimize the signal to noise ratio; the spectra of the background have been extracted from a larger circular region without sources. We performed the spectral analysis with XSPEC version 11.3.1. The spectrum of the first X-ray observation is well described by an absorbed power-law with $N_{\rm H}$ = 2.96 +0.60-0.65 $\times $ 1021 cm-2, photon index $\gamma=1.72^{+0.19}_{-0.20}$ and $\chi_{\nu}^{2}=0.76$with 9 d.o.f. The flux in 2-10 keV is $F=(5.75\pm0.86)$ $\times $ 10-14  $\rm erg~cm^{-2}~s^{-1}$. The spectrum of the first X-ray observation in the energy range between 0.2-9 keV is shown in Fig. 4.

In the second observation there are too few counts and we fitted its spectrum with an absorbed power-law with $N_{\rm H}$ and $\gamma$ kept at the value previously found. Thus the flux at 2-10 keV is $F=(5.58\pm1.45)$ $\times $ $10^{-15}~\rm erg~cm^{-2}~s^{-1}$. We obtained a temporal decay index of $\delta_x=-(2.25\pm0.60)$ between the two Chandra observations. We note that our results are in agreement with those calculated by Sako et al. (2005) and Gendre et al. (2006).

   
4.2 The lightcurves

The temporal profile of the X-ray afterglows are studied collecting all the available ToO observations made by BeppoSAX, Chandra and XMM-Newton. The detection epochs range from a few hours to more than a month. We obtained a sample of 15 bursts: 9 events have observations within 1 day and the other 6 events have later observations. We report in Fig. 5 the prompt and the afterglow X-ray data for the XRR/XRF sample.

To detect possible temporal changes in the X-ray lightcurve, we separately considered the decay indexes of the two previously defined sub-samples of events. For the 9 events with early-time observations, we found a weighted mean value of $\langle\delta_{\rm x}\rangle$ = $-(1.0\pm0.1)$. For the other sample (excluding two events with upper limits and including the late XMM-Newton observation of XRR 030329) we found instead $\langle\delta_{\rm x}\rangle$ = $-(1.5\pm0.1)$. The early and late time decay indexes are not compatible at a 5$\sigma$ level. This suggests the presence of breaks in the afterglow evolution as commonly observed for GRBs.


  \begin{figure} \par\includegraphics[angle=-90,width=6.8cm,clip]{4501fig4.ps}\end{figure} Figure 4: Spectrum of the first observation made by ACIS-I of Chandra of the afterglow of the XRR 011030 in 0.2-9 keV.
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=90,width=7.5cm,clip]{4501fig5.ps}\end{figure} Figure 5: X-ray light curves of 15 XRRs/XRFs with afterglow observations in the range 2-10 keV (the arrows indicate the upper limits); the points are connected with straight lines. For event XRR 991106 we used the afterglow flux by De Pasquale et al. (2003). For completeness we report also the prompt data. (This figure is available in color in electronic form.)
Open with DEXTER

In particular, XRR 030329 and XRR 021004 show a temporal decay index of $\delta _{\rm x}$ = $-(1.9\pm0.2)$ between 111-3222 ks and $\delta _{\rm x}$ = $-(1.8\pm0.5)$ between 12-4500 ks. These values are consistent with the decay index expected after the jet break, where jet matter expands laterally at a velocity close to the speed of light (Rhoads 1999). The presence of an achromatic break for XRR 030329 is also supported by optical data (Tiengo et al. 2003a). A possible break in the optical lightcurve was observed in 4 other cases: XRR 010921 (Price et al. 2001c), XRR 011211 (Holland et al. 2001), XRR 020124 (Bloom et al. 2002) and XRR 030725 (Pugliese et al. 2005). Thus, the presence of a break in the afterglow lightcurve of XRRs/XRFs seems to be, as in GRBs, a common feature.

We now focus on the early-time (<1 day) lightcurve. The X-ray afterglow data always show a decreasing temporal profile. In two cases, (XRR 030329 and XRR 011211), we have data as early as a few hours (5 and 10 respectively) after the trigger. Likewise, the optical lightcurves always show a fading behavior, sometimes together with a plateau transition (XRR 021004, Mirabal et al. 2002, and XRR 030723, Huang et al. 2004). The earliest data point is at $\sim$0.3 h for XRR 021004. The XRR/XRF X-ray and optical lightcurves never show evidence of a rising temporal behavior. If present, this should occur early as 0.3 h after the explosion.

   
4.3 The X-ray and optical flux distributions

We analysed the X-ray and optical flux distributions of XRRs/XRFs, and we compared them to the GRB ones. Ideally, we would like to compute and compare the luminosity distributions of the two classes. This is hampered by the paucity of bursts with known redshift in our sample. However, if the two populations have the same redshift distribution (as in the off-axis model) or the distributions do not overlap appreciably (as in the high-redshift scenario), the flux comparison is meaningful. We also used the available redshift measurements to further test our results.


  \begin{figure} \par\includegraphics[angle=90,width=7.5cm,clip]{4501fig6.ps}\end{figure} Figure 6: Distribution of the logarithm of X-ray flux at 40 ks in units of  $\rm erg~cm^{-2}~s^{-1}$ for 9 XRRs/XRFs (red dotted line) and 25 GRBs (black dashed line). OT = XRRs/XRFs with optical transient, HG = XRRs/XRFs with host galaxy, X = XRRs/XRFs without HG and OT. (This figure is available in color in electronic form.)
Open with DEXTER

In order to test the off-axis model, we studied the afterglow flux in 1.6-10 keV band at 40 ks ($F_{\rm x}$). At early times the three jet model lightcurves are strongly dependent on the viewing angle and they bear distinctive characteristics for each model.

For the analysis, we only used the subsample of 9 early afterglow events. This reduced the contribution from the presence of different decay slopes to the dispersion in the flux distribution. Moreover, for this sample the extrapolated flux $F_{\rm x}$ is more robustly constrained.

We calculated the mean value and the standard deviation of the total and parent distributions of $F_{\rm x}$, according to the likelihood method. We compared these results with those found with the same analysis for a sample of 25 GRBs by De Pasquale et al. (2003). Our results are reported in Table 8. The resulting distributions are shown in Fig. 6. The mean ratio between the GRB and the XRR/XRF flux is $\langle {\it HR}_{\rm x}\rangle_i=0.9$ $\pm$ 1.2.

Then, we calculated the X-ray luminosity at 40 ks for the XRRs/XRFs with known redshift,

 \begin{displaymath}% L(\nu,t)=F_{\nu}(\nu,t) 4\pi D^2(z)(1+z)^{1-\alpha+\delta_{\rm x}}, \end{displaymath} (1)

(Lamb & Reichart 2000), where $\alpha$ is the spectral energy index, $\delta _{\rm x}$ is the temporal decay index, $L_{\nu}(\nu,t)$ is the luminosity at the time t and at the frequency $\nu$ and D(z) is the comoving distance. We found 4 events with known redshift, 3 of them with an early X-ray observation. The light curves are plotted in Fig. 7. We adopt a cosmology $\Omega_{\Lambda}=0.7$, $\Omega_{\rm M}=0.3$, H0=70 km s-1 Mpc-1, q0=-0.55, k=0. The mean luminosity (units of $10^{45}~{\rm erg~s}^{-1}$) is $\langle \log L_{\rm x}\rangle_i$ = 0.6 $\pm$ 0.1, which favorably compares with that of the De Pasquale et al. (2003) sample of 12 GRBs: $\langle \log L_{\rm x}\rangle_i$ = 0.5 $\pm$ 0.2.


  \begin{figure} \par\includegraphics[angle=90,width=7.5cm,clip]{4501fig7.ps}\end{figure} Figure 7: X-ray light curves of XRRs/XRFs with known redshift in the rest frame of the sources in units of $10^{44}~{\rm erg}$, compiled using ${\it Chandra}, {\it BeppoSAX}, {\it RXTE}, {\it XMM-Newton}$ observations of the afterglow. The arrow indicates upper limit. (This figure is available in color in electronic form.)
Open with DEXTER

For the optical flux, we used OT observations at different times. We corrected the R magnitude, mR, for galactic extinction, following the calculations presented by De Pasquale et al. (2003). We extrapolated the flux at 40 ks ($F_{\rm o}$) using the temporal decay index  $\delta _{\rm o}$ of the OT, when available, and a value of $\delta_{\rm o}=1.15$ otherwise (De Pasquale et al. 2003). Our results are reported in Table 7. For XRF 020903 and XRR 011091 the flux extrapolated at 40 ks from the OT observations is overestimated compared to the observed upper limits. It may be due to a possible break in the light curve: in these cases we calculated $F_{\rm o}$ using the upper limits, measured respectively at 86.4 ks and 79.5 ks.

Table 7: The X-ray $(F_{\rm x})$ and optical $(F_{\rm o})$ flux of the afterglow at 40 ks and their ratio $ (F_{{\rm o}/{\rm x}})$; $N_{\rm H}$ is the hydrogen column density, $\delta _{\rm o}$ is the temporal index decay of the optical afterglow and $\delta _{\rm x}$ is the temporal decay index of the X-ray afterglow.

Table 8: Intrinsic mean value and variance of the logarithm of the X-ray [1.6-10 keV] and optical flux [R band], at 40 ks for XRRs/XRFs with early afterglow observations and GRBs. The X-ray flux is in units of $\rm erg~cm^{-2}~s^{-1}$ and the optical flux in units of $\rm W~m^{-2}~Hz^{-1}$.

We found 9 XRRs/XRFs with an optical detection within 1 day. We compared them with 11 OTGRBs (GRB with OT). The ratio between the OTGRBs and the XRRs/XRFs is $\langle HR_{\rm o} \rangle=0.9$ $\pm$ 1.2. Both the optical and X-ray flux distributions, shown in Fig. 8, are similar between GRBs and XRRs/XRFs.


  \begin{figure} \par\includegraphics[angle=90,width=7.25cm,clip]{4501fig8.ps}\end{figure} Figure 8: Distribution of the logarithm of optical flux at 40 ks in units of Wm-2Hz-1 for 9 XRRs/XRFs (red dotted line) and 11 GRBs (black dashed line). (This figure is available in color in electronic form.)
Open with DEXTER

We also analyzed the optical to X-ray flux correlation for both OT and DARK XRRs/XRFs. We find $\langle \log~(f_{\rm o}/f_{\rm x}) \rangle$ = 0.3 $\pm$ 0.3 and $\sigma=0.9$ for XRRs/XRFs and $\langle \log~(f_{\rm o}/f_{\rm x}) \rangle$ = 0.4 $\pm$ 0.1 and $\sigma=0.6$ for GRBs. The ratio is compatible within 1$\sigma$ between the two classes. Instead, the standard deviation of the XRRs/XRFs distribution is greater than a factor $\sim$3 compared to the GRBs, even if we remove the three bursts XRF 981226, XRF 990704 and XRR 020410, which have a value of the optical to X-ray flux ratio smaller than the minimum value found for the GRB sample.

We calculated the ratio between the afterglow X-ray flux (at 40 ks) and the prompt gamma-ray flux (40-700 keV). We considered 8 XRRs/XRFs (with early observations) and 9 GRBs (De Pasquale et al. 2006). We found for the XRR/XRF and GRB parent distributions $\langle \log~(F_{\rm x}/F_{\gamma})\rangle_i$ = 1.35 $\pm$ 0.33, $\sigma=0.61^{+0.28}_{-0.15}$ and $\langle \log~(F_{\rm x}/F_{\gamma})\rangle_i$ = 0.39 +0.18-0.24, $\sigma=0.56^{+0.26}_{-0.15}$, respectively. These value are not consistent at the 3$\sigma$ level.

   
5 Discussion

5.1 The high redshift scenario

In this section, we test the possibility that the observed global properties of the XRFs are only due to a distance effect. The population of XRRs/XRFs is therefore assumed to have the same intrinsic properties of the GRBs but a higher average redshift. This scenario would naturally explain the spectral parameter distributions of the prompt emission of XRRs/XRFs vs. GRBs: since XRRs/XRFs are on average more distant, the observed average spectrum is rigidly red-shifted. From the ratio of the observed peak energies, assuming $\langle z_{\rm grb} \rangle= 1$ for GRBs, we estimate $\langle z_{\rm xr} \rangle \approx 8$.

Under this assumption, the X-ray afterglow at a given time would appear dimmer. Assuming the same spectral and temporal slopes ( $\alpha=-1.1$and $\delta=-1.3$) (De Pasquale et al. 2003) and $\langle z_{\rm xr} \rangle=8$, Eq. (1) yields an X-ray flux ratio of $\sim$12. From our analysis we obtained $\langle {\it HR}_{\rm x} \rangle=0.9$ $\pm$ 1.1.

In order to estimate bias effects due to distance, we calculate the prompt X-Ray flux for a typical GRB with $E_{\rm iso}=10^{53}$ erg, spectral parameters $\beta_1=-1$, $\beta_2=-2.3$ and $E_{\rm peak}=300$ keV (value obtained using the Amati relation), at z=8. We obtain an observed flux in 2-10 keV (assuming a burst duration of 10 s) of Fl=1.2 $\times $ 10-8 erg cm-2 s-1, $\sim$3 and 1.3 times greater then the sensitivity of the WFC and WXM respectively. Thus we expect no relevant selection effects. They appear only for GRBs with  $E_{\rm iso} \le 10^{53}$ erg and $z\ge8$. In order to test the high redshift model, we compare the distribution of the redshift for 13 GRBs and 12 XRR/XRF of our sample, Fig. 9; the two distribution are similar with a mean value of $\langle z_{{\rm xr}} \rangle=1.7$ $\pm$ 0.3 and $\langle z_{\rm grb} \rangle=1.3$ $\pm$ 0.2, compatible within 1$\sigma$. Moreover, the probability that they belong to the same parent population is p=0.15. Even if we consider the subsample of events analysed for the X-ray afterglow,we find compatible values: $\langle z_{\rm xr} \rangle=1.6$ $\pm$ 0.7 and $\langle z_{\rm grb} \rangle=1.5$ $\pm$ 0.4 Thus this result suggests that the XRRs/XRFs and GRBs have similar redshift.

We also compare the rest frame energy peak for XRRs/XRFs and GRBs; we find that there are several event XRR/XRF with an intrinsic Peak energy significantly lower then to the GRB one. However there are also some events, like XRR 020124 and XRR 021004, with an $E_{\rm p}$ in the rest frame consistent with that of GRBs.

For high redshift objects ($z \geq 5$) no optical afterglow is expected: the Lyman-$\alpha$-forest completely absorbs the emission in the optical range (Fruchter 1999). We find that 7 XRR/XRF out of 40 are DARK and show neither a candidate host galaxy nor redshift estimation. Thus some of them could be at high redshift. We calculated the pseudo-redshift for these bursts (see Table 5). Excluding XRR 021112 with a pseudo-redshift pz=4.62 $\pm$ 4.33, all the other bursts have pz less than 1.2. If that estimation holds true, they are probably DARK because of absorption (De Pasquale et al. 2003; Jakobsson et al. 2004). In conclusion, the total sample of the XRRs/XRFs seems to be not compatible with the high redshift model, even though we cannot exclude that some of them could be GRBs at $z \geq 5$. This fraction can be under represented in our sample, if is biased toward brighter (i.e. closer) objects.


  \begin{figure} \par\includegraphics[angle=90,width=7.4cm,clip]{4501fig9.ps}\end{figure} Figure 9: Distribution of the redshift for 16 XRRs/XRFs (red dashed line) and 13 GRBs (black dashed line). U = XRR/XRF with upper limits, T = XRR/XRF with early X-ray afterglow detection (this figure is available in color in electronic form).
Open with DEXTER

5.2 The off-axis scenario

In this section, we discuss the viability of the "off-axis scenario'' to explain GRB, XRF and XRR dissimilarities as due to differences in the observer line of sight. We specifically consider three models. First, the Universal Power-law-shaped (UP) jet (Lamb et al. 2005). Then, the Quasi-Universal Gaussian (QUG) jet (Zhang et al. 2004) and the off-axis Homogeneous (OH) jet model (Yamazaki et al. 2004).

The three jet structures differ for the distribution of kinetic energy per unit solid angle  ${\rm d}E/{\rm d}\Omega$ across the jet surface. In the UP jet model, the jet is boundless ( $\theta_{\rm j}=90^{\circ})$ and the energy distribution, outside a core angle  $\theta _{\rm c}$, follows a power-law with index -2 (Rossi et al. 2002; Zhang & Meszaros 2002). In the QUG jet, ${\rm d}E(\theta)/{\rm d}\Omega=({\rm d}E/{\rm d}\Omega)_{0}$ $\times $ ${\rm e}^{-\theta^{2}/(2\theta_{\rm k} ^{2})}$, shows a nearly constant energy core ( $0<\theta \le\theta_{\rm k}$) and an exponential decrease for $\theta > \theta_{\rm k}$. In the uniform jet model, ${\rm d}E/{\rm d}\Omega$ is constant within the aperture ( $\theta _{\rm j}$) of the jet and it drops sharply to zero outside. All models assume the Amati relation (Amati et al. 2002) extended to XRF peak energies (Lamb & Graziani 2003); it allows us to relate the isotropic equivalent energy  $ E_{\rm iso}$ to the rest frame peak  $\tilde{E}_{\rm peak}$in the $\nu F_{\nu}$ spectrum of the prompt emission,

 \begin{displaymath}% \tilde{E}_{\rm peak}\sim C~{\rm keV} \left(\frac{E_{\rm iso}} {10^{52}~{\rm erg~s}} \right)^{0.5}, \end{displaymath} (2)

where C follows a log-normal distribution with best fit parameters $\langle C \rangle=90.4$ and $\sigma_C=0.7$ (Lamb et al. 2005). In the UP and QUG jet models there are not specific assumptions or predictions for the shape of the spectrum as a function of the viewing angle; instead, the spectral slopes are expected to be angle independent in the OH jet model. This is consistent with our observed spectral parameter distributions (Figs. 1 and 2).

The afterglow predictions and data are compared in the following discussion. Here we only consider the sub-sample of events used for the X-ray flux analysis in Sect. 4.3 and their $\langle E_{\rm p,xr}\rangle$reported in Table 4. We proceed as follows. We define the average parameters of the jet qualifying a XRR/XRF vs. GRB for each jet structure. XRR is defined by an observed hardness ratio of H>0.32. It corresponds to a peak energy $E_{\rm peak} \la 80$ keV, if we fix the spectral slopes to $\beta_1=-1$ and $\beta_2=-2$ in the Band spectrum. Thus, in the QUG and UP jet model, we can evaluate the viewing angle  $\theta _{\rm o}$ at which the transition between GRBs and XRRs occurs. In the OH jet model is $\theta_{\rm o}=\theta_{\rm j}$. Then, we deduce the average viewing angle for GRBs and XRRs/XRFs in our sample from the observed average peak energies: $\langle \tilde{E}_{\rm p,grb}\rangle\simeq 210~(1+z)=410$ keV and $\langle \tilde{E}_{\rm p,xr}\rangle\simeq 68~(1+z)=136$ keV (assuming $\langle z \rangle=1$). Simulations of X-ray afterglow light curves allow us an estimate of the expected GRBs over XRRs/XRFs flux ratio at $40/(1+\langle z\rangle)=20$ ks for our sample. We note here that the average  $E_{\rm peak}$s used in this discussion are obtained from a subsample of 7 out of 9 XRRs/XRFs and of 14 out of 25 GRBs; the associated uncertainties are $10\%$ (see Table 4). The uncertainties of the expected flux ratios are consequently at least of $10\%$. We comment on how the model predictions compare with our result of a flux ratio of the order of unity (Sect. 4.3).

The parameters adopted by Lamb et al. (2005) for the UP jet are: $\theta_{\rm c}=0.26^{\circ}$, $\theta _{\rm j}=90^{\circ }$ and $E_{\rm iso}(0)=2$ $\times $ 1054 ergs and $E_{\rm iso}\simeq\frac{E_{\gamma}} {29} \theta^{-2}$, where $E_{\gamma}\simeq 1.2$ $\times $ 1051 erg is the total standard energy. The off-axis angle is related to the peak energy by

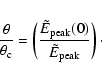
\begin{eqnarray*}\frac{\theta}{\theta_{\rm c}}=\left(\frac{\tilde{E}_{\rm peak}(0)}{\tilde{E}_{\rm peak}}\right)\cdot \end{eqnarray*}


This implies that for $\frac{\theta_{\rm o}}{\theta_{\rm c}}>8 \simeq 2^{\circ}$the observer detects XRRs/XRFs. The mean viewing angles for GRBs and XRRs/XRFs in our sample are $\frac{\theta_{\rm grb}}{\theta_{\rm c}}\simeq 3.1$and $\frac{\theta_{\rm xr}}{\theta_{\rm c}}\simeq 9.4$ respectively. The expected X-ray flux ratio is $\simeq$0.5. However, we note that using the parameters adopted by Lamb et al. (2005), it may be possible to explain the large range of  $ E_{\rm iso}$ needed to account for GRBs and XRFs but not the time of the break. Due to the small core angle, we would expect the afterglow break to occur on average before 40 ks. This is not, however, what we observe (see Sect. 4.2 and Fig. 5). If, instead, we use the standard geometrical relation between  $ E_{\rm iso}$ and  $E_{\gamma}$, we get $\theta_{\rm c}=\left(\frac{2 E_{\gamma}}{E_{\rm iso}}\right)^{0.5}\simeq 2$ degree. The break in the lightcurve is thus expected around $\sim$few days (Fig. 11), in better agreement with our results in Sect. 4.2. In this case, the expected X-ray flux ratio is $\simeq$20.

Zhang et al. (2004) constrain with data the average parameters of the QUG jet: $\theta_k\simeq 5.7$ degree and a standard total energy of $E_{\gamma}\simeq 1.3$ $\times $ 1051 erg. This implies an average $E_{\rm iso}(0)\simeq 2.6$ $\times $ 1053 erg. Since

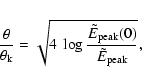
\begin{eqnarray*}\frac{\theta}{\theta_{\rm k}}=\sqrt{4~\log{\frac{\tilde{E}_{\rm peak}(0)} {\tilde{E}_{\rm peak}}}}, \end{eqnarray*}


XRRs/XRFs are detected for $\theta_{\rm o} \ga 2.1 \theta_{\rm k}$. In our sample, we detect GRBs observing at an average angle of $\frac{\theta_{\rm o}}{\theta_{\rm k}}=0.7$ and XRRs/XRFs at $\frac{\theta_{\rm o}}{\theta_{\rm k}}=2.2$. Thus, the expected X-ray flux ratio is $\sim$11 (Fig. 12).

In the off-axis homogeneous jet model, a GRB is detected for $\theta_{\rm o} \le\theta_{\rm j}$. Yamazaki et al. (2004) assume a power-low distribution of opening angles and a log-normal distribution for $E_{\gamma}$ with $\langle E_{\gamma}\rangle \simeq 1.2$ $\times $ 1051 erg. The parameters of the "average'' homogeneous jet corresponding to the observed events in Fig. 6 are: $E_{\rm iso}=2.1$ $\times $ 1053 erg and $\theta_{\rm j} \simeq 6.1$ degree, where we have used Eq. (2) and $\frac{1}{2}\theta_{\rm j}^{2}E_{\rm iso}=E_{\gamma}$. In this model,

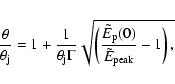
\begin{eqnarray*}\frac{\theta}{\theta_{\rm j}}=1+\frac{1}{\theta_{\rm j}\Gamma}\... ...(\frac{\tilde{E}_{\rm p}(0)} {\tilde{E}_{\rm peak}}-1 \right),} \end{eqnarray*}


where $\Gamma$ is the Lorentz factor. From the observed energy peak ratio, we derive $\frac{\theta_{\rm xr}}{\theta_{\rm grb}}\simeq 1.03$ (with $\Gamma=500$). Correspondingly, we expect a X-ray flux ratio of $\sim$1.1 (Fig. 13).

In summary, the OH predictions are in best agreement with data. The conclusions for the UP jet depend instead on the assumed core size, which is still a poorly constrained parameter of the model. If we chose the size core to match the large spread of  $ E_{\rm iso}$, the UP also favourably compares with the data.

Nevertheless, selection effects may weaken these conclusions. We have been assuming that the two classes of events in Fig. 6 have the same mean redshift. This assumption is tentatively supported but not proven true by the comparison of the distributions of GRBs and XRFs with known redshift. In fact, the mean value of the redshift is compatible within 1$\sigma$. Our sample of XRRs/XRFs seems to be biased towards high  $ E_{\rm iso}$ (for a given $E_{\rm p}$), allowed by the scattering in the Amati relation. This consideration comes from a direct comparison between our 3 events with know redshift and the "Amati'' relation as reported by Ghirlanda et al. (2004; see. Fig. 10). We have further selected events with an early afterglow observations. We cannot exclude that early follow up observations have been carried out following criteria linked to the property of the prompt emission (e.g. bright bursts). These uncertainties on the selection effects do not allow us to draw strong conclusions and, in particular, the QUG cannot be ruled out.


  \begin{figure} \par\includegraphics[width=6.8cm,clip]{4501fig10.ps}\end{figure} Figure 10: Amati relation for 12 XRRs/XRFs (red and blue point) and 22 GRBs (black point) from Ghirlanda et al. (2004). The blue point are XRRs/XRFs with early afterglow observation and known redshift. The right angles are the upper limits. (This figure is available in color in electronic form.)
Open with DEXTER

We now consider the temporal behavior of the X-ray afterglow lightcurves in the three models (Figs. 13-12) and compare it with our results (Sect. 4.2 and Figs. 5 and 7). At early times, the lightcurve is remarkably different as a function of  $\theta _{\rm o}$ in the three scenarios. The sharp edges of the homogeneous jet imply that no light is emitted along the line of sight for $\theta_{\rm o}>\theta_{\rm j}+1/\Gamma$. This gives the characteristic rising temporal slope as the fireball decelerates and $1/\Gamma<\theta_{\rm o}$ (Fig. 13). It also implies no jet breaks in the XRF lightcurve, unless $\theta_{\rm o} \sim \theta_{\rm j}$. The UP jet lightcurves, instead, always have the temporal evolution of an on-axis curve from a homogeneous jet (Fig. 11). An intermediate behavior is presented by the Gaussian jet (Fig. 12): as $\theta _{\rm o}$increases, the lightcurve becomes flatter and it eventually recovers the off-axis behavior for a homogeneous jet.


  \begin{figure} \par\includegraphics[angle=90,width=7.5cm,clip]{4501fig11.ps}\end{figure} Figure 11: Light curves for a power-law shaped jet (UP) observed from different viewing angles. From top to bottom: $\theta _{\rm o}$ = 0, 3.1, 9.4, 36  $\theta _{\rm c}$, where $\theta _{\rm c}=2^{\circ }$. The estimated viewing angle for a GRB is $\theta _{{\rm o},{\rm grb}}$ = $3.1\theta _{\rm c}$ (blue dotted line) and for an XRR/XRF is $\theta _{{\rm o},{\rm xr}}$ = $9.4\theta _{\rm c}$ (red dashed line). (This figure is available in color in electronic form.) The other parameters are: $\theta _{\rm j}=90^{\circ }$, $\Gamma _{0}=500$, rest frame frequency =10 keV, $\epsilon _{\rm b}=0.01$, $\epsilon _{\rm e}=0.1$, z=1, p=2.5, n=10 cm-1. The straight line marks the time (20 ks) when we extrapolated the observed fluxes.
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=90,width=7.5cm,clip]{4501fig12.ps}\end{figure} Figure 12: Light curves of a Gaussian jet (QUG) observed from different viewing angles using the model described by Zhang et al. (2004). From top to bottom: $\theta _{\rm o}$ = 0, 0.7, 2.2, 8.0  $\theta _{\rm k}$, where $\theta _{\rm k}=(5.7^{+3.4}_{-2.1})^{\circ }$. The estimated viewing angle for a GRB is $\theta _{{\rm o},{\rm grb}}$ = $0.7 \theta _{\rm k}$ (blue dotted line) and for an XRR/XRF is $\theta _{{\rm o},{\rm xr}}$ = $2.2\theta _{\rm k}$ (red dashed line) (this figure is available in color in electronic form). The other parameters are: $\theta _{\rm j}=90^{\circ }$, $\Gamma _{0}=500$, rest frame frequency =10 keV, $\epsilon _{\rm b}=0.01$, $\epsilon _{\rm e}=0.1$, z=1, p=2.5, n=10 cm-1. The straight line marks the time (20 ks) when we extrapolated the observed fluxes.
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=90,width=7.5cm,clip]{4501fig13.ps}\end{figure} Figure 13: Light curves of an homogeneous jet (OH) observed from the top to the bottom on axis, from different viewing angles using the model described by Yamazaki et al. (2004). From top to bottom: $\theta _{\rm o}$ = 0, 1, 1.03, 4  $\theta _{\rm j}$, where $\theta _{\rm j}=6.1^{\circ }$. The estimated viewing angle for a GRB is $\theta _{{\rm o},{\rm grb}}$ = $\theta _{\rm j}$ (blue dotted line) and for an XRR/XRF is $\theta _{{\rm o},{\rm xr}}$ = $1.03\theta _{\rm k}$ (red dashed line). (This figure is available in color in electronic form.) The other parameters are: $\Gamma _{0}=500$, the rest frame frequency =10 keV, $\epsilon _{\rm b}=0.01$, $\epsilon _{\rm e}=0.1$, z=1, p=2.5, n=10 cm-1. The straight line marks the the time (20 ks) when we extrapolated the observed fluxes.
Open with DEXTER

Unfortunately, our sample is biased towards viewing angles close to the jet core/aperture, where the lightcurve behaviour from then three jet structures becomes very similar. Thus, a comparison with our current data does not allow us to discriminate between the models. A Gaussian jet seen at small angles ( $(\theta_{\rm o}-\theta_{\rm j}) \sim (0.1{-}1) \theta_{\rm j}$) has been also claimed by Granot (2005) et al. to explain the afterglow of XRF 030723 and XRF 041006.

Another test that in principle could discriminate between the jet energy profiles is the ratio between the afterglow X-ray flux and the prompt $\gamma$-ray flux. This gives a robust estimate of the ratio of radiation efficiencies of the prompt and afterglow phases, if the emission is dominated by the line of sight part of the jet (Freedman & Waxman 2001). This is the case for GRBs in all three jet models. This is also true for XRRs/XRFs in the UP jet model and for the QUG jets seen close to the jet core. In those cases, we expect a similar flux ratio for XRRs/XRFs and GRBs, if the efficiency ratio is constant with the angular distance from the jet axis. Instead, the flux ratio may strongly depend on the viewing angle and on the Lorentz factor for the OH jet model. In fact, we find that the two classes have a mean flux ratio  $\log~(F_{\rm x}/F[40,700])_i$ not compatible at a $3\sigma$ level, with a difference of one order of magnitude. In particular, we may assume that the afterglow efficiency is the same in XRRs/XRFs and GRBs: therefore the mechanism responsible for the prompt emissio would be more efficient for GRBs.

Finally, the three jet profiles predict a larger width of the X-ray flux distribution of the XRRs/XRFs, compared to the GRB one. This is due to the larger $ E_{\rm iso}$ distribution expected for XRRs/XRFs (see e.g. Fig. 2 in Yamazaki et al. 2004). We found that $\sigma_i=0.45^{+0.14}_{-0.12}$ for GRBs and $\sigma_i=0.85^{+0.46}_{-0.30}$ for XRRs/XRFs; these values are compatible within the errors. Also in this case we may miss the dim/soft events; therefore, the observed XRR/XRF flux distribution can seem narrower than the intrinsic one.

   
6 Conclusions

In this work, we studied the prompt and afterglow emission properties of XRRs/XRFs, compared to GRB ones. We compiled a sample of 54 XRRs/XRFs and we classified them according to the same hardness spectral ratio.

We analyzed the spectral parameter distributions of the prompt emission and we found that the XRR/XRF Band spectral indexes (Band et al. 1993) $\beta _1$ and  $\beta _2$ are consistent with GRB ones, while the peak energy is lower by a factor $\sim$4.5.

We analyzed the light curves of the XRRs/XRFs; we found evidence of breaks both in X-ray and optical afterglow. It is supported also by the observed different values of the temporal decay index for the early and late afterglow.

We found that the optical and X-ray flux distributions are consistent for GRBs and XRRs/XRFs; the ratios are respectively of $ \langle {\it HR}_{\rm o} \rangle=0.9$ $\pm$ 1.1 and $\langle {\it HR}_{\rm x} \rangle=0.9$ $\pm$ 1.2;

We discussed our results in the framework of the high-redshift and the off-axis scenarios.

While the prompt emission spectral parameters are consistent with a redshifted spectrum, the X-ray and optical afterglow properties and the (few) measured redshifts argue against the interpretation of XRRs/XRFs as high redshift GRBs.

However, there are also some XRR/XRF events with an intrinsic energy peak consistent with that of classical GRBs. This suggests a high redshift nature for them.

Our analysis of the off-axis scenario favors the OH and UP jet models: both the X-ray flux ratio between XRRs/XRFs and GBRs and the light curve behavior seem consistent. However, the prediction of the X-ray flux ratio of the UP jet is parameter-dependent. The QUG jet may still be consistent with our results, if selection effects have reduced the distance between the mean X-ray fluxes of XRRs/XRFs and GRBs.

Finally, our result on the prompt over afterglow flux ratio are inconsistent with the simple picture of a constant prompt over afterglow efficiency ratio for the UP and QUG jet models.

These conclusions should be further tested, collecting a larger sample of XRRs/XRFs with known redshift and early afterglow observations, allowing one to compare direct luminosity distributions. The SWIFT data will be important for this goal, even if this satellite is sensitive only at energies greater than 15 keV, i.e. above the range of the softest XRFs. Future missions able to select dim/soft XRRs/XRFs with high sensitivity can provide a fundamental step to understand the origin of these events.

Acknowledgements
The authors are grateful to Enrico Massaro for his suggestions and advice. We thank Ehud Nakar and Edo Berger for useful discussion and comments as the anonymous referee for very useful suggestions. Support for this work was provided by NASA though Chandra Postdoctoral Fellowship grant number PF5-60040 awarded by the Chandra X-ray Center, which is operated by the smithsonian Astrophysical Observatory for NASA under contract NASA8-03060. This work was partially supported by the EU FPS RTN "Gamma Ray Burst: an enigma and a tool''.

References

 

  
Online Material

Table 1: Spectral parameters of 54 XRRs/XRFs. The models used are: BAND = Band function, PL = powerlaw as N(E) = $KE^{\Gamma }$, PLE = powerlaw $\times $ exponential cutoff as N(E) = $KE^{\beta_1}\times \exp~(-E/E_0)$, PLA = absorbed powerlaw as N(E) = $KE^{\Gamma}\times \exp~(-N_{\rm H}\sigma(E))$. When not given directly, we have derived $E_{\rm peak}=(2+\beta _1)\times E_{\rm o}$.

Table 2: General properties of 54 events XRRs/XRFs: Time UT of the burst trigger, instrument of the observation, fluences in $10^{-7}~{\rm erg~cm}^{-2}$ in the energy range 30-400 keV (S[30, 400]), 2-30 keV (S[2, 30]), 40-700 keV (S[40, 700]) and 2-10 keV (S[2, 10]).


Copyright ESO 2006