A&A 460, 583-595 (2006)
DOI: 10.1051/0004-6361:20065752
Reconstruction of solar irradiance variations in cycles 21-23 based on surface magnetic fields
T. Wenzler1,2 - S. K. Solanki2
- N. A. Krivova2 - C. Fröhlich3
1 - Institute of Astronomy, ETH Zentrum, 8092 Zurich, Switzerland
2 -
Max-Planck-Institut für Sonnensystemforschung, 37191 Katlenburg-Lindau, Germany
3 -
Physikalisch-Meteorologisches Observatorium Davos, World Radiation Center, 7260 Davos Dorf, Switzerland
Received 2 June 2006/ Accepted 17 August 2006
Abstract
Aims. We present a reconstruction of total solar irradiance (TSI) back to 1974, i.e. from the minimum of cycle 21 to the declining phase of cycle 23. We also present a cross-calibration between the magnetograms obtained by the 512 channel magnetograph and the spectromagnetograph at Kitt Peak.
Methods. The TSI reconstruction is carried out using data from the 512-channel Diode Array Magnetograph and the newer spectromagnetograph on Kitt Peak. The model is based on the assumption that all irradiance changes on time-scales of a day and longer are entirely due to the variations of the surface distribution of the solar magnetic field. The reconstructed irradiance is compared with the composite of total solar irradiance measurements from PMOD/WRC (version 41).
Results. A good correspondence is found with the PMOD TSI composite, with no bias between the three cycles on time-scales longer than the solar rotation period, although the accuracy of the TSI reconstruction is somewhat lower when 512 channel magnetograph data are used. This suggests that the same driver of the irradiance variations, namely the evolution of the magnetic flux at the solar surface, is acting in cycles 21-23. Different methods of comparing the magnetograms obtained by the two Kitt Peak magnetographs give somewhat different results, with factors by which 512 channel data must be divided in the range 1.38-1.63 being found. This is due to the non-linearity of the relationship between the magnetic field measured by the two instruments.
Key words: methods: data analysis - solar-terrestrial relations - Sun: activity - Sun: faculae, plages - Sun: magnetic fields - sunspots
1 Introduction
Models of TSI variations for cycle 23 and the declining part of cycle 22 (Krivova et al. 2003; Wenzler et al. 2005,2004), which are based on the assumption that all irradiance changes are entirely due to the evolution of solar surface magnetic features and which have a single free parameter, account for more than 88% of all changes in the TSI on time scales of days up to the solar cycle. These magnetic features are extracted from high resolution full-disk magnetograms and the corresponding intensity images obtained at regular intervals. Krivova et al. (2003) used data recorded by the Michelson Doppler Imager (MDI) on the Solar and Heliospheric Observatory (SoHO; Scherrer et al. 1995) to reconstruct irradiance variations recorded by the Variability of solar IRradiance and Gravity Oscillations (VIRGO) experiment on SoHO (Fröhlich et al. 1997) between 1996 and 2002, whereas Wenzler et al. (2005) reconstructed TSI variations based on magnetograms and intensity images obtained by the spectromagnetograph (abbreviated as NSO-SPM; Jones et al. 1992) at the Kitt Peak Vacuum Tower (KPVT; Livingston et al. 1976a) of the National Solar Observatory (NSO) between 1992 and 2003. The results show good agreement with the TSI composite measurements from Fröhlich (2003b) on both short (days to months) and long (solar cycle) time-scales. However, the reconstructed interval was too short to judge wether the model shows any significant trend over multiple cycles.
In this paper we extend the SATIRE (Spectral and Total Irradiance REconstruction) model back to the year 1974, i.e. to before the start of space-based TSI observations in 1978, using data recorded by the NSO/KPVT 512-channel Diode Array Magnetograph (hereinafter referred to as NSO-512; Livingston et al. 1976b). With this extension we test whether the assumption that the main driver of the solar irradiance changes on time-scales of days and longer is the magnetic field at the solar surface is valid also for cycle 21. In particular, we consider whether the TSI for all 3 cycles, 21-23, can be reproduced with a single value of the free parameter. Also, the reconstructed TSI values between 1974 and 1978 can be used to extend the TSI data set by a few years. In order to successfully reconstruct TSI using NSO-512 data, these have to be characterized, rid of any systematic errors present in them and intercalibrated with the NSO-SPM data. This forms a major part of the paper.
The paper is structured as follows. In Sect. 2 we present the data sets used. We compare magnetograms and continuum intensity images taken with the NSO-512 and the NSO-SPM at the KPVT in Sect. 3. In Sect. 4 we briefly describe the model of total solar irradiance based on NSO-SPM data and the results for cycles 22 and 23. The TSI model based on NSO-512 data and the results for cycles 21 and 22 are described in Sect. 5. Our results of the reconstruction of total solar irradiance variations in cycles 21-23 based on the combined KPVT/NSO-512 and KPVT/NSO-SPM data set are summarized and compared with the PMOD TSI composite in Sect. 6. Finally, our conclusions are presented in Sect. 7.
 |
Figure 1:
Examples of magnetograms (left) and continuum intensity images (right) for March 19, 1993. The magnetogram and the corresponding continuum intensity image in the upper row were recorded by NSO-SPM, those in the lower row by NSO-512. |
| Open with DEXTER |
2 Data
2.1 Magnetograms and continuum images
The TSI model discussed here is based on two sets of full-disk solar observations obtained daily at the KPVT. The first data set employed here (henceforth referred to as NSO-SPM) comprises daily full-disk magnetograms and corresponding continuum intensity images recorded by the NASA/NSO spectromagnetograph (SPM) at the KPVT in the Fe I 8688  spectral line. It is available from 1992 November 21 to 2003 September 21, after which the NSO-SPM was permanently turned off. The full-disk images with
spectral line. It is available from 1992 November 21 to 2003 September 21, after which the NSO-SPM was permanently turned off. The full-disk images with
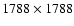 pixels were scanned in about one hour and have a field of view of
pixels were scanned in about one hour and have a field of view of
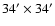 .
The corresponding pixel size is
.
The corresponding pixel size is
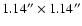 .
The two images in the upper row of Fig. 1 show a magnetogram and the corresponding intensity image recorded by NSO-SPM on March 19, 1993. Earlier full-disk images also observed with the NSO-SPM instrument exist between 1992 April 4 and 1992 November 19 but they were obtained in the Fe I 5507
.
The two images in the upper row of Fig. 1 show a magnetogram and the corresponding intensity image recorded by NSO-SPM on March 19, 1993. Earlier full-disk images also observed with the NSO-SPM instrument exist between 1992 April 4 and 1992 November 19 but they were obtained in the Fe I 5507  spectral line. Unfortunately there is no overlap between the two NSO-SPM data sets and therefore an independent crosscalibration is not possible. Thus for the present analysis we use only the NSO-SPM data set observed in the Fe I 8688
spectral line. Unfortunately there is no overlap between the two NSO-SPM data sets and therefore an independent crosscalibration is not possible. Thus for the present analysis we use only the NSO-SPM data set observed in the Fe I 8688  spectral line. NSO-SPM data for 2055 days are used here. On the other 839 days on which data are available, constituting
spectral line. NSO-SPM data for 2055 days are used here. On the other 839 days on which data are available, constituting 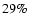 of the original data record, we identified regions with artifacts or obvious loss of data quality introduced by clouds, poor seeing and/or instrumental problems (see Wenzler et al. 2005,2004, for details).
of the original data record, we identified regions with artifacts or obvious loss of data quality introduced by clouds, poor seeing and/or instrumental problems (see Wenzler et al. 2005,2004, for details).
The second set (henceforth referred to as NSO-512) covers daily full-disk magnetograms and corresponding continuum intensity images from the NASA/NSO 512-channel Diode Array Magnetograph at the KPVT in the Fe I 8688  spectral line. The full-disk images with
spectral line. The full-disk images with
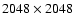 pixels were recorded in about 40 minutes and have a field of view of
pixels were recorded in about 40 minutes and have a field of view of
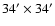 .
Each pixel corresponds to
.
Each pixel corresponds to
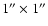 .
Data for 4620 days from 1974 February 1 to 1992 April 18 and for 45 days from 1992 November 28 to 1993 April 10 are available. A sample NSO-512 magnetogram and the corresponding continuum intensity image recorded on 19th March 1993 are shown in the lower row of Fig. 1. The NSO-512 data (magnetograms and intensity images) have a noticeably lower quality than the NSO-SPM data. This is particularly marked for the NSO-512 continuum intensity images, for which only 4 bits per pixel are stored, so that an exact determination of sunspot areas is difficult and on some days even impossible (see Sect. 3.2 for details). Furthermore, the NSO-512 magnetograms exhibit many more regions with artifacts or obvious loss of data quality than the NSO-SPM magnetograms (private communication by J. W. Harvey). Using the selection procedure of Wenzler et al. (2004) we have carefully examined the NSO-512 magnetograms, the corresponding intensity images and the constructed sunspot and facluar masks (see Sect. 4) on all of the 4620 days and found such problems on 2886 days, which is
.
Data for 4620 days from 1974 February 1 to 1992 April 18 and for 45 days from 1992 November 28 to 1993 April 10 are available. A sample NSO-512 magnetogram and the corresponding continuum intensity image recorded on 19th March 1993 are shown in the lower row of Fig. 1. The NSO-512 data (magnetograms and intensity images) have a noticeably lower quality than the NSO-SPM data. This is particularly marked for the NSO-512 continuum intensity images, for which only 4 bits per pixel are stored, so that an exact determination of sunspot areas is difficult and on some days even impossible (see Sect. 3.2 for details). Furthermore, the NSO-512 magnetograms exhibit many more regions with artifacts or obvious loss of data quality than the NSO-SPM magnetograms (private communication by J. W. Harvey). Using the selection procedure of Wenzler et al. (2004) we have carefully examined the NSO-512 magnetograms, the corresponding intensity images and the constructed sunspot and facluar masks (see Sect. 4) on all of the 4620 days and found such problems on 2886 days, which is 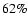 of the original data record. About
of the original data record. About 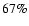 of these 2886 days are identified as problematic due to artifacts in the NSO-512 magnetograms and intensity images introduced by instrumental problems (e.g. heavily enhanced noise level or misalignment between different swaths across the Sun, blank images) and
of these 2886 days are identified as problematic due to artifacts in the NSO-512 magnetograms and intensity images introduced by instrumental problems (e.g. heavily enhanced noise level or misalignment between different swaths across the Sun, blank images) and 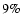 by artifacts introduced by clouds and/or very poor seeing. On a further
by artifacts introduced by clouds and/or very poor seeing. On a further 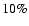 of these days the magnetograms are of good quality but not the continuum intensity images, while
of these days the magnetograms are of good quality but not the continuum intensity images, while 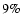 of the data were discarded due to incomplete coverage of the solar disk. On
of the data were discarded due to incomplete coverage of the solar disk. On 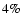 and
and 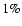 of these 2886 days the spot masks and facular masks, respectively, exhibit errors, i.e. often missing spot regions and/or problems at the solar limb. These data cannot be used for irradiance reconstructions. Therefore only data for 1734 days from 1974 August 23 to 1992 April 4 are used here. The data for the 45 days from 1992 November 28 to 1993 April 10 are used for the comparison between NSO-SPM and NSO-512 data (see Sect. 3 for details).
of these 2886 days the spot masks and facular masks, respectively, exhibit errors, i.e. often missing spot regions and/or problems at the solar limb. These data cannot be used for irradiance reconstructions. Therefore only data for 1734 days from 1974 August 23 to 1992 April 4 are used here. The data for the 45 days from 1992 November 28 to 1993 April 10 are used for the comparison between NSO-SPM and NSO-512 data (see Sect. 3 for details).
We stress that the faulty NSO-SPM and NSO-512 magnetograms and the corresponding continuum intensity images were rejected a priori and not on the basis of the reconstruction of total solar irradiance and its agreement or disagreement with observations. We also note that there probably is instrumental noise in many of the selected magnetograms at a level too low to be accurately identified as such, but sufficiently strong to have an effect on the irradiance reconstruction.
 |
Figure 2:
Noise level (in G) of the NSO-512 magnetograms as a function of location on the solar disk. Plotted is an average over the noise level surfaces of 6 magnetograms. Both the surface and the contours represent the standard deviation of the magnetogram signal (see text for details). The y-axis gives the direction from south to north, the x-axis from east to west. |
| Open with DEXTER |
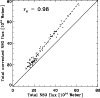 |
Figure 3:
Total (unsigned) photospheric magnetic flux (in 1014 Weber) based on corrected NSO-512 magnetograms vs. total photospheric magnetic flux based on uncorrected NSO-512 magnetograms for several Carrington rotations between 1974 and 1987 (Arge et al. 2002). The correlation coefficient, 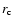 ,
is 0.98. The solid diagonal line represents the expectation values for identical data, the dashed line is a regression. ,
is 0.98. The solid diagonal line represents the expectation values for identical data, the dashed line is a regression. |
| Open with DEXTER |
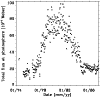 |
Figure 4:
Total (unsigned) photospheric magnetic flux for Carrington rotations between 1974 and 1987 based on NSO-512 magnetograms. Asterisks represent uncorrected values, filled circles corrected values obtained by Arge et al. (2002) and open circles represent the linearly scaled NSO-512 flux values (see text for details). |
| Open with DEXTER |
2.2 Noise level of the magnetograms
The noise level
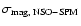 of the NSO-SPM magnetograms has been calculated by Wenzler et al. (2004), who applied the same method as Ortiz et al. (2002) and obtained a value of about 5 G (see Fig. 4 of Wenzler et al. 2004). We use the same method now to determine the noise level of the NSO-512 magnetograms. In order to avoid artifacts introduced by the presence of active regions, we use six low activity magnetograms from the year 1985. In Fig. 2 we show the noise level surface averaged over all 6 magnetograms. The mean value of the surface
of the NSO-SPM magnetograms has been calculated by Wenzler et al. (2004), who applied the same method as Ortiz et al. (2002) and obtained a value of about 5 G (see Fig. 4 of Wenzler et al. 2004). We use the same method now to determine the noise level of the NSO-512 magnetograms. In order to avoid artifacts introduced by the presence of active regions, we use six low activity magnetograms from the year 1985. In Fig. 2 we show the noise level surface averaged over all 6 magnetograms. The mean value of the surface
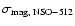 is 8.1 G, with maximum and minimum values of about 8.8 and 7.5 G, respectively. The values of the surface mean noise level for single magnetograms range from 7.5 G to 9.0 G. Jones et al. (1992) found a similar noise level, about 7 G, for the NSO-512 magnetograms taken under the best conditions.
is 8.1 G, with maximum and minimum values of about 8.8 and 7.5 G, respectively. The values of the surface mean noise level for single magnetograms range from 7.5 G to 9.0 G. Jones et al. (1992) found a similar noise level, about 7 G, for the NSO-512 magnetograms taken under the best conditions.
2.3 Magnetic flux correction in the earlier magnetograms
Arge et al. (2002) have compared total (unsigned) photospheric magnetic flux calculated for each Carrington rotation between 1974 and 2002 derived from magnetograms of the National (NSO, i.e. NSO-512 and NSO-SPM data), Wilcox (WSO) and Mount Wilson (MWO) Solar Observatories. They noticed that the NSO fluxes obtained with the NSO-512 data between 1974 and the end of 1989 are unusually low as compared to those from the other two observatories. Having identified the sources of these and other discrepancies (for details see Arge et al. 2002) they developed a procedure to correct the NSO-512 data before constructing Carrington maps. Since only a limited number of magnetograms were corrected by Arge et al. (2002), while we need here as many as possible, we took recourse to the following simplification. We plot in Fig. 3 the total (Carrington-rotation integrated) photospheric magnetic flux based on corrected NSO-512 data against the total photospheric flux based on original NSO-512 data for several Carrington rotations between 1974 June 18 and 1987 August 9 (private communication by C. N. Arge and J. W. Harvey, see also Arge et al. 2002, Fig. 1). We found that all points lie close to a straight line with a slope and intercept of
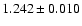 and
and
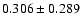 ,
respectively (dashed line in Fig. 3). The resulting correlation coefficient is
,
respectively (dashed line in Fig. 3). The resulting correlation coefficient is
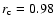 .
.
This allows us to approximately generate the missing corrected values by simply multiplying all NSO-512 fluxes between 1974 and the end of 1989 by a factor of 1.242. In Fig. 4 we plot the total photospheric NSO-512 flux for each Carrington rotation between 1974 and 1987. Asterisks represent flux values based on uncorrected NSO-512 data and filled circles those based on NSO-512 data corrected by Arge et al. (2002). The open circles are used for the flux values based on uncorrected NSO-512 data, but scaled with the factor of 1.242.
To highlight the results of the procedure described above we show in Fig. 5 the total photospheric flux integrated for each Carrington rotation between 1974 and 2002 for the NSO (circles), WSO (plus signs) and MWO (triangles) data (cf. Arge et al. 2002, Fig. 1). Before the end of 1989 the circles represent NSO-512 data that have either been corrected by Arge et al. (2002) or have been linearly scaled by the factor 1.242. Between 1990 and 2002 the circles denote the original NSO-512 and NSO-SPM data, whereby the official recommended factor of 1.46 for the intercalibration with NSO-SPM data (see Sect. 3) has been employed.
![\begin{figure}
\par\includegraphics[width=17cm]{5752fi5.eps} \end{figure}](/articles/aa/full/2006/47/aa5752-06/Timg34.gif) |
Figure 5:
Total (unsigned) photospheric magnetic flux for each Carrington rotation between 1974 and 2002 based on NSO (NSO-512 and NSO-SPM, circles), WSO (plus signs) and MWO (triangles) data (cf. Arge et al. 2002, Fig. 1). See text for details. |
| Open with DEXTER |
2.4 Composite record of total solar irradiance measurements
Total solar irradiance reconstructions based on NSO-512 and NSO-SPM data are compared with the newest PMOD composite of TSI (version 41) from the Physikalisch-Meteorologisches Observatorium Davos/World Radiation Center (PMOD/WRC) in Switzerland (Fröhlich 2006,2003b,2000), which is compiled from multiple, cross-calibrated independent radiometric measurements since 1978 November 16.
3 Comparison of NSO-SPM and NSO-512 data
In this section we compare and intercalibrate magnetograms and continuum intensity images taken with the two instruments NSO-SPM and NSO-512. The overlap between the NSO-SPM and NSO-512 data observed in the same Fe I 8688  spectral line extends for about five months between November 28, 1992 and April 10, 1993. We have selected 22 NSO-SPM and NSO-512 magnetograms and the corresponding continuum images, which are of sufficiently good quality and were obtained within a relatively short time to each other (in order to avoid changes due to evolution, solar rotation, etc.). We use a similar comparison method as Jones et al. (2000) and Jones & Ceja (2001), see Sect. 3.1, but also an alternative comparison method described in Sect. 3.3.
spectral line extends for about five months between November 28, 1992 and April 10, 1993. We have selected 22 NSO-SPM and NSO-512 magnetograms and the corresponding continuum images, which are of sufficiently good quality and were obtained within a relatively short time to each other (in order to avoid changes due to evolution, solar rotation, etc.). We use a similar comparison method as Jones et al. (2000) and Jones & Ceja (2001), see Sect. 3.1, but also an alternative comparison method described in Sect. 3.3.
3.1 Histogram comparison
The official conversion factor by which NSO-SPM magnetograms need to be multiplied to make them compatible with NSO-512 data is 1.46. In order to check this, we have calculated, following the histogram comparison method of Jones et al. (2000) and Jones & Ceja (2001), the histogram equating tables for the 22 selected NSO-512 and NSO-SPM magnetograms (see also Wenzler et al. 2004, Sect. 3.1). Since Wenzler et al. (2004) obtained good agreement between VIRGO data and reconstructed total solar irradiance based on NSO-SPM magnetograms without multiplying the latter by this factor, we also employ the unaltered NSO-SPM data. Rather, we divide the NSO-512 magnetograms by the intercalibration factor before employing them for irradiance reconstructions.
In Fig. 6 the NSO-512 equating tables are plotted against the NSO-SPM equating tables for the 22 individual days between November 1992 and April 1993. A linear fit to the 22 histogram-equating curves has been computed. The resulting slope is 1.514 (see Table 1). As can be seen from Fig. 6, there is a considerable scatter from one day to the other, so that the exact choice of dates is relevant. It is also evident that the equating curves are not exactly linear so that the linear fit tends to underestimate the factor for small magnetogram signals and overestimate it for large signals.
 |
Figure 6:
Histogram-equating curves for 22 individual days, calculated with NSO-SPM and NSO-512 magnetograms. The dotted diagonal line represents the expectation values for identical NSO-SPM and NSO-512 magnetograms, the dashed line is a linear regression. |
| Open with DEXTER |
Table 1:
Average of linear fits to histogram equating curves for 22 days between November 28, 1992 and April 10, 1993 based on NSO-512 and NSO-SPM magnetograms.
If we divide the magnetic signals in all the NSO-512 magnetograms between 1974 and 1992 by a factor of 1.514, the slope of a regression to the resulting histogram equating curves is not exactly unity. If instead we look for a factor between the NSO-512 and NSO-SPM magnetograms, which gives, after dividing the NSO-512 signal, a slope close to unity, we arrive at a slightly larger factor of 1.63 (see Table 1). This seeming inconsistency results because the conversion between the two data types is only approximately linear. In order to learn more about the difference between the two data sets, we also use an alternative comparison method (see Sect. 3.3).
3.2 Identification of magnetic features and computation of histograms
Following the method of Wenzler et al. (2004) we now determine the facular distributions and identify the sunspot areas using the 22 selected NSO-512 and NSO-SPM magnetograms and continuum intensity images.
First, we divide the NSO-512 magnetograms by the official factor 1.46. We then rebin the NSO-512 data to the same pixel size as in the NSO-SPM data, i.e. from
 to
to
 pixels. Next, the individual NSO-SPM images (magnetograms and continuum images) are rotated to the time at which the NSO-512 images were recorded, to compensate for solar rotation.
pixels. Next, the individual NSO-SPM images (magnetograms and continuum images) are rotated to the time at which the NSO-512 images were recorded, to compensate for solar rotation.
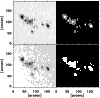 |
Figure 7:
Example of a sunspot group in an NSO-SPM continuum intensity image after removal of limb-darkening recorded on March 19, 1993 ( upper left). The same region in the corresponding NSO-512 continuum intensity image ( lower left). Note the jump in the continuum intensity due to the Sun's limb darkening and limited dynamic range of the data close to the location of the sunspots. The upper right frame represents the spot mask obtained from the sunpot region of the NSO-SPM continuum intensity image, the lower right frame from the NSO-512 continuum intensity image. In the NSO-SPM spot mask ( upper right) the umbral area is plotted white, while the penumbral area is grey. Since the NSO-512 continuum intensity images are not good enough to distinguish between umbrae and penumbrae, only entire spots are identified (white) in the NSO-512 spot mask ( lower right). |
| Open with DEXTER |
To identify sunspot umbrae and penumbrae we use continuum images. We follow Fligge et al. (2000b) and use a simple brightness threshold to distinguish between umbra, penumbra and the rest of the Sun. For NSO-SPM, the intensity images were corrected for limb-darkening effects following Neckel & Labs (1994). The brightness thresholds of umbrae and penumbrae are 0.70 and 0.92, respectively. Note that the umbral brightness threshold is somewhat larger than in our earlier analyses (0.64; Wenzler et al. 2005,2004). It provides a better agreement with published values of the ratio of umbral to total sunspot area (see Sect. 5.1 for details). The entries of the NSO-512 intensity images are integer values for each pixel ranging between 0 (outside the disk) and a maximum value m between 7 and 15. The extremely small dynamic range does not allow a useful correction of limb-darkening, since the observed limb-darkening profile in the NSO-512 intensity images has the contour of a step function, with noise introducing some irregularity (see Fig. 1 as an example). Therefore we cannot identify sunspot umbrae and penumbrae following the method of Fligge et al. (2000b) and we have had to develop an algorithm which allows us to identify the entire sunspot as follows (a separate identification of umbrae and penumbrae turned out to be too unreliable for these data). For each intensity level between the entries 1 and the maximum intensity level m we create a histogram of the intensity distribution
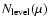 .
The
.
The 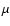 -values were binned linearly, with
-values were binned linearly, with
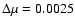 ,
resulting in a grid with 401 bins. For each level,
,
resulting in a grid with 401 bins. For each level, 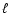 ,
the histogram has the largest population over a given
,
the histogram has the largest population over a given 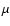 range where the quiet-Sun brightness
range where the quiet-Sun brightness
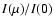 corresponds to
corresponds to 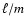 (Fig. 1). If, in addition to this ring (
(Fig. 1). If, in addition to this ring (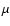 -band), pixels with brightness
-band), pixels with brightness 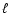 are found at larger
are found at larger 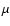 ,
then these are assigned to sunspot regions. This process is repeated for all
,
then these are assigned to sunspot regions. This process is repeated for all 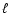 values, starting with 1 and going to m - 1 until we finally obtain the sunspot mask. As an example we show in Fig. 7 a region of the Sun with a field of view of about
values, starting with 1 and going to m - 1 until we finally obtain the sunspot mask. As an example we show in Fig. 7 a region of the Sun with a field of view of about
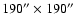 containing a sunspot group lying close to an intensity step in the NSO-512 data. The NSO-SPM continuum intensity image after removal of limb-darkening (left) recorded on March 19, 1993 and the corresponding mask with identified umbrae and penumbrae (right) are displayed in the upper row. The original NSO-512 intensity image (left) and the corresponding mask (right) are plotted in the lower row. In this case only entire spots can be identified. For the whole spot areas both NSO-SPM and NSO-512 data yield nearly identical masks. The same applies, if we consider the spot masks of the entire solar disk (see Fig. 8). Note that the NSO-SPM continuum image was recorded about 3 hours earlier than the NSO-512 image, so that the sunspot regions may have evolved slightly in the interval.
containing a sunspot group lying close to an intensity step in the NSO-512 data. The NSO-SPM continuum intensity image after removal of limb-darkening (left) recorded on March 19, 1993 and the corresponding mask with identified umbrae and penumbrae (right) are displayed in the upper row. The original NSO-512 intensity image (left) and the corresponding mask (right) are plotted in the lower row. In this case only entire spots can be identified. For the whole spot areas both NSO-SPM and NSO-512 data yield nearly identical masks. The same applies, if we consider the spot masks of the entire solar disk (see Fig. 8). Note that the NSO-SPM continuum image was recorded about 3 hours earlier than the NSO-512 image, so that the sunspot regions may have evolved slightly in the interval.
We now determine the facular fields and compare their distribution. We first identify the non-sunspot points above a threshold magnetogram signal which lies significantly above noise (3-4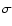 ). We introduce the same threshold in both data sets. After division by the factor of 1.46, the noise level of the corrected NSO-512 magnetograms,
). We introduce the same threshold in both data sets. After division by the factor of 1.46, the noise level of the corrected NSO-512 magnetograms, 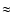 5.5 G, is of the same order as the NSO-SPM noise level. For the threshold we employ:
5.5 G, is of the same order as the NSO-SPM noise level. For the threshold we employ:
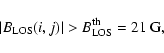 |
(1) |
where i and j are indices identifying the pixels,
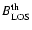 is the line-of-sight (LOS) component of the magnetic field threshold.
is the line-of-sight (LOS) component of the magnetic field threshold.
A visual inspection of masks displaying only facular pixels shows that the NSO-SPM and NSO-512 data coincide well. To compare the two data sets in more detail we create histograms of the spots and facular distributions following Wenzler et al. (2004), which will be discussed in Sect. 3.3. For spots we study histograms
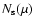 ,
while we consider the distribution
,
while we consider the distribution
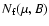 for faculae, where N is the number of pixels and
for faculae, where N is the number of pixels and
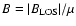 .
The factor
.
The factor 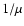 in B takes into account that a magnetogram underestimates the true flux in pixels close to the limb since facular and network fields on the Sun are mainly vertical (Martínez Pillet et al. 1997; Bernasconi 1997, cf. Solanki 1993) due to buoyancy (Schüssler 1986).
in B takes into account that a magnetogram underestimates the true flux in pixels close to the limb since facular and network fields on the Sun are mainly vertical (Martínez Pillet et al. 1997; Bernasconi 1997, cf. Solanki 1993) due to buoyancy (Schüssler 1986).
3.3 Comparison of the facular fields and sunspot areas
Here we compare histograms of the spot,
 ,
and facular,
,
and facular,
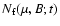 ,
distributions obtained from the NSO-SPM and NSO-512 data as described in Sect. 3.2. The spot and facular distributions are studied as a function of
,
distributions obtained from the NSO-SPM and NSO-512 data as described in Sect. 3.2. The spot and facular distributions are studied as a function of 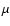 for each day individually and for the average over the selected 22 days (in which case we omit the time variable t). The facular distributions are in addition analysed as a function of the magnetic field strength B.
for each day individually and for the average over the selected 22 days (in which case we omit the time variable t). The facular distributions are in addition analysed as a function of the magnetic field strength B.
Figure 8 shows the NSO-SPM (dashed line) and NSO-512 (solid line) histograms of the spot area vs. 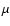 ,
,
 ,
deduced from continuum images recorded on March 19, 1993. The NSO-512 and NSO-SPM histograms agree very well with each other. This good agreement implies that firstly our algorithm is successful in identifying sunspots in NSO-512 continuum images and, secondly, for the chosen NSO-SPM thresholds not only are the average areas roughly the same, but also the location and distribution on the solar surface.
,
deduced from continuum images recorded on March 19, 1993. The NSO-512 and NSO-SPM histograms agree very well with each other. This good agreement implies that firstly our algorithm is successful in identifying sunspots in NSO-512 continuum images and, secondly, for the chosen NSO-SPM thresholds not only are the average areas roughly the same, but also the location and distribution on the solar surface.
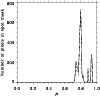 |
Figure 8:
Histogram of the spot mask vs. 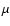 for March 19, 1993. Solid line represents NSO-512 data, the dashed line NSO-SPM data.
for March 19, 1993. Solid line represents NSO-512 data, the dashed line NSO-SPM data. 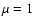 is the disk centre;
is the disk centre; 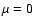 is the limb.
is the limb. |
| Open with DEXTER |
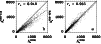 |
Figure 9:
a) Sunspot areas in millionths of the solar disk based on NSO-512 data for 1734 days between 1974 and 1992 vs. an independent composite record of sunspot areas. b) The same quantity, but now based on NSO-SPM data for 2055 days between 1992 and 2003 vs. the same independent composite record. The correlation coefficients, 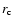 ,
are indicated. Solid lines represent expectation values for identical sunspot areas, the dashed lines are regressions. ,
are indicated. Solid lines represent expectation values for identical sunspot areas, the dashed lines are regressions. |
| Open with DEXTER |
In order to test whether we identify the correct total spot area in the NSO-512 and NSO-SPM data sets, we now compare all NSO-512 and NSO-SPM total daily sunspot areas in millionths of the solar disk,
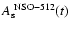 and
and
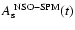 ,
with an independent sunspot area record. We use the composite data set
,
with an independent sunspot area record. We use the composite data set
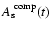 constructed by Balmaceda et al. (2005) based on an intercalibration between total daily sunspot areas collected by the Royal Greenwich Observatory (RGO) between 1874 and 1976, compiled in the Russian Stations Data (RSD) recorded between 1977 and 1984 and compiled at the Mount Wilson Solar Observatoy (MWO) between 1985 and 2003 (cf. Foster 2004). In Fig. 9
constructed by Balmaceda et al. (2005) based on an intercalibration between total daily sunspot areas collected by the Royal Greenwich Observatory (RGO) between 1874 and 1976, compiled in the Russian Stations Data (RSD) recorded between 1977 and 1984 and compiled at the Mount Wilson Solar Observatoy (MWO) between 1985 and 2003 (cf. Foster 2004). In Fig. 9
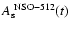 and
and
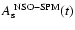 are plotted against
are plotted against
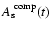 .
Linear fits to the dots (daily values) have been computed. The resulting slopes are
.
Linear fits to the dots (daily values) have been computed. The resulting slopes are
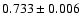 (NSO-512) and
(NSO-512) and
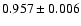 (NSO-SPM), respectively (see Table 2). The error bars are the formal errors of the regressions. The NSO-512 values are significantly (
(NSO-SPM), respectively (see Table 2). The error bars are the formal errors of the regressions. The NSO-512 values are significantly (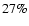 ), the NSO-SPM values only slightly (
), the NSO-SPM values only slightly (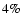 )
lower than the composite values. The NSO-SPM values agree very well with the observations. This means that the sunspot identification method of Fligge et al. (2000b) and the choice of the brightness threshold 0.92 (see Sect. 5.1) provide results that agree with widely used independent measurements when applied to NSO-SPM data. If we consider all days, the statistics are sufficiently good to show that the NSO-512 sunpost areas are too low. This means that the sunspot identification algorithm decribed in Sect. 3.2 misses some spot regions in the NSO-512 continuum images. We suspect that this is because smaller features, such as pores which generally exhibit a small contrast, are often not identifiable because of the low quality of the NSO-512 continuum images. In order to test this hypothesis and to be able to correct this deficit, we have identified pores using the NSO-SPM intensity images,
)
lower than the composite values. The NSO-SPM values agree very well with the observations. This means that the sunspot identification method of Fligge et al. (2000b) and the choice of the brightness threshold 0.92 (see Sect. 5.1) provide results that agree with widely used independent measurements when applied to NSO-SPM data. If we consider all days, the statistics are sufficiently good to show that the NSO-512 sunpost areas are too low. This means that the sunspot identification algorithm decribed in Sect. 3.2 misses some spot regions in the NSO-512 continuum images. We suspect that this is because smaller features, such as pores which generally exhibit a small contrast, are often not identifiable because of the low quality of the NSO-512 continuum images. In order to test this hypothesis and to be able to correct this deficit, we have identified pores using the NSO-SPM intensity images,
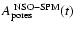 by searching for isolated features that are darker than the threshold for the penumbra, but not as dark as the umbral threshold. Such features are generally found to have a small size and to look like pores. Figure 10 shows the daily sunspot areas in millionths of the solar disk,
by searching for isolated features that are darker than the threshold for the penumbra, but not as dark as the umbral threshold. Such features are generally found to have a small size and to look like pores. Figure 10 shows the daily sunspot areas in millionths of the solar disk,
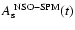 ,
vs. the same quantity but now without the pores,
,
vs. the same quantity but now without the pores,
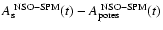 .
The resulting correlation coefficient is
.
The resulting correlation coefficient is
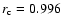 and the slope of the linear fit to the dots (daily values) is
and the slope of the linear fit to the dots (daily values) is
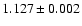 (see Table 2). Based on this result we correct all NSO-512 spot histograms in that we multiply the sunspot areas entries by the factor 1.127. This corresponds to assuming that the area covered by pores on a given day is proportional to the area covered by sunspots. This factor is smaller than the missing area factor
0.957/0.733 = 1.306 (see the slopes in Table 2) but may nevertheless be apropriate for producing the correct darkening due to sunspots and pores. This is because we assume a fixed umbra to penumbra area ratio for the NSO-512 data (since this ratio cannot be determined from the data) and use the same brightness for all dark features. In reality, however, pores are closer in brightness to sunspot penumbra than to umbrae and small sunspots are not as dark as large spots (Collados et al. 1994; cf. Solanki 2003). The use of this "pore''-factor does not affect the results significantly, although the use of this factor increases the agreement between the modelled and measured irradiance (increase in correlation by 0.01-0.03).
(see Table 2). Based on this result we correct all NSO-512 spot histograms in that we multiply the sunspot areas entries by the factor 1.127. This corresponds to assuming that the area covered by pores on a given day is proportional to the area covered by sunspots. This factor is smaller than the missing area factor
0.957/0.733 = 1.306 (see the slopes in Table 2) but may nevertheless be apropriate for producing the correct darkening due to sunspots and pores. This is because we assume a fixed umbra to penumbra area ratio for the NSO-512 data (since this ratio cannot be determined from the data) and use the same brightness for all dark features. In reality, however, pores are closer in brightness to sunspot penumbra than to umbrae and small sunspots are not as dark as large spots (Collados et al. 1994; cf. Solanki 2003). The use of this "pore''-factor does not affect the results significantly, although the use of this factor increases the agreement between the modelled and measured irradiance (increase in correlation by 0.01-0.03).
Table 2:
Daily sunspot areas in millionths of the solar disk based on NSO-512 data (1974-2003), on NSO-SPM data (1992-2003) and on an independent composite sunspot area data set (1974-2003).
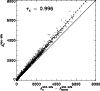 |
Figure 10:
Sunspot areas in millionths of the solar disk based on NSO-SPM data for 2055 individual days between 1992 and 2003 vs. the same quantity but now excluding pore areas. |
| Open with DEXTER |
 |
Figure 11:
22-day averaged histograms of the facular distributions. a) The number of facular points vs.
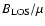 ,
b) the same quantity vs. ,
b) the same quantity vs. 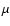 .
Solid lines represent NSO-512 data, dashed lines NSO-SPM data. .
Solid lines represent NSO-512 data, dashed lines NSO-SPM data. |
| Open with DEXTER |
 |
Figure 12:
Relative difference,
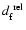 ,
of the facular magnetic distributions plotted vs. ,
of the facular magnetic distributions plotted vs.
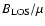 a) and vs.
a) and vs. 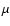 b). Positive values indicate that NSO-512 data show more pixels with signal at that
b). Positive values indicate that NSO-512 data show more pixels with signal at that
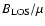 or
or 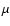 value. The solid lines represent relative differences based on histograms averaged over 22 days between 1992 November 28 and 1993 April 10. Dashed lines indicate
value. The solid lines represent relative differences based on histograms averaged over 22 days between 1992 November 28 and 1993 April 10. Dashed lines indicate
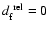 . . |
| Open with DEXTER |
The "pore'' area added to the sunspot histograms is next removed from the NSO-512 facular histograms. Since we know only the 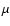 dependence of the pore pixels (not the exact position on the solar disk), we remove the entries of the facular histograms with the highest B values in the
dependence of the pore pixels (not the exact position on the solar disk), we remove the entries of the facular histograms with the highest B values in the 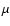 bins in which the pores are located.
bins in which the pores are located.
Next we compare in Fig. 11 the NSO-SPM and NSO-512 histograms of the facular distributions after integration over 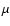 ,
,
 ,
and, alternatively, after integration over
,
and, alternatively, after integration over
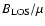 ,
,
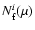 ,
after averaging over the 22 selected days, where i stands for NSO-SPM or NSO-512. The differences between the NSO-SPM and NSO-512 facular histograms are significant. At small
,
after averaging over the 22 selected days, where i stands for NSO-SPM or NSO-512. The differences between the NSO-SPM and NSO-512 facular histograms are significant. At small
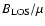 values more NSO-512 pixels show a signal, while more NSO-SPM pixels show a signal with
values more NSO-512 pixels show a signal, while more NSO-SPM pixels show a signal with
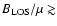 75 G. The latter result could reflect the Zeeman saturation of the NSO-512 magnetograph at higher field strengths (e.g. Frazier & Stenflo 1972), since fields in regions with higher filling factors tend to be somewhat stronger (Rüedi et al. 1992; Stenflo & Harvey 1985). The SPM does not suffer from this effect. The excess of
75 G. The latter result could reflect the Zeeman saturation of the NSO-512 magnetograph at higher field strengths (e.g. Frazier & Stenflo 1972), since fields in regions with higher filling factors tend to be somewhat stronger (Rüedi et al. 1992; Stenflo & Harvey 1985). The SPM does not suffer from this effect. The excess of
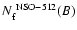 at small B may partly be due to the presence of electronic noise in these magnetograms (see Sect. 2.1), which we cannot distinguish from a real signal. When plotted vs.
at small B may partly be due to the presence of electronic noise in these magnetograms (see Sect. 2.1), which we cannot distinguish from a real signal. When plotted vs. 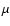 more NSO-SPM pixels lie above the threshold at small
more NSO-SPM pixels lie above the threshold at small 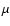 values, while more NSO-512 pixels lie above the threshold at
values, while more NSO-512 pixels lie above the threshold at
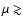 0.65.
0.65.
To highlight the difference between the 22-day averaged NSO-SPM and NSO-512 histograms, we compute and plot in Fig. 12 the relative differences
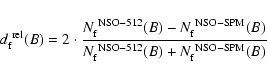 |
(2) |
and
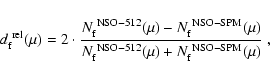 |
(3) |
cf. Eqs. (2) and (3) of Wenzler et al. (2004). Note that the official conversion factor of 1.46 was applied before this comparison was carried out. The complex relationship between the NSO-SPM and NSO-512 magnetograms indicated by Fig. 11 and demonstrated by Fig. 12 implies that it is possible to convert NSO-SPM magnetograms into NSO-512 ones or vice versa using a constant calibration factor only very approximately. The relative difference of the number of facular NSO-512 and NSO-SPM pixels integrated over all magnetic field strengths and  values is
values is
![\begin{displaymath}\Delta N_{\rm f}^{\rm ~rel} =
2\cdot\frac{\sum\limits_{B}[N...
...f}^{\rm ~NSO-512}(B)+N_{\rm f}^{\rm ~NSO-SPM}(B)]}
= 0.046\ ,
\end{displaymath}](/articles/aa/full/2006/47/aa5752-06/img79.gif) |
(4) |
i.e. there are 4.6% more facular NSO-512 pixels. However, the relative magnetic flux difference
![\begin{displaymath}\Delta \phi_{\rm f}^{\rm ~rel} =
2\cdot\frac{\sum\limits_{B...
...rm ~NSO-512}(B)+N_{\rm f}^{\rm ~NSO-SPM}(B)]}
= -0.093 \rm\ ,
\end{displaymath}](/articles/aa/full/2006/47/aa5752-06/img80.gif) |
(5) |
so that the NSO-SPM flux actually exceeds the NSO-512 flux by about 9%. If we divide the NSO-512 magnetograms by a factor of 1.53 instead of the standard factor of 1.46 then we obtain practically the same number of NSO-512 and NSO-SPM facular pixels (
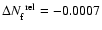 ), if we divide by 1.38 the NSO-512 and NSO-SPM facular magnetic fluxes are similar (
), if we divide by 1.38 the NSO-512 and NSO-SPM facular magnetic fluxes are similar (
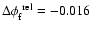 ).
).
In summary, we find conversion factors ranging between 1.38 and 1.63 depending on the quantity being compared and the employed technique. This is not surprising, given the complexity of the relationship between the two data sets suggested by Fig. 12. It is encouraging that the official conversion factor of 1.46 lies within the range found here. For the reconstruction of variations of total solar irradiance based on NSO-512 data we therefore first use the standard factor of 1.46, i.e. we divide the NSO-512 magnetograms by this constant factor (see Sect. 5 and 6.1). Then in Sect. 6.2 we vary this factor within the range 1.38-1.63 in order to find the best correlation with the measurements.
4 TSI reconstructions based on NSO-SPM data
4.1 Model based on NSO-SPM data
To reconstruct variations of total solar irradiance we use
the same model as Fligge et al. (2000b,a), Krivova et al. (2003) and Wenzler et al. (2005,2004). In this SATIRE model (Spectral And Total Irradiance REconstructions, Solanki et al. 2005) we describe the solar photosphere by four components, namely quiet Sun (q), sunspot umbrae (u), sunspot penumbrae (p) and faculae (f), whose time independent intensities
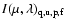 depend on the heliocentric angle
depend on the heliocentric angle 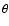 (
(
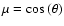 )
and the wavelength
)
and the wavelength 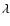 .
The intensities
.
The intensities
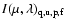 were calculated following Unruh et al. (1999). The variation of the reconstructed solar irradiance comes from the evolution in time of the fraction of the solar surface occupied by each component. Since the procedure for reconstructing the irradiance differs in detail for the NSO-512 and NSO-SPM data, we describe them separately.
were calculated following Unruh et al. (1999). The variation of the reconstructed solar irradiance comes from the evolution in time of the fraction of the solar surface occupied by each component. Since the procedure for reconstructing the irradiance differs in detail for the NSO-512 and NSO-SPM data, we describe them separately.
We use daily NSO-SPM full-disk magnetograms and the corresponding continuum intensity images to find the number of pixels, N, for every 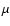 -value occupied by each component at a given time t following Wenzler et al. (2005,2004). The higher umbral threshold of 0.7 (see Sect. 3.2) implies an increased size of the umbra, at the cost of the penumbra. In order to maintain the contrast of sunspots as a whole we have increased the effective temperature of the penumbral model atmosphere by 50 K to
-value occupied by each component at a given time t following Wenzler et al. (2005,2004). The higher umbral threshold of 0.7 (see Sect. 3.2) implies an increased size of the umbra, at the cost of the penumbra. In order to maintain the contrast of sunspots as a whole we have increased the effective temperature of the penumbral model atmosphere by 50 K to
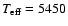 K. The reconstructed TSI values are very close to those from Wenzler et al. (2005) and are obtained from the relation:
K. The reconstructed TSI values are very close to those from Wenzler et al. (2005) and are obtained from the relation:
![\begin{displaymath}\begin{array}{rll}
S_{\rm NSO-SPM}(\lambda,t) = \sum\limits_...
...(\mu,B;t) \alpha_{\rm f}(\mu,B)]) I_q(\mu;\lambda)]
\end{array}\end{displaymath}](/articles/aa/full/2006/47/aa5752-06/img88.gif) |
(6) |
where
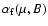 is used to convert the magnetogram signal, B, into the corresponding filling factor using Eq. (6) from Wenzler et al. (2004). With increasing B the magnetic filling factor and hence the contribution of the facular component to a given magnetogram pixel increases. A limiting value,
is used to convert the magnetogram signal, B, into the corresponding filling factor using Eq. (6) from Wenzler et al. (2004). With increasing B the magnetic filling factor and hence the contribution of the facular component to a given magnetogram pixel increases. A limiting value,
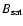 ,
is introduced beyond which the pixel is completely filled by faculae (and described purely by the facular atmosphere, for details see Fligge et al. 2000b).
,
is introduced beyond which the pixel is completely filled by faculae (and described purely by the facular atmosphere, for details see Fligge et al. 2000b).
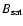 takes into account that magnetic features in regions with larger filling factors are less bright than their counterparts in regions with smaller magnetic filling (Solanki 1986; Solanki & Stenflo 1984). The value of
takes into account that magnetic features in regions with larger filling factors are less bright than their counterparts in regions with smaller magnetic filling (Solanki 1986; Solanki & Stenflo 1984). The value of
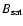 is the free parameter in our model.
is the free parameter in our model.
 gives the total number of pixels having a given
gives the total number of pixels having a given 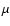 .
.
4.2 Results for cycles 22 and 23
Wenzler et al. (2005) have reconstructed the total solar irradiance over the whole operational period of NSO-SPM, i.e. from near the maximum of cycle 22 to the declining phase of cycle 23. The resulting correlation coefficient between the reconstructed and measured total solar irradiance (version 30 of the PMOD composite, Fröhlich 2003b) is 0.94. In this paper we employ the newest PMOD composite record (version 41). Since the difference between the two versions is mainly restricted to cycle 21, the correlation coefficient remains unchanged (see also Table 3).
Jones et al. (2003) also used NSO-SPM data in order to reconstruct the irradiance. In contrast to us they did not use model atmospheres to describe the contributions of different solar features to irradiance variations, but rather divided the solar surface into nine different types of features and carried out a principle components analysis. Unlike Wenzler et al. (2005) and the work described in this paper they were unable to reproduce the irradiance variations described by the PMOD composite over the analysed period of time. This may have to do with the fact that they compared with an older version of the PMOD composite (version 23, compared with version 41 that we employ). The older composite displays a steeper rise in irradiance into cycle 23 than the newer versions. This is mainly due to an underestimation of the sensitivity increase of DIARAD/VIRGO in the earlier versions (before 6) and explains the positive trend of the older versions since the start of VIRGO on SoHO. Thus the PMOD composites based on VIRGO versions 6 an higher would probably be closer to their reconstruction.
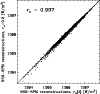 |
Figure 13:
Modelled total solar irradiance based on NSO-SPM data calculated with time independent ratio of umbral to total sunspot area
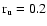 vs. modelled TSI based on NSO-SPM data calculated with time-dependent ratios of umbral to total sunspot area
vs. modelled TSI based on NSO-SPM data calculated with time-dependent ratios of umbral to total sunspot area
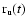 for 2055 individual days between 1992 and 2003 (see text for details). The correlation coefficient,
for 2055 individual days between 1992 and 2003 (see text for details). The correlation coefficient, 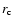 ,
is indicated. The solid diagonal line represents the expectation values for identical reconstructions, a regression (dashed line) is hardly distinguishable from it. ,
is indicated. The solid diagonal line represents the expectation values for identical reconstructions, a regression (dashed line) is hardly distinguishable from it. |
| Open with DEXTER |
5 TSI reconstructions based on NSO-512 data
5.1 Model based on NSO-512 data
Since we were only able to identify whole sunspots in the NSO-512 continuum intensity images, we need to make some assumption regarding the umbra/penumbra area ratio. From the umbra to total spot area ratio evaluated using the NSO-SPM data we obtained an average ratio of umbral to total sunspot area,
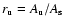 of 0.2 (Wenzler et al., in preparation).
of 0.2 (Wenzler et al., in preparation).
As a next step we have calculated and compared the TSI reconstructions based on the analysed NSO-SPM data using the real umbra/penumbra area ratio (Sect. 4.2) and using the constant value of
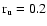 following Eq. (7). In Fig. 13 the reconstructed TSI based on NSO-SPM data using
following Eq. (7). In Fig. 13 the reconstructed TSI based on NSO-SPM data using
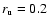 is plotted against the irradiance reconstructed using time dependent ratios,
is plotted against the irradiance reconstructed using time dependent ratios,
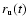 .
The correlation coefficient between the two models is
.
The correlation coefficient between the two models is
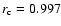 .
Therefore we can now calculate the TSI based on NSO-512 data as follows:
.
Therefore we can now calculate the TSI based on NSO-512 data as follows:
![\begin{displaymath}\begin{array}{rll}
S_{\rm NSO-512}(\lambda,t) = \sum\limits_...
...(\mu,B;t) \alpha_{\rm f}(\mu,B)]) I_q(\mu;\lambda)]
\end{array}\end{displaymath}](/articles/aa/full/2006/47/aa5752-06/img97.gif) |
(7) |
where
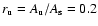 .
.
5.2 Results for cycles 21 and 22
The reconstructed TSI based on NSO-512 data using the standard correction factor for the magnetograms of 1.46 for 1734 days between August 1974 and May 1992 is plotted in the top panel of Fig. 14 (filled circles). The solid curve represents the PMOD composite record of total solar irradiance (version 41, Fröhlich 2006) since 1978 November 16. The two middle and two lower panels display extracts on an enlarged scale at different phases of the solar cycles 21 and 22, respectively. The enlargements I and IV reveal that the short-term variations of the total solar irradiance are well reproduced in both maxima of the solar cycles 21 and 22. Enlargements II and III show, however, that the agreement is not so optimal at all times. In both these enlargements the reconstructed TSI values generally lie too low compared with the measurements. The correlation coefficient between the reconstructed TSI values and the measured irradiance (PMOD composite) is
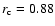 .
.
![\begin{figure}
\par\includegraphics[width=17cm]{5752fi14.eps} \end{figure}](/articles/aa/full/2006/47/aa5752-06/Timg100.gif) |
Figure 14:
PMOD composite record of total solar irradiance (solid line) and reconstructed daily TSI based on NSO-512 data (filled circles, connected by the dotted curve when there are no data gaps) for 1734 days between 1974 and 1992, i.e. from the minimum of cycle 21 to the maximum of cycle 22 (top panel). The middle and lower panels show enlargements of four shorter intervals at different activity levels. The times corresponding to these zoom-ins are marked in the top panel by the double-headed arrows under the roman numerals. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=16.7cm]{5752fi15.eps} \end{figure}](/articles/aa/full/2006/47/aa5752-06/Timg101.gif) |
Figure 15:
The five upper panels show the same as Fig. 14, but now with reconstructed daily TSI based on both NSO-512 and NSO-SPM data between 1974 and 2003. The bottom panel shows the difference between the reconstructed total solar irradiance based on KP (NSO-512 and NSO-SPM) data and the PMOD composite measurements. The solid line indicates difference = 0, the dashed line is a regression. The dotted vertical lines indicate periods, when the individual data sets from HF, AI & AII (ACRIM I & II) and V (VIRGO) were used for the composite. |
| Open with DEXTER |
6 TSI reconstructions in cycles 21, 22 and 23
In this section we compare the TSI reconstructed over the whole period over which NSO/KP data are available with the PMOD TSI composite record described in Sect. 2.4. First, in Sect. 6.1, we compare the reconstructed variations of the total solar irradiance based on the original NSO-SPM magnetograms and on the NSO-512 magnetograms, which were multiplied by the official conversion factor of 1/1.46 (henceforth referred to as the standard corrections to magnetograms; see Sect. 3 for details) with the PMOD composite. Then, in Sect. 6.2, we optimise the reconstructions to the PMOD irradiance composite by allowing the conversion factor between the NSO-SPM and NSO-512 data to vary between 1.38 and 1.63, i.e. the range found from our analysis. Note that a single
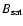 value is in all cases determined for the full period of time that KP data are available, i.e. between 1978 November 16 and 2003 September 21, such that the model best reproduces the full considered TSI composite.
value is in all cases determined for the full period of time that KP data are available, i.e. between 1978 November 16 and 2003 September 21, such that the model best reproduces the full considered TSI composite.
6.1 Standard reconstruction: Comparison with PMOD composite
We now compare the results of the TSI reconstructions based on NSO-SPM and standard corrected NSO-512 magnetograms with the PMOD composite record of Fröhlich (2006). In Fig. 15 the filled circles in the five upper panels are the reconstructed variations of the total solar irradiance for 3789 days between August 1974 and September 2003, i.e. from the minimum of cycle 21 to the declining phase of cycle 23. When there are no data gaps the filled circles are connected by dotted lines. The PMOD composite of TSI measurements (version 41; Fröhlich 2006) is represented by the solid line. The levels of the reconstructed irradiance during the three minima of the solar cycles 21-23 are similar. The PMOD composite, which has a negligible trend between the solar minima of the cycles 22 and 23, shows the same behaviour. The correlation coefficient between the model and the measurements is
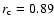 (Fig. 16). The solid line in Fig. 16 represents the expectation value for a perfect model fit and the almost overlapping dashed line represents the linear regression to the dots which represent daily values. The relatively large scatter is partly due to the decreased quality of the reconstructions in the earlier period, i.e. the noticeably lower quality of the NSO-512 data, but also gets some contribution from the lower stability of earlier TSI measurements. In the bottom panel of Fig. 15 we plot the difference between the reconstructed total solar irradiance and the PMOD composite measurements. The dots are daily values and the thick dashed line is a regression. The NSO-512 values (1978-1992) are scattered much more around the regression line than those based on the NSO-SPM data (1992-2003). The increased scatter during the maximum of cycles 21 and 22 relative to cycle 23 is evident. In addition, the general trend with time suggests a slightly different trend in the reconstruction than in the data. The reconstructed TSI values are somewhat higher than the PMOD measurements at earlier times. The trend is present mainly in the maxima, while model and measurements agree relatively well during the 2 minima. This suggests that the trend seen in the lower panel of Fig. 15 is due to the remaining uncertainty in the correction factor by which we divide the NSO-512 magnetograms and its non-linearity as seen in Fig. 6 and discussed in Sect. 3 (see also Sect. 6.2 for further details).
(Fig. 16). The solid line in Fig. 16 represents the expectation value for a perfect model fit and the almost overlapping dashed line represents the linear regression to the dots which represent daily values. The relatively large scatter is partly due to the decreased quality of the reconstructions in the earlier period, i.e. the noticeably lower quality of the NSO-512 data, but also gets some contribution from the lower stability of earlier TSI measurements. In the bottom panel of Fig. 15 we plot the difference between the reconstructed total solar irradiance and the PMOD composite measurements. The dots are daily values and the thick dashed line is a regression. The NSO-512 values (1978-1992) are scattered much more around the regression line than those based on the NSO-SPM data (1992-2003). The increased scatter during the maximum of cycles 21 and 22 relative to cycle 23 is evident. In addition, the general trend with time suggests a slightly different trend in the reconstruction than in the data. The reconstructed TSI values are somewhat higher than the PMOD measurements at earlier times. The trend is present mainly in the maxima, while model and measurements agree relatively well during the 2 minima. This suggests that the trend seen in the lower panel of Fig. 15 is due to the remaining uncertainty in the correction factor by which we divide the NSO-512 magnetograms and its non-linearity as seen in Fig. 6 and discussed in Sect. 3 (see also Sect. 6.2 for further details).
The correlation coefficients between the reconstructed and measured irradiance (PMOD composite measurements) during the NSO-512 time period (1978-1992), the NSO-SPM time period (1992-2003) and the whole period over which KP and composite data are available (1978-2003) as well as the slopes and 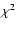 of the linear regressions (see Fig. 16 for the whole period of time) are listed under "Standard Reconstructions'' in Table 3. We find that the correlation coefficient,
of the linear regressions (see Fig. 16 for the whole period of time) are listed under "Standard Reconstructions'' in Table 3. We find that the correlation coefficient, 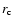 ,
is lower for the NSO-512 time period than for the NSO-SPM period, which is no surprise taking into account the lower quality of the NSO-512 data. This has the effect of diminishing
,
is lower for the NSO-512 time period than for the NSO-SPM period, which is no surprise taking into account the lower quality of the NSO-512 data. This has the effect of diminishing 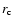 for the whole considered period of time. Note that we use the same value of the free parameter
for the whole considered period of time. Note that we use the same value of the free parameter
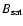 for the whole period (see Table 3 under Standard Reconstructions). Note that
for the whole period (see Table 3 under Standard Reconstructions). Note that
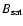 was chosen to maximize the correspondence with the whole TSI composite. Slightly different choices lead to improved correspondence over the considered subintervals, e.g.: 1978-1992 (
was chosen to maximize the correspondence with the whole TSI composite. Slightly different choices lead to improved correspondence over the considered subintervals, e.g.: 1978-1992 (
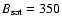 G,
G,
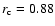 ,
slope =
,
slope =
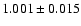 ,
,
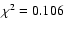 ).
).
6.2 TSI reconstruction with optimized factor between NSO-512 and NSO-SPM
In this section we have repeated the analysis described in Sect. 6.1, but now allowing the conversion factor between the NSO-SPM and NSO-512 data, i.e. the factor by which the NSO-512
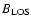 values have to be divided in order to make them compatible with NSO-SPM values, to vary within its range of uncertainty, i.e. between 1.38 and 1.63. Thus we have introduced another, although restricted free parameter to our SATIRE model in order to optimise the reconstructions to the PMOD composite. Note that both free parameters, the conversion factor and the
values have to be divided in order to make them compatible with NSO-SPM values, to vary within its range of uncertainty, i.e. between 1.38 and 1.63. Thus we have introduced another, although restricted free parameter to our SATIRE model in order to optimise the reconstructions to the PMOD composite. Note that both free parameters, the conversion factor and the
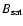 value, are fixed for the whole period for which TSI is reconstructed.
value, are fixed for the whole period for which TSI is reconstructed.
To best reproduce the PMOD composite irradiance time series (i.e. achieve the highest 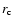 and lowest
and lowest 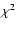 ), we need a slightly higher conversion factor of 1.6 compared with the official factor of 1.46 (see column 2 of Table 3).
), we need a slightly higher conversion factor of 1.6 compared with the official factor of 1.46 (see column 2 of Table 3).
Figure 17 shows the difference between the reconstructed total solar irradiance with optimized conversion factor and the PMOD TSI composite. In the comparison the regression line is very close to 0 for the whole period. In Fig. 18 we have plotted the reconstructed value based on corrected NSO-512 (factor 1.6) and NSO-SPM data against the measured irradiance for the full period of time for which both the TSI and the KP data are available. The resulting correlation coefficient is
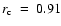 .
.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{5752fi16.eps} \end{figure}](/articles/aa/full/2006/47/aa5752-06/Timg107.gif) |
Figure 16:
Modelled total solar irradiance based on KP (NSO-512 and NSO-SPM) data vs. the PMOD TSI composite. The correlation coefficient, 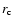 ,
is indicated. The solid diagonal line represents the expectation values for a perfect model fit, the dashed line is a regression. ,
is indicated. The solid diagonal line represents the expectation values for a perfect model fit, the dashed line is a regression. |
| Open with DEXTER |
7 Conclusions
We have extended the SATIRE (Spectral And Total Irradiance REconstructions) model back to the year 1974 using NSO/KPVT 512-channel Diode Array Magnetograph data. We have first compared these magnetograms and the corresponding continuum images with those obtained by the NSO/KPVT spectromagnetograph (SPM), in order to intercalibrate the magnetograms from the two instruments, needed before the NSO-512 data can be used to reconstruct total solar irradiance variations.
We find that a constant factor describes only approximately the complex relationship between the NSO-512 and NSO-SPM magnetograms. Such a factor depends on the magnetogram signal and 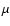 value (Fig. 12). Depending on the exact technique used to compare the magnetograms from the two instruments we obtain average factors ranging between 1.38 and 1.63. The older NSO-512 data also exhibit artifacts and systematic errors whose correction was started recently (Arge et al. 2002) and is still in progress (J. W. Harvey and H. P. Jones, priv. comm.). We have shown that a single correction factor serves as a reasonable first approximation. We apply these corrections and the same magnetic threshold for the noise level prior to carrying out the reconstructions.
value (Fig. 12). Depending on the exact technique used to compare the magnetograms from the two instruments we obtain average factors ranging between 1.38 and 1.63. The older NSO-512 data also exhibit artifacts and systematic errors whose correction was started recently (Arge et al. 2002) and is still in progress (J. W. Harvey and H. P. Jones, priv. comm.). We have shown that a single correction factor serves as a reasonable first approximation. We apply these corrections and the same magnetic threshold for the noise level prior to carrying out the reconstructions.
![\begin{figure}
\par\includegraphics[width=17cm]{5752fi17.eps} \end{figure}](/articles/aa/full/2006/47/aa5752-06/Timg108.gif) |
Figure 17:
The same as the bottom panel of Fig. 15, but now for the TSI reconstruction with optimized factor between NSO-512 and NSO-SPM
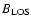 values.
values. |
| Open with DEXTER |
Table 3:
Correlation coefficients, 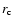 ,
slopes and
,
slopes and 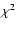 of the linear fits to the scatter plots of modelled total solar irradiance based on NSO-512 and NSO-SPM data vs. PMOD composite measurements for different periods. The reconstructed TSI values are calculated with different conversion factors between NSO-512 and NSO-SPM magnetograms in the upper and lower halves of the table.
of the linear fits to the scatter plots of modelled total solar irradiance based on NSO-512 and NSO-SPM data vs. PMOD composite measurements for different periods. The reconstructed TSI values are calculated with different conversion factors between NSO-512 and NSO-SPM magnetograms in the upper and lower halves of the table.
We have compared the TSI reconstructed between 1974 and 2003 with the PMOD composite of measured TSI. We find that our model, based on the assumption that the solar irradiance changes are entirely caused by the evolution of the solar surface magnetic fields, simultaneously reproduces the irradiance in all three cycles 21-23 as represented by the PMOD composite. The correlation coefficient between data and model for the whole period of time is
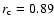 if we use the "official'' NSO-512/NSO-SPM conversion factor of 1.46. This implies that for this conversion factor a fraction of
if we use the "official'' NSO-512/NSO-SPM conversion factor of 1.46. This implies that for this conversion factor a fraction of
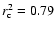 of the TSI variations over the last three solar cycles is due to the magnetic field at the solar surface. Yet better agreement (
of the TSI variations over the last three solar cycles is due to the magnetic field at the solar surface. Yet better agreement (
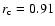 ,
,
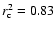 )
is achieved if we employ a conversion factor of 1.6, which is well within the allowed range (1.38-1.63). The true fraction is expected to be higher because, e.g., the imperfect employed model atmospheres degrade the quality of the reconstruction. Furthermore, the employed magnetograms contain noise and instrumental artifacts which lower the quality of the reconstruction. The importance of this point is underlined by the fact that the correlation coefficient obtained from the reconstruction employing the better SPM data is 0.94, while is only 0.88 when using the NSO-512 data (with space-based MDI data the correlation coefficient is even higher, 0.96). A final reason why the model underestimates the magnetic contribution to TSI variations lies in the lower quality of earlier TSI measurements and the uncertainty in producing a composite from TSI data recorded by different instruments.
)
is achieved if we employ a conversion factor of 1.6, which is well within the allowed range (1.38-1.63). The true fraction is expected to be higher because, e.g., the imperfect employed model atmospheres degrade the quality of the reconstruction. Furthermore, the employed magnetograms contain noise and instrumental artifacts which lower the quality of the reconstruction. The importance of this point is underlined by the fact that the correlation coefficient obtained from the reconstruction employing the better SPM data is 0.94, while is only 0.88 when using the NSO-512 data (with space-based MDI data the correlation coefficient is even higher, 0.96). A final reason why the model underestimates the magnetic contribution to TSI variations lies in the lower quality of earlier TSI measurements and the uncertainty in producing a composite from TSI data recorded by different instruments.
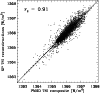 |
Figure 18:
The same as Fig. 16, but now for the TSI reconstruction with optimized factor between NSO-512 and NSO-SPM
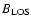 values.
values. |
| Open with DEXTER |
Improvements to the reconstructions can be achieved using magnetograms with higher sensitivity, such as those now being provided by the Synoptic Optical Long-term Investigations of the Sun (SOLIS) instrument at Kitt Peak (Harvey et al. 2003,2004). These magnetograms also show the weaker fields (weaker network and internetwork fields) not visible in the NSO-512 and NSO-SPM data. The advantages are particularly evident near the limb since the magnetograms used here missed even some of the stronger network elements close to the limb. These fields are nearly vertically oriented, so that only very sensitive line-of-sight magnetograms see them above the noise. SOLIS has the additional advantage that it measures vector magnetic fields, which also helps to detect the nearly vertical fields near the limb, as well as nearly horizontal fields at disk centre.
Finally, we find that the levels of the reconstructed irradiance during the three minima ahead of the solar cycles 21-23 are very similar. The similarity of the latter two has been reported by Fröhlich (2003a), but the minimum before cycle 21 occured prior to the start of TSI measurements, so that this is a new result obtained from the reconstructions.
Acknowledgements
We thank C. N. Arge, J. W. Harvey and H. P. Jones for providing the photospheric magnetic flux data and information on the NSO-512 and NSO-SPM data, Y.C. Unruh for providing the intensities of the model atmospheres and for helpful comments on the manuscript, L. Balmaceda for providing the sunspot area composite data set and M. Fligge and D.M. Fluri for helpful discussions. The work of T. Wenzler was carried out under Polyproject "Variability of the Sun and Global Climate'' at ETH Zurich. The excellent working conditions and the generous support are herewith gratefully acknowledged. This work was partly supported by the Deutsche Forschungsgemeinschaft, DFG project number SO 711/1-1.
- Arge,
C. N., Hildner, E., Pizzo, V. J., & Harvey,
J. W. 2002, J. Geophys. Res., 107, 16 [CrossRef] (In the text)
-
Balmaceda, L., Solanki, S. K., & Krivova, N. A. 2005,
Mem. S. A. It., 76, 929 [NASA ADS] (In the text)
-
Bernasconi, P. N. 1997, Stokes Vector-Polarimetry: Observation
and Analysis of Solar Magnetic Fields, Ph. D. Thesis, ETH,
Zurich
-
Collados, M., Martínez Pillet, V., Ruiz Cobo, B., del Toro
Iniesta, J. C., & Vázquez, M. 1994, A&A, 291,
622 [NASA ADS] (In the text)
-
Fligge, M., Solanki, S. K., Meunier, N., & Unruh,
Y. C. 2000a, in The Solar Cycle and Terrestrial Climate, ed.
A. Wilson, ESA Publ. SP-463, 117
-
Fligge, M., Solanki, S. K., & Unruh, Y. C. 2000b,
A&A, 353, 380 [NASA ADS] (In the text)
- Foster,
S. S. 2004, Ph. D. Thesis, University of Southampton (School
of Physics and Astronomy)
(In the text)
-
Frazier, E. N. & Stenflo, J. O. 1972,
Sol. Phys., 27, 330 [NASA ADS] [CrossRef] (In the text)
-
Fröhlich, C. 2000, Space Sci. Rev., 94, 15 [NASA ADS] [CrossRef]
-
Fröhlich, C. 2003a, Metrologia, 40, 60 [CrossRef] (In the text)
-
Fröhlich, C. 2003b, in Solar Variability as an Input to the
Earth's Environment, ed. A. Wilson, ESA Publ. SP-535, 183
(In the text)
-
Fröhlich, C. 2006, Space Sci. Rev., in press, DOI:
10.1007/s11214-006-9046-5
-
Fröhlich, C., Crommelynck, D., Wehrli, C., et al. 1997,
Sol. Phys., 175, 267 [NASA ADS] [CrossRef] (In the text)
- Harvey,
J., Giampapa, M., Henney, C., Jones, H., & Keller, C. 2003, AGU
Fall Meeting Abstracts, B545
- Harvey,
J., Giampapa, M., Henney, C., Keller, C., & Jones, H. 2004,
BAAS, 36, 708 [NASA ADS]
- Jones,
H. P., Branston, D. D., Jones, P. B., & Popescu,
M. D. 2003, ApJ, 589, 658 [NASA ADS] [CrossRef] (In the text)
- Jones,
H. P., Branston, D. D., Jones, P. B., &
Wills-Davey, M. J. 2000, ApJ, 529, 1070 [NASA ADS] [CrossRef] (In the text)
- Jones,
H. P. & Ceja, J. A. 2001, in Advanced Solar
Polarimetry - Theory, Observation, and Instrumentation, ed.
M. Sigwarth, ASP Conf. Ser., 236, 87
(In the text)
- Jones,
H. P., Duvall Jr., T. L., Harvey, J. W., et al.
1992, Sol. Phys., 139, 211 [NASA ADS] [CrossRef] (In the text)
-
Krivova, N. A., Solanki, S. K., Fligge, M., & Unruh,
Y. C. 2003, A&A, 399, L1 [EDP Sciences] [NASA ADS] [CrossRef] [EDP Sciences]
- Livingston, W. C., Harvey,
J., Pierce, A. K., et al. 1976a, Appl. Opt., 15,
33 [NASA ADS] (In the text)
- Livingston, W. C., Harvey,
J., Slaughter, C., & Trumbo, D. 1976b, Appl. Opt., 15,
40 [NASA ADS] (In the text)
- Martínez Pillet, V.,
Lites, B. W., & Skumanich, A. 1997, ApJ, 474, 810 [NASA ADS] [CrossRef]
- Neckel, H.
& Labs, D. 1994, Sol. Phys., 153, 91 [NASA ADS] [CrossRef] (In the text)
- Ortiz,
A., Solanki, S. K., Domingo, V., Fligge, M., & Sanahuja,
B. 2002, A&A, 388, 1036 [EDP Sciences] [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
-
Rüedi, I., Solanki, S. K., Livingston, W., & Stenflo,
J. O. 1992, A&A, 263, 323 [NASA ADS]
-
Schüssler, M. 1986, in Small Scale Magnetic Flux
Concentrations in the Solar Photosphere, ed. W. Deinzer, M.
Knölker, and H.H. Voigt, Abhandlungen der Akademie der
Wissenschaften in Göttingen, 103
(In the text)
-
Scherrer, P. H., Bogart, R. S., Bush, R. I.,
et al. 1995, Sol. Phys., 162, 129 [NASA ADS] [CrossRef] (In the text)
- Solanki,
S. K. 1986, A&A, 168, 311 [NASA ADS]
- Solanki,
S. K. 1993, Space Sci. Rev. 63, 1
(In the text)
- Solanki,
S. K. 2003, A&A Rev., 11, 153 [NASA ADS] (In the text)
-
Solanki, S. K., Krivova, N. A., & Wenzler, T. 2005,
Adv. Space Res., 35, 376 [NASA ADS] (In the text)
-
Solanki, S. K. & Stenflo, J. O. 1984, A&A, 140,
185 [NASA ADS]
-
Stenflo, J. O. & Harvey, J. W. 1985, Sol. Phys.,
95, 99 [NASA ADS] [CrossRef]
- Unruh,
Y. C., Solanki, S. K., & Fligge, M. 1999, A&A,
345, 635 [NASA ADS] (In the text)
-
Wenzler, T., Solanki, S. K., Krivova, N. A., & Fluri,
D. M. 2004, A&A, 427, 1031 [EDP Sciences] [NASA ADS] [CrossRef] [EDP Sciences]
-
Wenzler, T., Solanki, S. K., & Krivova, N. A. 2005,
A&A, 432, 1057 [EDP Sciences] [NASA ADS] [CrossRef] [EDP Sciences]
Copyright ESO 2006




![\begin{figure}
\par\includegraphics[width=17cm]{5752fi5.eps} \end{figure}](/articles/aa/full/2006/47/aa5752-06/Timg34.gif)


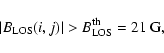



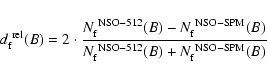
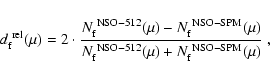
![\begin{displaymath}\Delta N_{\rm f}^{\rm ~rel} =
2\cdot\frac{\sum\limits_{B}[N...
...f}^{\rm ~NSO-512}(B)+N_{\rm f}^{\rm ~NSO-SPM}(B)]}
= 0.046\ ,
\end{displaymath}](/articles/aa/full/2006/47/aa5752-06/img79.gif)
![\begin{displaymath}\Delta \phi_{\rm f}^{\rm ~rel} =
2\cdot\frac{\sum\limits_{B...
...rm ~NSO-512}(B)+N_{\rm f}^{\rm ~NSO-SPM}(B)]}
= -0.093 \rm\ ,
\end{displaymath}](/articles/aa/full/2006/47/aa5752-06/img80.gif)
![\begin{displaymath}\begin{array}{rll}
S_{\rm NSO-SPM}(\lambda,t) = \sum\limits_...
...(\mu,B;t) \alpha_{\rm f}(\mu,B)]) I_q(\mu;\lambda)]
\end{array}\end{displaymath}](/articles/aa/full/2006/47/aa5752-06/img88.gif)

![\begin{displaymath}\begin{array}{rll}
S_{\rm NSO-512}(\lambda,t) = \sum\limits_...
...(\mu,B;t) \alpha_{\rm f}(\mu,B)]) I_q(\mu;\lambda)]
\end{array}\end{displaymath}](/articles/aa/full/2006/47/aa5752-06/img97.gif)
![\begin{figure}
\par\includegraphics[width=17cm]{5752fi14.eps} \end{figure}](/articles/aa/full/2006/47/aa5752-06/Timg100.gif)
![\begin{figure}
\par\includegraphics[width=16.7cm]{5752fi15.eps} \end{figure}](/articles/aa/full/2006/47/aa5752-06/Timg101.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{5752fi16.eps} \end{figure}](/articles/aa/full/2006/47/aa5752-06/Timg107.gif)
