A&A 460, 357-363 (2006)
DOI: 10.1051/0004-6361:20064805
S. Abbassi1 - J. Ghanbari2,3 - F. Salehi2,4
1 - Department of Physics, Damghan University of Basic
Sciences,
Damghan, Iran
2 -
Department of Physics, School of Sciences, Ferdowsi
University of Mashhad, Mashhad, Iran
3 -
Department of Physics and Astronomy, San Francisco State
University, 1600 Holloway, San Francisco, CA 94132, USA
4 -
Department of Physics, Khayam Institute of Higher
Education, Mashhad, Iran
Received 3 January 2006 / Accepted 20 June 2006
Abstract
Aims. We investigate the ![]() -prescription for viscosity in standard self-gravitating thin disks and predict that in a self-gravitating thin disk the
-prescription for viscosity in standard self-gravitating thin disks and predict that in a self-gravitating thin disk the ![]() -model will have a different dynamical behavior compared to the well-known
-model will have a different dynamical behavior compared to the well-known ![]() -prescription.
-prescription.
Methods. We used self-similar methods to solve the integrated equations that govern the dynamical behavior of the thin disk.
Results. We present the results of self-similar solutions of the time evolution of axisymmetric, polytropic, self-gravitating viscous disks around a new-born central object. We apply a ![]() -viscosity prescription derived from rotating shear flow experiments (
-viscosity prescription derived from rotating shear flow experiments (
![]() ). Using reduced equations in a slow accretion limit, we demonstrate inside-out self-similar solutions after core formation in the center. Some physical quantities for
). Using reduced equations in a slow accretion limit, we demonstrate inside-out self-similar solutions after core formation in the center. Some physical quantities for ![]() -disks are determined numerically. We compare our results with
-disks are determined numerically. We compare our results with ![]() -disks under the same initial conditions. The accretion rate onto the central object for
-disks under the same initial conditions. The accretion rate onto the central object for ![]() -disks is grater than for
-disks is grater than for ![]() -disks in the outer regions where
-disks in the outer regions where ![]() -disks are more efficient. Our results show that the Toomre instability parameter is less than one everywhere on the
-disks are more efficient. Our results show that the Toomre instability parameter is less than one everywhere on the ![]() -disk which means that in such disks gravitational instabilities can occur, so the
-disk which means that in such disks gravitational instabilities can occur, so the ![]() -disk model can be a good candidate for the origin of planetary systems. Our results show that the
-disk model can be a good candidate for the origin of planetary systems. Our results show that the ![]() -disks will decouple in the outer part of the disk where self-gravity plays an important role, in agreement with theoretical predictions.
-disks will decouple in the outer part of the disk where self-gravity plays an important role, in agreement with theoretical predictions.
Key words: accretion, accretion disks - stars: formation - planets and satellites: formation
Accretion disks are found around many astrophysical objects, such
as active galactic nuclei (AGN), binary stars and young stellar
objects. Observational evidence for disks in young stellar objects
gleaned both spectroscopically and through direct imaging is now
quite compelling (Beckwith & Sargent 1993; Storm et al. 1993).
Up to half of the solar type, pre-main sequence stars are
surrounded by disks of gas and dust, many having masses similar to
that expected for early solar nebula (Chandler 1998). The
accretion disks around pre-main sequence stars are good candidates
for the creation of planetary systems. The structure of such disks
is a subject of great interest and has been studied both through
self-similar solutions assuming an unsteady state
(Mineshige &
Umemura 1997; Mineshige et al. 1997; Tsuribe 1999) and through
direct numerical hydrodynamical simulations (Igumenshchev ![]() Abramowicz 1999; Stone et al. 1999; Torkelsson et al. 2000). It is
understood that the most crucial factors are self-gravity and
viscosity which play a role in angular momentum transportation on
the gas disk. Accretion takes place because of dissipation which
releases the free energy of the shear flow as heat, and so allows
the disk material to fall deeper into the potential well of the
central object. In a simple picture,
Lynden-Bell & Pringle
(1974) indicated that the dissipative processes must take the form
of a stress that transports angular momentum outwards. It plays a
significant role in many such systems, from protostellar disks to
active galactic nuclei (AGN). Self-gravity will modify the radial
and vertical equations and so can influence the dynamical behavior
of the accretion disks. In the standard thin accretion disk model,
the effect of self-gravity is neglected, and only pressure
supports the vertical structure. In contrast, the theory of
self-gravitating accretion disks is less developed and in the
traditional model of accretion disks, self-gravity is ignored for
simplicity (e.g. Pringle 1981), although self-gravity can describe
the deviation from Keplerian rotation velocity in some AGN and
flat infrared spectra of some T Tauri stars. From the
observational point of view, there are already some clues that the
disk self-gravity can be important both in the context of
proto-stellar disks and in the accretion disks around super
massive black holes in the AGN. However, comparison with
observations is limited by the lack of detailed models of
self-gravitating disks and by an incomplete understanding of the
basic physical processes involved.
Abramowicz 1999; Stone et al. 1999; Torkelsson et al. 2000). It is
understood that the most crucial factors are self-gravity and
viscosity which play a role in angular momentum transportation on
the gas disk. Accretion takes place because of dissipation which
releases the free energy of the shear flow as heat, and so allows
the disk material to fall deeper into the potential well of the
central object. In a simple picture,
Lynden-Bell & Pringle
(1974) indicated that the dissipative processes must take the form
of a stress that transports angular momentum outwards. It plays a
significant role in many such systems, from protostellar disks to
active galactic nuclei (AGN). Self-gravity will modify the radial
and vertical equations and so can influence the dynamical behavior
of the accretion disks. In the standard thin accretion disk model,
the effect of self-gravity is neglected, and only pressure
supports the vertical structure. In contrast, the theory of
self-gravitating accretion disks is less developed and in the
traditional model of accretion disks, self-gravity is ignored for
simplicity (e.g. Pringle 1981), although self-gravity can describe
the deviation from Keplerian rotation velocity in some AGN and
flat infrared spectra of some T Tauri stars. From the
observational point of view, there are already some clues that the
disk self-gravity can be important both in the context of
proto-stellar disks and in the accretion disks around super
massive black holes in the AGN. However, comparison with
observations is limited by the lack of detailed models of
self-gravitating disks and by an incomplete understanding of the
basic physical processes involved.
The study of self-gravity in the general case is difficult and
most authors usually study the effects related to self-gravity
either in the vertical structure of the disk (e.g. Bardou et al.
1998) or in the radial direction (e.g. Bodo ![]() Curir 1992).
Disks in the AGN are thought to be relatively light in the sense
that the ratio of
Curir 1992).
Disks in the AGN are thought to be relatively light in the sense
that the ratio of
![]() is around a few percent (where
M and M* are the masses of the disk and central star).
Usually self-gravity occurs at large distances from the central
objects (Shlosman
is around a few percent (where
M and M* are the masses of the disk and central star).
Usually self-gravity occurs at large distances from the central
objects (Shlosman ![]() Begelman 1987), and mainly in the direction
perpendicular to the plane of the disk. But in the accretion disks
around young stellar objects or pre-main-sequence stars,
self-gravity can be important in all parts of the disk in both
vertical and radial directions. Early numerical works of
self-gravitating accretion disks began with N-body modelling
(Cassen
Begelman 1987), and mainly in the direction
perpendicular to the plane of the disk. But in the accretion disks
around young stellar objects or pre-main-sequence stars,
self-gravity can be important in all parts of the disk in both
vertical and radial directions. Early numerical works of
self-gravitating accretion disks began with N-body modelling
(Cassen ![]() Moosman 1981; Tomley et al. 1991). Shlosman
Moosman 1981; Tomley et al. 1991). Shlosman ![]() Begelman (1987) investigated the role of
self-gravity in AGN. Recently, Ghanbari & Abbassi (2004)
introduced a model that shows that self-gravity is an important
effect in the equilibrium of a thick accretion disk.
Begelman (1987) investigated the role of
self-gravity in AGN. Recently, Ghanbari & Abbassi (2004)
introduced a model that shows that self-gravity is an important
effect in the equilibrium of a thick accretion disk.
Theoretical descriptions of accretion disks and these dynamics are
based on the underlying the physics of viscosity in the disks.
Because detailed modelling of the structure and evolution of
accretion disks depends on the viscosity and its dependence on the
physical parameters, choosing the best viscosity model is
important. There is a belief that the molecular viscosity is
inadequate to describe luminous accretion disks so that some kind
of turbulence viscosity is required. Most investigators adopt the
so-called ![]() -model introduced by Shakura (1972) and Shakura
-model introduced by Shakura (1972) and Shakura
![]() Sanyeav (1973) that gives the viscosity as the product of the
pressure scale height in the disk (h), the velocity of sound
(
Sanyeav (1973) that gives the viscosity as the product of the
pressure scale height in the disk (h), the velocity of sound
(![]() )
and a parameter
)
and a parameter ![]() which contains all the unknown
physics. The models for the structure and evolution of accretion
disks in close binary systems (e.g. dwarf novae and symbiotic
stars) show that Shakura and Sunyeav's parametrization with a
constant
which contains all the unknown
physics. The models for the structure and evolution of accretion
disks in close binary systems (e.g. dwarf novae and symbiotic
stars) show that Shakura and Sunyeav's parametrization with a
constant ![]() leads to results that reproduce the overall
observed behavior of the disks quite well. Accretion disks treated
by a weak magnetic field are subject to MHD instabilities (Balbus
leads to results that reproduce the overall
observed behavior of the disks quite well. Accretion disks treated
by a weak magnetic field are subject to MHD instabilities (Balbus
![]() Hawly 1991) that can induce turbulence in the disk, thereby
transporting angular momentum and promoting accretion processes.
However in many astrophysically interesting cases, such as the
outer part of proto-stellar disks, the ionization level is
expected to be low, significantly reducing the effect of the
magnetic field in the dynamical behavior of the disk. The
realization that molecular transport of angular momentum is
inefficient led theoreticians to look for another mechanism of
transport of angular momentum in accretion disks. A good candidate
is any kind of turbulence. The
Hawly 1991) that can induce turbulence in the disk, thereby
transporting angular momentum and promoting accretion processes.
However in many astrophysically interesting cases, such as the
outer part of proto-stellar disks, the ionization level is
expected to be low, significantly reducing the effect of the
magnetic field in the dynamical behavior of the disk. The
realization that molecular transport of angular momentum is
inefficient led theoreticians to look for another mechanism of
transport of angular momentum in accretion disks. A good candidate
is any kind of turbulence. The ![]() -prescription is based on
turbulence viscosity but there is no physical evidence for this as
the origin of turbulence in the model. On the other hand,
laboratory experiments of Taylor-Couette systems indicate that,
although the Coriolis force delays the onset of turbulence, the
flow is ultimately unstable to turbulence for Reynolds numbers
larger than a few thousand (e.g., see, Richard & Zahn 1999; Hure et al. 2001). Since in all self-gravitating disks
the Reynolds number is extremely high, it was thought that
hydrodynamically-driven turbulent viscosity based on the critical
Reynolds number probably plays a significant role in the
distribution of angular momentum in the accretion disk. The
resulting turbulence would then transport angular momentum
efficiently. Duschl et al. (2000) have
proposed a generalized accretion disk viscosity prescription based
on the hydrodynamically-driven turbulence at the critical
effective Reynolds number, the
-prescription is based on
turbulence viscosity but there is no physical evidence for this as
the origin of turbulence in the model. On the other hand,
laboratory experiments of Taylor-Couette systems indicate that,
although the Coriolis force delays the onset of turbulence, the
flow is ultimately unstable to turbulence for Reynolds numbers
larger than a few thousand (e.g., see, Richard & Zahn 1999; Hure et al. 2001). Since in all self-gravitating disks
the Reynolds number is extremely high, it was thought that
hydrodynamically-driven turbulent viscosity based on the critical
Reynolds number probably plays a significant role in the
distribution of angular momentum in the accretion disk. The
resulting turbulence would then transport angular momentum
efficiently. Duschl et al. (2000) have
proposed a generalized accretion disk viscosity prescription based
on the hydrodynamically-driven turbulence at the critical
effective Reynolds number, the ![]() -model, which is applied to
both self-gravitating and non self-gravitating disks and is shown
to yield the standard
-model, which is applied to
both self-gravitating and non self-gravitating disks and is shown
to yield the standard ![]() -model in the case of shock
dissipation limited, non self-gravitating disks. They have shown
that in the case of fully self-gravitating disks this model may
explain the observed spectra of proto-planetary disks and explain
the radial motion from the observed metallicity gradients in the
disk galaxy.
-model in the case of shock
dissipation limited, non self-gravitating disks. They have shown
that in the case of fully self-gravitating disks this model may
explain the observed spectra of proto-planetary disks and explain
the radial motion from the observed metallicity gradients in the
disk galaxy.
The basic equilibrium and dynamical structure of accretion disks
are now well understood, if the standard model based on the
![]() -viscosity prescription (Shakura
-viscosity prescription (Shakura ![]() Sunyeav 1973) is
believed. Nevertheless, it is not easy to follow its dynamical
evolution, mainly because the basic equations of the system are
highly non-linear, especially when the system is self-gravitating
(Paczynski 1978; Fukue
Sunyeav 1973) is
believed. Nevertheless, it is not easy to follow its dynamical
evolution, mainly because the basic equations of the system are
highly non-linear, especially when the system is self-gravitating
(Paczynski 1978; Fukue ![]() Sakamoto 1992). To follow the
non-linear evolution of dynamically evolving systems, in general,
the technique of self-similarity is sometimes useful. Self-similar
assumptions enable us to simplify the governing equations.
Self-similar solutions have a wide range of applications in
astrophysics. Several classes of solutions were disscussed
previously (Pringle 1974; Filipov 1984), but all of them
considered the disk in a fixed, central potential. But a class of
self-similar solution has been provided that use self-gravity
(Mineshige
Sakamoto 1992). To follow the
non-linear evolution of dynamically evolving systems, in general,
the technique of self-similarity is sometimes useful. Self-similar
assumptions enable us to simplify the governing equations.
Self-similar solutions have a wide range of applications in
astrophysics. Several classes of solutions were disscussed
previously (Pringle 1974; Filipov 1984), but all of them
considered the disk in a fixed, central potential. But a class of
self-similar solution has been provided that use self-gravity
(Mineshige ![]() Umemura 1997). These authors had found a
self-similar solution for the time evolution of an isothermal,
self-gravitating
Umemura 1997). These authors had found a
self-similar solution for the time evolution of an isothermal,
self-gravitating ![]() -viscous disk. This solution describes
the homologous collapse of a disk via self-gravity and viscosity.
They found that the disk structure and evolution are distinct in
the inner and outer parts. The effect of self-gravity in the
collapse of a polytropic self-gravitating viscous disk has been
investigated by Mineshige et al. (1997).
-viscous disk. This solution describes
the homologous collapse of a disk via self-gravity and viscosity.
They found that the disk structure and evolution are distinct in
the inner and outer parts. The effect of self-gravity in the
collapse of a polytropic self-gravitating viscous disk has been
investigated by Mineshige et al. (1997).
Following the Duschl et al. (2000) suggestion for a
![]() -prescription for viscosity, we apply this model for a thin
self-gravitating disk around newborn stars. It may seem that using
other forms of viscosity is not an important issue, because one
should just change the mathematical forms of the equations. But
this changes governing equations of the system that can effect the
dynamical behavior of the disks. This led us to explore the
self-gravitating disk using other viscosity prescriptions.
However, all viscosity prescriptions have phenomenological
backgrounds rather than physically confirmed backgrounds. While we
do not have a clear picture of the turbulence in disks, all such
prescriptions are equivalent regarding their physical backgrounds.
On the other hand, self-gravitation in a disk is a highly
nonlinear process as a result of the complex behaviors of the
various physical agents of the system, in which the turbulent
viscosity and its prescriptions play a vital role. What would
happen if other forms of viscosity prescriptions in a
self-gravitating disk are used? When we searched in the
literature, we found the
-prescription for viscosity, we apply this model for a thin
self-gravitating disk around newborn stars. It may seem that using
other forms of viscosity is not an important issue, because one
should just change the mathematical forms of the equations. But
this changes governing equations of the system that can effect the
dynamical behavior of the disks. This led us to explore the
self-gravitating disk using other viscosity prescriptions.
However, all viscosity prescriptions have phenomenological
backgrounds rather than physically confirmed backgrounds. While we
do not have a clear picture of the turbulence in disks, all such
prescriptions are equivalent regarding their physical backgrounds.
On the other hand, self-gravitation in a disk is a highly
nonlinear process as a result of the complex behaviors of the
various physical agents of the system, in which the turbulent
viscosity and its prescriptions play a vital role. What would
happen if other forms of viscosity prescriptions in a
self-gravitating disk are used? When we searched in the
literature, we found the ![]() -prescription as the only
experimentally tested viscosity prescription. There are a few
studies of the
-prescription as the only
experimentally tested viscosity prescription. There are a few
studies of the ![]() -prescription compared to the
-prescription compared to the
![]() -model. Many papers discuss physical considerations and
applications of the
-model. Many papers discuss physical considerations and
applications of the ![]() -model: Mayer & Duschl (2005); Weigelt
et al. (2004); Pott et al. (2004); Granato et al. (2004); Mathis et al. (2004); Richard & Davis (2004). We expect to
find a different dynamical behavior and we will show that
gravitational fragmentation can take place everywhere in the disk.
Thus it is a good description of the formation of a
proto-planetary disk.
-model: Mayer & Duschl (2005); Weigelt
et al. (2004); Pott et al. (2004); Granato et al. (2004); Mathis et al. (2004); Richard & Davis (2004). We expect to
find a different dynamical behavior and we will show that
gravitational fragmentation can take place everywhere in the disk.
Thus it is a good description of the formation of a
proto-planetary disk.
Self-similar behavior provides a set of non-steady state solutions to the self-gravitating fluid equations. On the other hand, many physical problems often attain self-similar limits for a wide range of initial conditions. Also self-similar properties allow us to investigate properties of the solutions in detail, without any of the associated difficulties of numerical hydrodynamics.
In order to study the accretion processes of a thin disk under the
effect of self-gravity and viscosity, we consider axisymmetric
polytropic disks using cylindrical coordinates (![]() ). We
assume that the accretion disks are geometrically thin in the
vertical direction and symmetric in the azimuthal direction. The
model is described by the fundamental governing equations:
). We
assume that the accretion disks are geometrically thin in the
vertical direction and symmetric in the azimuthal direction. The
model is described by the fundamental governing equations:
| (4) |
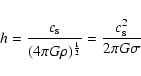 |
(5) |
The solution of these equations, gives us the dynamical evolution of the disk which strongly depends on the viscosity model. The study of the dynamical behavior the accretion disks is postponed until more information about viscosity is available.
Before we solve Eqs. (1-3), it is
convenient to nondimensionalize the equations. The essence of a
self-similar model is the existence of only two dimensional
parameters in the problem, viz., K and the gravitational
constant G. It is assumed, and this is born out by numerical
calculations, that any additional parameters, such as the initial
central density, have only transient effects that quickly lost,
at least in the part of the flow in which the density greatly
exceeds the initial central density. If that is the case, then
only one dimensionless combination of radius r and time t can be
found
(Mineshige et al. 1997; Yahil 1983):
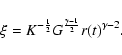 |
(6) |
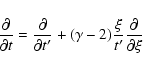 |
(7) |
 |
(8) |
To change the variables to the dimensionless form, we used K and G
because we require that all of the time-dependent terms disappear
in the self-similar forms of the equations. Other physical
quantities (functions of t and r) are transformed into
self-similar ones (functions of only ![]() )
as:
)
as:
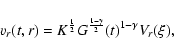 |
(9) |
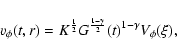 |
(10) |
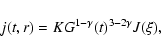 |
(11) |
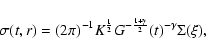 |
(12) |
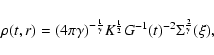 |
(13) |
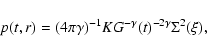 |
(14) |
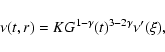 |
(15) |
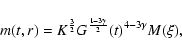 |
(16) |
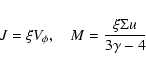 |
(17) |
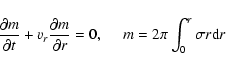 |
(18) |
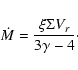 |
(19) |
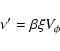 |
(20) |
Substituting the above transformations into Eqs. (1-3), we can introduce a set of coupled
ordinary differential equations. The basic equations are then
transformed into the following forms:
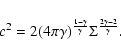 |
(25) |
We consider the fluid equations for a thin disk in the slow accretion approximation. The slow accretion approximation consists of rotationally supported disks when the viscous timescale is much larger than the dynamical timescale. In addition, the pressure gradient force and the acceleration term in this approximation are ignored. The slow accretion approximation in disks has been used by Tsuribe (1999) and Minshige et al. (1997) and many others.
In the slow accretion limit (
![]() ), and in
Eq. (2), the Euler equation, we have a radial
force-balance which means that only two terms on the right hand
side of the equation balance each other:
), and in
Eq. (2), the Euler equation, we have a radial
force-balance which means that only two terms on the right hand
side of the equation balance each other:
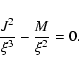 |
(26) |
To solve Eq. (32) numerically, we need one boundary
condition. We derived asymptotic solutions in the limits
![]() and
and
![]() for Vr where
these asymptotic values can be used as the boundary condition.
for Vr where
these asymptotic values can be used as the boundary condition.
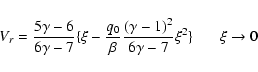 |
(33) |
![\begin{displaymath}V_r=-\frac{\beta}{q_0}\frac{[(2-\gamma)(22-18\gamma)-2(3\gamma-4)^2]}{(2-\gamma)^2}~~~~\xi\rightarrow\infty
\end{displaymath}](/articles/aa/full/2006/47/aa4805-06/img61.gif) |
(34) |
![\begin{figure}
{{\includegraphics[width=9cm]{4805fig1.EPS} }}
\end{figure}](/articles/aa/full/2006/47/aa4805-06/Timg64.gif) |
Figure 1:
Radial self-similar velocity distributions as a function
of the self-similar variable
|
| Open with DEXTER | |
![\begin{figure}
{{\includegraphics[width=9cm]{4805fig2.EPS} }}
\end{figure}](/articles/aa/full/2006/47/aa4805-06/Timg65.gif) |
Figure 2:
Azimuthal self-similar velocity distributions as a
function
of the self-similar variable
|
| Open with DEXTER | |
![\begin{figure}
{{\includegraphics[width=9cm]{4805fig3.EPS} }}
\end{figure}](/articles/aa/full/2006/47/aa4805-06/Timg66.gif) |
Figure 3:
Self-similar surface density distributions as a function
the of self-similar variable
|
| Open with DEXTER | |
![\begin{figure}
{{\includegraphics[width=9cm]{4805fig4.EPS} }}
\end{figure}](/articles/aa/full/2006/47/aa4805-06/Timg67.gif) |
Figure 4:
Self-similar mass accretion rate distributions as a
function of the self-similar variable
|
| Open with DEXTER | |
It is predicted that in the outer parts of a thin, viscous disk
around QSOs, self-gravity plays an important role. This effect is
investigated by the Toomre parameter (Toomre 1964), such that the
local gravitational instability occurs where Q<1 and where Q>1the disk is stable against gravitational fragmentation. It is
useful to calculate Q values to compare gravitational stability in
![]() and
and ![]() disks. The Toomre stability parameter for
epicyclic motion is:
disks. The Toomre stability parameter for
epicyclic motion is:
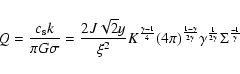 |
(35) |
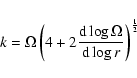 |
(36) |
In Fig. 5, we show the distribution of the Toomre Q value for
some ![]() and
and ![]() values. We also compare
values. We also compare ![]() and
and
![]() disks for
disks for
![]() .
In Fig. 6, the angular momentum
coefficient
.
In Fig. 6, the angular momentum
coefficient
![]() is plotted as a function of
is plotted as a function of ![]() for
some
for
some ![]() values at
values at
![]() .
Also we see its behavior
for
.
Also we see its behavior
for ![]() and
and ![]() disks.
disks.
To estimate the effect of viscosity on the evolution of accretion
disks we can compare the viscous time scale with the dynamical
time scale. The dynamical time scale
![]() is given by:
is given by:
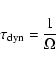 |
(37) |
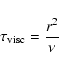 |
(38) |
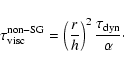 |
(39) |
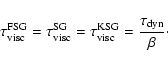 |
(40) |
The ![]() -prescription is based on the assumption that the
effective Reynolds number of the turbulence does not fall bellow
the critical Reynolds number. In this parametrization the
viscosity is proportional to the azimuthal velocity and the
radius. This yields physically consistent models of both Keplerian
and fully self-gravitating accretion disks which in the case of
thin disks with sufficiently small mass, recover the
-prescription is based on the assumption that the
effective Reynolds number of the turbulence does not fall bellow
the critical Reynolds number. In this parametrization the
viscosity is proportional to the azimuthal velocity and the
radius. This yields physically consistent models of both Keplerian
and fully self-gravitating accretion disks which in the case of
thin disks with sufficiently small mass, recover the ![]() -disk
solutions. Such
-disk
solutions. Such ![]() -disk models may be relevant for
protoplanetary accretion disks (Duschl et al. 2000). In the case
of protoplanetary disks they yield spectra that are considerably
flatter than those due to non-self-gravitating disks, in better
agreement with the observed spectra of these objects.
-disk models may be relevant for
protoplanetary accretion disks (Duschl et al. 2000). In the case
of protoplanetary disks they yield spectra that are considerably
flatter than those due to non-self-gravitating disks, in better
agreement with the observed spectra of these objects.
![\begin{figure}
{{\includegraphics[width=9cm]{4805fig5.EPS} }}
\end{figure}](/articles/aa/full/2006/47/aa4805-06/Timg89.gif) |
Figure 5:
Distribution of the Toomre Q value as a function of the
self-similar variable
|
| Open with DEXTER | |
![\begin{figure}
{{\includegraphics[width=9cm]{4805fig6.EPS} }}
\end{figure}](/articles/aa/full/2006/47/aa4805-06/Timg90.gif) |
Figure 6:
The angular momentum
coefficient profile, q, as a function the self-similar variable
|
| Open with DEXTER | |
In this paper, we have considered the time-dependent evolution of
self-gravitating disks with the ![]() -prescription by a
self-similar method for a thin, viscous disk. To do this, we
started from dimensionless basic fluid equations. In order to
consider gravity and the centrifugal force, we use the fluid
equations for a thin disk in the slow accretion approximation. It
has been found that the evolution is described by solving a simple
differential Eq. (32). We solved it numerically,
beginning the asymptotic solution of this equation near the origin
as a boundary condition. To obtain physical solutions from the
differential equations, we have to select
-prescription by a
self-similar method for a thin, viscous disk. To do this, we
started from dimensionless basic fluid equations. In order to
consider gravity and the centrifugal force, we use the fluid
equations for a thin disk in the slow accretion approximation. It
has been found that the evolution is described by solving a simple
differential Eq. (32). We solved it numerically,
beginning the asymptotic solution of this equation near the origin
as a boundary condition. To obtain physical solutions from the
differential equations, we have to select ![]() from a
specifical range of numbers.
from a
specifical range of numbers.
The presented method shows that an increase of the ![]() value
causes the azimuthal velocity to decrease but its general
distribution function does not change throughout the disk. Also,
azimuthal velocities in
value
causes the azimuthal velocity to decrease but its general
distribution function does not change throughout the disk. Also,
azimuthal velocities in ![]() -disks are greater than in
-disks are greater than in
![]() -disks (see Fig. 2). Thus we expect the
-disks (see Fig. 2). Thus we expect the ![]() -disks to
evolve in different ways to the
-disks to
evolve in different ways to the ![]() -disks.
-disks.
According to Fig. 4, ![]() -disks have larger mass accretion
rates than
-disks have larger mass accretion
rates than ![]() -disks. So, observably, we expect them to be
brighter than
-disks. So, observably, we expect them to be
brighter than ![]() -disks. Also, we note that with the increase
of the
-disks. Also, we note that with the increase
of the ![]() value,
value, ![]() increases. Mass flow thus increases
onto the central object. This implies greater radial velocity and
lower surface density (see Figs. 1, 3).
increases. Mass flow thus increases
onto the central object. This implies greater radial velocity and
lower surface density (see Figs. 1, 3).
Compared to ![]() -disks, the q is not a smooth distribution
(
-disks, the q is not a smooth distribution
(
![]() ). The q values are very small in the innermost
regions (see Fig. 6). They are almost constant in the outer
regions. It seems in the outer part of the disk where the beta
viscosity is more efficient, the angular momentum is proportional
to the disk's mass inside the radius r. In order to study the
effect of the self-gravity of thin
). The q values are very small in the innermost
regions (see Fig. 6). They are almost constant in the outer
regions. It seems in the outer part of the disk where the beta
viscosity is more efficient, the angular momentum is proportional
to the disk's mass inside the radius r. In order to study the
effect of the self-gravity of thin ![]() -disks, we plot the
Toomre parameter as a function of
-disks, we plot the
Toomre parameter as a function of ![]() .
It is obvious that the
gravitational instabilities in
.
It is obvious that the
gravitational instabilities in ![]() -disks are more pronounced
than in
-disks are more pronounced
than in ![]() -disks, Q<1. In Fig. 5, the Toomre parameter
profile can reveal this effect. It can be expected that the
-disks, Q<1. In Fig. 5, the Toomre parameter
profile can reveal this effect. It can be expected that the
![]() -disk is a good model to describe planet formation around
new-born stars. We showed that in the outer parts of the disk
there is a difference between
-disk is a good model to describe planet formation around
new-born stars. We showed that in the outer parts of the disk
there is a difference between ![]() and
and ![]() models. These
results were predicated by Duschl et al. (2000).
models. These
results were predicated by Duschl et al. (2000).
In order to study model and drive a realistic picture of a thin
self-gravitating disk, one must investigate the energy exchange of
the disk with its environment. This requires a mechanism to
transfer the thermal energy from the disk to the outside
environment; thus we should add energy equations to our model.
Both ![]() and
and ![]() models are phenomenological
prescriptions for disk viscosity. In an actual model of viscosity,
it is possible to combine these two models and establish an exact
description for different regions of the disk. In real accretion
disks, there are many important processes other than viscosity
that we have neglected, for example, non-axisymmetric waves which
are also expected to transport angular momentum outward. The
magnetic field and its influence are neglected and sometimes
magnetic braking may transport angular momentum. However, these
preliminary solutions can increase our understanding of the
physics governing the accretion disk.
models are phenomenological
prescriptions for disk viscosity. In an actual model of viscosity,
it is possible to combine these two models and establish an exact
description for different regions of the disk. In real accretion
disks, there are many important processes other than viscosity
that we have neglected, for example, non-axisymmetric waves which
are also expected to transport angular momentum outward. The
magnetic field and its influence are neglected and sometimes
magnetic braking may transport angular momentum. However, these
preliminary solutions can increase our understanding of the
physics governing the accretion disk.