A&A 460, 301-307 (2006)
DOI: 10.1051/0004-6361:20066123
J. Leenaarts1,2 - S. Wedemeyer-Böhm3
1 - Sterrekundig Instituut, Utrecht University,80000, 3508 TA Utrecht,Netherlands
2 - Institute of Theoretical Astrophysics, University of Oslo, PO Box 1029, Blindern,315 Oslo,
3 - Kiepenheuer Institut für Sonnenphysik,öneckstrasse 6, 79104 Freiburg,
Received 27 July 2006 / Accepted 16 August 2006
Abstract
Context. The hydrogen ionisation degree deviates substantially from statistical equilibrium under the conditions of the solar chromosphere. A realistic description of this atmospheric layer thus must account for time-dependent non-equilibrium effects.
Aims. Advancing the realism of numerical simulations of the solar chromosphere by improved numerical treatment of the relevant physics will provide more realistic models that are essential for interpretation of existing and future observations.
Methods. An approximate method for solving the rate equations for the hydrogen populations was extended and implemented in the three-dimensional radiation (magneto-)hydrodynamics code CO5BOLD. The method is based on a model atom with six energy levels and fixed radiative rates. It has been tested extensively in one-dimensional simulations. The extended method has been used to create a three-dimensional model that extends from the upper convection zone to the chromosphere.
Results. The ionisation degree of hydrogen in our time-dependent simulation is comparable to the corresponding equilibrium value up to 500 km above optical depth unity. Above this height, the non-equilibrium ionisation degree is fairly constant over time and space, and tends to be at a value set by hot propagating shock waves. The hydrogen level populations and electron density are much more constant than the corresponding values for statistical equilibrium, too. In contrast, the equilibrium ionisation degree varies by more than 20 orders of magnitude between hot, shocked regions and cool, non-shocked regions.
Conclusions. The simulation shows for the first time in 3D that the chromospheric hydrogen ionisation degree and electron density cannot be calculated in equilibrium. Our simulation can provide realistic values of those quantities for detailed radiative transfer computations.
Key words: Sun: chromosphere - radiative transfer
Hydrogen is the most abundant constituent of the solar gas and the major electron donor in the solar chromosphere. The assumption of local thermal equilibrium (LTE) for hydrogen atoms is not valid in the chromosphere because the radiative transition rates dominate over the collisional rates. Even the assumption of instantaneous statistical equilibrium, where the level populations of each species at all times are in equilibrium as determined by the local thermodynamic state and the non-local radiation field, is not valid in the dynamical chromosphere. The timescale on which the hydrogen level populations adjust to changes in the atmosphere (which is set by the transition rates between levels) is too long compared to the timescale on which the atmosphere changes. In order to properly model this behaviour one has to solve the rate equations for the populations of all relevant energy levels. We henceforth refer to this approach as time-dependent non-LTE modelling (TD-NLTE).
Kneer (1980) showed that the relaxation timescale for the ionisation of hydrogen varies from 100 s to 1000 s in the middle to upper chromosphere. In the nineties, time-dependent hydrogen ionisation was first implemented in one-dimensional (1D) hydrodynamics simulations of the solar chromosphere and corona (Carlsson & Stein 1992; Hansteen 1993; Carlsson & Stein 2002). Carlsson & Stein (2002, hereafter CS2002) gave a detailed analysis of dynamic hydrogen ionisation in 1D, where they included a transition region and a corona in their model. More recently, Rammacher & Ulmschneider (2003) also implemented a time-dependent treatment of magnesium in a 1D simulation.
The next step is obviously the inclusion of time-dependent hydrogen ionisation into 2D and 3D simulations. For reasons of numerical stability and current computer limitations, a full time-dependent NLTE treatment of hydrogen in the solar atmosphere is not yet possible in two- and three-dimensional models. In the 1D case a simplified treatment using fixed radiative rates gives a good approximation to the full solution (Sollum 1999). In this paper, we report on the implementation of this method in the 2D/3D radiation hydrodynamics code CO5BOLD code (Freytag et al. 2002). It yields electron densities that are more realistic than in the original simulation, assuming LTE. The electron densities can now directly be used for a more realistic synthesis of chromospheric spectral lines and continua, producing much more reliable results compared to earlier calculations based on instantaneous statistical equilibrium.
We give details on hydrogen ionisation in Sect. 2 and the numerical method in Sect. 3. The results of our numerical simulation are described in Sect. 4 and finally discussed in Sect. 5.
In this section we recapitulate the details of chromospheric hydrogen ionisation as found by CS2002.
Statistical equilibrium does not hold under chromospheric conditions
because the dynamical time scale of the chromosphere is much shorter
than the relaxation timescale of hydrogen level populations. The
timescale in cool inter-shock regions was found to be of the order of
104 s. Within shocks the relaxation timescale is typically 50 s,
owing to the higher temperatures and densities. This is still
sufficiently long to prevent equilibration of the hydrogen populations
within a shock. Thus, the time-dependent rate equations need to be
solved to obtain the correct hydrogen level populations. Up to just
below the transition region Lyman ![]() may be regarded as being in
detailed balance for all practical purposes. Lyman continuum
ionisation is negligible. To quote CS2002 literally: "the dominant
hydrogen ionization process is photoionization from the second level
[...]. There is a very rapid equilibration of the second and all
higher levels with the continuum, with a slow collisional leakage of
electrons from the ground state to the second level or visa versa,
depending on whether hydrogen is ionizing or recombining''. Because
the ionisation in shocks is much faster than the post-shock
recombination, the ionisation degree and electron density tend to
represent their shock value, also in the low temperature inter-shock
regions.
may be regarded as being in
detailed balance for all practical purposes. Lyman continuum
ionisation is negligible. To quote CS2002 literally: "the dominant
hydrogen ionization process is photoionization from the second level
[...]. There is a very rapid equilibration of the second and all
higher levels with the continuum, with a slow collisional leakage of
electrons from the ground state to the second level or visa versa,
depending on whether hydrogen is ionizing or recombining''. Because
the ionisation in shocks is much faster than the post-shock
recombination, the ionisation degree and electron density tend to
represent their shock value, also in the low temperature inter-shock
regions.
We assume that the radiation field in each transition, both
bound-bound and bound-free, can be described by a formal radiation
temperature
![]() so that the angle-averaged intensity
so that the angle-averaged intensity ![]() at
frequency
at
frequency ![]() is given by
is given by
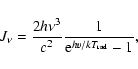 |
(1) |
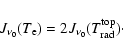 |
(2) |
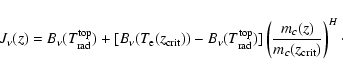 |
(3) |
This procedure ensures the radiation temperature connects smoothly
to the gas temperature in each column at
![]() .
There may be strong horizontal gradients in the radiation
temperature around this height if the gas temperature shows strong
horizontal gradients as well. The most important radiative
transition for hydrogen ionisation in the chromosphere is the Balmer
continuum. In this transition the radiation temperature ranges from
6250 K at
.
There may be strong horizontal gradients in the radiation
temperature around this height if the gas temperature shows strong
horizontal gradients as well. The most important radiative
transition for hydrogen ionisation in the chromosphere is the Balmer
continuum. In this transition the radiation temperature ranges from
6250 K at
![]() to 5237 K at the top of the computational
domain.
to 5237 K at the top of the computational
domain.
We restate the derivation of the radiative rate coefficients by Sollum (1999).
For lines, the assumption of a narrow line (
![]() is constant over the line profile) gives the following
expression for the radiative excitation rate coefficient:
is constant over the line profile) gives the following
expression for the radiative excitation rate coefficient:
| Rlu | = | 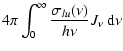 |
(4) |
| = | (5) | ||
| = | 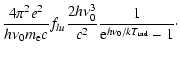 |
(6) |
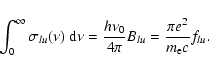 |
(7) |
| Ru l | = | (8) | |
| = | (9) |
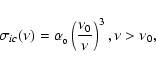 |
(10) |
| Ric | = | 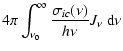 |
(11) |
| = | 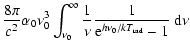 |
(12) | |
| = | ![$\displaystyle \frac{8 \pi}{c^2} \alpha_0
\nu_0^3 \sum_{n=1}^\infty E_1 \left[ n \frac{h \nu_0} {k
T_{{\rm r}{\rm a}{\rm d}}}\right],$](/articles/aa/full/2006/46/aa6123-06/img40.gif) |
(13) |
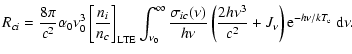 |
(14) |
![$\displaystyle R_{ci} = \frac{8 \pi}{c^2} \alpha_0 \nu_0^3 \left[
\frac{n_i}{n_c...
..._{{\rm r}{\rm a}{\rm d}}} +1 \right) \frac{h
\nu_0}{k T_{{\rm e}}} \right]\cdot$](/articles/aa/full/2006/46/aa6123-06/img43.gif) |
(15) |
We take the collisional rate coefficients Cij from Johnson (1972), who provides approximate cross sections for collisions of hydrogen with electrons.
As hydrogen is the most abundant element in the solar gas, ionisation
of hydrogen severely affects the electron densities, which in turn
enter into the collisional rate coefficients. LTE electron densities
are a poor choice at chromospheric heights. Hence, we adopt a hybrid
between LTE and TD-NLTE electron densities. The solution of the rate
equations in our TD-NLTE approach provides the population density of
the continuum level H II that is at the same time the contribution of
hydrogen to the electron number density. To this we add the LTE
electron densities from the other elements by solving the Saha
equation keeping the hydrogen ionization degree constant. For
computational speed, we use a pre-calculated table that gives the
electron density as a function of hydrogen ionisation degree, gas
temperature, and mass density. Parts of the RH code
(Uitenbroek 2001)
and partition functions by
Kurucz![]() were used
for the creation of the table.
were used
for the creation of the table.
The equations and methods described above are used for solving the
level population evolution equations for hydrogen,
| Pij = Cij + Rij. | (17) |
Numerically, Eq. (16) is solved in two steps. In the
first step, the populations from the previous time step are advected
with the flow in the hydrodynamics computation. In the second step,
the advected populations, mass density, and temperatures are used to
calculate the new rate coefficients. Then the rate equations (without
the advection term) form a system of linear ordinary differential
equations of first order, which is solved on the time interval between
the previous and current time step using the DVODE package
(Brown et al. 1989).
The solution yields the level populations for the current time
step. This system is solved with a relative accuracy of 10-4 for
each timestep. To ensure exact particle conservation we then scale the
updated population densities with the total hydrogen number density,
which is directly calculated from the mass density and the mass
fraction of hydrogen in the gas. This prevents cumulative buildup of
small errors. The code outputs the electron densities and hydrogen
level populations for the LTE case and the TD-NLTE case for each grid
cell.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{6123fig1.eps}
\end{figure}](/articles/aa/full/2006/46/aa6123-06/Timg46.gif) |
Figure 1: Time evolution of the ionisation degree F in a column of the simulation for the first 30 min of the simulation. Upper panel: LTE. Lower panel: TD-NLTE. The TD-NLTE simulation was started with LTE populations. The chromosphere shows large temporal variation in ionisation degree in the LTE case. The ionisation degree in the TD-NLTE case is relatively constant after the first 5 min, when the first few shocks have passed. |
| Open with DEXTER | |
We performed a three-dimensional numerical simulation using an upgraded version of the CO5BOLD code (Freytag et al. 2002). The relaxed end model by Wedemeyer et al. (2004) was adopted as initial model. The computational grid consists of 140 cells in each horizontal direction and 200 cells in the vertical direction. Horizontal resolution is 40 km, vertical resolution ranges from 46 km at the bottom to 12 km at the top of the computational domain. The horizontal extent is 5600 km. The vertical extent ranges from -1300 km below to 1783 km above average Rosseland optical depth unity. Radiative transfer is treated in the grey approximation. For more details on the hydrodynamics code see Wedemeyer (2003) and Wedemeyer et al. (2004). We let the simulation advance for 90 min of solar time. The first 30 min are reserved to ensure relaxation of the initial conditions, whereas the remaining 60 min are used for detailed analysis.
We used a five-level-plus-continuum hydrogen model atom with collisional transitions from each level to each other level. Radiative transitions from the ground level are not allowed, i.e., all Lyman transitions are put in detailed balance. Lyman cooling or heating is thus not possible, but as our model does not include a transition zone no significant effect even in the upper layers of our model is to be expected. The bound-bound oscillator strengths come from Johnson (1972) whereas the bound-free radiative cross sections are from Seaton (1960).
Figure 1 shows the time evolution of the ionisation
degree F along a column in the atmosphere. At
![]() min, the
simulation is started with LTE values for the hydrogen level
populations. The LTE panel (upper) shows the chromospheric shocks as
red streaks of high ionisation in the upper part of the atmosphere,
with cool, neutral gas in between. The typical time between successive
shocks is of the order of 2-3 min. In contrast, the ionisation
degree in the TD-NLTE case (lower panel) reaches a dynamical
equilibrium state of fairly constant ionisation already after 5 min,
when the first shocks have passed.
min, the
simulation is started with LTE values for the hydrogen level
populations. The LTE panel (upper) shows the chromospheric shocks as
red streaks of high ionisation in the upper part of the atmosphere,
with cool, neutral gas in between. The typical time between successive
shocks is of the order of 2-3 min. In contrast, the ionisation
degree in the TD-NLTE case (lower panel) reaches a dynamical
equilibrium state of fairly constant ionisation already after 5 min,
when the first shocks have passed.
Figure 2 shows horizontal slices through the
simulation after 60 min. At
![]() Mm the temperature and
density show little structure, as it is in between the reversed
granulation layer below
(see Leenaarts & Wedemeyer-Böhm 2005)
and the onset of strong shock formation in higher layers. The
time-dependent ionisation degree is almost in LTE, showing only a
somewhat higher ionisation degree in the cooler areas, where
over-ionisation in the Balmer continuum occurs. At
Mm the temperature and
density show little structure, as it is in between the reversed
granulation layer below
(see Leenaarts & Wedemeyer-Böhm 2005)
and the onset of strong shock formation in higher layers. The
time-dependent ionisation degree is almost in LTE, showing only a
somewhat higher ionisation degree in the cooler areas, where
over-ionisation in the Balmer continuum occurs. At
![]() Mm the
situation is different. Owing to the steady decline in average
density, the waves that are excited by the convective motions in the
photosphere have steepened into shocks. Both the temperature and
density fluctuations have increased. This has a profound effect on the
LTE ionisation degree. Because the ionisation degree is inversely
proportional to the electron density, the hydrogen ionisation at equal
temperature is much stronger than in deeper layers. In this particular
snapshot the peak ionisation degree at
Mm the
situation is different. Owing to the steady decline in average
density, the waves that are excited by the convective motions in the
photosphere have steepened into shocks. Both the temperature and
density fluctuations have increased. This has a profound effect on the
LTE ionisation degree. Because the ionisation degree is inversely
proportional to the electron density, the hydrogen ionisation at equal
temperature is much stronger than in deeper layers. In this particular
snapshot the peak ionisation degree at
![]() Mm is 0.89 at
Mm is 0.89 at
![]() K and the minimum is
K and the minimum is
![]() at T=1871 K. In
the time-dependent case the ionisation degree has less extreme values,
the maximum is 0.019 at 6443 K and the minimum is
at T=1871 K. In
the time-dependent case the ionisation degree has less extreme values,
the maximum is 0.019 at 6443 K and the minimum is
![]() at 2495 K. Note also that the positions of the extrema of
the TD-NLTE ionisation degree do not at all coincide with the
positions of the LTE extrema. The LTE ionisation degree depends on
the local mass density and temperature only, whereas in the
time-dependent case it also depends on the previous history of the
atmosphere.
at 2495 K. Note also that the positions of the extrema of
the TD-NLTE ionisation degree do not at all coincide with the
positions of the LTE extrema. The LTE ionisation degree depends on
the local mass density and temperature only, whereas in the
time-dependent case it also depends on the previous history of the
atmosphere.
At
![]() Mm this effect becomes even more striking. The average
density is lower, and temperature and density fluctuations are larger,
resulting in even larger LTE ionisation degree fluctuations. In
TD-NLTE the transition rates have become so small in the cool,
non-shocked areas that there is almost no recombination between the
passages of two shock waves. The transition rates are higher in shock
fronts as a direct result of higher temperature and density. Although
this leads to an increased ionisation degree in shock fronts, it
remains small compared to the LTE case. As a result the
time-dependent ionisation degree at this height is fairly constant, in
this snapshot varying only between 0.0014 and 0.021 with an average of
about 0.008.
Mm this effect becomes even more striking. The average
density is lower, and temperature and density fluctuations are larger,
resulting in even larger LTE ionisation degree fluctuations. In
TD-NLTE the transition rates have become so small in the cool,
non-shocked areas that there is almost no recombination between the
passages of two shock waves. The transition rates are higher in shock
fronts as a direct result of higher temperature and density. Although
this leads to an increased ionisation degree in shock fronts, it
remains small compared to the LTE case. As a result the
time-dependent ionisation degree at this height is fairly constant, in
this snapshot varying only between 0.0014 and 0.021 with an average of
about 0.008.
Figure 3 shows some physical quantities along a
vertical slice of the same snapshot as in Fig. 2.
Panel a shows the temperature, with granulation near 0 Mm, reversed
granulation around 0.2-0.3 Mm, and shocks above ![]() 0.7 Mm. The
mass density (panel b) decreases towards larger height, while its
horizontal fluctuations increase. Panels c and d show the hydrogen
ionisation degree F in LTE and TD-NLTE, respectively. The LTE case
follows the increase of horizontal inhomogeneities with height, with
high ionisation in the high-temperature shock waves. In contrast, the
TD-NLTE case shows only small horizontal variation and the presence of
shocks can hardly be discerned. Finally, panels e and f show the
electron density in LTE and TD-NLTE. The electron density is mainly
set by the hydrogen ionisation and - in first approximation - can be
thought of as a multiplication of the density with F. Contributions
from other elements are dominant only where F is lower than
0.7 Mm. The
mass density (panel b) decreases towards larger height, while its
horizontal fluctuations increase. Panels c and d show the hydrogen
ionisation degree F in LTE and TD-NLTE, respectively. The LTE case
follows the increase of horizontal inhomogeneities with height, with
high ionisation in the high-temperature shock waves. In contrast, the
TD-NLTE case shows only small horizontal variation and the presence of
shocks can hardly be discerned. Finally, panels e and f show the
electron density in LTE and TD-NLTE. The electron density is mainly
set by the hydrogen ionisation and - in first approximation - can be
thought of as a multiplication of the density with F. Contributions
from other elements are dominant only where F is lower than
![]() ,
i.e., around 0.4 Mm and - in the LTE case - in
the cool areas in the chromosphere. Again, in the time-dependent case
the extrema and horizontal variations are smaller in TD-NLTE than in LTE.
,
i.e., around 0.4 Mm and - in the LTE case - in
the cool areas in the chromosphere. Again, in the time-dependent case
the extrema and horizontal variations are smaller in TD-NLTE than in LTE.
![\begin{figure}
\par\includegraphics[width=17.1cm,clip]{6123fig2.eps}
\end{figure}](/articles/aa/full/2006/46/aa6123-06/Timg59.gif) |
Figure 2:
Horizontal slices through a simulation snapshot at
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6123fig3.eps}
\end{figure}](/articles/aa/full/2006/46/aa6123-06/Timg60.gif) |
Figure 3: Vertical cut through the snapshot along the line indicated in Fig. 2. a) gas temperature; b) mass density; LTE c) and TD-NLTE d) ionisation degree; LTE e) and TD-NLTE f) electron density. Note that the deepest layers of the model are not shown. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6123fig4.eps}
\end{figure}](/articles/aa/full/2006/46/aa6123-06/Timg61.gif) |
Figure 4: Departure coefficients of our model hydrogen atom in the same cut as Fig. 3 for the continuum and level n=5 down to level n=1 from top to bottom. The solution is nearly in LTE from the bottom of the computational domain up to 0.3 Mm above the average Rosseland optical depth unity. The largest deviations occur in cool chromospheric regions in between shocks, where, owing to the low temperature, the Saha-Boltzmann equation predicts a very low occupation fraction for all excited levels. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{6123fig5.eps}
\end{figure}](/articles/aa/full/2006/46/aa6123-06/Timg62.gif) |
Figure 5: Histogram of the logarithmic ionisation degree as a function of height for the LTE ( upper panel) and TD-NLTE ( lower panel) case. The averages in LTE and TD-NLTE are plotted as red dashed and blue solid lines, respectively. All columns have been individually scaled to maximum contrast to enhance visibility. |
| Open with DEXTER | |
Figure 4 shows the departure coefficients for each
level of our model atom in the same slice as Fig. 3.
The departure coefficient is defined as the ratio of the population
densities of a particular atomic energy level in NLTE and in LTE,
![]() .
Below z=0.3 Mm the
departure coefficients for all levels are close to 1, i.e., hydrogen is
in or very near LTE. Above these heights deviations occur. The
ground level (n =1, lowest panel) is very close to LTE for most of
the chromosphere, except in strong shocks. In the shocks the
ionisation lags behind compared to LTE, resulting in a slight
overpopulation of the ground level (which is the reservoir where
ionised hydrogen atoms are coming from). The other levels are strongly
collisionally coupled with each other and show similar behaviour in
the chromosphere. They are slightly underpopulated in the shock area
because the ionisation time scale is comparable or slightly longer
than the typical shock crossing time. The density of the ionised state
H II (the continuum level) is correspondingly lower than in LTE. Due
to the strong coupling to the H II density, b < 1 for all excited
levels of neutral hydrogen (
.
Below z=0.3 Mm the
departure coefficients for all levels are close to 1, i.e., hydrogen is
in or very near LTE. Above these heights deviations occur. The
ground level (n =1, lowest panel) is very close to LTE for most of
the chromosphere, except in strong shocks. In the shocks the
ionisation lags behind compared to LTE, resulting in a slight
overpopulation of the ground level (which is the reservoir where
ionised hydrogen atoms are coming from). The other levels are strongly
collisionally coupled with each other and show similar behaviour in
the chromosphere. They are slightly underpopulated in the shock area
because the ionisation time scale is comparable or slightly longer
than the typical shock crossing time. The density of the ionised state
H II (the continuum level) is correspondingly lower than in LTE. Due
to the strong coupling to the H II density, b < 1 for all excited
levels of neutral hydrogen (
![]() to
to
![]() ), too. In the cool
intershock areas all levels except
), too. In the cool
intershock areas all levels except
![]() are hugely
overpopulated. This is because the Saha and Boltzmann equations
predict extremely low population fractions for excited states and the
continuum for temperatures and electron densities typical for the
intershock regions. Thus, these enormous overpopulations simply
illustrate the complete failure of Saha-Boltzmann equilibrium
partitioning.
are hugely
overpopulated. This is because the Saha and Boltzmann equations
predict extremely low population fractions for excited states and the
continuum for temperatures and electron densities typical for the
intershock regions. Thus, these enormous overpopulations simply
illustrate the complete failure of Saha-Boltzmann equilibrium
partitioning.
Figure 5 shows a height-dependent histogram of the
ionisation degree. In LTE there is a strong bifurcation of the
ionisation degree as a result of the bimodal temperature distribution
in our model chromosphere
(cf. Fig. 7 of Wedemeyer et al. 2004).
In TD-NLTE this bifurcation is not present. For both cases there is a
minimum in average ionisation degree at
![]() Mm, roughly
corresponding to the classical temperature minimum in 1D static
quiet-Sun models. Quite surprisingly, the average ionisation degree in
the chromosphere is lower in the TD-NLTE case than in LTE. This is
because the average is determined mainly by the high LTE ionisation
degree in the shocks whereas in the TD-NLTE case the ionisation degree
is smaller there.
Mm, roughly
corresponding to the classical temperature minimum in 1D static
quiet-Sun models. Quite surprisingly, the average ionisation degree in
the chromosphere is lower in the TD-NLTE case than in LTE. This is
because the average is determined mainly by the high LTE ionisation
degree in the shocks whereas in the TD-NLTE case the ionisation degree
is smaller there.
| |
Figure 6:
Average TD-NLTE ionisation degree for our CO5BOLD model
(solid), CS2002's RADYN model (dashed) and the statistical
equilibrium FAL model C (dotted). The zero point of the
height scale is the average
|
| Open with DEXTER | |
| |
Figure 7: Vertical cut through the snapshot along the line indicated in Fig. 2 showing the relative contribution of other elements than hydrogen to the electron density. In the chromosphere the other elements contribute mostly in the high temperature shocks. |
| Open with DEXTER | |
Figure 6 shows a comparison of the average ionisation degree for our model, the detailed 1D study of CS2002, and the FAL model C (Fontenla et al. 1993). The latter is a static and one-dimensional semi-empirical model, constructed under the assumption of statistical equilibrium, while the RADYN and CO5BOLD models are dynamic but differ in the number of spatial dimensions. All models nevertheless show the same qualitative behaviour, with a minimum in ionisation degree between 200 and 500 km, and a rise of the average ionisation degree with height in the chromosphere. The cause of this behaviour, however, is different. In the static FAL-C model, the ionisation degree reflects a corresponding chromospheric temperature rise. In contrast the rise in ionisation degree in the dynamical RADYN and CO5BOLD models is due to the temperature in shock fronts, which increases with height, without need for a rise in average temperature (Carlsson & Stein 1995).
Qualitatively our CO5BOLD results are comparable to the detailed 1D study of CS2002. We attribute the remaining differences in ionisation degree to the different dimensionality of the code (1D vs. 3D) and the resulting different temperature structure. 1D simulations suffer from shock merging that lead to too high shock temperatures (Ulmschneider et al. 2005). Additionally, we do not include the effect of the time-dependent ionisation on the equation of state, causing too low shock temperatures in our CO5BOLD model (Carlsson & Stein 1992). Third, CS2002 include a transition region and corona in their model which influence the ionisation degree in the upper chromosphere, both by Lyman radiation ionising the upper chromosphere and the varying height of their transition zone. Their transition zone is sometimes considerably lower than 1.5 Mm, influencing the average ionisation degree. Fourth, it cannot be ascertained that the fixed radiative rates that we employ, which are accurate in 1D, are also accurate in 3D. This might affect our results as well.
Contributions to the electron density from other elements than hydrogen are still treated under the assumption of LTE. This will mostly affect the upper photosphere where the hydrogen ionisation degree is so low that metals such as iron, magnesium, and silicon are the main electron donors. Hydrogen is the dominant donor in all other regions. However, in the chromospheric shocks the other elements contribute around 10% of the electrons (see Fig. 7). Thus we expect a small error in the chromospheric electron density due to the LTE treatment of the other elements (see Rammacher & Ulmschneider 2003 for TD-NLTE effects on magnesium ionisation). For future simulations that take the transition region into account, a TD-NLTE treatment of helium might be of importance for the electron density as well, as the higher temperatures will lead to significant helium ionisation.
All in all we conclude that our 3D simulation with time-dependent hydrogen ionisation produces reasonably realistic - if probably somewhat too low - results for the ionisation degree and electron density, given the level of necessary simplification and resulting increase in computational speed.
With our method we can supply snapshots of 3D (M-)HD solar atmosphere simulations for detailed radiative transfer calculations containing time-dependent electron densities. Up until now most MHD simulations could only provide LTE electron densities, which are far from realistic in the chromosphere. The TD-NLTE electron densities are crucial in forward modelling of chromospheric diagnostics like the CaII H&K and infrared lines and (sub-)millimetre continua (see Leenaarts & Wedemeyer-Böhm 2006 for an example of the effect on TD-NLTE electron densities on the latter), as collisions between electrons and atoms provide the coupling of the state of the gas to the radiation field via the source function, and affect the opacities of for example H free-free and H- bound-free and free-free transitions.
As it is now, the code computes the ionisation degree and electron density from the state parameters defined by the hydrodynamics simulation. Future improvement of the method should take into account the back-coupling of the ionisation to the equation of state. The deviation from instantaneous ionisation equilibrium makes it impossible to use pre-computed lookup tables for the equation of state. In addition, the lookup tables that give the bin-averaged source function and opacity (computed in LTE as function of temperature and pressure) are then no longer consistent with the state of the gas. New methods have to be developed to handle this complex problem. In particular, implementing such physics in a Riemann-solver as used in CO5BOLD is non-trivial. Nevertheless this work is currently in progress. Significant influence on chromospheric wave propagation and temperature structure in the chromosphere can be expected (cf. Carlsson & Stein 1992).
Another necessary improvement is the relaxation of the assumption of the fixed radiative rates. This is mainly important for the Balmer continuum, which is the driver of the ionisation. A radiative rate that is proportional to the mean grey intensity, or, in the case of multi-group opacity methods, the mean intensity in the continuum is an obvious choice. Such a method would take the variation in the average radiation field due to the granulation pattern into account. It will give more accurate results in the case of strong horizontal inhomogeneities in gas temperature and density in the upper photosphere, as it is the case in the presence of magnetic fields.
Simulations for other stellar types than the Sun are possible but involve re-adjustment of the radiation temperatures. This requires a similar detailed 1D analysis and calibration as Sollum performed for the Sun for each spectral type separately.
Acknowledgements
The authors would like to thank O. Steiner, J. Bruls, and H.-G. Ludwig for illuminating discussions and R. J. Rutten, C. Keller and the referee for improvements to the manuscript. H. Uitenbroek provided his RH code. J. Leenaarts recognises support from the Deutscher Akademischer Austauschdienst, support from the USO-SP International Graduate School for Solar Physics (EU contract nr. MEST-CT-2005-020395) and hospitality at the Kiepenheuer-Institut für Sonnenphysik. S. Wedemeyer-Böhm was supported by the Deutsche Forschungsgemeinschaft (DFG), grant Ste 615/5.