A&A 460, 331-337 (2006)
DOI: 10.1051/0004-6361:20065860

Energy levels and radiative rates for transitions in Fe IX[*]

K. M. Aggarwal1 - F. P. Keenan - T. Kato2 - I. Murakami2


1 - Department of Physics and Astronomy, Queen's University, Belfast BT7 1NN, Northern Ireland, UK
2 - National Institute for Fusion Science, Oroshi-cho, Toki, Gifu 509-5292, Japan

Received 20 June 2006 / Accepted 30 August 2006

Abstract
Aims. In this paper we report calculations for energy levels and radiative rates for transitions in Fe IX.
Methods. The General purpose Relativistic Atomic Structure Package ( GRASP) has been adopted for the calculation of energy levels and radiative rates.
Results. Energies for the lowest 360 levels, including those from the (1s22s22p6) 3s23p6, 3s23p53d, 3s3p63d, 3s23p43d2, and 3s23p54$\ell$ configurations of Fe IX, are reported. Additionally, radiative rates, oscillator strengths, and line strengths are reported for all electric dipole (E1), magnetic dipole (M1), electric quadrupole (E2), and magnetic quadrupole (M2) transitions among these levels. Comparisons are made with the available results in the literature, and the accuracy of the present data is assessed. Finally, lifetimes for all excited levels are listed, and comparisons made with earlier available measurements and theoretical results.

Key words: atomic data - atomic processes

1 Introduction

This paper is a continuation of our work on generating atomic data (energy levels, radiative rates, collision strengths and excitation rates) for iron ions, for which we have already reported calculations for Fe X (Aggarwal & Keenan 2004b, 2005b), Fe XI (Aggarwal & Keenan 2003a,b), Fe XIII (Aggarwal & Keenan 2004a, 2005b), Fe XV (Aggarwal et al. 2001, 2003a), Fe XVI (Aggarwal & Keenan 2006a, b), Fe XVII (Aggarwal et al. 2003b, 2004), Fe XVIII (Jonauskas et al. 2004), Fe XXI (Aggarwal & Keenan 1999, 2001) and Fe XXIV (McKeown et al. 2004). Iron is an abundant element in solar and fusion plasmas, and its emission lines are observed over almost all ionization stages. To analyse the vast amount of observational data available from space missions such as SOHO, Chandra, XMM-Newton and Solar-B, theoretical atomic data for Fe ions are required, as there is a paucity of desired experimental results.

Here we report atomic data for transitions in Fe IX. Emission lines of Ar-like Fe IX in solar plasmas have been observed and analysed by many workers, such as: Behring et al. (1976), Dere (1978), Thomas & Neupert (1994), Brickhouse et al. (1995), and Young et al. (1998). These lines have also been measured in electron beam ion trap (EBIT) machines, and have been listed in the 50-175 $\AA$ range by Lepson et al. (2002). Particularly important are the bright solar lines in the 170-250 $\AA$ range, which belong to the levels of the 3s23p6 and 3s23p53d configurations. The ratio of the magnetic quadrupole (M2) transition (3s23p61S0-3s23p53d 3P$^\circ_2$) at 241.7 $\AA$ and the intercombination (E1) transition (3s23p6 1S0-3s23p53d 3P$^\circ_1$) at 244.9 $\AA$ is sensitive to electron density over the range 109-1013 cm-3 - see Fig. 4 of Storey et al. (2002). Since these two lines are not significantly blended, they provide an excellent density diagnostic. Therefore, many workers have reported atomic data for transitions in Fe IX, but almost all the earlier calculations have been limited to only a few levels/transitions. However, two calculations have appeared recently which have covered a wider range of levels/transitions, namely those of Storey et al. (2002) and Verma et al. (2006).

Storey et al. (2002) reported results for energy levels, radiative rates (A-values), and effective collision strengths ($\Upsilon$) for transitions among the lowest 140 levels of the (1s22s22p63s2) 3p6, 3p53d, 3p54s, 3p54p, and 3p43d2 configurations. For the calculations of energy levels and A-values, they adopted the SuperStructure (SS) code of Eissner et al. (1974), and for the scattering calculations the semi-relativistic R-matrix code of Berrington et al. (1978) was employed. In the generation of wavefunctions they included configuration interaction (CI), mainly within the n = 3 orbitals but also with (3s23p5) 4s and 4p, and noted the significant contribution of the 3p43d2 configuration in the determination of energy levels, which has also been highlighted earlier by Liedahl (2000). Since this configuration generates 111 levels, and most of these have energies between the levels of the 3p53d and 3p54p configurations (see Table 1), their inclusion in a scattering calculation becomes almost essential, because the resonances arising from these significantly contribute to the determination of $\Upsilon$values, even at the high temperatures ($\sim$106 K) at which data are required for Fe IX, as discussed and demonstrated by Storey et al. Therefore, considering that they have included reasonable CI in the generation of wavefunctions, the contribution of relativistic effects in the scattering process as well as of the resonances in the determination of $\Upsilon$ values, their results should be the most reliable. However, we find there is scope for improvement for the following reasons.

Firstly, Storey et al. (2002) did not report their results for all transitions among the 140 levels of their calculations, although they have recently made available a larger amount of data on the CHIANTI database at http://wwwsolar.nrl.navy.mil/chianti.html. This available data still covers less than a quarter of the permissible 9730 transitions. Secondly, they calculated A-values for the electric dipole (E1) transitions alone, whereas in a modelling calculation similar results for other types of transitions, namely magnetic dipole (M1), electric quadrupole (E2), and magnetic quadrupole (M2), may also be required. Both of these requirements of having a complete set of data and for all types of transitions have recently been emphasized by Liedahl (2000) and Del Zanna et al. (2004). Finally, and more importantly, CI is very important for defining the target, as mentioned by Storey et al. Inclusion of only moderate CI in the generation of wavefunctions may be the reason that their energy levels of the 3s23p54s and 3s23p54p configurations are in variance, in both magnitude and orderings with the more recent calculations of Verma et al. (2006), as discussed in Sect. 2. Therefore, apart from presenting a complete set of data, our aim is to improve the accuracy of the energy levels, and subsequently of the radiative rates. In doing so, we also avail the opportunity to extend their calculations by including additional levels from the higher excited configurations.

Recently, Verma et al. (2006) have reported results for energy levels, radiative rates and lifetimes among the lowest 87 levels of the 3s23p6, 3s23p53d, 3s23p54$\ell$, 3s3p63d, 3s3p64s, 3s3p64p, 3s23p55s, 3s23p55p, and 3s23p55d configurations of Fe IX. In their calculations, they have adopted the CIV3 code of Hibbert (1975a), and have included elaborate CI (up to n = 6 orbitals) along with the one-body relativistic operators. Unfortunately, their reported results are not much useful for applications in plasma analysis, mainly for three reasons. Firstly, and most importantly, they have excluded the levels of the 3p43d2configuration, the importance of which has already been discussed above. Secondly, in the generation of wavefunctions they have excluded the important 3s23p33d3configuration, whose levels closely interact with those of the 3s23p43d2 and 3s3p53d2 configurations, and hence have a direct impact on the accuracy of the energy levels. Since this configuration alone generates 350 levels, its inclusion in a calculation becomes computationally demanding. This is the reason that Verma et al. excluded this configuration and Storey et al. (2002) included only a few terms of it. Therefore, we find that there is ample scope for improving the accuracy of the available energy levels. Finally, Verma et al. also calculated A-values for the E1 transitions alone. Therefore, apart from providing a complete set of A-values for all types of transitions, we try to resolve differences between their calculations and those of Storey et al. for some of the levels, so that data can be applied with confidence in plasma modelling.

In the present work, we mostly focus on the lowest 360 levels of the 3s23p6, 3s23p53d, 3s3p63d, 3s23p43d2, 3s3p53d2, 3s23p33d3, 3s3p43d3, 3p63d2, 3s23p54$\ell$, 3s3p64$\ell$, 3s23p43d4$\ell$, and 3s3p53d4$\ell$ configurations of Fe IX, although calculations have been performed for a larger number of levels up to 2471. Additionally, our approach is fully relativistic, as we employ the GRASP (General purpose Relativistic Atomic Structure Package) code of Dyall et al. (1989) to calculate radiative rates (A-values) for the four types of transitions mentioned above. Finally, we also report lifetimes for all excited levels, and make comparisons with other available theoretical and experimental results.

2 Energy levels

The 3s23p6, 3s23p53d, 3s3p63d, 3s23p43d2, and 3s3p53d2 configurations of Fe IX give rise to 218 fine-structure levels. However, these levels closely interact with the 881 levels of the 3s23p33d3, 3s3p43d3 and 3p63d2 configurations. Inclusion of all of these configurations in a calculation is almost essential, because of their close interaction and almost continuous range of energy. This has already been noted by Liedahl (2000), and we too have arrived at the same conclusion after a few tests. This calculation, referred to as GRASP1, and performed with the above listed 8 configurations, includes a total of 1099 levels. Since many transitions arising from the n = 4 configurations are also observed (Lepson et al. 2002), and have the interacting energy range with the above 1099 levels, our GRASP1 calculation is not sufficient, and needs to be expanded for accuracy. Therefore, we have performed yet another calculation, referred to as GRASP2, in which we include a total of 2471 levels. The additional 1372 levels arise from the 3s23p54$\ell$, 3s3p64$\ell$, 3s23p43d4$\ell$ and 3s3p53d4$\ell$ configurations. This will help us in assessing the accuracy of results for the lowest levels in addition to fulfilling the requirement of those who need a larger amount of data for spectral modelling. Since it is not feasible to present and analyse the entire data in this paper, we focus our efforts on the lowest 360 levels only, which include all levels from the 3s23p6, 3s23p53d, 3s3p63d, 3s23p43d2, and 3s23p54$\ell$ configurations. However, the entire set of atomic data for energy levels and radiative rates for all four types of transitions (E1, E2, M1 and M2) are available in electronic form on request from KMA (K.Aggarwal@qub.ac.uk) or IM (mizumi@nifs.ac.jp), and a complete list of all the 2471 levels is also available in a printed form in Aggarwal et al. (2007a).

Table 2: Comparison of energy levels (in Ryd) of Fe IX.

Before we discuss our results, we would like to point out that CI, apart from relativistic effects, is very important for Fe IX, in spite of it being moderately heavy (Z = 26). Therefore, apart from including up to the n = 4 configurations in our above described GRASP calculations, we have also experimented with the n = 5 and 6 configurations, as well as with all other combinations of the n = 3 configurations, which have not been specifically listed above. This experimentation has mainly been performed with the Flexible Atomic Code ( FAC) of Gu (2003), which is available from the website http://kipac-tree.stanford.edu/fac. This is a fully relativistic code like GRASP, but is comparatively easier to run. Since results obtained from GRASP and FAC are generally in excellent agreement (see, for example, Aggarwal et al. 2007b, for Mg-like ions), our calculations from FAC enable us to assess the contribution of extensive CI in a fully relativistic work. We have performed several sets of calculations, and the largest one includes up to 6284 levels.

Our calculated energies obtained from the GRASP code, from both GRASP1 and GRASP2 calculations, are listed in Table 1 for the lowest 360 levels. For our calculations, we have used the option of extended average level (EAL), in which a weighted (proportional to 2j+1) trace of the Hamiltonian matrix is minimized. This produces a compromise set of orbitals describing closely lying states with moderate accuracy. The calculations also include corrections from the Breit and QED effects. Also included in Table 1 are the experimental compilations of the National Institute of Standards and Technology (NIST), which are available at the website http://physics.nist.gov/PhysRefData, and the available theoretical results of Storey et al. (2002) and Verma et al. (2006).

As can be seen in Table 1, experimental energies are available only for the lowest 17 levels plus some of the levels of the 3s23p54$\ell$ configurations. The energy levels of Verma et al. (2006), who adopted the CIV3 code of Hibbert (1975a), agree with the experimental ones within 1%, because they have adjusted their Hamiltonian accordingly. By contrast, the lowest 17 energy levels of Storey et al. (2002) differ up to 0.15 Ryd ($\sim$2%) with the experimental ones, as seen in their Table 6. However, the corresponding differences for the (3s23p54s) 3P$^\circ_1$ and 1P$^\circ_1$ levels (94 and 96) are up to 5%, and their energies are higher than all others listed in Table 1, including the experimental ones. Their calculated energies for the levels of the 3s23p54p configuration are also higher, up to 0.55 Ryd or equivalently $\le$6%, than our results or those of Verma et al. Furthermore, the ordering of their levels is also different from those of us or Verma et al. - see, for example, levels 118-120 and 137-139. This is because they included only limited CI in the construction of their wavefunctions, as discussed above in Sect. 1.

Our energy levels from the GRASP1 and GRASP2 calculations agree closely (within 1%), except for the 3s23p4(3P)3d2(3P) level (138), for which the difference is 0.24 Ryd. Since our calculations are ab initio, differences among the lower levels with the corresponding experimental energies are up to 0.15 Ryd (for example, see level 13). Among the higher levels, these differences are slightly higher (up to 0.4 Ryd) for some of the levels, such as: 273-288 and 323. However, the level orderings are the same between theory and experiment. Similarly, differences with the CIV3 calculations of Verma et al. (2006) are smaller than 0.4 Ryd (see, for example, levels 13, 131, 203 and 356), although there are only 87 common levels between the two calculations. More importantly, the level orderings of Verma et al. are different from ours in a few instances, such as for levels: 118-119, 125-131 and 203-206.

Before we comment on the accuracy of our energy levels, we would like to discuss the impact of more extensive CI. In Table 2, we focus on the lowest 17 levels of the 3s23p6, 3s23p53d and 3s3p63d configurations, because experimental data are mostly available for these levels alone, as mentioned earlier. Also included in this table are our results from the GRASP code (larger calculation with 2471 levels), as well as from the FAC code. There are 5 calculations from FAC, namely FAC1 (87 levels from the 3s23p6, 3s23p53d, 3s23p54$\ell$, 3s3p63d, 3s3p64s, 3s3p64p, 3s23p55s, 3s23p55p and 3s23p55d configurations, i.e. the same levels as included by Verma et al. 2006), FAC2 (136 levels, i.e. all those of FAC1 plus 3s23p55f, 3s23p55g, 3s3p64d and 3s3p64f), FAC3 (220 levels, i.e. all those of FAC2 plus 3s23p56$\ell$ and 3s3p66$\ell$), FAC4 (1219 levels of the 3s23p6, 3s23p53d, 3s3p63d, 3s23p43d2, 3s3p53d2, 3s23p33d3, 3s3p43d3, 3p63d2, 3s23p54$\ell$, 3s23p55$\ell$, 3s3p64$\ell$ and 3s3p65$\ell$ configurations), and finally FAC5, which includes all possible combinations of the n = 3 configurations plus 3s23p54$\ell$, 3s23p55$\ell$, 3s3p64$\ell$ and 3s3p65$\ell$.

The energy levels from our FAC1, FAC2 and FAC3 calculations are almost the same, because the levels of the n = 4-6 configurations have higher energies above 8.6 Ryd, as can be seen in Table 1. In these calculations, the agreement with the corresponding experimental energies is excellent for the lowest 12 levels, but differences for the levels of the 3s3p63d configuration are higher (up to 10%), and the theoretical results are invariably higher. On the other hand, results from the FAC4 and FAC5 calculations are similar, because they both include the two most important configurations, namely 3s23p43d2 and 3s23p33d3, whose energy levels closely interact with those of others. For this reason, both of these calculations have considerably improved the energies of the levels of the 3s3p63d configuration, but the energies of the lowest 12 levels have become slightly worse, in comparison to those obtained from FAC1, FAC2 and FAC3. Therefore, it is very difficult to strike a balance of the configurations, which can provide reasonably accurate energy levels covering a wider range. Based on these (and similar other) comparisons, we have arrived at the conclusion that our GRASP2 calculations are probably the best, and the accuracy for the majority of the levels is better than 1%.

Finally, we would like to mention that mixing among some of the levels (such as: 46 and 56 and 99 and 100) is very strong. As a result of this, the identification of a particular level is not unique, and is not based on the strength of the dominant eigenvector alone. This is a common problem in all atomic structure calculations, especially when the levels of a configuration are highly mixed. Therefore, the configuration and the J values given in Table 1 are definite, but the corresponding LSJ designation provided for a level is only for guidance, and is liable to interchange.

3 Radiative rates

The absorption oscillator strength (fij) and radiative rate Aji (in s-1) for a transition $i \to j$ are related by the following expression:


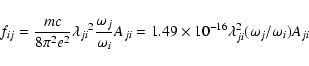\begin{displaymath}f_{ij} = \frac{mc}{8{\pi}^2{e^2}}{\lambda_{ji}}^2 \frac{{\ome... ...1.49 \times 10^{-16} \lambda^2_{ji} (\omega_j/\omega_i) A_{ji} \end{displaymath} (1)

where m and e are the electron mass and charge, respectively, c is the velocity of light, $\lambda_{ji}$ is the transition energy/wavelength in $\AA$, and $\omega_i$ and $\omega_j$ are the statistical weights of the lower (i) and upper (j) levels, respectively. An equally useful, but related, parameter is the line strength S:


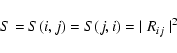\begin{displaymath}S = S(i,j) = S(j,i) = {\mid{R_{ij}}\mid}^2 \end{displaymath} (2)

where


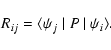\begin{displaymath}R_{ij} = \langle \psi_j \mid P \mid \psi_i\rangle. \end{displaymath} (3)

$\psi_i$ and $\psi_j$ are the initial and final state wavefunctions, and Rij is the transition matrix element of the appropriate mulipole operator P, and involves an integration over spatial and spin coordinates of all N electrons of the ion - see Sect. 5.1.2 of Hibbert (1975b) for further details. However, the oscillator strength fij (dimensionless) and the line strength S (in atomic unit, 1 a.u. = $6.460 \times 10^{-36}$ cm2 esu2) are related by the following standard equations:

For the electric dipole (E1) transitions:

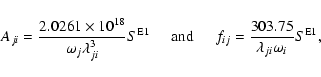\begin{displaymath}A_{ji} = \frac{2.0261\times{10^{18}}}{{{\omega}_j}\lambda^3_{... ... f_{ij} = \frac{303.75}{\lambda_{ji}\omega_i} S^{\rm E1}, \\ \end{displaymath} (4)

for the magnetic dipole (M1) transitions:

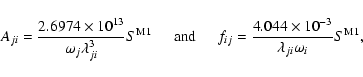\begin{displaymath}A_{ji} = \frac{2.6974\times{10^{13}}}{{{\omega}_j}\lambda^3_{... ...ac{4.044\times{10^{-3}}}{\lambda_{ji}\omega_i} S^{\rm M1}, \\ \end{displaymath} (5)

for the electric quadrupole (E2) transitions:

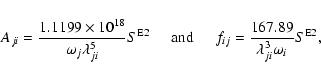\begin{displaymath}A_{ji} = \frac{1.1199\times{10^{18}}}{{{\omega}_j}\lambda^5_{... ...m} f_{ij} = \frac{167.89}{\lambda^3_{ji}\omega_i} S^{\rm E2}, \end{displaymath} (6)

and for the magnetic quadrupole (M2) transitions:

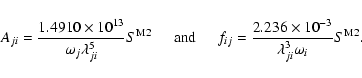\begin{displaymath}A_{ji} = \frac{1.4910\times{10^{13}}}{{{\omega}_j}\lambda^5_{... ...{2.236\times{10^{-3}}}{\lambda^3_{ji}\omega_i} S^{\rm M2}. \\ \end{displaymath} (7)

In Table 3 we present transition energies/wavelengths ($\Delta$Eij in $\AA$), radiative rates (Aji in s-1), oscillator strengths (fij, dimensionless), and line strengths (S in au), in length form only, for all 14 665 electric dipole (E1) and 22 292 electric quadrupole (E2) transitions among the lowest 360 levels of Fe IX. The indices used to represent the lower and upper levels of a transition have already been defined in Table 1. Similar results for 15 469 magnetic dipole (M1) and 20 970 magnetic quadrupole (M2) transitions are listed in Table 4.

Table 5: Comparison of oscillator strengths for some transitions of Fe IX. ( $a\pm b \equiv a\times 0^{{\pm }b}$).

Since the electric dipole (E1) transitions are comparatively more important, and most of the results available in the literature are confined to these transitions alone, we focus on the accuracy assessments of their f-values alone. In Table 5 we compare our results from the GRASP1, GRASP2 and FAC calculations with those from the CIV3 (Verma et al. 2006) and SS (Storey et al. 2002) codes. The FAC calculations correspond to the FAC4 configurations described in Sect. 2, and also included in this table are the ratio of the length and velocity forms of the f-values (fL/fV) from the GRASP2 and CIV3 calculations, because these give some indication of the accuracy of the results. Furthermore, in this table we restrict the comparisons for transitions among the lowest (and common to all calculations) 17 levels of Fe IX. This comparison will give us sufficient information about the accuracy of our radiative rates.

Our f-values from the GRASP1 and GRASP2 calculations generally agree within $\sim$10% for a majority of transitions, and the only exceptions are the two weak transitions (9-14 and 12-15), whose values are $\sim$10-6. This highly satisfactory agreement between the two calculations, with differing amount of CI included, clearly shows that the effect of additional CI with the n = 4 configurations has no noticeable effect on the f-values. The same conclusion can be drawn about the effect of the n= 5 configurations, because our f-values from the FAC calculations are comparable (within 10%) with those from the GRASP code. Similarly, the earlier obtained results of Storey et al. (2002) from the SS code generally agree within 20% for a majority of transitions, and the only exceptions are three weak transitions, namely 7-16, 9-14 and 12-15, whose f-values are $\le$10-5. For these very weak transitions, the f-values of Storey et al. differ by up to an order of magnitude. Such large differences for weak transitions are very common, and mainly arise from the cancellation effect of the mixing coefficients and/or the inclusion/exclusion of large CI. Although the f- or A-values for such transitions may also be required in any modelling or diagnostic work, their contribution is much less important in comparison to those from the stronger transitions. Therefore, a larger variation in their values among different calculations and/or between their fL and fV values, do not affect the overall accuracy of a calculation.

The other f-values listed in Table 5 are from the most recent calculations of Verma et al. (2006), who have adopted the semi-relativistic CIV3 code of Hibbert (1975a). Apart from the first three transitions (i.e. 1-3, 10 and 13), their reported f-values do not agree with any of the calculations listed in this table, and differ by up to a factor of two for stronger transitions, such as: 5-16, 6-15, 7-14 and 8-16. For weaker transitions ($f \le$ 0.01), their f-values differ by up to two orders of magnitude - see, for example, transitions 3-17, 9-14 and 12-15. Since the SS code adopted by Storey et al. (2002) is also semi-relativistic, the differences with the CIV3 calculations of Verma et al. cannot be attributed to the contribution of the two-body relativistic operators included in the fully relativistic GRASP and FAC codes. The major differences arise due to the fact that they have excluded the important 3s23p33d3 configuration in the generation of their wavefunctions, as discussed in Sect. 1, and have preferred to rely too much on the adjustment of their matrix elements in accordance with the available experimental energy levels. This procedure is only helpful to a certain extent, as it corrects the transition energies, but is mostly valid when the experimental energies are available for a majority of the levels, which is not the case for Fe IX as seen in Table 1, although levels of the transitions in Table 5 are not affected by this. This is because the basic errors in computing the matrix elements still remain, as mentioned by Hibbert (1975b) and recently demonstrated by Aggarwal et al. (2007b) for three Mg-like ions. Therefore, based on the comparison made in Table 5, the reported f-values of Verma et al. do not appear to be very accurate. However, before forming conclusions on the accuracy of our results, we make some other assessments below for a larger number of transitions, because the transitions in Table 5 represent only 0.27% (39) of a total of 14 665.

A general criterion to assess the accuracy of the A- or f-values is to compare their length and velocity forms. Before we discuss these we would like to remind readers that such comparisons are desirable, but are not a fully sufficient tests to assess the accuracies (Hibbert 1975b), as different calculations (or combinations of configurations) may give comparable f-values in the two forms, but entirely different results in magnitude - see Aggarwal et al. (2007b) for further details and comparisons. In fact, for the transitions discussed above in Table 5 the ratios fL/fV from the GRASP and CIV3 calculations are also comparable, yet the f-values are quite different, as already discussed. Nevertheless, we discuss the two forms below in order to make some assessment about the accuracy of the results.

Table 6: Comparison between experimental (Träbert et al. 2003) and theoretical lifetimes for some levels of Fe IX.

Among the stronger transitions (i.e. $f \ge$ 0.01), the length and velocity forms differ by over 20% for 114 (<0.8%) transitions, whereas only 83 (<0.6%) transitions have differing f-values of over 50%, but below a factor of five. Examples of such transitions are: 48-232, 63-269 and 112-203, and none of the transitions is a resonance line. However, two transitions, namely 98-193 ( f = 0.0106) and 100-203 ( f = 0.0104), have ratios ( AL/AV = fL/fV) of 0.003. Such large differences for some strong transitions are often observed, and are due to the inclusion (or exclusion) of extensive CI, as discussed in detail by Aggarwal (1998) for transitions in Fe XXI. However, differences between the two forms for weaker transitions (f < 0.01) are up to several orders of magnitude, particularly for those whose f-values are $\le$10-5. Examples of such transitions are: 3-21 ( $f = 3.5 \times 10^{-8}$), 20-187 ( $f = 1.2 \times 10^{-6}$) and 27-235 ( $f = 2.7 \times 10^{-6}$). However, all such transitions are very weak, and hence sensitive to mixing coefficients, but do not affect the overall accuracy of the calculations. To conclude, based on a satisfactory agreement between the two forms, we may state that the accuracy of our listed A-values is better than 20% for a majority of strong transitions.

4 Lifetimes

The lifetime $\tau$ for a level j is defined as follows:


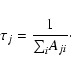\begin{displaymath}{\tau}_j = \frac{1}{{\sum_{i}^{}} A_{ji}}\cdot \end{displaymath} (8)

Since this is a measurable parameter, it provides a check on the accuracy of the calculations. In Table 1 we list our calculated lifetimes in the last column, which include the contributions from all four types of transitions, i.e. E1, E2, M1 and M2. These results are helpful for comparisons with theory or experiments.

To our knowledge, the only available measurements of lifetimes for Fe IX are those of Träbert et al. (2003) for the (3s23p53d) 3D$^\circ_3$, 3D$^\circ_2$ and 1F$^\circ_3$ levels (8, 11 and 12). In Table 6a we compare our calculated lifetimes with the measurements as well as with the earlier calculations of Flower (1977). For all three levels, theory and experiment agree well within the limits of uncertainty. The earlier calculations of Flower (1977) are also in good agreement with our results and the measurements, although their lifetime for the 1F$^\circ_3$ level is up to 10% higher. In Table 6b we compare our lifetimes with the most recent calculations of Verma et al. (2006) for 7 common levels of the 3s23p53d and 3s3p63d configurations. For all these levels, we would like to stress that the contributions of the E1 transitions are dominant, and those of the E2, M1 and M2 transitions are negligible. Therefore, differences between the two calculations are based on the calculations for the electric dipole transitions alone, and the lifetimes of Verma et al. are invariably higher for all the levels. However, for the levels of the 3s23p53d configuration, differences are only up to 10%, whereas for the levels of the 3s3p63d configuration differences between the two calculations are up to 70%. Since the A-values of Verma et al. are different from the present or earlier calculations, and are not assessed to be very accurate, as discussed in Sect. 3, their reported lifetimes are also expected to be different. However, we are confident of our results of lifetimes listed in Table 6. Nevertheless, additional measurements or calculations of lifetimes for a few more levels will be helpful to further assess the accuracy of our results.

5 Conclusions

In the present work, results for energy levels, radiative rates, oscillator strengths, and line strengths for transitions among the lowest 360 levels of Fe IX have been presented for all permissible transitions. Additionally, results for radiative rates have been presented for four types of transitions, namely E1, E2, M1 and M2. A complete set of results are likely to be useful for the modelling of a variety of plasmas.

Based on the comparison made among a variety of calculations, and adopting both the GRASP and FAC codes with differing amount of CI, as well as with the available compiled experimental and other theoretical results, our energy levels are assessed to be accurate to better than 1%. However, the level designations provided are only for guidance, and are likely to fluctuate for a few of them. Similarly, based on the comparison made between the length and velocity forms of the oscillator strengths, we assess that our radiative rates are accurate to better than 20% for a majority of strong transitions.

Lifetimes for all excited levels of Fe IX are listed, but comparison with the corresponding experimental results have been possible for only three levels, for which there are no discrepancies between theory and experiment. However, the reported lifetimes of Verma et al. (2006) are invariably higher, up to 70%, for all the 7 common levels.

The atomic data presented in this paper covers a wider range of transitions than available so far in the literature. However, the usefulness of the present data can only be fully assessed when the corresponding calculations for excitation rates are also available. Considering the large number of levels involved, these calculations will be computationally demanding and hence will take a considerably long time to perform. Nevertheless, we hope that with the availability of those calculations, along with the present work, the remaining discrepancy between theory and observations (Liedahl 2000; Storey et al. 2002) will be resolved for some of the prominent lines of Fe IX.

Acknowledgements
This work has been financed by the Engineering and Physical Sciences and Particle Physics and Astronomy Research Councils of the United Kingdom. Additionally, F.P.K. is grateful to A.W.E. Aldermaston for the award of a William Penney Fellowship, and K.M.A. would like to acknowledge the hospitality of NIFS, where a part of this work was performed during a visit in February, 2006.

References

 
Copyright ESO 2006