A&A 460, 349-355 (2006)
DOI: 10.1051/0004-6361:20065836
Deconvolution of multiple images with high dynamic range and an
application to LBT LINC-NIRVANA
B. Anconelli1 - M. Bertero1 - P. Boccacci1 - G. Desiderà1
- M. Carbillet2 - H. Lanteri2
1 - DISI, Università di Genova, via Dodecaneso 35,
16146 Genova, Italy
2 -
Laboratoire Universitaire d'Astrophysique de Nice,
UMR 6525, Parc Valrose, 06108 Nice Cedex 02, France
Received 15 June 2006 / Accepted 6 September 2006
Abstract
Context. The standard Richardson-Lucy method (RLM) does not work well in the deconvolution of astronomical images containing objects with very different angular scales and magnitudes. Therefore, modifications of RLM, applicable to this kind of objects, must be investigated.
Aims. We recently proposed a regularization of RLM which provides satisfactory results in the case of particular test objects with high dynamic range. In this paper we extend this method to the case of multiple image deconvolution, having in mind application to the reconstruction of the images provided by Fizeau interferometers such as LINC-NIRVANA, the German-Italian beam combiner for the Large Binocular Telescope.
Methods. RLM is an iterative method for the minimization of the Csiszár divergence, a problem equivalent to maximum likelihood estimation in the case of photon noise. In our approach, the problem is regularized by adding a suitable penalization term to the Csiszár divergence and an iterative method converging to the minimum of the resulting functional is derived from the so-called split gradient method (SGM).
Results. The method is tested on a model of young binary star consisting of a core binary surrounded by a dusty circumbinary ring. The results are quite good in the case of exact knowledge of the point spread functions (PSF). However, in the case of approximate knowledge of the PSFs, the accuracy of the reconstruction depends on the difference of magnitude between the ring and the central binary.
Key words: methods: numerical - techniques: image processing
In previous papers (Bertero & Boccacci 2000a,b;
Correia et al. 2002; Carbillet et al. 2002; Anconelli et
al. 2005) we developed methods and software for the deconvolution
of multiple interferometric images of the same astronomical target. One
of the results is the software package AIRY (Astronomical Image
Reconstruction in interferometrY) of which version 3.0 is now available
(see http://dirac.disi.unige.it and
http://www-luan.unice.fr/caos). This tool, described in Correia
et al. (2002), can be applied to
Fizeau interferometers such as LINC-NIRVANA (Lbt INterferometric Camera
and Near-InfraRed/Visible Adaptive iNterferometer for Astronomy), in the
following denoted by LN, the German-Italian beam combiner for the Large
Binocular Telescope (LBT). LBT, under completion on Mount Graham, Arizona,
will consist of two 8.4 m mirrors on a common mount, with a spacing of 14.4 m
between their centres, so that a maximum baseline of 22.8 m will be available.
The two primary mirrors have been already installed and aluminized; "first
light'' has been achieved on October 12, 2005.
The methods we have implemented and validated are, essentially, accelerated
versions of the multiple-image Richardson-Lucy method (RLM), in particular
the so-called ordered subset expectation maximization (OSEM) method. As it
is known both RLM and OSEM need an early stopping of the iterations in order
to avoid the so-called checkerboard effect in the case of diffuse
objects. Moreover, in the case of a field containing both diffuse and
pointwise objects, providing different signal-to-noise ratios (SNR) in
different regions of the image domain, both RLM and OSEM have different
convergence rates in these different regions. One can try to overcome this
difficulty by some kind of explicit adaptive regularization,
acting in a different way on diffuse and pointwise objects.
Methods with such a property have been already proposed and investigated.
For a recent review see Puetter et al. (2005). In this paper we
attack the problem with another method, based on a suitable global
regularization, which can be easily implemented and can work well in the
case of scientific targets satisfying the following conditions:
- the object consists of very bright stars and of faint diffuse
structures so that there exists a wide gap between their intensities;
- there exists an angular separation between the two kinds of objects,
i.e. they are located in different regions of the field of view (FOV).
An example of such an object is shown in Fig. 1. It is a model
of young binary star surrounded by a dusty circumbinary ring, described in
Carbillet et al. (2002). It is directly inspired by near-infrared
observations of the T-Tauri binary star of the quadruple system GG Tau and
subsequent modeling by Wood et al. (1999). The main features of the
model are the following: the object is an array
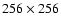 ,
so that,
with a pixel size corresponding to that of the LN detector (5.12 mas), it has
an extension of about 1.31 arcsec; it is observed in K band and has a total
magnitude of 9.63; the integrated magnitude of the ring is 15.25 while the
magnitudes of the two stars are 10 and 11, respectively. Moreover, the angular
separation of the binary is about twice the angular resolution of LN in K band
(20 mas). The cut of the object (normalized to unit maximum value) along the
direction of the binary star is plotted in the upper-right panel of Fig. 1, to show that there is about a factor 106 between the flux
of the primary and the average flux of the ring. The structure of the ring is
shown in the lower-left panel by means of a representation in terms of level
curves. It is obvious that, in such a situation, the side lobes of the images
of the two stars are superimposed to the ring and mask its structure. This
effect is illustrated in the lower-right panel of the same figure where we give
the image obtained by convolving the object with an ideal interferometric
PSF of LN. This object will be used in our numerical simulations.
,
so that,
with a pixel size corresponding to that of the LN detector (5.12 mas), it has
an extension of about 1.31 arcsec; it is observed in K band and has a total
magnitude of 9.63; the integrated magnitude of the ring is 15.25 while the
magnitudes of the two stars are 10 and 11, respectively. Moreover, the angular
separation of the binary is about twice the angular resolution of LN in K band
(20 mas). The cut of the object (normalized to unit maximum value) along the
direction of the binary star is plotted in the upper-right panel of Fig. 1, to show that there is about a factor 106 between the flux
of the primary and the average flux of the ring. The structure of the ring is
shown in the lower-left panel by means of a representation in terms of level
curves. It is obvious that, in such a situation, the side lobes of the images
of the two stars are superimposed to the ring and mask its structure. This
effect is illustrated in the lower-right panel of the same figure where we give
the image obtained by convolving the object with an ideal interferometric
PSF of LN. This object will be used in our numerical simulations.
![\begin{figure}
\par\includegraphics[height=3.9cm,width=3.9cm,clip]{5836fg1a.ps}\...
...*{2mm}
\includegraphics[height=3.9cm,width=3.8cm,clip]{5836fg1d.ps}\end{figure}](/articles/aa/full/2006/46/aa5836-06/Timg12.gif) |
Figure 1:
Upper-left panel: gray level representation of the model of young
binary star described in the text. Upper-right panel: the cut of the object
(normalized to unit maximum value) along the direction of the binary system.
Lower-left panel: representation of the ring by means of level curves
(corresponding to the values 2460, 4320, 7020, and 9720; the maximum value
of the ring is
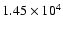 ,
while the maximum value of the binary is ,
while the maximum value of the binary is
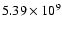 ). Lower-right panel: gray level representation, in a
log-scale, of the image corresponding to an ideal PSF of LN, with ). Lower-right panel: gray level representation, in a
log-scale, of the image corresponding to an ideal PSF of LN, with 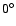 relative parallactic angle. relative parallactic angle. |
| Open with DEXTER |
Our approach will be based on a regularization functional containing a
thresholding parameter, assuring that the reconstruction of the bright
point objects above the value of the parameter is not regularized, while the
reconstruction of the faint objects, below the value of the parameter is
regularized in a Tikhonov-like manner (see, for instance, Bertero &
Boccacci 1998). Therefore it contains also a Tikhonov
regularization parameter, which must be optimized.
This approach has been recently proposed in the case of single image
deconvolution (Anconelli et al. 2006b) and, in this paper, it will be
extended to the problem of multiple image deconvolution in view of its
application to the reconstruction of LN interferometric images. In Sect. 2 we discuss the functional we propose for the regularization of the
maximum likelihood approach in the case of photon noise, by comparing its
effect with that of the standard Tikhonov functional. In Sect. 3 we derive
modified versions of RLM and OSEM able to minimize the regularized functional.
In Sect. 4 we present our numerical experiments based on the test object
of Fig. 1, using both ideal and AO corrected PSFs. Finally in
Sect. 5 we discuss the limitations of our approach.
We use bold letters for denoting
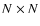 arrays, whose pixels are
indexed by a multi-index
arrays, whose pixels are
indexed by a multi-index
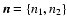 .
Moreover, we assume that
we have p images acquired with LN, corresponding to p different
orientations of the baseline and denoted by
.
Moreover, we assume that
we have p images acquired with LN, corresponding to p different
orientations of the baseline and denoted by
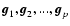 .
If
.
If
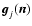 is the value of the jth image
at pixel
is the value of the jth image
at pixel 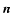 ,
then, according to the model proposed by Snyder et al.
(1993) for data acquired with a CCD camera, we can write:
,
then, according to the model proposed by Snyder et al.
(1993) for data acquired with a CCD camera, we can write:
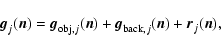 |
(1) |
where:
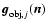 is the number of photoelectrons
due to radiation from the object;
is the number of photoelectrons
due to radiation from the object;
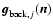 is
the number of photoelectrons due to external and internal background, dark
current, etc.;
is
the number of photoelectrons due to external and internal background, dark
current, etc.;
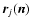 is the read-out noise due to the
amplifier. The first two terms are realizations of independent Poisson
processes (photon noise), so that their sum is also a Poisson process; its
expected value is given by:
is the read-out noise due to the
amplifier. The first two terms are realizations of independent Poisson
processes (photon noise), so that their sum is also a Poisson process; its
expected value is given by:
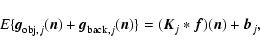 |
(2) |
where:
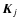 is the PSF corresponding to the jth orientation of
the baseline;
is the PSF corresponding to the jth orientation of
the baseline; 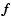 is the object array;
is the object array;
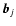 is the (constant)
expected value of the background. We assume, as usual, that the PSFs are
normalized to one:
is the (constant)
expected value of the background. We assume, as usual, that the PSFs are
normalized to one:
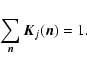 |
(3) |
If the images are dominated by photon noise, as in the cases we are
considering, the read-out noise can be neglected, and the likelihood function
is given by a product of Poisson distributions, one for each pixel of the
image domain. The maximization of this function is equivalent to the
minimization of the Csiszár divergence (Csiszár 1991) given by:
![$\displaystyle J({\vec f};{\vec g})=\sum_{j=1}^p \sum_{\vec n} \{
{\vec g}_j({\v...
...})+{\vec b}_j}
+ [(A_j {\vec f})({\vec n})+{\vec b}_j-{\vec g}_j({\vec n})] \},$](/articles/aa/full/2006/46/aa5836-06/img27.gif) |
|
|
(4) |
where 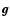 denotes the set of the p images
denotes the set of the p images
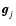 and Aj
is the matrix defined by:
and Aj
is the matrix defined by:
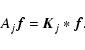 |
(5) |
Multiple-image RLM and OSEM (Bertero & Boccacci 2000b) are just
iterative methods for the minimization of this functional.
Regularization of the Csiszár divergence can be achieved by adding a
suitable penalty term and the problem becomes the minimization of
functionals of the following form:
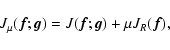 |
(6) |
where 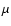 is the regularization parameter.
is the regularization parameter.
The standard Tikhonov regularization, can be obtained by taking:
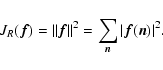 |
(7) |
However, in the case of bright point objects combined with diffuse faint
objects, this functional is dominated by the point objects and is not
significantly affected by the faint ones. For instance, in the case of the
object of Fig. 1, the value of this functional is
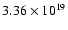 .
Since the brightness of the primary component of the binary
is
.
Since the brightness of the primary component of the binary
is
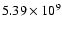 while the brightness of the secondary component is
while the brightness of the secondary component is
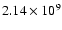 ,
we find that the ring contributes to the fourth digit of
the value of this functional. Therefore it is obvious that such a functional
regularizes the binary but does not regularize the faint ring.
,
we find that the ring contributes to the fourth digit of
the value of this functional. Therefore it is obvious that such a functional
regularizes the binary but does not regularize the faint ring.
This effect can be removed if it is possible to "mask'' in some way the
bright point objects. This goal can be achieved by a very simple modification
of the previous functional, already investigated in Anconelli et al.
(2006b):
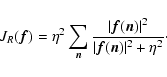 |
(8) |
Indeed this functional is constant (no penalty) in the regions where the
brightness of the object is much greater than 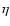 ,
while it provides
a Tikhonov-like penalty in the regions where the brightness is much
smaller than
,
while it provides
a Tikhonov-like penalty in the regions where the brightness is much
smaller than 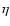 ;
moreover this penalty is smoothly varying when the
brightness increases.
;
moreover this penalty is smoothly varying when the
brightness increases.
We recall that this functional was first proposed for edge-preserving
regularization (hence with the object values replaced by the values of the
modulus of the gradient) by Geman & Mc Clure (1987). We also
point out that the function defined in Eq. (8) is not convex,
but quasi-convex, i.e. all its sub-level sets are convex, and that it has
a unique global minimum at
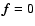 .
.
An iterative method for the minimization of the functional defined by Eqs. (6), (4), and (8), with the additional
constraints of non-negativity and flux conservation:
| |
|
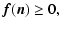 |
(9) |
| |
|
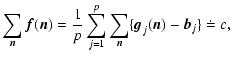 |
|
can be obtained by means of a general approach known as split gradient method
(SGM), proposed by Lanteri et al. (2001, 2002). The extension
of this approach to the problem of multiple image deconvolution is discussed
in Anconelli et al. (2004). The method provides iterative algorithms
that, in general, are not very efficient (they require a large number of
iterations) but have a very nice feature: for very broad classes of
regularization functionals they can be obtained by means of a very simple
modification of RLM or OSEM and therefore can be easily implemented by
everybody. In such a way it is easy to compare the results obtainable by means
of different regularization functionals. In particular we will apply the
method to the case of the two regularization functionals given by Eqs. (7) and (8) respectively. Of course, once a
specific regularized functional has been selected for the specific problem
at hand, one can use more efficient optimization methods for its minimization.
The basic point is the following decomposition of the gradient of the
functional of Eq. (6):
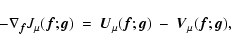 |
(10) |
where
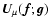 and
and
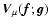 are
positive arrays depending on
are
positive arrays depending on 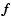 and
and 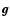 .
Then SGM can be obtained
by applying the method of successive approximations to the fixed point
equation derived from the Kuhn-Tucker conditions. A discussion is contained
in a recently published paper (Anconelli et al. 2006a). As a result,
the general structure of the iterative algorithm is the following:
.
Then SGM can be obtained
by applying the method of successive approximations to the fixed point
equation derived from the Kuhn-Tucker conditions. A discussion is contained
in a recently published paper (Anconelli et al. 2006a). As a result,
the general structure of the iterative algorithm is the following:
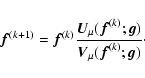 |
(11) |
The convergence of this algorithm has not been proved in general, but only
in some particular cases; nevertheless it has been verified experimentally
in all the applications we have considered. An interesting feature
of this algorithm is that non-negativity of the iterates is automatically
satisfied, as one can easily verify.
Now, by computing the gradient of the regularized functional, we find that
we can write:
| |
|
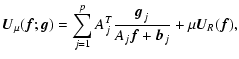 |
(12) |
| |
|
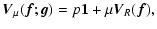 |
|
where 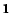 is the array whose entries are all equal to 1, and
is the array whose entries are all equal to 1, and
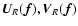 are the arrays from the
decomposition of the gradient of
are the arrays from the
decomposition of the gradient of
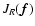 .
Then, from Eq. (11) we obtain the following modification of the
multiple-image RLM algorithm:
.
Then, from Eq. (11) we obtain the following modification of the
multiple-image RLM algorithm:
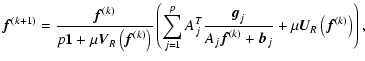 |
|
|
(13) |
which is the general structure of a regularized multiple-image RLM.
In the particular case of the regularization functional of Eq. (7), by taking into account that we are considering the
restriction of this functional to the cone of the non-negative arrays, we
can choose the following decomposition of its gradient:
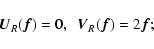 |
(14) |
analogously, in the case of the functional of Eq. (8), we can
choose the decomposition:
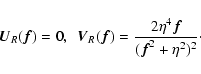 |
(15) |
Therefore, by looking at Eq. (13), we find that, in both cases, the
modification of the RLM algorithm consists uniquely in the insertion of a
multiplicative factor in the r.h.s. The OS-version of this algorithm,
including also the constraint on the total flux, as deduced from the general
form derived in Anconelli et al. (2004), is the following:
If 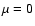 this algorithm is precisely the OSEM method as given, for
instance, in Anconelli et al. (2005). Moreover, if
this algorithm is precisely the OSEM method as given, for
instance, in Anconelli et al. (2005). Moreover, if
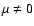 and
and
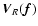 is given by Eq. (14), the algorithm
will be called TKR (TiKhonov Regularization) algorithm while it will be
called HDR (High Dynamic Regularization) algorithm if
is given by Eq. (14), the algorithm
will be called TKR (TiKhonov Regularization) algorithm while it will be
called HDR (High Dynamic Regularization) algorithm if
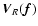 is given by Eq. (15). In this case it is easy to verify that,
if, in one pixel, the value of
is given by Eq. (15). In this case it is easy to verify that,
if, in one pixel, the value of
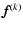 is large with respect to
is large with respect to
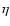 ,
then, in that pixel, we have a standard OSEM iteration; on the
other hand, if the value of
,
then, in that pixel, we have a standard OSEM iteration; on the
other hand, if the value of
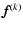 is small with respect to
is small with respect to 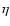 ,
then we have, in that pixel, a TKR iteration.
,
then we have, in that pixel, a TKR iteration.
The regularization methods described in the previous sections have been
validated by means of numerical simulations in the case of the test object
shown in Fig. 1.
In a first set of experiments we used the same PSFs for convolving the
object and deconvolving the images. This is the so-called inverse
crime and is investigated for establishing the best performance
achievable with the proposed HDR algorithm. For completeness we compared
the results with those provided by the TKR algorithm (Tikhonov
regularization). However it is expected that a poor knowledge of the PSFs
can significantly degrade the quality of the results, as a consequence of
the high ratio between the brightness of the stars and that of the ring. We
will verify that this is the case, indeed. Therefore, in a second set of
experiments we will use PSFs with different Strehl ratio (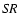 )
for convolving
the object and deconvolving the images and we will find that a reliable
reconstruction can be obtained only in the case of an object where the
difference of magnitude between the ring and the binary is decreased.
)
for convolving
the object and deconvolving the images and we will find that a reliable
reconstruction can be obtained only in the case of an object where the
difference of magnitude between the ring and the binary is decreased.
We investigate the case of LN observations by assuming that three different
images are obtained with three different orientations of the baseline,
corresponding to relative parallactic angles of
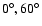 and
and
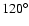 .
Moreover, in order to investigate the effect of partial
AO-correction, we use three different sets of PSFs: the first consists of
ideal PSFs while the second and third set consist of AO-corrected PSFs with
very different values of
.
Moreover, in order to investigate the effect of partial
AO-correction, we use three different sets of PSFs: the first consists of
ideal PSFs while the second and third set consist of AO-corrected PSFs with
very different values of 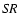 ,
i.e. 70% and 26%, respectively. These PSFs
are already described and used for numerical simulations in Anconelli et al.
(2004, 2005). The
,
i.e. 70% and 26%, respectively. These PSFs
are already described and used for numerical simulations in Anconelli et al.
(2004, 2005). The
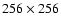 images are formed by convolving
the model with the PSFs of a given set. Sky background emission in K band
(12.5 mag/arcsec2) is added to the results, which are also perturbed with
Poisson and Gaussian (10 e- rms) noise. For image generation the
following parameters are used: a total efficency of 25%, an integration
time of 20 min and a telescope surface of 104 m2.
images are formed by convolving
the model with the PSFs of a given set. Sky background emission in K band
(12.5 mag/arcsec2) is added to the results, which are also perturbed with
Poisson and Gaussian (10 e- rms) noise. For image generation the
following parameters are used: a total efficency of 25%, an integration
time of 20 min and a telescope surface of 104 m2.
Since images are dominated by photon noise, the variation of the SNR over
the FOV can be estimated by remarking that, in the region of the binary,
the peak value of the images is of the order of 108, while, in the
region of the ring is of the order of 105. This large peak value is
due to contribution from the image of the binary, since, in the object,
the maximum value of the ring is of the order of 104.
As already discussed in the Introduction, our regularization functional
contains a thresholding parameter 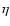 ,
related to the intensity gap
between bright and faint objects. This parameter, however, can not be
directly estimated from the detected images and therefore our approach
requires two steps: the first is a reconstruction based on standard OSEM,
which is used for estimating
,
related to the intensity gap
between bright and faint objects. This parameter, however, can not be
directly estimated from the detected images and therefore our approach
requires two steps: the first is a reconstruction based on standard OSEM,
which is used for estimating 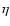 ;
the second is the reconstruction based
on the HDR algorithm, including an optimization of the value of the
regularization parameter
;
the second is the reconstruction based
on the HDR algorithm, including an optimization of the value of the
regularization parameter 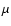 .
.
Before discussing the results of our simulations, we must introduce some
figures of merit (FOM) for quantifying the quality of the reconstructions.
For the ring we can use the relative rms defined by:
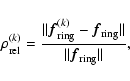 |
(18) |
where 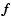
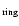 is the array obtained by masking the binary in
the original object while
is the array obtained by masking the binary in
the original object while 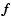
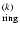 is the array obtained
in the same way from the result of the kth iteration of the iterative
method one is considering.
is the array obtained
in the same way from the result of the kth iteration of the iterative
method one is considering.
Moreover, for checking the accuracy in the reconstruction of the
photometry of the binary, we can compute, at each iteration, the fluxes of the
two stars, by using
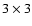 arrays centered on their positions. In such a
way it is also possible to compute their magnitudes and their difference of
magnitudes.
arrays centered on their positions. In such a
way it is also possible to compute their magnitudes and their difference of
magnitudes.
Finally, to check the statistical goodness of the reconstructions, we looked at
the normalized residuals of the solutions, defined by:
![\begin{displaymath}
{\vec R}_j({\vec n})=\frac{g_j({\vec n})-[(A_j {\vec f})({\v...
...j]}
{\sqrt{(A_j {\vec f})({\vec n})+{\vec b}_j}} ;~~j=1,...,p.
\end{displaymath}](/articles/aa/full/2006/46/aa5836-06/img67.gif) |
(19) |
If
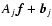 is the exact model corresponding to the images
is the exact model corresponding to the images
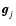 ,
then the corresponding residual is essentially a realization of
white noise. On the other hand, if
,
then the corresponding residual is essentially a realization of
white noise. On the other hand, if 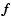 is the reconstructed image and
is free of artifacts, then the corresponding residual should have a similar
behaviour, otherwise it will exhibit spatial correlations (see Puetter et al.
2005, for a discussion).
is the reconstructed image and
is free of artifacts, then the corresponding residual should have a similar
behaviour, otherwise it will exhibit spatial correlations (see Puetter et al.
2005, for a discussion).
About the estimate of the thresholding parameter 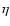 ,
we checked that
after 400 iterations, OSEM provides a satisfactory estimate of the maximum
value of the ring, that is about
,
we checked that
after 400 iterations, OSEM provides a satisfactory estimate of the maximum
value of the ring, that is about
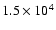 .
Therefore we expect
.
Therefore we expect
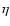 to be greater than this value. We have found that this is the correct
condition because, when it is satisfied, the results provided by the HDR
algorithm do not depend on the particular value of
to be greater than this value. We have found that this is the correct
condition because, when it is satisfied, the results provided by the HDR
algorithm do not depend on the particular value of 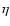 .
All our
computations have been done by taking
.
All our
computations have been done by taking
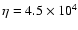 .
.
![\begin{figure}
\par\includegraphics[width=6.4cm,clip]{5836fg2a.eps}\vspace*{2mm}
\par\hspace*{-2mm}\includegraphics[width=6.4cm,clip]{5836fg2b.eps}\end{figure}](/articles/aa/full/2006/46/aa5836-06/Timg71.gif) |
Figure 2:
Upper panel: the relative rms error in the reconstruction
of the ring as a function of the number of iterations in the case of OSEM
(full line), TKR (dotted line) and HDR (dashed line); ideal PSFs are assumed.
Lower panel: behaviour of the flux of the primary star as a function of the
number of iterations in the same cases of the upper panel. |
| Open with DEXTER |
The next point is to understand where to search for the best value of the
regularization parameter 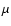 .
This problem arises both in the case of
TKR and in the case of HDR algorithm. In both cases one can guess that the
best choice is that providing a balance between the two terms of the
regularized functional of Eq. (6) when the reconstructed object
is close to the exact model
.
This problem arises both in the case of
TKR and in the case of HDR algorithm. In both cases one can guess that the
best choice is that providing a balance between the two terms of the
regularized functional of Eq. (6) when the reconstructed object
is close to the exact model 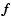 .
Therefore we computed the value of
the first term in Eq. (6) for the three sets of PSFs and we found
values ranging from
.
Therefore we computed the value of
the first term in Eq. (6) for the three sets of PSFs and we found
values ranging from
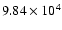 to
to
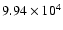 ,
values very close
to the expected value of this functional, namely
,
values very close
to the expected value of this functional, namely
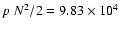 .
Since the value of the functional of Eq. (7) is
.
Since the value of the functional of Eq. (7) is
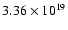 ,
we can guess that, in the case of TKR algorithm, we should have
,
we can guess that, in the case of TKR algorithm, we should have
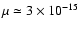 .
On the other hand, the value of the functional
of Eq. (8), with
.
On the other hand, the value of the functional
of Eq. (8), with
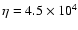 ,
is
,
is
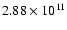 ,
so that we guess that for the HDR algorithm we should have
,
so that we guess that for the HDR algorithm we should have
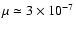 .
A rough search for the best values of the regularization
parameters in a region around the previously estimated values has
demonstrated that they work surprisingly well and that they can be used to
get the best reconstructions achievable by means of the two methods.
.
A rough search for the best values of the regularization
parameters in a region around the previously estimated values has
demonstrated that they work surprisingly well and that they can be used to
get the best reconstructions achievable by means of the two methods.
Table 1:
Values of the rms error in the reconstruction of the ring:
in the case of OSEM and TKR we give the minimum values and, in brackets, the
corresponding number of iterations; in the case of HDR we give the limiting
values, which are reached after a number of iterations of the order of 2000.
The values of the parameters 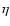 and
and 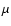 are those indicated in the text.
are those indicated in the text.
In Fig. 2 (upper panel) we plot the behaviour of the relative
rms error,
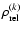 ,
defined in Eq. (18), as a
function of the number of iterations k, in the case of OSEM, TKR and HDR
algorithms (ideal PSFs). It is evident that both OSEM and TKR have a
minimum of the reconstruction error (semiconvergence of the method) while HDR
is convergent. We point out that OSEM and TKR provide the same value of the
minimum rms (the only difference is that TKR is a bit faster), while the
minimum rms provided by HDR is considerably smaller.
,
defined in Eq. (18), as a
function of the number of iterations k, in the case of OSEM, TKR and HDR
algorithms (ideal PSFs). It is evident that both OSEM and TKR have a
minimum of the reconstruction error (semiconvergence of the method) while HDR
is convergent. We point out that OSEM and TKR provide the same value of the
minimum rms (the only difference is that TKR is a bit faster), while the
minimum rms provided by HDR is considerably smaller.
In Table 1 we give the minimum values of the rms obtained by applying the
three algorithms (in brackets the number of iterations required for
reaching the minimum). We point out that both the reconstruction error
and the number of iterations increase with decreasing 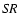 .
.
In the lower panel of Fig. 2, we plot the behaviour of the
flux of the primary star as a function of the number of iterations, for the
three cases considered in the upper panel. The convergence is very fast
and is faster for the regularized methods; we obtain a 9% error after 10
iteration and a 1% error after 50 iterations. However this accuracy
concerns the photometry, as computed in the way indicated above, and not
the pointwise structure of the binary, as we can see by looking at the
residuals
These are shown in Fig. 3 both in the case of the exact object
and in the case of the reconstructions corresponding to the minimum rms
error on the ring. It is evident that the residual corresponding to the
reconstruction provided by the HDR algorithm is free of artifacts while those
corresponding to the solutions provided by OSEM and TKR algorithms
show artifacts in the central region indicating, as expected, that the
reconstruction of the binary is not completely satisfactory.
We also checked the behaviour of the 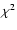 function. Since in each pixel
of our images we have a very large number of photons, we use the following
simplified form of the unbiased
function. Since in each pixel
of our images we have a very large number of photons, we use the following
simplified form of the unbiased
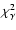 function introduced by Mighell
(1999):
function introduced by Mighell
(1999):
![\begin{displaymath}
\bar{\chi}^2_\gamma=\frac{1}{pN^2} \sum_{j=1}^{p} \sum_{\vec...
...{\vec f})({\vec n})+{\vec b}_j]\vert^2}
{g_j({\vec n})+1}\cdot
\end{displaymath}](/articles/aa/full/2006/46/aa5836-06/img81.gif) |
(20) |
In all cases of Table 1 this quantity is decreasing and tending to 1 as the
number of iterations increases. However, if we consider, for instance, the
case of ideal PSFs, for OSEM and TKR, the
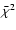 takes the value
1.04 in correspondence of the minimum rms error in the reconstruction of
the ring. If we increase the number of iterations, then this quantity
decreases but the reconstruction of the ring is considerably degraded. On
the other hand, in the case of HDR, the
takes the value
1.04 in correspondence of the minimum rms error in the reconstruction of
the ring. If we increase the number of iterations, then this quantity
decreases but the reconstruction of the ring is considerably degraded. On
the other hand, in the case of HDR, the
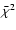 takes the value
1.01 after 2000 iterations and still decreases for a larger number of
iterations while the reconstruction of the ring remains stable. We think
that these results confirm the statistical significance of our approach.
takes the value
1.01 after 2000 iterations and still decreases for a larger number of
iterations while the reconstruction of the ring remains stable. We think
that these results confirm the statistical significance of our approach.
![\begin{figure}
\par\includegraphics[width=3.9cm,clip]{5836fg3a.eps}\hspace*{0.7m...
...eps}\hspace*{0.7mm}
\includegraphics[width=3.9cm,clip]{5836fg3d.eps}\end{figure}](/articles/aa/full/2006/46/aa5836-06/Timg83.gif) |
Figure 3:
Residuals corresponding to the original object and to the
reconstructed images obtained by the different methods. Upper-left panel: the
exact object. Upper-right panel: the OSEM reconstruction. Lower-left panel:
the TKR reconstruction. Lower-right panel: the HDR reconstruction. |
| Open with DEXTER |
The quality of the reconstructions of the ring can also be appreciated by
looking at the reconstruction of the level curves shown in Fig. 1 (lower-left panel). Therefore, in Fig. 4 we
compare the reconstructions of these level curves, as provided by OSEM and
by the HDR algorithm, while we do not show those provided by the TKR
algorithm because they look very similar to the OSEM reconstructions. We give
all the results we have obtained using both ideal and AO-corrected PSFs. We
see that the quality of the reconstruction decreases for decreasing values of
the 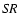 .
.
![\begin{figure}
\par\includegraphics[width=3.3cm,clip]{5836fg4a.eps}\hspace*{8mm}...
...e.eps}\hspace*{8mm}
\includegraphics[width=3.3cm,clip]{5836fg4f.eps}\end{figure}](/articles/aa/full/2006/46/aa5836-06/Timg84.gif) |
Figure 4:
Reconstruction of the level curves of the ring corresponding to the
values indicated in Fig. 1. In the left column we display the best
reconstructions provided by OSEM and in the right column those provided by
the HDR algorithm. From top to bottom: ideal PSFs, AO-corrected PSFs with
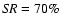 and AO-corrected PSFs with
and AO-corrected PSFs with
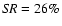 . . |
| Open with DEXTER |
![\begin{figure}
\par\mbox{\parbox{2.8cm}{\includegraphics[width=2.8cm,clip]{5836f...
...8mm}
\parbox{4cm}{\includegraphics[width=4cm,clip]{5836fg5b.eps}} }
\end{figure}](/articles/aa/full/2006/46/aa5836-06/Timg85.gif) |
Figure 5:
Left panel: picture of the different areas of the ring where we check
the accuracy of the restoration. Right panel: behaviour of the ratio between
the areas A and C as a function of the number of iterations both in the case
of ideal PSFs and in the case of AO-corrected PSFs (
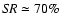 ). ). |
| Open with DEXTER |
Finally, we also considered FOMs defined as the ratio between the flux of
the main star and the flux of regions of the ring. To this purpose we
considered two domains, each
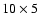 pixels, one on the front and the
other on the back of the ring. These areas are shown in the left panel of
Fig. 5. In the right panel of the same figure we plot,
as a function of the number of iterations, the ratio between the flux of A
and that of C. The correct value is reached after a few hundreds of
iterations in the case of both ideal and AO-corrected PSFs.
pixels, one on the front and the
other on the back of the ring. These areas are shown in the left panel of
Fig. 5. In the right panel of the same figure we plot,
as a function of the number of iterations, the ratio between the flux of A
and that of C. The correct value is reached after a few hundreds of
iterations in the case of both ideal and AO-corrected PSFs.
The previous results are quite promising but they are based on the assumption
of an exact knowledge of the PSFs. It is obvious that this is not the case
in practice. Therefore, in a second set of experiments, we attempted the
simulation of a real case using different sets of PSFs for convolving the
object and deconvolving the images. To this purpose, we assumed the same
orientations of the baseline considered in the previous set of experiments
but we used AO-corrected PSFs with
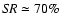 for convolution and
AO-corrected PSFs with
for convolution and
AO-corrected PSFs with
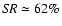 for deconvolution. These PSFs have
been generated by the method described in Anconelli et al. (2005)
and they simulate PSFs extracted from an off-line reference star.
for deconvolution. These PSFs have
been generated by the method described in Anconelli et al. (2005)
and they simulate PSFs extracted from an off-line reference star.
The attempt of reconstructing the same object used in the first set of
experiments was unsuccessful. Even if the two sets of PSFs are not very
different, the difference between their values is too large with respect to
the accuracy required in the reconstruction of such a hard astronomical
object. The reconstruction of the ring looks completely erased both with
OSEM and with the regularized algorithm. For this reason we
modified the model by decreasing the integrated magnitude of the ring, while
keeping fixed that of the binary, to reduce the gap between their fluxes.
In particular we considered two cases: in the first, the integrated magnitude
of the ring is 12.25 while, in the second, it is 10.25.
In Fig. 6 we show the reconstructions provided by OSEM. They do not
correspond to the minimum of the rms error on the ring, since this is
reached after a very small number of iterations (of the order of 10) so that
the binary is not yet resolved. For instance, in the case of integrated
magnitude 10.25, the minimum rms is 16%, while that of the reconstruction
of Fig. 6 is about 19%. Anyway, the reconstruction obtained in the case
of magnitude 12.25, does not allow an estimate of the parameter 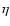 while
this is possible in the case of magnitude 10.25. We remark that, in this case,
there is a factor 103 between the flux of the primary star and the maximum
flux on the ring and that, if we deconvolve the images using the exact PSFs
(inverse crime), then OSEM already provides an excellent reconstruction, so
that the regularized algorithm is not needed. Indeed, after 1000
iterations, the reconstruction error of the ring is about 2% and also the
reconstruction of the binary is very accurate. However, the regularized
algorithm is required in the case of inexact knowledge of the PSFs, because,
as we will show, it can improve the quality of the reconstruction.
while
this is possible in the case of magnitude 10.25. We remark that, in this case,
there is a factor 103 between the flux of the primary star and the maximum
flux on the ring and that, if we deconvolve the images using the exact PSFs
(inverse crime), then OSEM already provides an excellent reconstruction, so
that the regularized algorithm is not needed. Indeed, after 1000
iterations, the reconstruction error of the ring is about 2% and also the
reconstruction of the binary is very accurate. However, the regularized
algorithm is required in the case of inexact knowledge of the PSFs, because,
as we will show, it can improve the quality of the reconstruction.
![\begin{figure}
\par\includegraphics[width=4cm,clip]{5836fg6a.ps}\hspace*{0.7mm}
\includegraphics[width=4cm,clip]{5836fg6b.ps}\end{figure}](/articles/aa/full/2006/46/aa5836-06/Timg87.gif) |
Figure 6:
Examples of reconstructions provided by OSEM when different PSFs
are used for convolution and deconvolution. The PSFs used to convolve the
object have
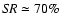 while the PSFs used to deconvolve the images
have
while the PSFs used to deconvolve the images
have
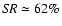 .
To the left, the case where the integrated magnitude
of the ring is 12.25 and to the right the case where it is 10.25. .
To the left, the case where the integrated magnitude
of the ring is 12.25 and to the right the case where it is 10.25. |
| Open with DEXTER |
As already mentioned, using PSFs with
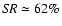 for deconvolution,
OSEM provides a minimum reconstruction error of about 16% after 10
iterations, with an estimate of about
for deconvolution,
OSEM provides a minimum reconstruction error of about 16% after 10
iterations, with an estimate of about
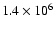 for the maximum
value of the ring. Therefore we use a value of
for the maximum
value of the ring. Therefore we use a value of 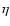 greater than this
one and precisely
greater than this
one and precisely
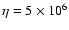 .
About the choice of
.
About the choice of 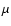 ,
if we use the expected value of the functional
,
if we use the expected value of the functional
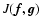 corresponding to the exact model (that is again of the
order of
corresponding to the exact model (that is again of the
order of
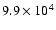 ), and the value of
), and the value of
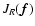 ,
that is now
,
that is now
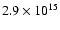 ,
we find a value of
,
we find a value of 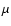 of the order of
of the order of
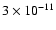 .
We checked by numerical simulations that this value is too small and does
not provide regularization of the ring.
.
We checked by numerical simulations that this value is too small and does
not provide regularization of the ring.
This result is interesting. Indeed, we discovered that the value of 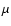 is
controlled by the value of
is
controlled by the value of
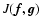 corresponding to the PSFs
used for deconvolving the object. This value is much greater than the previous
one and is of the order of
corresponding to the PSFs
used for deconvolving the object. This value is much greater than the previous
one and is of the order of
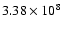 .
It implies a value of
.
It implies a value of 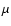 of the order of
of the order of
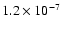 .
By performing a rough search around
this value, we obtained the best reconstruction with
.
By performing a rough search around
this value, we obtained the best reconstruction with
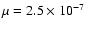 .
The rms error on the ring has a typical semiconvergent behaviour and a
minimum of 13.8% is reached after 10 iterations.
.
The rms error on the ring has a typical semiconvergent behaviour and a
minimum of 13.8% is reached after 10 iterations.
As a final experiment, we attempted an improvement of the result by means
of the iterative blind deconvolution (IBD) method we recently implemented
and tested (Desiderà et al. 2006). As a byproduct we have
recognized that an improvement of this method may be convenient: it consists
in introducing a constraint on the 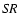 of the PSFs in the PSF boxes and it
will be described in detail in forthcoming papers. Therefore we assumed to
know the
of the PSFs in the PSF boxes and it
will be described in detail in forthcoming papers. Therefore we assumed to
know the 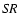 of the PSFs associated with the scientific object (about 70%).
of the PSFs associated with the scientific object (about 70%).
The IBD method was initialized with the reconstruction of the ring
provided by HDR and corresponding to the minimum reconstruction error
and with the PSFs previously used for deconvolution (
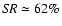 ). We
used 20 cycles of asymmetric IBD (1 iteration in the object box and 5
iterations in the PSFs boxes). The error on the ring increases, but this is
not unexpected since IBD does not contain a regularized algorithm. However,
the important point is that the PSFs are improved by IBD. Indeed, the rms
error between the PSFs with
). We
used 20 cycles of asymmetric IBD (1 iteration in the object box and 5
iterations in the PSFs boxes). The error on the ring increases, but this is
not unexpected since IBD does not contain a regularized algorithm. However,
the important point is that the PSFs are improved by IBD. Indeed, the rms
error between the PSFs with
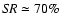 and those with
and those with
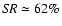 is about 11% while the rms error between the PSFs with
is about 11% while the rms error between the PSFs with
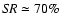 and
those at the exit of IBD is about 6%.
and
those at the exit of IBD is about 6%.
These PSFs are used in the HDR algorithm, with the value of 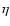 estimated above. About
estimated above. About 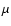 ,
we remark that the value of
,
we remark that the value of
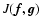 corresponding to the new PSFs is now 1.15
corresponding to the new PSFs is now 1.15
 ,
providing
,
providing
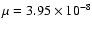 .
A rough search around this value
provided an optimal value that was again of the order of
.
A rough search around this value
provided an optimal value that was again of the order of
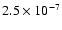 .
The rms error on the ring has now a nice convergent behaviour and an error
of about 13.2% is reached after 100 iterations. The improvement is not
spectacular but significant.
.
The rms error on the ring has now a nice convergent behaviour and an error
of about 13.2% is reached after 100 iterations. The improvement is not
spectacular but significant.
In Fig. 7 we show the level curves for the original object and the
reconstructions obtained with the different methods. The level curves of the
OSEM reconstruction correspond to that shown in Fig. 6 (right panel), while
the level curves of the HDR reconstruction correspond to the result provided
by 10 iterations, with a rms on the ring of about 14%. Since the
number of iterations is small, the binary is not yet well resolved. To this
purpose it should be necessary to use about 100 iterations, but then
the rms on the ring increases to 15.5%. It is obvious that the
main advantage of the reconstruction based on on the PSFs obtained by
means of IBD is that the rms has a convergent behaviour, so that it is
possible to have a good reconstruction of the binary, without degrading the
reconstruction of the ring.
The improvement in the reconstruction is confirmed by looking at the
normalized residuals. All the residuals show now strong space correlations
due to the fact that we do not know the correct PSFs. However these
correlations are weaker in the case of the reconstruction obtained by
means of the PSFs improved by IBD.
![\begin{figure}
\par\includegraphics[width=3.2cm,clip]{5836fg7a.eps}\hspace*{5mm}...
...c.eps}\hspace*{5mm}
\includegraphics[width=3.2cm,clip]{5836fg7d.eps}\end{figure}](/articles/aa/full/2006/46/aa5836-06/Timg100.gif) |
Figure 7:
Reconstructions of the level curves of the object with integrated
magnitude of the ring 10.25. The values of the level curves are obtained
from those of Fig. 1 by multiplying by a factor of 102. Different PSFs
for convolution and deconvolution are used (see the text). Upper-left panel:
the object. Upper-right panel: the OSEM reconstruction shown in Fig. 6.
Lower-left panel: the HDR reconstruction (the values of the parameters
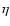 and
and 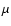 are indicated in the text). Lower-right panel: the HDR
reconstruction obtained using the PSFs corrected by the blind method.
are indicated in the text). Lower-right panel: the HDR
reconstruction obtained using the PSFs corrected by the blind method. |
| Open with DEXTER |
In this paper we propose a method for multiple image deconvolution in the
case of images with high dynamic range. The method applies to scenes
consisting of bright point objects and faint diffuse objects, that do not
superimpose. It is an iterative method derived from a regularization of
the Csiszàr I-divergence and consists in a simple modification of the
multiple image RLM or of its accelerated version OSEM. The method has
been tested on a difficult object derived from a model of young binary
star and it is very effective in the case of accurate knowledge of the
PSFs. If this condition is not satisfied, then reconstruction is still
possible in the case of a smaller difference of magnitude between
the binary and the surrounding ring.
Acknowledgements
We thank Rick Puetter for an accurate review of the paper and for suggesting
several corrections and additions that, we believe, have greatly improved the
quality of our paper.
- Anconelli, B., Bertero,
M., Boccacci, P., et al. 2004, Proc. SPIE, 5491, 932 [NASA ADS] (In the text)
- Anconelli, B., Bertero,
M., Boccacci, P., & Carbillet, M. 2005, A&A, 430, 731 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Anconelli, B.,
Bertero, M., Boccacci, P., Carbillet, M., & Lanteri, H. 2006a,
A&A, 448, 1217 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Anconelli, B., Bertero,
M., Boccacci, P., Carbillet, M., & Lanteri, H. 2006b, JCAM, to
appear
(In the text)
- Bertero, M., &
Boccacci, P. 1998, Introduction to Inverse Problems in Imaging
(Bristol: IOP Publishing)
(In the text)
- Bertero, M., &
Boccacci, P. 2000a, A&AS, 144, 181 [EDP Sciences] [NASA ADS] (In the text)
- Bertero, M., &
Boccacci, P. 2000b, A&AS, 147, 323 [EDP Sciences] [NASA ADS] (In the text)
- Carbillet, M., Correia, S.,
Boccacci, P., & Bertero, M. 2002, A&A, 387, 744 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Correia, S., Carbillet, M.,
Boccacci, P., Bertero, M., & Fini, L. 2002, A&A, 387,
733 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Csiszár, I. 1991, Ann.
Stat., 19, 2032 (In the text)
- Desiderà, G.,
Anconelli, B., Bertero, M., Boccacci, P., & Carbillet, M. 2006,
A&A, 452, 727 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Geman, S., & Mc
Clure, D. 1987, Proc. 46th Session of the ICI, Bulletin of the ICI,
5
(In the text)
- Lanteri, H., Roche, M.,
Cuevas, O., & Aime, C. 2001, Signal Processing, 81, 945 [CrossRef] (In the text)
- Lanteri, H., Roche, M.,
& Aime, C. 2002, Inverse Problems, 18, 1397 [NASA ADS] [CrossRef] (In the text)
- Mighell, K. J. 1999,
ApJ, 518, 380 [NASA ADS] [CrossRef] (In the text)
- Puetter, R. C.,
Gosnell, T. R., & Yahil, A. 2005, ARA&A, 43, 139 [NASA ADS] (In the text)
- Snyder, D. L., Hammoud,
A. M., & White, R. L. 1993, JOSA, A10, 1014 [NASA ADS] (In the text)
- Wood, K., Crosas, M., &
Ghez, A. 1999, ApJ, 516, 335 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2006
![\begin{figure}
\par\includegraphics[height=3.9cm,width=3.9cm,clip]{5836fg1a.ps}\...
...*{2mm}
\includegraphics[height=3.9cm,width=3.8cm,clip]{5836fg1d.ps}\end{figure}](/articles/aa/full/2006/46/aa5836-06/Timg12.gif)
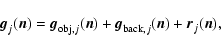
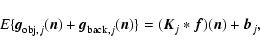
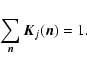
![$\displaystyle J({\vec f};{\vec g})=\sum_{j=1}^p \sum_{\vec n} \{
{\vec g}_j({\v...
...})+{\vec b}_j}
+ [(A_j {\vec f})({\vec n})+{\vec b}_j-{\vec g}_j({\vec n})] \},$](/articles/aa/full/2006/46/aa5836-06/img27.gif)
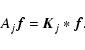
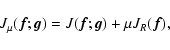
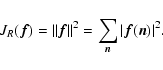
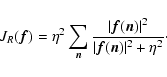
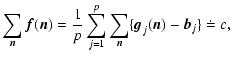
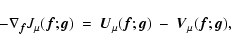
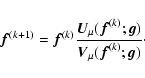
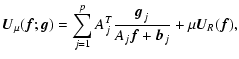
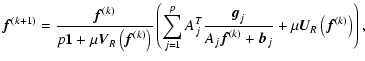
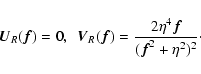
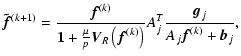
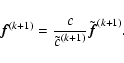
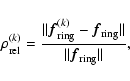
![\begin{displaymath}
{\vec R}_j({\vec n})=\frac{g_j({\vec n})-[(A_j {\vec f})({\v...
...j]}
{\sqrt{(A_j {\vec f})({\vec n})+{\vec b}_j}} ;~~j=1,...,p.
\end{displaymath}](/articles/aa/full/2006/46/aa5836-06/img67.gif)
![\begin{figure}
\par\includegraphics[width=6.4cm,clip]{5836fg2a.eps}\vspace*{2mm}
\par\hspace*{-2mm}\includegraphics[width=6.4cm,clip]{5836fg2b.eps}\end{figure}](/articles/aa/full/2006/46/aa5836-06/Timg71.gif)
![\begin{displaymath}
\bar{\chi}^2_\gamma=\frac{1}{pN^2} \sum_{j=1}^{p} \sum_{\vec...
...{\vec f})({\vec n})+{\vec b}_j]\vert^2}
{g_j({\vec n})+1}\cdot
\end{displaymath}](/articles/aa/full/2006/46/aa5836-06/img81.gif)
![\begin{figure}
\par\includegraphics[width=3.9cm,clip]{5836fg3a.eps}\hspace*{0.7m...
...eps}\hspace*{0.7mm}
\includegraphics[width=3.9cm,clip]{5836fg3d.eps}\end{figure}](/articles/aa/full/2006/46/aa5836-06/Timg83.gif)
![\begin{figure}
\par\includegraphics[width=3.3cm,clip]{5836fg4a.eps}\hspace*{8mm}...
...e.eps}\hspace*{8mm}
\includegraphics[width=3.3cm,clip]{5836fg4f.eps}\end{figure}](/articles/aa/full/2006/46/aa5836-06/Timg84.gif)
![\begin{figure}
\par\includegraphics[width=3.2cm,clip]{5836fg7a.eps}\hspace*{5mm}...
...c.eps}\hspace*{5mm}
\includegraphics[width=3.2cm,clip]{5836fg7d.eps}\end{figure}](/articles/aa/full/2006/46/aa5836-06/Timg100.gif)