1 - Observatoire de Paris, L.U.Th., 92190 Meudon, France
2 - AstroParticule & Cosmologie (APC)
3 - Max Planck Institute for Astrophysics, Box 1317, 85741 Garching, Germany
A&A 460, 1-14 (2006)
DOI: 10.1051/0004-6361:20065484
Z. Meliani1,2,3 - F. Casse2 - C. Sauty1
1 - Observatoire de Paris, L.U.Th., 92190 Meudon,
France
2 - AstroParticule & Cosmologie (APC)![]() , Université Paris 7, 11
place Marcelin Berthelot, 75231 Paris Cedex 05, France
, Université Paris 7, 11
place Marcelin Berthelot, 75231 Paris Cedex 05, France
3 - Max Planck Institute for Astrophysics, Box 1317, 85741 Garching,
Germany
Received 24 April 2006 / Accepted 4 August 2006
Abstract
Context. We present the first-ever simulations of non-ideal magnetohydrodynamical (MHD) stellar magnetospheric winds coupled with disc-driven jets where the resistive and viscous accretion disc is self-consistently described.
Aims. These innovative MHD simulations are devoted to the study of the interplay between a stellar wind (having different ejection mass rates) and an MHD disc-driven jet embedding the stellar wind.
Methods. The transmagnetosonic, collimated MHD outflows are investigated numerically using the VAC code. We first investigate the various angular momentum transports occurring in the magneto-viscous accretion disc. We then analyze the modifications induced by the interaction between the two components of the outflow.
Results. Our simulations show that the inner outflow is accelerated from the central object's hot corona thanks to both the thermal pressure and the Lorentz force. In our framework, the thermal acceleration is sustained by the heating produced by the dissipated magnetic energy due to the turbulence. Conversely, the outflow launched from the resistive accretion disc is mainly accelerated by the magneto-centrifugal force.
Conclusions. The simulations show that the MHD disc-driven outflow extracts angular momentum more efficiently than do viscous effects in near-equipartition, thin-magnetized discs where turbulence is fully developed. We also show that, when a dense inner stellar wind occurs, the resulting disc-driven jet has a different structure, namely a magnetic structure where poloidal magnetic field lines are more inclined because of the pressure caused by the stellar wind. This modification leads to both an enhanced mass-ejection rate in the disc-driven jet and a larger radial extension that is in better agreement with the observations, besides being more consistent.
Key words: stars: winds, outflows - magnetohydrodynamics (MHD) - accretion, accretion disks - acceleration of particles - stars: mass-loss - stars: pre-main sequence
Accreting stellar objects are often associated with collimated jets or winds from accretion discs. Most of those objects also show evidence of winds originating in a corona surrounding the central object. These accretion-ejection phenomena are observed in different astrophysical sources ranging from young stellar objects (YSOs), X-ray binaries, planetary nebulae to active galactic nuclei (AGNs) (see, e.g. Livio 1997 and references therein). The outflow provides an efficient way of extracting angular momentum and converting gravitational energy from the accretion disc or from the central object into outflow kinetic energy.
Observations show that most of the jets are launched very close to the central engine.
In the case of YSOs, there is direct observational evidence
(Burrows et al. 1996)
as well as in the case of some microquasars
(Mirabel 2003; Fender et al. 1997). For instance, it has been suggested that, in
microquasars, the fastest components of the outflow are
launched in the vicinity of the black hole (Meier 2003).
Another piece of evidence that the outflow may originate in a region relatively
close to the central object is that the observed asymptotic velocity of the jet
is close to the escaping speed from the central engine. Thus there is a
direct relation between the asymptotic speed and the depth of the gravitational
potential (Mirabel 1999; Livio 1999; Pringle 1993).
Moreover, the high-resolution images of H![]() and
and ![]() (Bacciotti et al. 2002) reveal a continuous transverse variation of the
jet's velocity, where the fastest and densest components are closer to the
central axis.
(Bacciotti et al. 2002) reveal a continuous transverse variation of the
jet's velocity, where the fastest and densest components are closer to the
central axis.
The high velocity of the observed jet
in YSOs suggests that they originate in a region that is no larger than
one astronomical unity (AU) in
extent (Kwan & Tademaru 1988) and between 0.3 to 4.0 AU from the star in the
case of the LVC of DG Tau (Anderson et al. 2003).
This theoretical prediction is supported, in the case of a disc wind,
by observations of the rotation of several jets associated with TTauris
(Coffey et al. 2004).
Moreover, in the case of classical TTauris (CTTS),
UV observations (Dupree et al. 2005; Beristain et al. 2001) reveal the presence of a
warm wind whose temperature is at least of
![]() .
It appears that the source of this wind is restricted to the star itself, where
X-ray observations support the presence of a hot
corona in CTT stars (Feigelson & Montmerle 1999).
These observations also suggest the existence in CTTS of stellar winds
comparable to the solar wind. These winds may be both thermally and
magneto-centrifugally accelerated.
.
It appears that the source of this wind is restricted to the star itself, where
X-ray observations support the presence of a hot
corona in CTT stars (Feigelson & Montmerle 1999).
These observations also suggest the existence in CTTS of stellar winds
comparable to the solar wind. These winds may be both thermally and
magneto-centrifugally accelerated.
Since the discovery of the existence of winds and jets in astrophysics, enormous progress has been made regarding the understanding of these phenomena. At the same time, we still do not know precisely how the wind from the central corona of the star or the compact object interacts with the disc outflow and the respective roles and differences between these two types of flows.
Several works have analytically and numerically studied the formation of outflows launched from the accretion disc (Vlahakis & Tsinganos 1998; Contopoulos & Lovelace 1994; Blandford & Payne 1982; Anderson et al. 2005; ,,; Casse & Ferreira 2000; Ustyugova et al. 1995; Pudritz et al. 2006; Ouyed et al. 1997). Other works have focused on the outflows from the hot corona of the central objects (; Fendt 2003; Sakurai 1985; Sauty & Tsinganos 1994).
In models dealing with outflows launched from accretion discs, the magnetic field plays a key role in the accretion, the acceleration, and the collimation of the associated vertical wind, which is also supported by recent observations (Donati et al. 2005).
The detection of rotation signatures in TTauri jets gives extra strong support to the magneto-centrifugal launching from the accretion disc. However in stellar ouflows, the wind must be thermally accelerated because of the strong heating of viscous and non-ideal magnetohydrodynamical (MHD) mechanisms. This acceleration increases and approaches the magneto-centrifugal acceleration at least near the polar axis. Some models have already investigated diffusive disc-driven jet launching. In some simulations the accretion disc was considered as a fixed, time-independent boundary condition, while a constant magnetic resistivity prevails through the entire outflow (Fendt & Cemeljic 2002). Kuwabara et al. (2005) have included an accretion disc in their resistive simulations but only considered an uniform magnetic resistivity everywhere in their computational domain. Because of the very different physical conditions prevailing in the disk, the jet and the external medium, it seems very unlikely that this kind of resistivity is physically relevant. Models involving two component bipolar outflows have been proposed in the case of AGN as such as in Sol et al. (1989) and Renaud & Henri (1998), where an electron-positron central wind component is surrounded by an external, ideal MHD disc-driven jet. Another two-component outflow model has been proposed by (Bogovalov & Tsinganos 2005) where a relativistic pulsar wind is surrounded and collimated by an ideal MHD disc-driven wind. In the case of YSOs, two-component models were considered, such as in X-wind outflows (Ferreira et al. 2000; Sauty & Tsinganos 1994). The inner component extracts its energies from the corona around the central region (the central object and the inner part of the accretion disc where an advection-dominated accretion flow may exist), while the second component is launched from the thin accretion disc.
The aim of this paper is to investigate the formation of a two-component outflow around YSOs, one coming from the thin accretion disc and the other one injected from the hot corona of the central star. This work is developed on the base of the disc wind simulations of Casse & Keppens (2002, 2004) (CK02, CK04). Its goal is to study the influence of the stellar wind on the structure and the dynamics of the jet around YSOs. Furthermore, we investigate the consequences of the energy dissipation in the outflow close to the polar axis. Before that, we present simulations of the outflow launched from a resistive and viscous accretion disc where magnetic Prandtl number (ratio of the anomalous viscosity to the anomalous resistivity) equals unity. This is the first time that viscosity and resistivity are considered together in the disc and included in an MHD simulation involving both the accretion disc and the related jet. In previous works, the viscous accretion disc was examined without taking the disc wind into account or with an imposed internal structure (Von Rekowski et al. 2006), which does not enable the authors to study the complete angular momentum transfer. Thus, the first part investigates the relative role of angular-momentum transport by viscosity and by the outflowing plasma and its influence on the formation of the outflow from the disc. Then in a second part, we present the results of our simulations of ideal MHD outflows launched from resistive, viscous, accretion discs surrounding the turbulent wind accelerated from the hot corona of the central star.
In this section we present the simulations of axisymmetric MHD outflows generated from thin accretion discs where for the first time viscosity is taken into account, together with resistivity. We recall that turbulence is believed to generate both anomalous resistivity and viscosity, such that the turbulent magnetic Prandtl number, which is the ratio of the viscous to the resistive transport coefficients, should be of order unity within flows where turbulence is fully developed (Pouquet et al. 1976; Kitchatinov & Pipin 1994). This is supposed to be the case of accretion discs and stellar winds. The presence of two braking torques inside the disc may achieve different disc-jet configurations, since the angular momentum transport is modified by the presence of viscosity.
To get the evolution of such a disc, we solve the system of
time-dependent resistive and viscous MHD equations, namely, the
conservation of mass,
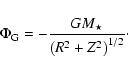 |
(4) |
The initial density profile and velocities are set as follows,
| |
= | ![$\displaystyle \rho_0\max\left[5\times 10^{-6},
\frac{R^{\frac{3}{2}}}{\left(R^2 + R_{0}^2\right)^{\frac{3}{4}}}\right]$](/articles/aa/full/2006/46/aa5484-06/img42.gif) |
|
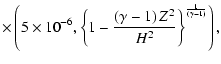 |
(6) | ||
| VR(R,Z) | = | 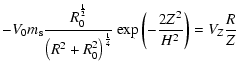 |
(7) |
| = | 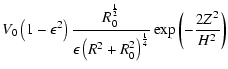 |
(8) |
The initial magnetic field configuration is taken as in CK04,
| |
= | 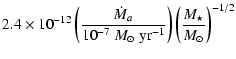 |
|
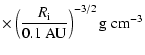 |
|||
| V0 | = | 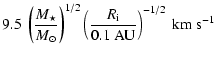 |
|
| T0 | = | 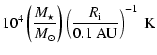 |
|
| B0 | = | 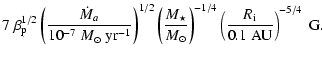 |
(10) |
The boundary conditions here are similar to CK04. We designed an absorbing sink
around the origin in order to avoid the gravitational singularity. In the first
quadrant of
the simulation, the sink region is a square of one unit length both
in the R and Z directions where matter can only enter the zone
(
![]() )
in order to avoid
any numerical artifact. We consider the axis and disc mid-plane as a
combination of symmetric and antisymmetric boundaries. The top and right
boundaries are set as free boundaries (with nil gradients) except for the
outer radius of the disc where we impose a fixed poloidal mass accretion
rate.
)
in order to avoid
any numerical artifact. We consider the axis and disc mid-plane as a
combination of symmetric and antisymmetric boundaries. The top and right
boundaries are set as free boundaries (with nil gradients) except for the
outer radius of the disc where we impose a fixed poloidal mass accretion
rate.
The numerical simulations presented in this paper were performed using the
Versatile Advection Code VAC (Tóth 1996), see
http://www.phys.uu.nl/~toth. We solve the full set of
resistive and
viscous MHD equations under the assumption of cylindrical symmetry. We
time-advance the initial conditions using the conservative, second-order
accurate total variation diminishing Lax-Friedrichs scheme
(Tóth & Odstr$"7015c$il 1996) with minmod limiting applied to the primitive
variables. We apply a projection scheme prior to each time step to enforce
![]() (Brackbill & Barnes 1980).
(Brackbill & Barnes 1980).
In order to study the angular momentum transport governing such an accretion disc, we direct our first simulation here to studying the sole resistive and viscous accretion disc threaded by a large-scale magnetic field. We do not set any additional outflow coming from the central star in this simulation.
Writing down the conservation of angular momentum in an axisymmetric
framework, we see the two mechanisms responsible for the angular momentum
transport and removal, namely the magnetic torque and the viscous torque
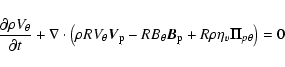 |
(12) |
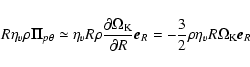 |
(13) |
![\begin{figure}
\par\includegraphics[height=8.4cm,width=5.1cm,clip]{5484fig1.ps}\end{figure}](/articles/aa/full/2006/46/aa5484-06/Timg81.gif) |
Figure 1:
Density contours in the poloidal plane of an
accretion-ejection structure where a viscous and resistive MHD disc is
launching a collimated jet. Magnetic field lines are drawn
in black solid lines, while the fast magnetosonic surface corresponds to the
white solid line (Alfvèn surface is the black dotted line).
The size of the sink region
is
|
| Open with DEXTER | |
The result of the simulation is displayed in
Fig. 1
logarithmic density;
the poloidal magnetic field lines. The
obtained accretion-ejection structure shows a super-fastmagnetosonic
collimated jet. In order to study the difference with the accretion-ejection
flows obtained by CK04, where the magnetic Prandtl number was set to zero,
we measured the various angular
momentum fluxes crossing the internal and external radii, as well as through
the disc surface. To do so, we define global variables characterizing the
angular momentum extracted from the accretion disc, namely,
| (14) |
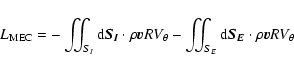 |
(15) |
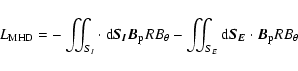 |
(16) |
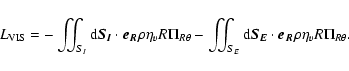 |
(17) |
When the outflow is arising from the accretion disc, we can evaluate the
angular momentum transported vertically into the jet by considering the
various fluxes through the disc surface,
| (18) |
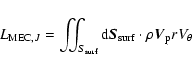 |
(19) |
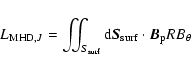 |
(20) |
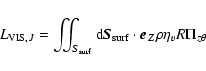 |
(21) |
![\begin{figure}
\par\includegraphics[height=4.9cm,width=6.6cm,clip]{5484fig2.eps}\end{figure}](/articles/aa/full/2006/46/aa5484-06/Timg104.gif) |
Figure 2:
Temporal evolution of several angular momentum fluxes occurring
inside the accretion-ejection structure displayed in
Fig. 1. The various fluxes are normalized to
the amount of angular momentum removed from the disc
|
| Open with DEXTER | |
In order to explain why the magnetic torque prevails in the accretion disc,
we can use some ordering to estimate the relative amplitude of the two
torques. The magnetic torque expression is
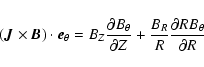 |
(22) |
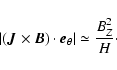 |
(23) |
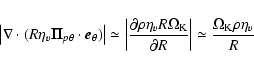 |
(24) |
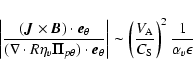 |
(25) |
However, in order to have a more consistent simulation of the accretion-ejection structures, we should take the interaction with the inner stellar coronal wind into account. Incontrast to previous simulations, we include the acceleration of the stellar wind, which is likely to start with a subsonic motion from the base of the corona and then accelerates, as well as the full description of the accretion-disc launching jets. The stellar wind acceleration close to the axis cannot be exclusively magnetic, since magneto-centrifugal effects vanish near the axis. Besides, the high coronal temperature is likely to induce a more efficient turbulent heating. We thus intend to use the turbulent wind viscosity and resistivity as the primary sources of acceleration for the inner stellar outflow. Turbulence may be induced in the stellar magnetospheric wind by its interaction with the disc-driven jet. The differences between both their dynamics and thermodynamics probably induce instabilities. The turbulence may also have a stellar origin and/or a possible connection to the accretion occurring near the surface of the star. In fact, the inner accretion surface, as well as the star surface, are time-dependent and inhomogeneous, leading to outwardly propagating Alfvén waves in the stellar wind and inducing turbulence. This origin of turbulence is based on an analogy with models and observations of the solar wind where the solar origin of turbulence is investigated (; Leamon et al. 1998) as the convection below the photosphere (Cranmer & Ballegooijen 2005; See also a review papers (Cranmer 2004; Goldstein et al. 1995)).
The aim of this section is to model the interplay between the two components of a YSO outflow, namely a jet launched from a magnetized resistive, viscous accretion disc and the second one, an non-ideal MHD spherical wind ejected from the protostar hot corona. In this section, we describe the method that we developed for the implementation of the stellar wind in the model. The results and the differences, with the non-ideal MHD stellar wind model, is discussed in the following section. We use the same initial conditions as in the previous section, except for is a change in the boundary condition located at the top of the sink region.
We now replace the accretion inflow by an outward mass flux whose amplitude is
![]() times the solar mass-loss rate and which is spherically ejected with a
speed that is a fraction
times the solar mass-loss rate and which is spherically ejected with a
speed that is a fraction ![]() of the fast-magnetosonic speed in the corona
of the fast-magnetosonic speed in the corona
![]() ;
;
In our simulations, we model neither the very inner part of the
accretion disc nor its interaction with the magnetosphere of the star
located at (
![]() ).
).
Nevertheless, we include the effect of the star rotation in our simulations
by imposing a solid rotation profile (
![]() )
on the outflow at
the top of the sink region. We set the angular velocity of the outflow at
this boundary to the Keplerian angular velocity at the inner radius
)
on the outflow at
the top of the sink region. We set the angular velocity of the outflow at
this boundary to the Keplerian angular velocity at the inner radius ![]() .
The rotation period associated is then
.
The rotation period associated is then
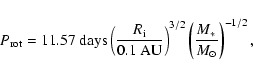 |
(29) |
We also consider two different cases of stellar winds. The
first one is consistent with a heavy hot wind whose mass loss is on the
order of
![]() yr (
yr (
![]() ). This mass-ejection
rate is in the range of typical mass losses for young B-star and O-star type.
This kind of YSO is characterized by strong outflows and dynamical timescales
around 104 years, and the stellar wind is believed to be the main
contributor to the outflow. The computational domain related to this simulation
is
). This mass-ejection
rate is in the range of typical mass losses for young B-star and O-star type.
This kind of YSO is characterized by strong outflows and dynamical timescales
around 104 years, and the stellar wind is believed to be the main
contributor to the outflow. The computational domain related to this simulation
is
![]() with a resolution of
with a resolution of
![]() cells.
The other simulation stands for systems where the stellar wind is a light
and hot one, namely with a mass
loss on the order of
cells.
The other simulation stands for systems where the stellar wind is a light
and hot one, namely with a mass
loss on the order of
![]() yr (
yr (
![]() )
(Fig. 3).
In these cases the stellar wind is lighter than the jet launched from
the accretion disc. The computational domain associated with the second
simulation is
)
(Fig. 3).
In these cases the stellar wind is lighter than the jet launched from
the accretion disc. The computational domain associated with the second
simulation is
![]() with a resolution of
with a resolution of
![]() cells. It is noteworthy that, since we
are expecting a widening of the jet due to the strong stellar mass loss in
the first simulation, we have designed a larger computational domain in order
to capture all the features of the resulting outflow.
We set the velocity parameter
cells. It is noteworthy that, since we
are expecting a widening of the jet due to the strong stellar mass loss in
the first simulation, we have designed a larger computational domain in order
to capture all the features of the resulting outflow.
We set the velocity parameter
![]() to 0.01 in both simulations,
which is consistent with an initial sub fast-magnetosonic and sub-Alfvénic
ejection from the corona.
We assume that part of the outflow acceleration has already taken place between
the star surface (hidden in the sink) and the top boundary of the sink region
although the flow is sometimes even sub-slow-magnetosonic, depending on the
magnetic configuration.
to 0.01 in both simulations,
which is consistent with an initial sub fast-magnetosonic and sub-Alfvénic
ejection from the corona.
We assume that part of the outflow acceleration has already taken place between
the star surface (hidden in the sink) and the top boundary of the sink region
although the flow is sometimes even sub-slow-magnetosonic, depending on the
magnetic configuration.
In most stellar wind models, the wind material is often subject to coronal
heating, contributing to the global acceleration of the flow.
In our simulations, we assume that the coronal heating is a
fraction
![]() of the energy released in the
accretion disc at the boundary of the sink region, which is
transformed into thermal energy in the stellar corona close to the polar axis.
This scenario was proposed by (Matt & Pudritz 2005) and is
supported by the current observations of hot stellar outflows (Dupree et al. 2005).
The thermal energy imposed at the lower boundary of the corona
is, at each step of the simulation, the sum of the
thermal energy
of the energy released in the
accretion disc at the boundary of the sink region, which is
transformed into thermal energy in the stellar corona close to the polar axis.
This scenario was proposed by (Matt & Pudritz 2005) and is
supported by the current observations of hot stellar outflows (Dupree et al. 2005).
The thermal energy imposed at the lower boundary of the corona
is, at each step of the simulation, the sum of the
thermal energy
![]() of the above stellar jet, i.e. the thermal energy of the
first cells above the sink border, plus a fraction
of the above stellar jet, i.e. the thermal energy of the
first cells above the sink border, plus a fraction
![]() of the thermal energy at the disc inner radius
of the thermal energy at the disc inner radius
![]() .
Thus the thermal energy at the upper boundary of the sink is
.
Thus the thermal energy at the upper boundary of the sink is
| (30) |
![\begin{figure}
\par\includegraphics[height=8.4cm,width=4.9cm,clip]{5484fig3.ps}\end{figure}](/articles/aa/full/2006/46/aa5484-06/Timg139.gif) |
Figure 3:
Same as in Fig. 1 but with a
ideal stellar wind emitted from the inner region whose ejection mass
rate is
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=8.4cm,width=3.6cm,clip]{5484F4_1.ps}\...
...F4_3.ps}\includegraphics[height=8.4cm,width=3.6cm,clip]{5484F4_4.ps}\end{figure}](/articles/aa/full/2006/46/aa5484-06/Timg140.gif) |
Figure 4:
Time evolution of a two-component jet launched from a thin accretion
disc threaded by a bipolar
magnetic field. The outflow is composed of a disc-driven jet embedding a non-ideal stellar wind
emitted from a YSO located at the center of the
simulation in the sink region. The density
contours are represented by greyscales while poloidal magnetic
field lines are displayed using solid lines. The various snapshots
represent the same system but at different stages (after five, ten, twenty,
and thirty inner disc rotations).The simulation was performed with a
stellar mass-loss rate of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=10.2cm,width=5.8cm,clip]{5484F5_1.ps}...
...*{4mm}
\includegraphics[height=10.2cm,width=5.8cm,clip]{5484F5_2.ps}\end{figure}](/articles/aa/full/2006/46/aa5484-06/Timg141.gif) |
Figure 5:
Left: plot of the initial temperature isocontours of the
accretion disc.
Right: plot of the temperature isocontours of the simulation displayed in
Fig. 3. Temperature isocontours are not displayed in the
external medium (outside of both the jet, stellar wind, and disc) as it is
considered a near vacuum medium with very low temperature.
The size of the sink region
is
|
| Open with DEXTER | |
The interaction between the different components of the outflow may be
responsible for energy dissipation inside the plasma, which is the outcome of
non-ideal MHD mechanisms occurring in the wind.
In this paragraph, we show how these non-ideal MHD effects are taken into
account when prescribing a turbulent magnetic resistivity
taking place in the wind region, in addition to the disc resistivity
![$\displaystyle \eta_{\rm m} = \alpha_{\rm m} \left.V_{A}\right\vert_{Z = 0} H \e...
... V_{A} H_{\rm w} \exp{\left[-2
\left(\frac{R}{H_{\rm w}}\right)^2\right]} \cdot$](/articles/aa/full/2006/46/aa5484-06/img142.gif) |
(31) |
We first focus on a simulation where the stellar mass loss is set to
![]() yr. The outcome of our simulation can be seen in
Fig. 4 where we display four different snapshots of the poloidal
cross-sections of the structure
at different times its evolution, i.e. at 8, 16, 24, and 32
rotation periods of the inner disc radius. In these snapshots we
display the density contours and the poloidal
magnetic field lines. The initial accretion disc
configuration is close to a hydrostatic equilibrium where the centrifugal
force and the total pressure gradient balance
the gravity. In the central region, the matter is continuously emitted at
the surface of the sink region (designed to be close to the star surface)
with sub fast-magnetosonic speed and with a solid
rotation velocity profile. Initially, a conical hot outflow (stellar wind)
propagates
above the inner part of the disc. Its inertia compresses the magnetic field
anchored to the accretion disc. As a result, the bending of the magnetic
surfaces increases, leading to a magnetic pinching of the disc. This pinching
delays the jet launching as the disc has to find a new vertical equilibrium.
Thus the disc takes a few more inner disc rotations before launching its jet
compared to CK04.
Once the jet has been launched, the structure reaches a quasi steady-state
where the outflow becomes parallel to the poloidal magnetic field that is
parallel to the vertical direction.
yr. The outcome of our simulation can be seen in
Fig. 4 where we display four different snapshots of the poloidal
cross-sections of the structure
at different times its evolution, i.e. at 8, 16, 24, and 32
rotation periods of the inner disc radius. In these snapshots we
display the density contours and the poloidal
magnetic field lines. The initial accretion disc
configuration is close to a hydrostatic equilibrium where the centrifugal
force and the total pressure gradient balance
the gravity. In the central region, the matter is continuously emitted at
the surface of the sink region (designed to be close to the star surface)
with sub fast-magnetosonic speed and with a solid
rotation velocity profile. Initially, a conical hot outflow (stellar wind)
propagates
above the inner part of the disc. Its inertia compresses the magnetic field
anchored to the accretion disc. As a result, the bending of the magnetic
surfaces increases, leading to a magnetic pinching of the disc. This pinching
delays the jet launching as the disc has to find a new vertical equilibrium.
Thus the disc takes a few more inner disc rotations before launching its jet
compared to CK04.
Once the jet has been launched, the structure reaches a quasi steady-state
where the outflow becomes parallel to the poloidal magnetic field that is
parallel to the vertical direction.
The obtained solution is fully consistent with an accretion-disc launching
plasma with a sub-slowmagnetosonic velocity. The solution crosses the three
critical surfaces, namely the slow-magnetosonic, the Alfvén, and the
fast-magnetosonic surfaces. The
other component of the outflow, namely the stellar wind, is injected with
sub-fastmagnetosonic velocity and crosses the Alfvén and
fastmagnetosonic surfaces.
The two components of the outflow become super-fastmagnetosonic before
reaching the upper boundary limit of the computational
domain. Figure 4 also shows that the outflow has achieved quite a
good collimation within our computational domain. We can distinguish between
the two components using the isocontours of temperature, which are displayed
as grey-scales in Fig. 5. In this figure, we can clearly see
a hot outflow coming from the central object embedded
in the cooler jet arising from the accretion disc. In Fig. 5
we also show that the thermal
energy released by the Ohmic and viscous heating in the accretion disc
is extracted by a hot jet that is compatible with the result in
CK04. In order to illustrate the thermal effect on the outflow, we have plotted
the temperature vertical profile in Fig. 6 along a radius located at
![]() from the axis. In this plot, the temperature increases
in the disc corona before reaching its maximum
from the axis. In this plot, the temperature increases
in the disc corona before reaching its maximum
![]() and
remaining constant.
and
remaining constant.
![\begin{figure}
\par\includegraphics[height=4.8cm,width=6.6cm,clip]{5484Fig6.ps}\end{figure}](/articles/aa/full/2006/46/aa5484-06/Timg150.gif) |
Figure 6:
Plot of the vertical variation at
|
| Open with DEXTER | |
To study the time evolution of both accretion and ejection
phenomena in the accretion disc and around the star, we
analyze the accretion and ejection mass loss rate in both components.
As in CK04 we draw the time evolution in Fig. 7 of the mass loss
rate
![]() in the disc-driven jet normalized to the accreted mass rate
in the disc-driven jet normalized to the accreted mass rate
![]() at the inner radius RI =1. We also display
at the inner radius RI =1. We also display
![]() normalized
to the fixed mass accreted
normalized
to the fixed mass accreted
![]() at the external radius of our
accretion disc at RI =40. Similar to CK04, we observe a strong increase,
on the accretion rate in the inner part with time (Fig. 7).
This behavior is related to the extraction of the rotational energy of the
accretion disc by the magnetic field. Indeed the creation of the toroidal
component of the magnetic field in the disc brakes the disc matter so that
the centrifugal force decreases, leading to an enhanced accretion motion.
The mass flux associated with the
disc-driven jet slowly increases to reach
at the external radius of our
accretion disc at RI =40. Similar to CK04, we observe a strong increase,
on the accretion rate in the inner part with time (Fig. 7).
This behavior is related to the extraction of the rotational energy of the
accretion disc by the magnetic field. Indeed the creation of the toroidal
component of the magnetic field in the disc brakes the disc matter so that
the centrifugal force decreases, leading to an enhanced accretion motion.
The mass flux associated with the
disc-driven jet slowly increases to reach ![]() of the accreted mass rate at the inner radius and contributes to
of the accreted mass rate at the inner radius and contributes to ![]() of the
total mass-loss rate of the outflow. In fact, in this simulation the mass-loss
rate from the central object is constant (
of the
total mass-loss rate of the outflow. In fact, in this simulation the mass-loss
rate from the central object is constant (
![]() yr), while the
inner accretion rate reaches
yr), while the
inner accretion rate reaches
![]() yr and the disc-driven jet mass rate
yr and the disc-driven jet mass rate
![]() yr. Hence the stellar outflow does not affect the
overall structure of the outflow much. This is confirmed by the shape of the
outflow since it reaches a very similar aspect to the one obtain in CK04 or
in the previous simulation without a stellar jet, i.e. a jet
confined within 20 inner disc radius.
yr. Hence the stellar outflow does not affect the
overall structure of the outflow much. This is confirmed by the shape of the
outflow since it reaches a very similar aspect to the one obtain in CK04 or
in the previous simulation without a stellar jet, i.e. a jet
confined within 20 inner disc radius.
In order to analyze this accretion-ejection engine, we have to identify the
forces responsible for the establishment of a steady accretion motion in
equilibrium with a continuous emission of matter at the surface of the
accretion disc. Furthermore we have to look at the collimation of the
outflow and its interaction with the stellar wind. We show in
Fig. 8 the various forces parallel to a given magnetic field line
anchored in the disc and a flow streamline anchored to the central object. The various
forces working along and across the field lines are
| |
= | (32) | |
| = | (33) | ||
| = | (34) | ||
| = | 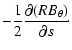 |
(35) | |
| = | (36) | ||
| = | (37) | ||
| = | (38) | ||
| = | (39) |
![\begin{figure}
\par\includegraphics[height=4.9cm,width=16.1cm,clip]{5484Fig7.ps}\end{figure}](/articles/aa/full/2006/46/aa5484-06/Timg187.gif) |
Figure 7:
a) Plot of the ejection mass rate from the accretion disc.
b) The inner
accretion rate. c) The ratio of the stellar mass-loss rate to the
disc-wind mass-loss rate
as a function of time. These plots are related to the simulation performed
with a stellar mass loss of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=6.5cm,width=7.7cm,clip]{5484F8R.eps}\...
...e*{6mm}
\includegraphics[height=6.5cm,width=7.6cm,clip]{5484F8L.eps}\end{figure}](/articles/aa/full/2006/46/aa5484-06/Timg188.gif) |
Figure 8:
Plot of the various forces Left: along a given magnetic field line
anchored in the accretion disc, Right: along a streamline anchored
to the stellar corona. These plots show the various forces accelerating the
flow:
|
| Open with DEXTER | |
The disc-driven jet behaves as in CK04. In particular,
we find that the mass acceleration encounters two different regimes. In
Fig. 8 we see that the vertical outflow is
lifted from the accretion disc by both the magneto-centrifugal force and the
pressure gradient up to the Alfvén surface. Beyond, the poloidal acceleration
is mainly sustained by the pressure gradient associated with the toroidal
component of the magnetic field. Inside the resistive accretion disc, the
toroidal component of the magnetic field increases because of the differential
rotation of the disc
![]() .
Conversely, outside
the disc, the advection of the toroidal
magnetic field balances the differential rotation
.
Conversely, outside
the disc, the advection of the toroidal
magnetic field balances the differential rotation
![]() exactly
(Ferreira 1997; Casse & Ferreira 2000). This change induces a decrease in
exactly
(Ferreira 1997; Casse & Ferreira 2000). This change induces a decrease in
![]() outside the accretion disc. As shown in CK04, this configuration
allows matter below the disc surface to be pinched and to remain in an
accretion regime, while beyond the disc surface, the change of sign of
outside the accretion disc. As shown in CK04, this configuration
allows matter below the disc surface to be pinched and to remain in an
accretion regime, while beyond the disc surface, the change of sign of
![]() enables acceleration of mass along the magnetic field
lines (cf. Fig. 8). This change in the magnetic poloidal force
also corresponds to a change in sign of the magnetic torque
(
enables acceleration of mass along the magnetic field
lines (cf. Fig. 8). This change in the magnetic poloidal force
also corresponds to a change in sign of the magnetic torque
(
![]() )
leading to the transformation of the MHD Poynting
flux generated by the disc into kinetic energy of the jet material.
)
leading to the transformation of the MHD Poynting
flux generated by the disc into kinetic energy of the jet material.
The cylindrical collimation of the external outflow is induced by the pressure
gradient of the poloidal component of the magnetic field (
![]() in
Fig. 9). In fact, the magnetic field
in the disc-driven jet undergoes an expansion that induces a decrease
in the poloidal magnetic field in the jet compared to the outer region
(Fig. 9). Conversely the pressure gradient of the toroidal magnetic
field (
in
Fig. 9). In fact, the magnetic field
in the disc-driven jet undergoes an expansion that induces a decrease
in the poloidal magnetic field in the jet compared to the outer region
(Fig. 9). Conversely the pressure gradient of the toroidal magnetic
field (
![]() )
acts to decollimate the outflow because the
value of
)
acts to decollimate the outflow because the
value of
![]() is low outside the outflow, and its absolute value
decreases between the massive part of the disc-driven outflow and the outer
medium. The magnetic field lines in the massive part of the outflow are
anchored to the inner part of the accretion disc and extract more angular
momentum than the magnetic lines in the outer medium.
The inner part of the jet is, on the other hand, collimated by the toroidal
pinching force.
is low outside the outflow, and its absolute value
decreases between the massive part of the disc-driven outflow and the outer
medium. The magnetic field lines in the massive part of the outflow are
anchored to the inner part of the accretion disc and extract more angular
momentum than the magnetic lines in the outer medium.
The inner part of the jet is, on the other hand, collimated by the toroidal
pinching force.
![\begin{figure}
\par\includegraphics[height=6.8cm,width=7.9cm,clip]{5484F9.eps}\end{figure}](/articles/aa/full/2006/46/aa5484-06/Timg194.gif) |
Figure 9:
Plot of the transverse forces as a function of R at a given
altitude Z = 75. It shows, across a
given cross section of the jet, the collimation processes acting in the
stellar and disc components
of the jet for the simulation with a stellar mass
loss
|
| Open with DEXTER | |
The stellar wind undergoes a thermal acceleration, as long as the shape of the
jet does not become cylindrical. Incontrast to the disc-driven jet, the
magneto-centrifugal force remains weak along the stellar wind flow.
The opening angle between magnetic field lines that emerge from the sink region
remains weak.
In fact the stellar outflow starts to be collimated by the surrounding
hollow jet induced by the accretion disc.
This explains the difference from a
model of Matt & Balick (2004) where the stellar wind is the only
outflow and which is prone to a dipolar expansion.
In our simulation, we self-consistently describe the acceleration of the
inner jet in addition to its collimation, something that can be compared
with analytical modeling (Sauty et al. 2002,2004). Part of both the thermal energy
deposited at the surface
of the corona near the polar axis and the energy deposited by the turbulence in
the stellar wind is transformed into kinetic energy (Fig. 10)
along the streamline. We have estimated the amount of Ohmic heating
released in the stellar outflow in the context of our simulation, namely,
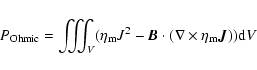 |
(40) |
![\begin{figure}
\par\includegraphics[height=6.4cm,width=7.2cm,clip]{5484F10.eps}\end{figure}](/articles/aa/full/2006/46/aa5484-06/Timg197.gif) |
Figure 10:
The vertical variations of specific energies, normalized to the
maximum kinetic energy flux, along a streamline in the stellar
wind with a rate
|
| Open with DEXTER | |
The collimation of the inner part of the jet is induced by the thermal pressure plus the pinching of the toroidal component of the magnetic field. They balance the centrifugal force and the pressure of the poloidal component of the magnetic field (Fig. 9). Besides that, the simulation shows that the inner portion of the stellar jet has a deep in density (Fig. 4) and a peak of velocity around the axis (Fig. 13). Thus, all these facts suggest that the very inner part of the outflow, the so-called spine jet, behave as a meridionally-self-similar jet as in Sauty et al. (2002,2004). We observe that this is a kind of "hollow'' stellar jet "thermally'' driven and both magnetically and thermally confined inside the "hollow'' disc jet. This result is to be compared to the analysis of CK04 where it is shown that the external disc jet is, partially at least, behaving as a radially self-similar one.
![\begin{figure}
\par\includegraphics[height=6.6cm,width=8cm,clip]{5484F11L.eps}\h...
...*{3mm}
\includegraphics[height=6.6cm,width=7.9cm,clip]{5484F11R.eps}\end{figure}](/articles/aa/full/2006/46/aa5484-06/Timg198.gif) |
Figure 11:
Same plots as in Fig. 8 but for a
simulation where the
stellar mass ejection rate is
|
| Open with DEXTER | |
In Fig. 12, we display temperature isocontours within
a small area around the sink region. Thanks to this plot, we can see that
the magnetic lever arm associated with the various outflow components is
different. In fact, the disc-driven jet exhibits a magnetic lever arm
(related to the ratio of the Alfvèn radius to the magnetic-field line
foot-point radius) varying approximately from 9 to 25, while the magnetic
lever arm associated with the stellar wind ranges from 0 near the axis to
several tens, if one considers the foot-point of magnetospheric magnetic-field
line to be anchored to the star. This last magnetic lever arm value may not
be very reliable since we have imposed the size of the sink and thus
influenced the radial extension of the magnetospheric outflow near the sink.
![\begin{figure}
\par\includegraphics[height=8.7cm,width=7.4cm,clip]{5484F12.ps}\end{figure}](/articles/aa/full/2006/46/aa5484-06/Timg199.gif) |
Figure 12:
Same density plot as in Fig. 3 but for a smaller zone around the
sink. The three critical surfaces are represented by dark lines
(slow-magnetosonic), dashed lines (Alfvèn), and white lines
(fast-magnetsonic). The size of the sink region
is
|
| Open with DEXTER | |
An alternative to the presence of turbulence in the stellar wind would
be to have a mechanism acting near the star corona and transforming a
part of the accretion energy into thermal energy (see for instance
Matt & Pudritz 2005 and reference therein). We performed several simulations
without turbulence inside the stellar wind (
![]() )
and with the
value of
)
and with the
value of
![]() regularly increased (and thus the amount
of thermal energy at the top of the sink). We find that, in our
simulations, the maximal
value of
regularly increased (and thus the amount
of thermal energy at the top of the sink). We find that, in our
simulations, the maximal
value of
![]() is around 10-3. Beyond that value,
the pressure above the sink is so high that it disrupts the accretion
disc structure and prevents the launching of the disc-driven jet. It is
noteworthy that this value of
is around 10-3. Beyond that value,
the pressure above the sink is so high that it disrupts the accretion
disc structure and prevents the launching of the disc-driven jet. It is
noteworthy that this value of
![]() is linked to very
high value of thermal energy released in the star corona.
is linked to very
high value of thermal energy released in the star corona.
Indeed, the reader has to keep in mind that the top boundary of the sink
is quite far from the stellar surface (typically 20 stellar radii) so that
if the flow undergoes a spherical expansion with a constant thermal energy
flux, the thermal energy deposited in the corona would represent
![]() of the energy released by
accretion. This amount of thermal energy may then represent a
significant fraction of the accretion energy. In our calculations done
without stellar outflow turbulence, we noticed that the
structures fulfilling observational constraints coincide with the highest
value of
of the energy released by
accretion. This amount of thermal energy may then represent a
significant fraction of the accretion energy. In our calculations done
without stellar outflow turbulence, we noticed that the
structures fulfilling observational constraints coincide with the highest
value of
![]() allowing disc-driven jet launching
(typically 10-3).
allowing disc-driven jet launching
(typically 10-3).
The resulting two-component outflow is very similar to simulations done with
turbulence in the stellar wind (and a very low
![]() ),
except the terminal velocity of the stellar outflow as shown in
Fig. 13 where we display the vertical velocity of matter along a
radial direction located at
),
except the terminal velocity of the stellar outflow as shown in
Fig. 13 where we display the vertical velocity of matter along a
radial direction located at
![]() .
In this figure we can clearly see that
the stellar wind prone to turbulent heating is faster than the ideal MHD
stellar wind. The poloidal mass acceleration in this zone is very sensitive
to thermal heating since magneto-centrifugal is vanishing here. A continuous
heating, as generated by Ohmic heating, seems more efficient for accelerating
the mass since it is
"refilling'' the thermal energy reservoir available for acceleration
along the flow.
.
In this figure we can clearly see that
the stellar wind prone to turbulent heating is faster than the ideal MHD
stellar wind. The poloidal mass acceleration in this zone is very sensitive
to thermal heating since magneto-centrifugal is vanishing here. A continuous
heating, as generated by Ohmic heating, seems more efficient for accelerating
the mass since it is
"refilling'' the thermal energy reservoir available for acceleration
along the flow.
![\begin{figure}
\par\includegraphics[height=4.4cm,width=5.8cm,clip]{5484F13L.ps}\...
...*{10mm}
\includegraphics[height=4.4cm,width=5.8cm,clip]{5484F13R.ps}\end{figure}](/articles/aa/full/2006/46/aa5484-06/Timg203.gif) |
Figure 13:
The transverse variation of the vertical velocity
at Z = 8 AU, for the simulation with stellar mass loss
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=11.2cm,width=6.5cm,clip]{5484F14.ps}\end{figure}](/articles/aa/full/2006/46/aa5484-06/Timg204.gif) |
Figure 14:
Same figure as in Fig. 1 but with a
non-ideal stellar wind emitted from the inner region with an ejection mass
rate
|
| Open with DEXTER | |
The angular momentum carried away by the stellar outflow now represents ![]() of
the accreted angular momentum at the inner radius of the accretion disc.
Regarding the acceleration of the outflow, we can distinguish two regions:
an internal one corresponding to the contribution from the stellar outflow
and an external one coming from the disc-driven
jet. This last component reaches velocities up to vz = 15(Fig. 16).
The acceleration of this component is thermally and
magneto-centrifugally driven, which is coherent with the larger radial
expansion of the stream
lines (see Fig. 11). In the inner stellar wind,
the flow undergoes a weak expansion, and its velocity does not exceed vz =
6.8. The acceleration of this component is achieved mainly via the
thermal pressure, which is expected since the mass density is much higher
than in previous simulations where
of
the accreted angular momentum at the inner radius of the accretion disc.
Regarding the acceleration of the outflow, we can distinguish two regions:
an internal one corresponding to the contribution from the stellar outflow
and an external one coming from the disc-driven
jet. This last component reaches velocities up to vz = 15(Fig. 16).
The acceleration of this component is thermally and
magneto-centrifugally driven, which is coherent with the larger radial
expansion of the stream
lines (see Fig. 11). In the inner stellar wind,
the flow undergoes a weak expansion, and its velocity does not exceed vz =
6.8. The acceleration of this component is achieved mainly via the
thermal pressure, which is expected since the mass density is much higher
than in previous simulations where
![]() yr. Let us
note that the fast-magnetosonic Mach number remains higher than one for the
whole outflow (Fig. 16).
yr. Let us
note that the fast-magnetosonic Mach number remains higher than one for the
whole outflow (Fig. 16).
In this paper we present numerical simulations of the
interaction between an accretion-ejection
structure launching a disc-driven jet and a stellar wind emitted either from the
central object and/or from its magnetosphere, in particular for the case of YSOs. In our framework, the
accretion disc is near
equipartition between thermal pressure and magnetic pressure where
turbulence is believed to occur. This turbulence is characterized by a time
and space-dependent anomalous resistivity and viscosity set by using an
![]() description. The origin of the turbulence is still unknown but is
not likely to arise from magneto-rotational instability since an
equipartition disc is inconsistent with the development of such instability
(Ogilvie & Livio 2001).
description. The origin of the turbulence is still unknown but is
not likely to arise from magneto-rotational instability since an
equipartition disc is inconsistent with the development of such instability
(Ogilvie & Livio 2001).
The properties of both the accretion disc and outflow were investigated in
this paper. In a first stage, we analyzed the contribution of the various
hydrodynamical and magnetohydrodynamical mechanisms
to the angular momentum transport in the thin accretion disc including, for the
first time, both anomalous viscosity and resistivity, with a magnetic
Prandtl number equal to unity. We demonstrated
that the MHD Poynting flux associated with the disc-driven jet plays a
major role in the removal of the angular momentum from
the thin accretion disc. The angular momentum radial transport provided by
the anomalous viscosity inside
the disc remains weak and contributes only ![]() of the total angular
momentum transport (this value agrees with analytical estimates
depending on disc thickness and
of the total angular
momentum transport (this value agrees with analytical estimates
depending on disc thickness and ![]() value). This is consistent with
the viscous torque depending upon the radial derivative of angular velocity,
while the magnetic torque is mainly controlled by the vertical derivative of the
toroidal component of the magnetic field. In a thin accretion disc, the
toroidal magnetic field varies from zero to an equipartition value on a
disc scale height
value). This is consistent with
the viscous torque depending upon the radial derivative of angular velocity,
while the magnetic torque is mainly controlled by the vertical derivative of the
toroidal component of the magnetic field. In a thin accretion disc, the
toroidal magnetic field varies from zero to an equipartition value on a
disc scale height
![]() ,
leading to a much more
efficient extraction of the rotational energy from the magnetic torque into
the MHD Poynting energy flux feeding the jet.
Basically, with our simulation and despite the disc viscosity, we have
reproduced very similar results to those obtained by CK04 where the
viscous torque was neglected.
,
leading to a much more
efficient extraction of the rotational energy from the magnetic torque into
the MHD Poynting energy flux feeding the jet.
Basically, with our simulation and despite the disc viscosity, we have
reproduced very similar results to those obtained by CK04 where the
viscous torque was neglected.
| |
Figure 15:
Plot of the temporal evolution of the ejection mass-loss rate from
the accretion disc in a) the ratio of
the stellar mass-loss rate to the ejection mass-loss rate
from the accretion disc as a function of time in b) for the simulation with a
stellar mass-loss rate of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=4.9cm,width=15.9cm,clip]{5484F16.eps}\end{figure}](/articles/aa/full/2006/46/aa5484-06/Timg212.gif) |
Figure 16:
The transverse variation of different physical quantities as
magnetic-field components, velocity components, and the fast-magnetosonic
Mach number
at Z = 100, for the simulation with stellar mass loss
|
| Open with DEXTER | |
We performed various simulations using different stellar mass ejection
rates from the central objects. These stellar ejection-mass rates range
from a Sun-like star (
![]() yr) to O and B type stars
(
yr) to O and B type stars
(
![]() yr).
The influence of the stellar wind on the
dynamics and the structure of jet and the accretion-ejection structure around the
stellar object gets stronger with higher stellar mass ejection rates. As an
example in the simulations where stellar mass ejection rates are
yr).
The influence of the stellar wind on the
dynamics and the structure of jet and the accretion-ejection structure around the
stellar object gets stronger with higher stellar mass ejection rates. As an
example in the simulations where stellar mass ejection rates are
![]() yr, we obtained a very similar disc-driven jet to the
one in CK04. The only difference lies in the presence of the internal, fast, hot
plasma coming from the central object. In this simulation, the ejection-mass
rate in the disc-driven jet is similar to the one in CK04, on the order of
yr, we obtained a very similar disc-driven jet to the
one in CK04. The only difference lies in the presence of the internal, fast, hot
plasma coming from the central object. In this simulation, the ejection-mass
rate in the disc-driven jet is similar to the one in CK04, on the order of
![]() of the inner disc accretion mass rate, while the stellar ejection
mass rate represents
of the inner disc accretion mass rate, while the stellar ejection
mass rate represents ![]() of the total mass loss in the outflow.
of the total mass loss in the outflow.
In our simulations, the collimation of the stellar outflow takes place once the jet from the accretion disc is launched and has reached a significant spatial extension. Its collimation is provided mainly by pinching the toroidal magnetic field in equilibrium with the thermal pressure gradient. Conversely the collimation of the jet from the accretion disc is induced by the poloidal magnetic field pressure gradient balancing the centrifugal force. Furthermore, in all the simulation the stellar wind keeps having a more or less conical expansion up to the asymptotic region where the disc-driven jet acts to collimate the stellar flow into a cylindrical flow.
These important results are self-consistently obtained, in contrast to simulations of Bogovalov & Tsinganos (2005) where a relativistic wind was collimated by a jet but which did not consider either the accretion disc, the jet launching, or the stellar wind acceleration. Indeed in our model, we self-consistent describe the launching and the collimation of disc and stellar wind. In particular, our simulations completely describe both the stellar flow acceleration (the stellar flow is injected with sub-Alfvènic velocity) and the launching mechanism of the jet from the accretion disc.
We have shown that the contribution of non-ideal MHD
mechanisms in the
acceleration of the stellar outflow can be significant since turning on
this dissipative mechanism leads, for instance, to higher terminal
velocities of the stellar jet-collimated flow. Our prescription of these
dissipative mechanisms is of course subject to improvements, but our goal
was to show that they enable an increase in the efficiency
of both the thermal and magnetic acceleration of the stellar wind.
The turbulence may be produced by the interaction of the stellar wind with
the disc-driven jet. Moreover, as in the solar wind, the turbulence in
the stellar wind may also have a stellar origin and/or a possible connection
to the accretion occurring near the surface of the star. In this scenario,
a part of the energy released by accretion is carried away in the wind by
outwardly propagating Alfvén waves inducing turbulence. This scenario
is a variant of models where a significant part of the accretion
energy is converted into thermal energy in the star corona (see
Matt & Pudritz 2005 and references therein). By performing
simulations with no stellar wind turbulence but with a large amount of
thermal energy at the base of the wind, we found quite similar result
except for the velocity field, the resistive continuous heating of the
stellar wind being more efficient in providing higher velocity. It is noteworthy
that, similarl to models depositing thermal energy near the stellar corona,
the amount of energy released by the turbulent heating is a significant
fraction of the accretion energy (in the particular case of our simulations,
it represents near ![]() of the accretion energy).
Note also that similar double-layer jets were found by Koide and
collaborators in various
simulations (e.g. Koide et al. 1998, 1999) but those
simulations were devoted to
rapidly variable jets (with only a few disc rotations) and not to steady
structures.
of the accretion energy).
Note also that similar double-layer jets were found by Koide and
collaborators in various
simulations (e.g. Koide et al. 1998, 1999) but those
simulations were devoted to
rapidly variable jets (with only a few disc rotations) and not to steady
structures.
We performed simulations with higher stellar ejection-mass rate,
typically with
![]() yr (compatible with O-B type
stars). The increase in the stellar mass-loss rate induces
a faster and larger expansion of the jet. Indeed the enhanced pressure
provoked by the stellar wind tends to bend the disc magnetic field lines over a
larger radial extension, leading to a larger disc-driven jet. The
corresponding disc-driven jet mass-ejection rate is much higher than in
previous simulations since it reaches
yr (compatible with O-B type
stars). The increase in the stellar mass-loss rate induces
a faster and larger expansion of the jet. Indeed the enhanced pressure
provoked by the stellar wind tends to bend the disc magnetic field lines over a
larger radial extension, leading to a larger disc-driven jet. The
corresponding disc-driven jet mass-ejection rate is much higher than in
previous simulations since it reaches ![]() of the disc inner accretion
rate (stellar ejection-mass rate on the order of
of the disc inner accretion
rate (stellar ejection-mass rate on the order of ![]() ).
The simulations give a quantitative
threshold beyond which the stellar jet gives a significant extra expansion
of the disc jet. Typically
a mass loss rate from the star on the order of
).
The simulations give a quantitative
threshold beyond which the stellar jet gives a significant extra expansion
of the disc jet. Typically
a mass loss rate from the star on the order of
![]() yr
gives a factor two in the radial
expansion of the disc-driven jet. Although the total jet remains small in
cross section, as in CK04, and compared to self-similar disc wind models. Moreover
the stellar jet play a very important role, also, in the formation of the disc
wind.
We verify that, part of the external disc wind may look quasi
radially-self-similar in nature, the
most inner part of the stellar wind is quasi meridionally self-similar.
In our work we neglected all radiative losses coming from the
central star or from the plasma itself. The implementation of these terms
and the study of their impact on the outflow structure is postponed to
future work.
yr
gives a factor two in the radial
expansion of the disc-driven jet. Although the total jet remains small in
cross section, as in CK04, and compared to self-similar disc wind models. Moreover
the stellar jet play a very important role, also, in the formation of the disc
wind.
We verify that, part of the external disc wind may look quasi
radially-self-similar in nature, the
most inner part of the stellar wind is quasi meridionally self-similar.
In our work we neglected all radiative losses coming from the
central star or from the plasma itself. The implementation of these terms
and the study of their impact on the outflow structure is postponed to
future work.
Acknowledgements
Z.M. thanks Henk Spruit, Andrea Merloni and Dimitrios Giannios for many valuable suggestions. Z.M. is grateful for the hospitality of the Garching group. Part of this research was supported by European FP5 RTN "Gamma Ray Burst: An Enigma and a Tool''. Z.M. thanks Kanaris Tsinganos for many valuable suggestions. Z.M. thanks Claudio Zanni for many valuable suggestions. Finally, F.C. would like to thank Sylvie Cabrit for many helpful remarks and advises.