A&A 460, 37-44 (2006)
DOI: 10.1051/0004-6361:20064965
Large-scale structure and the Cardassian fluid
S. Fay1,2 - M. Amarzguioui3
1 - School of Mathematical Science, Queen Mary, University of London, Mile End road, London E1 4NS, UK
2 - Laboratoire Univers et Théories (LUTH), UMR 8102, Observatoire de Paris, 92195 Meudon Cedex, France
3 -
Institute of Theoretical Astrophysics, University of Oslo, PO Box 1029 Blindern, 0315 Oslo, Norway
Received 3 February 2006 / Accepted 24 August 2006
Abstract
In this paper, we confront the predictions of the
power law Cardassian model for the baryon power
spectrum with the observations of the SDSS galaxy survey. We show that
they fit only for very unusual values of the cold dark matter or
baryon density parameters, the Hubble parameter or the spectral index
of the initial power spectrum. Moreover, the best-fit Cardassian models turn out to
be phantom models. If one wants to recover the usual values for these constants, as
quoted by the WMAP team, the power law Cardassian model turns out to
be indistinguishable from a 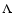 CDM model.
CDM model.
Key words: cosmology: theory - cosmological parameters - large-scale structure of Universe
1 Introduction
One of the greatest discoveries in cosmology in recent years is the accelerated expansion of the Universe. The first strong evidence that led to the conclusion that the expansion of the Universe appears to be accelerating, came in 1998 from observations of supernovae of type Ia (Perlmutter et al. 1999; Riess et al. 1998). Since then, more recent supernovae observations (Knop et al. 2003; Riess et al. 2004; Tonry et al. 2003) along with observations of the cosmic microwave background (Spergel et al. 2003) and large-scale structure (Tegmark et al. 2004) have strengthened this conclusion even further.
Now that the accelerated expansion of the Universe seems to have been
established, the task facing cosmologists is to explain its origin.
Several models have been proposed over the years that attempt to
explain the dark energy that gives rise to the accelerated
expansion. One such model is the power law Cardassian
(Freese & Lewis 2002). This is a model that has no additional energy
components other than baryons and cold dark matter. However, motivated
by brane world cosmology (Chung & Freese 2000), the Friedmann equation is
modified by the presence of an additional energy term that is
proportional to the cold dark matter density raised to a general
power, i.e.
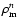 .
It is this term that gives rise to the
accelerated expansion or dark energy. Indeed, it can
be shown that the Hubble function can be written in the same form as
ordinary general relativity with a dark energy fluid
defined by a constant equation of state
.
It is this term that gives rise to the
accelerated expansion or dark energy. Indeed, it can
be shown that the Hubble function can be written in the same form as
ordinary general relativity with a dark energy fluid
defined by a constant equation of state
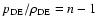 ,
where
,
where
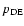 and
and
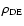 are respectively the pressure and
density of this special form of dark energy (Avelino et al. 2003).
Consequently, acceleration occurs for n<2/3 and the power law
Cardassian model cannot be distinguished from such dark energy
models by any observational tests based on the Hubble function only,
such as the redshift-luminosity distance relation inferred from
supernovae. However, this is no longer the case for tests based on
large-scale structure data (Koivisto et al. 2005; Sandvik et al. 2004), since they
probe more than just the background evolution.
More general Cardassian models exist where the
modification of the Friedmann equation cannot be written as a simple
power in the matter density. Examples of such model are the
Polytropic Cardassian Model (PC) and the Modified Polytropic
Cardassian Model (MPC), which were proposed in Gondolo & Freese (2003).
However, for such models it is more difficult to make a connection
to fundamental physics, hence rendering the model a purely
phenomenological model with little physical motivation. We stress
that we will consider only the original power law Cardassian model
in this work. Furthermore, the model will be considered in the
so-called fluid interpretation (Gondolo & Freese 2003), which will be
explained in Sect. 2. In the following, we will refer to
the power law Cardassian model as a phantom Cardassian
when n<0.
are respectively the pressure and
density of this special form of dark energy (Avelino et al. 2003).
Consequently, acceleration occurs for n<2/3 and the power law
Cardassian model cannot be distinguished from such dark energy
models by any observational tests based on the Hubble function only,
such as the redshift-luminosity distance relation inferred from
supernovae. However, this is no longer the case for tests based on
large-scale structure data (Koivisto et al. 2005; Sandvik et al. 2004), since they
probe more than just the background evolution.
More general Cardassian models exist where the
modification of the Friedmann equation cannot be written as a simple
power in the matter density. Examples of such model are the
Polytropic Cardassian Model (PC) and the Modified Polytropic
Cardassian Model (MPC), which were proposed in Gondolo & Freese (2003).
However, for such models it is more difficult to make a connection
to fundamental physics, hence rendering the model a purely
phenomenological model with little physical motivation. We stress
that we will consider only the original power law Cardassian model
in this work. Furthermore, the model will be considered in the
so-called fluid interpretation (Gondolo & Freese 2003), which will be
explained in Sect. 2. In the following, we will refer to
the power law Cardassian model as a phantom Cardassian
when n<0.
Constraints on Cardassian model imposed by the supernovae have been
investigated extensively in several papers, e.g. (Szydlowski et al. 2006; Bento et al. 2006; Frith 2004; Szydlowski et al. 2005; Gong & Duan 2004; Lazkoz et al. 2005; Sen & Sen 2003; Wang et al. 2003; Zhu et al. 2004; Nesseris & Perivolaropoulos 2004; Bento et al. 2005). These studies show that the parameter space of the model is quite degenerate. In order to get
better constraints one needs to consider additional cosmological
tests. In Amarzguioui et al. (2005), the MPC model is constrained by
comparing the matter power spectrum predicted by the model with that
inferred from the SDSS large-scale structure data. The authors show
that these data constrain the model severely. In fact, it is shown
that |n| has to be of order less than 10-5, which renders the
model virtually indistinguishable from the 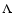 CDM model. In the
analysis leading to this conclusion the density and Hubble parameters
were fixed to the first-year values quoted by the WMAP team
(Spergel et al. 2003), i.e.
CDM model. In the
analysis leading to this conclusion the density and Hubble parameters
were fixed to the first-year values quoted by the WMAP team
(Spergel et al. 2003), i.e.
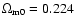 ,
,
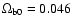 and
h=0.72. Here,
and
h=0.72. Here,
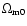 and
and
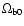 denote the density
parameters of dark matter and baryon respectively. In this paper we
want to generalise this approach. We restrict
ourselves to the power law Cardassian model, and perform a fit to
the baryon power spectrum while allowing these cosmological
parameters to take a range of constant values along with n.
Furthermore, we allow also the spectral index
denote the density
parameters of dark matter and baryon respectively. In this paper we
want to generalise this approach. We restrict
ourselves to the power law Cardassian model, and perform a fit to
the baryon power spectrum while allowing these cosmological
parameters to take a range of constant values along with n.
Furthermore, we allow also the spectral index 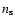 of the initial
power spectrum to take a range of possible values
rather than being just unity. This makes sense in view of the last
WMAP results (Spergel et al. 2006) which give
of the initial
power spectrum to take a range of possible values
rather than being just unity. This makes sense in view of the last
WMAP results (Spergel et al. 2006) which give
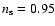
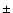 0.016compared with the first-year estimate of 0.99
0.016compared with the first-year estimate of 0.99 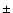 0.04. Does this
added freedom allow the Cardassian model to deviate from the
0.04. Does this
added freedom allow the Cardassian model to deviate from the
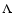 CDM model? This is what we intend to answer in this paper.
CDM model? This is what we intend to answer in this paper.
We find that all the best-fit models have negative n, which in the terminology defined above means that they are phantom models. The models that are compatible with the data fall
into two categories: |n| is either so small that the model is
indistinguishable from a 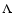 CDM model, or n can have a non-negligible negative value. But in the latter case, one finds that either the cold dark matter density, the Hubble parameter or
the spectral index must have very unusual values for the model to
differ substantially from a
CDM model, or n can have a non-negligible negative value. But in the latter case, one finds that either the cold dark matter density, the Hubble parameter or
the spectral index must have very unusual values for the model to
differ substantially from a 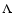 CDM model. Thus, if one wants
to recover the usual values for these constants, as quoted by the
WMAP team, the Cardassian model turns out to be indistinguishable
from a
CDM model. Thus, if one wants
to recover the usual values for these constants, as quoted by the
WMAP team, the Cardassian model turns out to be indistinguishable
from a 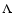 CDM model with
CDM model with
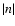 < 10-5.
< 10-5.
The structure of this paper is as follows: in Sect. 2 we
present the Friedmann equation of the power law
Cardassian model and look at how first order perturbations evolve in
the fluid interpretation of this model. In Sect. 3 we discuss
how to obtain the baryon power spectrum for the Cardassian model using
the perturbed equations presented in the preceding section, and what
initial condition to use for these. In Sect. 4 we present the
statistics we need to fit the predicted power spectrum of the model
with the observed. In Sect. 5, we fit the predictions of the
Cardassian model with the SDSS (Tegmark et al. 2004) baryonic power spectrum
by keeping three of the parameters
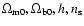 fixed
to their WMAP concordance values and allowing the remaining one
to take a range of possible values in addition to n.
fixed
to their WMAP concordance values and allowing the remaining one
to take a range of possible values in addition to n.
Finally, in Sect. 6 we summarise and conclude.
2 Field equations
We assume the universe to be homogeneous, isotropic and flat. The
metric can then be written in the usual form:
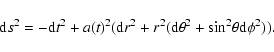 |
(1) |
The modified Friedmann equation for the Cardassian model is
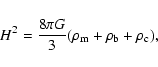 |
(2) |
where
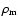 and
and
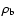 are respectively the CDM and baryonic matter densities and
are respectively the CDM and baryonic matter densities and
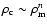 .
Note that we are looking at the ordinary Cardassian model and not the Modified Polytropic Cardassian Model (MPC) that was considered in Amarzguioui et al. (2005).
.
Note that we are looking at the ordinary Cardassian model and not the Modified Polytropic Cardassian Model (MPC) that was considered in Amarzguioui et al. (2005).
Energy conservation of pressureless matter implies that
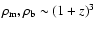 and hence,
and hence,
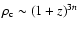 .
This allows us to write the Friedmann equation as
.
This allows us to write the Friedmann equation as
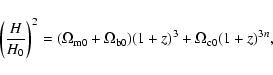 |
(3) |
where we have defined the density parameters
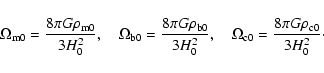 |
(4) |
In order to derive the matter power spectrum we need to go one step further than Eq. (3) which gives the evolution of the background. We need to consider first order perturbations. In order to do this, we follow the approach of Amarzguioui et al. (2005) and consider the fluid interpretation of the Cardassian model as introduced in Gondolo & Freese (2003). In this approach, the dark matter term and the term that gives rise to dark energy are treated as two "components'' of one single fluid - the Cardassian fluid. We write
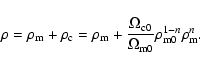 |
(5) |
Treating this as a perfect fluid and using energy-momentum conservation, we arrive at the usual continuity equation for the fluid 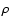 :
:
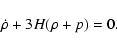 |
(6) |
Substituting from Eq. (5) and using energy conservation of ordinary matter, the effective pressure of the Cardassian fluid can be written as
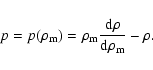 |
(7) |
The sound speed and the effective equation of state for the Cardassian fluid can now be calculated easily. We get
for the sound speed, and
for the equation of state.
In the fluid interpretation, the model we're considering contains two fluids, namely the Cardassian fluid and the baryon fluid. The evolution of density perturbation in these fluids is given by a coupled set of second order differential equations. The detailed derivation of these equations can be found in Lyth & Stewart (1990) and Padmanabhan (1993). Setting the equation of state parameter and sound speed of baryons equal to zero, we can write these differential equations as
| |
|
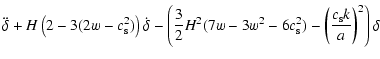 |
|
| |
|
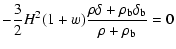 |
(10) |
and
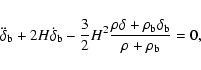 |
(11) |
where 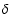 and
and
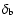 are the perturbations in the Cardassian and baryon fluids respectively. These equations are written with respect to cosmic time t. We want to solve them numerically, and in that respect it is more useful to write them in terms of a new time variable u defined by
are the perturbations in the Cardassian and baryon fluids respectively. These equations are written with respect to cosmic time t. We want to solve them numerically, and in that respect it is more useful to write them in terms of a new time variable u defined by
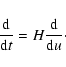 |
(12) |
This implies that
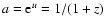 if we define the scale factor today as a0=1. Using this time parameter and marking a derivative with respect to it with a prime, the differential equations take the form
if we define the scale factor today as a0=1. Using this time parameter and marking a derivative with respect to it with a prime, the differential equations take the form
![$\displaystyle %
H^2\delta''+(H^2)' \frac{\delta'}{2}+\left[2-3(2\omega-c_{\rm s}^2)\right]H^2\delta'-\frac{3}{2}(7\omega-3\omega^2$](/articles/aa/full/2006/46/aa4965-06/img48.gif) |
|
|
|
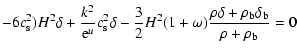 |
|
|
(13) |
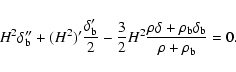 |
(14) |
3 Power spectrum
In this work we will use the large-scale structure data of the SDSS team to constrain the Cardassian model. The galaxy power spectrum inferred from these data![[*]](/icons/foot_motif.gif) is plotted in Fig. 1.
is plotted in Fig. 1.
The power spectrum of energy component i can be written as
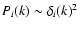 .
Thus, we can use Eqs. (13) and (14) with the appropriate initial conditions to predict the power spectrum of the baryons and/or the Cardassian fluid today. Taking the arguments presented in Beça et al. (2003) into account, we will consider the power spectrum arising from the baryons only and not from the dark matter component of the Cardassian fluid.
.
Thus, we can use Eqs. (13) and (14) with the appropriate initial conditions to predict the power spectrum of the baryons and/or the Cardassian fluid today. Taking the arguments presented in Beça et al. (2003) into account, we will consider the power spectrum arising from the baryons only and not from the dark matter component of the Cardassian fluid.
To determine the initial conditions for the coupled system of
differential Eqs. (13) and (14), we follow the
approach of Sandvik et al. (2004) and Amarzguioui et al. (2005): we assume the
evolution of the Cardassian and  CDM models to be similar very
early on, and use CMBFast (Seljak & Zaldarriaga 1996) to calculate the matter transfer function at redshift z=200 arising from an initial spectrum with a general spectral index
CDM models to be similar very
early on, and use CMBFast (Seljak & Zaldarriaga 1996) to calculate the matter transfer function at redshift z=200 arising from an initial spectrum with a general spectral index 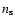 .
This allows us to write the density perturbations at z=200 as
.
This allows us to write the density perturbations at z=200 as
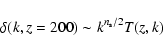 |
(15) |
where T(z,k) is the transfer function obtained from CMBFast. Next, we use (13) and (14) to evolve the perturbations until today. The power spectrum of baryons today is then obtained as
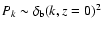 .
.
4 Statistics
To fit the 22 SDSS data points for the power spectrum we will use a least square test  .
It is defined by
.
It is defined by
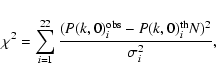 |
(16) |
where P(k,0) is the power spectrum of the baryons today and the superscripts th and obs denote the theoretical and the observed spectra respectively. Furthermore, 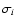 are the
are the 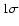 errors of the SDSS data and N is a normalisation factor that allows us to adjust the amplitude of the theoretical power spectrum. We want to find the values of N and the other cosmological parameters that minimise
errors of the SDSS data and N is a normalisation factor that allows us to adjust the amplitude of the theoretical power spectrum. We want to find the values of N and the other cosmological parameters that minimise  .
To simplify this procedure, we can define a new quantity
.
To simplify this procedure, we can define a new quantity
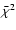 which minimises
which minimises  analytically with respect to the amplitude N. First, we define the following quantities:
analytically with respect to the amplitude N. First, we define the following quantities:
Substituting these into (16), we get the expression
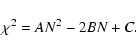 |
(20) |
Treating this as a function of N we find that its minimum is reached for N=B/A. We define the value of  corresponding to this minimising N as the new
corresponding to this minimising N as the new
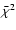 .
Thus, we write
.
Thus, we write
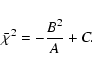 |
(21) |
This last expression defines a new  analytically minimised with respect to N. This is the definition of
analytically minimised with respect to N. This is the definition of  that we will use to fit the data.
that we will use to fit the data.
5 Fit to the SDSS matter power spectrum
In this section we perform the fitting of the
theoretical Cardassian model to the empirical values of the SDSS matter power spectrum. The parameters which are constrained in the fitting are the Cardassian parameter n, the CDM density parameter
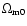 ,
the baryon density parameter
,
the baryon density parameter
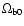 ,
the
Hubble parameter h, and the spectral index
,
the
Hubble parameter h, and the spectral index 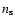 .
Ideally we would
like to get a constraint on all of these parameters
simultaneously, but the parameter space would be too large to handle
in a simple
.
Ideally we would
like to get a constraint on all of these parameters
simultaneously, but the parameter space would be too large to handle
in a simple  test. We will therefore restrict ourselves to
constraining pairs of these parameters with one parameter being n.
test. We will therefore restrict ourselves to
constraining pairs of these parameters with one parameter being n.
5.1 Constraining the n parameter only
In this first subsection we mainly try to recover the results of
Amarzguioui et al. (2005). In their analysis, the cosmological parameters
were set equal to the values quoted by the WMAP team. However, they
did not perform an explicit  fitting to the data. They
looked at the predicted power spectrum and noted that it deviates
strongly from the SDSS data even for extremely small deviation from
the
fitting to the data. They
looked at the predicted power spectrum and noted that it deviates
strongly from the SDSS data even for extremely small deviation from
the 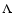 CDM model. Repeating their analysis, but doing an explicit fit to the data, we set
CDM model. Repeating their analysis, but doing an explicit fit to the data, we set
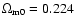 and
and
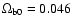 ,
implying
,
implying
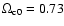 .
Furthermore, we set
the value of the Hubble parameter to h=0.72 and the spectral index
to
.
Furthermore, we set
the value of the Hubble parameter to h=0.72 and the spectral index
to
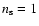 .
Using Eq. (21), we find the minimal value for
.
Using Eq. (21), we find the minimal value for  to be 27.08 when n=-5.6
to be 27.08 when n=-5.6 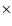 10-7. With 22 data
points and one free parameter, the
10-7. With 22 data
points and one free parameter, the  per degree of freedom (d.o.f.) is thus
per degree of freedom (d.o.f.) is thus
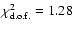 .
For n=0, corresponding to a cosmological constant,
.
For n=0, corresponding to a cosmological constant,
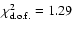 .
These values are not very
good but they are comparable to the values of
.
These values are not very
good but they are comparable to the values of
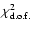 that were
obtained with the 56 supernovae of Perlmutter (Perlmutter et al. 1999)
published in 1999, and in works aiming to constrain quintessence
models (Di Pietro & Claeskens 2003). So maybe more precise data in the future will
decrease the
that were
obtained with the 56 supernovae of Perlmutter (Perlmutter et al. 1999)
published in 1999, and in works aiming to constrain quintessence
models (Di Pietro & Claeskens 2003). So maybe more precise data in the future will
decrease the
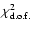 we get in this section, just as was the
case with the supernovae data. Figure 2 shows a plot
of
we get in this section, just as was the
case with the supernovae data. Figure 2 shows a plot
of  as a function of the parameter n.
as a function of the parameter n.
We see clearly that the SDSS data do not allow for as large values of n as the supernovae data: at 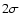 ,
n is limited to the
range
,
n is limited to the
range
![$n\in\left[-1.5\times 10^{-5},8.9\times 10^{-6}\right]$](/articles/aa/full/2006/46/aa4965-06/img70.gif) .
They
show that the Cardassian model must resemble a
.
They
show that the Cardassian model must resemble a 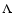 CDM model very
closely to be in agreement with the large-scale structure observations
and the WMAP values for the cosmological parameters.
Figure 3 compares the predictions of the Cardassian model with the SDSS data and is in agreement with the results of Amarzguioui et al. (2005). Note that negative values for n are not as strongly disfavoured as positive values. But still only a very small deviation from zero in the negative direction is allowed.
CDM model very
closely to be in agreement with the large-scale structure observations
and the WMAP values for the cosmological parameters.
Figure 3 compares the predictions of the Cardassian model with the SDSS data and is in agreement with the results of Amarzguioui et al. (2005). Note that negative values for n are not as strongly disfavoured as positive values. But still only a very small deviation from zero in the negative direction is allowed.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4965fig3.eps}\end{figure}](/articles/aa/full/2006/46/aa4965-06/Timg72.gif) |
Figure 3:
Power spectrum predicted by the Cardassian model versus SDSS data for several values of n. The curves are such that they best fit the data. The power spectrum predicted with the positive value n=0.0001 is totally excluded by the data. |
| Open with DEXTER |
5.2 Constraining n and the CDM density parameter
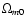
This section and the following ones generalise the work of
Amarzguioui et al. (2005). We consider n and
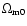 to be free
parameters and keep the other cosmological parameters fixed to
to be free
parameters and keep the other cosmological parameters fixed to
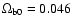 ,
h=0.72 and
,
h=0.72 and
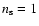 .
The minimal value for
.
The minimal value for  is then 21.86, which gives us
is then 21.86, which gives us
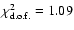 .
This is
obtained when
.
This is
obtained when
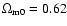 and n=-0.10. In
Fig. 4 we have plotted the
and n=-0.10. In
Fig. 4 we have plotted the  along with
the 1 and
along with
the 1 and 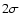 confidence contours as functions of n and
confidence contours as functions of n and
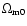 .
In Fig. 5 one can find an enlargement of this figure for the area
.
In Fig. 5 one can find an enlargement of this figure for the area
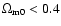 .
The 1 and
.
The 1 and 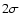 confidence levels for several ranges of values of n, in particular for the small n, are plotted in Fig. 6. At
confidence levels for several ranges of values of n, in particular for the small n, are plotted in Fig. 6. At 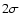 ,
the allowed ranges for the parameters are
,
the allowed ranges for the parameters are
![$n\in\left[-1.1,6.3\times 10^{-6}\right]$](/articles/aa/full/2006/46/aa4965-06/img76.gif) and
and
![$\Omega_{\rm m0}\in\left[0.22,0.73\right]$](/articles/aa/full/2006/46/aa4965-06/img77.gif) .
Thus, we see
that positive values for n are strongly disfavoured. But the data
do allow for negative values up to order of unity when treating only n and
.
Thus, we see
that positive values for n are strongly disfavoured. But the data
do allow for negative values up to order of unity when treating only n and
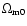 as free parameters.
as free parameters.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4965fig4.eps}\end{figure}](/articles/aa/full/2006/46/aa4965-06/Timg78.gif) |
Figure 4:
 and the 1 and
and the 1 and 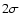 confidence contours (dashed lines) as functions of n and
confidence contours (dashed lines) as functions of n and
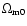 .
We only present the values of .
We only present the values of  smaller than 126 to clarify the colour of the plot.
smaller than 126 to clarify the colour of the plot. |
| Open with DEXTER |
In agreement with the previous section, for the fiducial value
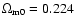 ,
the Cardassian model fits the data only if
,
the Cardassian model fits the data only if
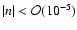 ,
that is: it is indistinguishable from a
,
that is: it is indistinguishable from a  CDM model. If we want the Cardassian model to be different from
CDM model. If we want the Cardassian model to be different from  CDM, one has to consider some unusual values of
CDM, one has to consider some unusual values of
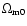 like 0.6. Figure 7 shows predictions of the Cardassian model for the power spectrum versus SDSS data for some values of
like 0.6. Figure 7 shows predictions of the Cardassian model for the power spectrum versus SDSS data for some values of
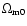 and n.
and n.
5.3 Constraining n and the baryon density parameter
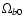
This time, we keep
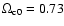 ,
h=0.72 and
,
h=0.72 and
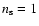 fixed, but
treat n and the baryon density parameter
fixed, but
treat n and the baryon density parameter
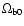 as free parameters when doing the fitting. The lowest
as free parameters when doing the fitting. The lowest  value is now obtained for a negative value of
value is now obtained for a negative value of
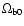 (even with a prior on
(even with a prior on
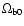 )
with
)
with
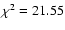 .
This is clearly an unphysical value. However degeneracy also allows positive values of
.
This is clearly an unphysical value. However degeneracy also allows positive values of
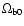 with reasonable
with reasonable  ,
e.g.
,
e.g.
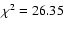 when
when
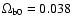 and n=-1.1
and n=-1.1 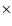 10-5.
10-5.
Figure 8 shows a plot of the  and
the 1 and
and
the 1 and 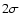 confidence contours as functions of
confidence contours as functions of
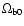 and n. An enlargement of the confidence contours is
shown in Fig. 9 for the most relevant area of the
parameter space. The allowed ranges for the parameters at
and n. An enlargement of the confidence contours is
shown in Fig. 9 for the most relevant area of the
parameter space. The allowed ranges for the parameters at 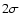 are
are
![$n\in\left[-4.3\times 10^{-5},5.3\times 10^{-6}\right]$](/articles/aa/full/2006/46/aa4965-06/img84.gif) and
and
![$\Omega_{\rm b0}\in\left[0,0.048\right]$](/articles/aa/full/2006/46/aa4965-06/img85.gif) .
Once again we find that the data
constrains n very strongly. Just as when we constrained n alone, we
find that the allowed range is smaller for positive than for negative
values. But the constraint is still so strong that n has to satisfy
|n|<10-5 in order for the Cardassian model to be in agreement
with the SDSS data.
.
Once again we find that the data
constrains n very strongly. Just as when we constrained n alone, we
find that the allowed range is smaller for positive than for negative
values. But the constraint is still so strong that n has to satisfy
|n|<10-5 in order for the Cardassian model to be in agreement
with the SDSS data.
![\begin{figure}
\par\includegraphics[width=3.8cm,clip]{4965fig6.eps}\includegraph...
...cm}\includegraphics[width=3.8cm,clip]{4965fig7.eps}\hspace*{1.9cm}}
\end{figure}](/articles/aa/full/2006/46/aa4965-06/Timg86.gif) |
Figure 6:
1 and 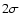 confidence contours for several ranges of n. Only very small values of n are possible when
confidence contours for several ranges of n. Only very small values of n are possible when
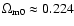 ,
the value of the CDM density parameter in agreement with CMB data of WMAP. ,
the value of the CDM density parameter in agreement with CMB data of WMAP. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4965fig9.eps}\end{figure}](/articles/aa/full/2006/46/aa4965-06/Timg87.gif) |
Figure 7:
Some power spectra predicted by the Cardassian model forseveral values of
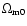 versus the SDSS data.
versus the SDSS data. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4965fig10.eps}\end{figure}](/articles/aa/full/2006/46/aa4965-06/Timg88.gif) |
Figure 8:
 and the 1 and
and the 1 and 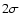 confidence contours (dashed lines) as functions of confidence contours (dashed lines) as functions of
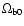 and n. Only the small value of n allow to fit the SDSS data.
and n. Only the small value of n allow to fit the SDSS data. |
| Open with DEXTER |
Figure 10 shows predictions of the Cardassian model for the power spectrum for some choices for n and
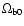 versus the SDSS data. We see from Fig. 9 that the data seem to prefer values for
versus the SDSS data. We see from Fig. 9 that the data seem to prefer values for
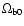 that are smaller than the WMAP value. But still, the allowed values of n are so small that it leaves the Cardassian model virtually indistinguishable from a
that are smaller than the WMAP value. But still, the allowed values of n are so small that it leaves the Cardassian model virtually indistinguishable from a  CDM model.
CDM model.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4965fig12.eps}\end{figure}](/articles/aa/full/2006/46/aa4965-06/Timg90.gif) |
Figure 10:
Some power spectra predicted by the Cardassian model forseveral values of
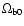 versus the SDSS data. versus the SDSS data. |
| Open with DEXTER |
5.4 Constraining n and the Hubble parameter h
Here, we treat n and h as free parameters in the
fitting, and keep
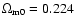 ,
,
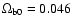 and
and
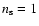 fixed. The best fit is now
fixed. The best fit is now
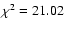 for h=1.11 and
n=-9.8
for h=1.11 and
n=-9.8  10-5 with
10-5 with
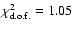 .
Plots of the
.
Plots of the  and the 1 and
and the 1 and 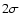 confidence contours as functions of hand n can be found in Fig. 11. A couple
of enlargements of the confidence contours are plotted in
Fig. 12. The parameter ranges allowed at
confidence contours as functions of hand n can be found in Fig. 11. A couple
of enlargements of the confidence contours are plotted in
Fig. 12. The parameter ranges allowed at 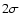 are n<1.8
are n<1.8 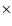 10-5 and h>0.76. We have not calculated the lower and upper limits for respectively n and hsince they are beyond h=1.40 (and then below n=-8
10-5 and h>0.76. We have not calculated the lower and upper limits for respectively n and hsince they are beyond h=1.40 (and then below n=-8 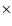 10-4).
Thus, the data appear to place a tight limit on positive
values for n, but not on negative values, at least if one does not
put a prior on h.
Clearly, as the confidence contours show us, the SDSS data are not able to constrain the Hubble parameter very well.
10-4).
Thus, the data appear to place a tight limit on positive
values for n, but not on negative values, at least if one does not
put a prior on h.
Clearly, as the confidence contours show us, the SDSS data are not able to constrain the Hubble parameter very well.
Note that the HST Key Project (Freedman et al. 2001) quotes a value for
the Hubble parameter of h=0.72 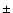 0.8, whereas the WMAP team quote a value of h=0.72
0.8, whereas the WMAP team quote a value of h=0.72 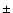 0.05 when using WMAP data alone. If we demand hto be around 0.7 in order to be in agreement with these
measurements, we find that |n| must be less than
0.05 when using WMAP data alone. If we demand hto be around 0.7 in order to be in agreement with these
measurements, we find that |n| must be less than
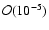 .
Again, this implies that the Cardassian model is indistinguishable from the
.
Again, this implies that the Cardassian model is indistinguishable from the 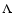 CDM model. The only way to make
it substantially different is to accept values for h larger than 1.0, which is quite unrealistic with respect to the measurements quoted above.
CDM model. The only way to make
it substantially different is to accept values for h larger than 1.0, which is quite unrealistic with respect to the measurements quoted above.
Figure 13 show plots of the power spectra predicted by the Cardassian model for some choices for the parameters n and h.
5.5 Constraining n and the spectral index ns
In all the previous sections we have chosen the Harrison-Zeldovich
power spectrum
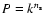 with
with
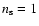 as the initial power spectrum.
In this section we will consider
as the initial power spectrum.
In this section we will consider 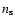 as a free parameter along with n. The other cosmological parameters are kept fixed with
as a free parameter along with n. The other cosmological parameters are kept fixed with
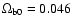 ,
,
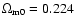 and h=0.72. The best fit is
then
and h=0.72. The best fit is
then
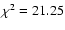 with
with
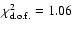 when
when
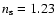 and
n=-4.0
and
n=-4.0  10-5. The
10-5. The  and the 1 and
and the 1 and 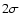 confidence contours are plotted in Fig. 14 as functions of
confidence contours are plotted in Fig. 14 as functions of 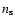 and n. At
and n. At 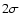 the allowed ranges for the parameters are
the allowed ranges for the parameters are
![$n\in\left[-0.3,4.2\times 10^{-6}\right]$](/articles/aa/full/2006/46/aa4965-06/img98.gif) and
and
![$n_{\rm s}\in\left[1,1.73\right]$](/articles/aa/full/2006/46/aa4965-06/img99.gif) .
Just as we saw in the constraints in
Sects. 5.2 and 5.4, positive values for n are tightly
constrained, whereas relatively large negative values are allowed.
.
Just as we saw in the constraints in
Sects. 5.2 and 5.4, positive values for n are tightly
constrained, whereas relatively large negative values are allowed.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{4965fig13.eps}\end{figure}](/articles/aa/full/2006/46/aa4965-06/Timg100.gif) |
Figure 11:
 and the 1 and
and the 1 and 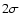 confidence contours (dotted line) as functions of H0 and n.
confidence contours (dotted line) as functions of H0 and n. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{4965fig14.eps}\hspace*{2mm}
\includegraphics[width=6.9cm,clip]{4965fig15.eps}\end{figure}](/articles/aa/full/2006/46/aa4965-06/Timg101.gif) |
Figure 12:
1 and 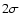 confidence contours as a function of H0 and n.
confidence contours as a function of H0 and n. |
| Open with DEXTER |
Thus, it is evident that the SDSS data do not tightly constrain 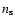 .
Indeed, we find that for
.
Indeed, we find that for
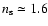 ,
large values of n<0 are in
agreement with the SDSS data. Thus, if we accept such large values for
the spectral index, it is then possible to construct a Cardassian model that differs considerably from
,
large values of n<0 are in
agreement with the SDSS data. Thus, if we accept such large values for
the spectral index, it is then possible to construct a Cardassian model that differs considerably from 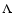 CDM and still agrees with the SDSS data. However, such values of
CDM and still agrees with the SDSS data. However, such values of 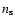 are
not compatible with the value measured by WMAP. For the special value
are
not compatible with the value measured by WMAP. For the special value
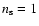 ,
i.e. a Harrison-Zeldovich spectrum, we find that |n| has to be less than
,
i.e. a Harrison-Zeldovich spectrum, we find that |n| has to be less than
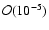 in order to be in agreement with the data.
in order to be in agreement with the data.
Once again, if we do not modify the usual Harrison-Zeldovich power spectrum with
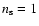 ,
the Cardassian model is equivalent to a
,
the Cardassian model is equivalent to a 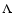 CDM model. Figure 13 shows plots of the predicted power spectrum for the Cardassian model for several values of n and
CDM model. Figure 13 shows plots of the predicted power spectrum for the Cardassian model for several values of n and 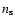 along with the SDSS data.
along with the SDSS data.
6 Conclusions
The purpose of this work has been to constrain the parameters of
the power law Cardassian model in the fluid
interpretation by using large scale structure data from the SDSS galaxy survey. We generalised the work of Amarzguioui et al. (2005) by
treating additional cosmological parameters as free in addition to nitself under a fitting to the galaxy power spectrum. In our analysis, we looked at five different
fits to the SDSS galaxy power spectrum. In the first fit, repeating
the analysis of Amarzguioui et al. (2005), we fixed the four cosmological
parameters
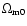 (CDM density),
(CDM density),
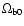 (baryon
density), h (Hubble parameter) and
(baryon
density), h (Hubble parameter) and 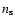 (spectral index of the
initial spectrum), and treated only the Cardassian parameter n as a free parameter. Then one finds that |n| has to be less that 10-5 so as to be in accordance with the data.
A similar conclusion was reached by Koivisto et al. (2005)
for the MPC model using the CMB power spectrum. These results are
also similar to those of Sandvik et al. (2004), who showed that a generalised Chaplygin gas has to resemble the
(spectral index of the
initial spectrum), and treated only the Cardassian parameter n as a free parameter. Then one finds that |n| has to be less that 10-5 so as to be in accordance with the data.
A similar conclusion was reached by Koivisto et al. (2005)
for the MPC model using the CMB power spectrum. These results are
also similar to those of Sandvik et al. (2004), who showed that a generalised Chaplygin gas has to resemble the 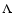 CDM model closely to avoid oscillations or blow ups of the matter power spectrum.
CDM model closely to avoid oscillations or blow ups of the matter power spectrum.
In the remaining four fits, we allowed one additional parameter to
take values freely along with n, while keeping the
remaining ones fixed to their WMAP best fit value.
First, constraining
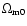 simultaneously with n, we find that positive values for |n| are tightly
constrained, but not the negative. While the
simultaneously with n, we find that positive values for |n| are tightly
constrained, but not the negative. While the 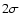 upper limit
for n is of order 10-6, the lower limit allows for negative
values of order unity. But for such negative values the Universe
would have to contain an unsual amount of cold dark matter. If we
demand that the dark matter content be within the bounds given by
WMAP, we again find that |n| has to be so small that the model
becomes indistinguishable from
upper limit
for n is of order 10-6, the lower limit allows for negative
values of order unity. But for such negative values the Universe
would have to contain an unsual amount of cold dark matter. If we
demand that the dark matter content be within the bounds given by
WMAP, we again find that |n| has to be so small that the model
becomes indistinguishable from 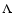 CDM.
CDM.
Next, varying
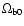 and n freely, we again
find that latter is strongly constrained both in the negative and
positive directions. More specifically, |n| has to be of order
smaller than 10-5 to be in agreement with the data. Next,
varying h and n freely, we again find that
positive values for n are tightly constrained, but negative values
are much less constrained. However, it turns out h has to be larger
than
and n freely, we again
find that latter is strongly constrained both in the negative and
positive directions. More specifically, |n| has to be of order
smaller than 10-5 to be in agreement with the data. Next,
varying h and n freely, we again find that
positive values for n are tightly constrained, but negative values
are much less constrained. However, it turns out h has to be larger
than  1.4 in order for n to be smaller than -10-3. This is an unrealistically high value for the Hubble parameter. Demanding a more realistic value for h will again render
the Cardassian model indistinguishable from
1.4 in order for n to be smaller than -10-3. This is an unrealistically high value for the Hubble parameter. Demanding a more realistic value for h will again render
the Cardassian model indistinguishable from  CDM.
CDM.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{4965fig16.eps}\end{figure}](/articles/aa/full/2006/46/aa4965-06/Timg103.gif) |
Figure 13:
Some power spectra predicted by the Cardassian model for several values of H0 versus the SDSS data. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{4965fig17.eps}\end{figure}](/articles/aa/full/2006/46/aa4965-06/Timg104.gif) |
Figure 14:
 and the 1 and
and the 1 and 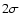 confidence contours (dotted lines) as functions of confidence contours (dotted lines) as functions of 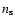 and n. Note that in the second plot, the
and n. Note that in the second plot, the 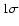 confidence contour is not visible at this scale. confidence contour is not visible at this scale. |
| Open with DEXTER |
Finally, allowing the spectral index 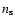 and n to vary freely, we find the same behaviour as in the last fit. Positive values for n are tightly constrained, while negative values
are not. But adding a reasonable prior on
and n to vary freely, we find the same behaviour as in the last fit. Positive values for n are tightly constrained, while negative values
are not. But adding a reasonable prior on 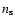 will restrict the
allowed negative values severely. In fact,
will restrict the
allowed negative values severely. In fact, 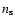 has to be larger than
has to be larger than  1.5 in order for n to be of order less than -10-1 and still agree with the SDSS data.
A summary of our results showing the best fit models can be found in Table 1.
1.5 in order for n to be of order less than -10-1 and still agree with the SDSS data.
A summary of our results showing the best fit models can be found in Table 1.
Hence, unless one is ready to accept very unusual values for the
cosmological parameters considered here, the SDSS data force the
power law Cardassian model to be virtually
indistinguishable from an ordinary  CDM model.
It thus seems difficult to unify dark energy and dark matter via the power law Cardassian model.
CDM model.
It thus seems difficult to unify dark energy and dark matter via the power law Cardassian model.
Does this spell the end for the power law Cardassian model - at least in the fluid interpretation? A more general treatment is probably needed to conclude this absolutely. For example,
one would ideally like to write a code like CMBFast for the Cardassian
model instead of using the  CDM model to generate the initial
perturbations. However, this work confirms that the SDSS data look
like a promising way to rule out this model. It shows that the galaxy
power spectrum imposes much tighter constraints on the Cardassian model
than the supernova data.
CDM model to generate the initial
perturbations. However, this work confirms that the SDSS data look
like a promising way to rule out this model. It shows that the galaxy
power spectrum imposes much tighter constraints on the Cardassian model
than the supernova data.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{4965fig18.eps}\end{figure}](/articles/aa/full/2006/46/aa4965-06/Timg105.gif) |
Figure 15:
Some power spectra predicted by the Cardassian model forseveral values of 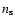 and n versus the SDSS data.
and n versus the SDSS data. |
| Open with DEXTER |
Table 1:
Best values of the Cardassian parameters fitting the SDSS baryon spectrum.
Finally, we wish to stress that we have only
considered the Cardassian model in the fluid interpretation. If
an alternative interpretation were to be found, where perturbative
calculation could be performed, a similar analysis might very well
produce a different result.
Acknowledgements
S.F. is supported by a Marie Curie Intra-European Fellowship Program of the Commission of the European Union (MEIF-CT-2005-515028) which is greatly appreciated. M.A. acknowledges support from the Norwegian Research Council through the project "Shedding Light on Dark Energy'', grant 159637/V30. MA also wishes to thank Øystein Elgarøy for helpful comments.
- Amarzguioui,
M., Elgarøy, Ø, & Multamäki, T. 2005, JCAP,
0501, 008 [NASA ADS] (In the text)
- Avelino, P. P.,
Beça, L. M., de Carvalho, J. P., Martins, C. J., & Pinto,
P. 2003, Phys. Rev. D, 67, 023511 [NASA ADS] [CrossRef] (In the text)
- Beça, L. M.,
Avelino, P. P., de Carvalho, J. P., & Martins, C. J. 2003,
Phys. Rev. D, 67, 101301 [NASA ADS] [CrossRef] (In the text)
- Bento, M. C.,
Bertolami, O., Santos, N. M., & Sen, A. A. 2005, Phys. Rev. D,
71, 063501 [NASA ADS] [CrossRef]
- Bento, M. C.,
et al. 2006, J. Phys. Conf. Ser., 33, 197
- Chung, D. J. H.,
& Freese, K. 2000, Phys. Rev. D, 61, 023511 [NASA ADS] [CrossRef] (In the text)
- Di Pietro, E.,
& Claeskens, J.-F. 2003, MNRAS, 341, 4 (In the text)
- Freedman, W.
L., Madore, B. F., Gibson, B. K., et al. 2001, ApJ, 553,
47 [NASA ADS] [CrossRef] (In the text)
- Freese, K., &
Lewis, M. 2002, Phys. Lett. B, 540, 1 [NASA ADS] (In the text)
- Frith, W. J. 2004,
MNRAS, 348, 916 [NASA ADS] [CrossRef]
- Gondolo, P.,
& Freese, K. 2003, Phys. Rev. D, 68, 063509 [NASA ADS] [CrossRef] (In the text)
- Gong, Y.-G., &
Duan, C.-K. 2004, MNRAS, 352, 847 [NASA ADS] [CrossRef]
- Knop, R. A., Aldering,
G., Amanullah, R., et al. 2003, ApJ, 598, 102 [NASA ADS] [CrossRef]
- Koivisto, T.,
et al. 2005, Phys. Rev. D, 71, 064027 [NASA ADS] [CrossRef]
- Lazkoz, R.,
Nesseris, S., & Perivolaropoulos, L. 2005, Exploring, JCAP,
0511, 010
- Lyth, D. H., &
Stewart, E. D. 1990, ApJ, 361, 343 [NASA ADS] [CrossRef] (In the text)
- Nesseris, S.,
& Perivolaropoulos, L. 2004, Phys. Rev. D, 70, 043531 [NASA ADS] [CrossRef]
- Padmanabhan, T. 1993
(Cambridge: Cambridge University Press)
(In the text)
- Perlmutter, S., Aldering,
G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef]
- Riess, A. G.,
Filippenko, A. V., Challis, P., et al. 1998, AJ, 116,
1009 [NASA ADS] [CrossRef]
- Riess, A. G., Strolger,
L.-G., Tonry, J., et al. 2004, ApJ, 607, 665 [NASA ADS] [CrossRef]
- Sandvik, H.,
et al. 2004, Phys. Rev. D, 69, 123524 [NASA ADS] [CrossRef]
- Seljak, U., &
Zaldarriaga, M. 1996, ApJ, 469, 437 [NASA ADS] [CrossRef] (In the text)
- Sen, S., & Sen, A. A.
2003, ApJ, 588, 1 [NASA ADS] [CrossRef]
- Spergel, D. N.,
Verde, L., Peiris, H. V., et al. 2003, ApJS, 148, 175 [NASA ADS] [CrossRef] (In the text)
- Spergel, D. N.,
et al. 2006, ApJ, submitted
(In the text)
- Szydlowski, M., &
Czaja, W. 2005, Ann. Phys., 320, 251 [NASA ADS]
- Szydlowski, M., &
Godlowski, W. 2006, Phys. Lett. B, 633, 427 [NASA ADS]
- Tegmark, M.,
Strauss, M. A., Blanton, M. R., et al. 2004, Phys. Rev. D, 69,
103501 [NASA ADS] [CrossRef] (In the text)
- Tegmark M., Blanton, M.
R., Strauss, M. A., et al. 2004, ApJ, 606, 702 [NASA ADS] [CrossRef] (In the text)
- Tonry, J. L.,
Schmidt, B. P., Barris, B., et al. 2003, ApJ, 594, 1 [NASA ADS] [CrossRef]
- Wang, Y., Freese, K.,
Gondolo, P., & Lewis, M. 2003, ApJ, 594, 25 [NASA ADS] [CrossRef]
- Zhu, Z.-H., Fujimoto,
M.-K., & He, X.-T. 2004, ApJ, 603, 365 [NASA ADS] [CrossRef]
Copyright ESO 2006
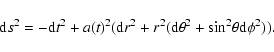
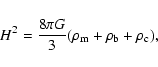
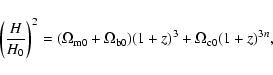
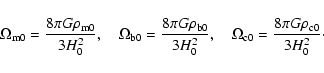
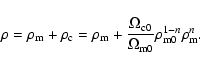
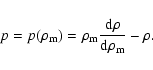
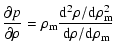
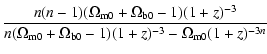
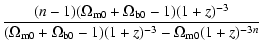
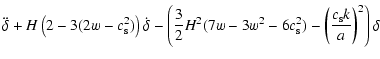
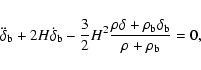
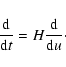
![$\displaystyle %
H^2\delta''+(H^2)' \frac{\delta'}{2}+\left[2-3(2\omega-c_{\rm s}^2)\right]H^2\delta'-\frac{3}{2}(7\omega-3\omega^2$](/articles/aa/full/2006/46/aa4965-06/img48.gif)
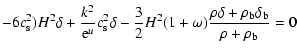
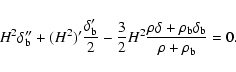
![\begin{figure}
\par\includegraphics[width=8.45cm,clip]{4965fig1.eps}\end{figure}](/articles/aa/full/2006/46/aa4965-06/Timg52.gif)
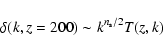
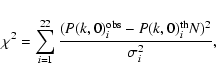
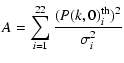
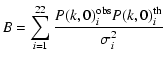
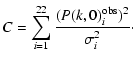
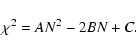
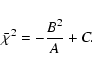
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4965fig2.eps}\end{figure}](/articles/aa/full/2006/46/aa4965-06/Timg71.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4965fig3.eps}\end{figure}](/articles/aa/full/2006/46/aa4965-06/Timg72.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4965fig4.eps}\end{figure}](/articles/aa/full/2006/46/aa4965-06/Timg78.gif)
![\begin{figure}
\par\includegraphics[width=14cm,clip]{4965fig5.eps}\end{figure}](/articles/aa/full/2006/46/aa4965-06/Timg79.gif)
![\begin{figure}
\par\includegraphics[width=3.8cm,clip]{4965fig6.eps}\includegraph...
...cm}\includegraphics[width=3.8cm,clip]{4965fig7.eps}\hspace*{1.9cm}}
\end{figure}](/articles/aa/full/2006/46/aa4965-06/Timg86.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4965fig9.eps}\end{figure}](/articles/aa/full/2006/46/aa4965-06/Timg87.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4965fig10.eps}\end{figure}](/articles/aa/full/2006/46/aa4965-06/Timg88.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{4965fig11.eps}\end{figure}](/articles/aa/full/2006/46/aa4965-06/Timg89.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4965fig12.eps}\end{figure}](/articles/aa/full/2006/46/aa4965-06/Timg90.gif)
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{4965fig14.eps}\hspace*{2mm}
\includegraphics[width=6.9cm,clip]{4965fig15.eps}\end{figure}](/articles/aa/full/2006/46/aa4965-06/Timg101.gif)
![\begin{figure}
\par\includegraphics[width=9cm,clip]{4965fig16.eps}\end{figure}](/articles/aa/full/2006/46/aa4965-06/Timg103.gif)
![\begin{figure}
\par\includegraphics[width=14cm,clip]{4965fig17.eps}\end{figure}](/articles/aa/full/2006/46/aa4965-06/Timg104.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{4965fig18.eps}\end{figure}](/articles/aa/full/2006/46/aa4965-06/Timg105.gif)