A&A 460, 23-28 (2006)
DOI: 10.1051/0004-6361:20064833
J. Tammi1,2 - R. Vainio3
1 -
Tuorla Observatory, Väisälä Institute for Space Physics and Astronomy,
Väisäläntie 20, 21500 Piikkiö, Finland
2 -
UCD School of Mathematical Sciences, University College Dublin,
Belfield, Dublin 4, Ireland
3 -
Department of Physical Sciences, PO Box 64,
00014 University of Helsinki, Finland
Received 10 January 2006 / Accepted 6 September 2006
Abstract
We apply a semi-classical approach of handling waves as
quasiparticle gas in a slowly varying flow - analogous to
ray tracing - to calculate the Alfvén wave transmission
parameters, the resulting cross-helicity of the waves and the
scattering-centre compression ratio, for cases where the shock
thickness is large enough for the turbulent waves in the plasma to
see the transition of the background flow parameters as smooth and
slowly varying. For nonrelativistic shocks the wave transmission
produces similar effects on the downstream turbulence and the
scattering-centre compression ratio as does the transmission through
a step shock: the downstream Alfvén waves propagate predominantly
towards the shock in the local plasma frame and, thus, the
scattering-centre compression ratio is larger than the gas
compression ratio. For thick relativistic shocks, however, we find
qualitative differences with respect to the step-shock case: for
low-Alfvénic-Mach-number shocks the downstream waves propagate
predominantly away from the shock, and the scattering-centre
compression ratio is lower than that of the gas. Thus, when taken
into account, the Alfvén wave transmission can decrease the
efficiency of the first-order Fermi acceleration in a thick
relativistic shock.
Key words: turbulence - shock waves - waves
A common approximation in shock-related particle acceleration studies
involving the first-order Fermi mechanism is to assume the scattering
turbulence frozen-in to the plasma. This is very well justified in
cases where the speed of the turbulent waves is negligibly small
compared to the flow speed. For cases where the wave speed increases
and becomes a notable fraction of the flow speed, however, the
deviation of the scattering centre speed from the speed of the
background flow can have notable effects on the particle acceleration
scenario; it was noted already by Bell (1978) that the
speed of the scattering centres is not necessarily that of the flow.
Furthermore, the compression ratio (of the scattering centres) is
known to have significant effect on the power-law spectral index of
particles accelerated in the shock for both steplike and thick shocks
(for modified shocks see Drury et al. 1982 and Drury
1983 for nonrelativistic analytical studies, and Virtanen
& Vainio 2005a, hereafter VV05
![]() , for numerical results for all speeds, and Keshet & Waxman
2005 for an analytical approach for step
shocks). The turbulent waves are, of course, also affected by the
shock, and thus one has to start from the transmission of turbulence
through the shock to arrive at describing particle acceleration in a
case where wave-propagation effects are taken into account.
, for numerical results for all speeds, and Keshet & Waxman
2005 for an analytical approach for step
shocks). The turbulent waves are, of course, also affected by the
shock, and thus one has to start from the transmission of turbulence
through the shock to arrive at describing particle acceleration in a
case where wave-propagation effects are taken into account.
The effect of the transmission of Alfvén waves through a step shock
was solved at the nonrelativistic limit by Vainio & Schlickeiser
(1998) and later generalised to include also relativistic
shocks by Vainio et al. (2003, hereafter referred to as
VVS03; 2005). They found that, regardless of
the shock speed, waves initially in equipartition were propagating
predominantly antiparallel to the flow direction (i.e. backwards
toward the shock in the downstream plasma frame) after being
transmitted through a step shock with Alfvénic Mach number
sufficiently low to yield non-negligible wave speeds compared to the
speed of the plasma flow. They showed that this leads to an increased
scattering-centre compression ratio, i.e., that the
scattering-centre speed can undergo compression that is significantly
higher than the compression of the flow itself. This effect thus
causes the first-order Fermi acceleration to lead to accelerated
particle energy spectral indices harder than ![]() 2.2, the
well-known outcome of parallel step shocks at the ultrarelativistic
limit in case of isotropic particle scattering (e.g., Kirk & Duffy
1999; Keshet & Waxman 2005). This
transmission analysis is, however, valid only for shocks of small
thickness and waves with wavelengths much longer than the width of the
shock transition.
2.2, the
well-known outcome of parallel step shocks at the ultrarelativistic
limit in case of isotropic particle scattering (e.g., Kirk & Duffy
1999; Keshet & Waxman 2005). This
transmission analysis is, however, valid only for shocks of small
thickness and waves with wavelengths much longer than the width of the
shock transition.
In this paper we continue studying the transmission of Alfvén waves through parallel shocks, but take an approach opposite to the step-shock approximation of VVS03. We calculate the transmission coefficients and their derivative parameters (the average cross-helicity of the waves, and the compression ratio of the scattering centres) for a continuous flow profile, approximating the transmission of waves through a shock with thickness sufficiently large for the waves to see the flow parameters varying slowly. The transmission coefficients for the nonrelativistic thick-shock case were calculated by VV05.
In general, a single shock wave is not either a step-shock nor a thick shock: as the turbulence in the upstream medium has a broad-band spectrum, some waves will see the shock as a thick while others see it as a thin structure. In addition, some waves have wavelengths matching the shock thickness. Thus, the general theory of wave propagation can not rely on either the thick or thin shock approximation. However, the general theory is mathematically very cumbersome and we have here chosen to limit our discussion to waves with wavelengths much shorter than the shock thickness. Combining these results with our earlier ones (VVS03) with the opposite assumption gives the first qualitative view on turbulence transmission through parallel shocks with finite thickness.
We adopt the idea of treating the waves as a quasiparticle gas. For
monochromatic waves, the number density of the wave quanta, or the
wave action density, is
![]() ,
where E' and
,
where E' and ![]() are the energy density and the angular frequency of the waves in the
plasma frame. We will use the prime to denote the quantities measured
in the plasma frame, while unprimed values are measured in the shock
frame. Below, we will consider a broad-band spectrum of waves and,
thus, the evolution of the quasi-particle distribution function in
the phase space
are the energy density and the angular frequency of the waves in the
plasma frame. We will use the prime to denote the quantities measured
in the plasma frame, while unprimed values are measured in the shock
frame. Below, we will consider a broad-band spectrum of waves and,
thus, the evolution of the quasi-particle distribution function in
the phase space
![]() .
.
Our approach is equivalent to the use of a variational principle in deriving the equation for the turbulent MHD wave-action density, pioneered by Dewar (1970) and extended to the relativistic case by Achterberg (1983).
In addition to the angular frequency ![]() ,
we will be needing the
wavenumber k and frequency
,
we will be needing the
wavenumber k and frequency
![]() ,
as well as their
values in the local plasma frame (
,
as well as their
values in the local plasma frame (![]() ,
k' and
,
k' and
![]() respectively). Because the medium consists of a
time-independent flow profile through the shock, the shock-frame
frequencies are conserved during shock crossing and we can write the
correspondence between the shock- and plasma-frame values as
respectively). Because the medium consists of a
time-independent flow profile through the shock, the shock-frame
frequencies are conserved during shock crossing and we can write the
correspondence between the shock- and plasma-frame values as
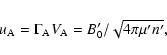 |
(3) |
We adopt the turbulence spectra in a power-law form
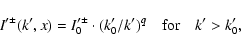 |
(4) |
Let us consider the propagation of an Alfvén wave in a
time-independent medium with spatial gradients only in the direction
of the background flow, aligned with the background magnetic field and
the x-axis. The Hamiltonian of the system is
| (5) |
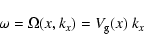 |
(6) |
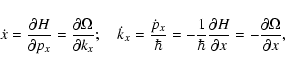 |
(7) |
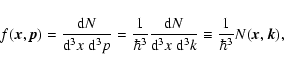
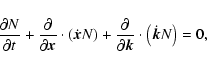 |
(8) |
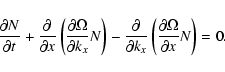 |
(9) |
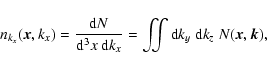
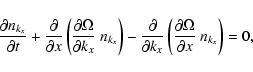 |
(10) |
From now on, we will assume that the wavevector is aligned with the
x-axis (i.e., that
ky=kz=0) and simplify the notation
by writing kx=k. Thus, using the explicit form of the dispersion
relation, we obtain in steady state
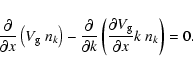 |
(11) |
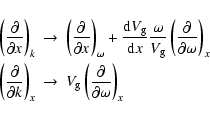
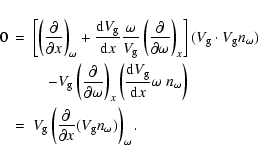
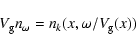 |
(12) |
Next we calculate the transmission coefficients for Alfvén waves with wavelengths much shorter than the shock thickness.
Transmission coefficients are needed for solving the turbulence
conditions at a given location in the shock. In contrast to the step
shock case (VVS03) where part of the waves are reflected at
the shock and change their mode (from parallel to antiparallel, or
vice versa), in the case of slowly changing medium all the waves are
transmitted through the shock without reflection, and the turbulence
at a given location can be obtained from equation
 |
(13) |
The co-moving intensity of the waves is related to the number-density
of wave quanta by
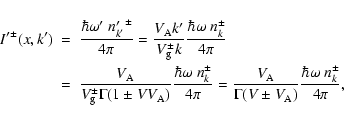
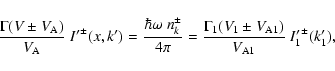
![\begin{displaymath}{I'}^{\pm}(x,k')
= {I'_{1}}^{\pm}(k')\frac{V_{{\rm A}}}{V_{...
...m V_{{\rm A}1})}{\Gamma(V\pm V_{{\rm A}})}
\right]^{q+1}\cdot
\end{displaymath}](/articles/aa/full/2006/46/aa4833-06/img60.gif) |
(14) |
From this point on, we deal only with plasma-frame quantities, so we omit the primes in variable symbols and assume them being measured in the plasma rest frame, unless otherwise mentioned. The local plasma speeds V and the location are, of course, still in the shock frame.
For a general view we first look at the case of vanishing upstream
cross-helicity. The ratio of forward-to-backward waves in the
downstream is
![\begin{displaymath}\frac{I^+}{I^-} =
\left[
\frac{ (V_1+V_{\rm A,1})(V_2-V_{...
...A,2}) }
{ (V_1-V_{\rm A,1})(V_2+V_{\rm A,2}) }
\right]^{q+1}
\end{displaymath}](/articles/aa/full/2006/46/aa4833-06/img63.gif) |
(16) |
In the following sections we study the cross-helicity of the transmitted waves in the downstream, and its development throughout the shock. We also calculate the scattering centre compression ratios in the downstream.
![\begin{figure}
\par\includegraphics[width=8.8cm]{4833fig1.eps}\end{figure}](/articles/aa/full/2006/46/aa4833-06/Timg67.gif) |
Figure 1:
The far downstream cross-helicity
|
| Open with DEXTER | |
Here we calculate the normalised cross-helicity of the waves,
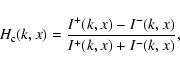 |
(17) |
For high-M shocks, where the effect of wave speeds is negligible,
the downstream cross-helicity approaches, of course, the cross
helicity upstream as
![]() .
As the Alfvénic Mach number
decreases and approaches the critical Mach number
.
As the Alfvénic Mach number
decreases and approaches the critical Mach number
![]() (i.e., as the downstream Alfvén speed starts to approach
the downstream flow speed), the cross-helicity for nonrelativistic
shocks starts to decrease and approach -1 (as shown by
VV05), as for step shocks of all speeds (VVS03).
(i.e., as the downstream Alfvén speed starts to approach
the downstream flow speed), the cross-helicity for nonrelativistic
shocks starts to decrease and approach -1 (as shown by
VV05), as for step shocks of all speeds (VVS03).
For relativistic speeds and Mach number a few times the critical
![]() ,
however, nearly all of the waves are streaming
parallel to the flow and
,
however, nearly all of the waves are streaming
parallel to the flow and
![]() as
as
![]() almost regardless of the upstream cross-helicity. For the
lowest
almost regardless of the upstream cross-helicity. For the
lowest
![]() the cross-helicity drops to -1 as the
downstream Alfvén speed becomes equal to the flow speed; this
happens because the transmission coefficients of the backward waves,
T2-, goes to infinity. The physicality and removal of this
mathematical singularity is discussed in Sect. 3.4.
the cross-helicity drops to -1 as the
downstream Alfvén speed becomes equal to the flow speed; this
happens because the transmission coefficients of the backward waves,
T2-, goes to infinity. The physicality and removal of this
mathematical singularity is discussed in Sect. 3.4.
The lack of wave reflection causes the special cases of only one
upstream wave field to keep also the downstream wave field at the same
state (i.e.,
![]() )
but the above-mentioned general behaviour is seen for all
)
but the above-mentioned general behaviour is seen for all
![]() .
The downstream cross-helicity as a function of
the Alfvénic Mach number is plotted in Fig. 1 for
non-to-highly relativistic shocks for vanishing upstream cross
helicity.
.
The downstream cross-helicity as a function of
the Alfvénic Mach number is plotted in Fig. 1 for
non-to-highly relativistic shocks for vanishing upstream cross
helicity.
![\begin{figure}
\par\includegraphics[width=8.8cm]{4833fig2.eps}\end{figure}](/articles/aa/full/2006/46/aa4833-06/Timg77.gif) |
Figure 2:
Form of the flow profile ( upper panel) and the local cross
helicity across the shock when
|
| Open with DEXTER | |
Next we want to study how the cross-helicity changes from the upstream
value to that of the downstream. We use a hyperbolic tangent profile
(Schneider & Kirk 1989; Virtanen & Vainio 2005)
to describe the flow speed as a function of location, and follow the
development of the local mean cross-helicity. Since the actual shock
thickness is of no importance for the spatial properties of the
test-wave transmission, as long as it is large enough to allow for the
"smoothly-varying-background'' assumption, we use only one flow
profile (and one thickness) to demonstrate the general behaviour. The
form of the flow speed profile is shown in the top panel of
Fig. 2. The unit of location x in that figure is
arbitrary and is chosen so that the shock transition takes place
within ![]() 1 location unit.
1 location unit.
While for nonrelativistic shocks the cross-helicity changes
monotonically from the upstream value to that calculated in Sect. 3.1, for faster shocks the local cross-helicity
![]() has non-monotonic behaviour: the cross-helicity forms a
maximum near the "centre'' of the flow profile, where the velocity
gradient has its largest value, after which it decreases to the
downstream value
has non-monotonic behaviour: the cross-helicity forms a
maximum near the "centre'' of the flow profile, where the velocity
gradient has its largest value, after which it decreases to the
downstream value
![]() .
.
An example of the non-monotonic cross-helicity is shown in
Fig. 2, where the local cross-helicity
![]() (here set equal to zero the far upstream) is plotted as a function of
location x for several shocks with speeds ranging from non- to fully
relativistic, but all having the Alfvénic Mach number
(here set equal to zero the far upstream) is plotted as a function of
location x for several shocks with speeds ranging from non- to fully
relativistic, but all having the Alfvénic Mach number
![]() .
The critical Mach number
.
The critical Mach number
![]() is calculated
separately for each shock speed following the scheme described in
VVS03. The spectral index of the turbulence is q=1.5 for
all cases.
is calculated
separately for each shock speed following the scheme described in
VVS03. The spectral index of the turbulence is q=1.5 for
all cases.
![\begin{figure}
\par\includegraphics[width=8.8cm]{4833fig3.eps} \end{figure}](/articles/aa/full/2006/46/aa4833-06/Timg82.gif) |
Figure 3:
Ratio of the scattering centre compression ratio rk to
that of the gas r for different shock proper speeds u1 as
functions of the Alvénic Mach number M. Lines are drawn for
upstream cross-helicity
|
| Open with DEXTER | |
While the assumption of small-amplitude waves leaves the compression
of the plasma itself unaffected, the compression felt by the
scattering particles, on the other hand, can be changed remarkably.
This is due to the fact that the particles are scattered by the
turbulent waves, and if the waves have speed non-neglibigle compared to
the speed of the flow (i.e. waves are not assumed to be frozen-in to
the plasma), the speed profile of the scattering centres can be
different from that of the plasma. Thus, also the effective
compression ratio felt by the particles, rk, can
differ from the gas compression ratio r.
Using the local cross-helicity ![]() we can express the
average wave speed as
we can express the
average wave speed as
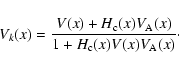 |
(18) |
As noted earlier, if the cross-helicity in the upstream equals ![]() it remains unchanged throughout the shock. So if there are e.g. only
forward waves in the upstream, the upstream scattering centre speed is
simply the (relativistic) sum of the flow speed and the local Alfvén
speed; and likewise in the downstream.
However, because of the compression and drop in the flow speed at the
shock, the ratio of the Alfvén and the flow speed in the downstream
is larger than in the upstream. Also its effect on the resulting
shock-frame scattering-centre speed is larger when the underlying flow
speed is not close to the speed of light.
For only forward waves in the upstream this results in rk < r,
and for only backward waves in the upstream rk > r. When the
Alfvén speed drops and becomes negligible compared to local flow
speeds (i.e.
it remains unchanged throughout the shock. So if there are e.g. only
forward waves in the upstream, the upstream scattering centre speed is
simply the (relativistic) sum of the flow speed and the local Alfvén
speed; and likewise in the downstream.
However, because of the compression and drop in the flow speed at the
shock, the ratio of the Alfvén and the flow speed in the downstream
is larger than in the upstream. Also its effect on the resulting
shock-frame scattering-centre speed is larger when the underlying flow
speed is not close to the speed of light.
For only forward waves in the upstream this results in rk < r,
and for only backward waves in the upstream rk > r. When the
Alfvén speed drops and becomes negligible compared to local flow
speeds (i.e.
![]() ),
), ![]() .
This is illustrated in
Fig. 3.
.
This is illustrated in
Fig. 3.
For vanishing upstream cross-helicity, the behaviour in a nonrelativistic shock was examined by VV05 and it was shown to be very similar to that in step shocks. Now for thick relativistic shock, because of the positive downstream cross-helicity, the average shock-frame wave speed in the downstream is higher than the local flow speed, and, thus, the compression ratio of the scattering centres is lower than that of the gas.
Resulting scattering-centre compression ratios (scaled to the gas
compression ratio) are plotted for upstream cross-helicities
![]() in Fig. 3, and for
in Fig. 3, and for
![]() in
Fig. 4. The nonrelativistic (u1 = 0.1) case is the
same as in VV05 and, as for step shocks, the compression
ratio increases also for higher speeds. However, on the
contrary to what VV05 expected, for the fastest low-Mshocks the scattering-centre compression ratio does not increase
steadily as
in
Fig. 4. The nonrelativistic (u1 = 0.1) case is the
same as in VV05 and, as for step shocks, the compression
ratio increases also for higher speeds. However, on the
contrary to what VV05 expected, for the fastest low-Mshocks the scattering-centre compression ratio does not increase
steadily as
![]() ,
but falls below the gas compression
ratio when the shock speed becomes relativistic.
,
but falls below the gas compression
ratio when the shock speed becomes relativistic.
In earlier studies by Vainio & Schlickeiser (1998) for nonrelativistic shocks and VVS03 for relativistic ones, the transmission properties were solved for waves of wavelengths essentially longer than the length scales of the shock. Here we have studied the opposite of "short'' waves flowing through a shock thicker than the wave length scales. Although these two transmission schemes work differently and in different parts of parameter space, it would be physically meaningful to apply both schemes in the same shock: the analysis of VVS03 for the part of the turbulence spectrum for which the wavelengths are longer than the width of the shock transition, and the method described in this paper for waves for which the plasma parameters vary slowly throughout the transition. Thus, the scattering-centre compression ratio is a function of wavenumber, and the resulting accelerated particle spectrum is not a simple power-law in energy (Fig. 5).
![\begin{figure}
\par\includegraphics[width=8.8cm]{4833fig4.eps} \end{figure}](/articles/aa/full/2006/46/aa4833-06/Timg90.gif) |
Figure 4:
Same as Fig. 3, but for
|
| Open with DEXTER | |
| |
Figure 5: Sketch of the scattering-centre compression ratio as a function of wavenumber ( left) and the resulting accelerated particle spectrum ( right) in a thick relativistic shock. L denotes the shock thickness. |
| Open with DEXTER | |
As the study here assumed no back-reaction of the waves to the shock
structure or dynamics, the approach is limited to small-amplitude
waves. The test-wave approach, on the other hand, leads to
mathematical singularities at
![]() ;
at this
limit the antiparallel waves are amplified infinitely. In the analysis
this limitation affects through the simplified calculation of the gas
compression ratio. In more detailed further analysis the effect of the
upstream wave parameters to the calculation of the gas compression
ratio should be taken into account in order to remove the
(non-physical) singularities, as demonstrated by Vainio &
Schlickeiser (1999) for nonrelativistic step shocks.
;
at this
limit the antiparallel waves are amplified infinitely. In the analysis
this limitation affects through the simplified calculation of the gas
compression ratio. In more detailed further analysis the effect of the
upstream wave parameters to the calculation of the gas compression
ratio should be taken into account in order to remove the
(non-physical) singularities, as demonstrated by Vainio &
Schlickeiser (1999) for nonrelativistic step shocks.
Also the inclusion of accelerating particles will have effects on the waves; in this treatise the effect of the particles on the waves have been omitted. However, the resonant wave-particle interactions could have a damping effect on the turbulence, thus rapidly changing the transmitted wave distributions, especially when moving downstream away from the shock. Similarily, our analysis also neglects the wave-wave interactions in the downstream medium (Vainio & Spanier 2005).
Finally we merely note that in the present study we have confined the analysis to strictly parallel shocks. For oblique magnetic field alignments the treatment of the turbulence transmission becomes very complicated and is beyond the scope of this study.
We have calculated the transmission coefficients for Alfvén (test) waves with short wavelengths through a modified shock with background plasma properties changing slowly compared to the wave length scales.
While the transmission trough a step shock was found similar throughout the whole shock speed range (VVS03), and, additionally, very similar behaviour was observed also for thick shocks in the nonrelativistic limit (VV05), qualitative and signifigant differences emerge for thick shocks when the speed increases. As a consequence, from the point of view of the particle acceleration studies, the compression felt by the particles (i.e. that of the scattering centres) at a thick relativistic low-M shock was shown to be weaker than the compression of the background flow. For slower (from non- to mildly relativistic) shocks the scattering centre compression ratio was shown to increase, like in step shocks.
Acknowledgements
The authors thank an anonymous referee for valuable suggestions on how to improve the manuscript. J.T. further thanks professors Reinhard Schlickeiser and Ian Lerche for constructive criticism and inspiring discussions.