A&A 459, 875-883 (2006)
DOI: 10.1051/0004-6361:20065741

Early spectral evolution of Nova Sagittarii 2004 (V5114 Sagittarii)[*],[*],[*]

A. Ederoclite1,2,3 - E. Mason2 - M. Della Valle4,5 - R. Gilmozzi2 - R. E. Williams6 - L. Germany2 - I. Saviane2 - F. Matteucci3 - B. E. Schaefer7 - F. Walter8 - R. J. Rudy9 - D. Lynch9 - S. Mazuk9 - C. C. Venturini9 - R. C. Puetter10 - R. B. Perry11 - W. Liller12 - A. Rotter13


1 - Vrije Universiteit Brussel, 2 Pleinlaan, Brussels, Belgium
2 - ESO - European Southern Observatory, Alonso de Cordova 3107, Casilla 91001, Santiago, Chile
3 - Department of Astronomy, University of Trieste, via Tiepolo 11, Trieste, Italy
4 - INAF - Osservatorio Astrofisico di Arcetri, L.go E. Fermi 5, Firenze, Italia
5 - Kavli Institute for Theoretical Physics, UC Santa Barbara, California, 93106, USA
6 - Space Telescope Science Institute 3700 San Martin Drive, Baltimore, MD, USA
7 - Department of Physics and Astronomy, Louisiana State University, Baton Rouge, Louisiana, 70803, USA
8 - Department of Physics and Astronomy, SUNY, Stony Brook, NY, 11794-3800, USA
9 - Aerospace Corporation, PO Box 92957, Los Angeles, CA 90009-2957, USA
10 - University of California San Diego, 9500 Gilman Dr., La Jolla, CA, USA
11 - NASA Langley Research Center, 100 NASA Road, Hampton, VA, USA
12 - Isaac Newton Institute, Casilla 8-9, Correo 9, Santiago, Chile
13 - Department of Astronomy and Astrophysics, Penn State University, 525 Davey Lab, University Park, PA, USA

Received 1 June 2006 / Accepted 28 July 2006

Abstract
Aims. We present optical and near-infrared spectral evolution of the Galactic nova V5114 Sgr (2004) during few months after the outburst.
Methods. We use multi-band photometry and line intensities derived from spectroscopy to put constrains on the distance and the physical conditions of the ejecta of V5114 Sgr.
Results. The nova showed a fast decline ( $t_2 \simeq 11$ days) and spectral features of Fe II spectroscopic class. It reached MV = -8.7 $\pm$ 0.2 mag at maximum light, from which we derive a distance of 7700 $\pm$ 700 kpc and a distance from the galactic plane of about 800 pc. Hydrogen and oxygen mass of the ejecta are measured from emission lines, leading to $\sim$10-6 and $10^{-7}~M_\odot$, respectively. We compute the filling factor of the ejecta to be in the range 0.1-10-3. We found the value of the filling factor to decrease with time. The same is also observed in other novae, then giving support to the idea that nova shells are not homogeneously filled in, rather being the material clumped in relatively higher density blobs less affected by the general expanding motion of the ejecta.

Key words: stars: novae, cataclysmic variables - stars: individual: V5114 Sgr

1 Introduction

Nova Sgr 2004 (V5114 Sgr) was independently discovered by Nishimura (2004) and Liller (2004) on Mar. 15.8 UT and Mar. 17.3 UT, respectively. West (2004) provided precise coordinates RA = 18$^{\rm h}$19$^{\rm m}$32 $.\!\!^{\rm s}$29, Dec = -28$^$36$^\prime$35 $.\!\!^{\prime\prime}$7 (gal. coord. l=3 $.\!\!^\circ$9 b=-6 $.\!\!^\circ$3). Early spectroscopy on Mar. 18.3 UT by Della Valle et al. (2004) confirmed this object to be a classical nova caught near maximum light. Here, we present photometric and spectroscopic observations taken at McDonald Observatory, Cerro Tololo Inter-American Observatory (CTIO), ESO-La Silla, and Lick Observatory. The spectra from ESO-La Silla have been obtained as part of the Target of Opportunity campaign for the observation of Classical Novae in the Galaxy and in the Magellanic Clouds. The paper is organized as follows: in Sect. 2 we present the analysis of the photometric and spectroscopic data, in Sects. 3 and 4 we analyze the evolution of the light curve and spectra of V5114 Sgr, in Sect. 5 we discuss the effects of interstellar absorption. In Sect. 6 we derive the physical parameters of the nova ejecta. Summary and conclusions are given in Sect. 7.


  \begin{figure} \par\includegraphics[width=12cm,clip]{5741fig1.eps} \end{figure} Figure 1: Upper left panel: V band light curve. Filled symbols represent our data points, empty symbols represent IAUC data. Vertical dotted lines represent maximum light, t2, and t3. Data points are affected by errors $\protect\la$0.04 mag in all bands but in U, where the error is 0.1 mag. Lower left panel: evolution of different colors: filled squares represent B-V, empty triangles U-B, crosses V-I and empty squares V-R. Upper right panel: J band light curve. Lower right panel: evolution of near-infrared colors: triangles represent J-H and squares H-K.
Open with DEXTER

2 Observations and data reduction

Optical photometry has been carried out during 8 nights in March and April 2004 with the 0.8-m telescope at McDonald Observatory. Another observing run has been carried out during 14 nights in June and July with the Small and Moderate Aperture Research Telescope System (SMARTS) 1.0-m telescope at CTIO. Optical and infrared photometry has been also carried out with the ANDICAM dual-channel imager on the SMARTS 1.3-m at CTIO during 25 nights from March to August. One night of observations has been carried out with a 0.3-m telescope equipped with an SBIG ST7E CCD camera, in Exmouth, Australia. A log of photometric observations is given in Table A.1.

Spectra at maximum and during the early decline have been obtained with FEROS (Kaufer et al. 1999) with a resolution $R \sim$ 48 000 and spectral range 4000-9000 Å. Spectrophotometric standard stars have not been observed each night, and in this case the spectra have been corrected with an "average response curve''. This procedure can introduce an uncertainty on the flux measurement up to 50%. Flux-determination is affected by undetermined uncertainty because FEROS is a fiber-fed spectrograph that was not equipped with an atmospheric distortion corrector at the time of these observations. Indetermination is due to the fact that the observations are carried out guiding on the V-band image of the star that is differently displaced (due to atmospheric refraction) in the other bands. During our analysis, fluxes were corrected in order to match the observed magnitudes.

An independent spectroscopic follow up has been carried out with the RC spectrograph on the SMARTS 1.5-m telescope at CTIO. A spectrophotometric standard star (either LTT 4364 or Feige 110) has been observed each night to remove the instrumental signature. Standard reduction has been carried out with an author's written IDL routine.

An IR spectrum was taken June 22, 2004 UT at Lick Observatory using the Aerospace Corporation's Near-Infrared and Visible Imaging Spectrograph (NIRIS). The standard star used was HR 6836.

All spectra have been analyzed with the onedspec package in IRAF. Line fluxes have been measured by the integration of the line profile and not by Gaussian fitting. Full width at half maximum (FWHM) of lines have been measured also via Gaussian fitting but show no significant difference from direct measure. A complete log of our spectroscopic observation is reported in Table A.2.

Table 1: Observed photometric properties for V5114 Sgr.

3 Light curve

The optical and near-infrared light curves of V5114 Sgr are shown in Fig. 1. The light curves have been derived using both our photometric data and photometry available in the literature (IAUC 8306, 8307, 8310). The V light curve shows that V5114 Sgr reached V = 8.0 mag on Mar. 17.17 UT (MJD = 53 081.556). West (2004) noted that nothing was visible at the same position in the red Digitized Sky Survey. After considering that the DSS limiting magnitude is $\sim$21 mag, we can infer that the outburst amplitude was $\ga$13 mag which is consistent with values observed for other novae with about the same rate of decline (see Warner 1995).


  \begin{figure} \par\includegraphics[width=7cm,clip]{5741fig2.eps} \end{figure} Figure 2: Spectral energy distribution of V5114 Sgr one day after maximum. The magnitudes in the various bands have been corrected for interstellar extinction.
Open with DEXTER

The nova decreased by two magnitudes from maximum in t2=11 days and by three magnitudes in t3=21 days. Adopting the maximum magnitude versus rate of decline (MMRD) relation by Della Valle & Livio (1995), V5114 Sgr achieved an absolute V magnitude at maximum light of MV=-8.7 $\pm$ 0.2 mag. Photometric properties are summarized in Table 1. The typical photometric errors are smaller than 0.04 mag in all bands but in $U \sim 0.1$ mag (J-H) color changes its slope after $\sim$day 40. This could be in principle due to formation of dust in the ejecta but an inspection of the B and V light curves rules out "DQ Herculis'' behavior, therefore the reddened color is likely due to to variations in intensity of emission lines in the NIR. The spectral energy distribution (SED) one day after maximum appears to be well fitted by a blackbody at T=9600 K as shown in Fig. 2.

4 Spectral evolution

Spectroscopic observations started immediately after discovery. Line identification for FEROS spectra (see Figs. 3 and 4) is given in Table 2 while in Table 3 we show line identification for spectra taken at CTIO (Williams et al., in preparation).

The first spectrum (phase +1[*]) was dominated by Balmer, Fe II and O I emission lines. This behavior characterized the nova as a typical "Fe II''  type object, according to the Cerro Tololo classification (Williams et al. 1991, 1994). P-Cyg profiles were clearly visible in Balmer lines as well as in Fe II, O I, and Na I lines. P-Cyg profiles were double, thus suggesting the presence of two expanding systems with velocities (obtained by averaging of measurements of Balmer lines) of 1400 $\pm$ 50 km s-1 and 850 $\pm$ 30 km s-1.

Eight days after maximum the spectrum was still dominated by low ionization species. The double P-Cyg profiles were still clearly visible and the velocities (as derived from both the P-Cyg profiles and FWHM) were increasing. The emission lines started developing a flat topped profile.

On April 9 (phase +23), we observe the 4640 Å emission band together with N II and N III, although Fe II emission lines were still present. The O I $\lambda$8446 emission line was more intense than the H$\beta $ one and showed a flatter profile.

By April 18 (phase +32) P-Cyg profiles had disappeared and Fe II emission lines were fading and forbidden and high excitation lines strengthened. The intensity of [O III] $\lambda 4363$indicated that V5114 Sgr entered the auroral phase, described in Williams et al. (1991, 1994). Fluxes of Balmer lines, that had decreased very slowly until this moment, started to decrease faster (see Fig. 7). The FWHM of Balmer lines reached a plateau (2000 $\pm$ 100 km s-1).


  \begin{figure} \par\includegraphics[width=12cm,clip]{5741fig3.eps} \end{figure} Figure 3: Dereddened spectra of V5114 Sgr (blue part). Fluxes are in logarithmic scale to show the less intense lines.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=12cm,clip]{5741fig4.eps} \end{figure} Figure 4: Dereddened spectra of V5114 Sgr (red part). Fluxes are in logarithmic scale to show the less intense lines.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=12cm,clip]{5741fig5.eps}\end{figure} Figure 5: Dereddened spectra of V5114 Sgr taken at CTIO and covering the region 3500-5200 $\AA$.
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=-90,width=12.7cm,clip]{5741fig6.eps}\end{figure} Figure 6: Dereddened IR spectrum of V5114 Sgr observed with NIRIS at Lick Observatory on June 22, 2004 UT. Upper panel shows the "blue'' part of the spectrum and the lower panel shows the "red'' part.
Open with DEXTER

The O I $\lambda$8446 and He I $\lambda$5876 lines show flat topped profiles while the hydrogen lines have a clearly asymmetric profile (the red side being more prominent than the blue one). At this stage the O I $\lambda$8446 emission line reached its maximum intensity.

By May 13 (phase +57) the hydrogen lines turn to flat topped profiles (like oxygen) while nitrogen lines were still rounded. It has been noted in the past (see Payne-Gaposchkin 1957) that different line profiles observed at the same stage indicate that the emission lines originate in different layers of the ejecta. Flat topped profiles originate from optically thin spherical shells while rounded profiles are related to optically thick winds. The NIR part of the spectrum (observed only on June 22, see Fig. 6, line identification given in Table 5) showed prominent Paschen and Brackett lines as well as oxygen and nitrogen lines. Common but unknown lines (1.10, 1.19, 1.55 and 2.10 $\mu$m) were present in this spectrum (see Venturini et al. 2004). Tentative identifications for these lines with van Hoof's line list[*] are given in Table 6. Few suggested identifications have already been suggested by Rudy et al. (2002) during analysis of lines of V723 Cas.

In September the spectrum was dominated by O I  $\lambda \lambda$ 4959-5007 lines. All lines showed saddle-shaped profiles. The O I $\lambda$8446 line had almost disappeared. H$\alpha $ was clearly strongly blended with N II.

The overall evolution of expansion velocities measured from P-Cyg absorption is shown in Fig. 8. Cassatella et al. (2004) have shown that the evolution of P-Cyg profiles as measured in the UV of Nova Cyg 1992 can be modelled with an exponential law $v(t) = v_\infty - (v_0 - v_\infty) {\rm e}^{-t/\tau} $, where v(t) is the velocity t days after maximum, v0 is the expansion velocity at maximum light, $v_\infty$ is the asymptotic velocity and $\tau$ is a time scale similar to t3. The best fit to the data gives $v_\infty = 2100$ $\pm$ 50 km s-1 and 1500 $\pm$ 50 km s-1, v0 = 1300 $\pm$ 50 km s-1 and 800 $\pm$ 50 km s-1 and $\tau = 18$ $\pm$ 1 day. Both $v_\infty$ and velocity measurements based on the FWHM of emission lines during the nebular stage are important quantities that should be considered in view of future observations aimed at determining the distance to V5114 Sgr, via nebular expansion parallax.

Table 5: Reddening-corrected near infra red line fluxes (in erg s-1 cm-2) observed with NIRIS at Lick Observatory on June 22, 2004, UT.


  \begin{figure} \par\includegraphics[width=7.25cm,clip]{5741fig7.eps} \end{figure} Figure 7: Upper panel: evolution of Balmer lines fluxes. Triangles represent H$\alpha $, squares H$\beta $, pentagons H$\gamma $and hexagons H$\delta $. Filled symbols represent data from FEROS, empty symbols from the RC spectrograph at the 1.5-m telescope at CTIO. Lines connecting the FEROS symbols are meant to show the trend of the data. Lower panel: evolution of ratios of Balmer lines divided by the H$\beta $ flux (symbols refer to the same lines as in the upper panel). Horizontal lines represent the Balmer lines ratios for case B at 10 000 K as from Osterbrock (1989) (from top to bottom H$\alpha $/H$\beta $, H$\gamma $/H$\beta $ and H$\delta $/H$\beta $).
Open with DEXTER

5 Reddening and distance

We have used several methods to estimate the reddening of V5114 Sgr. This piece of information is crucial to measure the distance to the object. The results of our various estimates of the interstellar reddening are summarised in Table 7.

Table 6: Tentative identification of previously unidentified NIR lines.


  \begin{figure} \par\includegraphics[angle=-90,width=6.9cm,clip]{5741fig8.eps} \end{figure} Figure 8: Velocities of the ejecta. Measures are derived as average of P-Cyg profiles of Balmer lines. Squares refer to the faster absorption system and triangles to the slower one. Filled symbols refer to FEROS observations and empty sybols to CTIO observations. Continuous lines are exponential description of the evolution (see text).
Open with DEXTER

Table 7: Measured values for reddening of V5114 Sgr.

We could not use the commonly used NaD lines because they are saturated. Nevertheless it has been shown by Munari & Zwitter (1997) that alternatively to these lines, the K I $\lambda$7699 line can be used. The advantage to use this line is that it has a less steep curve of growth, thus giving the opportunity to measure higher reddenings. After applying this method to V5114 Sgr, we found EB-V = 0.45 mag. Colors at maximum are a widely used empirical indicator of interstellar reddening. Van Den Bergh & Younger (1987) showed that novae at maximum have an intrinsic B-V of 0.23 $\pm$ 0.06 mag. The same authors showed also that novae, two magnitudes below maximum, have an intrinsic B-V = -0.02 $\pm$ 0.04 mag. As from Table 1, V5114 Sgr had $(B-V)_{{\rm max}} = 0.66$ mag and (B-V)t2 = 0.38 mag. This leads to EB-V = 0.43 $\pm$ 0.06 mag and EB-V = 0.40 $\pm$ 0.04 mag, respectively. From Schlegel et al. (1998) dust maps of the Milky Way, we have derived EB-V = 0.58 mag. Relations based on emission-line ratios are considered the best ones (see Williams 1994), unfortunately they can be used only at very late stages when the nova is in the optically thin phase. As an example, if we compute the reddening through O I $\lambda$8446 and O I $\lambda$13164 (following Rudy et al. 1991) we find EB-V=1.2 mag, which is very different from the reddening estimates derived with other methods (see Table 7). Williams (1994) suggested that if the He II  $\lambda \lambda$4686, 10124 and the H I  $\lambda \lambda$4861, 10049 are optically thin, then they can be used to measure the absorption to the nova via:

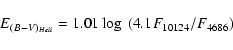
\begin{displaymath}E_{(B-V)_{He {\sc ii}}}=1.01 \log~ (4.1 F_{10124}/F_{4686}) \end{displaymath}

and

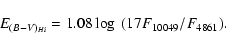
\begin{displaymath}E_{(B-V)_{H {\sc i}}}=1.08 \log~ (17 F_{10049}/F_{4861}). \end{displaymath}

The observed flat-topped profiles suggest that these lines likely originate in the ejected shell and therefore they may be optically thin. Therefore we can derive EB-V=0.57 mag and EB-V=0.65 mag, respectively. A last attempt has been carried out making use of the fact that the He I triplet ratios $\lambda \lambda$5876, 4471 and $\lambda \lambda$10830, 4471 are rather unsensitive to density. Robbins (1968) showed that $\frac{F_{5876}}{F_{4471}}\sim 2.9$ for different values of density and temperature, while, from Osterbrock (1989), $\frac{F_{10830}}{F_{4471}} = 4.4$ for typical values of temperature and density. From the observed He I  $\lambda \lambda$5876, 4471 lines we find zero extinction. This value is unlikely to be correct and Ferland (1977) adviced against the use of these two lines because of the small baseline and the faintness of the He I $\lambda$4471 line. On the other hand, the He I  $\lambda \lambda$4471, 10830 lines point towards EB-V=0.9 mag thus supporting rather high extinction. In the following we adopt EB-V=0.6 $\pm$ 0.3 mag.

After assuming the maximum magnitude obtained in Sect. 3 with the MMRD ( MV = -8.7 $\pm$ 0.2 mag) and the average absorption derived above, we derive a distance to V5114 Sgr of 9000 $\pm$ 900 pc. A complementary estimate of the distance has been obtained using the Buscombe-DeVaucouleurs relation (all novae show the same magnitude 15 days after maximum) as from Capaccioli et al. (1989). This second estimate leads to 6000 $\pm$ 1200 pc. After taking the average weight, we get d = 7700 $\pm$ 700 pc. For l=3 $.\!\!^\circ$9 and b=-6 $.\!\!^\circ$3, we find the nova to be located 770 $\pm$ 70 pc above the galactic plane

6 Physical parameters

Analysis of dereddened line fluxes is the only way to derive physical parameters of nova ejecta (e.g. masses and temperatures). Since ejecta are still evolving toward the nebular stage, the line ratios are not the ones expected from atomic transition probabilities. For example, looking at Fig. 7 the H$\alpha $/H$\beta $ ratio converges toward the theoretical value only after phase $\sim$100.

A different explanation (also at later stages) is invoked for the case of [O I]  $\lambda \lambda$6300, 6364. This is a well known example of lines that does not respect the theoretical ratio $\sim$3:1. Williams (1994) interpreted this as due to large optical depth in the 6300 Å line, and showed that the optical depth of that line can be derived from

 \begin{displaymath}% \frac{j_{6300}}{j_{6364}} =\frac{1-{\rm e}^{-\tau}}{1-{\rm e}^{-\tau/3}}\cdot \end{displaymath} (1)

Following this argument, we find $\tau _{6300}$ to be in the range 1.6-6.1, in good agreement with the values exhibited by other novae. The optical depth, together with the ratio of [O I]  $\lambda \lambda$6300, 5577 can be used to determine electron temperature of the zones of the ejecta where [O I] lines are formed through the formula:

\begin{displaymath}% T_{e}=\frac{11~200}{\log~[43\tau/(1-{\rm e}^{-\tau})\times F_{\lambda6300}/F_{\lambda5577}]}\cdot \end{displaymath} (2)

We find $T_{\rm e}$ to be between 3700 K and 6000 K.

The knowledge of the optical depth and electron temperature allows us to estimate the mass of oxygen in the ejecta using the 6300 Å line:

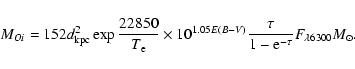\begin{displaymath}% M_{O {\sc i}}=152 d ^2 _{{\rm kpc}} \exp { \frac{22850}{T_{... ...B-V)} \frac{\tau}{1-{\rm e}^{-\tau}}F_{\lambda6300} {M}_\odot. \end{displaymath} (3)

We find $M_{O {\sc i}}= 1.9$ $\times$ 10-5-2.4 $\times$ $10^{-7}~M_\odot$.

Electron densities can be determined adopting the temperatures computed above and [O III] line ratios as in Osterbrock (1989)

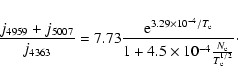\begin{displaymath}% \frac{j_{4959} + j_{5007}}{j_{4363}} = 7.73 \frac{{\rm e}... ...}{1+4.5 \times 10^{-4} \frac{N_{\rm e}}{T_{\rm e}^{1/2}}}\cdot \end{displaymath} (4)

The values we obtain are in the range 107-109 cm-3, close to the upper limit of the critical densities to give rise to nebular and auroral lines. This is an indication that these lines likely arise from regions characterized by a relatively high density.

Hydrogen mass can be derived following Mustel & Boyarchuk (1970). The H$\alpha $ line is given by

 \begin{displaymath}% j_{{\rm H}\alpha} = g_\alpha \times n^2 _{\rm e} \times \epsilon \times V \end{displaymath} (5)

where $g_\alpha$ is the emission coefficient, $n_{\rm e}$ is the electron density, $\epsilon $ is the so-called "filling factor'' (a measure of the clumpiness of the ejecta) and V is the volume that can be expressed as

 \begin{displaymath}% V = 4 \pi \times R^2 \times \delta \end{displaymath} (6)

where the radius R can be obtained by simple expansion $v_{{\rm exp}} \times \Delta t$ and $\delta = R ~ v_{{\rm ther}} / v_{{\rm exp}} $ is assumed to be representative of the thickness of the shell. Deriving $v_{{\rm exp}}$ from the FWHM of Balmer lines ($\sim$2000 km s-1) and $v_{{\rm ther}} = \sqrt{3kT/m_p}$ (for $T_{\rm e} \sim 5$ $\times$ 103 K, $v_{{\rm ther}} \sim 10$ km s-1) it follows that $\delta \sim 0.01$ $\times$ R (cf.  $v_{{\rm ther}}/v_{{\rm exp}} \sim 0.05$ for GK Per, Mustel & Boyarchuck 1970). On the other hand this is true only for the case of a very thin shell instantaneously ejected. In fact, the shell ejection process occurs on a much longer time scale, of the order of t3. Therefore the thickness of the shell can be computed, as order of magnitude, by the ratio between t3 $\times$ $v_{{\rm exp}}$ and $t_{{\rm neb}}$ $\times$ $v_{{\rm exp}}$, being  $t_{{\rm neb}}$ the time needed by the nova to reach the nebular stage, i.e. $\delta \sim 20~{\rm days}/100~{\rm days}$ = 0.2 $\times$ R. This is consistent with spectroscopic measurements obtained by Della Valle et al. (1997) for FH Ser ( $\delta=0.5 \times R$) and Humason (1940) for DQ Her ( $\delta=0.5 \times R$).

Solving Eq. (5) for $\epsilon $,

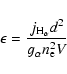\begin{displaymath}% \epsilon = \frac{j_{{\rm H}_\alpha} d^2}{ g_\alpha n_{\rm e}^2 V } \end{displaymath} (7)

we find that the filling factor spans a range of 7.1 $\times$ 10-2-7.9 $\times$ 10-4. Finally, we can determine from

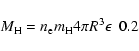\begin{displaymath}% M_{\rm H} = n_{\rm e} m_{\rm H} 4 \pi R^3 \epsilon ~~ 0.2 \end{displaymath} (8)

values of $M_{\rm H}$ to be $\sim$3.0 $\times$ 10-5-1.1 $\times$ $10^{-6}~M_\odot$.

The derived physical parameters are summarized in Tables 8 and 9.

7 Summary and conclusions

V5114 Sgr is an Fe II nova that occurred in the bulge of the Milky Way. The rate of decline characterizes V5114 Sgr as a borderline object between the fast (t2 < 12 days) and slow (t2 > 12 days) classes (Della Valle & Livio 1998). These authors have shown that He/N and Fe IIb (i.e. Fe II broad) novae belong to the fast class and are preferentially concentrated towards the galactic disc, i.e. at small z above the galactic plane (z<200 pc), while Fe II novae belong to both slow and fast classes and are observed both in the disk and in the bulge, extending up to $\sim$1 kpc. V5114 Sgr located at about 0.8 kpc above the galactic plane in the direction of the galactic bulge is an Fe II nova which does not represent an exception to this scenario (Della Valle et al. 1992).

Table 8: Physical parameters for V5114 Sgr: O I $\lambda \lambda 6300/6363$ line ratios, optical depth in $\lambda 6300$ ( $\tau _{6300}$), electron temperature, O I mass, [O III] line ratios and electron densities.

Spectroscopic observations showed a dramatic change in the overall appearance of the spectrum of the nova at about 30 days after maximum light (in coincidence with the entrance in the "auroral phase''): permitted lines start fading at a different rate, P-Cyg profiles disappear, and velocities reach a "plateau'' phase and U-V and J-K colors increase. The lack of detection of [Ne III] line hints for a "standard'' evolution of the nebular spectrum (see Williams et al. 1994).

The very high values of optical depth in the O I $\lambda 6300$ suggest very high densities for the zones of the ejecta where these lines are formed. We have derived the filling factor in the range $\sim$7.1 $\times$ 10-2 to 7.9 $\times$ 10-4. Comparing these values with other values reported in the literature (see Table 10), two facts emerge: a) the filling factors in nova ejecta are definitely smaller than 1, likely close to 0.1, during the early stages; b) these values decrease by 1-3 orders of magnitude with time. This fact indicates that the volume of the expanding shell (computed with Eq. (6)) increases with time more rapidly than the volume actually occupied by most of the ejected material. In other words, the decreasing trend exhibited by the filling factor suggests that the ejected matter tends to remain clumped in sub-structures having higher density than the average density characterizing the expanding shell. This is consistent with the [O I]  $\lambda \lambda$6300, 6364 ratio < 2 (Table 8), which suggests that [O I] lines should be formed in very dense small blobs of neutral material embedded within the ionized shell (see paragraph 6). However, recently Williams & Mason (2006) proposed an alternative interpretation of this behavior, assuming that the [O I] lines arise in regions of high magnetic field, and their intensity and profile are modified by Quadratic Zeeman Effect.

Table 9: Physical parameters for V5114 Sgr: $\epsilon $ and the hydrogen mass.

Table 10: Comparison between filling factors in literature.

Computed oxygen and hydrogen masses are in the ranges 1.9 $\times$ 10-5-2.4 $\times$ $10^{-7}~M_\odot$ and 3.0 $\times$ 10-5-1.1 $\times$ $10^{-6}~M_\odot$. This high mass ratio is close to the upper limit for classical novae shown in Warner (1995).

Acknowledgements
The authors are indebted to Pierluigi Selvelli and Chris Sterken for their critical reading of the manuscript. They also thank the anonymous referee and Steve Shore, who helped improving the presentation.
This work has been partly supported by "IAP P5/36'' Interuniversity Attraction Poles Programme of the Belgian Federal Office for Scientific, Technical and Cultural Affairs.

References

 

  
Online Material

Table 2: V5114 Sgr reddening-corrected emission line fluxes (in erg s-1 cm-2) from FEROS spectra.

Table 3: V5114 Sgr reddening-corrected emission line fluxes (in erg s-1 cm-2) from CTIO spectra with wavelength range larger than 2000 $\AA$and including the H$\alpha $ region.

Table 4: V5114 Sgr reddening-corrected emission line fluxes (in erg s-1 cm-2) from CTIO spectra shown in Fig. 5.

Appendix A: Logs of the observations

Table A.1: Measured magnitudes during photometric campaigns (described in text).

Table A.2: Log of the spectroscopic observations for V5114 Sgr.


Copyright ESO 2006