A&A 459, 969-976 (2006)
DOI: 10.1051/0004-6361:20065518
A. Alvarez-Candal1 -
R. Duffard1,![]() -
D. Lazzaro1 -
T. Michtchenko2
-
D. Lazzaro1 -
T. Michtchenko2
1 - Observatório Nacional, R. Gal. José Cristino 77, 20921-400,
Rio de Janeiro, Brazil
2 -
Instituto de Astronomia, Geofísica e Ciências Atmosféricas, USP,
Rua do Matão 1226, 05508-900 São Paulo, Brazil
Received 27 April 2006 / Accepted 17 August 2006
Abstract
Aims. To better understand the dynamical and collisional evolution of the inner Main Belt, we perform a visible spectroscopic survey and construct dynamical maps of the region.
Methods. The survey was performed between March 2002 and August 2005, at diverse observatories. The dynamical analysis was performed by the integration of 3131 massless particles homogeneously distributed in the region.
Results. We obtained new taxonomic classification for 88 asteroids representing a 13% increase in the sample of asteroids with know classification in the inner region of the Main Belt. The increase in the number of classified objects further confirms the notion that the inner region can be divided into three compositional zones: the innermost, where asteroids of the S-group concentrate, the outermost, where the C-group peaks, and in-between, with the highest concentration of V-type. The dynamical analysis shows that the region is covered by a dense web of mean-motion and secular resonances which may play an important role in the dynamical diffusion of the asteroids.
Key words: techniques: spectroscopic - minor planets, asteroids
A precise characterization of the inner region of the Asteroid Belt is important to better understand its formation and collisional evolution. This region is delimited by the ![]() and 3:1 secular and mean motion resonances, and it is densely populated, with more than 47 000 numbered asteroids divided in several groups and families. The identification of the diverse families, however, varies from author to author as a consequence of the complex structure of the region attributable to the presence of the strong
and 3:1 secular and mean motion resonances, and it is densely populated, with more than 47 000 numbered asteroids divided in several groups and families. The identification of the diverse families, however, varies from author to author as a consequence of the complex structure of the region attributable to the presence of the strong ![]() and 3:1 resonances, and the high density of objects.
and 3:1 resonances, and the high density of objects.
In the innermost part of the region, the Flora family, first identified by Hirayama (1919), has been split into one or more families over the time. The most obvious cause for these discrepancies is the proximity to the ![]() secular resonance, which makes the computation of the proper elements difficult. Another possible cause is a multi-collision origin of the family as proposed by some authors (Weisel 1978; Tedesco 1979). Indeed, Zappalà et al. (1994, 1995) classified Flora as a "clan'', a term first introduced by Farinella et al. (1992) to indicate a group where the membership strongly depends on the statistical criteria adopted and where diverse sub-structures are apparent. On the other hand, the Flora clan seems homogeneous from a compositional point of view, as shown by the quite uniform S-type classification of a large number of its members (Florczak et al. 1998). More recently, Mothé-Diniz et al. (2005) found that the Flora clan can be separated into the Baptistina family and many other small clumps.
secular resonance, which makes the computation of the proper elements difficult. Another possible cause is a multi-collision origin of the family as proposed by some authors (Weisel 1978; Tedesco 1979). Indeed, Zappalà et al. (1994, 1995) classified Flora as a "clan'', a term first introduced by Farinella et al. (1992) to indicate a group where the membership strongly depends on the statistical criteria adopted and where diverse sub-structures are apparent. On the other hand, the Flora clan seems homogeneous from a compositional point of view, as shown by the quite uniform S-type classification of a large number of its members (Florczak et al. 1998). More recently, Mothé-Diniz et al. (2005) found that the Flora clan can be separated into the Baptistina family and many other small clumps.
The outermost part of the region, near the 3:1 mean motion resonance, is dominated by the large Nysa-Polana clan as defined by Zappalà et al. (1994, 1995). Here, again, the complex structure of the clan shows substructures which could reflect the casual merging of different independent families, as well as possible second-generation events involving fragments created by an original break-up. This clan was studied spectroscopically by Cellino et al. (2001), revealing two distinct spectral behaviors: one group of S-type and a second one of B- or F-type asteroids. These authors proposed the existence of two families, each one with different spectral characteristics: Nysa and Polana. Interestingly, they also found that (44) Nysa and (135) Herta, the largest members of the Nysa family, do not share the same classification as the other members, being considered interlopers. The Nysa family was, therefore, renamed following its largest member, (878) Mildred. Mothé-Diniz et al. (2005) mostly confirmed the results by Cellino et al. (2001) about two distinct groups. However they point out that the Xc classification of (44) Nysa could be related to a metal-rich composition, coming from the nucleus of a completely differentiated body. In their analysis, Mothé-Diniz et al. identified other two families in the region: Massalia and Erigone.
Probably the most interesting family in the inner Main Belt is that associated with the asteroid (4) Vesta. (4) Vesta is unique in the sense that is the only large (![]() 470 km) asteroid with a basaltic crust discovered so far in the Main Belt. The Vesta family was first identified by Williams (1989) and the subsequent spectroscopic analysis of several of its members proved that their composition is indeed similar to that of (4) Vesta (Binzel & Xu 1993). Many other small asteroids having similar taxonomic classification have been found in the region (Florczak et al. 1998; Burbine et al. 2001; Florczak et al. 2002; Duffard et al. 2004). Although most of these objects are dynamically related to (4) Vesta, several are located far from it. It is believed that all these objects probably originated from a cratering event on (4) Vesta (Thomas et al. 1997; Asphaug 1997) and were subsequently diffused due to the interplay of the Yarkowsky effect and secular resonances (Carruba et al. 2005).
470 km) asteroid with a basaltic crust discovered so far in the Main Belt. The Vesta family was first identified by Williams (1989) and the subsequent spectroscopic analysis of several of its members proved that their composition is indeed similar to that of (4) Vesta (Binzel & Xu 1993). Many other small asteroids having similar taxonomic classification have been found in the region (Florczak et al. 1998; Burbine et al. 2001; Florczak et al. 2002; Duffard et al. 2004). Although most of these objects are dynamically related to (4) Vesta, several are located far from it. It is believed that all these objects probably originated from a cratering event on (4) Vesta (Thomas et al. 1997; Asphaug 1997) and were subsequently diffused due to the interplay of the Yarkowsky effect and secular resonances (Carruba et al. 2005).
To better understand the dynamical and collisional evolution of the inner Main Belt, we performed a visible spectroscopic survey and obtained a dynamical map of the region. The studied region was delimited by 2.1<a<2.5 AU, e<0.3 and
![]() .
This was done in order to avoid the Mars Crosser as well as the high inclination group of Phocaea. The observations have been carried out at diverse observatories and are described, along with the data reduction procedures, in the next section. In Sect. 3 we present the taxonomic classification of the data and an analysis of its distribution in the region. The dynamical analysis of the inner Main Belt is then described and analyzed in Sect. 4. In the last section we give a brief discussion of the obtained results.
.
This was done in order to avoid the Mars Crosser as well as the high inclination group of Phocaea. The observations have been carried out at diverse observatories and are described, along with the data reduction procedures, in the next section. In Sect. 3 we present the taxonomic classification of the data and an analysis of its distribution in the region. The dynamical analysis of the inner Main Belt is then described and analyzed in Sect. 4. In the last section we give a brief discussion of the obtained results.
The observations were carried out at three observatories: the European Southern Observatory at La Silla (ESO-Chile), the Complejo Astronómico el Leoncito at San Juan (CASLEO-Argentina) and the Observatório do Pico dos Dias (OPD-Brazil). The data were obtained in 9 observing runs: two in 2002 at ESO, two in 2003 and one in 2004 at CASLEO, and two in 2004 and 2005, each, at OPD. The observational conditions for all the objects are listed in Table 1.
At ESO we used the 1.52 m telescope equipped with a Boller and Chivens spectrograph and a CCD
![]() pixels with a readout noise of
pixels with a readout noise of
![]() rms and a square pixel of 15
rms and a square pixel of 15 ![]() m. A grating of 225 g/mm with a dispersion of 330 Å/mm in the first order was used. This configuration resulted in a useful spectral range of 0.49
m. A grating of 225 g/mm with a dispersion of 330 Å/mm in the first order was used. This configuration resulted in a useful spectral range of 0.49
![]() 0.92
0.92 ![]() m with a FWHM of 10 Å. The tracking procedure was the same used for the S3OS2 survey and described in Lazzaro et al. (2004). It consisted of one or more pauses during an exposure in order to guarantee that the asteroid would always be inside the slit.
m with a FWHM of 10 Å. The tracking procedure was the same used for the S3OS2 survey and described in Lazzaro et al. (2004). It consisted of one or more pauses during an exposure in order to guarantee that the asteroid would always be inside the slit.
At CASLEO we used the 2.15 m telescope equipped with a REOSC spectrograph in its simple dispersion mode, using the grating #320 of 300 lines per millimeter, with a dispersion of 168 Å/mm. The grating was set at ![]() .
The spectral coverage with this configuration ranges from 0.64 to 0.95
.
The spectral coverage with this configuration ranges from 0.64 to 0.95 ![]() m. The REOSC is equipped with a CCD camera TEL
m. The REOSC is equipped with a CCD camera TEL
![]() pixels. The telescope was guided at the sidereal rate. As the targets do not move at this rate, it was necessary to correct the position from time to time to match the apparent motion in the sky of the targets, the tracking was done manually using the CCD camera SBIG model ST-7 which allows one to follow targets up to
pixels. The telescope was guided at the sidereal rate. As the targets do not move at this rate, it was necessary to correct the position from time to time to match the apparent motion in the sky of the targets, the tracking was done manually using the CCD camera SBIG model ST-7 which allows one to follow targets up to ![]() .
.
At the OPD we used the 1.5 m telescope with a Boller and Chivens spectrograph and a CCD SITe
![]() pixels
with a readout noise of
pixels
with a readout noise of
![]() rms and a pixel of
rms and a pixel of
![]()
![]() m. A grating of 300 lines per millimeter with a
dispersion of 2.4 Å/pix in the first order was used. This configuration resulted in a useful spectral range from
0.55 to 0.90
m. A grating of 300 lines per millimeter with a
dispersion of 2.4 Å/pix in the first order was used. This configuration resulted in a useful spectral range from
0.55 to 0.90 ![]() m. The telescope allows for differential tracking on the targets, which is useful for the brighter
targets and/or good night conditions. Otherwise, we tracked the telescope at the sidereal rate, making differential corrections from time to time to match the apparent motion of the targets.
m. The telescope allows for differential tracking on the targets, which is useful for the brighter
targets and/or good night conditions. Otherwise, we tracked the telescope at the sidereal rate, making differential corrections from time to time to match the apparent motion of the targets.
The spectra at CASLEO and OPD were taken through a 5 arcsec slit oriented in the direction of the sidereal motion of the object. This slit direction and width was chosen in order to minimize the consequences of loss of light. At ESO the slit, of the same width, was oriented in the East-West direction (see Lazzaro et al. 2004). Most of the objects were observed at small zenith distances.
The spectral data reduction was performed using the Image Reduction and Analysis Facilities, IRAF, package. Classical procedures for median BIAS, dome FLAT-FIELDS, and sky subtraction, as well as for spectra extraction were followed. Wavelength calibration was performed using a He-Ar lamp, whose spectrum was obtained several times during each night.
At least two different solar analogs (Hardorp 1978) were observed during each observational night in order to compute
reflectivity. The solar analog spectra were reduced in the same fashion as the asteroids. After reduction, the
asteroid spectra were divided by that of the solar analog star thus yielding the reflectance spectrum of the asteroid.
Tests made using different solar analogs produced differences in the reflectance spectra smaller than
![]() Å. All the obtained asteroid spectra were normalized at 0.62
Å. All the obtained asteroid spectra were normalized at 0.62 ![]() m by convention. Some spectra, in particular those from CASLEO, have the initial wavelength at 0.64
m by convention. Some spectra, in particular those from CASLEO, have the initial wavelength at 0.64 ![]() m and were normalized to this initial value.
m and were normalized to this initial value.
Each spectrum has been filtered by applying a low-pass band filter (see Press et al. 1992).
The filtering technique was applied in order to improve the quality of some low signal-to-noise ratio spectra,
allowing us to obtain a good taxonomic classification. All the filtered spectra are shown in Appendix A, while the
original spectra are available on-line![]() .
The normalization described above is lost when filtering the spectra. The upturn at both ends of the spectrum are artifacts due to the filtering technique used, but does not interfere with the taxonomic classification.
In Fig. 1 we show examples of the filtering technique applied to a high and medium signal-to-noise
spectra, (126) Velleda and (854) Frostia, respectively. In the figures, the gray dashed and the continuous line
represent the original and the filtered spectra, respectively. No structure, other than the upturns at the borders, is added to the spectra, and the high-frequency noise has been removed.
.
The normalization described above is lost when filtering the spectra. The upturn at both ends of the spectrum are artifacts due to the filtering technique used, but does not interfere with the taxonomic classification.
In Fig. 1 we show examples of the filtering technique applied to a high and medium signal-to-noise
spectra, (126) Velleda and (854) Frostia, respectively. In the figures, the gray dashed and the continuous line
represent the original and the filtered spectra, respectively. No structure, other than the upturns at the borders, is added to the spectra, and the high-frequency noise has been removed.
 |
Figure 1: Applying the Fourier technique. On the left (126) Velleda and on the right (854) Frostia, examples of the technique in a high and medium signal-to-noise spectra. |
| Open with DEXTER | |
The obtained spectra have been used to classify the asteroids according to the Tholen taxonomy (Tholen & Barucci 1989). The classification was performed by visual comparison with templates of the Tholen classes and, therefore, we call this a "Tholen-like'' classification as described in Lazzaro et al. (2004). The taxonomic classification of all the observed asteroids is given in Table 2 along with the family (upper case) or clump (lower case) membership according to Mothé-Diniz et al. (2005), and the absolute magnitude. The diameter, whenever available, is given between parentheses.
A main result of the present work is the taxonomic classification of 88 asteroids. We did not use the Bus taxonomy (Bus & Binzel 2002b) because of our aim to have a general view of the taxonomic distribution in the region. Although the Bus taxonomy is more precise in classifying visible spectra, it has the disadvantage of separating the classes by small spectral differences, which results in a great number of these. In order to analyze the taxonomic distribution we would have needed to use the "complexes'', most of which are very similar to the Tholen classes. Furthermore, it would be impossible to apply the Bus taxonomy classification since it uses 0.44 ![]() m as starting point, where most of our spectra do not reach.
m as starting point, where most of our spectra do not reach.
The spatial distribution, in the proper element space, of the more than 47 000 numbered asteroids in the inner region
is shown in Fig. 2, where in (a) and (b) are plotted the semi-major axis versus eccentricity and
semi-major axis versus sine of inclination, respectively. The proper elements were extracted from the March
2006 version of the asteroid proper element database ASTDYS![]() (Knezevic & Milani 2003). The taxonomic distribution in the region was obtained including into the present survey all those objects having a classification in ECAS (Zellner et al. 1985, Tholen 1989), SMASS (Xu et al. 1995; Bus & Binzel 2002a), and S3OS2 (Lazzaro
et al. 2004), as well as some other sparse data, such as some targets of the Rosetta mission (Fornasier et al. 2003; Barucci et al. 2005) and objects from the Nysa region (Cellino et al. 2001; Manara et al. 2001).
(Knezevic & Milani 2003). The taxonomic distribution in the region was obtained including into the present survey all those objects having a classification in ECAS (Zellner et al. 1985, Tholen 1989), SMASS (Xu et al. 1995; Bus & Binzel 2002a), and S3OS2 (Lazzaro
et al. 2004), as well as some other sparse data, such as some targets of the Rosetta mission (Fornasier et al. 2003; Barucci et al. 2005) and objects from the Nysa region (Cellino et al. 2001; Manara et al. 2001).
| |
Figure 2: Proper element distribution of asteroids in the inner belt region: a) semi-major axis versus eccentricity and b) semi-major axis versus sine of inclination. |
| Open with DEXTER | |
In the inner region there are 671 asteroids with assigned taxonomic classification,
including those of the present work. This represents less than 2% of the total numbered population. However,
the data presented here account for an increase of 13% in the number of classified asteroids.
In Fig. 3 we present the taxonomic distribution where, to simplify the plot and the subsequent analysis,
we separated the objects as "featured'' (red) and "featureless'' (blue) according to the presence or not of an absorption band around 1 ![]() m.
m.
![\begin{figure}
\par\resizebox{18cm}{!}{\includegraphics[angle=270]{5518fg3a.ps}} \end{figure}](/articles/aa/full/2006/45/aa5518-06/Timg21.gif) |
Figure 3: Proper element distribution of the classified asteroids: a) semi-major axis versus eccentricity and b) semi-major axis versus sine of inclination space. The red (open) and blue (filled) points represent asteroids with featured and featureless spectra, respectively. |
| Open with DEXTER | |
The spatial distribution of the featureless spectral objects, Fig. 4-top, shows that they are more
conspicuous
at a>2.3 AU. In particular, one concentration of objects appears at the Nysa family location (
![]() AU,
AU,
![]() and
and
![]() ). As can be seen in the figure, few objects are found at low eccentricities and
with semi-major axes smaller than 2.3 AU.
). As can be seen in the figure, few objects are found at low eccentricities and
with semi-major axes smaller than 2.3 AU.
The total sample of featureless (as well as featured) spectra include objects classified using diverse taxonomies
which complicates the distribution analysis. Therefore, in what follows we consider the following generic groups:
the C-group, consisting of 107 objects classified as C, Cb, Cgh, Ch, Cb, B and F, the X-group with 56 objects
classified as X, M, P, E, Xk, Xe and Xc, and the D-group with only 16 objects. In Fig. 5 we show
the number distribution of each of the above groups in the
![]() space. Asteroids of both
the C- and D-groups are found mostly at
space. Asteroids of both
the C- and D-groups are found mostly at ![]() AU, while those of the X-group are more homogeneously distributed.
Only objects of the X-group are found at low eccentricities.
AU, while those of the X-group are more homogeneously distributed.
Only objects of the X-group are found at low eccentricities.
The spatial distribution of the asteroids with featured spectra, Fig. 4-bottom, shows a clear abundance at a semi-major axis around 2.15-2.25 AU. Another clear concentration appears at about 2.35-2.4 AU, the location of the Vesta family.
To study the spatial distribution of the featured spectra asteroids, we separated them into four groups: the S-group, including the S, Sl, Sk and Sq, the V-group, with the V-type asteroids, the AR-group, including the A, Sa, R and Sr, and the L-group, including the L, Ld and K. This grouping is arbitrary but it preserves the distribution of classes in the principal components space, as given in Bus & Binzel (2002b).
The S-group is the most populated, containing 370 objects, followed by the V-group with 71, the AR-group with 42 (36 being of the A- and Sa-type and 6 of the R- and Sr-type) and the L-group with just 9 objects. The distribution of asteroids in the various groups can be seen in Fig. 6, were the S-, AR- and V-group are shown in the upper, middle and lower panels, respectively. The L-group is not plotted due to the small number of objects, sparsely distributed in the region.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[angle=270,width=\textwi...
...x{8.8cm}{!}{\includegraphics[angle=270,width=\textwidth]{5518fg4c}} \end{figure}](/articles/aa/full/2006/45/aa5518-06/Timg27.gif) |
Figure 4: Number distribution of classified asteroids: left, semi-major axis versus eccentricity and right, semi-major axis versus sine of inclination. The top and bottom panels represent asteroids with featureless and featured spectra, respectively. The gray scale code used is given below the figure. |
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[angle=270,width=\textwi...
....8cm}{!}{\includegraphics[angle=270,width=\textwidth]{5518fg5d.ps}} \end{figure}](/articles/aa/full/2006/45/aa5518-06/Timg28.gif) |
Figure 5: Number distribution of asteroids with featureless spectra: left, semi-major axis versus eccentricity and right, semi-major axis versus sine of inclination. The upper, middle and lower panels represent asteroids of the C-, X- and D-groups as defined in the text, respectively. The gray scale code used is given below the figure. |
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[angle=270,width=\textwi...
....8cm}{!}{\includegraphics[angle=270,width=\textwidth]{5518fg6d.ps}} \end{figure}](/articles/aa/full/2006/45/aa5518-06/Timg29.gif) |
Figure 6: Number distribution of asteroids with featured spectra: left, semi-major axis versus eccentricity and right, semi-major axis versus sine of inclination. The upper, middle and lower panels represent asteroids of the S-, AR- and V-group as defined in the text, respectively. The gray scale used code is given below the figure. |
| Open with DEXTER | |
In the region between 2.1 and 2.3 AU are located most of the objects belonging to the S- and AR-group, decreasing in number at larger semi-major axis. In particular, few objects of the AR-group are found at a>2.3 AU. Nevertheless, there is a small concentration of asteroids of the S-group at 2.4 AU and high eccentricities. The V-group is the most compact, basically at the location of the Vesta family but with several objects at higher and lower eccentricities and/or inclinations. This distribution is clearly seen in Fig. 6-bottom.
The distributions discussed above represent the apparent distribution of compositions or spectral characteristics. The real distribution is affected by several observational biases which need to be identified and taken into account. For example, it is well known that there exists a strong bias toward observing nearer, larger, and brighter asteroids. Another important effect is the incompleteness of the numbered catalog of asteroids which, according to Jedicke & Metcalfe (1998), starts at apparent magnitude 12.75 in the inner belt. A third bias arises from the observing selection criterion, which generally focuses on specific families and/or groups at the expense of field asteroids. Sometimes this effect is corrected by representing each family by just one member, based on the assumption of the break-up of an original body. In order to compare our results with others, we will not try to correct this last bias, since, as already explained in Sect. 1, the identification of the diverse families has changed from author to author. Regarding the other biases we used the methodology originally developed by Zellner (1979) and Gradie & Tedesco (1982) with the modifications described in Mothé-Diniz et al. (2003) to which we refer the reader for more details.
We estimated the fraction, f, of numbered to classified objects computed in bins of 0.5 of absolute magnitude in the range 3 < H < 13.5. We then assumed that for each asteroid A, with a given absolute magnitude and taxonomic class, there exist f-1 objects in the same region with the same H and taxonomic class. The relative abundance was computed for the featured and featureless groups in bins of 0.025 AU and is shown in Fig. 7. From this figure we conclude that the featured objects dominate the innermost part, and decrease continuously until to a fraction of nearly 30% at 2.5 AU. The fraction of featureless objects, on the other hand, goes from zero in the innermost part up to nearly 70% around 2.4-2.5 AU.
Although the general behavior show in Fig. 7 is the same as in previous works (Gradie et al. 1989; Mothé-Diniz et al. 2003) a direct comparison is difficult due to the distinct taxonomic scheme used by each author. Moreover, our restriction to objects with
![]() and e < 0.3 further complicates the comparison, for example, with the Mothé-Diniz et al. (2003) results.
and e < 0.3 further complicates the comparison, for example, with the Mothé-Diniz et al. (2003) results.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[width=\textwidth]{5518fg7a.ps}} \end{figure}](/articles/aa/full/2006/45/aa5518-06/Timg31.gif) |
Figure 7: De-biased populations of the inner Main Belt. Featured, dashed line, and featureless, continuous line. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.3cm]{5518fg8a.eps}\includegraphics[width=8.3cm]{5518fg8b.eps} \end{figure}](/articles/aa/full/2006/45/aa5518-06/Timg32.gif) |
Figure 8: Dynamical maps of the inner region of the asteroidal belt on the (a,e)-plane ( left) and (a, I)-plane ( right) of the osculating elements (the initial inclination on the left panel and initial eccentricity on the right panel were fixed at the current values of those of Vesta). The domains of chaotic motion (the vertical dark strips) are associated with two- and three-body mean-motion resonances and are labeled on the top of the panels by numbers from 1 to 9 (see Table 3). For reference we also show the location in the proper elements space of Vesta family members, in cyan, Massalia, in blue, Nysa, in yellow, Erigone, in magenta, and Baptistina, in green. |
| Open with DEXTER | |
Although the spectroscopic survey was not designed to study families and clumps in the region, some members were observed. In particular, we classified three members of the Nysa family and two of the Baptistina, as well as nine objects as members of nine different clumps (see Table 2). These observations do not much change the results already obtained by Mothé-Diniz et al. (2005). The sole difference between their work and the present is that we have used all the taxonomic classifications available in the literature. In particular, the sample analyzed here contains 31 members of the Nysa family where 6 are of the X-group, 11 of the C-group and 14 of the S-group. This result confirms previous works (Cellino et al. 2001; Mothé-Diniz et al. 2005) about the probable existence of three clusters, two of them, Mildred and Hertha, composed of featured objects and the third, McCuskey, of featureless.
One very interesting family is the Baptistina, which was already recognized by Mothé-Diniz et al. (2005) as presenting an interesting mixture of compositions. Of the 9 objects with known classification three are of the S-group, two are of the X-group, another two of the AR-group, and one of the C- and V-group, respectively. With the sole exception of the C-group asteroid, the remaining are compatible with the fragmentation of a completely differentiated parent body. Even the X-group asteroid could be associated with the metal-rich nucleus of the body. Obviously, this is very speculative for the moment, since very few members of the family have a taxonomic classification and not even the albedo of these objects is known. This family deserves further observations.
About the Massalia and Erigone families, located at a semi-major axis around 2.35-2.45 AU, very little can be said since each one has just one member with known classification: of the S- and of the C-group, respectively.
The most homogeneous family in the inner region is clearly Vesta, containing 40 V-type asteroids, out of the 49
asteroids of the family with known classification. The Mothé-Diniz et al. (2005)
family definition![]() uses a very conservative cut-off and
several V-type asteroids found outside the limits of the dynamical family are very near it. Therefore, of the
31 V-type asteroids not being members of the Vesta dynamical family, only around 20 are escapees, or resulting
from the fragmentation of another differentiated body. The origin of these V-type "outliers'' is a very
interesting topic.
uses a very conservative cut-off and
several V-type asteroids found outside the limits of the dynamical family are very near it. Therefore, of the
31 V-type asteroids not being members of the Vesta dynamical family, only around 20 are escapees, or resulting
from the fragmentation of another differentiated body. The origin of these V-type "outliers'' is a very
interesting topic.
Most of the clumps that do have at least one classified object are of the S-group in the region around 2.1-2.3 AU and of the C-group around 2.3-2.4 AU. A mixture of featured and featureless objects is found only in the Matterania clump (S-, X-, and D-group). Obviously, as mentioned above, the small number of objects with a taxonomic classification makes it impossible to derive any conclusion.
In order to assess the possible dynamical mechanisms responsible for the observed taxonomic distribution in the inner belt and, in particular, the transport mechanisms of V-type asteroids, we investigated the occurrence of mean-motion and secular resonances in the region. The obtained dynamical maps of the region are described in the following section.
We present dynamical maps of the inner Main Belt. We have applied the Spectral Analysis Method
(SAM) developed by Michtchenko et al. (2002): 3131 massless particles with initial test orbits distributed in a
![]() grid in the (a, e) and (a,I) osculating planes have been integrated over 1 Myr, accounting for planetary
perturbations from Mars to Neptune. The initial angular elements,
grid in the (a, e) and (a,I) osculating planes have been integrated over 1 Myr, accounting for planetary
perturbations from Mars to Neptune. The initial angular elements,
![]() ,
and
,
and
![]() ,
of these test orbits have been fixed at those of (4) Vesta.
During the integration, a low pass-band digital filter has been applied to remove the short period
oscillations due to the synodic perturbations of the major planets. The output series of filtered elements for
each test orbit have been Fourier analyzed in order to identify the relevant peaks in the Fourier spectra of the
semi-major axis (see Michtchenko et al. 2002, for details). The number of the relevant peaks can be used to
characterize the chaoticity of the orbit: for regular orbits, a few well defined lines appear in the spectra, while
for chaotic orbits the number of peaks is large. This information has been translated to a gray scale code on the
(a,e)- and (a,I)-planes of the osculating semi-major axis, eccentricity and inclination in Fig. 8.
,
of these test orbits have been fixed at those of (4) Vesta.
During the integration, a low pass-band digital filter has been applied to remove the short period
oscillations due to the synodic perturbations of the major planets. The output series of filtered elements for
each test orbit have been Fourier analyzed in order to identify the relevant peaks in the Fourier spectra of the
semi-major axis (see Michtchenko et al. 2002, for details). The number of the relevant peaks can be used to
characterize the chaoticity of the orbit: for regular orbits, a few well defined lines appear in the spectra, while
for chaotic orbits the number of peaks is large. This information has been translated to a gray scale code on the
(a,e)- and (a,I)-planes of the osculating semi-major axis, eccentricity and inclination in Fig. 8.
The inner Main Belt region presents a very complex web of mean-motion and secular resonances. The principal groups of two- and three-body mean-motion resonances are labeled with numbers from 1 to 9 on the top of each panel in Fig. 8 and are listed in Table 3. Table 4 gives a list of the main nonlinear secular resonances up to order 6, detected in the inner region applying the SAM method. There are resonances involving the perihelia, nodes and both perihelia and nodes of the asteroid and the planets from Mars to Neptune. Figure 9 displays the locations of these resonances in the (a, e) osculating plane.
The location of the Vesta (cyan), Massalia (blue), Nysa (yellow), Erigone (magenta), and Baptistina (green) family
members in the proper element space is superimposed in Fig. 8 for comparison. In Fig. 9 we
superimposed the Vesta family members (cyan) along with the 31 V-type asteroids (red) which are not members of the
dynamical family, as defined by Mothé-Diniz et al. (2005). The dynamical map constructed over a grid of osculating
orbital elements cannot be directly compared to the proper elements of the actual asteroids, since the location
of the web of secular resonances on the (a, e) and (a, I)-planes is unique for each asteroid,
depending on the fixed values of the inclination or eccentricity. Thus, Figs. 8 and 9 provide
only an estimation of the dynamical behavior of a real object.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[width=\textwidth]{5518fg9a.eps}} \end{figure}](/articles/aa/full/2006/45/aa5518-06/Timg37.gif) |
Figure 9:
Location of the nonlinear secular resonances in the inner Main Belt computed for the inclination of
(4) Vesta (
|
| Open with DEXTER | |
The shading scale used in the dynamical map in Fig. 8 is related to the degree of stochastic behaviour
of the test
orbits: the lighter regions in the dynamical map correspond to initial conditions of regular motion, darker tones
indicate increasingly chaotic motion. The domains where the test particles escape from the region within the
time-interval of integration (![]() 1 Myr) are hatched. The large-scale instabilities in these regions are
caused by the
1 Myr) are hatched. The large-scale instabilities in these regions are
caused by the ![]() secular resonance (left-hand side of Fig. 8) and the strong 3:1 mean-motion
resonance with Jupiter (right-hand side). The linear
secular resonance (left-hand side of Fig. 8) and the strong 3:1 mean-motion
resonance with Jupiter (right-hand side). The linear ![]() secular resonance (of order 2) is well known from
previous work and occurs in the regions where the precessional rate of the asteroid's longitude of perihelion
equals the precessional rate of Saturn's perihelion. The strong effects of both phenomena, the
secular resonance (of order 2) is well known from
previous work and occurs in the regions where the precessional rate of the asteroid's longitude of perihelion
equals the precessional rate of Saturn's perihelion. The strong effects of both phenomena, the ![]() secular and
3:1 mean-motion resonances, form the physical boundaries of the inner asteroid belt.
secular and
3:1 mean-motion resonances, form the physical boundaries of the inner asteroid belt.
A relevant feature in Fig. 8 is the occurrence of several vertical thin stripes of chaotic motion, which are
associated with two-body mean-motion resonances with Jupiter or Mars, and to three-body mean-motion resonances with
both Jupiter and Saturn. Many of these resonances cut through the asteroid families and we may expect several Vesta
family members to involve these resonances. Among the mostly relevant ones, there are the 7:2 mean motion
with Jupiter that bounds the Vesta family at the side of smaller semi-major axes, the 1:2 resonance with Mars and
several three-body mean motion resonances of low order, such as the
![]() ,
,
![]() ,
and
,
and
![]() resonances, where the letters
resonances, where the letters
![]() denote Jupiter, Saturn, Mars and an asteroid, respectively.
denote Jupiter, Saturn, Mars and an asteroid, respectively.
It is known that nonlinear secular resonances are able to cause significant long-term variation in eccentricity and
inclination (Milani & Knezevic 1994). Among all the detected secular resonances, the
2(g-g6)+s-s6 (z2
by Milani & Knezevic 1994) and the
2(g-g6)+g5-g4 resonances seem to be the most interesting, since they
are the ones that affect the largest number of real objects in the inner Main Belt (see Carruba et al. 2005).
The secular resonances do not appear in the dynamical maps of Fig. 8 because the
total integration time was not long enough to detect the diffusive effects of the long-term secular
resonances. However, the SAM method allows us to identify the occurrence of secular resonances. These are determined
by searching for the orbits whose fundamental frequencies satisfy the condition
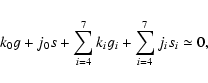
Figure 9 shows that the region of the inner Main Belt is covered by a dense web of secular resonances which may play an important role in the long term dynamical diffusion of the asteroids. Indeed, as was shown in Carruba et al. (2005), the V-group asteroids outside the Vesta family (at least part of them) are former family members that migrated to their current positions via the interplay of the Yarkovsky effect and nonlinear secular and mean-motion resonances.
A region of chaotic motions is also observed in the upper-left half of the dynamical maps, especially over a diagonal band crossing the map from the lower-left to the upper-right corners of the left panel in Fig. 8. This band seems to be associated with the overlap of several secular resonances which involve the longitude of perihelion and node of the asteroid simultaneously, and mean-motion resonances at middle-to-high eccentricities. All the families as well as the bulk of asteroids in the inner Main Belt are located below this band, although several asteroids may be also found over this band and in the region above it, moving in rather stable orbits (as stable as to allow computation of their proper elements).
In the present study we performed a visible spectral survey of asteroids in the inner Main Belt and a dynamical analysis of the region. We report the taxonomic classification of 88 asteroids. This number is very small when compared to the total number of asteroids in the region (more than 47 000), but represents an increase of 13% in the number of object with known taxonomic classification. This larger database does not change substantially the picture obtained from previous works on the distribution of compositions, as derived from taxonomic classification. The increase in the number of classified objects further confirms the notion that the inner region can be divided in three different compositional zones: the innermost, where asteroids of the S-group concentrate, the outermost, where the C-group peaks, and the in-between, with the highest concentration of V-type. This zoning does not, however, imply that mixtures of the diverse taxonomies do not exist in the region. The Nysa family is the most prominent example of this kind of mixture.
Dynamical maps of the inner Main Belt identify the presence of a complex structure of mean motion and secular resonances. All these resonances have played a major role in shaping the distribution of asteroids, the families in the region, and in the delimiting effect of the large chaotic band that crosses the region from the lower left side to the upper right (left panel in Fig. 8). All the families lie below this band. Moreover, all the clumps also are located below this chaotic belt (they are not shown in the figure for clarity). Most of the clumps in the inner belt are located around the Baptistina family, the former Flora clan.
Another interesting structure is the spread in semi-major axis of the Vesta family, compared to the other families within the region. Although this can be attributed to the dissipation effect of the Yarkovsky force, due to the small sizes of the Vesta family members, it should affect in similar way the smaller objects of the other families. One possibility is that the basaltic material is more affected by the Yarkovsky effect. According to Rubincam (1995) a basaltic asteroid will evolve due to the Yarkovsky force more efficiently than an iron one. Another possibility is that the Vesta family is older than the rest or, conversely, that these are so old that they were completely eroded by the diverse dynamical, collisional and/or dissipative processes (Marzari et al. 1999; Nesvorný et al. 2002).
Probably the most interesting family in the Main Belt is the one associated with asteroid (4) Vesta. The uniqueness of the basaltic crust of Vesta among the large asteroids as well as its similarity to the HED meteorites has led to the association between them, despite the initial difficulties in identifying the transport mechanism. The identification of a family (Williams 1989; Zappalà et al. 1990), along with the discovery of a large crater in (4) Vesta consolidated the hypothesis of a cratering event that formed the family and injected fragments in nearby resonances. This scenario was strengthen by the discovery (Binzel & Xu 1993) that many small asteroids, either members of the Vesta family or close to it, shared the same surface composition as Vesta. Recently several other V-group asteroids have been discovered outside the family, some even larger than most of the family members (Florczak et al. 2002). In the present survey one major result is the discovery of 6 new basaltic asteroids, all outside the limits of the dynamical family. Considering all the "outliers'', these asteroids represent almost 50% of the known V-group in the region. Note, however, that this must be considered as an observational bias since the present survey searched specifically for new V-type asteroids outside the limits of the dynamical family.
Duffard et al. (2004) studied the problem of the origin of the V-type asteroids near (4) Vesta from a mineralogical point of view. Their aim was to identify characteristics that could indicate different origins of the V-type asteroids members and not members of the dynamical family. Although distinct mineralogies were found, these could not be linked to an asteroid belonging or not to the Vesta family. Therefore, some, or all, the "outliers'' can indeed have come from the cratering event that formed the Vesta family and have been transported to their current location due to some dynamical diffusion mechanism. This point was explored by Carruba et al. (2005), showing that the interplay of the Yarkovsky effect and nonlinear secular resonances can transport bodies of intermediate size, such as (809) Lundia, 12.3 km, and (956) Elisa, 8.5 km. According to these authors, the smaller objects, on the other hand, would cross the secular resonances without being captured and would "fall'' inside a stronger resonance. Therefore, we continue to lack a secure link between most of these "outliers" and (4) Vesta. In particular, it seems very difficult to explain the V-type asteroids located at lower inclinations than the Vesta family. One possibility would be that these objects, or at least some of them, come from the disruption that generated the Baptistina family. The Baptistina family lies at lower inclinations than Vesta (Fig. 8, right panel) and the compositional (taxonomic) distribution of its members can be consistent with a differentiated original body. More substantial theoretical and observational work is required.
Acknowledgements
We thank the referee for thoughtful and valuable comments which much improved the paper. This work has been supported by the Brazilian National Research Council - CNPq, as well as the Rio de Janeiro State Science Foundation - FAPERJ, and the São Paulo State Science Foundation - FAPESP. The authors gratefully acknowledge the Computation Center of the University of São Paulo (LCCA-USP) for the use of their facilities.
![\begin{figure}
\par\resizebox{18cm}{!}{\includegraphics[width=\textwidth]{5518fg10.ps}}
\end{figure}](/articles/aa/full/2006/45/aa5518-06/Timg42.gif) |
Figure 10: Filtered spectra of the observed asteroids. |
| Open with DEXTER | |
![\begin{figure}\par\resizebox{18cm}{!}{\includegraphics[width=\textwidth]{5518fg11.ps}}
\end{figure}](/articles/aa/full/2006/45/aa5518-06/Timg43.gif) |
Figure 10: continued. |
| Open with DEXTER | |
![\begin{figure}\par\resizebox{18cm}{!}{\includegraphics[width=\textwidth]{5518fg12.ps}}
\end{figure}](/articles/aa/full/2006/45/aa5518-06/Timg44.gif) |
Figure 10: continued. |
| Open with DEXTER | |
![\begin{figure}\par\resizebox{18cm}{!}{\includegraphics[width=\textwidth]{5518fg13.ps}}
\end{figure}](/articles/aa/full/2006/45/aa5518-06/Timg45.gif) |
Figure 10: continued. |
| Open with DEXTER | |
Table 1:
Observational parameters. For each asteroid we give its denomination, the night of observation, the UT start time, the exposure time, the airmass, the apparent visual magnitude, the solar phase angle, ![]() ,
the solar analog star used in the reduction and an observatory code where E, C and O indicate ESO, CASLEO and OPD, respectively. In the last column s/n indicates, for each asteroid, the number of obtained spectra, s, distributed on how many different nights, n. The values for the night of observation, start and exposure time, apparent visual magnitude and phase angle refer to just one selected spectrum. This spectrum was chosen as the one with the smallest noise between 0.65 and 0.70
,
the solar analog star used in the reduction and an observatory code where E, C and O indicate ESO, CASLEO and OPD, respectively. In the last column s/n indicates, for each asteroid, the number of obtained spectra, s, distributed on how many different nights, n. The values for the night of observation, start and exposure time, apparent visual magnitude and phase angle refer to just one selected spectrum. This spectrum was chosen as the one with the smallest noise between 0.65 and 0.70 ![]() m since in this region all spectra are quite linear and with no strong features regardless of their taxonomic classification.
m since in this region all spectra are quite linear and with no strong features regardless of their taxonomic classification.
Table 2: Classification of the observed asteroids.
Table 3:
The groups of mean-motion resonances in the inner Main Belt. We use the notation
![]() ,
where
,
where
![]() are simple
integers and letters
are simple
integers and letters
![]() denote Jupiter, Saturn, Mars and an asteroid, respectively.
denote Jupiter, Saturn, Mars and an asteroid, respectively.
Table 4: Nonlinear secular resonances in the inner Main Belt.