Centrum voor Plasma Astrofysica, K. U. Leuven, Celestijnenlaan 200 B, 3001 Leuven, Belgium

Abstract
Aims. The initiation of solar Coronal Mass Ejections (CMEs) is studied in the framework of computational Magneto-Hydro-Dynamics (MHD).
Methods. The initial configuration includes a magnetic flux rope that is embedded in a gravitationally stratified solar atmosphere with a background dipole magnetic field in spherical, axi-symmetric geometry. The flux rope is in equilibrium due to an image current below the photosphere. An emerging magnetic flux triggering mechanism is used to make this equilibrium configuration unstable.
Results. When the magnetic flux emerges within the filament below the flux rope this results in a catastrophic behavior similar to earlier, more simple models. As a result, the flux rope rises and a current sheet forms below it. It is shown that the magnetic reconnection in the current sheet below the flux rope in combination with the outward curvature forces results in a fast ejection of the flux rope as observed for solar CMEs. We have done a parameter study of the effect of the flux emergence rate on the velocity and the acceleration of the resulting CMEs.

Key words: Sun: coronal mass ejections (CMEs) - Sun: magnetic fields - magnetohydrodynamics (MHD)

1 Introduction

Fast Coronal Mass Ejections (CMEs) play a crucial role in space weather and, thus, a careful study of the origin, the structure, and the propagation characteristics of these violent phenomena is essential for a deeper insight in basic space weather physics. The fast CMEs, with velocities of 1000 to 2000 km s^-1 and higher, owe this important role to the shock waves they generate. Clearly, the theoretical modelling of the initiation and the interplanetary (IP) evolution of CMEs can be divided into sub-problems. An important unresolved sub-problem is the initiation of CMEs, i.e. the question why CMEs occur at all and how are they triggered.

Klimchuk (2001) reviewed the many different theoretical models for CME initiation. Based on basic physical properties, such as energetics, structure and dynamics, this author distinguished two types of models, directly driven and storage and release models, and presented them by making simple analogues involving springs, ropes, and weights. However, Klimchuk concludes that "all these models have difficulty explaining one or more aspects of observations''. Hence, a lot of work remains to be done and the present models need to be improved: 3D extensions need to be created including fine structure, real (instead of numerical) dissipation, a more realistic shearing of magnetic foot points, etc. CME shock evolution studies very often apply simplified generation models for the CMEs. Groth et al. (2000) used a "density-driven'' model which simply means that a high-density (and high-pressure) plasma blob is superposed on the solar wind. Other simplified models generate a pressure pulse with or without an additional velocity change (i.e. a kind of "nozzle'' boundary condition), see e.g. Wang et al. (1995) and Odstrcil & Pizzo (1999). Keppens & Goedbloed (1999) on the other hand impose an extra mass flow to generate the CMEs.

More realistic CME evolution simulations make use of theoretical analytic CME initiation models such as the models of the self-similar Gibson & Low (1998) family (Gombosi et al. 2000) or the Titov & Démoulin model (Roussev et al. 2003), while Odstrcil & Pizzo (2002) and Odstrcil et al. (2003) still use another analytical flux rope model. What one really should do, however, is to simulate the evolution of reconstructed coronal structures (e.g. Aulanier et al. 2000) driven unstable by realistic foot point shearing and/or magnetic flux emergence or cancelation. Several groups are working on such simulations and results appeared recently (Lionello et al. 2005; Roussev et al. 2003).

The CME initiation model presented in this paper extends earlier results obtained by Lin et al. (1998) and Chen & Shibata (2000). These authors focused on the triggering mechanism. i.e. on the question whether the primary mechanism for driving eruptions is magnetic reconnection or a catastrophic loss of mechanical equilibrium. Lin et al. (1998) considered a two-dimensional (axial symmetry) flux-rope model for a CME consisting of a torus encircling the sun and studied the ability of the large-scale curvature of the flux rope to propel it outward from the sun. The initial balance between the magnetic tension and compression force and the curvature force is lost when the photospheric sources of the coronal field slowly decay in time. These authors showed that the system then shows a catastrophic evolution and it is especially the flux rope with large radius that is likely to erupt. The loss of ideal MHD equilibrium cannot fully open the magnetic field but it leads to the sudden formation of a current sheet. When the reconnection in this sheet is fast enough, the flux rope can escape from the sun. Chen & Shibata (2000) also considered a configuration with a detached flux rope in a two-dimensional simulation in a Cartesian plane. These authors considered an initial quadrupolar background field and the flux-rope is initially in equilibrium with its surroundings due to an image current below the photosphere. The quadrupolar field turned out to be more favourable for flux rope ejection than earlier tests with bipolar fields Forbes et al. (1994). These authors put the emphasis on the onset process of the CME and neglected gas pressure and gravity in their model.

Compared with the study of Linker et al. (2003) we have considered ideal MHD calculations and we rely on the numerical diffusion of the applied schemes while Linker et al. (2003) included a finite resistivity and viscosity. Moreover, we considered a background dipole field that is suitable for the low corona, close to the solar surface, while the model of Linker et al. contains a background solar wind. Moreover, as a triggering mechanism we only consider flux cancelation, i.e. the emergence of flux of opposite sign, while Linker et al. considered a combination of foot point shearing and flux cancelation. So in the terminology introduced by Klimchuk (2001) in his review paper, our model belongs to the "tether release'' type while Linker's model is in fact a combination of the "tether release'' CME type and the closely related "tether straining'' type, in which there is a slow build-up phase due to the shearing. In both cases, the flux cancelation is "cutting the tethers''. As a consequence, in our calculations the initial flux rope is strictly in equilibrium (due to an image current), while the flux rope of Linker et al. is created by the foot point shearing and is stable for some time but not in strict equilibrium. Linker et al. have shown that when a critical threshold of flux reduction is exceeded, the configuration erupts violently. While we have performed a parametric study of the effect of the amount of emerged flux and the flux emergence rate on the evolution and the velocity of the resulting CMEs. In the present paper, we will show that the amount of magnetic flux that emergences plays a more important role than the flux emergence rate.

The results presented here are based on a model that can be seen as an extension of the two papers described in the previous paragraph. Compared to the model of Chen & Shibata (2000), e.g., this extension includes: 1) geometry effects (spherical curvature, also included in the model of Lin et al. 1998); 2) gas pressure and gravity; 3) gravitational stratification of the ambient medium; and 4) a parameter study of the effect of the amount of magnetic flux and the flux emergence rate on the velocity and the acceleration of the resulting CMEs. The initial model is presented in the next section and Sect. 3 contains details on the applied numerical methods and time-dependent boundary conditions. Section 4 is devoted to discussion of the numerical results obtained in the parameter study. The conclusions are drawn in Sect. 5.

2 The initial model

Our pre-CME model is inspired by the models and results of Chen & Shibata (2000) and Lin et al. (1998). Chen & Shibata used three separate current elements to get a detached magnetic flux rope in equilibrium with its surroundings in a 2D Cartesian plane. These authors considered a line current to describe the flux rope in the corona, its image current below the photosphere, and four line currents to produce a quadrupole background magnetic field. We have considered only two separate current elements in a 2.5D (i.e. axi-symmetric) spherical geometry: a ring current centered at a distance h above the photosphere on the equator with finite radius r₀, and its image current located below the photosphere. As background, however, we use a global dipole field, very similar to that in Forbes (1990). Hence, in the present paper, we do not consider the actual formation of the flux ropes but in previous studies, several mechanisms have been suggested for this.

We use spherical coordinates $(r, \theta, \varphi)$ and express the magnetic field $\vec{B}$ in terms of a vector potential $A_{\varphi}$ , i.e. $\vec{B}= \nabla \times (A_{\varphi} \hat\varphi)+ B_\varphi\hat\varphi$ . The initial magnetic configuration is given by $A_{\varphi} = A_{\varphi r} + A_{\varphi i} + A_{\varphi b}$ , where the magnetic vector potential of the ring current ( $A_{\varphi r}$ ), its image current ( $A_{\varphi i}$ ) and the background dipole field ( $A_{\varphi b}$ ) have the following forms:

$\displaystyle A_{\varphi b}(r,\theta)$	=	$\displaystyle m \frac{\sin \theta}{r^2},$	(1)
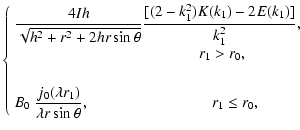$\displaystyle A_{\varphi r}(r,\theta)$	=	$\displaystyle \left\{ \begin{array}{l l} \displaystyle\frac{4I h}{\sqrt {h^2+r^... ... \sin\theta}, \qquad \qquad \qquad \qquad r_{1} \leq r_{0}, \end{array} \right.$	(2)
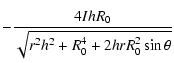$\displaystyle A_{\varphi i}(r,\theta)$	=	$\displaystyle -\frac{4I h R_{0}}{\sqrt {r^2 h^2+R_{0}^4+ 2h r R_{0}^2 \sin \theta}}$
		$\displaystyle \times \frac{[(2- k_{2}^2)K(k_{2})-2E(k_{2})]}{k_{2}^2},$	(3)

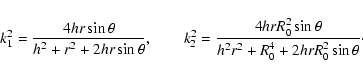
$\begin{displaymath}k_{1}^2=\frac{4hr \sin\theta}{h^2+r^2+2hr \sin\theta},\qquad ... ...}^2 \sin\theta}{h^2 r^2+ R_{0}^4+ 2hr R_{0}^2 \sin\theta}\cdot \end{displaymath}$

We assume that there are no magnetic field sources at infinity. The current within the initial flux rope, that is located at the equatorial plane, is the only current source within the region $r > R_\odot$ prior to the eruption. We have also taken account the effect of gravity in our model. As a result, the ambient plasma is stratified, i.e. $\rho_{\rm g}= \exp\left[{\frac{1}{2}(\frac{v_{\hbox{\tiny esc}}^2}{r} -1)}\right]$ , where $v_{\hbox{\tiny esc}}$ is the escape velocity of the Sun. The flux rope itself is initialized with a high density, much higher than the density of the ambient plasma, that is distributed as

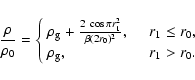$\begin{displaymath}\frac{\rho}{\rho_{0}}= \left\{ \begin{array}{l l} \rho_{\rm ... ... \rho_{\rm g}, & \quad r_{1} > r_{0}.\\ \end{array} \right. \end{displaymath}$

(4)

3 Numerical methods

The full time dependent ideal MHD equations are applied in our mathematical model. This set of partial differential equations is solved numerically by means of the VAC code (Versatile Advection Code, Tóth 1996) by a two-step Runge-Kutta scheme in time while for the spatial discretization we use a second-order finite volume scheme, viz. the so-called TVD Lax-Friedrichs method. The solenoidal condition, $\nabla\cdot\vec{B}=0$ , is maintained to machine precision using the approach suggested by Balsara (2003), which we implemented in the VAC code for a magnetic field representation in terms of a vector potential.

We have taken the following characteristic values for normalizing the density and temperature: $\rho_{0}= 1.6726 \times 10^{-16}\;$ g/cm³, and $T_{0}= 1.5 \times 10^6\;$ K, respectively. The solar radius $R_{\odot}= 6.9626\times 10^{10}\;$ cm is used to normalize the length scales so that the solar surface is at r=1 in dimensionless units. The numerical (dimensionless) units for the other quantities follow from these three, viz. velocity $v_{0}= \sqrt {T_{0} {2k_{\rm b}}/{m_{\rm p}}}= 1.574 \times 10^7\;$ cm/s, time $t_{0}={R_{\odot}}/{v_{0}}=4420\;$ s, $B_{0}= v_{0} \sqrt {4\pi \rho_{0}}= 0.7216\;$ Gauss, and magnetic flux $\psi_{0}= B_{0} R^{2}_{\odot}= 34.98 \times 10^{20}\;$ Mx. We have considered ideal MHD but reconnections of magnetic field lines can occur anyway due to the unavoidable numerical diffusion in the applied scheme. In the near future, we will take into account finite magnetic resistivity in our model. However, the magnetic resistivity in the solar corona is extremely small and in all current numerical simulations including dissipative effects, the numerical diffusion is much higher than in the real coronal plasma.

The computational domain is part of the $(r,\theta)$ -plane limited by $1 \leq r \leq 30$ and $0 \leq \theta \leq \pi$ . This domain is discretized by a grid off $600\times201$ points, which are non-uniformly distributed in both the r- and the $\theta$ -directions. The numerical grid is logarithmic accumulated near the solar surface at r=1 and near the equatorial plane at $\theta=\pi/2$ with a stretch factor of 50 and 10 in the r- and $\theta$ -direction, respectively. The bottom boundary of the simulation area is a line tying boundary, where all quantities except for the temperature T are fixed outside the flux emergence region while T is determined by constant extrapolation. The boundary conditions at the poles for the $\varphi$ - and $\theta$ -components of vector quantities are asymmetric, while for the r-components of the vector quantities and for the plasma density symmetric boundary conditions are applied (making the normal derivative across the boundary zero). At the outer boundary, we imposed superfast outlet boundary conditions. This means that all quantities are extrapolated.

The numerical simulations of the flux rope CME initiation are done in two phases. In a first phase, the initial state is "relaxed'' (i.e. fixed boundary conditions, no driving) for a rather long period, viz. until t=32 corresponding to 39.3 h, in order to assure that a numerical equilibrium is reached with a stable flux rope, i.e. a flux rope that is in equilibrium with its surroundings. In other words, the forces acting on the flux rope (gravitation, pressure, magnetic pressure and tension) are in balance so that, initially at least, the net force on the flux rope is zero. The resulting static equilibrium configuration is illustrated in Fig. 1. After this initial phase, the kinetic energy of the system and the changes in density and magnetic field are ignorable. Note, that in Eqs. (2) and (3), the current I has been determined by trial and error to make sure that the flux rope center approximately keeps stable for a long enough time, viz. 32 time units. In these simulations the (dimensionless) value of I we obtained in this way is 6.33.

$\begin{figure} \par\includegraphics[width=6.8cm,clip]{4719fg01.ps}\end{figure}$	Figure 1: The plasma density $\log_{10}~\rho$ (grey scale) and magnetic field lines for the initial relaxed configuration (i.e. at t=t₀=32.0 or 39.3 h).
Open with DEXTER

In analogy with Forbes et al. (1994) and Chen & Shibata (2000), the magnetic flux emergence is then implemented by changing the magnetic field at the lower boundary in time. This is done by changing the value of the vector potential $A_{\varphi}$ starting at t=t₀=32. The magnetic flux emergence region is limited to $\frac{\pi}{2} - 0.5 \leq \theta \leq \frac{\pi}{2} + 0.5$ . The emerging magnetic flux grows linearly in time in the time interval $\Delta t= t_{\rm e}-t_0$ . This is imposed as a boundary condition by setting the $\phi-$ component of the vector potential at r=1 equal to:

$\displaystyle \left. A_{\varphi}(t;\theta)\right\vert _{r=1} = \left.A_{\varphi... ...rac{\pi}{2}-\theta) \pi\right)}{\sin\theta}, \quad t_{0} \leq t \leq t_{\rm e}.$

(5)

$\displaystyle \left. B_{r}(t;\theta)\right\vert _{r=1}$	=	$\displaystyle \frac{1}{\sin\theta}~\left[ \frac{\partial\sin\theta A_{\varphi}}{\partial\theta}\right]$
	=	$\displaystyle -c_{\rm e} \pi~ \frac{(t-t_{0})}{\Delta t} \frac{\sin \left((2\theta-\pi) \pi\right)}{\sin\theta},\quad t_0\leq t \leq t_{\rm e}.$	(6)

$\begin{displaymath} \psi(t) = \int_0^{2\pi}\!\!\int_{\frac{\pi}{2} - 0.5}^{\fra... ...\pi c_{\rm e} \frac{(t-t_0)}{\Delta t} \right\vert _{r=1}\cdot \end{displaymath}$

(7)

$\begin{displaymath} \frac{{\rm d}\psi(t)}{{\rm d}t} = \left. 2\pi \frac{c_{\rm e}}{\Delta t} \right\vert _{r=1}\cdot \end{displaymath}$

(8)

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{4719fg02.ps} \end{figure}$	Figure 2: $A_{\varphi }\vert _{r=1}$ versus $\theta$ at t=t₀=32.0 (after the relaxation), after $7.5\;$ min (during the flux emergence), and after $30\;$ min, i.e. at the end of the flux emergence for the case $c_{\rm e}=-3$ and $\Delta t = 30\;$ min).
Open with DEXTER

4 Numerical results - parameter study

After the initial relaxation towards the static computational equilibrium (as described above) the triggering phase starts. In this phase we emerge magnetic flux at the lower boundary (r=1) in a limited time interval ( $\Delta t= t_{\rm e}-t_0$ ) and a limited $\theta-$ interval around the equator. Four cases are investigated here. In case A, we considered a range of different time intervals for the flux emergence, keeping the total amount of emerged magnetic flux (determined by the parameter ( $c_{{\rm e}}$ ) fixed. In case B, on the other hand, we keep the time interval, i.e. the parameter $t_{{\rm e}}$ , fixed and vary the amount of emerged magnetic flux in this interval, thereby again changing the flux emergence rate. Then, in case C both parameters $c_{{\rm e}}$ (the amount of flux) and $t_{{\rm e}}$ (the flux emergence time interval) are varied proportionally so that the flux emergence rate remains constant in this case. Finally, in case D we combine the largest amount of magnetic flux with the fastest flux emergence rate and the smallest amount of total flux with the slowest flux emergence rate. Hence, in this last case we get more extreme combinations and we cover a much larger flux emergence rate interval, spanning almost two orders of magnitude. The total magnetic flux, before we start emerging addition flux, amounts to $37.85\times10^{23}\;$ Mx in the Northern hemisphere.

$\begin{figure} \mbox{\includegraphics[bbllx=112pt,bblly=20pt,bburx=372pt,bbury=5... ...ly=20pt,bburx=372pt,bbury=501pt,width=144 pt,clip=]{4719fg04.ps} }\end{figure}$	Figure 3: The plasma density $\log_{10}~\rho$ (grey scale) and magnetic field lines at t=33.0 ( left) and at t=38.0 ( right, with a different scale on the abscissa) for the case with $t_{\rm e}=32.1357$ .
Open with DEXTER

4.1 Case A: varying flux emergence rate, fixed $c_{{\rm e}}$ (total flux)

We first consider different values of the parameter $t_{{\rm e}}$ in Eq. (5). The parameter $c_{{\rm e}}$ in Eq. (5) is set to -3 in all simulations so that the total amount of emerged flux is the same in all simulations of case A, viz. $2 \pi~c_{\rm e}~\psi_0\approx -6.6\times10^{22}\;$ Mx in the Northern hemisphere, and the exact opposite in the Southern hemisphere. This is 1.7437% of the initial flux. Notice that we have assumed axi-symmetry in the present model. Therefore, the total amount of emerged flux is larger than the amounts of flux emerging on the real sun. When comparing the two, one should take into account that on the real sun the flux emergence region is also limited in the $\varphi$ -direction and not only in the $\theta$ -direction, as in our model. This means that for comparison with real data the fluxes mentioned in the present paper have to be re-scaled by a factor $\Delta\varphi / 2\pi$ , where $\Delta\varphi$ denotes the width of the active region in the $\varphi$ -direction. Considering a flux emergence region with $\Delta\varphi =\pi/6$ , e.g., the mentioned total amount of flux emergence would be only $-6.6\times10^{22}\;$ Mx $\times \frac{1}{12} = -5.5\times10^{21}\;$ Mx.

The time-dependence of the flux emergence is linear as is clear from Eq. (5). The magnetic flux is emerged from time t=t₀ to $t=t_{\rm e}$ where t₀=32 and $\Delta t= t_{\rm e}-t_0$ is taken as 0.1357, 0.4072, and 1.2217, respectively. Hence, we effectively change the flux emergence rate, i.e. $2\pi~c_{\rm e}~\psi_0/\Delta t$ , in this parameter study as the same amount of flux is emerged in a time interval ranging from 10 $\;$ min to 90 $\;$ min. The flux emergence rate thus varies from $1.10\times10^{20}\;$ Mx/s (for $t_{\rm e}=32.1357$ , i.e. $\Delta t=10\;$ min) to $1.22\times10^{19}\;$ Mx/s (for $t_{\rm e}=33.2217$ , i.e. $\Delta t=90\;$ min). Note that the emerging magnetic flux has the opposite polarity from the ambient coronal magnetic field.

The effect of the applied flux emergence is is illustrated in Fig. 3. As the new magnetic flux emerges near the neutral line, magnetic field line reconnections take place below the flux rope leading to a partial magnetic flux cancelation. This, in turn, results in the loss of the equilibrium force balance. Consequently, the flux rope starts moving upwards and the region below the flux rope is evacuated and suffers a pressure drop. Therefore, magnetized plasma at both sides (left and right from the null point) is seen to move inward and a current sheet is formed in this extending region as the CME moves further upward. A clearly formed current sheet below the flux rope can be seen in Fig. 3. The current in the sheet has the same direction as that in the flux rope and, therefore, flux rope feels a downward Lorentz force due to this sheet current. With a finite resistivity, the current sheet would be dissipated and the escaping flux rope thus should be accelerated more than in this ideal MHD simulation. However, our numerical scheme, as any numerical scheme, introduces some numerical diffusion. The numerical diffusion may be higher than the real diffusion in the hot coronal plasma which is known to be extremely small.

The corresponding height-time curves of the center of the simulated flux rope ejections (i.e. defined as location of the magnetic axis) are shown in Fig. 4. It is clear that the flux emergence rate influences the velocity and the acceleration of the flux rope. From the height-time curves, one can easily derive these velocities. The related velocities are shown in Fig. 5. Note that we used a simple finite difference method to determine the derivative of the height-time curves, which yields the erratic oscillations in the velocity curves, which could be smoothed out. Clearly, an increasing the flux emergence rate leads to a higher initial acceleration and thus a higher upward speed of the flux rope while the total amount of emerged flux is same in all cases. The obtained velocities are in the range about 200-300 km s^-1, which is below the typical range for CMEs. Figure 5 also illustrates that the velocities at which the flux ropes are expelled are not constant in time. The triggered CMEs are first accelerated and then quickly decelerate due to the gravitational force that is working on the launched CME. In the next subsection we will see that this deceleration can even lead to negative velocities, i.e. to flux ropes falling back to the Sun.

4.2 Case B: varying flux emergence rate, fixed $t_{{\rm e}}$ (time interval)

$\begin{figure} \par\includegraphics[width=8.2cm,clip]{4719fg05.ps} \end{figure}$	Figure 4: Height (in $R_\odot$ ) of the flux rope center versus time (in hours) for the different flux emergence rates in case A (until the flux rope center leaves the computational domain).
Open with DEXTER

The resulting height-time curves of the flux rope center of mass and the time dependence of the related flux rope velocities are shown in Figs. 6 and 7, respectively. Clearly, for the highest flux emergence rate (obtained for $c_{\rm e}=-9$ ), we now get a fast acceleration of the flux rope up to a velocity of 450 $\;$ km s^-1 which is reached in less than one hour after the onset of the flux emergence. However, after this fast acceleration, the flux rope again gradually decelerates due to the effect of gravity. Of course, for lower flux emergence rates (i.e. smaller values of $\vert c_{\rm e}\vert$ ), we get less acceleration and thus slower CMEs.

Table 1: Parameter study: effect of changing the $c_{{\rm e}}$ and $t_{{\rm e}}$ values on the flux emergence rate. Case A corresponds to third row, case B to the third column, while case C corresponds to the main diagonal of the table and case D to the off-diagonal.

$\begin{figure} \par\includegraphics[width=8.7cm,clip]{4719fg06.ps} \end{figure}$	Figure 5: Velocity of the flux rope center versus time for different flux emergence rates in case A (until the flux rope center leaves the computational domain).
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.3cm,clip]{4719fg07.ps} \end{figure}$	Figure 6: Height (in $R_\odot$ ) of the flux rope center versus time (in hours) for the different flux emergence rates in case B.
Open with DEXTER

In Fig. 6 we see that, for an emerging flux rate that is smaller than some threshold value, the flux rope can not escape from the corona: it falls down (back to the Sun), again as a result of the deceleration due to gravity (see the lowest curve in the figure). The corresponding negative velocity of the flux rope, falling back to the Sun, is seen in Fig. 7. We remark that such a case has actually been observed recently by Wang & Sheeley (2002). Note that the flux rope then bounces up and down. At first sight, this behaviour looks very similar to that of the flux rope in our simulations with small amounts of emerging flux ( $c_{\rm e}=-1$ ). However, the dynamics of the observed flux rope are actually a direct consequence of the line-tying boundary conditions which make the flux rope oscillate in the vertical direction.

$\begin{figure} \par\includegraphics[width=8.4cm,clip]{4719fg08.ps} \end{figure}$	Figure 7: Velocity of the flux rope center versus time for different flux emergence rates in case B.
Open with DEXTER

4.3 Case C: fixed flux emergence rate, varying $t_{{\rm e}}$ and $c_{{\rm e}}$

In case C, we make different combinations of the values of the parameters $c_{{\rm e}}$ and $t_{{\rm e}}$ in order to keep the magnetic flux emergence rate, i.e. $2\pi\psi_0c_{\rm e}/(t_{\rm e}-t_0)$ in Eq. (5), constant. This is achieved by increasing $\vert c_{\rm e}\vert$ and $t_{\rm e}-t_0$ proportionally (by factors of 3, as in cases A and B, but now simultaneously). The time interval of the flux emergence, $\Delta t= t_{\rm e}-t_0$ , is taken equal to $10\;$ min, $30\;$ min, and $90\;$ min, respectively (i.e. the same values as considered in case A). For the parameter $c_{{\rm e}}$ we considered again the values -1, -3, and -9 (as in case B). The constant flux emergence rate thus is $3.67\times10^{19}\;$ Mx/s in this case. An overview of the considered parameter combinations and the resulting flux emergence rates in the three cases is given in Table 1. The corresponding height-time curves of flux rope center of mass and the corresponding flux rope velocities versus time are shown in Figs. 8 and 9, respectively. Clearly, for the longest flux emergence interval (90 $\;$ min), i.e. the largest amount of total emerged flux ( $-1.98\times10^{23}\;$ Mx), we now get an acceleration up to a velocity of slightly more than 300 $\;$ km s^-1, again decreasing quickly after this maximum, however.

4.4 Case D: varying flux emergence rate, extreme cases

For lower flux emergence rates, we get slower CMEs. Again, in Fig. 8 we see that, for a total emerged flux that is smaller than some threshold value, the flux rope can not escape from the solar corona: after a while it falls down again as a result of the deceleration due to gravity (see the lowest curve in the figure). The corresponding negative velocity of the flux rope, falling back to the Sun, is seen in Fig. 9. The flux rope again starts a slowly damped oscillation (see case B section). Finally, we again make different combinations of the values of the parameters $c_{{\rm e}}$ and $t_{{\rm e}}$ , but now we combine the smallest total emerged flux ( $c_{\rm e}=-1$ , i.e. $-2.2\times10^{22}\;$ Mx) with the slowest flux emergence ( $t_{\rm e}=1.2217$ , i.e. $\Delta t=90\;$ min) and the largest total emerged flux ( $c_{\rm e}=-9$ , i.e. $-1.98\times10^{23}\;$ Mx) with the fastest flux emergence ( $t_{\rm e}=0.1357$ , i.e. $\Delta t=10\;$ min). As a result, in this case the magnetic flux emergence rate now varies over a much wider range, viz. $4.07\times10^{18}\;$ Mx/s to $3.30\times10^{20}\;$ Mx/s (almost two orders of magnitude). In the overview of the considered parameter combinations and the resulting flux emergence rates given in Table 1, case D corresponds to the off-diagonal.

The corresponding height-time curves of flux rope center of mass and the corresponding flux rope velocities versus time are shown in Figs. 10 and 11, respectively. Clearly, the shortest flux emergence interval (10 $\;$ min) combined with the largest amount of total emerged flux ( $-1.98\times10^{23}\;$ Mx), we now get an acceleration up to a velocity of slightly more than 600 $\;$ km s^-1, again decreasing quickly after this maximum, however. For the lowest flux emergence rate, $4.07\times10^{18}\;$ Mx/s, the flux rope can again not escape from the solar corona and after a while it falls back to the Sun (see the lowest curve in Fig. 10). The corresponding negative velocity of the flux rope, falling back to the Sun, is seen in Fig. 11. The flux rope again starts a slowly damped oscillation, but with a much smaller amplitude in this extreme case.

5 Discussion and conclusion

The present numerical simulations and parameter study was inspired by the work of Chen & Shibata (2000). These authors considered an equilibrium in a 2D Cartesian box, consisting of a background plasma with a homogeneous density (no gravity) and a quadripole magnetic field. They superposed a flux rope on this background plasma and kept in in equilibrium by means of an image current below the lower edge of the box (corresponding to the photosphere on the Sun). By emerging reconnection favourable magnetic flux from this lower edge, the flux rope is then driven unstable and is launched upwards at a certain velocity. In the present paper, this CME initiation model of Chen & Shibata (2000) has been extended by including the effects of gravity, spherical geometry (curvature) in 2.5D (i.e. assuming axi-symmetry), and a stratified ambient medium. Moreover, we studied the effect of the flux emergence rate on the velocity of the resulting flux rope CMEs by changing the values of the parameters $c_{{\rm e}}$ (affecting the total amount of emerged magnetic flux) and $t_{{\rm e}}$ (affecting the time interval of the flux emergence). Hence, when the parameter $c_{{\rm e}}$ is kept constant while the parameter $t_{{\rm e}}$ is varied, the flux emergence rate varies. This is what we did in case A.

$\begin{figure} \par\includegraphics[width=8.4cm,clip]{4719fg09.ps} \end{figure}$	Figure 8: Height (in $R_\odot$ ) of the flux rope center versus time (in hours) for the fixed flux emergence rates (case C).
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.4cm,clip]{4719fg10.ps} \end{figure}$	Figure 9: Velocity of the flux rope center versus time for fixed flux emergence rates (case C).
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{4719fg11.ps} \end{figure}$	Figure 10: Height (in $R_\odot$ ) of the flux rope center versus time (in hours) for the extreme flux emergence rate range (case D).
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{4719fg12.ps}\end{figure}$	Figure 11: Velocity of the flux rope center versus time for very different flux emergence rates (case D).
Open with DEXTER

Comparing to the two upper curves of Fig. 9, which correspond to the case with the same flux emergence rate but a tripled amount of emerged flux, we see that tripling the total amount of emerged flux has a more substantial effect on the maximal velocity of the flux rope: it now increases by a factor of about 50%, i.e. more than in the first case, but less than in the second case.

The present model can not explain very fast CMEs, probably because our model is only 2.5D and, moreover, we did not take the effect of a background wind into account. The latter extension of the model is our next aim.

The initiation of coronal mass ejections by magnetic flux emergence