A&A 459, 423-440 (2006)
DOI: 10.1051/0004-6361:20065720
G. Battaglia1 - E. Tolstoy1 - A. Helmi1 - M. J. Irwin2 - B. Letarte1 - P. Jablonka3 - V. Hill4 - K. A. Venn5 - M. D. Shetrone6 - N. Arimoto7 - F. Primas8 - A. Kaufer9 - P. Francois4 - T. Szeifert9 - T. Abel10 - K. Sadakane11
1 - Kapteyn Institute, University of Groningen,
Postbus 800, 9700AV Groningen, The Netherlands
2 -
Institute of Astronomy, University of Cambridge,
Madingley Road, Cambridge CB3 0HA, UK
3 -
Observatoire de Genève, Laboratoire d'Astrophysique de
l'École Polytechnique Fédérale de Lausanne (EPFL), 1290 Sauverny, Switzerland
4 -
Observatoire de Paris-Meudon, 92195 Meudon Cedex, France
5 -
Department of Physics and Astronomy, University of Victoria, 3800 Finnerty Road,
Victoria, BC, V8P 1A1, Canada
6 -
University of Texas, McDonald Observatory, USA
7 -
National Astronomical Observatory, 2-21-1 Osawa,
Mitaka, Tokyo 181-8588, Japan
8 -
European Southern Observatory,
Karl-Schwarzschild str 2, 85748 Garching bei München, Germany
9 -
European Southern Observatory,
Alonso de Cordova 3107, Vitacura, Casilla 19001, Santiago, Chile
10 -
Kavli Institute for Particle Astrophysics and Cosmology, Department of Physics and Stanford Linear Accelerator Center, Stanford University, 2575 Sand Hill Road, Menlo Park, CA 94044, USA
11 -
Astronomical Institute, Osaka Kyoiku University, Kashiwara-shi,
Osaka 581-8582, Japan
Received 29 May 2006 / Accepted 26 July 2006
Abstract
Aims. As part of the DART project we have used the ESO/2.2m Wide Field Imager in conjunction with the VLT/FLAMES![]() GIRAFFE spectrograph to study the detailed properties of the resolved stellar population of the Fornax dwarf spheroidal galaxy out to and beyond its tidal radius. Fornax dwarf spheroidal galaxy has had a complicated evolution and contains significant numbers of young, intermediate age and old stars. We investigate the relation between these different components by studying their photometric, kinematic and abundance distributions.
GIRAFFE spectrograph to study the detailed properties of the resolved stellar population of the Fornax dwarf spheroidal galaxy out to and beyond its tidal radius. Fornax dwarf spheroidal galaxy has had a complicated evolution and contains significant numbers of young, intermediate age and old stars. We investigate the relation between these different components by studying their photometric, kinematic and abundance distributions.
Methods. We re-derived the structural parameters of the Fornax dwarf spheroidal using our wide field imaging covering the galaxy out to its tidal radius, and analysed the spatial distribution of the Fornax stars of different ages as selected from colour-magnitude diagram analysis. We have obtained accurate velocities and metallicities from spectra in the Ca II triplet wavelength region for 562 Red Giant Branch stars which have velocities consistent with membership of the Fornax dwarf spheroidal.
Results. We have found evidence for the presence of at least three distinct stellar components: a young population (few 100 Myr old) concentrated in the centre of the galaxy, visible as a Main Sequence in the colour-magnitude diagram; an intermediate age population (2-8 Gyr old); and an ancient population (>10 Gyr), which are distinguishable from each other kinematically, from the metallicity distribution and in the spatial distribution of stars found in the colour-magnitude diagram.
Conclusions. From our spectroscopic analysis we find that the "metal rich'' stars (
![]() )
show a less extended and more concentrated spatial distribution, and display colder kinematics than the "metal poor'' stars (
)
show a less extended and more concentrated spatial distribution, and display colder kinematics than the "metal poor'' stars (
![]() ). There is tentative evidence that the ancient stellar population in the centre of Fornax does not exhibit equilibrium kinematics. This could be a sign of a relatively recent accretion of external material, such as the merger of another galaxy or other means of gas accretion at some point in the fairly recent past, consistent with other recent evidence of substructure (Coleman et al. 2004, AJ, 127, 832; 2005, AJ, 129, 1443).
). There is tentative evidence that the ancient stellar population in the centre of Fornax does not exhibit equilibrium kinematics. This could be a sign of a relatively recent accretion of external material, such as the merger of another galaxy or other means of gas accretion at some point in the fairly recent past, consistent with other recent evidence of substructure (Coleman et al. 2004, AJ, 127, 832; 2005, AJ, 129, 1443).
Key words: galaxies: dwarf - galaxies: individual: Fornax - galaxies: kinematics and dynamics - galaxies: stellar content - galaxies: Local Group - stars: abundances
Similarly to Sagittarius, Fornax has its own globular cluster
population, but contrary to Sagittarius all of the Fornax globular
clusters appear to be metal poor (e.g. Letarte et al. 2006a; Strader et al. 2003).
Fornax is known to contain a large number of carbon
stars with a wide range of bolometric luminosities indicating
significant mass (and hence age) dispersion at intermediate ages
(e.g. Stetson et al. 1998; Azzopardi et al. 1999; Aaronson & Mould 1980; Demers & Kunkel 1979). This is supported
by a well populated intermediate age sub-giant branch and red clump.
Fornax also contains a sizable population of RR Lyrae variable stars
with an average metallicity of [Fe/H]
![]() (Bersier & Wood 2002). From detailed colour-magnitude
diagram (CMD) analysis (e.g. Stetson et al. 1998; Saviane et al. 2000; Pont et al. 2004; Buonanno et al. 1999)
it is clear that, unlike most dSphs in the Local Group,
Fornax has had a long history of star formation, which only
ceased a few hundred Myr ago. However,
in common with most dSph galaxies, Fornax does not appear to have any HI gas at present
(e.g. Young 1999). It is difficult to understand how Fornax lost all it gas.
It is possible that, as a consequence of the recent star
formation, the gas is fully ionized; however detections of ionized gas
are difficult.
(Bersier & Wood 2002). From detailed colour-magnitude
diagram (CMD) analysis (e.g. Stetson et al. 1998; Saviane et al. 2000; Pont et al. 2004; Buonanno et al. 1999)
it is clear that, unlike most dSphs in the Local Group,
Fornax has had a long history of star formation, which only
ceased a few hundred Myr ago. However,
in common with most dSph galaxies, Fornax does not appear to have any HI gas at present
(e.g. Young 1999). It is difficult to understand how Fornax lost all it gas.
It is possible that, as a consequence of the recent star
formation, the gas is fully ionized; however detections of ionized gas
are difficult.
A recent proper motion estimate suggests that Fornax has a low eccentricity polar orbit that crossed the path of the Magellanic Stream about 190 Myr ago (Dinescu et al. 2004), and that the excess of small scale structure in the Magellanic Stream, tracing back along the proposed orbit of Fornax, comes from gas lost by Fornax during this encounter. The authors propose this encounter as a viable mechanism to make Fornax lose its gas and stop forming stars. However, previous proper motion measurements do not suggest such an encounter (Piatek et al. 2002).
Fornax has been the centre of some attention recently for the discovery, in photometric surveys, of stellar over-densities in and around the system (Coleman et al. 2005,2004; Olszewski et al. 2006). These over-densities have been interpreted by Coleman et al. as shell structures caused by the recent capture of a small galaxy by Fornax.
There have been previous spectroscopic studies of individual
stars in Fornax.
Studies of kinematic properties
indicated a (moderate) central mass-to-light ratio
![]() (
(
![]() )
)![]() ,
possibly as high as 26 (e.g. Mateo et al. 1991),
and a global
,
possibly as high as 26 (e.g. Mateo et al. 1991),
and a global
![]() -40 larger than the
-40 larger than the
![]() of the luminous component (Walker et al. 2006).
This is much higher than is typical for globular clusters, which have
mass-to-light ratios in the range 1-3 (e.g. McLaughlin & van der Marel 2005),
but
considerably lower than that found for many other dSphs such as Draco and
Ursa Minor (M/L > 100 (
of the luminous component (Walker et al. 2006).
This is much higher than is typical for globular clusters, which have
mass-to-light ratios in the range 1-3 (e.g. McLaughlin & van der Marel 2005),
but
considerably lower than that found for many other dSphs such as Draco and
Ursa Minor (M/L > 100 (
![]() )
)![]() )
(e.g. Kleyna et al. 2003; Wilkinson et al. 2004).
)
(e.g. Kleyna et al. 2003; Wilkinson et al. 2004).
There have
been two previous Ca II triplet (CaT) studies of Red Giant Branch (RGB) stars in the
central region of Fornax (33 stars, Tolstoy et al. 2001; 117 stars, Pont et al. 2004),
both using VLT/FORS1. There are also detailed
abundance studies of 3 field stars
(Shetrone et al. 2003) and 9 globular cluster
stars (Letarte et al. 2006a) made with VLT/UVES. This is about to be
extended dramatically by VLT/FLAMES (![]() 100 stars, Letarte et al. 2006b).
These spectroscopic studies conclude that the bulk of the stellar population is more
metal rich than could be inferred from the position of the
RGB in the CMD, with a peak at
100 stars, Letarte et al. 2006b).
These spectroscopic studies conclude that the bulk of the stellar population is more
metal rich than could be inferred from the position of the
RGB in the CMD, with a peak at
![]() ,
a metal
poor tail extending out to
,
a metal
poor tail extending out to
![]() and a metal rich tail
extending beyond
and a metal rich tail
extending beyond
![]() with more than half the stars on the
RGB having ages <4 Gyr.
with more than half the stars on the
RGB having ages <4 Gyr.
Here we present the first results of a study of the Fornax dSph from
the Dwarf Abundances and Radial velocities Team (DART) large programme
at ESO.
The aim of DART is to analyse the chemical and kinematic behaviour of individual stars
in a representative
sample of dSphs in the Local Group, in order to derive their star formation and
chemical enrichment histories, and explore the kinematic status of these objects
and their mass distribution. Our targets are Sculptor (Tolstoy et al. 2004),
Fornax and Sextans dSphs. From our large program at ESO we obtained for each of these
galaxies: extended WFI imaging; intermediate resolution VLT/FLAMES spectra in the CaT region
to derive metallicity and velocity measurements for a large sample of RGB stars covering
an extended
area; and VLT/FLAMES high resolution
spectra in the central regions, which give detailed abundances over a large range of elements
for ![]() 100 RGB stars.
100 RGB stars.
In this work we present our results for both wide field imaging and
intermediate resolution FLAMES spectroscopy for 562 RGB kinematic members of Fornax
out to the tidal radius. The relatively high
signal-to-noise (
![]() -20 per Å) of our data has enabled
us to derive both accurate metallicities (
-20 per Å) of our data has enabled
us to derive both accurate metallicities (
![]() 0.1 dex from internal errors) and radial velocities (to
0.1 dex from internal errors) and radial velocities (to ![]()
![]() 2 km s-1). We can thus study the different stellar populations in
Fornax and how their metallicities and kinematic properties vary spatially
with a much larger sample than any previous study. Our study differs
from Walker et al. (2006) in that we have both abundance and kinematics and
this has been shown to be crucial information for disentangling
complicated galaxy properties (Tolstoy et al. 2004).
2 km s-1). We can thus study the different stellar populations in
Fornax and how their metallicities and kinematic properties vary spatially
with a much larger sample than any previous study. Our study differs
from Walker et al. (2006) in that we have both abundance and kinematics and
this has been shown to be crucial information for disentangling
complicated galaxy properties (Tolstoy et al. 2004).
In future works we will present our CaT calibration (Battaglia et al. 2006b), detailed kinematic modelling of Fornax dSph (Battaglia et al. 2006a) and accurate star formation history from our VLT/FLAMES high resolution abundances of Fornax (Letarte et al. 2006b).
Image reduction and analysis was based on the pipeline processing software developed by the Cambridge Astronomical Survey Unit for dealing with imaging data from mosaic cameras. Details of the pipeline processing can be found in Irwin (1985), Irwin & Lewis (2001) and Irwin et al. (2004). Each set of frames for a particular field is processed individually to remove gross instrumental artefacts (i.e. bias-corrected, trimmed, flatfielded, and defringed as necessary). An object catalogue is then constructed and used to derive accurate astrometric transformations to enable stacking of multiple images for each field in a common coordinate system. The stacked images, produced from a sequence of 3 dithered exposures, are then used to generate the final object catalogues, and the astrometric information is updated.
The astrometric solutions are based on a general Zenithal Polynomial projection
(e.g. Greisen & Calabretta 2002), which for the ESO WFI is particularly simple
since the radial distortion is effectively zero. Astrometric standard stars
were selected automatically from APM scans of UKST photographic survey plates
(http://www.ast.cam.ac.uk/casu) which in turn are calibrated with respect to
TYCHO 2. Each of the 8 detectors making up the mosaic is solved for
independently using a 6 constant linear solution linking detector x, y to
projected celestial coordinates. Residuals in the fit per star are
typically ![]() 200 mas, which is almost entirely due to the random error
in the photographic astrometry. Even in the outer parts of Fornax there are
more than 100 plate-based standards per detector which means that any
systematic errors in the solution are negligible (<100 mas).
200 mas, which is almost entirely due to the random error
in the photographic astrometry. Even in the outer parts of Fornax there are
more than 100 plate-based standards per detector which means that any
systematic errors in the solution are negligible (<100 mas).
Objects are morphologically classified on each stacked frame as either
noise artefacts, galaxies, or stars, primarily according to the properties
of the curve-of-growth light distribution using a series of aperture fluxes.
At the same time aperture corrections for stellar profiles are derived at
the detector level to enable accurate (![]() 1%) conversion to total
fluxes.
1%) conversion to total
fluxes.
The internal gain correction, applied at the flatfielding stage, ensures
a common photometric system across the mosaic (to ![]() 1%) and hence
photometric calibration simplifies to finding a single magnitude zero-point
for each science observation. A correction for scattered light, which
affects the flatfielding in addition to the science images for WFI data,
was also made. This was directly derived from the standard star observations
assuming a radially symmetric effect. This is a well-known problem with the
WFI (Manfroid & Selman 2001) and the correction was made prior to the
photometric calibration.
1%) and hence
photometric calibration simplifies to finding a single magnitude zero-point
for each science observation. A correction for scattered light, which
affects the flatfielding in addition to the science images for WFI data,
was also made. This was directly derived from the standard star observations
assuming a radially symmetric effect. This is a well-known problem with the
WFI (Manfroid & Selman 2001) and the correction was made prior to the
photometric calibration.
The first-pass photometric calibration is based on observations of
photometric standard fields taken during the same nights as the target
observations. Since these observations were undertaken
in service mode in mainly photometric conditions, we used the default La Silla
extinction for these passbands to derive an airmass correction (the range
in airmass and number of the standard star observations precluded any other
option). The colour equations to correct the data to the Johnson-Cousins system were
taken from the ESO web pages. Each photometric standard field observed
contains between ![]() 10-50 suitable standards and provides a single
zero-point with better than
10-50 suitable standards and provides a single
zero-point with better than ![]() 1% random error; assorted systematic
errors (e.g. aperture corrections, flatfielding gradients, scattered light
correction) contribute at about the same level.
1% random error; assorted systematic
errors (e.g. aperture corrections, flatfielding gradients, scattered light
correction) contribute at about the same level.
The zero-point trend over all the service observing is consistent within
the errors ![]() 1-2% with photometric conditions on all nights apart from
the standard star observation for the night of 2005 Jan 31st. Since no
science target frames were taken during this night this data point was
ignored and a constant zero-point adopted for both the V- and I-band
images. (Note that this was also the night with very poor seeing.)
1-2% with photometric conditions on all nights apart from
the standard star observation for the night of 2005 Jan 31st. Since no
science target frames were taken during this night this data point was
ignored and a constant zero-point adopted for both the V- and I-band
images. (Note that this was also the night with very poor seeing.)
As a final check of the overall calibration the overlap (![]() 5%)
between adjacent fields was used to determine the internal consistency of the
magnitude system and small
5%)
between adjacent fields was used to determine the internal consistency of the
magnitude system and small ![]()
![]() 2% adjustments were made to bring
all the observations to a common scale. This ensures that the whole
system is on the same photometric zero-point, which is essential for analysis
of large scale structure.
The final sensitivity of all the images is the same within 0.1 mag.
2% adjustments were made to bring
all the observations to a common scale. This ensures that the whole
system is on the same photometric zero-point, which is essential for analysis
of large scale structure.
The final sensitivity of all the images is the same within 0.1 mag.
The final step was to merge all the object catalogues in the V- and I-band to produce a unique set of object detections for the whole area studied. In the case of multiple measurements for a given object the one with the smallest error estimates were used. This catalogue forms the basis for all subsequent photometric and spectroscopic analysis.
The final sample was carefully checked to weed out any spurious objects (e.g. broken fibres, background galaxies, foreground stars, etc.). We removed 6 objects because they were inadvertently assigned to fibres which were not available during our observing runs; we found no background galaxies and removed 12 objects because the continuum shape or the presence of very broad absorption line was not consistent with what is expected for RGB stars spectra. Excluding the objects that did not meet our S/N and velocity error criteria, our final sample of acceptable measurements consists of 641 stars.
In this section we present the results of our wide field,
ESO/WFI photometry of Fornax, out to
its nominal tidal radius (see Fig. 1), and going down to V= 23 and
I= 22 (
MI= 1.2).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{5720f1.eps} %\end{figure}](/articles/aa/full/2006/44/aa5720-06/Timg58.gif) |
Figure 1:
ESO/WFI coverage for Fornax dSph. The inner shell-like feature detected by Coleman et al. (2004)
is located at
|
| Open with DEXTER | |
Previous studies have revealed the spatial structure
of Fornax to be far from regular. Hodge (1961), using photographic plates,
found that the ellipticity (defined as e= 1- b/a, where b and a
are respectively the semi-minor and semi-major axes of the galaxy)
increases with radius, from a value of 0.21 in the central regions to 0.36
in the outer parts.
Irwin & Hatzidimitriou (1995) noticed that in the inner regions the isopleths
showed departures from elliptical symmetry and that they were more closely spaced
on the east side of the major axis than on the west, as already noticed by Hodge (1961).
The asymmetry was found to be centred close to cluster 4 (
![]() ,
,
![]() in
Fig. 1). The ellipticity was again found to
increase with radius.
Coleman et al. (2005), using only RGB stars, found that the position
of the centre shifts 3' towards west within a radius of 20' and 4' towards south
at all radii. For radii larger than 35' they find an opposite trend for the ellipticity,
i.e. the outer contours become more circular.
in
Fig. 1). The ellipticity was again found to
increase with radius.
Coleman et al. (2005), using only RGB stars, found that the position
of the centre shifts 3' towards west within a radius of 20' and 4' towards south
at all radii. For radii larger than 35' they find an opposite trend for the ellipticity,
i.e. the outer contours become more circular.
Due to the variety of previous estimates, sometimes differing significantly from each other, we
decided to re-derive the structural parameters of Fornax dSph. We divided the 2D
spatial distribution of the stellar objects in our photometry
(Fig. 1) into a grid with a "pixel''
width of 0.02 deg and associated with each pixel the number of stars it contained.
We then used the IRAF task ELLIPSE to derive the variation with radius of the
central position, ellipticity and position angle (Fig. 2),
by fitting ellipses at radii between 15' and 60' with a ![]() 5' spacing.
We find that the centre is at (
5' spacing.
We find that the centre is at (
![]() ,
,
![]() )
= (
)
= (
![]() ,
,
![]() ),
west (
),
west (
![]() )
and
south (
)
and
south (
![]() )
with respect to the values listed in Mateo (1998).
The centre now appears to be located very close to cluster 4.
With this new analysis
the ellipticity, with an average value
)
with respect to the values listed in Mateo (1998).
The centre now appears to be located very close to cluster 4.
With this new analysis
the ellipticity, with an average value
![]() ,
does not show any trend with radius.
The position angle (PA) appears to be larger in the inner 15' and then to become
approximately constant with radius. A larger position angle for the inner region could be
caused, for example, by the presence of cluster 4 or, more likely, by
the presence of young stars
with a markedly different distribution (see Sect. 3.3). In our subsequent analysis we adopt
the average value of the PA to be 46.8
,
does not show any trend with radius.
The position angle (PA) appears to be larger in the inner 15' and then to become
approximately constant with radius. A larger position angle for the inner region could be
caused, for example, by the presence of cluster 4 or, more likely, by
the presence of young stars
with a markedly different distribution (see Sect. 3.3). In our subsequent analysis we adopt
the average value of the PA to be 46.8
![]() ,
consistent
with previous estimates. Our re-derived structural parameters are listed in Table 2.
With the exception of the position of the centre of the galaxy,
all the derived parameters are consistent with the values listed by Mateo (1998).
,
consistent
with previous estimates. Our re-derived structural parameters are listed in Table 2.
With the exception of the position of the centre of the galaxy,
all the derived parameters are consistent with the values listed by Mateo (1998).
We also rederived the
surface density profile for Fornax in bins
of 3' out to a radius of 83' (see Fig. 3).
The contamination by
field star density, from a weighted average of the
points beyond 68', is
![]() stars arcmin-2.
From previous estimates of the tidal radius (e.g. Irwin & Hatzidimitriou 1995)
we know that it is unlikely that our data extend out to
a pure background region. Thus our determination of the Galactic contamination
is of necessity an overestimate due to our limited spatial coverage.
We compared this Galactic contamination-subtracted profile
to several surface brightness models using a least-square fit to the data.
We used an empirical King profile (King 1962),
an exponential profile,
a Sersic profile (Sersic 1968) and a Plummer model (Plummer 1911).
stars arcmin-2.
From previous estimates of the tidal radius (e.g. Irwin & Hatzidimitriou 1995)
we know that it is unlikely that our data extend out to
a pure background region. Thus our determination of the Galactic contamination
is of necessity an overestimate due to our limited spatial coverage.
We compared this Galactic contamination-subtracted profile
to several surface brightness models using a least-square fit to the data.
We used an empirical King profile (King 1962),
an exponential profile,
a Sersic profile (Sersic 1968) and a Plummer model (Plummer 1911).
![\begin{figure}
\par\includegraphics[width=4.2cm,clip]{5720f2a.eps}\includegraphi...
...m,clip]{5720f2c.eps}\includegraphics[width=4.2cm,clip]{5720f2d.eps}
\end{figure}](/articles/aa/full/2006/44/aa5720-06/Timg65.gif) |
Figure 2:
The variation with radius of the central position (x and y coordinate,
a) and b) respectively), c) ellipticity and d) position angle for the entire stellar population of Fornax, from ESO/WFI imaging data. The variation of
the central position is with respect to the value listed in Mateo (1998). We find that the centre is at
|
| Open with DEXTER | |
Table 2: Table of Fornax parameters. 1. This work. 2. Mateo et al. (1998). The position angle is defined as the angle between North and the major-axis of the galaxy measured counter-clockwise; the ellipticity is e= 1 - b/a.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{5720f3.eps}
\end{figure}](/articles/aa/full/2006/44/aa5720-06/Timg73.gif) |
Figure 3:
The surface density profile for Fornax dSph galaxy with overlaid
best-fitting King, Sersic, exponential and Plummer models
(solid, dashed, dotted, dash-dot lines, respectively). The Galactic stellar contamination,
|
| Open with DEXTER | |
The King model has been extensively used to describe the
surface density profile of dSphs.
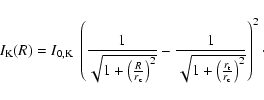 |
(1) |
Table 3:
Parameters of best-fitting King model (core radius, ![]() ,
tidal radius,
,
tidal radius, ![]() ),
Sersic model (Sersic radius,
),
Sersic model (Sersic radius, ![]() ,
shape parameter, m), exponential model (scale radius,
,
shape parameter, m), exponential model (scale radius, ![]() )
and Plummer model (scale radius, b)
for all stellar populations, intermediate age and old stellar components in Fornax dSph. For each model
we also compute the half-number radius,
)
and Plummer model (scale radius, b)
for all stellar populations, intermediate age and old stellar components in Fornax dSph. For each model
we also compute the half-number radius, ![]() ;
for the Plummer model this coincides with b. The
errors in the parameters are formal errors from the fitting procedure.
;
for the Plummer model this coincides with b. The
errors in the parameters are formal errors from the fitting procedure.
Another possibility to explain the excess of stars in the outer parts
of dSphs is that the King model
does not provide the best representation of the data at large radii.
The Sersic profile is known to provide a good empirical formula to fit the projected light distribution of
elliptical galaxies and
the bulges of spiral galaxies (e.g. Graham & Guzmán 2003; Trujillo et al. 2004; Caldwell 1999; Caon et al. 1993):
![\begin{displaymath}I_{\rm S}(R)= I_{\rm0,S} \exp \left[ - \left(\frac{R}{R_{\rm S}}\right)^{1/m}\right]
\end{displaymath}](/articles/aa/full/2006/44/aa5720-06/img83.gif) |
(2) |
In our analysis, King and Sersic profiles reproduce the data
much better than a Plummer or an exponential profile. Our best fit
is a Sersic profile with Sersic radius,
![]() arcmin, and m= 0.71, thus steeper than an exponential (Fig. 3).
arcmin, and m= 0.71, thus steeper than an exponential (Fig. 3).
For the best-fitting King model we find a core radius
![]() arcmin and a tidal radius
arcmin and a tidal radius
![]() arcmin.
The core radius determined here is 4' larger than previous estimates
whilst the tidal radius is
in agreement with the value of
arcmin.
The core radius determined here is 4' larger than previous estimates
whilst the tidal radius is
in agreement with the value of ![]() arcmin from IH95. The slightly
smaller value
we obtain for the tidal radius is likely due to our overestimated field star density.
arcmin from IH95. The slightly
smaller value
we obtain for the tidal radius is likely due to our overestimated field star density.
Figure 3 shows that in our determination of the density profile
there is an excess of stars with respect to the King profile (solid line) for radii
larger than 1 deg. At this distance the Sersic profile (dashed) best follows the data.
Both exponential and Plummer profiles (dotted and dash-dot)
over-predict the surface density at r<0.1 deg and
at radii larger than ![]() 0.8 deg, and under-predict it at intermediate distances.
A summary of the best-fitting parameters is given in Table 3.
0.8 deg, and under-predict it at intermediate distances.
A summary of the best-fitting parameters is given in Table 3.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{5720f4a.eps}\par\vspace*{3mm}
\includegraphics[width=8cm,clip]{5720f4b.eps}
\end{figure}](/articles/aa/full/2006/44/aa5720-06/Timg88.gif) |
Figure 4: CMD for objects classified as stellar from our ESO/WFI imaging covering the whole extent of the Fornax dSph. The boxes in panel b) indicate the regions we used to select different stellar populations (MS: main sequence; BL: Blue Loop; FOR: foreground; BHB: Blue Horizontal Branch; RRLy: RRLyrae; RHB: Red Horizontal Branch; B-RGB: Blue-Red Giant Branch; R-RGB: Red-Red Giant Branch; AGBb: AGB bump; RC: Red Clump). |
| Open with DEXTER | |
It is well established that the Fornax dSph has had a very complex star formation history (e.g. Stetson et al. 1998; Saviane et al. 2000; Buonanno et al. 1999). Stetson et al. (1998), in a photometric study covering a field of 1/3 deg2 near the centre of Fornax, found that the majority of stars fall into three distinct stellar populations: an old one represented by HB and RR Lyrae stars; an intermediate age population of He-core-burning clump stars (Red Clump, RC); and a young population, indicated by the presence of main sequence stars. Fornax displays a broad RGB, classically interpreted as due to a large spread in metallicity.
Figure 4a shows our WFI
colour-magnitude diagram for Fornax within the tidal radius
(![]()
![]() );
it contains 73 700 stars, including a quantity of foreground stars, which
lie in a fairly constant density sheet redwards of V-I = 0.6.
We notice the following features (highlighted in Fig. 4b, and
directly visible in the Hess diagram in Fig. 5):
);
it contains 73 700 stars, including a quantity of foreground stars, which
lie in a fairly constant density sheet redwards of V-I = 0.6.
We notice the following features (highlighted in Fig. 4b, and
directly visible in the Hess diagram in Fig. 5):
![\begin{figure}
\par\includegraphics[width=8cm,clip]{5720f5.eps}
\end{figure}](/articles/aa/full/2006/44/aa5720-06/Timg90.gif) |
Figure 5:
The Hess diagram for Fornax dSph CMD from ESO/WFI imaging, where
the structures, and their relative intensity, in the different regions of the CMD are visible.
Each cell is
|
| Open with DEXTER | |
The spatial distribution of different stellar components in a galaxy gives an indication of how and where the star formation took place at different times and how long the gas was retained as a function of radius.
Previous studies of dSphs in the Local Group (e.g. Majewski et al. 1999; Harbeck et al. 2001; Hurley-Keller et al. 1999; Tolstoy et al. 2004) have shown that HB properties vary as a function of the distance from the centre in several dSphs: in general the RHB is more centrally concentrated than the BHB. This indicates the dominance of old and/or metal poor stars in the outer regions and younger and/or more metal rich stars in the inner regions.
Fornax contains both old (e.g. HB),
intermediate (e.g. RC), and young stellar components (MS and Blue Loop
stars). Previous photometric studies of individual stars, which have been
limited to the central regions of Fornax dSph,
have found indications that the intermediate age stars have a more concentrated
distribution than the ancient stars (Stetson et al. 1998; Saviane et al. 2000).
Stetson et al. (1998) found that the MS stars displayed a centrally concentrated asymmetric distribution,
with a major axis tilted
![]() 30
30![]() with respect to the main body of Fornax.
with respect to the main body of Fornax.
Our WFI data, covering the entire extent of Fornax, allow us to analyse the
spatial distribution of the resolved stellar population of Fornax out to its nominal tidal radius.
We plot a CMD for 3 different spatial
samples, i.e. for stars found at elliptical radius r< 0.4 deg,
![]() ,
and r> 0.7 deg (Fig. 6). Clear differences are visible between the inner and the outer
regions: the main sequence and Blue Loop stars (young) are absent
in the outer regions.
The extent in
,
and r> 0.7 deg (Fig. 6). Clear differences are visible between the inner and the outer
regions: the main sequence and Blue Loop stars (young) are absent
in the outer regions.
The extent in ![]() of the RC decreases with the distance
to Fornax centre;
this means that the age of the dominant stellar component in this feature
is older in the outer parts (Caputo et al. 1995).
We also notice that the BHB, which is almost hidden by the main
sequence in the inner region, becomes more clearly visible the further out we go,
because the MS disappears. Finally,
we can see that the RGB changes: the red side, generally younger and more metal rich than
the blue side, becomes less evident in the outer regions.
of the RC decreases with the distance
to Fornax centre;
this means that the age of the dominant stellar component in this feature
is older in the outer parts (Caputo et al. 1995).
We also notice that the BHB, which is almost hidden by the main
sequence in the inner region, becomes more clearly visible the further out we go,
because the MS disappears. Finally,
we can see that the RGB changes: the red side, generally younger and more metal rich than
the blue side, becomes less evident in the outer regions.
Below we analyse
the spatial distribution of the different components, through their location
in the field of view and the trend of the cumulative fraction with radius.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{5720f6a.eps}\par\includegrap...
...clip]{5720f6b.eps}\par\includegraphics[width=7cm,clip]{5720f6c.eps}
\end{figure}](/articles/aa/full/2006/44/aa5720-06/Timg115.gif) |
Figure 6: ESO/WFI CMDs for the Fornax dSph at radii r< 0.4 a), 0.4 <r< 0.7 b), r> 0.7 deg c). We have normalized the number of stars in the 3 panels to allow a more meaningful comparison. Note the change in stellar population as function of radius: the young population (main sequence and Blue Loop stars) is absent beyond r>0.4 deg, whilst the ancient population becomes more dominant, as can be seen for example from the more visible BHB at r>0.4 deg, the bluer average colour of the RGB, and the less extended RC in V mag. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{5720f7a.eps}\par\vspace*{1...
...\par\vspace*{1.5mm}
\includegraphics[width=7.3cm,clip]{5720f7c.eps}
\end{figure}](/articles/aa/full/2006/44/aa5720-06/Timg116.gif) |
Figure 7: Spatial distribution of BHB, RHB and RC stars in the Fornax dSph as selected from the CMD shown in Fig. 4b. The RC stars show a more concentrated and less extended distribution than RHB and BHB stars. The number of RC stars has been normalised to the number of RHB stars. |
| Open with DEXTER | |
| |
Figure 8: Spatial distribution of Blue RGB and Red RGB stars in the Fornax dSph (as selected from the CMD shown in Fig. 4b). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{5720f9a.eps}\par\includegraphics[width=9cm,clip]{5720f9b.eps}
\end{figure}](/articles/aa/full/2006/44/aa5720-06/Timg118.gif) |
Figure 9: Surface number density ( top) and fraction of stars within elliptical radius r ( bottom) of ancient stellar populations in the Fornax dSph (solid line: RHB stars; dotted line: BHB stars; dash-dot-dot line: RRLyrae stars; dashed line: B-RGB stars). The surface number density has been Galactic stellar contamination subtracted. Note that all the ancient stars, even if found at different stages of stellar evolution, display a similar spatial trend with radius. In the bottom panel we show for comparison the fraction of stars within elliptical radius r for RC stars (long dashed line), representative of intermediate age stars: note the more extended and less concentrated spatial distribution of ancient stars with respect to intermediate age stars. |
| Open with DEXTER | |
In Fornax the BHB stars overlap the MS in the inner regions,
thus we reduce the selection box of BHB stars to
0.15 < V-I < 0.35.
In Figs. 7a,b we plot the spatial distribution of the BHB and RHB
components, and in Fig. 8a the location of B-RGB stars.
Figure 9 shows the Galactic contamination subtracted
density profile for the ancient populations (top) and the fraction of stars
within a radius r, f(<r), in bins
of 0.1 deg (bottom). The ancient stellar components clearly all have the same distribution,
the only exception being the trend at r<0.3 deg for the BHB population, which
suffers from small number statistics.
It is also likely that the BHB behaviour is altered by the
presence in the selection box of MS stars (see Fig. 4b).
A ![]() two-sample test applied to the percentage of stars within a radius r
out to the estimated Fornax tidal radius gives a
probability of 99.99% that the ancient stellar populations are drawn
from the same distribution.
two-sample test applied to the percentage of stars within a radius r
out to the estimated Fornax tidal radius gives a
probability of 99.99% that the ancient stellar populations are drawn
from the same distribution.
Taking as reference the RHB cumulative distribution, we can see that 95% of the ancient population is found within
![]() deg.
The dominant,
intermediate age stellar population in Fornax, i.e. RC stars,
shows a distinctly different distribution,
with 95% of its stars distributed within
deg.
The dominant,
intermediate age stellar population in Fornax, i.e. RC stars,
shows a distinctly different distribution,
with 95% of its stars distributed within
![]() deg.
Clearly, the ancient
populations display a more extended spatial distribution then the intermediate age stars.
The same
deg.
Clearly, the ancient
populations display a more extended spatial distribution then the intermediate age stars.
The same ![]() test applied to the RHB and RC stars
gives a low probability, 5%, that these two populations are drawn from
the same parent population, confirming the fact that intermediate and
ancient stars show very different spatial distributions.
test applied to the RHB and RC stars
gives a low probability, 5%, that these two populations are drawn from
the same parent population, confirming the fact that intermediate and
ancient stars show very different spatial distributions.
There is evidence for small scale spatial substructure in part of the ancient
stellar component of Fornax.
In Fig. 8a (B-RGB) there is a clear overdensity of stars
at
![]() and
and
![]() (
(
![]() ,
,
![]() );
this also appears to be present, though
less pronounced, in the
spatial distribution of RHB stars at similar position, however in
contrast the
distributions of BHB and RRLyrae stars appear to be smooth.
We find the number of B-RGB within 4'
of the above feature significantly larger (within 2
);
this also appears to be present, though
less pronounced, in the
spatial distribution of RHB stars at similar position, however in
contrast the
distributions of BHB and RRLyrae stars appear to be smooth.
We find the number of B-RGB within 4'
of the above feature significantly larger (within 2![]() )
than
the number within 3 control fields, of the same dimensions and at the same elliptical radius;
the overdensity of RHB is instead not statistically significant.
A CMD centred on this overdensity shows
a slightly bluer colour for the RGB in the over-density than in the 3 control fields.
)
than
the number within 3 control fields, of the same dimensions and at the same elliptical radius;
the overdensity of RHB is instead not statistically significant.
A CMD centred on this overdensity shows
a slightly bluer colour for the RGB in the over-density than in the 3 control fields.
There is no
evidence that the nearby cluster 2 (
![]() ,
,
![]() in Fig. 1) is
related to this over-density, because the stars in the over-density do not match
the cluster 2 CMD (e.g. Buonanno et al. 1998).
in Fig. 1) is
related to this over-density, because the stars in the over-density do not match
the cluster 2 CMD (e.g. Buonanno et al. 1998).
Similar overdensities in the stellar distribution have been found in previous works both in other dSphs as well as in Fornax dSph (e.g. Coleman et al. 2004).
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{5720f10a.eps}\par\vspace*{1.5mm}
\includegraphics[width=8.6cm,clip]{5720f10b.eps}
\end{figure}](/articles/aa/full/2006/44/aa5720-06/Timg128.gif) |
Figure 10: As in Fig. 9 but for intermediate age stellar populations (solid line: RC stars; dotted line: R-RGB stars; dash-dot-dot line: AGB bump stars). All the intermediate age populations display a similar spatial trend with radius. In the bottom panel we show for comparison the fraction of stars within elliptical radius r for RHB stars (long dashed line), representative of ancient stars, as in Fig. 9: note the more extended and less concentrated spatial distribution of ancient stars with respect to intermediate age stars. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.25cm,clip]{5720f11a.eps}\par\include...
...{5720f11b.eps}\par\includegraphics[width=7.25cm,clip]{5720f11c.eps}
\end{figure}](/articles/aa/full/2006/44/aa5720-06/Timg129.gif) |
Figure 11:
Spatial distribution of main sequence a) and Blue Loop b) stars
in the Fornax dSph (as selected from the CMD shown in Fig. 4b) and c)
the foreground contamination in the Blue Loop distribution as from
a CMD-selected sample of foreground stars to match the Blue Loop contamination density.
Note the asymmetric
distribution of MS stars in a),
elongated in the E-W direction and tilted by |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{5720f12.eps}
\end{figure}](/articles/aa/full/2006/44/aa5720-06/Timg130.gif) |
Figure 12:
CMD for stars within 0.4 degree of the
centre of the Fornax dSph; the box shows the selection region for the Blue Loop
stars. The colours and magnitudes of the Blue Loop
stars are consistent with theoretical Padua isochrones (Girardi et al. 2000)
of metallicity Z=0.004 (
|
| Open with DEXTER | |
We have already seen from the CMDs in Fig. 6 that young MS (<1 Gyr old) and BL stars
are only present within r< 0.4 deg, in the central region of Fornax.
Figure 11 shows the spatial distribution of MS and Blue Loop
stars (panels a, b).
The main sequence stars are
centrally concentrated and show a different, asymmetric distribution with respect
to the older stars. They predominantly form a structure extended
in the E-W direction, with a major axis
tilted at ![]()
![]() with respect to the bulk of the stellar population (as already
noted by Stetson et al. 1998). The overall spatial distribution of BL stars
is also asymmetric, although not as pronounced as the MS.
It is difficult to remove the effects of the foreground contamination (Fig. 11c)
but it appears that the blue
loop stars have a more relaxed distribution than the MS.
with respect to the bulk of the stellar population (as already
noted by Stetson et al. 1998). The overall spatial distribution of BL stars
is also asymmetric, although not as pronounced as the MS.
It is difficult to remove the effects of the foreground contamination (Fig. 11c)
but it appears that the blue
loop stars have a more relaxed distribution than the MS.
As mentioned in Sect. 3.2.3 the colour of the BL feature is
strongly dependent on metallicity. Overlaying
Padua stellar isochrones (Girardi et al. 2000)
on the CMD (Fig. 12),
we find that the Blue Loop stars are consistent
with ages between 400 and 700 Myr and metallicity Z=0.004.
Isochrones of lower metallicities (Z=0.001) predict
the presence of a plume of Blue Loop giants much closer to the MS than observed,
and the predicted average colour of the BL feature
for higher metallicities (Z=0.008) is significantly
redder than observed![]() .
.
Figure 12 also shows that the Girardi et al. (2000) Padua isochrones
suggest that the
MS contains stars as young as 200-300 Myr,
and as old as 1 Gyr, which is different to the BL stars age range.
Thus, to compare the spatial distribution of MS and BL stars,
we must separate the MS stars in two groups, those predominantly younger and
those older than 400 Myr. This is
achieved by splitting the MS in colour: the "young'' and "old'' MS stars are approximately
bluer and redder, respectively, than V-I=0. In this case we find that the spatial distribution
of "old'' MS stars is consistent with the BL spatial distribution, whilst "young'' MS
stars display a more asymmetric and centrally concentrated distribution.
Thus, it seems that the "young'' MS stars are found closer to the location
where they were formed, whilst "old'' MS and BL stars have diffused
to larger radii. To estimate the diffusion time, we use the dynamical time
(Binney & Tremaine 1987), which ranges between 350-800 Myr,
assuming a mass within the tidal radius between
108-
![]()
![]() . This is consistent with the age of the "old'' MS stars.
Thus the elongated structure of the MS is formed predominantly by the younger MS stars, and is
presumably the remaining signature of the collapsed gas from which the stars were formed.
. This is consistent with the age of the "old'' MS stars.
Thus the elongated structure of the MS is formed predominantly by the younger MS stars, and is
presumably the remaining signature of the collapsed gas from which the stars were formed.
We derived density profiles, from which Galactic contamination has been subtracted,
for these two components and compared them to the models used in Sect. 3.1.
The best-fitting profile for the old population is given
by the King model, that follows more closely the data beyond
1 deg than the Sersic profile. However, the density profile of the
intermediate age stars is better represented by a Sersic profile,
since the King model declines too steeply. In both cases the exponential and
Plummer models overpredict the density for
![]() deg and
deg and
![]() deg,
and underpredict it at intermediate radii.
Independently of the adopted model,
the results of the fit (see Table 3) show that intermediate age stars are more
centrally concentrated and less extended than old stars.
deg,
and underpredict it at intermediate radii.
Independently of the adopted model,
the results of the fit (see Table 3) show that intermediate age stars are more
centrally concentrated and less extended than old stars.
The spatial distribution of different stellar populations is a powerful way to identify stellar populations of different ages in a dwarf galaxy.
The discovery of two shell-like features
was recently reported in Fornax from photometric studies
(Coleman et al. 2005,2004). The first of these features
was identified outside the core radius at
![]() and
and
![]() (corresponding to
(corresponding to
![]() ,
,
![]() and elliptical radius of 0.33 deg in
Fig. 1) as a small over-density of stars in data
down to
and elliptical radius of 0.33 deg in
Fig. 1) as a small over-density of stars in data
down to ![]() (Coleman et al. 2004). Adding
deeper data from Stetson et al. (1998) to their sample the authors found the shell
to be consistent with being dominated by young, 2 Gyr old, ZAMS stars.
The authors proposed that this might be analogous to the
shells found in elliptical galaxies and suggested that Fornax might have accreted a smaller
gas-rich galaxy around 2 Gyr ago.
(Coleman et al. 2004). Adding
deeper data from Stetson et al. (1998) to their sample the authors found the shell
to be consistent with being dominated by young, 2 Gyr old, ZAMS stars.
The authors proposed that this might be analogous to the
shells found in elliptical galaxies and suggested that Fornax might have accreted a smaller
gas-rich galaxy around 2 Gyr ago.
A second "shell'' was found in the RGB distribution outside
the tidal radius, around 1.3![]() northwest of the centre (Coleman et al. 2005) and,
similarly to the inner shell,
located along the minor axis and elongated along the major axis.
northwest of the centre (Coleman et al. 2005) and,
similarly to the inner shell,
located along the minor axis and elongated along the major axis.
Olszewski et al. (2006) carried out much deeper imaging of this over-density, down to ![]() and
refined the age of the "feature'' and suggested that the excess of stars
in the shell might be the result of a burst of star formation
which occurred 1.4 Gyr ago with a metallicity Z=0.004 (
and
refined the age of the "feature'' and suggested that the excess of stars
in the shell might be the result of a burst of star formation
which occurred 1.4 Gyr ago with a metallicity Z=0.004 (
![]() ), favouring a
scenario in which the gas
from which these stars formed was pre-enriched within Fornax itself.
), favouring a
scenario in which the gas
from which these stars formed was pre-enriched within Fornax itself.
Our photometry covers the region of the inner shell,
and we do not detect such a feature, but comparing our sample with the additional
data-set from Stetson et al. (1998), we find signs of the shell when we include the stars
we had discarded from our analysis because they were detected in V but not in the I band.
This makes it clear that the feature is just at the detection limit of our data. We also note
that the MS stars are asymmetrically
distributed, and this could cause the presence of local overdensities
with respect to other regions in Fornax, at the same elliptical radius,
where young stars might be under-represented.
Deeper photometry covering the entire region at r<0.4-0.5 deg would make it possible
to resolve this issue.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{5720f13.eps}
\end{figure}](/articles/aa/full/2006/44/aa5720-06/Timg138.gif) |
Figure 13: Location of the observed FLAMES fields and targets (with S/N per Å > 10 and error in velocity <5 km s-1) in the Fornax dSph (squares: probable members; crosses: probable non-members). The black filled circles show the location of Fornax globular clusters, the black small ellipse shows the location of the "shell-like'' feature detected by Coleman et al. 2004, and the dashed circles indicate the observed FLAMES fields. The tidal radius is from this work. |
| Open with DEXTER | |
Our VLT/FLAMES spectroscopic survey of individual stars in the Fornax dSph allows us to determine velocities and metallicities ([Fe/H]) from the CaT equivalent width for a subsample of RGB stars out to the nominal tidal radius of Fornax dSph (see Fig. 13).
The dependence of CaT equivalent width on metallicity has been
empirically proved by extensive work in the literature
(e.g. Armandroff & Da Costa 1991; Armandroff & Zinn 1988; Olszewski et al. 1991). Rutledge et al. (1997a)
presented the largest compilation of CaT equivalent width measurements
for individual RGB stars in globular clusters, which Rutledge et al. (1997b)
calibrated with high resolution metallicities, proving the CaT method to be
reliable and accurate in the probed metallicity range,
![]() .
.
We obtained metallicities from the CaT equivalent widths by using the relation
derived by Rutledge et al. (1997b):
| (3) |
| (4) |
Since the Fornax dSph displays a very broad RGB (see Sect. 3.2 and Fig. 4) we chose our targets from a box around the RGB covering a wide colour range, to avoid biasing our sample in age or in metallicity. The spatial distribution of our targeted VLT/FLAMES is shown in Fig. 13, together with the position of Fornax globular clusters and the location of the shell-like feature (Coleman et al. 2004). The fields cover a wide range of radii. Since, as discussed in Sect. 3, the stellar population of different ages display different spatial distributions, our sample will contain predominantly intermediate age stars in the central fields, and ancient stars in the outermost fields. Previous studies, which were restricted to the central regions, were clearly biased towards the properties of the intermediate age population.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{5720f14.eps}
\end{figure}](/articles/aa/full/2006/44/aa5720-06/Timg146.gif) |
Figure 14: Histogram of velocities for the observed VLT/FLAMES targets in the Fornax dSph which passed our S/N and velocity error criteria (641 stars). |
| Open with DEXTER | |
Figure 14 shows the velocity histogram
of our VLT/FLAMES targets which met our S/N and velocity
error criteria (641 stars). To find the systemic velocity of Fornax we first selected
the stars found within 4![]() of the velocity
peak associated with Fornax. We used the
value of
of the velocity
peak associated with Fornax. We used the
value of
![]() km s-1
taken from the literature (e.g. Walker et al. 2005) as a first approximation.
We calculated the mean velocity and the velocity dispersion from the 4
km s-1
taken from the literature (e.g. Walker et al. 2005) as a first approximation.
We calculated the mean velocity and the velocity dispersion from the 4![]() sample and then
repeated the procedure selecting stars within 3
sample and then
repeated the procedure selecting stars within 3![]() and finally the stars within
2.5
and finally the stars within
2.5![]() .
We found a systemic velocity
.
We found a systemic velocity
![]() km s-1 and
a velocity dispersion
km s-1 and
a velocity dispersion
![]() km s-1 (3
km s-1 (3![]() ), and
), and
![]() km s-1,
km s-1,
![]() km s-1 (2.5
km s-1 (2.5![]() ).
).
Because Fornax has a systemic velocity that strongly overlaps with the Galaxy,
we tested to see if the large variation in velocity dispersion for different ![]() cuts
might be due to
foreground contamination. We performed Monte Carlo simulations
producing 10000 sets of 600 velocities about the mean velocity of Fornax
Gaussianly distributed with a trial dispersion
of 15 km s-1. The dispersions obtained cutting the artificial velocity
set at 3
cuts
might be due to
foreground contamination. We performed Monte Carlo simulations
producing 10000 sets of 600 velocities about the mean velocity of Fornax
Gaussianly distributed with a trial dispersion
of 15 km s-1. The dispersions obtained cutting the artificial velocity
set at 3![]() and 2.5
and 2.5![]() were consistent within 2
were consistent within 2![]() in 99.63% of the cases. We obtained very similar results when we fixed
the dispersion at 12 km s-1, and/or convolved the simulated velocities
with observational errors.
This means that the differences in velocity dispersion
we obtain with the
in 99.63% of the cases. We obtained very similar results when we fixed
the dispersion at 12 km s-1, and/or convolved the simulated velocities
with observational errors.
This means that the differences in velocity dispersion
we obtain with the ![]() and
and
![]() cuts for our data are most likely not
due to the cuts themselves, but to the presence of Galactic
contamination.
A similar result is obtained by adding a Galactic component to the simulated velocities of Fornax,
as a Gaussian with parameters determined from the Besançon model (Robin et al. 2003).
The input velocity dispersion for
the dSph velocity distribution is recovered with the
cuts for our data are most likely not
due to the cuts themselves, but to the presence of Galactic
contamination.
A similar result is obtained by adding a Galactic component to the simulated velocities of Fornax,
as a Gaussian with parameters determined from the Besançon model (Robin et al. 2003).
The input velocity dispersion for
the dSph velocity distribution is recovered with the
![]() cut,
whilst the dispersion from the
cut,
whilst the dispersion from the ![]() cut is overestimated.
We thus adopt the 2.5
cut is overestimated.
We thus adopt the 2.5![]() selection about the systemic velocity to limit the foreground
contamination.
selection about the systemic velocity to limit the foreground
contamination.
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{5720f15.eps}
\end{figure}](/articles/aa/full/2006/44/aa5720-06/Timg154.gif) |
Figure 15:
Heliocentric velocity with elliptical radius from VLT/FLAMES spectroscopic observations
of individual RGB stars in the Fornax dSph. We plotted all the stars which satisfy our selection criteria (S/N per Å > 10 and velocity error <5 km s-1).
The dashed line is the systemic velocity,
|
| Open with DEXTER | |
From our kinematic selection the number of probable Fornax members
(with S/N per Å > 10 and error in
velocity <5 km s-1) is 562 (see Fig. 15).
We list in Table 4 the relevant information for the observed
targets that passed our selection criteria.
Note that
probable members are also observed beyond the nominal tidal radius
(derived in Sect. 3.1).
In Fig. 16 we show the location on the CMD of probable velocity members and
non-members. Because of the low heliocentric velocity of Fornax it is
not always possible to firmly distinguish between members and non-members according to
a pure kinematic selection: some members are present in a region of the CMD
where none are expected. Visual inspection of these spectra shows that all but one
are consistent with a RGB spectrum. However it is difficult to distinguish between
dwarf and RGB stars in the spectral range covered by our data.
The distribution of metallicity versus velocity (Fig. 17)
shows that Fornax members are recognizable in this parameter space and the foreground
stars (kinematic non-members)
appear to cluster predominantly in the region between
![]() .
The Fornax members off the RGB (asterisks in Fig. 16)
are also identified in Fig. 17. All but one
fall in the region between
.
The Fornax members off the RGB (asterisks in Fig. 16)
are also identified in Fig. 17. All but one
fall in the region between
![]() ,
thus the distribution of
these stars in this parameter space again suggests that they are highly likely to be Galactic contamination.
As the number of these objects is very small and removing or including them
in our present analysis will not affect the conclusions, we decided
to include them in the sample. A more strict membership selection
will be carried out before analysing the detailed kinematics of Fornax (Battaglia et al. 2006a).
,
thus the distribution of
these stars in this parameter space again suggests that they are highly likely to be Galactic contamination.
As the number of these objects is very small and removing or including them
in our present analysis will not affect the conclusions, we decided
to include them in the sample. A more strict membership selection
will be carried out before analysing the detailed kinematics of Fornax (Battaglia et al. 2006a).
Several spectroscopic studies of individual stars in the Fornax dSph galaxy
have shown that it is the most metal rich of the Milky Way dSph
satellites (except for Sagittarius), with a peak metallicity at
![]() and a
large metallicity spread (Pont et al. 2004; Tolstoy et al. 2001).
The extent of the metal poor and metal rich tail has changed
depending mainly on the size and the spatial location
of the observations. The most
recent study, consisting of CaII triplet measurements of 117 RGB stars
(Pont et al. 2004), showed that Fornax contains
stars as metal poor as
and a
large metallicity spread (Pont et al. 2004; Tolstoy et al. 2001).
The extent of the metal poor and metal rich tail has changed
depending mainly on the size and the spatial location
of the observations. The most
recent study, consisting of CaII triplet measurements of 117 RGB stars
(Pont et al. 2004), showed that Fornax contains
stars as metal poor as
![]() and as metal rich as -0.4
with a peak at
and as metal rich as -0.4
with a peak at
![]() .
.
Figure 18 shows the metallicity distribution with elliptical radius for
the Fornax members kinematically selected from our VLT/FLAMES data.
A variation of metallicity with elliptical radius is clearly visible: a metal poor
population (
![]() )
is seen throughout
the galaxy; a
more metal rich population ([Fe/H]
)
is seen throughout
the galaxy; a
more metal rich population ([Fe/H]
![]() )
is present out to
0.7 deg from the centre; and an even more metal rich tail, extending out to
)
is present out to
0.7 deg from the centre; and an even more metal rich tail, extending out to
![]() ,
is present mainly in the inner 0.3-0.4 deg.
This is quantified in a histogram in Fig. 19, where the sample is divided
into 3 spatial bins (inner r<0.4 deg, middle 0.4<r<0.7 deg, and outer r>0.7 deg)
and we can see that the
metal poor component, centred at
,
is present mainly in the inner 0.3-0.4 deg.
This is quantified in a histogram in Fig. 19, where the sample is divided
into 3 spatial bins (inner r<0.4 deg, middle 0.4<r<0.7 deg, and outer r>0.7 deg)
and we can see that the
metal poor component, centred at
![]() ,
is present
in each bin and is thus spread throughout the galaxy;
another component, centred at
,
is present
in each bin and is thus spread throughout the galaxy;
another component, centred at
![]() ,
with a width at half
peak of about 0.3, is present in the middle and inner regions; only the innermost region
contains the most metal rich component.
,
with a width at half
peak of about 0.3, is present in the middle and inner regions; only the innermost region
contains the most metal rich component.
Such a large sample of velocity and metallicity measurements,
covering a much larger area than previous studies,
gives us the possibility to explore the relationship
between the kinematics and metallicity in this galaxy.
We divided the metallicity distribution into two parts: stars more metal
rich (MR) and more metal poor (MP) than
![]() .
This value
of the metallicity was chosen to minimise the overlap between
the two metallicity components. However a slightly different cut
(e.g. [Fe/H] = -1.2 or -1.4) does not significantly change the conclusions of our analysis.
.
This value
of the metallicity was chosen to minimise the overlap between
the two metallicity components. However a slightly different cut
(e.g. [Fe/H] = -1.2 or -1.4) does not significantly change the conclusions of our analysis.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{5720f16.eps}
\end{figure}](/articles/aa/full/2006/44/aa5720-06/Timg164.gif) |
Figure 16: Location on the CMD of the observed FLAMES targets for Fornax dSph (squares: probable members; crosses: probable non-members). The boundaries of our target selection region closely follow the location of the targets. The asterisks indicates stars selected as velocity members falling in unusual position in the CMD; they are likely to be Galactic foreground contamination (see Fig. 17). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{5720f17.eps}
\end{figure}](/articles/aa/full/2006/44/aa5720-06/Timg166.gif) |
Figure 17:
Metallicity versus heliocentric velocity for the observed FLAMES targets with
S/N per
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{5720f18.eps}
\end{figure}](/articles/aa/full/2006/44/aa5720-06/Timg167.gif) |
Figure 18:
Metallicity distribution with elliptical radius for the Fornax dSph. Note the trend
of decreasing metallicity with radius and the absence of very metal poor stars
(dotted line indicates
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{5720f19.eps}
\end{figure}](/articles/aa/full/2006/44/aa5720-06/Timg168.gif) |
Figure 19: Histogram of metallicity measurements for individual RGB stars in the Fornax dSph (solid line: all velocity members; dotted line: velocity members within r< 0.4 deg from the centre; dashed line: velocity members between 0.4<r<0.7 deg from the centre; dashed-dotted line: velocity members at r>0.7 deg from the centre). |
| Open with DEXTER | |
Figure 20 shows the velocity distributions for the two metallicity
components in 3 different spatial bins (inner r< 0.4 deg,
middle
0.4 <r< 0.7 deg, outer r> 0.7 deg). The metal poor population
exhibits a larger velocity dispersion than the metal rich
population![]() (see Table 5);
furthermore,
in the first bin the velocity distribution of the metal poor stars is far
from being Gaussian: it is flat or even double peaked (with peaks
between 37-42 km s-1 and 67-72 km s-1). Changing the
binning in the histogram leaves the main features of
the velocity distribution unchanged.
Figure 21 shows the cumulative function of the MP stars at r<0.4 deg
compared to the cumulative distribution for a Gaussian with the
same mean velocity and dispersion as the metal rich component
in the same distance bin. The two cumulative functions are
very different, and this also shows that the cumulative function
of the MP stars is similar to what
is expected for a uniform distribution, with two peaks at
(see Table 5);
furthermore,
in the first bin the velocity distribution of the metal poor stars is far
from being Gaussian: it is flat or even double peaked (with peaks
between 37-42 km s-1 and 67-72 km s-1). Changing the
binning in the histogram leaves the main features of
the velocity distribution unchanged.
Figure 21 shows the cumulative function of the MP stars at r<0.4 deg
compared to the cumulative distribution for a Gaussian with the
same mean velocity and dispersion as the metal rich component
in the same distance bin. The two cumulative functions are
very different, and this also shows that the cumulative function
of the MP stars is similar to what
is expected for a uniform distribution, with two peaks at ![]() 40 km s-1
and
40 km s-1
and ![]() 70 km s-1.
70 km s-1.
An issue is if the velocity distribution of MP stars in the first bin
is artificially biased by our choice of the metallicity cut, namely if by assigning
metal poor stars to the metal rich component we could cause the small observed
number of MP stars
with velocity close to the systemic in the inner bin.
This can be explored by changing the cut in
metallicity, e.g. using
![]() for the metal poor component, and
for the metal poor component, and
![]() for the metal rich one. We find the same features for the MP distribution at r< 0.4 deg
as in the case with a metallicity
division at
for the metal rich one. We find the same features for the MP distribution at r< 0.4 deg
as in the case with a metallicity
division at
![]() ,
showing that the choice of a different metallicity cutoff
does not alter our conclusions
and accentuates the differences between
the velocity distributions for metal rich and metal poor stars.
,
showing that the choice of a different metallicity cutoff
does not alter our conclusions
and accentuates the differences between
the velocity distributions for metal rich and metal poor stars.
We tested to see if the differences in velocity distribution between the metal poor and the metal rich components are statistically significant: can the metal poor population in the inner bin be drawn from the metal rich and how significant would this be? A two-sided KS-test applied to the velocity distributions gives a probability of 0.7%, 0.4% and 16% that the MP stars in the first bin might be drawn from the same distribution as respectively: the MR stars in the inner bin; the MR stars in the middle bin; the MP stars in the middle bin. Thus the differences in the velocity distribution of MR and MP stars are unlikely to be an artifact of the observed number of stars, and instead point to significantly different kinematic behaviour of different metallicity components.
We also tested to see if the differences between the velocity distribution
of MP stars in the inner and middle bins, reflected
in the relatively low value of the K-S test, are due to the peculiarities of
the velocity distribution of the MP stars at r< 0.4 deg, or
are intrinsic. Thus, we artificially "removed'' the two velocity peaks by considering
as the "expected'' number of stars at the velocities
of the peaks as the average of the number of stars in the adjacent bins.
We then randomly removed the stars in "excess''
from the velocity peaks (![]() for the peak at
for the peak at ![]() 40 km s-1
and
40 km s-1
and ![]() at
at ![]() 70 km s-1). The velocity distribution of the remaining stars
is compatible with a Gaussian distribution with velocity dispersion
70 km s-1). The velocity distribution of the remaining stars
is compatible with a Gaussian distribution with velocity dispersion
![]() km s-1 (probability of 99.85% from a KS-test).
In this case MP stars in the inner and middle distance bins
have a 93.7% probability of having been drawn from the same velocity distribution.
km s-1 (probability of 99.85% from a KS-test).
In this case MP stars in the inner and middle distance bins
have a 93.7% probability of having been drawn from the same velocity distribution.
Thus Fornax dSph shows clear differences in the kinematics of its
MR and MP component. Contrary to expectations, part of the metal poor component,
arguably the oldest component, displays
non-equilibrium kinematic behaviour at r< 0.4 deg. A possible explanation for this is that Fornax
recently captured external material
which is disturbing the underlying distribution. Since we detect signs of
disturbance only in the MP component, we argue that part of the object accreted by Fornax
must have been dominated by stars more metal poor than
![]() .
.
![\begin{figure}
\par\includegraphics[width=16cm,clip]{5720f20.eps}
\end{figure}](/articles/aa/full/2006/44/aa5720-06/Timg180.gif) |
Figure 20: Velocity histograms for 3 different distance bins for metal rich (dashed) and metal poor (dotted) stars in the Fornax dSph. The "metal rich'' stars display a colder kinematics than the "metal poor'' stars (see Table 3). Note the flat/double-peaked velocity distribution of MP stars in the inner bin. |
| Open with DEXTER | |
Table 5: Number of stars, weighted mean heliocentric velocity, and line of sight velocity dispersion for Fornax members (all mem), metal rich (MR) and metal poor (MP) stars at every elliptical radius (all r), and in 3 distance bins (r<0.4, 0.4<r<0.7, r>0.7 deg).
It is well known that the main uncertainty in deriving the absolute
ages of stars in a CMD of a complex stellar population (i.e. a galaxy)
is that the position of a star changes depending degenerately upon
both age and metallicity. We can break this degeneracy using
metallicities derived from spectroscopy. In Fornax we can use our
spectroscopic metallicities of 562 RGB stars to determine which
isochrone set to use to determine the ages of these stars, and thus
produce an age-metallicity relation for the galaxy over the age range
covered by RGB stars (>1 Gyr). The ages we determine in this way
remain uncertain in absolute terms due to the limitations in the
stellar models used to create the isochrones, but in relative terms
the ages are accurate. Given the low systemic velocity of Fornax
there will be foreground stars contaminating our samples.
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{5720f21.eps}
\end{figure}](/articles/aa/full/2006/44/aa5720-06/Timg185.gif) |
Figure 21:
The squares with errorbars show the cumulative velocity distribution for MP stars (
|
| Open with DEXTER | |
We chose to use the Yonsei-Yale isochrones (Yi et al. 2001; Kim et al. 2002)
because they cover the range of ages and metallicities we require in a
uniform way, and they allow for a variation in [![]() /Fe]. They also
provide a useful interpolation programme which allows us to
efficiently calculate the exact set of isochrones to compare with each
spectroscopic metallicity. These isochrones did have the problem that
they did not always extend up to the tip of the RGB for young metal
rich stars, but comparison with the Padua isochrones (Girardi et
al. 2000) of the same metallicity suggested that we could extrapolate
these Y-Y isochrones to the tip of the RGB which allowed us to
determine ages of the young metal rich stars in our sample.
/Fe]. They also
provide a useful interpolation programme which allows us to
efficiently calculate the exact set of isochrones to compare with each
spectroscopic metallicity. These isochrones did have the problem that
they did not always extend up to the tip of the RGB for young metal
rich stars, but comparison with the Padua isochrones (Girardi et
al. 2000) of the same metallicity suggested that we could extrapolate
these Y-Y isochrones to the tip of the RGB which allowed us to
determine ages of the young metal rich stars in our sample.
In Fig. 22a we plot the CMD of the 39 stars in our
spectroscopic sample with
![]() and over-plot the Y-Y
isochrones of the same metallicity for two different ages: the
majority of metal poor stars fall on the blue side of the RGB and are
consistent with old ages (>10 Gyr old), and thus
can be associated with the ancient component
from the photometric analysis in Sect. 3. The stars found outside the
range of the isochrones to the red (
and over-plot the Y-Y
isochrones of the same metallicity for two different ages: the
majority of metal poor stars fall on the blue side of the RGB and are
consistent with old ages (>10 Gyr old), and thus
can be associated with the ancient component
from the photometric analysis in Sect. 3. The stars found outside the
range of the isochrones to the red (
![]() )
may be Galactic
contamination. There are also several quite blue stars (at
)
may be Galactic
contamination. There are also several quite blue stars (at
![]() ;
;
![]() )
which are consistent with having young ages (2
Gyr), and these are most likely to be foreground contamination. The
more metal rich stars for which we have spectroscopy, with
)
which are consistent with having young ages (2
Gyr), and these are most likely to be foreground contamination. The
more metal rich stars for which we have spectroscopy, with
![]() (119 stars), are shown in Fig. 22b. They are
generally consistent with young, 2-5 Gyr old isochrones and match the
dominant intermediate age component found in the photometric
analysis. Fornax members at higher metallicity (
(119 stars), are shown in Fig. 22b. They are
generally consistent with young, 2-5 Gyr old isochrones and match the
dominant intermediate age component found in the photometric
analysis. Fornax members at higher metallicity (
![]() )
are better represented by ages of 1.5-2 Gyr (Fig. 22c).
)
are better represented by ages of 1.5-2 Gyr (Fig. 22c).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{5720f22a.eps}\par\includegra...
...ip]{5720f22b.eps}\par\includegraphics[width=8cm,clip]{5720f22c.eps}
\end{figure}](/articles/aa/full/2006/44/aa5720-06/Timg188.gif) |
Figure 22:
The comparison between measured metallicities and colours of Fornax stars (asterisks) with the
theoretical isochrones (lines) for the metallicity of the stars.
a) Stars with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{5720f23.eps}
\end{figure}](/articles/aa/full/2006/44/aa5720-06/Timg189.gif) |
Figure 23:
Ages and errorbars derived from isochrones fitting of the VLT/FLAMES
spectroscopic sample of RGB stars in Fornax dSph. The lines shows the average
value of [Fe/H] as a function of age assuming [ |
| Open with DEXTER | |
In Fig. 23 we show the age-metallicity relation obtained
for Fornax from fitting Y-Y isochrones to our entire spectroscopic
sample. We used [
![]() ,
in agreement with the average
value from preliminary HR measurements of RGB stars in the centre of
the Fornax dSph (Letarte et al. 2006b). We derived the errors in the age
determination from the errors in magnitude and colour of the
photometry, and assuming a metallicity error of 0.1 dex for each star.
This figure contains 466 stars (out of the total sample of 562 stars),
among which 103 were young stars which were too bright for the young
isochrones (but fainter than the tip of the RGB); 97 stars fell
completely outside the age range of the isochrones and therefore had
to be excluded.
,
in agreement with the average
value from preliminary HR measurements of RGB stars in the centre of
the Fornax dSph (Letarte et al. 2006b). We derived the errors in the age
determination from the errors in magnitude and colour of the
photometry, and assuming a metallicity error of 0.1 dex for each star.
This figure contains 466 stars (out of the total sample of 562 stars),
among which 103 were young stars which were too bright for the young
isochrones (but fainter than the tip of the RGB); 97 stars fell
completely outside the age range of the isochrones and therefore had
to be excluded.
If we change the [![]() /Fe] assumed, and repeat our age
determination for [
/Fe] assumed, and repeat our age
determination for [![]() /Fe] = 0.3; and for a variation in
/Fe] = 0.3; and for a variation in ![]() with [Fe/H] ([
with [Fe/H] ([
![]() for
for
![]() and
decreasing to [
and
decreasing to [![]() /Fe] = 0 between
/Fe] = 0 between
![]() and
then remaining constant), as found in HR studies of the central region
of Fornax (Letarte et al. 2006b) we obtain slightly different results
as shown by the relations plotted in Fig. 23. The
different trend is enhanced by the fact that previously excluded
groups of low metallicity stars could now be included when using [
and
then remaining constant), as found in HR studies of the central region
of Fornax (Letarte et al. 2006b) we obtain slightly different results
as shown by the relations plotted in Fig. 23. The
different trend is enhanced by the fact that previously excluded
groups of low metallicity stars could now be included when using [![]() /Fe] > 0 isochrones. Thus the
/Fe] > 0 isochrones. Thus the ![]() -element abundance of a star
has an impact on deriving accurate ages, and it would clearly be
desirable to be able to correct for this effect for each star.
Unfortunately [
-element abundance of a star
has an impact on deriving accurate ages, and it would clearly be
desirable to be able to correct for this effect for each star.
Unfortunately [![]() /Fe] determination requires HR spectroscopy and
for the large sample here this is a daunting task. However we can make
use of the HR study of the central region and use the general trends
found there. HR studies (Letarte et al. 2006b) find that
[
/Fe] determination requires HR spectroscopy and
for the large sample here this is a daunting task. However we can make
use of the HR study of the central region and use the general trends
found there. HR studies (Letarte et al. 2006b) find that
[![]() /Fe] < 0 for
/Fe] < 0 for
![]() ,
however as there are no
currently available sets of isochrones for [
,
however as there are no
currently available sets of isochrones for [![]() /Fe] < 0, it is
not clear how this will affect our age estimates. Assuming the
interpolation between [
/Fe] < 0, it is
not clear how this will affect our age estimates. Assuming the
interpolation between [![]() /Fe] = 0.3 and 0. continues to -0.3
this would go in the direction of reconciling the discrepancies
between the observations and the isochrones at high metallicities.
/Fe] = 0.3 and 0. continues to -0.3
this would go in the direction of reconciling the discrepancies
between the observations and the isochrones at high metallicities.
One of the main results of our imaging and spectroscopic survey of the Fornax dwarf spheroidal galaxy is the presence of a population gradient. The stellar population shows a clear variation in age and metallicity as a function of radius (e.g. Figs. 6, 14 and 19). We can associate most of the more metal poor component with an ancient population (>10 Gyr), and most of the more metal rich component with an intermediate age population (2-8 Gyr) with overlapping metallicity distributions.
Population gradients have been detected in several other dwarf
spheroidal galaxies in the Local Group from imaging
(e.g., Harbeck et al. 2001), and spectroscopy (e.g., Tolstoy et al. 2004).
This must point to some common process in the formation of stars in these
small systems, as this variation most likely reflects the original
spatial distribution of gas from which the different stellar
populations were formed. It is unlikely that the spatial distribution
of one stellar component can have changed significantly with
respect to another over time. Although weak encounters could
diffuse an older component, it is unlikely to be an important effect
because the relaxation time (Binney & Tremaine 1987)
of Fornax is >
![]() years,
i.e. longer than the age of the ancient population. Therefore, the
present spatial distribution of stars of different ages gives us an
indication of how the gas from which they were formed was distributed,
and requires an explanation for how gas has apparently been
progressively "removed'' from the outer regions, and more recently,
apparently, completely from the system.
years,
i.e. longer than the age of the ancient population. Therefore, the
present spatial distribution of stars of different ages gives us an
indication of how the gas from which they were formed was distributed,
and requires an explanation for how gas has apparently been
progressively "removed'' from the outer regions, and more recently,
apparently, completely from the system.
Star formation is likely to have a dramatic impact on the interstellar medium of these small galaxies. It is possible that gas is frequently blown away as the result of supernovae type II explosions of massive stars (e.g. Mac Low & Ferrara 1999; Mori et al. 2002). This expelled gas should be able to fall back onto the galaxy, if the galaxy has a large enough potential, and on its return the gas will sink deeper into the central regions, where further generations of star formation can occur, with potentially different spatial, kinematic, metallicity and age characteristics. This next generation stellar population will likely be a more centrally concentrated, younger, more metal rich component. In this case we should expect a direct correlation between the mass of the galaxy and the fraction of gas retained by the system, as the deeper potential well of the most massive dSphs is more capable of retaining more of the original gas (e.g., Ferrara & Tolstoy 2000). Consistent with this picture, Fornax differs from the less massive Sculptor dSph in having a much more extended star formation history.
However this correlation is not a straight forward prediction of the properties of all the dwarf galaxies in the Local Group. This is because it is not only the mass of galaxies that determines their ability to retain an interstellar medium; dSph typically live in a fairly active environment with competing effects of the tidal field of our much larger Milky Way and several fairly large interacting companions (e.g., the Magellanic Clouds), and the debris left around by these interactions (e.g., the Magellanic Stream). N-body simulations indicate that tidal stripping combined with ram pressure stripping is a feasible combination to explain the lack of gas at the present time in dSphs (Mayer 2005). The importance of these effects depends strongly on the orbital parameters of the satellite, the apocenter-to-pericenter ratio, and the time at which the satellite enters the Milky Way potential. Whilst the satellite is orbiting the Galaxy, part of its gas may be ionized by the Milky Way corona, perhaps in combination with the cosmic UV background. The gas can be then removed over time, with varying degrees of efficiency, if the apocenter-to-pericenter ratio is large enough.
Recent proper motion measurements for Fornax suggest
a pericentric distance of the order of
the present Galactocentric distance (Dinescu et al. 2004; Piatek et al. 2002),
and an almost circular orbit with an orbital period of ![]() 4-5 Gyr (Dinescu et al. 2004). Even though proper motion measurements are rather uncertain,
this would suggest that we can exclude strong interaction with the
Milky Way. Thus, as suggested by Mayer (2005), an object like Fornax
may not be completely stripped of its gas, but would be able to retain
it in its central regions and thus maintain an extended star
formation history.
4-5 Gyr (Dinescu et al. 2004). Even though proper motion measurements are rather uncertain,
this would suggest that we can exclude strong interaction with the
Milky Way. Thus, as suggested by Mayer (2005), an object like Fornax
may not be completely stripped of its gas, but would be able to retain
it in its central regions and thus maintain an extended star
formation history.
N-body models that predict dIrr to be the progenitors of dSphs, transformed into
spheroids by tidal stirring from the Milky Way (Mayer et al. 2001a,b),
predict an increase in the star formation activity of a
satellite after pericentric passage. The pericentric passage can
also provoke the formation of a bar that funnels gas into the central
region, making the gas distribution more centrally concentrated. These models are highly
dependent upon the starting conditions for the satellite. It is found
that an apocentre-to-pericentre ratio of ![]() 5 and a pericentre
distance of
5 and a pericentre
distance of ![]() 50 kpc would be required to transform a dIrr into a
dSph. Fornax has never been specifically modelled; however, as it is
now thought to be close to its pericentre and the previous
passage probably occurred around 4-5 Gyr ago, this would correspond well to the time
frame of the last period of intense star formation. This scenario could
explain both the variation in the spatial distribution of the Fornax
stellar population and the large fraction of intermediate age
stars. Specific simulations, emulating the orbital parameters of
Fornax, are required for a more detailed comparison between these
observations and N-body simulations.
50 kpc would be required to transform a dIrr into a
dSph. Fornax has never been specifically modelled; however, as it is
now thought to be close to its pericentre and the previous
passage probably occurred around 4-5 Gyr ago, this would correspond well to the time
frame of the last period of intense star formation. This scenario could
explain both the variation in the spatial distribution of the Fornax
stellar population and the large fraction of intermediate age
stars. Specific simulations, emulating the orbital parameters of
Fornax, are required for a more detailed comparison between these
observations and N-body simulations.
In addition to the different spatial distribution of ancient, intermediate age and young stars, we also find a different kinematic behaviour of metal rich and metal poor stars. This behaviour appears similar to what is seen, for example, in our Milky Way. The stellar bulge of our Galaxy is much less extended and kinematically colder than the stellar halo. This distinction may merely reflect the different spatial distribution required by a star moving with a larger velocity to reach larger distances or it may be telling us something more fundamental about the different conditions of the formation of these two different components. To test this we can use the Jeans equation to derive the line of sight velocity dispersion predicted for stars following the different density profiles of old and intermediate age stars (Binney & Tremaine 1987). This calculation shows that it is difficult to interpret the observed differences in velocity dispersion of MR and MP stars as being only due to their different spatial distribution (Battaglia et al. 2006a), and the same result is found in N-body simulations (e.g Kawata et al. 2006). In a future paper we will present detailed kinematic modelling of these distinct stellar populations, taking into account the possibility of different orbital properties for the two populations (Battaglia et al. 2006a).
Another aspect that deserves further investigation is the apparently
non-equilibrium
kinematics of the metal poor, presumably the oldest,
stellar population in the centre of Fornax. A possible interpretation of
this is that we are seeing a remnant of accreted material. Given the
presence of 5 globular clusters in Fornax, it would not be surprising for
this to be a disrupted globular cluster. In this case we would expect
the metallicity distribution of the stars forming the velocity feature
to be extremely narrow, however the metallicity of the stars in the
double peak ranges from
![]() ,
showing a
much larger spread than can be accounted for by a globular cluster.
,
showing a
much larger spread than can be accounted for by a globular cluster.
An alternative explanation, as proposed by Coleman et al. (2005,2004), is that Fornax accreted a smaller galaxy at some point in
the recent past. These authors propose the accretion of a gas-rich
dwarf ![]() 2 Gyr ago. In this case the MP stars with unrelaxed
kinematics could be the remnant of the disrupted old stellar component of
this accreted galaxy, and the asymmetric spatial distribution of the
young stars (BL and MS) could be a result of the gas which subsequently formed
stars as a consequence of the accretion process.
Measuring the metallicities of the young stars in Fornax could help to answer this
question by determining whether or not they are consistent with the bulk of the
older stellar population in Fornax. Unfortunately we do not have
spectroscopic metallicities of these stars, but
the indications from the colour of the Blue Loops in the CMD (see
Sect. 3.3.3) suggest that these stars have a metallicity of
2 Gyr ago. In this case the MP stars with unrelaxed
kinematics could be the remnant of the disrupted old stellar component of
this accreted galaxy, and the asymmetric spatial distribution of the
young stars (BL and MS) could be a result of the gas which subsequently formed
stars as a consequence of the accretion process.
Measuring the metallicities of the young stars in Fornax could help to answer this
question by determining whether or not they are consistent with the bulk of the
older stellar population in Fornax. Unfortunately we do not have
spectroscopic metallicities of these stars, but
the indications from the colour of the Blue Loops in the CMD (see
Sect. 3.3.3) suggest that these stars have a metallicity of
![]() ,
consistent with the mean of the youngest
RGB stars (age >1-2 Gyr) in our VLT/FLAMES sample.
However, our FLAMES sample also contains a significant number of stars
with higher metallicity, up to
,
consistent with the mean of the youngest
RGB stars (age >1-2 Gyr) in our VLT/FLAMES sample.
However, our FLAMES sample also contains a significant number of stars
with higher metallicity, up to
![]() .
Assuming we can
directly compare metallicities derived with these two different
methods, this could be an indication that Fornax has recently
(<1-2 Gyr ago) been polluted with external gas of lower metallicity than
the gas in Fornax at that time. This
would also explain the peculiar kinematics of the MP stars in the
centre of Fornax. However, this conclusion requires further
confirmation, such as high resolution follow-up of the metal rich
RGB stars in the central region (Letarte et al. 2006b),
spectroscopic analysis of the Blue Loop and/or main sequence stars, and detailed dynamical modelling.
.
Assuming we can
directly compare metallicities derived with these two different
methods, this could be an indication that Fornax has recently
(<1-2 Gyr ago) been polluted with external gas of lower metallicity than
the gas in Fornax at that time. This
would also explain the peculiar kinematics of the MP stars in the
centre of Fornax. However, this conclusion requires further
confirmation, such as high resolution follow-up of the metal rich
RGB stars in the central region (Letarte et al. 2006b),
spectroscopic analysis of the Blue Loop and/or main sequence stars, and detailed dynamical modelling.
Using our ESO/WFI photometry
we re-derive basic structural parameters of Fornax such as central position,
ellipticity and position angle.
In common with previous imaging studies we show that
the Fornax dwarf spheroidal galaxy
contains 3 stellar components: an ancient component, with ages between
10-15 Gyr old, which is spatially extended; an intermediate age component,
with ages 2-8 Gyr old, that contains the bulk of the stellar population
(![]() 40%), which is more centrally concentrated and
less extended than the older component; a young population,
with stars younger than
40%), which is more centrally concentrated and
less extended than the older component; a young population,
with stars younger than ![]() 1 Gyr old. The youngest component
(<1 Gyr old) is the most
centrally concentrated and is completely absent beyond a radius of 0.4 deg
from the centre, and
it shows an asymmetric, disc-like (or bar-like) distribution. Within
this component, the 200-300 Myr old stars show the most asymmetric
and centrally concentrated distribution. The colour of the plume formed in the CMD by Blue Loop
stars indicates that this young population has a metallicity [Fe/H]
between -0.7 and -1.0. Spatial analysis shows that
substructures might be present in the ancient stellar
population represented by the B-RGB.
1 Gyr old. The youngest component
(<1 Gyr old) is the most
centrally concentrated and is completely absent beyond a radius of 0.4 deg
from the centre, and
it shows an asymmetric, disc-like (or bar-like) distribution. Within
this component, the 200-300 Myr old stars show the most asymmetric
and centrally concentrated distribution. The colour of the plume formed in the CMD by Blue Loop
stars indicates that this young population has a metallicity [Fe/H]
between -0.7 and -1.0. Spatial analysis shows that
substructures might be present in the ancient stellar
population represented by the B-RGB.
The VLT/FLAMES spectroscopy in the CaT wavelength region for a
sample of 562 Fornax RGB velocity members shows that the mean metallicity
of the stellar population changes with radius with the central regions
more metal rich than the outer regions. No stars more metal poor than
![]() are found anywhere in the galaxy, but we can distinguish a metal poor
component, with a mean of
are found anywhere in the galaxy, but we can distinguish a metal poor
component, with a mean of
![]() and extending from
and extending from
![]() ,
that is found throughout the
galaxy; a more metal rich component, with a mean of
,
that is found throughout the
galaxy; a more metal rich component, with a mean of
![]() and
extending from
and
extending from
![]() ,
present mainly
within 0.7 deg from the centre and is thus more spatially concentrated than
the metal poor stars; a metal rich tail,
,
present mainly
within 0.7 deg from the centre and is thus more spatially concentrated than
the metal poor stars; a metal rich tail,
![]() ,
is
found at radii less than 0.4 deg from the centre. "Metal rich'' and "metal poor''
populations (stars with
,
is
found at radii less than 0.4 deg from the centre. "Metal rich'' and "metal poor''
populations (stars with
![]() and <-1.3, respectively) show
different kinematics: metal rich stars have a colder velocity
dispersion than metal poor stars, and these differences are not dependent
on the metallicity cut. The metal
poor component shows signs of non-equilibrium kinematics in the inner
regions (r<0.4 deg), arguably due to the accretion of external
material. A more complete modelling of chemo-dynamics of Fornax is the subject
of a future paper (Battaglia et al. 2006a).
and <-1.3, respectively) show
different kinematics: metal rich stars have a colder velocity
dispersion than metal poor stars, and these differences are not dependent
on the metallicity cut. The metal
poor component shows signs of non-equilibrium kinematics in the inner
regions (r<0.4 deg), arguably due to the accretion of external
material. A more complete modelling of chemo-dynamics of Fornax is the subject
of a future paper (Battaglia et al. 2006a).
Acknowledgements
G.B. would like to thank Andrew Cole for useful suggestions. E.T. gratefully acknowledges support from a fellowship of the Royal Netherlands Academy of Arts and Sciences A.H. acknowledges financial support from the Netherlands Organization for Scientific Research (NWO). M.D.S. would like to thank the NSF for partial support under AST-0306884. K.A.V. would like to thank the NSF for support through a CAREER award, AST 99-84073, as well as the University of Victoria for additional research funds.
Table 1: Table of Fornax ESO/WFI observations. The seeing is the average stellar FWHM from the final image.
Table 4:
Data for the observed VLT/FLAMES targets in Fornax dSph. Column (1) ID; (2)
![]() ;
(3)
;
(3)
![]() ;
(4) V magnitude; (5)
;
(4) V magnitude; (5) ![]() ;
(6) I magnitude; (7)
;
(6) I magnitude; (7) ![]() ;
(8) signal-to-noise ratio per Å ; (9) [Fe/H]; (10)
;
(8) signal-to-noise ratio per Å ; (9) [Fe/H]; (10)
![]() ;
(11) membership (Y= kinematic member; N= kinematic non-member).
The errors in metallicity are based on S/N computations and adjusted to agree with repeated measurements.
;
(11) membership (Y= kinematic member; N= kinematic non-member).
The errors in metallicity are based on S/N computations and adjusted to agree with repeated measurements.