A&A 459, 353-360 (2006)
DOI: 10.1051/0004-6361:20065678
XMM-Newton high-resolution spectroscopy reveals the chemical evolution of M 87
N. Werner1 - H. Böhringer3 - J. S. Kaastra1 - J. de Plaa1,2 - A. Simionescu3 - J. Vink2
1 - SRON Netherlands Institute for Space Research, Sorbonnelaan 2,
3584 CA Utrecht, The Netherlands
2 -
Astronomical Institute, Utrecht University, PO Box 80000,
3508 TA Utrecht, The Netherlands
3 -
Max-Planck-Institut für extraterrestrische Physik, 85748 Garching, Germany
Received 23 May 2006 / Accepted 17 July 2006
Abstract
We present a study of chemical abundances in the giant elliptical galaxy M 87 using high-resolution spectra obtained with the Reflection Grating Spectrometers during two deep XMM-Newton observations.
While we confirm the two-temperature structure of the inter-stellar medium (ISM) in M 87, we also show that a continuous temperature distribution describes the data equally well.
The high statistics allow us, for the first time, to also determine relatively accurate abundance values for carbon and nitrogen. The comparison of the abundance ratios of C, N, O, and Fe in the ISM of M 87 with those in the stellar population of our Galaxy shows that the relative contribution of core-collapse supernovae to the enrichment of the ISM in M 87 is significantly less than in the Milky Way and indicates that the enrichment of the ISM by iron through Type Ia supernovae and by carbon and nitrogen is occurring in parallel.
This suggests that the main sources of carbon and nitrogen in M 87 are the low- and intermediate-mass asymptotic giant branch stars. From the oxygen to iron abundance ratio in the hot gas,
we estimate that the relative number of core collapse and type Ia supernovae contributing to the enrichment of the ISM in the core of M 87 is 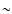 60% and
60% and 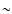 40% respectively. The spatial distributions of iron and oxygen are different. Although the oxygen abundance distribution is flat, the iron abundance peaks in the core and has a gradient throughout the
40% respectively. The spatial distributions of iron and oxygen are different. Although the oxygen abundance distribution is flat, the iron abundance peaks in the core and has a gradient throughout the
 wide field of view of the instrument, suggesting early enrichment by core-collapse supernovae and a continuous contribution of type Ia supernovae.
wide field of view of the instrument, suggesting early enrichment by core-collapse supernovae and a continuous contribution of type Ia supernovae.
Key words: galaxies: individual: M 87 - galaxies: intergalactic medium - galaxies: ISM - galaxies: abundances - cooling flows -
X-rays: galaxies: clusters
1 Introduction
The giant elliptical galaxy M 87 resides at the centre of the nearby Virgo Cluster. Its relatively small distance of 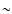 16 Mpc makes it a perfect target for studying the
processes that are important in all clusters of galaxies, but in much greater detail than possible elsewhere. Among such studies, the investigation of the structure and physics of cooling cores (previously thought to harbour cooling flows) and of the heavy element enrichment of the intra-cluster medium (ICM) gain a central importance. This is due to the fact that M 87 is, on one hand, a famous cooling core cluster and, on the other, with ICM temperature range of about 1-3 keV provides an X-ray spectrum that is very rich in metal emission lines that allow us to perform detailed diagnostics of the chemical ICM abundances. Consequently, M 87 is among the best-studied objects in the sky. Studies of M 87 at all wavelengths offer detailed insight into the balance of the ICM cooling and the heating by the central active galactic nucleus (AGN).
16 Mpc makes it a perfect target for studying the
processes that are important in all clusters of galaxies, but in much greater detail than possible elsewhere. Among such studies, the investigation of the structure and physics of cooling cores (previously thought to harbour cooling flows) and of the heavy element enrichment of the intra-cluster medium (ICM) gain a central importance. This is due to the fact that M 87 is, on one hand, a famous cooling core cluster and, on the other, with ICM temperature range of about 1-3 keV provides an X-ray spectrum that is very rich in metal emission lines that allow us to perform detailed diagnostics of the chemical ICM abundances. Consequently, M 87 is among the best-studied objects in the sky. Studies of M 87 at all wavelengths offer detailed insight into the balance of the ICM cooling and the heating by the central active galactic nucleus (AGN).
The radio map of M 87 shows two lobes of synchrotron emission located about 20-30 kpc East and Southwest of the nucleus (Owen et al. 2000). The AGN and its inner jet probably supply the lobes with
energy and relativistic electrons.
Based on the previous XMM-Newton observation, Belsole et al. (2001) and Matsushita et al. (2002) find that the ICM in M 87 has locally a single-phase structure, except for the regions
associated with radio lobes, where the X-ray emission can be modelled with two thermal components with temperatures of about 2 and 1 keV. The cooler gas fills a small volume
compared to the hotter component and is confined to the radio arms, rather than being associated with the potential well of the galaxy (Molendi 2002). Based on radio and
X-ray observations, Churazov et al. (2001) developed a model, according to which the bubbles seen in radio buoyantly rise through the hot plasma in the cluster, and during their
rise, they lift cooler X-ray emitting gas up from the central region out to larger distances.
This scenario has also been studied in numerical hydrodynamical simulations by Brüggen & Kaiser (2002) who illustrated the turbulent mixing of hot, cooler, and relativistic plasma initiated by the bubble-ICM interaction. This effect probably gives rise to the observed two-phase, or multi-phase, temperature structure in the interaction region. Plasma cooling below a temperature of 0.8 keV is observed neither in the XMM Reflection Grating Spectrometers (RGS) X-ray spectra (Sakelliou et al. 2002) nor in the XMM European Photon Imaging Camera (EPIC) spectra of M 87 (Böhringer et al. 2002).
Böhringer et al. (2001) and Finoguenov et al. (2002) show that oxygen has a relatively flat radial
abundance distribution compared to the steep gradients of silicon, sulfur, argon, calcium, and iron. The strong abundance increase of iron in the core of M 87 compared to that
of oxygen indicates an enhanced contribution of type Ia supernovae (SN Ia) in the central regions of the galaxy. The flatter oxygen gradient was also confirmed by
Matsushita et al. (2003). On the other hand, while Gastaldello & Molendi (2002) confirm the strong heavy-element gradient, they also find a significant increase in abundance for light
elements, in particular oxygen, toward the centre of the galaxy, which contradicts the results of Böhringer et al. (2001), Finoguenov et al. (2002), and Matsushita et al. (2003).
In this paper we report the results obtained by combining two deep observations with the Reflection Grating Spectrometer (RGS, den Herder et al. 2001) aboard XMM-Newton. The strongly-peaked high X-ray luminosity makes M 87 an ideal target for the RGS. The high statistics allow us to reliably determine the abundance of carbon and nitrogen for the first time.
While it is well known that elements from oxygen up to the iron group are primarily produced in supernovae, the main sources of carbon and nitrogen are still being debated. Both elements are believed to originate from a wide range of sources, including winds of short-lived massive metal-rich stars, longer-lived low- and intermediate-mass stars, and also an early generation of massive stars (e.g. Meynet & Maeder 2002; Gustafsson et al. 1999; Chiappini et al. 2003).
Shi et al. (2002) find that carbon is enriched by winds of metal-rich massive stars at the beginning of the Galactic disk evolution, while at the later stage it is produced mainly by low-mass stars.
They also conclude that nitrogen is mainly produced by intermediate-mass stars.
Bensby & Feltzing (2006) find that the carbon enrichment in the Galaxy is happening on a time scale very similar to that of iron. They conclude that, while at low metallicities the main carbon contributors are massive stars, carbon is later produced mainly by asymptotic giant branch (AGB) stars.
The deep observation also allows us to extract spatially-resolved high-resolution spectra and to determine radial temperature profiles and abundance profiles of several elements out
to
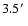 from the core of M 87.
from the core of M 87.
For the distance to M 87, we adopt a value of 16.1 Mpc (Tonry et al. 2001), which implies a linear scale of 4.7 kpc arcmin-1.
Unless specified otherwise, all errors are at the 68% confidence level for one interesting parameter (
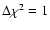 ).
).
M 87 was observed with XMM-Newton on June 19, 2000 for 60 ks and re-observed in January 2005 with an exposure time of 109 ks.
We process the RGS data from both observations with the 6.5.0 version of the XMM-Newton Science Analysis System (SAS) following the method described in Tamura et al. (2001).
In order to minimise the effect of soft protons in our spectral analysis, we extract a light-curve using the events on CCD 9 of the RGS outside the central area, with a distance larger than 30
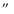 from the dispersion axis, and cut out all time intervals where the count rate deviates from the mean by more than
from the dispersion axis, and cut out all time intervals where the count rate deviates from the mean by more than 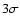 .
After removing the high background periods from the data, the net effective exposure time is 40 ks for the first observation and 84 ks for the second observation.
.
After removing the high background periods from the data, the net effective exposure time is 40 ks for the first observation and 84 ks for the second observation.
Because the extended emission fills the entire field-of-view of the RGS, we model the background using the standard RGS background model available in SAS. We correct the standard response for the RGS instruments by additional, time-dependent large-scale effective area corrections found by one of us (Jacco Vink;
more information can be found on the website of the XMM-Newton users group![[*]](/icons/foot_motif.gif) ), which are based on the standard XMM-Newton calibration sources MRK 421 and PKS 2155-304. These corrections will be implemented
in the forthcoming release of the XMM-Newton SAS software package and calibration data files.
), which are based on the standard XMM-Newton calibration sources MRK 421 and PKS 2155-304. These corrections will be implemented
in the forthcoming release of the XMM-Newton SAS software package and calibration data files.
To derive spatial temperature and abundance profiles from the RGS, we extract spectra from four
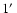 wide regions along the cross-dispersion axis of the instrument. We select the events from rectangular areas on the CCD strip in the cross-dispersion direction (see Fig. 3).
wide regions along the cross-dispersion axis of the instrument. We select the events from rectangular areas on the CCD strip in the cross-dispersion direction (see Fig. 3).
The observed line emission of the hot gas is broadened by the spatial extent of the source along the dispersion direction. In order to account for this effect in the spectral modelling, we convolve the model with the surface brightness profile of the galaxy along the dispersion direction (Tamura et al. 2004). We derive the surface brightness profile for each extraction region from the EPIC/MOS1 image in the 0.8-1.4 keV band along the dispersion direction of the RGS and convolve it with the RGS response to produce a predicted line spread function (lsf). Because the radial profile for an ion can be different from this intensity profile, this method is not ideal. Therefore, we introduce two additional parameters, the width and the centroid of the lsf, which are left free during spectral fitting in order to match the observed profiles of the main emission lines. The scale parameter s for the width is the ratio of the observed lsf width and the width of the intensity profile.
3 Spectral models
For the spectral analysis we use the SPEX package (Kaastra et al. 1996).
We model the Galactic absorption using the hot model of that package, which calculates
the transmission of a plasma in collisional ionization equilibrium (CIE) with cosmic abundances. We mimic
the transmission of a neutral gas by putting its temperature to 0.5 eV. Compared to the older standard absorption models like Morrison & McCammon (1983), the hot model is using continuum opacities from Verner & Yakovlev (1995). Line opacities for most ions are from Verner et al. (1996).
To find the best description of the emission of the hot plasma in M 87, we use a combination of two
CIE plasma models (MEKAL) with coupled abundances. We also try to model the emission of the hot plasma with a differential emission measure
(DEM) model with a cut-off power-law distribution of emission measures versus temperature (wdem). The wdem model appears to be a good empirical approximation for
the spectrum in cooling cores of clusters of galaxies (e.g. de Plaa et al. 2006; Kaastra et al. 2004; Werner et al. 2006).
The emission measure
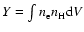 (where
(where
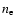 and
and
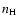 are the electron and proton densities, V is the volume of the
source) in the wdem model is specified in Eq. (1) as adapted from Kaastra et al. (2004):
are the electron and proton densities, V is the volume of the
source) in the wdem model is specified in Eq. (1) as adapted from Kaastra et al. (2004):
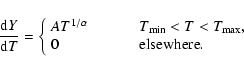 |
(1) |
The emission measure distribution has a cut-off at
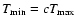 .
For
.
For
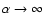 ,
we obtain a flat emission measure distribution.
The emission measure weighted mean temperature
,
we obtain a flat emission measure distribution.
The emission measure weighted mean temperature
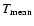 is given by:
is given by:
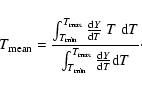 |
(2) |
By integrating this equation between
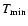 and
and
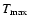 ,
we obtain a direct relation between
,
we obtain a direct relation between
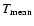 and
and
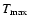 as a function of
as a function of 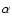 and c:
and c:
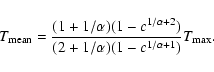 |
(3) |
A comparison of the wdem model with the classical cooling-flow model can be found in de Plaa et al. (2005). We note that the wdem model contains less cool gas than
the classical cooling-flow model, which is consistent with recent observations (Peterson et al. 2003,2001).
The spectral lines in the MEKAL model are fitted self consistently. From the fits we obtain the abundances of all elements with detected line emission.
Throughout the paper we give the measured abundances relative to the proto-solar values given by Lodders (2003).
We note that the values of the fitted elemental abundances do not depend on the chosen values for the solar abundances, and we give the values of the elemental abundances with
respect to solar for convenience. The recent solar abundance determinations by Lodders (2003)
give significantly lower abundances of oxygen, neon, and iron than those measured by Anders & Grevesse (1989).
The centre of M 87 harbours an active galactic nucleus (AGN). Its emission can be fitted well with a power-law. A correct description of the AGN emission is essential for determining the absolute abundances in the core of M 87 with the RGS. In the first observation we determine the parameter values of the power-law by fitting the EPIC spectrum of the core of the galaxy. We extract the spectrum from a small circular region with a radius of 20
 and fit it with a power-law and two thermal models. The parameter values of the power-law strongly depend on the value for the absorption column density in the model. For the best value measured for the absorption column density
and fit it with a power-law and two thermal models. The parameter values of the power-law strongly depend on the value for the absorption column density in the model. For the best value measured for the absorption column density
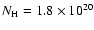 cm-2 (Lieu et al. 1996), we obtain a power-law with a photon index of
cm-2 (Lieu et al. 1996), we obtain a power-law with a photon index of
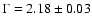 and a 2-10 keV luminosity of (
and a 2-10 keV luminosity of (
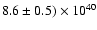 erg s-1.
erg s-1.
The AGN was much brighter during the second observation than during the first one, and its photon index also changed.
However, the strong pile-up both in EPIC/MOS and EPIC/pn does not allow us to determine the properties of the AGN emission from the EPIC observations. We have to do it using the RGS, which is much less susceptible to pile-up.
Because the two observations were performed with similar position angles, the thermal cluster emission in the two datasets is the same. We determine the parameter values of the cluster emission in the first dataset.
While we fit the parameter values for the power-law emission in the second dataset, we keep the parameter values of the cluster emission fixed. We find a power-law with a photon index of
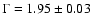 and a 2-10 keV luminosity of
and a 2-10 keV luminosity of
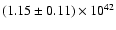 erg s-1.
To confirm this high flux, we scale the RGS spectrum obtained during the first observation to the exposure time of the second observation and subtract it from the RGS spectrum from the second dataset. This way we get rid of most of the cluster emission, which allows us to analyse the excess power-law emission from the central AGN detected during the second observation. With this exercise we confirm our previous results on the high AGN luminosity in the second dataset.
erg s-1.
To confirm this high flux, we scale the RGS spectrum obtained during the first observation to the exposure time of the second observation and subtract it from the RGS spectrum from the second dataset. This way we get rid of most of the cluster emission, which allows us to analyse the excess power-law emission from the central AGN detected during the second observation. With this exercise we confirm our previous results on the high AGN luminosity in the second dataset.
While fitting the thermal ICM/ISM emission, we keep the power-law parameters fixed at the best determined values. The uncertainties in the AGN luminosity introduce systematic uncertainties in the emission measure of the thermal components and in the absolute abundance values. The uncertainties in the photon index of the power-law emission are much smaller than those in the luminosity and thus have less of an influence on the best-fit parameters of the thermal components. If the luminosity of the AGN in the second observation is 10% lower than the adopted value, then the best-fit emission measures of the thermal components will be 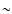 15% higher and the absolute abundance values will be
15% higher and the absolute abundance values will be 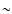 15% lower. If the luminosity of the AGN is 10% higher than the adopted value, then the best-fit emission measures will be
15% lower. If the luminosity of the AGN is 10% higher than the adopted value, then the best-fit emission measures will be 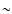 15% lower and the absolute abundance values
15% lower and the absolute abundance values 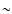 15% higher. The best-fit temperatures and relative abundance values are, however, robust and the systematic uncertainties arising from the uncertainty in the AGN emission are smaller than their statistical errors.
15% higher. The best-fit temperatures and relative abundance values are, however, robust and the systematic uncertainties arising from the uncertainty in the AGN emission are smaller than their statistical errors.
Since the difference in the position angles of the two observations is
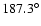 ,
the strips used to extract the spectra from the RGS are rotated with respect to each other by only
,
the strips used to extract the spectra from the RGS are rotated with respect to each other by only
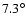 .
While in the first observation the core of the emission falls on the centre of the RGS detector, in the second observation the core of the emission is offset from the centre of the detector by
.
While in the first observation the core of the emission falls on the centre of the RGS detector, in the second observation the core of the emission is offset from the centre of the detector by 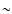 1.5
1.5
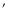 .
To obtain a combined spectrum with the highest possible statistics for the core of the galaxy, we extract spectra from a
.
To obtain a combined spectrum with the highest possible statistics for the core of the galaxy, we extract spectra from a
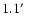 wide strip centred on the core of M 87 from both observations. We fit these spectra simultaneously. The fit to the total spectrum is shown in Fig. 1.
wide strip centred on the core of M 87 from both observations. We fit these spectra simultaneously. The fit to the total spectrum is shown in Fig. 1.
We try two different thermal models to fit the emission of the hot gas in M 87: a combination of
two thermal components and a differential emission measure model (see Sect. 3). The results of these two fits are shown in Table 1. The reduced 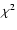 s of both fits are
s of both fits are 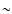 1.4, so neither of the thermal models can be ruled out by our analysis.
1.4, so neither of the thermal models can be ruled out by our analysis.
![\begin{figure}
\par\includegraphics[angle=270,width=8.6cm,clip]{5678f1.ps}
\end{figure}](/articles/aa/full/2006/44/aa5678-06/Timg32.gif) |
Figure 1:
1st-order RGS spectra obtained during two observations with different luminosities of the central AGN. The two spectra are extracted from a
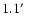 wide strip centred on the core of M 87 and are fitted simultaneously. The total useful exposure time is 124 ks. The continuous line represents the best-fit model of the spectrum.
wide strip centred on the core of M 87 and are fitted simultaneously. The total useful exposure time is 124 ks. The continuous line represents the best-fit model of the spectrum. |
| Open with DEXTER |
Since the continuum is not determined very well by the RGS, absolute abundance values obtained by fitting different thermal models are slightly different. However, the relative abundances are consistent for both thermal models. In Table 1 we show our best-fit abundances relative to iron, which is, due to the strong iron lines in the spectrum, the element with the best determined abundance value. The excellent statistics of the combined spectrum allow us, for the first time, to determine relatively accurate abundance values also for carbon and nitrogen. All the detected spectral lines are shown in Fig. 2, which shows the residuals of the RGS spectrum with line emission set to zero in the model.
We note that Sakelliou et al. (2002) use a cooling-flow model with
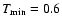 keV, in combination with a single-temperature model. By fitting this model we do not obtain a
better fit than with the 2-temperature model and the determined abundances (also the absolute abundances) are consistent with those obtained with the 2-temperature model. The abundance values determined by Sakelliou et al. (2002) are different from our values due to a different power-law slope and normalisation used to account for the AGN emission. They obtained different parameter values for the power-law because they used a different (obtained by a survey at lower spatial resolution) Galactic absorption column density of
keV, in combination with a single-temperature model. By fitting this model we do not obtain a
better fit than with the 2-temperature model and the determined abundances (also the absolute abundances) are consistent with those obtained with the 2-temperature model. The abundance values determined by Sakelliou et al. (2002) are different from our values due to a different power-law slope and normalisation used to account for the AGN emission. They obtained different parameter values for the power-law because they used a different (obtained by a survey at lower spatial resolution) Galactic absorption column density of
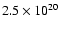 cm-2.
cm-2.
The spectra lack emission from lines that trace gas cooling below 0.8 keV (e.g. O VII line emission), which confirms the previous results of Sakelliou et al. (2002). The spectra, however, allow us to put strong upper limits on the amount of the cooling gas. Our upper limit on the emission measure of the gas with a temperature of 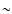 0.2 keV with the same oxygen abundance as the ambient hot gas is
0.2 keV with the same oxygen abundance as the ambient hot gas is
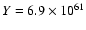 cm-3. If
we assume that all this gas is in a sphere with a radius of
cm-3. If
we assume that all this gas is in a sphere with a radius of
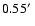 ,
then our upper limit for the total mass of the
,
then our upper limit for the total mass of the 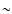 0.2 keV gas is
0.2 keV gas is 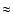
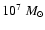 ,
which is
,
which is 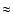 8% of the total gas in the sphere (
8% of the total gas in the sphere (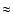
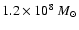 ).
).
Table 1:
Fit results for the RGS spectra extracted from a 1.1
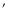 wide strip centred on the core of M 87.
The iron abundance is given with respect to the proto-solar values by Lodders (2003)
and the other abundances with respect to iron. Emission measures (
wide strip centred on the core of M 87.
The iron abundance is given with respect to the proto-solar values by Lodders (2003)
and the other abundances with respect to iron. Emission measures (
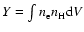 )
are given in 1064 cm-3.
)
are given in 1064 cm-3.
![\begin{figure}
\par\includegraphics[angle=90,width=8.6cm,clip]{5678f2.ps}
\end{figure}](/articles/aa/full/2006/44/aa5678-06/Timg65.gif) |
Figure 2:
Residuals of the fit to the combined RGS spectrum with a total exposure time of 124 ks with line emission set to zero in the
model. We indicate the positions of all the detected spectral lines. |
| Open with DEXTER |
In order to detect intrinsic absorption by the putative cooling gas in the core of M 87, and/or by the warm-hot intergalactic medium associated with the Virgo cluster (reported by Fujimoto et al. 2004), we subtract the first observation from the second one. This way we get rid of most of the cluster emission, which allows us to analyse the excess power-law emission from the central AGN detected during the second observation. We do not see any absorption lines in the power-law spectrum. However, we find an upper limit of 1016 cm-2 for the O VII absorption column.
Resonant scattering of line emission is expected to be important in the dense cores of clusters of galaxies (e.g. Gilfanov et al. 1987). Its detection in the RGS spectra of the elliptical galaxy NGC 4636 in the Virgo cluster was reported by Xu et al. (2002). The best lines to detect resonant scattering in M 87 are the
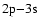 and the
and the
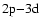 Fe XVII lines at 17.1 Å and 15.01 Å, respectively. The oscillator strength of the
Fe XVII lines at 17.1 Å and 15.01 Å, respectively. The oscillator strength of the
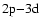 transition is substantially higher than that of the
transition is substantially higher than that of the
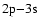 transitions. Their ratios at different distances from the core of the galaxy can reveal resonant scattering of the line at 15.01 Å. Since these lines originate from the same ion of the same element, the observed spatial dependence of their ratios cannot be due to gradients in temperature or elemental abundances in the ISM. However, these lines can be determined well only close to the core of the galaxy. We determine the ratios of their equivalent widths in a 30
transitions. Their ratios at different distances from the core of the galaxy can reveal resonant scattering of the line at 15.01 Å. Since these lines originate from the same ion of the same element, the observed spatial dependence of their ratios cannot be due to gradients in temperature or elemental abundances in the ISM. However, these lines can be determined well only close to the core of the galaxy. We determine the ratios of their equivalent widths in a 30
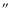 wide strip going through the core of the galaxy and in the combined spectrum extracted from two 15
wide strip going through the core of the galaxy and in the combined spectrum extracted from two 15
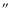 strips next to the central extraction region. While the ratio of the equivalent widths of the
strips next to the central extraction region. While the ratio of the equivalent widths of the
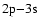 lines to that of the
lines to that of the
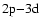 line in the central region is
line in the central region is 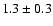 ,
the ratio in the neighbouring bins is
,
the ratio in the neighbouring bins is 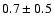 .
This result indicates that 15.01 Å photons emitted in the core of the galaxy get scattered before they exit the interstellar medium. However, the large errors do not allow us to make definite conclusions.
.
This result indicates that 15.01 Å photons emitted in the core of the galaxy get scattered before they exit the interstellar medium. However, the large errors do not allow us to make definite conclusions.
The excellent statistics of the RGS spectra obtained during the second observation allow us to extract spectra from four
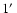 wide strips in the cross-dispersion
direction of the instrument and to make radial temperature and abundance profiles up to
wide strips in the cross-dispersion
direction of the instrument and to make radial temperature and abundance profiles up to
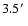 from the core of the galaxy. Unfortunately the core of the emission was offset
from the centre of the RGS detector so we could not determine the profiles from both sides of the core.
from the core of the galaxy. Unfortunately the core of the emission was offset
from the centre of the RGS detector so we could not determine the profiles from both sides of the core.
Since the 2-temperature model describes the data just as well as the wdem model and because the 2-temperature model may also be justified by two separate thermal
components within and outside of the radio lobes in M 87, we fit all the spectra with the simpler 2-temperature model.
The best-fit results are shown in Table 2.
We note that the extraction regions from which we determine the RGS radial profiles are actually sampling the Southwestern lobe at different distances from the core (see Fig. 3).
Table 2:
Fit results for spatially-resolved RGS spectra. We model the plasma with two thermal components.
Abundances are given with respect to the proto-solar values by Lodders (2003). The emission measures are given in 1064 cm-3.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{5678f3.eps}\end{figure}](/articles/aa/full/2006/44/aa5678-06/Timg107.gif) |
Figure 3:
The RGS extraction regions used for fitting the radial profiles overplotted on a temperature map by
Aurora Simionescu (in preparation). Our radial profiles go along the Southwestern lobe filled with cooler gas - clearly seen on the temperature map. |
| Open with DEXTER |
The radial temperature profiles for the two thermal components are shown in Fig. 4. They both show an increase in temperature in the
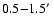 region and
do not show a radial gradient. The radial distribution of the emission measures shows a
region and
do not show a radial gradient. The radial distribution of the emission measures shows a 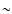 3 times larger relative contribution of the cooler gas in the central region than
in the
3 times larger relative contribution of the cooler gas in the central region than
in the
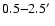 region.
region.
The radial abundance profiles for oxygen and iron are
shown in Fig. 5. We see that the radial distributions of oxygen and iron, the two best-determined abundances, are different. Both elements have a peak in the core of the cluster, but while the oxygen abundance drops at
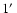 distance from the core by
distance from the core by
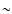 17% and then its distribution stays flat, the distribution of iron shows a gradient all the way out in our investigated region.
17% and then its distribution stays flat, the distribution of iron shows a gradient all the way out in our investigated region.
The radial distribution of neon also seems to show a gradient throughout the investigated region. But its abundance values are less certain. In the extraction regions not going through the core of the cluster, the spatial extent of the source along the dispersion direction broadens the lines in the RGS, and the neon line gets blended with the iron lines. Thus, for extraction regions farther away from the core of the galaxy, the systematic uncertainties on the neon abundance get higher. The radial distribution of carbon and nitrogen seems to be consistent with that of iron; however, their values are too uncertain to draw conclusions.
We note that the best-fit temperature and abundance values determined from the RGS are actually the mean values along the dispersion direction of the instrument and the true radial profiles have stronger gradients than those derived from the RGS spectra.
![\begin{figure}
\par\includegraphics[angle=270,width=7.6cm,clip]{5678f4.ps}\end{figure}](/articles/aa/full/2006/44/aa5678-06/Timg110.gif) |
Figure 4:
Radial temperature profiles of the two thermal components obtained by fitting spectra extracted from rectangular regions in the cross-dispersion direction of the RGS. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=270,width=8.3cm,clip]{5678f5.ps}
\end{figure}](/articles/aa/full/2006/44/aa5678-06/Timg111.gif) |
Figure 5:
Radial abundance profiles for oxygen and iron obtained by fitting spectra extracted from rectangular regions in the cross-dispersion direction of the RGS. |
| Open with DEXTER |
5 Discussion
5.1 Chemical enrichment by type Ia and core collapse supernovae
The ISM/ICM in M 87 was enriched by heavy elements primarily by core collapse supernovae (SN
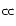 ), type Ia supernovae (SN Ia), and stellar winds. To investigate the relative contribution of SN Ia and SN
), type Ia supernovae (SN Ia), and stellar winds. To investigate the relative contribution of SN Ia and SN
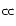 ,
one can use the observed ratios of elements (produced by supernovae) with detected line emission to iron to find the best fit to the function:
,
one can use the observed ratios of elements (produced by supernovae) with detected line emission to iron to find the best fit to the function:
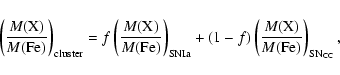 |
(4) |
where the expression
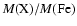 represents the fraction of the mass of a given element to the mass of iron as observed in the galaxy (cluster), as predicted for the
yield of SN Ia and as predicted for the yield of SN
represents the fraction of the mass of a given element to the mass of iron as observed in the galaxy (cluster), as predicted for the
yield of SN Ia and as predicted for the yield of SN
 ;
f represents the fraction of iron produced by SN Ia relative to the total mass of iron produced by the two main types of supernovae.
;
f represents the fraction of iron produced by SN Ia relative to the total mass of iron produced by the two main types of supernovae.
For nucleosynthesis products of SN
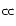 ,
we adopt an average yield of stars on the mass range from 10
,
we adopt an average yield of stars on the mass range from 10 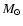 to 50
to 50 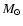 calculated by Tsujimoto et al. (1995)
assuming a Salpeter initial mass function. For nucleosynthesis products of SN Ia, we adopt values calculated for the delayed-detonation model WDD2 by Iwamoto et al. (1999).
calculated by Tsujimoto et al. (1995)
assuming a Salpeter initial mass function. For nucleosynthesis products of SN Ia, we adopt values calculated for the delayed-detonation model WDD2 by Iwamoto et al. (1999).
The best determined are the oxygen and iron abundance. Assuming that all iron and oxygen is produced by supernovae, we estimate from their ratios that 86% of iron is coming
from SN Ia. Then the relative number of SN Ia contributing to the enrichment of the ICM is 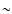 40%, while the relative number of SN
40%, while the relative number of SN
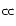 is
is 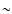 60%. We note that Böhringer et al. (2005), based on the XMM-Newton EPIC measurements analysed by Matsushita et al. (2003), estimate that about 80% of iron comes from SN Ia. Given the different extraction regions and the gradient in the iron abundance, this estimate agrees with our result. The measured neon abundance is not matched well by the supernova models, because it is much higher than what the models predict (see Table 3), which was also observed previously in the cluster of galaxies 2A 0335+096 (Werner et al. 2006). The best fit for the magnesium abundance value may be influenced by the uncertainties in the effective area calibration of the RGS at short wavelengths. Therefore, we do not discuss it here.
60%. We note that Böhringer et al. (2005), based on the XMM-Newton EPIC measurements analysed by Matsushita et al. (2003), estimate that about 80% of iron comes from SN Ia. Given the different extraction regions and the gradient in the iron abundance, this estimate agrees with our result. The measured neon abundance is not matched well by the supernova models, because it is much higher than what the models predict (see Table 3), which was also observed previously in the cluster of galaxies 2A 0335+096 (Werner et al. 2006). The best fit for the magnesium abundance value may be influenced by the uncertainties in the effective area calibration of the RGS at short wavelengths. Therefore, we do not discuss it here.
The supernovae produce only small amounts of carbon and nitrogen.
As shown in Table 3, we observe about 300 times more nitrogen and 10 times more carbon in M 87 than what can be explained by the employed supernova models.
The difference between the predicted mass produced by all supernovae (as calculated from the total mass of iron, relative numbers of SN Ia and SN
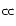 ,
and the theoretical yields) and the total observed mass of these elements can be used to put an upper limit on the contribution from stellar winds to the chemical enrichment of the ICM.
,
and the theoretical yields) and the total observed mass of these elements can be used to put an upper limit on the contribution from stellar winds to the chemical enrichment of the ICM.
However, to estimate the total mass of these metals is difficult. The long and narrow extraction region of RGS and the disturbed nature of the core only allow us to make rough estimates. If we assume that the measured central abundances are typical of the inner
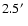 of the galaxy and we consider an average density of
of the galaxy and we consider an average density of
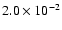 cm-3 (based on Matsushita et al. 2002), then the total mass of carbon and nitrogen in the ISM is
cm-3 (based on Matsushita et al. 2002), then the total mass of carbon and nitrogen in the ISM is 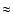
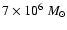 and
and 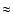
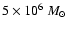 ,
respectively. However, the radial abundance profiles of nitrogen and carbon suggest abundance gradients, which means that, since the measured abundance values are an average along the dispersion direction of the RGS, the true central abundance is probably higher. Because of the assumptions, the estimated masses can be considered as lower limits.
,
respectively. However, the radial abundance profiles of nitrogen and carbon suggest abundance gradients, which means that, since the measured abundance values are an average along the dispersion direction of the RGS, the true central abundance is probably higher. Because of the assumptions, the estimated masses can be considered as lower limits.
Table 3:
Comparison of the observed mass ratios in the core of M 87 for five elements to iron with the predicted mass ratios, assuming that all the elements were produced only by supernovae with 86% of all iron produced by SN Ia. The observed to predicted ratio for oxygen is here by definition one.
![\begin{figure}
\par\includegraphics[angle=270,width=7cm,clip]{5678f6a.ps}\par\vspace*{2mm}
\includegraphics[angle=270,width=7cm,clip]{5678f6b.ps}\end{figure}](/articles/aa/full/2006/44/aa5678-06/Timg121.gif) |
Figure 6:
Comparison of the [C/Fe] and [O/Fe] enrichment in M 87 with those
of the Galactic thin and thick disk stars of Bensby & Feltzing (2006). Thin and thick disk stars are marked by open and filled circles, respectively. The value for M 87 is indicated by the asterisk. |
| Open with DEXTER |
Although, it is well-known that elements from oxygen up to the iron group are produced primarily in supernovae, the main sites of the carbon and nitrogen production are still being debated. It is believed that both elements are being contributed by a wide range of sources. The main question is whether their production is dominated by the winds of short-lived massive stars or by the longer-lived progenitors of AGB stars.
An analysis of the enrichment history of carbon in our Galaxy has, for example, been performed
by Bensby & Feltzing (2006). They find that the
ratio C/Fe is fairly constant with a decrease of
about a factor of 1.5 over the chemical evolution
history involving [Fe/H] values from -1 to +0.4
as covered in their survey. At the same time, the
O/Fe ratio decreases by about a factor of 5. The general
explanation of this large decrease in the relative oxygen
abundance is an early enrichment by SN
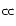 with
high O/Fe values and a subsequent production of primarily iron
by SN Ia, which go off on much longer time scales than do the SN
with
high O/Fe values and a subsequent production of primarily iron
by SN Ia, which go off on much longer time scales than do the SN
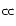 .
In contrast, the flat C/Fe ratio then implies
that the enrichment by Fe through SN Ia and the C pollution
has occurred very much in parallel. The similar enrichment time-scale
suggests that the main sites of carbon production are the longer-lived progenitors of AGB stars.
.
In contrast, the flat C/Fe ratio then implies
that the enrichment by Fe through SN Ia and the C pollution
has occurred very much in parallel. The similar enrichment time-scale
suggests that the main sites of carbon production are the longer-lived progenitors of AGB stars.
For our case of the, on average, much older stellar population
of M 87, it is now interesting to compare the enrichment
situation with that of our Galaxy. In Fig. 6 we compare
the C/Fe and O/Fe enrichment in M 87 with that
of the Galactic thin and thick disk stars of Bensby & Feltzing (2006).
We see that, while O/Fe is significantly lower in the ISM of M 87
than in the stellar population of our Galaxy, C/Fe is comparable to
the lowest C/Fe values detected in the Milky Way. The O/Fe ratio in M 87
is so low probably due to the fact that the contribution of SN Ia to the enrichment of the ISM in M 87 is approximately 3 times as large as in our Galaxy; according to Tsujimoto et al. (1995), the relative number of SN Ia for our Galaxy is
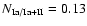 .
The low O/Fe ratio also suggests that the star formation in M 87 has essentially stopped.
The C/Fe ratio is consistent with the Galactic value, which indicates that the enrichment by Fe from SN Ia and by C through AGB stars is also occurring in parallel in M 87.
.
The low O/Fe ratio also suggests that the star formation in M 87 has essentially stopped.
The C/Fe ratio is consistent with the Galactic value, which indicates that the enrichment by Fe from SN Ia and by C through AGB stars is also occurring in parallel in M 87.
In Fig. 7 we compare the N/Fe and N/O enrichment with a sample of Galactic stars published by Chen et al. (2000) and Shi et al. (2002). The measured N/O ratio in M 87 is higher than in the sample of Galactic stars. However, the N/Fe ratio is comparable to the highest values detected in this sample. Given the old stellar population in M 87, the high N/O ratio in the ISM is not surprising. While the oxygen (and probably also some of the nitrogen) was supplied by core collapse supernovae early in the enrichment history, nitrogen is still being constantly supplied by intermediate mass AGB stars on a time scale possibly similar to the enrichment by iron.
While the chemical abundances of all elements have a peak in the centre of the galaxy, the radial abundance profiles indicate that the spatial distributions of oxygen and iron are different. The radial distribution of iron, primarily a type Ia supernova product, has a gradient throughout the field of view of the RGS. However, the radial distribution of oxygen, primarily a product of core collapse supernovae, seems to be flat with a projected abundance of 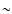 0.5 solar, with only a modest peak in the extraction region centred on the core of the galaxy.
While the flat component of the distribution of core collapse supernova products has been produced by
supernovae going off primarily in the earlier stages of the evolution of the galaxy, type Ia supernova still continue to enrich the ISM/ICM in M 87.
0.5 solar, with only a modest peak in the extraction region centred on the core of the galaxy.
While the flat component of the distribution of core collapse supernova products has been produced by
supernovae going off primarily in the earlier stages of the evolution of the galaxy, type Ia supernova still continue to enrich the ISM/ICM in M 87.
Our results confirm the previous results of Böhringer et al. (2001), Finoguenov et al. (2002), and Matsushita et al. (2003), who showed, based on observations with EPIC, that oxygen has a relatively flat radial abundance distribution compared to the steep gradients of the heavier elements. While the low spectral resolution of EPIC combined with the relative closeness of the iron lines and calibration problems at low energies left some room for doubts about these early results, the RGS with its high spectral resolution showed conclusively that the spatial distributions of oxygen and iron are different.
However, the systematic uncertainties in the absolute abundance values still leave open the possibility of more enhanced abundance values in the innermost bin fitted with the RGS, which would mean not only an even stronger central peak in the distribution of iron, but also a peak in the oxygen distribution.
We have analysed the temperature structure and the chemical abundances in the giant elliptical galaxy M 87 using high-resolution spectra obtained during two deep XMM-Newton observations with the Reflection Grating Spectrometers.
We found that:
-
Even though we confirm the two-temperature structure of the ISM, we show that a multi-temperature wdem fit also describes the data well and gives the same relative abundances as the two-temperature fit.
-
The O/Fe and O/N ratios in the ISM of M 87 are lower than in the stellar population of our Galaxy, which shows that the relative contribution of core collapse supernovae in the old stellar population of M 87 to the enrichment of the ISM was significantly less than in our Galaxy.
-
The comparison of the C/Fe and N/Fe ratios in the ISM of M 87 with those in the stellar population of our Galaxy suggests that the enrichment of the ISM by iron through Type Ia supernovae and by carbon and nitrogen is occurring in parallel and thus the dominant sources of carbon and nitrogen in M 87 are the intermediate- and low-mass AGB stars.
-
From the oxygen to iron abundance ratio we estimate that the relative number of core collapse and type Ia supernovae contributing to the enrichment of the ISM in the core of M 87 is
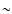 60% and
60% and 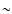 40%, respectively.
40%, respectively.
-
The spatial distributions of oxygen and iron in M 87 are different. While the oxygen abundance distribution is flat, the iron abundance peaks in the core and has a gradient throughout the field of view of the instrument, suggesting an early enrichment by core-collapse supernovae and a continuous contribution of SN Ia.
Acknowledgements
This work is based on observations obtained with XMM-Newton, an ESA science mission with instruments
and contributions directly funded by ESA member states and the USA (NASA). The Netherlands Institute
for Space Research (SRON) is supported financially by NWO, the Netherlands Organization for Scientific Research.
We would like to thank Onno Pols for reading and giving constructive comments on a draft version of the paper.
- Anders, E.,
& Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53,
197 [NASA ADS] [CrossRef] (In the text)
- Belsole, E.,
Sauvageot, J. L., Böhringer, H., et al. 2001,
A&A, 365, L188 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Bensby, T.,
& Feltzing, S. 2006, MNRAS, 367, 1181 [NASA ADS] [CrossRef] (In the text)
-
Böhringer, H., Belsole, E., Kennea, J., et al. 2001,
A&A, 365, L181 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
-
Böhringer, H., Matsushita, K., Churazov, E., Ikebe, Y., &
Chen, Y. 2002, A&A, 382, 804 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
-
Böhringer, H., Matsushita, K., Finoguenov, A., Xue, Y., &
Churazov, E. 2005, Adv. Space Res., 36, 677 [NASA ADS] (In the text)
- Brüggen,
M., & Kaiser, C. R. 2002, Nature, 418, 301 [NASA ADS] [CrossRef] (In the text)
- Chen, Y. Q.,
Nissen, P. E., Zhao, G., Zhang, H. W., & Benoni, T.
2000, A&AS, 141, 491 [EDP Sciences] [NASA ADS] (In the text)
-
Chiappini, C., Matteucci, F., & Meynet, G. 2003, A&A, 410,
257 [EDP Sciences] [NASA ADS] [CrossRef]
- Churazov,
E., Brüggen, M., Kaiser, C. R., Böhringer, H., &
Forman, W. 2001, ApJ, 554, 261 [NASA ADS] [CrossRef] (In the text)
- de Plaa, J.,
Kaastra, J. S., Méndez, M., et al. 2005, Adv. Space
Res., 36, 601 [NASA ADS] (In the text)
- de Plaa, J.,
Werner, N., Bykov, A., Kaastra, J. S., & Bleeker,
J. A. M. 2006, A&A, 452, 397 [EDP Sciences] [NASA ADS] [CrossRef]
- den Herder,
J. W., Brinkman, A. C., Kahn, S. M., et al.
2001, A&A, 365, L7 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
-
Finoguenov, A., Matsushita, K., Böhringer, H., Ikebe, Y.,
& Arnaud, M. 2002, A&A, 381, 21 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Fujimoto,
R., Takei, Y., Tamura, T., et al. 2004, PASJ, 56, L29 [NASA ADS] (In the text)
-
Gastaldello, F., & Molendi, S. 2002, ApJ, 572, 160 [NASA ADS] [CrossRef] (In the text)
- Gilfanov,
M. R., Sunyaev, R. A., & Churazov, E. M. 1987,
Sov. Astron. Lett., 13, 3 [NASA ADS] (In the text)
-
Gustafsson, B., Karlsson, T., Olsson, E., Edvardsson, B., &
Ryde, N. 1999, A&A, 342, 426 [NASA ADS]
- Iwamoto, K.,
Brachwitz, F., Nomoto, K., et al. 1999, ApJS, 125, 439 [NASA ADS] [CrossRef] (In the text)
- Kaastra,
J. S., Mewe, R., & Nieuwenhuijzen, H. 1996, in UV and
X-ray Spectroscopy of Astrophysical and Laboratory Plasmas, ed. K.
Yamashita, & T. Watanabe (Tokyo: Universal Academy Press),
411
(In the text)
- Kaastra,
J. S., Tamura, T., Peterson, J. R., et al. 2004,
A&A, 413, 415 [EDP Sciences] [NASA ADS] [CrossRef]
- Lieu, R., Mittaz,
J. P. D., Bowyer, S., et al. 1996, ApJ, 458, L5 [NASA ADS] [CrossRef] (In the text)
- Lodders, K.
2003, ApJ, 591, 1220 [NASA ADS] [CrossRef] (In the text)
-
Matsushita, K., Belsole, E., Finoguenov, A., & Böhringer,
H. 2002, A&A, 386, 77 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
-
Matsushita, K., Finoguenov, A., & Böhringer, H. 2003,
A&A, 401, 443 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Meynet, G.,
& Maeder, A. 2002, A&A, 381, L25 [EDP Sciences] [NASA ADS] [CrossRef]
- Molendi, S.
2002, ApJ, 580, 815 [NASA ADS] [CrossRef] (In the text)
- Morrison, R., &
McCammon, D. 1983, ApJ, 270, 119 [NASA ADS] [CrossRef] (In the text)
- Owen, F. N.,
Eilek, J. A., & Kassim, N. E. 2000, ApJ, 543,
611 [NASA ADS] [CrossRef] (In the text)
- Peterson,
J. R., Paerels, F. B. S., Kaastra, J. S.,
et al. 2001, A&A, 365, L104 [EDP Sciences] [NASA ADS] [CrossRef]
- Peterson,
J. R., Kahn, S. M., Paerels, F. B. S.,
et al. 2003, ApJ, 590, 207 [NASA ADS] [CrossRef]
-
Sakelliou, I., Peterson, J. R., Tamura, T., et al. 2002,
A&A, 391, 903 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Shi, J. R.,
Zhao, G., & Chen, Y. Q. 2002, A&A, 381, 982 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Tamura, T.,
Bleeker, J. A. M., Kaastra, J. S., Ferrigno, C.,
& Molendi, S. 2001, A&A, 379, 107 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Tamura, T.,
Kaastra, J. S., den Herder, J. W. A., Bleeker,
J. A. M., & Peterson, J. R. 2004, A&A, 420,
135 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Tonry,
J. L., Dressler, A., Blakeslee, J. P., et al. 2001,
ApJ, 546, 681 [NASA ADS] [CrossRef] (In the text)
-
Tsujimoto, T., Nomoto, K., Yoshii, Y., et al. 1995, MNRAS,
277, 945 [NASA ADS] (In the text)
- Verner,
D. A., Verner, E. M., & Ferland, G. J. 1996,
Atomic Data and Nuclear Data Tables, 64, 1 [NASA ADS] [CrossRef] (In the text)
- Verner,
D. A., & Yakovlev, D. G. 1995, A&AS, 109,
125 [NASA ADS] (In the text)
- Werner, N., de
Plaa, J., Kaastra, J. S., et al. 2006, A&A, 449,
475 [EDP Sciences] [NASA ADS] [CrossRef]
- Xu, H., Kahn,
S. M., Peterson, J. R., et al. 2002, ApJ, 579,
600 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2006
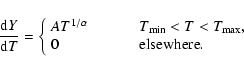
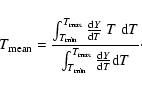
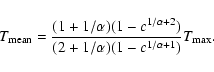
![\begin{figure}
\par\includegraphics[angle=270,width=8.6cm,clip]{5678f1.ps}
\end{figure}](/articles/aa/full/2006/44/aa5678-06/Timg32.gif)
![\begin{figure}
\par\includegraphics[angle=90,width=8.6cm,clip]{5678f2.ps}
\end{figure}](/articles/aa/full/2006/44/aa5678-06/Timg65.gif)
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{5678f3.eps}\end{figure}](/articles/aa/full/2006/44/aa5678-06/Timg107.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.6cm,clip]{5678f4.ps}\end{figure}](/articles/aa/full/2006/44/aa5678-06/Timg110.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=8.3cm,clip]{5678f5.ps}
\end{figure}](/articles/aa/full/2006/44/aa5678-06/Timg111.gif)
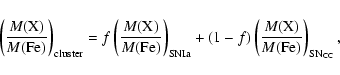
![\begin{figure}
\par\includegraphics[angle=270,width=7cm,clip]{5678f6a.ps}\par\vspace*{2mm}
\includegraphics[angle=270,width=7cm,clip]{5678f6b.ps}\end{figure}](/articles/aa/full/2006/44/aa5678-06/Timg121.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7cm,clip]{5678f7a.ps}\par\vspace*{2mm}
\includegraphics[angle=270,width=7cm,clip]{5678f7b.ps}
\end{figure}](/articles/aa/full/2006/44/aa5678-06/Timg122.gif)