A&A 459, 407-414 (2006)
DOI: 10.1051/0004-6361:20065149
Microlensing towards the Large Magellanic Cloud: a study of the LMC halo contribution
S. Calchi Novati1,2,4 - F. De Luca1,2
- Ph. Jetzer1 - G. Scarpetta2,3,4
1 -
Institute for Theoretical Physics, University of Zürich,
Winterthurerstrasse 190, 8057 Zürich, Switzerland
2 -
Dipartimento di Fisica "E. R. Caianiello'',
Università di Salerno,
Via S. Allende, 84081 Baronissi (SA), Italy
3 -
International Institute for Advanced Scientific Studies,
Vietri sul Mare (SA), Italy
4 -
Istituto Nazionale di Fisica Nucleare, sez. Napoli, Italy
Received 7 March 2006 / Accepted 10 July 2006
Abstract
We carry out a new analysis of the sample of MACHO microlensing candidates
towards the LMC.
Our main purpose is to determine the lens population
to which the events may belong. We give particular
emphasis to the possibility of characterising
the Milky Way dark matter halo population
with respect to the LMC one. Indeed,
we show that only a fraction of the events
have characteristics that
match those expected for lenses belonging
to the MACHO population of the Galactic halo.
This suggests that this component cannot explain all the candidates.
Accordingly, we challenge the view that the dark matter
halo fraction of both the Galaxy
and the LMC halos are equal, and indeed we show that,
for a MACHO mass in the range 0.1-0.3 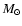 ,
the LMC halo
fraction can be significantly larger than the Milky Way's.
In this perspective, our main conclusion is
that up to about half of the observed events
could be attributed to the LMC MACHO dark matter halo.
,
the LMC halo
fraction can be significantly larger than the Milky Way's.
In this perspective, our main conclusion is
that up to about half of the observed events
could be attributed to the LMC MACHO dark matter halo.
Key words: gravitational lensing - Galaxy: halo - galaxies: Magellanic clouds -
cosmology: dark matter
Since the original proposal of Paczynski (1986), microlensing has been shown
to be a powerful tool
for investigating the MACHO composition of galactic halos.
The microlensing surveys
towards the LMC and the SMC probed the existence
of compact halo objects along these lines of sight;
however, the assessment of these results with respect to the actual
fraction of the Milky Way (hereafter "MW'')
halo in the form of MACHOs is still highly debated.
The MACHO collaboration reported the detection
of 13-17 microlensing candidates towards the LMC (Alcock et al. 2000b),
arguing in favour of a MACHO halo fraction
of 
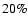 of objects of
of objects of 
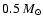 and estimating a microlensing optical depth towards the LMC of
and estimating a microlensing optical depth towards the LMC of
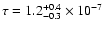 .
The reported microlensing
rate towards the LMC significantly exceeds the expected one
from known visible components of our Galaxy.
Further analysis mainly confirmed these conclusions
(Bennett et al. 2005). On the other hand, the EROS collaboration,
from observations towards both the LMC and the SMC,
put more and more lower upper limits
on the MACHO contribution to galactic halos (Tisserand & Milsztajn 2005; Lasserre et al. 2000; Afonso et al. 2003),
which are no longer compatible with the MACHO results.
.
The reported microlensing
rate towards the LMC significantly exceeds the expected one
from known visible components of our Galaxy.
Further analysis mainly confirmed these conclusions
(Bennett et al. 2005). On the other hand, the EROS collaboration,
from observations towards both the LMC and the SMC,
put more and more lower upper limits
on the MACHO contribution to galactic halos (Tisserand & Milsztajn 2005; Lasserre et al. 2000; Afonso et al. 2003),
which are no longer compatible with the MACHO results.
These questions have also been addressed
by microlensing surveys towards M 31 (Ansari et al. 1997),
and a first evidence of a MACHO contribution along
this line of sight have been reported (Calchi Novati et al. 2005),
although challenged in de Jong et al. (2006).
Overall, the picture remains unclear, in particular the problem
of the nature and location of the observed events.
For example, Green & Jedamzik (2002) have cast doubts on
the interpretation of the microlensing data towards LMC as due to
a dominant lens population made by Galactic halo MACHOs.
In fact they show, at a high level of confidence, that the distribution
of the duration of the
observed microlensing events is significantly narrower
than what is expected from a standard halo-lens population.
We have already addressed some of these questions in Jetzer et al. (2002) and
Mancini et al. (2004) (hereafter Papers I and II, respectively).
A main issue in both works is that the microlensing events towards the LMC,
as observed by the MACHO collaboration, do not necessarily all belong
to the same lens population.
In particular in Paper II, we considered the issue of self lensing
in the framework of the van der Marel et al. (2002) picture of the
luminous components of the LMC. The main conclusion,
based both on the predicted number and characteristics
of self-lensing events, was that self lensing alone cannot
explain all the observed events.
In the present work we extend the analysis by fully considering
the LMC and MW dark matter halo MACHO lens populations.
The main question we want to address
is whether and to what extent events due to the lens population
residing in the LMC halo can contribute to the observed rates.
This issue was first proposed and discussed in Gould (1993).
Here we consider
again the question taking into account both the results
of the MACHO collaboration
and the most recent results on the modeling of the LMC.
The paper is organised as follows. In Sect. 2
we review the models of the LMC and Galactic components we consider.
In Sect. 3 we discuss the evaluation
of the microlensing rate and present the results
for the expected number and duration of the microlensing events.
In Sect. 4 we carry out
our new analysis and present
our main conclusions on the LMC MACHO halo contribution,
and in Sect. 5 we present our conclusions.
2 Models
We consider the LMC as composed of a luminous part,
the bar, and the disc, plus a stellar and a dark matter halos. We also include
the Galactic dark matter halo, but we do not include
the Galactic disc and spheroid populations.
These components have already been shown to give
smaller contributions than the LMC self lensing (Alcock et al. 2000b),
which we include instead. Accordingly, we exclude
from our analysis the single event whose lens,
upon a direct search, has been acknowledged
to be part of these components.
For the structure and dynamics of the luminous components
of the LMC we follow Paper II closely.
From the analysis in van der Marel et al. (2002), who derive
their results on the assumption that the carbon star population
is representative of the bulk of the LMC disc stars,
we take up the results on the
LMC disc intrinsic ellipticity, vertical thickness, line-of-sight velocity
dispersion, rotation curve, and the coincidence
of the centre of mass of the disc and the bar components.
We assume the following values for the bar and disc components
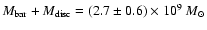 (van der Marel et al. 2002), and
(van der Marel et al. 2002), and
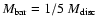 (Gyuk et al. 2000),
which we consider to be both centred at
(Gyuk et al. 2000),
which we consider to be both centred at
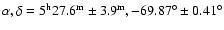 (J2000)
at a distance from us of
(J2000)
at a distance from us of
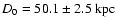 (van der Marel et al. 2002).
We use the same density star distribution as in Paper II,
characterised by a vertical distribution for the exponential disc
described by a sech2 function and a boxy bar, with a Gaussian
profile along the major axis and the section described
by a
(van der Marel et al. 2002).
We use the same density star distribution as in Paper II,
characterised by a vertical distribution for the exponential disc
described by a sech2 function and a boxy bar, with a Gaussian
profile along the major axis and the section described
by a
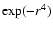 function.
The vertical structure of the LMC has been recently the object
of an intensive debate (for a discussion see van der Marel 2004).
We considered this issue with respect to the expected
self lensing signal in Paper II.
In the present analysis, where we focus on the contribution of the two halos,
we do not enter into this discussion but consider only
the configuration with coplanar disc and bar.
function.
The vertical structure of the LMC has been recently the object
of an intensive debate (for a discussion see van der Marel 2004).
We considered this issue with respect to the expected
self lensing signal in Paper II.
In the present analysis, where we focus on the contribution of the two halos,
we do not enter into this discussion but consider only
the configuration with coplanar disc and bar.
The presence of a significant LMC stellar halo population
is a matter of debate (Gallart et al. 2004; Alves 2004; Minniti et al. 2003).
In the present analysis we include the contribution
of such a possible component following Alves (2004),
who proposes a spherically symmetric spheroid with density profile
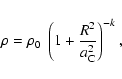 |
(1) |
with k=3/2, central density
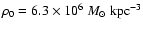 ,
and core radius
,
and core radius
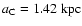 for a total mass,
within 8.9 kpc,
of
for a total mass,
within 8.9 kpc,
of
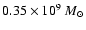 somewhat smaller than that of the bar.
The optical depth profile of this component shows a near-far
asymmetry due to the LMC disc inclination, whose overall shape recalls
that of the optical depth profile of the LMC MACHO halo component
(Paper II, Fig. 4), with a maximum value around
somewhat smaller than that of the bar.
The optical depth profile of this component shows a near-far
asymmetry due to the LMC disc inclination, whose overall shape recalls
that of the optical depth profile of the LMC MACHO halo component
(Paper II, Fig. 4), with a maximum value around
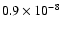 reached in correspondence of the field MACHO 6.
reached in correspondence of the field MACHO 6.
Following van der Marel et al. (2002),
who present observational evidence based
on the rotation curves, we include a significant
LMC dark matter halo component.
We assume a total LMC mass of
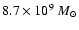 within 8.9 kpc with a truncation radius of 15 kpc (van der Marel et al. 2002),
which we consider to also include the contribution from the stellar halo.
We assume a spherical isothermal model (k=1 in Eq. (1)) with
a core radius of
within 8.9 kpc with a truncation radius of 15 kpc (van der Marel et al. 2002),
which we consider to also include the contribution from the stellar halo.
We assume a spherical isothermal model (k=1 in Eq. (1)) with
a core radius of
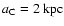 (Alcock et al. 2000b).
(Alcock et al. 2000b).
This spherical symmetric configuration might not be a realistic
description of this component
given that the dynamical environment of the LMC can induce
tidal distortions and disruptions,
especially in the outer parts. To take this issue into account, in Paper II
we compared the LMC halo optical depth profiles for both a spherical
and an elliptical configuration (Figs. 4 and 5 respectively):
the overall shape is similar even if in the latter case the maximum
value rises by about 20%
and the near-far asymmetry is enhanced. However, as we lack any strong constraint,
we prefer not to introduce a further parameter in the present analysis; therefore,
we only consider the spherical configuration, in view also of the possibility
of carrying out a more direct comparison with previous works.
In this same perspective, we consider
the "standard'' isothermal profile for the Galactic dark matter halo
with a core radius of 5 kpc, local density
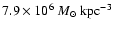 ,
and a distance from the Galactic centre of 8.5 kpc (Alcock et al. 2000b).
,
and a distance from the Galactic centre of 8.5 kpc (Alcock et al. 2000b).
3 The microlensing rate
The main tool of investigation we use is
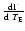 ,
the
differential rate of microlensing events with respect to the
Einstein time
,
the
differential rate of microlensing events with respect to the
Einstein time
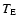 (Griest 1991; de Rujula et al. 1991; Roulet & Mollerach 1997).
This allows us to make predictions on the timescale,
the number, and the spatial distribution of the expected events,
which we can compare with the corresponding observed quantities.
With respect to the self-lensing configuration that we analysed in Paper II
(Sect. 4.2), we can no longer adopt the useful approximation
(Griest 1991; de Rujula et al. 1991; Roulet & Mollerach 1997).
This allows us to make predictions on the timescale,
the number, and the spatial distribution of the expected events,
which we can compare with the corresponding observed quantities.
With respect to the self-lensing configuration that we analysed in Paper II
(Sect. 4.2), we can no longer adopt the useful approximation
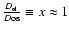 .
Moreover we now have to take the bulk velocity of
the LMC components and the relative motion between the LMC and the
Galaxy (van der Marel et al. 2002) fully into account.
.
Moreover we now have to take the bulk velocity of
the LMC components and the relative motion between the LMC and the
Galaxy (van der Marel et al. 2002) fully into account.
The source stars belong to the luminous components, disc or bar, of the LMC,
whereas the lenses can belong either to the LMC or the MW halo.
We assume an isotropic Maxwellian profile![[*]](/icons/foot_motif.gif) for the velocity distribution for both lenses and sources.
For the flattened LMC luminous components,
this is a rough approximation; still,
it gives a fair description of the average properties of these populations
that we consider to be sufficient in the present framework.
for the velocity distribution for both lenses and sources.
For the flattened LMC luminous components,
this is a rough approximation; still,
it gives a fair description of the average properties of these populations
that we consider to be sufficient in the present framework.
For the LMC disc component we consider the rotational
velocity as in van der Marel et al. (2002) with
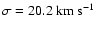 .
For the LMC bar stars we use a higher value
of the velocity dispersion than for the disc,
.
For the LMC bar stars we use a higher value
of the velocity dispersion than for the disc,
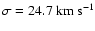 (Cole et al. 2005).
For both the LMC halo components, stellar and MACHO, we use
(Cole et al. 2005).
For both the LMC halo components, stellar and MACHO, we use
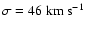 (van der Marel et al. 2002; Alves 2004)
(we tested that our results remain qualitatively unaltered
by changing this value up to 20%);
for the Galactic halo,
(van der Marel et al. 2002; Alves 2004)
(we tested that our results remain qualitatively unaltered
by changing this value up to 20%);
for the Galactic halo,
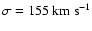 .
.
The expression for the random motion velocity for
the lenses reads![[*]](/icons/foot_motif.gif)
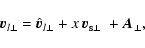 |
(2) |
where
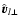 is the velocity
relative to the microlensing tube at position x, whose modulus is the ratio
between the Einstein radius and the Einstein time
(
is the velocity
relative to the microlensing tube at position x, whose modulus is the ratio
between the Einstein radius and the Einstein time
(
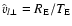 ), and
), and
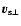 the random component
of the velocity of the sources.
All the bulk motions are included in
the random component
of the velocity of the sources.
All the bulk motions are included in
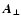 ,
defined as
,
defined as
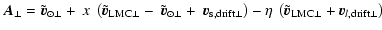 |
|
|
(3) |
where
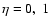 for lenses in the Galaxy and in the LMC, respectively;
for lenses in the Galaxy and in the LMC, respectively;
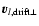 is the drift velocity of the lens star
belonging to the LMC disc (for the bar sources as well as
for the halo lenses we only consider a random motion component),
and a tilde over a vector indicates a quantity measured
by an observer comoving with the Galactic centre.
In the self-lensing configuration,
is the drift velocity of the lens star
belonging to the LMC disc (for the bar sources as well as
for the halo lenses we only consider a random motion component),
and a tilde over a vector indicates a quantity measured
by an observer comoving with the Galactic centre.
In the self-lensing configuration,
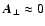 ,
and Eq. (2)
reduces to Eq. (13) of Paper II.
,
and Eq. (2)
reduces to Eq. (13) of Paper II.
We call 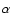 the angle between the inner normal to the tube,
the angle between the inner normal to the tube,
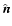 ,
and the source velocity
,
and the source velocity
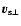 ;
;
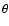 the angle between
the angle between
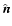 and
and
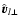 ,
,
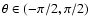 ;
;
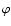 the angle between
the angle between
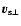 and
and
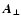 ;
so that the angle between
;
so that the angle between
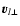 and
and
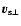 is
is
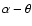 ,
and that between
,
and that between
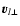 and
and
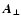 is
is
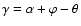 .
Both
.
Both 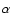 and
and 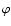 vary
in the range (
vary
in the range (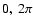 )
(Fig. 1).
)
(Fig. 1).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{5149f1}
\end{figure}](/articles/aa/full/2006/44/aa5149-06/Timg47.gif) |
Figure 1:
Scheme of a section of the microlensing tube with
indicated the positions of the vectors and the angles involved. |
| Open with DEXTER |
In the case of
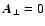 ,
all the integrations over the angular
variables can be carried out analytically. This is now only possible for
the
,
all the integrations over the angular
variables can be carried out analytically. This is now only possible for
the 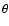 variable. Altogether, after an analytical integration
on the modulus of the source velocity, we are left with the following expression
of the differential rate with respect to the Einstein time
variable. Altogether, after an analytical integration
on the modulus of the source velocity, we are left with the following expression
of the differential rate with respect to the Einstein time
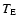 :
:
where the normalization factor 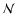 is the integral over the line of
sight of the sources
is the integral over the line of
sight of the sources
having assumed that the number of detectable stars varies
with the distance as
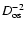 .
We define
.
We define
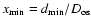 ,
,
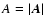 ;
the integration limits along the line of sight,
;
the integration limits along the line of sight,
 and
and
 ,
represent the distances
from the observer to the intersection with the LMC tidal surface,
for lenses in the LMC, whereas
,
represent the distances
from the observer to the intersection with the LMC tidal surface,
for lenses in the LMC, whereas
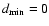 for lenses in the Galactic halo.
We use solar mass units, defining
for lenses in the Galactic halo.
We use solar mass units, defining
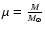 ,
where M is the lens mass.
For lenses belonging either to the disc or the bar
of the LMC, as well as for the stellar LMC halo contribution,
we use the exponential function as in Chabrier (2001)
for the mass function
,
where M is the lens mass.
For lenses belonging either to the disc or the bar
of the LMC, as well as for the stellar LMC halo contribution,
we use the exponential function as in Chabrier (2001)
for the mass function
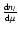 ,
with integration limits
,
with integration limits
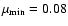 and
and
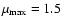 .
If the lenses belong to the MW halo or to the LMC halo, the would be MACHOs, we
use a set of delta functions with values going from 10-5 up to 10
.
If the lenses belong to the MW halo or to the LMC halo, the would be MACHOs, we
use a set of delta functions with values going from 10-5 up to 10 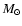 .
.
Finally, to compare with the results of the observations,
we have to take the expression
for the detection efficiency into account, so that we obtain
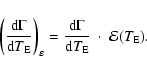 |
(5) |
To discuss the results of the MACHO collaboration
we use the efficiency as a function of 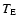 as in Alcock et al. (2000b)
for which an analytical approximation is given in Paper II.
We take the correction reported in Bennett (2005) into account.
as in Alcock et al. (2000b)
for which an analytical approximation is given in Paper II.
We take the correction reported in Bennett (2005) into account.
Following the prescription outlined in the previous section,
we evaluate the differential microlensing rate,
for each different lens population we consider,
along the lines of sight towards the MACHO fields.
In particular for each lens population, we
calculate the expected number of events per field as
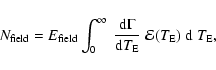 |
(6) |
where the "field exposure''
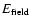 is defined in Alcock et al. (2000b), as the product
of the number of distinct light curves per field
and the relevant time span. Furthermore, we take care
to eliminate the field overlaps.
is defined in Alcock et al. (2000b), as the product
of the number of distinct light curves per field
and the relevant time span. Furthermore, we take care
to eliminate the field overlaps.
To characterise the expected timescale, we report
the median value of the asymmetric distribution
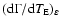 ,
together with the values
,
together with the values
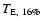 and
and
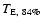 that single out the extremes of the 68% probability range around the median.
that single out the extremes of the 68% probability range around the median.
In Table 1 we report, for both MW and LMC MACHO lens populations,
the total number of the expected events in all the MACHO fields,
in the case of a full MACHO halo, together with the expected timescales.
We recall that the expected timescale varies with the square root of
the mass of the MACHO,
and that very short timescales are strongly suppressed by the detection
efficiency function.
Table 1:
Expected duration, median values with 68% CL errors,
and expected number of events for a full dark matter halo, respectively averaged
and summed over the MACHO fields, as a function of the MACHO mass.
The predicted durations turn out to be almost independent of the position
for both the halo populations we consider, whereas the issue of the variation of
the expected timescales with the position across the fields for the
self-lensing population was discussed thoroughly in Paper II.
Indeed, for lenses in the Galactic halo, we find
a dispersion of the median timescales towards the different fields smaller
than 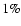 .
In the case of the LMC lenses, the dispersion
is only slightly larger, at most
.
In the case of the LMC lenses, the dispersion
is only slightly larger, at most 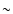
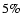 .
The expected total number of events due to the LMC stellar halo
turns out to be
.
The expected total number of events due to the LMC stellar halo
turns out to be 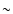 0.6, about half of those due to
the LMC disc-bar self-lensing contribution (Paper II).
The expected median timescale, averaged on the 30 fields,
is
0.6, about half of those due to
the LMC disc-bar self-lensing contribution (Paper II).
The expected median timescale, averaged on the 30 fields,
is
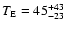 days.
days.
Overall, we recover the result (Alcock et al. 2000b) that stellar
lensing alone cannot explain the signal,
so that most of the detected events must belong either
to the MW or to the LMC dark matter halo.
4 The LMC MACHO contribution to microlensing events
A straightforward conclusion to be drawn from the results
on the expected number of events due to the dark matter MW and LMC halos
is that, with the implicit hypothesis that the halo fractions
in both the MW and the LMC halos are the same,
most of the lenses should indeed belong to the Galactic halo.
Our aim is to challenge this point of view.
First, we recall the current status about the microlensing
events observed by the MACHO collaboration.
Next, we carry out a statistical analysis
of the observed characteristics of the events
(timescale and spatial distribution).
The purpose here is to determine to what extent
the available data allow the two halo populations to be distinguished.
Eventually, using a likelihood analysis
based on the microlensing rate,
we study whether a viable solution
to the MACHO puzzle can come
from a significant contribution
of a lens population belonging to the LMC halo.
4.1 The microlensing MACHO candidates
In the final analysis of 5.7 years of data in 30 fields towards the LMC,
the MACHO group presented two sets of microlensing candidates,
sets A and B, with 13 and 17 candidates, respectively, the former being
a subsample of the latter (Alcock et al. 2000b).
Further works allowed more information to be gathered on some of these candidates.
The lens for the event LMC-5 is located in the Galactic disc (Alcock et al. 2001b).
LMC-22 has been identified as a very likely supernova (Alcock et al. 2001a).
LMC-23 has been acknowledged as a probable variable star (Bennett et al. 2005).
LMC-9 is a double-lens system with caustic crossing (Alcock et al. 2000a).
The microlensing candidates LMC-9, LMC-20, LMC-22, and LMC-27 only belong
to set B. For most of the remaining events, a further photometric follow-up
allowed confirmation of the microlensing origin of the flux variation
(Bennett et al. 2005).
We restrict the present analysis to a homogeneous set
of Paczynski-like events, so we exclude LMC-9. Furthermore,
we do not include the Galactic disc lens population, so that we exclude LMC-5,
as well as all those candidates whose microlensing origin has been
put in doubt. Accordingly, in the following we consider
a subset of 13 events taken from the original
larger set B, from which we exclude the candidates LMC-5, LMC-9, LMC-22, and LMC-23.
Furthermore, we have verified that our main conclusions
would not change had we started from the smaller set of 11 events, a
subsample of the original set A, just excluding the candidates LMC-5 and LMC-23.
4.2 Duration and position: a statistical analysis
As previously noted, the expected timescale distributions
for microlensing events due to lenses either in the LMC or in the MW halo
are almost independent
of the position. This property allows us to carry on
an analysis in which we compare the observed
timescales to the predicted one for each population. In particular,
we investigate whether it is possible to draw from such an analysis any conclusion
on the relative fraction of the Galactic over the LMC dark matter halo events.
Here we neglect the stellar lensing contributions.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{5149f2}
\end{figure}](/articles/aa/full/2006/44/aa5149-06/Timg95.gif) |
Figure 2:
Normalised differential rate
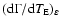 for both MW and LMC halos for 0.2 and 0.5 for both MW and LMC halos for 0.2 and 0.5 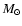 ,
dashed
and solid lines, respectively. Superimposed is the value of the observed durations.
The y-axis values are in 10-2 units. ,
dashed
and solid lines, respectively. Superimposed is the value of the observed durations.
The y-axis values are in 10-2 units. |
| Open with DEXTER |
For a given value of the MACHO mass, the expected LMC
median timescales are larger than the MW ones (Gould 1993).
We show in the same plot (Fig. 2) the normalised differential
rate distribution for lenses in the LMC and the MW halo, corresponding to
two values of the MACHO mass (0.2 and
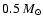 ).
Superimposed, the vertical lines indicate the Einstein time
of the observed events.
To investigate this issue further, we make use of the Kolmogorov-Smirnov test
(hereafter KS). This allows us to test the null hypothesis
that the events are drawn from a given population.
The resulting KS coefficient gives the significance level of the test.
In the first place, we apply the KS hypothesis test separately
to the two populations of lenses in the MW and the LMC halo. Then we introduce
a parameter
).
Superimposed, the vertical lines indicate the Einstein time
of the observed events.
To investigate this issue further, we make use of the Kolmogorov-Smirnov test
(hereafter KS). This allows us to test the null hypothesis
that the events are drawn from a given population.
The resulting KS coefficient gives the significance level of the test.
In the first place, we apply the KS hypothesis test separately
to the two populations of lenses in the MW and the LMC halo. Then we introduce
a parameter 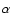 ,
defined as the ratio of the MW events over the total
(MW plus LMC events),
in order to explore the possibility that an intermediate solution,
with the two populations mixed, has to be preferred.
To this purpose we look for the value of
,
defined as the ratio of the MW events over the total
(MW plus LMC events),
in order to explore the possibility that an intermediate solution,
with the two populations mixed, has to be preferred.
To this purpose we look for the value of 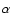 that minimises
the corresponding KS coefficient.
that minimises
the corresponding KS coefficient.
Table 2:
Kolmogorov-Smirnov test results.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{5149f3}
\end{figure}](/articles/aa/full/2006/44/aa5149-06/Timg99.gif) |
Figure 3:
Kolmogorov-Smirnov and 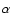 coefficients
as a function of the MACHO mass, with
coefficients
as a function of the MACHO mass, with 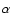 the ratio
of the MW over the total number of dark matter halo events.
the ratio
of the MW over the total number of dark matter halo events. |
| Open with DEXTER |
To take the variations of the microlensing rate across
the fields into account, mainly in the case of lenses in the LMC halo, we carry out
the test on each of the MACHO fields separately. We then evaluate and report
the value averaged on the 30 MACHO fields. The associated dispersion gives
the error bars drawn in Fig. 3.
In Table 2 and Fig. 3 we present the results
of this analysis. We report the value of the parameter 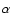 and
the KS coefficient in the three cases considered,
and
the KS coefficient in the three cases considered,
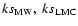 ,
and
,
and 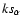 ,
respectively, as a function of the MACHO mass. We report
the results only in the range 0.01-1
,
respectively, as a function of the MACHO mass. We report
the results only in the range 0.01-1 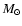 where the
preferred solution are found (see below).
where the
preferred solution are found (see below).
When we consider the MW and the LMC halos separately, the solutions
with the highest level of confidence are found for a MACHO mass of
 0.5
0.5  and
and 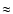 0.15
0.15 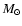 ,
respectively.
This result is confirmed by the microlensing-rate-normalised
distributions in Fig. 2, where the profile
corresponding to the case of
,
respectively.
This result is confirmed by the microlensing-rate-normalised
distributions in Fig. 2, where the profile
corresponding to the case of
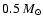 MW lenses is almost
coincident with that of
MW lenses is almost
coincident with that of
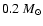 LMC lenses.
LMC lenses.
For the case of the combined populations, we find that the coefficient
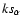 presents two minima near the two values of
mass found in the previous case.
The absolute minimum, which we note is lower than the values obtained
in the case of the separate test analysis, is found at
presents two minima near the two values of
mass found in the previous case.
The absolute minimum, which we note is lower than the values obtained
in the case of the separate test analysis, is found at
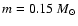 with
with
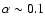 ,
and it gives us
the parameters with the highest confidence level. Moreover
we observe that the
,
and it gives us
the parameters with the highest confidence level. Moreover
we observe that the 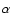 parameter grows monotonically
as a function of the mass from 0 up to 1 (Fig. 3).
parameter grows monotonically
as a function of the mass from 0 up to 1 (Fig. 3).
We conclude that the statistical analysis made
on the duration of the events
gives a first suggestion that a significant fraction of the
observed events could belong to the LMC MACHO halo population.
Next we consider the issue of the spatial distribution of the
observed events (Gould 1993).
The optical depth profiles clearly show that the LMC halo events are
characterised, with respect
to LMC self-lensing and to MW halo ones, by a strong
asymmetry with respect to the line of nodes (Paper II). Looking
at the expected number of events per field, this asymmetry is somewhat weakened
but still present, because of the different source density as a function
of the position. In order to get insight into the more complex
two-dimensional situation we have to deal with,
we show the normalised number of the expected
events (
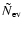 )
in Fig. 4, for the different lens populations
we consider, evaluated along the axis orthogonal to the line
of nodes passing through the LMC centre (the
)
in Fig. 4, for the different lens populations
we consider, evaluated along the axis orthogonal to the line
of nodes passing through the LMC centre (the 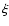 axis in the plot).
axis in the plot).
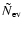 has been calculated in the LMC centre and
in six more positions, specularly symmetric two
by two with respect to the centre.
This plot shows clearly that the distribution in the case of self-lensing
events is symmetric and, moreover, that outside the bar region
it declines sharply. The profile for MW events presents
a slight asymmetry with respect to the line
of nodes, whereas that corresponding to LMC MACHO lenses have a pronounced
asymmetric distribution.
has been calculated in the LMC centre and
in six more positions, specularly symmetric two
by two with respect to the centre.
This plot shows clearly that the distribution in the case of self-lensing
events is symmetric and, moreover, that outside the bar region
it declines sharply. The profile for MW events presents
a slight asymmetry with respect to the line
of nodes, whereas that corresponding to LMC MACHO lenses have a pronounced
asymmetric distribution.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{5149f4}
\end{figure}](/articles/aa/full/2006/44/aa5149-06/Timg106.gif) |
Figure 4:
Normalised expected number profiles along the axis,
pointing south-west, orthogonal to the line of nodes
and passing through the LMC centre, for different lens populations:
self lensing, dot dashed line; MW MACHO, solid line;
LMC MACHO, dashed line. Values on the 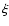 axis are in kpc. axis are in kpc. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{5149f5}
\end{figure}](/articles/aa/full/2006/44/aa5149-06/Timg107.gif) |
Figure 5:
Location of the 30 MACHO fields in a reference frame
centred in the LMC centre with the x-axis antiparallel
to the right ascension, the y-axis parallel to the declination,
and the z-axis (not shown) pointing towards the observer.
The location of the 13 microlensing candidates, a subset of the
original set B of MACHO candidates that we use
in thepresent analysis (Sect. 4.1),
is shown. Also shown is the position
of the line of nodes and the central band around it, which
we exclude inthe asymmetry analysis. |
| Open with DEXTER |
In Paper II we addressed the question of whether the
observed asymmetrical distribution of the detected events,
which goes indeed in the same sense predicted
by a halo LMC population, really does reflect the observational
strategy, mainly to argue against the self-lensing origin
of the events. Here we take advantage of knowing
the expected number of events for all the
populations of interest to study this issue in more detail.
We take the line of nodes as the symmetry axis, and
as in Paper II we bin the observed space in two regions,
the north-east "near'' and the south-west "far'' ones
(Fig. 5).
We delimit them by two straight lines parallel
to the line of nodes, each at a distance from the latter
of 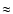
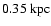 ,
the 1
,
the 1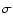 error in position as calculated by van der Marel et al. (2002).
Note that this way the innermost LMC regions are excluded
from the asymmetry analysis.
Our purpose is to test the asymmetry with respect to the prediction
of the different lens populations,
assigning the probability pi that a microlensing
event would fall in the first or second region to be proportional
to the expected number of events of the given population.
As in Paper II we make use of the non-parametric Pearson test,
which allows us to evaluate the probability to accept the null hypothesis
that the pi match the measured distribution, for which we get
1 and 7 observed events in the near and far regions, respectively.
This analysis is carried out by normalising
the number of expected events of each population to that of the observed events.
error in position as calculated by van der Marel et al. (2002).
Note that this way the innermost LMC regions are excluded
from the asymmetry analysis.
Our purpose is to test the asymmetry with respect to the prediction
of the different lens populations,
assigning the probability pi that a microlensing
event would fall in the first or second region to be proportional
to the expected number of events of the given population.
As in Paper II we make use of the non-parametric Pearson test,
which allows us to evaluate the probability to accept the null hypothesis
that the pi match the measured distribution, for which we get
1 and 7 observed events in the near and far regions, respectively.
This analysis is carried out by normalising
the number of expected events of each population to that of the observed events.
The result of this analysis gives us a probability of 46% and 26% for a
MACHO LMC and MW halo lens population, respectively.
This outcome makes the lack
of a predominant lens population very clear.
Indeed, the expected smoother spatial
distribution of MW halo lenses is barely
coherent with the observed distribution,
thus challenging the explanation that attributes most
of the events to this population.
Rather, we find much better agreement
with the expected asymmetric distribution
of LMC halo events.
Finally, we note that, contrary to the previous analysis
based on the timescale distribution,
this result turns out to be independent of the value of the MACHO mass.
As a byproduct of the present analysis (confirming
that carried out in Paper II), we note that
the probability of accepting the hypothesis
of a self-lensing origin on the basis of the observed
spatial distribution turns out to be only 19%.
Both these analyses, carried out working on
normalised distributions (i.e. independent of the actual
halo fraction) indicate that a large fraction of the lenses
could indeed belong to the LMC dark matter halo.
4.3 The Galaxy and the LMC: two different halo fractions?
The previous analysis has provided us with two important clues, both showing that a significant
fraction of the events detected by the MACHO collaboration
could be part of the LMC dark matter halo.
To reconcile this result with the predicted number
of events (Table 1),
we now drop the hypothesis of equal halo MACHO fractions
in the Galactic and the LMC halo.
![\begin{figure}
\par\mbox{\includegraphics[width=5.7cm,clip]{5149f6a}\includegrap...
...cm,clip]{5149f6c}\includegraphics[width=5.7cm,clip]{5149f6d} }
\par
\end{figure}](/articles/aa/full/2006/44/aa5149-06/Timg110.gif) |
Figure 6:
Probability isocontours with 34%, 68% and 90% regions
for the LMC and MW dark matter halo fraction for four values of the MACHO mass. |
| Open with DEXTER |
We start by evaluating the likelihood function
![$\displaystyle L\left(f_{{\rm MW}},~f_{{\rm LMC}}\right) =
\exp\left(-N_{\rm exp...
...~ \frac{{\rm d}\Gamma}
{{\rm d}T_{{\rm E}}}~\left(T_{{\rm E}_i}\right)
\right],$](/articles/aa/full/2006/44/aa5149-06/img111.gif) |
|
|
(7) |
where
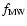 and
and
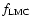 are the halo fractions
for the MW and the LMC, respectively.
For both
are the halo fractions
for the MW and the LMC, respectively.
For both
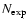 ,
the expected number of events,
and the differential rate
,
the expected number of events,
and the differential rate
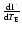 ,
we sum over all the lens populations (including the stellar ones), multiplying
the MACHO contributions for the appropriate halo fraction.
The product runs over the
,
we sum over all the lens populations (including the stellar ones), multiplying
the MACHO contributions for the appropriate halo fraction.
The product runs over the
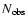 observed events.
By Bayesian inversion, using a flat prior probability,
it is then possible to compute the probability
distribution for the halo fractions given the observed events,
observed events.
By Bayesian inversion, using a flat prior probability,
it is then possible to compute the probability
distribution for the halo fractions given the observed events,
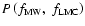 .
Note that we are now taking the MACHO mass as a parameter, equal for
both halo populations.
.
Note that we are now taking the MACHO mass as a parameter, equal for
both halo populations.
In Fig. 6 we show the 2-dimensional probability isocontour
for the two halo fractions for four
values of the MACHO mass. Eventually, after marginalisation
over one variable with respect to the other, we get the results
for the two halo fractions as a function of the MACHO mass
shown in Fig. 7.
The main outcome of this analysis is that
in a significant range of the MACHO mass, the LMC and MW
dark matter halo fractions are not expected to be equal.
In particular, from 0.1 up to 0.3 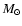 ,
both a high value for
,
both a high value for
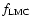 and a low one for
and a low one for
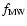 are expected.
are expected.
This behaviour is mainly due to the observed timescales.
It is therefore not surprising that this result
is coherent with the one obtained with the KS test,
where we found a preferred value of the mass of about
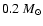 ,
with a significant expected contribution from LMC MACHO halo lenses.
The likelihood analysis gives, for
,
with a significant expected contribution from LMC MACHO halo lenses.
The likelihood analysis gives, for
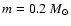 ,
,
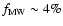 and
and
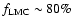 .
At face value, given the number of expected events,
we get to the overall prediction
of about 6-7 events to be attributed to the
LMC dark matter halo lens population,
2-3 to the MW halo one, to be looked for
among those with the shorter durations,
still allowing for a contribution of about 2-3 events,
distributed among self-lensing and LMC stellar halo lenses.
.
At face value, given the number of expected events,
we get to the overall prediction
of about 6-7 events to be attributed to the
LMC dark matter halo lens population,
2-3 to the MW halo one, to be looked for
among those with the shorter durations,
still allowing for a contribution of about 2-3 events,
distributed among self-lensing and LMC stellar halo lenses.
For higher values of the mass, the LMC MACHO halo fraction
turns out to be almost degenerate though compatible with zero, and,
for 0.5 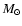 ,
we recover the result of a Galactic MACHO
halo fraction of about 20% (Alcock et al. 2000b). This is again coherent
with the issue of the KS test.
,
we recover the result of a Galactic MACHO
halo fraction of about 20% (Alcock et al. 2000b). This is again coherent
with the issue of the KS test.
We stress that the outcome of this analysis has to be looked at together
with the outcomes of the previous analysis
on the timescale and the spatial distributions of the observed events.
Overall, they indicate that
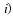 a sizeable fraction
of the observed events show characteristics in accord with those
expected for a MACHO LMC halo population;
a sizeable fraction
of the observed events show characteristics in accord with those
expected for a MACHO LMC halo population;
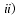 such a contribution may be expected by dropping the hypothesis
that the halo fractions in the form of MACHOs in the Galactic and the LMC
dark matter halo are equal.
such a contribution may be expected by dropping the hypothesis
that the halo fractions in the form of MACHOs in the Galactic and the LMC
dark matter halo are equal.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{5149f7}
\end{figure}](/articles/aa/full/2006/44/aa5149-06/Timg122.gif) |
Figure 7:
MW and LMC dark matter halo fraction, median value
with 68% CL errors, as a function of the MACHO mass. |
| Open with DEXTER |
As a last point, we discuss the dependence of our results on the choice
of the LMC dark matter halo parameters, the central density, and
the truncation radius (Sect. 2).
We find that any variation in the parameters in a reasonable range
around their fiducial values does not change, at least qualitatively, our results.
As for the central density, any variation
downward (upward) is linearly related to a
corresponding change in the total number of expected
events. This implies a scaling upward (downward)
for the halo fraction without affecting the main conclusion
on the contribution of the LMC halo.
As for the truncation radius (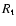 ), as a first approximation
the situation is similar, as a lower (higher) value of
), as a first approximation
the situation is similar, as a lower (higher) value of 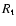 roughly give rises to
a lower (higher) total LMC mass. However, the issue is slightly subtler.
First, the problem is not symmetric with respect to the choice
of our fiducial value,
roughly give rises to
a lower (higher) total LMC mass. However, the issue is slightly subtler.
First, the problem is not symmetric with respect to the choice
of our fiducial value,
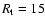 kpc. Second,
different choices for
kpc. Second,
different choices for 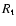 enhance different spatial distributions
for the number of expected events.
In particular,
enhance different spatial distributions
for the number of expected events.
In particular,
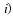 the decrease in the number of expected events, for lower
values of
the decrease in the number of expected events, for lower
values of 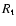 than the fiducial value, is relatively larger
than the increase obtained
by choosing higher values;
than the fiducial value, is relatively larger
than the increase obtained
by choosing higher values;
 the spatial asymmetry
of MACHO LMC halo events is enhanced for a lower value of
the spatial asymmetry
of MACHO LMC halo events is enhanced for a lower value of 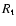 .
(Both effects are easily explained, as most of the lenses
are expected to be located in the innermost LMC region.)
We tested our results
with 4 values of
.
(Both effects are easily explained, as most of the lenses
are expected to be located in the innermost LMC region.)
We tested our results
with 4 values of 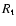 ,
respectively lower (higher) of our
fiducial value by 20% and 40%.
The relative average decrease in the number of expected
events for
,
respectively lower (higher) of our
fiducial value by 20% and 40%.
The relative average decrease in the number of expected
events for
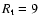 and 12 kpc with respect to the
and 12 kpc with respect to the
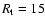 kpc case
is
kpc case
is 
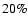 and 8.7%, whereas the relative increase for
and 8.7%, whereas the relative increase for
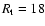 and 21 kpc
is
and 21 kpc
is 
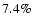 and 14%, respectively. As for the spatial
distribution, we characterise the asymmetry by the relative difference
between the number of expected events
evaluated at the extremes of the
and 14%, respectively. As for the spatial
distribution, we characterise the asymmetry by the relative difference
between the number of expected events
evaluated at the extremes of the  axis
(as defined in Fig. 4)
axis
(as defined in Fig. 4) 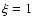 kpc and
kpc and 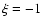 kpc.
Where the fiducial case turns out to be of
kpc.
Where the fiducial case turns out to be of 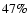 ,
for
,
for
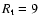 and 12 kpc we find a relative increase of 11% and 4%, and
for
and 12 kpc we find a relative increase of 11% and 4%, and
for
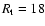 and 21 kpc a relative decrease of 2% and 6%, respectively.
Overall, lower values of
and 21 kpc a relative decrease of 2% and 6%, respectively.
Overall, lower values of 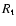 strengthen our conclusions.
strengthen our conclusions.
5 Conclusions
In this paper we have addressed the issue
of the interpretation of the microlensing results
toward the LMC. In particular, starting from
the sample of microlensing candidates reported
by the MACHO collaboration, we discussed the contingent
contribution of a lens component belonging to
the LMC dark matter halo besides that of the Galactic one.
As a main result of the present analysis, we show that
a sizeable fraction of the observed events,
up to about half of the total,
could indeed be part of the first component.
We summarise our analysis as follows.
First, we compared the observed timescales
with those expected for the two different
MACHO populations, the MW and the LMC.
As a result, we have shown that the preferred
values for the MACHO mass are about 0.5 and 0.2 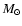 ,
respectively and, through a KS test,
that the latter solution is preferred.
Second, we studied the spatial distribution of the observed events,
recalling that, because of the inclination of the LMC disc
with respect to our line of sight, an asymmetry is expected
for LMC halo events. As a result we have shown
that, independent of the value of the MACHO mass,
the observed distribution better matches
that expected for a LMC halo population
than for a MW halo population.
Overall, these are clues suggesting the presence
of a significant MACHO LMC halo population among the observed events.
,
respectively and, through a KS test,
that the latter solution is preferred.
Second, we studied the spatial distribution of the observed events,
recalling that, because of the inclination of the LMC disc
with respect to our line of sight, an asymmetry is expected
for LMC halo events. As a result we have shown
that, independent of the value of the MACHO mass,
the observed distribution better matches
that expected for a LMC halo population
than for a MW halo population.
Overall, these are clues suggesting the presence
of a significant MACHO LMC halo population among the observed events.
The extremely high value of the overall Galactic halo mass compared to the LMC one
implies that generally one can safely ignore the LMC halo component.
To explain such a large contribution of the latter,
one way out is to consider that the halo fractions in the form of MACHOs of the two components,
the MW, and the LMC halos may be different.
Coherently with the timescale analysis, this issue turns out to be
strongly dependent on the value of the MACHO mass.
In order to get to more quantitative results, we tested this hypothesis through
a likelihood analysis. Eventually we have shown that for a wide range of mass values
a different (and larger) fraction for the LMC halo compared to the MW one is indeed expected.
In particular, for a MACHO mass of 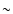
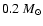 ,
we evaluated a high halo fraction for the LMC,
,
we evaluated a high halo fraction for the LMC, 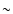
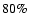 ,
together with a small one for the MW,
,
together with a small one for the MW, 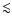
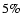 ,
thus implying that about half of the observed events
should belong to the LMC dark matter halo.
On the other hand, for MACHOs of
,
thus implying that about half of the observed events
should belong to the LMC dark matter halo.
On the other hand, for MACHOs of 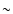
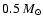 ,
we recovered the well-known result of a MW halo fraction
,
we recovered the well-known result of a MW halo fraction 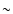
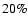 with a (possibly) negligible contribution from the LMC dark matter halo.
with a (possibly) negligible contribution from the LMC dark matter halo.
A possible explanation of the origin of different halo fractions
could come from the different formation histories of the two galaxies,
or more simply, could be related to the fact that one observes
all the LMC halo but, practically, only a line of sight through the Galactic halo.
These conclusions should be taken
cum grano salis. The overall implicit
assumption is the validity of the MACHO results, whereas they are actually
challenged by the EROS collaboration.
Furthermore, an intrinsic limit for all the analyses
carried out up to now is the result of the lack of available statistics.
The SuperMACHO collaboration (Becker et al. 2004)
is expected to provide a larger sample of candidates
spread over a much larger field of view, and this should allow
the problem to be constrained further.
Eventually we stress that the model issue,
in particular for the LMC components, is still a matter of debate.
Our analysis shows, however, that it is in principle possible to characterise
and distinguish the two halo lens populations and,
moreover, challenge
the usual implicit assumption of equal halo fractions
in the form of MACHO for both the Galactic and the LMC dark matter halos.
Acknowledgements
We thank Andy Gould for useful comments and discussions.
S.C.N. was partly supported by the Swiss National Science Foundation.
F.D.L. work was performed under the auspices of the EU, which has provided
financial support to the "Dottorato di Ricerca Internazionale in
Fisica della Gravitazione ed Astrofisica'' of Salerno University,
through "Fondo Sociale Europeo, Misura III.4''.
G.S. acknowledges support for this work provided by MIUR through PRIN 2004
"Astroparticle Physics'', protocol number 2004024710_006,
and by research funds of Salerno University.
- Afonso, C., Albert,
J. N., Andersen, J., et al. 2003, A&A, 400, 951 [EDP Sciences] [NASA ADS] [CrossRef]
- Alcock, C.,
Allsman, R. A., Alves, D., et al. 2000a, ApJ, 541,
270 [NASA ADS] [CrossRef] (In the text)
- Alcock, C., Allsman,
R. A., Alves, D. R., et al. 2000b, ApJ, 542,
281 [NASA ADS] [CrossRef] (In the text)
- Alcock, C.,
Allsman, R. A., Alves, D. R., et al. 2001a, ApJ,
552, 582 [NASA ADS] [CrossRef] (In the text)
- Alcock, C.,
Allsman, R. A., Alves, D. R., et al. 2001b, Nature,
414, 617 [NASA ADS] [CrossRef] (In the text)
- Alves, D. R.
2004, ApJ, 601, L151 [NASA ADS] [CrossRef]
- Ansari, R.,
Aurière, M., Baillon, P., et al. 1997, A&A, 324,
843 [NASA ADS] (In the text)
- Becker, A. C.,
Rest, A., Stubbs, C., et al. 2004
[arXiv:astro-ph/0409167]
(In the text)
- Bennett,
D. P. 2005, ApJ, 633, 906 [NASA ADS] [CrossRef] (In the text)
- Bennett,
D. P., Becker, A. C., & Tomaney, A. 2005, ApJ, 631,
301 [NASA ADS] [CrossRef] (In the text)
- Calchi Novati, S.,
Paulin-Henriksson, S., An, J., et al. 2005, A&A, 443,
911 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Chabrier, G.
2001, ApJ, 554, 1274 [NASA ADS] [CrossRef] (In the text)
- Cole, A. A.,
Tolstoy, E., Gallagher, J. S., & Smecker-Hane, T. A.
2005, AJ, 129, 1465 [NASA ADS] [CrossRef] (In the text)
- de Jong,
J. T. A., Widrow, L. M., Cseresnjes, P., et al.
2006, A&A, 446, 855 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- de Rujula, A.,
Jetzer, P., & Masso, E. 1991, MNRAS, 250, 348 [NASA ADS]
- Gallart, C.,
Stetson, P. B., Hardy, E., Pont, F., & Zinn, R. 2004, ApJ,
614, L109 [NASA ADS] [CrossRef]
- Gerhard,
O. E. 1993, MNRAS, 265, 213 [NASA ADS]
- Gould, A. 1993, ApJ,
404, 451 [NASA ADS] [CrossRef] (In the text)
- Green, A. M.,
& Jedamzik, K. 2002, A&A, 395, 31 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Griest, K. 1991,
ApJ, 366, 412 [NASA ADS] [CrossRef]
- Gyuk, G., Dalal, N.,
& Griest, K. 2000, ApJ, 535, 90 [NASA ADS] [CrossRef] (In the text)
- Jetzer, P.,
Mancini, L., & Scarpetta, G. 2002, A&A, 393, 129 [EDP Sciences] [NASA ADS] [CrossRef],
Paper I
(In the text)
- Lasserre, T., Afonso,
C., Albert, J. N., et al. 2000, A&A, 355, L39 [NASA ADS]
- Mancini, L.,
Calchi Novati, S., Jetzer, P., & Scarpetta, G. 2004, A&A,
427, 61 [EDP Sciences] [NASA ADS] [CrossRef] (Paper II)
(In the text)
- Minniti, D.,
Borissova, J., Rejkuba, M., et al. 2003, Science, 301,
1508 [NASA ADS] [CrossRef]
- Paczynski, B. 1986,
ApJ, 304, 1 [NASA ADS] [CrossRef] (In the text)
- Roulet, E., &
Mollerach, S. 1997, Phys. Rep., 279, 67 [NASA ADS] [CrossRef]
- Tisserand, P., &
Milsztajn, A. 2005 [arXiv:astro-ph/0501584]
- van der
Marel, R. P. 2004 [arXiv:astro-ph/0404192]
(In the text)
- van der Marel,
R. P., Alves, D. R., Hardy, E., & Suntzeff,
N. B. 2002, AJ, 124, 2639 [NASA ADS] [CrossRef] (In the text)
- van der Marel,
R. P., & Franx, M. 1993, ApJ, 407, 525 [NASA ADS] [CrossRef]
Copyright ESO 2006
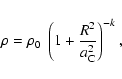
![\begin{figure}
\par\includegraphics[width=8cm,clip]{5149f1}
\end{figure}](/articles/aa/full/2006/44/aa5149-06/Timg47.gif)
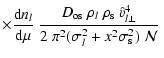
![$\displaystyle \times\Bigg\{ \exp\Big[{-\frac{A^{2}+{\hat v}_{{l}\perp}^{2}+2 A~
{\hat v}_{{l}\perp} \cos(\alpha+\varphi)} {2~\sigma^{2}_{l}}}\Big]$](/articles/aa/full/2006/44/aa5149-06/img52.gif)
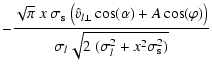
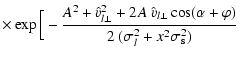
![$\displaystyle -\frac{x^2 ~ \sigma_{\rm s}^2~({\hat v}_{{l}\perp}
\sin(\alpha)-A...
...(\varphi))^2}{\sigma_{l}^2 ~2~(\sigma^{2}_{l}+
x^{2} \sigma^{2}_{\rm s})}
\Big]$](/articles/aa/full/2006/44/aa5149-06/img55.gif)
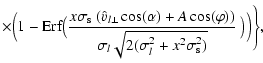
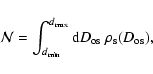
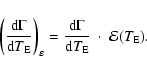
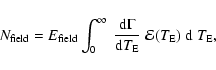
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{5149f2}
\end{figure}](/articles/aa/full/2006/44/aa5149-06/Timg95.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{5149f3}
\end{figure}](/articles/aa/full/2006/44/aa5149-06/Timg99.gif)
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{5149f4}
\end{figure}](/articles/aa/full/2006/44/aa5149-06/Timg106.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{5149f5}
\end{figure}](/articles/aa/full/2006/44/aa5149-06/Timg107.gif)
![\begin{figure}
\par\mbox{\includegraphics[width=5.7cm,clip]{5149f6a}\includegrap...
...cm,clip]{5149f6c}\includegraphics[width=5.7cm,clip]{5149f6d} }
\par
\end{figure}](/articles/aa/full/2006/44/aa5149-06/Timg110.gif)
![$\displaystyle L\left(f_{{\rm MW}},~f_{{\rm LMC}}\right) =
\exp\left(-N_{\rm exp...
...~ \frac{{\rm d}\Gamma}
{{\rm d}T_{{\rm E}}}~\left(T_{{\rm E}_i}\right)
\right],$](/articles/aa/full/2006/44/aa5149-06/img111.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{5149f7}
\end{figure}](/articles/aa/full/2006/44/aa5149-06/Timg122.gif)