A&A 459, 341-352 (2006)
DOI: 10.1051/0004-6361:20065034
J.-B. Melin1,2,![]() - J. G. Bartlett1 - J. Delabrouille1
- J. G. Bartlett1 - J. Delabrouille1
1 - APC, 11 pl. Marcelin Berthelot, 75231
Paris Cedex 05, France
(UMR 7164 - CNRS, Université
Paris 7, CEA, Observatoire de Paris)
2 - Department of Physics, University of California Davis,
One Shields Avenue, Davis, CA, 95616, USA
Received 16 February 2006 / Accepted 30 June 2006
Abstract
We present a method based on matched multifrequency filters
for extracting cluster catalogs from Sunyaev-Zel'dovich (SZ) surveys. We evaluate
its performance in terms of completeness, contamination rate and photometric
recovery for three representative types of SZ survey: a high resolution
single frequency radio survey (AMI), a high resolution ground-based
multiband survey
(SPT), and the Planck all-sky survey. These surveys are not purely flux limited,
and they loose completeness significantly before their point-source detection
thresholds. Contamination remains relatively low at <5% (less than 30%)
for a detection threshold set at S/N=5 (S/N=3). We identify photometric recovery
as an important source of catalog uncertainty: dispersion in recovered flux from
multiband surveys is larger than the intrinsic scatter in the Y-M relation
predicted from hydrodynamical simulations, while photometry in the single frequency
survey is seriously compromised by confusion with primary cosmic microwave
background anisotropy. The latter effect implies that follow-up observations in other
wavebands (e.g., 90 GHz, X-ray) of single frequency
surveys will be required. Cluster morphology can cause a bias in
the recovered Y-M relation, but has little effect on the scatter;
the bias would be removed during calibration of the relation.
Point source confusion only slightly decreases multiband survey
completeness; single frequency survey completeness could be significantly reduced
by radio point source confusion, but this remains highly uncertain because we
do not know the radio counts at the relevant flux levels.
Key words: large-scale structure of Universe - galaxies: clusters: general - methods: data analysis
Cosmological studies demand statistically pure catalogs with well understood selection criteria. As just said, SZ surveys are intrinsically good in this light; however, many other factors - related, for example, to instrumental properties, observing conditions, astrophysical foregrounds and data reduction algorithms - influence the selection criteria. This has prompted some authors to begin more careful scrutiny of SZ survey selection functions in anticipation of future observations (Bartlett 2001; Schulz & White 2003; White 2003; Vale & White 2006; Melin et al. 2005; Juin et al. 2005).
In Melin et al. (2005), we presented a general formalism for the
SZ selection function together with some preliminary applications
using a matched-filter cluster detection method.
In this paper we give a thorough presentation of
our cluster detection method and evaluate its performance
in terms of catalog completeness, contamination and photometric recovery.
We focus on three types of SZ survey: single frequency radio surveys like
the Arcminute MicroKelvin Imager (AMI interferometer) survey![]() , multi-band ground-based bolometric surveys such as
the South Pole Telescope (SPT) survey
, multi-band ground-based bolometric surveys such as
the South Pole Telescope (SPT) survey![]() , and the space-based Planck survey
, and the space-based Planck survey![]() .
In each case, we quantify the selection function using the formalism of
Melin et al. (2005).
.
In each case, we quantify the selection function using the formalism of
Melin et al. (2005).
We draw particular attention to the oft-neglected issue of photometry. Even if the SZ flux-mass relation is intrinsically tight, what matters in practice is the relation between the observed SZ flux and the mass. Photometric errors introduce both bias and additional scatter in the observed relation. Calibration of the Y-M relation will in principal remove the bias; calibration precision, however, depends crucially on the scatter in the observed relation. Good photometry is therefore very important. As we will see, observational uncertainty dominates the predicted intrinsic scatter in this relation in all cases studied.
We proceed as follows. In Sect. 2, we discuss cluster detection techniques and present the matched filter formalism. We describe our detection algorithm in Sect. 3. Using Monte Carlo simulations of the three types of survey, we discuss catalog completeness, contamination and photometry. This is done in Sect. 4 under the ideal situation where the filter perfectly matches the simulated clusters and in the absence of point sources. In Sect. 5 we examine effects caused by cluster morphology, using N-body simulations, and then the effect of point sources. We close with a final discussion and conclusions in Sect. 6.
The detection and photometry of extended sources presents a complexity well appreciated in Astronomy. Many powerful algorithms, such as SExtractor (Bertin & Arnouts 1996), have been developed to extract extended sources superimposed on an unwanted background. They typically estimate the local background level and group pixels brighter than this level into individual objects. Searching for clusters at millimeter wavelengths poses a particular challenge to this approach, because the clusters are embedded in the highly variable background of the primary CMB anisotropies and Galactic emission. Realizing the importance of this issue, several authors have proposed specialized techniques for SZ cluster detection. Before detailing our own method, we first briefly summarize some of this work in order to motivate our own approach and place it in context.
Diego et al. (2002) developed a method designed for the Planck mission that is based on application of SExtractor to SZ signal maps constructed by combining different frequency channels. It makes no assumption about the frequency dependance of the different astrophysical signals, nor the cluster SZ emission profile. The method, however, requires many low-noise maps over a broad range of frequencies in order to construct the SZ map to be processed by SExtractor. Although they will benefit from higher resolution, planned ground-based surveys will have fewer frequencies and higher noise levels, making application of this method difficult.
In another approach, Herranz et al. (2002a,b; see also López-Caniego et al. 2005 for point-source applications) developed an ingenious filter (Scale Adaptive Filter) that simultaneously extracts cluster size and flux. Defined as the optimal filter for a map containing a single cluster, it does not account for source blending. Cluster-cluster blending could be an important source of confusion in future ground-based experiments, with as a consequence poorly estimated source size and flux.
Hobson & McLachlan (2003) recently proposed a powerful Bayesian detection method using a Monte Carlo Markov Chain. The method simultaneously solves for the position, size, flux and morphology of clusters in a given map. Its complexity and run-time, however, rapidly increase with the number of sources.
More recently, Schäfer et al. (2006) generalized scale adaptive and matched filters to the sphere for the Planck all-sky SZ survey. Pierpaoli et al. (2005) propose a method based on wavelet filtering, studying clusters with complex shapes. Vale & White (2006) examine cluster detection using different filters (matched, wavelets, mexican hat), comparing completeness and contamination levels.
Finally, Pires et al. (2006) introduced an independent component analysis on simulated multi-band data to separate the SZ signal, followed by non-linear wavelet filtering and application of SExtractor.
Our aim is here is two-fold: to present and extensively evaluate our own SZ cluster catalog extraction method, and to use it in a comprehensive study of SZ survey selection effects. The two are in fact inseparable. First of all, selection effects are specific to a particular catalog extraction method. Secondly, we require a robust, rapid algorithm that we can run over a large number of simulated data sets in order to accurately quantify the selection effets. This important consideration conditions the kind of extraction algorithm that we can use. With this in mind, we have developed a fast catalog construction algorithm based on matched filters for both single and multiple frequency surveys. It is based on the approach first proposed by Herranz et al., but accounts for source blending.
After describing the method, we apply the formalism given in Melin et al. (2005) to quantify the selection function and contamination level in up-coming SZ surveys. We take as representative survey configurations AMI, SPT and Planck, and Monte Carlo simulate the entire catalog extraction process from a large ensemble of realizations for each configuration. By comparing to the simulated input catalogs, we evaluate the extracted catalogs in terms of their completeness, contamination and photometric accuracy/precision. We will place particular emphasis on the importance of the latter, something which has received little attention in most studies of this kind.
The SZ effect is caused by the hot gas (
![]() keV) contained in
galaxy clusters known as the intracluster medium (ICM); electrons in
this gas up-scatter CMB photons and create a unique spectral distortion
that is negative at radio wavelengths and positive in the
submillimeter, with a zero-crossing near 220 GHz. The form of this
distortion is universal (in the non-relativistic limit applicable to
most clusters), while the amplitude is given by the Compton yparameter, an integral of the gas pressure along the line-of-sight.
In a SZ survey, clusters will appear as sources extended over
arcminute scales (apart from the very nearby objects, which are
already known) with brightness profile
keV) contained in
galaxy clusters known as the intracluster medium (ICM); electrons in
this gas up-scatter CMB photons and create a unique spectral distortion
that is negative at radio wavelengths and positive in the
submillimeter, with a zero-crossing near 220 GHz. The form of this
distortion is universal (in the non-relativistic limit applicable to
most clusters), while the amplitude is given by the Compton yparameter, an integral of the gas pressure along the line-of-sight.
In a SZ survey, clusters will appear as sources extended over
arcminute scales (apart from the very nearby objects, which are
already known) with brightness profile
| (1) |
Matched filters for SZ observations were first proposed by Haehnelt & Tegmark (1996) as a tool to estimate cluster peculiar velocities from the kinetic effect, and Herranz et al. (2002a,b) later showed how to use them to detect clusters via the thermal SZ effect. They are designed to maximally enhance the signal-to-noise for a SZ cluster source by optimally (in the least square sense) filtering the data, which in our case is a sky map or set of maps at different frequencies. They do so by incorporating prior knowledge of the cluster signal, such as its spatial and spectral characteristics. The unique and universal frequency spectrum of the thermal SZ effect (in the non-relativistic regime) is hence well suited for a matched-filter approach.
Less clear is the choice of the spatial profile
![]() to adopt for cluster SZ emission.
One aims to choose a spatial
template that represents as well as possible the average SZ emission
profile. In other words, we want
to adopt for cluster SZ emission.
One aims to choose a spatial
template that represents as well as possible the average SZ emission
profile. In other words, we want
![]() ,
where the
average is over many clusters of size
,
where the
average is over many clusters of size
![]() .
In the following, we
choose to describe clusters with a projected spherical
.
In the following, we
choose to describe clusters with a projected spherical ![]() -profile:
-profile:
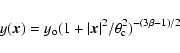 |
(2) |
In reality, of course, we know neither this average profile precisely nor the dispersion of individual clusters around it beforehand. This is an important point, because our choice for the template will affect both the detection efficiency and photometric accuracy. Detection efficiency will be reduced if the template does not well represent the average profile and, as will become clear below, the photometry will be biased. In general, the survey selection function unavoidably suffers from uncertainty induced by unknown source astrophysics (in addition to other sources of uncertainty).
In the following, we first study (Sect. 4) the ideal case where the filters
perfectly match the cluster profiles, i.e., we use the ![]() -model
for both our simulations and as the detection template. In a later
section (5), we examine the effects caused by non-trivial cluster
morphology, as well as by point source confusion.
-model
for both our simulations and as the detection template. In a later
section (5), we examine the effects caused by non-trivial cluster
morphology, as well as by point source confusion.
Consider a cluster with core radius
![]() and central
y-value
and central
y-value ![]() positioned at an arbitrary point
positioned at an arbitrary point
![]() on the sky. For generality, suppose that the
region is covered by several maps
on the sky. For generality, suppose that the
region is covered by several maps
![]() at N different
frequencies
at N different
frequencies ![]() (i=1,...,N). We arrange the survey maps
into a column vector
(i=1,...,N). We arrange the survey maps
into a column vector
![]() whose ith component is
the map at frequency
whose ith component is
the map at frequency ![]() ;
this vector reduces to a scalar map in
the case of a single frequency survey. Our maps contain the
cluster SZ signal plus noise:
;
this vector reduces to a scalar map in
the case of a single frequency survey. Our maps contain the
cluster SZ signal plus noise:
| (3) |
We now build a filter
![]() (in general, a column
vector in frequency space) that returns an estimate,
(in general, a column
vector in frequency space) that returns an estimate,
![]() ,
of
,
of
![]() when centered on the cluster:
when centered on the cluster:
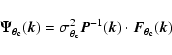 |
(5) |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{ami_spt_filters.eps}
\end{figure}](/articles/aa/full/2006/44/aa5034-06/Timg61.gif) |
Figure 1:
Two examples of the matched filter for
|
| Open with DEXTER | |
We write the noise power spectrum as a sum
![]() ,
where
,
where
![]() represents the instrumental noise power in band i,
represents the instrumental noise power in band i,
![]() the observational beam and
the observational beam and
![]() gives the foreground power (non-SZ signal) between channels i and j.
As explicitly written, we assume uncorrelated instrumental noise between observation
frequencies. Note that we treat the astrophysical foregrounds as
isotropic, stationary random fields with zero mean. The zero
mode is, in any case, removed from each of the maps, and the model
certainly applies to the primary CMB anisotropy. It should
also be a reasonable model for fluctuations of other foregrounds
about their mean, at least over cluster scales
gives the foreground power (non-SZ signal) between channels i and j.
As explicitly written, we assume uncorrelated instrumental noise between observation
frequencies. Note that we treat the astrophysical foregrounds as
isotropic, stationary random fields with zero mean. The zero
mode is, in any case, removed from each of the maps, and the model
certainly applies to the primary CMB anisotropy. It should
also be a reasonable model for fluctuations of other foregrounds
about their mean, at least over cluster scales![]() .
.
Two examples of the matched filter for
![]() arcmin
are shown in Fig. 1,
one for an AMI-like single frequency survey with a 1.5 arcmin beam
(left-hand panel) and the other for a SPT-like 3-band filter (right-hand
panel); see Table 1 for the experimental characteristics.
The filters are circularly symmetric, with the figures giving their radial
profiles, because we have chosen a spherical cluster model.
We clearly see the spatial weighting used by the single frequency filter
to optimally extract the cluster from the noise and CMB backgrounds.
The multiple frequency filter
arcmin
are shown in Fig. 1,
one for an AMI-like single frequency survey with a 1.5 arcmin beam
(left-hand panel) and the other for a SPT-like 3-band filter (right-hand
panel); see Table 1 for the experimental characteristics.
The filters are circularly symmetric, with the figures giving their radial
profiles, because we have chosen a spherical cluster model.
We clearly see the spatial weighting used by the single frequency filter
to optimally extract the cluster from the noise and CMB backgrounds.
The multiple frequency filter
![]() is a 3-element column
vector containing filters for each individual frequency.
In this case, the filter employs both spectral and spatial
weighting to optimally extract the cluster signal.
is a 3-element column
vector containing filters for each individual frequency.
In this case, the filter employs both spectral and spatial
weighting to optimally extract the cluster signal.
Figure 2 shows the filter noise as a function of
template core radius
![]() .
We plot the filter noise expressed in terms
of an equivalent noise
.
We plot the filter noise expressed in terms
of an equivalent noise
![]() on the integrated SZ flux Y. The dashed-triple-dotted red curve with
on the integrated SZ flux Y. The dashed-triple-dotted red curve with ![]() is shown
for comparison to gauge the impact of changing this parameter, otherwise fixed at
is shown
for comparison to gauge the impact of changing this parameter, otherwise fixed at ![]() throughout this work. Melin et al. (2005) use
the information in this figure to construct survey completeness functions. At fixed
signal-to-noise q, the completeness of a survey rapidly increases to
unity in the region above the curve
throughout this work. Melin et al. (2005) use
the information in this figure to construct survey completeness functions. At fixed
signal-to-noise q, the completeness of a survey rapidly increases to
unity in the region above the curve
![]() .
The figure shows that high angular resolution ground-based surveys
(e.g., AMI, SPT) are not purely flux limited, because their noise
level rises significantly with core radius. The lower resolution of the
Planck survey, on the other hand, results in more nearly flux limited
sample.
.
The figure shows that high angular resolution ground-based surveys
(e.g., AMI, SPT) are not purely flux limited, because their noise
level rises significantly with core radius. The lower resolution of the
Planck survey, on the other hand, results in more nearly flux limited
sample.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{cy_vs_tc_beta.eps}
\end{figure}](/articles/aa/full/2006/44/aa5034-06/Timg70.gif) |
Figure 2:
Filter noise expressed in terms of integrated SZ flux Y -
|
| Open with DEXTER | |
Catalog construction proceeds in three steps, the last two of which
are repeated![]() :
:
Table 1:
Characteristics of the three types of experiments considered.
We run our extraction method on
100 sky patches of
![]() square degrees (for AMI and SPT) and
square degrees (for AMI and SPT) and
![]() square degrees (for Planck).
square degrees (for Planck).
In the first step, we convolve the observed map(s) with matched filters
covering the expected range of core radii. For AMI and SPT, for example,
we vary ![]() from 0.1 to
from 0.1 to
![]() in 0.1 steps
(i.e.,
in 0.1 steps
(i.e.,
![]() )
and add
three values for the largest clusters:
)
and add
three values for the largest clusters:
![]() .
We thus filter the map(s)
.
We thus filter the map(s)
![]() times (
times (
![]() for AMI and SPT) to obtain
for AMI and SPT) to obtain
![]() filtered maps,
filtered maps,
![]() et
et
![]() .
The
.
The
![]() maps
maps
![]() give the SZ amplitude
(obtained using
give the SZ amplitude
(obtained using
![]() ), while the
), while the
![]() maps
maps
![]() give the signal-to-noise ratio:
give the signal-to-noise ratio:
![]() ).
We set a detection threshold at fixed signal-to-noise qand identify candidates at each filter scale
).
We set a detection threshold at fixed signal-to-noise qand identify candidates at each filter scale
![]() as pixels with
as pixels with
![]() .
Common values for the threshold are q=3 and q=5;
the choice is a tradeoff between detection
and contamination rates (see below).
.
Common values for the threshold are q=3 and q=5;
the choice is a tradeoff between detection
and contamination rates (see below).
We begin the second step by looking for the brightest candidate
pixel in the set of maps
![]() .
The candidate cluster is assigned the spatial coordinates
(x,y) of this pixel, and its core radius is defined as the
filter scale of the map containing the pixel:
.
The candidate cluster is assigned the spatial coordinates
(x,y) of this pixel, and its core radius is defined as the
filter scale of the map containing the pixel:
![]() .
We then calculate the total integrated flux using
.
We then calculate the total integrated flux using
![]() ,
where
,
where
![]() is taken from the map
is taken from the map
![]() at the same filter scale.
We refer to this step as the photometric step, and the parameters
at the same filter scale.
We refer to this step as the photometric step, and the parameters
![]() ,
,
![]() and Y as photometric parameters. Note that measurement error
on Y comes from errors on both
and Y as photometric parameters. Note that measurement error
on Y comes from errors on both
![]() and
and
![]() (we
return to this in greater detail in Sect. 4.4).
(we
return to this in greater detail in Sect. 4.4).
The candidate cluster is now added to the final cluster catalog,
and we proceed by removing it from the set of filtered maps
![]() and
and
![]() before returning to step 2. To this end, we
construct beforehand a 2D array (library) of un-normalized, filtered cluster
templates (postage-stamp maps)
before returning to step 2. To this end, we
construct beforehand a 2D array (library) of un-normalized, filtered cluster
templates (postage-stamp maps)
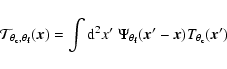 |
(8) |
We then return to step 2 and repeat the process until there are no remaining candidate pixels. Thus, clusters are added to the catalog while being subtracted from the maps one at a time, thereby de-blending the sources. By pulling off the brightest clusters first, we aim to minimize uncertainty in the catalog photometric parameters. Nevertheless, it must be emphasized that the entire procedure relies heavily on the use of templates and that real clusters need not conform to the chosen profiles. We return to the effects of cluster morphology below.
In the end, we have a cluster catalog with positions (x,y), central
Compton y parameters, sizes ![]() and fluxes Y.
and fluxes Y.
We tested our catalog construction method on simulated observations
of the three representative types of SZ survey specified in Table 1. The simulations include SZ emission, primary CMB
anisotropy and instrumental noise and beam smearing. We do not include diffuse Galactic foregrounds in this study. We begin in this section with the
ideal case where the filter perfectly matches the simulated clusters
(spherical ![]() -model profiles) and in the absence of extragalactic point sources. We return to the additional effects of cluster morphology and
point source confusion in Sect. 5.
-model profiles) and in the absence of extragalactic point sources. We return to the additional effects of cluster morphology and
point source confusion in Sect. 5.
The simulated maps are generated by Monte Carlo. We first create a realization of the linear matter distribution in a large box using the matter power spectrum. Clusters are then distributed according to their expected number density, given by the mass function, and bias as a function of mass and redshift. We also give each cluster a peculiar velocity consistent with the matter distribution according to linear theory. The simulations thus featuring cluster spatial and velocity correlations accurate first order, which is a reasonable approximation on cluster scales. In this paper, we use these simulations but we do not study the impact of the correlations on the detection method, leaving this issue to forthcoming work.
The cluster gas is modeled by a spherical isothermal ![]() -profile with
-profile with ![]() and
and
![]() ,
where
,
where
![]() is the angular projection
of the virial radius and which varies with cluster mass and redshift following a self-similar relationship. We choose an M-T relation consistent with the local abundance of X-ray clusters and our value of
is the angular projection
of the virial radius and which varies with cluster mass and redshift following a self-similar relationship. We choose an M-T relation consistent with the local abundance of X-ray clusters and our value of ![]() ,
given below (Pierpaoli et al. 2005).
Finally, we fix the gas mass fraction at
,
given below (Pierpaoli et al. 2005).
Finally, we fix the gas mass fraction at
![]() (e.g., Mohr et al. 1999). The input catalog consists of clusters with
total mass
(e.g., Mohr et al. 1999). The input catalog consists of clusters with
total mass
![]() ,
which is sufficient given the experimental characteristics listed in Table 1. Delabrouille et al. (2002) describe the simulation method in more detail.
,
which is sufficient given the experimental characteristics listed in Table 1. Delabrouille et al. (2002) describe the simulation method in more detail.
We generate primary CMB anisotropies using the power spectrum calculated
by CMBFAST![]() (Seljak & Zaldarriaga 1996)
for a flat concordance model with
(Seljak & Zaldarriaga 1996)
for a flat concordance model with
![]() (Spergel et al. 2003), Hubble constant
(Spergel et al. 2003), Hubble constant
![]() km s-1 Mpc-1 (Freedman et al. 2001) and a power
spectrum normalization
km s-1 Mpc-1 (Freedman et al. 2001) and a power
spectrum normalization
![]() .
As a last step we smooth the map
with a Gaussian beam and add Gaussian white noise to model
instrumental effects
.
As a last step we smooth the map
with a Gaussian beam and add Gaussian white noise to model
instrumental effects![]() .
.
We simulate maps that would be obtained from the proposed surveys
listed in Table 1. The first is an
AMI![]() -like
experiment (Jones et al. 2005), a single frequency, high resolution
interferometer; the sensitivity corresponds to a one-month integration
time per 0.1 square degree (Kneissl et al. 2001).
The SPT
-like
experiment (Jones et al. 2005), a single frequency, high resolution
interferometer; the sensitivity corresponds to a one-month integration
time per 0.1 square degree (Kneissl et al. 2001).
The SPT![]() -like
experiment (Ruhl et al. 2004) is a high resolution, multi-band bolometer array.
We calculate the noise levels assuming
an integration time of 1 hour per square degree, and a split of
2/3, 1/6, 1/6 of the 150, 220, 275 GHz channels for the 1000 detectors
in the focal plane array (Ruhl et al. 2004).
Finally, we consider the space-based
Planck
-like
experiment (Ruhl et al. 2004) is a high resolution, multi-band bolometer array.
We calculate the noise levels assuming
an integration time of 1 hour per square degree, and a split of
2/3, 1/6, 1/6 of the 150, 220, 275 GHz channels for the 1000 detectors
in the focal plane array (Ruhl et al. 2004).
Finally, we consider the space-based
Planck![]() -like
experiment, with a nominal sensitivity for a
14 month mission. For the AMI and SPT maps we use pixels
-like
experiment, with a nominal sensitivity for a
14 month mission. For the AMI and SPT maps we use pixels![]() of
of
![]() ,
while for Planck the pixels are
,
while for Planck the pixels are
![]() .
.
We simulate 100 sky patches of ![]() square degrees
for both AMI and SPT, and of
square degrees
for both AMI and SPT, and of
![]() square degrees for Planck.
This is appropriate given the masses of detected clusters in each experiment.
In practice, AMI will cover a few square degrees, similar to the
simulated patch, while SPT will cover 4000 square degrees and Planck will
observe the entire sky. Thus, the surveys decrease in sensitivity
while increasing sky coverage from top to bottom in Table 2
(see also Table 1).
square degrees for Planck.
This is appropriate given the masses of detected clusters in each experiment.
In practice, AMI will cover a few square degrees, similar to the
simulated patch, while SPT will cover 4000 square degrees and Planck will
observe the entire sky. Thus, the surveys decrease in sensitivity
while increasing sky coverage from top to bottom in Table 2
(see also Table 1).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{integrated_counts_inset_reass.eps}
\end{figure}](/articles/aa/full/2006/44/aa5034-06/Timg104.gif) |
Figure 3: Cluster counts N(>Y) per square degree as a function of true SZ flux Y for a threshold of S/N>5. The dash-dotted black line gives the cluster counts from the mass function (Jenkins et al. 2001). The dashed blue line gives the recovered cluster counts for AMI, the red solid line for SPT and the dotted green line for Planck. The inset shows the completeness ratio (relative to the mass function prediction) for each survey. All the surveys are significantly incomplete at their point-source sensitivities (5 times the y-intercept in Fig. 2). |
| Open with DEXTER | |
Table 2: Extracted counts/sq. deg. from simulations of the three types of survey. The numbers in parenthesis give the counts predicted by our analytic cluster model; the difference is due to cluster overlap confusion (see text).
An important issue for catalog evaluation is the association between a detected object (candidate cluster) with a cluster from the simulation input catalog (real cluster); in other words, a candidate corresponds to which, if any, real cluster. Any association method will be imprecise, and estimates of catalog completeness, contamination and photometric accuracy will unavoidably depend on the choice of association criteria.
We proceed as follows: for each detection, we
look at all input clusters with centers positioned within a distance
![]() ,
where d is
the pixel size (
,
where d is
the pixel size (
![]() for AMI and SPT,
for AMI and SPT,
![]() for Planck); this covers the neighboring 24 pixels.
If there is no input cluster, then we have a false detection;
otherwise, we identify the candidate with the cluster whose flux is
closest to that of the detection. After running through all the
candidates in this fashion, we may find that different candidates
are associated with the same input cluster. In this case, we only
keep the candidate whose flux is closest to the common input cluster, and
we flag the other candidates as false detections (multiple detections).
for Planck); this covers the neighboring 24 pixels.
If there is no input cluster, then we have a false detection;
otherwise, we identify the candidate with the cluster whose flux is
closest to that of the detection. After running through all the
candidates in this fashion, we may find that different candidates
are associated with the same input cluster. In this case, we only
keep the candidate whose flux is closest to the common input cluster, and
we flag the other candidates as false detections (multiple detections).
At this stage, some associations may nevertheless be chance alignments.
We therefore employ a second parameter,
![]() :
a candidate
associated with a real cluster of flux
:
a candidate
associated with a real cluster of flux
![]() is flagged as a false detection. We indicate these false detections
as diamonds in Figs. 7, 8,
9 and 11. The idea is
that such clusters are too faint to have been detected and the
association is therefore by chance. In the following, we take
is flagged as a false detection. We indicate these false detections
as diamonds in Figs. 7, 8,
9 and 11. The idea is
that such clusters are too faint to have been detected and the
association is therefore by chance. In the following, we take
![]() for AMI and SPT, respectively, and
for AMI and SPT, respectively, and
![]() for Planck.
Note that these numbers are well below the point-source sensitivity
(at S/N=5) in each case (see below and Fig. 2).
for Planck.
Note that these numbers are well below the point-source sensitivity
(at S/N=5) in each case (see below and Fig. 2).
Figure 3 shows completeness for the three experiments in terms of true integrated Y, while Table 2 summarizes the counts. In Fig. 4 we give the corresponding limiting mass as a function of redshift. Given our cluster model, AMI, SPT and Planck should find, respectively, about 16, 11 and 0.35 clusters/deg.2 at a S/N>5; these are the numbers given in parentheses in Table 2. Cluster overlap confusion accounts for the fact that the actual counts extracted from the simulated surveys are higher: some clusters that would not otherwise pass the detection cut enter the catalog because the filter adds in flux from close neighbors.
A detection threshold of S/N=5 corresponds to a point-source
sensitivity of just below
![]() arcmin2 for both
AMI and SPT, as can be read off the left-hand-side of
Fig. 2. The surveys approach a high level of
completeness only at Y>10-4 arcmin2, however, due to the rise
of the selection cut with core radius seen in Fig. 2.
For these high resolution surveys, point-source sensitivity gives
a false idea of the survey completeness flux limit.
arcmin2 for both
AMI and SPT, as can be read off the left-hand-side of
Fig. 2. The surveys approach a high level of
completeness only at Y>10-4 arcmin2, however, due to the rise
of the selection cut with core radius seen in Fig. 2.
For these high resolution surveys, point-source sensitivity gives
a false idea of the survey completeness flux limit.
At the same signal-to-noise threshold,
Planck is essentially complete above
![]() and should detect about 0.4 clusters per square degree. Since most
clusters are unresolved by Planck, the survey reaches a high completeness
level near the point-source sensitivity. We also see this from
the small slope of the Planck selection cut in Fig. 2.
and should detect about 0.4 clusters per square degree. Since most
clusters are unresolved by Planck, the survey reaches a high completeness
level near the point-source sensitivity. We also see this from
the small slope of the Planck selection cut in Fig. 2.
We emphasize that the surveys (in particular, the high resolution surveys) are not flux limited for any value of q, because increasing q simply
translates the curve in Fig. 2 along the y axis. However, one can approach a flux-limited catalog by selecting clusters at S/N>q and then cutting the resulting catalog at
![]() ,
where the constant Q>q.
As Q increases we tend towards a catalog for which
,
where the constant Q>q.
As Q increases we tend towards a catalog for which
![]() .
In the case
of SPT with q=3, for example, we find that large values of Q (>10)
are required to approach a reasonable flux-limited catalog; this construction, however, throws away a very large number of detected clusters.
.
In the case
of SPT with q=3, for example, we find that large values of Q (>10)
are required to approach a reasonable flux-limited catalog; this construction, however, throws away a very large number of detected clusters.
Although the AMI (single frequency) and
SPT (multi-band) survey maps have comparable depth,
SPT will cover ![]() 4000 sq. degrees, compared to AMI's
4000 sq. degrees, compared to AMI's ![]() 10 sq.
degrees. Planck will only find the brightest clusters, but with
full sky coverage. Predictions for the counts suffer from cluster modeling
uncertainties, but the comparison between experiments is robust and of
primary interest here.
10 sq.
degrees. Planck will only find the brightest clusters, but with
full sky coverage. Predictions for the counts suffer from cluster modeling
uncertainties, but the comparison between experiments is robust and of
primary interest here.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{mz_limit_lin_lin.eps}
\end{figure}](/articles/aa/full/2006/44/aa5034-06/Timg116.gif) |
Figure 4: Mininum detectable cluster mass as a function of redshift, M(z), corresponding to S/N=5 for the three experiments discussed in the text. The rise at low redshift for the single-frequency (AMI) curve is caused by confusion with primary CMB anisotropy. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{contamination_5_zoom_reass.eps}
\end{figure}](/articles/aa/full/2006/44/aa5034-06/Timg117.gif) |
Figure 5:
Contamination as a function of the core radius
|
| Open with DEXTER | |
Figure 5 shows the contamination level at S/N>5 for
each survey type as a function of recovered flux ![]() .
The multiband experiments (SPT and Planck) benefit from low
contamination at all fluxes.
Single frequency surveys (e.g., AMI), on the other hand, experience a
slightly higher contamination level at large flux due to confusion from
primary CMB anisotropy. This confusion also degrades the photometry,
as we discuss below.
.
The multiband experiments (SPT and Planck) benefit from low
contamination at all fluxes.
Single frequency surveys (e.g., AMI), on the other hand, experience a
slightly higher contamination level at large flux due to confusion from
primary CMB anisotropy. This confusion also degrades the photometry,
as we discuss below.
At S/N>5, the AMI, SPT and Planck catalogs have less than 2% total contamination
rate. These numbers
increase to ![]() 23, 20 and 27 percent, respectively, for AMI, SPT and
Planck at a detection threshold of S/N>3. Note that the total
contamination rate is an average over the histogram of Fig. 5
weighted by the number of objects in each bin; thus, the higher contamination
at large flux is down-weighted in the total rate.
23, 20 and 27 percent, respectively, for AMI, SPT and
Planck at a detection threshold of S/N>3. Note that the total
contamination rate is an average over the histogram of Fig. 5
weighted by the number of objects in each bin; thus, the higher contamination
at large flux is down-weighted in the total rate.
In all cases, the contamination rate is higher than expected from pure Gaussian noise fluctuations; there is an important contribution from cluster-cluster confusion (residuals from cluster subtraction and overlaps). We expect even higher contamination rates in practice, because of variations in cluster morphology around the filter templates. We quantify this latter effect below.
A useful summary of these results is a completeness-purity plot, as
shown in Fig. 6. Proper comparison of the
different experiments requires an appropriate choice of input catalog
used to define the completeness in this plot. Here, we
take the input catalog as all clusters with (true) flux geater than
three times the point source sensitivity for each experiment.
If the clusters were point sources and the detection method perfect (i.e. not affected by confusion), the completeness would be 1 for q=3 in the top-left corner. These curves summarize the efficiency of our cluster detection method; however, they give no information on the photometric capabilities of the experiments.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{completeness_purity_pssens_reass_true.eps}
\end{figure}](/articles/aa/full/2006/44/aa5034-06/Timg119.gif) |
Figure 6:
Completeness-Purity plot. For each curve, q varies from 3 ( top-left) to 10 ( bottom-right). For each experiment, the input catalog contains clusters with true flux greater than three times the point source sensitivity (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{spt_photometry_dots_conf.eps}
\end{figure}](/articles/aa/full/2006/44/aa5034-06/Timg121.gif) |
Figure 7:
Recovered vs. true flux for SPT clusters extracted at S/N>5from 100 survey simulations. The diamonds indicate cluster detections
with
|
| Open with DEXTER | |
We now turn to the important, but often neglected issue of cluster SZ photometry. The ability of a SZ survey to constrain cosmology relies on application of the Y-M relation. As mentioned, we expect the intrinsic (or true) flux to tightly correlate with cluster mass (Bartlett 2001), as indeed borne out by numerical simulations (da Silva et al. 2004; Motl et al. 2005; Nagai 2005). Nevertheless, unknown cluster physics could affect the exact form and normalization of the relation, pointing up the necessity of an empirical calibration (referred to as survey calibration), either with the survey data itself (self-calibration; Hu 2003; Majumdar & Mohr 2003; Lima & Hu 2004; Lima & Hu 2005) or using external data, such as lensing mass estimates (Bartelmann 2001) (although the latter will be limited to relatively low redshifts).
Photometric measurement
accuracy and precision is as important as cluster physics in this context:
what matters in practice is the relation between recovered SZ flux ![]() and cluster mass M. Biased SZ photometry (bias in the
and cluster mass M. Biased SZ photometry (bias in the
![]() )
relation
will change the form and normalization of the
)
relation
will change the form and normalization of the
![]() relation and noise will
increase the scatter. One potentially important source of photometric
error for the matched filter comes from cluster morphology, i.e.,
the fact that cluster profiles do not exactly follow the filter shape
(see Sect. 5).
relation and noise will
increase the scatter. One potentially important source of photometric
error for the matched filter comes from cluster morphology, i.e.,
the fact that cluster profiles do not exactly follow the filter shape
(see Sect. 5).
Survey calibration will help remove the bias, but with an ease that depends on the photometric scatter: large scatter will increase calibration uncertainty and/or necessitate a larger amount of external data. In addition, scatter will degrade the final cosmological constraints (e.g., Lima & Hu 2005). Photometry should therefore be considered an important evaluation criteria for cluster catalog extraction methods.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{plk_photometry_dots_conf.eps}
\end{figure}](/articles/aa/full/2006/44/aa5034-06/Timg124.gif) |
Figure 8:
Recovered vs. true flux for Planck clusters extracted at
S/N>5 from 100 survey simulations. The diamonds indicate
cluster detections with
|
| Open with DEXTER | |
Consider, first, SPT photometry. Figure 7 shows the
relation between observed (or recovered) flux ![]() and true flux Y
for a detection threshold of S/N>5. Fitting for the average trend
of
and true flux Y
for a detection threshold of S/N>5. Fitting for the average trend
of ![]() as a function of Y, we obtain
as a function of Y, we obtain
![\begin{figure}
\par\includegraphics[width=8cm,clip]{ami_photometry_dots_reass.eps}
\end{figure}](/articles/aa/full/2006/44/aa5034-06/Timg127.gif) |
Figure 9:
Recovered vs. true flux for AMI clusters extracted at S/N>5from 100 survey simulations. The diamonds indicate cluster detections
with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{ami_histogram_cy_back_1_reass.eps}
\end{figure}](/articles/aa/full/2006/44/aa5034-06/Timg128.gif) |
Figure 10:
The full blue histogram gives the cluster counts from
Fig. 9 in the bin
(
10-4<Y<2.10-4,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{ami_photometry_tc_dots_reass.eps}
\end{figure}](/articles/aa/full/2006/44/aa5034-06/Timg129.gif) |
Figure 11: Single-frequency photometry when we artificially set the core radii of detected clusters to their true values from the input catalog. The dispersion decreases dramatically, demonstrating that the inability to recover the core radius is the origin of the bad photometry seen in Fig. 9. |
| Open with DEXTER | |
The scatter about the fit is consistent with a Gaussian
distribution with a roughly constant
standard deviation of
![]() over the entire interval.
over the entire interval.
The scatter is a factor of 10 larger than expected from instrumental noise alone, which is given by the selection curve in Fig. 2. Uncertainty in the recovered cluster position, core radius and effects from cluster-cluster confusion all strongly influence the scatter. Photometry precision, therefore, cannot be predicted from instrumental noise properties alone, but only with simulations accounting for these other, more important effects.
Figure 8 shows the photometry for the Planck survey.
Apart from some catastrophic cases (the diamonds), the photometry is
good and fit by
We emphasize that the observational scatter in the
![]() relation
for both SPT and Planck dominates the intrinsic scatter of less
than 5% seen in the Y-M relation from numerical simulations
(da Silva et al. 2004; Motl et al. 2005).
relation
for both SPT and Planck dominates the intrinsic scatter of less
than 5% seen in the Y-M relation from numerical simulations
(da Silva et al. 2004; Motl et al. 2005).
We now turn to single frequency surveys, which Fig. 9
shows to have seriously compromised photometry. The distribution
at a given true flux Y is in fact bimodal, as illustrated by the solid
blue histogram in Fig. 10 that
gives the distribution of the recovered flux ![]() for clusters with
true flux and core radius in a bin centered on
for clusters with
true flux and core radius in a bin centered on
![]() arcmin2 and
arcmin2 and
![]() arcmin.
We have traced this effect to an inability to accurately determine the
core radius of the candidate clusters. We demonstrate this in
Fig. 11 by artificially setting the candidate
core radius to its true value taken from the associated input
cluster; the photometry now cleanly scatters about the mean trend.
arcmin.
We have traced this effect to an inability to accurately determine the
core radius of the candidate clusters. We demonstrate this in
Fig. 11 by artificially setting the candidate
core radius to its true value taken from the associated input
cluster; the photometry now cleanly scatters about the mean trend.
This inability to determine the core radius mainly arises from confusion with
primary CMB anisotropy, as we now show using
Fig. 10.
We performed 1000 simulations of a single cluster
(
![]() arcmin2,
arcmin2,
![]() arcmin) placed at
the middle of a beam-convolved map containing background SZ clusters
(from our general simulations), primary CMB anisotropy and
instrumental noise. We then estimate its core radius and flux with
our matched filters centered on the known position (to avoid any
positional uncertainty) and trace the histogram of resulting
measured flux. This is the red dot-dashed histogram in the figure,
which displays a bi-modality similar to that of the blue solid
histogram. We then follow the same procedure after first removing the
primary CMB anisotropy from the simulated map.
The resulting histogram of recovered flux is given
by the black dot-dashed line with much less pronounced bimodality.
The remaining tail reaching towards high flux is caused by cluster-cluster
confusion.
arcmin) placed at
the middle of a beam-convolved map containing background SZ clusters
(from our general simulations), primary CMB anisotropy and
instrumental noise. We then estimate its core radius and flux with
our matched filters centered on the known position (to avoid any
positional uncertainty) and trace the histogram of resulting
measured flux. This is the red dot-dashed histogram in the figure,
which displays a bi-modality similar to that of the blue solid
histogram. We then follow the same procedure after first removing the
primary CMB anisotropy from the simulated map.
The resulting histogram of recovered flux is given
by the black dot-dashed line with much less pronounced bimodality.
The remaining tail reaching towards high flux is caused by cluster-cluster
confusion.
With their additional spectral information, multiband surveys remove the primary CMB signal, thereby avoiding this source of confusion. The result suggests that follow-up observations of detected clusters at a second frequency will be required for proper photometry; without such follow-up, the scientific power of a single frequency survey may be seriously compromised, as can be appreciated from inspection of Fig. 9.
As emphasized, our previous results follow for a filter that perfectly matches the (spherical) clusters in our simulations and in the absence of any point sources. In this section we examine the effects of both cluster morphology and point sources.
We find that cluster morphology has little effect on catalog completeness, but that it does increase contamination. More importantly, it can bias photometric recovery, although it does not significantly increase the scatter. This bias changes the observed Y-M relation from its intrinsic form, adding to the modeling uncertainty already caused by cluster gas physics. For this reason, the relation must be calibrated in order to use the SZ catalog for any cosmological study. The observational bias would be removed during this calibration step.
Completeness is the most affected by point source confusion, decreasing somewhat for the multi-band surveys in the presence of IR point sources. The level of confusion for the single frequency survey remains highly uncertain due to the unknown point source counts at low flux densities. Contamination and photometry are essentially unaffected.
To assess the influence of cluster morphology, we ran our
catalog extraction algorithm on maps constructed from numerical simulations.
We use the simulations presented by Schulz & White (Schulz & White 2003) and kindly
provided to us by M. White. Their simulations follow dark matter clustering with
a N-body code in a flat concordance cosmology,
and model cluster gas physics with semi-analytical
techniques by distributing an isothermal gas of mass fraction
![]() according to the halo dark matter distribution. For details, see Schulz & White.
In the following, we refer to these simulations as the "N-body'' simulations.
according to the halo dark matter distribution. For details, see Schulz & White.
In the following, we refer to these simulations as the "N-body'' simulations.
We proceed by comparing catalogs
extracted from the N-body map to those from a corresponding
simulation made with spherical clusters. The latter is constructed by applying
our spherical ![]() -model gas distribution to the cluster halos taken
from the N-body simulation and using them as input to our Monte Carlo
sky maps. In the process, we renormalize our Y-M relation to the one
used in the N-body SZ maps. We thus obtain two SZ maps containing the same
cluster halos, one with spherical clusters (referred to hereafter as the "
-model gas distribution to the cluster halos taken
from the N-body simulation and using them as input to our Monte Carlo
sky maps. In the process, we renormalize our Y-M relation to the one
used in the N-body SZ maps. We thus obtain two SZ maps containing the same
cluster halos, one with spherical clusters (referred to hereafter as the "![]() -model''
maps) and the other with more complex cluster morphology (the N-body maps).
Comparison of the catalogs extracted from the two different types of
simulated map gives us an indication of the sensitivity of
our method to cluster morphology. We make this comparative study only for the
SPT and Planck like surveys.
-model''
maps) and the other with more complex cluster morphology (the N-body maps).
Comparison of the catalogs extracted from the two different types of
simulated map gives us an indication of the sensitivity of
our method to cluster morphology. We make this comparative study only for the
SPT and Planck like surveys.
Catalog completeness is essentially unaffected by cluster morphology; the integrated counts, for example, follow the same curves shown in Fig. 3 with very little deviation, the only difference being a very small decrease in the Planck counts at the lowest fluxes. The effect, for example, is smaller than that displayed in Fig. 13 due to point source confusion (and discussed below).
Non-trivial cluster morphology, however, does significantly
increase the catalog contamination rate; for example, in the SPT survey
the global contamination rises from less than 2% to 13% at S/N=5 for the N-body simulations. We trace this to residual flux left in the maps after
cluster extraction: cluster SZ signal that deviates from the assumed spherical ![]() -model filter profile remains in the map and is
picked up later as new cluster candidates. Masking those
regions where a cluster has been previously extracted (i.e.,
forbidding any cluster detection) drops the contamination to 4% (SPT case), but causes a decrease
of 2.8 clusters per square degree in the recovered counts; this technique would also
have important consequences for clustering studies.
-model filter profile remains in the map and is
picked up later as new cluster candidates. Masking those
regions where a cluster has been previously extracted (i.e.,
forbidding any cluster detection) drops the contamination to 4% (SPT case), but causes a decrease
of 2.8 clusters per square degree in the recovered counts; this technique would also
have important consequences for clustering studies.
From Fig. 12, we clearly see that cluster
morphology induces a bias in the photometry. This arises from the fact
that the actual cluster SZ profiles differ from the template adopted
for the filter. The differences are of two types: an overall difference
in the form of radial profile and local deviations about the average radial profile due to cluster substructure. It is the former that is primarily
responsible for the bias. In our case, the N-body simulations have
much more centrally peaked SZ emission than the filter templates, which
causes the filter to systematically underestimate the total SZ flux.
Cluster substructure will increase the scatter about the mean
![]() relation. This latter effect is not large, at least for
the N-body simulations used here, as can be seen by comparing the scatter
in Figs. 12 and 7.
relation. This latter effect is not large, at least for
the N-body simulations used here, as can be seen by comparing the scatter
in Figs. 12 and 7.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{spt_photometry_nbody_dots_sca_reass.eps}
\end{figure}](/articles/aa/full/2006/44/aa5034-06/Timg135.gif) |
Figure 12: Photometry for the SPT catalog from the N-body simulations. Cluster morphology (mismatch between the filter profile and the actual cluster SZ profile) clearly induces a bias between the recovered and true SZ flux. The scatter, on the other hand, is not very affected, as can be seen in comparing with Fig. 7. |
| Open with DEXTER | |
We emphasize, however, that the quantitative effects on photometry depend on the intrinsic cluster profile, and hence are subject to modeling uncertainty. The simulations used here do not include gas physics and simply assume that the gas follows the dark matter. The real bias will depend on unknown cluster physics, thus adding to the modeling uncertainty in the Y-M relation. This uncertainty, due to both cluster physics and the photometric uncertainty discussed here, must be dealt with by empirically calibrating the relation, either with external data (lensing) and/or internally (self-calibration).
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{integrated_counts_sources_reass.eps}
\end{figure}](/articles/aa/full/2006/44/aa5034-06/Timg136.gif) |
Figure 13: Integrated cluster counts for the three types of survey. The upper curve in each pair reproduces the results of Fig. 3, while the lower curve shows the effect of point source confusion. Despite the large IR point source population, multiband surveys efficiently eliminate confusion. The AMI-like survey is, on the other hand, strongly affected. This latter effect remains uncertain due to a lack of information on the faint end of the radio point source counts (see text). |
| Open with DEXTER | |
We next examine the effect of point sources. In a previous paper (Bartlett & Melin 2005, hereafter BM) we studied their influence on survey detection sensitivity. We extend this work to our present study in this section.
Low frequency surveys, such as our AMI example, contend with an important radio source population, while higher frequency bolometer surveys face a large population of IR sources. Radio source counts down to the sub-mJy flux levels relevant for SZ surveys are unfortunately poorly known. The IR counts are somewhat better constrained at fluxes dominating the fluctuations in the IR background, although at higher frequencies (850 microns) than those used in SZ surveys; an uncertain extrapolation in frequency is thus necessary.
For the present study, we use the radio counts fit by Knox et al. (2004) to a combination of
data from CBI, DASI, VSA and WMAP (see also Eq. (6) in BM), and
IR counts fit to blank-field SCUBA observations at 850 microns by Borys et al. (2003)
(and given by Eq. (8) in BM). We further
assume that all radio sources brighter than 100 ![]() Jy have been subtracted from
our maps at 15 GHz (AMI case); this is the target sensitivity of the long baseline
Ryle Telescope observations that will perform the source subtraction for AMI.
No such explicit point source subtraction is readily available for the higher
frequency bolometer surveys; they must rely solely on their frequency coverage to
reduce point source confusion. We therefore include all IR sources in our
simulations, and fix their effective spectral index
Jy have been subtracted from
our maps at 15 GHz (AMI case); this is the target sensitivity of the long baseline
Ryle Telescope observations that will perform the source subtraction for AMI.
No such explicit point source subtraction is readily available for the higher
frequency bolometer surveys; they must rely solely on their frequency coverage to
reduce point source confusion. We therefore include all IR sources in our
simulations, and fix their effective spectral index ![]() with no
dispersion
with no
dispersion![]() .
We refer the reader to BM for details of our point source model.
Note that for this study we use the spherical cluster model for direct comparison
to our fiducial results.
.
We refer the reader to BM for details of our point source model.
Note that for this study we use the spherical cluster model for direct comparison
to our fiducial results.
Figure 13 compares the integrated counts from Fig. 3 (upper curve in each case) to those extracted from the simulations including point sources (lower curves). We see that point source confusion only slightly decreases the completeness of the multiband surveys, but greatly affects the single frequency survey.
In the case of SPT, this is because point source confusion remains modest compared to the noise: the two are comparable at 150 GHz, but the noise power rises more quickly with frequency than the confusion power (see BM for details) - in other words, the noise is bluer than the confusion. This is an important consideration when looking for the optimal allocation of detectors to the observation bands.
For Planck, confusion power dominates at all frequencies, but the spectral coverage provides sufficient leverage to control it. In this light, it must be emphasized that we only include three astrophysical signals (SZ, CMB & point sources) in these simulations, so that three observation bands are sufficient. In reality, one will have to deal with other foregrounds, e.g., diffuse Galactic emission, which will require the use of additional observation bands.
The single frequency observations, on the other hand, are strongly affected. This is consistent with the estimate in BM (Eq. (15)) placing confusion noise well above instrumental noise for the chosen point source model and source subtraction threshold. We emphasize the uncertainty in this estimate, however: in BM we showed, for example, that a model with flattening counts has much lower source confusion while remaining consistent with the observed counts at high flux densities. The actual confusion level remains to be determined from deeper counts at CMB frequencies (see Waldram et al. 2003; Waldram et al. 2004 for recent deep counts at 15 GHz).
Contamination in the multiband surveys is practically unaffected by point source confusion. For AMI we actually find a lower contamination rate, an apparent gain explained by the fact that the catalog now contains only the brighter SZ sources, due to the lowered sensitivity caused by point source confusion.
The photometry of the multiband surveys also shows little effect from the point sources. Fits to the recovered flux vs. true flux relation do not differ significantly from the no-source case, and the dispersion remains essentially the same. This is consistent with the idea that point source confusion is either modest compared to the noise (SPT) or controlled by multiband observations (Planck).
We have described a simple, rapid method based on matched multi-frequency filters for extracting cluster catalogs from SZ surveys. We assessed its performance when applied to the three kinds of survey listed in Table 1. The rapidity of the method allows us to run many simulations of each survey to accurately quantify selection effects and observational uncertainties. We specifically examined catalog completeness, contamination rate and photometric precision.
Figure 2 shows the cluster selection criteria in terms of total SZ flux and source size. It clearly demonstrates that SZ surveys, in particular high resolution ground-bases surveys, will not be purely flux limited, something which must be correctly accounted for when interpreting catalog statistics (Melin et al. 2005).
Figure 3 and Table 2 summarize the expected yield for each survey. The counts roll off at the faint end well before the point-source flux limit (intercept of the curves in Fig. 2 multiplied by the S/N limit) even at the high detection threshold of S/N=5; the surveys loose completeness precisely because they are not purely flux-limited. These yields depend on the underlying cluster model and are hence subject to non-negligible uncertainty. They are nonetheless indicative, and in this work we focus on the nature of observational selection effects for which the exact yields are of secondary importance.
At our fiducial S/N=5 detection threshold, overall catalog contamination remains below 5%, with some dependence on SZ flux for the single frequency survey (see Fig. 5). The overall contamination rises to between 20% and 30% at S/N>3. We note that the contamination rate is always larger than expected from pure instrumental noise, pointing to the influence of astrophysical confusion.
We pay particular attention to photometric precision, an issue often neglected
in discussions of the scientific potential of SZ surveys. Scatter plots for the
recovered flux for each survey type are given in Figs. 7-9. In the two multiband surveys, the
recovered SZ flux is slightly biased, due to the flux cut, with a dispersion
of
![]() and
and
![]() for SPT and Planck, respectively.
This observational dispersion
is significantly larger than the intrinsic dispersion in the Y-M relation predicted
by hydrodynamical simulations. This uncertainty must be properly accounted for
in scientific interpretation of SZ catalogs; specifically, it will degrade survey
calibration and cosmological constraints.
for SPT and Planck, respectively.
This observational dispersion
is significantly larger than the intrinsic dispersion in the Y-M relation predicted
by hydrodynamical simulations. This uncertainty must be properly accounted for
in scientific interpretation of SZ catalogs; specifically, it will degrade survey
calibration and cosmological constraints.
Even more importantly, we found that astrophysical confusion seriously compromises the photometry of the single frequency survey (Fig. 9). The histogram in Fig. 10 shows that the recovered flux has in fact a bimodal distribution. We traced the effect to an inability to determine source core radii in the presence of primary CMB anisotropy. If cluster core radius could be accurately measured, e.g., with X-ray follow-up, then we would obtain photometric precision comparable to the multiband surveys (see Fig. 11). This confusion can also be removed by follow-up of detected sources at a second radio frequency (e.g., 90 GHz). Photometric uncertainty will therefore be key limiting factor in single frequency SZ surveys.
All these results apply to the ideal case where the filter exactly matches the (simulated) cluster profiles. We then examined the potential impact of cluster morphology and point sources on these conclusions.
Using N-body simulations, we found that cluster morphology has little effect on catalog completeness, but that it does increase the contamination rate and bias the photometry. The increased contamination is caused by deviations from a smooth radial SZ profile that appear as residual flux in the maps after source extraction. More importantly, the photometry is biased by the mismatch between the filter template and the actual cluster profile. This observational bias adds to the modeling uncertainty in the Y-M relation, which will have to be empirically determined in order to use the catalog for cosmology studies.
As shown by Fig. 13,
point sources decrease survey completeness. The multiband surveys effectively
reduce IR point source confusion and suffer only a small decrease. Radio source
confusion, on the other hand, greatly decreased the completeness of the single
frequency survey. This is consistent with the expectation that, for our adopted
radio point source model and source subtraction threshold, point source
confusion dominates instrumental noise. Modeling uncertainty here is, however,
very large: radio source counts are not constrained at relevant fluxes
(![]()
![]() Jy), which requires us to extrapolate counts from mJy levels
(see BM for a more detailed discussion).
Jy), which requires us to extrapolate counts from mJy levels
(see BM for a more detailed discussion).
Surveys based on the SZ effect will open a new window onto the high redshift universe. They inherit their strong scientific potential from the unique characteristics of the SZ signal. Full realization of this potential, however, requires understanding of observational selection effects and uncertainties. Overall, multiband surveys appear robust in this light, while single frequency surveys will most likely require additional observational effort, e.g., follow-up in other wavebands, to overcome large photometric errors caused by astrophysical confusion with primary CMB anisotropy.
Acknowledgements
We thank T. Crawford for useful comments on matched filters and information about SPT, and A. Schulz and M. White for kindly providing us with their N-body simulations. We are also grateful to the anonymous referee for helpful and insightful comments. JBM wishes to thank L. Knox, the Berkeley Astrophysics group and E. Pierpaoli for discussions on the detection method, and D. Herranz and the Santander group for discussions on matched filters. JBM was supported at UC Davis by the National Science Foundation under Grant No. 0307961 and NASA under Grant No. NAG5-11098.