A&A 459, 103-111 (2006)
DOI: 10.1051/0004-6361:20065816
S. S. Larsen1,2 - T. Richtler3
1 - European Southern Observatory, ST-ECF,
Karl-Schwarzschild-Str. 2, 85748 Garching b. München, Germany
2 -
Astronomical Institute, University of Utrecht, Princetonplein 5,
3584 CC Utrecht, The Netherlands
3 -
Astronomy Group, Universidad de Concepción, Departamento de Física,
Casilla 160-C, Concepción, Chile
Received 13 June 2006 / Accepted 16 August 2006
Abstract
Context. During an analysis of optical spectra of 80 young star clusters in several nearby spiral galaxies, [O III] and [N II] emission lines were noted in some cases. Three of these emission line sources are associated with clusters older than 30 Myr, and are identified as likely planetary nebula (PN) candidates.
Aims. These objects may represent a rare opportunity to study PNe whose progenitor stars are known to be of intermediate masses, although detailed analysis is challenging because of the underlying strong continuum from the cluster stars. This paper presents and discusses basic properties of the PN candidates and their host clusters.
Methods. Based on the observed emission line fluxes, the excitation parameters and luminosities of the nebulae are derived. This allows a crude placement of the central stars in two of the objects on the H-R diagram. Cluster ages and masses are estimated from broad-band colours and by fitting model SSP spectra to the observed spectra.
Results. The two PN candidates where central star luminosities and temperatures can be estimated are found to be consistent with post-AGB model tracks for a central star mass of about 0.60 ![]() .
One of the host clusters has an age of 32-65 Myr, corresponding to a main sequence turn-off mass of
.
One of the host clusters has an age of 32-65 Myr, corresponding to a main sequence turn-off mass of
![]() = 6.6-9.0
= 6.6-9.0 ![]() .
For the other cluster the age is 282-407 Myr, corresponding to
.
For the other cluster the age is 282-407 Myr, corresponding to
![]() = 3.2-3.6
= 3.2-3.6 ![]() .
By estimating the number of stars evolving off the main sequence per year, a total of 6 PNe are expected in the full sample of 80 clusters for a PN lifetime of 104 years. The factor of two disagreement with the actual observed number may be due, among other things, to uncertainties in PN lifetimes. It is interesting to note that all three PN candidates are associated with clusters which are more diffuse than average.
.
By estimating the number of stars evolving off the main sequence per year, a total of 6 PNe are expected in the full sample of 80 clusters for a PN lifetime of 104 years. The factor of two disagreement with the actual observed number may be due, among other things, to uncertainties in PN lifetimes. It is interesting to note that all three PN candidates are associated with clusters which are more diffuse than average.
Conclusions. While PNe have previously been found in some old globular clusters, the candidates identified here are among the first identified in young star clusters.
Key words: galaxies: spiral - galaxies: star clusters - stars: AGB and post-AGB - planetary nebulae: general
Star clusters and planetary nebulae (PNe) can both be observed at distances well beyond the Local Group, and are thus valuable extragalactic population tracers. However, much remains to be understood about the post-main sequence evolution of low- and intermediate stars leading up to the PN stage, partly because of the difficulty in determining the distances and progenitor stellar masses of planetary nebulae in the Milky Way. For PNe associated with stellar clusters the initial mass of the progenitor star can be assumed to be that corresponding to the main sequence turn-off (unless the progenitor star is a close binary in which mass exchange has occurred), but the number of PNe known to be associated with stellar clusters remains small. Less than a handful of such objects are known to exist in Milky Way open clusters (Pedreros 1987,1989; O'Dell 1963) and four PNe have been found in Galactic globular clusters (M15, M22, Pal 6, NGC 6441; Jacoby et al. 1997).
The distance problem can be alleviated by studying PNe in external galaxies with well determined distances. Many such searches have been carried out or are currently under way (Kwok 2000; Feldmeier 2006; Magrini 2006), but the detected candidates are typically field objects and the initial mass thus remains unknown. PNe have been identified in a few GCs in the nearby giant elliptical NGC 5128 (Minniti & Rejkuba 2002; Rejkuba et al. 2003), and the significant number of on-going large spectroscopic surveys of extragalactic globular cluster systems are likely to reveal many more candidates. However, by studying PNe in ancient globular clusters one remains fundamentally limited to low-mass stars. One way to sample a larger range of stellar masses would be to collect a sample of PN candidates in younger stellar clusters. So far, the number of such objects are limited to the small number of PNe in Milky Way open clusters.
We have recently obtained optical spectra for a number of young star
clusters in several nearby galaxies. The original aim of this programme was
to carry out a detailed test of simple stellar population (SSP) models,
but during the analysis we noted
emission lines in some of the spectra. As discussed below, the
clusters in question span a range of ages from a few tens of Myr to several hundreds of Myr, corresponding to main sequence turn-off masses between 3
and 9 ![]() .
These objects potentially represent a valuable addition
to the very few cases where PNe have been associated with young star clusters, and
could provide a unique opportunity to study PNe where the
distances and initial masses
are known with some accuracy. The full spectroscopic dataset and analysis
will be presented in a forthcoming paper, and here we concentrate on the
few spectra where PN candidates were identified.
.
These objects potentially represent a valuable addition
to the very few cases where PNe have been associated with young star clusters, and
could provide a unique opportunity to study PNe where the
distances and initial masses
are known with some accuracy. The full spectroscopic dataset and analysis
will be presented in a forthcoming paper, and here we concentrate on the
few spectra where PN candidates were identified.
Spectra of a sample of young massive clusters (YMCs) in several nearby spiral
galaxies were obtained with the EMMI instrument on the
ESO New Technology Telescope from March 16-March 18, 2004. The observations
were carried out in multi-slit mode, using the RILD ("Red Imaging and
Low-Dispersion Spectroscopy'') mode and grism #3, which provided a spectral
resolution of
![]() over the wavelength range
4000-9000 Å. In each of the 7 slitmasks, typically 3 exposures of
3600 s each were obtained with the CCDs read out in 2
over the wavelength range
4000-9000 Å. In each of the 7 slitmasks, typically 3 exposures of
3600 s each were obtained with the CCDs read out in 2 ![]() 2 binned mode.
The full spectroscopic sample included 80 clusters in four galaxies
(NGC 2835, NGC 2997, NGC 3621 and NGC 5236), selected primarily from the sample
presented in Larsen (1999). In order to maximise the fraction of
bona-fide star clusters (as opposed to "asterisms'' or loose
associations), as many objects as possible with imaging from the Hubble Space
Telescope (HST) were included (Larsen 2004).
The astrometry for the slitmask design was based on pre-imaging data obtained
with EMMI in service mode on Jan. 28, 2004, exposed for 5 min in the R-band.
2 binned mode.
The full spectroscopic sample included 80 clusters in four galaxies
(NGC 2835, NGC 2997, NGC 3621 and NGC 5236), selected primarily from the sample
presented in Larsen (1999). In order to maximise the fraction of
bona-fide star clusters (as opposed to "asterisms'' or loose
associations), as many objects as possible with imaging from the Hubble Space
Telescope (HST) were included (Larsen 2004).
The astrometry for the slitmask design was based on pre-imaging data obtained
with EMMI in service mode on Jan. 28, 2004, exposed for 5 min in the R-band.
The spectra were reduced with standard tools in the
IRAF![]() ONEDSPEC package
and were wavelength- and flux calibrated using observations of HeAr calibration lamps and the flux standards Hiltner 600 and LTT 2415
(Stone & Baldwin 1983; Hamuy et al. 1994). Small additional
corrections (on order
ONEDSPEC package
and were wavelength- and flux calibrated using observations of HeAr calibration lamps and the flux standards Hiltner 600 and LTT 2415
(Stone & Baldwin 1983; Hamuy et al. 1994). Small additional
corrections (on order ![]() 1 Å) to the wavelength
scale were applied using the [O I] 5577.35 Å night sky line.
1 Å) to the wavelength
scale were applied using the [O I] 5577.35 Å night sky line.
Accurate absolute flux calibration of slit spectra is always challenging due to slitlosses, which depend on the seeing and accurate centring of objects on the slit. Because EMMI does not have a functioning atmospheric dispersion corrector, an additional complication for multislit spectroscopy is differential refraction, which causes the slitlosses to be wavelength dependent as the slits cannot be aligned with the parallactic angle for the entire duration of an exposure. Other factors, such as the spatial distribution of the targets, also limit the freedom to choose the orientation of the slits. Although the observations were carried out at low airmass (generally <1.2), some differences were noted in the flux calibration between individual observations of the same targets.
We attempted to bring our spectra closer to an absolute flux scale by scaling
them to match the fluxes derived from the ground-based photometry. Since the
wavelength range covered by the EMMI spectra includes four of the photometric
passbands (![]() )
for which broad-band photometry is available, the
wavelength-dependent
nature of the slit losses could also be accommodated. This was done
by forming the ratio of the photometric fluxes (
)
for which broad-band photometry is available, the
wavelength-dependent
nature of the slit losses could also be accommodated. This was done
by forming the ratio of the photometric fluxes (
![]() )
in each band to
the fluxes measured in the corresponding wavelength ranges of the
spectra (
)
in each band to
the fluxes measured in the corresponding wavelength ranges of the
spectra (
![]() ), and then producing
a correction function by fitting a second-order polynomial to the
resulting ratio
), and then producing
a correction function by fitting a second-order polynomial to the
resulting ratio
![]() .
Within a given exposure, differences in the overall scaling of individual spectra
could be as large as
.
Within a given exposure, differences in the overall scaling of individual spectra
could be as large as ![]() 25%. This may reflect uncertainties in the
photometric as well as the spectroscopic measurements. The shapes of
the individual correction functions showed better agreement. Furthermore,
for some objects (e.g. H II regions dominated by strong emission
lines) it was not possible to construct reliable
correction functions. We therefore applied
one average correction function to all spectra obtained in
a given exposure, based on about half of the objects in a given
slitmask. Typically, the correction amounted to 10-20%, but
in the most extreme cases it could be as much as a factor of 2.
Each spectrum was then multiplied by the correction
function, and the several individual spectra of each object were
averaged (using a sigma-clipping algorithm to reject cosmic-ray hits)
to produce the final spectra.
25%. This may reflect uncertainties in the
photometric as well as the spectroscopic measurements. The shapes of
the individual correction functions showed better agreement. Furthermore,
for some objects (e.g. H II regions dominated by strong emission
lines) it was not possible to construct reliable
correction functions. We therefore applied
one average correction function to all spectra obtained in
a given exposure, based on about half of the objects in a given
slitmask. Typically, the correction amounted to 10-20%, but
in the most extreme cases it could be as much as a factor of 2.
Each spectrum was then multiplied by the correction
function, and the several individual spectra of each object were
averaged (using a sigma-clipping algorithm to reject cosmic-ray hits)
to produce the final spectra.
Visual inspection of the reduced spectra generally revealed A-type
spectra with strong Balmer lines, as expected for young star clusters
with ages on the order of ![]() 108 years. Some very young objects, known
from ground-based narrow-band imaging to be embedded in H
108 years. Some very young objects, known
from ground-based narrow-band imaging to be embedded in H![]() emission,
were also included, and showed the expected strong emission
lines from H, N, and O characteristic of H II regions. Here we
concentrate on three spectra which showed weaker [O III] and [N II] emission lines
superimposed on A-type stellar spectra, for which both broad-band photometry
and a comparison with model
spectra suggest ages significantly greater than 107 years (Sect. 3.2). Ground-based H
emission,
were also included, and showed the expected strong emission
lines from H, N, and O characteristic of H II regions. Here we
concentrate on three spectra which showed weaker [O III] and [N II] emission lines
superimposed on A-type stellar spectra, for which both broad-band photometry
and a comparison with model
spectra suggest ages significantly greater than 107 years (Sect. 3.2). Ground-based H![]() images showed no line emission in the
immediate vicinity of these objects, again suggesting that the emission-line
objects contained in the star clusters are not H II regions. As
discussed below, a more likely (although not entirely
unique) explanation is that these clusters contain
planetary nebulae (PNe).
images showed no line emission in the
immediate vicinity of these objects, again suggesting that the emission-line
objects contained in the star clusters are not H II regions. As
discussed below, a more likely (although not entirely
unique) explanation is that these clusters contain
planetary nebulae (PNe).
The three clusters discussed here are located in the two galaxies
NGC 5236 and NGC 3621, both of which are actively star-forming, nearby spiral
galaxies. Throughout this paper, we assume distance moduli of
m-M=28.25 ![]() 0.15 for NGC 5236 (Thim et al. 2003) and
29.10
0.15 for NGC 5236 (Thim et al. 2003) and
29.10 ![]() 0.20 for NGC 3621 (Rawson et al. 1997). For the foreground
extinction we use the Schlegel et al. (1998) values of
AB=0.284 mag (NGC 5236) and AB=0.346 mag (NGC 3621).
For a more comprehensive listing of the properties of the host galaxies we
refer to Larsen & Richtler (2000).
0.20 for NGC 3621 (Rawson et al. 1997). For the foreground
extinction we use the Schlegel et al. (1998) values of
AB=0.284 mag (NGC 5236) and AB=0.346 mag (NGC 3621).
For a more comprehensive listing of the properties of the host galaxies we
refer to Larsen & Richtler (2000).
![\begin{figure}
\par\includegraphics[width=8.05cm,clip]{5816f1.ps}\end{figure}](/articles/aa/full/2006/43/aa5816-06/Timg25.gif) |
Figure 1: EMMI spectra of the three YMCs with PN candidates. Each panel shows the raw spectrum (thick lines) and the residuals when the best-fitting solar-metallicity model spectrum from González-Delgado et al. (2005) is subtracted (thin lines, blue in the on-line edition). |
| Open with DEXTER | |
| |
Figure 2:
HST/WFPC2 F606W ( |
| Open with DEXTER | |
The EMMI spectra of the three objects are shown in Fig. 1.
All three objects happened to have images from the Wide Field Planetary
Camera 2 (WFPC2) on board the Hubble Space Telescope (HST), as shown in
Fig. 2. Two of
the objects are located in NGC 5236 (N5236-254, N5236-487 in the
list of Larsen 1999), while the third is in NGC 3621
(N3621-1106). The morphological appearance of all three objects
is generally consistent with that of star clusters, all of them being
significantly more extended than the WFPC2 point-spread function, but still
fairly compact and with regular, symmetric profiles. Note, though, that
N3621-1106 has a fainter companion at a projected separation of
![]() (
(![]() 22 pc). The companion is also resolved in the HST images, and thus also a likely cluster candidate. Whether the two objects represent a chance alignment or a real physical pair is difficult
to tell, however. Similar colours would suggest similar ages for the
two objects and thus make a chance alignment less likely, but the ground-based
imaging has insufficient resolution to address this question and the HST data are available in only one band. The half-light radii listed
in Larsen (2004) are 10.1 pc, 6.7 pc and 7.2 pc for N5236-254,
N5236-487 and N3621-1106, respectively. While these sizes are
consistent with those of star clusters, it is interesting to note that
all three clusters have larger half-light radii than the mean
value of 3-4 pc which is typical for both young and old clusters
(Whitmore et al. 1999; Larsen 2004; Jordán et al. 2005).
22 pc). The companion is also resolved in the HST images, and thus also a likely cluster candidate. Whether the two objects represent a chance alignment or a real physical pair is difficult
to tell, however. Similar colours would suggest similar ages for the
two objects and thus make a chance alignment less likely, but the ground-based
imaging has insufficient resolution to address this question and the HST data are available in only one band. The half-light radii listed
in Larsen (2004) are 10.1 pc, 6.7 pc and 7.2 pc for N5236-254,
N5236-487 and N3621-1106, respectively. While these sizes are
consistent with those of star clusters, it is interesting to note that
all three clusters have larger half-light radii than the mean
value of 3-4 pc which is typical for both young and old clusters
(Whitmore et al. 1999; Larsen 2004; Jordán et al. 2005).
The spectral signal-to-noise ratio per pixel in the dispersion direction is
about 106, 30 and 24 at 5000 Å for N5236-254, N5236-487 and N3621-1106,
respectively. The [O III] ![]() 4959, 5007 Å and
[N II]
4959, 5007 Å and
[N II] ![]() 6548, 6584 Å lines are noticeable in all three spectra, but much weaker than typically seen in H II regions. Balmer lines are expected to be seen in emission in both
planetary nebulae and H II regions, but in our cluster spectra
the Balmer lines are dominated by the underlying strong absorption
lines from the stellar component.
6548, 6584 Å lines are noticeable in all three spectra, but much weaker than typically seen in H II regions. Balmer lines are expected to be seen in emission in both
planetary nebulae and H II regions, but in our cluster spectra
the Balmer lines are dominated by the underlying strong absorption
lines from the stellar component.
In order to remove the stellar component from the spectra, model spectra from
the library of González-Delgado et al. (2005) were subtracted
from the observed spectra.
The library contains model spectra for the
integrated light of simple stellar populations with ages between
1 Myr and 17 Gyr, tabulated at 0.3 Å resolution. A Salpeter
(1955)-like IMF is assumed.
The best-fitting model spectra were selected by
minimising the rms residuals between the observed spectra (shifted
to zero radial velocity) and smoothed model spectra. Because of the
uncertainties in the absolute flux calibration and the reddening
corrections, the model spectra were multiplied by a polynomial to
follow the same large-scale spectral energy distribution as the
observed spectra.
This was done by fitting the ratio of the observed to model spectra
with a 5th-order polynomial and multiplying the model spectra with
this polynomial, rather than scaling them by a single constant, before
calculating the rms residuals. The González-Delgado et al. library includes
models based on both the Geneva and Padua stellar isochrones and for a range
of metallicities, but for this work we only used Solar metallicity models
based on the Padua isochrones. The analysis carried out in the following
does not depend strongly on the model choice.
For NGC 5236, analysis of H II regions
(Bresolin & Kennicutt 2002) yields an oxygen
abundance very close to Solar [12+log(O/H) = 8.9] at the galactocentric
distance of the two clusters (
![]() for N5236-254 and
for N5236-254 and
![]() for N5236-487). For NGC 3621, the work of Ryder (1995) indicates
12+log(O/H) = 9.0 at the position of N3621-1106,
for N5236-487). For NGC 3621, the work of Ryder (1995) indicates
12+log(O/H) = 9.0 at the position of N3621-1106,
![]() from the centre.
The use of Solar metallicity models thus appears justified. The only
remaining free parameter is then the age, and for each cluster we selected
the model spectrum of the age which gave the best fit to the data.
from the centre.
The use of Solar metallicity models thus appears justified. The only
remaining free parameter is then the age, and for each cluster we selected
the model spectrum of the age which gave the best fit to the data.
Figure 3 shows the regions around the H![]() [O III] and
H
[O III] and
H![]() [N II] lines after subtraction of the best-fitting, scaled
solar-metallicity models. Emission line fluxes were measured by fitting
Gaussian line profiles to the emission line spectra. The
[O III]
[N II] lines after subtraction of the best-fitting, scaled
solar-metallicity models. Emission line fluxes were measured by fitting
Gaussian line profiles to the emission line spectra. The
[O III] ![]() 5007/4959 Å and [N II]
5007/4959 Å and [N II] ![]() 6584/6548 Å
line ratios were kept fixed at 3.0 as dictated by
atomic physics (e.g. Osterbrock 1988), while the
[O III]/H
6584/6548 Å
line ratios were kept fixed at 3.0 as dictated by
atomic physics (e.g. Osterbrock 1988), while the
[O III]/H![]() and [N II]/H
and [N II]/H![]() ratios were allowed to vary. The resulting best-fitting Gaussian models
are overplotted on the spectra in Fig. 3.
For the two emission-line sources associated with YMCs in NGC 5236, no
further shifts in wavelength were required
to match the line profiles and the sources are likely to be physically
associated with the clusters. The best fit for N3621-1106 was
obtained if an additional shift of about +150 km s-1 was applied to
the observed spectrum, so in this case the source of the emission lines
may not be physically associated with the cluster.
ratios were allowed to vary. The resulting best-fitting Gaussian models
are overplotted on the spectra in Fig. 3.
For the two emission-line sources associated with YMCs in NGC 5236, no
further shifts in wavelength were required
to match the line profiles and the sources are likely to be physically
associated with the clusters. The best fit for N3621-1106 was
obtained if an additional shift of about +150 km s-1 was applied to
the observed spectrum, so in this case the source of the emission lines
may not be physically associated with the cluster.
Table 1 lists the emission line fluxes obtained from
the fits in Fig. 3. Errors were estimated by fitting
emission lines at 8 different wavelengths where none were expected.
The mean errors in the table represent the standard deviation of
these 8 test measurements.
It should be emphasised that these error estimates only account for
random measurement errors. The
line fluxes may be further affected by systematic errors, for example due to
inaccurate subtraction of the stellar continuum. To investigate this issue,
we repeated the emission
line measurements after subtracting Z=0.008 SSP models based on the
Padua isochrones, and Z=0.008 and Z=0.020 models based on the
Geneva isochrones. The resulting emission line fluxes generally agreed with
those listed in Table 1 within the stated one-sigma errors.
Only for the H![]() line in the spectrum of N5236-254 was a somewhat larger
deviation encountered - for this line, a flux of
2.5
line in the spectrum of N5236-254 was a somewhat larger
deviation encountered - for this line, a flux of
2.5 ![]() 10-17 erg-1 cm-2 was returned when using the
Z=0.008 Padua-based SSP model, i.e. a 2.7
10-17 erg-1 cm-2 was returned when using the
Z=0.008 Padua-based SSP model, i.e. a 2.7![]() deviation. In
conclusion, although some systematic errors cannot be entirely ruled out,
the error estimates in Table 1 appear to be fairly
realistic overall. The flux calibration may account for
a further
deviation. In
conclusion, although some systematic errors cannot be entirely ruled out,
the error estimates in Table 1 appear to be fairly
realistic overall. The flux calibration may account for
a further ![]() 10-20% uncertainty on the line fluxes, although relative
line ratios are probably more accurate. Finally, the m5007 magnitudes, defined
as
10-20% uncertainty on the line fluxes, although relative
line ratios are probably more accurate. Finally, the m5007 magnitudes, defined
as
![]() (Jacoby 1989),
are also listed.
(Jacoby 1989),
are also listed.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{5816f3a.ps}\vspace*{3mm}
\...
...6f3b.ps}\vspace*{3mm}
\includegraphics[width=7.5cm,clip]{5816f3c.ps}\end{figure}](/articles/aa/full/2006/43/aa5816-06/Timg37.gif) |
Figure 3:
Gaussian emission line fits to the spectra after subtraction of
best-fitting solar-metallicity SSP models. In each panel, the thick lines
represent the observed
spectra while the thin lines (red in the on-line edition) are the
Gaussian fits. The regions
around H |
| Open with DEXTER | |
Table 1: Emission line fluxes in units of 10-17 erg s-1 cm-2. Note that both lines in the [O III] and [N II] doublets were fitted together.
Table 2:
Cluster data. Photometry is corrected for foreground
reddening only.
![]() is the additional amount of reddening
required to best match the SSP model colours. The ranges of turn-off
and total cluster masses reflect the differences between spectroscopic
and photometric age estimates. The masses are for a Salpeter-like
IMF with a lower mass limit of
is the additional amount of reddening
required to best match the SSP model colours. The ranges of turn-off
and total cluster masses reflect the differences between spectroscopic
and photometric age estimates. The masses are for a Salpeter-like
IMF with a lower mass limit of
![]()
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{5816f4.ps}\end{figure}](/articles/aa/full/2006/43/aa5816-06/Timg69.gif) |
Figure 4:
|
| Open with DEXTER | |
Photometry for the clusters was taken from Larsen (1999).
Table 2 lists the ![]() broad-band colours for each
cluster, corrected for foreground extinction only. From the broad-band
colours, rough age estimates can be obtained by comparison
with predictions by simple stellar population (SSP) models, or by using
the empirical "S''-sequence calibration (based on LMC clusters)
by Girardi et al. (1995). Figure 4 shows the
broad-band colours for each
cluster, corrected for foreground extinction only. From the broad-band
colours, rough age estimates can be obtained by comparison
with predictions by simple stellar population (SSP) models, or by using
the empirical "S''-sequence calibration (based on LMC clusters)
by Girardi et al. (1995). Figure 4 shows the
![]() vs.
vs. ![]() two-colour diagram, including the S-sequence and photometry
for the three clusters. Based on this plot, N5236-487 appears to be
the youngest of the three objects with
two-colour diagram, including the S-sequence and photometry
for the three clusters. Based on this plot, N5236-487 appears to be
the youngest of the three objects with ![]() (age)
(age) ![]() 7.8, while
N5236-254 is the oldest (
7.8, while
N5236-254 is the oldest (![]() (age)
(age) ![]() 8.6). Including all the
colours available in Table 2 and comparing with solar metallicity
SSP models from Bruzual & Charlot (2003),
the photometric age and extinction estimates listed in
Table 2 were obtained. Here,
8.6). Including all the
colours available in Table 2 and comparing with solar metallicity
SSP models from Bruzual & Charlot (2003),
the photometric age and extinction estimates listed in
Table 2 were obtained. Here,
![]() denotes the
extinction required to best match the observed colours in addition
to the foreground extinction. Errors on the age- and extinction estimates
were estimated by a Monte-Carlo procedure: first, random offsets
denotes the
extinction required to best match the observed colours in addition
to the foreground extinction. Errors on the age- and extinction estimates
were estimated by a Monte-Carlo procedure: first, random offsets
![]() were added to the observed colours, and the age- and
extinction were then re-derived. The offsets
were added to the observed colours, and the age- and
extinction were then re-derived. The offsets
![]() were
drawn from a Gaussian distribution with standard deviation equal to the
photometric errors on each colour. The errors on the ages and extinctions
were then estimated as the standard deviation of the individual
values obtained from 100 such experiments. The ages derived
from the comparison with SSP models agree quite well with those inferred
from Fig. 4.
were
drawn from a Gaussian distribution with standard deviation equal to the
photometric errors on each colour. The errors on the ages and extinctions
were then estimated as the standard deviation of the individual
values obtained from 100 such experiments. The ages derived
from the comparison with SSP models agree quite well with those inferred
from Fig. 4.
The extinction estimates in Table 2 can be compared with
those derived from the H![]() /H
/H![]() line ratios in
Table 1. Assuming the Case B recombination
ratio F(H
line ratios in
Table 1. Assuming the Case B recombination
ratio F(H![]() )/F(H
)/F(H![]() ) = 2.85 (e.g. Osterbrock 1988),
we derive
) = 2.85 (e.g. Osterbrock 1988),
we derive
![]()
![]() 0.95 mag for N5236-254 and
0.95 mag for N5236-254 and
![]()
![]() 1.53 mag for N5236-487. These values are consistent
with the photometric
1.53 mag for N5236-487. These values are consistent
with the photometric
![]() values, although the errors are larger.
In the case of N3621-1106,
both H
values, although the errors are larger.
In the case of N3621-1106,
both H![]() and H
and H![]() are essentially non-detections, and it is
not possible to derive a meaningful extinction estimate.
are essentially non-detections, and it is
not possible to derive a meaningful extinction estimate.
Also listed in Table 2 are the spectroscopic age estimates,
which are simply the ages of the best-fitting SSP model spectra. The
spectroscopic ages tend to be lower than the photometric ones, although for
any individual cluster the difference between the two age estimates is not
much larger than the ![]() error. However, the relative ranking of the
clusters remains the same. A detailed comparison of photometric and
spectroscopic ages, using the full sample, will be carried out in a separate paper. Because the continuum shape was not fitted, no constraints
on the extinction are available from the spectral fits.
error. However, the relative ranking of the
clusters remains the same. A detailed comparison of photometric and
spectroscopic ages, using the full sample, will be carried out in a separate paper. Because the continuum shape was not fitted, no constraints
on the extinction are available from the spectral fits.
Once the ages and reddenings are known, the cluster masses can be estimated
by combining the SSP model predictions for mass-to-light ratios with
the observed magnitudes and adopting the distances for the galaxies
quoted above. Table 2 lists these photometric mass estimates,
assuming a stellar mass function with the Salpeter slope
(
![]() )
extending down to 0.1
)
extending down to 0.1 ![]() .
For a more realistic IMF (e.g. Kroupa 2002) the masses would be
lower by a factor of
.
For a more realistic IMF (e.g. Kroupa 2002) the masses would be
lower by a factor of ![]() 1.6. The mass ranges given in the table
correspond to the difference between the photometric and spectroscopic
ages, with the lower masses corresponding to the younger ages.
1.6. The mass ranges given in the table
correspond to the difference between the photometric and spectroscopic
ages, with the lower masses corresponding to the younger ages.
The main sequence turn-off masses,
![]() ,
corresponding to the cluster
ages were obtained from the Salasnich et al. (2000) stellar model
tracks. Again, Table 2 lists a range corresponding to
the photometric and spectroscopic ages. If the emission line sources
are indeed PNe associated
with their putative host clusters, then their progenitor stars should have
started out with masses close to the cluster turn-off masses.
,
corresponding to the cluster
ages were obtained from the Salasnich et al. (2000) stellar model
tracks. Again, Table 2 lists a range corresponding to
the photometric and spectroscopic ages. If the emission line sources
are indeed PNe associated
with their putative host clusters, then their progenitor stars should have
started out with masses close to the cluster turn-off masses.
Several classes of objects show emission line spectra, but not
all are consistent with the characteristics of the objects studied here.
First, H II regions are common in star-forming galaxies. Our full
sample contains several such objects, which generally show very different
spectra than those in Fig. 1. The emission line equivalent
widths of H II regions are generally much larger than in the spectra
in Fig. 1, and the excitation is typically
lower (e.g. Acker et al. 1987). Furthermore,
young star-forming regions tend to have a much less regular structure than
the smooth profiles indicated by the images in Fig. 2.
Finally, only clusters younger than ![]() 10 Myr contain stars which
are hot enough to produce the ionising radiation required to excite an H II region, while we derive significantly higher ages for the
three objects studied here (Sect. 3.2). We can therefore exclude
with fairly high confidence that the objects are H II regions.
10 Myr contain stars which
are hot enough to produce the ionising radiation required to excite an H II region, while we derive significantly higher ages for the
three objects studied here (Sect. 3.2). We can therefore exclude
with fairly high confidence that the objects are H II regions.
Wolf-Rayet stars also show strong emission lines, but again the spectra
are quantitatively (and qualitatively) very different from those observed
here. In particular, the lines in W-R star spectra are very broad
(several 1000 km s-1) and would be easily resolvable at the spectral resolution
of our EMMI data. As for H II regions, the ages of the clusters
studied here make it highly unlikely that they contain W-R stars, whose
progenitors are believed to be massive (>
![]() ;
Humphreys et al. 1985) stars with
lifetimes of only a few Myr. We note, however, that a few objects in our full
sample do show the characteristic W-R bumps at 4650 Å and 5812 Å
(e.g. Torres & Massey 1987), but these features are entirely absent
from the spectra in Fig. 1.
;
Humphreys et al. 1985) stars with
lifetimes of only a few Myr. We note, however, that a few objects in our full
sample do show the characteristic W-R bumps at 4650 Å and 5812 Å
(e.g. Torres & Massey 1987), but these features are entirely absent
from the spectra in Fig. 1.
A third possibility, which is more difficult to dismiss, is symbiotic stars (SSs). These are binary systems in which a red giant is transferring material to a hot compact companion, such as a white dwarf (Kenyon 1986). Mass loss from the red giant results in a nebula which is ionised by the hot companion, producing a spectrum very similar to that of a planetary nebula. The main difference is that the spectrum of a SS contains an extra component in addition to the emission-line spectrum and the spectrum of the hot star, namely that of the red giant. However, for our sources it is impossible to detect this small addition to the continuum on top of the cluster spectrum. On the basis of the data at hand, it is difficult to distinguish between symbiotic stars and planetary nebulae as the most likely sources of the emission lines seen in our spectra. The progenitor stars are also expected to be similar, in both cases involving red giants or AGB stars.
Most surveys of Galactic and extra-galactic emission-line objects identify a larger number of PNe than SSs, and we might thus expect on statistical grounds that our candidates are more likely to be PNe. About 1500 PNe are known in the Milky Way (Kohoutek 2001), while less than 200 symbiotic stars are catalogued (Belcynski et al. 2000). Unfortunately, the completeness of these catalogues is very difficult to assess for either type of object, and the classification of at least 50 objects in the Milky Way alone is still ambiguous (Kohoutek 2001). The total number of PNe in the Milky Way is estimated to be about 25 000 (Buzzoni et al. 2006), but this is little better than an order-of-magnitude estimate. The uncertainty on the number of SSs may be even greater, with estimates ranging from 3000 (Kenyon 1986) to as many as 300.000 (Munari & Renzini 1992).
Surveys of PNe and SSs in the Magellanic Clouds have the
advantage that the distances are known with reasonable accuracy.
About a dozen SSs are known in the LMC and SMC. These have H![]() luminosities in the range 7.7
luminosities in the range 7.7 ![]() 1033-5
1033-5 ![]() 1034 erg s-1(Morgan 1992), i.e. all are fainter than the H
1034 erg s-1(Morgan 1992), i.e. all are fainter than the H![]() fluxes derived for the objects studied here (Sect. 3.4).
For typical effective temperatures of the hot component of
fluxes derived for the objects studied here (Sect. 3.4).
For typical effective temperatures of the hot component of ![]() 105 K
(Mürset et al. 1996), the [O III]
105 K
(Mürset et al. 1996), the [O III] ![]() 5007 flux is about an order of magnitude greater than the H
5007 flux is about an order of magnitude greater than the H![]() flux. As a crude estimate, there may then be about 10 SSs in the Clouds with
L([O III]) > 1035 erg s-1 (although, again, an unknown
completeness correction may apply). For comparison, more than 100 PNe with L([O III]) > 1035 erg s-1 are catalogued in the
Clouds (Jacoby et al. 1990). Thus, at least at the high-luminosity
end, PNe appear to outnumber SSs by about an order of magnitude in
the Magellanic Clouds. Furthermore, Mürset et al. (1996)
conclude that the LMC SSs most likely belong to a population older than
flux. As a crude estimate, there may then be about 10 SSs in the Clouds with
L([O III]) > 1035 erg s-1 (although, again, an unknown
completeness correction may apply). For comparison, more than 100 PNe with L([O III]) > 1035 erg s-1 are catalogued in the
Clouds (Jacoby et al. 1990). Thus, at least at the high-luminosity
end, PNe appear to outnumber SSs by about an order of magnitude in
the Magellanic Clouds. Furthermore, Mürset et al. (1996)
conclude that the LMC SSs most likely belong to a population older than
![]() 4 Gyr, which is much older than the clusters studied here
(Sect. 3.2). It is also worth noting that no SSs are
known to be associated with stellar clusters in the Milky Way while about
7 PNe have been found in Galactic globular or open clusters, as noted
in the Introduction.
4 Gyr, which is much older than the clusters studied here
(Sect. 3.2). It is also worth noting that no SSs are
known to be associated with stellar clusters in the Milky Way while about
7 PNe have been found in Galactic globular or open clusters, as noted
in the Introduction.
We thus proceed under the assumption that the emission-line objects
found here are most likely planetary nebulae, although symbiotic stars
cannot be entirely ruled out as an alternative. Repeat observations
might help clarify this issue, as SSs often show significant variability
on time scales of days, weeks or months. A detailed analysis of the
nebular properties using high-dispersion spectroscopy might also help
distinguish between SSs and PNe, since SSs typically have ![]() 100 times
higher densities than PNe (Kenyon 1986). As a further note, it
seems to us that the identification issue frequently receives less
attention than it merits in extragalactic PN surveys.
100 times
higher densities than PNe (Kenyon 1986). As a further note, it
seems to us that the identification issue frequently receives less
attention than it merits in extragalactic PN surveys.
Table 3:
Derived nebular properties.
![]() is the luminosity of the central star. Note that H
is the luminosity of the central star. Note that H![]() fluxes are derived from the H
fluxes are derived from the H![]() fluxes assuming standard case B
recombination.
fluxes assuming standard case B
recombination.
Because only the strongest emission lines can be measured in the spectra,
it is not possible to derive basic nebular properties such as temperature
and density directly. While this limits the amount of physical information
that can be extracted from the spectra, some constraints can be put
on the total luminosities and effective temperatures of the ionising sources.
Dopita et al. (1992) have published an extensive set of
model calculations, allowing estimates of these properties from observations
of the Balmer lines and strong forbidden lines. They define the excitation
parameter as
![]() for
0.0 < E < 5.0.
For higher excitation parameters the He II
for
0.0 < E < 5.0.
For higher excitation parameters the He II ![]() 4686 Å line
is required. This line is not detected in our spectra, but as will be
seen below the excitation parameters derived here are sufficiently low
that only the O and H lines are needed.
4686 Å line
is required. This line is not detected in our spectra, but as will be
seen below the excitation parameters derived here are sufficiently low
that only the O and H lines are needed.
Measurements of the Balmer emission lines
rely critically on correct subtraction of the underlying cluster spectra.
From Fig. 3 it is difficult to assess the reliability
of this subtraction for H![]() .
The H
.
The H![]() line, on the other hand,
is stronger and less diluted by the stellar absorption, and therefore
easier to measure reliably, at least for the two objects in NGC 5236.
For the object in NGC 3621, neither H
line, on the other hand,
is stronger and less diluted by the stellar absorption, and therefore
easier to measure reliably, at least for the two objects in NGC 5236.
For the object in NGC 3621, neither H![]() nor
H
nor
H![]() can be reliably measured. Thus, in the following discussion we
concentrate on the two objects in NGC 5236, for which the association
with the star clusters is anyway more secure.
can be reliably measured. Thus, in the following discussion we
concentrate on the two objects in NGC 5236, for which the association
with the star clusters is anyway more secure.
Table 3 lists the basic parameters derived for the nebulae.
The H![]() fluxes were estimated from the measured H
fluxes were estimated from the measured H![]() values
assuming the Case B recombination ratio,
but the results do not change much if we use
the measured H
values
assuming the Case B recombination ratio,
but the results do not change much if we use
the measured H![]() fluxes directly. For N5236-254, the de-reddened
H
fluxes directly. For N5236-254, the de-reddened
H![]() flux [(1.80
flux [(1.80 ![]() 0.47)
0.47) ![]() 1035 erg s-1] agrees almost
exactly with that derived from the H
1035 erg s-1] agrees almost
exactly with that derived from the H![]() flux. For N5236-487 the
de-reddened H
flux. For N5236-487 the
de-reddened H![]() flux is (0.95
flux is (0.95 ![]() 0.37)
0.37) ![]() 1035 erg s-1,
about 40% lower than the value derived from H
1035 erg s-1,
about 40% lower than the value derived from H![]() ,
but with a larger
formal error. All line fluxes have been de-reddened using the Cardelli et al. (1989)
extinction curve and the extinction estimates from Table 2.
The quoted error estimates include a 0.15 (0.20) mag
uncertainty on the distance modulus of NGC 5236 (NGC 3621). For
reference, the [O III] luminosities have been converted to
absolute M5007 magnitudes. These are well within the range
expected for planetary nebulae; the tip of the planetary nebula luminosity
function is at
,
but with a larger
formal error. All line fluxes have been de-reddened using the Cardelli et al. (1989)
extinction curve and the extinction estimates from Table 2.
The quoted error estimates include a 0.15 (0.20) mag
uncertainty on the distance modulus of NGC 5236 (NGC 3621). For
reference, the [O III] luminosities have been converted to
absolute M5007 magnitudes. These are well within the range
expected for planetary nebulae; the tip of the planetary nebula luminosity
function is at
![]() (e.g. Kwok 2000).
(e.g. Kwok 2000).
![\begin{figure}
\par\includegraphics[width=6.85cm,clip]{5816f5.ps}\end{figure}](/articles/aa/full/2006/43/aa5816-06/Timg88.gif) |
Figure 5:
H-R diagram for the PN candidates in NGC 5236, with
|
| Open with DEXTER | |
Based on the excitation parameters and the H![]() luminosities, the
effective temperatures and total luminosities of the central stars (
luminosities, the
effective temperatures and total luminosities of the central stars (
![]() )
were
derived using the relations given in Dopita et al. (1992).
The errors on
)
were
derived using the relations given in Dopita et al. (1992).
The errors on
![]() and
and
![]() were estimated simply by
propagating the random measurement errors, and thus do not include any
systematic errors in the calibration. Such errros might result, for example,
from metallicity differences between the LMC and SMC calibrator PNe used
by Dopita et al. and the objects studied here. For the relevant
temperature range, Dopita et al. find that the
L(H
were estimated simply by
propagating the random measurement errors, and thus do not include any
systematic errors in the calibration. Such errros might result, for example,
from metallicity differences between the LMC and SMC calibrator PNe used
by Dopita et al. and the objects studied here. For the relevant
temperature range, Dopita et al. find that the
L(H![]() )/
)/
![]() ratio changes by only
ratio changes by only ![]() 1 percent for
O abundances between 0.1 and 2 times Solar (their Fig. 1). Over the same
metallicity range,
1 percent for
O abundances between 0.1 and 2 times Solar (their Fig. 1). Over the same
metallicity range,
![]() varies by
varies by ![]() 0.05 dex for
a fixed
0.05 dex for
a fixed ![]() .
The error estimates in Table 3 do not
include uncertainties on the reddening. For E and
.
The error estimates in Table 3 do not
include uncertainties on the reddening. For E and
![]() the effect on the error budget is negligible (
the effect on the error budget is negligible (
![]() mag for N5236-487) while the additional uncertainty on
mag for N5236-487) while the additional uncertainty on
![]() is
is
![]() dex for N5236-487. In both cases, the
associated errors for N5236-254 are even smaller.
dex for N5236-487. In both cases, the
associated errors for N5236-254 are even smaller.
The H-R diagram for the two nebulae in NGC 5236 is shown in
Fig. 5 together with H-burning post-AGB evolutionary tracks
from Vassiliadis & Wood (1994).
Curiously, the two central stars have very similar luminosities and effective temperatures, in both cases corresponding to a mass close to 0.60 ![]() .
This is somewhat
lower than predicted by the Vassiliadis & Wood tracks for
initial masses of 3.2-3.6
.
This is somewhat
lower than predicted by the Vassiliadis & Wood tracks for
initial masses of 3.2-3.6 ![]() (for N5236-254) and >
(for N5236-254) and >
![]() (N5236-487).
Empirically, the initial-final mass relation for
AGB and post-AGB evolution shows a fairly large scatter. It may be nearly
flat for
(N5236-487).
Empirically, the initial-final mass relation for
AGB and post-AGB evolution shows a fairly large scatter. It may be nearly
flat for
![]()
![]() ,
although most studies suggest that a star with an initial mass
>
,
although most studies suggest that a star with an initial mass
>
![]() is more likely to produce a
is more likely to produce a ![]()
![]() remnant (Kwok 2000; Ferrario et al. 2005;
Weidemann 2000). It would clearly be desirable to put stronger constraints on the physical
properties of these PNe.
remnant (Kwok 2000; Ferrario et al. 2005;
Weidemann 2000). It would clearly be desirable to put stronger constraints on the physical
properties of these PNe.
We have used the solar-metallicity
(Z=0.016) tracks in Fig. 5, but the Z=0.004 tracks do not
differ much and the inferred core masses would be lower by only ![]()
![]() .
The formal errors from Table 3 are smaller than
the plot symbols, but we emphasise
that a more robust analysis, using better data, would be desirable.
However, since the
model tracks are nearly horizontal in the H-R diagram, uncertainties on
.
The formal errors from Table 3 are smaller than
the plot symbols, but we emphasise
that a more robust analysis, using better data, would be desirable.
However, since the
model tracks are nearly horizontal in the H-R diagram, uncertainties on
![]() are of minor importance for the comparison with the post-AGB
tracks. Likewise, uncertainties on the flux calibration and reddening
correction should lead to shifts of no more than 10-20%, or
are of minor importance for the comparison with the post-AGB
tracks. Likewise, uncertainties on the flux calibration and reddening
correction should lead to shifts of no more than 10-20%, or ![]() 0.1 dex in
0.1 dex in
![]() .
The difference between the measured and
derived H
.
The difference between the measured and
derived H![]() flux for N5236-487 corresponds to a shift of 0.2 dex (downward) in
flux for N5236-487 corresponds to a shift of 0.2 dex (downward) in
![]() .
.
From Fig. 3 one notes significant differences in
the relative strengths of the [N II] and [O III] lines.
In N5236-254 and N3621-1106 the
[N II] lines are only slightly weaker than the [O III] lines, while in N5236-487 they are about factor of 6 weaker. This may appear somewhat puzzling, considering the very similar
parameters derived for the central stars in the two PNe in NGC 5236.
However, the PNe studied here fall well within the range of
[O III]/[N II] line ratios seen in Galactic PNe
(Cuisinier 1996), which indeed show a very large range in the relative abundances
of N and O. This is likely related to CNO processing in the progenitor stars
(Peimbert & Serrano 1980) and the ratio of N to O is expected
on theoretical grounds to increase steeply with
progenitor mass (Renzini & Voli 1981). With the current data
we cannot carry out an actual abundance analysis, but it may
be worth noting that the spectrum having the weakest N lines is that
associated with the youngest cluster (and thus the highest progenitor
star mass).
The H![]() line is also stronger relative to the [N II] doublet in N5236-487 than in the other objects. At least qualitatively,
this seems consistent with the overall decrease in the [N/O] abundance ratio with decreasing [N II]/H
line is also stronger relative to the [N II] doublet in N5236-487 than in the other objects. At least qualitatively,
this seems consistent with the overall decrease in the [N/O] abundance ratio with decreasing [N II]/H![]() line ratio
noted by Perinotto & Corradi (1998), again hinting that
N5236-487 may have a decreased [N/O] ratio, rather than an enhanced one
as expected for a massive progenitor.
line ratio
noted by Perinotto & Corradi (1998), again hinting that
N5236-487 may have a decreased [N/O] ratio, rather than an enhanced one
as expected for a massive progenitor.
Figure 6 shows the absolute magnitude MV vs. the
(photometric) age estimate for all 80 clusters included in the full
spectroscopic sample. Ages were estimated by matching the observed ![]() colours against SSP model predictions from Bruzual & Charlot
(2003) as described in Sect. 3.2.
Of the 80 clusters, 28 have ages less than
colours against SSP model predictions from Bruzual & Charlot
(2003) as described in Sect. 3.2.
Of the 80 clusters, 28 have ages less than
![]() and are thus unlikely to host planetary nebulae. For the
remaining 52 clusters, it is of interest to compare the expected number
of PNe with the 2-3 objects actually detected (in the clusters marked
by filled circles).
and are thus unlikely to host planetary nebulae. For the
remaining 52 clusters, it is of interest to compare the expected number
of PNe with the 2-3 objects actually detected (in the clusters marked
by filled circles).
Recently, Buzzoni et al. (2006) have given an extensive discussion
of planetary nebulae as population tracers. However, their main focus
is on populations older than about 1 Gyr and their results are not
directly applicable to our case.
In the following it is assumed that a stellar cluster consists of stars
born in a single burst of negligible duration compared to the age of
the cluster. As the age spread within a cluster is typically
only a few Myr at most, this is a reasonable assumption for clusters
which are old enough to host PNe. If the (initial) mass of a TP-AGB star
which is just about to become a PN is labelled MP, then the stellar
death rate is the number of stars with masses in a small range (
![]() ), divided by the difference in the stellar lifetime (
), divided by the difference in the stellar lifetime (
![]() )
across the mass interval
)
across the mass interval ![]() .
The predicted number of PNe in the cluster is then
.
The predicted number of PNe in the cluster is then
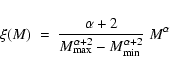 |
(3) |
![\begin{figure}
\par\includegraphics[width=7.35cm,clip]{5816f6.ps}\end{figure}](/articles/aa/full/2006/43/aa5816-06/Timg117.gif) |
Figure 6: Absolute MV magnitude versus log(age) for all clusters in the spectroscopic sample. The clusters containing PN candidates are indicated with filled circles. Ages in this figure are estimated from broad-band colours. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{5816f7.ps}\end{figure}](/articles/aa/full/2006/43/aa5816-06/Timg118.gif) |
Figure 7: Stellar lifetime as a function of initial mass, according to Salasnich et al. (2000) model tracks. The curve is a power-law fit to the points. |
| Open with DEXTER | |
Using mass-to-light ratios from the Bruzual & Charlot SSP models, the number
of PNe per unit luminosity can be calculated. This is shown in
Fig. 9 for the V-band. While the expected frequency of
PNe still depends on age, the dependence on assumptions about the
low-mass end of the IMF disappears when
normalising to luminosity instead of mass. This is because the PNe progenitors
are among the most luminous stars in a SSP while the low-mass stars contribute
very little to the luminosity of a SSP. This makes the curve in
Fig. 9 more directly comparable to observations.
Of course, the same IMF has to be used when computing the number of
PNe per mass (Eq. (2)) and for the subsequent evaluation of
the mass-to-light ratios. Here we are assuming a Salpeter-like IMF
extending down to 0.1 ![]() .
The PN formation rate derived here
agrees within about a factor of two with the estimates by Renzini &
Buzzoni (1986).
.
The PN formation rate derived here
agrees within about a factor of two with the estimates by Renzini &
Buzzoni (1986).
![\begin{figure}
\par\includegraphics[width=7.1cm,clip]{5816f8.ps}\end{figure}](/articles/aa/full/2006/43/aa5816-06/Timg119.gif) |
Figure 8:
Predicted number of planetary nebulae per 106 |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.1cm,clip]{5816f9.ps}\end{figure}](/articles/aa/full/2006/43/aa5816-06/Timg120.gif) |
Figure 9:
Predicted number of planetary nebulae per 106
|
| Open with DEXTER | |
We can now estimate the number of PNe expected in each cluster in
Fig. 6. From Figs. 8 and 9 it
is clear that, on average, less than 1 PN is expected per cluster. By
summing up the expected numbers of PNe in all clusters in the sample we
estimate a total of 6 PNe in the age range
![]() .
This
is to be compared with the 2-3 objects actually observed. Note that
this assumes an observable PN lifetime of 104 years - if, for example,
the lifetimes are shorter by a factor of two, then the predicted number
of PNe would be lower by the same factor. Since the PN lifetimes are a steep function of the central star mass, with more massive progenitor
stars expected to produce shorter lifetimes (Schönberner & Blöcker
1996), the agreement appears
satisfactory and these rough estimates certainly suggest that the detection
of a small number of PNe in a spectroscopic survey like the one carried out here
is indeed expected. Alternatively, we can compare with the empirical
estimate of the PN specific frequency from Magrini et al. (2003),
who estimate an average of one PN per 106.92 V-band
.
This
is to be compared with the 2-3 objects actually observed. Note that
this assumes an observable PN lifetime of 104 years - if, for example,
the lifetimes are shorter by a factor of two, then the predicted number
of PNe would be lower by the same factor. Since the PN lifetimes are a steep function of the central star mass, with more massive progenitor
stars expected to produce shorter lifetimes (Schönberner & Blöcker
1996), the agreement appears
satisfactory and these rough estimates certainly suggest that the detection
of a small number of PNe in a spectroscopic survey like the one carried out here
is indeed expected. Alternatively, we can compare with the empirical
estimate of the PN specific frequency from Magrini et al. (2003),
who estimate an average of one PN per 106.92 V-band ![]() for
Local Group galaxies (ignoring any age dependence). The integrated V-band
luminosity of all clusters in our sample older than 30 Myr is about
3.3
for
Local Group galaxies (ignoring any age dependence). The integrated V-band
luminosity of all clusters in our sample older than 30 Myr is about
3.3 ![]()
![]() ,
corresponding to 4 PNe. A search of PNe in a larger sample of young and intermediate-age star clusters might prove rewarding.
,
corresponding to 4 PNe. A search of PNe in a larger sample of young and intermediate-age star clusters might prove rewarding.
In a sample of optical spectra of 80 young extragalactic star clusters, 3 emission line objects were detected which we identify as likely PN candidates. Two of these have radial velocities consistent with those of their host clusters, while the third displays a shift of about 150 km s-1 and may be a field object falling on the slit by chance. The analysis of the candidate PN spectra is complicated by the relatively low spectral resolution and the strong underlying stellar spectra. This is a problem especially for the Balmer lines, which are very strong in absorption in the cluster spectra and thus mask the comparatively weak line emission from the PNe. However, it was found that the line emission can be reasonably well separated by subtracting out synthetic SSP model spectra from the library of González-Delgado (2005).
All three objects have [O III] emission line fluxes consistent with
those expected from
PNe. For the two objects where the association with clusters is most
robust (both
in NGC 5236), the excitation parameters and total luminosities were estimated
and the central stars were placed on the H-R diagram. Comparison with
post-AGB evolutionary tracks from Vassiliadis & Wood (1994)
indicates central star masses of about 0.60 ![]() .
.
Based on stellar evolutionary timescales, we estimate that a total of about 6 PNe are expected in the 80 star clusters for a PN lifetime of 104 years. Instead, 2-3 are detected here, which we consider reasonable agreement. Scaling the empirical estimate of the PN specific frequency from Magrini et al. (2003) predicts a total of 4 PNe in our sample, although the age distribution of our PN host clusters is likely different from that of the Local Group stellar populations on which the Magrini et al. estimate is based. A systematic search for PNe in a larger sample of extragalactic star clusters might put useful constraints on the PN lifetimes and the range of stellar masses that produce PNe. High-dispersion spectroscopy would allow a better subtraction of the underlying cluster spectra and thus more accurate measurements of the emission lines, and would provide constraints on the kinematic properties (expansion velocities) of the nebulae. Further observations would also provide constraints on time variability, and thus help distinguish between PNe and other possibilities (e.g. symbiotic stars).
Acknowledgements
We thank J. Walsh and A. Zijlstra for their encouragement and several useful discussions. S.S.L. thanks G. Pugliese for assistance and company during the observations. The anonymous referee provided several helpful comments which led to significant improvements in the paper. This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.