A&A 459, 229-240 (2006)
DOI: 10.1051/0004-6361:20065781

Non-LTE models for synthetic spectra of type Ia supernovae / hot stars with extremely extended atmospheres

II. Improved lower boundary conditions for the numerical solution of the radiative transfer

D. N. Sauer1,2,3 - T. L. Hoffmann3 - A. W. A. Pauldrach3


1 - INAF, Osservatorio Astronomico di Trieste, via G. B. Tiepolo 11, 34131 Trieste, Italy
2 - Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85741 Garching, Germany
3 - Universitätssternwarte München, Scheinerstr. 1, 81679 München, Germany

Received 8 June 2006 / Accepted 4 August 2006

Abstract
Context. Realistic atmospheric models that link the properties and the physical conditions of supernova ejecta to observable spectra are required for the quantitative interpretation of observational data of type Ia supernovae (SN Ia) and the assessment of the physical merits of theoretical supernova explosion models. The numerical treatment of the radiation transport - yielding the synthetic spectra - in models of SN Ia ejecta in early phases is usually carried out in analogy to atmospheric models of "normal'' hot stars. Applying this analogy indiscriminately leads to inconsistencies in SN Ia models because a diffusive lower boundary, while justified for hot stars, is invalid for hydrogen and helium-deficient supernova ejecta. In type Ia supernovae the radiation field does not thermalize even at large depths, and large optical depths are not reached at all wavelengths.
Aims. We aim to derive an improved description of the lower boundary that allows a more consistent solution of the radiation transfer in SN Ia and therefore yields more realistic synthetic spectra.
Methods. We analyze the conditions that lead to a breakdown of the conventional diffusion approximation as the lower boundary in SN Ia. For the radiative transfer, we use a full non-LTE code originally developed for radiatively driven winds of hot stars, with adaptations for the physical conditions in SN Ia. In addition to a well-tested treatment of the underlying microphysical processes, this code allows a direct comparison of the results for SN Ia and hot stars.
Results. We develop a semi-analytical description that allows us to overcome some of the limiting assumptions in the conventional treatment of the lower boundary in SN Ia radiative transfer models. We achieve good agreement in a comparison between the synthetic spectrum of our test model and an observed spectrum.

Key words: radiative transfer - methods: numerical - line: formation - supernovae: general - stars: atmospheres - stars: winds, outflows

1 Introduction

Type Ia supernovae (SN Ia) have become an invaluable tool for the determination of the cosmological parameters (Riess et al. 1998,2001; Tonry et al. 2003; Perlmutter et al. 1999) as their exceptional brightness makes them observable even at large cosmological distances. Using SN Ia for distance determination requires knowledge of their absolute luminosities; however, SN Ia are not perfect "standard candles'' in this respect because they show an intrinsic scatter in their properties, in particular in the peak brightness. The application of SN Ia for cosmology therefore relies on empirical relationships between the peak brightness and other observed characteristics (e.g., Perlmutter et al. 1997; Phillips 1993; Hamuy et al. 1996; Riess et al. 1996). To first order the shape of the light curves and certain spectral properties is determined by the mass of synthesized \ensuremath{^{56}{\rm Ni}} and its distribution within the ejecta (Nugent et al. 1995b; Pinto & Eastman 2000; Höflich et al. 1995). However, the details of the physical processes that cause the observed variation are still unclear (see Hillebrandt & Niemeyer 2000, for a review). This uncertainty is an essential problem because the different calibration methods used to derive the peak brightness yield partly different results, implying an unaccounted source of systematic error (Leibundgut 2004). In addition, the application of SN Ia for cosmological distance measurement relies on the crucial assumption that objects observed at high redshifts have the same properties as objects in the nearby universe, so that the same calibration method for the luminosity differences can be applied to all objects. It is, therefore, of fundamental interest to derive a physical model that can explain the explosion mechanism of SN Ia in detail, including the observed intrinsic variability. This will allow a more reliable estimate of the systematic errors of the distance measurement.

The currently favored models for the explosion mechanism of SN Ia involve the thermonuclear explosion of a carbon-oxygen white dwarf (WD) in a binary system. Two progenitor scenarios are generally considered: the "single degenerate'' scenario and the "double degenerate'' scenario. In the single degenerate scenario the WD accretes mass from a red-giant companion star. When the WD reaches a mass close to the Chandrasekhar mass ( $M_{\rm Ch}\approx 1.4~\ensuremath{M_{\odot}} $) the compressional heating at the center of the star triggers carbon burning. After a period of a few thousand years of quiet burning a thermonuclear runaway disrupts the star (Iben & Tutukov 1984; Woosley et al. 2004; Han & Podsiadlowski 2004; Webbink 1984). In the "double degenerate'' scenario the companion star is also a WD with a mass such that the total mass of the system exceeds $M_{\rm Ch}$. Due to energy loss by gravitational waves the orbital separation of the binary system gradually decreases, leading to a merger, which triggers the thermonuclear runaway that explodes the star (Nomoto 1982; Whelan & Iben 1973). Potential progenitor systems have been found in recent years; their numbers, however, are too low to explain the observed rates of SN Ia (Cappellaro et al. 1999). Pauldrach (2005) suggests on basis of the results of Pauldrach et al. (2004) a potential connection of SN Ia progenitors to a subgroup of central stars of planetary nebulae (CSPN).

The details of the explosion process itself are also still subject to a lively debate. The general picture is that a subsonic deflagration wave ("flame'') is ignited near the center of the star. The flame travels outward, burning part of the star to nuclear statistical equilibrium (NSE). Because the flame propagates subsonically, the star can expand while undergoing burning. This allows partial burning of C and O to intermediate mass elements (Si, S, Mg, Ca) which dominate the composition. In contrast to the deflagration, a prompt, supersonic detonation of the star would generate predominantly iron group elements. This outcome contradicts the observed composition. No agreement has been reached in the debate whether the explosion continues subsonically until the end of the explosion (Reinecke et al. 2002; Woosley et al. 1984; Röpke 2005; Nomoto et al. 1984; Niemeyer & Hillebrandt 1995; Röpke & Hillebrandt 2005) or if a (yet unknown) mechanism triggers the deflagration to turn into a supersonic detonation toward the end of the explosion (delayed detonation transition, DDT) (Höflich & Khokhlov 1996; Iwamoto et al. 1999). At present, the resulting composition of DDT models seem to favor the latter scenario; however, those models are not self-consistent and depend on ad hoc assumptions of the occurrence of the DDT.

Judging the validity of numerical explosion models requires a comparison of the observational consequences predicted by the explosion models to the de facto observations of SN Ia. Realistic radiative transfer models provide the crucial link between explosion models and observations. It is possible to predict the observational implications of the hydrodynamical models only if the radiative transfer models are sufficiently realistic and detailed. Conversely, such radiative transfer models make it possible to establish constraints on the composition and structure of SN Ia from the spectroscopic interpretation of observed spectra.

SN Ia in phases before and shortly after maximum exhibit a spectrum dominated by a few very broad absorption features in a non-thermal continuum. These absorption features are mostly due to blends of several lines, while the "continuum'' itself is formed by the overlap of a large number of Doppler-broadened metal lines. The true continuum opacities and emissivities that determine the overall shape of the spectrum in stars are of minor significance in supernovae. At later epochs, the "pseudo-continuum'' photosphere recedes deeper and deeper into the ejecta and eventually disappears as the ejecta become transparent. Unlike stars, the radiation in SN Ia is generated within the expanding medium itself by the deposition of the energy of $\gamma $-photons that result from the decay chain \ensuremath{^{56}{\rm Ni}} \ensuremath{\rightarrow} \ensuremath{^{56}{\rm Co}} \ensuremath{\rightarrow} \ensuremath{^{56}{\rm Fe}} (Colgate & McKee 1969).

The early epochs where a photosphere is still present are referred to as the photospheric phase. In the photospheric phase the ejecta can be treated in analogy to hot stars as expanding, extended atmospheres. Only the radiative transfer in the photosphere and in the outer envelope above the photosphere needs to be considered. In this setup a steady state is assumed because the photon escape timescale in the thin medium generally will be much shorter than the expansion timescale.

In principle, a complete radiative transfer model for SN Ia would require consistent, time-dependent solutions of the populations of all atomic levels and the continuum and line transfer, including the treatment of energy deposition by the decay products of \ensuremath{^{56}{\rm Ni}} and \ensuremath{^{56}{\rm Co}}.

Current models implement various simplifications according to the specific model's purpose. These simplifications are necessary because the solution of time-dependent radiative transfer in three dimensions, including the full coupling of radiation and matter, is not yet feasible and some of the terms involved in such a consistent solution are shown to be or regarded to be of second order. In recent decades synthetic spectra of SN Ia have been modeled by several groups with a variety of approaches involving different levels of complexity depending on the application (Stehle et al. 2005; Nugent et al. 1995a; Höflich et al. 1995; Mazzali & Lucy 1993; Baron et al. 2006; Kasen et al. 2006; Eastman & Pinto 1993; Nugent et al. 1997; Mazzali et al. 1993; Pauldrach et al. 1996; Lentz et al. 2001; Branch et al. 1985; Höflich 2005).

Highly parametrized models, which implement a simplified treatment of physical processes to achieve short run-times seem to be suitable for the comparative analysis of a large number of observed spectra, while more realistic models are required for a deeper understanding of the physical effects leading to specific observed properties. In particular, judging the validity of hydrodynamic explosion models, as mentioned above, can only be performed using radiative transfer models that include a very detailed treatment of relevant physical processes. Such detailed models may also be used to validate or invalidate specific simplifying assumptions used in less elaborate models.

In spite of the analogy mentioned before, SN Ia ejecta differ from ordinary stellar atmospheres in several important aspects. Techniques and methods that are adopted for stellar atmosphere modeling must be carefully checked to verify whether the applied approximations are still justified for SN Ia. In this work we present an improved description for the lower boundary of the radiative transfer calculation. This is required because the assumption of thermalization at large depths, justified for stellar atmospheres, breaks down for SN Ia.

In the work we present here, we use the computer program WMbasic (Pauldrach et al. 1994,2001) to obtain a consistent solution of the full non-LTE rate equations and a detailed observer's frame solution of the radiative transfer. This code was originally designed for the analysis of the spectra of hot stars with radiatively driven winds, but an earlier version has already been used by Pauldrach et al. (1996) (Paper I) to quantitatively investigate the effects of line blocking in SN Ia. While they used a consistent treatment of line blocking, the back-reaction of the line opacities on the temperature structure (line blanketing) was not taken into account. In our present work the current version of the code has been further adapted to treat the radiative transfer in supernovae in a more sophisticated way.


  \begin{figure} \par\includegraphics[width=11.25cm,clip]{5781fig1.eps} \end{figure} Figure 1: Overview of the physical equations that must be consistently solved for the non-LTE model. The input is fixed by an external explosion model. In the middle-left box the rate equations which determine the occupation numbers ni of the atomic levels are given. The middle-right box shows the radiative transfer equation for the radiation field. The lower-right box gives the energy equation that fixes the temperature structure within the atmosphere. The energy deposition by $\gamma $ photons, shown in the lower-left box, is currently taken into account only approximately. This means that the models rely on the input of the total luminosity L at the lower boundary of the computational grid instead of the 56Ni-mass.
Open with DEXTER

Section 2 describes the setup of the non-LTE model and introduces the numerical scheme used to solve the radiative transfer. In Sect. 3 the physical conditions in the "pseudo-photosphere'' of SN Ia are discussed with respect to the solution of the radiative transfer and are compared to the situation in normal stars (i.e., stars that have a well defined photosphere). Section 4 describes the derivation of an improved treatment of the inner boundary for the numerical solution of the radiative transfer. The results are discussed in Sect. 5, and a comparison of a model spectrum with an observed SN Ia spectrum is shown. The conclusions are provided in Sect. 6.

  
2 The radiative transfer model

The code WMbasic has been successfully used to model extended, radiation-driven stellar atmospheres, assuming a homogeneous, stationary, spherically symmetric outflow. Here we provide a brief outline of the main concepts; details relevant to the derivation in Sect. 4 will be discussed as well. A more comprehensive description of the numerical methods can be found in Pauldrach et al. (2001) and Pauldrach (2003) and references therein.

2.1 General setup

To derive synthetic spectra of supernovae in early phases the analogy to hot stars with extended atmospheres can be used to apply similar concepts for the solution. The radiative transfer model for supernovae requires the following input:

The computation of a self-consistent non-LTE-model requires the simultaneous solution of a number of physical equations, in particular the radiative transfer, the rate equations, and the energy equation. Figure 1 gives an overview of the physical equations and the physical quantities by which these equations are interconnected.

The general concept behind our code, WMbasic, is to first obtain a rough solution with a fast, approximate method, and then, based on this solution, obtain a completely consistent solution with an exact, detailed method. The approximate method should provide a solution that is sufficiently close to the final solution so that only a few iterations with the much more time-consuming detailed method are necessary.

Our fast, approximate method is based on a Doppler-broadened sampling technique for line opacities and emissivities. The idea behind this method is to solve the radiative transfer for a representative sample of frequency points in the relevant spectral range.

In the final iterations, a detailed radiative transfer method that does not suffer from the approximations of the first iteration cycle is used. This method uses an exact observer's frame solution, equivalent to a comoving frame solution, which correctly treats the angular variation of line opacities and emissivities. The line profiles are spatially resolved. Multi-line effects and back-reactions of the line opacities on the model structures are treated correctly.

The temperature structure is in practice obtained from balancing energy gains and losses to the electron gas (heating and cooling rates). This description is equivalent to the condition of radiative equilibrium (indicated in the energy equation in Fig. 1), but is numerically advantageous for physical conditions where the opacity is dominated by scattering events that do not couple the radiation field to the thermal pool (see Pauldrach et al. 2001).

   
2.2 Solution of the radiative transfer

To introduce the nomenclature and equations used later, the solution applied to solve the radiative transfer in the observer's frame employing the fast opacity sampling method is recapitulated in this section.

To determine the radiation field that enters into the Thomson emissivity, an iteration alternating between the ray-by-ray solution and the angular-integrated moments equation is performed. Both systems are solved with a Feautrier-type scheme (Feautrier 1964) as discussed, e.g., in Mihalas (1978). For each frequency point, the iteration is performed twice: first for a pure continuum model and afterwards for the full problem with continuum and lines. The solution is carried out in the usual Cartesian-like p-z-coordinate system where each p-ray at a given radius shell corresponds to a  $\mu=\cos\vartheta$-direction in spherical coordinates (see Fig. 2). The transfer equation for each p-ray is rewritten for the intensities in positive and negative z-direction

 \begin{displaymath}% \ensuremath{\frac{{\rm d} I^{\pm}_{\nu}}{{\rm d} \tau_{\nu}... ...\quad \ensuremath{{\rm d}}\tau_{\nu} = -\chi_{\nu} {\rm d} z. \end{displaymath} (1)

These equations have to be evaluated at each frequency point of the computational grid. In the remainder of this section the index $\nu$ is omitted for brevity. By introducing the new variables $u = \ensuremath{{\textstyle\frac{1}{2}}}\left(I^{+}+I^{-}\right)$ and $v=\ensuremath{{\textstyle\frac{1}{2}}}\left( I^{+}-I^{-} \right)$ these two first order differential equations with a single boundary condition (initial value problems) can be converted into a second order differential equation with a boundary condition for each side:

 \begin{displaymath}% \ensuremath{\frac{{\rm d} u}{{\rm d} \tau}} = v, \quad \ens... ...ad \ensuremath{\frac{{\rm d}^{2} u}{{\rm d} \tau^{2}}} = u - S \end{displaymath} (2)

where S is the source function.


  \begin{figure} \par\includegraphics[width=7.5cm,clip]{5781fig2.eps} \end{figure} Figure 2: p-z coordinate system used to solve the transfer equation in spherical symmetry. R denotes the radius of the inner core.
Open with DEXTER

To close the system, suitable boundary conditions must be specified. At the outer boundary the condition $I^{-}\equiv 0$ (no radiation incident from outside) leads to

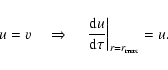\begin{displaymath}% u = v \quad \ensuremath{\Rightarrow}\quad \left.\ensuremath{\frac{{\rm d} u}{{\rm d} \tau}}\right\vert _{r=r_{\rm max}}=u. \end{displaymath} (3)

At the inner boundary one has to distinguish between those p-rays that intersect the photospheric core (p<R) and those that do not (p>R) (see Fig. 2). For core rays the incident intensity has to be explicitly specified, $I^{+}=I_{\rm core}$, while for non-core rays a reflecting boundary I+=I- is used. Noting that v=I+-u, one gets

 \begin{displaymath}% \left.\ensuremath{\frac{{\rm d} u}{{\rm d} \tau}}\right\vert _{\tau_{\rm max}}=I_{\rm core} - u \qquad(p<R) \end{displaymath} (4)

for core rays and

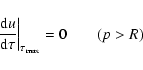\begin{displaymath}% \left.\ensuremath{\frac{{\rm d} u}{{\rm d} \tau}}\right\vert _{\tau_{\rm max}}=0\qquad(p>R) \end{displaymath} (5)

for non-core rays. Using a suitable discretization scheme (e.g., the standard scheme as modified by Pauldrach et al. 2001; see also Hoffmann et al. 2006, in prep.), the numerical solution of this system can be carried out very efficiently.

A very similar method can be used to obtain a solution for the moments equation in spherical symmetry

  
$\displaystyle % \ensuremath{\frac{{\rm d} \tilde{H}}{{\rm d} \tilde{\tau}}} =\f... ...quad \ensuremath{\frac{{\rm d} (qf\tilde{J})}{{\rm d} \tilde{\tau}}} =\tilde{H}$      
$\displaystyle \ensuremath{\Rightarrow}\quad\ensuremath{\frac{{\rm d}^{2} (qf\tilde{J})}{{\rm d} \tilde{\tau}^{2}}} = \frac{1}{q}\left(\tilde{J}-\tilde{S}\right),$     (6)

where $J=\int_{-1}^1 I(\mu)~\ensuremath{{\rm d}}\mu$, $H=\int_{-1}^1 I(\mu)~\mu~\ensuremath{{\rm d}}\mu$, and all symbols with a tilde denote the respective quantity times r2. The Eddington factor $f_{\nu }$ is defined as

 \begin{displaymath}% f=\frac{J}{K}=\frac{\int_{-1}^1 I(\mu)~\ensuremath{{\rm d}}\mu}{\int_{-1}^1 I(\mu)~\mu^2~\ensuremath{{\rm d}}\mu} \end{displaymath} (7)

(at each frequency point $\nu$); q denotes the sphericality factor, defined by
 
    $\displaystyle \ensuremath{\frac{{\rm d} (r^{2}q)}{{\rm d} r}} := r^{2}q\frac{3f-1}{rf}$ (8)
    $\displaystyle \ensuremath{\Rightarrow}\quad qr^{2}=\exp\left({\int_{1}^{r}\frac{3f(r')-1}{r'f(r')}~\ensuremath{{\rm d}} r'}\right).$ (9)

One advantage of the moments equation, as compared to the ray-by-ray solution, is that one can implicitly solve for the contribution of Thomson scattering to the source function S. Separating the emissivity due to true processes ( $\eta^{\rm true}$) and that due to Thomson-scattering ( $\eta^{\rm Th} = \chi^{\rm Th}J$), one can write

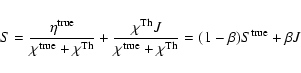\begin{displaymath}% S = \frac{\eta^{\rm true}}{\chi^{\rm true}+\chi^{\rm Th}} +... ...i^{\rm true}+\chi^{\rm Th}} = (1-\beta)S^{\rm true} + \beta J \end{displaymath} (10)

with the definitions

 \begin{displaymath}% S^{\rm true}:=\frac{\eta^{\rm true}}{\chi^{\rm true}}\qquad... ...beta:=\frac{\chi^{\rm Th}}{\chi^{\rm true}+\chi^{\rm Th}}\cdot \end{displaymath} (11)

Using this in Eq. (6) gives

 \begin{displaymath}% \ensuremath{\frac{{\rm d}^{2} (qf\tilde{J})}{{\rm d} \tilde{\tau}^{2}}} = \tilde{J}(1-\beta)-\tilde{S}^{\rm true}(1-\beta). \end{displaymath} (12)

At the boundaries, the system is closed by employing factors

 \begin{displaymath}% h := \frac{\int_{0}^{1}u(\mu)~\mu~\ensuremath{{\rm d}}\mu}{\int_{0}^{1}u(\mu)~\ensuremath{{\rm d}}\mu} \end{displaymath} (13)

similar to the second Eddington factor[*], with $u(\mu)$ coming from the solution of the ray-by-ray solution. At the outer boundary, because $u(r_{\rm max})\equiv v(r_{\rm max})$, this is

 \begin{displaymath}% h(r=r_{\rm max}) = \left.\frac{H}{J}\right\vert _{r=r_{\rm max}}. \end{displaymath} (14)

Thus, the outer boundary equation is

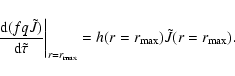\begin{displaymath}% \left.\ensuremath{\frac{{\rm d} (fq\tilde{J})}{{\rm d} \til... ...t _{r=r_{\rm max}} = h(r=r_{\rm max})\tilde{J}(r=r_{\rm max}). \end{displaymath} (15)

The inner boundary (r=R) is treated similarly; however, because $\int u~\mu~\ensuremath{{\rm d}}\mu \ne H$, $I_{\rm core}$ from the ray-by-ray solution has to be employed here as well, noting that

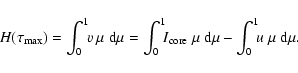\begin{displaymath}% H(\tau_{\rm max}) = \int_{0}^{1}\!\! v~\mu~\ensuremath{{\rm... ...{{\rm d}}\mu - \int_{0}^{1}\!\!u~\mu~\ensuremath{{\rm d}}\mu. \end{displaymath} (16)

This results in

 \begin{displaymath}% \left.\ensuremath{\frac{{\rm d} (fq\tilde{J})}{{\rm d} \til... ...ore}~\mu~\ensuremath{{\rm d}}\mu - h(\tau_{\rm max})\tilde{J}. \end{displaymath} (17)

In the final, detailed solution, the radiative transfer is solved through the total hemisphere using a formal integral on an adaptive micro-grid. This also requires the specification of boundary conditions. For consistency, the $I^{+}_{\rm core}$ values used for the sampling method must be used for the core rays in the iterations using this method. Therefore, only the boundary condition for the sampling iteration will be discussed here.

   
3 Physical conditions at the photosphere of a SN Ia

In normal stellar atmospheres the exponential increase of the density at the bottom of the atmosphere provides a clear definition of a photospheric radius because large optical depths are reached at all wavelengths within a very short spatial distance. In contrast, SN Ia do not have a clearly defined photosphere: because the material is unbound, no exponential density structure comparable to a stellar atmosphere can develop. As a result, the optical depth scale depends strongly on the wavelength. (This makes the concept of a mean optical depth like the Rosseland optical depth much less useful, if not entirely meaningless, in SN Ia.) In addition, the absolute densities are much lower than in stellar atmospheres and the composition in SN Ia is dominated by intermediate-mass and iron-group elements. When compared to stellar atmospheres this behavior leads to very low number densities of ions and electrons, resulting in a significantly weaker free-free continuum. The absence of hydrogen and helium in the ejecta further reduces the contribution of the bound-free continuum in the optical and infrared part of the spectrum. Going from red to blue wavelengths the first strong continuum edge is the O I ionization edge at 911 Å.


  \begin{figure} \par\hspace*{1mm} \includegraphics[width=8.1cm,clip]{5781fig3a.eps}\vspace*{3mm} \includegraphics[width=8.2cm,clip]{5781fig3b.eps} \end{figure} Figure 3: Comparison of the different contributions to the total opacity near the photosphere in a stellar atmosphere (upper panel; model D40 in Pauldrach et al. 2001) and a SN Ia model (lower panel); note the logarithmic scale. $\chi _{\rm true}$ represents the total true opacity (continuum and lines), $\chi _{\rm cont}$ the true continuum alone and $\chi _{\rm thom}$ the Thomson scattering opacity. The dotted lines show the shape of a blackbody spectrum at the respective temperature on an arbitrary scale to indicate the position of the flux maximum.
Open with DEXTER

Figure 3 shows a comparison of the contributions to the total opacity in the photospheric region of a hot star (Model D40 from Pauldrach et al. 2001) and a SN Ia. The dotted line shows a blackbody spectrum corresponding to a typical temperature (40 000 K for D40, 12 000 K for the supernova) to indicate the approximate position of the maximum flux in the spectrum. It can be seen that in the supernova, the bound-free continuum opacity is irrelevant compared to the line opacity in the major part of the spectrum. The plot also illustrates the formation of the "pseudo-continuum'' by the overlap of thousands of lines.

The most significant qualitative difference between a supernova and a star, however, is that at wavelengths redward of about 5000 Å, the electron scattering opacity becomes the dominating source of opacity, even in deep layers of the ejecta. Note that this situation cannot be changed significantly by computing down to smaller radii because the mild increase of density does not permit the formation of a significant free-free opacity. On the contrary, one encounters a lower contribution of true opacities because higher ionization stages tend to have less lines, and thus the line opacity decreases inwards. (In addition, the validity of the stationarity assumption needs to be considered because the photon trapping time at deep layers becomes comparable to the escape time.) Figure 4 shows the logarithm of the total opacity as a function of velocity and wavelength for a SN Ia model (epoch: 25 days after explosion) where the effect of decreasing line opacity can be seen clearly.


  \begin{figure} \par\includegraphics[width=8.25cm,clip]{5781fig4.eps} \end{figure} Figure 4: Logarithm of the total opacity in a SN Ia model (sampling iteration) versus velocity and wavelength. Note that the line opacity decreases toward the inside (front) because higher ionization stages with less lines dominate.
Open with DEXTER

Compared to a blackbody spectrum at the respective temperature, the radiation field in the innermost regions is more likely to have a bluer characteristic because it is the result of radiation from the deposition of $\gamma $ rays that is not entirely thermalized. Furthermore, no emission from down-scattering of $\gamma $-photons can be generated further out in the ejecta in wavelength regions that do not have significant continuum or line opacity. This effect results in the characteristic shape of SN Ia spectra in red and infrared wavelengths where the slope of the pseudo-continuum is generally steeper than the slope of a corresponding blackbody spectrum. In synthetic spectra computed assuming thermalization this effect generally results in an offset of the model spectrum in the red and infrared wavelengths (see e.g., Pauldrach et al. 1996 and Nugent et al. 1997 and the spectral fits in Stehle et al. 2005).

In summary, the ejecta of early SN Ia form an intermediate object between an extended stellar atmosphere and a planetary nebula. For both extreme cases the choice for the boundary conditions is clear: for the star, the LTE diffusion approximation Eq. (18) is a suitable choice. For a gaseous nebula, the incident radiation field from the illuminating star naturally defines the radiation field at the inner boundary (because there is essentially no back-reaction of the nebula on the stellar atmosphere). In SN Ia neither of these choices can be strictly applied.

In the next section we will discuss an extension to the diffusion approximation that eliminates most of the restrictive requirements of LTE and therefore allows a more consistent description of the inner boundary for supernova conditions.

   
4 An improved inner boundary for the radiation transfer at non-LTE conditions

   
4.1 The standard case for stellar atmospheres: the LTE diffusion approximation

The numerical solution of the radiative transfer equation requires a set of boundary conditions. For the objects discussed here, this requires an assumption about the incoming radiation  $I_{\nu}^{+}$ at the core. $I_{\nu}^{+}$ should be chosen so that it describes the radiation field as accurately as possible under the physical conditions present. Ideally, the expression for the boundary equation is an analytic extrapolation of the radiation field at the innermost points.

For the calculations done here, the incident radiation from outside the ejecta is assumed to be zero. Therefore, the boundary condition for the outer boundary is $I^{-}(\nu,\mu)\vert _{r=r_{\rm max}}=0$. The common choice for the  $I_{\nu}^{+}$ at the inner boundary in stellar atmospheres is derived from the LTE-diffusion approximation (see, e.g., Mihalas 1978)

 \begin{displaymath}% I^{+}(\nu,\mu) \approx B_{\nu}(T) + 3\mu \ensuremath{\frac{{\rm d} B_{\nu}(T)}{{\rm d} \tau_{\nu}}}\cdot \end{displaymath} (18)

This result is more generally obtained by applying a harmonic expansion for I+ that leads to the expression (see, e.g., Pomraning 1973)

 \begin{displaymath}% I^{+}(\nu,\mu) \approx I^{0}(\nu) + 3\mu I^{1}(\nu)\equiv I^{0}_{\nu} + 3\mu H^{0}_{\nu} \end{displaymath} (19)

where the zeroth term $I^{0}_{\nu}$ is isotropic and the first term has an angular dependence proportional to $\mu$. The term I1 has the properties of a flux (it is, however, in general not identical to the real flux $H_{\nu}$ that results from a solution of the transfer equation with this boundary condition). We therefore associate the symbol  $H^{0}_{\nu}\equiv I^{1}(\nu)$ with the analytical expression for the anisotropic term of the boundary equation. In the following we will discuss expressions of different refinement for the terms  $I^{0}_{\nu}$ and  $H^{0}_{\nu}$.

For the classical derivation of the LTE diffusion approximation, commonly used in stellar atmospheres, a Taylor expansion of $S_{\nu}$ in the limit of large $\tau $

 \begin{displaymath}% S_{\nu}(\tau_{\nu}') \approx \ensuremath{B_{\nu}} = \sum_{n... ...tial\tau_{\nu}^{(n)}} \frac{(\tau_{\nu}'-\tau_{\nu}^{n})}{n!} \end{displaymath} (20)

is used. Through the formal solution of the transfer equation this leads to the terms

 \begin{displaymath}% I^{0}_{\nu} \approx I^{0}_{\rm classic}(\nu)\equiv B_{\nu}(T) \end{displaymath} (21)

and

 \begin{displaymath}% H^{0}_{\nu} \approx H^{0}_{\rm classic}(\nu) \equiv \frac{... ...u}}}{\partial T}}\ensuremath{\frac{{\rm d} T}{{\rm d} r}}\cdot \end{displaymath} (22)

In the standard implementation, the (lower) boundary equations for the ray-by-ray solution (core rays), Eq. (4) and the moments equation Eq. (17), are therefore given by
    $\displaystyle \left.\ensuremath{\frac{{\rm d} u_{\nu}}{{\rm d} \tau_{\nu}}}\rig... ...u}^{\rm max}} = I_{\nu}^{0} + 3\mu H_{\nu}^{0} - u_{\nu}(\tau_{\nu}^{,\rm max})$ (23)
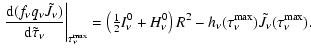    $\displaystyle \left.\ensuremath{\frac{{\rm d} (f_{\nu}q_{\nu}\tilde{J}_{\nu})}{... ...ght)R^{2} - h_{\nu}(\tau_{\nu}^{\rm max})\tilde{J}_{\nu}(\tau_{\nu}^{\rm max}).$ (24)

The expansion Eq. (20) and, therefore, Eq. (21) is applicable if the radiation field is thermalized (i.e., the mean free paths of photons are much shorter than any significant hydrodynamic length scale). In SN Ia, however, this condition is not fulfilled over the full spectrum (as discussed in Sect. 3). Hence, the use of Eq. (21) leads to incorrect spectral properties of the radiation field at the inner boundary. The inconsistency between the radiation field and the physical state of the matter caused by enforcing a thermal radiation field at the core boundary leads to spurious results in the rate equations and, in particular, in the heating and cooling rates for the temperature determination. The unstable behavior results from a feedback effect between the radiation field and the temperature. The radiation field at the inner points is used to determine the temperature, which (through the boundary equation) sets the incoming intensity and, therefore, partially sets the radiation field at those points.

Part of this work focuses on deriving an analytical expression for the radiation field at the inner boundary that reflects the physical conditions in SN Ia more accurately and reproduces the slope of the pseudo-continuum in the red and infrared wavelengths better.

4.1.1 Flux constraint

To constrain the total flux at the inner boundary, the frequency integrated input flux $H^0 =\int_{0}^{\infty}\!\!H^{0}_{\nu}~\ensuremath{{\rm d}}\nu$ is compared to the total integrated input flux ${\cal H}_{0} =L/(16\pi^{2}R^{2})$. This results in a (frequency-independent) scaling factor

 \begin{displaymath}% FC = \frac{{\cal H}_{0}}{\int_{0}^{\infty}\!\! H^{0}_{\nu}~\ensuremath{{\rm d}}\nu} \end{displaymath} (25)

that is applied to the flux term of the inner boundary condition, so that (cf. Eq. (22))

 \begin{displaymath}% H^{0}_{\rm classic{'}}(\nu) = -\frac{1}{3}\frac{1}{\chi_{\... ...l T}}\ensuremath{\frac{{\rm d} T}{{\rm d} r}} FC_{\rm classic} \end{displaymath} (26)

with

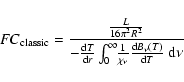\begin{displaymath}% FC_{\rm classic} = \frac{\frac{L}{16\pi^{2}R^{2}}}{-\ensur... ...frac{{\rm d} B_{\nu}(T)}{{\rm d} T}} ~\ensuremath{{\rm d}}\nu} \end{displaymath} (27)

(Mihalas 1978, p. 252). The purpose of applying this flux correction factor is to induce the model to converge to a solution with the correct total flux. The factor $\it FC$ not only accounts for small numerical differences (in particular in the derivation of the temperature gradient) but also for inconsistencies between the assumptions implied in the construction of the boundary flux and the physical conditions that are actually encountered at the boundary layer of the model. For the case of the classical diffusion approximation, deviations from $\it FC=1$ in the converged model indicate departures from ideal LTE diffusion conditions.

With respect to the moments equation for the flux at the inner boundary the derived flux is actually

 \begin{displaymath}% H_{\nu}(R) = \!\!\int_{0}^{1}\!\!\left(I^{0}_{\nu}+3\mu H_... ...th{{\textstyle\frac{1}{2}}} I^{0}_{\nu}-h_{\nu}J_{\nu}\right). \end{displaymath} (28)

Thus, constraining the flux by adjusting $H^{0}_{\nu}$ only with respect to H0 implicitly assumes that the second term in Eq. (28) vanishes, which requires

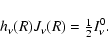\begin{displaymath}% h_{\nu}(R)J_{\nu}(R) = \ensuremath{{\textstyle\frac{1}{2}}} I^{0}_{\nu}. \end{displaymath} (29)

As can be seen in Fig. 5, even for the D40 star model (cf. Pauldrach et al. 2001) this condition is not exactly fulfilled. In this case, however, the deviations are certainly negligible, whereas in SN Ia the effect is much stronger (bottom panel in Fig. 5). This leads to a significant discrepancy between $\it FC$ and the actually derived flux. The modifications discussed in the next section require that this effect is taken into account. Therefore, the correct flux correction factor has to be used:

 \begin{displaymath}% FC = \frac{\frac{L}{16\pi^{2}R^{2}} - \int_{0}^{\infty}\lef... ...nt_{0}^{\infty}\!\! H^{0}_{\nu}~\ensuremath{{\rm d}}\nu}\cdot \end{displaymath} (30)

Without the additional term that accounts for small deviations from LTE the integrated flux at the inner boundary deviates from the desired input flux even if $\it FC=1$. With the formulation in Eq. (30), it is possible to achieve $\it FC=1$ and the correct flux at r=R.


  \begin{figure} \par\includegraphics[width=8.1cm,clip]{5781fig5a.eps}\vspace*{1.5mm} \includegraphics[width=8.1cm,clip]{5781fig5b.eps} \end{figure} Figure 5: The ratio $(\ensuremath{{\textstyle\frac{1}{2}}}\ensuremath{B_{\nu}} -h_{\nu}J_{\nu})/\ensuremath{B_{\nu}} $ at the inner boundary (see text). Upper panel: O-star model D40 (Pauldrach et al. 2001). Lower panel: SN Ia model. Note the different y-scales in these plots.
Open with DEXTER

As already noted above, in the formulation of Eq. (26) the factor $\it FC$effectively represents a correction to the temperature gradient at the inner boundary:

 \begin{displaymath}% I^{+}(\nu,\mu) = B_{\nu}(T) + \mu\frac{1}{\chi_{\nu}}\ensu... ...al T}}\left(FC\ensuremath{\frac{{\rm d} T}{{\rm d} r}}\right). \end{displaymath} (31)

We have found that it is numerically more stable to determine the temperature T1 of the innermost grid point directly from requiring that the correct flux be reached, instead of applying FC as above and waiting for the temperature-correction mechanism of the code (based on heating and cooling rates) to adjust the temperature accordingly. One reason for an unstable behavior of the latter approach is that in Eq. (31) the first term is also temperature dependent, and, in case of the physical conditions in a supernova, is of the same order as the second term. Therefore, a correction of the second term alone can lead to an inconsistency between the shape of the radiation field that results and the actual temperature. (An additional problem under near-LTE conditions (e.g., at the inner boundary in "normal'' stellar atmospheres) is that determining the temperature from the balance of the kinetic heating and cooling rates becomes inaccurate, because in thermal equilibrium the heating and cooling rates balance at all temperatures. In stellar atmosphere models we avoid the problem by computing the temperature in the optically thick inner region either via the condition of radiative balance, or as a parametrized function of the optical depth, with the parameters adjusted to conserve the flux (cf. Pauldrach et al. 2001).) From Eq. (30) and the condition FC=1 the temperature of the innermost point is derived by requiring

 \begin{displaymath}% \int_{0}^{\infty}\!\!H^{0}_{\nu}~\ensuremath{{\rm d}}\nu-\l... ..._{\nu}\right)~\ensuremath{{\rm d}}\nu\right) \stackrel{!}{=}0 \end{displaymath} (32)

where, for the case of the standard diffusion approximation, $H^{0}_{\nu}$corresponds to the flux term  $H^{0}_{\rm classic}(\nu )$ of the boundary condition (Eq. (22)). The conditional Eq. (32) implicitly defines $T_1 = T_2 + (\ensuremath{{\rm d}} T/\ensuremath{{\rm d}} r) \Delta r_{1,2}$ because $I^{0}_{\nu}$ and  $H^{0}_{\nu}$ are functions of T and  $\ensuremath{{\rm d}} T/\ensuremath{{\rm d}} r$(Eqs. (21) and (22)). The temperature T2 of the second grid point (and all other grid points) is derived conventionally via heating and cooling rates. In practice, Eq. (32) is solved numerically in each iteration, assuming that the temperature-dependence of the second integral is negligible.

Note that the expression Eq. (28) implicitly contains the assumption of thermalization. Only then is the degree of isotropy given that is necessary to make the expansion Eq. (19) meaningful, neglecting quadratic and higher order terms.

   
4.2 I+ for a non-thermal radiation field at the inner boundary

In this section we will consider modifications to the inner boundary that allow deviations of the radiation field from thermal equilibrium conditions, which reflects the physical situation in SN Ia better. A consistent treatment of the boundary becomes increasingly important for models of later epochs, as long as the luminosity emitted at the boundary is still significant compared to the flux originating from the $\gamma $-ray energy deposition above that boundary.

All modifications must be carried out in such a way that, in the limit of LTE-conditions at the inner points, the standard diffusive boundary condition Eq. (18) is retained. While it will not be possible to determine a boundary condition entirely free of analytical approximations (the model would not be sufficiently constrained) some of the assumptions entering into Eq. (21) can be relaxed without affecting the stability of the solution.

Starting from Eq. (19) one can give up the assumption of strictly thermal conditions by allowing deviations of the terms  $I^{0}(\nu)$ and  $I^{1}(\nu)$ from the Planck function. Thus, instead of Eq. (18) we set more generally

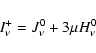\begin{displaymath}% I^{+}_{\nu}=J^{0}_{\nu} + 3\mu H^{0}_{\nu} \end{displaymath} (33)

with an intensity term $J^{0}_{\nu}$ and a flux term  $H^{0}_{\nu}$ to be determined. We will consider those two terms separately because we will choose a fundamentally different treatment.

The isotropic term ${J}_{\nu }^{0}$

We have found that the isotropic term  $J^{0}_{\nu}$ can be determined numerically by a simple iteration procedure. This does not involve very much additional computational effort compared to the standard solution for the boundary condition because the iteration is carried out to determine the intensity term for the Thomson scattering source function anyway.

In the solution of the moments equation, one can solve for this term implicitly by writing the boundary equation as

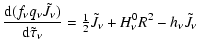    $\displaystyle \ensuremath{\frac{{\rm d} (f_{\nu}q_{\nu}\tilde{J}_{\nu})}{{\rm d... ...xtstyle\frac{1}{2}}}\tilde{J}_{\nu} + H_{\nu}^{0}R^{2} - h_{\nu}\tilde{J}_{\nu}$ (34)
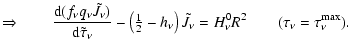    $\displaystyle \ensuremath{\Rightarrow}\qquad\ensuremath{\frac{{\rm d} (f_{\nu}q... ...ght)\tilde{J}_{\nu}= H_{\nu}^{0}R^{2} \qquad (\tau_{\nu}=\tau_{\nu}^{\rm max}).$ (35)

An equivalent expression for the ray-by-ray solution is not as straightforward and may lead to slightly inconsistent results for $J_\nu $ in the iteration because there is no constraint that requires the angular integral of the converged analogous quantities $u_\nu$ for each ray to equal $J_\nu $. For the boundary equation in the ray-by-ray solution we therefore also use the $J_\nu $that results from the moments equation.

Compared to the standard diffusion approximation this effectively means that the inner boundary is less strongly constrained, which may lead to numerical instability. To ensure that the boundary condition is still well behaved and to understand its general behavior we have studied this modification on a simple toy model before applying it to the radiative transfer code.


  \begin{figure} \par\includegraphics[width=7.3cm,clip]{5781fig6.eps} \end{figure} Figure 6: Simple toy model to illustrate the new treatment of the zeroth term of I+ at the inner boundary for the situation of an optically thin true continuum. The dotted line represents the run of J if the traditional setting $I^{0}=\ensuremath {\rm const.} $ is assumed, the solid line shows the new treatment (see text). The true source function is indicated by the dash-dotted line. Panel  a) shows the case of an optically thin model (line and continuum) where $\tau _{\rm line}=0.001$. Panel  b) shows an intermediate case ( $\tau _{\rm line}=0.2$). Panel  c) and  d) show the case of an optically thick line ( $\tau _{\rm line}=5$) where the modification only influences the inner part because the emergent radiation is entirely separated from the inner region by the line. Panel  d) shows a situation where the method would overestimate J in the inner region: the case where in the conventional treatment I0 at the inner boundary is smaller than  $S_{\rm line}$. In this case the iteratively determined I0 is not appropriate, and instead an I0 based on that of a neighboring frequency point is used.
Open with DEXTER

The results of this toy model are shown in Fig. 6. The basic parameters are the same for all cases considered. The Thomson-opacity is $\chi_{\rm Th}=1$ and the background opacity (continuum) is $\chi_{\rm c}=10^{-3}$with a corresponding source function of $S_{\rm c}=1$. We also consider a line with a source function of $S_{\rm l}=5$at a certain radius point. (The idea here is that the line is Doppler-shifted by the velocity field and appears at the frequency point being considered at that particular radius point.) The zeroth term of the traditional boundary condition is set to I0=10 for the first three cases and to I0=2 for the last. H0 is set equal to 0 in all cases. The radiation field is obtained by an iteration of a ray-by-ray solution with a solution of the moments equation in spherical symmetry. A Feautrier scheme similar to the one in the radiative transfer code is used. Generally, in the main code, convergence is obtained within less than 15 iterations - depending on the physical conditions and on the relevance of Thomson-scattering in particular. (For comparison, the iteration for Thomson-scattering alone with a fixed boundary usually converges within 5 iterations.) All plots show the comparison of J as a function of radius obtained from the solution of the moments equation. The result from the traditional choice of using a pre-specified $I^{0}=\ensuremath {\rm const.} $ (in practice $B_{\nu}$) is shown as a dotted line in red. The result of allowing I0 to consistently converge to I0=Jis shown as a solid blue line. The black dash-dotted line represents the true source function (line and background).

Panel a in Fig. 6 shows the situation for an optically thin model ( $\tau _{\rm line}=0.001$). Panel b shows an intermediate case with $\tau _{\rm line}=0.2$. The last two panels, c and d, show the case of an optically thick line ( $\tau _{\rm line}=5$). Here the modification only influences the radiation field in the inner region as the emergent radiation is entirely separated from the inner region by the optically thick line. Compared to the conventional treatment with a small I0, in the new treatment J is significantly larger inner region. The physical conditions cannot cause this increase in intensity because of the low true opacity. Thus, in this situation a shortcoming of this method becomes apparent: one would expect $J_\nu $ to drop to  $\ensuremath{{\textstyle\frac{1}{2}}} S_{\rm l}$toward the inner boundary because the absence of emission toward the inner region means that $I^{+}\equiv 0$. The model, however, effectively sets I+=I-. Unfortunately, this situation occurs quite frequently in SN Ia: at each frequency point where the opacity at the boundary is low but increases outward as a line is shifted into that frequency by the large velocity gradient.

Table 1: Conditions for the correction of enhanced $J_\nu $ at the inner boundary. The reference radius  $R_{\rm ref}$ is set to the radius of $\tau _{\rm Ross}\approx 2/3$. $R_{\rm ref2}$ refers to the radius where $\tau _{\rm c+l}\ge 3$. All $\tau $ values are derived radially from the inside outward.

This behavior follows from the assumption that the conditions and the radiation field $J_\nu $ within the inner zones of the computational grid are representative for the region below the innermost point. In cases where a strong line is present further out this assumption is, however, not justified. If this is not taken into account by an additional correction, an artificial emission will build up in the iteration between the moments equation and the formal ray-by-ray solution. Eventually this additional emission also affects the rate equations and the temperature in the inner region because the respective line transition can pump itself in an unphysical way.

As a first step for an ad hoc correction of this behavior, criteria have to be established to determine when a correction should be applied. No correction is needed if the continuum is optically thick or if the local opacity at the first two radius points is large (e.g., for a strong continuum or if a line is present at the inner boundary). Another criterion has to include a comparison of the local opacity to an average opacity over a reference $\Delta R$-step. If the average opacity is higher than the local opacity, a line is likely to be present further out. The reference $\Delta R$ is chosen according to a step $\Delta\tau_{\rm c}\ge 3$for pure continuum opacity (true and Thomson). The exact conditions for the correction used in the current implementation are listed in Table 1.

Secondly, a suitable correction has to be used for each frequency point. We found that a suitable approach was to use a fixed value $I^{0}_{\nu}=J_{\nu'}$with $J_{\nu'}$ being $J_\nu $ of the previous (redder) uncorrected frequency point. To prevent excessively large values for  $I^{0}_{\nu}$ in frequency regions where many subsequent points have to be corrected, an upper cut-off at  $\ensuremath{B_{\nu}} $ is applied.

The flux term ${H}_{\nu }^{0}$

Instead of the expansion Eq. (20) of $S_{\nu}$, we now start from a general expression for the source function, which explicitly takes a contribution from Thomson scattering into account

 \begin{displaymath}% S_{\nu}=\left(1-\beta_{\nu}\right)\ensuremath{B_{\nu}} + \b... ...\nu}^{\rm Th}}{\chi_{\nu}^{\rm Th}+\chi_{\nu}^{\rm true}}\cdot \end{displaymath} (36)

From the moments equation in spherical symmetry, Eq. (6), one then gets

 \begin{displaymath}% \ensuremath{\frac{{\rm d}^{2} \left(q_{\nu}f_{\nu}\tilde{J}... ...a_{\nu})}{q_{\nu}}\left(\tilde{J}_{\nu}-\tilde{B}_{\nu}\right) \end{displaymath} (37)

(with the Eddington factor $f_{\nu }=J_{\nu }/K_{\nu }$, cf. Eq. (7)) which can be solved analytically by rewriting it to

 \begin{displaymath}% \ensuremath{\frac{{\rm d}^{2} }{{\rm d} \tilde{\tau}_{\nu}^... ...nu}f_{\nu}\left(\tilde{J}_{\nu}-\tilde{B}_{\nu} \right)\right) \end{displaymath} (38)

under the assumption that

 \begin{displaymath}% \ensuremath{\frac{{\rm d}^{2} q_{\nu}f_{\nu}\tilde{B}_{\nu}... ...\frac{1-\beta_{\nu}}{{q}_{\nu}^{2}f_{\nu}}\approx {\rm const.} \end{displaymath} (39)

The first assumption can be justified by considering only up to first order terms in an expansion of $q_{\nu}f_{\nu}\tilde{B}_{\nu}$ in  $\tilde{\tau}_{\nu}$. The second assumption is not strictly fulfilled, however in practice a representative mean value $\langle(1-\beta_{\nu})/(q_{\nu}^{2}f_{\nu})\rangle$ is used. The general solution for $J_\nu $ in Eq. (38) is then derived to
 
    $\displaystyle q_{\nu}f_{\nu}\tilde{J}_{\nu} = q_{\nu}f_{\nu}\tilde{B}_{\nu} + C... ...1-\beta_{\nu}}{q_{\nu}^{2}f_{\nu}}\right\rangle} \tilde{\tau}_{\nu}} + C_{\nu}'$  
    $\displaystyle \ensuremath{\Rightarrow}\qquad J_{\nu} = \ensuremath{B_{\nu}} + \... ...{\nu}}\right\rangle} \tilde{\tau}_{\nu}} + \frac{C_{\nu}'}{q_{\nu}f_{\nu}r^{2}}$ (40)

with integration constants $C_{\nu}$ and $C_{\nu}'$ to be determined. Given the condition that $\tilde{\tau}\ensuremath{\rightarrow}\infty$, $\tilde{J}_{\nu}=\tilde{B}_{\nu}$has to be obtained. It follows that $C_{\nu}'\equiv 0$.

This result can be used to determine the flux term  ${H}_{\nu }^{0}$ from the moments equation Eq. (6), which leads to

 
                             $\displaystyle % \tilde{H}_{\nu}^{0}$ = $\displaystyle \ensuremath{\frac{{\rm d} }{{\rm d} \tilde{\tau}_{\nu}}}\left(q_{\nu} f_{\nu} r^{2}J_{\nu}\right)$ (41)
  = $\displaystyle \ensuremath{\frac{{\rm d} }{{\rm d} \tilde{\tau}_{\nu}}}\left(q_{... ...angle\frac{1-\beta_{\nu}}{q_{\nu}^{2}f_{\nu}}\right\rangle}\tilde{\tau}_{\nu}}.$ (42)

For the first term one derives the expression
 
                   $\displaystyle % \ensuremath{\frac{{\rm d} }{{\rm d} \tilde{\tau}_{\nu}}}\left(q_{\nu}f_{\nu}r^{2}B_{\nu}\right)$ = $\displaystyle \ensuremath{\frac{{\rm d} (r^{2}q_{\nu})}{{\rm d} \tilde{\tau}_{\... ...+ f_{\nu}\ensuremath{\frac{{\rm d} B_{\nu}}{{\rm d} \tilde{\tau}_{\nu}}}\right)$  
  = $\displaystyle \left\{ -\left(\frac{3f_{\nu}-1}{q_{\nu}\chi_{\nu} r} - \ensurema... ...{{\rm d} \ensuremath{B_{\nu}}}{{\rm d} \tilde{\tau}_{\nu}}}\right\}r^{2}q_{\nu}$  
  = $\displaystyle \left\{ -\left(\frac{3f_{\nu}-1}{\chi_{\nu} r} - \ensuremath{\fra... ...nsuremath{\frac{{\rm d} \ensuremath{B_{\nu}}}{{\rm d} \tau_{\nu}}}\right\}r^{2}$ (43)

making use of the definition of the sphericality factor $q_{\nu}$(Eq. (9)). Note that the last line in Eq. (43) contains only derivatives in  $\tau_{\nu}$, not $\tilde{\tau}_{\nu}$, because $q_{\nu}$ cancels in $\ensuremath{{\rm d}}\tilde{\tau}_{\nu}=-q_{\nu}\chi_{\nu}~\ensuremath{{\rm d}} r$.

Next we consider the integration constant $C_{\nu}$ in Eq. (40). This constant can be obtained by considering that in the outer part of the atmosphere

 \begin{displaymath}% j_{\nu}(\tilde{\tau}_{0})=\left.\frac{H_{\nu}}{J_{\nu}}\rig... ...x 2 \qquad\ensuremath{\rm for}\quad\tilde{\tau}_{0}(\nu)\ll 1 \end{displaymath} (44)

holds. It therefore follows that

 \begin{displaymath}% \tilde{J}_{\nu}(\tilde{\tau}_{0}(\nu))=j_{\nu}(\tilde{\tau}... ...}{{\rm d} \tilde{\tau}_{\nu}}}\right\vert _{\tilde{\tau}_{0}}. \end{displaymath} (45)

Inserting the result of Eq. (40) into Eq. (45) gives
 
$\displaystyle % \tilde{B}_{\nu}(\tilde{\tau}_{0}(\nu)) + \frac{C_{\nu}}{(q_{\nu... ...c{1-\beta_{\nu}}{q_{\nu}^{2}f_{\nu}}\right\rangle}\tilde{\tau}_{0}(\nu)}\right)$     (46)

and hence the expression for $C_{\nu}$ where $\tilde{\tau}_{0}\ll 1$

 \begin{displaymath}% C_{\nu}=\frac{-\tilde{B}_{\nu}(\tilde{\tau}_{0}(\nu)) + j_... ...\nu}}{q_{\nu}^{2}f_{\nu}}\right\rangle}\tilde{\tau}_{0}(\nu)}. \end{displaymath} (47)

In practice, $\tilde{\tau}_{0}$ has been chosen such that, at the corresponding depth point, the radiation field is not entirely decoupled from matter (e.g., $\tilde{\tau}_{0}\approx0.1$). This is necessary because the temperature in $\ensuremath{B_{\nu}} (T(\tilde{\tau}_{0}))$ at this depth point still has to be meaningful to characterize the radiation field. Using the result of Eq. (43), $C_{\nu}$can be expressed as
 
$\displaystyle % C_{\nu} = \frac{r(\tilde{\tau}_{0})^{2} \left\{j_{\nu} \left( \... ...e\frac{1-\beta_{\nu}}{q_{\nu}^{2}f_{\nu}}\right\rangle} \tilde{\tau}_{0}(\nu)}.$     (48)

As a further approximation we adopt an expansion in $1/\tau_{\nu}$ for $f_{\nu }$assuming that $f_{\nu}\ensuremath{\rightarrow}\ensuremath{{\frac{1}{3}}} $ for $\tau_{\nu}\ensuremath{\rightarrow}\infty$ to avoid mixing terms of $\ensuremath{\frac{{\rm d} f_{\nu}}{{\rm d} \tau}} $ and $f_{\nu }$ in Eq. (41):

 \begin{displaymath}% f_{\nu}(1/\tau_{\nu}) \approx \ensuremath{{\frac{1}{3}}} + ... ...uremath{\frac{{\rm d} f_{\nu}}{{\rm d} \tau_{\nu}}}\tau_{\nu}. \end{displaymath} (49)

Introducing Eq. (49) and Eq. (43) in Eq. (41) gives a new expression for the first term of the inner boundary condition[*]
 
$\displaystyle % H^{0}_{\rm new}(\nu)\equiv H^{0}_{\nu} = \frac{1}{3}\ensuremath... ...ngle\frac{1-\beta_{\nu}}{q_{\nu}^{2}f_{\nu}} \right\rangle}\tilde{\tau}_{\nu}}.$     (50)

This expression resembles the original diffusion flux  $H^{0}_{\rm classic}(\nu )$ plus additional correction terms that vanish for large optical depths and an isotropic radiation field.

In the radiative transfer code, a slightly different form was used by solving Eq. (49) for $\ensuremath{\frac{{\rm d} f}{{\rm d} \tau}} $ because the gradient of the Eddington factor is numerically less accurate than $f_{\nu }$ itself

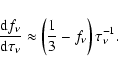\begin{displaymath}% \ensuremath{\frac{{\rm d} f_{\nu}}{{\rm d} \tau_{\nu}}}\app... ...eft(\ensuremath{{\frac{1}{3}}} -f_{\nu}\right)\tau_{\nu}^{-1}. \end{displaymath} (51)

This leads to the alternative form of
 
$\displaystyle % H^{0}_{\rm new'}(\nu) =f_{\nu}\ensuremath{\frac{{\rm d} \ensure... ...ngle\frac{1-\beta_{\nu}}{q_{\nu}^{2}f_{\nu}} \right\rangle}\tilde{\tau}_{\nu}}.$     (52)

In the equation for the temperature at the inner boundary Eq. (32) accordingly the expression $H^{0}_{\rm new'}(\nu)$ has to be used for  $H^{0}_{\nu}$. The Eddington factor $f_{\nu }$ is calculated from the moments $J_{\nu}=\int_{0}^1 u_{\nu}(\mu)~\ensuremath{{\rm d}}\mu$ and $K_{\nu}=\int_{0}^1 u_{\nu}(\mu)~\mu^2~\ensuremath{{\rm d}}\mu$ of the radiation field, obtained from the ray-by-ray solution (which represents an angular-resolved computation of the intensity, $I_{\nu}(\mu)$). Note that $f_{\nu }$ is a quantity not directly imposed by the boundary condition, which only specifies I+ but not I-.


  \begin{figure} \par\includegraphics[width=8.25cm,clip]{5781fig7.eps} \end{figure} Figure 7: The Eddington factor $f_{\nu }=J_{\nu }/K_{\nu }$ at the innermost radius points as a function of wavelength for the case of a SN Ia model. The deviation of $f_{\nu }$ from its LTE value of  $\ensuremath{{\frac{1}{3}}} $ (indicated by the dotted line) allows the new flux term of the inner boundary $H^{0}_{\rm new}(\nu )$ to deviate substantially from the LTE value of $H^{0}_{\rm classic}(\nu )$. The radii are given in units of the innermost radius.
Open with DEXTER

The crucial modification with respect to the classical formulation Eq. (22) of the flux term is achieved by the Eddington factor $f_{\nu }$that can deviate substantially from its value of  $\ensuremath{{\frac{1}{3}}} $ in the LTE diffusion limit. This deviation can be seen in Fig. 7 which shows $f_{\nu }$as a function of wavelength for the four innermost radial grid points of a SN Ia model.

   
5 Discussion and test calculations


  \begin{figure} \par\includegraphics[width=8.15cm,clip]{5781fig8.eps} \end{figure} Figure 8: The radiation field $J_\nu $ at the inner boundary for different treatments of I+. The dotted green line shows the radiation field for the uncorrected iterative method, which produces large artificial peaks at wavelength points where a line is present further out within a small $\tau $-interval. The blue solid line represents the new method including the correction for those wavelength points. The red line is calculated with the traditional treatment of the inner boundary. It is clear that the new method significantly reduces the radiation field in the red part of the spectrum. All three models are shown after a few iterations before the first temperature update.
Open with DEXTER

Figure 8 shows the radiation field $J_\nu $ at the innermost grid point for the case where the new method is used with and without correction (indicated by the blue solid line and the green dotted line, respectively). The third model shown in Fig. 8 uses the standard boundary condition (red solid line). One can see that the uncorrected new boundary treatment may create large artificial emission peaks. These peaks occur at wavelengths where a line is present further out within a small $\tau $-interval.

Additionally, Fig. 8 clearly shows that the characteristic of the radiation field is far from Planckian, which causes the standard diffusion approximation to be inappropriate. Also it can be seen that the new method produces less radiation in the red and infrared regions compared to the old boundary treatment.

Looking at the structure of the newly derived flux term Eq. (52), we note that the original flux term of the diffusion approximation Eq. (22) is obtained in the limit of large $\tau $ and  $f_{\nu}\ensuremath{\rightarrow}\ensuremath{{\frac{1}{3}}} $, equivalent to the requirement of a isotropic radiation field. Under these conditions the radiation field approaches LTE and the iterated $I_{\nu}^{0}=J_{\nu}$ term will therefore approach the Planck function  $\ensuremath{B_{\nu}} (T)$. This behavior complies with the requirement that the original diffusion approximation has to be recovered for LTE conditions.


  \begin{figure} \par\includegraphics[width=8.1cm,clip]{5781fig9.eps} \end{figure} Figure 9: Comparison of two test models using the old and the new treatments of the inner boundary. One can see that the flux in the red wavelengths is diminished in the model using the new boundary treatment. Note that the two models are not strictly comparable because the occupation numbers, ionization, and temperature structure adjust differently. For comparison the observed spectrum of SN 1992A 5 d after maximum is shown (Kirshner et al. 1993).
Open with DEXTER

Figure 9 shows a comparison of two full test models with the old and the new treatments of the boundary. One can see that in the red wavelength region as well as in the peaks of the spectrum, the radiation field in the model using the new method is slightly diminished compared to the model using the standard procedure. A direct comparison of the two models, however, is difficult because the treatment of the boundary condition has a significant influence on the occupation numbers, the ionization fractions, and the temperature structure. This influence can be seen especially in the UV part of the spectrum. The observed spectrum of SN 1992A 5 d after maximum (Kirshner et al. 1993), is shown in gray in this figure. Note that even though these models are test cases only and have not been tuned to fit the observation in detail, the overall shape of the observed spectrum is reproduced quite well. The model shown here uses the density distribution of the model f1 by Röpke & Hillebrandt (2005) which has been averaged over angles to obtain spherical symmetry. For the velocity field a homologous expansion law $v\propto r$ is assumed. For simplicity, we adopt a "generic'', homogeneous composition, independent of the predictions of the underlying explosion model. Also, the luminosity was not determined from the \ensuremath{^{56}{\rm Ni}} content of the explosion model but set to L=1 $\times$ 1043  \ensuremath{{\rm erg}~{\rm s}^{-1}}. The entire luminosity is emitted at the lower boundary implying conservation of the radiation flux through the ejecta. Table 2 summarizes the parameters of this model. v0 is the velocity at the innermost radius of the computational grid. The velocity at the "photosphere'', $v_{\rm ph}$ (where the photosphere is defined as the point at which $\tau _{\rm Rosseland}=2/3$), is actually an output quantity of the model because it depends on the opacities that change with the occupation numbers over the course of the iterations. Due to the strong wavelength-dependence of the opacities, however, this "photospheric velocity'' is not necessarily an observationally meaningful quantity. We note that the absorption minimum of the Si II $~\lambda6355$ feature in the model corresponds to a velocity of $\sim$8800  \ensuremath{{\rm km}~{\rm s}^{-1}} which is significantly larger than the  $v_{\rm ph}$ defined via $\tau_{\rm Rosseland}$. This should be kept in mind when using  $v_{\rm Si {\sc ii}}$ to track the photospheric velocity observationally (e.g., Benetti et al. 2005; Hachinger et al. 2006).

Table 2: Model parameters for the test model shown in Fig. 9. The composition is given in fractions by mass. The photospheric velocity  $v_{\rm ph}$ denotes the velocity where $\tau _{\rm Rosseland}=2/3$. v0 is the velocity of the actual innermost point of the model while  $v_{\rm ph}$ is an output of the calculation.

   
6 Conclusions

We have shown that the physical conditions in the expanding atmospheres of SN Ia are such that even at early times a complete thermalization of photons cannot be assumed. Therefore the common approach using an LTE diffusive boundary condition at the inner point of the computational grid does not provide a consistent description of the radiation field and may lead to non-realistic synthetic spectra. Observationally this can be seen in the red and infrared wavelength bands where the spectral slope of typical SN Ia spectra deviates significantly from a thermal continuum. The assumption of such a thermal continuum in radiative transfer models generally results in an overestimate of the radiation flux in those wavelengths. We have developed a theoretical framework to eliminate some of the restrictions that are imposed by the assumption of LTE conditions.

With the formalism discussed in this work we are able to self-consistently derive the isotropic term of the boundary condition. Only the flux term has to be specified analytically by taking the physical conditions in the photospheric region into account. Of course, removing constraints in the boundary conditions may cause the system to become numerically less stable. For this reason the consistency of the solution is much more important than in the classical case where the explicit specification of the Planck-function forces the system into LTE-conditions naturally.

Our modifications to the LTE-diffusion approximation have been derived in a very general way. Therefore, this formalism can also be applied to other objects (such as Wolf-Rayet stars with very extended atmospheres) where the physical conditions are such that the assumption of LTE at the photosphere is not justified.

The comparison of the synthetic spectrum from a SN Ia test model to an observed SN Ia spectrum shows that the overall shape and prominent features of observed SN Ia are well reproduced by the model. A more detailed analysis of observed spectra will be the subject of forthcoming publications.

Late epochs of SN Ia have not been considered here in more detail because the energy deposition by $\gamma $-photons above the photosphere has not yet been fully implemented in our code. The description developed here nevertheless provides a basis for a reliable implementation of this energy deposition, since even if a fraction of the radiative energy is created above the photosphere the remaining radiation has to originate from below the computational grid. However, given that the photospheric conditions are such that thermalization occurs only partially, it is impossible that the energy deposited in the outer ejecta will be completely thermalized. Instead, excitation and ionization by fast electrons and $\gamma $-photons above the photosphere may provide a non-thermal contribution to the spectrum. This might already be an issue even for epochs around maximum, as recent three-dimensional explosion models indicate extensive mixing of \ensuremath{^{56}{\rm Ni}} into the outer layers of the ejecta.

Furthermore, to derive a model with a luminosity that is consistently determined from the \ensuremath{^{56}{\rm Ni}} distribution of an explosion model, the time-dependent effects of photon trapping in earlier epochs have to be incorporated into the boundary luminosity (Nugent et al. 1997; Höflich & Khokhlov 1996; Arnett 1982).

Acknowledgements
This work was supported in part by the Sonderforschungsbereich 375 of the Deutsche Forschungsgemeinschaft, DFG, the European Union's Human Potential Programme "Gamma-Ray Bursts: An Enigma and a Tool'', under contract HPRN-CT-2002-00294, and the National Science Foundation under Grant No. PHY99-07949. D. N. S. thanks the Kavli Institute for Theoretical Physics at the University of California, Santa Barbara for its hospitality during the program on "The Supernova Gamma-Ray Burst Connection''. We also want to thank our colleague Wolfgang Hillebrandt for helpful discussions and his support during the course of this work.

References

 
Copyright ESO 2006