A&A 459, 297-305 (2006)
DOI: 10.1051/0004-6361:20065718
Rotational excitation of SiO by collisions with helium
F. Dayou
-
C. Balança
Laboratoire d'Étude du Rayonnement et de la Matière en Astrophysique,
UMR 8112 du CNRS, Observatoire de Paris-Meudon, 5 place Jules Janssen, 92195 Meudon Cedex, France
Received 29 May 2006 / Accepted 4 July 2006
Abstract
Context. Within shocked regions of the interstellar medium and circumstellar environment of AGB stars the proper modelling of SiO line emission through non-LTE radiative transfer calculations requires accurate values of collisional rate coefficients.
Aims. The present study focuses on the transitions among the rotational levels of the SiO molecule in its ground vibrational state induced by collision with He. The H2 molecule being the main colliding partner for the astrophysical regions of interest, the collisional process between SiO and para-H2(j=0) is also investigated in an approximated way.
Methods. A new 2D SiO-He potential energy surface is computed by means of highly correlated ab initio calculations. Collisional rate coefficients corresponding to the pure rotational (de)excitation of SiO by collision with He are obtained from close-coupling quantum scattering calculations of inelastic cross sections. The SiO-He potential energy surface is also employed to compute rate coefficients for the rotational (de)excitation of SiO by collision with para-H2(j=0).
Results. Rate coefficients for rotational levels up to j=26 and kinetic temperatures in the range 10-300 K are obtained for the SiO-He colliding system. The large asymmetry of the SiO-He potential energy surface induces a propensity rule that favours odd  transitions over even
transitions over even  .
The estimated values of the SiO-para-H2(j=0) rate coefficients are compared with those of Turner et al. (1992) for the twenty first rotational levels. As a result of significant differences between the SiO-He interaction potentials employed in the two studies, the rate coefficients are found to differ by a factor 2.5-5 for the main rotational transitions, whatever the temperature range.
.
The estimated values of the SiO-para-H2(j=0) rate coefficients are compared with those of Turner et al. (1992) for the twenty first rotational levels. As a result of significant differences between the SiO-He interaction potentials employed in the two studies, the rate coefficients are found to differ by a factor 2.5-5 for the main rotational transitions, whatever the temperature range.
Key words: ISM: molecules - molecular processes - molecular data
The silicon monoxide (SiO) molecule was detected for the first time in the interstellar medium by Wilson et al. (1971) through the
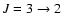 radio line emission from the galactic source Sagittarius B2, shortly after the first detection of the interstellar CO molecule (Wilson et al. 1970). Since then, SiO has been detected in a variety of astrophysical objects, and the modelling of observed molecular spectra showed that the SiO molecule, in contrast to CO, is mostly present in regions associated with warm, dense, and shocked gas. In quiescent cold clouds the SiO abundance is less than 10-12 relative to H2 (Ziurys et al. 1989), but it can increase by several orders of magnitude in high velocity molecular outflows from young stellar objects (Martin-Pintado et al. 1992; Acord et al. 1997; Codella et al. 1999; Nisini et al. 2002). To date, the most likely explanation of such an enhancement of the SiO abundance comes from the sputtering of dust grains in shocked regions and the subsequent release of Si-bearing material into the gas phase (Schilke et al. 1997; Jiménez-Serra et al. 2005; Flower & Pineau des Forets 1995; Dayou & Spielfiedel 2003; Le Picard et al. 2001). Rotational line emissions of SiO are thus currently used as tracers of shocked gas in molecular outflows surrounding low- and high-mass star-forming regions (Martin-Pintado et al. 1992; Gueth et al. 1998; Acord et al. 1997; Codella et al. 1999; Nisini et al. 2002), as well as shocked regions of galactic nuclei (Usero et al. 2006; Martin-Pintado et al. 1997). The fact that Si-bearing species probably are major components of dust grains for an oxygen-rich composition of the gas (Jeong et al. 1999) also makes SiO very useful for gaining information about the formation and evolution of dust grains. SiO radio line emissions detected towards outer atmospheres and circumstellar envelopes (CSE's) of Asymptotic Giant Branch (AGB) stars, especially M-type stars (
radio line emission from the galactic source Sagittarius B2, shortly after the first detection of the interstellar CO molecule (Wilson et al. 1970). Since then, SiO has been detected in a variety of astrophysical objects, and the modelling of observed molecular spectra showed that the SiO molecule, in contrast to CO, is mostly present in regions associated with warm, dense, and shocked gas. In quiescent cold clouds the SiO abundance is less than 10-12 relative to H2 (Ziurys et al. 1989), but it can increase by several orders of magnitude in high velocity molecular outflows from young stellar objects (Martin-Pintado et al. 1992; Acord et al. 1997; Codella et al. 1999; Nisini et al. 2002). To date, the most likely explanation of such an enhancement of the SiO abundance comes from the sputtering of dust grains in shocked regions and the subsequent release of Si-bearing material into the gas phase (Schilke et al. 1997; Jiménez-Serra et al. 2005; Flower & Pineau des Forets 1995; Dayou & Spielfiedel 2003; Le Picard et al. 2001). Rotational line emissions of SiO are thus currently used as tracers of shocked gas in molecular outflows surrounding low- and high-mass star-forming regions (Martin-Pintado et al. 1992; Gueth et al. 1998; Acord et al. 1997; Codella et al. 1999; Nisini et al. 2002), as well as shocked regions of galactic nuclei (Usero et al. 2006; Martin-Pintado et al. 1997). The fact that Si-bearing species probably are major components of dust grains for an oxygen-rich composition of the gas (Jeong et al. 1999) also makes SiO very useful for gaining information about the formation and evolution of dust grains. SiO radio line emissions detected towards outer atmospheres and circumstellar envelopes (CSE's) of Asymptotic Giant Branch (AGB) stars, especially M-type stars ( ), are thus employed as a probe of circumstellar dust formation and dynamics (González Delgado et al. 2003; Schöier et al. 2004; Bieging et al. 2000), shedding light on the mechanisms responsible for the mass-loss of AGB stars.
), are thus employed as a probe of circumstellar dust formation and dynamics (González Delgado et al. 2003; Schöier et al. 2004; Bieging et al. 2000), shedding light on the mechanisms responsible for the mass-loss of AGB stars.
Within shocked regions of the interstellar medium and circumstellar environment of AGB stars, the proper modelling of SiO line emission through non-LTE radiative transfer calculations requires accurate values of collisional rate coefficients with H2, the most abundant molecule, and to a lesser extent with H and He. In most cases the observed SiO line emissions involve rotational transitions within the ground vibrational state of SiO, although vibrationally excited states of SiO may also have to be considered in the case of circumstellar SiO maser line emissions from evolved stars (Pardo et al. 1998; Chen et al. 2006; Herpin et al. 2006). Pure rotational excitation rate coefficients for SiO in collision with para-H2(j=0) were calculated by Turner et al. (1992) in the temperature range
20-300 K for rotational levels up to j=20. The latter rate coefficients were calculated within the coupled-states approximation using a SiO-He potential energy surface (PES) that was obtained from an electron gas model (Bieniek & Green 1981). Although the coupled-states approximation may provide reliable results at moderate to high temperatures, the electron gas model is known to induce large inaccuracies in the PES and hence in the leading rate coefficients (Thomas et al. 1980). Moreover, the use of a SiO-He PES to approximate the SiO-H2 colliding system may also be a source of significant errors given the results obtained for systems such as CO (Wernli et al. 2006) and H2O (Phillips et al. 1996), for which both collision partners were considered.
The goal of the present work is to provide accurate rotational excitation rate coefficients for the SiO-He colliding system by means of highly correlated ab initio methods to compute the PES and close-coupling (CC) quantum scattering calculations. Since H2 is the main colliding partner within the astrophysical regions of interest, the SiO-He PES is also employed to provide estimated values of SiO-H2 collisional rate coefficients. Comparison with the results of Turner et al. (1992) obtained in the same way serves to probe the sensitivity of collisional rate coefficients on the description of the PES. As it will be shown below, quite important discrepancies are found between the two sets of rate coefficients. Hence the present results are thought to represent an important improvement and should be relevant to the modelling of SiO line emission until the SiO-H2 colliding system is considered explicitly. This work represents a first step of a thorough theoretical study of ro-vibrational excitation rate coefficients of SiO by collision with He and, in the near future, with H2. This is motivated by the perspective of future observations of SiO line emission by the Herschel Space Observatory, which will acquire data from far-IR to submillimeter domains with both high resolution and sensitivity from a variety of astrophysical regions.
The paper is organised as follows. Details on the ab initio calculations, fitting procedure, and features of the resulting SiO-He PES are given in Sect. 2. The collisions dynamics calculations are described in Sect. 3. Section 4 is devoted to the results obtained for the SiO-He collisional cross sections and rate coefficients, and the approximated SiO-H2 rate coefficients are compared to those of Turner et al. (1992).
The two interacting species are taken in their ground electronic states SiO
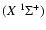 and He
and He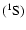 .
The SiO-He interaction potential is expressed in Jacobi coordinates
.
The SiO-He interaction potential is expressed in Jacobi coordinates
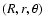 where R is the distance between the SiO centre of mass and the He atom, r is the SiO bond length, and
where R is the distance between the SiO centre of mass and the He atom, r is the SiO bond length, and 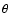 is the angle between the two distance vectors oriented such that
is the angle between the two distance vectors oriented such that
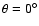 holds for He approaching the O-side of the SiO molecule. In the present work the SiO bond length is held fixed at its equilibrium value
holds for He approaching the O-side of the SiO molecule. In the present work the SiO bond length is held fixed at its equilibrium value
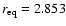 bohr (Huber & Herzberg 1979). A proper description of the van der Waals interaction potential for the SiO-He closed-shell system demands the use of highly correlated electronic calculations. This is needed to properly describe the balance between the short-range repulsion and the attractive long-range dispersion energies. To this aim we performed ab initio calculations in the supermolecular approach using the coupled-cluster method at the RCCSD(T) level of theory (Watts et al. 1993). The basis sets employed to describe the Si, O, and He atoms consisted of the standard aug-cc-pVQZ basis sets (Woon & Dunning 1994; Dunning 1989; Woon & Dunning 1993; Kendall et al. 1992). Added to this set, the
bohr (Huber & Herzberg 1979). A proper description of the van der Waals interaction potential for the SiO-He closed-shell system demands the use of highly correlated electronic calculations. This is needed to properly describe the balance between the short-range repulsion and the attractive long-range dispersion energies. To this aim we performed ab initio calculations in the supermolecular approach using the coupled-cluster method at the RCCSD(T) level of theory (Watts et al. 1993). The basis sets employed to describe the Si, O, and He atoms consisted of the standard aug-cc-pVQZ basis sets (Woon & Dunning 1994; Dunning 1989; Woon & Dunning 1993; Kendall et al. 1992). Added to this set, the
![$\rm [3s2p2d1f1g]$](/articles/aa/full/2006/43/aa5718-06/img16.gif) bond functions optimised by Cybulski & Toczylowski (1999) were placed at the midpoint between the He atom and the SiO centre of mass. At each geometry the calculated energy
bond functions optimised by Cybulski & Toczylowski (1999) were placed at the midpoint between the He atom and the SiO centre of mass. At each geometry the calculated energy
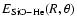 was corrected for the basis set superposition error (BSSE) using the Boys & Bernardi (1970) counterpoise procedure:
was corrected for the basis set superposition error (BSSE) using the Boys & Bernardi (1970) counterpoise procedure:
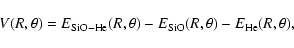 |
(1) |
where the SiO and He subsystems are computed with the SiO-He basis set. Additional calculations of
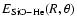 at a large number of
at a large number of
 geometries were performed using the multiconfigurational CASSCF approach (Werner & Knowles 1985; Knowles & Werner 1985). The weight associated with the closed-shell electronic configuration used as a reference in the coupled-cluster calculations was found to be by far the dominant one (the weight at least equals 0.94 for all studied geometries). Under such circumstances, and owing to the rather extended basis sets used in the present work, the coupled-cluster approach is expected to yield reliable results for the SiO-He interaction potential. All ab initio calculations have been carried out with the MOLPRO (Werner et al. 2003) suite of programs.
geometries were performed using the multiconfigurational CASSCF approach (Werner & Knowles 1985; Knowles & Werner 1985). The weight associated with the closed-shell electronic configuration used as a reference in the coupled-cluster calculations was found to be by far the dominant one (the weight at least equals 0.94 for all studied geometries). Under such circumstances, and owing to the rather extended basis sets used in the present work, the coupled-cluster approach is expected to yield reliable results for the SiO-He interaction potential. All ab initio calculations have been carried out with the MOLPRO (Werner et al. 2003) suite of programs.
Using the computational scheme described above, a total of 640 geometries were computed for the SiO-He system. The radial scattering coordinate R ranged from 4 to 16 bohr by steps of 0.25 bohr, and the angle 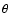 varied from
varied from 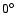 to
to
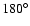 by steps of
by steps of
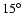 .
At a short atom-diatom separation, additional geometries were computed in such a way that the interaction energy becomes at least 3500 cm-1 at any angle.
.
At a short atom-diatom separation, additional geometries were computed in such a way that the interaction energy becomes at least 3500 cm-1 at any angle.
An analytic representation of the two-dimensional interaction potential
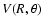 ,
suitable for use in dynamics calculations, was constructed following the method developed by Werner et al. (1989). At each computed angle
,
suitable for use in dynamics calculations, was constructed following the method developed by Werner et al. (1989). At each computed angle 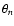 the R-dependent potentials
the R-dependent potentials
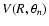 were fitted to the form:
were fitted to the form:
![$\displaystyle B_n(R)= \exp\left(-a_n\ R\right)\ .\ \left[{\displaystyle\sum_{i=...
...tanh(R)\right]\ .\ \left[{\displaystyle\sum_{j=6,8}}\ c_n^{(j)}\ R^{-j}\right],$](/articles/aa/full/2006/43/aa5718-06/img26.gif) |
|
|
(2) |
where the first and second parts of Eq. (2) hold for the short- and long-range parts of the potential, respectively. For each of the angles 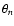 ,
a set of seven parameters was determined from the calculated interaction energies
,
a set of seven parameters was determined from the calculated interaction energies
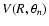 ,
leading to a global root-mean-square deviation between the fit and the whole set of ab initio points of 0.85 cm-1 (the mean relative error is 0.07
,
leading to a global root-mean-square deviation between the fit and the whole set of ab initio points of 0.85 cm-1 (the mean relative error is 0.07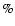 with a largest deviation of 0.54
with a largest deviation of 0.54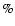 ). The one-dimensional functions Bn(R) were then used to express the analytic interaction potential
). The one-dimensional functions Bn(R) were then used to express the analytic interaction potential
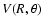 as an expansion into a basis of Legendre polynomials up to
as an expansion into a basis of Legendre polynomials up to
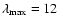 :
:
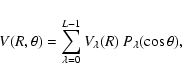 |
(3) |
where L=13 is the number of computed angle values and
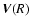 is a vector column obtained from
is a vector column obtained from
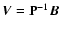 ,
with matrix elements of
P given by
,
with matrix elements of
P given by
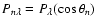 .
.
As a check of our fitting procedure, the ab initio points were interpolated along the angular coordinate to generate an additional PES expressed onto 25 angle values. The latter PES was then fitted using the polynomial expansion of Eq. (3) up to
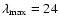 .
For
.
For 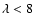 the resulting anisotropic terms
the resulting anisotropic terms
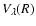 were found to be almost identical to those obtained from the ab initio PES defined onto 13 angle values. For the higher order components, discrepancies appear only at short R values, i.e. within classically forbidden regions of the PES. Such a check pointed out that our ab initio PES defined onto 13 angle values was sufficient to properly describe the anisotropy of the SiO-He interaction potential.
were found to be almost identical to those obtained from the ab initio PES defined onto 13 angle values. For the higher order components, discrepancies appear only at short R values, i.e. within classically forbidden regions of the PES. Such a check pointed out that our ab initio PES defined onto 13 angle values was sufficient to properly describe the anisotropy of the SiO-He interaction potential.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{5718fig1}
\end{figure}](/articles/aa/full/2006/43/aa5718-06/Timg35.gif) |
Figure 1:
Contour plot of the analytical ground PES of the SiO-He system obtained from the present ab initio calculations, as a function of Jacobi coordinates R and 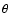 .
The SiO bond length is held fixed to .
The SiO bond length is held fixed to
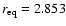 bohr. Contours are drawn in steps of 1 cm-1 with a maximum energy of 0 cm-1.
bohr. Contours are drawn in steps of 1 cm-1 with a maximum energy of 0 cm-1. |
| Open with DEXTER |
A contour plot of the analytical PES
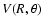 is shown in Fig. 1 as a function of Jacobi coordinates R and
is shown in Fig. 1 as a function of Jacobi coordinates R and 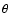 for the SiO bond length kept fixed at
for the SiO bond length kept fixed at
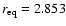 bohr. The interaction potential is found to be highly anisotropic, with both long- and short-range interactions weaker for the perpendicular approach (
bohr. The interaction potential is found to be highly anisotropic, with both long- and short-range interactions weaker for the perpendicular approach (
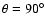 )
of the He atom toward the SiO molecule than for collinear approaches (
)
of the He atom toward the SiO molecule than for collinear approaches (
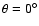 and
and
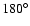 ). The linear He-OSi geometry (
). The linear He-OSi geometry (
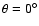 )
is found to be favoured over the linear He-SiO (
)
is found to be favoured over the linear He-SiO (
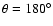 ), due to weaker short-range interactions as He approaches the O-side of the SiO molecule. Such features result in a global minimum for the PES at the linear He-OSi geometry (and R=7.993 bohr) and an associated well depth
), due to weaker short-range interactions as He approaches the O-side of the SiO molecule. Such features result in a global minimum for the PES at the linear He-OSi geometry (and R=7.993 bohr) and an associated well depth
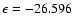 cm-1.
cm-1.
The main features of the PES described above are consistent with what one might expect from the features associated with the polarizability of the SiO molecule (
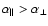 )
and with the polarizabilities of the Si and O atoms (
)
and with the polarizabilities of the Si and O atoms (
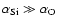 ). As a check, the SiO-He PES was also computed by means of an empirical model developed by Pirani et al. (2001) and further extended by Bartolomei et al. (2006) to account for heteronuclear diatoms. The resulting
PES
). As a check, the SiO-He PES was also computed by means of an empirical model developed by Pirani et al. (2001) and further extended by Bartolomei et al. (2006) to account for heteronuclear diatoms. The resulting
PES![[*]](/icons/foot_motif.gif) qualitatively reproduces the main features of our ab initio PES. The empirical model told us that the location of the global minimum at
qualitatively reproduces the main features of our ab initio PES. The empirical model told us that the location of the global minimum at
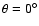 is mainly due to a combination of dipole-induced dipole and (dipole, quadrupole)-induced dipole interactions that favour the linear He-OSi geometry over the other ones. From the empirical PES a global minimum of a depth
is mainly due to a combination of dipole-induced dipole and (dipole, quadrupole)-induced dipole interactions that favour the linear He-OSi geometry over the other ones. From the empirical PES a global minimum of a depth
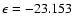 cm-1 is found at
cm-1 is found at
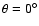 (and R=7.667 bohr), which is in quite good agreement with the results obtained from our ab initio PES.
(and R=7.667 bohr), which is in quite good agreement with the results obtained from our ab initio PES.
A comparison can be made with the SiO-He PES computed by Bieniek & Green (1981) using the electron-gas method (Gordon & Kim 1972) and an analytic form for long-range interactions. The PES was originally fitted (FIT1) with the aim of calculating ro-vibrational excitation rate coefficients at high temperatures and was not expressed in terms of a Legendre polynomial expansion. A second analytical fit (FIT2) to the energy points of Bieniek and Green (BK) was obtained by Sisak & Secrest (1991) to compute rotational excitation cross sections at low collision energies, using a Legendre polynomial expansion up to
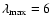 .
The rotational excitation rate coefficients calculated by Turner et al. (1992) were obtained from a third fit, with an interpolation procedure for the angular coordinate that allowed them to express the PES in terms of a Legendre polynomial expansion up to
.
The rotational excitation rate coefficients calculated by Turner et al. (1992) were obtained from a third fit, with an interpolation procedure for the angular coordinate that allowed them to express the PES in terms of a Legendre polynomial expansion up to
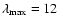 .
Details on the latter PES were not published, but it is believed to be rather similar to FIT2. We report in Fig. 2 cuts of the two available BK PESs at given values of the Jacobi angle
.
Details on the latter PES were not published, but it is believed to be rather similar to FIT2. We report in Fig. 2 cuts of the two available BK PESs at given values of the Jacobi angle 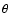 ,
together with the result of the present ab initio calculations. It is readily seen that both BK PESs are markedly different from the ab initio one. At whatever geometry, they show potential wells deeper by at least a factor of 2 and shifted to shorter R values compared to the ab initio PES. Moreover, the global minima associated with the PESs FIT1 and FIT2 are found at
,
together with the result of the present ab initio calculations. It is readily seen that both BK PESs are markedly different from the ab initio one. At whatever geometry, they show potential wells deeper by at least a factor of 2 and shifted to shorter R values compared to the ab initio PES. Moreover, the global minima associated with the PESs FIT1 and FIT2 are found at
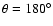 (
(
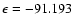 cm-1) and
cm-1) and
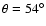 (
(
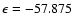 cm-1), respectively, in direct contrast to the global minimum found at
cm-1), respectively, in direct contrast to the global minimum found at
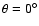 for both the ab initio and empirical PESs.
for both the ab initio and empirical PESs.
To assess the main features of the SiO-He PES likely to influence the scattering processes we report in Fig. 3 the first four radial terms
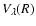 of Eq. (3) associated with the ab initio PES together with the results obtained by Sisak & Secrest (1991). One has to recall that the isotropic component
of Eq. (3) associated with the ab initio PES together with the results obtained by Sisak & Secrest (1991). One has to recall that the isotropic component  only contributes to the elastic scattering process. Moreover, each
only contributes to the elastic scattering process. Moreover, each
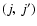 pair of states characterised by even (or odd)
pair of states characterised by even (or odd)
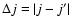 values are directly coupled by even (or odd)
values are directly coupled by even (or odd)
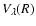 terms which verify
terms which verify
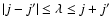 .
For each
.
For each  inelastic transition, the remaining
inelastic transition, the remaining
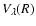 terms contribute through indirect coupling with other rotational states. The isotropic term V0 depicted in Fig. 3 is found to be much less attractive for the ab initio PES compared to the BK PES, with a repulsive wall displaced toward larger R values. A similar trend is found for the anisotropic V2 term. By contrast, the anisotropic terms V1 and V3 are found much more attractive for the ab initio PES than for the BK PES, with a repulsive wall slightly displaced toward shorter R values. The higher order components
terms contribute through indirect coupling with other rotational states. The isotropic term V0 depicted in Fig. 3 is found to be much less attractive for the ab initio PES compared to the BK PES, with a repulsive wall displaced toward larger R values. A similar trend is found for the anisotropic V2 term. By contrast, the anisotropic terms V1 and V3 are found much more attractive for the ab initio PES than for the BK PES, with a repulsive wall slightly displaced toward shorter R values. The higher order components
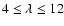 associated with the ab initio PES are mainly repulsive terms and their magnitudes rapidly decrease as
associated with the ab initio PES are mainly repulsive terms and their magnitudes rapidly decrease as 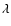 increases. No significant differences are found between the ab initio and BK PESs for the components
increases. No significant differences are found between the ab initio and BK PESs for the components
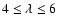 .
However, the large differences found between the two PESs on the isotropic component
.
However, the large differences found between the two PESs on the isotropic component 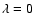 and the main anisotropic components
and the main anisotropic components
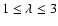 are expected to yield inelastic cross sections, and hence rate coefficients, that are significantly different. This will be discussed in the next sections.
are expected to yield inelastic cross sections, and hence rate coefficients, that are significantly different. This will be discussed in the next sections.
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{5718fig4}
\end{figure}](/articles/aa/full/2006/43/aa5718-06/Timg61.gif) |
Figure 4:
Rotational de-excitation and excitation cross sections ( upper and lower panel, respectively) of the SiO molecule in collision with He as a function of the relative kinetic energy. A logarithmic scale is used for both axes. Bold lines: odd
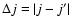 inelastic transitions; thin lines: even
inelastic transitions; thin lines: even
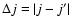 inelastic transitions.
inelastic transitions. |
| Open with DEXTER |
The analytic SiO-He interaction potential fitted to the ab initio points was used to perform CC calculations of the rotational excitation and de-excitation cross sections using the MOLSCAT code (Hutson & Green 1994). The
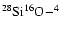 He system was considered (
He system was considered (
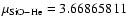 a.m.u.). The rotational energy levels were described using a
set of Dunham ro-vibrational constants (Lovas et al. 1981) that were fitted to experimental line frequencies. The coupled-channel Schrödinger equations were solved using the
diabatic modified log-derivative method of Manolopoulos (1986). Terms up to
a.m.u.). The rotational energy levels were described using a
set of Dunham ro-vibrational constants (Lovas et al. 1981) that were fitted to experimental line frequencies. The coupled-channel Schrödinger equations were solved using the
diabatic modified log-derivative method of Manolopoulos (1986). Terms up to
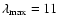 were retained in the Legendre polynomial expansion of the potential defined by
Eq. (3), and a 13 point Gauss-Legendre quadrature was used to obtain the radial expansion coefficients
were retained in the Legendre polynomial expansion of the potential defined by
Eq. (3), and a 13 point Gauss-Legendre quadrature was used to obtain the radial expansion coefficients
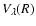 .
The minimum propagation distance was held fixed at about 5 bohr for low energies (typically 100 cm-1), whereas an automatic search of this parameter was used at higher energies with the criterion that the wavefunction amplitude should be less than 10-9 in all channels at the starting point. The minimum value of the maximum propagation distance was set to 40 bohr, and this value was increased when necessary according to the location of the outer classical turning point on the centrifugal energy barrier. The maximum value of the total angular momentum J used in the calculations was chosen according to a convergence criterion of 0.005
.
The minimum propagation distance was held fixed at about 5 bohr for low energies (typically 100 cm-1), whereas an automatic search of this parameter was used at higher energies with the criterion that the wavefunction amplitude should be less than 10-9 in all channels at the starting point. The minimum value of the maximum propagation distance was set to 40 bohr, and this value was increased when necessary according to the location of the outer classical turning point on the centrifugal energy barrier. The maximum value of the total angular momentum J used in the calculations was chosen according to a convergence criterion of 0.005 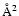 on the inelastic cross sections value. CC calculations were carried out for total energies ranging from the first excited rotational energy level up to 3000 cm-1. Owing to the relatively low value of the SiO rotational constant (
Bv=0=0.724 cm-1), a large number of rotational levels had to be included in the basis set to ensure convergence of the inelastic cross sections. The size of the basis set varied from
on the inelastic cross sections value. CC calculations were carried out for total energies ranging from the first excited rotational energy level up to 3000 cm-1. Owing to the relatively low value of the SiO rotational constant (
Bv=0=0.724 cm-1), a large number of rotational levels had to be included in the basis set to ensure convergence of the inelastic cross sections. The size of the basis set varied from
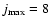 up to
up to
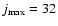 according to the range of energies studied. Test calculations were performed over the whole range of energies to check that the chosen propagation parameters and basis set size ensure an accuracy of about 1
according to the range of energies studied. Test calculations were performed over the whole range of energies to check that the chosen propagation parameters and basis set size ensure an accuracy of about 1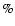 for the inelastic cross sections values.
for the inelastic cross sections values.
Using the computational scheme described above, inelastic cross sections associated with a transition from an initial rotational state j to a final state
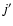 were obtained at each kinetic energy Ek from (Arthurs & Dalgarno 1963):
were obtained at each kinetic energy Ek from (Arthurs & Dalgarno 1963):
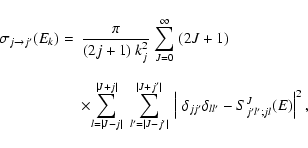 |
(4) |
where J and l are the total and orbital angular momentum quantum numbers respectively, E is the total energy, and
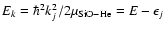 ,
where
,
where
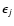 is the rotational energy level of the initial j state. From the rotational excitation cross sections
is the rotational energy level of the initial j state. From the rotational excitation cross sections
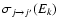 ,
one obtains the rotational excitation rate coefficient at a temperature T by performing a Boltzmann thermal average of the cross sections:
,
one obtains the rotational excitation rate coefficient at a temperature T by performing a Boltzmann thermal average of the cross sections:
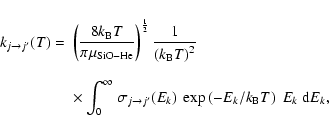 |
(5) |
where 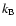 is the Boltzmann constant. The numerical integration over the collision energies was performed using a Simpson rule. Care was taken to span the energy range with a step size low enough to account for resonance structures in the cross sections. To this aim the energy step size was progressively increased from
0.05 to 1 cm-1 for total energies from 1.4 up to 850 cm-1, from 2 to 50 cm-1 for energies up to 2000 cm-1, and then set equal to 500 cm-1 for energies up to 3000 cm-1. Such an energy range was found large enough to calculate rotational excitation rate coefficients up to 300 K for rotational levels up to j=26, the highest energy point for each transition being at least at the threshold energy plus 12 kT. The rotational excitation rate coefficients
is the Boltzmann constant. The numerical integration over the collision energies was performed using a Simpson rule. Care was taken to span the energy range with a step size low enough to account for resonance structures in the cross sections. To this aim the energy step size was progressively increased from
0.05 to 1 cm-1 for total energies from 1.4 up to 850 cm-1, from 2 to 50 cm-1 for energies up to 2000 cm-1, and then set equal to 500 cm-1 for energies up to 3000 cm-1. Such an energy range was found large enough to calculate rotational excitation rate coefficients up to 300 K for rotational levels up to j=26, the highest energy point for each transition being at least at the threshold energy plus 12 kT. The rotational excitation rate coefficients
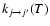 obtained from Eq. (5) can then be used to compute the de-excitation rate coefficients
obtained from Eq. (5) can then be used to compute the de-excitation rate coefficients
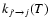 from the detailed balance:
from the detailed balance:
![\begin{displaymath}k_{j^{\prime}\rightarrow j}(T)=\frac{\left(2j+1\right)}{\left...
...ime}}\right)/k_{\rm B}T\right]
k_{j\rightarrow j^{\prime}}(T).
\end{displaymath}](/articles/aa/full/2006/43/aa5718-06/img77.gif) |
(6) |
The de-excitation rate coefficients obtained from the de-excitation cross sections by means of Eq. (5) were used as a check of our numerical integration procedure.
We report in Fig. 4 the de-excitation and excitation cross sections obtained from the present CC calculations for a few selected rotational levels of the SiO molecule. The de-excitation cross sections are almost decreasing functions of collision energies Ek. Interestingly, the present SiO-He PES leads to
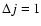 and
and
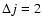 de-excitation cross sections that behave roughly like
Ek-1/2 and
Ek-1/6, respectively, at high collision energies. For collision energies below 30 cm-1 many resonances are found in the de-excitation cross sections. This relates to the presence of an attractive potential well, of a depth of
de-excitation cross sections that behave roughly like
Ek-1/2 and
Ek-1/6, respectively, at high collision energies. For collision energies below 30 cm-1 many resonances are found in the de-excitation cross sections. This relates to the presence of an attractive potential well, of a depth of
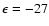 cm-1 at the linear He-OSi geometry, which allows the He atom to be temporarily trapped into the well and hence quasibound states to be formed before the complex dissociates (Smith et al. 1979; Christoffel & Bowman 1983). Quasibound states may arise from tunneling through the centrifugal energy barrier (shape resonances) or they may form through excitation of the molecule to an asymptotically closed channel where the complex is still temporarily trapped before it de-excites to open channels (Feshbach resonances). Owing to the rather small energy spacing between the SiO rotational levels with respect to the potential well depth, both types of resonance may be found in the same energy range. This was confirmed on selected transitions by strong changes in the resonance structure when the basis set size or the rotational energy spacing are modified in the scattering calculations.
cm-1 at the linear He-OSi geometry, which allows the He atom to be temporarily trapped into the well and hence quasibound states to be formed before the complex dissociates (Smith et al. 1979; Christoffel & Bowman 1983). Quasibound states may arise from tunneling through the centrifugal energy barrier (shape resonances) or they may form through excitation of the molecule to an asymptotically closed channel where the complex is still temporarily trapped before it de-excites to open channels (Feshbach resonances). Owing to the rather small energy spacing between the SiO rotational levels with respect to the potential well depth, both types of resonance may be found in the same energy range. This was confirmed on selected transitions by strong changes in the resonance structure when the basis set size or the rotational energy spacing are modified in the scattering calculations.
The de-excitation cross sections shown in Fig. 4 exhibit further interesting features that have important consequences on the magnitude of rotational de-excitation rate coefficients: (i) for a given initial j state the de-excitation cross sections decrease on increasing  ,
with propensity rules giving rise to odd
,
with propensity rules giving rise to odd  cross sections larger than even
cross sections larger than even  cross sections; (ii) for a given
cross sections; (ii) for a given  the de-excitation cross sections increase with j, the effect being more pronounced for low j values. The features described above follow the trend suggested by the anisotropic terms
the de-excitation cross sections increase with j, the effect being more pronounced for low j values. The features described above follow the trend suggested by the anisotropic terms
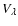 ,
which couple directly each
,
which couple directly each
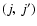 pair of states: (i) for a given initial j state the order
pair of states: (i) for a given initial j state the order 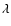 increases with
increases with  and the magnitude of
and the magnitude of
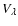 terms decreases on increasing
terms decreases on increasing 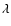 for the classically allowed regions of the PES. This may explain the rapidly diminished coupling between the rotational states as
for the classically allowed regions of the PES. This may explain the rapidly diminished coupling between the rotational states as  increases. The propensity rule observed for odd and even
increases. The propensity rule observed for odd and even  cross sections is probably due to the large well depths associated with the V1 and V3 terms (see Fig. 3) that favour odd
cross sections is probably due to the large well depths associated with the V1 and V3 terms (see Fig. 3) that favour odd  transitions over even ones. Interestingly, the propensity rule is still observed up to
transitions over even ones. Interestingly, the propensity rule is still observed up to
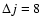 ,
i.e., for rotational transitions where the V1 and V3 terms only contribute through indirect coupling with other rotational states. (ii) For a given value of
,
i.e., for rotational transitions where the V1 and V3 terms only contribute through indirect coupling with other rotational states. (ii) For a given value of  the number of
the number of
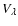 terms involved increases with j, which may yield a stronger coupling between the rotational states. The latter effect becomes rapidly saturated with j due to the decreasing magnitude of
terms involved increases with j, which may yield a stronger coupling between the rotational states. The latter effect becomes rapidly saturated with j due to the decreasing magnitude of
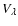 terms as
terms as 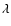 increases.
increases.
The features shown by excitation cross sections in Fig. 4 can be understood from the detailed balance:
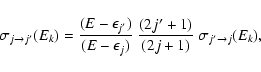 |
(7) |
which relates excitation and de-excitation cross sections. For the relatively low j and  values considered in Fig. 4 the energy factor
values considered in Fig. 4 the energy factor
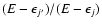 ,
responsible for the shape of excitation cross sections above energy thresholds, rapidly goes to 1 with increasing energy. Hence the main contribution to the observed features of excitation cross sections with respect to de-excitation ones comes from the degeneracy factor
,
responsible for the shape of excitation cross sections above energy thresholds, rapidly goes to 1 with increasing energy. Hence the main contribution to the observed features of excitation cross sections with respect to de-excitation ones comes from the degeneracy factor
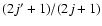 .
For a given initial j state it increases continuously with
.
For a given initial j state it increases continuously with  ,
while for a given
,
while for a given  it decreases with j.
it decreases with j.
The present results have been compared to inelastic cross section values reported by Sisak & Secrest (1991,1992) for selected transitions and given values of the total energy. The (de)excitation cross sections were computed by means of CC calculations using the PES of Bieniek & Green (1981). For collision energies above the well depths of both PESs, the comparison points out that the present ab initio SiO-He interaction potential leads to greater odd  cross sections than the BK PES (see Fig. 5). The enhancement is about 30
cross sections than the BK PES (see Fig. 5). The enhancement is about 30 for the
for the
 transition, 70
transition, 70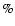 for the
for the
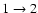 transition, and up to a factor of 3.5 for the
transition, and up to a factor of 3.5 for the
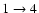 and
and
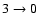 transitions (not shown in Fig. 5). By contrast, a decrease of the cross section by a factor close to 2.5 is observed for the
transitions (not shown in Fig. 5). By contrast, a decrease of the cross section by a factor close to 2.5 is observed for the
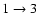 transition corresponding to an even
transition corresponding to an even  value. Consequently the two PESs yield opposite propensity rules for even and odd
value. Consequently the two PESs yield opposite propensity rules for even and odd  cross sections. In the present case the propensity rule
cross sections. In the present case the propensity rule
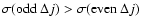 arises from the large asymmetry of the ab initio SiO-He interaction potential, leading to odd V1 and V3 anisotropic terms characterised by deep well depths. It is worth noticing that such an unusual propensity rule for rotational excitation cross sections has been already discussed by McCurdy & Miller (1977) in terms of model potentials, and that it has been observed experimentally (Carty et al. 2004) as well as from theoretical calculations (Cecchi-Pestellini et al. 2002) for the CO-He collision system.
arises from the large asymmetry of the ab initio SiO-He interaction potential, leading to odd V1 and V3 anisotropic terms characterised by deep well depths. It is worth noticing that such an unusual propensity rule for rotational excitation cross sections has been already discussed by McCurdy & Miller (1977) in terms of model potentials, and that it has been observed experimentally (Carty et al. 2004) as well as from theoretical calculations (Cecchi-Pestellini et al. 2002) for the CO-He collision system.
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{5718fig6}
\end{figure}](/articles/aa/full/2006/43/aa5718-06/Timg93.gif) |
Figure 6:
Rotational de-excitation rate coefficients of the SiO molecule in collision with He.
Upper-left panel: rate coefficients for SiO(j=6) as a function of
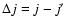 for several temperatures; upper-right panel: rate coefficients for SiO(j=2-6) and T=100 K as a function of
for several temperatures; upper-right panel: rate coefficients for SiO(j=2-6) and T=100 K as a function of  ;
lower panel: rate coefficients for SiO(j=1-6) as a function of temperature for ;
lower panel: rate coefficients for SiO(j=1-6) as a function of temperature for
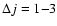 . . |
| Open with DEXTER |
The rotational excitation and de-excitation rate coefficients of SiO(j) in collision with He have been computed for rotational levels up to j=26 and kinetic temperatures up to 300 K through a Boltzmann thermal average of inelastic cross sections (Eq. (5)). We report in Fig. 6 the de-excitation rate coefficients as a function of
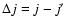 for selected transitions and temperatures. It is seen that: (i) for a given initial j state the de-excitation rate coefficients decrease with increasing
for selected transitions and temperatures. It is seen that: (i) for a given initial j state the de-excitation rate coefficients decrease with increasing  ,
with propensity rules giving rise to odd
,
with propensity rules giving rise to odd  rate coefficients larger than even
rate coefficients larger than even  ones; (ii) for a given
ones; (ii) for a given  the de-excitation rate coefficients increase with j, the effect being more pronounced for low j values. The features described above were expected from the results obtained for the de-excitation cross sections and discussed in the previous section.
the de-excitation rate coefficients increase with j, the effect being more pronounced for low j values. The features described above were expected from the results obtained for the de-excitation cross sections and discussed in the previous section.
Figure 6 also shows the variation of selected de-excitation rate coefficients with temperature. As can be seen the rate coefficients associated with a given value of  evolve in a similar fashion with temperature. This comes from the dominant contribution of the first anisotropic term
evolve in a similar fashion with temperature. This comes from the dominant contribution of the first anisotropic term
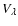 ,
with
,
with
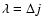 ,
specific to each
,
specific to each  inelastic transition. Furthermore,
inelastic transition. Furthermore,
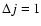 rate coefficients are almost constant over the whole temperature range. This is a direct consequence of the variation close to
Ek-1/2 of the associated de-excitation cross sections (the integral of Eq. (5) behaves like T3/2 in such a case). The rate coefficient corresponding to the
rate coefficients are almost constant over the whole temperature range. This is a direct consequence of the variation close to
Ek-1/2 of the associated de-excitation cross sections (the integral of Eq. (5) behaves like T3/2 in such a case). The rate coefficient corresponding to the
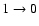 transition deviates from this rule. It rather behaves like T4/3 due to the steeper variation of its associated de-excitation cross section, close to
Ek-2/3. For
transition deviates from this rule. It rather behaves like T4/3 due to the steeper variation of its associated de-excitation cross section, close to
Ek-2/3. For
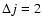 ,
the variation close to
Ek-1/6 of de-excitation cross sections at high collision energies produces an increase in the rate coefficient close to T1/3 above 100 K. The complete set of (de)excitation rate coefficients is available as on-line material from the BASECOL web site
,
the variation close to
Ek-1/6 of de-excitation cross sections at high collision energies produces an increase in the rate coefficient close to T1/3 above 100 K. The complete set of (de)excitation rate coefficients is available as on-line material from the BASECOL web site![[*]](/icons/foot_motif.gif) .
.
![\begin{figure}
\par\includegraphics[width=16.4cm,clip]{5718fig7}
\end{figure}](/articles/aa/full/2006/43/aa5718-06/Timg95.gif) |
Figure 7:
Estimated values of the rotational de-excitation rate coefficients of SiO(j) in collision with para-H2(j=0) obtained from: CC scattering calculations using the SiO-H2 reduced mass and the SiO-He ab initio PES (filled circles); SiO-He de-excitation rate coefficients corrected from the square root of the reduced mass ratio
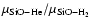 (dotted line); coupled-states scattering calculations of Turner et al. (1992) using the SiO-H2 reduced mass and the SiO-He PES of Bieniek & Green (1981) (empty circles).
(dotted line); coupled-states scattering calculations of Turner et al. (1992) using the SiO-H2 reduced mass and the SiO-He PES of Bieniek & Green (1981) (empty circles). |
| Open with DEXTER |
In the circumstellar environment of evolved stars and shocked regions of the interstellar medium, the relatively large abundance of H2 makes this species the main colliding partner for other molecules. The collisional rate coefficients corresponding to molecules in collision with H2 are thus needed to infer both the molecular abundances and physical conditions in these regions from the observed molecular spectra. Unless these rate coefficients are available, it is generally assumed (Schöier et al. 2005) that rate coefficients with He as a collision partner are likely to provide a first estimate of rate coefficients with para-H2(j=0). The underlying approximation is to consider identical cross section values for the two colliding systems, and then apply a scaling factor to the rate coefficients to correct for the associated different reduced masses. For a given molecule X, the scaling factor is
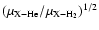 (see Eq. (5)) and equals about 1.4 if the molecule X is much heavier than He and H2. However, results on systems such as CO (Wernli et al. 2006) and H2O (Phillips et al. 1996), for which both collision partners were considered, pointed out that rate coefficients associated with p-H2(j=0) were within a factor of 1-3 larger than those with He depending on the selected transition. Another widely used approximation is to consider the interaction potential between a given molecule X and He identical to the one associated with p-H2(j=0), and then perform scattering calculations using the reduced mass
(see Eq. (5)) and equals about 1.4 if the molecule X is much heavier than He and H2. However, results on systems such as CO (Wernli et al. 2006) and H2O (Phillips et al. 1996), for which both collision partners were considered, pointed out that rate coefficients associated with p-H2(j=0) were within a factor of 1-3 larger than those with He depending on the selected transition. Another widely used approximation is to consider the interaction potential between a given molecule X and He identical to the one associated with p-H2(j=0), and then perform scattering calculations using the reduced mass
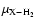 to get the associated rate coefficients. This was indeed the case for the SiO-H2 rate coefficients calculated by Turner et al. (1992) and currently used in radiative transfer modelling of interstellar regions. Thus, to probe the effect of the new SiO-He interaction potential on collisional rate coefficients, we employed the same approximation as Turner et al. (1992) to compute the SiO-H2 rate coefficients.
to get the associated rate coefficients. This was indeed the case for the SiO-H2 rate coefficients calculated by Turner et al. (1992) and currently used in radiative transfer modelling of interstellar regions. Thus, to probe the effect of the new SiO-He interaction potential on collisional rate coefficients, we employed the same approximation as Turner et al. (1992) to compute the SiO-H2 rate coefficients.
The scattering calculations were performed by means of the CC method. Similar basis sets and energy grid spacing as used before were employed for total energies up to 350 cm-1. For energies above 500 cm-1 we took advantage of the smooth variation of collisional cross sections (see Fig. 4) to use an energy grid spacing of 500 cm-1 up to 3000 cm-1. This allowed the determination of rate coefficients for the twenty first rotational energy levels up to 300 K. The dominant rate coefficients obtained from the two approximations described above are shown in Fig. 7, together with the results of Turner et al. (1992). As can be seen first, the scaled SiO-He rate coefficients compare rather well with our estimated values for the SiO-H2 collision system for low  transitions, the discrepancies being around 10
transitions, the discrepancies being around 10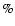 and 30
and 30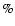 at high and low temperatures, respectively. Nevertheless, for higher
at high and low temperatures, respectively. Nevertheless, for higher  transitions the typical errors rise continuously, up to factors of 2 and 25 for
transitions the typical errors rise continuously, up to factors of 2 and 25 for
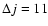 at high and low temperatures, respectively. This illustrates the role played by the reduced mass accounted for in collision dynamics calculations. On the other hand, the comparison between our rate coefficients and those of Turner et al. (1992) show quite important disagreements even for low
at high and low temperatures, respectively. This illustrates the role played by the reduced mass accounted for in collision dynamics calculations. On the other hand, the comparison between our rate coefficients and those of Turner et al. (1992) show quite important disagreements even for low  transitions: (i) for odd
transitions: (i) for odd  transitions our rate coefficients are larger than those of Turner et al. (1992) by about a factor of 5, up to an order of magnitude larger for high j levels at low temperatures; (ii) for even
transitions our rate coefficients are larger than those of Turner et al. (1992) by about a factor of 5, up to an order of magnitude larger for high j levels at low temperatures; (ii) for even  transitions our rates are smaller than those of Turner et al. (1992) by about a factor of 2.5 whatever the temperature; (iii) for higher
transitions our rates are smaller than those of Turner et al. (1992) by about a factor of 2.5 whatever the temperature; (iii) for higher  transitions (not shown here) the discrepancies can rise up to an order of magnitude even at high temperatures; (iv) the two sets of rate coefficients display opposite propensity rules for even and odd
transitions (not shown here) the discrepancies can rise up to an order of magnitude even at high temperatures; (iv) the two sets of rate coefficients display opposite propensity rules for even and odd  transitions.
transitions.
Such large differences may be attributed to several factors, the main one being the distinct SiO-He interaction potentials employed in dynamics calculations. Indeed, the SiO-He interaction potential of Bieniek & Green (1981) computed by means of an electron gas method has been found markedly different from the present ab initio SiO-He PES. It is worth mentioning that details of the SiO-He PES resulting from the fitting procedure of Turner et al. (1992) were not published. Nevertheless, the leading rate coefficients and cross section values of Sisak & Secrest (1991,1992) yield close differences when compared to our results (see end of Sect. 4.1). Thus the SiO-He PES employed by Turner et al. (1992) is thought to be almost similar to the one of Sisak & Secrest (1991,1992) discussed in Sect. 2. At low temperatures, the discrepancies between the two sets of rate coefficients may also be attributed both to the use of the coupled-states approximation in dynamics calculations and to the description of resonance structure in collisional cross sections.
We have to stress that the underlying approximation to the determination of our SiO-H2 collisional rate coefficients is identical to the one employed by Turner et al. (1992). Since accurate values for SiO-H2 rate coefficients are still lacking, the values of Turner et al. (1992) have been employed so far for the SiO line emission modelling of many astrophysical regions (see for instance Gibb et al. (2004); González Delgado et al. (2003) for the most recent studies). However, discrepancies as large as a factor of 2.5-5 between two sets of collisional rate coefficients for the main rotational transitions are expected to be relevant in radiative transfer modelling since they should strongly modify the estimated values of column density (Lique et al. 2006). Hence, although the present study focused on the determination of accurate rate coefficients for the SiO-He collision system, our estimated values for SiO-H2 are thought to be the most appropriate for an astrophysical purpose until the SiO-H2 colliding system be explicitly considered.
Inelastic cross sections corresponding to pure rotational (de)excitation of SiO by collision with He have been computed from CC quantum scattering calculations in the energy range 1.4-3000 cm-1, using a rotational basis set extending up to
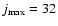 .
This allowed the determination of thermally averaged rate coefficients associated with transitions among the rotational levels of SiO up to j=26 for kinetic temperatures up to 300 K. A new 2D SiO-He PES was employed, computed by means of highly correlated ab initio calculations and extended basis sets. The overall features of the ab initio PES agree with the results of a new empirical model (Bartolomei et al. 2006), but differ significantly from those associated with the electron-gas PES of Bieniek & Green (1981). Particularly, the asymmetric character of the SiO-He PES is found to be much more pronounced in the ab initio case, leading to large odd anisotropic terms in the polynomial expansion of the PES. Consequently, the inelastic cross sections resulting from both PESs show opposite propensity rules for even and odd
.
This allowed the determination of thermally averaged rate coefficients associated with transitions among the rotational levels of SiO up to j=26 for kinetic temperatures up to 300 K. A new 2D SiO-He PES was employed, computed by means of highly correlated ab initio calculations and extended basis sets. The overall features of the ab initio PES agree with the results of a new empirical model (Bartolomei et al. 2006), but differ significantly from those associated with the electron-gas PES of Bieniek & Green (1981). Particularly, the asymmetric character of the SiO-He PES is found to be much more pronounced in the ab initio case, leading to large odd anisotropic terms in the polynomial expansion of the PES. Consequently, the inelastic cross sections resulting from both PESs show opposite propensity rules for even and odd  transitions and differ significantly in their magnitudes. In the present case, the inelastic cross sections as well as the leading rate coefficients are found to be larger for odd
transitions and differ significantly in their magnitudes. In the present case, the inelastic cross sections as well as the leading rate coefficients are found to be larger for odd  transitions than for even ones.
transitions than for even ones.
Additional calculations were performed using the SiO-He PES to compute approximated values of SiO-para-H2(j=0) collisional rate coefficients for rotational levels up to j=19 and kinetic temperatures up to 300 K. These rate coefficients have been compared first to the SiO-He rate coefficients scaled by a factor of 1.4 to account for the different reduced mass of the two colliding systems. Although the two sets of rate coefficients agree within 10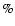 for low
for low  transitions at high temperatures, differences up to a factor of 2 are found for higher
transitions at high temperatures, differences up to a factor of 2 are found for higher  transitions, that rise up to an order of magnitude for both high
transitions, that rise up to an order of magnitude for both high  and low temperatures. Such a comparison allows us to assess the effect of the reduced mass on collision dynamics. Our calculated SiO-para-H2(j=0) collisional rate coefficients have been also compared to those of Turner et al. (1992) for which the SiO-He PES of Bieniek & Green (1981) was employed. In such a case quite important discrepancies are found even for low
and low temperatures. Such a comparison allows us to assess the effect of the reduced mass on collision dynamics. Our calculated SiO-para-H2(j=0) collisional rate coefficients have been also compared to those of Turner et al. (1992) for which the SiO-He PES of Bieniek & Green (1981) was employed. In such a case quite important discrepancies are found even for low  transitions and high temperatures. For odd
transitions and high temperatures. For odd  transitions our rate coefficients are larger by a factor of 5, while for even
transitions our rate coefficients are larger by a factor of 5, while for even  transitions they are found to be smaller by about a factor of 2.5. For higher
transitions they are found to be smaller by about a factor of 2.5. For higher  transitions or low temperatures the discrepancies can rise up to an order of magnitude. Since both sets of rate coefficients rest upon identical approximations, this illustrates the need for a proper description of the PES to achieve accurate values of collisional rate coefficients.
transitions or low temperatures the discrepancies can rise up to an order of magnitude. Since both sets of rate coefficients rest upon identical approximations, this illustrates the need for a proper description of the PES to achieve accurate values of collisional rate coefficients.
The quite large discrepancies found between our results and those of Turner et al. (1992) for the SiO-para-H2(j=0) colliding system may have an important impact on the diagnostic of column densities derived from SiO line modelling. Hence, given the improved accuracy of the present SiO-He PES, our collisional rate coefficient values are thought to be the most appropriate for an astrophysical purpose, until the SiO-H2 colliding system is explicitly considered. Indeed, results on systems such as CO (Wernli et al. 2006) and H2O (Phillips et al. 1996), for which both collision partners were considered, showed that the value of 1.4 assumed for the scaling factor of rates with He was in fact within a range 1-3. The sets of rotational (de)excitation rate coefficients for both the SiO-He and SiO-para-H2(j=0) colliding systems are available from the BASECOL web site![[*]](/icons/foot_motif.gif) . The range of higher temperatures (300-2000 K) is currently under investigation to provide the ro-vibrational rate coefficients needed, for instance, in the case of circumstellar SiO maser line emissions from evolved stars.
. The range of higher temperatures (300-2000 K) is currently under investigation to provide the ro-vibrational rate coefficients needed, for instance, in the case of circumstellar SiO maser line emissions from evolved stars.
Acknowledgements
The PES calculations were performed on the MPOPM cluster at the Paris-Meudon Observatory. Quantum scattering calculations were carried out at the IDRIS French national computing centre under project no. 060883. This work was supported by the EU FP6 Program "Molecular Universe''. We would like to acknowledge F. Lique, F. Daniel, and A. Spielfiedel for the very helpful discussions, as well as M. Bartolomei for his contribution to this work. We also acknowledge G. Dhont for providing us the fitting code employed in the present study.
- Acord, J. M.,
Walmsley, C. M., & Churchwell, E. 1997, ApJ, 475, 693 [NASA ADS] [CrossRef]
- Arthurs,
A. M., & Dalgarno, A. 1963, Proc. Roy. Soc. A, 256,
540 [NASA ADS] (In the text)
-
Bartolomei, M., Cappelletti, D., & Pirani, F. 2006, Private
Communication
(In the text)
- Bieging,
J. H., Shaked, S., & Gensheimer, P. D. 2000, ApJ,
543, 897 [NASA ADS] [CrossRef]
- Bieniek,
R. J., & Green, S. 1981, Chem. Phys. Lett., 84, 380 [NASA ADS] [CrossRef] (In the text)
- Boys, S. F.,
& Bernardi, F. 1970, Mol. Phys., 19, 553 [NASA ADS] [CrossRef] (In the text)
- Carty, D., Goddard,
A., Sims, I. R., & Smith, I. W. M. 2004,
J. Chem. Phys., 121, 4671 [NASA ADS] [CrossRef] (In the text)
-
Cecchi-Pestellini, C., Bodo, E., Balakrishnan, N., & Dalgarno,
A. 2002, ApJ, 571, 1015 [NASA ADS] [CrossRef] (In the text)
- Chen, X., Shen,
Z.-Q., Imai, H., & Kamohara, R. 2006, ApJ, 640, 982 [NASA ADS] [CrossRef]
-
Christoffel, K. M., & Bowman, J. M. 1983,
J. Chem. Phys., 78, 3952 [NASA ADS] [CrossRef]
- Codella, C.,
Bachiller, R., & Reipurth, B. 1999, A&A, 343, 585 [NASA ADS]
- Cybulski,
S. M., & Toczylowski, R. R. 1999,
J. Chem. Phys., 111, 10520 [NASA ADS] [CrossRef] (In the text)
- Dayou, F., &
Spielfiedel, A. 2003, J. Chem. Phys., 119, 4237 [NASA ADS] [CrossRef]
- Dunning,
T. H. 1989, J. Chem. Phys., 90, 1007 [NASA ADS] [CrossRef]
- Flower,
D. R., & Pineau des Forets, G. 1995, MNRAS, 275, 1049 [NASA ADS]
- Gibb, A. G.,
Richer, J. S., Chandler, C. J., & Davis, C. J.
2004, ApJ, 603, 198 [NASA ADS] [CrossRef]
- González
Delgado, D., Olofsson, H., Kerschbaum, F., et al. 2003,
A&A, 411, 123 [NASA ADS] [CrossRef] [EDP Sciences]
- Gordon,
R. G., & Kim, Y. S. 1972, J. Chem. Phys.,
56, 3122 [CrossRef] (In the text)
- Gueth, F.,
Guilloteau, S., & Bachiller, R. 1998, A&A, 333, 287 [NASA ADS]
- Herpin, F.,
Baudry, A., Thum, C., Morris, D., & Wiesemeyer, H. 2006,
A&A, 450, 667 [NASA ADS] [CrossRef] [EDP Sciences]
-
Honerjäger, R., & Tischer, R. 1974, Z. Nature A, 29,
1695
- Huber, K. P.,
& Herzberg, G. 1979, Constants of Diatomic Molecules
(New York: Van Nostrand Reinhold Co.)
(In the text)
- Hutson, J. M.,
& Green, S. 1994, MOLSCAT computer code version 14, distributed
by Collaborative Computational Project No. 6 of the Engineering and
Physical Sciences Research Council
(In the text)
- Jeong, K. S.,
Winters, J. M., & Sedlmayr, E. 1999, in IAU Symp., 191,
Asymptotic Giant Branch Stars, ed. T. Le Bertre,
A. Lebre, & C. Waelkens, 233
(In the text)
-
Jiménez-Serra, I., Martín-Pintado, J.,
Rodríguez-Franco, A., & Martín, S. 2005, ApJ, 627,
L121 [NASA ADS] [CrossRef]
- Kendall,
R. A., Dunning, T. H., & Harrison, R. J. 1992,
J. Chem. Phys., 96, 6796 [NASA ADS] [CrossRef]
- Knowles,
P. J., & Werner, H.-J. 1985, Chem. Phys. Lett., 115,
259 [NASA ADS] [CrossRef]
- Le Picard,
S. D., Canosa, A., Pineau des Forêts, G., Rebrion-Rowe,
C., & Rowe, B. R. 2001, A&A, 372, 1064 [NASA ADS] [CrossRef] [EDP Sciences]
- Lique, F.,
Spielfiedel, A., & Cernicharo, C. 2006, A&A, 451, 1125 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Lovas, F., Maki,
A., & Olson, W. 1981, J. Mol. Spectrosc., 87, 449 [NASA ADS] [CrossRef] (In the text)
-
Manolopoulos, D. E. 1986, J. Chem. Phys., 85,
6425 [NASA ADS] [CrossRef] (In the text)
- Martin-Pintado,
J., Bachiller, R., & Fuente, A. 1992, A&A, 254, 315 [NASA ADS]
- Martin-Pintado,
J., de Vicente, P., Fuente, A., & Planesas, P. 1997, ApJ, 482,
L45 [NASA ADS] [CrossRef]
- McCurdy,
C. W., & Miller, W. H. 1977,
J. Chem. Phys., 67, 463 [NASA ADS] [CrossRef] (In the text)
- Nisini, B.,
Codella, C., Giannini, T., & Richer, J. S. 2002, A&A,
395, L25 [NASA ADS] [CrossRef] [EDP Sciences]
- Olney, T. N.,
Cann, N. M., & Cooper, G. E. B. C. 1997, Chem. Phys.,
223, 59 [CrossRef]
- Pardo, J. R.,
Cernicharo, J., Gonzalez-Alfonso, E., & Bujarrabal, V. 1998,
A&A, 329, 219 [NASA ADS]
- Phillips,
T. R., Maluendes, S., & Green, S. 1996, ApJS, 107,
467 [NASA ADS] [CrossRef] (In the text)
- Pirani, F.,
Cappelletti, D., & Liuti, G. 2001, Chem. Phys. Lett., 350,
286 [CrossRef] (In the text)
- Ramonda,
J. W., Muenter, J. S., & Klemperer, W. A. 1970,
J. Chem. Phys., 52, 3458 [CrossRef]
- Reinsch, E.-A.,
& Meyer, W. 1976, Phys. Rev. A, 14, 915 [NASA ADS] [CrossRef]
- Schilke, P.,
Walmsley, C. M., Pineau des Forets, G., & Flower,
D. R. 1997, A&A, 321, 293 [NASA ADS]
- Schöier,
F. L., Olofsson, H., Wong, T., Lindqvist, M., &
Kerschbaum, F. 2004, A&A, 422, 651 [NASA ADS] [CrossRef] [EDP Sciences]
- Schöier,
F. L., van der Tak, F. F. S., van Dishoeck,
E. F., & Black, J. H. 2005, A&A, 432, 369 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Sisak, M., &
Secrest, D. 1991, J. Chem. Phys., 94, 5488 [NASA ADS] [CrossRef] (In the text)
- Sisak, M., &
Secrest, D. 1992, J. Chem. Phys., 96, 230 [NASA ADS] [CrossRef] (In the text)
- Smith, L. N.,
Malik, D. J., & Secrest, D. 1979,
J. Chem. Phys., 71, 4502 [NASA ADS] [CrossRef]
- Thomas, L.,
Kraemer, W., & Diercksen, G. 1980, Chem. Phys., 51, 131 [CrossRef] (In the text)
- Turner,
B. E., Chan, K.-W., Green, S., & Lubowich, D. A.
1992, ApJ, 399, 114 [NASA ADS] [CrossRef] (In the text)
- Usero, A.,
García-Burillo, S., Martín-Pintado, J., Fuente, A., &
Neri, R. 2006, A&A, 448, 457 [NASA ADS] [CrossRef] [EDP Sciences]
- Watts, J. D.,
Gauss, J., & Bartlett, R. J. 1993,
J. Chem. Phys., 98, 8718 [NASA ADS] [CrossRef] (In the text)
- Werner, H.-J.,
& Meyer, W. 1976, Phys. Rev. A, 13, 13 [NASA ADS] [CrossRef]
- Werner, H.-J.,
& Knowles, P. J. 1985, J. Chem. Phys., 82,
5053 [NASA ADS] [CrossRef]
- Werner, H.-J.,
Follmeg, B., Alexander, M. H., & Lemoine, D. 1989,
J. Chem. Phys., 91, 5425 [NASA ADS] [CrossRef] (In the text)
- Werner, H.-J., Knowles,
P. J., Lindh, R., et al. 2003, MOLPRO, version 2002.6, a
package of ab initio programs, see http://www.molpro.net
(In the text)
- Wernli, M.,
Valiron, P., Faure, A., et al. 2006, A&A, 446, 367 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Wilson,
R. W., Jefferts, K. B., & Penzias, A. A. 1970,
ApJ, 161, L43 [NASA ADS] [CrossRef] (In the text)
- Wilson,
R. W., Penzias, A. A., Jefferts, K. B., Kutner, M.,
& Thaddeus, P. 1971, ApJ, 167, L97 [NASA ADS] [CrossRef] (In the text)
- Woon, D. E.,
& Dunning, T. H. 1993, J. Chem. Phys., 98,
1358 [NASA ADS] [CrossRef]
- Woon, D. E.,
& Dunning, T. H. 1994, J. Chem. Phys., 100,
2975 [NASA ADS] [CrossRef]
- Ziurys,
L. M., Friberg, P., & Irvine, W. M. 1989, ApJ, 343,
201 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2006
![$\displaystyle B_n(R)= \exp\left(-a_n\ R\right)\ .\ \left[{\displaystyle\sum_{i=...
...tanh(R)\right]\ .\ \left[{\displaystyle\sum_{j=6,8}}\ c_n^{(j)}\ R^{-j}\right],$](/articles/aa/full/2006/43/aa5718-06/img26.gif)
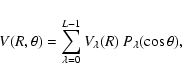
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{5718fig1}
\end{figure}](/articles/aa/full/2006/43/aa5718-06/Timg35.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{5718fig2}
\end{figure}](/articles/aa/full/2006/43/aa5718-06/Timg39.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{5718fig3}
\end{figure}](/articles/aa/full/2006/43/aa5718-06/Timg60.gif)
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{5718fig4}
\end{figure}](/articles/aa/full/2006/43/aa5718-06/Timg61.gif)
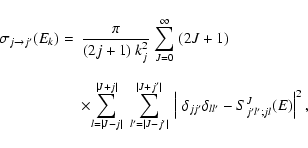
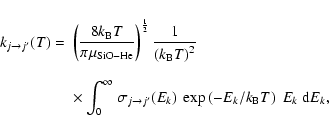
![\begin{displaymath}k_{j^{\prime}\rightarrow j}(T)=\frac{\left(2j+1\right)}{\left...
...ime}}\right)/k_{\rm B}T\right]
k_{j\rightarrow j^{\prime}}(T).
\end{displaymath}](/articles/aa/full/2006/43/aa5718-06/img77.gif)
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{5718fig5}
\end{figure}](/articles/aa/full/2006/43/aa5718-06/Timg83.gif)
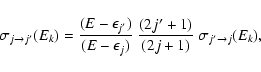
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{5718fig6}
\end{figure}](/articles/aa/full/2006/43/aa5718-06/Timg93.gif)
![\begin{figure}
\par\includegraphics[width=16.4cm,clip]{5718fig7}
\end{figure}](/articles/aa/full/2006/43/aa5718-06/Timg95.gif)