Contents

A&A 459, 43-54 (2006)
DOI: 10.1051/0004-6361:20064945

The cosmological history of accretion onto dark halos and supermassive black holes[*]

L. Miller1 - W. J. Percival2,3 - S. M. Croom4 - A. Babic1


1 - Dept. of Physics, University of Oxford, Denys Wilkinson Building, Keble Road, Oxford OX1 3RH, UK
2 - Institute for Astronomy, University of Edinburgh, Blackford Hill, Edinburgh EH9 3HJ, UK
3 - Institute of Cosmology and Gravitation, University of Portsmouth, Portsmouth, PO1 2EG, UK
4 - Anglo-Australian Observatory, PO Box 296, Epping, NSW 2121, Australia

Received 1 February 2006 / Accepted 8 August 2006

Abstract
Aims. We investigate the cosmological growth of dark halos and follow the consequences of coeval growth for the accretion history of associated supermassive black holes.
Methods. The Press-Schechter approximation is used to obtain an analytic expression for the mean rate of growth of dark matter halos. Dark halo accretion rates are compared with numerical work and the consequences for understanding AGN evolution are described.
Results. The mean accretion rate onto dark matter halos is shown to have a simple analytic form that agrees with previous numerical work and that may easily be calculated for a wide range of halo mass, redshift and cosmological parameters. The result offers a significant improvement over published fitting formulae deduced from merger trees. We then consider the growth of associated supermassive black holes, and make a basic test of the simple hypothesis of "Pure Coeval Evolution'' (PCE) in which, on average, black hole growth tracks dark halo growth. We demonstrate that both the absolute value of the integrated AGN bolometric luminosity density and its cosmological evolution derived from hard X-ray surveys are well-reproduced by PCE. Excellent agreement is found at $z \ga 0.5$, although the observed luminosity density drops by a factor 2 compared with PCE by z=0: black hole growth appears to decouple from halo growth at low redshifts, and this may be related to the phenomenon of "cosmic downsizing''. Overall, AGN evolution appears either to be caused by or to be closely linked to the slow-down in the growth of cosmic structure. We also discuss the mean Eddington ratio averaged over all galaxies, which is predicted to show strong evolution to higher values with redshift.

Key words: accretion, accretion disks - galaxies: formation - galaxies: active - cosmology: theory

1 Introduction

One of the great mysteries in the study of active galaxies and QSOs is the physical origin of the strong cosmological evolution in their space density at a given luminosity. For many years it has appeared that, at least in broad terms, the evolution was best described as "pure luminosity evolution'' in which QSOs appeared on average to have dimmed with time rather than changing in comoving space density (Croom et al. 2004; Marshall et al. 1983; Boyle et al. 1988). This is in accord with recent evidence that almost all galaxies with a massive spheroid component contain a supermassive black hole at the present epoch (Magorrian et al. 1998; Ferrarese & Merritt 2000; Onken et al. 2004; Tremaine et al. 2002; Gebhardt et al. 2000), the great majority of which must be largely inactive today. If these black holes were luminous in a phase of accretion and growth at higher redshift then their luminosities must indeed have declined with time.

Yet this picture is not easily in accord with modern ideas of galaxy formation, since if the matter content of the universe is dominated by cold dark matter we expect galaxies to grow hierarchically, and we expect the mass function of black holes at the centres of galaxies to increase with time - what then is the mechanism that allows the mass function to increase but the luminosity to decrease with cosmic epoch? One obvious possibility is that black holes may increase in mass but with a decreasing mean accretion rate. This picture has been incorporated into models such as those of Haehnelt & Rees (1993) and Kauffmann & Haehnelt (2000) in which simple parameterisations of such cosmological evolution in accretion rate were allowed, and it was shown that with a suitable choice of parameters the evolution in the QSO optical luminosity function could be matched. The physical origin of this variation in accretion rate has not yet been determined, however, and explanations range from a systematic depletion in available gaseous material with cosmic epoch to long-term variations in the accretion process itself: these latter explanations would of course only work if black holes were formed at high redshift and the luminosity evolution that has been observed were a reflection of the variation in accretion history of individual black holes.

More recently however it has become clear that optically luminous QSOs are a short-lived phenomenon, at least compared with the Hubble time. Measurement of the clustering of QSOs in the 2dF QSO Redshift Survey (2QZ: Croom et al. 2005) has shown that their clustering amplitude does not increase with time as would be expected if QSOs were long-lived, given that cosmic structure is expected still to be growing at $z \sim 2$ in a Universe with a cosmological matter density parameter  $\Omega_M \sim 0.3$. This implies that we must look for a universal variation in accretion rate rather than anything intrinsic to an individual accretion "event''.

The simple picture of QSO luminosity evolution itself has now been shown to be more complicated when active galaxies are selected at X-ray wavelengths. First, it now seems likely that the hard X-ray background is produced by X-rays emitted from active galaxies, but in that case a large fraction of those active galaxies must be highly absorbed, with equivalent X-ray absorption column densities in neutral hydrogen >1023 cm-2(Risaliti et al. 1999; Comastri et al. 2001; Ueda et al. 2003). These active galaxies would be likely to be optically obscured also. A second significant discovery from X-ray surveys however has been that low luminosity X-ray selected active galaxies, that would be classified as Seyfert galaxies were they optically selected, display cosmological evolution in their space density that appears to have a maximum at lower redshift than their high luminosity QSO counterparts (Zheng et al. 2004; Barger et al. 2005; Steffen et al. 2003; Ueda et al. 2003; Cowie et al. 2003). It may be to some extent that the identification of these weak active galaxies may be less complete at higher redshifts, but early indications are that there is a significant shift of the space density maximum to lower redshifts with decreasing luminosity.

Hence it appears that there is much still to understand both observationally and theoretically about the evolution of active galaxies. Nonetheless, the basic inference that there must have been evolution in accretion rate seems inescapable. In this paper we test the extent to which the growth of black holes may be linked to the growth of galaxies, and argue that cosmological evolution in accretion rate can be understood primarily as arising from the cosmological evolution in the rate of accretion of matter onto galaxies. In Sect. 3 we present a new calculation of the accretion rate onto dark halos using the extended Press-Schechter approximation. We find that the analytic expression agrees well with both our own and previous numerical estimation of the accretion rate calculated from merger trees. The analytic approach here circumvents the need for such numerical estimation, and we also find that it provides mathematically better behaviour than fitting functions to the numerical results that have previously been proposed in the literature.

In Sect. 4 we argue that coeval growth of black holes with their associated galaxies and dark halos leads to a simple expression for the total mass accretion rate onto all black holes. We calculate the expected integrated luminosity density arising from accretion onto black holes and show that it agrees remarkably well with observation. When expressed as the Eddington ratio (the ratio of the actual mass accretion rate to the rate required to attain the Eddington limiting luminosity) it shows significant cosmological evolution almost independent of halo mass and without depending strongly on the choice of cosmological parameters.

   
2 Coeval growth of supermassive black holes and their host galaxies and halos

One hypothesis, whose consequences will be followed in this paper, is that the population of supermassive black holes, that in the nearby universe inhabit the nuclei of massive galaxies, grew coevally with their host galaxies and associated dark halos. Before launching into detailed calculation, in this section we first consider the rationale for testing this hypothesis.

First, given present data on the black hole/bulge relationship, some degree of coeval growth seems hard to avoid, at least for galaxies with measurable bulge components. In all massive galaxies where both a bulge mass and a black hole mass have been measured dynamically, there is an extremely tight correlation between the two (Onken et al. 2004; Tremaine et al. 2002; Gebhardt et al. 2000). At lower masses, with velocity dispersion $\sigma < 100$ km s-1, the correlation is less well-established, but does appear to extend at least down to $\sigma \sim 30$ km s-1(Barth et al. 2005). When the bulge mass is determined from velocity dispersion measurements, the cosmic scatter in the relation appears smaller than the measurement errors, and probably is less than a factor three (Onken et al. 2004; Tremaine et al. 2002). But it is thought that galaxies have grown hierarchically over a wide range of cosmic epoch, and with galaxies at any observed redshift having accumulated their masses at many different times. In order for the tight present-day black-hole/bulge relation to exist, the process of formation of black hole and galaxy must have been interrelated, the simplest explanation being that they grew in mass at the same time.

Second, the luminosity emitted by AGN is thought to arise from accretion, and therefore is a signature of ongoing black hole growth at low redshifts. Ueda et al. (2003) and Marconi et al. (2004) have shown that both the X-ray background and the local mass density in black holes are consistent with being created by the luminous phase of accretion visible in hard X-ray AGN surveys, and that the bulk of that black hole growth occurs at low redshifts (z < 3). The picture of supermassive black holes forming at high redshifts and then remaining largely unchanged since then is not consistent with the observed AGN luminosity density and the inferred local black hole mass density, unless the radiative efficiency of the AGN luminosity we can see is unfeasibly high ( $\epsilon \gg 0.1$, Marconi et al. 2004). So it appears that black holes have been continuing to form during the cosmic epochs in which dark halos and their associated galaxies have also continued to grow.

Previous AGN models (e.g. Kauffmann & Haehnelt 2000) have assumed a relationship between dark halo mass and black hole mass. It is hard to see how the black hole could know what mass of halo it is in unless there has been some causal link between halo growth and black hole growth. The link does not need to be direct, and it may be that feedback processes have an important role in regulating the black hole/halo relationship, but in effect, these models have implicitly assumed that coeval growth has occurred. Whether coeval growth is still occurring in the present-day universe is another question, and one that we shall attempt to investigate in this paper.

The growth of galaxies by hierarchical mergers implies that there is a contribution of mergers to black hole growth, too. Thus we expect the mass function of black holes to be determined by hierarchical merging, as is the mass function of galaxies. Mergers of black holes cannot change the integrated irreducible mass in black holes, however, so the integrated mass in black holes should depend on the total amount of matter accreted and not on the merger history. The importance of mergers does not violate the argument originally due to Soltan (1982) that black holes in the local universe are produced by accretion at earlier cosmic epochs. The growth of supermassive black holes through mergers does in principle allow high black hole masses to be attained at rates faster than the Salpeter rate without violating the Eddington limit, which may help us to understand how supermassive black holes can exist at high redshift, $z \sim 6$ (e.g. Willott et al. 2003).

In practice we might expect the phases of significant mass accretion in the life of a black hole to be correlated with periods of galaxy merging: it has long been suggested that mergers may drive matter into galaxy centres and trigger phases of black hole accretion (e.g. Barnes & Hernquist 1992). This picture creates an attractive link between galaxy mergers and prompt AGN activation but is not required in what follows.

3 The mean accretion rate onto dark matter halos

3.1 Structure growth from the Press-Schechter approximation

If the matter content of the universe is dominated by cold dark matter, then dark matter halos associated with galaxies form hierarchically. Bond et al. (1991) have shown that a more rigorous treatment of the work of Press & Schechter (1974) ("extended Press-Schechter'', hereafter EPS) can be used to obtain information about the build-up of structure, and the resulting evolving mass functions agree with the results of N-body simulations, especially if some additional modification of EPS theory is allowed (Sheth et al. 2001; Sheth & Tormen 1999,2002).

In this picture of hierarchical galaxy formation, at any moment in time, any given overdensity is increasing in mass through the process of accretion of matter. There has been much discussion in the literature about whether one can use EPS theory to further analyse this accretion in terms of merger events (Benson et al. 2005; Lacey & Cole 1993; Cole et al. 2000; Lacey & Cole 1994) but we are not interested here in attempting such a detailed view of the build-up of galaxies. In previous papers (Percival et al. 2000; Percival & Miller 1999) the formation rate of halos within EPS theory has been calculated, and hence if the space density of halos is also known this may be converted into a mean accretion rate onto halos as a function of their mass and redshift, measuring the overall accretion of matter, not broken down into individual events.

In those papers it was shown that a joint distribution function in mass M and cosmic time t of new overdensities, F(M,t), could be defined that is related to the mass function, F(M|t), by the relation

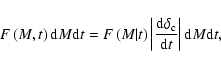\begin{displaymath}F\left(M,t\right) {\rm d}M {\rm d}t = F\left(M\vert t\right) ... ...{\rm d}\delta_{\rm c}}{{\rm d}t}\right\vert {\rm d}M {\rm d}t, \end{displaymath} (1)

where $\delta_{\rm c}(z)$ is the linear-theory overdensity at redshift z=0 that would be required for an overdensity to have collapsed at some redshift z>0. For an Einstein-deSitter universe

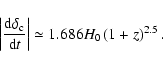\begin{displaymath}\left\vert\frac{{\rm d}\delta_{\rm c}}{{\rm d}t}\right\vert \simeq 1.686 H_0 \left(1+z\right)^{2.5}. \end{displaymath} (2)

In Appendix A we discuss alternative methods of calculating $\vert{\rm d}\delta_{\rm c}/{\rm d}t\vert$ for other choices of cosmological parameters, and describe an analytic approximation based on the linear growth factor of cosmological perturbations.

However, the normalisation of the joint distribution F(M,t) is problematic, as discussed by Percival et al. (2000). In Sect. 3.2 we follow a different approach and calculate the mean accretion rate analytically from the EPS conditional mass function. This is complemented in Sect. 3.3 by a numerical derivation of the rate from Monte-Carlo realisations of the EPS process.

   
3.2 Analytic derivation of the mean halo accretion rate

Lacey & Cole (1993,1994) give the conditional probability that a location in a halo of mass M at cosmic time t was previously part of a halo of lower mass M' at earlier time t':

 \begin{displaymath}\frac{{\rm d}f}{{\rm d}M'}\left(M',t' \vert M,t \right) = \fr... ...{\left(\Delta\delta_{\rm c}\right)^2}{2\Delta\sigma^2}\right], \end{displaymath} (3)

where $\Delta\delta_{\rm c} = \delta_{\rm c}(t')-\delta_{\rm c}(t)$, $\delta_{\rm c}(t') > \delta_{\rm c}(t)$, and where $\Delta\sigma^2 = \sigma'^2 - \sigma^2$ with $\sigma'^2$ being the variance on the mass scale M', $\sigma^2$ the variance on the mass scale Mand $\sigma'^2 > \sigma^2$ for M' < M.

Hence the expectation value for the halo's increase in mass $\Delta M \equiv M - M'$ is

\begin{displaymath}\left\langle \Delta M \right\rangle = \int_0^{M} \frac{\left(... ...rm c}\right)^2}{2\left(\Delta\sigma^2\right)}\right]{\rm d}M'. \end{displaymath} (4)

Making the substitution $y^2 = 1/\Delta\sigma^2$ this can be rearranged to give

 \begin{displaymath}\left\langle \Delta M \right\rangle = M \Delta\delta_{\rm c} ... ...eft[-y^2\left(\Delta\delta_{\rm c}\right)^2/2\right] {\rm d}y. \end{displaymath} (5)

As $y \rightarrow \infty$, $M'(y) \rightarrow M$ and $\left(1-\frac{M'(y)}{M}\right) \rightarrow 0$. Hence we can make $\Delta\delta_{\rm c}$ sufficiently small that the exponential term can be ignored in this integral, and in the limit $\Delta t = (t - t') \rightarrow 0$, $\Delta\delta_{\rm c} \rightarrow 0$ and
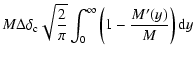                        $\displaystyle \left\langle \Delta M \right\rangle$ $\textstyle \rightarrow$ $\displaystyle M \Delta\delta_{\rm c} \sqrt{\frac{2}{\pi}} \int_0^{\infty} \left(1-\frac{M'(y)}{M}\right) {\rm d}y$ (6)
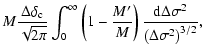  $\textstyle \rightarrow$ $\displaystyle M \frac{\Delta\delta_{\rm c}}{\sqrt{2\pi}} \int_0^{\infty} \left(... ...{M'}{M}\right) \frac{{\rm d}\Delta\sigma^2}{\left(\Delta\sigma^2\right)^{3/2}},$ (7)

where $\Delta\sigma^2 \rightarrow \infty$ as $M' \rightarrow 0$for CDM power spectra and $\Delta\sigma^2 \rightarrow 0$ as $M' \rightarrow M$. The kernel of this integral was derived by Cole et al. (2000) but those authors were interested in considering the distribution of merger events rather than integrating to find the overall mean accretion rate, which forms the basis of this paper.

Hence we can write the mean rate of mass accretion as

 \begin{displaymath}\left\langle \dot{M} \right \rangle = \lim_{\Delta\delta_{\r... ...rm d}\delta_{\rm c}}{{\rm d}t} \right \vert f\left( M \right), \end{displaymath} (8)

where

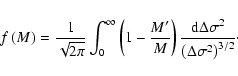\begin{displaymath}f\left( M \right) = \frac{1}{\sqrt{2\pi}} \int_0^{\infty} \l... ...{\rm d}\Delta\sigma^2}{\left(\Delta\sigma^2\right)^{3/2}}\cdot \end{displaymath} (9)

Integrating by parts we find
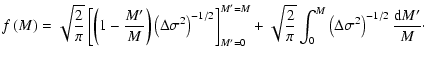$\displaystyle f\left( M \right) = \sqrt{\frac{2}{\pi}} \left[ \left(1-\frac{M'}... ...{\pi}} \int_{0}^{M} \left(\Delta\sigma^2\right)^{-1/2} \frac{{\rm d}M'}{M}\cdot$     (10)

The first term is zero provided $\left\vert \frac{{\rm d}\sigma^2}{{\rm d}M'} \right\vert _{M'=M} > 0$, leaving

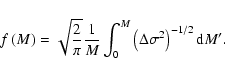\begin{displaymath}f\left( M \right) = \sqrt{\frac{2}{\pi}} \frac{1}{M} \int_{0}^{M} \left(\Delta\sigma^2\right)^{-1/2} {\rm d}M'. \end{displaymath} (11)

It should be noted that this particular definition of mass accretion rate is not the only one possible. One could also calculate the accretion rate by considering the future accretion of halos and taking the limit of small time intervals: this produces a different analytic form, involving an integration over masses larger then the mass being considered, and highlights that the mass accretion process for a mass M at time t is discontinuous within EPS theory. In Sect. 3.3 we also consider the relationship of this "instantaneous'' mass accretion rate to the process of the build-up of halos on longer timescales: the mean accretion rate is a function of the time interval being considered, as may be seen from inspection of Eq. (5).

The function f(M) may be evaluated numerically for an assumed matter power spectrum. For cold dark matter power spectra it depends only weakly on mass and varies little with shape of the power spectrum. It varies inversely with the normalisation parameter $\sigma_8$. Figure 1 shows the variation of f(M) with halo mass for a $\Lambda $CDM power spectrum approximated as in Efstathiou et al. (1992) for a range of values of the shape parameter $\Gamma \equiv \Omega_M h$and with fixed $\sigma _8 = 0.74$, h=0.7. The relationship between variance $\sigma^2$ and mass was calculated assuming a spherical top-hat smoothing function, although we should note that strictly Eq. (3) is derived assuming smoothing with a top-hat function in k-space. At a halo mass of $10^{12.5} h^{-1}~M_{\odot}$, appropriate for the halo masses of luminous QSOs (Croom et al. 2005), f(M) varies only by a factor 2 over the range $0.1 < \Omega_M < 0.4$ for h=0.7. The variation with mass is also weak for masses in the range appropriate for massive galaxies: at $\Omega_M = 0.3, h=0.7$, f(M) varies by a factor 2 over the range  $10 < \log_{10}(M/M_{\odot}) < 13$.


  \begin{figure} \par\includegraphics[angle=-90,width=7.8cm,clip]{4945fig1.ps} \end{figure} Figure 1: The variation of the function f(M) with log10(halo mass) as a function of the power-spectrum shape parameter $\Gamma $, with h=0.7and $\sigma _8 = 0.74$. Curves from top to bottom have $\Gamma = 0.07$,0.14, 0.21, 0.28, 0.35, 0.7; solid curves show the calculated function, dashed curves show the fitting function, Eq. (12).

For convenience we provide a fitting formula for f(M). Over the range of $\Gamma $ and mass shown in Fig. 1, we adopt the relation

 \begin{displaymath}\log_{10}\left(f\left[M\right]\right) = A\left(\Gamma\right) ... ...t( \frac{(h/0.7)^2 M}{10^{17}~{M_\odot}}\right)\right]^{\beta} \end{displaymath} (12)

with B = 1.117, $\beta = 4.82$ and $A\left(\Gamma\right) = -0.7349 - 0.9808(\log_{10}\Gamma) - 0.2055(\log_{10}\Gamma)^2$. This function fits to an rms accuracy of 1.6 percent over the range $0.07 \le \Gamma \le 0.7$, or $0.1 \le \Omega_0 \le 1$ for h=0.7, and is shown by dashed lines in Fig. 1. For $\sigma_8 = 0.84$ the best fitting function parameters are B = 1.072, $\beta = 4.57$ and $A\left(\Gamma\right) = -0.8665 - 1.002(\log_{10}\Gamma) - 0.2093(\log_{10}\Gamma)^2$. This formula may be used together with the analytic approximation to $\vert{\rm d}\delta_{\rm c}/{\rm d}t\vert$ described in Appendix A to calculate the mean cosmological accretion rate for a wide range of cosmological parameters. It is worth noting that the accretion rate has a simple dependence on mass and redshift, and either weak or at least linear dependence on cosmological parameters.

   
3.3 Numerical calculation of the mean halo accretion rate


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{4945fig2.ps} \end{figure} Figure 2: Comparison of the mean mass accretion rate calculated analytically (solid curves) and measured from Monte-Carlo realisations (solid symbols), shown as a function of redshift for a variety of masses.

To validate the derivation presented in Sect. 3.2, we now compare the analytic instantaneous rate with the rate calculated from Monte-Carlo realisations of the EPS process. In EPS theory, the overdensity recovered if a realisation of the density field is smoothed on different scales around a fixed point can be matched to a one-dimensional Brownian random walk. The collapsed mass at a given time is given by the trajectory's first upcrossing of a barrier at the critical overdensity corresponding to the chosen time. Because we can only calculate finite representations of these trajectories, there are a number of numerical issues that complicate their use. In particular

By appropriate choice of the step size, we can minimize these problems. We have created a sample of 106 trajectories each consisting of 213 steps of varying size in $\sigma^2$. A varying step size was chosen to more closely match the expected upcrossing distribution and allow a larger range in $\sigma^2$ to be probed. The barrier height was set at 4 times the initial step size to minimise problems owing to missed upcrossing in the first few steps of the trajectories. Because the trajectories can be arbitrarily scaled in $\delta_{\rm c}^2/\sigma^2$, we can use this single set of trajectories (and associated upcrossings) to determine the mass accretion rate for any halo mass and epoch. For the masses and times chosen, we have determined that the problems owing to the finite extent of the trajectories are negligible. By comparing with the expected conditional mass function (Eq. (3)), we have also optimised the step size to reduce problems owing to the discreteness of the realisations.

Figure 2 shows the result from the Monte-Carlo measurements, calculated from the average mass accreted within $\Delta\delta_{\rm c}=0.032$, corresponding to 0.0035 Gyr at z=7 and 0.5 Gyr at z=0. Decreasing $\Delta\delta_{\rm c}$ further does not significantly change the recovered rate. The agreement with the analytic instantaneous rate is extremely close. Any differences may be revealed by comparing f(M) with the equivalent quantity from the Monte-Carlo realisations by factoring out the analytic linear dependence on mass and ${\rm d}\delta_{\rm c}\protect/{\rm d}t$ (Fig. 3). The maximum difference between the analytic and numerical results is <5% and is likely to be caused by remaining problems owing to the discrete nature of the numerical trajectories. Note that the curves in Fig. 2 show the immediate mass accretion rate onto a halo which has a specified mass at a specified redshift, not how the mean accretion rate varies with time for an individual halo.

This comparison has shown that the results obtained from numerical realisations of the Press-Schechter process are indeed consistent with the analytic results that we have obtained. This type of realisation forms the basis of the commonly-used "merger trees'' and in the next section we compare our results with earlier numerical attempts to understand the growth of dark matter halos.


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{4945fig3.ps} \end{figure} Figure 3: Comparison of f(M) (solid curve) with that deduced from the Monte-Carlo realisations by factoring out the linear dependence on M and ${\rm d}\delta_{\rm c}\protect/{\rm d}t$.

3.4 Comparison with previous numerical calculations

Van den Bosch (2002) has calculated the average mass accretion histories of dark matter haloes based on the extended Press-Schechter formalism and the N-branch merger-tree construction algorithm of Somerville & Kolatt (1999). He provides a fit to the numerically-obtained mass accretion histories by fitting a function of the form

 \begin{displaymath}\log\left\langle \frac{M(z)}{M_0}\right\rangle = -0.301\left[\frac{\log (1+z)}{\log (1+z_f)}\right]^\nu , \end{displaymath} (13)

where M(z) is a halo's mass at redshift z, M0 is its present-day mass, and $\nu$ and zf are non-independent parameters. The best-fit set of parameter values is $\nu = 1.362 + 1.858\log (1+z_f)-0.032\log \left[M_0/(10^{11}h^{-1}~{M_\odot})\right]$. zf is obtained from the root of equation:

\begin{displaymath}\delta_{\rm c}(z_f) = \delta_{\rm c}(0) + 0.477 \sqrt{2\left[\sigma^2(f_{i}M_0)-\sigma^2(M_0)\right]} \end{displaymath} (14)

where fi is set to a value fi=0.254. Van den Bosch (2002) recommends differentiating M(z) in order to find the mean mass accretion rate. As discussed by Van den Bosch (2002), construction of such accretion histories numerically is not trivial, and depends on the definition of a halo's progenitor within a merger tree. However, it will be interesting to compare the results of the analytic result presented here with these earlier numerical attempts.


  \begin{figure} \par\includegraphics[angle=-90,width=7.8cm,clip]{4945fig4.ps} \end{figure} Figure 4: Comparison of the mean accretion rate from this paper (dotted lines) with the two alternative numerical fits proposed by Van den Bosch (2002) (solid lines) and by Wechsler et al. (2002) with parameter values estimated by Van den Bosch (2002) (dot-dashed lines). See the text for more details of the calculation of these curves, which are shown for values of $\log_{10}(M(z)/{M_\odot})=8,10,12,14$. The Van den Bosch (2002) curves becomes unphysical at low redshift and depart significantly from the analytic results. Both numerical fits become unphysical at high redshift and are truncated outside the region of validity, as discussed in the text.

Wechsler et al. (2002) have also discussed the growth of halos in merger trees, and find a reasonable parameterisation of the accretion histories of halos to have the form:

 \begin{displaymath}M(z) = M_0 {\rm e}^{-\alpha z} \end{displaymath} (15)

where $\alpha$ is a parameter. In fact, comparison with Eq. (8) suggests this is a good approximating function for Wechsler et al. (2002) to have chosen. From Eq. (8) we find

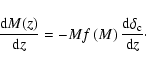\begin{displaymath}\frac{{\rm d}M(z)}{{\rm d}z} = -M f\left( M \right) \frac{{\rm d}\delta_{\rm c}}{{\rm d}z}\cdot \end{displaymath} (16)

In the case of an Einstein-de-Sitter universe ${\rm d}\delta_{\rm c}/{\rm d}z = 1.686$ and a solution for M(z) of the form of Eq. (15) immediately follows if we ignore the slight redshift dependence introduced by the f(M(z)) term. This solution will not be correct for other cosmologies, but should still qualitatively be of the correct form. Van den Bosch (2002) has related the parameter $\alpha$ to the previous parameter zf by the relation  $\alpha = \left(z_f/1.43\right)^{-1.05}$.

In Fig. 4 we compare our accretion rate with those obtained from these two alternative fits to the numerical mass accretion histories. The solid line shows the mean accretion rate obtained by differentiating Eq. (13) and the dot-dashed line from differentiating Eq. (15), both with the prescriptions for the free parameters given by Van den Bosch (2002) that are quoted above. The dotted line shows the mass accretion rate from Eq. (8) (note that, as in Fig. 2, each curve corresponds to a fixed value of mass at each redshift: i.e. these are curves of constant M(z) and not constant M0). The comparison is made for several values of halo mass: $\log_{10}\left(M(z)/{M_\odot}\right)=8,10,12,14$. There is excellent agreement between the three curves over most of the range of redshifts. However, at the lowest redshifts the Van den Bosch (2002) accretion rate shows significant departures, and it is straightforward to see that this arises from the choice of fitting function in Eq. (13): in the limit $z \rightarrow 0$, ${\rm d}M/{\rm d}t \rightarrow 0$ if calculated from that equation, for parameter values $\nu > 1$. Such behaviour is unphysical, it implies that all halos at the present day have stopped growing. This is purely an artefact of the choice of fitting function and leads to significant departures from the analytic calculation for z<0.5. The result from the Wechsler et al. (2002) form consistently results in slightly higher values of accretion rate, but predicts the same behaviour as the analytic calculation at redshifts approaching zero.

We also find a further limitation of the numerical prescriptions, which is that the calculated growth histories become unphysical at high masses and redshifts, with problems arising when the present-day mass $M_0\ga 10^{15}~{M_\odot}$. The problem is that the M(z)functions for differing masses cross at high redshift, such that a high mass halo might be predicted to have had a lower-mass progenitor than a lower mass halo. For example, the main progenitor mass of a $M_0=10^{16}~{M_\odot}$ halo is predicted by Eq. (13) to be smaller than that of a $M_0=10^{14}~{M_\odot}$ halo at redshifts $z\ga 2.5$. We roughly estimate that the Van den Bosch (2002) fit can be used up to $(\log_{10}(M_0/{M_\odot}),z)=\{(14.5,1),(13.3,2),(11.7,4),(10.8,6),(10.2,8.)\}$, where the pairs of numbers denote the locus on the M0, z plane beyond which the prescription becomes unreliable. The same problem is found when using the parameterisation of Eq. (15), with the range of valid redshift and present-day halo mass moved to lower values: $(\log_{10}(M_0/{M_\odot}),z)=\{(13.3,1),(11.8,2.),(9.8,4),(8.3,6),(7.7,7)\}$. Given the relationship between the Wechsler et al. (2002) and analytic functions, it can be seen that the problem in this case arises from the prescription for the value of $\alpha$rather than being an intrinsic problem with the choice of numerical function.

Overall we conclude that the analytic and previous numerical results are in reasonable agreement in the regions of mass and redshift space where the numerical parameterisations are reliable, but that there exist significant regions of that space where the previous numerical fits become unusable.

3.5 How good is extended Press-Schechter theory?

So far, both the analytic calculation and the numerical realisations have relied on the EPS formalism. This formalism effectively amounts to being a linearised approximation to the true process of non-linear growth of structure, and a priori we should have no right to expect that this will be an accurate approximation. How can we be confident that the work presented here has relevance to the real process of halo growth? There have been many comparisons of the calculation of the halo mass function predicted by EPS with that obtained from N-body dark matter simulations and, with some caveats, good agreement is found. Jenkins et al. (2001) show the level of agreement when compared with Virgo consortium simulations. The mass functions agree to a factor 1.6 over a wide range of halo mass. In this paper we investigate the rate of growth of dark halos: if the EPS growth rate were significantly wrong it would be hard to then reproduce a good estimate of the mass function, and it seems likely therefore that the calculations presented here are correct when compared with dark-matter-only simulations to this level of accuracy.

Sheth & Tormen (1999) have shown, however, that the EPS mass function may be modified to produce even closer agreement with the N-body simulations. This work has been developed further by Sheth et al. (2001) and Sheth & Tormen (2002) and confirmed in the Jenkins et al. (2001) simulations. The principal modification is to reduce the critical density for collapse, $\delta _{\rm c}$, by a factor $\sqrt{a}$ where a is determined from comparison with the simulations to have a value $a \simeq 0.7$. Insertion of this factor into Eq. (3) would simply imply that f(M) is also reduced by a factor $\sqrt{a} \simeq 0.84$. This causes a slight shift in the curves plotted here but otherwise has no effect on the redshift or mass dependence.

We note that the merger trees of Van den Bosch (2002) have also been compared with N-body simulations, and reasonable agreement was found there too, albeit with a tendency for halos to form at higher redshifts which could also be reproduced by introduction of the factor $\sqrt{a}$. In the case of the Van den Bosch (2002) simulations the best-fitting value for $\sqrt{a}$ varied over the range $0.82 < \sqrt{a} < 0.94$, depending on halo mass. Hence it may be that there is some systematic and possibly mass-dependent departure of the EPS accretion rate from the "true'' (dark-matter N-body) rate, but most likely at a level <20% in accretion rate. Finally, we note that Benson et al. (2005) have also argued that the distribution of mass discontinuities in EPS does not allow a self-consistent interpretation of these as merger events. This casts doubt on one of the fundamental assumptions of EPS-based merger trees, but should not affect the calculation of the mean accretion rate, which does not rely on that assumption.

4 The accretion history of supermassive black holes

   
4.1 Pure coeval evolution

We now move on to consider what effect the evolution in mass accretion might have on the ultimate accretion onto a supermassive black hole lying at the heart of a massive galaxy. In principle, understanding not only the formation of galaxies within dark halos but also the accretion of baryonic matter onto a central black hole requires complex and poorly-constrained physics. However, we could make a very simple assumption for the net effect of these complex processes, and see how well the predictions compare with observation. The assumption we shall make is that, on average, the relative growth rates of central black holes track the growth rates of their associated dark halos (Sect. 2). That is,

 \begin{displaymath}\left\langle\frac{1}{M_{\rm BH}}\frac{{\rm d}M_{\rm BH}}{{\rm... ...left\vert \frac{{\rm d}\delta_{\rm c}}{{\rm d}t} \right \vert, \end{displaymath} (17)

where $M_{\rm H}$ is a dark halo's mass, $M_{\rm BH}$ a black hole's mass, and where $\left\langle\right\rangle$ denotes averaging over an ensemble of halos and black holes. Note also that we haven't needed to specify what fraction of mass ends up accreting onto a black hole - that calculation would indeed need some detailed physics - the hypothesis simply assumes that the ensemble-averaged relative growth rates are the same. We shall term this simple hypothesis "Pure Coeval Evolution'' (PCE).

A simple extension of this hypothesis would allow some non-linear evolution of the relation between black holes and dark halos. Equation (17) could be modified by a factor $\alpha$ such that

 \begin{displaymath}\left\langle\frac{1}{M_{\rm BH}}\frac{{\rm d}M_{\rm BH}}{{\rm... ...left\vert \frac{{\rm d}\delta_{\rm c}}{{\rm d}t} \right \vert, \end{displaymath} (18)

which would lead to a relation of the form $M_{\rm BH} \propto M_{\rm H}^{\alpha}$ as inferred by Ferrarese (2002). We can see that the effect of such a non-linear term would be to modify the accretion rate calculations only by a constant factor.

   
4.2 The AGN luminosity density and its evolution

In this section we calculate the observationally-determined AGN luminosity density and compare with the value predicted by PCE. We define the integrated luminosity density to be the luminosity emitted during the black hole accretion process per comoving cubic Mpc, summing over AGN of all luminosities, as previously calculated by a number of authors (e.g. Marconi et al. 2004). The quantity predicted by the PCE hypothesis is the bolometric luminosity density, so we will need to apply bolometric corrections to observed quantities.

4.2.1 The bolometric luminosity density derived from X-ray surveys
We shall first estimate the bolometric luminosity density from the Ueda et al. (2003) AGN luminosity function. It has recently been recognised that hard X-ray surveys currently provide the most complete way of selecting AGN of all types, and Ueda et al. (2003) incorporate into their analysis correction for X-ray obscuration in the detected AGN (although if there is a population of extremely absorbed, Compton-thick, AGN these will be missing from Ueda et al. 2003's census - see below).

Figure 5 shows the bolometric luminosity density $\rho_{\rm BOL}$derived from the Ueda et al. (2003) LDDE model at 2-10 keV integrated over the absorption-corrected luminosity range $10^{40}<L_{\rm X}<10^{48}$ erg s-1. The X-ray luminosity density has been converted to a bolometric luminosity density and a small correction for missing Compton-thick AGN has also been applied, as described below. The luminosity density is not sensitive to the precise limits of integration: increasing the lower limit to $L_{\rm X} > 10^{42}$ erg s-1 decreases the z=0 luminosity density only by 0.08 dex without changing the maximum value (to 0.01 dex) or its redshift. Decreasing the upper limit to $L_{\rm X} < 10^{46}$ erg s-1 has no effect to within 0.01 dex. Most of the bolometric luminosity density is produced by AGN with $L_{\rm X} \sim 10^{44}$ erg s-1.

Also shown in Fig. 5 are estimates of the uncertainty in $\rho_{\rm BOL}$. To calculate the uncertainty, we first refit the binned data shown in Fig. 11 of Ueda et al. (2003), kindly provided by Y. Ueda, with the same six-parameter model (see Ueda et al. 2003, for details of the model), but with the normalisation parameterised instead as the integrated luminosity density. We then estimate confidence intervals on the integrated luminosity density for each of the five redshift slices (0.015-0.2,0.2-0.4,0.4-0.8,0.8-1.6,1.6-3.0) in turn, marginalising over the remaining five parameters of the fit. This procedure thus includes the full statistical uncertainty in the data and includes an element of uncertainty arising from the fact that to cover the full luminosity range requires some extrapolation of the model, although with the caveat that only the set of model functions that may be parameterised by the six-parameter function are allowed. The best-fit values for each redshift slice and the deduced uncertainties are shown in Fig. 5. Some points deviate somewhat from the nominal curve deduced from Ueda et al. (2003)'s best fit: this is likely because their best fit was obtained from a maximum likelihood fit to unbinned data whereas our points and errors were evaluated from fits to the binned data. We nonetheless expect that the size of the error bars should also be a good indication of the size of the 68 percent confidence region for the likelihood-determined function.


  \begin{figure} \par\includegraphics[angle=270,width=7.8cm,clip]{4945fig5.ps} \end{figure} Figure 5: The bolometric luminosity density deduced from the best-fit model of Ueda et al. (2003), integrating over the range $10^{40}<L_{\rm X}<10^{48}$ erg s-1 and applying the bolometric correction of Marconi et al. (2004) and correction for Compton-thick AGN of Ueda et al. (2003) (see text) (dashed curve). Also shown are uncertainties estimated from refitting to the binned data of Ueda et al. (2003) (points with error bars: see text; horizontal bars indicate the range of redshifts included in each point). For comparison, we show the equivalent calculation from the pure-luminosity-evolution fit of Richards et al. (2005) to the optical 2SLAQ QSO survey in the redshift range 0.4<z<2.1 (lower dashed curve). The luminosity density expected in PCE is shown for two cases: (i) no evolution in the comoving black hole mass density (dotted upper curve); (ii) evolution in the comoving black hole mass density that tracks the evolution of massive dark halos with $M_{\rm H}>10^{11.5}~{M_\odot}$(solid curve). Both curves assume average radiative efficiency $\langle\epsilon\rangle=0.04$ (see text). Note that the PCE calculation predicts a value for the luminosity density at z=0, dependent only on $\langle\epsilon\rangle$ and cosmological parameters, with the higher redshift evolution further dependent only on choice of dark halo mass: the normalisation is not allowed to float arbitrarily.

4.2.2 X-ray absorption and the Compton-thick fraction

It is recognised that 2-10 keV X-ray fluxes must be corrected for absorption, and Ueda et al. (2003) derive an estimate for the luminosity-dependent distribution of absorption column which has been incorporated into their analysis. In addition, it is likely that some fraction of AGN are Compton-thick, that the Compton-thick fraction is a function of intrinsic luminosity and that even hard X-ray surveys miss these objects (Ueda et al. 2003). Ueda et al. (2003) assume the (very uncertain) correction, based on the results of Risaliti et al. (1999), that there are $\sim$1.6 times as many Compton-thick AGN as there are AGN with absorption column densities in the range $10^{23} < N_{\rm H} < 10^{24}$ cm-2. We apply the same correction here. Although very uncertain, the net effect is to increase the bolometric luminosity density by only a factor 1.48 (i.e. 0.17 dex). Varying the Compton-thick fraction from this nominal value would have an equivalent effect on the value of $\langle\epsilon\rangle$ deduced, but does not significantly affect the conclusions of this paper.

4.2.3 The bolometric correction
To convert 2-10 keV luminosity to bolometric luminosity we use the bolometric correction of Marconi et al. (2004), averaged over the distribution of luminosities of the Ueda et al. (2003) model as a function of redshift. Because the luminosity function is distributed to higher luminosities at higher redshifts, the average fraction of the bolometric luminosity that appears in the X-ray band varies from 0.056 at z=0 to 0.023 at z=3, resulting in a variation in $\log_{10}(\rho_{\rm BOL})$ of 0.4 over this redshift range arising from the change in mean bolometric correction. Hence the bolometric luminosity density shows stronger evolution, and has a maximum at higher redshift, than the 2-10 keV X-ray luminosity density alone. The bolometric correction is notoriously uncertain, and one key uncertainty is the non-linear dependence between X-ray and optical luminosity that leads to the strong luminosity-dependence of the bolometric correction. Marconi et al. (2004) assume the relation of Vignali et al. (2003), which has recently been extended to lower luminosities by Steffen et al. (2006) and which now seems fairly robust. To test this further we also compare with the bolometric luminosity density derived from optical QSO surveys.

4.2.4 The bolometric luminosity density from optical QSO surveys
Optical QSO surveys do not probe to sufficiently low intrinsic luminosities to pick up the significant population of Seyfert and type II AGN, and they are dominated by broad-line, type I objects. (e.g. Steffen et al. 2006; Barger et al. 2005; Richards et al. 2005). However, it will be a useful test of the Marconi et al. (2004) bolometric correction to attempt to measure the bolometric luminosity density from an optical QSO survey: the X-ray and optical bolometric corrections have a dependence on bolometric luminosity of opposite signs (Marconi et al. 2004), arising from the $L_{\rm X}-L_{\rm opt}$ correlation already mentioned, so if the bolometric correction is wrong this will be manifest in this test.

The optical QSO survey that to date has most successfully probed to low intrinsic luminosity is the 2SLAQ survey (Richards et al. 2005). In Fig. 5 we plot the bolometric luminosity density obtained by integrating the pure luminosity evolution model derived from the 2SLAQ data alone, integrating over the equivalent luminosity range as for the X-ray determination, with the Marconi et al. (2004) optical bolometric correction and Ueda et al. (2003) Compton-thick fraction as above. Because of optical selection biases the valid redshift range is restricted to 0.4<z<2.1 (Richards et al. 2005).

The function shown is more sensitive to the limits of integration than the X-ray case above, because although the large survey areas allow optical QSO surveys to probe to higher AGN bolometric luminosities, the range of bolometric luminosity covered is substantially smaller than the composite X-ray surveys discussed above (Richards et al. 2005). Increasing the lower luminosity limit to match a value $L_{\rm X} > 10^{42}$ erg s-1 decreases the z=0.4bolometric luminosity density by 0.19 dex and the maximum value by 0.14 dex. Again, decreasing the upper luminosity limit to match a value $L_{\rm X} < 10^{46}$ erg s-1 leads to no significant change in luminosity density, to 0.01 dex.

Considering the differing selection of AGN types in optical and X-ray surveys, the X-ray- and optical-derived bolometric luminosity densities show remarkably good agreement. This demonstrates that the corrections applied are unlikely to be too far wrong, at least over the optical-X-ray part of the spectrum (both bolometric corrections could be missing components in other parts of the spectrum such as the far infrared - this is discussed further by Marconi et al. 2004). The differences between the two functions are most apparent at $z\sim 0.7$, although even here they agree within a factor 1.6. This difference arises from the additional low-luminosity AGN that are found by hard X-ray surveys but not by the large-area optical QSO surveys (see Richards et al. 2005, for further discussion).

This diagram also illustrates the limited effect of possible "cosmic downsizing'' on the luminosity density: the optical density is derived from a pure luminosity-evolution model, the X-ray from a luminosity-dependent density evolution model. We can see that the two models are measurably different, but that any "cosmic downsizing'' does not dominate the redshift evolution of the luminosity density.

4.2.5 The predicted bolometric luminosity density
To calculate the luminosity density expected from PCE, we assume an average fraction $\langle\epsilon\rangle$ of the rest energy of accreted baryonic material is radiated. Since the fractional accretion rate is almost independent of mass, we can write the expected bolometric luminosity density as
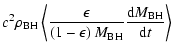                    $\displaystyle \left\langle\rho_{\rm L}\right\rangle$ $\textstyle \simeq$ $\displaystyle c^2 \rho_{\rm BH} \left\langle \frac{\epsilon}{\left(1-\epsilon\right)M_{\rm BH}} \frac{{\rm d}M_{\rm BH}}{{\rm d}t} \right\rangle$  
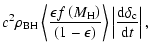  $\textstyle \simeq$ $\displaystyle c^2 \rho_{\rm BH} \left\langle \frac{\epsilon f\left(M_{\rm H}\ri... ... \right\rangle \left \vert \frac{{\rm d}\delta_{\rm c}}{{\rm d}t} \right \vert,$ (19)

where $\rho_{\rm BH}$ is the cosmic black hole mass density. For the latter quantity we follow Marconi et al. (2004) and integrate the black hole mass function obtained by convolving the Nakamura et al. (2003) luminosity function with the luminosity- $M_{\rm BH}$ relation of Marconi & Hunt (2003), which integrated for $M_{\rm BH} > 10^{5}~{M_\odot}$yields a z=0 mass density $\rho_{\rm BH} = 4.8\times 10^5~{M_\odot}$ Mpc-3 with an uncertainty of about 30 percent (Marconi et al. 2004).

The result is shown in Fig. 5 for two cases. The first shows what would happen if the black hole mass density did not change with cosmic epoch: the luminosity density would then be determined entirely by the invariant black hole mass density and the epoch-dependent accretion rate, as shown by the dotted curve. For consistency with Ueda et al. (2003) we assume a $\Lambda $CDM cosmology with parameters $\Omega_M=0.3$, H0=73 km s-1 Mpc-3 (the observational values are also adjusted to this value of H0) and $\sigma _8 = 0.74$ (Spergel et al. 2006). The remaining parameter is the average radiative efficiency $\langle\epsilon\rangle$ which we have set to a value 0.04 to approximately match data and prediction at $z \ga 0.5$. Such a value is consistent both with the range of values that might be expected for accretion onto black holes and with determinations that compare the X-ray background with the local black hole mass function, leading to a luminosity-function-dependent value for the radiative efficiency specifically of luminous AGN of $\langle\epsilon_{\rm AGN}\rangle \sim 0.08^{+0.08}_{-0.04}$ (Marconi et al. 2004). Note that this could differ from the average efficiency for all black holes if a proportion were growing by radiatively-inefficient accretion: taken literally the agreement with the PCE model with $\langle\epsilon\rangle=0.04$implies that such inefficient growth does not dominate the overall growth of black holes at $z \ga 0.5$, although some "ADAF'' contribution is allowed. However, the deduced value of $\langle\epsilon\rangle$ is degenerate with the rather uncertain values of the bolometric correction and black hole mass density and with the value of $\sigma_8$. The local black hole mass density is uncertain by $\sim$30 percent and the value of $\sigma_8$ currently has an uncertainty $\sim$10 percent (Spergel et al. 2006). The uncertainty in the bolometric correction is not well determined. Also, introduction of non-linear coupling between black hole and dark halo growth (Sect. 4.1) would also modify the deduced value of $\langle\epsilon\rangle$ by a factor $\alpha$ (Eq. (18)). Hence we should not attach too much importance to its value, provided that it is in the range expected for accretion onto supermassive black holes (e.g. $\sim$0.06 for a Schwarzschild black hole). However, a significantly lower value might imply a significant contribution to black hole growth either from radiatively inefficient accretion or from obscured growth.

The second case shown in Fig. 5 considers also the expected evolution in the black hole mass function: if black holes do indeed grow coevally with their host galaxies and halos we expect their mass function to show similar evolution. The lower solid curve shows the result expected if the integrated black hole mass density evolves the same way as massive dark halos with $M_{\rm H}>10^{11.5}~{M_\odot}$. This evolution was calculated by integrating the Sheth & Tormen (2002) mass function above this limit[*]. We find that imposing an upper limit has little effect, but that the amount of turn-down with increasing redshift in the integrated luminosity density does depend on the lower halo mass limit, with lower masses having less high-z turn-down, as expected from standard CDM models.

4.2.6 Comparison of observed and predicted luminosity densities
At $z \ga 0.5$ the simple hypothesis that black holes grow with their parent halos seems remarkably successful. With a fixed set of cosmological parameters, an independently determined estimate of the local mass density in black holes and a radiative efficiency in the expected range for AGN, this simple model of mass build-up predicts the local AGN luminosity density to within the observational uncertainties. No other tuning of the model or variation of parameters is required.

Further, the integrated luminosity density is dominated by the contribution from AGN around the "break'' in the luminosity function, with $L_{\rm X} \sim 10^{44}$ erg s-1: AGN of this luminosity typically have black hole masses around  $10^8~{M_\odot}$ (Fine et al. 2006) and QSOs of this luminosity in the 2dF QSO Redshift Survey (2QZ) have dark halo masses independently estimated from their clustering bias of $M_{\rm H} \sim 10^{12.5}h^{-1}~{M_\odot}$ (Croom et al. 2005). Thus the higher-redshift evolution of the luminosity density is entirely in accord with the expectation that it is dominated by accretion onto black holes contained within massive galaxy halos.

At z<0.5 the luminosity density falls off faster than predicted, although even at z=0 the predicted and observed values agree to a factor two. The implication is that although halos and black holes grow coevally at higher redshifts, in the more nearby universe black hole growth may have decoupled from halo growth. There is growing evidence that accretion rate in the low-redshift universe depends on host galaxy mass, with lower mass galaxies having black holes that at low redshift are preferentially growing with respect to their higher-mass counterparts (e.g. Heckman et al. 2004) - so-called "cosmic downsizing''. In detail, to explain cosmic downsizing we may need to recognise that in the late universe higher mass galaxies have slowed down their growth more than lower-mass galaxies, perhaps as a result of the environment they find themselves in at late epochs, or perhaps as a result of feedback. An alternative explanation is that the mean radiative efficiency may fall if AGN accreting at lower Eddington ratios switch to an ADAF mode of accretion (e.g. Beckert & Duschl 2002).

What we can learn from the PCE model however is that these processes are secondary to the primary cause of AGN evolution: the cosmic build-up of structure and its rate of change. We reiterate that the success of the PCE hypothesis does not mean that complex physics is not operating: it simply means that averaged across all massive galaxies, there is a mean net effect which corresponds to black holes growing at about the same rate as their host dark halos. Individually we expect black holes to go through periods of inactivity punctuated by bursts of accretion probably associated with merger events between galaxies, remembering that the galaxy mass function itself is also built up hierarchically by mergers between less massive progenitors. But just as the average effect on the galaxy mass function is a steady build-up of mass, so there is a steady build-up of mass in the black hole population.

A final consistency check is to ask whether the inferred local black hole mass density could indeed have been built up during the process of luminous accretion. This question has largely been answered by Marconi et al. (2004), who have shown that the Ueda et al. (2003) luminosity function correctly predicts not only the hard extragalactic X-ray background spectrum but also the local black hole mass density, as already discussed above. The implication is that not only are the estimates of bolometric luminosity density consistent with the relic black hole population, but that there cannot have been any substantially larger amount of "hidden'' (Compton-thick or radiatively-inefficient) black hole growth, unless the observed AGN have an uncomfortably high radiative efficiency ( $\epsilon \gg 0.1$).

4.3 The evolution in the Eddington ratio of supermassive black holes

An alternative view of the evolution expected from the PCE hypothesis is to calculate the mean Eddington ratio $\langle\lambda\rangle$, where $\lambda $ is the ratio of the actual mass accretion rate $\dot{M}_{\rm acc}$to the Eddington mass accretion rate $\dot{M}_{\rm Edd}$ defined by $L_{\rm Edd} = \epsilon \dot{M}_{\rm Edd} c^2$, so that
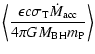                 $\displaystyle \left\langle\lambda\right\rangle$ = $\displaystyle \left\langle\frac{\epsilon c \sigma_{\rm T}\dot{M}_{\rm acc}}{4\pi GM_{\rm BH}m_{\rm P}}\right\rangle$  
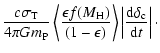  = $\displaystyle \frac{c \sigma_{\rm T}}{4\pi Gm_{\rm P}} \left\langle\frac{\epsil... ...ght\rangle \left \vert \frac{{\rm d}\delta_{\rm c}}{{\rm d}t} \right \vert\cdot$ (20)

In deriving this expression, it is important to remember that we have calculated the PCE-predicted average Eddington rate of all black holes in galaxies, not simply those that happen to be visible as AGN at any particular epoch. As we don't expect accretion to be a smooth continuous process for any one galaxy, this is an important distinction. An individual galaxy with an observed high rate of mass accretion could have an individual Eddington ratio approaching unity as seen in even local AGN (e.g. Onken et al. 2004) but the whole population of galaxies would have a much lower mean Eddington ratio.

So what significance can we attach to the mean Eddington ratio? If $\langle\lambda\rangle$ has a high value, it implies that, on average, there is plenty of matter available to fuel luminous accreting black holes at or close to their Eddington rate. In fact, values significantly higher than unity would imply that there is actually too much accreting matter available: we should expect that black hole growth by accretion would be limited to the Salpeter rate but that overall growth by mergers might be important. Conversely, a low value implies that, on average, there is insufficient new material accreting onto massive galaxies to maintain Eddington-limited black hole growth. Figure 6 shows $\left\langle\lambda\right\rangle$ as a function of redshift for a flat, $\Lambda $CDM cosmology, assuming $\Omega_M=0.3$, H0 = 73 km s-1 Mpc-1, $\sigma _8 = 0.74$, $M_{\rm H} = 10^{12.5} h^{-1}~{M_\odot}$, radiative efficiency $\epsilon=0.04$and without non-linear modification (Sect. 4.1).


  \begin{figure} \par\includegraphics[angle=270,width=7.8cm,clip]{4945fig6.ps} \end{figure} Figure 6: Ratio of mean accretion rate to the limiting Eddington rate, $\lambda $, as a function of (1+z) over the range 0<z<20, plotted logarithmically to demonstrate the near power-law dependence. Results are shown for $M_{\rm H}= 10^{12.5} ~h^{-1}~{M_\odot}$ and mean radiative efficiency $\langle\epsilon\rangle=0.04$ for: (a) $\Lambda $CDM cosmology, $\Omega _0=0.3$, $\Omega _{\Lambda }=0.7$, H0 = 73 km s-1 Mpc-1, $\sigma _8 = 0.74$ (solid curve); (b) Einstein-de Sitter cosmology with parameters as in (a) except $\Omega _0=1$, $\Omega _{\Lambda }=0$ (dashed curve).

The result plotted is remarkable in two respects. As already discussed, $\langle\lambda\rangle$ depends only weakly on the mass of dark matter halo and on the shape of the dark matter power spectrum, with no dependence on the fraction of a halo's total mass (dark matter plus baryons), that ends up in the black hole. Even the dependence on cosmology is weak, with a near power-law dependence on 1+z with exponent $n \simeq 2.4$ at z<1 for the $\Lambda $CDM cosmology compared with n = 2.5 for Einstein-de Sitter. Second, in principle there was no reason why the growth of dark matter halos should have any interesting relationship to the Eddington limit, except that both are governed by gravity. Yet it turns out that at low redshifts the mean ratio $\langle\lambda\rangle$ is consistent with the range of observationally determined values $\lambda_L$ (determined as the ratio of bolometric luminosity to estimated Eddington luminosity) for galaxy samples with a mean value $\langle\lambda_L\rangle \sim 0.0035$(Ho 2004) as discussed below. At moderate redshifts the mean ratio increases to a value $\langle\lambda\rangle \sim 0.1$ at $z \sim 4$, implying that at that epoch every galaxy has an actively accreting nuclear black hole (although typically with lower mass than today's black holes).

5 Discussion

5.1 Dispersion in Eddington ratio

The above analysis has only enabled us to calculate the mean evolution in luminosity density and in $\langle\lambda\rangle$. Since accretion events are discrete, we expect there to be a distribution of $\lambda $ values at any given cosmic epoch. In principle one could either attempt to calculate that distribution from EPS theory (e.g. Cole et al. 2000) or from numerical simulation (e.g. Hopkins et al. 2006; Di Matteo et al. 2005), or one could look at the observational constraints on the distribution. Ho (2004) has estimated the distribution of $\lambda_L$ for Palomar galaxies, with bolometric luminosities estimated from H$\alpha$ and black hole mass estimated from applying the Tremaine et al. (2002) relation to measured stellar velocity dispersions. The distribution at essentially zero redshift is broad, with a mean $\langle\lambda_L\rangle \sim 0.0035$, and although there are large uncertainties associated with the determination of $\lambda_L$the agreement to a factor about 2 with the value $\langle\lambda\rangle \sim 0.0015$ obtained at z=0 for $\langle\epsilon\rangle=0.04$ (shown in Fig. 6) is encouraging. The Ho (2004) values have a large dispersion, which results in there being a small number of galaxies with $\lambda_L \sim 0.1$ that are visible as AGN (Onken et al. 2004), and the vast majority of galaxies accreting at rates closer to $\langle\lambda_L\rangle$.

We again emphasise that the mean value $\langle\lambda\rangle$calculated here is the mean for all galaxies and is not the mean value expected for samples of AGN. By definition AGN are selected because they are actively accreting and they must therefore be biased to higher values than the mean. Using the results from this paper to predict the distribution and evolution of AGN requires knowledge of or assumptions about the distribution of $\lambda $ and will be discussed further by Babic et al. (in preparation).

5.2 AGN evolution and accretion at high redshift

As seen in Sect. 4.2, the absolute value and the evolution of either the observed space or luminosity density appears to be a combination of two competing but inter-related effects: the build-up of massive halos and hence black holes with decreasing redshift, and the decreasing accretion rate with decreasing redshift calculated in this paper. Croom et al. (2005) have shown that luminous QSOs inhabit dark matter halos of mass $\sim$ $10^{12.5} h^{-1}~M_{\odot}$: at low redshifts (z<1) the halo mass function, and hence the black hole mass function, is changing little at this mass, and AGN evolution is dominated by the evolution in $\lambda $. In this case we expect the evolution of the population to be dominated by apparent luminosity evolution: on average black holes at lower redshift accrete at a lower rate than black holes at higher redshift. Broadly speaking, this is what is observed (Boyle et al. 2000), although it's not the whole story (Zheng et al. 2004; Barger et al. 2005; Steffen et al. 2003; Ueda et al. 2003; Cowie et al. 2003). At higher redshifts (z>2) the growth of the black hole mass function is significant and probably dominates the evolution, causing a decline in space density with redshift (Fig. 5).

At $z \sim 4$ $\langle\lambda\rangle$ approaches the values found for the most luminous QSOs at lower z: at this epoch in cosmic history the average dark matter halo is accreting at a rate sufficient to supply close to the Eddington luminosity of its nuclear black hole: the majority of galaxies with such a black hole would be active. At higher redshifts still the rate of accretion of matter onto dark halos exceeds that required to supply the Eddington rate. In this case it is unlikely that super-Eddington accretion onto black holes would occur: it is more likely that nuclear outflows would limit the accretion process of individual black holes to about the Eddington rate and it is also possible that the black-hole/bulge relation may be built up during this phase of galaxy and black hole growth (King 2003; King & Pounds 2003).

5.3 Comparison with previous work

In previous numerical (e.g. Kauffmann & Haehnelt 2000; Volonteri et al. 2003; Croton et al. 2006) and analytic (e.g. Percival & Miller 1999) attempts to understand AGN evolution and supermassive black hole growth, AGN activity was hypothesised to be directly associated with merger events, and prescriptions were adopted that describe the relationship between the halo mass of a galaxy and the resulting AGN's luminosity, and between the rate of mergers and the evolving space density of AGN. Implicitly, a relationship between black hole mass and halo mass is assumed. To obtain the correct space density of AGN it was also necessary to assume a timescale for the luminous phase of a black hole following a merger. In these models, the evolution in EPS merger rate effectively produces number density evolution, whereas the dominant component of observed QSO evolution takes the form of luminosity evolution. As argued in the introduction, there must in fact have been evolution in mean accretion rate if local massive galaxies contain dormant supermassive black holes. This work shows how that evolution arises naturally in $\Lambda $CDM models. There has been no requirement to make assumptions about the luminosity/halo relation or the link with mergers and no assumption required about the timescale of AGN activity. The calculation presented here has assumed coeval growth of black holes: similar assumptions are made in, for example, Volonteri et al. (2003), but this assumption certainly needs further testing and evaluation. Overall, the extremely good agreement between the predicted and observed AGN luminosity density and its evolution, without any "model-tuning'', points to a close link between AGN cosmological evolution and the evolution in accretion onto galaxy halos. Conversely, predictions of recent semi-analytic models that attempt to provide recipes for the complex physics governing black hole growth (Croton et al. 2006) predict a peak in black hole formation rate (and hence presumably emitted luminosity density arising from accretion) at $z \sim 3$, with a decline to z=0 of a factor $\sim$6, in disagreement with the observed luminosity density presented in Sect. 4.2.

Numerical simulations have also been used to try to understand the link between black hole growth and galaxy mergers, and in particular to understand the role of feedback in forming the well-defined relation between galaxy velocity dispersion and black hole mass (e.g. Hopkins et al. 2005; Di Matteo et al. 2005; Hopkins et al. 2006; Robertson et al. 2006). These approaches are directly complementary to the question addressed in this paper, namely to understand analytically the effect that the cosmic slowdown in halo growth has on the typical black hole accretion rate. It may be that combining the two approaches will finally lead us to a detailed understanding of AGN evolution.

6 Conclusions

The results from this work may be summarised as follows.

1.
Press-Schechter theory may be used to calculate analytically the mean mass accretion rate of dark matter halos. The result of the calculation is in good agreement with previous numerical work but offers a significant improvement over previously-published fits to numerical simulations. The mass accretion rate depends almost linearly on mass but is very insensitive to choice of cosmological parameters within the range normally considered. We present fitting formulae to allow easy calculation of the accretion rate.

2.
It seems likely that the deduced strong decline in halo mass accretion will have an effect not only on the build-up of dark halos but also on the baryonic structures they contain. There may therefore be a close link between the cosmological evolution in star formation rate, in AGN accretion and dark halo accretion.

3.
We have investigated arguably the simplest hypothesis one could make for black hole growth, "Pure Coeval Evolution'' (PCE), which postulates that, on average, supermassive black holes have growth that tracks the growth of their parent dark halos. In this case it is straightforward to calculate the expected mass accretion rate onto black holes and, estimating the local black hole mass density, we predict a value for the integrated AGN luminosity density in remarkable agreement at $z \ga 0.5$with the value deduced from hard X-ray surveys.

4.
The evolution in integrated AGN luminosity density at z > 0.5 is well-matched by this model if the integrated black hole mass density tracks the mass density in massive $M_{\rm H}>10^{11.5}~{M_\odot}$ halos, consistent with the value obtained by inferring the clustering bias of QSOs in the 2dF QSO redshift survey (Croom et al. 2005)

5.
At z<0.5 the observed luminosity density falls off faster than predicted, although even by z=0 the overprediction is only a factor two. It seems that in the recent universe the black hole growth has started to decouple from dark halo growth, although a decrease in mean radiative efficiency associated with an increasing prevalence of ADAFs may also occur.

6.
Expressed in terms of the Eddington ratio, at sufficiently high redshifts ($z \ga 4$), halos would have black holes accreting at a significant fraction of the Eddington rate - we expect all massive galaxies to contain an active AGN. At higher redshifts still, the nominal Eddington ratio could greatly exceed unity. The response of the black hole would be to limit its growth to the Salpeter rate, but such systems might produce significant outflows (King 2003; King & Pounds 2003) which in turn would produce a significant feedback effect on their hosts. It is also likely that in this phase of black hole growth, growth by mergers between halos is faster than growth by accretion. Merger-dominated growth is one way of avoiding the problem of high-mass black holes at high redshift that have had insufficient time to grow at the Salpeter rate from solar- or intermediate-mass black hole progenitors (Willott et al. 2003).
Further work will model the AGN luminosity function and the contribution to the X-ray background (Babic et al. in preparation).

Acknowledgements
We are grateful to Y. Ueda for supplying data from Ueda et al. (2003). A.B. acknowledges support from the Clarendon Fund.

References

 

  
7 Online Material

   
Appendix A: Calculating d $\delta _{{\rm c}}/$dt

In this section we discuss the calculation of ${\rm d}\delta_{\rm c}\protect/{\rm d}t$ and approximations to it for cosmologies with a cosmological constant (the analysis could be extended to include more general dark energy cosmologies following the approach of Percival (2005) but this is beyond the scope of this appendix). We consider quantities that evolve as a function of scale factor a=(1+z)-1. If no dependence is quoted, the quantities should be assumed to be calculated at a=1 (z=0).

The critical overdensity for collapse $\delta _{\rm c}(a)$ in the spherical top-hat collapse model is the linear overdensity, extrapolated to the present day, that leads to the collapse of a homogeneous spherical region to a singularity at scale factor a. This is used in EPS theory to link overdensities with their predicted collapse times. However, two alternative formalisms are often considered for the collapse of perturbations in EPS theory.


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{4945fA1.ps} \end{figure} Figure A.1: Plot showing the mismatch between contours of constant $\delta _{\rm c}$ (black lines) and the lines along which $\Omega _M$ and $\Omega _\Lambda $ vary with the evolution of the universe (grey lines). The contours of constant $\delta _{\rm c}$ are plotted as a ratio of $\delta _{\rm EdS}$, the critical overdensity for collapse at redshift zero in an Einstein-de Sitter cosmology. Because these lines cross, the evolution of $\delta _{\rm c}(a)$ is not solely dependent on the linear growth factor.

1.
The overdensity field is assumed to grow with the linear growth factor, and when perturbations reach a particular critical overdensity they are said to have collapsed. This suggests that, given  $\delta _{\rm c}$, we can calculate  $\delta_{\rm c}(a)=\delta_{\rm c}D/D(a)$, where D(a) is the linear growth factor.
2.
An overdense region is considered to be spherical and to evolve according to the Friedmann equations, and hence its collapse time may be calculated. The overdensity value is extrapolated to the epoch at which the density field is normalised (conventionally, the present day) using the linear growth factor.
These two alternatives give different formulae for $\delta _{\rm c}(a)$. In Fig. A.1 we plot contours of constant $\delta _{\rm c}$ (black lines) within the plane of ( $\Omega_M,\Omega_\Lambda$) values, calculated using the method of Percival et al. (2000). Contours are plotted as a function of the value of $\delta _{\rm c}$ in an Einstein-de Sitter cosmology:

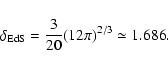\begin{displaymath}\delta_{\rm EdS} = \frac{3}{20}(12\pi)^{2/3} \simeq 1.686 . \end{displaymath} (A.1)

We also plot lines along which universes evolve (grey lines) given by
$\displaystyle \Omega_M(a) = \frac{\Omega_M}{a+(1-a)\Omega_M+(a^3-a)\Omega_\Lambda}$     (A.2)
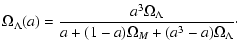$\displaystyle \Omega_\Lambda(a) = \frac{a^3\Omega_\Lambda}{a+(1-a)\Omega_M+(a^3-a)\Omega_\Lambda}\cdot$     (A.3)

Because $\delta _{\rm c}$ changes along the lines of evolution, we see that the spherical top-hat collapse model does not predict evolution of the critical overdensity given by $\delta_{\rm c}(a)=\delta_{\rm c}D/D(a)$.
  \begin{figure} \par\includegraphics[width=7.8cm,clip]{4945fA2.ps} \end{figure} Figure A.2: The percentage error in approximating the time derivative of $\delta _{\rm c}(a)$ as $\delta _{\rm c}(a)=\delta _{\rm EdS}D/D(a)$, where D(a) is the linear growth factor. Open symbols incorporate the approximation for D(a) given by Eq. (A.6), while solid symbols calculate D(a) by numerically integrating Eq. (A.4). Results are shown for three cosmological models: for an Einstein-de Sitter cosmology, both approximations reduce to the exact behaviour.

The first picture of EPS theory as corresponding to a growing field does not follow from the spherical top-hat collapse model. However, Fig. A.1 shows that the evolution of  $\delta _{\rm c}$ along lines of evolving ( $\Omega_M(a),\Omega_\Lambda(a)$) is small. In the remainder of this appendix we consider the error introduced in $\vert{\rm d}\delta_{\rm c}(a)/{\rm d}t\vert$ by assuming that the evolution in $\delta _{\rm c}(a)$ is governed solely by the linear growth factor. The linear growth factor D(a) is given by

 \begin{displaymath}D(a) = \frac{5}{2}\Omega_M H_0^2 H(a) \int^a_0\frac{{\rm d}a}{\left(aH\left(a\right)\right)^3}, \end{displaymath} (A.4)

where

 \begin{displaymath}\left(\frac{1}{a}\frac{{\rm d}a}{{\rm d}t}\right)^2\!= \!H(a)... ...ambda+\Omega_Ma^{-3}-(\Omega_m+\Omega_\Lambda-1)a^{-2}\right). \end{displaymath} (A.5)

D(a) may be approximated using the fitting formula of Carroll et al. (1992):
 
$\displaystyle D(a) \simeq \frac{5\Omega_M(a)a}{2} \left[\Omega_M(a)^{4/7}-\Omeg... ...a_M(a)}{2}\right) \left(1+\frac{\Omega_\Lambda(a)}{70}\right) \right]^{-1}\cdot$     (A.6)

Equation (A.4) can be differentiated to obtain
 
                  $\displaystyle \frac{{\rm d}D(a)}{{\rm d}a}$ = $\displaystyle \frac{H_0^2}{H(a)^2} \left[\frac{5}{2}\frac{\Omega_M}{a^3} -\frac{3}{2}\frac{D(a)\Omega_M}{a^4}\right.$ (A.7)
    $\displaystyle \left.+(\Omega_M+\Omega_\Lambda-1)\frac{D(a)}{a^3} \right]\cdot$ (A.8)

Finally, the approximation to ${\rm d}\delta_{\rm c}(a)/{\rm d}t$ is given by

 \begin{displaymath}\frac{{\rm d}\delta_{\rm c}(a)}{{\rm d}t} \simeq \delta_{\rm ... ...2} \frac{{\rm d}D(a)}{{\rm d}a}\frac{{\rm d}a}{{\rm d}t}\cdot \end{displaymath} (A.9)

Equations (A.5)-(A.9) combine to provide an analytic approximation to ${\rm d}\delta_{\rm c}\protect/{\rm d}t$. In Fig. A.2, we plot the percentage error introduced by this approximation compared with numerically integrating the behaviour of $\delta _{\rm c}(a)$, calculated using the method of Percival et al. (2000) (open symbols). We also consider calculating D(a) exactly and use this instead of the Carroll et al. (1992) approximation in Eq. (A.8) (solid symbols). The solid symbols show the error in ${\rm d}\delta_{\rm c}\protect/{\rm d}t$ from ignoring the evolution in  $\delta _{\rm c}$ because of changing $\Omega _M$ and  $\Omega _\Lambda $. Comparison of solid and open symbols shows the error introduced by Eq. (A.6). Errors are plotted for three cosmologies: for the Einstein-de Sitter cosmology, the approximations reduce to the exact result. For the $\Lambda $ and open cosmologies, the maximum error is less than 2%.


Copyright ESO 2006