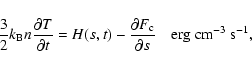A&A 458, 987-995 (2006)
DOI: 10.1051/0004-6361:20065691

Explosive heating of low-density coronal plasma

S. J. Bradshaw - P. J. Cargill

Space and Atmospheric Physics, Blackett Laboratory, Imperial College London, Prince Consort Road, London, SW7 2BZ, UK

Received 25 May 2006 / Accepted 9 August 2006

Abstract
Context. This paper addresses the impulsive heating of very diffuse coronal loops, such as can occur in a nanoflare-heated corona with low filling factor.
Aims. We study the physics associated with nanoflare heating in this scenario and aim to determine whether there exist any observable signatures.
Methods. We derive an analytical model in order to gain some simple physical insights into the system and use a one dimensional hydrodynamic model that treats the electrons and ions as a coupled fluid to simulate nanoflare heating with time-scales of 30 s. Our analytical model also provide a means of verifying our numerical results.
Results. We find that diffuse loops containing plasma at T> 20 MK can be rapidly created and subsequently filled by the violent evaporation of chromospheric plasma driven by near-saturated thermal conduction. Most importantly, we find order-of-magnitude departures from equilibrium of the ionisation balance for iron and use this result to identify a potential signature of this heating mechanism.
Conclusions. We conclude that nanoflare heating can account for the presence of extremely high temperature plasma in a corona with low filling factor. We find that near-saturated thermal conduction may play a key role at the onset of chromospheric evaporation and a non-equilibrium ionisation balance is absolutely inevitable. The high temperatures could never be directly measured in the corona due to the small emission measure and the most promising signature of such heating is blue-shifted plasma from the loop footpoints. We find reason for cautious optimism that this signature can be detected by future space-based spectroscopic instrumentation (e.g. SolarB-EIS).

Key words: atomic processes - hydrodynamics - Sun: corona - Sun: UV radiation

   
1 Introduction

It is now recognised that a determination of the coronal heating mechanism in closed magnetic loops requires a strong connection between data obtained at EUV and X-ray wavelengths and theoretical models. One approach relies on relating observations of magnetic field-aligned temperature and density profiles to numerical models in order to determine how energy is deposited spatially in a loop (Priest et al. 2000; Mackay et al. 2000; Aschwanden et al. 2001). Difficulties with this approach include the non-uniqueness of the calculated heating function, the lack of consideration of impulsive, non-steady heating, and the fact that the observations almost certainly do not resolve the fine structure of the loop.

An alternative approach developed in the past two decades involves so-called forward modelling. Here, the intensity of emission that one may expect a particular instrument to measure is synthesised. For example, given the temperature, number density and bulk velocity from a numerical simulation, along with the relevant atomic data provided by a database such as CHIANTI (Dere et al. 1997; Landi et al. 2006), and the optical properties, performance characteristics and orbital geometry parameters of the observing instrument, it is possible to estimate the measured intensity of emission (in instrument units) for direct comparison with actual observational data. Furthermore, such an approach can predict the wavelength regions in the EM spectrum where strong signatures may be seen, hence guiding future instrument development.

A popular scenario for coronal heating is small-scale magnetic reconnection events (commonly referred to as nanoflares: Parker 1983, 1988). In earlier work, (Cargill 1993; Cargill 1994; Cargill & Klimchuk 1997; Cargill & Klimchuk 2004), we calculated observable signatures of such models, especially for high temperature plasma such as observed by Yohkoh-SXT. Features of this modelling were the prediction of significant high-temperature plasma components, and coronal structures with low filling factors. By the latter we mean that in any observed coronal volume, a significant fraction of the volume is empty, i.e. the radiation comes from relatively few high-density strands. However, nanoflare heating is likely to be distributed quasi-randomly in the corona, so that strong heating will occur in what are effectively evacuated regions of the corona.

In our early work (Cargill 1994) we dealt with strong plasma heating of such tenuous strands in an approximate way, but in fact such a process raises many new questions that need to be addressed if we are to understand present and future observations. In this paper we use numerical simulations and forward modelling to address these questions and investigate the heating of initially very tenuous and cool active region loops to very high temperatures, which represents the situation in the corona at low filling factor. As we shall see, of particular importance are saturated and non-local heat-fluxes, non-equilibrium ionisation, fast cooling, small emission measures and remote dynamical signatures.

The work most closely comparable to that presented in this paper is by Patsourakos & Klimchuk (2005), though our work differs in several important ways. We explore a substantially different temperature and density regime; our initial conditions have much lower temperature and density, and our plasma reaches a much higher temperature during heating. Since reconnection rates are related to the local Alfven speed, one may argue that reconnection will be more efficient in evacuated regions and so we consider far more rapid heating (30 s pulses compared with 250 s pulses in Patsourakos & Klimchuk 2005). Our low density and fast heating regime also forces us to consider the effect of non-equilibrium processes on the temperatures of different particle species and on the ionisation balance because the rate of heating is far greater than the relevant collisional equilibration rates. Therefore, we introduce a two-fluid model (electrons and ions) and include the effects of energy exchange between particle species. Our inclusion of the effects of a non-equilibrium ionisation balance becomes crucially important when synthesising emission lines in our forward-modelling procedure. However, in common with Patsourakos & Klimchuk (2005) we also consider a saturated heat-flux.

In Sect. 2 we derive a simple analytical model for a more intuitive understanding of the interaction between the dominant physical processes and provide a discussion of the accompanying numerical experiment (see also Appendix A). In Sect. 3 we discuss the results from our numerical experiment and compare them with our analytical model. In Sect. 4 we use the technique of forward-modelling to search for potentially observationable signatures of explosive heating, with particular reference to the SolarB Extreme ultra-violet Imaging Spectrometer (EIS). In Sect. 5 we summarise our findings, present our conclusions and state our intentions for future work.

   
2 The model

   
2.1 Heat flux saturation

We consider the evolution of a loop initially in hydrostatic equilibrium having length 2L = 30 Mm, a uniform temperature of T = 0.02 MK and gravitationally stratified, with a density of n= 10⁷ cm^-3 at the apex. Such a cool and tenuous loop may arise in the model of a nanoflare-heated corona described in the Introduction, or immediately after emergence of new magnetic field through the photosphere. As we will see, the release of energy into such a loop results in fast heating and high temperatures, so we refer to it as explosive heating. We consider only one-dimensional evolution (i.e. along a magnetic flux element, or a bundle of field lines) and assume that the rigid magnetic field guides heat conduction and plasma flows. The full set of equations solved are presented in Sect. 2.2.

An analytical model will be a useful guide to the computational results presented later on. In it we assume that two processes determine the loop pressure and temperature during explosive heating: plasma heating and thermal conduction. Thermal conduction is highly efficient at this time and dominates energy transfer/loss due to mass motions and optically thin radiation. The equation of energy balance describing this system can be written as:

$$% \frac{3}{2} k_{\rm B} n \frac{\partial T}{\partial t} = H(s... ...\partial F_{\rm c}}{\partial s} ~~~~ {\rm erg~cm^{-3}~s^{-1}},$$ (1)

where we have considered only a single particle species, $k_{\rm B}$ is the Boltzmann constant, n and T are the number density and temperature of the particle species, H(s,t) is energy input and $F_{\rm c}$ is the heat flux. The spatial coordinate, s, is taken along the field and t is time. n = n(s) since flows are neglected. All physical quanities are in c.g.s. units throughout.

For constant heating we may estimate an equilibrium temperature reached at the loop apex:

$$\begin{eqnarray*}H_0 \approx \frac{\partial F_{\rm c}}{\partial s}\cdot \end{eqnarray*}$$

Assuming a classical (Spitzer) conduction ( $F_{\rm c} = \kappa_0 T^{5/2}{\rm d}T/{\rm d}s$), where $\kappa_0 = 7.8$ $\times$ 10^-7, and integrating over a characteristic coronal length scale (L) gives:

$$% H_0 = \frac{\kappa_0 T^\frac{7}{2}}{L^2} ~~~~ {\rm and} ~~~~ T = \left[\frac{H_0 L^2}{\kappa_0}\right]^\frac{2}{7}\cdot$$ (2)

However, this is not the full picture because in our rarefied initial conditions the free-streaming or flux-saturation limit, describing the maximum conducted flux that the plasma is capable of supporting, may easily be reached. The flux becomes saturated when all of the particles travel in the same direction at the electron thermal speed, $v = \left[\frac{k_{\rm B} T}{m_{\rm e}}\right]^\frac{1}{2}$. This saturated flux is given by:

$$% F_{\rm s} = \frac{3}{2\sqrt{m_{\rm e}}} n \left(k_{\rm B} T\right)^\frac{3}{2}.$$ (3)

Thus, $H_0 = F_{\rm s}/L$ and

$$% T = \left[\frac{2\sqrt{m_{\rm e}}H_0 L}{3 k_{\rm B}^\frac{3}{2} n}\right]^\frac{2}{3}\cdot$$ (4)

It is important to note that in Eq. (2) the equilibrium temperature reached is independent of the density, whereas Eq. (4) shows that in the saturated regime lower densities give rise to higher temperatures. This is due to the reduced heat capacity of lower density plasma and its inability to conduct the excess energy away.

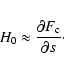
In order to assess the importance of flux-saturation in our model, we may equate the two fluxes and establish that it is important for temperatures ( $T_{\rm crit}$) exceeding:

$$% T_{{\rm crit}} = \left[\frac{3 k_{\rm B}^\frac{3}{2}}{2\sqrt{m_{\rm e}}\kappa_0} n L\right]^\frac{1}{2}\cdot$$ (5)

For a plasma with n= 10⁸ cm^-3, L= 1.5 $\times$ 10⁹ cm and assuming only electrons are heated, we find $T_{\rm crit} \approx$ 4 MK. Thus, flux-saturation is important in this parameter regime. Note also that at the apex itself $F_{\rm c} = 0$ due to symmetry. However, if flux saturation is important further down the loop then this will result in thermal energy being bottled up between the location of saturation and the apex, causing the plasma in this region to reach and maintain a higher temperature than would otherwise be expected.

   
2.2 Numerical model

We use the numerical code HYDRAD (Bradshaw & Mason 2003a,b; Bradshaw et al. 2004; Taroyan et al. 2006) to solve the one-dimensional, two-fluid hydrodynamic equations for a loop geometry. (Appendix A contains a detailed discussion of the difficulties encountered when attempting to solve these equations numerically, and the approach adopted to obtain solutions that are appropriate to the problem at hand.)

$$% \frac{\partial \rho}{\partial t} + \frac{\partial}{\partial s}\left(\rho v\right) = 0,$$ (6)

$$% \frac{\partial}{\partial t}\left(\rho v\right) + \frac{\par... ...al s}\left(P_{\rm e} + P_{\rm i}\right) - \rho g_{\vert\vert},$$ (7)

 

$$% \frac{\partial E_{\rm e}}{\partial t} + \frac{\partial}{\partial s}\left[\left(E_{\rm e} + P_{\rm e}\right)v\right] -\frac{\partial F_{{\rm ce}}}{\partial s} + v\frac{\partial P_{\rm e}}{\partial s}$$ =

$$+ \frac{k_{\rm B} n}{\gamma-1}\nu_{{\rm ie}}\left(T_{\rm i}-T_{\rm e}\right) - R + H,$$ (8)

 

$$% \frac{\partial E_{\rm i}}{\partial t} + \frac{\partial}{\partial s}\left[\left(E_{\rm i} + P_{\rm i}\right)v\right] -\frac{\partial F_{{\rm ci}}}{\partial s} - v\frac{\partial P_{\rm e}}{\partial s}$$ =

$$+ \frac{k_{\rm B} n}{\gamma-1}\nu_{{\rm ie}}\left(T_{\rm e}-T_{\rm i}\right) + \rho v g_{\vert\vert}.$$ (9)

The plasma is effectively considered to be composed of two particle species (electrons and protons) except insofar as the mass density, the bulk flow and optically-thin radiation are concerned, where significant contributions from the heavier elements are included. In these equations a subscript e (i) denotes a property of the electron (ion) fluid. $\rho = m_{\rm i}n$, where $m_{\rm i}$ is the average ion mass and accounts for the fact that while hydrogen is by far the most abundant element, the presence of heavy metals has a non-negligible influence on the mass density and the bulk flow.

The first term on the right-hand side of Eqs. (8) and (9) represents the thermally conducted flux carried by each particle species. The Spitzer coefficient for the electron thermal conduction is $\kappa_{\rm0e} = 7.8$ $\times$ 10^-7 and we assume that protons dominate the ion thermal conduction, giving $\kappa_{\rm0i} = 3.2$ $\times$ 10^-8. A flux-limiter is built into the numerical code to ensure that the free-streaming limit is not exceeded (see also Patsourakos & Klimchuk 2005). The second term on the right-hand side of Eqs. (8) and 9, the flux of the electron pressure, $P_{\rm e}$, represents the work done by/on the particles due to the weak electric fields that arise from the quasi-neutral conditions. The third term represents the thermal equilibration between the particle species via collisions, where  $\nu_{\rm ie}$ is the Coulomb collision frequency:

$$\begin{eqnarray*}\nu_{\rm ie} = \frac{16\sqrt{\pi}}{3} \frac{e^4}{m_{\rm e} m_{\... ...e}}{m_{\rm e}}\right)^{-\frac{3}{2}} n \left(\ln \Lambda\right), \end{eqnarray*}$$

where $\ln \Lambda$ is the Coulomb logarithm. The gravitational potential energy has been included for the ions and neglected for the electrons. R is the optically-thin radiative emission, which includes: a non-equilibrium contribution from iron; equilibrium contributions from the remaining most abundant elements of the solar atmosphere; and thermal bremmstrahlung. H is the heating function given by Eqs. (11) to (13). The remaining closure conditions for Eqs. (6) to (9) are:

$$% P_{\rm e} = k_{\rm B} n T_{\rm e},~P_{\rm i} = k_{\rm B} n ... ...~E_{\rm i} = \frac{P_{\rm i}}{\gamma-1} + \frac{1}{2}\rho v^2,$$ (10)

since the electron kinetic energy is a factor  $m_{\rm i}/m_{\rm e}$ smaller than the ion kinetic energy. We use a piece-wise expression for H(s,t) comprised of three stages:

$$% H(s,t) = H_0 \left(1-\exp\left[-\frac{t}{\tau_H}\right]\rig... ...\exp\left[-\frac{\vert s-s_0\vert}{s_H}\right], t < t_{\rm i};$$ (11)

$$% H(s,t) = H_0 \exp\left[-\frac{\vert s-s_0\vert}{s_H}\right], t_{\rm i} < t < t_{\rm f};$$ (12)

$$% H(s,t) \!=\! H_0 \left(1\!-\!\exp\left[-\frac{t_D - t}{\tau... ...frac{\vert s-s_0\vert}{s_H}\right], t_{\rm f} < t < t_{\rm D}.$$ (13)

$\tau_H$ is the e-folding period of the ramp-up time, and s₀and s_H are the location of maximum heating and the scale-length of heat deposition. The heating ramps up to $t_{\rm i}$, remains constant between $t_{\rm i}$ and $t_{\rm f}$, and ramps down to zero between $t_{\rm f}$ and $t_{\rm D}$. The parameters in the heating function have been chosen to closely match the characteristic properties of a classical nanoflare as detailed in the theory of Parker (1988): H₀ = 1 erg cm^-3 s^-1; $\tau_H$ = 0.1 s; s₀ = 1.5 $\times$ 10⁹ cm; s_H = 2 $\times$ 10⁸ cm; $t_{\rm i}$ = 1 s; $t_{\rm f}$ = 29 s; and $t_{\rm D}$ = 30 s. We have chosen a constant cross-sectional area for the filament of 10⁷ $\times$ 10⁷ cm², which yields an energy release of just over 10²⁴ erg in total. Observations suggest that coronal loop cross-sections are roughly constant (Watko & Klimchuk 2000), implying in turn a roughly uniform magnetic field.

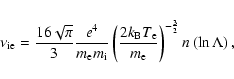
Our initial equilibrium solution (described at the beginning of Sect. 2.1) is obtained by forcing a balance between the heat input and the radiative emission, which is assumed to be negligible (and thus zero) at 0.02 MK. Consequently, the initial heat input is identically zero and all of the energy released into the loop is due to the explosive heating event alone. Therefore, we do not assume any background heating to derive our initial hydrostatic configuration. We follow the evolution of the plasma for a period of 100 s.

   
3 Results

   
3.1 Dynamical behaviour

The evolution of the electron temperature and density profiles along the loop at 5 s intervals during the 30 s period of explosive heating is shown in Fig. 1. The release of energy heats the plasma locally, rapidly raising its temperature above 10 MK, and sends a thermal conduction front propagating towards each footpoint (see also Fig. 3), which drives the evaporation of lower lying plasma, carrying it towards the apex and increasing the density in the upper part of the loop. Though the loop was initially isothermal and gravitationally stratified, steep temperature and density gradients are quickly created, which lead to the formation of the familiar chromosphere-transition region-corona structure.

	Figure 1: Temperature and density profiles from the footpoint (s=0 cm) to the apex (s=1.5 $\times$ 109 cm) of the loop during explosive heating. Times: 5 s (solid); 10 s (dot); 15 s (dash); 20 s (dot-dash); 25 s (triple dot-dash); and 30 s (long dash).
Open with DEXTER

	Figure 2: The time-evolution of the apex temperature and density during and following explosive heating.
Open with DEXTER

The temperature and density at the apex of the loop during the first 100 s of the numerical experiment is shown in Fig. 2. The nature of the explosive heating is clear; the plasma reaches a peak temperature of $\approx$25 MK in 0.5 s and maintains a temperature greater than 10 MK for the first 20 s. Thereafter, the temperature reaches an equilibrium plateau of $\approx$8 MK, where it remains until the heating is switched off at 30 s. The apex density increases from an initial value of 10⁷ cm^-3 to over 10⁹ cm^-3 during the first 30 s. The periodic behaviour evident in the apex density after 30 s is due to the compresssion and rarefaction of the plasma as material evaporated from each footpoint collides and rebounds. After 30 s the loop proceeds to cool, first by thermal conduction and subsequently by radiation. The cooling phase has been studied in detail in previous work (Cargill et al. 1995; Bradshaw & Cargill 2005) and we refer the interested reader to these publications.

Given the extreme parameter regime we are working within it is desirable to be able to check and otherwise validate our numerical results. In Sect. 2.1 we predicted the existence of an equilibrium temperature reached via the balance of heat input and thermal conduction; the two physical mechanisms considered to dominate during the initial stages of explosive heating. By first considering thermal conduction in the unsaturated regime we derived Eq. (2), which should apply at the apex of the loop where $F_{\rm c} = 0$ due to symmetry. Indeed, given H₀=1, L=1.5 $\times$ 10⁹ and $\kappa_{\rm0e} = 7.8$ $\times$ 10^-7, Eq. (2) gives an equilibrium temperature of $\approx$9.7 MK, compared with our numerical value of 8 MK. There are several reasons why the numerical value is slightly less than our analytical estimate. Firstly, the apex density is sufficiently large by the time the temperature equilibrium is established that optically-thin radiative emission makes a non-negligible contribution to the energy balance. This is good news because it increases our chances of actually observing something! Secondly, the electron fluid loses energy to the unheated ion fluid via Coulomb collisions and as the density increases so does the rate of energy exchange. Neither of these effects are accounted for in the analytical estimate but they are present in the numerical model and act to remove energy from the electrons, thus reducing their temperature. However, for the purpose of validating the numerical results the two estimates of the equilibrium temperature are sufficiently close, with the reasons for any differences well-understood, that we can be confident the code is working as expected and providing reliable results.

	Figure 3: The ratio of thermal flux ($F_{\rm c}$) to saturated thermal flux ($F_{\rm s}$) from the footpoint to the apex of the loop during explosive heating. Times: 1 s (solid); 5 s (dot); 10 s (dash); 20 s (dot-dash); and 30 s (triple dot-dash).
Open with DEXTER

   
3.2 Heat flux saturation

The ratio $\frac{F_{\rm c}}{F_{\rm s}}$, where $F_{\rm s}$ is the saturated thermal flux at the corresponding temperature and density, is given as a function of position along the loop at a selection of times during the heating event in Fig. 3. At 1 s, as expected, the flux in the apex region is unsaturated and remains so thereafter. However, between 1 s and 10 s we see that the flux is near-saturated along a significant fraction of the length of the loop, which means that thermal conduction is operating extremely efficiently in these regions and at first sight justifies the assumptions we made in order to derive our analytical model. As the loop is evaporatively filled the value of $F_{\rm s}$ becomes relatively large compared with $F_{\rm c}$ in proportion to the increase in density, as predicted by Eq. (3), and after 20 s the flux is unsaturated along the entire length of the loop. This corroborates the match between the analytical and numerical equilibrium temperatures discussed above.

We see a spike at s=5 $\times$ 10⁸ cm after 1 s of heating where the flux does become saturated and which subsequently propagates in the direction of the footpoint, though the flux in the region of the spike is unsaturated at later times. We must appreciate that $F_{\rm c}$ is almost certainly artificially limited by the resolution of our computational grid, which limits the temperature gradient, and given a higher resolution $F_{\rm c}$ may also be saturated at later times. However, since our analytical and numerical predictions are in good agreement we don't expect increasing the resolution to qualitatively affect our numerical results. The spike corresponds to the location at each given time where the temperature gradient is most rapidly steepening as a result of high density plasma being heated and then radiating strongly. The region of strongest radiation will always be at the location where the plasma has just been heated by the downward propagating thermal conduction front since this is where the density is highest; recall that the loop is gravitationally stratified and the radiative energy loss is proportional to n². The only way to balance this energy loss is by increasing the thermal flux, which can only be achieved by a steepening temperature gradient. As we have already said, no significant dynamical behaviour has developed at 1 s and so no other process such as convection, for example, can come to the aid of the energy balance.

	Figure 4: The ionisation balance of several ions of iron during explosive heating. The ion populations are far from equilibrium.
Open with DEXTER

   
3.3 Ionisation balance

Given the high temperatures maintained by the coronal plasma throughout the period of heating one may expect the emission to be dominated by very highly charged ions if, as is commonly assumed, the ionisation balance of the plasma remains in equilibrium. While this may be a reasonable (though possibly not entirely satisfactory) assumption for the high densities encountered during large-scale solar flares, Fig. 4 clearly shows that the ionisation balance in low density plasma during small-scale explosive heating may exist far from equilibrium. For example, the peak population temperatures of Fe VIII and Fe IX in equilibrium are 10^5.6 K and 10^5.8 K, respectively; however, at 5 s the peak population temperatures of Fe VIII and Fe IX are 10^6.5 K and 10^6.4 K. The peak population temperature for each of these ions continues to increase during the heating phase and at 20 s the peak population temperatures of Fe VIII and Fe IX are both in the region of 10^6.8 K. This is an order of magnitude departure from equilibrium!

The series of ionisation balances in Fig. 4 reveal that lower charge states (e.g. Fe VIII to Fe XII) tend to be created in the higher density, lower temperature plasma located further down the loop and are then carried upwards into higher temperature regions by the evaporative upflows; higher charge states (e.g. Fe XIII and Fe XIV) tend to be created closer to their equilibrium formation temperatures when the local density (and thus the rate of ionisation) is increased by the arrival of evaporated material. Consequently, we may expect to observe emission from relatively low charge states far from equilibrium. However, the emission observed from higher charge states may be closer to equilibrium; essentially because the density must have increased sufficiently for these higher charge states to be reached before the onset of significant cooling. These processes are a direct consequence of the ionisation balance as it is coupled to the hydrodynamics of the loop plasma and this aspect of plasma physics must be considered when studying observational data, as we will show in Sect. 4.

	Figure 5: The ratio of total energy (thermal + kinetic) to total heat input during explosive heating.
Open with DEXTER

   
3.4 Estimated radiative energy loss during explosive heating

An important quantity is the ratio of the thermal energy in the loop as a function of time to the energy released by the heating mechanism:

$$% R_{EQ} = \frac{E}{Q} = \frac{\int{\left( 3 k_{\rm B} n T + ... ...} \rho v^2 \right){\rm d}s}}{\int{\int{H {\rm d}s {\rm d}t}}},$$ (14)

where the quantity in the denominator can be obtained by a straightforward integration of Eqs. (11) to (13). This provides information on how much energy actually goes into increasing the temperature of the plasma during the heating event, and how much is transformed/lost by other processes. This is of particular importance because the energy required to heat a coronal structure is often calculated from the observed radiative intensity of the structure (in a relatively narrow temperature and wavelength range) and the dimensions of the observable part of the structure. However, a considerable amount of the energy released may be radiated away at lower temperatures and higher densities (e.g. from the transition region) before the coronal structure even becomes visible. Furthermore, when estimating the energy released into a particular volume the filling factor becomes a crucial parameter. It may be the case that only a small fraction of the resolved volume actually contains plasma at temperatures within the sensitivity range of the observing instrument. Using Eq. (14), we see from Fig. 5 that a negligible amount of the total energy supplied by 1 s has been radiated by the system, which is as expected. By 10 s about 3% of the total energy supplied has been radiated; by 20 s the figure is 21%; and by 30 s just over 35% has been radiated away. The question we must ask ourselves is: does this radiated energy contain any observable signatures of the heating event that we can use to determine its properties?

   
4 Observable signatures of explosive heating

Figure 1 shows that the plasma in the region of explosive heating at its onset is sufficiently tenuous (n $\approx$ 10⁷ cm^-3) that there would be little or no chance of making a direct observation. By the time at which the density has increased by an order of magnitude the structuring of the temperature profile induced by explosive heating has been smoothed out by the extremely efficient thermal conduction and any information contained within the radiative emission that may have provided clues to the nature of the heating event has been lost by 30 s. Therefore, a study of the cooling phase will not reveal anything about the heating phase (Winebarger & Warren 2004) and we must look to the possibility of indirect signatures in the emission during the period of explosive heating for observational clues to its nature (Klimchuk 2006).

	Figure 6: The predicted counts (as functions of temperature and spatial location) at 2 s intervals, between 4 s and 20 s, for the Fe VIII emission in the SolarB-EIS short wavelength (170-210 Å) range during explosive heating. Times: 4 s (solid); 6 s (dot); 8 s (dash); 10 s (dot-dash); 12 s (triple dot-dash); 14 s (long dash); 16 s (cross); 18 s (asterisk); and 20 s (diamond).
Open with DEXTER

	Figure 7: The predicted counts (as a function of temperature) for the emission from higher charge states of iron in the SolarB-EIS short wavelength (170-210 Å) range during explosive heating. Charge states: Fe VIII (solid); Fe IX (dot); Fe X (dash); Fe XI (dot-dash); Fe XII (triple dot-dash); and Fe XIII (long dash).
Open with DEXTER

	Figure 8: The predicted counts (as a function of spatial location) for the emission from higher charge states of iron in the SolarB-EIS short wavelength (170-210 Å) range during explosive heating. Charge states: Fe VIII (solid); Fe IX (dot); Fe X (dash); Fe XI (dot-dash); Fe XII (triple dot-dash); and Fe XIII (long dash).
Open with DEXTER

The behaviour of Fe VIII in Fig. 4 suggests one such possibility. Figure 6 shows Fe VIII emission (in instrument units of DN pixel^-1 s^-1) as a function of temperature and spatial location at 2 s intervals between 4 s and 20 s. The emission was calculated by a forward-modelling procedure using our numerical results and the short wavelength response function of SolarB-EIS. The emission is not spatially coincident with the region of heating (hence indirect) and has two components; a more-or-less stationary component below 10^6.4 K; and a higher temperature component, which is clearly associated with an upflow and therefore blue-shifted during the heating event. Figures 7 and 8 shows the emission from higher charge states of iron at 2 s intervals between 16 s and 20 s in the EIS short wavelength band; this emission is spatially coincident with the strongest of the earlier Fe VIII emission and also has a blue-shifted component. We may thus characterise explosive heating by two phases: the initial phase ($\approx$15 s) dominated by blue-shifted emission from Fe VIII; the final phase dominated by blue-shifted emission from higher charge states. Could this characterisation provide an indirect but observable signature of explosive heating?

The answer to this question depends upon the answers to two further questions. The first of these questions is: are the counts high enough to observe anything of this potential signature? The answer: possibly. We have considered only a single, filamentary loop of very small cross-section; in reality several neighbouring strands might be heated together and their emission integrated along the line-of-sight would increase the counts. Conversely, the strands might be heated separately; in this case the signature could be smoothed from the detected emission, though one might still observe blue-shifted emission from successive ionisation stages which may by itself be indicative, if the emission is spatially coincident.

The second question is: does EIS have the capability to resolve this signature? The answer: a cautious yes. The design specifications for EIS require a spatial resolution of 2'' and it is clear from Fig. 6, and Figs. 7 and 8, that the spatial scales of the emission structures are greater than 2''. The spatial resolution of EIS may even be sufficient to resolve the stationary and blue-shifted components of the emission. The temporal resolution of EIS is expected to be $\approx$10 s (though below 1 s in sit-and-stare mode) which acts to our advantage by increasing the counts, though it is close to the limit at which the two phases of explosive heating can be temporally resolved. However, given a sufficient number of observations a clear signature may be observed, though again it may be enough to observe blue-shifted emission from successive ionisation stages, if the emission is spatially coincident. The question of spectral resolution depends upon whether there are any emission lines sufficiently close to the Fe VIII lines for blending to be a potential problem and then whether these lines can be excited simultaneously with their neighbouring Fe VIII lines in the situation we are considering. The strongest Fe VIII lines in the EIS short wavelength region are at 193.97 Å, 194.66 Åand 195.97 Å, and nearby lines are emitted by S X, Ar XI, Ar XIV, Ca XIV, Fe X, Fe XII, Fe XIII and Ni XV (http://www.mssl.ucl.ac.uk/solarb/line_lists/activelines.html). We can discount the iron lines during the initial phase of explosive heating only if this phase can be temporally distinguished from the final phase, which has itself been characterised by the onset of emission from higher charge states of iron. The other ions with nearby lines are all formed at considerably higher temperatures than Fe VIII and so we may expect these stages to be reached only during the final phase, which is dominated by the emission from iron (particularly Fe XII at 195.12 Å).

   
5 Summary and conclusions

We have carried out a numerical experiment to investigate explosive heating in a cool, evacuated loop, of the type we expect to exist in a corona of low filling factor, or following the initial emergence of magnetic flux through the photosphere. Although there is a long history of simulating energy release in one dimensional loop models, we believe the conditions modelled here are the most appropriate for a low filling-factor corona (very low density and fast heating). (The closest comparable work (Patsourakos & Klimchuk 2005) considered an initial density of 3 $\times$ 10⁸ cm^-3 and nanoflares lasting 250 s.)

We found that explosive heating can rapidly produce loops containing plasma at T> 20 MK, filled by the violent evaporation of low lying, high density plasma, which is driven by near-saturated thermal conduction. We found order-of-magnitude departures from equilibrium of the ionisation balance for iron, proving beyond all doubt the importance of this effect in diagnostic studies, and used this result to identify a potential signature of explosive heating characteristed by two phases: an initial phase dominated by blue-shifted emission from Fe VIII; and a final phase dominated by blue-shifted emission from higher charge states. We assessed the capability of the EIS instrument due to fly on Solar-B to unambiguously detect this signature and found reason for cautious optimism. If small-scale, bursty (nanoflare) heating is indeed responsible for the extremely high temperature regions of the corona then such an observation will provide the first direct evidence for this mechanism in operation.

In terms of the generic process of conductive energy transport to the chromosphere, and subsequent evaporation of heated material, our results confirm the existing picture. The importance of this work instead lies in the difficulties that become apparent in measuring signatures of heating in very hot coronal plasma. While heat flux saturation undoubtedly extends the lifetime of hot coronal sources by inhibiting conductive energy transport, there are considerable difficulties in creating the ionisation states with the emission lines that would actually provide the signatures of heating. Furthermore, the small coronal emission measure in an explosively heated loop would make the detection of high temperature plasma very difficult. Indeed, it seems as if the most plausible observable of explosive heating in a low filling-factor corona would be strong blue-shifts in somewhat cooler emission lines.

The approach adopted in this paper has treated heat flux limiting within the fluid description. However, it should be noted that a full solution to the problem addressed here requires a kinetic approach (or at least a multi-fluid treatment of the electrons). This may be modelled through a solution of the Boltzmann equation for energetic electrons in conjunction with the hydrodynamic equations and will be the subject of a future paper.

Another issue of interest is the process through which coronal charge and current neutrality is maintained. Escaping hot coronal electrons require the generation of a return current of cooler, background electrons. The interaction between two such electron populations, and the background ions, has been the subject of extensive discussion in the literature in the past decades, albeit for rather different scenarios than in the present work. In particular, the impulsive injection of electron beams and strong local heating on scales of a few Debye lengths have been studied (Emslie 1980; D'Iakonov & Somov 1988; McKean et al. 1990). There is potential for energy loss from the return current through collisions, presumably leading to plasma heating. For beam injection in particular, this can lead to important differences in hard X-ray signatures.

The present work addresses distributed electron heating extending over many thousand km (millions of Debye lengths). While one can expect similar effects (such as a return current) to arise, the problem of ascertaining the importance of these effects is at this time close to unsolvable due to the discrepancy between the large scales of energy release in our simulation and the small scales (a few Debye lengths) required to model the plasma processes. (We note that even modern particle in cell (PIC) codes are limited to scales of thousands of Debye lengths.) However, one can conjecture that any energy loss from the return current will lead to hot electrons, hence reinforcing the downward heat flux. We hope that our work will stimulate new research in this area.

Acknowledgements

S.J.B. is grateful to PPARC for the award of a Post-Doctoral Fellowship. CHIANTI is a collaborative project involving the NRL (USA), RAL (UK), and the following Universities: College London (UK), Cambridge (UK), George Mason (USA), and Florence (Italy). We thank the referee for their insightful comments, in particular regarding return current generation.

   
Appendix A: numerical considerations

The combination of our chosen initial conditions and range of parameter values for the heating function drives the plasma temperature from 0.02 MK to over 25 MK in 0.5 s at the loop apex. Obviously there will be no significant bulk motions developing in this period and so the number density remains at 10⁷ cm^-3. The dominant physical process at this time is thermal conduction and one of the major difficulties in solving Eqs. (6) to (9) is due to the associated time-scale, given by:

$$% \tau_{F_{\rm c}} = \frac{k_{\rm B} n (\Delta s)^2}{2 \kappa_0 T^{\frac{5}{2}}}\cdot$$ (A.1)

For a plasma of T = 10 MK, n = 10⁷ cm^-3 Eq. (A.1) gives:

$$\begin{eqnarray*}\tau_{F_{\rm c}} = (2\times10^{-21}) (\Delta s)^2. \end{eqnarray*}$$

Clearly, thermal conduction can place severe restrictions on the time-step over which the equations can be stably integrated and drastically limit the time-frame over which the evolution of the plasma can be followed. Equation (A.1) shows that a computational grid with 1'' (700 km) resolution (comparable with current observations) requires a time-step of 10^-5 s and a grid with 100 km resolution (assuming a filling-factor of 1/7 for convenience) requires a time-step of 2 $\times$ 10^-7 s. This is the principle time-scale of the system during explosive heating.

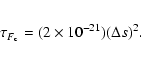
One might say that an implicit method for integrating the conductive term of the energy equation is required, however, there are several reasons why this might not necessarily be advantageous: the many matrix inversions that are necessary are far more computationally demanding than a straightforward explicit technique; many numerical implementations of implicit techniques for solving diffusion equations assume that the diffusion coefficient is everywhere constant or constant across a single cell, which is not acceptable for the strongly non-linear conduction in the solar corona ( $\kappa \propto T^{5/2}$); and the accuracy condition for an implicit technique is equivalent to the stability condition for an explicit technique. The last point is often overlooked, though it is extremely important. An implicit solution is guaranteed to converge to the equilibrium solution (if one exists), however, we are actually interested in the details of the solution at intermediate stages and so we must resolve the principle time-scale. This is extremely difficult and our strategy is to adopt an explicit method of solution with a uniform grid of 300 km resolution. We are able to obtain stable solutions with the expected physical behaviour (i.e. chromospheric evaporation, etc.), over a satisfactory time-frame and good agreement with our analytical model (Sect. 3.1).

As a consequence of the low density of the plasma the rate of thermalising Coulomb collisions between particle species is less than the rate of heating. Since it is likely that the mechanism of energy release will resonate (and thus heat) with one species in preference to another and consequently we must treat our plasma as composed of at least two separate fluid elements (electrons and, collectively, ions) and take explicit account of their collisional coupling and energy exchange. In our simulation we assume that the electrons are preferentially heated. Our argument for this is simply that electrons must exist at the temperatures we observe because the corona is dominated by collisionally excited (by electrons) emission lines and thermal bremmstrahlung (from electrons).

Another major difficulty that faces modelling efforts in our chosen parameter range is the appropriate treatment of optically-thin radiative emission. We have already stated that the plasma is dominated by heating and thermal conduction, which is true during the initial phase of explosive heating. However, the propagating thermal conduction fronts that arise as a consequence of the energy release at the loop apex inevitably result in the evaporation of higher density material into the corona and so eventually optically-thin radiative emission, proportional to n², will contribute significantly to the energy balance of the plasma. Furthermore, even during the initial phase of heating we are interested in the emission, regardless of its negligible contribution to the energy balance, because we wish to determine whether there will be any observational manifestations of such a heating event.

The major difficulty in accurately calculating the optically-thin radiative emission lies in the ionisation balance. A coronal density of 10⁷ cm^-3 and an increase in temperature from 0.02 MK to over 25 MK in 0.5 s means that the usual assumption of an equilibrium ionisation balance is entirely invalid. Obtaining a realistic ionisation balance during explosive heating of such tenuous plasma is a matter of solving the time-dependent form of the system of ionisation balance equations; an extremely stiff system of coupled differential equations and a substantial drain on computational resources. For a discussion of the solution of the ionisation balance equations and the calculation of non-equilibrium radiative emission see Bradshaw & Mason (2003b).

In order to obtain solutions within a reasonable time-frame we choose to solve the system of ionisation balance equations for iron only, as it is the most abundant element in the corona with many observable emission lines. Therefore, we are able to treat the radiative emission from iron in a time-dependent manner and the remaining elements in equilibrium. Since the lower-lying layers of the solar atmosphere are characterised by higher density plasma, the populations of the dominant emitting elements in these regions (helium, carbon, oxygen) are closer to equilibrium, especially during the early stages of explosive heating before the onset of significant dynamical behaviour.

References

• Aschwanden, M. J., Schrijver, C. J., & Alexander, D. 2001, ApJ, 550, 1036 [NASA ADS] [CrossRef] (In the text)
• Bradshaw, S. J., & Mason, H. E. 2003a, A&A, 401, 699 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Bradshaw, S. J., & Mason, H. E. 2003b, A&A, 407, 1127 [CrossRef] [EDP Sciences] (In the text)
• Bradshaw, S. J., & Cargill, P. J. 2005, A&A, 437, 311 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Bradshaw, S. J., Del Zanna, G., & Mason, H. E. 2004, A&A, 425, 287 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Cargill, P. J. 1993, Sol. Phys., 147, 263 [NASA ADS] [CrossRef] (In the text)
• Cargill, P. J. 1994, ApJ, 422, 381 [NASA ADS] [CrossRef] (In the text)
• Cargill, P. J., & Klimchuk, J. A. 1997, ApJ, 478, 799 [NASA ADS] [CrossRef] (In the text)
• Cargill, P. J., & Klimchuk, J. A. 2004, ApJ, 605, 911 [NASA ADS] [CrossRef] (In the text)
• Cargill, P. J., Mariska, J. T., & Antiochos, S. K. 1995, ApJ, 439, 1034 [NASA ADS] [CrossRef] (In the text)
• Dere, K. P., Landi, E., Mason, H. E., Monsignori Fossi, B. C., & Young, P. R. 1997, A&AS, 125, 149 [NASA ADS] (In the text)
• D'Iakonov, S. V., & Somov, B. V. 1988, Sol. Phys., 116, 119 [NASA ADS] (In the text)
• Emslie, A. G. 1980, ApJ, 235, 1055 [NASA ADS] [CrossRef] (In the text)
• Klimchuk, J. A. 2006, Sol. Phys., 234, 41 [NASA ADS] [CrossRef] (In the text)
• Landi, E., Del Zanna, G., Young, P. R., et al. 2006, ApJS, 162, 261 [NASA ADS] [CrossRef] (In the text)
• Mackay, D. H., Galsgaard, K., Priest, E. R., & Foley, C. R. 2000, Sol. Phys., 193, 93 [NASA ADS] [CrossRef] (In the text)
• McKean, M. E., Winglee, R. M., & Dulk, G. A. 1990, ApJ, 364, 295 [NASA ADS] [CrossRef] (In the text)
• Parker, E. N. 1988, ApJ, 330, 474 [NASA ADS] [CrossRef] (In the text)
• Patsourakos, S., & Klimchuk, J. A. 2005, ApJ, 628, 1023 [NASA ADS] [CrossRef] (In the text)
• Priest, E. R., Foley, C. R., Heyvaerts, J., et al. 2000, ApJ, 539, 1002 [NASA ADS] [CrossRef] (In the text)
• Taroyan, Y., Bradshaw, S. J., & Doyle, J. G. 2006, A&A, 446, 315 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Watko, J. A., & Klimchuk, J. A. 2000, Sol. Phys., 193, 77 [NASA ADS] [CrossRef] (In the text)
• Winebarger, A. R., & Warren, H. P. 2004, ApJ, 610, L129 [NASA ADS] [CrossRef] (In the text)