A&A 458, 941-951 (2006)
DOI: 10.1051/0004-6361:20065679
Photospheric modeling through spectral line inversion
Temperature and radial velocity stratifications and fluctuations
J. Koza1,2 -
A. Kucera2 -
J. Rybák2 -
H. Wöhl3
1 - Sterrekundig Instituut, Universiteit Utrecht, PO Box 80000, 3508 TA Utrecht, The Netherlands
2 -
Astronomical Institute, Slovak Academy of Sciences, 059 60 Tatranská Lomnica, Slovakia
3 -
Kiepenheuer-Institut für Sonnenphysik, Schöneckstrasse 6, 79104
Freiburg, Germany
Received 23 May 2006 / Accepted 6 July 2006
Abstract
Aims. We aim to determine average radial stratifications of various physical parameters throughout the solar photosphere at high angular resolution for non-magnetic and magnetic areas and to compare these with standard semiempirical 1D modeling and with 3D hydrodynamics (HD) and magnetohydrodynamics (MHD) simulations.
Methods. We analyse a 15-min sequence of adaptive-optics spectrograms of very high angular resolution taken at solar disk centre. We split the data between a quiet area and a magnetic one and derive mean temperature and velocity stratifications and fluctuations for these separately by applying LTE inversion based on response functions.
Results. The mean temperature stratifications in the non-magnetic region agree well with the classical 1D models and the 3D simulations at all heights. However, the observed rms temperature is much lower than in the simulations, the observed mean velocities indicate more upflows, and the observed velocity fluctuations are smaller except in upper layers. Some of the discrepancies are likely to result from remaining smearing by atmospheric seeing and instrumental limitations. The magnetic area shows conspicuous behaviour at large height. We also find evidence of fast low-photosphere downflows in the magnetic area and of enhanced temperature above a small pore.
Key words: Sun: photosphere - Sun: granulation - Sun: oscillations - stars: atmospheres
Solar high-resolution spectroscopy provides a framework for
quantitative comparison of actual photospheric properties with
classical semiempirical 1D models of the quiet solar photosphere and
with newer 3D radiation-hydrodynamics simulations of the solar
granulation. In this paper, we analyse new high-resolution
spectrocopic data in this context. We apply an inversion method to a 15-min time sequence of high-resolution spectrograms to obtain the
space-time evolution and the vertical
stratification of different physical parameters throughout the solar
photosphere (cf. Puschmann et al. 2005,2003).
In this paper we concentrate on temperature fluctuations,
line-of-sight velocities, and the macroturbulent velocity.
![\begin{figure}
\par\includegraphics[height=6.15cm,width=6cm,clip]{5679fg1a.eps}\...
....eps}\includegraphics[height=6.15cm,width=5.35cm,clip]{5679fg1c.eps}\end{figure}](/articles/aa/full/2006/42/aa5679-06/Timg22.gif) |
Figure 1:
Left: MDI/SoHO magnetogram. Middle: G-band
slit-jaw filtergram. Right: example spectrogram. The slit
position is indicated by the vertical black line. In the magnetogram
the completely black and white regions involve 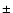 300 G and higher
field strengths.
The regions at 300 G and higher
field strengths.
The regions at
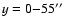 and
and
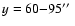 (measured along the slit)
are indicated as non-magnetic and magnetic, respectively.
(measured along the slit)
are indicated as non-magnetic and magnetic, respectively. |
| Open with DEXTER |
Solar 3D hydrodynamics simulations such, as the one by
Stein & Nordlund (1998), were recently extended to the low
chromosphere by Wedemeyer et al. (2004) and to the realm of
magneto-convection by Vögler et al. (2005). These 3D simulations all
assume strict LTE but differ in their treatment of opacity and in
how they use the opacity packages.
In this paper, we use the inversion code SIR by
Ruiz Cobo & del Toro Iniesta (1992) as a powerful tool for filling the gap
between these 3D numerical simulations of the solar photosphere and
the older semiempirical 1D modeling. We aim to add verification of
the 3D simulations to their comparison with various observations
summarised in Stein & Nordlund (2000). We do this by comparing the
results of our data inversions to the temporally and spatially-averaged
simulation stratifications tabulated in
Asplund et al. (2004,2005). The pertinent results are the
mean temperature stratifications, rms fluctuations, and the relations
between the continuum intensity and the velocity.
In our comparisons, we distinguish
between a non-magnetic region and a small region with enhanced
magnetic activity. We also investigate whether the magnetic field in
a pore is the single one responsible for the observed increase in the full
width at half minimum (FWHM) and in line-centre intensities. This
provides further evidence of enhanced
temperatures above small pores as reported by
Sütterlin et al. (1996) and Sütterlin (1998) and predicted by the
simulation of Stein & Nordlund (2000).
This work goes well beyond our previous attempts aimed at temporal
evolution of physical parameters within a single granule and
intergranular lane (see Kucera et al. 2004, and references therein)
and continues the quantitative confrontation of observations with
simulations.
We use a time sequence of spectrograms obtained at the German Vacuum Tower
Telescope (VTT, Schröter et al. 1985) at the Observatorio del Teide on April 28, 2000.
The adaptive optics of the National Solar Observatory
at Sacramento Peak (Rimmele et al. 1999) was operated in observations.
The spectrograms around 4993.8 Å and 6456.5 Å (Fig. 1) were
taken synchronously at a 3-s cadence with an exposure time of 1 s,
and the observing run lasted for 15 min from 9:26:39 UT to 9:41:33 UT.
The width of the slit was 100 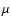 m equivalent to 0
m equivalent to 0
 46.
The spectral data were acquired with two 2k
46.
The spectral data were acquired with two 2k  2k
12 bit XEDAR XS-2048-A-12 CCD cameras using 2
2k
12 bit XEDAR XS-2048-A-12 CCD cameras using 2  2 pixel hardware
binning, doubling the linear dimension of an individual pixel to 28
2 pixel hardware
binning, doubling the linear dimension of an individual pixel to 28 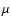 m.
The spatial sampling was 0.126
m.
The spatial sampling was 0.126
 /pixel, and the
dispersion was 2.528 mÅ/pixel and 3.066 mÅ/pixel
for the first and second spectral regions, respectively.
The corresponding Doppler velocities per pixel were
142 m s-1 and 152 m s-1.
In particular, we used the G-band filter of 9 Å bandpass
centred at 4306 Å for the slit-jaw image acquisition.
For more details, see Rybák et al. (2004) and Odert et al. (2005).
/pixel, and the
dispersion was 2.528 mÅ/pixel and 3.066 mÅ/pixel
for the first and second spectral regions, respectively.
The corresponding Doppler velocities per pixel were
142 m s-1 and 152 m s-1.
In particular, we used the G-band filter of 9 Å bandpass
centred at 4306 Å for the slit-jaw image acquisition.
For more details, see Rybák et al. (2004) and Odert et al. (2005).
Table 1:
Parameters of the spectral lines.
The entrance slit of the spectrograph was positioned almost in the
centre of the solar disk (
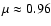 )
near the AR 8976, partly on
a quiet photosphere ranging from 0
)
near the AR 8976, partly on
a quiet photosphere ranging from 0
 to 55
to 55
 (Fig. 1) and partly on a small unipolar region of
enhanced magnetic activity ranging from 60
(Fig. 1) and partly on a small unipolar region of
enhanced magnetic activity ranging from 60
 to 95
to 95
 .
Hereafter, these regions are referred to as non-magnetic and magnetic,
respectively.
Inspecting the MDI/SoHO magnetogram and the G-band slit-jaw filtergram (Fig. 1)
of the magnetic region we conclude that the region involved
anomalous granulation and many G-band bright points harboring the flux tubes,
so the region would reveal itself as a plage in the chromosphere and the faculae was its limb counterpart.
Moreover, the spectrograph slit grazed a pore situated at
.
Hereafter, these regions are referred to as non-magnetic and magnetic,
respectively.
Inspecting the MDI/SoHO magnetogram and the G-band slit-jaw filtergram (Fig. 1)
of the magnetic region we conclude that the region involved
anomalous granulation and many G-band bright points harboring the flux tubes,
so the region would reveal itself as a plage in the chromosphere and the faculae was its limb counterpart.
Moreover, the spectrograph slit grazed a pore situated at
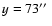 whose longitudinal component of the magnetic field strength was approximatively -900 G.
Another dark band is also conspicuous between
whose longitudinal component of the magnetic field strength was approximatively -900 G.
Another dark band is also conspicuous between
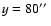 and
and
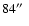 at the spectrogram and the map of continuum intensity (Figs. 1 and 6).
We suspect that the small micropore and the area of higher concentration of intergranular
lanes visible in the G-band filtergram at the positions
at the spectrogram and the map of continuum intensity (Figs. 1 and 6).
We suspect that the small micropore and the area of higher concentration of intergranular
lanes visible in the G-band filtergram at the positions
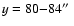 are responsible
for this feature.
The shift in the micropore with respect to the slit apparent on this particular G-band
filtergram was probably caused by the seeing.
The estimated diameters of the pores are not larger than 2-3
are responsible
for this feature.
The shift in the micropore with respect to the slit apparent on this particular G-band
filtergram was probably caused by the seeing.
The estimated diameters of the pores are not larger than 2-3
 .
.
Generally, the seeing conditions were of good quality allowing for
sub-arcsecond resolution.
The quality of the spectra, indicated by the relative
contrast of the continuum intensity
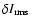 is displayed in Fig. 2.
The mean
is displayed in Fig. 2.
The mean
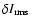 measured in the non-magnetic region are 3.4%
and 2.5% in the spectral regions 4993.8 Å and 6456.5 Å, respectively.
measured in the non-magnetic region are 3.4%
and 2.5% in the spectral regions 4993.8 Å and 6456.5 Å, respectively.
In the process of data reduction no correction for the 5-min
oscillations was performed. After the various reduction steps (Wöhl et al. 2002),
the spatial dimension of the spectra resulted in the value
of 1008 pixels (127
 ).
).
The orientation of the slit perpendicular to the horizon
allowed compensation for the differential refraction. The value of the
displacement was determined empirically by correlation of the intensities
of the continua in each pair of spectra recorded synchronously by the
cameras. The variation of differential refraction in the range
of values from 3 pixels to 4 pixels, i.e. from 0
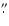 4 to 0
4 to 0
 5
was found, in perfect agreement with the theoretical value of 0
5
was found, in perfect agreement with the theoretical value of 0
 5 when actual air column mass and the geographical location are taken into account.
To compensate for this displacement, the spectra were shifted
parallel to the slit for quoted values.
After the compensation of the differential refraction
the spatio-temporal extent of the investigated data volume was
118
5 when actual air column mass and the geographical location are taken into account.
To compensate for this displacement, the spectra were shifted
parallel to the slit for quoted values.
After the compensation of the differential refraction
the spatio-temporal extent of the investigated data volume was
118

 15 min.
15 min.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{5679fg2.eps}\end{figure}](/articles/aa/full/2006/42/aa5679-06/Timg32.gif) |
Figure 2:
Variations in the rms of the continuum intensity in the non-magnetic
region. The triangles mark the records selected for inversion. |
| Open with DEXTER |
The wavelength calibration of the spectrograms was carried out
for the mean profiles by applying the method outlined in Allende Prieto & García López (1998a),
which proved that the FTS solar atlas (Neckel 1999) can be used as a benchmark to
perform wavelength calibrations of astronomical spectra and also
to set up an accurate wavelength scale for solar spectra.
The standard deviations of the used wavelength standards
were  2 mÅ (Allende Prieto & García López 1998b) corresponding
to an uncertainty of 90 m s-1 in the inferred line-of-sight
velocities.
By applying this wavelength calibration method, we also compensated
for the velocity of 90 m s-1 of the spectrograph
toward the Sun caused by the orbital and rotation velocities of the Earth.
2 mÅ (Allende Prieto & García López 1998b) corresponding
to an uncertainty of 90 m s-1 in the inferred line-of-sight
velocities.
By applying this wavelength calibration method, we also compensated
for the velocity of 90 m s-1 of the spectrograph
toward the Sun caused by the orbital and rotation velocities of the Earth.
To limit the considerable processing, we performed several reduction steps
decreasing the volume of the original data but keeping sufficiently high spatial, temporal,
and spectral resolution.
Thus the final dimension of the data cube entering the inversion was
471 spectral rows  448 spectral points
448 spectral points 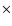 100 spectrograms.
100 spectrograms.
![\begin{figure}
\par\includegraphics[height=5.4cm,width=8.05cm,clip]{5679fg3a.eps...
...{5mm}
\includegraphics[height=5.4cm,width=7.85cm,clip]{5679fg3b.eps}\end{figure}](/articles/aa/full/2006/42/aa5679-06/Timg34.gif) |
Figure 3:
Example of synthetic profiles (solid lines) resulting from the inversion and the
observed profiles (circles) taken at 09:32:12 UT in the granule at
y=94
 close to the upper border of the magnetic region.
The lower panels show the relative residuals of the fits. close to the upper border of the magnetic region.
The lower panels show the relative residuals of the fits. |
| Open with DEXTER |
The inversion code SIR (Ruiz Cobo & del Toro Iniesta 1992) used
in this study consists in two basic modules.
The radiative transfer module assumes LTE, homogeneous plane-parallel layers,
and hydrostatic equilibrium.
The inversion module implements a nonlinear least-square Marquardt
algorithm (Press et al. 1992) minimizing the misfit between observed and
synthetic spectral line profiles by iterative modifications for the starting
model of the solar photosphere.
As a result of the inversion, SIR returns the stratification of temperature,
electron pressure, line-of-sight velocity, microturbulent velocity, total gas
pressure, and density throughout the atmosphere.
The resulting physical parameters are given both on an optical depth scale
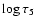 at
at
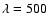 nm and as a function of geometrical height
assuming hydrostatic equilibrium.
The code also provides a macroturbulent velocity, which is assumed to be
independent of depth.
The chosen starting model Grevesse & Sauval (1999)
(Fig. 4) was discretised in equally-spaced logarithmic grid
of the optical depth scale from
nm and as a function of geometrical height
assuming hydrostatic equilibrium.
The code also provides a macroturbulent velocity, which is assumed to be
independent of depth.
The chosen starting model Grevesse & Sauval (1999)
(Fig. 4) was discretised in equally-spaced logarithmic grid
of the optical depth scale from
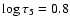 to
to
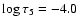 (step size
(step size
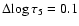 and 49 depth points).
The microturbulent velocity
and 49 depth points).
The microturbulent velocity
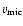 ,
the line-of-sight velocity
,
the line-of-sight velocity
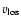 and the magnetic field strength B were initialised to the depth-independent values
of 800 m s-1, 636 m s-1 and 0 G, respectively, at all depth points.
For the macroturbulent velocity
and the magnetic field strength B were initialised to the depth-independent values
of 800 m s-1, 636 m s-1 and 0 G, respectively, at all depth points.
For the macroturbulent velocity
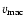 ,
the starting value of 1.6 km s-1was adopted.
Once the starting model was specified, the SIR code also needed to prescribe
the number of equidistantly distributed nodes in which the code is allowed to
modify the starting model.
In this analysis, the temperature and line-of-sight velocity were
perturbed subsequently in one, three, and five nodes.
One node was assigned to both micro- and macroturbulent velocity throughout
the inversion, whereas the initial B=0 G was kept unchanged.
,
the starting value of 1.6 km s-1was adopted.
Once the starting model was specified, the SIR code also needed to prescribe
the number of equidistantly distributed nodes in which the code is allowed to
modify the starting model.
In this analysis, the temperature and line-of-sight velocity were
perturbed subsequently in one, three, and five nodes.
One node was assigned to both micro- and macroturbulent velocity throughout
the inversion, whereas the initial B=0 G was kept unchanged.
Table 1 lists selected parameters of the five spectral lines
used in the inversion.
The sources of laboratory central wavelength
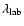 are
Nave et al. (1994) for the Fe I lines, Kupka et al. (1999) (VALD database) for the Ca I and Fe II 6456.4 Å lines, and Borrero & Bellot Rubio (2002)
for the Fe II 4993.3 Å line. The equivalent widths W
are
Nave et al. (1994) for the Fe I lines, Kupka et al. (1999) (VALD database) for the Ca I and Fe II 6456.4 Å lines, and Borrero & Bellot Rubio (2002)
for the Fe II 4993.3 Å line. The equivalent widths W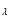 and multiplet numbers were taken from Moore et al. (1966).
The formation heights of the line cores h were taken
from Gurtovenko & Kostyk (1989) and Sheminova (1998) for the
strong line Fe I 4994.1 Å. The optical depth of formation
of the line cores
and multiplet numbers were taken from Moore et al. (1966).
The formation heights of the line cores h were taken
from Gurtovenko & Kostyk (1989) and Sheminova (1998) for the
strong line Fe I 4994.1 Å. The optical depth of formation
of the line cores
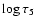 corresponds to the optical depth in
continuum at
corresponds to the optical depth in
continuum at
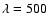 nm in the model atmosphere HOLMU
(Holweger & Müller 1974). The effective Landé factors
nm in the model atmosphere HOLMU
(Holweger & Müller 1974). The effective Landé factors
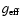 were taken from VALD and the values in parenthesis were computed
according to Beckers (1969). The sources of the excitation
potential of the lower level EP
were taken from VALD and the values in parenthesis were computed
according to Beckers (1969). The sources of the excitation
potential of the lower level EP
 are Nave et al. (1994) for
the Fe I lines and the database VALD for Fe II and
Ca I lines. The term designations were taken from
Moore (1972) and the values of the velocity parameter
are Nave et al. (1994) for
the Fe I lines and the database VALD for Fe II and
Ca I lines. The term designations were taken from
Moore (1972) and the values of the velocity parameter 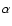 and
collisional broadening
and
collisional broadening 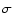 (given in Bohr radius
(given in Bohr radius 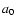 )
from Barklem et al. (2000).
)
from Barklem et al. (2000).
The estimated reliability ranges for temperature and line-of-sight velocity
of these lines are specified in Koza et al. (2006).
The formation heights of the line cores and corresponding optical
depths specified in Table 1 demonstrate the large extent of the height of the photospheric layers probed by the selected spectral lines.
The reliability of the inversion also depends strongly
on the accuracy of the atomic parameters.
To avoid systematic errors in temperature and line-of-sight velocity
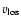 ,
we checked the accuracy of
,
we checked the accuracy of
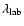 and oscillatory strengths
and oscillatory strengths 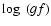 by a two-component model of the solar photosphere and by the method suggested in Borrero & Bellot Rubio (2002).
The advantage of this method is that the check on
by a two-component model of the solar photosphere and by the method suggested in Borrero & Bellot Rubio (2002).
The advantage of this method is that the check on
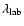 and
and 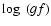 can be performed at the same time.
Table 1 shows the
can be performed at the same time.
Table 1 shows the 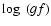 values with the best match of the synthetic
and atlas profiles extracted from Neckel (1999).
An exception was the Fe I 4994.1 Å line, where the value for
values with the best match of the synthetic
and atlas profiles extracted from Neckel (1999).
An exception was the Fe I 4994.1 Å line, where the value for 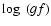 adopted from Bard et al. (1991) did not need any modification.
The check showed that the positions of the line centres of the synthetic profiles
and the atlas profiles extracted from the FTS solar atlas agreed very well
with only one exception: the laboratory central wavelength of the weak Fe I 4992.8 Å line
was decreased about 5 mÅ.
We used the classical Unsöld theory (Unsöld 1955)
to compute the collisional broadening of
Fe II 4993.3 Å and Fe II 6456.4 Å spectral lines.
We checked the adequacy of the Unsöld theory synthesising the line profiles
using the two-component model of the solar photosphere (Borrero & Bellot Rubio 2002).
The comparison of the synthetic profiles with the atlas profiles (Neckel 1999) showed
a satisfactory match of the line wings without any need to increase the collisional
broadening through an ad hoc enhancement (Bellot Rubio 1999).
For the inversion we adopted the iron abundance
adopted from Bard et al. (1991) did not need any modification.
The check showed that the positions of the line centres of the synthetic profiles
and the atlas profiles extracted from the FTS solar atlas agreed very well
with only one exception: the laboratory central wavelength of the weak Fe I 4992.8 Å line
was decreased about 5 mÅ.
We used the classical Unsöld theory (Unsöld 1955)
to compute the collisional broadening of
Fe II 4993.3 Å and Fe II 6456.4 Å spectral lines.
We checked the adequacy of the Unsöld theory synthesising the line profiles
using the two-component model of the solar photosphere (Borrero & Bellot Rubio 2002).
The comparison of the synthetic profiles with the atlas profiles (Neckel 1999) showed
a satisfactory match of the line wings without any need to increase the collisional
broadening through an ad hoc enhancement (Bellot Rubio 1999).
For the inversion we adopted the iron abundance
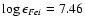 recommended in Asplund et al. (2000)
and the calcium abundance
recommended in Asplund et al. (2000)
and the calcium abundance
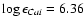 given in Thévenin (1989).
given in Thévenin (1989).
As a result of the inversion we obtained in total 47 100 individual 1D models representing the space-time evolution of the physical parameters
throughout the solar photosphere. We start the presentation of the
results with a qualitative assessment of the final fits by the
typical values of 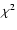 and equivalent
signal-to-noise ratio eqS/N. In the following
we provide insight into the structure of the solar photosphere by
the maps of the observed intensities and the inferred macroturbulent
and line-of-sight velocities, and temperatures in selected optical
depths. In order to compare them with some classical 1D models and
the 3D numerical simulations we show the mean temperature and
velocity stratifications, root-mean-square (rms) fluctuations, as well
as an empirical relation between observed continuum intensity and
line-of-sight velocity.
and equivalent
signal-to-noise ratio eqS/N. In the following
we provide insight into the structure of the solar photosphere by
the maps of the observed intensities and the inferred macroturbulent
and line-of-sight velocities, and temperatures in selected optical
depths. In order to compare them with some classical 1D models and
the 3D numerical simulations we show the mean temperature and
velocity stratifications, root-mean-square (rms) fluctuations, as well
as an empirical relation between observed continuum intensity and
line-of-sight velocity.
We plot an example of the observed and best-fit
profiles resulting from the inversion in Fig. 3.
The Doppler shifts and the asymmetrical shape of the profiles,
which are the result of the velocity field present at the point of the observation,
are reproduced to a reasonable degree of accuracy.
Notice the highly asymmetric line core of the strong line Fe I 4994.1 Å.
The quality of the final fits resulting from the inversion is characterised
by the values of 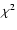 and equivalent signal-to-noise ratio eqS/N, which is defined
following Borrero & Bellot Rubio (2002) as the inverse of the standard
deviation of the residuals.
Table 2 summarises the typical values of eqS/N and
and equivalent signal-to-noise ratio eqS/N, which is defined
following Borrero & Bellot Rubio (2002) as the inverse of the standard
deviation of the residuals.
Table 2 summarises the typical values of eqS/N and 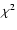 of individual
lines obtained by averaging along the slit and in time.
For the examples in Fig. 3, the inversion yielded eqS/N=50
and
of individual
lines obtained by averaging along the slit and in time.
For the examples in Fig. 3, the inversion yielded eqS/N=50
and 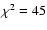
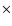 10-5 for the strong line Fe I 4994.1 Å, while
better values of eqS/N=131 and
10-5 for the strong line Fe I 4994.1 Å, while
better values of eqS/N=131 and
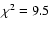
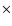 10-5
were obtained for the fit of the second line Fe II 6456.4 Å.
Generally, the best fits were achieved for the medium-strong line Ca I 6455.6 Å,
while the fits of the strong line Fe I 4994.1 Å exhibited the largest discrepancies.
10-5
were obtained for the fit of the second line Fe II 6456.4 Å.
Generally, the best fits were achieved for the medium-strong line Ca I 6455.6 Å,
while the fits of the strong line Fe I 4994.1 Å exhibited the largest discrepancies.
Table 2:
Quality of the fits evaluated by typical equivalent signal-to-noise ratio
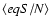 and typical value of
and typical value of
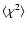 computed as time averages along the slit.
computed as time averages along the slit.
![\begin{figure}
\par\includegraphics[height=4.55cm,width=8.2cm,clip]{5679fg5a.eps...
...s}\par\includegraphics[height=5.15cm,width=8.2cm,clip]{5679fg5d.eps}\end{figure}](/articles/aa/full/2006/42/aa5679-06/Timg65.gif) |
Figure 5:
Space-time evolution of the observed line-center
intensities. The optical depth of formation of the line cores
from top to bottom are:
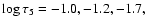 and -4.7.
The greyscales are given as fractions of the continuum intensity.
and -4.7.
The greyscales are given as fractions of the continuum intensity. |
| Open with DEXTER |
Because response functions vary considerably both with optical depth and
wavelength (e.g. Koza & Kucera 2003), the uncertainties also change with optical depth and
increase towards the limits of the sampled range.
We estimated by the response functions for temperature and line-of-sight velocity (Koza et al. 2006) that these spectral lines are sensitive to temperature and velocity changes within
the ranges of the optical depths
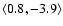 and
and
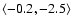 ,
respectively.
,
respectively.
The horizontally and temporally averaged gas temperatures and line-of-sight
velocities are shown in Fig. 4 separately for
the non-magnetic and magnetic regions. Because we averaged more than 104 values in each optical depth, the uncertainties are small so are not shown in the figures.
All figures and results hereafter that are pertinent to the line-of-sight velocity keep the usual
astrophysical sign convention, i.e. negative velocity indicates upflow, while positive
suggests downflow.
![\begin{figure}
\par\includegraphics[height=4.55cm,width=8.1cm,clip]{5679fg6a.eps...
...}\par\includegraphics[height=5.15cm,width=7.75cm,clip]{5679fg6d.eps}\end{figure}](/articles/aa/full/2006/42/aa5679-06/Timg70.gif) |
Figure 6:
Space-time evolution of continuum intensity,
temperature differences at
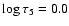 compared
to the mean temperaturs in the non-magnetic region,
macroturbulent velocity, and
line-of-sight velocities at
compared
to the mean temperaturs in the non-magnetic region,
macroturbulent velocity, and
line-of-sight velocities at
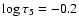 ,
respectively from top to bottom.
The greyscales are given as fractions of the continuum intensity, K, km s-1,
and km s-1, respectively.
The gravitational redshift of -636 m s-1 was subtracted from line-of-sight
velocities. Negative velocities indicate upflows.
The images were smoothed out by boxes of ,
respectively from top to bottom.
The greyscales are given as fractions of the continuum intensity, K, km s-1,
and km s-1, respectively.
The gravitational redshift of -636 m s-1 was subtracted from line-of-sight
velocities. Negative velocities indicate upflows.
The images were smoothed out by boxes of 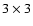 pixels. pixels. |
| Open with DEXTER |
The mean temperatures in the non-magnetic region is consistent
with the classical 1D semiempirical models as well as with the mean
of the 3D simulation by Stein & Nordlund (1998).
In the magnetic region the mean temperature stratification indicates that the sub-photospheric
layers are cooler by about 100 K and the upper layers (
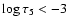 )
are hotter
by about 300 K than the 1D models and the 3D simulation.
The velocities averaged in the non-magnetic region exhibit upflows over
)
are hotter
by about 300 K than the 1D models and the 3D simulation.
The velocities averaged in the non-magnetic region exhibit upflows over
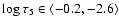 with the velocity decreasing toward the upper
layers. In contrast, the 3D simulation by Stein & Nordlund (1998) shows
velocities of
with the velocity decreasing toward the upper
layers. In contrast, the 3D simulation by Stein & Nordlund (1998) shows
velocities of 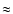 0.1 km s-1 in these photospheric layers.
In the upper layers of
0.1 km s-1 in these photospheric layers.
In the upper layers of
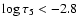 ,
both the observations and the 3D simulation show an almost
zero mean velocity. In the magnetic region, the mean velocity exhibits wavy behaviour unlike
both the non-magnetic region and the 3D simulation.
,
both the observations and the 3D simulation show an almost
zero mean velocity. In the magnetic region, the mean velocity exhibits wavy behaviour unlike
both the non-magnetic region and the 3D simulation.
Figure 5 shows the space-time evolution of the observed
line-centre intensities of four selected lines ordered with decreasing
optical depth formation of the line cores.
While the line center of the weak line Fe I 4992.8 Å maps
the lower photospheric layers at
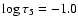 ,
the line core
of the strong line Fe I 4994.1 Å brings information about
the low chromosphere at
,
the line core
of the strong line Fe I 4994.1 Å brings information about
the low chromosphere at
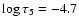 .
These observations are supplemented by the map of continuum intensity
shown in Fig. 6.
The granulation is recognisable by white and dark strips in the non-magnetic
region both in the continuum intensity map and in the low photospheric layers.
In upper layers the oscillation pattern prevails in the line-centre intensity
maps and dominates in the low chromosphere, as can be seen from the line-centre
intensity of Fe I 4994.1 Å.
In these layers the magnetic region is identifiable by bright bands
without any oscillatory pattern to indicate an increase of the line-centre intensities.
An exception is the white band at y=80
.
These observations are supplemented by the map of continuum intensity
shown in Fig. 6.
The granulation is recognisable by white and dark strips in the non-magnetic
region both in the continuum intensity map and in the low photospheric layers.
In upper layers the oscillation pattern prevails in the line-centre intensity
maps and dominates in the low chromosphere, as can be seen from the line-centre
intensity of Fe I 4994.1 Å.
In these layers the magnetic region is identifiable by bright bands
without any oscillatory pattern to indicate an increase of the line-centre intensities.
An exception is the white band at y=80
 in the line-centre intensity map
of the line Fe I 4994.1 Å, which shows brightenings with an estimated period of 5 min.
in the line-centre intensity map
of the line Fe I 4994.1 Å, which shows brightenings with an estimated period of 5 min.
The structure of the solar photosphere resulting from the inversion is illustrated in Fig. 6 showing the layers where the continuum is formed and in Fig. 7
characterising the upper layers by maps of the macroturbulent velocity, temperature differences, and absolute velocities at the selected optical depths
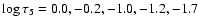 ,
and -2.5 out of the 49 layers considered in the inversion.
The continuum intensity map and the map of temperature differences in Fig. 6
show that the observed intensity contrast of 0.8-1.1 corresponds to temperature
differences of 400-500 K between granules, intergranular lanes, and pores.
Depending upon the time and the actual position with respect to the granular structure, the
macroturbulent velocity
,
and -2.5 out of the 49 layers considered in the inversion.
The continuum intensity map and the map of temperature differences in Fig. 6
show that the observed intensity contrast of 0.8-1.1 corresponds to temperature
differences of 400-500 K between granules, intergranular lanes, and pores.
Depending upon the time and the actual position with respect to the granular structure, the
macroturbulent velocity
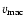 varies between 0.9 km s-1 and 1.9 km s-1, which is consistent with our results presented in Kucera et al. (2004).
Detailed comparison of the continuum intensity map and
varies between 0.9 km s-1 and 1.9 km s-1, which is consistent with our results presented in Kucera et al. (2004).
Detailed comparison of the continuum intensity map and
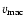 shows that in the non-magnetic region the lower values of
shows that in the non-magnetic region the lower values of
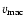 correspond to the granules, while
correspond to the granules, while
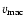 in the intergranular lanes near to the upper limit of the interval.
Owing to this, the map of
in the intergranular lanes near to the upper limit of the interval.
Owing to this, the map of
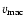 mirrors the continuum intensity map but on a reversed scale.
The bright granule and the fragmenting granule at the positions y=10
mirrors the continuum intensity map but on a reversed scale.
The bright granule and the fragmenting granule at the positions y=10
 and 19
and 19
 along the slit are good examples of this behaviour.
This result is a manifestation of what has already been concluded by many previous, studies namely
that the upflows appear laminar, while the downflows are more turbulent; i.e., they contain more unresolved velocity patterns.
This picture was also supported by the numerical simulation by Stein & Nordlund (1998).
These characteristics generally hold in the magnetic region as well; however, the dark tracks
resulting from the pore and the micropore at the positions y=75
along the slit are good examples of this behaviour.
This result is a manifestation of what has already been concluded by many previous, studies namely
that the upflows appear laminar, while the downflows are more turbulent; i.e., they contain more unresolved velocity patterns.
This picture was also supported by the numerical simulation by Stein & Nordlund (1998).
These characteristics generally hold in the magnetic region as well; however, the dark tracks
resulting from the pore and the micropore at the positions y=75
 and 80
and 80
 are
co-spatial with the regions of increased
are
co-spatial with the regions of increased
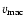 .
The granular overshoot prevails on the velocity map at
.
The granular overshoot prevails on the velocity map at
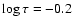 ,
and the strong upflows
between
,
and the strong upflows
between 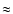 -1.5 and -2 km s-1 are co-spatial with the fragmenting granule at
y=30
-1.5 and -2 km s-1 are co-spatial with the fragmenting granule at
y=30
 and the bright granules at y=57
and the bright granules at y=57
 and 94
and 94
 .
On the other hand, the intensive downdrafts of 1.7 km s-1 are observed in the vicinity
of the pores at y=75
.
On the other hand, the intensive downdrafts of 1.7 km s-1 are observed in the vicinity
of the pores at y=75
 and 80
and 80
 .
Fast downflows on the borders of a pore and inside a bright point
were found in the 3D MHD simulation by Stein & Nordlund (2000, see Fig. 18, p. 106).
Granular fragmentations seen at 17
.
Fast downflows on the borders of a pore and inside a bright point
were found in the 3D MHD simulation by Stein & Nordlund (2000, see Fig. 18, p. 106).
Granular fragmentations seen at 17
 and 30
and 30
 are
recognisable in the continuum intensity map (Fig. 6) and the temperature maps (Fig. 7) throughout the lower photosphere
up to the optical depth
are
recognisable in the continuum intensity map (Fig. 6) and the temperature maps (Fig. 7) throughout the lower photosphere
up to the optical depth
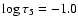 .
This layer exhibits signatures of the temperature reversal apparent in the cases of
both fragmenting granules, which are dark in contrast to their counterparts in the continuum.
At the optical depth
.
This layer exhibits signatures of the temperature reversal apparent in the cases of
both fragmenting granules, which are dark in contrast to their counterparts in the continuum.
At the optical depth
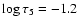 and partly at
and partly at
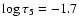 ,
the temperature reversal can be still seen in the granules
at 5
,
the temperature reversal can be still seen in the granules
at 5
 ,
17
,
17
 ,
24
,
24
 ,
30
,
30
 ,
and 47
,
and 47
 .
Positive correlation with continuum is re-established at
.
Positive correlation with continuum is re-established at
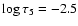 where the granules are again hotter than the surroundings, but now the granulation
pattern is overlaid by 5-min oscillations.
The temperature differences increase progressively with height, reaching
maximum amplitude of
where the granules are again hotter than the surroundings, but now the granulation
pattern is overlaid by 5-min oscillations.
The temperature differences increase progressively with height, reaching
maximum amplitude of 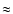 1300 K at the optical depth
1300 K at the optical depth
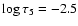 .
In the middle photosphere the magnetic region can be identified easily by its
track of temperature, which is about 300 K higher
than in the non-magnetic region.
.
In the middle photosphere the magnetic region can be identified easily by its
track of temperature, which is about 300 K higher
than in the non-magnetic region.
While the granular overshoot prevails in the velocity map around
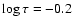 ,
the 5-min oscillations dominate in the upper layers of the non-magnetic region.
The patches of oscillation with coherent amplitude have an estimated size around 5
,
the 5-min oscillations dominate in the upper layers of the non-magnetic region.
The patches of oscillation with coherent amplitude have an estimated size around 5
 ;
however, their smooth pattern is perturbed in the magnetic region.
Some exceptional events of granular evolution are also clearly seen in
the velocity structure of the middle photosphere;
see e.g. the fragmenting granule at y=30
;
however, their smooth pattern is perturbed in the magnetic region.
Some exceptional events of granular evolution are also clearly seen in
the velocity structure of the middle photosphere;
see e.g. the fragmenting granule at y=30
 still visible at
still visible at
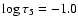 and -1.2.
Even the upper photosphere at
and -1.2.
Even the upper photosphere at
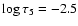 still exhibits velocity structures
induced by granulation as the upflows at y=17, 24, and 47
still exhibits velocity structures
induced by granulation as the upflows at y=17, 24, and 47
 demonstrate.
demonstrate.
Most inversions yielded negligible microturbulence (not shown).
In some cases the inversion finished with the values between 0.3 km s-1 and 0.9 km s-1 but without some clear and systematic relation to the granular structure in both regions.
Figure 8 shows our observed rms fluctuations of temperature and line-of-sight velocity
in the non-magnetic and magnetic regions.
Following Wedemeyer et al. (2004), the fluctuations were computed as a square root
of variance for the pertinent quantities using the mean stratifications inferred in the non-magnetic
and magnetic regions (Fig. 4).
Because the errors of the rms fluctuations are smaller than 1 K and 1 m s-1,
they are not shown.
The sub-photospheric layers are characterised by a sharp drop in the rms temperature fluctuation with height both in the 3D simulations and the results inferred by the inversion, which are systematically lower at about 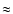 400 K.
Particularly, in the non-magnetic region they fall to
400 K.
Particularly, in the non-magnetic region they fall to 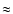 50 K at
50 K at
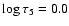 ,
and higher they remain small up to
,
and higher they remain small up to
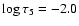 .
At larger heights the upper photosphere becomes more inhomogeneous.
The subsequent rise of the observed fluctuations up to 200 K over
the
.
At larger heights the upper photosphere becomes more inhomogeneous.
The subsequent rise of the observed fluctuations up to 200 K over
the
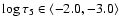 range is followed by a rather steep increase in the upper photosphere.
In the magnetic region, the rms temperature fluctuations behave similarly, but their
values are higher and a slight rise up to 100 K is present over
the low and the middle photosphere at
range is followed by a rather steep increase in the upper photosphere.
In the magnetic region, the rms temperature fluctuations behave similarly, but their
values are higher and a slight rise up to 100 K is present over
the low and the middle photosphere at
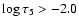 .
.
![\begin{figure}
\par\includegraphics[height=4.7cm,width=8.4cm,clip]{5679fg7a.eps}...
...g.eps}\includegraphics[height=5.25cm,width=7.5cm,clip]{5679fg7h.eps}\end{figure}](/articles/aa/full/2006/42/aa5679-06/Timg84.gif) |
Figure 7:
Space-time evolution of temperature differences compared
to the mean temperature stratification in the non-magnetic region ( left)
and line-of-sight velocities ( right) in the selected optical depths.
The greyscales are expressed in Kelvin and km s-1.
The gravitational redshift of -636 m s-1 was subtracted from
line-of-sight velocities. Negative velocities indicate upflows. The images
were smoothed out by boxes of 3 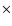 3 pixels. 3 pixels. |
| Open with DEXTER |
In the same figure we also show the temperature fluctuations in the 3D granulation simulations of
Wedemeyer et al. (2004, see p. 1131, Fig. 9# and Stein & Nordlund (1998).
In the low photosphere the 3D simulations exhibit a decrease in the rms temperature fluctuations
with height reaching a minimum of 150 K at
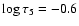 and then increasing monotonically with height.
Both 3D simulations behave rather similarly over
and then increasing monotonically with height.
Both 3D simulations behave rather similarly over
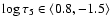 ,
but from
,
but from
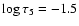 upwards the 3D simulation by Stein & Nordlund (1998) exhibits nearly constant rms temperature fluctuations of about 200 K
in discrepancy with our observational results, as well as, with the numerical results of Wedemeyer et al. (2004).
Note the similarity of the gradients of the curves in the sub-photospheric layers and
over interval
upwards the 3D simulation by Stein & Nordlund (1998) exhibits nearly constant rms temperature fluctuations of about 200 K
in discrepancy with our observational results, as well as, with the numerical results of Wedemeyer et al. (2004).
Note the similarity of the gradients of the curves in the sub-photospheric layers and
over interval
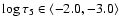 in which our observed rms temperature
fluctuations mimic the trend of the 3D simulation WFSLH by Wedemeyer et al. (2004).
in which our observed rms temperature
fluctuations mimic the trend of the 3D simulation WFSLH by Wedemeyer et al. (2004).
Our observed velocity fluctuations in the non-magnetic region show the nearly constant value of 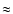 0.35 km s-1 over
0.35 km s-1 over
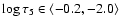 ,
above which they rise up to
,
above which they rise up to 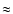 0.8 km s-1 at
0.8 km s-1 at
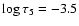 .
The increase in velocity fluctuations is more pronounced in the magnetic
region, reaching 3 km s-1 in the highest layers.
In the same optical depths the 3D simulation by Stein & Nordlund (1998) exhibits a decrease of rms velocity fluctuations
from 2.22 km s-1 to 0.84 km s-1 followed by a slight increase to 1 km s-1at
.
The increase in velocity fluctuations is more pronounced in the magnetic
region, reaching 3 km s-1 in the highest layers.
In the same optical depths the 3D simulation by Stein & Nordlund (1998) exhibits a decrease of rms velocity fluctuations
from 2.22 km s-1 to 0.84 km s-1 followed by a slight increase to 1 km s-1at
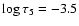 .
.
![\begin{figure}
\par\includegraphics[height=5.75cm,width=8cm,clip]{5679fg9.eps}\end{figure}](/articles/aa/full/2006/42/aa5679-06/Timg91.gif) |
Figure 9:
Scatter plot of observed continuum intensity versus line-of-sight
velocity inferred by the inversion at the optical depth
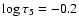 in the non-magnetic and magnetic regions. The thin solid line
outlines the extents of these quantities obtained at the optical depth
in the non-magnetic and magnetic regions. The thin solid line
outlines the extents of these quantities obtained at the optical depth
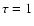 in the 3D numerical simulation SN by Stein & Nordlund (1998, see p. 917, Fig. 3#.
Negative velocities indicate upflows, and the intensity axis shows relative
continuum intensity reduced by unity.
in the 3D numerical simulation SN by Stein & Nordlund (1998, see p. 917, Fig. 3#.
Negative velocities indicate upflows, and the intensity axis shows relative
continuum intensity reduced by unity. |
| Open with DEXTER |
Figure 9 shows the empirical relation between observed continuum intensity
and line-of-sight velocity at
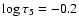 inferred by inversion in the non-magnetic and magnetic regions, and outlines the estimated border of the area occupied by the results of the
3D numerical simulation by Stein & Nordlund (1998, see p. 917, Fig. 3#, who showed
their simulated continuum intensity versus vertical velocity at the optical depth
inferred by inversion in the non-magnetic and magnetic regions, and outlines the estimated border of the area occupied by the results of the
3D numerical simulation by Stein & Nordlund (1998, see p. 917, Fig. 3#, who showed
their simulated continuum intensity versus vertical velocity at the optical depth 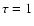 .
Obviously our observations and inversion give narrower ranges of continuum intensity
and velocity than does the 3D numerical simulation.
However, Stein & Nordlund (1998) show these data without smoothing by some point
spread function.
The centroid of our data is shifted about
.
Obviously our observations and inversion give narrower ranges of continuum intensity
and velocity than does the 3D numerical simulation.
However, Stein & Nordlund (1998) show these data without smoothing by some point
spread function.
The centroid of our data is shifted about 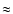 -1.0 km s-1 toward upflows.
In this plot typical granules should be in the upper left quadrant and typical intergranular lanes
in the lower right quadrant.
However, both simulation and observations indicate unusual granular dynamics.
A certain fraction of granules should exhibit downflows (Fig. 9, upper right quadrant)
and in turn the upflows should occur in the abundant clump of intergranular lanes
(Fig. 9, lower left quadrant).
Thus the simulation predicts the occurrence of unresolved dark upflows and bright downflows
associated with granular dynamics, which have not yet been observed and reported.
The scatter ellipse of the non-magnetic region is asymmetric towards bright
upflows, simply indicating that granules predominate
over intergranular lanes in an averaged sample.
Comparison of scatter plots from both regions shows
that downflows occur much more frequently in magnetic than in the non-magnetic region.
-1.0 km s-1 toward upflows.
In this plot typical granules should be in the upper left quadrant and typical intergranular lanes
in the lower right quadrant.
However, both simulation and observations indicate unusual granular dynamics.
A certain fraction of granules should exhibit downflows (Fig. 9, upper right quadrant)
and in turn the upflows should occur in the abundant clump of intergranular lanes
(Fig. 9, lower left quadrant).
Thus the simulation predicts the occurrence of unresolved dark upflows and bright downflows
associated with granular dynamics, which have not yet been observed and reported.
The scatter ellipse of the non-magnetic region is asymmetric towards bright
upflows, simply indicating that granules predominate
over intergranular lanes in an averaged sample.
Comparison of scatter plots from both regions shows
that downflows occur much more frequently in magnetic than in the non-magnetic region.
We applied the inversion code SIR on the sequence of the spectrograms with
the typical signal-to-noise of about 140 and 640 in the spectral regions
around 4993.8 Å and and 6456.5 Å and the
quality of the resulting fits was summarised in Table 2.
The largest departures in terms of the equivalent signal-to-noise (eqS/N), 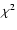 and the largest relative errors occurred in the case of the strong line Fe I 4994.1 Å.
Borrero & Bellot Rubio (2002) inverted 22 medium-strong Fe I spectral
line profiles extracted from the FTS solar atlas (Neckel 1999) with S/N=2500,
and their inversion finished with the eqS/N of about 211.
This quality evaluation suggests that further improvements in the fits
are possible by the enhancement of the S/N of the observations especially in the spectral region
involving the strong lines.
and the largest relative errors occurred in the case of the strong line Fe I 4994.1 Å.
Borrero & Bellot Rubio (2002) inverted 22 medium-strong Fe I spectral
line profiles extracted from the FTS solar atlas (Neckel 1999) with S/N=2500,
and their inversion finished with the eqS/N of about 211.
This quality evaluation suggests that further improvements in the fits
are possible by the enhancement of the S/N of the observations especially in the spectral region
involving the strong lines.
From the deep investigations of Rutten (1988) and Shchukina & Trujillo Bueno (2001),
we know that almost all neutral iron lines show departures from LTE.
A later paper concludes that it is possible to obtain good fits to the observed lines
by assuming LTE with a suggested iron abundance of 7.46.
Besides, the limited extent of the inversion just to the photospheric layers largely
eliminates the influence of the NLTE effects, which become important in the
lower chromosphere, i.e. at the optical depths
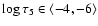 .
Moreover, the NLTE effects can also be minimised using lines spanning a wide
range of atomic parameters because each transition is influenced by the NLTE effects in different or even in opposite ways (Borrero & Bellot Rubio 2002).
Since we kept all these precautions as much in the selection of the iron abundance
and the spectral lines as in the determination of upper boundary, we
suppose that the NLTE effects do not exceed other uncertainties entering
into the inversion much thereby influencing the results (e.g. instrumental profile of the
spectrograph, atmospheric smearing, uncertainties in atomic parameters; etc.).
.
Moreover, the NLTE effects can also be minimised using lines spanning a wide
range of atomic parameters because each transition is influenced by the NLTE effects in different or even in opposite ways (Borrero & Bellot Rubio 2002).
Since we kept all these precautions as much in the selection of the iron abundance
and the spectral lines as in the determination of upper boundary, we
suppose that the NLTE effects do not exceed other uncertainties entering
into the inversion much thereby influencing the results (e.g. instrumental profile of the
spectrograph, atmospheric smearing, uncertainties in atomic parameters; etc.).
Also, ubiquitous magnetic fields play no less a role than
the NLTE effects in formation of the spectral lines observed with high resolution.
Since we lack the spectropolarimetric observations, the impact of the magnetic
fields on our results can only be judged by the effective Landé factors
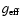 of selected spectral lines shown in Table 1.
Generally, the analysed spectral lines exhibit low or medium sensitivity to the magnetic
field. Nevertheless, we observed the solar photosphere by the spectral line with
of selected spectral lines shown in Table 1.
Generally, the analysed spectral lines exhibit low or medium sensitivity to the magnetic
field. Nevertheless, we observed the solar photosphere by the spectral line with
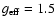 and in the red portion of the solar spectrum keeping in mind that the Zeeman broadening depends upon the square power of the wavelength.
Thus we can expect that the results characterising the pore and
its surroundings are especially biased,
as in the example of the high value of the macroturbulent velocity seen
in Fig. 6 at the positions y=75 and
and in the red portion of the solar spectrum keeping in mind that the Zeeman broadening depends upon the square power of the wavelength.
Thus we can expect that the results characterising the pore and
its surroundings are especially biased,
as in the example of the high value of the macroturbulent velocity seen
in Fig. 6 at the positions y=75 and
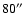 along the slit
nearly where the pore and micropore are seen in the G-band filtergram (Fig. 1).
Because there is no physical reason to expect the increased turbulence in the presence
of the strong magnetic field, the inversion code interpreted the line profiles broadening
in terms of higher values of macroturbulent velocity than usually obtained in the granules.
Interestingly, the inversion finished with a zero microturbulent velocity in the same locations.
along the slit
nearly where the pore and micropore are seen in the G-band filtergram (Fig. 1).
Because there is no physical reason to expect the increased turbulence in the presence
of the strong magnetic field, the inversion code interpreted the line profiles broadening
in terms of higher values of macroturbulent velocity than usually obtained in the granules.
Interestingly, the inversion finished with a zero microturbulent velocity in the same locations.
Applying the inversion code SIR to the spectral lines profiles emerging from the magnetic
region, we found an increase in temperature compare to the external non-magnetic environment,
which varies between 100 and 500 K (Fig. 8).
Many authors reported on the enhanced internal temperature in the flux-tube models
of solar plage (e.g. Solanki & Stenflo 1985; Bellot Rubio et al. 2000; Walton 1987)
and hotter atmosphere above a small pore (Sütterlin et al. 1996; Sütterlin 1998).
Several factors were identified as potentially responsible for the increased
internal temperature in the flux tubes.
Usually the nearly evacuated interior of the flux tubes is taken as the main
reason that the optical level 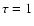 in the flux tube is situated
several tens of kilometers deeper than the same optical level in the
surrounding non-magnetic photosphere that is an analogy of the Wilson depression.
The scatter of hot-wall irradiance makes a spurious effect of the hot flux-tube interior.
Keller et al. (2004) prove that the brightness of the solar
faculae out of disk centre comes from irradiation of the limb-ward granules.
But in the disk centre, a nudge from a nearby granule (Steiner et al. 1998)
may bring the deeper and hotter flank of the granule into the
line-of-sight of
an observer through a nearly transparent flux-tube interior.
The results of the 3D simulation (Stein & Nordlund 1998) show a steep
temperature gradient near the surface in the ascending flows that also
determines the high contrast of the bright points.
Bellot Rubio et al. (2000) propose that UV radiation emanating from the walls
of the flux tubes causes overionization of
the iron and leads to the weakening of the Fe I lines compared to their
LTE strengths. Since all previous studies have treated the observations and the simulations in LTE, they interpreted the missing opacities in the line cores by increasing the internal temperature.
Probably the most comprehensive account of increased temperature above a small pore
and a hot flux-tube interior has been achieved by the 3D MHD simulation by Stein & Nordlund (2000, Fig. 18, p. 106).
in the flux tube is situated
several tens of kilometers deeper than the same optical level in the
surrounding non-magnetic photosphere that is an analogy of the Wilson depression.
The scatter of hot-wall irradiance makes a spurious effect of the hot flux-tube interior.
Keller et al. (2004) prove that the brightness of the solar
faculae out of disk centre comes from irradiation of the limb-ward granules.
But in the disk centre, a nudge from a nearby granule (Steiner et al. 1998)
may bring the deeper and hotter flank of the granule into the
line-of-sight of
an observer through a nearly transparent flux-tube interior.
The results of the 3D simulation (Stein & Nordlund 1998) show a steep
temperature gradient near the surface in the ascending flows that also
determines the high contrast of the bright points.
Bellot Rubio et al. (2000) propose that UV radiation emanating from the walls
of the flux tubes causes overionization of
the iron and leads to the weakening of the Fe I lines compared to their
LTE strengths. Since all previous studies have treated the observations and the simulations in LTE, they interpreted the missing opacities in the line cores by increasing the internal temperature.
Probably the most comprehensive account of increased temperature above a small pore
and a hot flux-tube interior has been achieved by the 3D MHD simulation by Stein & Nordlund (2000, Fig. 18, p. 106).
Table 3:
Full width at half minimum differences 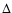 FWHM of
synthetic profiles computed with constant 900 G and zero field strength ( synt),
profiles observed in the pore and a granule (pore - gr) and in the pore, and an intergranular lane (pore - ig).
FWHM of
synthetic profiles computed with constant 900 G and zero field strength ( synt),
profiles observed in the pore and a granule (pore - gr) and in the pore, and an intergranular lane (pore - ig).
To estimate whether 900 G magnetic field alone can account for the broadening of spectral lines
interpreted by the SIR code by increasing temperature and macroturbulent velocity
in the pores at y=75 and 80
 ,
we performed the following numerical experiment along with measurements of the FWHM both of the synthetic and observed spectral line
profiles (Table 3).
With the model atmosphere of Grevesse & Sauval (1999) we calculated
the synthetic profiles of all lines, whose atomic parameters are shown in Table 1.
Adding the magnetic field strength of 900 G with zero value of inclination and azimuth
to the model, we repeated this once again, thus simulating the influence
of the magnetic field found in the pore.
The resulting synthetic profiles were used as an input of the SIR code and were inverted
under the same conditions as the observed ones.
The resulting temperatures were about 100-150 K higher than the starting one
at the optical depths
,
we performed the following numerical experiment along with measurements of the FWHM both of the synthetic and observed spectral line
profiles (Table 3).
With the model atmosphere of Grevesse & Sauval (1999) we calculated
the synthetic profiles of all lines, whose atomic parameters are shown in Table 1.
Adding the magnetic field strength of 900 G with zero value of inclination and azimuth
to the model, we repeated this once again, thus simulating the influence
of the magnetic field found in the pore.
The resulting synthetic profiles were used as an input of the SIR code and were inverted
under the same conditions as the observed ones.
The resulting temperatures were about 100-150 K higher than the starting one
at the optical depths
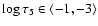 .
Obviously this cannot fully account for the temperature enhancement found at the
optical depths
.
Obviously this cannot fully account for the temperature enhancement found at the
optical depths
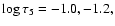 and -1.7 (Fig. 7) at the positions
of y=75 and
and -1.7 (Fig. 7) at the positions
of y=75 and
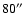 corresponding to the pore and micropore.
Furthermore in Table 3 we demonstrate the
influence of 900 G magnetic field on the FWHM of the synthetic line profiles.
Table 3 lists the FWHM differences (
corresponding to the pore and micropore.
Furthermore in Table 3 we demonstrate the
influence of 900 G magnetic field on the FWHM of the synthetic line profiles.
Table 3 lists the FWHM differences (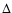 FWHM)
of synthetic lines profiles computed by 900 G and zero field strengths
as a function of the magnetic sensitivity of the spectral lines expressed
by the factor
FWHM)
of synthetic lines profiles computed by 900 G and zero field strengths
as a function of the magnetic sensitivity of the spectral lines expressed
by the factor
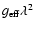 .
To highlight the inability of this field strength to explain
the observed spectral line broadening, we also show the
.
To highlight the inability of this field strength to explain
the observed spectral line broadening, we also show the 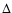 FWHM measured in the pore,
the selected granule, and the intergranular lane.
FWHM measured in the pore,
the selected granule, and the intergranular lane.
For this purpose we chose the line profiles observed at one of the best seeing moments
(Fig. 2) at t=11.5 min and coming from the spatial points
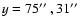 ,
and
,
and
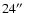 corresponding to the pore, a granule, and an intergranular lane in the non-magnetic region (see the
map of the continuum intensity in Fig. 6).
Except for the weak spectral line Fe I 4992.8 Å and Fe II 4993.3 Å observed in the intergranular lane, all line profiles exhibited considerably larger broadening than one would
expect from the adopted field strength.
All these results suggest the presence of some additional broadening mechanism presented above
pore and micropore.
However, we used field strength derived from the MDI magnetogram,
which is considerably lower than the typical values of a pore.
Bumba (1967), Beckers & Schröter (1968), Steshenko (1968), and Keppens & Martinez Pillet (1996) give an average value of 1400-1700 G.
An increase in temperature above a small pore with a diameter of
corresponding to the pore, a granule, and an intergranular lane in the non-magnetic region (see the
map of the continuum intensity in Fig. 6).
Except for the weak spectral line Fe I 4992.8 Å and Fe II 4993.3 Å observed in the intergranular lane, all line profiles exhibited considerably larger broadening than one would
expect from the adopted field strength.
All these results suggest the presence of some additional broadening mechanism presented above
pore and micropore.
However, we used field strength derived from the MDI magnetogram,
which is considerably lower than the typical values of a pore.
Bumba (1967), Beckers & Schröter (1968), Steshenko (1968), and Keppens & Martinez Pillet (1996) give an average value of 1400-1700 G.
An increase in temperature above a small pore with a diameter of 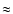
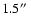 has
already been found by the 3D MHD simulation by Stein & Nordlund (2000).
Also a small pore with a diameter of 2
has
already been found by the 3D MHD simulation by Stein & Nordlund (2000).
Also a small pore with a diameter of 2
 analysed by
Sütterlin et al. (1996) and Sütterlin (1998) exhibits over
analysed by
Sütterlin et al. (1996) and Sütterlin (1998) exhibits over
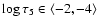 a temperature higher by about 400 K than the model atmosphere VALC (Vernazza et al. 1981)
in the same layers.
a temperature higher by about 400 K than the model atmosphere VALC (Vernazza et al. 1981)
in the same layers.
Figure 8 shows that our observed temperature fluctuations are significantly smaller than the computed ones at all depths, with flatter height dependence over
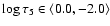 .
These disagreements are likely to be due to atmospheric smearing,
limited spatial resolution of the telescope, instrumental scattered light,
the instrumental profile of the spectrograph, and misfits between observed and synthetic line profiles resulting from imperfect inversion.
The same accounts for the narrower ranges of continuum intensities and line-of-sight velocities
in Fig. 9. In particular, the steep increase in the observed rms temperature fluctuation in the upper photosphere
(
.
These disagreements are likely to be due to atmospheric smearing,
limited spatial resolution of the telescope, instrumental scattered light,
the instrumental profile of the spectrograph, and misfits between observed and synthetic line profiles resulting from imperfect inversion.
The same accounts for the narrower ranges of continuum intensities and line-of-sight velocities
in Fig. 9. In particular, the steep increase in the observed rms temperature fluctuation in the upper photosphere
(
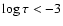 )
in Fig. 8 is uncertain and may be due to acoustic modulation, which
the SIR code interprets in terms of enhanced temperature variations.
On the other hand, the simulations are likely to overestimate the rms temperature
fluctuations in the upper photosphere through the wrong assumption on LTE.
)
in Fig. 8 is uncertain and may be due to acoustic modulation, which
the SIR code interprets in terms of enhanced temperature variations.
On the other hand, the simulations are likely to overestimate the rms temperature
fluctuations in the upper photosphere through the wrong assumption on LTE.
The bright downflows and the dark upflows indicated by Fig. 9 have a physical
as well as an observational origin. Approaching the photosphere, the buoyancy weakens and some hot parcels may begin to sink
even before they have cooled down enough to become dark, so we observe them as
bright downflows (Keller 2005).
On the other hand, the turbulence
causes certain recirculation of the cool matter back to the surface, which can be
potentially identified by the dark upflows as proposed by Stein & Nordlund (1998).
Additionally, atmospheric smearing and instrumental limitations in observations
are likely to contribute to their occurrence.
Finally, we suggest the plausible explanation for the non-zero mean velocity
(Fig. 4) in the low and the middle photospheres and the offset of the centroid
of velocities in the non-magnetic region (Fig. 9) with an estimated position
of about (-1.0 km s-1, 0.0).
These features are likely to be due neither to a methodological error in the
wavelength calibration nor to uncertainties of the wavelengths of the the reference spectral lines.
We recall that the relative velocity of the spectrograph with respect to the disc centre was only
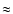 90 m s-1 and the wavelength uncertainties had a similar value.
Nonetheless, a gravitational redshift of 636 m s-1 was subtracted
from the resulting velocities.
We consider that the predominance of the granules in the averaged sample, along with
atmospheric smearing and instrumental limitations, are responsible for these
features. The behaviour of the observed mean velocity in the non-magnetic region is also determined
by the properties of the 5-min oscillations in different layers.
Odert et al. (2005) show that, while the velocity autocorrelation function oscillates but keeps the sign for the spectral line formed in the low photosphere,
for the spectral line formed in the upper photosphere, the function oscillates
around zero, having a character of damped oscillations.
This high regularity of the oscillatory pattern in the upper photosphere results
in a zero observed mean velocity in the non-magnetic region at
90 m s-1 and the wavelength uncertainties had a similar value.
Nonetheless, a gravitational redshift of 636 m s-1 was subtracted
from the resulting velocities.
We consider that the predominance of the granules in the averaged sample, along with
atmospheric smearing and instrumental limitations, are responsible for these
features. The behaviour of the observed mean velocity in the non-magnetic region is also determined
by the properties of the 5-min oscillations in different layers.
Odert et al. (2005) show that, while the velocity autocorrelation function oscillates but keeps the sign for the spectral line formed in the low photosphere,
for the spectral line formed in the upper photosphere, the function oscillates
around zero, having a character of damped oscillations.
This high regularity of the oscillatory pattern in the upper photosphere results
in a zero observed mean velocity in the non-magnetic region at
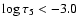 .
.
Using the time sequence of high-resolution spectrograms and the SIR inversion code, we
inferred temporal evolution of the temperature, line-of-sight velocity, and macroturbulent
velocity through the quiet solar photosphere and in a small area of enhanced magnetic activity.
The most important aspects are our avoiding of spatial and temporal averaging and
comparison of the results with the 3D numerical simulations of the solar granulation.
According to our results, the lower photosphere is thermally homogeneous, exhibiting small
rms temperature fluctuations, while the sub-photospheric and upper layers over
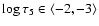 show an increase in the fluctuations with similar gradient to the one in the 3D simulation by Wedemeyer et al. (2004).
In contrast, the comparison with the 3D simulation by Stein & Nordlund (1998)
shows contradictory behaviour of the observed and predicted temperature fluctuations
at
show an increase in the fluctuations with similar gradient to the one in the 3D simulation by Wedemeyer et al. (2004).
In contrast, the comparison with the 3D simulation by Stein & Nordlund (1998)
shows contradictory behaviour of the observed and predicted temperature fluctuations
at
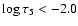 .
Our results generally exhibit reduced rms temperature fluctuations
compared with the 3D models of Wedemeyer et al. (2004) and Stein & Nordlund (1998)
and narrower ranges of the observed continuum intensities and the velocities than the 3D simulation by Stein & Nordlund (1998).
We found a flat distribution of the rms velocity fluctuations in the low and middle photospheres
over
.
Our results generally exhibit reduced rms temperature fluctuations
compared with the 3D models of Wedemeyer et al. (2004) and Stein & Nordlund (1998)
and narrower ranges of the observed continuum intensities and the velocities than the 3D simulation by Stein & Nordlund (1998).
We found a flat distribution of the rms velocity fluctuations in the low and middle photospheres
over
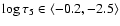 ,
which are smaller than in the 3D simulation
by Stein & Nordlund (1998).
The centroid of the observed continuum intensity-velocity distribution and the mean
velocity in the low and middle photospheres are shifted toward upflows.
We conclude that the predominance of the granules in the averaged sample,
along with atmospheric smearing and instrumental limitations, causes these differences
and the shifts.
Our observations and the inversion confirm the existence of the region
of enhanced temperature extended above the small pores found by Sütterlin et al. (1996)
and Sütterlin (1998) and the dominance of the fast downflows in the magnetic region at the low photospheric layers at
,
which are smaller than in the 3D simulation
by Stein & Nordlund (1998).
The centroid of the observed continuum intensity-velocity distribution and the mean
velocity in the low and middle photospheres are shifted toward upflows.
We conclude that the predominance of the granules in the averaged sample,
along with atmospheric smearing and instrumental limitations, causes these differences
and the shifts.
Our observations and the inversion confirm the existence of the region
of enhanced temperature extended above the small pores found by Sütterlin et al. (1996)
and Sütterlin (1998) and the dominance of the fast downflows in the magnetic region at the low photospheric layers at
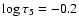 .
These findings agree with predictions by the 3D MHD simulation by Stein & Nordlund (2000).
However, further study of this feature will have to be inevitably backed up by the spectropolarimetric observations.
.
These findings agree with predictions by the 3D MHD simulation by Stein & Nordlund (2000).
However, further study of this feature will have to be inevitably backed up by the spectropolarimetric observations.
Acknowledgements
The VTT is operated by the Kiepenheuer-Institut für Sonnenphysik, Freiburg, at the Observatorio del Teide of the Instituto de Astrofísica de Canarias.
We are grateful to S. Wedemeyer-Böhm (KIS) for kindly
providing the WFSLH data in Fig. 8. J.K. thanks M. Collados (IAC) for supervision and advice during his stay at the IAC in the early 2003 in the framework of
Marie Curie Fellowship. The authors are grateful to R. J. Rutten for many comments.
This work was supported by the Slovak grant agency
VEGA (2/6195/26) and by the Deutsche Forschungsgemeinschaft grant (DFG 436 SLK 113/7).
This research is part of the European Solar Magnetism Network
(EC/RTN contract HPRN-CT-2002-00313). J. Koza's research is supported by a Marie Curie
Intra-European Fellowships within the 6th European Community Framework Programme.
- Allende Prieto, C., &
García López, R. J. 1998a, A&AS, 129,
41 [NASA ADS] (In the text)
- Allende Prieto, C., &
García López, R. J. 1998b, A&AS, 131,
431 [NASA ADS] (In the text)
-
Asplund, M., Nordlund, Å., Trampedach, R., & Stein,
R. F. 2000, A&A, 359, 743 [NASA ADS] (In the text)
-
Asplund, M., Grevesse, N., Sauval, A. J., Allende Prieto,
C., & Kiselman, D. 2004, A&A, 417, 751 [NASA ADS] [CrossRef] [EDP Sciences]
-
Asplund, M., Grevesse, N., Sauval, A. J., Allende Prieto,
C., & Kiselman, D. 2005, A&A, 435, 339 [NASA ADS] [CrossRef] [EDP Sciences]
- Bard, A., Kock,
A., & Kock, M. 1991, A&A, 248, 315 [NASA ADS] (In the text)
- Barklem,
P. S., Piskunov, N., & O'Mara, B. J. 2000, A&AS,
142, 467 [NASA ADS] (In the text)
- Beckers,
J. M. 1969, A table of Zeeman Multiplets, Sacramento Peak
Observatory Contribution No. 141 - Physical Science
Research Papers No. 371 (Sacramento Peak Observatory and Air
Force Cambridge Research Laboratories)
(In the text)
- Beckers, J. M., &
Schröter, E. H. 1968, Sol. Phys., 4, 142 [NASA ADS] [CrossRef] (In the text)
-
Bellot Rubio, L. R. 1999, A user guide to SIR,
Version 2, Instituto de Astrofísica de Canarias
(In the text)
-
Bellot Rubio, L. R., Ruiz Cobo, B., & Collados, M. 2000,
ApJ, 535, 489 [NASA ADS] [CrossRef]
- Borrero, J. M., &
Bellot Rubio, L. R. 2002, A&A, 385, 1056 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Bumba, V. 1967,
Sol. Phys., 1, 371 [NASA ADS] [CrossRef] (In the text)
- Grevesse, N., & Sauval,
A. J. 1999, A&A, 347, 348 [NASA ADS] (In the text)
- Gurtovenko, E. A., &
Kostyk, R. I. 1989, Fraunhofer spectrum and a system of solar
oscillator strengths (Naukova Dumka, Kiev)
(In the text)
- Holweger, H., & Müller,
E. A. 1974, Sol. Phys., 39, 19 [NASA ADS] [CrossRef] (In the text)
- Keller, C. U.
2005, private communication
(In the text)
- Keller,
C. U., Schüssler, M., Vögler, A., & Zakharov, V.
2004, ApJ, 607, L59 [NASA ADS] [CrossRef] (In the text)
- Keppens, R., & Martinez
Pillet, V. 1996, A&A, 316, 229 [NASA ADS] (In the text)
- Koza,
J., & Kucera, A. 2003, Contrib. Astron. Obs. Skalnaté
Pleso, 33, 224 [NASA ADS] (In the text)
- Koza, J.,
Kucera, A., Rybák, J., & Wöhl, H. 2006, in
Proceedings of NSO Workshop #23: Solar MHD: Theory and
Observations - a High Spatial Resolution Perspective,
ed. J. Leibacher, H. Uitenbroek, & R. Stein, ASP Conf.
Proc. Ser., 43
(In the text)
- Kucera, A.,
Koza, J., Bellot Rubio, L. R., et al. 2004, Hvar Obs.
Bull., 28, 19 [NASA ADS] (In the text)
- Kupka, F.,
Piskunov, N. E., Ryabchikova, T. A., Stempels,
H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS],
(VALD-2)
(In the text)
- Moore, C. E.
1972, A multiplet table of astrophysical interest - Pt.1:
Table of multiplets - Pt.2: Finding list of all lines in the
table of multiplets, rev. edn. (NSRDS-NBS, Washington: US
Department of Commerce)
(In the text)
- Moore,
C. E., Minnaert, M. G. J., & Houtgast, J. 1966,
The solar spectrum 2935 Å to 8770 Å (National
Bureau of Standards Monograph, Washington: US Government Printing
Office)
(In the text)
- Nave, G.,
Johansson, S., Learner, R. C. M., Thorne, A. P., &
Brault, J. W. 1994, ApJS, 94, 221 [NASA ADS] [CrossRef] (In the text)
- Neckel, H. 1999,
Sol. Phys., 184, 421 [CrossRef] (In the text)
- Odert, P.,
Hanslmeier, A., Rybák, J., Kucera, A., & Wöhl, H.
2005, A&A, 444, 257 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Press,
W. H., Teukolsky, S. A., Vetterling, W. T., &
Flannery, B. P. 1992, Numerical recipes in FORTRAN. The art of
scientific computing, 2nd edn. (Cambridge: University
Press)
(In the text)
-
Puschmann, K., Vázquez, M., Bonet, J. A., Ruiz Cobo,
B., & Hanslmeier, A. 2003, A&A, 408, 363 [NASA ADS] [CrossRef] [EDP Sciences]
-
Puschmann, K. G., Ruiz Cobo, B., Vázquez, M., Bonet,
J. A., & Hanslmeier, A. 2005, A&A, 441, 1157 [NASA ADS] [CrossRef] [EDP Sciences]
- Rimmele,
T., Dunn, R., Richards, K., & Radick, R. 1999, in Proc. High
Resolution Solar Physics: Theory, Observations, and Techniques,
ed. T. R. Rimmele, K. S. Balasubramaniam, &
R. R. Radick, ASP Conf. Ser., 183, 222
(In the text)
- Ruiz Cobo, B., & del
Toro Iniesta, J. C. 1992, ApJ, 398, 375 [NASA ADS] [CrossRef] (In the text)
- Rutten, R. J.
1988, in ASSL Vol. 138: IAU Coll. 94: Physics of Formation of FE II
Lines Outside LTE, 185
(In the text)
- Rybák,
J., Wöhl, H., Kucera, A., Hanslmeier, A., & Steiner, O.
2004, A&A, 420, 1141 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
-
Schröter, E. H., Soltau, D., & Wiehr, E. 1985, Vistas
in Astronomy, 28, 519 [NASA ADS] [CrossRef] (In the text)
- Shchukina, N., &
Trujillo Bueno, J. 2001, ApJ, 550, 970 [NASA ADS] [CrossRef] (In the text)
- Sheminova,
V. A. 1998, A&A, 329, 721 [NASA ADS] (In the text)
- Solanki, S. K., &
Stenflo, J. O. 1985, A&A, 148, 123 [NASA ADS]
-
Stein, R. F., & Nordlund, Å. 1998, ApJ, 499, 914 [NASA ADS] [CrossRef] (In the text)
-
Stein, R. F., & Nordlund, Å. 2000, Sol. Phys.,
192, 91 [NASA ADS] [CrossRef] (In the text)
- Steiner,
O., Grossmann-Doerth, U., Knoelker, M., & Schuessler, M. 1998,
ApJ, 495, 468 [NASA ADS] [CrossRef] (In the text)
- Steshenko,
N. V. 1968, in Structure and Development of Solar Active
Regions, ed. K. O. Kiepenheuer, IAU Symp., 35, 201
(In the text)
-
Sütterlin, P. 1998, A&A, 333, 305 [NASA ADS] (In the text)
-
Sütterlin, P., Schröter, E. H., & Muglach, K.
1996, Sol. Phys., 164, 311 [NASA ADS] [CrossRef] (In the text)
- Thévenin,
F. 1989, A&AS, 77, 137 [NASA ADS] (In the text)
- Unsöld, A.
1955, Physik der Sternatmosphären, Zweite Auflage
(Springer-Verlag)
(In the text)
-
Vernazza, J. E., Avrett, E. H., & Loeser, R. 1981,
ApJS, 45, 635 [NASA ADS] [CrossRef] (In the text)
-
Vögler, A., Shelyag, S., Schüssler, M., et al. 2005,
A&A, 429, 335 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Walton, S. R.
1987, ApJ, 312, 909 [NASA ADS] [CrossRef]
-
Wedemeyer, S., Freytag, B., Steffen, M., Ludwig, H.-G., &
Holweger, H. 2004, A&A, 414, 1121 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Wöhl, H.,
Kucera, A., Rybák, J., & Hanslmeier, A. 2002, A&A,
394, 1077 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Copyright ESO 2006
![\begin{figure}
\par\includegraphics[height=6.15cm,width=6cm,clip]{5679fg1a.eps}\...
....eps}\includegraphics[height=6.15cm,width=5.35cm,clip]{5679fg1c.eps}\end{figure}](/articles/aa/full/2006/42/aa5679-06/Timg22.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{5679fg2.eps}\end{figure}](/articles/aa/full/2006/42/aa5679-06/Timg32.gif)
![\begin{figure}
\par\includegraphics[height=5.4cm,width=8.05cm,clip]{5679fg3a.eps...
...{5mm}
\includegraphics[height=5.4cm,width=7.85cm,clip]{5679fg3b.eps}\end{figure}](/articles/aa/full/2006/42/aa5679-06/Timg34.gif)
![\begin{figure}
\par\includegraphics[height=5.9cm,width=8.4cm,clip]{5679fg4a.eps}...
...1.5mm}
\includegraphics[height=5.9cm,width=8.3cm,clip]{5679fg4b.eps}\end{figure}](/articles/aa/full/2006/42/aa5679-06/Timg63.gif)
![\begin{figure}
\par\includegraphics[height=4.55cm,width=8.2cm,clip]{5679fg5a.eps...
...s}\par\includegraphics[height=5.15cm,width=8.2cm,clip]{5679fg5d.eps}\end{figure}](/articles/aa/full/2006/42/aa5679-06/Timg65.gif)
![\begin{figure}
\par\includegraphics[height=4.55cm,width=8.1cm,clip]{5679fg6a.eps...
...}\par\includegraphics[height=5.15cm,width=7.75cm,clip]{5679fg6d.eps}\end{figure}](/articles/aa/full/2006/42/aa5679-06/Timg70.gif)
![\begin{figure}
\par\includegraphics[height=4.7cm,width=8.4cm,clip]{5679fg7a.eps}...
...g.eps}\includegraphics[height=5.25cm,width=7.5cm,clip]{5679fg7h.eps}\end{figure}](/articles/aa/full/2006/42/aa5679-06/Timg84.gif)
![\begin{figure}
\par\hspace*{-1mm}\includegraphics[height=5.75cm,width=8.15cm,cli...
...e*{3mm}
\includegraphics[height=5.75cm,width=8cm,clip]{5679fg8b.eps}\end{figure}](/articles/aa/full/2006/42/aa5679-06/Timg90.gif)
![\begin{figure}
\par\includegraphics[height=5.75cm,width=8cm,clip]{5679fg9.eps}\end{figure}](/articles/aa/full/2006/42/aa5679-06/Timg91.gif)