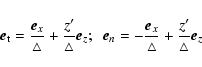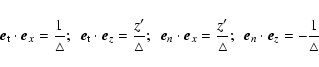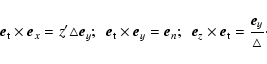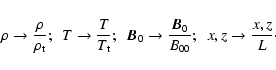A&A 458, 953-963 (2006)
DOI: 10.1051/0004-6361:20065206

Stability and mode analysis of solar coronal loops using thermodynamic irreversible energy principles

A. Costa¹ - R. González^2,3

1 - Instituto de Astronomía y Física del Espacio (CONICET-Argentina)
2 - Universidad Nacional de General Sarmiento (UNGS)
3 - Departamento de Física (FCEyN-UBA-Argentina)

Received 14 March 2006 / Accepted 7 July 2006

Abstract
Aims. We study the modes and stability of non-isothermal coronal loop models with different intensity values of the equilibrium magnetic field.
Methods. We use an energy principle obtained via non-equilibrium thermodynamic arguments. The principle is expressed in terms of Hermitian operators and allow to consider together the coupled system of equations: the balance of energy equation and the equation of motion.
Results. We determine modes characterized as long - wavelength disturbances that are present in inhomogeneous media. This character of the system introduces additional difficulties for the stability analysis because the inhomogeneous nature of the medium determines the structure of the disturbance, which is no longer sinusoidal. Moreover, another complication is that we obtain a continuous spectrum of stable modes in addition to the discrete one.
Conclusions. We obtain a unique unstable mode with a characteristic time that is comparable with the characteristic life-time observed for loops. The feasibility of wave-based and flow-based models is examined.

Key words: standards - waves - Sun: corona

1 Introduction

1.1 Variational principles

Stability is a crucial requirement for a model to produce realistic descriptions. Thus, different stability analyzed of solar structures can be found in the literature, generally restricted to special types of perturbations and specific equilibrium models. These includes, models that consider adiabatic configuration such as the ones analyzed via the classical criterion of Bernstein et al. (1958) or those that presuppose static equilibrium and analyze thermal stability. In the application of Bernstein's criterion, the adiabatic assumption implies that the energy balance equation is not required and thus dissipation is impossible. Also the assumption of static models is a strong, and often unjustified, restriction for open systems. Thus, a crucial question for any theoretical model is whether the much more common far-from-equilibrium states are stable, where the consideration of both thermal and mechanical coupled equations must be included.

A more realistic analysis of the stability of configurations represented by non-conservative equations was presented by Lerche & Low (1981). They proposed a Lagrangian principle in order to analyze quiescent prominences that can undergo thermal instabilities. However the non-self-adjoint character of the operators involved in the obtained principle makes the physical interpretation difficult.

In this paper we apply an energy principle to analyze the stability of solar coronal loops. The principle was obtained in a previous paper (Paper I: Costa et al. 2004; see also Sicardi et al. 2004; see also Sicardi et al. 1991, 1989a,b, 1985) using a general procedure of irreversible thermodynamics - based on firmly established thermodynamic laws - that can be understood as an extension of Bernstein's MHD principle to situations far from thermodynamic equilibrium. This fact has the advantage that many known results obtained by simpler criteria can be re-examined by a direct comparison with our criterion, and that, as it is obtained via a thermodynamic approach, allows a straightforward physical interpretation. The principle associates stability with the sign of a quadratic form avoiding non-self-adjoint operators. Obtaining a self-adjoint operator is a requirement for our principle to hold. When this is accomplished the calculus is simplified. The self-adjoint character of an operator implies that the eigenvalues  $\omega^{2}$ are real. Hence stability transitions always occur when  $\omega^{2}$ crosses zero, rather than at particular points of the real axis where the real part of the eigenvalue is different from zero, i.e. Re $(\omega) \neq 0$, leading to an efficient formulation to test stability. Thus, the symmetry considerations of the self-adjoint operators, the fact that there is a diagonal form associated with these operators, and that the Rayleigh-Ritz theorem states the existence of a minimum eigenvalue, are important reasons to try to maintain self-adjointness in the consideration of stability.

1.2 Solar coronal loops

The theoretical modeling and the interpretation of observations of coronal loop systems deal, among others, with the discussion whether the propagating observed disturbances in loops and post-flare loops are waves or plasma flow.

Dynamical features of brightening coronal loops have been traditionally interpreted as field-aligned flow of matter generated by asymmetries in the energy input. Most classical theoretical models have difficulties in determining the physical conditions that make them compatible with observations. Both static loops and steady state models - for the two classes of temperatures models: hot (isothermal coronas with $T \approx 10^{6}$ K) and cool (gradually increasing temperatures up to  $T \approx 10^{5}$ K) - fail to provide a satisfactory explanation for both the emission measure distribution and the Doppler shift observations (Jordan 1980; Serio 1981; Craig & McClymont 1978; Mariska 1984). Thus, this suggests that in traditional model scenarios radiative losses cannot be compensated by thermal conduction. Therefore, other heating mechanisms must be assumed (Aschwanden et al. 1999, 2000; Walsh & Galtier 2000). Also, theoretical time-dependent models of individual loops where the plasma evolves in response to a cyclical process of heating and cooling of the flow have difficulties in fitting observations (Klimchuk & Mariska 1988).

The assumption of propagating disturbances associated with slow magnetoacoustic waves in high Alfvén speed media is also a field of investigation. Several wave-based models were developed to explain observations (Nakariakov et al. 2000; Tsiklauri & Nakariakov 2001). These authors suggest that - depending on the relative importance of dissipation by magnetic resistivity - upwardly propagating waves (of observed periods between 5-20 min) that decay significantly in the vicinity of the loop apex could explain the rarity of observational detection of downwardly propagating waves. However, upwardly propagating disturbances with non-decaying or even growing amplitudes were observed in coronal EIT plumes. Analytic models have shown that slow magnetoacoustic waves may be trapped and nonlinearly steepened with height, providing a possible interpretation of this phenomenon (Ofman et al. 1999).

However, due to the intensity of the flaring, the plasma dynamic of flare loops is generally associated with flows rather than with waves. In fact, systematic intensity perturbations in post-flare loops can suggest that they are the result of evaporation-condensation cycles caused by the efficient heating of the flaring plasma from the chromosphere. Thus, chromospheric evaporation seems to be the main initial matter inflow source for flare loops. De Groof et al. (2004) analyzed an off-limb half loop structure from an EIT shutterless campaign and gave arguments to reject the slow magnetoacoustic description and to support the flowing/falling plasma one. Nevertheless, these authors admit that the wave theory cannot be excluded yet.

Other authors have suggested that a combination of phenomena can be at the basis of a better interpretation. Alexander et al. (1998) examined 10 flares and concluded that plasma turbulence could be the source of the observed intensity changes rather than hydrodynamic flows such as chromospheric evaporation. They pointed out that it cannot be excluded that there is a degree of "gentle evaporation'' occurring early in the event with associated hard X-ray emission below their threshold of detection. A series of more recent papers (Tsiklauri et al. 2004a-c) that combine theoretical and observational analysis showed that oscillations in white, radio and X-ray light curves observed during solar and stellar flares may be produced by slow standing magnetoacoustic modes of the loops. They found that a transient heat deposition at the loop bottom - or at the apex - leads to a posterior up-flow evaporation of material of the order of a few hundreds of km s^-1. During the peak of the flare, the simulations showed that a combined action of heat input and conductive and radiate losses could yield an oscillatory pattern with typical amplitudes of up to a few tens of km s^-1. Then, a cooling phase of plasma draining with velocities of the order of hundreds of km s^-1 occurs. The numerical quasi-periodic oscillations in all the physical quantities, that resemble observational features, were interpreted as being produced by standing sound waves caused by impulsive and localized heating.

In previous papers (Borgazzi & Costa 2004; Costa & Stenborg 2004) one of us developed a diagnostic observational method to describe loop intensity variations, both in space and time, along coarse-grain loop structures. We find that none of the arguments leading to the determination of whether waves or flow models can better fit observations was conclusive. Some of our results suggested wave-based model interpretations i.e. the periodic behaviour of the disturbances observed, the almost constant speed of some brightening features and the fact that the estimated speeds were not higher that the sound speed in the coronal loops. However, as we mentioned, the period behaviour can also be attributed to flows (Gómez et al. 1990; De Groof et al. 2004). Also, even when the calculated speeds were not greater than the sound ones, some of the velocity patterns were far from being constant and their values were comparable to the free-fall case.

Another open question is the relation between the loop's coronal dynamics and the physical conditions on the chromospheric bases. Borgazzi & Costa (2004) found a longitude of chromospheric coherence that characterizes the behaviour of a whole loop-system of evolving coronal-isolated filaments. This description is in accordance with limit-cycle models that require that the triggering mechanism of the dynamics is located at the bottom of the structure giving rise to the observed similar coronal conditions of the isolated filaments. Another aspect that deserves attention is whether it is physically possible that the periodicity observed could be related to, or could be the consequence of propagating magnetoacoustic modes from the chromosphere that have suffered distortion due to the dispersing media.

Other point that is under debate is the thermal structure of the loops. Loop observations with TRACE (Transition Region and Coronal Explorer, Handy et al. 1999) suggest that hot coronal loops are isothermal and more dense than the predictions of static loop models. However this scenario is not conclusive and other interpretations are possible. Reale & Peres (2000) showed that bundles of thin strands, each one behaving as a static loop, with its characteristic thermal structure, convoluted with the TRACE temperature response could appear as a single almost isothermal loop. A wide range of configurations can be proposed to fit observations. The fact that images form a compound of complex integrated time-varying data that are not easy to resolve is at the basis of this difficulty. The loops under analysis are surrounded by other structures that usually intersect them along the line of sight and the change of the brightening of the loops is also affected by background emission. Thus, efforts are made to produce observational and theoretical results of coronal loop dynamics.

The aim of this paper is to investigate whether the propagating observed disturbances in loops are waves or plasma flow and their thermal structure. Non-isothermal loops are traditional candidates for Hopf instabilities with cycles of flow evaporating and condensing, thus the analysis of frequencies and mode structures can provide insight into a possible wave model interpretation of these types of configurations. We consider the stability analysis as the leading criterion to select possible theoretical wave models. The fact that a number of non-linear equilibria are possible due to the open character of the systems makes it necessary to consider both thermal and mechanical stability in a coupled way.

2 The stability criterion

The thermodynamics of irreversible processes is described in terms of phenomenological relations between conjugate pairs of thermodynamic variables: the flows and the forces that cause them. The linear thermodynamic approximation treats small deviations from the equilibrium state by including fluctuations in the neighborhood of this state. It describes the behaviour of the system around the equilibrium state or around a non-equilibrium stationary one that is linearly close to it.

If the system is isolated, as is stated by the second law of thermodynamics, the entropy grows exponentially up to its maximum value. That the system is in an open-near-equilibrium state means that energy and matter is exchanged with the neighbors and the entropy of the system is not necessarily positive. Even when the entropy produced in the system's interior, due to irreversible processes, is never negative, a negative flow of entropy produced by the exchange of matter and energy can make the system remain indefinitely in a near-equilibrium state. These states are known as stationary states and a coherent dynamic of the system could last if sufficient negative entropy flow is provided to it. Thus, the criterion that states the stability of this stationary state gives insight into the dynamic structures that can be found in nature. These stationary states are also known as detailed balanced. As Onsager pointed out (1931), the balance consists of the compensation between the fluctuations and dissipation produced by the flows and forces that have a microscopic reversible character near the thermodynamic equilibrium. The empirical relations between flows and forces are linear and related by the so-called resistance matrix $\bf {R}$ that is symmetric and positive definite. Its symmetric character is guaranteed by the principle of microscopic reversibility and its positive definiteness by the proximity of the reference state to the thermodynamic equilibrium, where the entropy has a maximum.

However, there is no continuity between linear and nonlinear thermodynamical processes. When the system is beyond the immediate neighborhood of the stationary state the nonlinearities become visible. Instabilities that cause dynamic transitions in open systems are responsible for the qualitative difference between linear and nonlinear thermodynamics. Therefore, dynamic cooperative phenomena can only arise in nonlinear thermodynamics. Thus, nonlinear thermodynamics is related to the stability properties of non-equilibrium stationary states, where the linear relation between flows and forces can become state dependent (i.e. $\bf {R}$ is not necessarily a symmetric positive definite matrix), and the problem of having a thermodynamic theory to provide a general criterion for the stability of the system - which is not evident through the integration of the variational equations - becomes a fundamental point. Non-linear thermodynamics is the extension of the linear theory to situations far from thermodynamic equilibrium where the relaxation of the processes to a steady state of non-equilibrium (nonlinear state) is not assured and requires a stability analysis (Glansdorff & Prigogine 1971; Keizer 1976; Graham 1978; Lavenda 1993, 1987).

In Paper I we showed how to obtain the variational principle from the equations that describe the dynamics of the system of interest. The method consists of obtaining a Lyapunov function, also known as generalized potential, that represents the mathematical expression of the stability conditions. This function is determined by the analysis of the thermodynamic properties of the system linearized around a non-linear stationary state also called non-linear equilibrium state. The equations governing the dynamics are written as a system of two coupled equations: the balance energy equation and the equation of motion. Thus, the perturbation analysis around a stationary state is performed considering a variable state vector of four independent components: the three space component displacement and the temperature variation. Once the linearization is done, the Lyapunov function can be immediately obtained by inspection of the resulting expression written in a compact matrix form. Each of the matrices of the compact expression are linear operators (that could include spatial derivatives) and have a clear physical interpretation that is given by its role in the equation. The matrix that multiplies the second time derivative of the perturbation is associated with the inertia of the system, the one that multiplies the first time derivative of the perturbation is associated with dissipation and the one that multiplies the perturbation itself is associated with potential forces over the system. The principle is subject to physically reasonable requirements of hermiticity and antihermiticity over the matrices. For a more detailed presentation see Paper I and the references presented there.

2.1 The magnetohydrodynamic expression

The specific model we analyze is taken to be composed of a magnetohydrodynamic ideal plasma (i.e. with infinite electrical conductivity $\sigma \gg 1$). The fundamental ideal magnetohydrodynamic equations to be considered are as follows. The mass conservation equation,

$$\frac{\partial \rho}{\partial t}+\nabla\cdot(\rho\vec{v})=0$$ (1)

where $\rho$ is the density of the plasma, $\vec{v}$ is the plasma velocity, and t the time. The perfect gas law or state equation,

$$p=\frac{k_{\rm B}}{m}\rho T$$ (2)

$k_{\rm B}$ is the Boltzmann constant, p the pressure, T the temperature and $m\equiv m_{\rm p}$ the proton mass. For a fully ionized H plasma $\rho = \mu n_{\rm e} m_{\rm p}$; the solar coronal abundances (H:$\rm He=10$:1) correspond to a molecular weight $\mu=1.27$; $n_{\rm e}$ is the number density of electron particles (Aschwanden 2004). The induction equation,

$$\frac{\partial \vec{B}}{\partial t}=\nabla\times(\vec{v}\times\vec{B})$$ (3)

$\vec{B}$ is the magnetic field vector. The magnetic diffusivity was discarded. The equation of motion for the problem is:

$$\rho\frac{D\vec{v}}{Dt}=-\nabla(p)+\frac{1}{4\pi\mu}(\nabla\times\vec{B})\times\vec{B} -\rho\nabla\phi$$ (4)

where $g=-\nabla\phi$ is the gravity expression and $j=1/4\pi \nabla\times\vec{B}$ the current density. The energy balance equation takes the form:

$$\frac{\rho^{\gamma}}{(\gamma-1)}\frac{D}{D t}\left(\frac{p}{\rho^{\gamma}}\right)=-L$$ (5)

where $\gamma$ is the ratio of specific heats and L is the energy loss function:

$$L=-\nabla\cdot\vec{F_{\rm c}}-L_{\rm r}+H.$$ (6)

$\vec{F_{\rm c}}$ is the heat flux due to particle conduction along the loop, $L_{\rm r}$ is the net radiation flux. Neither the dominant heating mechanism of coronal loops nor the spatial distribution function of the energy input is known. So, the heating function is the least known term in the energy balance equation. Thus, the usual situation is to try reasonable arbitrary mathematical functions which must fit the constraint imposed by the equilibrium conditions. As our model considers inhomogeneous temperature gradients and isothermality is usually associated with footpoint heated loops more than with uniformly heated ones we discard the first case and tried the general expression ${H} = h \rho + H_{0}$. A time varying dependence of H was not considered for simplicity. However, it could be a requirement for modeling special events such as micro-flares or while considering magnetic reconnection phenomena. Equation (5) expresses the fact that the gain in particle energy (internal plus kinetic) is due to heating sources, heat flow and radiation losses; ohmic dissipation $j^{2}/\sigma$ and all other heating sources were considered as vanishing terms implying that the optically thin assumption holds. Then $L_{\rm r}=n_{\rm e}n_{\rm H}Q(T)$; the temperature variation ( $Q(T)=\chi T^{\alpha}$) was taken from Priest (1982). Also $F_{\rm c}=-k \nabla T$ and, as conduction across the magnetic field has been discarded, for a total ionized plasma $F_{\rm c}=-k_{0}T^{\frac{5}{2}}\nabla_{\parallel}T$. Finally Eq. (5) can be written as

$$\frac{\rho^{\gamma}}{\gamma-1}\frac{D(\frac{p}{\rho^{\gamma}}... ...{2}}{m^{2}} \chi T^{\alpha}+\frac{\upsilon}{m^{2}}\rho + H_{0}$$ (7)

where $\upsilon$ is a constant value to be determined from the equilibrium conditions.

The linearization procedure is performed by replacing $\rho=\rho_{0}+\rho_{1}$, T=T₀+T₁, B=B₀+B₁ and $\vec{v}=\vec{v_{0}}+\partial\vec{\xi}/\partial t$ in the last equations, and assuming hydrostatic conditions for the equation of motion. Thus, $\vec{v_{0}}=0$ and $\vec{v_{1}}=\partial\vec{\xi}/\partial t$ where $\xi$ is the perturbation around the equilibrium of the equation of motion (the stationary state), also $\partial\rho_{0}/\partial t=0$ and $\partial B_{0}/\partial t=0$. Using the relation $\partial/\partial t\simeq i\omega$ in Eqs. (1) and (3), the corresponding linearized equations (Eqs. (8)-(12)) are:

$$\rho_{1}+\nabla\cdot(\rho_{0}\vec{\xi})=0$$ (8)

$$p_{1}=\frac{k_{\rm B}}{m}(\rho_{0}T_{1}-T_{0}\nabla\cdot(\rho_{0}\vec{\xi}))$$ (9)

$$\vec{B_{1}}=-\nabla\times(\vec{B}_{0}\times\vec{\xi})$$ (10)

 

$$\rho_{0}\ddot{\vec{\xi}}=\displaystyle\frac{k_{\rm B}}{m}\nabla(T... ... B_{0} ) \times Q ] + \bigtriangledown \phi \nabla \cdot ( \rho_{0} \vec{\xi })$$ (11)

or equivalently $\rho_{0}\ddot{\vec{\xi}}-F\xi+\frac{k_{\rm B}}{m}\nabla(\rho_{0}T_{1})=0$ and

$$\frac{k_{\rm B}}{m(\gamma-1)}[\rho_{0}\dot{T_{1}}-(\gamma-1)T_{0} \nabla\cdot(\rho_{0}\dot{\vec{\xi}})]-AT_{1}+B\vec{\xi}=0$$ (12)

being

$$A=-\left[c\nabla \cdot \left(T_{0}^{\frac{5}{2}}\nabla _{\par... ...frac{\rho _{0}^{2}}{m^{2}}\chi \alpha T_{0}^{\alpha -1}\right]$$

and

$$B=\ \left\{\frac{k_{\rm B}}{m}\beta \nabla _{\bullet }(\rho _... ...rac{-2(\rho _{0}\chi T_{0}^{\alpha }- \upsilon /2)}{k_{\rm B}m}$$

$$c=\frac{1.8\times 10^{-10}}{\ln\Lambda} \ {\rm W~m}^{-1}~{\rm K}^{-1}, \; \ Q=\vec{B}_{0}\times\vec{\xi}.$$

The term $\ \nabla \cdot (\rho _{0}\dot{\xi}) \$ was discarded because it represents the total net flux of material through the magnetic tube. The two obtained equations are expressed in terms of the displacement and temperature perturbed variables $\vec{\xi}$ and T₁. $\star$represents the location of the perturbed variables when performing the matrix product.

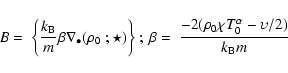
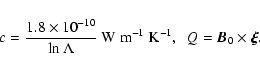
Following Paper I the resulting energy principle is:

 

$$\delta^{2} S = \frac{ 1}{ 2} \ \int \big[ \-\dot{\vec{\xi^{*}}}\b... ...{*} AT_{1} +T_{1}^{*}B\vec{\xi} -\vec{\xi}^{*}B T_{1})\big] {\rm d}^{3}x \geq 0$$ (13)

where F is the known Bernstein operator for the system.

For the non-dissipative cases, last expression reduces to the well-known Bernstein MHD energy principle

$$\delta^{2} S = \frac{ 1}{ 2}\int \left[\-\dot{\vec{\xi^{*}}}\... ...{ \vec{\xi^{*}} \beta F \vec{\xi}} \right] {\rm d}^{3}x \geq 0$$ (14)

from where the eigenmodes and eigenfrequencies are calculated as

$$\omega^{2}=-\frac{\int \vec{\xi}^{*} \beta F\vec{\xi} {\rm d}^{3}x}{\int\vec{\xi}^{*}\beta \rho_{0}\vec{\xi} {\rm d}^{3}x }$$ (15)

and the stability criterion is obtained by requiring the positivity of the potential energy of the perturbation (Galindo Trejo 1987)

$$\delta^{2} W_{p({\rm Bernstein})} = \frac{1}{2}\int \vec{\xi}^{*} \beta F\vec{\xi} {\rm d}^{3}x$$ (16)

subject to the normalization condition that the total kinetic energy is equal to one. Thus, the dissipative principle and the new frequencies are respectively:

$$\delta^{2} W_{\rm p} =\frac{1}{ 2}\int ( \vec{\xi}^{*} \beta ... ... +T_{1}^{*}B\vec{\xi} -\vec{\xi}^{*}BT_{1}){\rm d}^{3}x\geq 0,$$ (17)

$$\omega^{2} =- \frac{\int ( \vec{\xi}^{*} \beta F\vec{\xi} + T... ...}x}{\int (\vec{\xi^{*}} \beta \rho_{0}\vec{\xi} ){\rm d}^{3}x}$$ (18)

with the same normalization condition.

3 Application to the stability of a coronal inhomogeneous loop model

We are interested in analyzing the stability of non-homogeneous loops. This is, loops with inhomogeneous distributions of plasma density and temperatures. This character of the system poses additional difficulties for the stability analysis because the inhomogeneous nature of the medium determines the structure of the disturbance which is no longer sinusoidal, making the traditional normal mode analysis useless for this treatment. Moreover, there may exist a continuous spectrum of stable modes besides the discrete one. As a first order approximation we neglect the effect of gravitational stratification and thus confine the analysis to characteristic spatial scales lower than the pressure scale height in the solar corona. In order to analyze the stability and to obtain the frequencies and modes the physical quantities in Eqs. (17) and (18) must be calculated along the loop structure.

3.1 Mechanical equilibrium

In order to determine an equilibrium configuration we assume force-free equations due to the fact that in plasma with low  $\mathcal{\beta}$ (gas pressure over the magnetic pressure) the pressure gradient can be neglected in comparison to the Lorentz force. The coronal arcade is obtained from the equations

$$\nabla \times \vec{B}_{0}=\alpha \vec{B}_{0}=0$$ (19)

$$\vec{j} \times \vec{B}_{0}=0.$$ (20)

Also, $\vec{B}_{0} \cdot \nabla p =0$ and thus the pressure has a constant value along the loop. We assume that the unperturbed magnetic field is $\vec{B}_{0} = (B_{0,x}(x,z), 0 , B_{0,z}(x,z))$ and obtain the equilibrium field components

$$B_{0x}= - B_{00} \cos\left(\frac{\pi}{2L} x\right) {\rm e}^{-\frac{\pi}{2L}z}$$ (21)

$$B_{0z}= B_{00} \sin\left(\frac{\pi}{2L} x\right) {\rm e}^{-\frac{\pi}{2L}z}$$ (22)

with

$$\vec{B}_{0}= B_{00} {\rm e}^{-\frac{\pi}{2L}z}\vec{e}_{s}.$$ (23)

The relation

$$z= z_{\rm t}+\frac{2L}{\pi}\ln\left[\cos\left(\pi \frac{x}{2L}\right)\right]$$ (24)

is straightforward. The arc element s (see Fig. 1) can be expressed as

$${\rm d}s= {\rm d}x \sqrt{\left(1+\frac{{\rm d}z}{{\rm d}x}\right)^{2}} = {\rm d}x\; \triangle$$ (25)

with $\Delta= \sqrt{1+(z')^{2}}.$

	Figure 1: Schematic figure of the magnetic arcade with $z(x)= z_{\rm t}+\frac{2L}{\pi}\ln\left[\cos(\pi \frac{x}{2L})\right]$, x and z the Cartesian coordinates. $e_{\rm t}$ and $e_{\rm n}$ the tangential and normal versors respectively. $T_{\rm b}$ and $T_{\rm t}$ are the temperature values at the bottom and top respectively. The same notation is used for the density $\rho$.
Open with DEXTER

3.2 Thermal equilibrium

The thermal equilibrium is obtained from Eq. (7) with L=0(in Eq. (6)). Thus expressions $F_{\rm c}=-k_{0}T^{\frac{5}{2}}\nabla_{\parallel}T$ satisfies the two relations

$$\frac{\partial F_{\rm c}}{\partial T} \frac{\partial T}{\part... ...rtial F_{\rm c}}{\partial T }= -\frac{\rho^{2}}{m^{2}}Q(T)+ H,$$ (26)

from where we obtain the two equations

 

$$F_{\rm c} \frac{- {\rm d}T k_{0}T^{\frac{5}{2}}}{{\rm d}s}$$ =

$$\frac{{F_{\rm c}}^{2}}{2} {\int_{T_{0}}}^{T} k_{0}T'^{\frac{5}{2}}\left[\frac{\rho^{2}}{m^{2}}Q(T')-H_{0}\right] {\rm d}T'$$ = (27)

where we assume $F_{\rm c}(s=0)=0$ as ${\rm d}T/{\rm d}s=0$ at s=0 and H = H₀, so the constant value of Eq. (7) is $\upsilon =0$. We then can replace $F_{\rm c}$ in Eqs. (27) and give Q(T) its explicit expression. Then integrating between $T_{\rm t}$ and $T_{\rm b}$(the temperatures at the top and the bottom of the loop respectively) and using $({\rm d}T/{\rm d}s)_{T=T_{\rm b}}=0$ and $T_{\rm t}\gg T_{\rm b}$we obtain the constant value of the heating function $H_{0}= 7 p^{2} \chi T^{\alpha -2}_{\rm t}/\left(8 k_{\rm B}^{2}\left(\alpha +\frac{3}{2}\right)\right)$. Also, we find

$$\left[\frac{{\rm d}T}{{\rm d}s}\right]^{2}=\frac{p^{2}\chi}{2... ...} \left[1 - \left(\frac{T}{T_{\rm t}}\right)^{2-\alpha}\right]$$ (28)

which is equivalent to the calculus in Chap. 6 of Priest (1982). Our aim is to obtain T as a function of the line element s. From Eq. (28) s=f(T) given as an integral expression of the temperature, which has to be inverted. Thus, for calculus purposes, we define $v=1-(T/T_{\rm t})^{2-\alpha}$ and replace T as a function of v in Eq. (28). Then we obtain s=f(v) as

$$s=\frac{1}{\mathcal{A}}\mathbb{B}_{v}\left(\frac{1}{2},q\right)$$ (29)

where

$$\mathbb{B}_{v}\left(\frac{1}{2},q\right)=\int_{0}^{v}t^{p-1}(1-t)^{q-1}{\rm d}t$$

(Arfken & Weber 1995) with

$$p=\frac{1}{2}, \ q=\left(\frac{\alpha}{2}+\frac{3}{4}\right)(2-\alpha)+1,$$

$$\mathcal{A}=(2-\alpha)T_{\rm t}^{\frac{\alpha}{2}-\frac{11}{4... ...ha+\frac{3}{2}\right)k_{\rm B}^{2}\right)\right)^{\frac{1}{2}}.$$

Then, T=f^-1(s) as

$$\frac{{\rm d}T}{{\rm d}s}=\mathcal{A}\left[\frac{{\rm d}\mathbb{B}_{v}}{{\rm d}v}\frac{{\rm d}v}{{\rm d}T}\right]^{-1}\cdot$$ (30)

3.3 The perturbation

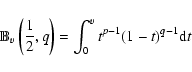
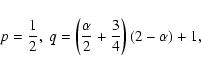
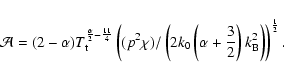
In order to calculate the stability and structure modes the general perturbation expression along the equilibrium loop is written

$$\vec{\xi}=[\zeta(x) \vec{e}_{\rm t}+\eta(x)\vec{e}_{n}+\xi_{y}(x)\vec{e}_{y}]{\rm e}^{{\rm i}ky}$$ (31)

and

$$T_{1}=T_{1}(x){\rm e}^{{\rm i}ky}.$$ (32)

Then, representing the equilibrium functions of the different quantities with a 0 sub-index and using the loop parameters and the mathematical relations presented in the Appendix, we obtain the non-dimensional expression for the energy principle (Eq. (17))

 

$$\delta^{2} W_{\rm p}=\frac{1}{2}\int_{-1}^{1}{\rm d}x \left \{ \l... ...{0}}{{\rm d}x}\right)f+\rho_{0}D_{x}f-k\rho_{0}\xi_{y} \right ) \right. \right.$$

$$\hspace*{2mm}+\beta T_{0}f \left ( \frac{{\rm d}^{2}\rho_{0}}{{\r... ...d}\rho_{0}}{{\rm d}x}\xi_{y}-k \rho_{0} \frac{{\rm d}\xi_{y}}{{\rm d}x}\right )$$

$$\hspace*{2mm}-k \beta T_{0} \xi_{y}\left ( \frac{{\rm d}\rho_{0}}{{\rm d}x} f-k\rho_{0}\xi_{y} \right ) \left. \right. {\Bigg ]}$$

$$\hspace*{2mm}+C_{1}\left [ \beta \frac{{\rm d}}{{\rm d}x} \left (... ...ft ( \frac{-z'}{\triangle}\zeta+\frac{\eta}{\triangle} \right ) \right. \right.$$

$$\hspace*{2mm} + \left ( k\frac{z'}{\triangle} \vec{B}_{0}\xi_{y}-... ...ta \left(\left ( k\frac{\vec{B}_{0}}{\triangle} \right )^{2}\xi_{y}^{2} \right.$$

$$\hspace*{2mm} + \left ( \frac{{\rm d}}{{\rm d}x}\left(\frac{\vec{... ...eta}{{\rm d}x}-k\frac{z'}{\triangle}\vec{B}_{0}\xi_{y})^{2} {\Bigg )} {\Bigg ]}$$

$$\hspace*{2mm}+ C_{2}\left [ -\zeta T_{0}^{\frac{3}{2}} \frac{1}{\... ...\left ( \frac{1}{\triangle} \right ) T_{1}\frac{{\rm d}T_{1}}{{\rm d}x} \right.$$

$$\hspace*{2mm} -\frac{T_{0}^{\frac{5}{2}}}{\triangle^{2}} T_{1} \f... ...- \rho_{0}T_{0}^{\alpha-1}T_{1}^{2}+\beta\frac{{\rm d}\rho_{0}}{{\rm d}x}T_{1}f$$

$$\hspace*{2mm} +\beta\rho_{0} \left ( D_{x}f-k\xi_{y} \right ) T_{1}$$

$$\hspace*{2mm} -\beta \left [ \frac{1}{\triangle}\frac{{\rm d}\rho... ...}x}\eta\frac{{\rm d}T_{1}}{{\rm d}x}+k\rho_{0}\xi_{y} T_{1} \right ] {\Bigg \}}$$ (33)

where the non-dimensional quantity $\delta^{2} W_{\rm p}/\left(\chi T_{\rm t}^{\alpha+1}\rho_{\rm t}^{2}L/m^{2}\right)$ replaces $\delta^{2} W_{\rm p}$, and $C_{1}=B_{00}^{2}k_{\rm B} T_{\rm t}\rho_{\rm t}/m\mu$ and $C_{2}=c \; m^{2} T_{\rm t}^{\frac{7}{2}}/(L^{2} T_{\rm t}\alpha\rho_{\rm t}^{2})$ were used. From this variational principle we can then analyze stability and obtain the mode structure and the associated frequencies for the general mode given by Eq. (31).

4 Results and discussion

In order to calculate modes and frequencies we followed the schematic procedure described in Paper I and in Galindo Trejo (1987). We used a symbolic manipulation program to integrate the equations. $\delta^{2} W_{\rm p}$ and the perturbations were expanded in a three dimensional-Fourier basis that adjusts to border conditions. Thus, a quadratic form for $\delta^{2} W_{\rm p}$was obtained and was minimized with the Ritz variational procedure. A matrix discrete eigenvalue problem subject to a normalization constraint was obtained. The procedure is equivalent to solving Eq. (18) of our modified principle. Once the modes are obtained, the stability condition of Eq. (17) for the generalized potential energy: $\delta^{2}W_{\rm p}\geq0$ must be corroborated. The following values were used for the numerical calculation of the modes

$$\alpha=-\frac{1}{2} \ \ \rightarrow \ \ q=\frac{6}{5}$$

$$s= \frac{1}{\mathcal{A}} \mathbb{B}_{v}\left(\frac{1}{2}, \fr... ...frac{p^{2}\chi}{2k_{0}k_{\rm B}^{2}}\right)^{ \frac{1}{2}}\cdot$$

Coronal loop parameters: L=10¹⁰ cm (or L=100 Mm), $T_{\rm b}=10^{4}$ K $T_{\rm t}=10^{6}$ K $n_{\rm e}=10^{8}$ cm^-3 electron number density $p_{\rm t} =2k_{\rm B}T_{\rm t}$; $\rho_{\rm t}=mp_{\rm t}/k_{\rm B}T_{\rm t}$.

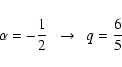
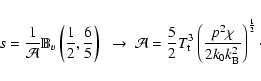
Our main concern was to know whether the magnetic configuration of equilibrium could be stable under linear perturbations. For non homogeneous configurations it is well known that the stable eigenvalues can have continuous spectra while the unstable ones have a discrete spectrum (see Freidberg 1982; or Priest 1982). If the resulting mode components have a characteristic wavelength of the order of the equilibrium structure, the non-homogeneous character of modes could determine, for the stable modes, a continuous spectrum. Thus, in this case, the traditional normal mode analysis gives only a rough description because one of the consequence of the existence of the continuum is that an accumulation of discrete eigenvalues can take place at either boundary, generally at $\omega^{2}=0$ or $\omega^{2}=\infty$, indicating the presence of a continuum stable spectrum. Note that as the basis used is discrete, the spectrum is necessarily discrete. However, the additional evaluation of the generalized potential energy provides the correct unstable modes and gives an approximate value of the most probable stable period when the smaller $\omega^{2}$ is not located at the boundaries.

We used different values for k: k=0, k=0.5 and k=10 (k is the wavenumber associated with the perturbation component transverse to the plane that contains the magnetic configuration). We also calculated the frequencies and modes for two different values of the magnetic field: B₀₀=11 G and B₀₀=100 G.

Table 1: Periods associated with the unstable and stable eigenvalues (minutes) for B₀₀=11 G.

Table 2: Periods associated with the unstable and stable eigenvalues (minutes) for B₀₀=100 G.

Tables 1 and 2 show the eigenvalues (periods) associated with the different modes for the cases B₀₀=11 G and  B₀₀=100 G respectively, considering k=0 and obtained by solving Eq. (18). We obtained 12 eigenfrequencies and 12 eigenmodes for each of the magnetic field values i.e. we used a three-component expansion and a four-component perturbation vector. We evaluated the mode behaviour for $k\neq0$. For each mode corresponding to a complex eigenvalue, the perturbation $\xi _{y}$ was at least two orders of magnitude smaller that the parallel $\zeta$ component and the normal $\eta$ components. For the modes with real eigenvalue, in only one case was $\xi _{y}$comparable to the smaller of the two other spatial perturbations. Thus, for numerical simplicity, we used k=0 and we discarded three zero eigenvalues associated with this choice of k. We then analyzed only the 9 relevant modes. This means that a two-dimensional analysis of the dynamics of the problem is reasonably able to obtain the overall behaviour within the approximations we are considering. Thus, we decided to investigate the unstable modes and to consider the most stable one as a reference value for stability. The most stable mode is the one that has a real $\omega$ value and minimizes $\delta^{2} W_{\rm p}$ (it is the mode that gives the minimum positive value of the functional  $\delta^{2} W_{\rm p}$) and the most unstable one is the mode that has a complex $\omega$ value with the minimum value of $\tau \simeq 1/\vert\omega\vert$ ($\tau$ the instability time).

	Figure 2: Mode components corresponding to the first mode P1=36.3 min for the cases: a) $\zeta$ and B00=11 G; b) $\eta$ and B00=11 G; c) $\zeta$ and  B00=100 G; d) $\eta$ and  B00=100 G.
Open with DEXTER

	Figure 3: Mode components corresponding to the second modes: a) $\zeta$ component of P2=6.6 min with B00=11 G; b) $\eta$ component of P2=6.6 min with B00=11 G; c) $\zeta$ component of P2=0.7 min with B00=11 G; d) $\eta$ component of P2=0.7 min with B00=100 G.
Open with DEXTER

From the analysis of the table data we can conclude: 1) for each of the two investigated magnetic values we have three complex values of $\omega$ and six real ones; 2) in the two magnetic field cases the eigenvalues of the first mode are the same; 3) in all the other cases the eigenvalues with B₀₀=100 G are almost an order of magnitude smaller than the corresponding values of B₀₀=11 G; 4) the series of eigenvalues is such that it could be possible that the stable periods accumulate at $\omega=0$, thus the definite stability characterization is subject to the evaluation of the generalized potential energy of the modes.

We analyzed the structure of the modes with complex values of $\omega$ as they are possible candidates for instability (Freidberg 1982). We noted that in the two first modes the component that is tangent to the magnetic field $\mid\zeta\mid$ is greater than the component $\mid\eta\mid$ that is normal to it. This can be seen from Figs. 2 and 3 where $\zeta$ and $\eta$ are shown for the cases: B₀₀=11 G and B₀₀=100 G respectively, also using k=0. The third mode (see Fig. 4) has comparable values of $\mid\zeta\mid$ and $\mid\eta\mid$.

The fact that for the first mode the two values of B₀₀ give the same time eigenvalue $P_{1}=2\cdot 60\pi / \omega = 36.3 i$ min indicates independence from the magnetic structure. This is consistent with the relative values between the two components in the two B₀₀ cases: $\mid\zeta\mid\gg\mid\eta\mid$ (see Fig. 2). Thus, these magnetoacoustic modes are more of the acoustic type $\mid\zeta\mid\gg\mid\eta\mid$ than of the Alfvén type, i.e. $\mid\zeta\mid\ll\mid\eta\mid$ (see Fig. 5). Also, the obtained period is included in a range ( $10~{\rm min}<P<60$ min) where MHD slow acoustic modes are expected (Aschwanden 2004).

Figure 3 shows the second mode for B₀₀=11 G and B₀₀=100 G respectively. Also for both cases the $\mid\zeta\mid$ perturbation is greater than the normal perturbation $\mid\eta\mid$ by an order of magnitude.

Figure 4 show the superposition of $\zeta$ and $\eta$ for the third modes corresponding to P=4.3 min, B₀₀=11 G and P=0.5 min, B₀₀=100 G respectively. Note that in these cases, when the component $\eta$ is relevant, resembling an Alfvén wave, the relation between the eigenvalues (periods) of the different magnetic fields is $P_{11~{\rm G}}\simeq 10 P_{100~{\rm G}}$, in accordance with the relation between the two values of $B_{00}(11~{\rm G})\simeq B_{00}(100~{\rm G})/10$ and with the corresponding values of the Alfvén velocities of the medium $v_{\rm A}=B_{00}/\sqrt{\mu\rho}$.

	Figure 4: $\zeta$ and $\eta$ components for the third mode. a) left: P3=4.3 min with B00=11 G and  b)  right: P3=0.5 min with B00=100 G. $\xi _{y}$ has vanishing values.
Open with DEXTER

	Figure 5: Schematic classification of fast and slow magnetoacoustic waves. $\theta$ is the angle between the mode and the magnetic field: $\theta =0$ corresponds to large values of $\zeta$ and $\theta =\pi /2$ corresponds to large values of $\eta$.
Open with DEXTER

Figure 5 gives a schematic classification of fast and slow magnetoacoustic waves from where we can analyze the behaviour of the modes. The first mode corresponds to $\theta \approx 0$ and as its eigenvalue is independent of the magnetic field it gives a slow magnetoacoustic mode. The third mode corresponds to $0 < \theta < \pi/2$ and as $P_{3,11~{\rm G}}\simeq 10 P_{3,100~{\rm G}}$ it looks like a fast magnetoacoustic mode (Priest 1982).

Then, in order to establish the final unstable modes we integrated Eq. (17) for each of the normal modes, i.e., the integrand is the generalized potential energy density.

Figure 6 shows the generalized potential energy density as a function of the independent variable x for the three first modes (see Table 1), and for the most stable one which was P₄. We show the case B₀₀=11 G, the case with B₀₀=100 G has the same functional dependence. Table 3 shows the eigenvalues and the potential energy for the modes with complex eigenvalues and for the most stable one. Note that, even when $\omega$ has complex values for the three first modes, as $\delta^{2} W_{\rm p}$ is positive in the second and third case, the P₁ = 36.3 min mode is the only unstable one. The fact that, on the contrary to what happens with the first mode, the other modes with complex $\omega$ seemed to accumulate at the origin is an indication of non-real unstable modes.

	Figure 6: Generalized potential energy density as a function of x for the modes a) P1=36. min with $\delta ^{2}W_{\rm p}=-16.$; b) P2=6.6 min with $\delta ^{2}W_{\rm p}=2.9$; c) P3=4.3 min with $\delta ^{2}W_{\rm p}=6.63$; d) P4=3.4 min with $\delta ^{2}W_{\rm p}=2143$, (B00=11 G for all the cases).
Open with DEXTER

Table 3: Potential energy (non dimensional) of the three first modes (complex eigenvalues) and the fourth (most stable mode) B₀₀=11 G.

Figure 7 shows the structure of the components $\zeta$ and $\eta$ for the most stable mode P₄ and for the two cases: B₀₀=11 G and B₀₀=100 G. Note that $\mid\eta\mid~\geq~\mid\zeta\mid$ and that $P_{4,B(11~{\rm G})}=3. 4~{\rm min} \simeq 10 \times 0.36~{\rm min} = 10\cdot P_{4,B(100~{\rm G})}$

	Figure 7: components of the most stable periods a) $\zeta$ component of P4=3.4 min with B00=11 G; b) $\eta$ component of P4=3.4 min with B00=11 G; c) $\zeta$ component of P4=0.36 min with B00=100 G; d) $\eta$ component of  P4=0.36 min with  B00=100 G.
Open with DEXTER

The mode structure of the stable eigenvalues can also be compared with recent results from the literature. Magnetoacoustic oscillations of the fast kink type have been studied theoretically (Edwin & Roberts 1983) and directly observed in EUV wavelengths with TRACE (an updated review of theoretical and observational results in Aschwanden 2004, and references therein). The observations are usually modeled by cylinders with a surface boundary representing coronal loops. The dispersion relation is obtained matching the internal and external MHD solutions via the requirement of continuity of pressure and perpendicular velocity. As in our model, the observed kink-mode oscillations correspond to the long-wavelength regime. In coronal conditions the magnetic field is almost equal inside and outside of the loop and the kink oscillation speed is almost the Alfvén one depending on the ratio of external and internal density values, i.e., outside and inside the loop. On the contrary, our model is performed by perturbing a magnetic arcade, without considering a cylinder with different inside and outside conditions. In eleven observational kink-mode oscillations from which the magnetic field of the events can be inferred were obtained by Aschwanden et al. (2002) and (2003). The comparison of our stable mode data P_i>1 in the B₀₀=11 G case is in good agreement with the kink-mode observational results. The period range (see Table 1), the magnetic strength (B₀₀=11 G) and the wave speed (Alfvén speed) fit the observations for similar loop densities and loop lengths. Also, the stable modes P_{i >1} with B₀₀=100 G (see Table 2) have periods that are comparable with the expected range of fast sausage-mode periods ( $P\pm 1{-}60$ s) and wave speeds of the order of the Alfvén speed (Aschwanden 2004). However - even when a more precise comparison requires a modeling that takes into account differences between external and internal conditions - it is worth investigating whether these type of modes could be associated with more intense magnetic fields in comparison to the associated kink-mode magnetic fields. This will be attempted in future work.

A main result regarding stability is that the characteristic time $\tau= 36$ min in which the instability grows is large enough to guarantee a relative permanence of the structure before it fades away: $\tau \simeq t_{\rm obs}$; where  $t_{\rm obs}$ is the typical characteristic time in which loops seem stable (see Costa & Stenborg 2004). Thus, even when the non-linear stationary configuration of Fig. 1 is unstable it lasts long enough for the observations to be made. Moreover, we confirm that the dynamic brightenings usually observed could be due to magnetoacoustic waves i.e. the perturbations have short periods in comparison with the time that instability occurs: P₄= 3.4 min and P₄=0.36 min satisfy $P_{4} \ll \tau$.

Thus, even when further calculation is needed in order to adjust the characteristic times, it seems that wave-based models could be able to describe the scenario of non-isothermal coronal loops for sufficiently short times comparable with the characteristic time in which the instability grows and the structure fades away. A more speculative argument about the relation between wave-based models and flow-based ones is given in the conclusions.

5 Conclusions

We investigated - via a thermodynamic energy principle - the stability of a coronal inhomogeneous loop model in a non-linear equilibrium state, i.e. a given thermal and magnetic equilibrium configuration. We also obtained the frequencies and their associated modes. The perturbation chosen was of the general type described by Eq. (31) which allowed the study of a more complex mode structure with coupled thermal and mechanical displacements from the equilibrium state. We used a three-component Fourier basis expansion on the independent coordinate x to characterize the unstable modes. We obtained three complex eigenvalues and six real ones with their corresponding eigenvectors for each of the magnetic field values B₀₀ analyzed. The other three modes were discarded. The definite stability condition of the modes is given by integrating the generalized potential energy density of Eq. (17), allowing the interpretation of long-wavelength disturbances that are present in inhomogeneous media.

1.

We used different values of k (k=0, k=0.5 and k=10) to calculate the eigenvectors with complex eigenvalues and for all cases we obtained vanishing values of $\xi _{y}$ with respect to the other perturbed quantities. When we repeated the procedure to calculate the modes with real eigenvectors we obtained small but not vanishing values of $\xi _{y}$ in comparison with the other components. Thus, two dimensional loop coronal models with a temperature gradient of two orders of magnitude between the bottom and top are a good approximation to study the whole three dimensional stability.

2.

We can classify the structure of the modes obtained as follows: a) those for which $\zeta\gg\eta$ and b) those for which $\eta\geq\zeta$. In the first case the perturbation  $v_{1}=\partial\vec{\xi}/\partial t$ is almost parallel to the magnetic field and the eigenvalue is relatively independent of its intensity resembling the acoustic waves where $v_{\rm s}$ is independent of the magnetic field (see Fig. 5). This basic longitudinal mode describes an oscillation between parallel plasma kinetic energy and plasma internal energy. In the second case $v_{1}=\partial\vec{\xi}/\partial t$ has an important orthogonal component and the eigenvalue varies with the magnetic field $P_{11~{\rm G}}\simeq 10 P_{100~{\rm G}}$ resembling the dependence of the Alfvén waves $v_{\rm A}\simeq B_{00}$. When the wave is nearly transverse it describes an oscillation between perpendicular plasma kinetic energy and the combined magnetic compressional and line bending energies. Thus, the first case can be thought of as slow magnetoacoustic waves and the second one as fast magnetoacoustic waves. The period of the slow magnetoacoustic mode is also in accordance with observational data. Between the fast magnetoacoustic modes and in the long wavelength regime we distinguish two possible types, depending of the strength of the magnetic field. For the modes with P_i>1 and B₀₀=11 G we found that the period range, the magnetic strength and the speed of the modes resemble a fast kink-mode. Also, through the consideration of period range values we suggest that modes with P_i>1 and B₀₀=100 G could be thought of as sausage modes. However, to go further with the classification of mode type a modeling that takes into consideration differences between the inside and outside of the loop is required. Also, the non-homogeneous character of the problem places serious limitations on conclusions in relation to stable modes.

	Figure 8: Thermal perturbation (T1 component) for the cases: a) P=36 min; B00=11 G b) P=36 min; B00=100 G.
Open with DEXTER

3.

We found only one unstable mode with characteristic growing time: $\tau_{u}=36$ min. The approximate and most stable mode is P₄=3.4 min for B₀₀=11 G and P₄=0.36 min for B₀₀=100 G. The fact that there is an unstable mode means that the equilibrium state is unstable and that wave-based models are not adequate to fit observations. However, as $\tau_{u} > P_{4}$ by an order of magnitude or two (depending on the B₀₀ value) the equilibrium appearance of the loop and the brightening effects of the most stable mode could be sustained by a characteristic time which is in accordance with observational data ($\tau_{u}$ the characteristic time of the instability).

4.

A much more speculative argument, which needs further analysis and numerical calculation of the non-linear behaviour of the modes, is as follows: the non-linear growth of unstable modes influences the stable modes (they are called slaves), the resulting behaviour is fundamentally governed by the most unstable modes. As we obtained a unique unstable mode, of the type of a slow magnetoacoustic wave, this indicates an overall unstable behaviour governed by the tangential $\zeta$ component and the thermal one. The thermal component of the unstable mode is shown in Fig. 8. As a characteristic wavelength of the components $\zeta$ and T₁ is L/2, it would be worth investigating whether this instability could be associated with a limit-cycle solution generally characterized as a flow-based model (Gómez et al. 1990; De Groof et al. 2004). If this is the case, $\tau$ should be the growth of the instability, before it reaches its non-linear saturated value, in a new equilibrium state of an oscillatory type in the $\zeta$ and T₁ components.

	Figure 9: Schematic description of the unstable mode superimposed on the magnetic structure. At a definite phase the perturbation is always positive, it grows until it reaches $x=\pm L/2$, then decreases until it becomes zero at $Z=Z_{\rm t}$.
Open with DEXTER

	Figure 10: The curve formed by the resulting component perturbations in the vector space of perturbations for a) B00=11 G and  b)  B00=100 G.
Open with DEXTER

Thus, both types of models (waves and flow) converge in explaining the instability of a magnetic structure with long wavelength perturbations of the order of the magnetic structure. Also, even when the modes were linearly unstable, the fact that the dominant varying components are T₁ and $\zeta$, with the last one parallel to the magnetic field could imply that the magnetic structure (but not the equilibrium state) lasts much longer than what is stated by $\tau$. Moreover, this is in accordance with the energetic description of the type of perturbation. Slow, nearly longitudinal magnetoacoustic modes describe a basic oscillation between parallel plasma kinetic energy and plasma internal energy where the magnetic energy plays no relevant role. This could justify long lasting loop observations with dynamic plasma inside. Figure 9 is a scheme of the unstable mode superimposed on the magnetic structure. In half of the period the perturbation is always positive and grows until it reaches $x=\pm L/2$, then decreases until it becomes zero at x=0 and $Z=Z_{\rm t}$. The perturbation gives the tangential velocity $v_{1}=\partial\vec{\xi}/\partial t$ of the plasma particles at each point of the magnetic configuration. Thus, in half of the period, as described in the figure, the plasma is emerges from the chromosphere i.e., $\vec{\xi}=\zeta \vec{e}_{n}$. In the other half, the perturbation is inverted with respect to the figure, it is always negative, i.e. $\vec{\xi}= -\zeta \vec{e}_{n}$, and the plasma particles fall into the chromosphere. A limit cycle is known to be a closed curve (a cycle) in the vector space formed by the perturbations. Figure 10 shows the resulting curve in the space of perturbations $(T_{1}, \zeta)$ for the two magnetic fields studied. It seems that only for relatively large values of the magnetic field limit cycle are possible solutions.

Acknowledgements

This paper is dedicated to the memory of our Professor and guide Constantino Ferro Fontán, and also to the memory of our colleague and friend Aníbal Sicardi Schifino.

6 Appendix: Mathematical tools

The following equations and relations are needed in order to obtain Eq. (33)

$$\rho_{\rm t}=\frac{mp}{k_{\rm B}T_{\rm t}}$$

$$\frac{{\rm d}\rho_{0}}{{\rm d}x}=\frac{{\rm d}\rho_{0}}{{\rm ... ...{\rm d}T_{0}}{{\rm d}x}=\triangle\frac{{\rm d}T_{0}}{{\rm d}s}$$ (34)

with $\triangle=\sqrt{1+(z')^{2}}$. From Fig. 1 it is easy to show

$$\vec{e}_{\rm t}= \frac{\vec{e}_{x}}{\triangle} +\frac{z'}{\tr... ...rac{\vec{e}_{x}}{\triangle} + \frac{z'}{\triangle} \vec{e}_{z}$$

$$\vec{e}_{\rm t}\cdot \vec{e}_{x}=\frac{1}{\triangle}; \ \ \ve... ...angle}; \ \ \vec{e}_{n}\cdot \vec{e}_{z}= - \frac{1}{\triangle}$$

and

$$\vec{e}_{\rm t} \times \vec{e}_{x}=z'{\triangle} \vec{e}_{y};... ...}_{z}\times \vec{e}_{\rm t}=\frac{\vec{e}_{y}}{\triangle}\cdot$$

Then, the spatial perturbation $\xi$ can be written in the Cartesian system as

$$\vec{\xi}=\left[f(\zeta,\eta) \vec{e}_{x}+{\rm i} \xi_{y}\vec{e}_{y} +g(\zeta,\eta)\vec{e}_{z}\right]{\rm e}^{{\rm i}ky}$$ (35)

taking into account

$$\vec{\xi}\cdot\vec{e}_{x}=\left(\frac{\zeta(x)}{\triangle}+\f... ...(x)\right){\rm e}^{{\rm i}ky}=f(\zeta,\eta){\rm e}^{{\rm i}ky}$$ (36)

and

$$\vec{\xi}\cdot\vec{e}_{z}=\left(\frac{\zeta(x)z'}{\triangle}-... ...x)\right){\rm e}^{{\rm i}ky}=g(\zeta,\eta){\rm e}^{{\rm i}ky}.$$ (37)

Then,

$$g(\zeta,\eta)=\eta(x)(1+z'^{2}-f(\zeta,\eta)z')$$ (38)

and

  

$$\frac{{\rm d}}{{\rm d}x}\left( \frac{1}{\triangle}\right)\zeta(x)... ...'}{\triangle} \eta(x)\frac{z'}{\triangle}\frac{{\rm d}}{{\rm d}x}\eta(x)\right)$$                            D_xf = (39)

$$\frac{{\rm d}^{2}}{{\rm d}x^{2}}\left( \frac{1}{\triangle}\right)... ...\zeta(x)}{{\rm d}x}+\frac{1}{\triangle}\frac{{\rm d}^{2}}{{\rm d}x^{2}} \eta(x)$$ D_xxf =

$$+\frac{{\rm d}^{2}}{{\rm d}x^{2}}\left(\frac{z'}{\triangle}\right... ...\eta(x)}{{\rm d}x}+\frac{z'}{\triangle}\frac{{\rm d}^{2}}{{\rm d}x^{2}}\eta(x).$$ (40)

Finally to obtain a non-dimensional equation the following changes were made

$$\rho\rightarrow\frac{\rho}{\rho_{\rm t}}; \ \ T\rightarrow\fr... ...frac{\vec{B}_{0}}{B_{00}}; \ \ x,z\rightarrow\frac{x,z}{L}\cdot$$

The other non-dimensional quantities are obtained immediately from these ones.

References

• Alexander, D., Harra-Murnion, L. K., Khan, J. I., & Matthews, S. A. 1998, ApJ, 494, L235 [NASA ADS] [CrossRef] (In the text)
• Arfken, G., & Weber, H. 1995, Mathematical methods for physicists (San Diego: Academic Press) (In the text)
• Aschwanden, M. J. 2002, ApJ, 580, L79 [NASA ADS] [CrossRef] (In the text)
• Aschwanden, M. J. 2004, Physics of the Solar Corona (New York: Springer-Verlag) (In the text)
• Aschwanden, M. J., Newmark, J. S., Delaboudiniere, J.-P., et al. 1999, ApJ, 515, 842 [NASA ADS] [CrossRef] (In the text)
• Aschwanden, M. J., Alexander, D., Hurlburt, N., et al. 2000, ApJ, 531, 1129 [NASA ADS] [CrossRef] (In the text)
• Aschwanden, M. J., Nightingale, R. W., Andries, J., et al. 2003, ApJ, 598, 1375 [NASA ADS] [CrossRef] (In the text)
• Bernstein, I. B., Frieman, E. A., Kruskal, M. D., & Kulsrud, R. M. 1958, Proc. Roy. Soc. A., 244, 17 [NASA ADS] (In the text)
• Borgazzi, A., & Costa, A. 2005, A&A, 441, 327 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Craig, I. J., & McClymont, A. 1978, A&A, 70, 1 [NASA ADS] [EDP Sciences] (In the text)
• Costa, A., & Stenborg, G. 2004, Sol. Phys., 222, 2 [CrossRef] (In the text)
• Costa, A., González, R., & Sicardi Schifino, A. C. 2004, A&A, 427, 353 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Edwin, P. M., & Roberts, B. 1983, Sol. Phys., 88, 179 [CrossRef] (In the text)
• Freidberg, J. P. 1982, Rev. Mod. Phys., 54, 3 [CrossRef] (In the text)
• De Groof, A., Berghmans, D., van Driel-Gesztelyi, L., & Poedts, S. 2004, A&A, 415, 1141 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Galindo Trejo, J. 1987, Sol. Phys., 108, 2, 265 (In the text)
• Glansdorff, P., & Prigogine, I. 1971, Structure Stability and Fluctuations (New York: Wiley Interscience) (In the text)
• Glansdorff, P., Nicolis, G., & Prigogine, I. 1974, Proc. Nat. Acad. Sci., 71, 197 [NASA ADS]
• Gómez, D., Sicardi Schifino, A., & Ferro Fontán, C. 1990, ApJ, 352, 318 [NASA ADS] [CrossRef] (In the text)
• Graham, R. 1978, Lec. Notes in Phys., 84, 83 [NASA ADS] (In the text)
• Handy, B. N., Acton, L. W., & Kankelborg, C. C. 1999, Sol. Phys., 184, 229 [NASA ADS] [CrossRef] (In the text)
• Jordan, C. 1980, A&A, 86, 355 [NASA ADS] (In the text)
• Keizer, J. 1976, J. Chem. Phys. 69, 2609 (In the text)
• Klimchuk, J. A., & Mariska, J. T. 1988, ApJ, 328, 324 [CrossRef] (In the text)
• Lavenda, B. H. 1985, Nonequilibium Statistical Thermodynamics (Chichester: Wiley-Interscience); J. Keizer 1987, Statistical Thermodynamics of Nonequilibium Processes (New York: Springer-Verlag) (In the text)
• Lavenda, B. H. 1993, Thermodynamics of Irreversible Processes (New York: Dover) (In the text)
• Lerche, I., & Low, B. C. 1981, Sol. Phys., 69, 327L [NASA ADS] [CrossRef] (In the text)
• Mariska, J. T. 1984, ApJ, 281, 435 [NASA ADS] [CrossRef] (In the text)
• Nakariakov, V. M., Verwichte, E., Berghmans, D., & Robbrecht, E. 2000, A&A, 362, 1151 [NASA ADS] (In the text)
• Ofman, L., Nakariakov, V. M., & DeForest, C. E. 1999, ApJ, 514, 441 [NASA ADS] [CrossRef] (In the text)
• Onsager, L. 1931, Phys. Rev., 37, 405 [NASA ADS] [CrossRef] (In the text)
• Priest, E. 1982, Solar Magneto-hydrodynamcis (Boston: Publishing Company) (In the text)
• Reale, F., & Peres, G. 2000, ApJ, 528, L45 [NASA ADS] [CrossRef] (In the text)
• Serio, S., Peres, G., Vaiana, G. S., Golub, L., & Rosner, R. 1981, ApJ, 243, 288 [NASA ADS] [CrossRef], 1981 (In the text)
• Sicardi Schifino, A. C., & Ferro Fontán, C. 1985, Phys. Lett., 113A, 263 [NASA ADS] (In the text)
• Sicardi Schifino, A. C., & Ferro Fontán, C. 1989, Phys. Lett. A, 134, 371 [NASA ADS] [CrossRef] (In the text)
• Sicardi Schifino, A. C., González, R., & Ferro Fontán, C. 1989, Phys. Lett. A, 137, 44 [NASA ADS] [CrossRef]
• Sicardi Schifino, A. C., Costa, A., & Ferro Fontán, C. 1991, J. Math. Phys., 32, 1350 [NASA ADS] [CrossRef] (In the text)
• Sicardi Schifino, A. C., Ferro Fontán, C., González, R., & Costa, A. 2004, Physica A, 334, 201 [NASA ADS] [CrossRef] (In the text)
• Tsiklauri, D., & Nakariakov, V. M. 2001, A&A, 379, 1106 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Tsiklauri, D., Aschwnaden, M. J., Nakariakov, V. M., & Arber, T. D. 2004a, A&A, 419, 1149 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
• Tsiklauri, D., Nakariakov, V. M., Arber, T. D., & Aschwnaden, M. J. 2004b, A&A, 422, 351 [NASA ADS] [CrossRef] [EDP Sciences]
• Tsiklauri, D., Nakariakov, V. M., Arber, T. D., & Aschwnaden, M. J. 2004c, Proc. of the SOHO 15 Workshop - Coronal Heating. 6-9 September 2004, St. Andrews, Scotland, UK (ESA SP-575), ed. R. W. Walsh, J. Ireland, D. Danesy, & B. Fleck. Paris: European Space Agency
• Walsh, R. W., & Galtier, S. 2000, Sol. Phys., 197, 57 [NASA ADS] [CrossRef] (In the text)