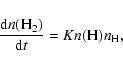 |
(1) |
A&A 458, 497-505 (2006)
DOI: 10.1051/0004-6361:20065913
Q. Chang1 - H. M. Cuppen1 - E. Herbst1,2
1 - Department of Physics, The Ohio State University,
Columbus, Ohio 43210, USA
2 - Departments of Chemistry and Astronomy, The Ohio State
University, Columbus, OH 43210, USA
Received 26 June 2006 / Accepted 1 August 2006
Abstract
Aims. A method to determine effective rate coefficients for H2 formation on grain surfaces is proposed based on the continuous-time, random-walk Monte Carlo simulation.
Methods. Our Monte Carlo simulation is used to calculate the efficiency of molecular hydrogen formation via recombination of H atoms on flat and rough surfaces of olivine and amorphous carbon under a variety of diffuse cloud conditions. The results are then fitted to two types of rate laws to determine effective rate coefficients for use in rate equation treatments. These rate coefficients can be utilized in pure gas-phase models, where the rate of molecular formation is associated with a grain collision rate for H atoms multiplied by an efficiency factor, and in gas-grain models, where the actual diffusion of H atoms on a grain surface is considered.
Results. The effective rate coefficients are tabulated as a function of incoming atomic hydrogen flux and surface temperature, over temperature ranges for which the surfaces show a reasonable efficiency of molecular hydrogen formation. For the flat surfaces studied, corrections to the standard rate treatment do not exceed a factor of three.
Key words: ISM: abundances - ISM: molecules - molecular processes - dust, extinction
Laboratory experiments have shown that efficient molecular hydrogen formation only occurs within narrow windows of temperature for "flat'' surfaces typically modeled by single diffusion barriers and desorption energies for a given adsorbate such as atomic hydrogen. For olivine, this window occurs only between 6 K and 10 K (Pirronello et al. 1997a; Katz et al. 1999; Pirronello et al. 1997b) for estimated interstellar fluxes of atomic hydrogen upon grains, while for amorphous carbon, it lies between 13 K and 17 K (Pirronello et al. 1999; Katz et al. 1999). These ranges of temperature, especially that for olivine, a metallic silicate, are somewhat below the surface temperature deduced for grains in diffuse clouds that are large enough to have a constant temperature (Cuppen et al. 2006). Since molecular hydrogen is formed efficiently in these clouds, it is likely that the surfaces studied in the laboratory are not good analogs of interstellar grain surfaces in diffuse clouds. It would indeed appear that a more complex surface model is required to explain the efficient formation of molecular hydrogen in diffuse clouds. The effect of porosity has been considered by Perets & Biham (2006) and found to be small. Recently, we showed that on a "rough'' surface, with sites on which adsorbates can have different binding energies, molecular hydrogen can be formed efficiently over a wider range of temperature (Cuppen & Herbst 2005; Chang et al. 2005; Cuppen et al. 2006). This result is in qualitative agreement with the results of Cazaux & Tielens (2004), who considered grains with sites of both physisorption and chemisorption. Amorphous surfaces, with continuous distributions of binding energies, can have the same effect (Chang et al. 2005). Theoretical studies on amorphous ice surfaces have also been undertaken (Perets et al. 2005).
In order to simulate H2 recombination on rough surfaces and determine its efficiency in the diffuse interstellar medium, we adopted a detailed Monte Carlo simulation (Montroll & Weiss 1965), which tracks the actual position of each H atom on grain surfaces and the local binding energy of each site. In this approach, known as the continuous-time, random-walk (CTRW) method, we consider granular surfaces as lattices of binding sites, and assume that H atoms hop from one site to another on the lattice. Incoming H atoms are randomly assigned a position on the lattice. Hopping, evaporation and deposition are considered to be Markovian processes; i.e., processes with no memory. The detailed procedure has been discussed in our first paper (Chang et al. 2005), while the construction of rough surface models is discussed in a subsequent paper (Cuppen & Herbst 2005).
Despite our success in explaining molecular hydrogen formation in diffuse clouds, it is very difficult to incorporate
this computer-intensive method into large chemical networks. In gas-phase networks, the formation of molecular hydrogen on surfaces is simulated by a simple rate law:
In large gas-grain networks, surface reactions are typically treated by rate equations (Ruffle & Herbst 2000). Such a rate equation for H2 formation from surface H atoms would look like the following:
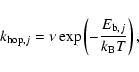 |
(4) |
In this paper, we propose an effective way to incorporate the results of the CTRW method in large gas-phase and gas-grain models, although here we only consider one reaction in diffuse clouds - the formation of H2 - as an example. The treatment can in principle be generalized to systems with more than one surface reaction. The essence of our approach is as follows: by simulating the actual rate of formation of H2 via the CTRW approach, it should be possible to fit the result to either of the two rate equations above and so determine an effective rate coefficient, which may not be constant for a given temperature because the rate equation approach is an approximation. For example, the rate coefficient can change with changing H atom flux onto a grain. Despite its variability, the effective rate coefficient under different conditions can be tabulated, and used in a rate law. Then, this most important surface reaction can be included in a model with a more accurate rate coefficient. For atomic hydrogen, we also have to simulate an effective rate law for evaporation on rough surfaces.
The paper is organized as follows. In the next section, we discuss how to extract rate coefficients from our Monte Carlo calculations on flat and rough grains. The results for H2 formation on flat surfaces are discussed in Sect. 3 and for rough surfaces in Sect. 4. We summarize our results in Sect. 5.
We consider granular surfaces to be square lattices of binding sites and assume that hydrogen atoms hop on the sites of the lattices. Both flat and rough surfaces for olivine and amorphous carbon are considered.
Although the barrier to diffusion ![]() and the desorption energy
and the desorption energy ![]() for a hydrogen atom have only single values on flat surfaces, to simulate a rough surface we assume that five different sets of these energies exist and can be expressed by the equations (Cuppen & Herbst 2005)
for a hydrogen atom have only single values on flat surfaces, to simulate a rough surface we assume that five different sets of these energies exist and can be expressed by the equations (Cuppen & Herbst 2005)
| (5) |
| (6) |
The rough surface chosen is hardly a unique choice. However, to within reasonable limits, we do not expect the level of roughness and the particular topology of the surface to have a strong influence on the results. Cuppen & Herbst (2005) showed that two surfaces with different topology but the same number of sites give very similar efficiencies of H2 formation. As for the strength of the lateral interaction, this value was chosen in part to account for the efficient production of H2 in diffuse clouds with an olivine substrate and to account for efficient H2 production at higher temperatures with a carbonaceous substrate. Any surface with these tendencies will yield similar effective rate parameters over relevant temperature ranges.
The parameters characterizing the four surfaces are listed in Table 1; these derive from the temperature-programmed-desorption experiments of Vidali and co-workers (Katz et al. 1999) for the flat surfaces. The fractions of the surface divided among the different types of sites are denoted as Fi.
Table 1: Parameters used for different surfaces.
In the continuous-time, random-walk Monte-Carlo simulation, instead of keeping track of the rate of reactions, we keep track of individual events. For the formation of molecular hydrogen, there are basically four events: the deposition of new H atoms on a grain, the hopping of H atoms from one site to another, the evaporation of H atoms,
and the formation of molecular hydrogen, which occurs when two H atoms reside in the same site. The first three are assumed to be independent Markovian processes. Thus, if we know the average time interval between events, ![]() ,
then the next time the event happens is given by the equation
,
then the next time the event happens is given by the equation
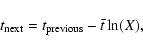 |
(7) |
For deposition, ![]() can be easily calculated as (fN)-1where f is the flux of incoming H atoms in units of monolayers per second (ML s-1), while N, the total number of sites on a grain, can be obtained from
can be easily calculated as (fN)-1where f is the flux of incoming H atoms in units of monolayers per second (ML s-1), while N, the total number of sites on a grain, can be obtained from
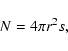 |
(8) |
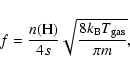 |
(9) |
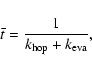 |
(11) |
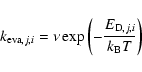 |
(12) |
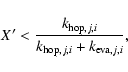 |
(13) |
The simulation is done by continuously determining which event will occur next and then using that event to propel the clock forward. Molecular hydrogen is formed if one H atom jumps into a site where there is already one. The newly formed H2 is assumed to be ejected immediately after formation for simplicity. In the last section of the paper, we consider the consequences if the H2 product stays on the grain until it evaporates. We take into account the Langmuir-Hinshelwood rejection term, which refers to the situation in which an adsorbing H atom cannot be deposited on a site that is already occupied. An alternative procedure would be to assume that H2 formation occurs via the Eley-Rideal mechanism. If this procedure were adapted, then at temperatures below those where the Langmuir-Hinshelwood mechanism is active, H2 formation could still occur efficiently.
The Monte Carlo simulations were performed on two square lattices, a large lattice 316 ![]() 316 in size, which corresponds to a large grain with an approximate radius of 0.063
316 in size, which corresponds to a large grain with an approximate radius of 0.063 ![]() m for olivine and 0.13
m for olivine and 0.13 ![]() m for amorphous carbon given the site densities utilized, and a 50
m for amorphous carbon given the site densities utilized, and a 50 ![]() 50 lattice, corresponding to a much smaller grain, with radii 0.01
50 lattice, corresponding to a much smaller grain, with radii 0.01 ![]() m and 0.02
m and 0.02 ![]() m for olivine and amorphous carbon, respectively. Grains smaller than 0.01-0.02
m for olivine and amorphous carbon, respectively. Grains smaller than 0.01-0.02 ![]() m will be strongly affected by stochastic heating in diffuse clouds and will not have a constant temperature (Cuppen et al. 2006).
m will be strongly affected by stochastic heating in diffuse clouds and will not have a constant temperature (Cuppen et al. 2006).
The recombination efficiency ![]() is calculated from the equation
is calculated from the equation
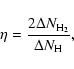 |
(14) |
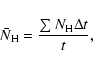 |
(15) |
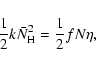 |
(16) |
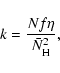 |
(17) |
In addition to the effective rate coefficient for H2 formation, one must calculate an effective evaporation rate for hydrogen atoms in gas-grain models. On flat surfaces, the evaporation rate is the same as shown above with i=0. On rough surfaces, however, since
hydrogen atoms spend time on sites of different binding energy, we proceed as follows. First, we determine the number of hydrogen atoms H that evaporate,
![]() ,
during a time
,
during a time ![]() with our CTRW model. Then, we calculate the ratio
with our CTRW model. Then, we calculate the ratio ![]() of evaporated hydrogen atoms to the total number of incoming atoms:
of evaporated hydrogen atoms to the total number of incoming atoms:
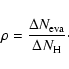 |
(18) |
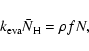 |
(19) |
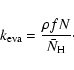 |
(20) |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{5913fig1.eps}\end{figure}](/articles/aa/full/2006/41/aa5913-06/Timg50.gif) |
Figure 1:
The recombination efficiency |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{5913fig2.eps} \end{figure}](/articles/aa/full/2006/41/aa5913-06/Timg51.gif) |
Figure 2:
The normalized effective rate coefficient computed via the CTRW method on a flat olivine surface at 10 K is shown as a function of incoming H flux. The circles are for larger grains (0.063 |
| Open with DEXTER | |
Using the CTRW method, we calculated the recombination efficiency ![]() for H2 formation for a variety of parameters and used it to determine what we term the "normalized effective rate coefficient'' k/k0, where k0 is the rate coefficient used in the standard rate treatment; i.e., the sum of the hopping rates of the reactant partners divided by the number of sites on the grain. The normalized effective rate coefficient is labeled as
for H2 formation for a variety of parameters and used it to determine what we term the "normalized effective rate coefficient'' k/k0, where k0 is the rate coefficient used in the standard rate treatment; i.e., the sum of the hopping rates of the reactant partners divided by the number of sites on the grain. The normalized effective rate coefficient is labeled as
![]() .
Figure 1 shows the recombination efficiency for large and small grains with flat olivine surfaces plotted against H atom flux in units of f0 at 10 K. At this temperature, the efficiency of H2 formation on olivine is declining from rather large values at lower temperatures at standard fluxes in diffuse interstellar clouds. The plotted recombination efficiency is seen to increase from a value less than 0.1 for a standard flux to greater than 0.5 for a flux 30
.
Figure 1 shows the recombination efficiency for large and small grains with flat olivine surfaces plotted against H atom flux in units of f0 at 10 K. At this temperature, the efficiency of H2 formation on olivine is declining from rather large values at lower temperatures at standard fluxes in diffuse interstellar clouds. The plotted recombination efficiency is seen to increase from a value less than 0.1 for a standard flux to greater than 0.5 for a flux 30 ![]() standard. A strong increase in recombination efficiency with flux occurs at temperatures above that of the optimum efficiency, while at temperatures below the optimum efficiency, an increased flux results in a lowered efficiency because the H atoms do not move rapidly. The difference in
standard. A strong increase in recombination efficiency with flux occurs at temperatures above that of the optimum efficiency, while at temperatures below the optimum efficiency, an increased flux results in a lowered efficiency because the H atoms do not move rapidly. The difference in ![]() between our two grain sizes is small but not zero, indicating that the large grain limit, in which
between our two grain sizes is small but not zero, indicating that the large grain limit, in which ![]() is independent of grain size, has not yet been reached (Chang et al. 2005).
is independent of grain size, has not yet been reached (Chang et al. 2005).
Table 2: Normalized effective rate coefficients for flat olivine1 and amorphous carbon2 surfaces.
Translating reaction efficiencies into normalized effective rate coefficients allows us to construct Fig. 2, in which
![]() for the same conditions is plotted against f/f0. We see immediately that the
for the same conditions is plotted against f/f0. We see immediately that the
![]() are not completely independent of flux, although the variation is a slight one. Also, the values of
are not completely independent of flux, although the variation is a slight one. Also, the values of
![]() are significantly below unity. For the larger grain,
are significantly below unity. For the larger grain,
![]() is about 1/3, while for the smaller grain it increases from 0.2 to 0.3 over the range of flux studied. The normalized effective rate coefficients are less than unity at even the highest fluxes because of the phenomenon of "back diffusion'', in which the detailed nature of random walk, handled exactly by the CTRW approach, manifests itself (Chang et al. 2005; Krug 2003). Back diffusion tends to become less important at higher fluxes, since the hydrogen atom population increases with increasing flux so that long random walks with backward steps become less noticeable. At the same time, evaporation, the major loss process, also becomes less important for the same reason.
is about 1/3, while for the smaller grain it increases from 0.2 to 0.3 over the range of flux studied. The normalized effective rate coefficients are less than unity at even the highest fluxes because of the phenomenon of "back diffusion'', in which the detailed nature of random walk, handled exactly by the CTRW approach, manifests itself (Chang et al. 2005; Krug 2003). Back diffusion tends to become less important at higher fluxes, since the hydrogen atom population increases with increasing flux so that long random walks with backward steps become less noticeable. At the same time, evaporation, the major loss process, also becomes less important for the same reason.
The dependence of
![]() on granular size originates from another phenomenon - the small number of H atoms on a grain. When the average number of H atoms per grain is less than unity, a phenomenon known loosely as the "accretion limit'', it is even more important to utilize stochastic methods because the rate equation approach can strongly overestimate the rate of H2 formation. Figure 3 shows the average number of H atoms per grain for both grain sizes as a function of flux. The smaller grain lies in the accretion limit for all fluxes, while the larger grain only approaches it at the lowest fluxes considered. Not surprisingly, therefore, the normalized effective rate coefficient for the smaller grain is the smaller.
on granular size originates from another phenomenon - the small number of H atoms on a grain. When the average number of H atoms per grain is less than unity, a phenomenon known loosely as the "accretion limit'', it is even more important to utilize stochastic methods because the rate equation approach can strongly overestimate the rate of H2 formation. Figure 3 shows the average number of H atoms per grain for both grain sizes as a function of flux. The smaller grain lies in the accretion limit for all fluxes, while the larger grain only approaches it at the lowest fluxes considered. Not surprisingly, therefore, the normalized effective rate coefficient for the smaller grain is the smaller.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{5913fig3.eps} \end{figure}](/articles/aa/full/2006/41/aa5913-06/Timg53.gif) |
Figure 3:
The average atomic H population per grain computed via the CTRW method is shown for flat olivine grains at 10 K as a function of incoming H flux. The circles are for larger grains (0.063 |
| Open with DEXTER | |
We summarize in Table 2 our effective normalized rate coefficients for flat olivine and amorphous carbon as a function of H atom flux (f/f0) derived from our large-grain calculations. The values for the smaller grains are smaller, but not significantly so in an astronomical context. Results are only shown at 10 K for olivine because lower temperatures are unphysical in space while at higher temperatures the effective rate coefficient is very small. Results for amorphous carbon are shown in the range 10-19 K, where H2 formation is efficient. It is important to note that the k/k0 values all lie in the range 0.3-1.0, showing that the simple rate method is not strongly in error for the flat surfaces considered here. This difference is mainly due to back diffusion, and the factors we found are in agreement with the predicted values of Lohmar & Krug (2006) in the high temperature end of the efficiency peak. Lohmar & Krug (2006) derived an analytical expression for the actual sweeping rate of an atom as compared with the one used in rate equations (and master equations). They found a value of 0.33 for olivine at 10 K and 0.37 for amorphous carbon at 18 K. The agreement is much less for lower surface temperatures of carboneous grains (1.0 versus 0.21 for 10 K). This discrepancy is most likely due to the Langmuir rejection that we are using and to the fact that they assume a very low surface coverage in their derivation whereas the hydrogen surface abundance in this regime is close to one monolayer.
To proceed to the actual effective rate coefficient, one just multiplies the value of the normalized rate coefficient by the rate coefficient k0, which is simply twice the hopping rate of hydrogen atoms divided by the number of sites. As an example, consider amorphous carbon at 15 K. The hopping rate of each H atom is obtained from Eq. (4) to be 1.6 ![]() 10-3 s-1 using the value of Eb in Table 1. For a large grain with 105 sites, the value of k0 is then 3.2
10-3 s-1 using the value of Eb in Table 1. For a large grain with 105 sites, the value of k0 is then 3.2 ![]() 10-8 s-1. If one uses a system in which
10-8 s-1. If one uses a system in which
![]() is given not in numbers per grain but in actual concentration, one must divide k0 by the granular concentration (Hasegawa et al. 1992).
is given not in numbers per grain but in actual concentration, one must divide k0 by the granular concentration (Hasegawa et al. 1992).
Table 3:
![]() values (10-17 cm3 s-1) for flat olivine1 and amorphous carbon2 surfaces.
values (10-17 cm3 s-1) for flat olivine1 and amorphous carbon2 surfaces.
In order to include H2 formation in a gas-phase code, we need to determine the effective rate coefficient K for molecular hydrogen formation in Eq. (1), which entails multiplying the standard K - itself obtained by multiplying the rate coefficient for atom-grain collisions by the grain-to-gas number density ratio - with the efficiency factor ![]() .
To remove the dependence on the gas-phase temperature, we can write K in terms of a parameter
.
To remove the dependence on the gas-phase temperature, we can write K in terms of a parameter ![]() (Cuppen et al. 2006), which incorporates the standard grain-size distribution:
(Cuppen et al. 2006), which incorporates the standard grain-size distribution:
Rough surfaces are important because they are probably better analogs of the surfaces of interstellar grains. Moreover, they can explain the efficient formation of H2 over a wide range of temperatures. If we try to simulate the formation of H2 on a rough surface with a single rate and single evaporation coefficient, we are effectively averaging the reaction and evaporation rate coefficients for atomic H on sites with different binding energies. This is different from the approach by Cazaux & Tielens (2004) and Perets et al. (2005), in which H atoms with different binding energies were treated as different atoms, with different rate coefficients. We have used the CTRW approach to study H2 formation on rough olivine and amorphous carbon grains at temperatures up to 20 K and 40 K, respectively, in the temperature regions where the recombination efficiency is highest. Once again, two grain sizes have been used.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{5913fig4.eps} \end{figure}](/articles/aa/full/2006/41/aa5913-06/Timg60.gif) |
Figure 4:
Recombination efficiency |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{5913fig5.eps} \end{figure}](/articles/aa/full/2006/41/aa5913-06/Timg61.gif) |
Figure 5: Effective rate coefficients k multiplied by the number of sites Nas a function of H flux for large and small rough olivine grains at 18 K and 19 K. The symbols are the same as these in Fig. 4.The sets of symbols for small and large grains at a given temperature overlap considerably. |
| Open with DEXTER | |
Figure 4 shows the recombination efficiency ![]() as a function of f/f0 at 18 K and 19 K on rough olivine grains of both sizes. Contrary to that on flat olivine grains, the recombination efficiency
is almost independent of grain size even at high temperature. This lack of size dependence is associated with the fact that the average number of H atoms is always greater than unity for rough
grains as long as the temperature is not above 19 K,
even for the small grains at the lowest fluxes. The large H population occurs because strong binding sites on the surface can trap the atoms so that they are more numerous than on
flat olivine. At lower temperatures (10-17 K), the recombination efficiency
is almost independent of f/f0 while on the analogous flat surface, this is only true around the temperature where the efficiency is at its peak.
as a function of f/f0 at 18 K and 19 K on rough olivine grains of both sizes. Contrary to that on flat olivine grains, the recombination efficiency
is almost independent of grain size even at high temperature. This lack of size dependence is associated with the fact that the average number of H atoms is always greater than unity for rough
grains as long as the temperature is not above 19 K,
even for the small grains at the lowest fluxes. The large H population occurs because strong binding sites on the surface can trap the atoms so that they are more numerous than on
flat olivine. At lower temperatures (10-17 K), the recombination efficiency
is almost independent of f/f0 while on the analogous flat surface, this is only true around the temperature where the efficiency is at its peak.
Table 4: Effective rate coefficients k (s-1) multiplied by number of sites N on rough olivine grains.
Table 5:
Effective evaporation rate coefficients
![]() (s-1) on rough olivine grains.
(s-1) on rough olivine grains.
Unlike the case of smooth surfaces, it makes little sense to normalize the effective rate coefficients by those of simple rate equation theory for a flat surface, since the ratios will in general be quite smaller than unity given that the binding sites of high barrier slow down diffusion on average. So, instead we plot kN (s-1), the effective rate coefficient multiplied by the number of sites on small (N = 2500) and
large (
N = 10 5) grains. Figure 5 shows kN as a function of f/f0 for rough olivine grains at 18 K and 19 K. In the rate equation approach on a flat olivine surface,
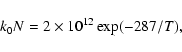 |
(23) |
Tables 4 and 5 contains calculated values of kN and
![]() for rough olivine grains in the temperature range 10-20 K at a variety of useful fluxes. These coefficients
are for the large grain, but they apply to grains with any size above the minimum considered here. Their increase with H flux can be more clearly seen at the lower temperatures. The increase is much weaker on the flat surfaces studied and is therefore an effect caused by the different binding sites: as the flux increases, the high energy sites fill up first. Thereafter the population of H atoms in sites with weak binding increases more rapidly than the population in sites with strong binding.
for rough olivine grains in the temperature range 10-20 K at a variety of useful fluxes. These coefficients
are for the large grain, but they apply to grains with any size above the minimum considered here. Their increase with H flux can be more clearly seen at the lower temperatures. The increase is much weaker on the flat surfaces studied and is therefore an effect caused by the different binding sites: as the flux increases, the high energy sites fill up first. Thereafter the population of H atoms in sites with weak binding increases more rapidly than the population in sites with strong binding.
As an example for obtaining effective rate coefficients in a gas-grain code, consider a diffuse cloud with gaseous H density 125 cm-3, and rough grain surface temperature 18 K.
From Eq. (10), we find the H flux to be 12.5f0. Since the rate coefficient
is approximately linear with flux over small ranges, we can linearly interpolate the tabulated rate coefficients at 10f0 and 15f0. In this manner, kN,
the recombination rate coefficient multiplied by the number of grain sites, is estimated to be
3.6 ![]() 10-5 s-1 while
10-5 s-1 while
![]() is 2.65
is 2.65 ![]() 10-7 s-1.
10-7 s-1.
For use in a gas-phase code, we convert the recombination efficiency into the parameter ![]() ,
defined in Eq. (22), from which the effective rate coefficient K (Eqs. (1) and (21)) can be determined. The method is
the same as that for flat surfaces. The values of
,
defined in Eq. (22), from which the effective rate coefficient K (Eqs. (1) and (21)) can be determined. The method is
the same as that for flat surfaces. The values of ![]() are shown in Table 6, where it can be seen that large values extend to surface temperatures at least as high as 19 K, unlike the case for flat olivine, where 10 K is the highest temperature of interest.
are shown in Table 6, where it can be seen that large values extend to surface temperatures at least as high as 19 K, unlike the case for flat olivine, where 10 K is the highest temperature of interest.
Table 6:
![]() values (10-17 cm3 s-1) for rough olivine.
values (10-17 cm3 s-1) for rough olivine.
Table 7: Calculated values for kN (s-1) for rough amorphous carbon grains.
Table 8:
Calculated values for
![]() (s-1) for rough amorphous carbon grains.
(s-1) for rough amorphous carbon grains.
Table 9:
![]() values (10-17 cm3 s-1) for rough amorphous carbon.
values (10-17 cm3 s-1) for rough amorphous carbon.
Significant values for the recombination efficiency ![]() on rough amorphous carbon grains extend to much higher temperatures than they do for olivine because of the larger binding energy for H and larger barrier against diffusion. Tables 7 and 8 show calculated effective values of kN and
on rough amorphous carbon grains extend to much higher temperatures than they do for olivine because of the larger binding energy for H and larger barrier against diffusion. Tables 7 and 8 show calculated effective values of kN and
![]() ,
respectively,
while Table 9 lists values of
,
respectively,
while Table 9 lists values of ![]() .
At a surface temperature of 35 K, it is clear that H2 can still be produced efficiently on amorphous carbon grains (Jura 1974), while at 40 K, the low value of
.
At a surface temperature of 35 K, it is clear that H2 can still be produced efficiently on amorphous carbon grains (Jura 1974), while at 40 K, the low value of ![]() shows that the reaction is no longer efficient. Note that the evaporation rate at 10 K is too small to be determined by the Monte Carlo approach.
shows that the reaction is no longer efficient. Note that the evaporation rate at 10 K is too small to be determined by the Monte Carlo approach.
Despite its use in the simulation of the recombination efficiency of molecular hydrogen on various grain surfaces (Cuppen & Herbst 2005; Chang et al. 2005; Cuppen et al. 2006), the continuous-time random-walk Monte Carlo simulation is still very difficult to employ, especially if one wishes to use it to simulate a large reaction network. In this paper, we used the simulation to derive effective parameters for the formation of molecular hydrogen from hydrogen atoms that land on both flat and rough olivine and amorphous carbon surfaces so that two types of rate equation methods can be used by astronomers interested in modeling H2 formation in diffuse and translucent regions. Rough surfaces are those in which a variety of different environments for binding exist (Cuppen & Herbst 2005).
The idea is to replace the standard rate coefficient used with an effective one derived and tabulated here. Two grain sizes were used: small grains, of radius 0.01-0.02 ![]() m, and large, or standard, grains, of radius 0.06-0.13
m, and large, or standard, grains, of radius 0.06-0.13 ![]() m, depending on whether the surface is olivine or amorphous carbon. For "pure'' gas-phase models in which the artificial rate equation for H2 formation is of the form shown in Eq. (1), the rate coefficient K can be obtained from the parameter
m, depending on whether the surface is olivine or amorphous carbon. For "pure'' gas-phase models in which the artificial rate equation for H2 formation is of the form shown in Eq. (1), the rate coefficient K can be obtained from the parameter ![]() tabulated here as a function of surface temperature and H-atom flux onto the grains followed by the use of Eq. (21), which only requires the gas-phase temperature. For gas-grain models in which the diffusive nature of the surface chemistry is treated by the rate equation listed in Eq. (2) with rate coefficient k, we have provided two different types of tables. For the flat olivine and amorphous carbon surfaces, we have tabulated as a function of H atom flux and surface temperature a normalized effective rate coefficient, which is k divided by the actual rate coefficient k0 used in the simple rate expression. This latter rate coefficient is simply the sum of the diffusion rates of the two hydrogen atoms over the entire grain, as expressed in Eqs. (3) and (4), and calculated in Sect. 3. We have found that the ratio k/k0 lies in the range 0.3-1.0, showing that the standard rate treatment for the production of H2 is not greatly in error for flat surfaces.
tabulated here as a function of surface temperature and H-atom flux onto the grains followed by the use of Eq. (21), which only requires the gas-phase temperature. For gas-grain models in which the diffusive nature of the surface chemistry is treated by the rate equation listed in Eq. (2) with rate coefficient k, we have provided two different types of tables. For the flat olivine and amorphous carbon surfaces, we have tabulated as a function of H atom flux and surface temperature a normalized effective rate coefficient, which is k divided by the actual rate coefficient k0 used in the simple rate expression. This latter rate coefficient is simply the sum of the diffusion rates of the two hydrogen atoms over the entire grain, as expressed in Eqs. (3) and (4), and calculated in Sect. 3. We have found that the ratio k/k0 lies in the range 0.3-1.0, showing that the standard rate treatment for the production of H2 is not greatly in error for flat surfaces.
For the rough olivine and carbonaceous surfaces, on which efficient H2 formation takes place over a much wider temperature range (Cuppen & Herbst 2005; Chang et al. 2005; Cuppen et al. 2006), we have tabulated the product kN, where N is the number of sites on the grain. The effective rate coefficient is then obtained by division by the number of sites on the size of grain being considered. In addition, we have also tabulated rates of evaporation for rough surfaces, since given the different binding sites, these must first be obtained by a Monte Carlo procedure. For the rough grains, the parameters ![]() and kN are independent of grain size as long as the grain is large enough that temperature fluctuations are not important. For the flat grains, the parameters do have a small size dependence, and the tables refer to standard grains.
Using these tables, astronomers should be able to compute the rate of H2 formation in diffuse and translucent clouds, or even diffuse portions of weak PDR's, for a variety of surfaces, densities, and temperatures. The extension to systems of multiple surface reactions, as occurs in dense cloud models, is feasible although at a greatly increased level of complexity according to preliminary calculations.
and kN are independent of grain size as long as the grain is large enough that temperature fluctuations are not important. For the flat grains, the parameters do have a small size dependence, and the tables refer to standard grains.
Using these tables, astronomers should be able to compute the rate of H2 formation in diffuse and translucent clouds, or even diffuse portions of weak PDR's, for a variety of surfaces, densities, and temperatures. The extension to systems of multiple surface reactions, as occurs in dense cloud models, is feasible although at a greatly increased level of complexity according to preliminary calculations.
The calculations discussed up to now have contained the assumption that all H2 is ejected from the surface immediately after being formed. We have also investigated the effect of making the opposite assumption, that the molecular hydrogen remains on the grain surface until evaporation. For flat surfaces, we find no change in the reported results over the temperature and flux ranges studied. Presumably, a large enough surface abundance of H2 does not build up even at low temperatures to influence the sticking and diffusion of H atoms. For rough surfaces, we find an increase in the rate coefficients k at the lower temperatures, depending on which surface is being studied. Qualitatively, the reason for the increase is the resistance to evaporation of those H2 molecules formed in those sites with deeper potential wells. The H atoms then tend to occupy the binding sites with shallower wells, and therefore diffuse more rapidly. But they also evaporate more rapidly and the net effect in the recombination efficiency is very small at all temperatures studied.
The method discussed here uses single parameters even for rough surfaces. An alternative procedure being considered is the use of rate equations in which adsorbates on different binding sites are considered to be different species. For example, consider very simple rough grains with only two types of binding - standard (weak) and stronger - as in Cazaux & Tielens (2004). Since the stronger binding site will guarantee that a large number of H atoms and other reactive species can reside on a grain over a wide temperature range, the rate equation method may be usable without significant corrections of the type advocated here, even for large networks.
Acknowledgements
E.H. acknowledges the support of the National Science Foundation (US) for his research program in astrochemistry.