A&A 458, 669-678 (2006)
DOI: 10.1051/0004-6361:20065253

Hubble Space Telescope observations of the nucleus and inner coma of comet 67P/Churyumov-Gerasimenko[*],[*]

P. L. Lamy1 - I. Toth1,2 - H. A. Weaver3 - L. Jorda1 - M. Kaasalainen4 - P. J. Gutiérrez1,5


1 - Laboratoire d'Astrophysique de Marseille, BP 8, 13376 Marseille Cedex 12, France
2 - Konkoly Observatory, Budapest, Hungary
3 - Applied Physics Laboratory, The Johns Hopkins University, Laurel, MD, USA
4 - Department of Mathematics and Statistics, University of Helsinki, Finland
5 - Instituto de Astrofisica de Andalucia, Granada, Spain

Received 22 March 2006 / Accepted 16 June 2006

Abstract
Context. Following the postponement of the launch of the Rosetta spacecraft scheduled in January 2003, comet 67P/Churyumov-Gerasimenko emerged as the most suitable new target. However a critical issue was the size, that is, the mass of its nucleus, as the surface module Philae was designed to land on a nucleus with a radius no larger than approximately 1.5 km.
Aims. It was therefore crucial to the success of the mission to achieve a timely characterization of the nucleus of 67P/C-G so as to take any proper action on the design needed before the new launch.
Methods. We used the Wide Field Planetary Camera 2 (WFPC2) of the Hubble Space Telescope (HST) whose superior spatial resolution enabled us to accurately separate the signal of the nucleus from that of the coma. The observations were performed on 12 and 13 March 2003, when the comet was 2.50 AU from the Sun, 1.52 AU from the Earth, and at a phase angle of 4.8$^\circ $.
Results. The nucleus of comet 67P/Churyumov-Gerasimenko was easily detected, and we measured its V and R magnitudes in the Johnson-Kron-Cousins photometric system. Assuming that the nucleus is spherical, with a geometric albedo of 0.04 and a phase coefficient of 0.04 mag/deg for the R band, we derived a radius of $1.98\pm0.02$ km. The spheroidal solution has semiaxes a = 2.41 km and b = c = 1.55 km and a rotational period of $12.41\pm0.41$ h. We inverted the light curve and solved it for a full three-dimensional nucleus having an overall size of $4.56\times3.81\times3.44$ km viewed at an aspect angle of ${\sim}80^\circ$ (i.e., near equatorial view) at the time of our observations. When combined with other constraints, the direction of the pole is found at either RA = $40^\circ$ $^{+70^\circ}_{-20^\circ}$ and Dec = $+70\pm10^\circ$ (prograde rotation) or RA = $250\pm30^\circ$ and Dec = $-70\pm10^\circ$ (retrograde rotation). The color of the nucleus is moderately red with $(V-R)=0.52\pm0.05$. From an analysis of the dust coma, we derived $Af\rho = 40.2\pm0.3$ cm, a dust production rate $Q_{\rm d} \sim 4$ kg s-1, and we characterized its color.

Key words: comets: general - comets: individual: 67P/Churyumov-Gerasimenko - techniques: image processing

1 Introduction

Following the postponement of the launch of the Rosetta spacecraft scheduled in January 2003, the mission's target had to be reconsidered and 67P/Churyumov-Gerasimenko emerged as the most suitable candidate on the basis of orbital considerations (Schwehm 2003; Ellwood et al. 2004). A critical issue, however, was the size, i.e., the mass of its nucleus, since a radius larger than approximately 1.5 km would endanger the landing of the surface module Philae. The only information available on the nucleus of 67P/C-G was a short report by Mueller (1992) based on ground-based CCD observations performed on 10, 11, 12 April and 15, 16 May 1991, which suggested an effective radius of $2.8\pm 0.1$ km (assuming a geometric albedo of 0.04) and a spheroidal shape with an axial ratio a/b > 1.7, where a and b are the semi-axes of the assumed prolate spheroid nucleus. However, there were some large random variations in the mean magnitude between each set of observations, indicating that some of the results may be unreliable. Other investigations had only established upper limits for the radius: 3.0 km from the radio observations of Kamoun et al. (1999) and 2.9 km from the visible observation of Lowry et al. (1999).

Based on our successful technique of detecting cometary nuclei with the Hubble Space Telescope (see the review by Lamy et al. 2004), including that of comet 46P/Wirtanen, the original target of the Rosetta mission (Lamy et al. 1998a), we initiated a program of HST observations to support ESA in its assessment of the new target. We issued a report within a few weeks following our observations that enabled ESA to take proper action and reinforce the landing gear of the surface module to insure a safe landing on a nucleus appreciably larger than that of 46P/Wirtanen (a radius of 2 km compared to 0.6 km). The Rosetta spacecraft was successfully launched on 2 March 2004 and is now on its way to rendezvous comet 67P/C-G in May 2014 at a heliocentric distance of 4.5 AU, some 15 months before its perihelion passage.

The purpose of the present article is to present a detailed analysis of our HST observations and the resulting characterization of the nucleus and inner coma of 67P/Churyumov-Gerasimenko, a Jupiter-family comet discovered by K. I. Churyumov and S. I. Gerasimenko during the night of 11-12 September 1969 (UT) at the Alma Ata Observatory, Kazakhstan (Smakova et al. 1970).

The orbital elements of 67P/C-G have undergone significant variations in the recent past following a number of close encounters with Jupiter (Carusi et al. 1985). From $\sim$1600 to $\sim$1959, both its perihelion and aphelion distances (respectively q and Q) increased, while its inclination ikept decreasing slightly. Then considerable reduction of q (from $\sim$2.7 to $\sim$1.3 AU) and i(from $\sim$$28^\circ$ to $\sim$$7^\circ$) took place, followed by a complete reorientation of the nodal line. These events probably triggered extra activity of the comet, leading to its discovery in 1969. The present orbit is characterized by a period of 6.57 years, q = 1.292 AU, e = 0.632, and $i = 7.12^\circ$. The comet has now completed only 7 perihelion passages on its new orbit ($q \sim1.3$ AU).

2 Observations

The observations were performed with the Planetary Camera (PC) mode of the Wide Field and Planetary Camera 2 of the HST between 11.4 and 12.3 March 2003, $\sim$205 days after the perihelion passage of 18.3 August 2002. They spanned a time interval of 21 h. The geometric parameters varied only slightly over this interval. The heliocentric distance changed from 2.5027 to 2.5090 AU and the geocentric distance from 1.5223 to 1.5296 AU. The solar phase angle increased from 4.7 to 4.9$^\circ $ and the image scale from 50.24 to 50.48 km pixel-1 (the PC has a pixel scale of 0.0455 arcsec). The observing program consisted of 11 visits carefully planned to sample a rotational light curve of unknown period ranging from hours up to days, without using inordinate amounts of precious HST observing time. The first eight visits were performed during eight consecutive orbits, followed by three observations every other orbit. Observed rotational periods for cometary nuclei range from 5 to 70 h, but the vast majority fall between 5 and 18 h (Lamy et al. 2004). For a rotational period of about 2 days, which is near the upper limit of the observed range, our strategy would have provided observations that sampled half the rotation, which is a full sinusoid because of the double-peaked nature of the light curve.

Our nominal program for each visit consisted of the following sequence of images:

The nominal exposure time of 300 sec was required to reach half of the CCD full-well signal level in the peak pixel of the PC, calculated assuming a radius of 2.5 km, an albedo of 0.04, and a phase law with a phase coefficient $\beta = 0.04$ mag/deg. The three short-duration exposures ( ${\sim} 3\times$ shorter than our nominal exposure) were used to ensure non-saturation of the CCD, in case the comet was unexpectedly bright. This sequence was fully implemented during the first six orbits and entirely filled the time available during those orbits. Thereafter, the available time was reduced as a consequence of observational constraints (notably the South Atlantic Anomaly), and the two F555W images were deleted. The worst case took place during orbit #10, as we could only secure two 120 s images with the F675W filter (Table 1).

The quality of the ephemerides was such that the pointing and tracking were excellent, the comet always falling close to the center of the PC chip. All images were processed using the standard "On the Fly'' (OTF) processing system at the Space Telescope Science Institute. Figure 1 displays a typical image of 67P/C-G, on which we have superimposed isophotal contours.


  \begin{figure} \par\includegraphics[width=7.5cm,height=7.5cm,clip]{5253fig1.ps}\end{figure} Figure 1: Image of comet 67P/Churyumov-Gerasimenko obtained with the WFPC2 (PC mode) of the Hubble Space Telescope on 11.734 March 2003 (UT) with the F675W filter. The inner circular isophotal contours highlight the nucleus, while the outer ones indicate a slightly asymmetric coma. The arrows indicate the anti-solar direction (prolonged radius vector ${\vec r}$), the direction of celestial North (N), and the heliocentric orbital velocity vector ( $V_{\rm orb}$) of the comet projected onto the sky plane.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.4cm,height=11.3cm,clip]{5253fig2.ps}\end{figure} Figure 2: Azimuthally averaged radial surface brightness profiles in log-log representation corresponding to the image displayed in Fig. 1 ( top panel). The thick solid line represents data, and the other curves are models for the signal from the nucleus (dashed line), the coma (thin solid line), and the total cometary signal (dash-dot line). The residuals (data-model, in percent of the observed signal) are also shown ( bottom panel).
Open with DEXTER

3 Data analysis

To analyze the data, we applied our standard method of fitting a parametric model of the expected surface brightness to the observed images. Our most general model for a 2-dimensional array of brightness values is simply given by:

\begin{displaymath}{\rm Model} = [{\rm nucleus + coma}] \otimes {\it PSF} \end{displaymath} (1)

where $PS\!F$ represents the point spread function of the telescope and $\otimes$ represents the convolution operator. The nucleus is not resolved so that

\begin{displaymath}{\rm nucleus} = k_n \; \delta(\rho) \end{displaymath} (2)

where $\delta$ is the Dirac delta function, $\rho$ the projected radial distance from the center, and kn a scaling factor. Specifying a model for the coma very much depends on its complexity in the observed images, and we have developed several approaches (Lamy et al. 2004). The inner coma of 67P appears to depart slightly from circular symmetry (Fig. 1), but not to the point of warranting the most general procedure implemented for comets 19P/Borrelly (Lamy et al. 1998b) and C/Hale-Bopp (1995 O1) (Weaver & Lamy 1997). We therefore used the simple isotropic model

\begin{displaymath}{\rm coma } = k_{\rm c}\;\; \rho^p \end{displaymath} (3)

where $k_{\rm c}$ is a scaling factor for the coma, and p the power exponent of the brightness variation versus distance from the nucleus (optocenter) in the image plane. The Point Spread Function (PSF) of the telescope was modeled using version 4.0 b of the TinyTIM software written by Krist (1995), which has the capability of including the jitter of the HST, which is sometimes conspicuous on long exposures. To account for the the sub-pixel location of the nucleus, which can cause a marked asymmetry of the brightness profiles, the model images were generated on a finer grid than the original PC pixel, with a resampling factor of 9. The fit to the observed images was performed after integrating the model over $9\times9$ sub-pixels to recover the original pixel of the PC. Note that the $\rho^p$ function was rigorously calculated in the central $3\times3$ pixels to take into account the finite extent of the pixels; this effect is negligible beyond this central area.

On each image, the sub-pixel location of the nucleus (xn, yn) was first determined using the X and Y-profiles through the pixel displaying the peak signal, as well as first estimates of the model parameters kn, $k_{\rm c}$, and p. Their final determinations, as well as those of the jitter if any, were performed on azimuthally averaged radial profiles, as performed in the case of comet 46P/Wirtanen (Lamy et al. 1998a). This is implemented by performing a polar transformation of the images centered on the nucleus (the pixel having the largest signal) with an angular resolution of 1$^\circ $, and summing the 360 individual profiles. All coma profiles could be adequately fit using the canonical value p=-1, indicating that the coma was in steady state. As illustrated in Fig. 2, the fits of the model profiles to the observed profiles were almost perfect, and the nucleus was easily detected, with nucleus to coma contrast ratios of $\sim$30 at the peak pixel.

The 1$\sigma$ error of the data can be expressed as

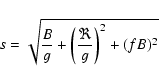\begin{displaymath}s = \sqrt{{B\over g} + {\left({\Re \over g}\right)^2} + (f B)^2} \end{displaymath} (4)

where B is the observed signal in DN, g=7 electrons DN-1 is the gain, $\Re = 5$ electrons is the readout noise, and f=0.01 expresses the flat field noise as a fraction of the signal. The azimuthal averaging of the 360 profiles reduces the error, typically by $\sqrt{360}$, although, strictly speaking, the profiles are not uncorrelated. The error resulting from the fitting procedure is obtained by a global quantification of the residuals (see example in Fig. 2) and is expressed as a fraction of the scaling factors. It typically ranges from 2 to 5% and always dominates over the error of the data.

The determination of the absolute magnitudes was performed on the kn PSFimages, which represent the brightness of the nucleus in the absence of coma. The procedure for calculating the nuclear magnitudes followed the recommendations of Holtzman et al. (1995). The so-called instrumental magnitudes were calculated by integrating the scaled PSFs in an aperture of 0.5'' radius, so that no aperture correction is required. The formulae converting the instrumental WFPC2 magnitudes to the standard Johnson-Kron-Cousins V and R magnitudes require a color correction in first and second orders of the (V-R) color index. Since observations were obtained in both filters for the first six orbits, we could combine the formulae and solved it for the V and R magnitudes without any assumption for the color of the nucleus. We then used the resulting average color index (V-R) = 0.52 to solve for the R magnitudes of the remaining five orbits. The errors affecting the scaling factors kn of the nucleus were propagated through the transformation formulae, and the final uncertainties for the magnitudes listed in Table 1 include the systematic errors in the zero-points of the calibration. Note that they are the same for the apparent and absolute magnitudes.

4 The properties of the nucleus

4.1 Size of the nucleus

The apparent V and R magnitudes of the nucleus of 67P/Churyumov-Gerasimenko in the Johnson-Kron-Cousins photometric system are listed in Table 1, along with the absolute magnitudes m(1,1,0), and are plotted in Fig. 3. The light curves clearly suggest that we are observing the apparent cross-sections of a rotating, elongated nucleus. As a first step, the observed light curve in the R band was analyzed by taking a Fourier decomposition limited to the first sine term, and the period was searched in the expected range of 10-13 h. We found $P_{\rm rot} = 12.41\pm0.5$ h, and the corresponding light curve is plotted in Fig. 3. The light curve has a mean value of R=18.92, and maximum - minimum amplitude of 0.44 mag.

Using the standard formula relating magnitudes to cross-sections (Russell 1916; Jewitt 1991), and assuming a geometric albedo of 0.04 and a linear phase law with a coefficient $\beta = 0.04$ mag/deg for the R band as used in our previous work (Lamy et al. 2004), we obtained a mean radius of $1.98\pm0.02$ km, and extreme radii of 2.12 and 1.85 km corresponding to the extrema of the light curve. An albedo of 0.03 increases the sizes by 15%. Since the observations were obtained at a small phase angle ($\sim$4.8$^\circ $), the derived sizes are not very sensitive to the particular phase law adopted. A phase law coefficient of 0.025 mag/deg as measured on 28P/Neujmin 1 (Delahodde et al. 2001) decreases the mean size to 1.92 km while a coefficient of 0.06 mag/deg typical of comets 2P/Encke (Fernández et al. 2000) and 48P/Johnson (Jewitt & Sheppard 2004) increases it to 2.07 km. Other sources of uncertainty lead to negligible errors in the derived values.

The upper limits on the radius of the nucleus set by Lowry et al. (1999) based on their undetection at aphelion (5.72 AU), $r_n \leq 2.9$ km, and consequently that of Kamoun et al. (1999) were therefore correct. It is possible that the observations at 4.87 and 4.97 AU by Mueller (1992), which yielded $r_n = 2.8 \pm 0.1$ km (scaled to pR = 0.04) and a/b > 1.7, were contaminated by a weak coma and/or a dust trail.


  \begin{figure} \par\includegraphics[width=7.3cm,height=7.2cm,clip]{5253fig3.ps}\end{figure} Figure 3: Light curves of the nucleus of comet 67P/Churyumov-Gerasimenko. The data points are the apparent V (circles) and R (dots) magnitudes, and the dashed line represents the calculated light curve as described in the text.
Open with DEXTER

4.2 Color of the nucleus

The (V-R) color index of the nucleus was calculated separately for the six orbits when images were obtained with both the F555W and F675W filters. For each orbit, we averaged the two magnitudes obtained with the green filter to derive a mean value of the V magnitude, and we averaged the five magnitudes obtained with the red filter (that time interval bracketed the time when the green images were obtained) to derive a mean value of the R magnitude. All values are averages weighted by the errors in the measurements, and the resulting (V-R) colors of the nucleus of 67P are reported in Table 1 with their respective uncertainties. The color is not constant, and, in fact, the light curve in the V band does not strictly follow that in the R band (Fig. 3). The most plausible explanation is a variation of the color across the surface of the nucleus, as detected, for example, on comet 2P/Encke (Lowry et al. 2003). The global average of the six color determinations is $(V-R)=0.52\pm0.05$, almost identical to the mean value of $0.49\pm0.03$ obtained for the nuclei of 34 ecliptic comets (Lamy & Toth 2006). The normalized reflectivity of the nucleus of 67P/C-G was calculated from the above color index, minus that of the Sun, and normalized to a value of 1 at 550 nm, the effective wavelength of the V band: $S(\lambda = 650~~ {\rm nm}) = 1.17\pm0.05$. The corresponding reflectivity gradient is $S^\prime (550,650~~ {\rm nm}) = 17$% per kÅ.

4.3 Period analysis

The R-band light curve of the nucleus of 67P/C-G was analyzed using seven different period-searching methods. We first removed low frequency trends in the data, such as the effect of the varying phase angle, in order to obtain cleaner periodograms and more accurate period determinations. A straight line was fitted to the data, this trend was subtracted, and the data were shifted to give a mean level of zero.


  \begin{figure} \par\includegraphics[width=6.9cm,height=7cm,clip]{5253fig4.ps}\end{figure} Figure 4: Autocorrelation periodogram of the R light curve of the nucleus of 67P/Churyumov-Gerasimenko using the modified autocorrelation method (MAC $\Theta $). The arrow indicates the most probable sine period at the first minimum of the periodogram.
Open with DEXTER

We started with the autocorrelation analysis, which is well-suited to detecting quasi-periodic trends in a time series and generally yields robust results. We implemented the modified autocorrelation (MAC) technique described by Burki et al. (1978), based on the calculation of the autocorrelation parameter $\Theta(\tau)$, where $\tau$ is the time lag or trial period. This parameter is defined as the ratio of the mean square value of the successive differences $\delta^2$, and the variance $\sigma^2$, i.e., $\Theta=\delta^2/\sigma^2$. Even if the data are extremely noisy, $\Theta $ has several properties that allow the detection of trends in segments of data. Three regimes may be distinguished (Burki et al. 1978):

In the second case, when the $\Theta(\tau)$ function exhibits a succession of maxima and minima, the first minimum indicates the most probable period of the signal, if it is periodic. This situation applies to the nucleus of 67P, as illustrated in Fig. 4, and the first broad minimum indicates a sine period $P_{\sin}$ in the range 5.5 to 7 h with a central value of 6.29 h. This converts to a rotational period $P_{\rm rot} = 2\ P_{\sin}$ of 12.58 h, assuming that the nucleus light curve is double-peaked.

Having ascertained the periodic nature of the light curve, we next considered six classical methods:

1.
The information entropy spectrum of a time series, as defined by Cincotta et al. (1995), for which a minimum occurs at the value of the trial period where the data shows periodicity (Fig. 5).
2.
The power spectrum of the data using Kurtz's (1985) implementation of Deeming's (1975) discrete Fourier transform (DFT) algorithm for unequally-spaced data.
3.
The Lomb-Scargle method (Lomb 1976; Scargle 1982).
4.
The period dispersion minimization method (PDM, Stellingwerf 1978).
5.
The analysis of variance (AoV) method (Schwarzenberg-Czerny 1989, 1991), which improves and corrects for the statistics of the original version of the PDM method (Stellingwerf 1978).
6.
The WindowCLEAN method (Belton & Gandhi 1988).
The periodograms corresponding to methods 2, 3, 4, and 5 are presented in Fig. 6, and that of the WindowCLEAN method in Fig. 7. The rotational periods determined with the different methods are regrouped in Table 2. The distribution of values range from 11.58 to 13.09 h with a mean of $P_{\rm rot} = 12.41$ h and $\sigma = 0.41$ h. The convergence of the seven independent methods to this value with an rms dispersion of only 4% suggests that it is a very robust result. In addition, we calculated the statistical significance of the peak in the PDM method as described by Schwarzenberg-Czerny (1997) and found 99.99%.
  \begin{figure} \par\includegraphics[width=6.9cm,height=7.1cm,clip]{5253fig5.ps}\end{figure} Figure 5: Information entropy periodogram of the R-band light curve of the nucleus of comet 67P/Churyumov-Gerasimenko. Information entropy S is defined by Eq. (1) of Cincotta et al. (1995). The most probable (sine) period is at the minimum of the periodogram.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=6.6cm,height=6.5cm,clip]{5253fig6a.ps}... ...*{5mm} \includegraphics[width=6.3cm,height=6.5cm,clip]{5253fig6d.ps}\end{figure} Figure 6: Periodograms of the R-band light curve of the nucleus of comet 67P/Churyumov-Gerasimenko obtained from four different methods: discrete Fourier power spectrum ( top left panel), phase dispersion minimization method ( top right panel), Lomb-Scargle method ( bottom left panel), and analysis of variance ( bottom right panel).
Open with DEXTER

4.4 Reconstruction of the shape of the nucleus

As a first approach, we considered the simple model of a prolate spheroid with semi-axes a > b=c rotating about its axis of largest moment of inertia (the shortest axis of the body), and we calculated its apparent light curve with the following assumptions. We used the Hapke formalism with the scattering law determined for asteroid 253 Mathilde, i.e., the parameters given by Clark et al. (1999, their Table V), because the surface properties of this asteroid (albedo pV = 0.047, coefficient of the phase function $\beta_V = 0.04$ mag/deg, and phase integral q = 0.28) appear to be typical of cometary nuclei (Groussin et al. 2004). We also used the mean rotation period $P_{\rm rot} = 12.41$ h. The semi-axes of the spheroid a = 2.41  km, b = c = 1.55  km, its aspect angle of 81$^\circ $ and its phasing were determined by best-fitting the model light curve to the data (Fig. 8). The axis ratio is a/b = 1.6 For comparison, we also display the light curve calculated from the projected cross-section corresponding to the illuminated fraction of the spheroid visible to the observer.

Figure 8 clearly indicates that the spheroidal shape does not provide a good fit to the observed light curve; consequently (and not surprisingly) the real shape of the nucleus of 67P is more complex. In order to find a possible/plausible solution for its shape, we inverted the light curve using the technique developed by Kaasalainen et al. (2001, 2002). This method makes use of all data points (both relative and calibrated photometry) and finds a physical model, albeit with a large number of free parameters, that accurately reproduces the photometric data down to the noise level. The simultaneously determined parameters describe the sidereal period, the pole direction, the shape, and the light-scattering properties of the body. To restrict the range of possible solutions (one light curve is obviously not enough to constrain the inversion), we imposed the realistic condition that the spin axis be close to the principal axis corresponding to the maximum moment of inertia in order to insure a stable rotation. This is expected to be the case for a moderately active but relatively large nucleus.

The inversion requires a scattering law (combined with a phase function), so we considered two cases: (i) a dirty snowball with a scattering law composed of a combination of the Lommel-Seeliger law (weight = 1.) and the Lambert law (weight = 0.2), yielding a very slight limb darkening, (ii) a nucleus extensively covered by an ice-free dust mantle in agreement with a fractional active area of a few percents (see Sect. 5). In this case, we adopted the same scattering law as described above for the spheroidal solution, i.e., the Hapke formalism with the parameters of asteroid 253 Mathilde.


  \begin{figure} \par\includegraphics[width=12.7cm,height=12.9cm,clip]{5253fig7.ps}\end{figure} Figure 7: WindowClean periodogram of the V-band light curve of the nucleus of comet 67P/Churyumov-Gerasimenko. The dirty Fourier spectrum ( top left panel), the spectral window ( top right panel), the cleaned spectrum ( bottom left panel), and the residuals ( bottom right panel) are displayed. The most probable (sine) period is 6.03 h, which corresponds to a rotational period of 12.07 h.
Open with DEXTER

We present a possible solution for the shape of the nucleus of 67P/Churyumov-Gerasimenko in Fig. 9. In this case, the inversion model was described by the cartesian coordinates of 650 vertices or directions. The corresponding light curve is displayed in Fig. 10; the rms value of the residuals (data-model) is 0.033 mag. The inversion procedure tends to choose equatorial viewing geometries (the proposed solution corresponds to an aspect angle of 79$^\circ $), since these give the simplest shapes. Furthermore, smaller aspect angles give very rapidly deteriorating fits, and a reasonable limit seems to be about 70$^\circ $. An aspect angle of 60$^\circ $ results in a rms deviation of 0.038 mag and is unlikely (Fig. 10). Apparently, during the HST observations we were extremely lucky to have a nearly equatorial view of the nucleus. We discuss this issue further below and show that such an orientation is now supported by several independent observations and considerations. There are, of course, many different solutions that match the observed light curve and maintain relatively simple pole/shape relationships, but all of them qualitatively have similar global shape characteristics. Above all, the pole-on views are similar, which is understandable: the silhouette that reproduces the observed light curve maxima and minima tends to be somewhat "rectangular''. The best estimate of the rotational period for this solution is $12.69\pm0.10$ h, and all acceptable solutions fall within that interval. This period also falls within the range of the various determinations presented in Table 2 and is identical to the result derived from the method of information entropy. The angle between the spin axis and the principal axis corresponding to the maximum moment of inertia is 4$^\circ $. Angles of a few degrees or so never make any difference in this kind of analysis and, therefore, have no visible effect at all. The two scattering laws produce essentially identical results with similar rms deviations of $\sim$0.03 mag.

Table 2: Period determinations.

Photometric inversion is basically size-scale free. In order to obtain the size of the modeled nucleus presented in Fig. 9, we performed two different normalizations.

The volume of the model body was forced to be equal to that of a sphere having a radius of 1.98 km, i.e., the mean radius we derived assuming pR = 0.04 and $\beta = 0.04$ mag/deg. The overall dimensions of the body are then 4.64, 3.87, and 3.50 km along the x-, y-, and z-axes, respectively.
The mean cross-section of the body as it rotates around the z-axis was forced to be equal to that of the above sphere. We adopted a step of 10$^\circ $ and calculated 35 cross-sections, which were averaged. The overall dimensions of the body are then 4.56, 3.81, and 3.44 km.
The differences between the two cases are $\sim$1.8%, so we conclude that the two normalizations yield essentially identical solutions for the size of the nucleus. In the following discussion, we adopt the second solution since it provides a somewhat better match to the observations.

The total surface area and volume of the nucleus are, respectively, 50 km2 and 31 km3, to be compared with 49 km2 and 32.5 km3 for the spherical model. For a bulk density of 500 kg m-3, the mass is $1.55\times10^{13}$ kg. According to the work of Davidsson & Gutiérrez (2005), this density represents an upper limit, and the true value is more likely to fall in the range 100-370 kg m-3. Then the mass of the nucleus would lie in the range $3.1\times10^{12}{-}1.2\times10^{13}$ kg.

From a rotational dynamics perspective, the shape can be assimilated to that of a prolate body, for which we calculated the ratios of the moments of inertia assuming uniform density. Introducing a body-fixed, triaxial coordinate system whose origin is at the center of mass of the body and whose axes (x, y, z) correspond to the principal axes of respectively smallest, intermediate, and largest moments of inertia, we found: Ix/Iz = 0.816 Iy/Iz = 0.998.

Finally, we performed a first-order analysis of the gravity field of this body, along the lines described by Scheeres et al. (1998) for asteroid 4179 Toutatis. The most important terms of the harmonic expansion of the gravity field correspond to the coefficients of second degree and order, C20 and C22. Assuming that the body is rotating in the minimum energy state of its angular momentum, i.e., about the principal axis of the largest moment of inertia (z-axis), and assuming that the body is homogeneous with a uniform density, we found the following dimensionless values: $C_{20} = -0.158/r_{\rm o}^2$ $C_{22} = 0.077/r_{\rm o}^2$where $r_{\rm o}$ is an arbitrary normalization radius. $r_{\rm o}$ may be suppressed as it has no real dynamical significance, in which case the C20 and C22 coefficients then have dimensions of km2.

4.4.1 Orientation of the spin axis

There have been several recent efforts to determine the orientation of the spin axis. Królikowska (2003) used the force precession model that resulted in a slightly prolate nucleus rotating around its largest principal axis, a quite unusual situation with direction defined by $\rm RA \sim 17^\circ$ and Dec $\sim$ $+5^\circ$. Davidsson & Gutiérrez (2005) have convincingly shown that this solution requires such special conditions that it is unlikely. Consequently, we did not include it in our analysis. Weiler et al. (2004) detected two significant radial features in the coma of 67P observed in March 2003 and speculated that they might correspond to the two sides of a side-on cone swept by an isolated source with each rotation. Since the spin axis of the nucleus is expected to be the axis of this cone, the inclination of its projected direction would be approximately 40$^\circ $ with respect to the orbital plane. Chesley (2004) modeled the outgassing-induced accelerations as "jets'' that thrust according to the insolation level, and he fitted the available astrometry for a wide range of pole orientations. His solution "B'' favored by the above observations of Weiler et al. (2004) has $\rm RA = 90\pm10^\circ$ and Dec = $+75\pm5^\circ$ implying an obliquity of 45$^\circ $ and one source at mid-latitude. Schleicher (2006) detected a sunward radial feature in an image of the coma of 67P obtained near perihelion in 1996, which he interpreted as the side of a cone swept by a mid-latitude source. Combined with other constraints, he proposed a possible pole solution with $\rm RA \sim 223^\circ$ and Dec $\sim$ $-65^\circ$, implying an obliquity of $\sim$134$^\circ $.

Davidsson & Gutiérrez (2005) applied a sophisticated thermophysical model to an ellipsoidal body and constrained the orientation of its spin axis by requiring that the solution must reproduce the observed light curve of the nucleus of 67P, the observed water production rates as a function of heliocentric distance, and the non-gravitational changes of the orbit, i.e., the orbital period, the longitude of the perihelion, and the longitude of the ascending node. They found that the spin axis is constrained to two well defined regions defined by its argument and obliquity (see definitions in Sekanina 1981). The first region is characterized by an argument in the range 45 to 75$^\circ $and an obliquity in the range 90 to 150$^\circ $, while the second one has an argument in the range 225 to 255$^\circ $ and an obliquity in the range 30$^\circ $ to 90$^\circ $.


  \begin{figure} \par\includegraphics[width=7.1cm,height=7cm,clip]{5253fig8.ps}\end{figure} Figure 8: Light curve (apparent R magnitude) of the nucleus of comet 67P/Churyumov-Gerasimenko. The dots are the observational data points. The solid line corresponds to the best prolate spheroid solution based on the Hapke photometric model with the parameters of asteroid 253 Mathilde. The dashed line corresponds to the projected cross-section of the illuminated fraction of the spheroid visible to the observer. The cross-section of the nucleus is displayed at different phase angles labeled 1 to 6.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.1cm,height=7cm,clip]{5253fig9.ps}\end{figure} Figure 9: Three-dimensional shape of the nucleus of 67P/Churyumov-Gerasimenko reconstructed from the inversion of the R light curve. The directions of the cartesian axes are indicated for each viewing geometry.
Open with DEXTER

These various solutions are displayed in Fig. 11, together with the constraint from our work that the aspect angle was ${\sim}80^\circ$ at the time of our observations. It should be kept in mind that the above solutions leave the sense of rotation undetermined, so each one leads to two diametrically opposed directions of the spin axis.

There is a remarkable convergence of these various determinations to two directions that are approximately opposed diametrically. The first one is defined by $\rm RA = 40_{-20^\circ} ^{+70^\circ}$ and $\rm Dec = +70\pm10^\circ$ and corresponds to a prograde sense of rotation and an obliquity of ${\sim}50^\circ$. The second one is defined by $\rm RA = 250\pm30^\circ$ and $\rm Dec = -70\pm10^\circ$, and corresponds to a retrograde sense of rotation and an obliquity of ${\sim}130^\circ$.


  \begin{figure} \par\includegraphics[width=6.2cm,height=6.3cm,clip]{5253fig10.ps}\end{figure} Figure 10: Light curve (apparent R magnitude) of the three-dimensional model of the nucleus of comet 67P/Churyumov-Gerasimenko as reconstructed by the inversion of the observations (data points). The phase folding is performed using the corresponding rotational period of 12.69 h. The best solution (dashed line) corresponds to an aspect angle of 79$^\circ $. Another solution with a 60$^\circ $ aspect angle is also displayed (dotted line) to illustrate the degradation of the fit.
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=90,width=6.8cm,clip]{5253fig11.ps}\end{figure} Figure 11: Direction of the spin axis of the nucleus of 67P/Churyumov-Gerasimenko according to different pole solutions.
Open with DEXTER

5 Activity of the nucleus

Production rates of OH by Hanner et al. (1985), Osip et al. (1992), Crovisier et al. (2002), Schleicher (2006) and of H2O by Mäkinen (2004) have been thoroughly reviewed and discussed by Davidsson & Gutiérrez (2005) and by Schleicher (2006). This ensemble of data spanning a wide range of heliocentric distances reveals a strong pre- to post-perihelion asymmetry, with peak productivity occurring $\sim$1 month after perihelion passage, as well as large rotational variability. Rotationally-averaged peak values of the water-production rate $Q_{\rm H_2O}$ at $r_{\rm h} \sim 1.36$ AU amount to $1\times10^{28}$ mol s-1 from the SOHO/SWAN Ly-$\alpha$ measurements of Mäkinen (2004) and to $8\times10^{27}$ mol s-1from the ground-based OH measurements of Schleicher (2006), hence in good agreement considering the different techniques. Following the standard (but oversimplified) practice, we calculated the fraction of active surface area on the nucleus on the basis of a simple water sublimation model that assumes a permanently illuminated isotropic source (Cowan & A'Hearn 1979). Active areas of 2.8 and 2.2 km2 are required to yield the above water production rates. For our model nucleus with a total surface area of 50 km2, this corresponds to active fractions of 5.6 and 4.5%, implying that the bulk of the surface of the nucleus of 67P is inactive. Schleicher (2006) argues that the simple model above overestimates the active area, as it is probably close to sub-solar latitudes, thus resulting in more efficient sublimation, and he favors an even smaller fraction of 3%. The survey of A'Hearn et al. (1995) gives an active area of 1.3 km2 to produce $Q_{\rm OH} = 4.1\times10^{27}$ mol s-1 at $r_{\rm h} = 1.41$ AU yielding an active fraction of 2.6%. These low values are consistent with the detection of structures in its coma and their probable association with a single or a few sources of limited spatial extent. No measurements have been obtained beyond 1.86 AU post-perihelion, but we can use available power laws to extrapolate the water production rate of water at $r_{\rm h} = 2.5$ AU post-perihelion corresponding to our HST observations. According to Schleicher (2006), the heliocentric variation of $Q_{\rm H_2O}$ beyond its post-perihelion peak is characterized by a power exponent of -6.8leading to $Q_{\rm H_2O}\sim1.2\times10^{26}$ mol s-1 at 2.5  AU. According to A'Hearn et al. (1995), $Q_{\rm OH}~r_{\rm h}^{-5.36}$, implying $Q_{\rm H_2O}~r_{\rm h}^{-5.86}$ (an extra -0.5 comes from the variation of the gas outflow velocity); extrapolating their OH production rate at 1.41 AU, we obtained $Q_{\rm H_2O}\sim1.4\times10^{26}$ mol s-1 at 2.5  AU. Taking the average of ${\sim} 1.3\times10^{26}$ mol s-1, we conclude that the active fraction had dropped to 0.1% at 2.5 AU. It is also conceivable that the seasonal effect implied by the large obliquity of the nucleus has changed the illumination conditions for the active region(s).

6 The properties of the coma

We now turn our attention to the coma of comet 67P and present below results for the standard quantity $Af\rho$ (A'Hearn et al. 1984), the dust production rate, and the reflectivity gradient. These three quantities all involve the ratio ${\sf R} = F_{\rm coma}/F_\odot$, where $F_{\rm coma}$ and $F_\odot$ are the brightness fluxes of the coma and of the Sun (expressed, for example, in erg s-1 cm-2 Å-1) and averaged over a given spectral band). A convenient way to calculate ${\sf R}$ is to express it in terms of the signals measured on the images and expressed in DN/s:

$\displaystyle {\sf R} = S_{\rm coma}/S_\odot$     (5)

where $S_\odot$, the signal that would be produced by the Sun if observed by the HST WFPC2 in a given filter, is directly obtained from the transformation formulae of Holtzman et al. (1995) using the known magnitudes and color indices of the Sun.

As pointed out in Sect. 3, the coma was found to be in steady state in all our images (p = -1), so that $S_{\rm coma}$ and the quantity $Af\rho$are independent of aperture size and can be directly expressed in terms of $k_{\rm c}$, the scaling factor of the coma model. We found very little variation among the 48 determinations of $k_{\rm c}$on the F675W red images, all lying within $\pm$5% of the mean, the typical uncertainty of the fitting process. We therefore averaged the individual results and obtained a value of $Af\rho = 40.2\pm0.3$ cm, valid at $\lambda = 670$ nm (the effective wavelength of the F675W filter) and at a phase angle of 4.8$^\circ $. Note that at such a small angle, an opposition effect can artificially increase the albedo A and therefore the quantity $Af\rho$.

An initial estimate for the dust production rate $Q_{\rm d}$ was obtained by assuming a very simple model of an isotropic, force-free steady state outflow of dust grains, all having the same radius a (see Toth et al. 2005 for a previous application). Then $Q_{\rm d}$ is related to $Af\rho$ by:

$\displaystyle Q_{\rm d} = 66.7\; {\rho_{\rm d}\; v_{\rm d}\; a \over p_{\rm d} \Phi(\theta)}\; Af\rho \quad {\rm\left(g\; s^{-1}\right)}$     (6)

where $v_{\rm d}$ (m s-1), $\rho_{\rm d}$ (g cm-3), a (cm), $p_{\rm d}$, and $\Phi(\theta)$, are, respectively, the velocity, the bulk density, the geometric albedo, and the scattering function of the dust grains. For a typical grain size $a = 3\times10^{-4}$ cm (3 $\mu$m) with $\rho_{\rm d} = 1$ g cm-3, we found $v_{\rm d} = 180$ m s-1 (see below). Further, assuming $p_{\rm d} = 0.04$ and the normalized scattering function of Divine (1981), $\Phi = 0.89$ at the phase angle of our observations, and using our determination $Af\rho = 40$ cm, we finally obtained $Q_{\rm d} = 4.6$ kg s-1.

The dust production rate was then estimated using the standard method we applied in our past studies (e.g., Lamy et al. 1998a,b; Toth et al. 2005). It is based on the formalism developed by Newburn & Spinrad (1985) and later re-formulated by Singh et al. (1992). The various parameters required by this method are unknown, so we have no other choice than to adopt "standard'' values except for those directly relevant to the nucleus of 67P. We used our determination of its radius, rn = 1.98 km, and a bulk density of 500 kg m-3. We assumed that the activity is still mostly driven by the sublimation of water ice at 2.5 AU and adopted our extrapolated value of the water production rate of $1.3\times10^{26}$ mol s-1 and an active fraction of 0.001 (Sect. 5). Applying this model to our measurements of the coma of 67P leads to $Q_{\rm d} \sim 4$ kg s-1. As pointed out by Newburn & Spinrad (1985), $Q_{\rm d}$ is most sensitive to the active fraction. Using the maximum (but improbable) value of 0.056 determined in Sect. 5 at the time of our observations indeed significantly reduces $Q_{\rm d}$ to 1 kg s-1. Not surprisingly, there are huge discrepancies among the currently published values of $Q_{\rm d}$, probably resulting from the different models being used and, particularly, the size of the largest liftable grain (see the discussion in Weiler et al. 2004). An in-depth study of this question is certainly warranted but beyond the scope of the present article.

The reflectivities of the coma were calculated from the ratios $S_{\rm coma}/S_\odot$, normalized at 540 nm, the effective wavelength of the F555W filter. For each orbit, we separately averaged the determinations of $k_{\rm c}$ from all images obtained with the F675W and the F555W filters, respectively. The resulting six values of the normalized reflectivity were further averaged, and we finally obtained $S[540, 670~\rm nm] = 1.41\pm0.01$. The corresponding reflectivity gradient is $S^\prime [540, 670~\rm nm] = 32\pm6\%$ per kÅ. The F675W filter is probably free of any major gas emission, but the F555W filter may contain several C2 bands, so that the above values are, strictly speaking, upper limits. However, 67P is a very dusty comet, and it is likely that, at 2.5 AU, the C2 bands make a negligible contribution with respect to the dust continuum. Therefore, our color measurements are probably representative of the properties of the dust grains of 67P, which are therefore quite red. From their spectrophotometric observations performed in 1982 and early 1983, Storrs et al. (1992) extracted seven continuum measurements spanning the spectral range 370-640 nm. Their average reflectivity gradient, restricted to the spectral range 446-626 nm, is $24\pm1$% per k$\AA$. Their reflectivity curve, however, exhibits an "S'' shape; interpolating a first value at 540 nm and extrapolating a second one at 670 nm, we found a gradient of ${\sim}30\pm6$% per kÅ, quite consistent with our own measurement. For the sake of completeness, we mention two results obtained in different spectral ranges: Weiler et al. (2004) found $S^\prime [407, 460~\rm nm] = -0.7\pm5.1\%$ per kÅ (but probably contaminated by a C3 band) and Schleicher (2006) $S^\prime [365, 484.5~\rm nm] = 30\pm42\%$ per kÅ (note, however, the very large error bar).

7 Conclusions

Our HST observations of comet 67P/Churyumov-Gerasimenko, the new target of the Rosetta mission, performed in March 2003 have enabled us to obtain a detailed portrait of its nucleus and to characterize its coma. Our main findings are summarized below.

1.
The solution for a spherical body, with a geometric albedo of 0.04 and a phase coefficient of 0.04 mag/deg for the R band, has a radius of $1.98\pm0.02$ km.
2.
The spheroidal solution implied by the double-peaked light curve has semiaxes a = 2.41 km and b = c = 1.55 km.
3.
The rotation period of the nucleus was determined from seven different period searching methods and is $12.41\pm0.41$ h, making it a moderate rotator among cometary nuclei having well-determined rotational periods.
4.
Inversion of the light curve led to a possible three-dimensional solution of the nucleus having an overall size of $4.56\times3.81\times3.44$ km viewed at an aspect angle of ${\sim}80^\circ$ (i.e., near equatorial view) at the time of our observations.
5.
Assuming a bulk density of 500 kg m-3, the nucleus with a shape coming from the inversion of the light curve has a mass of $1.55\times10^{13}$ kg. If the density lies in the range 100-370 kg m-3, as suggested by the work of Davidsson & Gutiérrez (2005), then its mass is in the range $3.1\times10^{12}{-}1.2\times10^{13}$ kg.
6.
When combined with other constraints, the direction of the pole is found at either RA = $40^\circ$ $^{+70^\circ}_{-20^\circ}$ and Dec = $+70\pm10^\circ$ (prograde rotation) or RA = $250\pm30^\circ$ and Dec = $-70\pm10^\circ$ (retrograde rotation)
7.
The color of the nucleus is moderately red with $(V-R)=0.52\pm0.05$, which corresponds to a reflectivity gradient of 17.4% per kÅ at optical wavelengths, the most common value for cometary nuclei.
8.
At its peak water production rate, which occurs $\sim$30 days after perihelion passage, the active fraction of the nucleus is only $\sim$5.6%, implying that the bulk of its surface is inactive with probably a single active area located at mid-latitude and responsible for a jet. At the time of our observations at $r_{\rm h} = 2.50$ AU, the active fraction had dropped to about 0.1%. It is also conceivable that the seasonal effect has changed the illumination conditions for the active region.
9.
The coma is characterized by $Af\rho = 40.2\pm0.3$ cm, a dust production rate $Q_{\rm d} \sim 4$ kg s-1(with a large uncertainty), a normalized reflectivity $S[540, 670~\rm nm] = 1.41\pm0.01$, and a reflectivity gradient $S^\prime [540, 670~\rm nm] = 32\pm6$% per kÅ.

Acknowledgements
We express our gratitude to S. Beckwith, Director of the Space Telescope Science Institute, for granting us Director's Discretionary time on very short notice. We thank the HST ground system personnel for their prompt and efficient scheduling of the observations. I. Toth acknowledges a special grant from the CNES (Centre National d'Études Spatiales), and P. Gutiérrez an ESA postdoctoral fellowship to support their stays at Laboratoire d'Astrophysique de Marseille. H. A. Weaver acknowledges financial support from NASA through grant number GO-9713 from the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS5-26555.

References

 

  
Online Material

Table 1: Journal of observations.


Copyright ESO 2006