A&A 458, 523-532 (2006)
DOI: 10.1051/0004-6361:20065241

Consistency between deep crustal heating of strange stars in superbursters and soft X-ray transients

M. Stejner - J. Madsen

Department of Physics and Astronomy, University of Aarhus, 8000 Århus C, Denmark

Received 21 March 2006 / Accepted 4 August 2006

Abstract
Context. Both superbursters and soft X-ray transients probe the process of deep crustal heating in compact stars. It was recently shown that the transfer of matter from crust to core in a strange star can heat the crust and ignite superbursts provided certain constraints on the strange quark matter equation of state are fulfilled.
Aims. We derive corresponding constraints on the equation of state for soft X-ray transients assuming their quiescent emission is powered in the same way, and further discuss the time dependence of this heating mechanism in transient systems.
Methods. We approach this using a simple parametrized model for deep crustal heating in strange stars assuming slow neutrino cooling in the core and blackbody photon emission from the surface.
Results. The constraints derived for hot frequently accreting soft X-ray transients are always consistent with those for superbursters. The colder sources are consistent for low values of the quark matter binding energy, heat conductivity and neutrino emissivity. The heating mechanism is very time dependent which may help explain cold sources with long recurrence times. Thus deep crustal heating in strange stars can provide a consistent explanation for superbursters and soft X-ray transients.

Key words: stars: neutron - dense matter - equation of state - X-rays: binaries - X-rays: bursts - X-rays: general

1 Introduction

Strange stars are a class of compact stars made entirely of absolutely stable strange quark matter except for a possible thin crust of ordinary nuclear matter below the neutron drip density separated from the core by a strong Coulomb barrier (Baym & Chin 1976; Witten 1984; Alcock et al. 1986; Itoh 1970; Haensel et al. 1986). The stability of strange quark matter depends on poorly constrained strong interaction properties and remains to be decided by observation or experiment (see Weber et al. 2006; Madsen 1999; Weber 2005, for reviews). If true, the strange matter hypothesis would imply that all compact stars are likely to be strange stars (because the galactic flux of quark matter lumps from strange star collisions will trigger the hadron-to-quark transition in neutron stars and supernova cores (Caldwell & Friedman 1991; Madsen 1988)), and so strange star models should be able to reproduce observed characteristics of compact stars. Specifically strange stars should be able to reproduce the bursting behavior of low mass X-ray binaries (LMXBs) expected to contain some of the heaviest compact stars due to accretion, and here we test the consistency of the recent model for superburst ignition in strange stars by Page & Cumming (2005) with similar considerations for the quiescent emission from soft X-ray transients; two of the most important LMXB activities.

Superbursts, first discovered by Cornelisse et al. (2000), are a rare kind of type I X-ray bursts from LMXBs distinguishing themselves by extreme energies ($\sim$1042 erg), long durations (4-14 h) and long recurrence times ($\sim$1 year) - see Kuulkers (2004) for a recent review of their observational properties. The mechanism behind superbursts is thought to be unstable thermonuclear burning of carbon in the crust at densities around $10^{9}~\mbox{g~cm}^{-3}$ (Cumming & Bildsten 2001; Brown 2004; Cooper & Narayan 2005; Cumming & Macbeth 2004; Strohmayer & Brown 2002; Cumming et al. 2005; in't Zand et al. 2004). The fuel for such an event is provided by the burning of accreted hydrogen and helium at the surface, which may take place either stably or unstably. In the latter case it gives rise to ordinary type I X-ray bursts. The ashes from this process, containing about 10% carbon by mass, are compressed under the increasing weight of the layers above, and when enough carbon has been accumulated it may be ignited and burn unstably. Observed superburst light curves require the ignition to take place at temperatures around $6\times 10^8$ K and column depths of approximately $10^{12}~\mbox{g~cm}^{-2}$, and as the heat released by accretion and burning at the surface is quickly reradiated and does not penetrate to this depth, these ignition conditions must be set by the process of deep crustal heating and therefore probe the physics of the deep crust and core (Cooper & Narayan 2005; Brown 2004).

In neutron stars deep crustal heating refers to the heat released as the sinking ashes undergo electron captures and most importantly - at densities above $10^{12}~\mbox{g~cm}^{-3} $ - pycnonuclear reactions (Haensel & Zdunik 2003; Brown et al. 1998; Haensel & Zdunik 1990). This amounts to about 1.4 MeV per nucleon and heats the core to $\sim$108 K depending on the accretion rate. It has however been difficult to achieve superburst ignition at the appropriate column depth, and in a recent investigation Cumming et al. (2005) showed that neutrino emission from Cooper pairing of neutrons at densities in the range $10^{12}{-}10^{13}~\mbox{g~cm}^{-3}$ limits the crust temperature below $5\times 10^8$ K. Thus unstable carbon ignition seems impossible at the observed depth unless Cooper pair emission is less efficient than currently thought or some additional heating source can be found.

In strange stars there can be no pycnonuclear reactions because the crust density is limited by the neutron drip density, but for the same reason there can be no Cooper pair emission from neutrons either. Furthermore the energy released by matter tunneling through the Coulomb barrier at the base of the crust and converting to quark matter could be much greater than that released by pycnonuclear reactions in neutron stars. Thus it seems reasonable to expect that strange stars in LMXBs can be heated to higher temperatures than neutron stars, and Page & Cumming (2005) recently showed that this can lead to superburst ignition at the observed column depths if certain constraints on the strange quark matter core parameters are fulfilled.

Soft X-ray transients are LMXBs which undergo accretion outbursts lasting days to years separated by long periods of quiescence in which no or very little accretion takes place and the X-ray luminosity drops to $\sim$ $10^{32}~\mbox{erg~s}^{-1}$(Tomsick et al. 2004; Campana et al. 1998; Rutledge et al. 1999). When accretion stops, the heat deposited at the surface quickly radiates away, and so in the absence of any residual accretion the surface temperature should reflect the temperature of the core including the effects of deep crustal heating. This has been thoroughly investigated for neutron stars in the literature (Yakovlev et al. 2004; Colpi et al. 2001; Brown et al. 1998; Ushomirsky & Rutledge 2001; Rutledge et al. 2002a; Brown et al. 2002; Yakovlev et al. 2003, and references therein) establishing deep crustal heating as an unavoidable heating mechanism in the core, which should at least provide a "rock bottom'' luminosity for these sources. Residual accretion may still play a role however - indeed the power law components in the spectra of many of these sources are often taken as a sign of residual accretion or shock emission from a rotation powered pulsar - and furthermore the properties of the core remains uncertain, so the precise nature of the quiescent emission is not firmly established.

Considering the many possible phases and poorly constrained properties of strange quark matter one would expect - for the same general reasons they were able to fit superbursters - that a wide range of strange star models can reproduce the observed properties of soft X-ray transients. Our approach is therefore to use a simple parametrized model for deep crustal heating in strange stars to discuss the consistency between constraints on strange quark matter derived from superbursters and soft X-ray transients, as such a mutual fit is likely to constrain the strange quark matter equation of state further.

We describe the overall structure of strange stars and their crusts in Sect. 2 and then turn to deep crustal heating in Sect. 3. In Sect. 4 we compare models with different assumptions about the cooling mechanism to observations of soft X-ray transients, and we discuss the importance of time dependence in Sect. 5 before concluding in Sect. 6.

  
2 Strange stars and their crusts

If strange stars are stable they contain roughly equal numbers of up, down and strange quarks in their core, but due to the higher mass of the negative s-quark, these will normally be slightly disfavored giving the core an overall positive quark charge to be compensated by electrons. Even color-flavor locked strange quark matter, which is strictly charge neutral in bulk (Rajagopal & Wilczek 2001) has an overall positive quark charge due to surface effects (Madsen 2001; Usov 2004; Madsen 2000). Because strange quark matter is self bound the density is largely constant in the core dropping by only a factor of a few from the center to the surface, where it goes from above nuclear density to zero within a few fm - see e.g. Kettner et al. (1995); Glendenning & Weber (1992); Zdunik (2002); Weber (1999); Alcock et al. (1986); Zdunik et al. (2001); Glendenning (2000); Haensel et al. (1986) for details on the global properties of strange stars. Since the electrostatic force is much weaker than the strong force confining the quarks, some of the electrons necessary to create an overall charge neutral object will form a thin atmosphere outside the quark phase held in place by a huge electric field. The electric field - up to $10^{18}~\mbox{V~cm}^{-1}$ - is capable of sustaining a nuclear matter crust decoupled from the quark phase by a small electron filled gap (Kettner et al. 1995; Stejner & Madsen 2005; Alcock et al. 1986). The crust is electrically neutral in bulk however, so beyond the boundary layer its structure is given by hydrostatic equilibrium with an equation of state corresponding to the chemical composition of the ashes from the surface burning (Glendenning & Weber 1992; Zdunik et al. 2001). The crust mass roughly follows (Zdunik et al. 2001)
 
                          $\displaystyle M_{\rm C}$ = $\displaystyle \frac{4\pi R^4 P_{\rm b}}{GM}\left(1-\frac{2GM}{Rc^2}\right)$ (1)
  = $\displaystyle 8.1\times 10^{-5}\frac{R_6^4}{M_*}\left(\frac{\rho_{\rm b}}{\rho_{\rm D}}\right)^{\gamma}\left[1-0.295\frac{M_*}{R_6}\right] M_\odot$ (2)

where $P_{\rm b}$ is the pressure at the bottom of the crust, $M_*=M/M_\odot$ is the stellar mass in units of the solar mass, $R_6=R/ 10~\mbox{km}$ is the stellar radius, $\rho_{\rm b}$ is the density at the bottom of the crust, $\rho_{\rm D}=7.8 \times 10^{11}~\mbox{g~cm}^{-3}$ is the neutron drip density, $\gamma\simeq 4/3$ is the adiabatic index in the crust and the last equality assumes the crust composition found by Haensel & Zdunik (2003) for accreting neutron stars. The density at the bottom of the crust may be limited by the neutron drip density if the Coulomb barrier from the core is sufficiently high, which depends on the details of the equation of state of strange quark matter. In most cases this will not be possible though and the maximum crust density is then determined by the rate at which ions tunnel through the Coulomb barrier such that the tunneling rate for an accreting star is equal to the accretion rate or corresponds to the inverse stellar age if the star is isolated (see Stejner & Madsen 2005, for a detailed discussion). The tunneling rate close to this equilibrium is very sensitive to the crust density so there is no great difference between these two cases in terms of crust density, but for the same reason one may expect that in soft X-ray transients the tunneling rate will vary with the accretion rate - we return to this point in Sect. 5.

Since the crust has no significant heating sources of its own (electron captures in the crust amount to less than 40 keV per nucleon (Haensel & Zdunik 2003)) its thermal profile is set by the diffusion of heat from the core towards the surface. The surface temperature, $T_{\rm S}$, is therefore only a function of the core surface temperature, $T_{\rm i}$, and thus probes the process of deep crustal heating. A detailed account for such $T_{\rm S}{-}T_{\rm i}$ relations can be found in e.g. Yakovlev et al. (2004), but in a reasonable approximation $T_{\rm i,9} \simeq 0.1T^2_{\rm S,6}$ (Gudmundsson et al. 1983), which will be sufficient for our purpose. Here $T_{\rm S,6}=T_{\rm S}/10^6$ K and $T_{\rm i,9}=T_{\rm i}/10^9$ K is actually the temperature at a density of $10^{10}~\mbox{g~cm}^{-3}$, but as the crust is largely isothermal at this depth, one can take this to be the core surface temperature (Yakovlev et al. 2004; Gudmundsson et al. 1983).

In the discussion above and in what follows we have assumed the conventional description of strange stars with a sharp core surface, an electron filled gap and a nuclear crust. It should be mentioned however that Jaikumar et al. (2006) recently showed, that if the surface tension of strange quark matter is not too high, it may be unstable to phase separation at low pressure leading to a crust of quark nuggets embedded in a degenerate electron gas, which would in many ways resemble the nuclear crust on neutron stars. The consequences of such a crust in an accreting system are not clear at present, and we restrict ourselves to the traditional scenario.

   
3 Deep crustal heating in accreting strange stars

Deep crustal heating in strange stars was recently studied by Page & Cumming (2005) as a means of achieving superburst ignition conditions at the appropriate column depth and thus constrain the properties of strange quark matter (see also the work on continuously accreting strange stars by Miralda-Escude et al. 1990). It was shown that observed ignition conditions are achieved for a wide range of crust density, $\rho_{\rm b}$, strange quark matter binding energy, $Q_{\rm SQM}$, neutrino emissivity, $\epsilon_\nu$, and thermal conductivity, K, provided that the direct Urca process does not operate in the core implying that strange quark matter should be a color superconductor. Furthermore a set of useful analytical approximations to the core surface temperature were shown to reasonably approximate numerical calculations. Here we will use those same approximations to find the corresponding constraints on strange quark matter in soft X-ray transients and a relationship between the observable parameters of superbursters and soft X-ray transients. For clarity and to emphasize the approximations we therefore briefly review the calculation by Page & Cumming (2005) in the following subsection.

3.1 Approximate thermal structure

As accretion on the strange star drives the crust towards its maximum density, the rate at which nuclei (or neutrons if the neutron drip density can be reached) tunnel through the Coulomb barrier into the quark matter core will increase until an equilibrium crust density is reached. This density may vary as a function of the unknown Coulomb barrier height at the quark matter surface but this would not change the qualitative features of the model and for our purpose we will assume that the equilibrium crust density is $\sim$ $10^{11}~\mbox{g~cm}^{-3}$. As the nuclei cross into the strange quark matter core at the rate $\dot{m}$ (in units of nucleons cm-2 s-1unless otherwise stated) and are dissolved, they release an energy, $Q_{\rm SQM}\leq 100$ MeV per nucleon (the actual value depends on uncertain values for strong interaction parameters but is fixed if these parameters were known). This heats the core until an equilibrium or steady state temperature is reached as the heating balances energy loss by neutrino emission in the core. This is assumed to take place at a (slow) rate of

 \begin{displaymath} \epsilon_\nu\simeq Q_\nu\times T^8_9 \mbox{ erg cm}^{-3}\mbox{ s}^{-1}, \quad Q_\nu \sim 10^{18}{-}10^{22} \end{displaymath} (3)

with $T_{9}=T/10^9~\mbox{K}$, corresponding to modified Urca and bremsstrahlung processes (Yakovlev & Pethick 2004; Page et al. 2005). We thus neglect a slow dependence on density in $Q_\nu $ which would only amount to a factor of order unity since the core density is nearly constant.

We will - at first - assume that this equilibrium is simply determined by the average accretion rate, which would be reasonable in systems where the tunneling is more or less continuous. We return to this point in Sect. 5 however as this steady state assumption may not be sufficient for all systems.

Following Page & Cumming (2005) we model the thermal profile of the core in a plane parallel approximation with heat transport taking place by conduction and with a heat sink from neutrino emission. The inward directed heat flux from the conversion of nucleons to strange quark matter, F, is determined by

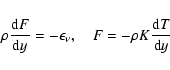\begin{displaymath}\rho\frac{{\rm d}F}{{\rm d}y}=-\epsilon_\nu, \quad F=-\rho K\frac{{\rm d}T}{{\rm d}y} \end{displaymath} (4)

where $\rho$ is the density, K is the thermal conductivity of strange quark matter, assumed to lie the range $10^{19}{-}10^{22}~\mbox{cgs}$, and y is the column density. Again we will neglect slow dependencies of K on density and temperature so assuming that $\rho$, $Q_\nu $ and K are constant in the core this gives

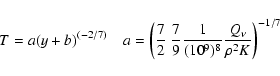\begin{displaymath}T=a(y+b)^{(-2/7)}\quad a=\left(\frac{7}{2}\;\frac{7}{9}\frac{1}{(10^9)^8}\frac{Q_\nu}{\rho^2 K}\right)^{-1/7} \end{displaymath} (5)

where b is a constant of integration determined by the requirement that all heat entering the core is emitted as neutrinos, $\dot{m}Q_{\rm SQM}=\rho^{-1}\int \epsilon_\nu {\rm d}y$. Assuming that the integral is dominated by the surface contribution this gives for the core surface temperature

 \begin{displaymath} T_{\rm i,9}=0.87~ Q_{\nu,21}^{-1/9} K_{20}^{-1/9}\left(\frac... ...{2/9}\left(\frac{\dot{m}}{0.3\;\dot{m}_{\rm Edd}}\right)^{2/9} \end{displaymath} (6)

where $Q_{\nu,21}=Q_\nu/10^{21}$, $K_{20}=K/10^{20}\mbox{ cgs}$ and $\dot{m}_{\rm Edd}\simeq 1.6\times10^{-8}~{M}_\odot~\mbox{yr}^{-1}/4\pi R^2m_u$ is the Eddington accretion rate in units of nucleons cm-2 s-1with R being the stars radius and mu the atomic mass unit.

If however the thermal conductivity of strange quark matter is sufficiently large the core becomes isothermal with the temperature given by $4\pi R^2\dot{m}Q_{\rm SQM}=(4\pi R^3/3)Q_\nu T_{\rm i,9}^8$ so

 \begin{displaymath} T_{\rm i,9}=0.54~ Q_{\nu,21}^{-1/8}\left(\frac{Q_{\rm SQM}}{... ...\frac{\dot{m}}{0.3\;\dot{m}_{\rm Edd}}\right)^{1/8}R_6^{-1/8} \end{displaymath} (7)

where R6 is the core radius in units of 10 km. Equating this to Eq. (6) shows that the core becomes isothermal at a critical thermal conductivity $K_{\rm crit}=4.3\times 10^{21}\mbox{ cgs } Q_{\nu,21}^{1/8}(Q_{\rm SQM}/100~{\rm MeV})^{7/8}(\dot{m}/0.3\;\dot{m}_{\rm Edd})^{7/8}$.

It should be noted that although Eqs. (6) and (7) are certainly oversimplified they were shown by Page & Cumming (2005) to agree reasonably well with numerical calculations of a full general relativistic model. Furthermore they offer a physical transparency, which given the many poorly constrained properties of strange quark matter, is perhaps just as desirable in what follows as full numerical models. Specifically Eqs. (6) and (7) are general enough not to depend on the properties of a particular strange quark matter phase - except for the assumption of slow neutrino emissivity necessary to obtain superburst ignition. They are in fact general enough to also describe neutron stars at the same level of detail, and indeed Eq. (7) corresponds entirely to case (ii.a) in Yakovlev et al. (2003) for low-mass neutron stars with slow neutrino emission. Thus much of what follows would also apply for neutron stars - although in that case it has of course been done in much greater detail.

In deriving Eqs. (6) and (7) we assumed that cooling by neutrino emission dominated photon emission from the surface. This is certainly the case in superbursters, where the core is very hot, but for cold enough cores this may not be the case and one should take the surface luminosity into account. Approximating the surface with a blackbody we can estimate when this becomes important by setting, $4\pi R^2 \dot{m}Q_{\rm SQM}=4\pi R^2\sigma T_{\rm S}^4$, which using the Gudmundsson et al. (1983) relation, $T_{\rm i,9}\simeq 0.1 T_{\rm S,6}^2$, gives a core temperature

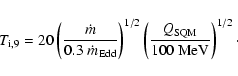\begin{displaymath}T_{\rm i,9}=20 \left(\frac{\dot{m}}{0.3\;\dot{m}_{\rm Edd}}\r... ...1/2}\left(\frac{Q_{\rm SQM}}{100~\mbox{MeV}}\right)^{1/2}\cdot \end{displaymath} (8)

Equating this to Eq. (7) shows that cooling by photon emission becomes important in the isothermal case below an accretion rate of

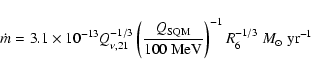\begin{displaymath}\dot{m}=3.1\times 10^{-13} Q_{\nu,21}^{-1/3} \left(\frac{Q_{\... ...100~\mbox{MeV}}\right)^{-1} R_6^{-1/3}~{M}_\odot~{\rm yr}^{-1} \end{displaymath} (9)

with a similar expression giving a somewhat lower limit for a non-isothermal core. Similar conclusions for neutron stars were reached by Yakovlev et al. (2003). Given the right combination of core parameters photon emission may therefore be important in soft X-ray transients with the lowest accretion rates as low as a few times $10^{-12}~{M}_\odot~{\rm yr}^{-1}$.

In the following subsections we shall ignore photon cooling from the surface, which allows analytical constraints on the core parameters and simple scaling relations for the surface temperature independent of assumptions about the core parameters. This approach is justified for high  $Q_{\rm SQM}$, but we return to discuss the importance of photon cooling in Sect. 4 as we shall find neutrino cooling unable to account for the coldest soft X-ray transients.

3.2 Constraints on the core parameters

Equations (6) and (7) relate quark matter properties represented by $Q_\nu $, $Q_{\rm SQM}$ and K to the stellar accretion rate and core surface temperature under the assumption that the accretion rate is high enough for neutrino cooling to dominate. In case there are independent constraints on the core surface temperature and the accretion rate Eqs. (6) and (7) can also be regarded as necessary relations between the quark matter core parameters $Q_\nu $, $Q_{\rm SQM}$ and K. This approach was taken for superbursts in Page & Cumming (2005) assuming that the crust below the superburst ignition depth is approximately isothermal so the core surface temperature can be approximated by the superburst ignition temperature, $T_{\rm i,9}\simeq 0.7$ at $\dot{m}=0.1{-}0.3~\dot{m}_{\rm Edd}$. We will make the same assumption and take over the superburst parameter constraints from Page & Cumming (2005).

Assuming that soft X-ray transients are also powered by deep crustal heating, a different independent constraint on the quark core parameters can be obtained by applying Eqs. (6) and (7) to observations of the accretion rate and surface temperature of soft X-ray transients using a $T_{\rm S}{-}T_{\rm i}$ relation such as the one in Yakovlev et al. (2004) or Gudmundsson et al. (1983).

Aql X-1 is an example of a well studied soft X-ray transient which has $\langle\dot{m}\rangle\simeq 10^{-10}~{M}_\odot~{\rm yr}^{-1}$, $T^\infty_S\simeq 113~\mbox{eV}$(Rutledge et al. 2002a; Yakovlev et al. 2003) and therefore $T_{\rm i,9}\simeq 0.3$ using a canonical mass-radius relationship, $R=10~\mbox{km}$, M/R=0.2, and $T_{\rm S}=T_{\rm S}^\infty /(1-2GM/R)^{1/2}$. The relations between the quark matter core parameters thus obtained for superbursts and for the soft X-ray transient Aql X-1 are compared in Fig. 1. If we keep $Q_\nu $ fixed and increase  $Q_{\rm SQM}$ then K must also increase to produce the required temperature until the critical conductivity is reached and the star must be isothermal. Therefore only the regions below the isothermal curves contain possible solutions for each class of object and there can be no common solution for superbursters and Aql X-1 between the two isothermal curves shown. It is clear that the range of quark matter parameters permitted for the soft X-ray transient Aql X-1 is significantly smaller than that allowed by the superbursters; in particular the quark matter binding energy per baryon, $Q_{\rm SQM}$, necessary to fit the soft X-ray transient must be in the lower part of the range allowed for fitting superbursters, other parameters being equal. We further note that the non-isothermal relations from Eq. (6) agree remarkably well in the range where common parameters fit superbursters and Aql X-1, whereas no simultaneous isothermal solutions for the two classes of objects seem to exist.

  \begin{figure} \par\includegraphics[width=8cm,clip]{5241fig1.ps} \end{figure} Figure 1: Constraints on quark core parameters obtained from superbursters (solid) and the soft X-ray transient Aql X-1 (dashed) assuming slow neutrino cooling for both. $Q_{\rm SQM}$ is given as a function of $Q_\nu $ for different choices of K. Thin lines show non-isothermal constraints from Eq. (6) with $K=10^{19},~ 10^{20},~ 10^{21},~ 10^{22}\mbox{ cgs}$ from the bottom up. Non-isothermal constraints for Aql X-1 are nearly indistinguishable from those for superbursters. Thick lines show isothermal constraints from Eq. (7). We take $\dot{m}=0.3 \dot{m}_{\rm Edd}$ for the superbursters.
Open with DEXTER

For a fixed (albeit unknown) set of strong interaction parameters neither the quark matter binding energy  $Q_{\rm SQM}$, nor the quark core surface density should vary between stars, because both are given directly by the strong interaction parameters. The neutrino luminosity is dominated by the core surface contribution and strange stars are furthermore characterized by an almost constant density in the core unless we are very close to the maximum mass strange star, so the slow variations with density of $Q_\nu $ and K should be unimportant. K may be inversely proportional to the temperature (Haensel 1991) and can therefore vary by a small factor between the coldest soft X-ray transients with quark core temperature $\sim$108 K and superbursters with core temperature $\sim$ $7\times 10^8$ K. If no density thresholds between phases or emission mechanisms are crossed when going from superbursters to soft X-ray transients it should therefore be reasonable to expect approximate agreement between the relations in Fig. 1, as seen for the non-isothermal solutions, but not order of magnitude differences as found in the isothermal case.

3.3 Scaling relations for the surface temperature

In this subsection we will use Eqs. (6) and (7) to relate the parameters for strange stars with deep crustal heating that can fit soft X-ray transient data and superbursters simultaneously, assuming slow neutrino cooling to be the dominant cooling mechanism. In particular we will derive relations between surface temperature and accretion rate for soft X-ray transients for strange star model parameters that fit superbursts. These relations will then be compared to observational data for soft X-ray transients in the following section.

To the extent that $Q_{\rm SQM}$ and $Q_\nu $ do not vary between stars we can utilize Eqs. (6) and (7) to compare the other parameters for two arbitrary strange stars with deep crustal heating. In the following we shall in particular be interested in cases where one of the stars is a superburster (SB) and the other a soft X-ray transient (X). From Eq. (6) we have in the non-isothermal case

 
                          $\displaystyle \alpha_{\rm SB}$ $\textstyle \equiv$ $\displaystyle \left(T_{\rm i,9}^{9/2}\left[\frac{\langle\dot{m}\rangle}{0.3~\dot{m}_{\rm Edd}}\right]^{-1}\right)_{\rm SB}$  
  = $\displaystyle \left(\frac{K_{\rm 20,X}}{K_{\rm 20,SB}}\right)^{1/2}\left(T_{\rm... ...[\frac{\langle\dot{m}\rangle}{0.3~\dot{m}_{\rm Edd}}\right]^{-1}\right)_{\rm X}$ (10)

and from Eq. (7) in the isothermal case
 
                         $\displaystyle \alpha_{\rm SB}$ $\textstyle \equiv$ $\displaystyle \left(T_{\rm i,9}^{8}\left[\frac{\langle\dot{m}\rangle}{0.3~\dot{m}_{\rm Edd}}\right]^{-1}\right)_{\rm SB}$  
  = $\displaystyle \left(\frac{R_{6,X}}{R_{6,SB}}\right)\left(T_{9,i}^{8}\left[\frac{\langle\dot{m}\rangle}{0.3~\dot{m}_{\rm Edd}}\right]^{-1}\right)_{\rm X} \cdot$ (11)

In a soft X-ray transient the temperature at the quark core surface can be obtained from a $T_{\rm S}{-}T_{\rm i}$ relation with $T_{\rm S}=T_{\rm S}^\infty /(1-2GM/R)^{1/2}$. The average accretion rate can be estimated from the outburst luminosity, $L_{\rm o}\sim (\Delta M/t_{\rm o})(GM/R)$, where $\Delta M$ is the accreted mass and $t_{\rm o}$ is the outburst duration, so if $t_{\rm q}$ is the time spent in quiescense $\langle\dot{m}\rangle= \frac{\Delta M/m_u}{4\pi R^2(t_{\rm o}+t_{\rm q})}$. In Eqs. (10) and (11) we should therefore further allow for different M/R ratios. If we use a detailed  $T_{\rm S}{-}T_{\rm i}$relation such as in Yakovlev et al. (2004) there is no point in doing this analytically. As noted such relations can however be approximated reasonably well by $T_{\rm i,9}\simeq 0.1~T_{\rm S,6}^2$ which allows a physically transparent interpretation.

We will use Eqs. (10) and (11) to compare superbursters and soft X-ray transients so writing  $\alpha_{\rm SB}$ for the left hand side scaled to fit the superburst data and dropping the subscript on the soft X-ray transient parameters we get

 
$\displaystyle T_{\rm S,6}=10^{1/2}\left[\alpha_{\rm SB} \left(\frac{K_{\rm 20,S... ...}}\right)^{1/2}\frac{\langle\dot{m}\rangle}{0.3~\dot{m}_{\rm Edd}}\right]^{1/9}$     (12)
$\displaystyle \alpha_{\rm SB}=0.2\left(\left(\frac{T_{\rm i,9}}{0.7}\right)^{9/... ...\frac{\langle\dot{m}\rangle}{0.3~\dot{m}_{\rm Edd}}\right]^{-1}\right)_{\rm SB}$     (13)

in the non-isothermal case and correspondingly in the isothermal case
 
$\displaystyle T_{\rm S,6}=10^{1/2}\left[\alpha_{\rm SB} \left(\frac{R_{\rm 6,SB}}{R_6}\right)\frac{\langle\dot{m}\rangle}{0.3~\dot{m}_{\rm Edd}}\right]^{1/16}$     (14)
$\displaystyle \alpha_{\rm SB}=0.058\left(\left(\frac{T_{\rm i,9}}{0.7}\right)^{... ...{\langle\dot{m}\rangle}{0.3~\dot{m}_{\rm Edd}}\right]^{-1}\right)_{\rm SB}\cdot$     (15)

As a last possibility we note from Fig. 1 that solutions can be found with non-isothermal superbursters and isothermal soft X-ray transients. In this case we use  $K_{\rm crit}$ in Eq. (6) to obtain a relation between  $Q_{\rm SQM}$ and $Q_\nu $ which when inserted in Eq. (7) gives
 
$\displaystyle T_{\rm S,6}=10^{1/2}\left[\alpha_{\rm SB} \frac{\langle\dot{m}\rangle}{0.3~\dot{m}_{\rm Edd}}\right]^{1/9}$     (16)
$\displaystyle \alpha_{\rm SB}=0.154\left(\left(\frac{T_{\rm i,9}}{0.7}\right)^{... ...{\langle\dot{m}\rangle}{0.3~\dot{m}_{\rm Edd}}\right]^{-1}\right)_{\rm SB}\cdot$     (17)

These expressions can be used to test the constancy of the quark core parameters when going from superbursters to soft X-ray transients, with $\alpha_{\rm SB}$ incorporating the constraints imposed by superbursters. We note that small variations in the quantities in square brackets will be strongly suppressed and specifically it will not matter whether we use a canonical mass radius relation for neutron stars to find the accretion rate or one more relevant to strange stars where the radius may be smaller by a few kilometers. This would translate into a temperature correction of about one percent which is far below the observational uncertainty so we can use the accretion rates in the literature even though they are derived for neutron stars. There is also no reason to expect that $(R_{\rm 6,SB}/R_6)^{1/16}$ will deviate much from unity so we drop this in the following. The $(K_{\rm SB}/K)^{1/18}$ term can give a factor $\sim$0.9 if K depends on the temperature and $\alpha_{\rm SB}\la 0.2$ so we keep both of these terms but note that uncertainties in these parameters are strongly suppressed too.

  
4 Comparison with observations

Table 1: Properties of the observational sample commonly used to test deep crustal heating. The temperature quoted for Aql X-1 is the redshifted  $T_{\rm S}^\infty $. We use $T_{\rm S}=T_{\rm S}^\infty /(1-2GM/R)^{1/2}$ with the canonical M/R=0.2. For Cen X-4 we quote the temperatures from both Rutledge et al. (2001) and Campana et al. (2004).


  \begin{figure} \par\includegraphics[width=16.8cm,clip]{5241fig2.ps} %\end{figure} Figure 2: Left: comparing cooling by a non-isothermal (dashed and dot-dashed; cf. Eq. (12)) and isothermal (dashed-doubledot and solid; cf. Eq. (14)) core to the observations in Table 1. For Cen X-4 the quoted temperature intervals overlap. Right: the "mixed'' case with non-isothermal superbursts and isothermal soft X-ray transients (dashed and solid; cf. Eq. (16)) and photon cooling (dotted) assuming a pure blackbody with  $Q_{\rm SQM}$ as labelled for each curve.
Open with DEXTER

The observational sample most commonly used to test relations for deep crustal heating such as Eqs. (14) and (12) consists of soft X-ray transients in the field with short outburst durations and recurrence times, for which X-ray observations in quiescense have determined or limited the surface temperature. The outburst duration should be short so the crust has not been significantly heated by the release of nuclear energy from the accreted matter and the surface temperature is therefore set by deep crustal heating. The recurrence time should be short enough that at least a few outbursts have been observed allowing a reasonable estimate of the time averaged accretion rate - although one should remember that the last 37 years of X-ray observations are not necessarily representative of the $\sim$104 years of accretion history needed to reach thermal equilibrium. Similarly since the accretion history for stars in globular clusters is uncertain one should only use systems in the field.

Useful lists of such systems and their properties including references can be found in e.g. Yakovlev et al. (2003) and Tomsick et al. (2004). We will take this data, summarized in Table 1, as our observational basis and briefly discuss each system below. The best examples of such systems are Aql X-1, Cen X-4 and 4U 1608-522 being short outburst field soft X-ray transients with detected thermal components. Tomsick et al. (2004) discuss the outburst history of these sources and we cite their accretion rates which are based on the review of soft X-ray transient activity by Chen et al. (1997) using

 \begin{displaymath} \langle\dot{m}\rangle=\frac{\bar{L}_{\rm Peak}Nt_{\rm\rm o}f}{\epsilon c^2 (33\mbox{ yr})} \end{displaymath} (18)

where $\bar{L}_{\rm Peak}$ is the time averaged peak outburst luminosity, N is the number of outbursts, f=0.4 is a factor which accounts for the shape of the light curve, $\epsilon=0.2$ is the fraction of rest mass energy released during the accretion and the time average is taken over 33 years of observation. Aql X-1, Cen X-4 and 4U 1608-522 have gone though 21, 2 and 16 outburst respectively between 1969 and 2003 allowing estimates of the accretion rate. Temperatures are found from spectral fits to absorbed neutron star atmosphere models assuming a mass of  $1.4~{M}_\odot$ - this also yields the best fit radius cited. Cen X-4 and some observations of Aql X-1 further require a power law component possibly indicating residual accretion during quiescense.

For SAX J1808.4-3658, SAX J1810.8-2609 and XTE J2123-058 no thermal components have been detected and so we only cite upper limits to the surface temperature. SAX J1810.8-2609 and XTE J2123-058 have each shown only one outburst so the accretion rate is actually an upper limit. The accretion rate cited for SAX J1808.4-3658 is based on the two outbursts in 1996 and 1998, but further outburst have ocurred in 2000, 2002 and 2005 (see Wijnands 2004, for a review). These systems are therefore not expected to agree well with the theory, but at least the upper limits to their surface temperatures should not lie significantly below the prediction of deep crustal heating if they have accreted for long enough to have reached thermal equilibrium.

XTE J1709-267 lies 9-10 arcmin from NGC 6293 which has a tidal radius of 14.2 arcmin and so may be associated with this globular cluster although distance measurements are inconclusive on this (Jonker et al. 2004). It has shown two outbursts since 1995 and has a varying power law component.

As should be clear from the discussion above the data is rather uncertain and should be treated with some caution. In particular the time averaged accretion rates are hardly more than estimates, and the surface temperatures, when they can be found, are uncertain and may not only reflect deep crustal heating. Nevertheless deep crustal heating should provide a minimum temperature for systems that have accreted long enough and so we should at least test for consistency with the observations if not perfect agreement. In Fig. 2 we plot the data from Table 1 and compare with photon cooling curves as well as Eqs. (12), (14) and (16), that assume neutrino cooling, for values of  $\alpha_{\rm SB}$corresponding to  $\dot{m}_{\rm SB}=0.1$ and  $0.3 ~\dot{m}_{\rm Edd}$.

The overall agreement with our predictions from neutrino emission in superbursts is not impressive. Except Aql X-1 and 4U 1608-522 the observations fall significantly below the predicted temperature for neutrino cooling, and actually pure photon cooling does better if $Q_{\rm SQM}\la 1$ MeV although it should not be dominant for the high accretion rates in Aql X-1 and 4U 1608-522. This raises two issues.

First it is noteworthy that the two sources which fall close to the superburst prediction without photon cooling, are the hottest and most frequently accreting sources thus resembling superbursters the most. In turn this raises the question whether the accretion history may lead to heating with a pronounced time dependence and whether the time averaged accretion rate is then still a good predictor for the temperature - we discuss this possibility in the next section.

  \begin{figure} \par\includegraphics[width=17.6cm,clip]{5241fig3.ps} %\end{figure} Figure 3: Left: comparing combined photon and neutrino cooling of an isothermal core (solid; cf. Eq. (22)) to the observations in Table 1 with $Q_{\rm SQM}$ as labelled for each curve. For reference we also show curves with neutrino cooling only (dashed; cf. Eq. (14)) and photon cooling only (dotted). The curves assuming $Q_{\rm SQM}=100$ MeV and neutrino cooling only are nearly identical. For Cen X-4 the quoted temperature intervals overlap. Right: corresponding curves for a non-isothermal core.
Open with DEXTER

Second we see that if $Q_{\rm SQM}$ is sufficiently low, photon emission from the surface may be very important and so we should combine the two cooling mechanisms. Thus we now demand - similarly to the procedure in Yakovlev et al. (2003) - $L_{\rm DH}=4\pi R^2\dot{m}Q_{\rm SQM}=L_\gamma+L_\nu$ where $L_{\rm DH}$ is the luminosity required to carry away the energy released by deep crustal heating and $L_\gamma=4\pi R^2\sigma T_{\rm S}^4$ is the usual blackbody luminosity. Following the calculation that leads to Eq. (6) the non-isothermal neutrino luminosity is

 \begin{displaymath}L_\nu=4\pi R^2\cdot0.3~ \dot{m}_{\rm Edd}\cdot 100 \mbox{ MeV... ..._{\rm i,9}}{0.87}\right)^{9/2} Q_{\nu,21}^{1/2} K_{20}^{1/2} . \end{displaymath} (19)

Neutrino cooling should dominate in superbursters, $L_{\rm DH}=L_\nu$ with $T_{\rm i,9}^{\rm SB}=0.7$, so using the constraints this imposes on the core parameters Eq. (19) gives

 \begin{displaymath}L_\nu=4\pi R^2\left(\frac{T_{\rm i,9}}{0.7}\right)^{9/2}~\dot{m}_{\rm SB}~Q_{\rm SQM} , \end{displaymath} (20)

and using $T_{\rm i,9}=0.1~T_{\rm S,6}^2$ the condition $L_{\rm DH}=4\pi R^2\dot{m}Q_{\rm SQM}=L_\gamma+L_\nu$ then becomes

 \begin{displaymath}\dot{m}~Q_{\rm SQM}=\left(\frac{0.1}{0.7}\right)^{9/2} \dot{m}_{\rm SB}~Q_{\rm SQM} T_{\rm S,6}^9+\sigma T_{\rm S}^4 . \end{displaymath} (21)

Correspondingly in the isothermal case

 \begin{displaymath}\dot{m}~Q_{\rm SQM}=1.8\times 10^{-7} \dot{m}_{\rm SB}~Q_{\rm SQM} T_{\rm S,6}^{16}+\sigma T_{\rm S}^4 . \end{displaymath} (22)

This can be solved numerically and in Fig. 3 we show representative solutions for a range in  $Q_{\rm SQM}$ and compare with pure photon and neutrino cooling. We see that photon cooling dominates at low accretion rates and low $Q_{\rm SQM}$whereas for high accretion rates and  $Q_{\rm SQM}$ we recover the neutrino cooling curves relevant to superbursters. In particular we note that $Q_{\rm SQM}=0.4~\mbox{MeV}$ while still fulfilling the superburst requirements at high accretion rates provides a close fit to some of the sources at low accretion rates that were difficult to explain with neutrino cooling alone. In this case other processes must be heating the surfaces of Aql X-1 and 4U 1608-522 though.

Brown et al. (1998) similarly found that deep crustal heating of neutron stars could explain the quiescent emission from Cen X-4 if only 0.1 MeV of the energy released by pycnonuclear reactions during an outburst was conducted into the core and deposited there. Yakovlev et al. (2004,2003) instead interpreted Cen X-4 and SAX J1808.4-3658 as massive neutron stars with enhanced neutrino emission. In the context of strange stars the energy is deposited directly in the core, but no enhanced neutrino cooling is required if the quark matter binding energy $Q_{\rm SQM}$ is small.

  
5 Time dependence of the mass transfer rate

The quiescent luminosity from some of the sources discussed here (i.e. Aql X-1 (Rutledge et al. 2002a), and Cen X-4 (Campana et al. 2004,1997; Rutledge et al. 2001; van Paradijs et al. 1987)) have been found to vary by factors of a few on timescales of days to years raising the question of how time dependent the heating mechanism is following an outburst. Furthermore the time dependence of the heating mechanism may be important in sources with long recurrence times and help explain their relatively low temperatures reducing the need to keep $Q_{\rm SQM}$ small.

To fully demonstrate either of these points would require a detailed time dependent model for cooling strange stars, which is beyond our scope here. Thus the calculations below are concerned only with the time dependence of the tunneling rate - and hence the heating - following an outburst, but we note that with respect to its consequences for the surface temperature we may be guided by similar considerations for neutron stars.

In neutron stars heat is released during and after an accretion event at the depth and on the time scale (months for the pycnonuclear reactions) corresponding to the individual electron captures, neutron emissions and pycnonuclear reactions. It then takes about 1 yr for the heat from the pycnonuclear reactions to diffuse to the surface (Ushomirsky & Rutledge 2001; Brown et al. 1998) and since it spreads out along the way, it is seen there as a heat wave lasting approximately the thermal diffusion time to the surface. Ushomirsky & Rutledge (2001) investigated the time dependence of this process for 1-day long outbursts, and found that energy deposited at depths, where the diffusion time to the surface was shorter than the outburst recurrence time, could produce significant variations in the surface luminosity following a pattern in time corresponding to the diffusion time for each nuclear reaction. If for instance the recurrence time was 1 year and assuming a low thermal conductivity in the crust, the luminosity variations were a few percent of the average, and only one heat wave could be seen because the diffusion time from the depth of the pycnonuclear reactions was on the order of the recurrence time. If the recurrence time was 30 years the variations in the luminosity could be up to 30 percent for cores with standard cooling and a factor of 3-4 for cores with accelerated cooling (e.g. pion condensates). In this case two separate heat waves were seen - one corresponding to electron captures in the outer crust visible a few days after the outburst and the other to the pycnonuclear reactions deeper in the crust emerging about a year later. For higher thermal conductivity variations were larger and happened on shorter time scales.

By analogy if the tunneling rate at the bottom of the crust - and hence the heating - is sufficiently time dependent following an accretion event, we would expect the qualitative conclusions in Ushomirsky & Rutledge (2001) to apply, possibly leading to strong variations in the surface temperature following an outburst as the resulting heat waves reach the surface. One difference may be though that in strange stars the heat is released at a lower density in the crust with a shorter diffusion time to the surface so the two heat waves may be closer in time.

The transfer of mass from crust to core by tunneling takes place at a rate of (Stejner & Madsen 2005; Alcock et al. 1986)

 
              $\displaystyle \frac{{\rm d}M_{\rm C}}{{\rm d}t}$ = $\displaystyle -m_{\rm N}N_{\rm ion}\times \nu\times \tau(\rho_{\rm b})$  
  = $\displaystyle -4\pi R^2d~\rho_{\rm b}\times \nu\times \tau(\rho_{\rm b})$ (23)
  = $\displaystyle -23.8\frac{\rho_{\rm b}}{\rho_{\rm D}}\tau(\rho_{\rm b})~{M}_\odot~\mbox{s}^{-1}$  

where $m_{\rm N}$ is the mass of ions at the bottom of the crust, $N_{\rm ion}$is the number of such ions whose motion allow them to strike the Coulomb barrier taken to be the number within one lattice distance, $d\sim 200$ fm, $\rho_{\rm b}$ is the density at the bottom of the crust, $\nu\la 1$ MeV is the frequency of this motion and $\tau(\rho)$ is the transmission rate. In Stejner & Madsen (2005) we found that the transmission rate can be approximated by
 
                      $\displaystyle \log{\tau(\rho)}$ = $\displaystyle -51Z\sqrt{\frac{2}{\Delta\phi_{\rm g}}}\Bigg[\arccos{\left(\frac{m_{\rm N}\Delta\phi_{\rm g}}{Ze\phi_{\rm e}(R_{\rm S})}\right)^{1/2}}$  
    $\displaystyle -\left(\frac{m_{\rm N}\Delta\phi_{\rm g}}{Ze\phi_{\rm e}(R_{\rm S... ...rm N}\Delta\phi_{\rm g}}{Ze\phi_{\rm e}(R_{\rm S})}\right)^2\right)^{1/2}\Bigg]$ (24)
$\displaystyle \Delta\phi_{\rm g}$ = $\displaystyle 1.9\times 10^{-4} \left(\frac{\rho_{\rm b}}{\rho_{\rm D}}\right)^{1/3}\left(\frac{56}{A}\right)^{4/3}\sqrt{Z^{8/3}-1}$ (25)

where Z is the ion charge number, A is the mass number, $e\phi_{\rm e}(R_{\rm S})$ is the height of the Coulomb barrier (i.e. the electric potential at the core surface, $R_{\rm S}$) and $\Delta\phi_{\rm g}=\phi_{\rm g}(R)-\phi_{\rm g}(R_S)$ is the difference in the (Newtonian) gravitational potential between the surface of the star and the core. We plot this behaviour in Fig. 4 assuming $e\phi_{\rm e}(R_{\rm S})=20\mbox{ MeV}$ and the crust composition in Haensel & Zdunik (2003) ( 106Ge at maximum density). From Eq. (23) a star accreting  $10^{-10}~{M}_\odot~{\rm yr}^{-1}$ must have $\log{\tau} \lesssim -42$ in equilibrium, so as previously mentioned the tunneling rate close to equilibrium is very sensitive to the density.


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{5241fig4.ps} \end{figure} Figure 4: Plot of Eq. (24) assuming $e\phi _{\rm e}(R_S)=20$ MeV and 106Ge at the crust boundary. Note that for this barrier height the gap width goes to zero and $\tau $ to 1 somewhat below the neutron drip density, which can then not be reached.
Open with DEXTER

Equation (2) gives a relation between $M_{\rm C}$ and  $\rho_{\rm b}$ so we can solve Eq. (23) to find the crust mass and tunneling rate for given accretion scenarios. Assuming the same parameters as in Fig. 4 we show a solution in Fig. 5 with 10 day long accretion outbursts separated by quiescent intervals of 30 years and an average accretion rate of $1.9\times 10^{-11}~{M}_\odot~\mbox{ yr}^{-1}$ - roughly corresponding to Cen X-4. We start the integration with a crust mass sufficiently low that the tunneling rate is negligible and let it build up until the mass transferred to the core during each cycle matches the average accretion rate. At this point the crust mass is at its maximum - as determined by the choice of $e\phi _{\rm e}(R_S)=20$ MeV - during the accretion outbursts and then relaxes to a state with very little tunneling within about a year after each outburst. Figure 6 shows the corresponding result for a system resembling Aql X-1 accreting 10 in every 220 days with an average accretion rate of  $10^{-10}~{M}_\odot~\mbox{yr}^{-1}$. Here we more clearly see the crust reach a maximum mass during the 10 day long outbursts.


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{5241fig5.ps} \end{figure} Figure 5: A crude model of Cen X-4. Crust mass in a system accreting with 10 day long accretion outbursts separated by quiescent intervals of 30 years and an average accretion rate of $1.9\times 10^{-11}~{M}_\odot~{\rm yr}^{-1}$. The inset shows a few equilibrium cycles. The peaks seen here have a flat top which is not resolved in time on the scale shown.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{5241fig6.ps} \end{figure} Figure 6: A crude model of Aql X-1. Crust mass in a system accreting with 10 day long accretion outbursts separated by quiescent intervals of 220 days and an average accretion rate of $10^{-10}~{M}_\odot~{\rm yr}^{-1}$. The inset shows a few equilibrium cycles.
Open with DEXTER

Thus practically all the heating takes place during and immediately after the outburst when the transfer rate is essentially the accretion rate, and the heating mechanism is indeed extremely time dependent. In systems such as Aql X-1 and 4U 1608-522 the outburst recurrence time is comparable to the diffusion time to the surface however. The heat wave resulting from an accretion outburst will therefore be smeared out, and the crust temperature will not vary significantly between outbursts unless one assumes a high thermal conductivity in the crust, so a steady state model using the average accretion rate should be able to predict the temperature. Conversely in systems such as Cen X-4 where the recurrence time is significantly longer than the diffusion time to the surface one would expect larger temperature variations following an outburst.

Furthermore in such systems the core - or the surface layers of the core in the non-isothermal case - may have time to cool significantly between outbursts. In this case we would not expect Eqs. (12), (14) and (16) to hold, but if (speculatively) the tunneling rate late in the cycle is a better predictor of the temperature at this point, Eq. (12) assuming neutrino cooling only would actually give a surface temperature around 76 eV for Cen X-4 as observed. The same argument for XTE J1709-267 assuming a 6 year recurrence time would lead to surface temperatures as low as 83 eV. Here the recurrence time may not be quite long enough however, and furthermore the temperature we cite was measured in May 2003 not very long after the March-April 2002 outburst, so the argument may be too simple. The temperature we cite for Cen X-4 was measured in 1997-2000 long after the 1979 outburst so this should provide a more clear-cut case. For the temperature of the three remaining sources to reach their upper bounds in this way with the cited accretion rates, the outburst recurrence times would have to be very long ($\sim$50, 100 and 800 years for SAX J1810.8-2609, XTE J2123-058 and SAX J1808.4-3658 respectively).

This shows how the the time dependence of the heating mechanism may potententially help explain the coldest soft X-ray transients, even if $Q_{\rm SQM}$ is too high for photon cooling to dominate. More work including details on the cooling of the core and the transport properties of both crust and core would be required though to show that it is possible for the temperature to change this rapidly.

  
6 Conclusion

Using a simple scaling argument for the steady state temperature of accreting strange stars we have presented a consistency check between the constraints on strange quark matter derived from superburst ignition conditions, and the temperature of quiescent soft X-ray transients - both assumed to derive from deep crustal heating by transfer of matter from crust to core.

For systems with short recurrence times where the steady state temperature may be expected to be a good approximation we found reasonable agreement assuming neutrino cooling only - although the range of quark matter parameters giving superbursters between the isothermal curves in Fig. 1 is then excluded by soft X-ray transients. Assuming a combination of photon and neutrino cooling for soft X-ray transients, we saw in Fig. 3 that if $Q_{\rm SQM}\la 1$ MeV even the coldest sources may be explained while still fulfilling superburst ignition conditions at high accretion rates.

We further showed that the tunneling rate near the equilibrium crust mass depends sensitively on the crust density and consequently that essentially all the heating takes place during or immediately after an outburst. This points to the need for a fully time dependent model to fit systems with recurrence times significantly longer than the thermal diffusion time to the surface, but if the low level tunneling rate long after the outburst is a better predictor for such systems, it would provide a fit for Cen X-4 assuming only neutrino cooling as well. The upper temperature bounds on SAX J1810.8-2609, XTE J2123-058 and SAX J1808.4-3658 can not be reached for the cited accretion rates in this way unless the recurrence times are very long. This is consistent with the outburst histories of SAX J1810.8-2609 and XTE J2123-058 - one known outburst each - but does not compare well with the $\sim$2 yr recurrence time for SAX J1808.4-3658. Similarly to the situation with neutron stars (Yakovlev et al. 2004; Campana et al. 2002) some form of enhanced cooling would thus seem to be required if SAX J1808.4-3658 has accreted for long enough to heat the core to its equilibrium temperature and  $Q_{\rm SQM}$ is too high for photon cooling to dominate. XTE J1709-267 has an intermediate recurrence time, and its temperature was measured shortly after an outburst making interpretation difficult.

If - as seems reasonable - a combination of the two cooling mechanisms is required to explain the observations we should further note that the constraints imposed by Aql X-1 in Fig. 1 are not relevant since they were derived assuming only neutrino cooling. The requirement that $Q_{\rm SQM}\la 1$ MeV can therefore be met - even if only just - for the quoted range in $Q_\nu $ and K assuming the parameters fit superburst ignition conditions in Fig. 1. Although such fine tuning in the binding energy can not be ruled out it is rather conspicuous, but given the simplicity of our model and that we have not dealt with the uncertainties or the time dependence in detail such quantitative conclusions should be treated with caution. We have attempted to test for consistency, not to determine the quark matter parameters. This would require more detailed modelling, possibly taking the individual accretion history of each source into account, which may alleviate the need to keep  $Q_{\rm SQM}$ small.

Thus even assuming a high $Q_{\rm SQM}$ the model seems consistent for the systems where it should be most credible and with the exception of SAX J1808.4-3658 no clear inconsistency can be demonstrated for the other sources studied here. However SAX J1808.4-3658 is difficult to explain with neutron stars as well, and its precise nature remains to be decided. At this point strange stars thus seem to do no worse than neutron stars in explaining the quiescent emission of soft X-ray transients regardless of the assumed core parameters, and for a low $Q_{\rm SQM}$ they explain even the coldest sources including SAX J1808.4-3658. Because the two cooling mechanisms are important in different accretion regimes it finally seems likely that detailed modelling along with more accurate temperature measurements at low accretion rates would constrain the core parameters further - or perhaps demonstrate a clear inconsistency.

Finally we should not omit a short discussion of the interesting quasi persistent transients KS 1731-260 and MXB 1659-29 (Wijnands et al. 2004; Cackett et al. 2006; Wijnands et al. 2002; Rutledge et al. 2002b; Wijnands et al. 2001,2003). These are systems with prolonged accretion outbursts - 12.5 and 2.5 years duration respectively - and a convincing case has been built for the suggestion that their crusts are significantly heated during these outbursts and brought out of thermal equilibrium with the core. The thermal components in their spectrum therefore show the cooling of the crust to thermal equilibrium and recently Cackett et al. (2006) using new Chandra and XMM-Newton data found that both systems are now close to equilibrium allowing the core temperatures and thermal cooling time scales of the crusts to be determined. Fitting the cooling curves with an exponential decay towards a constant temperature presumably reflecting the core temperature the constant was found to be $71.3\pm 1.6$ eV for KS 1731-260 and $52.1\pm 1.6$ eV for MXB 1659-29 at infinity. Using a canonical mass-radius relationship this implies surface temperatures of $93.1\pm 2.1$ eV and $68.0\pm 2.1$ eV respectively, so these sources are both cold but not unusually so. Only upper limits to the accretion rates can be established with any certainty however due to the very limited number of observed outbursts. For KS 1731-260 (one outburst in 1988-2001) this is  $5.1\times 10^{-9}~{M}_\odot~\mbox{yr}^{-1}$ (Yakovlev et al. 2003) using the time-averaged flux of Rutledge et al. (2002b). For MXB 1659-29 Wijnands et al. (2003) find bolometric fluxes of $5{-}10\times 10^{-10}~\mbox{erg~cm}^{-2}~\mbox{s}^{-1}$ for the 1999-2001 outburst and $2{-}12\times 10^{-10}~\mbox{erg~cm}^{-2}~\mbox{s}^{-1}$ for the 1976-1979 outburst which using the highest of these values in Eq. (18) (with f=1) means an upper limit of  $1.6\times 10^{-10}~{M}_\odot~\mbox{yr}^{-1}$ for a distance of 10 kpc. Referring to Fig. 3 both of these limits are very high given the surface temperatures, and would require enhanced cooling for both strange stars and neutron stars - but then the accretion rates are hardly certain enough to back up such a claim. Perhaps more interesting the e-folding times for the crust temperature relaxing back to the core temperature were determined both sources. Both of these were rather short ( $246 \pm 62$ days for KS 1731-260 and $501\pm 61$ days for MXB 1656-29) and by comparison with the neutron star cooling curves computed by Rutledge et al. (2002b) for the accretion history of KS 1731-260 may be taken as evidence for high thermal conductivity in the crust. Strange stars are missing the deep crust between 1011 and  $10^{15}~\mbox{g~cm}^{-3}$ and as we have seen there is very little tunnelling in quiescence, so although it would go too far to show this in detail here, it should be safe to assume that they cool faster than neutron stars relaxing the need for high thermal conductivity in the crust. This new development therefore further underlines how rewarding a time dependent model for accreting strange stars might be.

Acknowledgements
This work was supported by The Danish Natural Science Research Council.

References

 
Copyright ESO 2006