A&A 458, 417-426 (2006)
DOI: 10.1051/0004-6361:20065187
S. Muller1,2 - M. Guélin 2 - M. Dumke3,2 - R. Lucas2 - F. Combes4
1 - Academia Sinica Institute of Astronomy and Astrophysics (ASIAA), PO Box 23-141, 106 Taipei, Taiwan
2 -
Institut de RadioAstronomie Millimétrique (IRAM), 300 rue de la piscine, 38406 St-Martin-d'Hères, France
3 -
European Southern Observatory (ESO), Alonso de Cordova 3107, Casilla 19001, Santiago 19, Chile
4 -
Observatoire de Paris, LERMA, 61 Av. de l'Observatoire, 75014 Paris, France
Received 13 March 2006 / Accepted 26 July 2006
Abstract
With the Plateau de Bure interferometer, we have measured
the C, N, O and S isotopic abundance ratios in the arm of a spiral
galaxy with a redshift of 0.89. The galaxy is seen face-on according
to HST images. Its bulge intercepts the line of sight to the
radio-loud quasar PKS 1830-211, giving rise at mm wavelengths to two
Einstein images located each behind a spiral arm. The arms appear in
absorption in the lines of several molecules, giving the opportunity
to study the chemical composition of a galaxy only a few Gyr old. The
isotopic ratios in this spiral galaxy differ markedly from those
observed in the Milky Way. The 17O/18O and 14N/15N
ratios are low, as one would expect from an object too young to let
low mass stars play a major role in the regeneration of the gas.
Key words: quasars: individual: PKS 1830-211 - quasars: absorption lines - astrochemistry - galaxies: ISM - abundances - ISM: molecules - ISM: abundances
The C, N, O, S isotopic abundances are enlightening relics of the interstellar medium (ISM) past history. Not only are these elements the most abundant ones after H and He, but they are those whose synthesis in stars has been the best investigated. The CNO isotopes are tentatively classified into primary elements (12C, 16O, ...), formed directly by He burning, and secondary ones (13C, 14N, 17O, ...) formed at a later stage from primary elements, e.g. through the CNO cycles. In simple evolution models, the fraction of secondary elements increases with time. Actually, chemical evolution is not so straightforward and we know that isotopes like 14N and perhaps 13C are already in part produced in the first generation of stars.
Whereas isotopic abundances can be precisely measured in the Sun and on the Earth, their values in the Galactic ISM and, mostly, in the extragalactic ISM are hard to derive. In a pioneering work, Penzias and co-workers (Penzias et al. 1980, 1981) used the millimeter (mm) emission lines of molecular isotopologues to infer the isotopic ratios in a dozen molecular sources. They found significant differences between the Solar System, the local ISM, the Galactic Center and circumstellar envelopes that they interpreted in terms of degree of nuclear processing, the Solar System representing the state of the local ISM some 4.5 Gyr ago. This picture of the Galactic ISM remains essentially valid today, although it has been recognized that the molecular ratios involving D and 13C are affected by isotopic fractionation or selective photodissociation and may not reflect the elemental isotopic abundance ratios (Wilson & Matteucci 1992).
So far, only a few isotopic abundance ratios have been reported in external galaxies. Those are mostly the C, N, O and S isotopic ratios derived in the nuclei of four nearby starburst galaxies, M 82, IC 342, NGC 253 and NGC 4945, from the mm emission of CO, CS and HCN (Henkel & Mauersberger 1993; Henkel et al. 1998; Chin et al. 1999; Wang et al. 2004; Martín et al. 2005). These ratios are very uncertain due to beam dilution, because the lines of the rare isotopologues are weak, and because the line opacity of the main isotopologues is unknown. Moreover, the studies deal with nuclear regions that may not reflect the disk ISM abundances, as is the case in the Milky Way.
Another powerful way of studying the composition of the ISM consists in observing the molecular lines in absorption. The method needs only a strong background source and is insensitive to distance and to primary beam dilution. It yields directly the line opacities, provided the background source is fully covered by the intercepting clouds (e.g. Lucas & Liszt 1998). As far as molecular isotopic ratios are concerned, the method is limited to the line of sight to the brightest radio galaxies and quasars intercepted by deep absorption line systems. Few such absorption systems have been identified so far at millimeter wavelengths. They arise in the Milky Way (Lucas & Liszt 1996, 1998) and in a few distant galaxies with redshifts in the range z = 0.2-0.9(Wiklind & Combes 1994, 1995, 1996; Combes 1999).
In this article, we present high sensitivity absorption spectra arising from
the most remote presently known such system, located at z = 0.89.
The spectra cover the lines of a dozen
of molecular species, including the rare isotopomers HC17O+, H15NC
and C34S. From these spectra, we derive the C, N, O and S isotopic ratios
in the spiral arm of a young, seemingly normal galaxy![]() .
.
PKS 1830-211 is a radio loud quasar with a redshift of z = 2.5 (Lidman et al. 1999),
whose line of sight is intercepted by at least two galaxies: a relatively nearby
one, responsible for narrow HI line absorption at redshift z = 0.19 (Lovell et al.
1996), and a more distant one that gives rise to broad molecular and HI line absorption
at z = 0.89 (Wiklind & Combes 1996, 1998, hereafter WC96 and WC98;
Gérin et al. 1997; Menten et al. 1999; Chengalur et al. 1999;
Muller & Guélin 2003). No molecular absorption is detected in the first galaxy
(WC98) while the latter galaxy acts as
a gravitational lens and gives rise, at radio wavelengths, to two compact sources
(NE and SW) embedded in a faint Einstein ring (see Fig. 3 from Chengalur et al. 1999;
see also Jauncey et al. 1991).
The ring has a steep spectral index and fades away at short wavelengths
(Carilli et al. 1998), so that at mm wavelengths, the quasar image reduces essentially
to the NE and SW sources that are distant by ![]() 1
1
![]() ,
plus two weak "tails''
(Frye et al. 1997; WC98; Carilli et al. 1998).
,
plus two weak "tails''
(Frye et al. 1997; WC98; Carilli et al. 1998).
The z = 0.89 absorption system shows two main velocity components: a broad one at z = 0.88582 (assuming V = 0 km s-1 in heliocentric coordinates), associated with the SW source, and a narrow component, 147 km s-1 lower in velocity, associated with the NE source (Frye et al. 1997; WC98). Although both components are detected in absorption in HI and in molecular lines, the NE component is more conspicuous in the HI line and the SW one in the molecular lines (WC98; Chengalur et al. 1999).
Recently, Winn et al. (2002) have published a HST I-band image of the z = 0.89 lensing
galaxy (see Fig. 1). This latter appears as a typical nearly face-on spiral
(probably of type Sb or Sc).
The low inclination of the galaxy is confirmed by Koopmans & de Bruyn (2005), who modelled
its kinematics from the HI absorption profile and find
![]() .
The bulge of the galaxy is located near the
center of the radio ring. The SW radio source appears to lie right on
top of a spiral arm, at a (model dependent) distance of
.
The bulge of the galaxy is located near the
center of the radio ring. The SW radio source appears to lie right on
top of a spiral arm, at a (model dependent) distance of ![]() 2 kpc
from the center. The NE source lies at about twice this distance
(
2 kpc
from the center. The NE source lies at about twice this distance
(![]() 4 kpc) on the other side of the nucleus. Both absorption
components seem thus to arise in the counterpart of what we call in the
Milky Way the Molecular Ring.
4 kpc) on the other side of the nucleus. Both absorption
components seem thus to arise in the counterpart of what we call in the
Milky Way the Molecular Ring.
Adopting the cosmological parameters H0 = 70 km s-1 Mpc-1,
![]() and
and
![]() ,
the redshift
z = 0.89 corresponds to a lookback time of 7.2 Gyr, yielding an age
,
the redshift
z = 0.89 corresponds to a lookback time of 7.2 Gyr, yielding an age ![]() 6 Gyr for the galaxy. Assuming that the first generation of stars
formed 1 Gyr after the Big Bang, stars with masses <1.5
6 Gyr for the galaxy. Assuming that the first generation of stars
formed 1 Gyr after the Big Bang, stars with masses <1.5![]() barely
had the time to contribute to the enrichment of the interstellar medium.
barely
had the time to contribute to the enrichment of the interstellar medium.
![\begin{figure}
\par {\includegraphics[width=7cm,clip]{5187fig1.eps} }\end{figure}](/articles/aa/full/2006/41/aa5187-06/Timg10.gif) |
Figure 1:
Positions of the SW and NE absorption components as observed with
PdBI in the HCO+ (
|
| Open with DEXTER | |
Table 1: Basic data for PKS 1830-211 and the intervening galaxy.
With the Plateau de Bure Interferometer (PdBI), we have carried out a
high sensitivity and high spectral resolution survey of a dozen of mm
absorption lines in the line of sight to PKS 1830-211. This survey is
the result of a number of 2-4 h-long observing sessions, carried out
between 1999 and 2005 (see Table 2). The antennas were most of the time in a compact
configuration which led to a synthesized beam ![]() 10
10
![]() at
at ![]() GHz (
GHz (
![]() 21
21![]() ), much larger than the source size.
The phase reference was set at
), much larger than the source size.
The phase reference was set at
![]() 39
39
![]() 937,
937,
![]() $^$03
$^$03![]() 39
39
![]() 80 (J2000). The spectral resolution was 1.25 MHz before
2000, and 2 or 4 times better afterwards. For calibration
purpose, a strong continuum source (usually 3C 273 or 3C 345), free of
any absorption at the frequencies of interest was observed for 10 min shortly before and after PKS 1830-211.
80 (J2000). The spectral resolution was 1.25 MHz before
2000, and 2 or 4 times better afterwards. For calibration
purpose, a strong continuum source (usually 3C 273 or 3C 345), free of
any absorption at the frequencies of interest was observed for 10 min shortly before and after PKS 1830-211.
The data were reduced and analyzed with the GILDAS/CLIC software. The data from each observing session were first calibrated for instrumental RF bandpass by fitting a high order polynomial on the spectrum observed for the strong continuum source. We checked that this calibration was accurate to better than 1%.
Next, the spectral data were calibrated in amplitude and phase
with respect to the PKS 1830-211 continuum, whose flux was ![]() 2 Jy
at
2 Jy
at
![]() mm. PKS 1830-211 being unresolved in the
compact antenna configurations, the phases in this process were
referenced to the barycenter of the continuum emission and the
amplitudes normalized to the total continuum flux. Finally, the
spectra observed on the different sessions and with the different
baselines were co-added and a third-degree baseline withdrawn from
the global spectrum, in order to remove small RF bandpass residuals (amplitude
mm. PKS 1830-211 being unresolved in the
compact antenna configurations, the phases in this process were
referenced to the barycenter of the continuum emission and the
amplitudes normalized to the total continuum flux. Finally, the
spectra observed on the different sessions and with the different
baselines were co-added and a third-degree baseline withdrawn from
the global spectrum, in order to remove small RF bandpass residuals (amplitude ![]() 2%) caused by
instrumental drifts and/or strong atmospheric fluctuations.
2%) caused by
instrumental drifts and/or strong atmospheric fluctuations.
The total integration time per line ranges from 1 h to 20 h; the rms noise on the weakest lines is between 2 and 7 mJy per 1.25 MHz channel.
In addition to the compact configuration observations just described,
and which served as the basis of our molecular line survey, we
observed on 2003 February 26th and March 1st the HCO+ (
![]() )
line in the extended A configuration. This configuration
includes 400 m-long E-W and E-NW baselines that allow to spatially
resolve the NW and SW source components. We used a special procedure
to reduce these data. This procedure is described in Sect. 4.1.
)
line in the extended A configuration. This configuration
includes 400 m-long E-W and E-NW baselines that allow to spatially
resolve the NW and SW source components. We used a special procedure
to reduce these data. This procedure is described in Sect. 4.1.
Finally, we also observed on 2003 August 3rd the (
![]() )
line of HCN with
the IRAM 30-m telescope. The spectrum shown in Fig. 3 is the sum
of the 30-m and PdBI data.
)
line of HCN with
the IRAM 30-m telescope. The spectrum shown in Fig. 3 is the sum
of the 30-m and PdBI data.
Using the BIMA array, Frye et al. 1997 (see also Swift et al. 2001)
successfully resolved the two continuum components. They derived
an angular separation of
![]() .
Further evidence that
the NE component was indeed responsible for the second absorption at
V = -147 km s-1 was shown by WC98. They used the BC configuration
of the PdBI and fitted the position of the barycenter of emission
directly from the visibilities.
.
Further evidence that
the NE component was indeed responsible for the second absorption at
V = -147 km s-1 was shown by WC98. They used the BC configuration
of the PdBI and fitted the position of the barycenter of emission
directly from the visibilities.
Our A configuration PdBI observations of the HCO+ (
![]() )
line,
which combine high sensitivity and high angular resolution enable
us to locate with a much higher relative accuracy the velocity
components. For this, we used the following procedure.
)
line,
which combine high sensitivity and high angular resolution enable
us to locate with a much higher relative accuracy the velocity
components. For this, we used the following procedure.
The RF bandpass was first calibrated using the quasar 1749+096 (on
2003 Feb. 26th) or 3C 273 (on 2003 Mar. 1st). Next, the
continuum data on PKS 1830-211 were self-calibrated by calculating the
complex gains (amplitude and phase) corresponding to a point-like
source of flux unity at the phase center. The latter was fixed through
this procedure at the barycenter of the continuum emission. Then, the
calculated gains were applied to the line visibilities and the continuum
was subtracted. The resulting visibilities were fitted by a point source,
channel by channel, to trace the position of the absorption. At this step,
the absorptions at ![]() 147 km s-1 and
147 km s-1 and ![]() km s-1 were already
clearly found to arise from two different locations (NE and SW respectively)
separated by
km s-1 were already
clearly found to arise from two different locations (NE and SW respectively)
separated by
![]() at a position angle of
at a position angle of ![]() 42
42![]() .
.
The whole process was iterated: i) a new input continuum model, consisting of two point-like sources, located at the previously derived NE and SW positions and with fluxes in the ratio 1.7 (see Table 3), was used to self-calibrate the data; ii) the new continuum was subtracted from the calibrated visibilities to yield the amplitude of the absorption and its position in each velocity channel (Fig. 1).
We confirm that the two main absorption components (around V = 0 km s-1and V = -147 km s-1) arise from two distinct compact sources, whose
relative positions, estimated from weighted averages over each component,
are (
![]() ;
;
![]() )
for the NE component and
(
)
for the NE component and
(
![]() ;
;
![]() )
for the SW component.
This corresponds to a separation of
)
for the SW component.
This corresponds to a separation of
![]() and a position angle
of
and a position angle
of
![]() ,
in good agreement with the separation and position
angle of the continuum sources derived from BIMA, MERLIN and VLA observations.
,
in good agreement with the separation and position
angle of the continuum sources derived from BIMA, MERLIN and VLA observations.
One purpose of our extended configuration observations was to check
whether the 80 km s-1-broad absorption component centred at 0 km s-1 was arising entirely from the compact SW image, or if
the line shoulders and/or wings were arising from the dimmer "tails'' and
"knots'' visible at longer wavelengths, or from the weak Einstein ring.
It should be noted that the V = 0 km s-1 HCO+ and HCN absorption
profiles observed at 3-mm at low angular resolution are almost twice broader
than those observed at 6-mm with a 0.1
![]() resolution (Carilli et al. 1998).
resolution (Carilli et al. 1998).
Figure 1 shows that the absorption arises within 0.1
![]() (0.2
(0.2
![]() in
the weak wings of the line) from a point-like source and shows no obvious
velocity/position gradient. In particular, the wing emission at V < -20 km s-1
and V > 20 km s-1, which is not observed in the high resolution VLA and
VLBA observations, does not arise from the "tails'' and "knots'', but comes
from the compact SW "core''.
in
the weak wings of the line) from a point-like source and shows no obvious
velocity/position gradient. In particular, the wing emission at V < -20 km s-1
and V > 20 km s-1, which is not observed in the high resolution VLA and
VLBA observations, does not arise from the "tails'' and "knots'', but comes
from the compact SW "core''.
![\begin{figure}
\par {\includegraphics[width=7cm,clip]{5187fig2.eps} }\end{figure}](/articles/aa/full/2006/41/aa5187-06/Timg34.gif) |
Figure 2:
HCO+ absorption lines observed at different epochs from 1999 to 2002.
For comparison, all spectra have been smoothed to the same spectral resolution of 1.25 MHz ( |
| Open with DEXTER | |
The flux of PKS 1830-211 is known to be variable. For example, van Ommen et al. (1995) report a variation of the 15 GHz flux by a factor of 2 between 1990 and 1991, whereas Wiklind & Combes (1999) observe a similar increase of the 3-mm flux between 1997 and 1998. Although the 3-mm flux was mostly stable and close to 2.5 Jy in the course of our survey, we noted 20-30% changes between 1999 and 2001 and between 2001 and 2002. There was no significant change around August 2002, the period when the HNC line was observed.
A question central to this study is whether the magnification ratio of the NE and SW sources,
![]() ,
is also variable, as this would affect the amplitude
of the V = 0 and -147 km s-1 absorption components with respect to the
continuum flux.
,
is also variable, as this would affect the amplitude
of the V = 0 and -147 km s-1 absorption components with respect to the
continuum flux. ![]() is expected to vary after a sudden increase of the flux
of the background quasar, since the increase will first appear in the NE source,
then in the SW source after a delay
is expected to vary after a sudden increase of the flux
of the background quasar, since the increase will first appear in the NE source,
then in the SW source after a delay
![]() .
The path length from the quasar
to the observer is indeed shorter for the rays passing through the NE source
(Nair et al. 1993).
.
The path length from the quasar
to the observer is indeed shorter for the rays passing through the NE source
(Nair et al. 1993).
![]() has been measured by Lovell et al. (1998) and by
Wiklind & Combes (1999) and found to be about 25 days. Micro-lensing
events caused e.g. by stars may also randomly affect
has been measured by Lovell et al. (1998) and by
Wiklind & Combes (1999) and found to be about 25 days. Micro-lensing
events caused e.g. by stars may also randomly affect ![]() for short periods of time.
for short periods of time.
In order to check for variations of ![]() during the period of our observations,
we have regularly observed the absorption spectrum of the HCO+ (
during the period of our observations,
we have regularly observed the absorption spectrum of the HCO+ (
![]() ) line. Figure 2 shows the line profiles on 4 different epochs. We see no
variations in the lineshape or absorption depth that exceeds the 1-sigma rms
uncertainty (typically a few percent - see Table 3). The 0 km s-1component is known to be saturated in the HCO+ line. Assuming all the emission
near 0 km s-1 comes from the NE source, we derive relative intensities of 37% and 63% for the SW and NE continuum sources, and a magnification ratio
) line. Figure 2 shows the line profiles on 4 different epochs. We see no
variations in the lineshape or absorption depth that exceeds the 1-sigma rms
uncertainty (typically a few percent - see Table 3). The 0 km s-1component is known to be saturated in the HCO+ line. Assuming all the emission
near 0 km s-1 comes from the NE source, we derive relative intensities of 37% and 63% for the SW and NE continuum sources, and a magnification ratio
![]() (Table 3). The lack of obvious variations of
(Table 3). The lack of obvious variations of ![]() during our
observing period simply means that the flux variations over intervals of time of
25 days were either small, or constant.
during our
observing period simply means that the flux variations over intervals of time of
25 days were either small, or constant.
During their 3-year long monitoring of the HCO+ (
![]() )
line with
the 30-m telescope (1996-98) Wiklind and Combes also observed magnification ratios
in the range 1.4-1.7 with only a few excursions to values differing from
)
line with
the 30-m telescope (1996-98) Wiklind and Combes also observed magnification ratios
in the range 1.4-1.7 with only a few excursions to values differing from ![]() by more than 2
by more than 2![]() (1
(1![]() was typically 0.1). Swift et al. (2001) reported
a significantly smaller ratio (1.2) for Dec 1999, but this low ratio comes from the
separation of the two continuum sources in a half-resolved map. Our average ratio is
close to that measured with the VLA at 15 GHz and 23 GHz by Nair et al. (1993) in
1987-1990 (1.5-1.6).
was typically 0.1). Swift et al. (2001) reported
a significantly smaller ratio (1.2) for Dec 1999, but this low ratio comes from the
separation of the two continuum sources in a half-resolved map. Our average ratio is
close to that measured with the VLA at 15 GHz and 23 GHz by Nair et al. (1993) in
1987-1990 (1.5-1.6).
We therefore assumed in the following that the relative fluxes of the NE and SW sources remained constant during our observations and simply co-added, when necessary,
the calibrated spectra observed on different sessions. A variation of ![]() (e.g.
by 20%) for short periods of time is however not excluded: it would merely change
the absorption depths measured on those short periods (by
(e.g.
by 20%) for short periods of time is however not excluded: it would merely change
the absorption depths measured on those short periods (by ![]() 13%). This would
have no significant effect on most isotopic ratios, that average data of different
observing periods (see Table 2).
13%). This would
have no significant effect on most isotopic ratios, that average data of different
observing periods (see Table 2).
Table 3: Measurements of the magnification factors.
Figure 3 presents the absorption profiles for the (
![]() ) lines of HCO+, HCN and HNC. Both the V = 0 km s-1 and V = -147 km s-1 components
are detected in these 3 lines. The V = -147 km s-1 component had been previously
observed by WC98, but only for the HCO+ line and with a lower signal to noise ratio.
) lines of HCO+, HCN and HNC. Both the V = 0 km s-1 and V = -147 km s-1 components
are detected in these 3 lines. The V = -147 km s-1 component had been previously
observed by WC98, but only for the HCO+ line and with a lower signal to noise ratio.
The absorption profiles of the V = 0 km s-1 and V = -147 km s-1 components are not Gaussian.
The HNC (
![]() )
V = 0 km s-1 component consists of at least 3 Gaussian
sub-components (Fig. 5) and the V = -147 km s-1 component of 2 sub-components,
which implies the presence of several clouds in front of the SW and NE sources. The 5 Gaussian sub-components have velocities of
)
V = 0 km s-1 component consists of at least 3 Gaussian
sub-components (Fig. 5) and the V = -147 km s-1 component of 2 sub-components,
which implies the presence of several clouds in front of the SW and NE sources. The 5 Gaussian sub-components have velocities of ![]() -155, -150, -21, -3 and +7 km s-1.
Their widths (
-155, -150, -21, -3 and +7 km s-1.
Their widths (![]() 10-20 km s-1) are typical of the width of Milky Way Giant Molecular Clouds.
10-20 km s-1) are typical of the width of Milky Way Giant Molecular Clouds.
A comparison of the HNC, HCN and HCO+ line profiles suggests a similar set
of clouds with similar relative abundances, but with an increasing opacity
from HNC to HCO+. A modelling of the line opacities, assuming that the SW
source contains 37% of the total continuum flux, as derived in Sect. 3,
and that the source filling factor by the absorbing clouds is close to 1,
yields an opacity
![]() at the peak of the HNC line, and a HCN/HNC
opacity ratio of
at the peak of the HNC line, and a HCN/HNC
opacity ratio of ![]() 3, fairly constant across the entire spectrum, from -160 to +20 km s-1.
3, fairly constant across the entire spectrum, from -160 to +20 km s-1.
![\begin{figure}
\par {\includegraphics[width=7cm,clip]{5187fig3.eps} }\end{figure}](/articles/aa/full/2006/41/aa5187-06/Timg45.gif) |
Figure 3: Spectra of the main isotopomers of HCO+, HCN and HNC ( from top to bottom respectively). The velocity resolution is 2 km s-1. |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=7cm,clip]{5187fig4.eps} }
\end{figure}](/articles/aa/full/2006/41/aa5187-06/Timg46.gif) |
Figure 4:
Spectra of the different species and isotopomers observed for this survey.
From top to bottom: HNC, HCO+, HCN, CS and H2S isotopomers.
The velocity resolution is |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=7cm,clip]{5187fig5.eps} }\end{figure}](/articles/aa/full/2006/41/aa5187-06/Timg47.gif) |
Figure 5:
Line opacity profiles of the
|
| Open with DEXTER | |
| |
Figure 6:
Spectrum observed at the frequency of the DNC (
|
| Open with DEXTER | |
Figure 4 shows the
![]() line profiles of the rare 13C,
15N, 17O and 18O isotopologues of HCO+, HCN and HNC, as
well as those of CS and C34S
line profiles of the rare 13C,
15N, 17O and 18O isotopologues of HCO+, HCN and HNC, as
well as those of CS and C34S
![]() ,
and H2S and H234S
(
,
and H2S and H234S
(
![]() .
For these species, only the SW
absorption is detected. The profiles of HNC and of the rare isotopomers
are not flat-topped, but show narrow peaks near 0 km s-1. They are
not only sharper than those of the main HCO+ and HCN isotopomers,
but also shallower, indicating that they are not saturated. The absorption
lines of H13CO+, HC18O+, H13CN and HC15N
show very similar profiles, while the spectra of CS and H2S look
different: the +7 km s-1 sub-component is much enhanced for those species.
The similarity of the line opacity profiles of H13CO+ and HNC is
illustrated in Fig. 5.
.
For these species, only the SW
absorption is detected. The profiles of HNC and of the rare isotopomers
are not flat-topped, but show narrow peaks near 0 km s-1. They are
not only sharper than those of the main HCO+ and HCN isotopomers,
but also shallower, indicating that they are not saturated. The absorption
lines of H13CO+, HC18O+, H13CN and HC15N
show very similar profiles, while the spectra of CS and H2S look
different: the +7 km s-1 sub-component is much enhanced for those species.
The similarity of the line opacity profiles of H13CO+ and HNC is
illustrated in Fig. 5.
Assuming, again, that the SW source represents 37% of the total flux
and that its filling factor is unity, the line opacity ![]() is given by:
is given by:
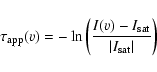 |
(1) |
The flat shape of the HCO+ and HCN profiles around 0 km s-1suggests that the clouds cover entirely the SW source. This coverage,
however, may not be uniform, as the SW source size (![]() 2.5 mas,
Carilli et al. 1998) is
2.5 mas,
Carilli et al. 1998) is ![]() 10 pc at the distance of the galaxy and
presumably large with respect to individual clouds. The apparent
opacities in Eq. (1) are thus strictly speaking lower limits to
the true opacities. However, the similarity of the absorption
profiles in Fig. 4, which yet have very different
opacities, suggests that the true opacities are not large, except for
HCO+ and HCN near 0 km s-1, and that the values derived from
Eq. (1) are close to the true opacities. This is illustrated in
Fig. 5 which shows the opacity profiles of the HNC,
H13CO+ and HC18O+ (
10 pc at the distance of the galaxy and
presumably large with respect to individual clouds. The apparent
opacities in Eq. (1) are thus strictly speaking lower limits to
the true opacities. However, the similarity of the absorption
profiles in Fig. 4, which yet have very different
opacities, suggests that the true opacities are not large, except for
HCO+ and HCN near 0 km s-1, and that the values derived from
Eq. (1) are close to the true opacities. This is illustrated in
Fig. 5 which shows the opacity profiles of the HNC,
H13CO+ and HC18O+ (
![]() )
lines, all of
which are indeed very similar despite their very different opacities.
We note that Carilli et al. (1998)
measure for the HCN (
)
lines, all of
which are indeed very similar despite their very different opacities.
We note that Carilli et al. (1998)
measure for the HCN (
![]() )
line an integrated apparent
opacity
)
line an integrated apparent
opacity
![]() km s-1 for the NE (V = -147 km s-1) component
that is 5 times smaller than our value of 3.5 km s-1 for the
(
km s-1 for the NE (V = -147 km s-1) component
that is 5 times smaller than our value of 3.5 km s-1 for the
(
![]() )
line, demonstrating that the the component is indeed
optically thin.
)
line, demonstrating that the the component is indeed
optically thin.
We have fitted the opacity profiles (e.g. Fig. 5) derived with
Eq. (1) for all the observed species with 4 Gaussian components:
3 for the SW source (
![]() km s-1), and one for the
NE source (
km s-1), and one for the
NE source (
![]() km s-1), which is too weak to be
resolved, except in the HCO+ line.
The fitted parameters (sub-component velocities, peak opacities and
velocity widths) and integrated opacities are listed in Tables 4
and 5 for the SW and NE components, respectively.
The uncertainties on the integrated opacities were estimated as
km s-1), which is too weak to be
resolved, except in the HCO+ line.
The fitted parameters (sub-component velocities, peak opacities and
velocity widths) and integrated opacities are listed in Tables 4
and 5 for the SW and NE components, respectively.
The uncertainties on the integrated opacities were estimated as
![]() where
where
![]() is the rms uncertainty on the opacity for the velocity
resolution
is the rms uncertainty on the opacity for the velocity
resolution ![]() and
and
![]() the half maximum velocity width.
For non detections, upper limits were calculated as 3
the half maximum velocity width.
For non detections, upper limits were calculated as 3
![]() where
where
![]() was taken as the velocity width of the
same component of the main isomer or isotopomer.
was taken as the velocity width of the
same component of the main isomer or isotopomer.
The mean central velocities of the 3 absorption components towards SW are -21, -3 and 7 km s-1, and their mean linewidths are 13, 8 and 10 km s-1. The linewidths of these different components are typical of Giant Molecular Clouds in the Milky Way Molecular Ring.
Note that we could not derive reliable parameters for the rare isotopomer HC15N because of low S/N, and fixed the velocities of 2 Gaussian profiles to -3 and 7 km s-1. For the same reason, the NE absorption of the CS spectrum was fitted with velocity and width fixed to the same values as the HCN NE fit.
Table 5: Fit of the NE opacity profiles.
In order to derive the line opacity ratios and the column density ratios of the different isotopologues, we assume that all the isotopologues from a same molecular species have the same spatial distribution and are similarly excited, hence that their line opacity profiles are similar.
The first hypothesis should be fulfilled, except for the species deeply affected by isotopic fractionation. In cold Galactic clouds, the abundances of molecules bearing 13C and, mostly, D atoms are known to be significantly affected by fractionation reactions and selective photodissociation. This is not the case, however, for the other species (see e.g. Langer et al. 1984), and we will assume that their relative abundances do reflect the elemental isotopic abundance ratios. The hypothesis of similar spatial distribution is not critical in the sense that it yields isotopic ratios averaged over the (small) continuum source, as long as the line is not too optically thick.
The hypothesis of similar excitation is certainly correct for most line
components and species: all the species studied here have large dipole moments
and are hard to excite. Since the bulk of the absorption caused by a cloud >10 pc with N(H
![]() cm-2 (Menten et al. 1999) is
likely to arise in a low density envelope (
cm-2 (Menten et al. 1999) is
likely to arise in a low density envelope (
![]() cm-2),
the molecules are essentially heated by the 5.1 K cosmic background, so that
cm-2),
the molecules are essentially heated by the 5.1 K cosmic background, so that
![]() K. The lines of the main HCO+ and HCN isotopologues,
the opacity of which is large between -10 and +10 km s-1, were not considered
inside this velocity range for the derivation of the isotopic ratios.
K. The lines of the main HCO+ and HCN isotopologues,
the opacity of which is large between -10 and +10 km s-1, were not considered
inside this velocity range for the derivation of the isotopic ratios.
The line opacity ratios derived for the different pairs of isotopologues are shown
in Table 6. These ratios were calculated in the following way: five line
opacity profiles, assumed to be identical for all isotopologues of a given molecular
species, were derived by fitting the line opacity profiles of H13CO+,
H13CN, HNC, CS and H2S with Gaussian components, as explained in Sect. 4.3 (see Fig. 5 and Table 4). Those species
were selected because they are observed with a good signal-to-noise ratio and
have a low or moderate opacity. The fitted opacity profiles were then sampled at
the velocity resolution of the observations and squared to yield weights. The
rare-to-abundant isotope line opacity ratio was then calculated as the weighted
average ![]() of the ratios measured for each velocity channel, in the velocity
ranges
-10 < V < 10 km s-1 (SW absorption line center)
or
-40 < V < -10 km s-1 (SW absorption line wing).
Finally,
of the ratios measured for each velocity channel, in the velocity
ranges
-10 < V < 10 km s-1 (SW absorption line center)
or
-40 < V < -10 km s-1 (SW absorption line wing).
Finally, ![]() was inverted to yield the abundant-to-rare line
opacity ratio,
was inverted to yield the abundant-to-rare line
opacity ratio,
![]() .
.
Similarly, the uncertainties on the line opacity ratios were first estimated
for the rare-to-abundant ratios, R. In all cases, the uncertainties are
dominated by the noise on the rare isotopologue. Then, R can be roughly decribed
as a normal variable of variance ![]() .
The error bars on the inverse
(abundant-to-rare) ratio
.
The error bars on the inverse
(abundant-to-rare) ratio
![]() were then derived as equal to
were then derived as equal to
![]() and +
and +
![]() .
Note that the bars are asymmetric for low signal-to-noise ratios. A more accurate
evaluation of the errors from the likelihood function yields identical results.
The errors quoted in Tables 4 and 6 (1
.
Note that the bars are asymmetric for low signal-to-noise ratios. A more accurate
evaluation of the errors from the likelihood function yields identical results.
The errors quoted in Tables 4 and 6 (1![]() )
reflect the
noise and baseline uncertainties, but not the uncertainties on the magnification
ratio (see Sect. 4.2), which was assumed to remain constant.
)
reflect the
noise and baseline uncertainties, but not the uncertainties on the magnification
ratio (see Sect. 4.2), which was assumed to remain constant.
Within our hypothesis of similar spatial distribution and similar excitation, the values of Table 6, multiplied by the inverse ratio of the square of the line frequencies, reflect the molecular isotopic abundance ratios.
We note that the 12C/13C and 14N/15N ratios derived from different species (e.g. HCN and HNC) and velocity components (e.g. wings vs. center of line) agree within the quoted uncertainties. We come back to this point when we discuss the elemental isotopic ratios individually.
Table 6: Line opacity ratios derived from our PdBI observations.
The elemental isotopic ratios derived by averaging![]() the values of Table 6 are given
in Table 7, where we list, for comparison, the isotopic ratios in a number
of Galactic and extragalactic sources. The former are the Solar System (SS),
whose isotopic ratios probably represent the state of the ISM 4.5 Gyr ago, the
local ISM, the Galactic Center (GC), which can be considered at a later stage
of evolution, and the carbon rich circumstellar envelope IRC+10216 that consists
of material entirely reprocessed in the core of a
the values of Table 6 are given
in Table 7, where we list, for comparison, the isotopic ratios in a number
of Galactic and extragalactic sources. The former are the Solar System (SS),
whose isotopic ratios probably represent the state of the ISM 4.5 Gyr ago, the
local ISM, the Galactic Center (GC), which can be considered at a later stage
of evolution, and the carbon rich circumstellar envelope IRC+10216 that consists
of material entirely reprocessed in the core of a ![]() 2
2 ![]() AGB star. The
latter are giant clouds from the Large Magellanic Could (LMC), that are
characterized by a low metallicity, and the nuclear regions of two nearby
starburst galaxies, NGC 253 and NGC 4945.
AGB star. The
latter are giant clouds from the Large Magellanic Could (LMC), that are
characterized by a low metallicity, and the nuclear regions of two nearby
starburst galaxies, NGC 253 and NGC 4945.
The local ISM values come from Lucas & Liszt (1998) and were derived through absorption measurements against extragalactic continuum sources. They probably refer to the same type of clouds as those observed in our remote galaxy and are the most accurate values of Table 7. The envelope IRC+10216 is probably typical of the matter recycled to the ISM by low-mass stars. It is thought that two-third of the matter presently ejected by the stars in the Galactic ISM comes from such low mass stars. The sequence SS-ISM-GC-IRC+10216 may thus be considered in the first approximation as one of increasing processing of the gas by low-mass stars.
The 12C/13C elemental isotopic ratio is difficult to measure,
since the main 12C isotopologues tend to be saturated when its 13C counterpart becomes detectable. This ratio, on the other hand, can be derived
in our survey from 3 different molecules: HCO+, HCN and HNC. H13CO+,
H13CN and HN13C are all detected in the SW component (V = -3 km s-1component), but both HCO+ and HCN are heavily saturated at the peak of the
line. The 12C/13C ratio can thus be measured only in the line wings
(V <-10 and V > 10 km s-1). The opacity of the HNC line (![]() 2, see Fig. 5)
is low enough to allow an estimate of the 12C/13C ratio even at the
center of the line. Within the uncertainties, we find the same ratio for the 3 molecular species:
2, see Fig. 5)
is low enough to allow an estimate of the 12C/13C ratio even at the
center of the line. Within the uncertainties, we find the same ratio for the 3 molecular species: ![]() 30. The mean isotopic ratio, estimated from a weighted average of the HCO+, HCN and HNC line opacity ratios, is
30. The mean isotopic ratio, estimated from a weighted average of the HCO+, HCN and HNC line opacity ratios, is ![]() ,
where the
uncertainty only reflects the noise and the calibration errors, but not residual
opacity effects linked e.g. to a change in the magnification ratio. Considering
these restrictions, our ratio is in good agreement with that derived by Menten et al.
(1999) from VLA HNC (
,
where the
uncertainty only reflects the noise and the calibration errors, but not residual
opacity effects linked e.g. to a change in the magnification ratio. Considering
these restrictions, our ratio is in good agreement with that derived by Menten et al.
(1999) from VLA HNC (
![]() )
line observations for the same velocity component:
)
line observations for the same velocity component: ![]() 35. The
35. The
![]() HNC line is less optically thick than the
HNC line is less optically thick than the
![]() line, but
the VLA HN13C spectrum has a lower velocity resolution and is noisier than
our spectra.
line, but
the VLA HN13C spectrum has a lower velocity resolution and is noisier than
our spectra.
The relative abundances of 12C and 13C can be affected by isotopic
fractionation (Lucas & Liszt 1998). Milam et al. (2005), however, argue that
the effects are limited and should not affect the isotopic ratios at the scales
involved here. The agreement between the ratios derived from three different
species and from two lines of the same species gives us confidence that the
12C/13C ratio in the SW source is indeed close to 27. Unfortunately,
none of the 13C species is detected in the NE component (V = -147 km s-1).
The upper limit on H13CO+ yields a 3![]() lower limit to the
HCO+/H13CO+ ratio of 31, close to the value of this ratio in the SW
component.
lower limit to the
HCO+/H13CO+ ratio of 31, close to the value of this ratio in the SW
component.
The interpretation of the 12C/13C ratio in terms of nucleosynthesis is also not straightforward. 12C is a primary product of helium burning in intermediate and massive stars. 13C forms from 12C through the CNO cycles in the H-burning shell. It may form in the H-burning shell of the very massive stars that produce 12C and/or could be produced later in a second generation of intermediate or low mass stars (Prantzos et al. 1996). In the later scheme, the abundance of 13C relative to 12C is expected to increase with time and the degree of processing of the gas; yet the observed 12C/13C ratio is not significantly lower in the IRC+10216 envelope than in the local interstellar medium (45 vs. 59, see Table 7) which suggests that 13C behaves at least partly as a primary element. Thus, the low value of the 12C/13C ratio in the z = 0.89 galaxy may not be very meaningful.
A direct measurement of the 14N/15N ratio is even more difficult
than for the 12C/13C ratio, as it is larger. We derive this ratio
directly from HNC for the V = -3 km s-1 component, or indirectly from the
double (H13CN/HC15N
![]() C/13C] ratio. The isotopic ratios
we arrive at are consistent and yield an average ratio 14N/15N =
C/13C] ratio. The isotopic ratios
we arrive at are consistent and yield an average ratio 14N/15N =
![]() ,
a factor of two smaller than its Solar System and local ISM values.
,
a factor of two smaller than its Solar System and local ISM values.
The relative abundances of 14N and 15N are strongly affected
by nuclear processing. In low mass stars, where the temperature of the
H-burning zone is ![]() 108 K, the cold CNO cycles convert essentially C, N and O into 14N and destroy most of 15N. In massive stars,
15N is produced at equilibrium through the hot CNO cycle. In explosive
episodes that mark the end of those stars (novae and supernovae), 14N
is quickly converted into 15N and 18O. As a result, the
14N/15N ratio is a sensitive probe of the type of stars governing
the nucleosynthesis; it should increase with the degree of processing by
low mass stars. Indeed, 14N/15N is found to be much larger in the
Galactic Center region than in the local ISM or in the Solar System and
reaches an even larger value in the circumstellar shell IRC+10216
(Table 7). In contrast, the low ratio measured toward PKS 1830-211 fits
well with the scenario where low mass stars played almost no role in the
composition of the ISM in the z = 0.89 galaxy.
108 K, the cold CNO cycles convert essentially C, N and O into 14N and destroy most of 15N. In massive stars,
15N is produced at equilibrium through the hot CNO cycle. In explosive
episodes that mark the end of those stars (novae and supernovae), 14N
is quickly converted into 15N and 18O. As a result, the
14N/15N ratio is a sensitive probe of the type of stars governing
the nucleosynthesis; it should increase with the degree of processing by
low mass stars. Indeed, 14N/15N is found to be much larger in the
Galactic Center region than in the local ISM or in the Solar System and
reaches an even larger value in the circumstellar shell IRC+10216
(Table 7). In contrast, the low ratio measured toward PKS 1830-211 fits
well with the scenario where low mass stars played almost no role in the
composition of the ISM in the z = 0.89 galaxy.
Because its value is very large, the 16O/18O ratio is usually
measured through the double [13C/12C
![]() O/18O] ratio.
The value we derive in this way,
O/18O] ratio.
The value we derive in this way, ![]() 60, is very low compared to the
Solar and interstellar values (
60, is very low compared to the
Solar and interstellar values (![]() 600), even though allowance should
be made for a possible underestimation of 12C/13C, due to
fractionation or residual opacity effects. That the actual ratio is low
is confirmed by our direct measurement of the H12C16O+/H12C18O+ ratio in the wings of the SW component (Table 6), which also yields
600), even though allowance should
be made for a possible underestimation of 12C/13C, due to
fractionation or residual opacity effects. That the actual ratio is low
is confirmed by our direct measurement of the H12C16O+/H12C18O+ ratio in the wings of the SW component (Table 6), which also yields ![]() 60. This result is surprising because both 16O and 18O
form in massive stars and are predicted to behave about similarly, except
at early ages, since 16O is a primary element and 18O a secondary
element. And indeed, the 16O/18O ratio is found to decrease mildly
or not at all between the local ISM to the Galactic Center (see Table 7
and Polehampton et al. 2005). At early ages, the 16O/18O ratio is
supposed to be larger (Prantzos et al. 1996). The 16O/18O ratio in
the Solar System, 1.6 times smaller than in the ISM, is however a well known
puzzle in this context and is sometimes interpreted by an overabundance of 16O in the Solar Nebula.
60. This result is surprising because both 16O and 18O
form in massive stars and are predicted to behave about similarly, except
at early ages, since 16O is a primary element and 18O a secondary
element. And indeed, the 16O/18O ratio is found to decrease mildly
or not at all between the local ISM to the Galactic Center (see Table 7
and Polehampton et al. 2005). At early ages, the 16O/18O ratio is
supposed to be larger (Prantzos et al. 1996). The 16O/18O ratio in
the Solar System, 1.6 times smaller than in the ISM, is however a well known
puzzle in this context and is sometimes interpreted by an overabundance of 16O in the Solar Nebula.
The 18O/17O ratio, which is small and stems from lines that are certainly optically thin, may be more accurately derived. According to the current nucleosynthesis models, the 16O/18O and 16O/17O isotopic ratios are sensitive indicators of the stellar mass, 18O being essentially formed and released by short-lived massive stars while 17O comes mostly from long-lived low-mass stars (see e.g. Landré et al. 1990; Prantzos et al. 1996). Our ratio 18O/17O = 12 is very large, compared to the canonical ISM value of 3-4 (Penzias 1981; Bensch et al. 2001; Wouterloot et al. 2005) and to the Solar System value of 5.5. It is especially large with respect to the value observed in IRC+10216 and in other late type giant envelopes which are all <1 (Kahane et al. 1992).
The high 18O/17O and low 16O/18O ratios, compared to the ISM and, mostly, to IRC+10216, are probably linked to the relative youth of the z = 0.89 galaxy. They may help us to better understand the puzzling 18O nucleosynthesis. It is worth noting that Combes & Wiklind (1995) derived from similar absorption observations a limit C18O/C17O > 15 in another high redshift galaxy (z = 0.68) on the line of sight to the quasar B0218+357.
The 18O/17O ratio has been estimated in the starburst nuclei of M 82, NGC 253 and NGC 4935 (Sage et al. 1991, Henkel & Mauersberger 1993). The values, which are much more uncertain than in the cases of the ISM and the z = 0.89 galaxy, seem larger than the Local ISM value and may be explained by a initial mass function biased towards massive stars (Henkel & Mauersberger 1993).
Figure 7 compares in a single diagram the relative abundances of 16O, 17O and 18O as observed for the main Galactic and extragalactic sources. 17O appears particularly abundant in IRC+10216 and 16O unabundant in the z = 0.89 galaxy. The LMC stands in this diagram at the opposite of the z = 0.89 galaxy, but this could be an artifact of low metallicity and strong UV radiation field, which may lead to selective photodissociation of the rare C18O and C17O isotopes.
![\begin{figure}
\par {\includegraphics[width=7.8cm,clip]{5187fig7.eps} }%\end{figure}](/articles/aa/full/2006/41/aa5187-06/Timg88.gif) |
Figure 7: Oxygen isotopic ratios 16O/17O vs. 16O/18O for different sources. |
| Open with DEXTER | |
The 32S/34S ratio we derive from CS and H2S, ![]() ,
is at the same time accurate, since it is directly measured on optically
thin lines for two different species, and meaningful, since only few
molecular sources show such a clear departure of this ratio from its
Solar System value, 22.
,
is at the same time accurate, since it is directly measured on optically
thin lines for two different species, and meaningful, since only few
molecular sources show such a clear departure of this ratio from its
Solar System value, 22.
The 32S/34S ratio is found to be the same in the processed stellar envelope IRC+10216, in the Solar System and in the local ISM. The 34CS/33CS ratio is the same in all Galactic molecular sources, and the 13CS/C34S ratio, which is used to estimate the 32S/34S ratio in Giant Molecular Clouds where 12CS is optically thick, shows no variations across the Galaxy (Frerking et al. 1980; Chin et al. 1996).
Because the 12C/13C ratio derived from H2CO and CO seems to decrease between the Solar neighbourhood and the Galactic Center, Chin et al. (1996) argue that the constancy of 13CS/C34S implies a similar decrease of 32S/34S. The 12C/13C gradient, however, is shallow, except perhaps near the Galactic Center. Moreover, CO and H2CO yield for the same galactocentric radius discrepant values (Wilson & Rood 1994). Thus, the observed 12CO/13CO and H212CO/H213CO ratios may well be affected by 13C fractionation and/or line opacity effects and may not reflect the 12CS/13CS ratio, so that the presence of a 32S/34S gradient in the Galaxy is not established. As a matter of fact, it would be quite surprising to find a low 32S/34S ratio in the Galactic Center, where nucleosynthesis, we believe, is mainly driven by low mass stars.
The sulfur isotopes are produced and destroyed in massive and very massive
stars. Their abundances stem from a critical balance between equilibrium
and explosive nucleosynthesis. In a 25 ![]() star, according to
Woosley & Hoffman (1986),
34S is 20 times more efficiently produced at equilibrium than 32S
and 100 times more than 33S. In an explosive oxygen burning episode,
the three isotopes are produced about evenly. Our 32S/34S ratio
of 10, twice smaller that in the local ISM, could imply that the IMF in the
z = 0.89 galaxy is different from that of the Milky Way at the same age.
Unfortunately, our non-detection of H233S brings little information
on this respect.
star, according to
Woosley & Hoffman (1986),
34S is 20 times more efficiently produced at equilibrium than 32S
and 100 times more than 33S. In an explosive oxygen burning episode,
the three isotopes are produced about evenly. Our 32S/34S ratio
of 10, twice smaller that in the local ISM, could imply that the IMF in the
z = 0.89 galaxy is different from that of the Milky Way at the same age.
Unfortunately, our non-detection of H233S brings little information
on this respect.
Wang et al. (2004) and Martín et al. (2005) report measurements of the
32S/34S ratio in the nuclear regions of two starburst galaxies,
NGC 4945 and NGC 253. The values they derive (
![]() and
and ![]() ,
respectively) are similar to that we find in the z = 0.89 galaxy. They are
much more uncertain, since they rely on the integrated intensity of the
broad and weak 13CS line and on the knowledge of the 12C/13C ratio. In contrast, the 32S/34S in the LMC (
,
respectively) are similar to that we find in the z = 0.89 galaxy. They are
much more uncertain, since they rely on the integrated intensity of the
broad and weak 13CS line and on the knowledge of the 12C/13C ratio. In contrast, the 32S/34S in the LMC (![]() ,
according to
Chin 1999) is close to that in the local ISM.
,
according to
Chin 1999) is close to that in the local ISM.
Deuterium is produced in the Big Bang nucleosynthesis with a primordial
[D/H] ratio of
![]() (Spergel et al. 2003). It is completely
destroyed in the interior of stars, so that, ignoring infall of unprocessed
gas, the D/H ratio is an indicator of the degree of evolution. In the local
ISM, the average ratio D/H is
(Spergel et al. 2003). It is completely
destroyed in the interior of stars, so that, ignoring infall of unprocessed
gas, the D/H ratio is an indicator of the degree of evolution. In the local
ISM, the average ratio D/H is ![]()
![]() .
.
The deuterium abundance can be greatly enhanced in molecules in the cold and dense gas. Extensive modelling of D-chemistry (see e.g. Roberts & Millar 2000) predicts D/H values as large as 0.01-0.1 for molecules embedded in very cold clouds, and such high ratios have been observed in Galactic dark clouds (Guélin et al. 1982), pre-stellar cores (Parise et al. 2002) and in the LMC (Chin et al. 1996).
We searched during 3 h for the DNC
![]() line with the PdB interferometer; no absorption was detected down to a level of
line with the PdB interferometer; no absorption was detected down to a level of
![]() (3
(3![]() )
with a velocity resolution of
)
with a velocity resolution of
![]() km s-1. Assuming a
linewidth similar to the main isotopomer HNC, we obtain an upper limit from
the ratio DNC(
km s-1. Assuming a
linewidth similar to the main isotopomer HNC, we obtain an upper limit from
the ratio DNC(
![]() )/HNC(
)/HNC(
![]() ):
):
![]() for the
-3 km s-1 component.
for the
-3 km s-1 component.
Our upper limit is less constraining than that derived by Shah et al. (1999) from the double isotopic ratio: [DCO+]/[H13CO+].[13C/12C ] < 0.0022. The latter, however, contrary to our result, depends on the knowledge of the C isotopic ratio, a ratio that can be affected by fractionation. Both limits remain far higher than the primordial ratio and tell us little about stellar processing.
We have argued in Sect. 5 that the molecules studied here,
which all have a large dipole moment, are likely to be at equilibrium with
the cosmic background radiation, whose temperature at z = 0.89 is 5.1 K. The
observations support this conclusion: Menten et al. (1999) measure a rotation
temperature
![]() K from the observations of two
rotational transitions of HC3N, and WC96 from
similar measurements find
K from the observations of two
rotational transitions of HC3N, and WC96 from
similar measurements find
![]() for CS, H13CO+ and N2H+ and
for CS, H13CO+ and N2H+ and
![]() K for HNC. We therefore assume
K for HNC. We therefore assume
![]() K in our calculations.
K in our calculations.
The column densities of Table 8 were calculated from the equation:
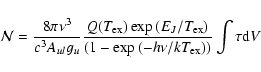 |
(2) |
As concerns HCO+ and HCN, whose lines are optically thick, we calculated their column densities by multiplying those of their 13C isotopologues by 12C/13C = 27. This assumes that the 12C/13C ratio is the same for all molecules and all velocity components. Our results are in good agreement with the values of Menten et al. (1999), which were derived from rotational transitions with lower J and lower opacities.
A crude analysis of the chemistry in the z = 0.89 galaxy has been made
by WC96 and Menten et al. (1999), who concluded that
the molecular abundances in the SW velocity component (
![]() km s-1)
are similar to those of Galactic dark clouds such as TMC 1. The HNC/HCN
ratio we find (0.4) is indeed similar to that in those cold clouds
(Hirota et al. 1998) and two orders of magnitude larger than in the hot
and dense clouds, such as Orion MC-1. A high HNC/HCN ratio probably means
that these two species are formed by gas phase ion-molecule reactions via
HCNH+. Note that a high HNC/HCN ratio has also been reported in the
center of nearby starburst galaxies (e.g. Martín et al. 2006).
km s-1)
are similar to those of Galactic dark clouds such as TMC 1. The HNC/HCN
ratio we find (0.4) is indeed similar to that in those cold clouds
(Hirota et al. 1998) and two orders of magnitude larger than in the hot
and dense clouds, such as Orion MC-1. A high HNC/HCN ratio probably means
that these two species are formed by gas phase ion-molecule reactions via
HCNH+. Note that a high HNC/HCN ratio has also been reported in the
center of nearby starburst galaxies (e.g. Martín et al. 2006).
The HCO+/N2H+ ratio, which reflects in the medium dense gas
the CO/N2 ratio, is 6 (adopting the N2H+ integrated (
![]() ) line opacity measured by WC96). Its value is close to the "cosmic''
O/N elemental ratio, 7.
) line opacity measured by WC96). Its value is close to the "cosmic''
O/N elemental ratio, 7.
Until now, H2S extragalactic detection was only reported in the LMC
(Heikkilä et al. 1999) and NGC 253 (Martín et al. 2005).
The abundance of H2S in the SW component is large (
![]() with
respect to H2, adopting
with
respect to H2, adopting
![]() (H
(H
![]() cm-2, WC96),
compared to the standard values of
cm-2, WC96),
compared to the standard values of
![]() measured in the quiescent
regions of OMC-1 and in the dark clouds (Minh et al. 1989). It is also a
factor of
measured in the quiescent
regions of OMC-1 and in the dark clouds (Minh et al. 1989). It is also a
factor of ![]() 10 larger than in the local diffuse clouds, as measured
by Lucas & Liszt (2002). This overabundance could reflect a large abundance
of S in the gas, although the CS abundance seems normal. It could also mean
that the absorbing gas at z = 0.89 is not that quiescent and that H2S
molecules could be released from dust grains either by intense UV radiation
from star forming regions or by shocks generated by young stellar objects,
as is observed in the Orion (KL) outflow (Minh et al. 1990). The very wide
absorption profile observed in a few pc-large SW absorbing cloud may
support this last scenario.
10 larger than in the local diffuse clouds, as measured
by Lucas & Liszt (2002). This overabundance could reflect a large abundance
of S in the gas, although the CS abundance seems normal. It could also mean
that the absorbing gas at z = 0.89 is not that quiescent and that H2S
molecules could be released from dust grains either by intense UV radiation
from star forming regions or by shocks generated by young stellar objects,
as is observed in the Orion (KL) outflow (Minh et al. 1990). The very wide
absorption profile observed in a few pc-large SW absorbing cloud may
support this last scenario.
Although we have measured only a few column densities for the NE velocity component (V = -147 km s-1), those also yield relative abundances similar to those of the cold dark clouds. In particular, the HNC/HCN ratio (0.3) is large.
The presence of an intervening nearly face-on spiral galaxy at z = 0.89in the line of sight of the radio loud quasar PKS 1830-211 offers an unique chance to study the chemical and isotopic compositions of the interstellar medium in the spiral arm of a galaxy 2-3 times younger than the Milky Way. The use of the PdB interferometer has enabled us to combine very flat baselines and high sensitivity, making it possible to measure reliably the C, N, O and S isotopic abundance ratios in HCO+, HCN, HNC, CS, and H2S. The ratios derived from different species or velocity components are fully consistent, which supports the view that they are not affected by residual opacity effects and/or fractionation effects and that they reflect the elemental isotopic ratios.
A comparison of the isotopic ratios in the z = 0.89 galaxy with those
observed in the local ISM, the Galactic Center, the circumstellar
envelope IRC+10216 and the Solar System shows major differences with
these sources. Mainly, the 17O/18O, and 14N/15N ratios, which are sensitive probes of the degree of processing of the
gas by low mass stars and which are expected to increase with time are
found to be smaller than in the ISM or the Solar System and much
smaller than in the Galactic Center and in the fully processed
low-mass star envelope IRC+10216. Most remarkably, the observed
16O/18O ratio is a factor of 10 lower than in the ISM and
the Solar System and the 32S/34S ratio is twice lower
than in the Galactic sources. These latter ratios result mainly from
nucleosynthesis in high mass stars and it is likely that the stellar
Initial Mass Function in the z = 0.89 galaxy is different from that of
the Milky Way at the same age. The low 17O/18O, and 14N/15N ratios are consistent with the young age of the
galaxy (<6 Gyr) which is smaller than the lifetime of stars with
masses <1.5 ![]() and severly limits the importance of low mass
stars in the regeneration of the ISM.
and severly limits the importance of low mass
stars in the regeneration of the ISM.
The isotopic ratios observed towards PKS 1830-211, although more extreme, are not unsimilar to those derived in the starburst nuclei of nearby galaxies, such as NGC 253, M 82 and NGC 4945 (see e.g. Martín et al. 2006). The later ratios, which result from the observation of weak and broad emission lines, are however far more uncertain.
The extension of this study to other remote galaxies is hampered by the small number of millimeter radio sources whose line-of-sight intercepts the plane of a remote galaxy. PKS 1830-211 is by far the brightest such source. The second best, at present, is the gravitational lens B0218+357 and several molecular lines have been observed in absorption at z = 0.68toward this object (Wiklind & Combes 1995; Menten & Reid 1996; Combes & Wiklind 1997). Even in this object, the detection of less abundant species is difficult (Henkel et al. 2005). Fortunately, the flux of this source has been growing lately at millimeter wavelengths, giving hope that the rare carbon, oxygen and sulfur isotopes can be studied in the near future.
Acknowledgements
We would like to thank all the members of the IRAM staff from the Plateau de Bure who made these observations possible. S.M. thanks Dr. Y. C. Minh for fruitful and stimulating discussions. We wish to thank the referee, whose comments helped to improve the paper. Based on observations carried out with the IRAM Plateau de Bure Interferometer. IRAM is supported by INSU / CNRS (France), MPG (Germany) and IGN (Spain).
Note added in proof. Follow-up observations of the
H234S (
![]() )
absorption yields to a better estimation of the
H2S/H234S line ratio of 10.6
)
absorption yields to a better estimation of the
H2S/H234S line ratio of 10.6 ![]() 0.9, fully consistent with our measurement of
C32S/C34S = 10.4
-0.7+0.8.
Combining these two results points to a ratio
32S/34S = 10.5
0.9, fully consistent with our measurement of
C32S/C34S = 10.4
-0.7+0.8.
Combining these two results points to a ratio
32S/34S = 10.5 ![]() 0.6 (Muller et al., in prep.).
0.6 (Muller et al., in prep.).
Table 2: Observational data.
Table 4: Results of the decomposition of the SW opacity profiles into multiple Gaussian components.
Table 7: Comparison of the C, N, O and S isotopic ratios in the z = 0.89 galaxy (SW absorption) with different other environments.
Table 8: Total molecular column densities towards the SW and NE absorption.