A&A 458, 357-367 (2006)
DOI: 10.1051/0004-6361:20065179
B. Aryal1,2 - S. M. Kandel2 - W. Saurer1
1 - Institut für
Astrophysik, Universität
Innsbruck, Technikerstraße 25, 6020 Innsbruck, Austria
2 -
Central Department of Physics, Tribhuvan University,
Kirtipur, Kathmandu, Nepal
Received 10 March 2006 / Accepted 15 May 2006
Abstract
We present an analysis of the spatial orientations of
323 galaxies in the cluster Abell 3558. Our aim is to examine
non-random effects in galaxy orientations in the subsample of the
cluster. The "position angle-inclination'' method is used to find
the three-dimensional rotation axes. To check for anisotropy or
isotropy we carried out three statistical tests: Fourier,
Kolmogorov-Smirnov, and Kuiper-V. We assumed a spatially isotropic
distribution to examine non-random effects. The galaxies found in
the investigated cluster region show isotropy in both two- and
three-dimensional analyses of the galactic coordinate system. In
addition, it is found that the overall isotropic appearance cannot
be maintained when looking at the subsamples. The low
radial-velocity galaxies in A 3558 showed anisotropy in both two-
and three-dimensional analyses. A weak anisotropy is noticed in the
hard X-ray emission region. Few subsamples shows similar
alignments with respect to both the galactic and Supergalactic
coordinate systems. We offer possible explanations of these
anisotropies.
Key words: galaxies: clusters: general - galaxies: evolution - galaxies: spiral - galaxies: distances and redshifts - galaxies: formation - galaxies: statistics
The Shapley Concentration is the richest supercluster within a
distance of 300 h-1 Mpc (h=H0/100). The core of the
Shapley Concentration is a chain formed by the ACO (Abell et al. 1989) clusters A 3558, A 3562, A 3556 and by the
two poor clusters SC 1327-312 and SC 1329-313. The main cluster A 3558, also known as Shapley 8, is the richest cluster listed in
the ACO catalogue, the only one with a richness class 4. Within a
circle of 1 Abell radius (![]() 1.5 h-1 Mpc) around this
cluster, about 267 galaxies with measured redshifts in the
velocity range 10 260-18 516 km s-1 are given in
catalogues, so this cluster complex is one of the best-sampled
galaxy clusters in the catalogue. The cluster A 3558 is in fact the
most evolved system in the group, termed as a early-type or B-M
type I (Bautz & Morgan 1970) cluster. These clusters have
systematically higher X-ray luminosities than other types (Ledlow
et al. 2003). Cooling flows are found in a large fraction
of them because of the presence of a cD galaxy and a
correspondingly deeper gravitational potential (McHardy
1978). These clusters are dynamically very active and
are still in the process of forming from their parent clusters or
vice versa.
1.5 h-1 Mpc) around this
cluster, about 267 galaxies with measured redshifts in the
velocity range 10 260-18 516 km s-1 are given in
catalogues, so this cluster complex is one of the best-sampled
galaxy clusters in the catalogue. The cluster A 3558 is in fact the
most evolved system in the group, termed as a early-type or B-M
type I (Bautz & Morgan 1970) cluster. These clusters have
systematically higher X-ray luminosities than other types (Ledlow
et al. 2003). Cooling flows are found in a large fraction
of them because of the presence of a cD galaxy and a
correspondingly deeper gravitational potential (McHardy
1978). These clusters are dynamically very active and
are still in the process of forming from their parent clusters or
vice versa.
A substructure analysis (Bardelli et al. 1998) briefly discusses the core of the Shapley Concentration and suggests that the core complex is the result of a series of incoherent group-group and cluster-group mergings. Venturi et al. (2000) studied radio properties in connection with the dynamical state of the cluster Abell 3558 complex and found that the ratio between the radio and the optical flux for the Shapley radio galaxies is not affected by the local galaxy density. This result suggests that the high optical density in the cluster has no effect on the radio galaxy emissivity. The core of the Shapley Concentration is dynamically very active (Bardelli et al. 1994), and the main cluster A 3558 appears to be interacting with the other clusters, A 3562 and A 3556; it is therefore very interesting to study the spatial distribution of angular momentum in the cluster galaxies. Because spatial orientations of the angular momentum of disk galaxies can indicate the initial conditions when galaxies and clusters formed. The study of the orientations of the rotation axes of cluster galaxies is very important for understanding the process of formation of this large structure.
Many theories use this distributions to develop scenarios. The "Pancake model'' by Doroshkevich (1973), the "Hierarchy model'' by Peebles (1969), and the "Primordial vorticity model'' of Ozernoy (1978) predict different scenarios concerning the origin of angular momentum of galaxies in clusters. Thus, studies of the angular momentum distribution of galaxies in clusters may explore important ideas in order to understand galaxy evolution scenarios. The "pancake model'' (see, e.g. Doroshkevich 1973; Shandarin 1974; Doroshkevich & Shandarin 1978) predicts that the rotation axes of galaxies tend to lie within the cluster plane. According to the "hierarchy model'' the directions of the rotation axes should be distributed randomly. The "primordial vorticity theory'' predicts that the rotation axes of galaxies are primarily distributed perpendicular to the cluster plane.
We use the "position angle - inclination'' method (Flin & Godlowski 1986) to compute three-dimensional spatial orientation vectors from two-dimensional measured parameters. Their method has been applied by several authors in galaxy orientation studies (Flin 1988; Kashikawa & Okamura 1992; Godlowski 1993, 1994; Hu et al. 1995, 1998; Wu et al. 1997; Yuan et al. 1997; Godlowski et al. 1998; Godlowski & Ostrowski 1999; Flin 2001; Aryal & Saurer 2004, 2005a,b,c, 2006; Baier et al. 2003; etc.). Their method, not only analyzed the distributions of galaxy PAs, but also considered another important parameter - the galaxy's inclination with respect to the observer's line of sight. These two angles allowed us to find the orientations of the two possible vectors normal to the galactic plane, one of them assumed to be the galactic rotation axis or spin vector of the galaxy.
Aryal & Saurer (2004) studied the spatial orientation of 296 galaxies in A 3558 and found anisotropy in both the two-dimensional (equatorial PA-distribution) and three-dimensional analysis (polar and azimuthal angle distributions). In the three-dimensional analyses, they found that the spin vector (SV hereafter) orientation of galaxies tends to lie parallel to the Local Supercluster plane and that SV projections of galaxies tend to be directed towards the Local Supercluster center (or Virgo cluster center). In this paper, we intend to find the local anisotropies in A 3558 and explain the role of such anisotropies in the merging environment (within the cluster A 3558) and in the cluster-cluster collision environment (with other clusters A 3556 and A 3562).
Kitzbichler & Saurer (2003) studied the Coma cluster, where they noticed local anisotropies in the X-ray emission region and concluded that the X-ray subcluster of the Coma cluster might be falling in on the main cluster. We are interested in studying the preferred alignments of galaxies in hard X-ray emission region of the cluster A 3558 in order to test a possible coincidence of hot-gas features with the local anisotropy.
Godlowski et al. (2003) describe a relation between angular momentum and the mass of a galaxy and tested this relation for Tully's galaxy group (Godlowski et al. 2005). A random galaxy alignment for that group is noticed. They conclude that the minima of the relation between angular momenta and masses of galaxy structures can be verified observationally.
We expect to carry out the following studies: (1) study the preferred alignment of the rotation axes of galaxies in the cluster with respect to the galactic coordinate system; (2) test the existence of a morphological, magnitudinal, diameter, and radial velocity (RV) dependence in the galaxy orientation; (3) investigate the emission region in other wavelengths and study the preferred alignment in that particular region; and, finally, (4) see what else we can say about the origin of angular momenta from this study.
This paper is organized as follows. In Sect. 2 we describe the sample used and the method of data reduction. We give the results of a multiwavelength study in Sect. 3. In Sect. 4 we describe the methods, statistical tools and the selection effects. Finally, a discussion of the statistical results and the conclusions are presented in Sects. 5 and 6.
We inspected all galaxies found in the cluster A 3558 region on the film copies (red-sensitive ESO) with the aid of a binocular microscope. The galaxies in the cluster were not too faint and it was relatively easy to determine diameters and position angles of many galaxies with relatively good accuracy. The galactic contamination in and around the clusters was minimum. A list of the data for A 3558 cluster as given in the ACO catalogue is given in Table 1.
![\begin{figure}
\par\includegraphics[height=5.8cm,clip]{5179f01a.eps}\includegrap...
...lip]{5179f01b.eps}\includegraphics[height=5.8cm,clip]{5179f01c.eps}
\end{figure}](/articles/aa/full/2006/41/aa5179-06/Timg27.gif) |
Figure 1:
The positions of 366 galaxies investigated in the cluster
A 3558 region in the equatorial coordinate system a) and galactic
coordinate system b), c)). The cross in the figure represents the
cluster center. The symbol " |
| Open with DEXTER | |
| |
Figure 2: a) Logarithm of the total number of galaxies greater than a given diameter versus the logarithm of this very diameter. The solid line represents the theoretical line having slope -3. The axial ratio (a/b) and the magnitude (m) distribution of galaxies in A 3558 is shown in Figs. 3b and 3c. The histogram of the morphological classification of galaxies is shown d). |
| Open with DEXTER | |
Table 1: Data of the cluster A 3558 as given in the ACO (Abell et al. 1989) catalogue.
To locate the cluster region on the films, the coordinates of the
cluster center as given in the ACO catalogue was used. A circular
survey area was defined using a radius
![]() /z (Thompson 1976). Here z represents the redshift of the cluster. The foreground field
galaxies in the investigated cluster region were identified with
the help of the Uppsala General Catalogue of Galaxies (Nilson
1973, UGC hereafter), the Third Reference Catalogue of
Bright Galaxies (de Vaucouleurs et al. 1991), the
ESO/Uppsala Survey of the ESO (B) Atlas (Lauberts 1982,
ESO hereafter), the Morphological Galaxy Catalogue
(Vorontsov-Vel'Yaminov et al. 1962-74; MGC hereafter), and
the Southern Galaxy Catalogue (Corwin et al. 1985). These
field galaxies have been removed from the database.
/z (Thompson 1976). Here z represents the redshift of the cluster. The foreground field
galaxies in the investigated cluster region were identified with
the help of the Uppsala General Catalogue of Galaxies (Nilson
1973, UGC hereafter), the Third Reference Catalogue of
Bright Galaxies (de Vaucouleurs et al. 1991), the
ESO/Uppsala Survey of the ESO (B) Atlas (Lauberts 1982,
ESO hereafter), the Morphological Galaxy Catalogue
(Vorontsov-Vel'Yaminov et al. 1962-74; MGC hereafter), and
the Southern Galaxy Catalogue (Corwin et al. 1985). These
field galaxies have been removed from the database.
Aryal & Saurer (2004) have roughly estimated the number
of background galaxies in the cluster region on the basis of the
area distribution of background galaxies around the cluster
region. The number of background galaxies per unit area around the
cluster region is calculated and divided by the number of galaxies
per unit area in the cluster region. They estimated that the
background contamination of galaxies in the investigated cluster
region is ![]() 12%.
12%.
The method of investigation and the measurements of positions, PAs, and diameters (a, b) of galaxies were the same as in Aryal & Saurer (2004). We measured positions (using DSS images with the help of the software ESO/ECF/CADC, Association of Universities for Research in Astronomy, Inc., version 1.3), diameters (using a transparent scale with units of one tenth of a millimeter), and PAs (using a protractor of 15 cm radius and a transparent glass with a thin line) for the investigated galaxies in the cluster region. We investigated 366 galaxies in the Abell 3558 cluster region. The diameters and position angle was measured for 366 (100%) and 323 (88.3%) galaxies. In the NED (NASA Extragalactic Database, http://nedwww.ipac.caltech.edu), the radial velocities of 217 (59.3%) galaxies were listed until the cutoff date (September 2005). Our database includes 53 (16.4%) spiral and S0 galaxies.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{5179f03a.eps}
\end{figure}](/articles/aa/full/2006/41/aa5179-06/Timg37.gif) |
Figure 3: The radial velocity distribution of galaxies in the cluster A 3558 region. |
| Open with DEXTER | |
We studied the distribution of the apparent diameters of the
galaxies to get the knowledge of the completeness of the data. For
this, a constant spatial density for the galaxies with equal
linear diameter was assumed. It was expected that the logarithm of
the total number of galaxies having an apparent diameter greater
or equal to a given limit is increasing with a slope of -3. As
indicated in Fig. 2a, the optical search is complete down to a
diameter of 1![]() (corresponding to a=0.85 mm on the
film-copies). We calculated 83 and 240 galaxies up to the search
limit (SL) and the below limit (BL). The histograms of the axial
ratio (b/a), magnitude, and the morphological distribution are
shown in Figs. 2b-d. The lack of nearly face-on galaxies can
be seen in Fig. 2b. The spiral galaxies are found to be dominated
by S0 galaxies in A 3558. The radial velocity distribution of
galaxies can be seen in Fig. 3. About 75% of the galaxies in A 3558 have
RVs in the range 13 000 to 16 000 km s-1.
(corresponding to a=0.85 mm on the
film-copies). We calculated 83 and 240 galaxies up to the search
limit (SL) and the below limit (BL). The histograms of the axial
ratio (b/a), magnitude, and the morphological distribution are
shown in Figs. 2b-d. The lack of nearly face-on galaxies can
be seen in Fig. 2b. The spiral galaxies are found to be dominated
by S0 galaxies in A 3558. The radial velocity distribution of
galaxies can be seen in Fig. 3. About 75% of the galaxies in A 3558 have
RVs in the range 13 000 to 16 000 km s-1.
The cluster position angle is estimated assuming that the galaxies
in the cluster are approximately equidistance. A straight
line is fitted using the least-square fit method for the total galaxy,
as well as for galaxies having
![]() ,
,
![]() ,
,
![]() in the cluster region.
The statistics of the samples are given in Table 2. The standard deviation
and standard error is at a minimum for the
total galaxies. The cPA for the all galaxies is estimated to
be 18
in the cluster region.
The statistics of the samples are given in Table 2. The standard deviation
and standard error is at a minimum for the
total galaxies. The cPA for the all galaxies is estimated to
be 18![]() north-west.
north-west.
Table 2:
Major diameter statistics. The first two columns give the
samples and the number of galaxies. The next three columns give
the mean value, standard deviation (![]() sd), and standard error
(
sd), and standard error
(![]() se) of the galaxy samples for
se) of the galaxy samples for
![]() ,
,
![]() ,
,
![]() ,
and all. The last column
gives the cluster position angle (cPA) in the galactic coordinate
system. The cPA is estimated using the least-square fit method (see
Fig. 1c).
,
and all. The last column
gives the cluster position angle (cPA) in the galactic coordinate
system. The cPA is estimated using the least-square fit method (see
Fig. 1c).
We classified these galaxies into 7 subsamples according to
their morphologies, radial velocities, diameters, and magnitudes,
as follows: (1) spirals and S0 galaxies: S+S0; (2) radial velocity
in the range
![]() (km s
(km s
![]() :
RV1; (3)
radial velocity in the range
:
RV1; (3)
radial velocity in the range
![]() (km s
(km s
![]() :
RV2; (4)
:
RV2; (4)
![]() :
SL (search
limit); (4)
:
SL (search
limit); (4)
![]() :
BL (below limit) (6) magnitude
(m):
:
BL (below limit) (6) magnitude
(m):
![]() (M1); and (7) magnitude (m):
(M1); and (7) magnitude (m):
![]() (M2).
(M2).
We classified the radial velocity and magnitude on the basis of
the minimum standard deviation. The subsamples RV1 (M1) and RV2 (M2)
showed approximately identical standard deviation values (within
their standard error limit). The center cD galaxy (
![]() )
falls into the subsamples RV1, M1, and SL.
)
falls into the subsamples RV1, M1, and SL.
We used SkyView (http://skyview.gsfc.nasa.gov/) to search
for counterparts to the investigated cluster region (the cluster A 3558). The SkyView Virtual Observatory gives hard X-ray,
soft X-ray, infrared, optical, UV, and radio surveys. We inspected
21 surveys focusing on our region of interest (RA (J2000):
![]() 0, Dec. (J2000):
0, Dec. (J2000):
![]() 00
00
![]() ;
2
;
2
![]() ). No emission is noted in the following surveys: HEAO 1 A-2 (Shafer
1983; Allen et al. 1994), INTEGRAL/SPI Survey of
the Galactic Centre (20-40 keV), Rossi X-ray Timming Explorer
(RXTE), All Sky Slew Survey (XSS) (Revnivtsev et al. 2004),
HRI Survey, ROSAT PSPC, ROSAT All Sky Survey (RASS3), ROSAT All
Sky Survey (Snowden et al. 1995), Two Micron All Sky
Survey (2MASS), COBE Diffuse Infrared Background Experiment
(DIRBE) (Hauser et al. 1990), SFD Dust Maps (Schlegel et al. 1998), The H-alpha Full Sky Map (Finkbeiner
2003), The Southern H-Alpha Sky Survey Atlas (SHASSA)
(Gaustad et al. 2001), Near Earth Asteroid Tracking (NEAT)
/ SkyMorph Survey, Sloan Digital Sky Survey (SDSS), 34.5 MHz
(Dwarakanath & Udaya Shankar 1990), 408 MHz (Haslam et al.
1982), VLA FIRST Survey, NRAO VLA Sky Survey (NVSS), 4850 Mhz and 4850 Mhz (OLD) (Condon et al. 1993,
1991). We found a noticeable emission in two surveys:
the GRANAT/SIGMA hard X-ray survey (40-100 keV) and 100
). No emission is noted in the following surveys: HEAO 1 A-2 (Shafer
1983; Allen et al. 1994), INTEGRAL/SPI Survey of
the Galactic Centre (20-40 keV), Rossi X-ray Timming Explorer
(RXTE), All Sky Slew Survey (XSS) (Revnivtsev et al. 2004),
HRI Survey, ROSAT PSPC, ROSAT All Sky Survey (RASS3), ROSAT All
Sky Survey (Snowden et al. 1995), Two Micron All Sky
Survey (2MASS), COBE Diffuse Infrared Background Experiment
(DIRBE) (Hauser et al. 1990), SFD Dust Maps (Schlegel et al. 1998), The H-alpha Full Sky Map (Finkbeiner
2003), The Southern H-Alpha Sky Survey Atlas (SHASSA)
(Gaustad et al. 2001), Near Earth Asteroid Tracking (NEAT)
/ SkyMorph Survey, Sloan Digital Sky Survey (SDSS), 34.5 MHz
(Dwarakanath & Udaya Shankar 1990), 408 MHz (Haslam et al.
1982), VLA FIRST Survey, NRAO VLA Sky Survey (NVSS), 4850 Mhz and 4850 Mhz (OLD) (Condon et al. 1993,
1991). We found a noticeable emission in two surveys:
the GRANAT/SIGMA hard X-ray survey (40-100 keV) and 100 ![]() m
IRAS survey.
m
IRAS survey.
![\begin{figure}
\par\includegraphics[height=8cm,clip]{5179f04a.eps} \includegraphics[height=8cm,clip]{5179f04b.eps}
\end{figure}](/articles/aa/full/2006/41/aa5179-06/Timg53.gif) |
Figure 4:
Significant emission in the investigated
cluster region in a) the GRANAT/SIGMA hard X-ray (40-100 keV)
and b) the 100 |
| Open with DEXTER | |
A significant emission can be found in the GRANAT/SIGMA survey of
hard X-ray sky (40-100 keV) (Paul et al. 1991; Revnivtsev
et al. 2004) in the A 3558 cluster region (see Fig. 4a).
Similarly, we found a significant 100 ![]() m infrared emission in
IRAS Survey (Wheelock et al. 1991) in our region of
interest (Fig. 4b).
m infrared emission in
IRAS Survey (Wheelock et al. 1991) in our region of
interest (Fig. 4b).
Figure 4a displays 2
![]() hard X-ray (40-100 keV)
contour maps overlayed on an image centered at A 3558. In this figure,
one notices that i) strong emission is found in the central
region; ii) the maxima of the central emission is not at the
cluster center; iii) the central emission is
hard X-ray (40-100 keV)
contour maps overlayed on an image centered at A 3558. In this figure,
one notices that i) strong emission is found in the central
region; ii) the maxima of the central emission is not at the
cluster center; iii) the central emission is ![]() 0.4
0.4
![]() east of the cluster center; iv) the emission is more or less
rounded; and v) there is no connection between the central
emission and the surrounding weak-emission region. The hard X-ray
contours span 11.5 to 23 MJy/str in steps separated by 2.3 MJy/str. A total number of 216 galaxies are found in this emission
region. A study of the spatial orientation of galaxies in this
central emission region could be important. Any preferred
alignment of galaxies in this region might indicate the
coincidence of the hot-gas feature with optical condensations. We
classify the galaxies found in this region as the 8th subsample
(abbreviated as HX) for the alignment study.
east of the cluster center; iv) the emission is more or less
rounded; and v) there is no connection between the central
emission and the surrounding weak-emission region. The hard X-ray
contours span 11.5 to 23 MJy/str in steps separated by 2.3 MJy/str. A total number of 216 galaxies are found in this emission
region. A study of the spatial orientation of galaxies in this
central emission region could be important. Any preferred
alignment of galaxies in this region might indicate the
coincidence of the hot-gas feature with optical condensations. We
classify the galaxies found in this region as the 8th subsample
(abbreviated as HX) for the alignment study.
In the IRAS survey, the emission is discernible not only at 100 ![]() m, but also at 60
m, but also at 60 ![]() m. Figure 4b shows
1
m. Figure 4b shows
1
![]() m HIRES contour maps (resolution
m HIRES contour maps (resolution ![]() 1
1
![]() )
projected on the image. The contours span 1.15 to 4.75 MJy/str in steps separated by 0.60 MJy/str. In Fig. 4b, three
emission regions are seen towards northeast. These emissions seem
to be connected. The total number of galaxies found in this region is
only 38. As we know that the IRAS sky region is relatively nearby sky and the
cluster A 3558 is a distant cluster. Are these chance
superpositions? Unfortunately there is no convincing way to find this
out, since a lot of the structure in the IRAS maps exists on different
scales. One of us (BA) has started a study to
address this problem of superpositions on IRAS maps, although here we
study the preferred alignment of galaxies found in this region
(9th subsample - abbreviated as IR).
)
projected on the image. The contours span 1.15 to 4.75 MJy/str in steps separated by 0.60 MJy/str. In Fig. 4b, three
emission regions are seen towards northeast. These emissions seem
to be connected. The total number of galaxies found in this region is
only 38. As we know that the IRAS sky region is relatively nearby sky and the
cluster A 3558 is a distant cluster. Are these chance
superpositions? Unfortunately there is no convincing way to find this
out, since a lot of the structure in the IRAS maps exists on different
scales. One of us (BA) has started a study to
address this problem of superpositions on IRAS maps, although here we
study the preferred alignment of galaxies found in this region
(9th subsample - abbreviated as IR).
We followed the usual method (see e.g. Flin & Godlowski
1986) to derive the spatial orientations of SVs of
galaxies. The three-dimensional orientation of the SV of a galaxy
is characterized by two angles: the polar angle (![]() )
between
the galactic SV and a reference plane, and the azimuthal angle (
)
between
the galactic SV and a reference plane, and the azimuthal angle (![]() )
between the projection of a galactic SV on this reference
plane and the X-axis within this plane. When using the galactic
coordinate system as reference,
)
between the projection of a galactic SV on this reference
plane and the X-axis within this plane. When using the galactic
coordinate system as reference, ![]() and
and ![]() can be
obtained from measurable quantities as follows:
can be
obtained from measurable quantities as follows:
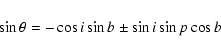 |
(1) |
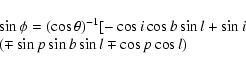 |
(2) |
There is no information from which we can define a physically-based reference frame for the cluster A 3558. The reference plane is complex because of the merging and collisional environment in the cluster A 3558, so we used the galactic plane (i.e., the plane of the Milky Way) as a reference for the analysis.
In the galactic coordinate system, the principal axis is the galactic
equator (the intersection of the plane of the Milky Way with the
celestial sphere) and the reference points are the north galactic
pole and the zero point on the galactic equator; the coordinates
of a celestial body are its galactic longitude and latitude.
In this system, the zero point on the galactic equator
has the equatorial coordinates RA (J2000
![]() and
Dec (J2000
and
Dec (J2000
![]() ;
this lies in the direction of the
center of our galaxy, the Milky Way.
;
this lies in the direction of the
center of our galaxy, the Milky Way.
To calculate the SV orientation (![]() ,
,
![]() )
of a given disk
galaxy, the measured quantities
)
of a given disk
galaxy, the measured quantities ![]() ,
,
![]() ,
PA (equatorial
system) have to be transformed to the galactic variables l, b,
p. We used the NED coordinate calculator for this transformation.
,
PA (equatorial
system) have to be transformed to the galactic variables l, b,
p. We used the NED coordinate calculator for this transformation.
It is evident that, for a given value of i, the expressions (1)
and (2) give two solutions for both ![]() and
and ![]() and hence
4 solutions for the angular momentum vector of a galaxy. For a large
sample of galaxies, however, it is hardly possible to determine
- for each galaxy - which one is physically correct. For the
statistical analysis we took each of these
possibilities into account independently, as usual.
and hence
4 solutions for the angular momentum vector of a galaxy. For a large
sample of galaxies, however, it is hardly possible to determine
- for each galaxy - which one is physically correct. For the
statistical analysis we took each of these
possibilities into account independently, as usual.
We assumed a spatial isotropic distribution of SVs of galaxies as a
theoretical reference. This spatial reference distribution
gives further reference distributions for the angles ![]() and
and ![]() .
As a next step, our observations was compared with these
isotropic distribution curves in both
.
As a next step, our observations was compared with these
isotropic distribution curves in both ![]() and
and ![]() .
For
this comparison we used three different statistical tests: Fourier
test, Kolmogorov-Smirnov test, and Kuiper-V statistics.
.
For
this comparison we used three different statistical tests: Fourier
test, Kolmogorov-Smirnov test, and Kuiper-V statistics.
We applied the Fourier (Godlowski 1993), K-S (Stephens
1970; Press et al. 1992; Kanji 1995) and
Kuiper-V (Kuiper 1962; Stephens 1970) tests to
the distribution of galactic position (p), polar (![]() ), and
azimuthal angle (
), and
azimuthal angle (![]() ). Note that these tests are a proper
method in our case, because p,
). Note that these tests are a proper
method in our case, because p, ![]() and
and ![]() are
independent data. The significance level was chosen to be 95%, as
the null hypothesis is established to be an equidistribution for
the p,
are
independent data. The significance level was chosen to be 95%, as
the null hypothesis is established to be an equidistribution for
the p, ![]() ,
and
,
and ![]() .
A spatial isotropy of the spin
vectors was chosen as null hypothesis. In cases of too small a
sample size, only the K-S and Kuiper-V tests are meaningful,
because they can be applied to small samples, too.
.
A spatial isotropy of the spin
vectors was chosen as null hypothesis. In cases of too small a
sample size, only the K-S and Kuiper-V tests are meaningful,
because they can be applied to small samples, too.
![\begin{figure}
\par\mbox{\includegraphics[height=4.3cm,clip]{5179f05a.eps} \incl...
...5179f05c.eps} \includegraphics[height=4.3cm,clip]{5179f05d.eps} }
\end{figure}](/articles/aa/full/2006/41/aa5179-06/Timg62.gif) |
Figure 5:
The galactic longitude a), latitude b), inclination angle c) and equatorial position
angle d) distribution of galaxies in A 3558 region.
|
| Open with DEXTER | |
The inhomogeneous distributions of positions (l, b) of
galaxies in A 3558 can be seen in Figs. 5a,b. The humps at 312
![]() in l and at 30.6
in l and at 30.6
![]() in b-distributions
are caused by the cluster center (Figs. 5a,b). In the
axial ratio distributions, the decline at 0.70-0.90 is due to the
selection effect against nearly face-on galaxies. This effect can
also be seen very clearly in the inclination angle distribution
(Fig. 5c). No galaxies can be seen in the first bin
(
in b-distributions
are caused by the cluster center (Figs. 5a,b). In the
axial ratio distributions, the decline at 0.70-0.90 is due to the
selection effect against nearly face-on galaxies. This effect can
also be seen very clearly in the inclination angle distribution
(Fig. 5c). No galaxies can be seen in the first bin
(
![]() ), and the number of galaxies in the first three
bins is less than expected (Fig. 5c). The decline in the number of
galaxies in the last two bins is probably due to the faint edge-on
galaxies that could not be included in the database. Hence, we
noticed three kinds of selection effects in our database: (1) inhomogenous distribution of positions of galaxies; (2) lack of
knowledge of PAs of nearly face-on galaxies; and (3) lack of
edge-on galaxies. These are thus the main selection effects.
), and the number of galaxies in the first three
bins is less than expected (Fig. 5c). The decline in the number of
galaxies in the last two bins is probably due to the faint edge-on
galaxies that could not be included in the database. Hence, we
noticed three kinds of selection effects in our database: (1) inhomogenous distribution of positions of galaxies; (2) lack of
knowledge of PAs of nearly face-on galaxies; and (3) lack of
edge-on galaxies. These are thus the main selection effects.
As was shown by Aryal & Saurer (2000, 2001),
any selection criteria imposed on the data may cause severe
changes in the shapes of the expected isotropic distribution
curves. The inhomogeneous distribution of galaxy positions and the
lack of our knowledge of the PAs of nearly face-on galaxies are
the main selection effects. Because our galaxy samples are taken
from the limited region of the sky, it is important to remove both
the positional and the inclination effects. To do this we use the
method described by Aryal & Saurer (2000). In their
method, a true spatial distribution of the galaxy rotation axis is
assumed to be isotropic. Then, due to the projection effects, i can be distributed ![]()
![]() ,
b can be distributed
,
b can be distributed ![]()
![]() ,
the variables l and p can be distributed
randomly, and formulae (1) and (2) can be used to calculate the
corresponding values of
,
the variables l and p can be distributed
randomly, and formulae (1) and (2) can be used to calculate the
corresponding values of ![]() and
and ![]() .
The isotropic
distribution curves are based on calculations including
.
The isotropic
distribution curves are based on calculations including
![]() virtual galaxies. These isotropic distribution curves in
virtual galaxies. These isotropic distribution curves in ![]() (Fig. 7) and
(Fig. 7) and ![]() (Fig. 8) are compared with the observations.
(Fig. 8) are compared with the observations.
Due to poor knowledge of the real shapes of galaxies (Godlowski & Ostrowski 1999; Godlowski et al. 2005) in the cluster, it is difficult to get correct theoretical distributions concerning the spatial orientation of galaxies. We believe that the relation between angular momenta and masses of galaxy structures in A 3558 gives the clue needed for the preferred alignment. This should be verified in the future.
To remove the Holmberg effect we adopted the method of Fouque &
Paturel (1985) in order to convert the measured diameters
to standard photometric diameters. For this aim we measured the
diameters of 78 galaxies for which diameters were given in the
catalogue and compared those values with the measurements. The
ratio of the measured and given diameters is found to be 1.07 to 1.12 (7-12% larger). We used an additive constant for the ESO,
UGC, and MGC catalogues to reduce the visual diameters of galaxies
to photometric ones. We found that our data need an additive
constant 0
![]() 17 to the visual diameters to put them on the
photometric system.
17 to the visual diameters to put them on the
photometric system.
Both ![]() and
and ![]() are assigned to be functions of b, l,
i, and p. The errors in the coordinates and PAs were determined
by comparing the measured values with known values in the
catalogues (UGC, ESO, and MGC) and the errors turned out to be less
than 10
are assigned to be functions of b, l,
i, and p. The errors in the coordinates and PAs were determined
by comparing the measured values with known values in the
catalogues (UGC, ESO, and MGC) and the errors turned out to be less
than 10
![]() and
and ![]() 10
10![]() .
The error in
major and minor diameters, mainly due to a limited step size, was
estimated to be 5
.
The error in
major and minor diameters, mainly due to a limited step size, was
estimated to be 5![]() .
Using the standard tool of error
propagation, the errors in i,
.
Using the standard tool of error
propagation, the errors in i, ![]() ,
and
,
and ![]() can be
estimated to be 6
can be
estimated to be 6![]() ,
12
,
12![]() ,
and 17
,
and 17![]() ,
respectively.
,
respectively.
We first give the results of two-dimensional analysis (galactic
PA-distribution) and later discuss their significance in
three-dimentional analysis (![]() and
and ![]() -distribution).
-distribution).
Table 3: Statistics of the galactic position angle distribution of galaxies in the total sample and subsamples.
Here we analyze the distribution of the PAs (i.e., the PA of the major
diameter) of galaxies instead of the rotation axes. The rotation axis is
perpendicular to the galactic planes therefore, the conditions for
anisotropy are the same as for the ![]() and
and ![]() -distributions. Only the
sign of
-distributions. Only the
sign of
![]() is opposite:
is opposite:
![]() indicates an excess of galaxies
with the galactic plane parallel to the equatorial plane.
indicates an excess of galaxies
with the galactic plane parallel to the equatorial plane.
![\begin{figure}
\par\includegraphics[height=4cm,clip]{5179f06a.eps}\includegraphi...
...,clip]{5179f06i.eps}\includegraphics[height=4cm,clip]{5179f06j.eps}
\end{figure}](/articles/aa/full/2006/41/aa5179-06/Timg71.gif) |
Figure 6:
The galactic position angle (p) distribution of
galaxies found in a) A 3558 region (total sample). The subsamples
are: b) S+S0 galaxies, c) galaxies with radial velocity in the
range 13 000-14 250 km s-1 (RV1), d) galaxies with
radial velocity |
| Open with DEXTER | |
Figure 6 shows the p-distribution of galaxies in the total sample
and subsample. The statistical parameters for the galactic position angle (p)
distribution of the total sample and subsamples are given in Table 3. The first three columns give the samples, the dips and humps in the galactic position angle (p)
distribution (Fig. 6). The next two columns give the results of
Kolmogorov-Smirnov test and Kuiper-V test: a "0'' denotes that the
null hypothesis (isotropy) cannot be rejected at the chosen
significance level, "1'' designates that the null hypothesis can be rejected. The last two columns
give the first-order Fourier coefficient (
![]() /
/![]() (
(
![]() )) and first-order
Fourier probability (P(>
)) and first-order
Fourier probability (P(>![]() )).
)).
The total sample shows the isotropy in all three statistical tests (Table 3). Similar to the total sample, the subsamples S+S0, RV2, SL, BL, M2, HX and IR show no preferred alignment in the position angle distribution. Hence, a random orientation of PA of galaxies is found with respect to the galactic coordinate system.
The Kolmogorov-Smirnov and Kuiper-V tests show anisotropy in two
subsamples: RV1 and M1. A significant hump at 90
![]() can be
seen in these subsamples (Figs. 6c,g). In the Fourier test, the
P(>
can be
seen in these subsamples (Figs. 6c,g). In the Fourier test, the
P(>![]() )
is found <15% in these subsamples. The
)
is found <15% in these subsamples. The
![]() value is found at the >1.3
value is found at the >1.3![]() level, suggesting
that the galactic planes of the galaxies tend to lie parallel to
the plane of the Milky Way, i.e., the galactic plane. In other
words, the rotation axes of the galaxies tend to be oriented
perpendicular to the galactic plane.
level, suggesting
that the galactic planes of the galaxies tend to lie parallel to
the plane of the Milky Way, i.e., the galactic plane. In other
words, the rotation axes of the galaxies tend to be oriented
perpendicular to the galactic plane.
To understand the evolution of a cluster, a good
knowledge of its reference system is needed. Using the least-square
fit, we fitted a straight line for all galaxies in the
investigated cluster region and estimated the cluster position angle
as 18![]() .
We studied the p-distributions of galaxies in the
total sample and subsamples with respect to the estimated cluster PA. In the total sample, a hump at
.
We studied the p-distributions of galaxies in the
total sample and subsamples with respect to the estimated cluster PA. In the total sample, a hump at ![]() 10
10![]() is noticed;
however, it shows isotropy in the statistics. We do
not notice any correlation between the estimated cluster position
angle (i.e., 18
is noticed;
however, it shows isotropy in the statistics. We do
not notice any correlation between the estimated cluster position
angle (i.e., 18![]() )
and the humps or dips in the subsamples. No
preferred alignment is noticed in the cluster position angle.
)
and the humps or dips in the subsamples. No
preferred alignment is noticed in the cluster position angle.
Hence, the total sample shows isotropy with respect to the cluster PA,
as well as to the galactic plane. The low RV (RV1) and the low-magnitude (M1)
galaxies in the cluster Abell 3558 show anisotropy.
We compare our results of two-dimensional analysis
(p-distribution) and three-dimensional analysis (![]() and
and ![]() distribution) in Sect. 5.4.
distribution) in Sect. 5.4.
Table 4 gives the statistical parameters and Fig. 7 shows this distribution in the galactic plane:
![]() (90
(90
![]() )
corresponds to the galactic SV and tends to
lie parallel (perpendicular) the galactic plane.
We assume weak anisotropy if,
)
corresponds to the galactic SV and tends to
lie parallel (perpendicular) the galactic plane.
We assume weak anisotropy if,
![]() /
/![]() (
(
![]() .
.
Table 4: Statistics of the polar angle distribution of galaxies in the total sample and subsamples. See text for an explanation of the columns.
![\begin{figure}
\par\includegraphics[height=4.1cm,clip]{5179f07a.eps}\includegrap...
...}\includegraphics[height=4.1cm,clip]{5179f07j.eps}\hspace*{4.1cm}}\end{figure}](/articles/aa/full/2006/41/aa5179-06/Timg74.gif) |
Figure 7:
The polar angle ( |
| Open with DEXTER | |
The total sample shows isotropy in all three statistics (Table 4). The
expected isotropic distribution almost fits the
observed distribution (Fig. 7a). A small dip at 57.5
![]() was not enough
to change the statistical result to anisotropy. It should be noted
that the dips at larger angles (>45
was not enough
to change the statistical result to anisotropy. It should be noted
that the dips at larger angles (>45
![]() )
and the humps at
smaller angles (<45
)
and the humps at
smaller angles (<45
![]() )
cause a negative
)
cause a negative
![]() value, suggesting that the SVs of galaxies tend to lie parallel
to the galactic plane. Here the
value, suggesting that the SVs of galaxies tend to lie parallel
to the galactic plane. Here the
![]() value
is found well within the
value
is found well within the ![]() 1
1![]() error limit. Hence, no
preferred alignment is noticed in the spatial orientation of 323
galaxies found in the A 3558 cluster region.
error limit. Hence, no
preferred alignment is noticed in the spatial orientation of 323
galaxies found in the A 3558 cluster region.
In the ![]() -distribution of the S+S0 galaxies in A 3558, both
K-S and Kuiper-V tests show isotropy. In these tests, the symbol "0''
indicates that the null hypothesis cannot be rejected. In other
words, our hypothesis (isotropy and homogeneous) is confirmed for
this subsample. Here we do not discuss the results of the Fourier
test because of poor statistics (number of the solution <5 in
many bins, see Fig. 7b). Hence, we conclude a random orientation
for S+S0 galaxies.
-distribution of the S+S0 galaxies in A 3558, both
K-S and Kuiper-V tests show isotropy. In these tests, the symbol "0''
indicates that the null hypothesis cannot be rejected. In other
words, our hypothesis (isotropy and homogeneous) is confirmed for
this subsample. Here we do not discuss the results of the Fourier
test because of poor statistics (number of the solution <5 in
many bins, see Fig. 7b). Hence, we conclude a random orientation
for S+S0 galaxies.
Five humps at 17.5
![]() (>1
(>1![]() ), 32.5
), 32.5
![]() (>1.5
(>1.5![]() ), 37.5
), 37.5
![]() (>1
(>1![]() ), 42.5
), 42.5
![]() (>1
(>1![]() ), and 67.5
), and 67.5
![]() (>1
(>1![]() )
can be seen in the
)
can be seen in the
![]() -distribution of the galaxies with a radial velocity in
the range 13 000 km s-1 and 14 250 km s-1 (RV1) (Fig. 7c). Four humps at smaller angles (<45
-distribution of the galaxies with a radial velocity in
the range 13 000 km s-1 and 14 250 km s-1 (RV1) (Fig. 7c). Four humps at smaller angles (<45
![]() )
cause a
negative
)
cause a
negative
![]() value at >1.2
value at >1.2![]() level, suggesting
that the SVs of low-RV galaxies tend to be aligned parallel
to the galactic plane. The dips at 52.5
level, suggesting
that the SVs of low-RV galaxies tend to be aligned parallel
to the galactic plane. The dips at 52.5
![]() (>1
(>1![]() )
and 72.5
)
and 72.5
![]() (
(![]() 1
1![]() )
support this
result. The
)
support this
result. The
![]() /
/![]() (
(
![]() ,
because of dips at smaller angles (<45
,
because of dips at smaller angles (<45
![]() ). The first-order
Fourier probability is found to be 20% because of these dips. Thus,
the Fourier test shows weak anisotropy for this subsample. The results
of the K-S and Kuiper-V tests suggest anisotropy and thus that
the null hypothesis can be rejected here. Hence, the SV orientation of RV1 galaxies in the cluster A 3558 tends to lie
parallel to the galactic plane. All three statistical tests show
isotropy in the subsample RV2 (Table 3). No significant hump can
be seen in Fig. 7d. The low RV galaxies in the A 3558 region show a
preferred alignment, whereas the high RV galaxies show a random
alignment.
). The first-order
Fourier probability is found to be 20% because of these dips. Thus,
the Fourier test shows weak anisotropy for this subsample. The results
of the K-S and Kuiper-V tests suggest anisotropy and thus that
the null hypothesis can be rejected here. Hence, the SV orientation of RV1 galaxies in the cluster A 3558 tends to lie
parallel to the galactic plane. All three statistical tests show
isotropy in the subsample RV2 (Table 3). No significant hump can
be seen in Fig. 7d. The low RV galaxies in the A 3558 region show a
preferred alignment, whereas the high RV galaxies show a random
alignment.
Similar to the subsamples RV1, the subsample M1 shows anisotropy in
all three statistics. A hump at 82.5
![]() (>1.5
(>1.5![]() )
and a
dip at 2.5
)
and a
dip at 2.5
![]() (>2
(>2![]() )
make a positive
)
make a positive
![]() value at the
value at the ![]() 1.4
1.4![]() level in the subsample M1 (Table 3,
Fig. 7g). Thus, the galaxies with lower magnitudes (mostly low-optical
surface brightness galaxies) in the cluster A 3558 show that
their SVs tend to be oriented perpendicular to the
galactic plane. A random orientation is found for the galaxies
having magnitudes greater than 18.
level in the subsample M1 (Table 3,
Fig. 7g). Thus, the galaxies with lower magnitudes (mostly low-optical
surface brightness galaxies) in the cluster A 3558 show that
their SVs tend to be oriented perpendicular to the
galactic plane. A random orientation is found for the galaxies
having magnitudes greater than 18.
No preferred alignment is shown by the galaxies found in both the hard
X-ray and 100 ![]() m emission regions in the cluster field. All
three statistics give isotropy in the subsamples HX and IR. A
small dip at 2.5
m emission regions in the cluster field. All
three statistics give isotropy in the subsamples HX and IR. A
small dip at 2.5
![]() and humps at 22.5
and humps at 22.5
![]() and 82.5
and 82.5
![]() were not enough to change the statistical result to show anisotropy
in the subsample HX (Fig. 7i). We do not discuss the results of
the Fourier test for subsample IR because of poor statistics
(number of the
were not enough to change the statistical result to show anisotropy
in the subsample HX (Fig. 7i). We do not discuss the results of
the Fourier test for subsample IR because of poor statistics
(number of the
![]() in many bins, see Fig. 7j). We
conclude isotropy for this subsample because of the results of the K-S
and Kuiper-V statistics.
in many bins, see Fig. 7j). We
conclude isotropy for this subsample because of the results of the K-S
and Kuiper-V statistics.
Thus, two subsamples RV1 and M1 show weak anisotropy in the polar
angle distribution. The SVs of the low RV galaxies (13 000 km s-1 to 14 250 km s-1) in the cluster A 3558 tend to lie
parallel to the galactic plane, whereas the low-magnitude galaxies
(![]() )
in the cluster A 3558 tend to be oriented
perpendicular to the galactic plane. No preferred
alignment of SVs of galaxies in the total sample and the
subsamples S+S0, RV2, SL, BL, M2, HX, and IR is noticed.
)
in the cluster A 3558 tend to be oriented
perpendicular to the galactic plane. No preferred
alignment of SVs of galaxies in the total sample and the
subsamples S+S0, RV2, SL, BL, M2, HX, and IR is noticed.
Statistical parameters for the azimuthal angle (![]() )
distribution of the total sample and subsamples are given in Table 5. Figure 8 shows the distribution of the SV projections (
)
distribution of the total sample and subsamples are given in Table 5. Figure 8 shows the distribution of the SV projections (![]() )
of galaxies in the total sample and subsamples with respect to the
galactic coordinate system. In the figures,
)
of galaxies in the total sample and subsamples with respect to the
galactic coordinate system. In the figures,
![]() means the direction towards the galactic center.
means the direction towards the galactic center.
Table 5: Statistics of the azimuthal angle distribution of galaxies in the total sample and subsamples. See text for an explanation of the columns.
![\begin{figure}
\par\includegraphics[height=4.1cm,clip]{5179f08a.eps}\includegrap...
...}\includegraphics[height=4.1cm,clip]{5179f08h.eps}\hspace*{4.1cm}}\end{figure}](/articles/aa/full/2006/41/aa5179-06/Timg78.gif) |
Figure 8:
The azimuthal angle ( |
| Open with DEXTER | |
It is relatively easy to interpret the humps and dips in the
histograms of the ![]() -distribution. This is not the case with
those of the
-distribution. This is not the case with
those of the ![]() -distribution because of their ranges,
-90
-distribution because of their ranges,
-90
![]() to 90
to 90
![]() .
In the histograms of the
.
In the histograms of the
![]() -distribution,
-distribution,
![]() means the direction towards
the center of the galactic coordinate system (e.g. Fig. 8). Humps
in the region -50
means the direction towards
the center of the galactic coordinate system (e.g. Fig. 8). Humps
in the region -50
![]() to +50
to +50
![]() and the dips at -90
and the dips at -90
![]() to -50
to -50
![]() (first 4 bins) and at 50
(first 4 bins) and at 50
![]() to 90
to 90
![]() (last 4 bins) make the
(last 4 bins) make the
![]() value positive in
the
value positive in
the ![]() -distribution. A positive
-distribution. A positive
![]() suggests that
the SV projections of galaxies tend to point towards the galactic
center. Similarly, a negative
suggests that
the SV projections of galaxies tend to point towards the galactic
center. Similarly, a negative
![]() suggests that the SV projections of galaxies tend to be oriented perpendicular with
respect to the galactic center. In the
suggests that the SV projections of galaxies tend to be oriented perpendicular with
respect to the galactic center. In the ![]() -distribution, the
-distribution, the
![]() value would be negative for
value would be negative for ![]() when humps are at -90
when humps are at -90
![]() to -50
to -50
![]() (first 4 bins) and at 50
(first 4 bins) and at 50
![]() to 90
to 90
![]() (last 4 bins) and dips are at -50
(last 4 bins) and dips are at -50
![]() to +50
to +50
![]() .
.
Selection effects make the shape of the expected isotropic
![]() -distribution curves rather complex (solid lines in Fig. 8).
We ran simulations to examine the possible effects on the results
of the Fourier test of the errors in
-distribution curves rather complex (solid lines in Fig. 8).
We ran simulations to examine the possible effects on the results
of the Fourier test of the errors in ![]() (17
(17
![]() ). It turned
out that the results of the Fourier test remains unchanged, so
we regard the Fourier test as more reliable. We assumed weak
anisotropy if
). It turned
out that the results of the Fourier test remains unchanged, so
we regard the Fourier test as more reliable. We assumed weak
anisotropy if
![]() /
/![]() (
(
![]() .
.
The total sample shows isotropy in all three statistics (Table 5),
meaning the distributions of SV projections of galaxies in the
cluster A 3558 were found to be random. Similar to the total sample, the
subsamples RV2, BL, M1, M2, and IR show isotropy in the
![]() -distribution. The Fourier probability is >40% in
these samples. The results of the K-S and Kuiper-V tests for these
samples give isotropy suggesting that the null hypothesis cannot
be rejected here. Hence, no preferred alignment is found in the
total sample as well as in the subsamples RV2, SL, M1, M2, and IR.
-distribution. The Fourier probability is >40% in
these samples. The results of the K-S and Kuiper-V tests for these
samples give isotropy suggesting that the null hypothesis cannot
be rejected here. Hence, no preferred alignment is found in the
total sample as well as in the subsamples RV2, SL, M1, M2, and IR.
Anisotropy is found in the subsamples S+S0, RV1, and SL (Figs. 8b,c,f). This can be seen in the results of the statistics (Table 5). The
![]() value is positive at >1.5
value is positive at >1.5![]() level for these subsamples, suggesting that the SV projections of
galaxies tend to point towards the center of the galactic
coordinate system.
level for these subsamples, suggesting that the SV projections of
galaxies tend to point towards the center of the galactic
coordinate system.
Thus, total sample and 6 subsamples show isotropy, and three
subsamples (S+S0, RV1, and SL) show anisotropy in the
![]() -distribution. These three subsamples show a similar
tendency: the SVs projections of the galaxies tend to point
towards the galactic center of the Milky Way.
-distribution. These three subsamples show a similar
tendency: the SVs projections of the galaxies tend to point
towards the galactic center of the Milky Way.
![\begin{figure}
\par\includegraphics[height=4.7cm,clip]{5179f09a.eps}\par\include...
...5179f09b.eps}\par\includegraphics[height=4.8cm,clip]{5179f09c.eps}
\end{figure}](/articles/aa/full/2006/41/aa5179-06/Timg79.gif) |
Figure 9:
The orientation parameter (the first-order Fourier coefficient,
|
| Open with DEXTER | |
Aryal & Saurer (2004) find anisotropy when analyzing 296 galaxies in A 3558 region in both the two-dimensional (equatorial
PA-distribution) and three-dimensional analysis (![]() and
and
![]() -distributions). In the three-dimensional analysis, they
studied the preferred orientation with respect to the
Supergalactic coordinate system and found that the SV of galaxies
tend to lie parallel to the Local Supercluster plane and SV
projections of galaxies tend to be directed towards the Local
Supercluster center (Virgo cluster center). In this work, no
preferred alignment was noticed in both the two- and
three-dimensional analyze when analyzing 324 galaxies.
Interestingly, we noticed a similar tendency to the one in Aryal
& Saurer (2004) for few subsamples of A 3558.
-distributions). In the three-dimensional analysis, they
studied the preferred orientation with respect to the
Supergalactic coordinate system and found that the SV of galaxies
tend to lie parallel to the Local Supercluster plane and SV
projections of galaxies tend to be directed towards the Local
Supercluster center (Virgo cluster center). In this work, no
preferred alignment was noticed in both the two- and
three-dimensional analyze when analyzing 324 galaxies.
Interestingly, we noticed a similar tendency to the one in Aryal
& Saurer (2004) for few subsamples of A 3558.
Figure 9 shows the orientation parameter (Fourier coefficient,
![]() /
/![]() (
(
![]() )) plot for the position (a)
polar (b) and azimuthal angle (c) of the total sample and
subsamples. It can be seen in Fig. 9 that the general trend to alignment
(
)) plot for the position (a)
polar (b) and azimuthal angle (c) of the total sample and
subsamples. It can be seen in Fig. 9 that the general trend to alignment
(
![]() is negative for PA and polar angle distributions;
positive for azimuthal angle distributions) is found to be similar
to both the galactic and Supergalactic systems.
is negative for PA and polar angle distributions;
positive for azimuthal angle distributions) is found to be similar
to both the galactic and Supergalactic systems.
The subsamples (total sample, RV2, SL, M2, HX, and IR) that showed isotropy in the two-dimensional analysis showed similar results in the three-dimensionl analysis. Thus, the projection effects in the two-dimensional analysis is studied better in the three-dimensional analysis.
The core of the Shapley Concentration is dynamically very active; the main cluster A 3558 appears to be interacting with the other clusters A 3562 and A 3556 (Bardelli et al. 1994). In a substructure analysis, Bardelli et al. (1998) briefly discuss the core of the Shapley concentration and suggest that the core complex is the result of a series of incoherent group-group and cluster-group mergings. Bardelli et al. (1998) studied the fraction of blue galaxies in the whole substructure and found that the bluest group is located between A 3558 and A 3562, i.e., in the expected position for the scenario of cluster-cluster collision. Metcalfe et al. (1994) suggest that there may already have been an encounter between A 3558 and A 3562. In our study, high RV (14 250 km s-1 to 16 000 km s-1) galaxies in A 3558 show random alignment. Thus, no preferred orientation is noticed in the bluest group of galaxies, suggesting that the cluster-cluster collision might be in an early phase or the collision environment has nothing to do with alignments of galaxies in A 3558.
Venturi et al. (2000) carried out detailed statistical analysis of the radio properties in connection with the dynamical state of the A 3558 cluster complex and found that the ratio between the radio and the optical flux for the Shapley radio galaxies is not affected by the local galaxy density. It indicates that the high optical density in the cluster has no effect on the radio galaxy emissivity. Thus the merging environment plays no role in the radio power distribution of radio sources. Probably, this result could suggest that the merging environments have nothing to do with the random alignment of spin vector of galaxies in A 3558 with respect to the galactic coordinate system.
Kitzbichler & Saurer (2003) studied the Coma cluster and
suggest that there are deviations from a completely random galaxy
orientation on small scales. They noticed local anisotropies in
the X-ray emission region and concluded that the X-ray subcluster
of the Coma cluster might be falling in on the main cluster. We
found that the galaxies found in the hard X-ray emission region
(subsample HX) in A 3558 show a weak anisotropy (
![]() )
in the azimuthal angle distribution. This indicates a
significant coincidence of hot-gas features identified in the hard
X-ray observation (GRANAT/SIGMA Survey, Paul et al. 1991)
of A 3558 with this local anisotropy.
)
in the azimuthal angle distribution. This indicates a
significant coincidence of hot-gas features identified in the hard
X-ray observation (GRANAT/SIGMA Survey, Paul et al. 1991)
of A 3558 with this local anisotropy.
The only subsample RV1 showed anisotropy in both the two and
three-dimensional analyses. The centre CD galaxy (equatorial
![]() )
belongs to this subsample. The spin vector orientations
of low RV (13 000 km s-1 to 14 250 km s-1) galaxies in
A 3558 tend to lie parallel to the galactic plane and their SV projections tend to point towards the galactic center. This result
might support the idea that the galaxies are falling in
towards the centrally located cD galaxy.
)
belongs to this subsample. The spin vector orientations
of low RV (13 000 km s-1 to 14 250 km s-1) galaxies in
A 3558 tend to lie parallel to the galactic plane and their SV projections tend to point towards the galactic center. This result
might support the idea that the galaxies are falling in
towards the centrally located cD galaxy.
We ran simulations to observe the changes in the results when the
galactic plane of the Milky Way is rotated by an angle ![]() .
Our
results for the subsample RV1 remain the same when
.
Our
results for the subsample RV1 remain the same when
![]() .
This indicates that the
low-RV galaxies in the A 3558 region support the pancake model, if the
reference plane of the clusters does not deviate by more than
.
This indicates that the
low-RV galaxies in the A 3558 region support the pancake model, if the
reference plane of the clusters does not deviate by more than ![]() 20
20
![]() from that of the galactic plane.
from that of the galactic plane.
We compare our results for the subsample "S+S0'' to Godlowski's
(1993) subsample "S''. He analyzed the S galaxies given
in the UGC ESO Catalogue (Nilson 1973) and NGC Tully
Catalogue (Tully 1988) separately. In the
![]() -distribution (
-distribution (![]() in our notation), he found
isotropy for the spiral galaxies, similar to our result. He found
anisotropy for the spirals (taken from the NGC Tully Catalogue) in
the
in our notation), he found
isotropy for the spiral galaxies, similar to our result. He found
anisotropy for the spirals (taken from the NGC Tully Catalogue) in
the ![]() -distribution (
-distribution (![]() in our notation). Interestingly,
we obtained a similar result for the "S+S0'' subsamples of the
A 3558 although not at a very high significance level. Godlowski
(1993) found that the SV projections of Spiral galaxies in the
Local Supercluster tend to be oriented tangentially with respect
to the Virgo cluster center. Godlowski (1994) used an
identical sample. Obviously, the results for S in Godlowski
(1994) are almost identical to those of Godlowski
(1993). It is an interesting result that the spatial orientation
of spiral galaxies in the nearby cluster (Local Supercluster,
in our notation). Interestingly,
we obtained a similar result for the "S+S0'' subsamples of the
A 3558 although not at a very high significance level. Godlowski
(1993) found that the SV projections of Spiral galaxies in the
Local Supercluster tend to be oriented tangentially with respect
to the Virgo cluster center. Godlowski (1994) used an
identical sample. Obviously, the results for S in Godlowski
(1994) are almost identical to those of Godlowski
(1993). It is an interesting result that the spatial orientation
of spiral galaxies in the nearby cluster (Local Supercluster,
![]() km s-1; Godlowski 1993) and the
distant cluster (A 3558,
km s-1; Godlowski 1993) and the
distant cluster (A 3558,
![]() km s-1; present
work) is identical to Supergalactic and galactic coordinate
systems, respectively. It indicates that there is a good
correlation between the physical reference plane of the
investigated cluster and Local Supercluster plane, as well as the
galactic plane of our Milky-way.
km s-1; present
work) is identical to Supergalactic and galactic coordinate
systems, respectively. It indicates that there is a good
correlation between the physical reference plane of the
investigated cluster and Local Supercluster plane, as well as the
galactic plane of our Milky-way.
The galaxies investigated in the core of the Shapley Concentration, i.e., the cluster Abell 3558, shows isotropy in both the two- and three-dimensional analysis when analyzing with respect to the galactic coordinate system. Thus, our results for the total sample support the hierarchy model (Peebles 1969), which predicts that the directions of the spin vectors are entirely random. In addition, it is found that the overall isotropic appearance of galaxy orientation in A 3558 cannot be maintained when looking at the subsamples.
A few subsamples (RV1, M1 in ![]() -distribution and S+S0, RV1,
SL in
-distribution and S+S0, RV1,
SL in ![]() -distribution) show anisotropy in the same direction,
as concluded by Aryal & Saurer (2004). The spin vector
orientations of galaxies in these subsamples tend to lie parallel
to the reference plane, and the spin vector projections tend to be
directed towards the center of the reference system. This is an
interesting result in that similar preferred alignments of
galaxies in A 3558 is noticed with respect to both Supergalactic
(Aryal & Saurer 2004) and galactic coordinate systems (present
study). Finding similar alignments with respect to the
Supergalactic and galactic systems is a noticeable result.
Probably, this result could indicate that the physical reference
plane of the cluster might coincide with a plane of a higher
concentration of galaxies at much larger scales.
-distribution) show anisotropy in the same direction,
as concluded by Aryal & Saurer (2004). The spin vector
orientations of galaxies in these subsamples tend to lie parallel
to the reference plane, and the spin vector projections tend to be
directed towards the center of the reference system. This is an
interesting result in that similar preferred alignments of
galaxies in A 3558 is noticed with respect to both Supergalactic
(Aryal & Saurer 2004) and galactic coordinate systems (present
study). Finding similar alignments with respect to the
Supergalactic and galactic systems is a noticeable result.
Probably, this result could indicate that the physical reference
plane of the cluster might coincide with a plane of a higher
concentration of galaxies at much larger scales.
The low-RV galaxies in A 3558 showed anisotropy in such a way that their spin-vector orientations tend to lie parallel to the galactic plane, and their spin vector projections tend to point towards the galactic center. This result supports the pancake model (Doroshkevich 1973; Shandarin 1974; Doroshkevich & Shandarin 1978), which predicts that spin vectors of galaxies tend to lie within the cluster plane. A weak anisotropy is noticed in the hard X-ray emission region. We suspect that this result indicates an interesting coincidence of hot-gas features identified in the hard X-ray observation of A 3558 with this local anisotropy. We intend to work on this coincidence in the future.
Acknowledgements
The authors wish to thank the referee for the careful reading of the manuscript and the useful suggestions helped us improve the paper. This research has made use of the NASA/IPAC Extragalactic Database (NED), which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration, and the SkyView virtual observatory, operated at http://skyview.gsfc.nasa.gov/. We acknowledge Profs. Udayraj Khanal & Mukunda Mani Aryal for their comments and suggestions. One of the authors (S.M.K.) acknowledges the Central Department of Physics, Tribhuvan University, Kirtipur, for providing various forms of support for his masters (M.Sc.) thesis.