A&A 458, 661-668 (2006)
DOI: 10.1051/0004-6361:20053689
K. Kornet1,2 - S. Wolf1 - M. Rózyczka2
1 - Max Planck Institute for Astronomy, Königstuhl 17, 69117 Heidelberg, Germany
2 -
Nicolaus Copernicus Astronomical Center, Bartycka 18, Warsaw 00-716, Poland
Received 23 June 2005 / Accepted 7 March 2006
Abstract
We examine the predictions of the core accretion - gas
capture model concerning the efficiency of planet formation around
stars with various masses. First, we follow the evolution of gas
and solids from the moment when all solids are in the form of
small grains to the stage when most of them are in the form of
planetesimals. We show that the surface density of the
planetesimal swarm tends to be higher around less massive stars.
Then, we derive the minimum surface density of the planetesimal
swarm required for the formation of a giant planet both in a numerical and in an approximate analytical approach. We combine
these results by calculating a set of representative disk models
characterized by different masses, sizes, and metallicities, and
by estimating their capability of forming giant planets. Our results
show that the set of protoplanetary disks capable of giant planet
formation is larger for less massive stars. Provided that the
distribution of initial disk parameters does not depend too
strongly on the mass of the central star, we predict that the
percentage of stars with giant planets should increase with
decreasing stellar mass. Furthermore, we identify the
radial redistribution of solids during the formation of
planetesimal swarms as the key element in explaining these effects.
Key words: accretion, accretion disks - planetary systems: protoplanetary disks - planetary systems: formation
Radial velocity surveys led to the discovery of over 150 extrasolar planets around main sequence stars. Published descriptions of most of them can be found in the references given by Marcy et al. (2005) and Mayor et al. (2004). Those surveys have been the most successful in the case of G dwarf stars, because such stars have well-defined spectroscopic features and show only a little photospheric activity. Consequently, most of the known extrasolar planets orbit stars similar to our Sun. Due to the constant progress in the detection techniques, the observational programs recently started to also include stars with lower masses on a larger scale, namely M dwarfs. Moreover, some of these surveys are now particularly dedicated to lower-mass stars (e.g. Bonfils et al. 2004; Endl et al. 2003). So far, these efforts have led to the discovery of three planets around two M dwarf stars: Gliese 876b,c (Marcy et al. 2001,1998) and GJ436b (Butler et al. 2004).
From the theoretical point of view, the problem of giant planet formation around M dwarfs was studied recently by Laughlin et al. (2004). They addressed it within the core accretion - gas capture model (CAGCM) that provides the most widely accepted scenario explaining the formation of giant planets in both the Solar System and extrasolar planetary systems. This model predicts that first a solid planetary core is formed by collisional accumulation of planetesimals. When the core reaches a mass of a few Earth masses, it starts to accrete gas, and an extended hydrostatic envelope is built around it. As the accretion rate of gas is greater than the accretion rate of solids at this time, the envelope eventually becomes more massive than the core. When this happens, a runaway accretion of gas ensues, which is terminated either by tidal interactions of the planet with the protoplanetary disk or by the dissipation of the disk. CAGCM has found supporting evidence in the discovery that stars with planets have higher metallicities than field stars (Fischer & Valenti 2003; Santos et al. 2000). This is because the formation time of giant planets decreases with increasing surface density of the planetesimal swarm (Pollack et al. 1996), which in turn increases with the primordial metallicity of the protoplanetary disk. Thus, giant planets are expected to form more easily in disks with higher metallicity.
Laughlin et al. (2004) conclude that M dwarfs have a limited ability to form Jupiter-mass planets. This is a direct consequence of their assumption that the surface density of the planetesimal swarm out of which planetary cores are formed scales linearly with the mass of the central star. However, the solid component of the protoplanetary disk evolves in a different way than the gaseous component (Weidenschilling & Cuzzi 1993). Due to the gas drag, a significant redistribution of solids takes place, and in the inner disk their surface density can be substantially enhanced compared to the initial one (Weidenschilling 2003; Stepinski & Valageas 1997). In general, the efficiency of the processes responsible for the redistribution of dust depends on the mass of the central star. An obvious conclusion is that analysis of the formation of giant planets around stars with various masses should include the global evolution of solids in protoplanetary disks. A simple model of the evolution of solids was proposed by Kornet et al. (2005,2002). Applying it to solar-like central stars, these authors reproduced the observed correlation between stellar metallicity and the probability of a planet occurring (a similar result was independently obtained by Ida & Lin 2004b).
The rapid progress in observational techniques opens up the possibility
of testing the correctness and predictive power of the model proposed
by Kornet et al. (2005). To that end, we extend their analysis and
calculate probabilities of planet occurrence around stars with
different masses (both smaller and larger than ![]() ), which
may be compared to future observational data. In Sect. 2 we explain our approach to the evolution of protoplanetary disks and planet formation. The results of our
calculations are presented in Sect. 3 and discussed in Sect. 4.
), which
may be compared to future observational data. In Sect. 2 we explain our approach to the evolution of protoplanetary disks and planet formation. The results of our
calculations are presented in Sect. 3 and discussed in Sect. 4.
We model the protoplanetary disk as a two-component fluid,
consisting of gas and solids. The gaseous component is described
by the analytical model of Stepinski (1998), which gives the surface
density of gas,
![]() ,
as a function of distance afrom the star and time t, in terms of a selfsimilar solution to
the viscous diffusion equation. The viscosity coefficient is given
by the standard
,
as a function of distance afrom the star and time t, in terms of a selfsimilar solution to
the viscous diffusion equation. The viscosity coefficient is given
by the standard ![]() prescription:
prescription:
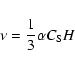 |
(1) |
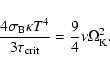 |
(6) |
The evolution of solids is governed by two equations. The first of
them is the continuity equation for the surface density of solid
material,
![]() .
The second one, describing
the evolution of grain sizes, can be interpreted as the continuity
equation for size-weighted surface density of solids,
.
The second one, describing
the evolution of grain sizes, can be interpreted as the continuity
equation for size-weighted surface density of solids,
![]() ,
where s(a)is the radius of solid particles at a distance a from the star.
The equations are solved numerically on a moving grid whose outer
edge follows the outer edge of the dust disk. The details of the
method can be found in Kornet et al. (2001).
,
where s(a)is the radius of solid particles at a distance a from the star.
The equations are solved numerically on a moving grid whose outer
edge follows the outer edge of the dust disk. The details of the
method can be found in Kornet et al. (2001).
![\begin{figure}
\par\includegraphics[angle=-90,width=7.55cm,clip]{3689sig.ps}\includegraphics[angle=-90,width=7.45cm,clip]{3689T.ps}\end{figure}](/articles/aa/full/2006/41/aa3689-05/Timg31.gif) |
Figure 1:
The initial surface density ( left panel) and temperature
( right panel) as a function of distance from the star in the
protoplanetary disk with an initial mass
|
| Open with DEXTER | |
We model the formation of a giant planet in situ, so the
orbital parameters of the planet do not vary in time. Our
procedure for the evolution of the protoplanetary cores is based
on the following assumptions: (1) core accretion starts when
solids at a given distance a from the star reach radii of
![]() ;
(2) at each time, the planetesimals are mixed well through the feeding zone of the planet, so their surface
density
;
(2) at each time, the planetesimals are mixed well through the feeding zone of the planet, so their surface
density
![]() is always uniform in space, but
usually decreasing with time as planetesimals accrete onto
the planet; (3) the planetesimals do not migrate into the feeding
zone from outside or inside and vice versa, but they can be
overtaken by the boundary of the feeding zone as it expands due to
the growing mass of the planet. Under these assumptions the growth
of protoplanetary core mass
is always uniform in space, but
usually decreasing with time as planetesimals accrete onto
the planet; (3) the planetesimals do not migrate into the feeding
zone from outside or inside and vice versa, but they can be
overtaken by the boundary of the feeding zone as it expands due to
the growing mass of the planet. Under these assumptions the growth
of protoplanetary core mass ![]() can be described by
the formula given by Papaloizou & Terquem (1999),
can be described by
the formula given by Papaloizou & Terquem (1999),
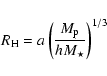 |
(8) |
To calculate the rate of gas accretion onto the protoplanet, one should
solve the equations of mass conservation,
hydrostatic equilibrium, energy generation from accretion of
planetesimals and quasi-static contraction, and radiative or
convective energy transport, as given e.g. in Bodenheimer & Pollack (1986).
Following Ida & Lin (2004a), we use a simplified approach based
on fits to the numerical results. We assume that the accretion of
gas starts when the core reaches critical mass of
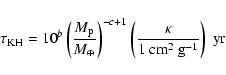 |
(11) |
In the CAGCM the process of planet formation is naturally split into two main phases. In the first one, dominated by collisional accumulation of dust grains, a planetesimal swarm is formed in the protoplanetary disk. In the second phase, dominated by gravitational interactions, planetary cores are assembled and subsequently accrete planetesimals and gas from the disk. In the following subsections we investigate how each phase is influenced by the mass of the central star.
To illustrate how the mass of the central star influences the
formation of the planetesimal swarm, we follow the evolution of a protoplanetary disk with an initial mass
![]() and initial outer radius
and initial outer radius
![]() for three values of
for three values of ![]() (0.5,1 and 4
(0.5,1 and 4 ![]() ). Figure 1 shows the
initial distributions of
). Figure 1 shows the
initial distributions of
![]() and T in the
midplane of the disk. In all three cases the gas is distributed
very similarly, with
and T in the
midplane of the disk. In all three cases the gas is distributed
very similarly, with
![]() dropping monotonically
from
dropping monotonically
from ![]()
![]() at 0.01 AU from the star to
at 0.01 AU from the star to
![]() at the outer edge of the disk. The
changes of slopes in the distribution of
at the outer edge of the disk. The
changes of slopes in the distribution of
![]() correspond to transitions between different powerlaws describing
the opacity of the disk matter in different temperature ranges
(Ruden & Pollack 1991). The distribution of temperature is qualitatively
very similar to the distribution of
correspond to transitions between different powerlaws describing
the opacity of the disk matter in different temperature ranges
(Ruden & Pollack 1991). The distribution of temperature is qualitatively
very similar to the distribution of
![]() .
In the
disk around a
.
In the
disk around a ![]() star T drops from
star T drops from
![]() at
at
![]() to a few Kelvins at the outer edge of the
disk. The evaporation temperature assumed for the dust grains in
our models (
to a few Kelvins at the outer edge of the
disk. The evaporation temperature assumed for the dust grains in
our models (
![]() )
is reached at
)
is reached at
![]() .
Note that at a given radius T increases as the mass of the central star is increased. It is the result of the
increasing vertical component stellar gravity, due to which the
scale height of the disk is reduced.
.
Note that at a given radius T increases as the mass of the central star is increased. It is the result of the
increasing vertical component stellar gravity, due to which the
scale height of the disk is reduced.
Initially, the dust is well mixed with the gas, with the ratio
![]()
![]() 10-3 being
constant everywhere in the disk. As the disk evolves, surface
density and temperature of gas slowly decrease due to accretion
and viscous spreading; however, the dust component evolves in
quite a different way. The grains grow in size due to mutual
collisions and gain inward radial velocities due to the gas drag.
If they cross the evaporation radius, they sublimate and are
accreted onto the star on the viscous timescale as a vapour.
However, if their growth time is shorter than the timescale of
inward migration, they manage to reach sizes of a few km before reaching the evaporation radius. Their radial motions are
then stopped and the planetesimal swarm attains its final form.
Figure 2 shows the distribution of planetesimals in our
model after 106 yr from the beginning of its evolution. In all
three cases, the outer radius of the planetesimal swarm is much
smaller than the initial outer radius of the disk. The difference
is larger for models with smaller
10-3 being
constant everywhere in the disk. As the disk evolves, surface
density and temperature of gas slowly decrease due to accretion
and viscous spreading; however, the dust component evolves in
quite a different way. The grains grow in size due to mutual
collisions and gain inward radial velocities due to the gas drag.
If they cross the evaporation radius, they sublimate and are
accreted onto the star on the viscous timescale as a vapour.
However, if their growth time is shorter than the timescale of
inward migration, they manage to reach sizes of a few km before reaching the evaporation radius. Their radial motions are
then stopped and the planetesimal swarm attains its final form.
Figure 2 shows the distribution of planetesimals in our
model after 106 yr from the beginning of its evolution. In all
three cases, the outer radius of the planetesimal swarm is much
smaller than the initial outer radius of the disk. The difference
is larger for models with smaller ![]() .
This is because small
solid bodies evolving in disks around less massive stars gain
higher inward velocities and tend to migrate to smaller radius
before reaching km-sizes. The maximum velocity of the inward drift
can be estimated as
.
This is because small
solid bodies evolving in disks around less massive stars gain
higher inward velocities and tend to migrate to smaller radius
before reaching km-sizes. The maximum velocity of the inward drift
can be estimated as
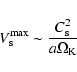 |
(13) |
Due to the inward migration of solids and their
confinement to much smaller radii, the final surface density of
planetesimals is increased locally within a factor of a few in
comparison with the initial value of
![]() .
As this
effect is larger in disks around less massive stars, their final
planetesimal swarms tend to be more favourable to the formation
of giant planets.
.
As this
effect is larger in disks around less massive stars, their final
planetesimal swarms tend to be more favourable to the formation
of giant planets.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.35cm,clip]{3689sig_.ps}\end{figure}](/articles/aa/full/2006/41/aa3689-05/Timg68.gif) |
Figure 2:
The surface density of solids as a function distance from the
star in the protoplanetary disk with the same parameters as in
Fig. 1 after
|
| Open with DEXTER | |
To quantify the influence of ![]() on the effectiveness
of giant planet formation from a planetesimal swarm, we introduce
the concept of the minimum surface density
on the effectiveness
of giant planet formation from a planetesimal swarm, we introduce
the concept of the minimum surface density
![]() .
We define it as the minimum value of the initial surface density of planetesimals
.
We define it as the minimum value of the initial surface density of planetesimals
![]() needed to form a Jupiter-mass (1
needed to form a Jupiter-mass (1 ![]() )
planet in less than the lifetime of
the protoplanetary disk
)
planet in less than the lifetime of
the protoplanetary disk
![]() .
For
.
For
![]() we adopt a value of 3
we adopt a value of 3 ![]()
![]() .
.
First, by solving the set of Eqs. (7), (9), and (12) with different values of
![]() ,
we determine
,
we determine
![]() as
a function of distance from the star. The results are shown in Fig. 3 for the same values of
as
a function of distance from the star. The results are shown in Fig. 3 for the same values of ![]() as before. Close to the star (
as before. Close to the star (
![]() ),
),
![]() is a decreasing function a. In this regime, the accreting
protoplanetary core rapidly accumulates all planetesimals in its
feeding zone and reaches the isolation mass
is a decreasing function a. In this regime, the accreting
protoplanetary core rapidly accumulates all planetesimals in its
feeding zone and reaches the isolation mass
![]() .
Afterwards, the accretion of planetesimals is negligible and the
planet grows mainly due to the accretion of gas. Upon integrating
Eq. (12), we obtain the minimum isolation mass
needed to form a 1
.
Afterwards, the accretion of planetesimals is negligible and the
planet grows mainly due to the accretion of gas. Upon integrating
Eq. (12), we obtain the minimum isolation mass
needed to form a 1 ![]() planet within
planet within
![]() :
:
![\begin{displaymath}%
M_{\rm iso}\ge[M_{\rm J}^{1-c}+(c-1) \tilde{A}
\tau_{\rm f}]^{1/(1-c)},
\end{displaymath}](/articles/aa/full/2006/41/aa3689-05/img73.gif) |
(14) |
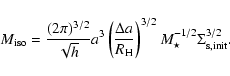 |
(15) |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.25cm,clip]{3689sigc.ps}\end{figure}](/articles/aa/full/2006/41/aa3689-05/Timg78.gif) |
Figure 3:
The minimum surface density of a planetesimal swarm
needed to from a 1 |
| Open with DEXTER | |
For sufficiently large radii
![]() ,
,
![]() changes its slope and becomes an increasing function of a. In this regime, the time scale of accretion of the planetesimals onto the core is larger than the
lifetime of the disk and becomes the main factor to determine
changes its slope and becomes an increasing function of a. In this regime, the time scale of accretion of the planetesimals onto the core is larger than the
lifetime of the disk and becomes the main factor to determine
![]() .
Consequently, the surface density of
planetesimals in the feeding zone never drops much below its
initial value. To describe the formation of a planet analytically
under these conditions, we divide the whole process into two phases. During the first phase the planet exclusively due to the accretion of planetesimals grows. We assume that the surface density
of planetesimal swarm
.
Consequently, the surface density of
planetesimals in the feeding zone never drops much below its
initial value. To describe the formation of a planet analytically
under these conditions, we divide the whole process into two phases. During the first phase the planet exclusively due to the accretion of planetesimals grows. We assume that the surface density
of planetesimal swarm
![]() does not change in time,
because the core only accumulates a negligible fraction of solids
present in the feeding zone. From Eq. (7) we obtain
does not change in time,
because the core only accumulates a negligible fraction of solids
present in the feeding zone. From Eq. (7) we obtain
![\begin{figure}
\par\includegraphics[angle=-90,width=8.25cm,clip]{3689scon.ps}\end{figure}](/articles/aa/full/2006/41/aa3689-05/Timg92.gif) |
Figure 4:
The minimum surface density of the planetesimal swarm
needed to form a 1 |
| Open with DEXTER | |
As we see, the minimum surface density of the planetesimal
swarm required for the formation of a gas giant planet in a time
shorter than the lifetime of protoplanetary disk is a complicated
function of ![]() .
In a given planetesimal swarm such a planet
forms more easily around less massive star if its orbital radius
is smaller than
.
In a given planetesimal swarm such a planet
forms more easily around less massive star if its orbital radius
is smaller than ![]() 10 AU, and around a more massive star if
its orbital radius is larger than
10 AU, and around a more massive star if
its orbital radius is larger than ![]() 10 AU.
10 AU.
The results of the last two subsections allow us to
investigate the influence of ![]() on the whole process of
giant planet formation for a broad set of models of protoplanetary
disks. We calculate the grid of models similar to the one
described in Sect. 3.1, but with different values of the
initial disk mass M0 and outer radius R0. To cover the range
of masses and sizes of disks observed in nature, we choose M0in the range of 0.02 to 0.2
on the whole process of
giant planet formation for a broad set of models of protoplanetary
disks. We calculate the grid of models similar to the one
described in Sect. 3.1, but with different values of the
initial disk mass M0 and outer radius R0. To cover the range
of masses and sizes of disks observed in nature, we choose M0in the range of 0.02 to 0.2 ![]() .
The range of R0 is
adjusted for every metallicity so that all models in which
formation of giant planets is possible could be accounted for. For
the viscosity coefficient
.
The range of R0 is
adjusted for every metallicity so that all models in which
formation of giant planets is possible could be accounted for. For
the viscosity coefficient ![]() we chose a value of 0.001
(Papaloizou & Nelson 2003). We follow each model until all solids are in
the form of planetesimals or are accreted onto the star. Then, we
evaluate every model with planetesimals to determine whether the
surface density of planetesimals exceeds the minimum surface
density
we chose a value of 0.001
(Papaloizou & Nelson 2003). We follow each model until all solids are in
the form of planetesimals or are accreted onto the star. Then, we
evaluate every model with planetesimals to determine whether the
surface density of planetesimals exceeds the minimum surface
density
![]() anywhere in the disk. Models with
this property are labeled as planet bearing. For each
such model we determine the minimum and maximum distances from the
star at which the surface density of the planetesimal swarm is
larger than
anywhere in the disk. Models with
this property are labeled as planet bearing. For each
such model we determine the minimum and maximum distances from the
star at which the surface density of the planetesimal swarm is
larger than
![]() .
The results obtained for
different values of the stellar mass are shown in Figs. 5-7.
.
The results obtained for
different values of the stellar mass are shown in Figs. 5-7.
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{36891.0_.eps}\end{figure}](/articles/aa/full/2006/41/aa3689-05/Timg94.gif) |
Figure 5:
The plane of initial parameters of protoplanetary disk models [M0, |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{36890.5_.eps}\end{figure}](/articles/aa/full/2006/41/aa3689-05/Timg96.gif) |
Figure 6:
Same as Fig. 5 but for the central star with a mass of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{36894.0_.eps}\end{figure}](/articles/aa/full/2006/41/aa3689-05/Timg98.gif) |
Figure 7:
Same as Fig. 5 but for the central star with a mass
of |
| Open with DEXTER | |
The area of the region occupied on the [M0,R0] plane by the planet bearing disks is clearly anticorrelated with the mass of the central star. As we have shown in Sect. 3.1, solid grains gain higher inward velocities in disks around less massive stars, and the resulting planetesimal swarms have higher surface densities. We see that reducing the mass of the central star increases the maximum R0 for which planet formation is possible in disks with the same initial mass M0.
We can also see that in a given disk the inner edge of the
planet-bearing region moves inward as we decrease the mass of the star
(for
![]() its radius is on the average equal to
its radius is on the average equal to
![]() 0.55 that for
0.55 that for
![]() ). This effect is mainly
caused by the larger surface density of planetesimal swarms produced
by disks around less massive stars. Differences in
). This effect is mainly
caused by the larger surface density of planetesimal swarms produced
by disks around less massive stars. Differences in
![]() ,
while appreciable, are much less important (when
,
while appreciable, are much less important (when ![]() is reduced by a factor of 2,
is reduced by a factor of 2,
![]() drops by 20% only; see Eq. (16)). The outer edge of the
planet-bearing region also moves closer to the star (for
drops by 20% only; see Eq. (16)). The outer edge of the
planet-bearing region also moves closer to the star (for
![]() its radius is on the average equal to
its radius is on the average equal to ![]() 0.75 that for
0.75 that for
![]() ). This is because in most cases it coincides with
the outer edge of the planetesimal swarm, which is more compact around
less massive stars. The difference in the minimum surface density
). This is because in most cases it coincides with
the outer edge of the planetesimal swarm, which is more compact around
less massive stars. The difference in the minimum surface density
![]() also tends to decrease the outer radius of the
planet-bearing region, but it is again a second-order factor.
also tends to decrease the outer radius of the
planet-bearing region, but it is again a second-order factor.
Generally, our model predicts that giant planets tend to form at tighter orbits around less massive stars, and wider orbits around more massive stars. However, at least in some cases their locations may be influenced by the effects of migration. We return to this point in Sect. 4.
One of the main results of extrasolar planet searches is the
discovery that planet-bearing stars tend to have higher
metallicities than field stars (Fischer & Valenti 2003; Santos et al. 2000). That
correlation can be easily explained within CAGCM. In this scenario,
the formation time of giant planets decreases with increasing
surface density of the planetesimal swarm (see Eqs. (16)
and (22)), which in turn is an increasing function
of the original metal content of the protoplanetary disk.
Consequently, the giant planets form more easily in disks with
higher metallicities. Kornet et al. (2005) calculated the rates of giant-planet
occurrence in disks with different metallicities around
stars with mass
![]() .
Their approach to the
evolution of solids and to the formation of giant planets was the same as
the one used in this paper. They were able to reproduce the
observational correlation for disk models with viscosity parameter
.
Their approach to the
evolution of solids and to the formation of giant planets was the same as
the one used in this paper. They were able to reproduce the
observational correlation for disk models with viscosity parameter
![]() .
Herein we extend their calculations
onto disks around stars with various masses.
.
Herein we extend their calculations
onto disks around stars with various masses.
The change in the disk metallicity influences the processes
leading to the formation of planets in two ways. First, it
changes the structure of the gaseous disk by changing the opacity
in the disk. In our models we scaled the opacity by a constant
factor Z equal to the metallicity of the disk expressed in solar
units. This approach is justified by the fact that the opacity in
protoplanetary disks is mainly due to dust grains and molecules.
Second, the primordial metallicity of the disk determines the
initial ratio of dust-to-gas surface densities. In our models this
ratio is initially independent of the distance from the star and
is equal to
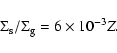 |
(23) |
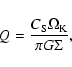 |
(24) |
Following the procedure described by Kornet et al. (2005), for every Zwe calculate the area
![]() of the region occupied on
the
of the region occupied on
the
![]() plane by disks that form planets at
distances smaller than 5 AU from the central star. The last
restriction comes from the fact that currently we know only one extrasolar planet on a larger orbit
plane by disks that form planets at
distances smaller than 5 AU from the central star. The last
restriction comes from the fact that currently we know only one extrasolar planet on a larger orbit![]() - 55 Cnc d (Marcy et al. 2002). A measure of the rate of planet occurrence can be defined as
- 55 Cnc d (Marcy et al. 2002). A measure of the rate of planet occurrence can be defined as
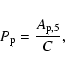 |
(25) |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.7cm,clip]{3689P_p.ps}\end{figure}](/articles/aa/full/2006/41/aa3689-05/Timg111.gif) |
Figure 8: The rate of planet occurrence as a function of the primordial metallicity of protoplanetary disks. Different lines are obtained for models with different masses of the central star, as labeled in solar units in the upper left corner. The histogram shows the observational data compiled by Fischer & Valenti (2003). |
| Open with DEXTER | |
The results are presented in Fig. 8. It shows the rate
of planet occurrence as a function of disk metallicity for three values of ![]() .
As expected,
.
As expected, ![]() is an increasing function of Z. The minimum value of Z below which no giant
planets are formed at orbits smaller than 5 AU decreases with the
mass of the central from
is an increasing function of Z. The minimum value of Z below which no giant
planets are formed at orbits smaller than 5 AU decreases with the
mass of the central from
![]() for
for
![]() ,
to
,
to
![]() for
for
![]() .
.
We see that for Z smaller than ![]() 0.2,
0.2, ![]() is
an increasing function of
is
an increasing function of ![]() .
This is because most disks in
which planets formation would be possible around less massive
stars have outer parts that are gravitationally unstable, and the amount of
solids present in their stable parts is too low to enable
subsequent formation of giant planets according to CAGCM.
However, as Z increases, smaller and smaller disks become
planet-bearing for every M0, and the percentage of
gravitationally unstable disks in which formation of giant planets is
not possible decreases.
Consequently, the factors promoting the formation of a giant planet
around less massive stars as described in previous sections become
important, and
.
This is because most disks in
which planets formation would be possible around less massive
stars have outer parts that are gravitationally unstable, and the amount of
solids present in their stable parts is too low to enable
subsequent formation of giant planets according to CAGCM.
However, as Z increases, smaller and smaller disks become
planet-bearing for every M0, and the percentage of
gravitationally unstable disks in which formation of giant planets is
not possible decreases.
Consequently, the factors promoting the formation of a giant planet
around less massive stars as described in previous sections become
important, and ![]() changes into a decreasing function
of
changes into a decreasing function
of ![]() .
.
Based on a simple approach to the evolution of solids in
protoplanetary disks, we investigated the influence of the mass of the
central star on the formation of giant planets.
We showed that due to the more efficient redistribution of
solids the planetesimal swarms around less massive stars tend to
have higher surface densities. Next, we derived the minimum
surface density of the planetesimal swarm needed to enable
formation of a giant planet within the lifetime of the
protoplanetary disk, and we found that at distances from the star
smaller than ![]() 10 AU it increases with the stellar mass.
Farther away from the star the minimum density becomes
anticorrelated with the mass of the star. However this effect is
offset by the anticorrelation mentioned already between the mass
of the star and the surface density of the planetesimals.
10 AU it increases with the stellar mass.
Farther away from the star the minimum density becomes
anticorrelated with the mass of the star. However this effect is
offset by the anticorrelation mentioned already between the mass
of the star and the surface density of the planetesimals.
These two effects determine the set of initial parameters
characterising protoplanetary disks that are capable of giant
planet formation within the core accretion - gas capture scenario.
We showed that this set is larger for less massive stars.
This means that the percentage of stars with massive planets
should increase with decreasing stellar mass (at least in the
range 0.5-4 ![]() ). However, as discussed below,
in the currently accessible range of orbital radii (<5 AU), the
situation is not all that clear.
). However, as discussed below,
in the currently accessible range of orbital radii (<5 AU), the
situation is not all that clear.
Based on the sets obtained for different metallicities, we
determined the occurrence rate of planets with orbits smaller than
5 AU as a function of the mass and metallicity of the star. We took
into account the fact that the outer region of the
disk is gravitationally unstable in some models. Such regions are located farther
than 5 AU from the central star, and planets formed there by
disk fragmentation are not included in our occurrence rate.
However, their presence reduces the amount of solid material
available for the formation of planetesimals. For less massive
stars this effect is so strong that it overcomes factors promoting
planet formation, so that for metal-poor disks the rate of planet
occurrence decreases with the mass of the central star. As a result, the minimum metallicity at which giant planets can form at
orbits smaller than
![]() decreases from
decreases from ![]() 0.6 for
stars with masses of
0.6 for
stars with masses of
![]() to
to ![]() 0.2 for
0.2 for ![]() .
.
In the metal-rich regime the percentage of entirely stable disks in which formation of giant planets is possible is larger, and stable regions of partly unstable disks contain enough solids to produce planetesimal swarms capable of giant planet formation. Consequently, both factors promoting planet formation around less massive stars are in play, and a clear anticorrelation between the stellar mass and planet occurrence rate is observed. At the same time, our model does not account for the presence of giant planets around metal-poor stars. This may be due to the fact that we do not include planets that have formed beyond 5 AU and later migrated inward. Such an assumption is valid as long as the number of these planets is small compared to the number of planets that have formed within 5 AU. However, as we move to lower metallicities, the percentage of giant planets with silicate cores decreases (the silicates simply become too scarce), while the percentage of planets forming from ice grains increases. Thus, in metal-poor systems the number of planets with ice cores that migrated from large orbits can become a large fraction of planets at orbits smaller than 5 AU.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.7cm,clip]{3689P_p_.ps}\end{figure}](/articles/aa/full/2006/41/aa3689-05/Timg116.gif) |
Figure 9:
The rate of planet occurrence as a function of the
primordial metallicity of protoplanetary disks. Disks around stars with masses
of |
| Open with DEXTER | |
Obviously, our description of the evolution of solids is very
simplified. The basic underlying assumptions like the single-size
distribution of solid grains or the neglect of planet migration
already have been discussed by Kornet at al. (2004, 2005).
The main
additional assumption introduced in the present paper is the
independence of the initial parameters of protoplanetary disks on
the mass of the central star. While admittedly ad hoc, it
seems to be better than the one adopted by Laughlin et al. (2004), who
scaled their initial surface density of planetesimals linearly
with the mass of the star. They did not take into account the
antecedent evolution of solids leading to the formation of
planetesimal swarms, and concluded that the formation of giant
planets around low-mass stars is difficult. Recent
observations suggest that masses of protoplanetary disks do not
strongly depend on masses of the central stars (Guilloteau 2005).
Nevertheless, to investigate the influence of our assumption, we
performed additional set of calculations with a mass of the central
star of
![]() and with the initial masses of disks scaled by
factor of 0.5. The results are shown in Fig. 9.
In this case the probability of finding a planet does not seem to
depend strongly on the mass of the central star, which is true
for the whole range of metallicities we have considered. Still,
our models show that the evolution of solids leading to the
formation of planetesimal swarms is a vital factor facilitating
the formation of giant planets, whose role should be particularly
clear for low-mass stars.
and with the initial masses of disks scaled by
factor of 0.5. The results are shown in Fig. 9.
In this case the probability of finding a planet does not seem to
depend strongly on the mass of the central star, which is true
for the whole range of metallicities we have considered. Still,
our models show that the evolution of solids leading to the
formation of planetesimal swarms is a vital factor facilitating
the formation of giant planets, whose role should be particularly
clear for low-mass stars.
Our models of gaseous disks do not reproduce recent observations by (Muzerolle et al. 2005), which show that the accretion rate in protoplanetary disks increases with the mass of the central star. However, in the mass range considered here this dependence is very weak, and for a given value of stellar mass the spread in accretion rates reaches two orders of magnitude. In our opinion these data do not invalidate our basic assumption that initial disk parameters do not depend on the mass of the star. We also assumed that heating by stellar radiation is negligible, whereas at least in some cases it can be a dominant source of energy in the outer regions of the disk (more efficient than the turbulent dissipation). As such, it may substantially change the structure of the disk and the radial velocities of solids. Currently we are working on models that will take these effects into account.
Acknowledgements
This project was supported by the German Research Foundation (DFG) through the Emmy Noether grant WO 857/2-1 and the European Community's Human Potential Programme through the contract HPRN-CT-2002-00308, PLANETS. K.K. and M.R. acknowledge support from the grant No. 1 P03D 026 26 from the Polish Ministry of Science.