A&A 458, 331-337 (2006)
DOI: 10.1051/0004-6361:20065713
Ro-vibrational excitation of the SO molecule by collision with the He atom
F. Lique1 - A. Spielfiedel1 - G. Dhont2 - N. Feautrier1
1 - LERMA and UMR 8112 of CNRS, Observatoire de
Paris-Meudon, 92195 Meudon Cedex, France
2 -
Université du Littoral Côte d'opale, LPCA, 189A avenue Maurice Schumann, 59140 Dunkerque, France
Received 29 May 2006 / Accepted 13 July 2006
Abstract
Context. Over the next few years, ALMA and Herschel missions will perform high spatial and spectral resolution studies at infrared and sub-millimeter wavelengths. This will provide much greater detail about the composition and evolution of molecules in space. Modeling of the spectra will require accurate radiative and collisional rates for species of astrophysical interest.
Aims. We calculate ro-vibrational excitation rate coefficients of SO by He, useful for studies of high-temperature environments.
Methods. A new accurate three dimensional (3D) potential energy surface was calculated for the SO-He system which explicitly takes into account the r-dependence of the SO vibration as well as the R-distance and 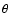 angle which describe the relative position of the collision partners. The dynamics calculations were performed according to the VCC-IOS approximation.
angle which describe the relative position of the collision partners. The dynamics calculations were performed according to the VCC-IOS approximation.
Results. The new rate coefficients between the ro-vibrational levels are calculated for temperatures from 300 K to 800 K.
Key words: ISM: molecules - molecular data - molecular processes
Observations of molecular emission at millimeter and infrared wavelengths, supplemented by careful and detailed modeling, are powerful tools to investigate the physical and chemical conditions of astrophysical objects. First observed by Gottlieb & Ball (1973) in the interstellar gas, SO has been used extensively to study shocked molecular gas in various environments
(Turner et al. 1992; van Dishoeck & Blake 1998; Blake et al. 1987). The modeling of the line intensities requires comparison with model excitation calculations using radiative as well as collisional rates. Collisional excitation in shocked regions and in photon dominated regions involves excitation of high-rotational levels as well as vibrational excitation by the most abundant species, He and H2.
Rotational excitation rate coefficients for collisions among fine structure levels of SO with He atoms, based on an accurate ab initio potential energy surface (PES), have been calculated recently (Lique et al. 2005; Lique et al. 2006). For pure rotational excitation, the SO r-distance was kept at its equilibrium geometry for the calculation of the PES. In Lique et al. (2005) the sensitivity of the cross sections to different basis sets used in the calculation of the SO-He surface has been studied. In the present paper we focus on calculations of rate coefficients for the v=0-1 vibrational excitation by He. The potential energy surface was calculated for different SO r-distances in order to account for the vibration of SO. The same strategy of calculation of the surface for each SO r-distance as in Lique et al. (2005) was adopted here.
A full close coupling approach for the dynamics calculations is prohibitively expensive in computer time for heavy molecules when transitions among highly excited rovibrational levels are involved. We therefore used the vibrational close-coupling rotational infinite order sudden (VCC-IOS) method (Parker & Pack 1978; Goldflam et al. 1977a,b) to perform the calculations. Cross-sections among the 118 first rotational levels of v=0 and v=1 have been calculated for total energies up to 5000 cm-1. After Boltzmann thermal average, they give rate coefficients up to 800 K.
The paper is organized as follows: Sect. 2 describes the ab initio calculation of the potential energy surface. Section 3 provides a rapid description of the theory and of the calculations. In Sect. 4 we present and discuss our results.
The present work uses a Jacobi coordinate system, in which r is the SO distance, R is the distance from the center of mass of SO to the He atom and 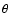 is the angle between the two distance vectors (
is the angle between the two distance vectors (
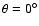 :
He adjacent to oxygen atom,
:
He adjacent to oxygen atom,
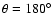 :
He adjacent to sulfur atom). The SO-He potential energy surface was calculated in the supermolecular approach based on the single and double excitation open-shell coupled cluster method with perturbative contributions of connected triple excitations (RCCSD(T)) computed as defined by
Knowles et al. (1993, 2000). To check the validity of this mono-configurational method, we have performed calculations for the first triplet electronic states with the Multi-Configuration Self-Consistent-field (MCSCF) approach. For all investigated geometries, it was found that the weight of the dominant configuration in the ground electronic state of the SO-He complex was between 0.92 and 0.94 which justifies the choice of the RCCSD(T) approach. Calculations were performed for three SO r-distances (2.4, 2.8 and 3.3 bohr) and the same grid of R and
:
He adjacent to sulfur atom). The SO-He potential energy surface was calculated in the supermolecular approach based on the single and double excitation open-shell coupled cluster method with perturbative contributions of connected triple excitations (RCCSD(T)) computed as defined by
Knowles et al. (1993, 2000). To check the validity of this mono-configurational method, we have performed calculations for the first triplet electronic states with the Multi-Configuration Self-Consistent-field (MCSCF) approach. For all investigated geometries, it was found that the weight of the dominant configuration in the ground electronic state of the SO-He complex was between 0.92 and 0.94 which justifies the choice of the RCCSD(T) approach. Calculations were performed for three SO r-distances (2.4, 2.8 and 3.3 bohr) and the same grid of R and 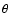 values (R was assigned values from 4.0 bohr to 16.0 bohr by steps of 0.25 bohr, the angular grid was uniform with a 15 degree spacing from 0 to 180 degree) as described in Lique et al. (2005).The three atoms were described by the standard correlation consistent polarized valence quadruple zeta set of Woon & Dunning (1994) augmented by the (3s3p2d2f1g) bond functions optimized by Cybulski & Toczylowski (1999), placed at mid-distance between the SO centre-of-mass and He. In all calculations, the basis set superposition error (BSSE) is corrected at all geometries with the Boys & Bernardi (1970) counterpoise procedure. The PES calculations were performed with the MOLPRO 2002 package (MOLPRO 2002).
values (R was assigned values from 4.0 bohr to 16.0 bohr by steps of 0.25 bohr, the angular grid was uniform with a 15 degree spacing from 0 to 180 degree) as described in Lique et al. (2005).The three atoms were described by the standard correlation consistent polarized valence quadruple zeta set of Woon & Dunning (1994) augmented by the (3s3p2d2f1g) bond functions optimized by Cybulski & Toczylowski (1999), placed at mid-distance between the SO centre-of-mass and He. In all calculations, the basis set superposition error (BSSE) is corrected at all geometries with the Boys & Bernardi (1970) counterpoise procedure. The PES calculations were performed with the MOLPRO 2002 package (MOLPRO 2002).
The fitting procedure described by Werner et al. (1988) for the CN-He system was adopted in order to obtain the
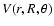 numerical expansion routine required to perform the dynamical calculations. The potential was fitted to the functional form:
numerical expansion routine required to perform the dynamical calculations. The potential was fitted to the functional form:
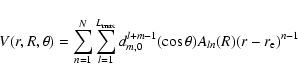 |
(1) |
where the
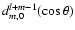 are reduced Wigner rotation matrix elements.
are reduced Wigner rotation matrix elements.
N equals the number of SO bond distances and
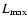 the number of angles
the number of angles 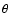 for which the potential has been calculated.
for which the potential has been calculated.
Table 1:
Vibrational matrix elements (
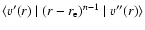 )
used in the vibrational averaging of the interaction potential;
)
used in the vibrational averaging of the interaction potential; 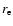 was taken to be 2.8 bohr.
was taken to be 2.8 bohr.
![\begin{figure}
\par\includegraphics[width=7.8cm,angle=270.]{5713fig1.ps}\par\end{figure}](/articles/aa/full/2006/40/aa5713-06/Timg16.gif) |
Figure 1:
Contour plot of the
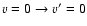 matrix elements of the interaction potential for elastic scattering of He+SO as a function of R and
matrix elements of the interaction potential for elastic scattering of He+SO as a function of R and 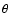 .
The energies are in cm-1 with a distance of 1.0 cm-1 between two adjacent contours, the zero of energy is taken as that of the He+SO asymptote. .
The energies are in cm-1 with a distance of 1.0 cm-1 between two adjacent contours, the zero of energy is taken as that of the He+SO asymptote. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.8cm,angle=270.]{5713fig2.ps}\par\end{figure}](/articles/aa/full/2006/40/aa5713-06/Timg17.gif) |
Figure 2:
Contour plot of the
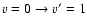 matrix elements of the interaction potential for inelastic scattering of He+SO as a function of R and
matrix elements of the interaction potential for inelastic scattering of He+SO as a function of R and 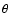 .
The energies are in cm-1 with a distance of 0.1 cm-1 between two adjacent contours, the zero of energy is taken as that of the He+SO asymptote. .
The energies are in cm-1 with a distance of 0.1 cm-1 between two adjacent contours, the zero of energy is taken as that of the He+SO asymptote. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.8cm,angle=0.]{5713fig3.eps}\par\end{figure}](/articles/aa/full/2006/40/aa5713-06/Timg18.gif) |
Figure 3:
Variation of the vibrationally elastic rotational cross sections for v=0 with the v=0 and v=1 basis set (full curve) and without vibrational coupling (diamonds). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.8cm,angle=0.]{5713fig4.eps}\par\end{figure}](/articles/aa/full/2006/40/aa5713-06/Timg19.gif) |
Figure 4:
"Fundamental IOS cross sections'' (see Eq. (4)) for vibrationally elastic rotational excitation of SO out of the v=1, N=0 level to v=0, L level calculated including 2, 3 and 4 vibrational levels in the dynamical calculations. |
| Open with DEXTER |
For a VCC-IOS calculation, matrix elements of the potential between the vibrational states of the SO molecule are required for fixed values of the Jacobi scattering angle and for all the R-values. We write these matrix elements as:
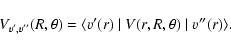 |
(2) |
The SO vibrational wave functions were obtained by the Fourier grid Hamiltonian (FGH) method of Clay Marston & Balint-Kurti (1989) from a SO potential calculated with the MOLPRO 2002 package at the Complete Active Space Self-Consistent-field (CASSCF) + Multi-Reference Configuration Interaction (MRCI) level using the aug-cc-pVQZ basis set of Woon and Dunning (1994). The vibrational wave functions were taken with j=0.
The relevant
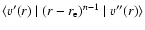 matrix elements are given in Table 1.
matrix elements are given in Table 1.
Contour plots of the
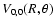 and
and
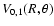 surfaces are respectively shown in Figs. 1 and 2. In these plots the value
surfaces are respectively shown in Figs. 1 and 2. In these plots the value
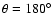 corresponds to colinear He-SO. The
corresponds to colinear He-SO. The
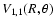 surface is indistinguishable from the
surface is indistinguishable from the
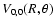 surface. The global minimum in the V0,0 and V1,1 surfaces is found to be -34.62 cm-1 (R=7.35 bohr,
surface. The global minimum in the V0,0 and V1,1 surfaces is found to be -34.62 cm-1 (R=7.35 bohr, 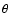 = 180
= 180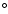 ).
).
Table 2:
Energy in cm-1 of the fine structure levels of SO (v=0) (E=0 cm-1 for
v=0, NJ=10).
In the SO (
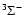 )
electronic ground state, the rotational levels are split by spin-rotation coupling. In the intermediate coupling scheme, the rotational wave function of SO can be written for
)
electronic ground state, the rotational levels are split by spin-rotation coupling. In the intermediate coupling scheme, the rotational wave function of SO can be written for 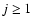 as:
as:
where
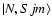 denotes pure Hund's case (b) basis functions and the mixing angle
denotes pure Hund's case (b) basis functions and the mixing angle 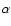 is obtained by diagonalisation of the molecular Hamiltonian. In the pure case (b) limit,
is obtained by diagonalisation of the molecular Hamiltonian. In the pure case (b) limit,
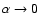 ,
the F1 level corresponds to N=j-1 and the F3 level to N=j+1. For SO, the case (b) limit becomes valid beyond N=5. The calculations of the rotational energy levels were done with the F1, F2 and F3 functions but, since the dynamical calculations were performed in the IOS approach (the levels are described in the Hund case (b) limit), the usual level labeling Nj with N=j-1, N=j, N=j+1 corresponding to the F1, F2 and F3 levels as defined in
Eq. (3) will be used in the following.
,
the F1 level corresponds to N=j-1 and the F3 level to N=j+1. For SO, the case (b) limit becomes valid beyond N=5. The calculations of the rotational energy levels were done with the F1, F2 and F3 functions but, since the dynamical calculations were performed in the IOS approach (the levels are described in the Hund case (b) limit), the usual level labeling Nj with N=j-1, N=j, N=j+1 corresponding to the F1, F2 and F3 levels as defined in
Eq. (3) will be used in the following.
Table 3:
Energy in cm-1 of the fine structure levels of SO (v=1) (E=0 cm-1 for
v=0, NJ=10).
The energies of the first fine structure levels pertaining to the v=0 and v=1 vibrational levels are given in Tables 2 and 3. They were computed with the experimental spectroscopic constants of Bogey et al. (1982). Due to the low rotational constant there are 118 Nj levels with an energy lower than the first excited vibrational level.
In the VCC-IOS method, the rotational levels are treated as degenerate. Within this approximation the problem reduces to the computation of vibrationally inelastic S-matrix elements calculated with a close coupling approach at fixed 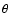 Jacobi angles for a given L-value. These fixed-angle S-matrix elements must then be mutiplied by the appropriate spherical harmonics and integrated over
Jacobi angles for a given L-value. These fixed-angle S-matrix elements must then be mutiplied by the appropriate spherical harmonics and integrated over 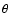 to give the "fundamental IOS cross sections''
to give the "fundamental IOS cross sections''
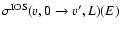 out of the v, N=0 level.
out of the v, N=0 level.
In the Hund's case (b) limit, the de-excitation ro-vibrational cross sections are expressed in a reduced form in terms of the
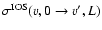 cross sections (Corey & McCourt 1983):
cross sections (Corey & McCourt 1983):
where
 and
and
 are respectively the "3-j'' and "6-j'' symbols.
v, Nj and
v', N' j' are the initial and final vibrational and rotational states. The summation in Eq. (4) was performed for
are respectively the "3-j'' and "6-j'' symbols.
v, Nj and
v', N' j' are the initial and final vibrational and rotational states. The summation in Eq. (4) was performed for 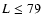 which allows us to obtain converged cross sections for rotational angular momenta
which allows us to obtain converged cross sections for rotational angular momenta 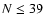 .
All the calculations were performed using the MOLSCAT computer program of Hutson & Green (1994). The calculations were carried out using the propagator of Manolopoulos (1986). The reduced mass of the system is 3.694 amu. Typically, the minimum and maximum integration distances are
.
All the calculations were performed using the MOLSCAT computer program of Hutson & Green (1994). The calculations were carried out using the propagator of Manolopoulos (1986). The reduced mass of the system is 3.694 amu. Typically, the minimum and maximum integration distances are
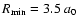 and
and
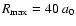 .
.
Rate coefficients are obtained by averaging the appropriate cross sections over a Boltzmann distribution of velocities at a given kinetic temperature T:
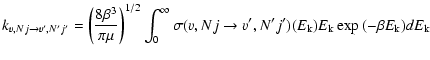 |
|
|
(5) |
where
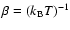 ,
,
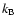 is the Boltzmann constant,
is the Boltzmann constant, 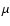 is the reduced mass of the colliding system. The total energy E is related to the kinetic energy according to
is the reduced mass of the colliding system. The total energy E is related to the kinetic energy according to
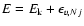 where
where
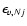 is the energy of the initial rovibrational level. Rate coefficients for the reverse transitions may be obtained by detailed balance.
is the energy of the initial rovibrational level. Rate coefficients for the reverse transitions may be obtained by detailed balance.
As the IOS approximation neglects the energy structure of the rotational levels, it is expected to be poor at low energies, so the results presented here refer to high temperatures. The validity of this approach was checked in Lique et al. (2006) for pure rotational excitation. It was found to be appropriate, especially for transitions involving levels with N > 5.
However it may not be so applicable to vibrational quenching as resonant vibrational energy transfer may occur. This type of near-resonant energy transfer has been observed experimentally
(Stewart et al. 2000; McCaffery & Marsh 2000) and obtained theoretically (Stewart et al. 1988, 2000; Miklavc et al. 1992; Krems et al. 2001) for diatomic molecules with a small moment of inertia (H2, HF, Li2). Molecules with smaller rotational constants (CO for example) can exhibit resonant vibrational relaxation when they are initially in very high rotational levels. The role of near-resonant vibrational relaxation has been investigated systematically in CO (Krems 2002). This study shows that the contribution of this resonant process is negligible for low j levels and high energy, and only becomes important when the initial rotational state of v=1 is close in energy to high rotational states of v=0. These cases were not considered in this paper.
![\begin{figure}
\par\includegraphics[width=7.8cm,angle=0.]{5713fig5.eps}\end{figure}](/articles/aa/full/2006/40/aa5713-06/Timg55.gif) |
Figure 5:
Temperature variation of the
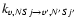 collision rates for:
collision rates for:
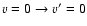 ( upper panel),
( upper panel),
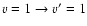 ( medium panel),
( medium panel),
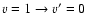 ( lower panel).
( lower panel). |
| Open with DEXTER |
In order to compute cross sections and rate coefficients for vibrational relaxation of SO, we have tested the convergence of the vibrational close-coupling expansion by including several vibrational wave functions in the basis set.
We first considered the effect of vibrational coupling on the rotational excitation cross sections. Figure 3 compares the fundamental IOS cross sections (see Eq. (4)) for vibrationally elastic rotational excitation of SO out of the v=0, N=0 level calculated with and without vibrational coupling between v=0 and v=1.
As already found for other systems like CO (Krems 2002) and HF (Krems & Nordholm 2001; Krems et al. 2001), the pure rotational transitions are unaffected by the vibrational channel included in the calculation. This result is directly the consequence of the very small non-diagonal vibrational matrix elements of the interaction potential compared to the diagonal ones. In addition, there is an excellent agreement between the cross sections calculated with the 3D PES and the one previously calculated (Lique et al. 2006) with the 2D PES. This result validates the choice of a 2D PES for pure rotational excitation.
We have also considered the convergence of the vibrational expansion on inelastic vibrational cross sections. Figure 4 shows the "fundamental IOS cross sections'' out of v=1, N=0 (see Eq. (4)) for vibrational v=0,1, v=0,1,2 and
v=0,1,2, 3 basis sets.
![\begin{figure}
\par\includegraphics[width=16.2cm,angle=0.]{5713fig6.eps}\end{figure}](/articles/aa/full/2006/40/aa5713-06/Timg56.gif) |
Figure 6:
Distribution of the final fine structure levels N'j' in v'=0,n' identified by the number n' (given in Table 2 following vibrational relaxation of
v=1, Nj states) at T=500 K. Upper panel is for
Nj = 01 (F1 level), middle panel is for
Nj = 1010 (F2 level) and bottom panel is for
Nj = 3534 (F3 level). |
| Open with DEXTER |
It follows from this plot that the "fundamental IOS cross sections'' from v=1 can be obtained by neglecting coupling with vibrational states higher than v=1. Therefore, all the calculations presented in the following were performed with the v=0,1 basis set.
Calculations were performed for the 118 first fine structure levels of v=0 and v=1 and for energies up to 5000 cm-1 leading to converged rate coefficients for all the considered levels and temperatures up to 800 K. The temperature variation of the rate coefficients involving the first rotational levels are displayed in Fig. 5 for
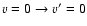 ,
for
,
for
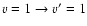 and for
and for
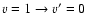 transitions.
transitions.
One observes a slow variation with temperature of the vibrationally elastic rate coefficients when the variation of the vibrational excitation
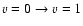 coefficients vary more rapidly. As found for other systems, the rate coefficients for
coefficients vary more rapidly. As found for other systems, the rate coefficients for
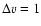 transitions are lower than the elastic coefficients by several orders of magnitude. It would be necessary to consider much higher temperatures and/or high-j levels leading to near-resonant j-levels belonging to v=0 and v=1 to get much higher vibrational excitation rate coefficients. It is thus expected that the values obtained in the present VCC-IOS approximation for vibrational excitation and desexcitation give the correct order of magnitude of the rate coefficients.
transitions are lower than the elastic coefficients by several orders of magnitude. It would be necessary to consider much higher temperatures and/or high-j levels leading to near-resonant j-levels belonging to v=0 and v=1 to get much higher vibrational excitation rate coefficients. It is thus expected that the values obtained in the present VCC-IOS approximation for vibrational excitation and desexcitation give the correct order of magnitude of the rate coefficients.
Figure 6 presents diagrams of the distribution of the final rotational states
v'=0, N'j' (identified by the number n') after vibrational relaxation of various
v=1, Nj states at a temperature of 500 K.
The vibrational relaxation of low j levels exhibits a first peak centered in the region of low j' levels and a second broad peak decreasing slowly for large j' levels. As the initial rotational excitation increases, the first peak becomes larger than the second one and shifts toward larger j' values. One can also observe in this figure a strong propensity for F-conserving transitions in the large j limit. This was already found in pure rotational cross sections and rate coefficients (Lique et al. 2005) and predicted theoretically (Alexander & Dagdigian 1988).
All the rate coefficients are available on our web site (http://amdpo.obspm.fr/basecol/).
In this work, we use the vibrational close coupling - rotational IOS approach to investigate the ro-vibrational energy transfer in collisions of SO with He atoms. The calculations are performed with a new accurate 3D potential energy surface. The results can be summarized as follows:
- (i)
- The vibrationally elastic rotational energy transfer in v=0 is essentially unaffected by the vibrational coupling with v=1. An analogous behaviour has been observed by Krems & Nordholm (2001) in their study of vibrational and rotational excitation of HF by collisions with Ar. From an analysis of the rotational excitation of HF (v, j=0) for different v-values, these authors conclude that the vibrational motion of HF plays no role in pure rotational transitions. This result, if confirmed for other colliding systems, is important as cross sections and rate coefficients for rotational excitation may be obtained without considering the vibration of the diatomic molecule.
- (ii)
- In the energy range considered (
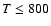 K) the rate coefficients for vibrational excitation of v=1 are several orders of magnitude lower than the rotational rate coefficients. As a consequence, vibrational excitation of SO by He may be considered as negligible in comparison with radiative vibrational excitation in the majority of non-Local Thermodynamic Equilibrium (LTE) astrophysical environments.
K) the rate coefficients for vibrational excitation of v=1 are several orders of magnitude lower than the rotational rate coefficients. As a consequence, vibrational excitation of SO by He may be considered as negligible in comparison with radiative vibrational excitation in the majority of non-Local Thermodynamic Equilibrium (LTE) astrophysical environments.
- (iii)
- The calculations performed within the VCC-IOS approximation cannot take into account the near-resonant interactions that may occur between highly excited rotational levels in v=0 and v=1. Such an effect is small for low or moderately high rotational levels and high energies.
It is difficult to assess the absolute accuracy of our calculated rates. The typical error may be lower than an order of magnitude, and we believe that the results are probably accurate within a factor of 2-3. Some caution must be exercised concerning the use of the present rate coefficients for collisions with He to provide a first estimate of rate coefficients with para-H2 (j=0). The underlying approximation is to consider identical cross sections for the two colliding systems and apply a scaling factor to account for the different associated reduced masses. Recent results on rotational excitation of CO (Wernli et al. 2006), SiO (Dayou & Balança 2006) and CS (Lique 2006) pointed out that rate coefficients with para-H2 (j=0) are within a factor 1-3 larger or lower than those with He, depending on the selected transition.
This indicates that accurate rate coefficients for collisions with H2 cannot be obtained from the present results although they give the correct order of magnitude.
Acknowledgements
The calculations of ab initio potential energy surfaces were
performed on the parallel machine MPOPM of Paris Observatory, and
the scattering calculations were performed at the IDRIS-CNRS center
(Institut de Développement et des Ressources en Informatique
Scientifique du Centre National de la Recherche Scientifique) under
project 050883.
- Alexander, M.
A., & Dagdigian, P. J. 1988, J. Chem. Phys., 79, 302 [NASA ADS] [CrossRef] (In the text)
- Blake, G. A., Surron,
E. C., Masson, C. R., & Phillips, T. G. 1987, ApJ, 315,
621 [NASA ADS] [CrossRef] (In the text)
- Basecol:
http://amdpo.obspm.fr/basecol/
- Bogey, M., Demuynck
C., & Destombes, J. L. 1982, Chem. Phys., 66, 99 [CrossRef] (In the text)
- Boys, S. F., &
Bernardi, F. 1970, Mol. Phys., 19, 553 [NASA ADS] [CrossRef] (In the text)
- Clay Marston, C., &
Balint-Kurti, G. G. 1989, J. Chem. Phys., 91 3571
(In the text)
- Corey, G., &
McCourt, F. R. 1983, J. Chem. Phys., 87, 2723 [CrossRef]
- Cybulski, S.
M., & Toczylowski, R. R. 1999, J. Chem. Phys., 111, 10520 [NASA ADS] [CrossRef] (In the text)
- Dayou, F.,
Balança, C. 2006, A&A, submitted
(In the text)
- Goldflam, R.,
Green, S., & Kouri, D. J. 1977a, J. Chem. Phys., 67, 4149 [NASA ADS] [CrossRef] (In the text)
- Goldflam, R.,
Kouri, D. J., & Green, S. 1977b, J. Chem. Phys., 67, 5661 [NASA ADS] [CrossRef]
- Gottlieb, C.
A., & Ball, J. A. 1973, ApJ, 184, L59 [NASA ADS] [CrossRef] (In the text)
- Hutson, J. M., &
Green, S. 1994, MOLSCAT computer code, version 14, Collaborative
Computational Project No. 6 of the Science and Engineering Research
Council, UK
(In the text)
- Knowles, P. J.,
Hampel, C., & Werner, H.-J. 1993, J. Chem. Phys., 99, 5219 [NASA ADS] [CrossRef] (In the text)
- Knowles, P. J.,
Hampel, C., & Werner, H.-J. 2000, J. Chem. Phys., 112,
3106 [NASA ADS] [CrossRef] (In the text)
- Krems, R. V. 2002, J.
Chem. Phys., 116, 4517 [NASA ADS] [CrossRef] (In the text)
- Krems, R. V., &
Nordholm, S. 2001, J. Chem. Phys., 115, 257 [NASA ADS] [CrossRef] (In the text)
- Krems, R. V.,
Markovic, N., Buchachenko, A. A., & Nordholm, S. 2001, J. Chem.
Phys., 114, 1249 [NASA ADS] [CrossRef] (In the text)
- Lique, F. 2006,
unpublished data
- Lique, F.
Spielfiedel, S., Dubernet M.-L., & Feautrier, N. 2005, J. Chem.
Phys., 123, 134316 [CrossRef] (In the text)
- Lique, F.
Spielfiedel, S. & Feautrier, N. 2006, A&A, 450, 399 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- McCaffery, A.
J., & Marsh, R. J. 2000, J. Phys. Chem., 104, 10442 (In the text)
-
Manolopoulos, D. E. 1986, J. Chem. Phys., 85, 6425 [NASA ADS] [CrossRef] (In the text)
- Miklavc, A.,
Markovic, N., Nyman., G., Harb., V., & Nordholm., S. 1992, J.
Chem. Phys., 97, 3348 [NASA ADS] [CrossRef] (In the text)
- MOLPRO is a package of
ab initio programs written by: Werner, H.-J., & Knowles, P. J.
with contributions from Almlöf, J., Amos, R. D., Deegan, M.
J., et al.
- Parker, G. A.,
& Pack, R. T. 1978, J. Chem. Phys., 68, 1585 [NASA ADS] [CrossRef] (In the text)
- Stewart, B.,
Magil, P. D., Scott, T. P., Derouard, J., & Pritchard, D. E.
1988, Phys. Rev. Lett., 60, 282 [NASA ADS] [CrossRef] (In the text)
- Stewart, B.,
Magil, P. D., & Pritchard, D. E. 2000, J. Phys. Chem., 104,
10565 (In the text)
- Turner, B. E.,
Chan, K.-W., Green, S., & Lubowich, D. A. 1992, ApJ, 399,
114 [NASA ADS] [CrossRef] (In the text)
- van
Dishoeck, E. F., & Blake G. A., 1998, ARA&A, 36, 317 [NASA ADS] (In the text)
- Wernli, M.,
Valiron, P., Faure, A., et al. 2006, A&A, 446, 367 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Werner, H.-J.,
Follmeg B., Alexander, M. H., & Lemoine D. 1988, J. Chem.
Phys., 89, 3139 [NASA ADS] [CrossRef] (In the text)
- Woon, D. E., &
Dunning, T. H. Jr 1994, J. Chem. Phys., 100, 2975 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2006
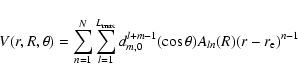
![\begin{figure}
\par\includegraphics[width=7.8cm,angle=270.]{5713fig1.ps}\par\end{figure}](/articles/aa/full/2006/40/aa5713-06/Timg16.gif)
![\begin{figure}
\par\includegraphics[width=7.8cm,angle=270.]{5713fig2.ps}\par\end{figure}](/articles/aa/full/2006/40/aa5713-06/Timg17.gif)
![\begin{figure}
\par\includegraphics[width=7.8cm,angle=0.]{5713fig3.eps}\par\end{figure}](/articles/aa/full/2006/40/aa5713-06/Timg18.gif)
![\begin{figure}
\par\includegraphics[width=7.8cm,angle=0.]{5713fig4.eps}\par\end{figure}](/articles/aa/full/2006/40/aa5713-06/Timg19.gif)
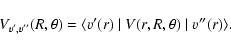
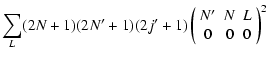
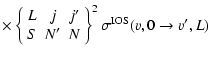
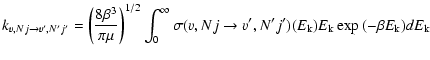
![\begin{figure}
\par\includegraphics[width=7.8cm,angle=0.]{5713fig5.eps}\end{figure}](/articles/aa/full/2006/40/aa5713-06/Timg55.gif)
![\begin{figure}
\par\includegraphics[width=16.2cm,angle=0.]{5713fig6.eps}\end{figure}](/articles/aa/full/2006/40/aa5713-06/Timg56.gif)