A&A 458, 31-37 (2006)
DOI: 10.1051/0004-6361:20065551
1st Experimental Lyceum of Athens, Ipitou 15, Plaka, 10557 Athens, Greece
Received 5 May 2006 / Accepted 29 June 2006
Abstract
We combine the results of merger trees realizations, predicted by the extended Press-Schechter
theory, to the assumption of "stable clustering'' in order to calculate density profiles of dark matter
haloes. Our results show that:
1) Haloes of different masses have different concentrations.
More specifically, concentration is a decreasing function of
the mass. The relation between concentration and virial mass predicted by our results is
in good agreement with the predictions of large cosmological N-body
simulations.
2) The slope of the density profile of dark matter haloes is flatter at the inner regions and steepens
outwards. At a given fraction of the virial radius the slope (defined as minus the derivative of
the logarithm of the density with respect to the logarithm of the radial distance) is a decreasing function
of the virial mass of the halo. At 0.01 of the virial
radius
![]() the slope ranges from 0.4 to
1.5 for masses in the range
the slope ranges from 0.4 to
1.5 for masses in the range
![]() to
to
![]() .
At distance
.
At distance
![]() the values of the slope
are in the range 2.5 to 5.5. We note that the small values of the inner slope predicted in
this paper are closer to the predictions of observations than the results of N-body simulations.
3) Comparing haloes of the same present day mass we found that:
a) Haloes with large rate of recent mass increase, show flatter outer density
profiles than those with small recent mass increase.
b) The concentration becomes larger for increasing recent mass growth
rate.
the values of the slope
are in the range 2.5 to 5.5. We note that the small values of the inner slope predicted in
this paper are closer to the predictions of observations than the results of N-body simulations.
3) Comparing haloes of the same present day mass we found that:
a) Haloes with large rate of recent mass increase, show flatter outer density
profiles than those with small recent mass increase.
b) The concentration becomes larger for increasing recent mass growth
rate.
Key words: galaxies: formation - galaxies: halos - galaxies: structure - methods: numerical - methods: analytical - cosmology: dark matter
It is likely that structures in the Universe grow from small initially Gaussian density perturbations that progressively detach from the general expansion, reach a maximum radius and then collapse to form bound objects. Larger haloes are formed hierarchically by mergers between smaller ones.
The above scenario of formation is usually studied by two different kinds of methods. The first kind is the N-body simulations that are able to follow the evolution of a large number of particles under the influence of the mutual gravity, from initial conditions to the present epoch. The second kind consists of semi-analytical methods. Among them, the Press-Schechter (PS) approach and its extensions (EPS) are of great interest since they allow us to compute mass functions (Press & Schechter 1974; Bond et al. 1991) to approximate merging histories (Lacey & Cole 1993, LC93 hereafter; Bower 1991; Sheth & Lemson 1999b) and to estimate the spatial clustering of dark matter haloes (Mo & White 1996; Catelan et al. 1998; Sheth & Lemson 1999a).
One of the interesting problems related to the formation of dark
matter haloes is that of their density profiles. Numerical
simulations show that a good model for the density profile
![]() of a halo is that given by the formula,
of a halo is that given by the formula,
![\begin{displaymath}\rho_{\rm M}(r)=\frac{\rho_{\rm c}}{(r/r_{\rm s})^{\kappa}[1+(r/r_{\rm s})^{\lambda}]^{\mu}}
\end{displaymath}](/articles/aa/full/2006/40/aa5551-06/img8.gif) |
(1) |
![\begin{displaymath}\gamma(r)\equiv-\frac{{\rm d}\ln[\rho_{\rm M}(r)]}{{\rm d}\ln...
... \mu \frac{(r/r_{\rm s})^{\lambda}}{1+(r/r_{\rm s})^{\lambda}}
\end{displaymath}](/articles/aa/full/2006/40/aa5551-06/img11.gif) |
(2) |
We define the concentration c by the common way,
![]() ,
that is the ratio of the virial radius of
the system
,
that is the ratio of the virial radius of
the system
![]() to the radius r2, where the above logarithmic slope becomes equal to 2. For the NFW profile,
r2 equals the scale radius
to the radius r2, where the above logarithmic slope becomes equal to 2. For the NFW profile,
r2 equals the scale radius ![]() but this is not true for other values of
but this is not true for other values of
![]() and
and ![]() .
.
The results of N-body simulations show that concentration is a decreasing function of the mass of the halo. This shows that in a hierarchical clustering scenario, larger haloes are formed later.
As regards the inner asymptotic slope, given by the value of ![]() ,
the results differ
not only between them but also with the predictions of
observations that report significantly smaller values of
,
the results differ
not only between them but also with the predictions of
observations that report significantly smaller values of ![]() (Sand et al.
2002, 2004).
(Sand et al.
2002, 2004).
In this paper, we present density profiles predicted by semi-analytical methods based on the EPS theory. We hope, in this way, to better understand the physics involved during the collapse and relaxation of dark matter haloes. We compare our results to empirical formulas resulted from the predictions of numerical simulations. We find a satisfactory agreement.
The paper is organized as follows: in Sect. 2, basic equations are summarized. In Sect. 3, we present our results while a discussion is given in Sect. 4.
![\begin{displaymath}B(S,t)=\sqrt{aS_*}[1+\beta(S/aS_*)^{\gamma}].
\end{displaymath}](/articles/aa/full/2006/40/aa5551-06/img24.gif) |
(3) |
The spherical collapse model has a barrier that does not
depend on the mass (e.g. LC93). For this model, the values of the parameters are
a=1 and ![]() .
The ellipsoidal collapse model (EC)
(Sheth & Tormen 1999) has
a barrier that depends on the mass (moving barrier). The values of the
parameters are a=0.707,
.
The ellipsoidal collapse model (EC)
(Sheth & Tormen 1999) has
a barrier that depends on the mass (moving barrier). The values of the
parameters are a=0.707,
![]() ,
,
![]() and are adopted
either from the dynamics of ellipsoidal collapse or from
fits to the results of N-body simulations.
and are adopted
either from the dynamics of ellipsoidal collapse or from
fits to the results of N-body simulations.
Sheth & Tormen (2002) showed
that given a mass element - that is a
part of a halo of mass M0 at time t0 - the probability that at earlier
time t this mass element was a part of a smaller halo with mass M, is
given by the equation:
![$\displaystyle f(S,t/S_0,t_0){\rm d}S=
\frac{1}{\sqrt{2\pi}}\frac{\vert T(S,t/S_...
...ert}{(\Delta
S)^{3/2}} \exp\left[-\frac{(\Delta B)^2}{2\Delta S}\right]{\rm d}S$](/articles/aa/full/2006/40/aa5551-06/img34.gif) |
(4) |
The function T is given by:
![$\displaystyle T(S,t/S_0,t_0)\!=\!B(S,t)-B(S_0,t_0)\!+\! \sum_{n=1}^{5}\frac{[S_0-S]^n}{n!}
\frac{{\rm\partial ^n}}{\partial S^n}B(S,t)$](/articles/aa/full/2006/40/aa5551-06/img37.gif) |
(5) |
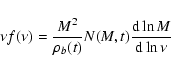 |
(6) |
Using a barrier of the form of Eq. (3) in the unconditional mass probability, one finds for
![]() the expression:
the expression:
| |
= | ||
| (7) |
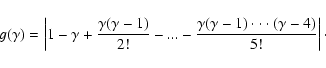 |
(8) |
We assume a number of haloes with the same present day mass M0 - at present epoch t0 - and we study their
past using merger-trees. This is done
by finding their progenitors -haloes that merged
and formed the present day haloes- at previous times. The procedure for a single halo is
as follows: A new time t<t0 is chosen. Then a value ![]() is chosen from the desired distribution
given by Eq. (4). The mass Mp of a progenitor is found by solving for Mp the equation
is chosen from the desired distribution
given by Eq. (4). The mass Mp of a progenitor is found by solving for Mp the equation
![]() .
If the mass left to be resolved M0-Mp is large enough, the above procedure is repeated
so a distribution of the progenitors of the halo is created at t. If the mass left to be resolved - that equals to M0 minus the sum of the masses of its progenitors - is less than a threshold then we proceed to the next
time by analyzing with the same procedure the mass of each progenitor. The most massive progenitor at t is considered as the mass of the initial halo at that
time.
.
If the mass left to be resolved M0-Mp is large enough, the above procedure is repeated
so a distribution of the progenitors of the halo is created at t. If the mass left to be resolved - that equals to M0 minus the sum of the masses of its progenitors - is less than a threshold then we proceed to the next
time by analyzing with the same procedure the mass of each progenitor. The most massive progenitor at t is considered as the mass of the initial halo at that
time.
The above procedure is repeated for a large number of haloes of the same mass and at every time step, the average mass is found. Thus a smooth curve is derived that shows the growth of mass as a function of time (or the scale factor). A complete description of the above numerical method is given in Hiotelis & Del Popolo (2006). The algorithm - known as N-branch merger-tree- is based on the pioneered works of LC93, Somerville & Kollat (1999) and van de Bosch (2002).
In our calculations, we use a flat model for the Universe with
present day density parameters
![]() and
and
![]() .
.
![]() is the cosmological constant and H0 is the present day value of Hubble's
constant. We used the value
is the cosmological constant and H0 is the present day value of Hubble's
constant. We used the value
![]() with h=0.7 and a system of units with
with h=0.7 and a system of units with
![]() ,
,
![]() and a gravitational constant G=1. At this system of units
and a gravitational constant G=1. At this system of units
![]()
As regards the power spectrum, we used the
![]() form proposed by
Smith et al. (1998). The power spectrum is smoothed using the top-hat window function and
is normalized for
form proposed by
Smith et al. (1998). The power spectrum is smoothed using the top-hat window function and
is normalized for
![]() .
.
We proceed by calculating density profiles using the assumption of "stable clustering'' (e.g. Nusser & Sheth 1999; Manrique et al. 2003; Hiotelis 2003). According to this assumption the haloes grow inside-out. The accreted mass is deposited at an outer spherical shell without changing the inner density profile. Although this is an ideal situation, it may not be far from reality. For example, Taylor & Babul (2005), among other results of their N-body simulations, state that "The density of the main system changes with time, although in practice this change is mainly confined to the outer parts of the halo''.
The radial extent of a halo is defined by its virial radius
![]() ,
that
is the radius containing a mass with mean density
,
that
is the radius containing a mass with mean density
![]() times the current mean density
of the Universe,
times the current mean density
of the Universe, ![]() .
.
![]() is, in general, a function of
time that depends on the assumed cosmology (Bryan & Norman 1998). Consequently, the mass
is, in general, a function of
time that depends on the assumed cosmology (Bryan & Norman 1998). Consequently, the mass
![]() contained
inside
contained
inside
![]() at scale factor a, satisfies the following equations:
at scale factor a, satisfies the following equations:
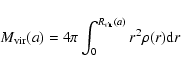 |
(9) |
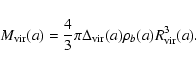 |
(10) |
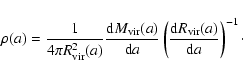 |
(11) |
![\begin{displaymath}\rho(a)=\frac{3X(a)}{8\pi
G}\left[1-\frac{{\rm d}\ln X(a)/{\...
...}\ln a}{{\rm d}\ln M_{\rm vir}(a)/{\rm d}\ln a}
\right]^{-1}
\end{displaymath}](/articles/aa/full/2006/40/aa5551-06/img71.gif) |
(12) |
![\begin{displaymath}R_{\rm vir}(a)=\left[\frac{2GM_{\rm vir}(a)}{X(a)}\right]^{1/3}
\end{displaymath}](/articles/aa/full/2006/40/aa5551-06/img72.gif) |
(13) |
Let us assume that
![]() while
while
![]() .
It is interesting to study approximate predictions of the above two equations. First, X(a) depends on the assumed cosmology alone. Since
.
It is interesting to study approximate predictions of the above two equations. First, X(a) depends on the assumed cosmology alone. Since
![]() ,
where subscripts 0 stand
for the present day values and
,
where subscripts 0 stand
for the present day values and
![]() is a slowly varying function of a, we see that X(a) scales approximately as a-3 so
is a slowly varying function of a, we see that X(a) scales approximately as a-3 so
![]() .
On the other hand, g varies significantly
during the evolution. It is well known that the mass of
a forming object grows fast at the early stages of its evolution, while the growth rate drops at later
times when its mass grows very slow. Using (12) and (13) one can show that the slope
.
On the other hand, g varies significantly
during the evolution. It is well known that the mass of
a forming object grows fast at the early stages of its evolution, while the growth rate drops at later
times when its mass grows very slow. Using (12) and (13) one can show that the slope ![]() follows
follows
![]() .
Obviously, f<0 and g>0 so
.
Obviously, f<0 and g>0 so ![]() .
Hiotelis
& Del Popolo (2006) have shown that the values of
.
Hiotelis
& Del Popolo (2006) have shown that the values of
![]() for values of a close to unity
(present time) are in the range
0.4/a - 0.8/a, from small to large haloes. This gives a rough estimation of the
slope at the virial radius in the range 2.64 to 2.36, which is in satisfactory agreement
with the models based on the results of N-body simulations as those described in the introduction.
For
for values of a close to unity
(present time) are in the range
0.4/a - 0.8/a, from small to large haloes. This gives a rough estimation of the
slope at the virial radius in the range 2.64 to 2.36, which is in satisfactory agreement
with the models based on the results of N-body simulations as those described in the introduction.
For
![]() ,
we use the model
,
we use the model
![]() resulting in
resulting in
![]() at present epoch (a=1) (see Solanes et al. 2005).
at present epoch (a=1) (see Solanes et al. 2005).
From the above approximate expression we see that ![]() is a decreasing function of g. Since g is
a decreasing function of the scale factor a (the mass growth rate decreases with time),
is a decreasing function of g. Since g is
a decreasing function of the scale factor a (the mass growth rate decreases with time), ![]() increases
during the build-up of the halo. Thus, the inner region
is characterized by smaller values of
increases
during the build-up of the halo. Thus, the inner region
is characterized by smaller values of ![]() than the outer one. Hiotelis & Del Popolo (2006)
found that for haloes of the same present day mass, different analytical models
predict different mass growth rates. Namely, at the early stages of the evolution, EC model predicts haloes that
grow with a larger mass growth rate than those haloes formed by the spherical model. Thus formation times are smaller
in the EC model. This result is in the correct direction since it improves the agreement between the
results of analytical and numerical methods (Lin et al. 2003). This improvement is also a motive for the study
of density profiles that are predicted by EC model. Some of the differences to be expected are clear:
The inner density profile should be flatter in the EC model than the spherical model since at their
early stages, haloes evolve with larger g for the first model. However, since the spherical model predicts
density profiles in good agreement with the NFW profile (Manrique et al. 2003), we expect inner density profiles
with logarithmic slope
than the outer one. Hiotelis & Del Popolo (2006)
found that for haloes of the same present day mass, different analytical models
predict different mass growth rates. Namely, at the early stages of the evolution, EC model predicts haloes that
grow with a larger mass growth rate than those haloes formed by the spherical model. Thus formation times are smaller
in the EC model. This result is in the correct direction since it improves the agreement between the
results of analytical and numerical methods (Lin et al. 2003). This improvement is also a motive for the study
of density profiles that are predicted by EC model. Some of the differences to be expected are clear:
The inner density profile should be flatter in the EC model than the spherical model since at their
early stages, haloes evolve with larger g for the first model. However, since the spherical model predicts
density profiles in good agreement with the NFW profile (Manrique et al. 2003), we expect inner density profiles
with logarithmic slope ![]() smaller than 1.
smaller than 1.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{5551-fig1}
\end{figure}](/articles/aa/full/2006/40/aa5551-06/Timg82.gif) |
Figure 1: Density profiles for four of the cases studied. From top to bottom dotted lines correspond to the results of the cases 1, 4, 6 and 7, respectively. Solid lines are fits by the formula of Eq. (1). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{5551-fig2}
\end{figure}](/articles/aa/full/2006/40/aa5551-06/Timg83.gif) |
Figure 2: Triangles show the concentrations predicted by the model studied while the solid line shows the predictions of the toy-model of Bullock et al. |
| Open with DEXTER | |
In Fig. 1, we show the density profiles of four of the seven cases
studied. From top to bottom, dotted lines show our predictions
for cases 1, 4, 6 and 7, respectively, while
solid lines show the fits of the above dotted curves by models of the
form of Eq. (1) where
![]() and
and ![]() are
fitting parameters. The values of the parameters are found by
minimizing the sum
are
fitting parameters. The values of the parameters are found by
minimizing the sum
![]() ,
where
,
where ![]() are the values of the density predicted by our results. The minimization is performed using the unconstrained
subroutine ZXMWD of IMSL mathematical library. The fits are shown to be very good. We also tried minimizations
for
are the values of the density predicted by our results. The minimization is performed using the unconstrained
subroutine ZXMWD of IMSL mathematical library. The fits are shown to be very good. We also tried minimizations
for
![]() and
and ![]() and
and
![]() free parameters corresponding to the NFW model with
free parameters corresponding to the NFW model with
![]() and
and
![]() free parameters, corresponding to the R05 model
but the respective fits were found less satisfactory. The resulting values of the parameters are used in order to calculate
the concentrations of the haloes. Equation (2) yields that the logarithmic slope
free parameters, corresponding to the R05 model
but the respective fits were found less satisfactory. The resulting values of the parameters are used in order to calculate
the concentrations of the haloes. Equation (2) yields that the logarithmic slope ![]() equals n at distance rn given
by
equals n at distance rn given
by
![\begin{displaymath}r_n=\left[\frac{n-k}{\lambda\mu+k-n}\right]^{1/\lambda}r_{\rm s}.
\end{displaymath}](/articles/aa/full/2006/40/aa5551-06/img92.gif) |
(14) |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{5551-fig3}
\end{figure}](/articles/aa/full/2006/40/aa5551-06/Timg93.gif) |
Figure 3: Solid lines show the logarithmic slopes of the density profiles given by Eq. (2) for all seven cases studied. From top to bottom, these lines correspond to cases 1, 2, 3, 4, 5, 6 and 7, respectively. Dashed lines show, with the same order, the predictions of the model of Reed et al. (2005), based on the results of their N-body simulations. |
| Open with DEXTER | |
| (15) |
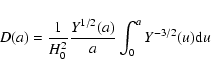 |
(16) |
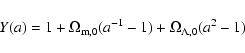 |
(17) |
We note that for the cosmology used in this paper, the present-day value of M* is
![]() .
It is obvious from Fig. 2, that the agreement is very satisfactory.
.
It is obvious from Fig. 2, that the agreement is very satisfactory.
In Fig. 3, we compare the logarithmic slopes resulting by our calculations to those proposed by R05 to fit the results of N-body simulations. Solid lines are the predictions of the logarithmic slopes predicted by our modes while dashed lines are the predictions of the procedure proposed by the above authors. From top to bottom, the slopes correspond to the cases 1, 2, 3, 4, 5, 6 and 7, respectively. The procedure proposed by R05 is as follows:
For a halo of mass M, we find the exponent ![]() by the formula
by the formula
![]() .
Then a concentration ck, defined by
.
Then a concentration ck, defined by
![]() ,
is calculated
by the empirical formula
,
is calculated
by the empirical formula
![]() ,
that is a satisfactory fit to the results of N-body simulations, and then the formula
,
that is a satisfactory fit to the results of N-body simulations, and then the formula
![]() is applied. This formula results from
Eq. (2) for
is applied. This formula results from
Eq. (2) for ![]() ,
and
,
and
![]() ,
while
,
while
![]() is the radial
distance in units of the virial radius. We also note that R05 report
a significant scatter in the values of
is the radial
distance in units of the virial radius. We also note that R05 report
a significant scatter in the values of
![]() in the results of their N-body simulations, which obviously
leads to significant scatter to the values of the logarithmic slope.
in the results of their N-body simulations, which obviously
leads to significant scatter to the values of the logarithmic slope.
There are some interesting features in this figure. First, the
density profiles of heavier haloes are flatter. This order is obvious in both our results and those of N-body
simulations. Second, the values of inner slope (at
![]() )
resulting from our models are significantly
smaller than those resulting from N-body simulations while the inverse occurs
at the outer slopes (at
)
resulting from our models are significantly
smaller than those resulting from N-body simulations while the inverse occurs
at the outer slopes (at
![]() ).
).
In Fig. 4, dotted lines show the central density profiles of the cases 3, 4, 5, 6 and
7 while solid ones show the fits by the formula of Eq. (1). This figure is drawn to show the high quality of the fit and to ensure that
the logarithmic slope can be estimated with a good accuracy.
Figure 5 presents the central slopes of the five more massive haloes that are represented by
the cases 3, 4, 5, 6 and 7. It is clear that the asymptotic slope at the center of the system varies in the range
of 0.35 to 0.4.
![\begin{figure}
\par\includegraphics[width=8.3cm]{5551-fig4}
\end{figure}](/articles/aa/full/2006/40/aa5551-06/Timg108.gif) |
Figure 4: Fits of the density profiles of inner regions. From top to bottom dotted lines correspond to the cases 3, 4, 5, 6, 7 of our model while solid lines are the fits by the formula of Eq. (1). The quality of the fit is sufficient for a reasonable estimation of the logarithmic slope. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{5551-fig5}
\end{figure}](/articles/aa/full/2006/40/aa5551-06/Timg109.gif) |
Figure 5:
The logarithmic slopes of the density profiles for the
cases of Fig. 4. From top to bottom the lines correspond to cases 3, 4, 5, 6, 7. It is clear that larger haloes have at the same
radial distance (measured in units of the virial radius) flatter
inner density profiles. Additionally, it is clear that |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{5551-fig6}
\end{figure}](/articles/aa/full/2006/40/aa5551-06/Timg110.gif) |
Figure 6:
The same as in Fig. 5 but for the outer region. From top
to bottom, lines correspond to the cases 1, 2, 3, 4, 5, 6 and 7,
respectively. It is clear that the slope |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{5551-fig7}
\end{figure}](/articles/aa/full/2006/40/aa5551-06/Timg111.gif) |
Figure 7: The dependence of the concentration on the mass growth rate of the halo. Triangles represent the concentrations of haloes with large recent mass growth, squares represent the concentrations of all haloes of every case and circles the concentrations of haloes with small recent mass growth. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{5551-fig8}
\end{figure}](/articles/aa/full/2006/40/aa5551-06/Timg112.gif) |
Figure 8: The dependence on the outer slope on the mass growth rate. Solid lines correspond to case 3, dashed lines to case 4 and dotted lines to case 7. Upper lines correspond to haloes with small recent mass growth while lower lines correspond to haloes with large recent mass growth. It is obvious that haloes which recently increased significantly their masses have flatter outer density profiles. |
| Open with DEXTER | |
We have to note here that there are difficulties concerning the calculation of the slope of the density profile at inner and outer regions of a halo. If the derivation of slopes is carried out by finding the logarithmic derivative of the analytic formula designed to fit the density profile, it is clear that this could lead to large inaccuracies. For example, an analytic formula could fit well a large part of the curve but not its inner and/or outer region. Such an example can be seen in Fig. 8 of Tasitsiomi et al. (2004), where analytic formulas are presented along with the results of N-body simulations. It is obvious that, in some cases presented in that figure, analytic formulas are bad estimators of inner and outer slopes. Regarding our fits we note that in cases where the formula given by Eq. (1) is not able to fit the whole curve to a desired high accuracy, we used it to fit the inner or the outer regions separately. Thus, the resulting inner and outer slopes as well as the values of concentration are calculated with a high accuracy.
We additionally examined the role of the mass growth rate to the resulting concentrations and density
profiles So, we analyze our samples of haloes by the following procedure:
First, for every case we find the value of the scale factor
![]() at which about half of the haloes have mass smaller
than one half of the present day mass. Thus, we divide the haloes of every case into two groups. The first
group, called group S (small), contains haloes whose mass satisfies
at which about half of the haloes have mass smaller
than one half of the present day mass. Thus, we divide the haloes of every case into two groups. The first
group, called group S (small), contains haloes whose mass satisfies
![]() while the second
group, called group L (large), contains haloes whose mass satisfies
while the second
group, called group L (large), contains haloes whose mass satisfies
![]() .
It is clear that haloes of group S have to
show a larger recent mass growth rate than those of group L since the haloes of both groups have the same present day
mass. Then, we found the concentration of every group. The
results are presented in Fig. 7.
Triangles are the concentrations of group S for every case, squares are those of all haloes and circles
show the concentrations of group L. It is obvious that, although the differences are not large, haloes of group S
show systematically larger concentrations than those of group L.
.
It is clear that haloes of group S have to
show a larger recent mass growth rate than those of group L since the haloes of both groups have the same present day
mass. Then, we found the concentration of every group. The
results are presented in Fig. 7.
Triangles are the concentrations of group S for every case, squares are those of all haloes and circles
show the concentrations of group L. It is obvious that, although the differences are not large, haloes of group S
show systematically larger concentrations than those of group L.
In Fig. 8, we plot the outer slopes for every group of the cases 3, 4 and 7. The upper solid line at the right of the
figure corresponds to the group L of case 3, while the lower solid line corresponds to the
group S of the same case. The upper and
lower dashed lines correspond to the groups L and S of the case 4, respectively, while the upper and lower dotted lines
correspond to the groups L and S of the case 7. The role of the mass growth is obvious in this
figure Haloes which recently increased significantly their masses (they belong to groups S) have flatter outer density
profiles than haloes of the same mass but which show no recent significant growth of their masses (group L).
We note that the results of Fig. 8 are fully consistent with the approximate predictions of the method that are analyzed
above. A significant recent increase of mass corresponds to large values of the exponent g and consequently to
small values of ![]() .
.
No systematic dependence of the inner slope on the mass growth rate is found.
It has been reported (Ascasibar et al. 2003; Tasitsiomi et al. 2004) that haloes, which experienced a recent
merger event, have lower concentrations and steeper inner profiles than more relaxed systems. We note that in N-body
simulations a recent merger event probably leads to a redistribution
of particles even inside the virial radius while in our model the halo remains always in
virial equilibrium. However, a recent merging event does not necessarily correspond to a recent and significant
mass growth rate. Thus the difference that appears (a recent merger event leads to lower concentration while
a recent significant mass growth rate to a larger concentration) is due to the obvious inability of
the "stable clustering'' approach to deal with all kinds of merger events. Virial equilibrium assumed for
our approach holds under certain conditions that are related to the masses and the amounts of
the intrinsic and orbital angular momentum of merging haloes. Further
studies by both numerical and analytical methods are needed to improve our understanding
about the physics of merger events. However, the limits of validity of "stable clustering'' approach
are not clear yet. Manrique et al. (2003) and Hiotelis (2003) proposed that the "stable clustering'' approach is
valid if the fractional increase of halo's mass by a merger is below a given threshold
![]() (with
(with
![]() in the range
0.2-0.5). Although for the above values models seem to work well, it is obvious that kinematic parameters
(as the amounts of angular momentum) have also to be taken into account.
in the range
0.2-0.5). Although for the above values models seem to work well, it is obvious that kinematic parameters
(as the amounts of angular momentum) have also to be taken into account.
It is clear that the formation history of a halo is a very complicated process. Its mass growth history
consists of periods of gentle increase, corresponding to the accretion of small amounts of the surrounding matter,
and periods of sharp increase that correspond to mergers with other haloes. It is obvious that our assumption
of stable clustering can hardly hold in cases of mergers between haloes of similar masses. On the other hand, the
prediction of smooth density profiles requires a sufficient smooth approximation of mass growth. Smooth mass growth curves
are derived by using a large number of haloes of the same mass for every case. We show that inner and outer slopes depend on the present day mass of the
halo. Heavier haloes have smaller values of ![]() in both inner and outer regions. We also show that heavier haloes
have smaller concentrations than those of less heavy ones. The predicted values of concentration are very close to those
predicted by the results of N-body simulations.
in both inner and outer regions. We also show that heavier haloes
have smaller concentrations than those of less heavy ones. The predicted values of concentration are very close to those
predicted by the results of N-body simulations.
Inner and outer slopes predicted by the model studied here are different from those predicted from N-body simulations.
Our results indicate that inner slopes depend mainly on the mass of the halo (or equivalently on the power spectrum)and
not on the rate of its mass growth.
The values of inner slope are close to those derived from observations. Outer slopes do not depend on the present day
mass of the halo only but on the rate of its mass growth too. A low recent mass growth
rate results in steep outer density profiles. In any case, these values seem to be different from those
reported by numerical simulations. Only very massive haloes seem to have slopes at
![]() smaller than 3.
Less massive haloes show outer slopes even larger than 5.
smaller than 3.
Less massive haloes show outer slopes even larger than 5.
Since the predictions presented in this paper are so close to the results of observations for the central regions, we believe that the simple physical model used is very promising and further improvements could help us to understand better the physics involved in the formation of central regions of dark matter haloes.
Acknowledgements
We are grateful to the anonymous referee for helpful and constructive comments and discussions. We also acknowledge the Empirikion Foundation for its financial support, Dr. M. Vlachogiannis and K. Konte for assistance in manuscript preparation.