A&A 458, 13-20 (2006)
DOI: 10.1051/0004-6361:20065540
H.-J. Fahr - M. Siewert
Institut für Astrophysik und Extraterrestrische Forschung (now part of the Argelander Institut für Astronomie) der Universität Bonn, Auf dem Huegel 71, 53121 Bonn, Germany
Recieved 4 May 2006 / Accepted 30 June 2006
Abstract
Aims. We study the classical problem of the transition of a pressure-anisotropic plasma over a hydrodynamical shock using a purely Boltzmann-kinetical treatment.
Methods. We derive the Boltzmann equation for a plasma crossing a shock at a random orientation and evaluate the velocity space integral of the distribution function over the shock analytically. We then try to reproduce the classical MHD behavior and to evaluate the pressures parallel and perpendicular to the magnetic field by integrating the resulting Boltzmann equation over velocity space.
Results. We obtain, for the first time, a completely analytical result for the downstream pressure anisotropy in the case of a perpendicular shock, closing the set of MHD jump conditions. For the parallel shock, it turns out that a single-fluid description without relaxation terms is not sufficient to describe the shock, no matter how much we fine-tune our external parameters. All these results are completely independent of the fine structure of the shock and the upstream distribution function.
Key words: plasmas - shock waves - solar wind - magnetohydrodynamics (MHD)
As is well known from the literature, the solar wind termination shock, and in most cases also other astrophysical shocks, are theoretically well described by the application of hydrodynamical or magnetohydrodynamical fluid concepts (for more recent different model approaches to the solar wind termination shock see Zank et al. 1993; Chalov & Fahr 1995; Fahr & Scherer 2005; Chalov & Fahr 1994; Zank 1999; Chalov & Fahr 1996). For purely hydrodynamical fluids the so-called Rankine-Hugoniot relations are developed respecting the usual physical conservation laws for the mass, the momentum, the energy, and the entropy flows. Usually they appear in the form given by, e.g., Serrin (1959), Zel`dovich & Raizer (1966) or Landau & Lifshitz (1977). If the plasma is magnetized and magnetic pressures and tensions cannot be neglected, then these relations have to be enlarged by corresponding magnetic terms and, under the simplifying assumption of scalar ion/electron pressures, one in that case is lead to a system of MHD shock relations given in e.g. Baumjohann & Treumann (1996), Gombosi (1998) or Diver (2001).
The outstanding problem in these approaches is that most of
the astrophysical shocks are classified by their nature as collisionless
shocks, i.e., the randomization or thermalization of particle kinetic energies
on the upstream side at the passage over the small scales of the shock
transition (that is of the order of the ion inertial length or a proton skin
depth) cannot be achieved by usual binary particle collisions. Hereby the ion
inertial length, or the proton skin depth, is given by
![]() with
with
![]() being the ion plasma frequency. So-called "collisionless
shocks'' establish themselves when collsionless plasmas counterstream to
each other with super-alfvénic velocities or encounter an obstacle.
Different types of such shocks appear in the heliosphere in the form of solar wind
bowshocks ahead of cometary or planetary objects, shocks in-between corotating
interaction regions, travelling interplanetary shocks, or the heliospheric
termination shock. The problem, however, with these types of shocks is that
they do not permit a hydrodynamical or
magnetohydrodynamical treatment, at least not based on the lowest velocity
moments of the distribution function, i.e., the density, the bulk velocity, and
the scalar pressure. Nevertheless HD approaches based on
low-order velocity moments of the distribution function are most often
used to describe these shocks, though it is not explained in these approaches
how the dynamic bulk energy of the upstream ions is irreversibly converted
into thermal energy of the downstream ions. It is tacitly understood in the
scientific community that this entropisation of the plasma flow is achieved by
collective wave-particle interaction processes, which require upstream and
downstream wave turbulences, not consistently included in the usual MHD approach.
being the ion plasma frequency. So-called "collisionless
shocks'' establish themselves when collsionless plasmas counterstream to
each other with super-alfvénic velocities or encounter an obstacle.
Different types of such shocks appear in the heliosphere in the form of solar wind
bowshocks ahead of cometary or planetary objects, shocks in-between corotating
interaction regions, travelling interplanetary shocks, or the heliospheric
termination shock. The problem, however, with these types of shocks is that
they do not permit a hydrodynamical or
magnetohydrodynamical treatment, at least not based on the lowest velocity
moments of the distribution function, i.e., the density, the bulk velocity, and
the scalar pressure. Nevertheless HD approaches based on
low-order velocity moments of the distribution function are most often
used to describe these shocks, though it is not explained in these approaches
how the dynamic bulk energy of the upstream ions is irreversibly converted
into thermal energy of the downstream ions. It is tacitly understood in the
scientific community that this entropisation of the plasma flow is achieved by
collective wave-particle interaction processes, which require upstream and
downstream wave turbulences, not consistently included in the usual MHD approach.
General weaknesses of the MHD approach have been extensively discussed in
the Proceedings of the COSPAR Colloquium "Physics of Collisionless Shocks''
(Russell 1995) and in a recent review by Lembege et al. (2004).
Unsolved questions concerning the behavior and the role of
electrons at the shock passage and of shock-reflected ions that could be
candidates to drive upstream MHD wave turbulences supporting nonlinear
wave-particle dissipation processes, which are especially important.
These counterflowing ion populations that
cannot be described in the frame of a fluid theory where kinetic
two-stream- or Buneman-instabilities are responsible for a viscous heating of
the electron fluid. Different from fluid concepts, a local description of the
dissipation via reflected ions needs kinetic aspects to be taken into account.
The downstream concentration of the magnetic field and of the density
self-consistently produces the electric field of the shock ramp that
decelerates most of the ions, but also reflects a fraction of the inflowing
ions, thus moving opposite to the inflowing upstream plasma. At present, the
only hope to bring this complicated kinetic particle-field system to at least
some degree of conistency is connected with shock simulation calculations
within hybrid or full particle codes (e.g., see Hada et al. 2003; Scholer et al. 2003)
Yet even these computationally highly pretentious simulation
runs most often do not offer a stationary solution for the shock profile, but
due to the accumulation of spectuularly reflected ions upstream of the shock cause
the formation and repeated reformation of ramp shocks on timescales of
gyroperiods of the ramp magnetic fields. While for unrealistic ion/electron
mass ratios (i.e.,
![]() the average shock profile attains a relatively regular shape, for realistic ratios
the average shock profile attains a relatively regular shape, for realistic ratios
![]() a completely
erratic profile is found. Most unclear in all the simulation runs remains the
role of shock-heated electrons. Hybrid simulation codes show that
they can only achieve reasonable results for unresasonably high electron
resistivities (Scudder 1995), which perhaps could be ascribed to ion-acoustic
instabilities or to Coulomb collision mediation, but, as could be shown in
particle-particle simulations, neither ion-acoustic instabilities nor Coulomb
collision effects are likely to become of the required importance
(see Wilkinson 1991; Thomsen et al. 1985). Thus it may be concluded here that
neither hybrid codes nor full particle in cell codes are able at present to
adequately represent the full physics of collisionless shocks. We thus may
try another way to study the kinetic structure of collisionless shocks
starting from MHD shock solutions, which yield the basic shock structure of
the plasma density, the bulk velocity, and the magnetic field, and then solve the
kinetic transport equation for the ion distribution function at the ion passage over this shock structure.
a completely
erratic profile is found. Most unclear in all the simulation runs remains the
role of shock-heated electrons. Hybrid simulation codes show that
they can only achieve reasonable results for unresasonably high electron
resistivities (Scudder 1995), which perhaps could be ascribed to ion-acoustic
instabilities or to Coulomb collision mediation, but, as could be shown in
particle-particle simulations, neither ion-acoustic instabilities nor Coulomb
collision effects are likely to become of the required importance
(see Wilkinson 1991; Thomsen et al. 1985). Thus it may be concluded here that
neither hybrid codes nor full particle in cell codes are able at present to
adequately represent the full physics of collisionless shocks. We thus may
try another way to study the kinetic structure of collisionless shocks
starting from MHD shock solutions, which yield the basic shock structure of
the plasma density, the bulk velocity, and the magnetic field, and then solve the
kinetic transport equation for the ion distribution function at the ion passage over this shock structure.
We start from solutions of the well-known MHD shock relations, which are considered to give valid connections of the fluid and field properties of the upstream with the downstream MHD plasma flows. From these solutions we obtain the main plasma properties like the plasma density and the magnitude and direction of the plasma bulk velocity and of the frozen-in magnetic field (e.g., see Gombosi 1998; Baumjohann & Treumann 1996; Diver 2001).
What we furthermore aim at here, is the change of the kinetic properties of
the ion distribution function at the ion passage from the upstream to the
downstream side of the shock. To learn about these changes we
integrate the Boltzmann-Vlasow equation that kinetically describes the
phase-space change of the ion distribution function
![]() .
Here
.
Here
![]() is the individual ion velocity vector, and s is a streamline coordinate counted along the streamline that leads from the upstream
to the downstream side. For a local planar shock, which may be
considered here, this coordinate simply measures the distance
in the direction of the shock
normal from the shock. Neglecting in the first step an explicit local time
dependence and any form of stochastic interaction processes like wave-particle
interactions, the Boltzmann equation is simply
is the individual ion velocity vector, and s is a streamline coordinate counted along the streamline that leads from the upstream
to the downstream side. For a local planar shock, which may be
considered here, this coordinate simply measures the distance
in the direction of the shock
normal from the shock. Neglecting in the first step an explicit local time
dependence and any form of stochastic interaction processes like wave-particle
interactions, the Boltzmann equation is simply
Now we want to make use of the knowledge of the MHD quantities and for that
purpose want to transform the upper Boltzmann equation into the plasma bulk
frame moving with the plasma bulk velocity
![]() .
In this frame
the distribution function may be denoted by
.
In this frame
the distribution function may be denoted by
![]() ,
where
,
where
![]() denotes the individual ion velocity in the plasma
bulk frame. In this frame, no electric forces are operating since these are
just compensated by the Lorentz forces
denotes the individual ion velocity in the plasma
bulk frame. In this frame, no electric forces are operating since these are
just compensated by the Lorentz forces
![]() .
However,
some additional forces are appearing in this frame,
since it is accelerated with
respect to the solar frame due to the change of the velocity
.
However,
some additional forces are appearing in this frame,
since it is accelerated with
respect to the solar frame due to the change of the velocity
![]() with the proper time
with the proper time ![]() given by
given by
![]() .
.
The most general covariant 8-dimensional phase-space formulation of the
Boltzmann-Vlasow equation that can be applied to that case was given in the
following form (see Landau & Lifshitz 1977):
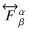 is the electromagnetic field
tensor and
is the electromagnetic field
tensor and 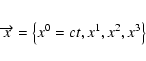
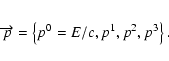
For the homogeneous region far upstream of the termination shock, where
temporal and spatial derivatives of the distribution function disappear,
the actions of Lorentz forces on the distribution function also have to cancel, at
least if an averaging over times large compared to the gyroperiod
![]() is considered.
is considered.
This explicitly means that the distribution function
![]() has to be of a form such that:
has to be of a form such that:
Now we want to solve the Boltzmann equation in the plasma bulk reference frame
that moves locally with the plasma bulk velocity
![]() ;
however, considering the inhomogeneous transition region just upstream and
downstream of the shock, where
;
however, considering the inhomogeneous transition region just upstream and
downstream of the shock, where
![]() and
and
![]() ,
for a locally planar shock, are functions only of the streamline coordinate s. In this system the distribution function is given by
,
for a locally planar shock, are functions only of the streamline coordinate s. In this system the distribution function is given by
![]() ,
where the individual ion velocity
,
where the individual ion velocity
![]() is connected with the associated velocity
is connected with the associated velocity
![]() in the
solar rest frame by
in the
solar rest frame by
![]() .
Neglecting explicit time-dependences in this bulk reference system, the
total time derivative of
.
Neglecting explicit time-dependences in this bulk reference system, the
total time derivative of ![]()
![]() thus is given by
the Boltzmann equation (Eq. (8)).
thus is given by
the Boltzmann equation (Eq. (8)).
The gyro-average of the Lorentz acceleration, in application to the gyrotropic
distribution function
![]() ,
explicitly assuming the
conservation of the magnetic moment of each individual ion (i.e., assuming that
,
explicitly assuming the
conservation of the magnetic moment of each individual ion (i.e., assuming that
![]() ,
where
,
where
![]() and L are the gyrofrequency of
the ion and the normal extent of the shock transition layer, respectively),
can then be given by two separately contributing parts connected a) with the change of the
magnitude, and b) with the change of the direction of
and L are the gyrofrequency of
the ion and the normal extent of the shock transition layer, respectively),
can then be given by two separately contributing parts connected a) with the change of the
magnitude, and b) with the change of the direction of
![]() .
These two parts then lead to:
.
These two parts then lead to:
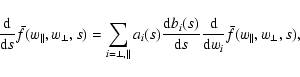 |
(21) |
To integrate Eq. (22) over the shock, it is necessary to start from the basic MHD solutions for the shock transition. Nevertheless there are two essentially different approaches possible to this problem, i.e., the shock with finite extent and the infinitesimally thin, rapid shock transition. Since the latter case is a limit of the former one, we first focus on shock with finite extent.
We assume that the extended shock ranges from
![]()
![]() .
For the specific form of the quantities ai and bi, we
chose the ansatz
.
For the specific form of the quantities ai and bi, we
chose the ansatz
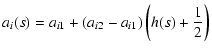 |
(23) | ||
| (24) |
Next, we separate these functions into a symmetrical and an antisymmetrical
part,
| (25) | |||
| (26) | |||
| h(s) = hs(s) + ha(s). | (27) |
It is also obvious that this result even holds for an infinitesimal shock. There are other instances, though, when the thickness of the shock does matter. For example, if the shock is thicker than the average ion gyroradius, heavy ions in an astrophysical plasma will conserve their magnetic moments at the passage, while for an abrupt shock, these ions cannot adiabatically adapt to the change in the B-field magnitude and direction (Bzowski et al. 2006).
Next, we use these results to evaluate Eq. (22). For the angular
expressions we use
| (29) | |||
| (30) |
| [[A]] = A2-A1 | (32) | ||
| (33) |
First we investigate the reaction of the distribution
function to a purely perpendicular shock, which leads to the conditions
Bt1=B1,
Bt2=B2, and
Bn1=Bn2=0. In addition, from
classical high Mach
number MHD it follows that
Un2=Un1/s and
B2=sB1. Using these
results the MHD parameters introduced in Eqs. (35) to (37) reduce to
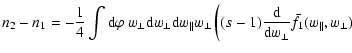 |
|||
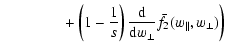 |
|||
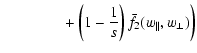 |
|||
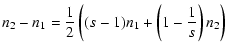 |
|||
| n2-n1 = (s-1)n1 | |||
| n2 = sn1. | (42) |
The other extreme situation in MHD shock theory is the
parallel shock, which leads to the conditions
Bt1 = Bt2 = 0and
Bn1=Bn2=B. In this case we obtain the following equations
for the parameters:
| (43) | |||
| (44) | |||
| (45) |
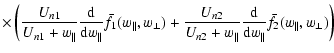 |
|||
| = |
(46) |
Solving the integral in Eq. (47) is complicated by the presence
of the singularity in the form of
![]() .
In plasma
physics, i.e., plasma wave dispersion theories, integrals of this form are
common in the theory of wave damping and excitation, where they are solved by
moving the singularity off the real axis and applying the residual theorem. In
our case, this procedure allows us to apply Cauchys integral formula and we
obtain
.
In plasma
physics, i.e., plasma wave dispersion theories, integrals of this form are
common in the theory of wave damping and excitation, where they are solved by
moving the singularity off the real axis and applying the residual theorem. In
our case, this procedure allows us to apply Cauchys integral formula and we
obtain
| (49) |
From this we conclude that for
practically all physical distribution functions it is not possible
to reproduce the MHD equations from a Boltzmann-kinetic treatment of
the shock transition, as was developed in the section before.
This is a direct result of the singularity
at
![]() .
Considering the source of this expression
(Eq. (17)), it may be
interpreted as an effective velocity at which the individual particles
with velocity
.
Considering the source of this expression
(Eq. (17)), it may be
interpreted as an effective velocity at which the individual particles
with velocity
![]() cross the shock. Obviously, not only
will some of these particles never make it past the shock,
but they will cross it in
the "wrong'' direction, going from the downstream to the upstream
region. This essentially splits up the system into (at least) two different streams moving in antiparallel directions.
cross the shock. Obviously, not only
will some of these particles never make it past the shock,
but they will cross it in
the "wrong'' direction, going from the downstream to the upstream
region. This essentially splits up the system into (at least) two different streams moving in antiparallel directions.
Despite the complications involved with a general solution of Eq. (38), we now investigate the downstream pressure anisotropy, which
is of special interest because it cannot be predicted from classical MHD theories, not even if extended to non-scalar pressures such as those
carried out by Erkaev et al. (2000). As shown by these authors, the system of shock relations
resulting in this more complicated case can only be solved if the
assumption is made that, according to derivations presented in the CGL-theory
(Chew et al. 1956), the first and second adiabatic plasma
invariants are conserved at the shock passage. However, even then the downstream
pressure anisoptropy
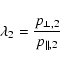 |
(52) |
In the case of a purely perpendicular shock, where the MHD mass flux
conservation can always be fulfilled (see Sect. 5.1), no matter what
the distribution function in detail looks like, we take Eq. (41)
and apply cylindrical velocity space coordinates
(
![]() ),
which lead to the relations
),
which lead to the relations
The partial pressures in the plasma wind system are defined as the second-order velocity moments,
| (55) | |||
| (56) |
The equations then reduce to
| |
= | ||
| = | (57) |
| |
= | ||
| = | (58) |
| (59) | |||
| (60) |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{5540fig1.eps}\end{figure}](/articles/aa/full/2006/40/aa5540-06/Timg177.gif) |
Figure 1:
Ratio of iterated downstream to upstream pressure anisotropy for a perpendicular shock as a function of the mach number |
| Open with DEXTER | |
From this above result it is possible to draw two important conclusions: first, for a perpendicular shock, the downstream pressure anisotropy is a simple, monotonously growing function of the MHD compression ratio s. Furthermore, the downstream anisotropy will always be larger than the upstream one.
The second result is even more important, since the downstream pressures do
not need the knowledge of the specific form of the ion velocity distribution function.
As already mentioned, a pure MHD treatment of the shock is not able to predict
the pressure anisotropy downstream. Now, however, we have the possibility of
evaluating this expression numerically: we first select an initial
![]() ,
calulate the new
,
calulate the new
![]() using
using
![]() and
Eq. (61), and repeat this procedure until
and
Eq. (61), and repeat this procedure until
![]() .
Since the MHD compression factor s is, at
least for a perpendicular shock, almost independent of
.
Since the MHD compression factor s is, at
least for a perpendicular shock, almost independent of
![]() (Erkaev et al. 2000), this algorithm typically already converges after the first or
second step. Iterated compression ratios are presented in
Fig. 1, where we have demonstrated that the downstream
pressure anisotropy depends strongly on the sonic mach parameter As and
somewhat less on the upstream pressure anisotropy
(Erkaev et al. 2000), this algorithm typically already converges after the first or
second step. Iterated compression ratios are presented in
Fig. 1, where we have demonstrated that the downstream
pressure anisotropy depends strongly on the sonic mach parameter As and
somewhat less on the upstream pressure anisotropy
![]() and the
Alfven mach number MA.
and the
Alfven mach number MA.
We now test if this above-derived result is consistent with the CGL-asumption
of the conservation of the two adiabatic invariants as adopted in the MHD model by Chew et al. (1956) and Erkaev et al. (2000),
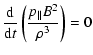 |
(62) | ||
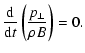 |
(63) |
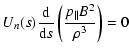 |
(64) | ||
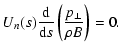 |
(65) |
![\begin{eqnarray*}\frac{1}{2}\{\{U_{n}(s)\}\}[[g(s)]]=0,
\end{eqnarray*}](/articles/aa/full/2006/40/aa5540-06/img187.gif)
From Sect. 3 and Eq. (28) it also follows
that any adiabatic invariant of the form
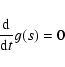 |
(69) |
| (70) |
We have developed a kinetic treatment of a pressure-anisotropic plasma crossing a classical MHD shock. To do this, we first derived the Boltzmann equation for such a plasma, taking the nonrelativistic limit from the general covariant form of the Boltzmann equation and adapting it to typical anisotropic MHD shock transitions. We have proven that for practically all physical situations the fine structure of the transition region does not influence the downstream quantities at all.
Next, we investigated the shock transition in more detail for two extreme situations, the perpendicular shock where the magnetic field is orthogonal to the shock normal, and the parallel shock, where B is parallel to the shock normal. We have proven that in the case of the perpendicular shock, the kinetic treatment of the shock is in perfect agreement with the MHD one, and it is possible to give an analytical expression for the downstream pressure anisotropy, closing the (incomplete) set of MHD equations (see, e.g. Erkaev et al. 2000) without any specific knowledge of the velocity distribution function.
For the parallel shock, we have proven that MHD is usually not an adequate description, which is a direct result from a singularity in the Boltzmann equation. We have physically interpreted this as a distribution in the bulk velocity system, where particles with different local velocities will also cross the shock at different timescales. This situation can be identified as (at least) two different plasma streams crossing the shock with two different velocities, both parallel and antiparallel to the shock normal. This effect will automatically lead to a two-stream instability leading to viscous-type dissipation, as was already often envisaged in the literature (e.g. Scholer et al. 2003), which, however, will be analyzed in more detail in a further publication.
While we have not yet solved the Boltzmann equation to obtain the downstream distribution function, we were already able to derive several results from the equation itself, including the lower order momenta of the downstream plasma. The full solution of the equation, as well as more detailed properties of this distribution function (e.g. higher downstream momenta, or the entropy change when crossing the shock) will be published in the near future. We have also recently begun investigating the generation of MHD waves and their coupling to the charged particles, including determining what kind of wave generation and radiation is possible from within the system. After finishing this, we intend to revisit the parallel shock (and, more generally, the inclined shock with an arbitrary angle between the magnetic field and the shock normal).
Our results suggest that a perpendicular shock is well described by simple analytical expressions, which do not depend on the fine structure of the shock at all. This in turn provides an excellent test criterium for numerical simulations aiming to describe more complex shock structures in plasmas. Inaddition, this relation and the formalism developed here should considerably simplify calculations related to less simple systems, e.g. where there are more than one particle population (see, e.g. Bzowski et al. 2006).
Finally, we were able to derive a simple relation which allows to turn any adiabatic invariant into an additional jump condition, which should allow us to study more complicated jump conditions.
Acknowledgements
We are grateful for financial support to the DFG within the frame of the DFG-Project Fa 97/31-1.