A&A 458, 135-149 (2006)
DOI: 10.1051/0004-6361:20065374
On the self-enrichment scenario of galactic globular clusters: constraints
on the IMF
N. Prantzos1 - C. Charbonnel2,3
1 - Institut d'Astrophysique de Paris, UMR7095 CNRS, Univ. P. & M. Curie, 98bis Bd. Arago, 75104 Paris, France
2 -
Geneva Observatory, 1290 Sauverny, Switzerland
3 -
Laboratoire d'Astrophysique de Toulouse et Tarbes - CNRS UMR 5572 CNRS - Université Paul Sabatier Toulouse 3, 14, Av. E. Belin, 31400 Toulouse, France
Received 6 April 2006 / Accepted 22 June 2006
Abstract
Aims. Galactic globular cluster (GC) stars exhibit abundance patterns that are not shared by their field counterparts, e.g. the well-documented O-Na and Mg-Al anticorrelations. Recent spectroscopic observations of GC turnoff stars have provided compelling evidence that these abundance anomalies were already present in the gas from which the observed stars formed. A widely held hypothesis is that the gas was "polluted'' by stars that were more massive (and evolving faster) than the presently observed low-mass stars. In the framework of this "self-enrichment'' scenario for GCs, we present a new method of deriving the initial mass function (IMF) of the polluters, by using the O/Na abundance distribution.
Methods. We focus on NGC 2808, a GC for which the largest sample of O and Na abundance determinations is presently available. We use the abundance distribution of [O/Na] to derive the amount of polluted material with respect to the original composition. We explore two scenarios in detail for the self-enrichment of the cluster, which differ by the assumptions made on the composition of the polluter ejecta. In each case we consider two classes of possible "culprits'': massive asymptotic giant branch (AGB) stars (4-9  )
and winds of massive stars (WMS) in the mass range 10-100
)
and winds of massive stars (WMS) in the mass range 10-100  .
.
Results. We obtain upper limits for the slope of the IMF (assumed to be given by a power-law) of the stars initially more massive than the present turnoff mass. We also derive lower limits for the amount of stellar residues in NGC 2808.
Conclusions. We find that the polluter IMF had to be much flatter than the presently observed IMFs in stellar clusters, which agrees with the results of two other GC IMF determination methods, which we also discuss. Likewise, we find that the present mass of the GC should be totally dominated by stellar remnants if the polluters were AGB stars, which is not the case if the culprits are WMS. We critically analyse the advantages and shortcomings of each potential polluter class and find the WMS scenario more attractive.
Key words: stars: abundances - stars: luminosity function, mass function - Galaxy: abundances - globular clusters: general - globular clusters: individual: NGC 2808
Globular cluster (GC) studies are linked to a wide variety of astrophysical issues.
These stellar systems indeed provide insight into the formation and early chemical evolution
of galaxies and of their substructures. They also represent unique laboratories
for dynamical processes that occur on shorter timescales
than Hubble time (such as two-body relaxation, mass segregation from equipartition
of energy, stellar encounters, collisions and mergers, core collapse, tidal stripping).
Because they are large aggregates of coeval stars, all located at the same distance from us
and containing both very common and unusual (e.g., blue stragglers) stellar objects,
they provide invaluable tests of stellar evolution theory. However, and despite
their broad astrophysical importance, their origin and formation processes still remain uncertain.
For all these reasons,
galactic GCs have been subject to intensive scrunity over the past decades.
The advent of very large telescopes and of multiple-object spectrometers allowed
detailed investigation of their chemical composition
(see Gratton et al. 2004; and Sneden 2005, for recent and extended reviews).
We briefly recall here the fundamental chemical properties of the galactic GCs:
- (i)
- most of them appear to be
mono-metallic as far as the Fe-group elements (Fe, Ni, Cu) are concerned
(with the notable exception of Omega Cen);
- (ii)
- they present very low scatter and the same trends as field stars
for the neutron-capture elements (both s- and r-; Ba, La, Eu) and the alpha-elements (Si, Ca);
- (iii)
- for the lighter elements (from C to Al), they exhibit complex patterns
and large star-to-star abundance variations, which are not shared by their field counterparts.
Among these anomalous patterns, the most striking ones are the anticorrelations between
the abundances of O and Na (see Pilachowski 1989; Drake et al. 1992; and Sneden et al. 1991,
for the early studies; for complete references see Gratton et al. 2004) and
of Mg and Al (see e.g. Shetrone 1996; Ivans et al. 1999; Ramirez & Cohen 2002)
![[*]](/icons/foot_motif.gif) .
.
These anticorrelations are easily understood as the result
of proton-capture nucleosynthesis in the CNO-cycle and the NeNa- and MgAl-chains
of H-burning (Denissenkov & Denissenkova 1990; Langer et al. 1993).
Proton-captures on 16O and 22Ne respectively lead to the destruction
of O and to the production of 23Na at temperatures >
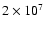 K.
At higher temperatures (
K.
At higher temperatures (
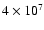 K),
20Ne generates 23Na.
On the other hand, the MgAl-chain is only active at temperatures higher
than
K),
20Ne generates 23Na.
On the other hand, the MgAl-chain is only active at temperatures higher
than 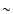
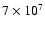 K.
K.
Although the underlying nucleosynthesis is unambiguous, the identification of the
corresponding astrophysical site still remains a challenge.
For a long time the main question was whether such patterns were inherited at the
birth of the stars that we are currently observing
(the so-called self-enrichment hypothesis that implies pollution of the
intracluster gas by more massive and faster evolving stars)
or if they were generated in the course of the evolution of these objects
(the so-called evolution hypothesis that requires non-canonical mixing
inside the star itself).
A major breakthrough was made in that respect from high-resolution spectrographs on
very large telescopes that allowed one to determine the abundances of the
concerned elements in faint subgiant and turnoff stars in a couple of GCs
(Gratton et al. 2001; Grundhal et al. 2002;
Carretta et al. 2003, 2004; Ramirez & Cohen 2002, 2003).
The discovery of the above-mentioned anticorrelations in these scarcely evolved objects
has given a new spin to the self-enrichment scenario.
Indeed, turnoff stars are not hot enough for the required nuclear reactions to occur
in their interiors.
Additionally, the spread of abundances cannot be explained by in situ mechanisms
like gravitational settling and thermal diffusion (Richard et al. 2002;
Michaud et al. 2004).
This implies that the O, Na, Mg, and Al abundance anomalies pre-existed
in the material out of which these objects formed; their gas must have been polluted
early in the history of the cluster by more massive and faster evolving
stars (Cottrell & Da Costa 1981)![[*]](/icons/foot_motif.gif) .
.
It has long been debated whether GCs were made out of totally metal-free material or out of the same gas as the halo field stars (progressively metal-enriched, during the halo chemical evolution). The former is the "classical''
self-enrichment scenario (Cayrel 1986; Fall & Rees 1985; Truran et al. 1991;
Brown et al. 1991; Parmentier et al. 1999; Parmentier 2004), while the latter is a
"pre-enrichment'' scenario (e.g. Harris & Pudritz 1994).
The classical self-enrichment scenario assumes that stars within the GCs created the totality
of the metals (light and heavy), and it involves three stellar generations.
A first generation of exclusively massive stars is clustered in the central regions
of the progenitor cloud, and their SNII explosions rapidly enrich the intra-cluster
gas in iron, 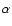 -, and heavy elements, but not in s-elements; the resulting [Ba/Eu]
and [Sr/Ba] ratios should thus reflect pure r-process synthesis (Truran 1988).
A second stellar generation is formed out of this gas, and a sub-class of rapidly evolving
stars injects into the ISM products of H-burning (and nothing else).
The third generation formed from these ejecta has the same uniform heavy-element content
(in alpha- and heavier than Fe elements) as the second one, but a dispersion in its
light metal abundances. The long-lived stars of the second and third generations are
those observed today.
-, and heavy elements, but not in s-elements; the resulting [Ba/Eu]
and [Sr/Ba] ratios should thus reflect pure r-process synthesis (Truran 1988).
A second stellar generation is formed out of this gas, and a sub-class of rapidly evolving
stars injects into the ISM products of H-burning (and nothing else).
The third generation formed from these ejecta has the same uniform heavy-element content
(in alpha- and heavier than Fe elements) as the second one, but a dispersion in its
light metal abundances. The long-lived stars of the second and third generations are
those observed today.
On the other hand, the pre-enrichment scenario assumes that GCs were born with their current
heavy metal content and invokes only two stellar generations: the first of them produces
only the light metals, which contaminate the gas of the second generation,
and builds up the observed anticorrelations
(i.e. they are
equivalent to the second and third generations of the previous scenario).
The two scenarios differ on a key point, the slow neutron capture component of the heavy elements (s-component). In the first scenario, only the rapid neutron capture component (r-component), produced in SNII, may exist, whereas in the latter the s-component appears naturally (exactly as in the field stars of similar metallicity).
A recent high-resolution and high-S/N spectroscopic analysis of turnoff and early
subgiant stars in three GCs spanning a wide range in [Fe/H] values (James et al. 2004a,b)
showed that the [Ba/Eu] and [Sr/Ba] ratios in GCs
follow the trends found in field stars over the same metallicity range. Since Ba and Sr are s-elements, while Eu is an r-element, these findings
clearly indicate a similar and uniform enrichement
by both r- and s-process nucleosynthesis in both populations (halo field stars and GCs).
Consequently, the "classical'' self-enrichment scenario is disfavoured.
Another important result of the work of James et al. (2004a,b) is that no dispersion
is found for s-element abundances within each individual GC (see also Armosky et al. 1994),
nor any correlation with the O and Na patterns.
This indicates that the stars responsible for the light element anticorrelations
did not produce significant amounts of s-process elements.
In view of the aforementioned observational constraints, one concludes that
the GC heavy metals must come from pre-enrichment and that
only light metals up to Al are produced in situ.
It is this scenario that will be called hereafter "the self-enrichment scenario''.
One key aspect of the problem is that the O-Na anticorrelation is found in all GCs
where it has been looked for, independent of their characteristics, i.e., in disk
and halo GCs spanning a wide range in metallicity and in physical properties
(such as horizontal branch morphology, total cluster mass, concentration, and density;
see Carretta 2006; and Carretta et al. 2006).
It appears to be an intrinsic property of those stellar systems.
Understanding the related self-enrichment process would obviously shed light
on GC formation and on the physical processes that dominate the primordial phases
of their evolution.
In particular, one may try to constrain the initial mass function (IMF) of GCs
in the framework of the self-enrichment scenario.
Such an attempt was first made by Smith & Norris (1982) on the basis of the then available data
on C-N anticorrelation in NGC 6752 and 47 Tuc. They found that the observed depletion of C in the cyanogen
enhanced stars of those clusters can be achieved only if the IMF of the first generation stars had
a slope X<-0.4 (where X=1.35 is the Salpeter value) and an upper mass limit <11  .
.
In the present work we discuss the case of NGC 2808 as it is the GC for which the largest sample
of O and Na abundance determinations is available. On the basis of recent data, we derive
the O/Na abundance distribution of the cluster (Sect. 2).
We explore two scenarios for the self-enrichment (Sect. 3) and, in both cases, consider
two possible classes of "polluters'': (i) massive AGB stars (4 to 9  )
which undergo hot-bottom burning and which are usually considered as the most likely culprits;
and (ii) winds of rotating massive stars (WMS), which offer
an interesting alternative, as we argue in Sect. 5.
From the analysis of NGC 2808 data, we constrain the IMF of the stars that are
initially more massive than the ones surviving today, i.e., the GC IMF above
0.8
)
which undergo hot-bottom burning and which are usually considered as the most likely culprits;
and (ii) winds of rotating massive stars (WMS), which offer
an interesting alternative, as we argue in Sect. 5.
From the analysis of NGC 2808 data, we constrain the IMF of the stars that are
initially more massive than the ones surviving today, i.e., the GC IMF above
0.8  ,
and we discuss the implications for the amount of stellar residues (Sect. 4).
In (Sect. 5) we discuss the various (often extreme) assumptions made in the course of our analysis
and argue that, in a realistic scenario, the IMF should be even flatter than the ones we derive
in Sect. 4. We also discuss the advantages and shortcomings of the two classes of polluters, AGBs
and WMS. In Sect. 6 we summarize our work.
,
and we discuss the implications for the amount of stellar residues (Sect. 4).
In (Sect. 5) we discuss the various (often extreme) assumptions made in the course of our analysis
and argue that, in a realistic scenario, the IMF should be even flatter than the ones we derive
in Sect. 4. We also discuss the advantages and shortcomings of the two classes of polluters, AGBs
and WMS. In Sect. 6 we summarize our work.
In the case of NGC 2808, the O-Na anticorrelation
was established for the first time by Carretta et al. (2004).
In an extended survey, Carretta et al. (2006) detected both Na and O in
91 RGB stars of the cluster and obtained upper limits
for O abundances for another 36 giants with Na abundance determinations.
The spread in O and Na abundances is seen
in stars of all luminosities along the RGB,
pointing out a primordial origin with no significant
contribution from the internal evolution of the stars (see also Carretta et al. 2003).
The data of Carretta et al. (2006) for the 91 stars where both O and Na
are detected are displayed in Fig. 1.
It is clearly seen that the ratio [O/Fe]![[*]](/icons/foot_motif.gif) varies from
varies from 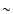 0.5 down to
0.5 down to 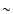 -1, i.e. by a factor of
-1, i.e. by a factor of 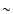 30,
while at the same time Na increases from [Na/Fe
30,
while at the same time Na increases from [Na/Fe![$]\sim-0.2$](/articles/aa/full/2006/40/aa5374-06/img18.gif) to
to 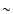 0.8,
i.e. by a factor of
0.8,
i.e. by a factor of 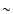 10.
Regarding the O-depletion levels, NGC 2808 is very similar to M13
(Sneden et al. 2004); both clusters display the severest variations
reported up to now.
Since the value of [O/Fe] = 0.5 is typical of
field halo stars (e.g. Spite et al. 2005), it is usually assumed that stars displaying
that ratio (and correspondingly low [Na/Fe]) are those that maintain their
original composition, the one
of the proto-cluster gas.
In contrast, stars displaying the lowest [O/Fe] and highest [Na/Fe]
have been severely contaminated by some external agent
(in the framework of the self-enrichment scenario).
Stars with intermediate compositions
are born from gas that was contaminated to a lesser extent.
10.
Regarding the O-depletion levels, NGC 2808 is very similar to M13
(Sneden et al. 2004); both clusters display the severest variations
reported up to now.
Since the value of [O/Fe] = 0.5 is typical of
field halo stars (e.g. Spite et al. 2005), it is usually assumed that stars displaying
that ratio (and correspondingly low [Na/Fe]) are those that maintain their
original composition, the one
of the proto-cluster gas.
In contrast, stars displaying the lowest [O/Fe] and highest [Na/Fe]
have been severely contaminated by some external agent
(in the framework of the self-enrichment scenario).
Stars with intermediate compositions
are born from gas that was contaminated to a lesser extent.
Because of the anticorrelation, the ratio [O/Na] varies more than
either [O/Fe] or [Na/Fe], from -1.55 to 0.55, and offers a larger basis
for statistical analysis of the abundance distribution within NGC 2808.
Such a distribution has already been presented in Carretta et al. (2006),
but we adopt a different (and, in our opinion, more appropriate)
one here, obtained along the following lines:
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{5374fig1.eps}
\end{figure}](/articles/aa/full/2006/40/aa5374-06/Timg19.gif) |
Figure 1:
Na vs. O anticorrelation in NGC 2808. Data for a sample of 91 stars,
with both Na and O detections, are from Carretta et al. (2006).
Open squares indicate average abundances in the seven bins of
the adopted O/Na distribution
(see Fig. 2 and Sect. 2). |
| Open with DEXTER |
The average error bars for [O/Fe] and [Na/Fe] in the 91-star sample of Carretta et al.
(2006) are
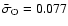 dex
and
dex
and
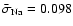 dex, respectively. For each star, the error
in the [O/Na] ratio
dex, respectively. For each star, the error
in the [O/Na] ratio
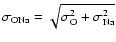 is calculated, and the
average is found to be
is calculated, and the
average is found to be
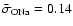 .
We then consider bins in [O/Na] of width
.
We then consider bins in [O/Na] of width
 [O/Na]=0.30, i.e. slightly larger than twice the average error on that ratio.
Provided the quoted error bars reflect statistical errors reliably,
it can be reasonably argued that stars found in different bins have a
truly different composition (in a statistically significant way), at least as far as O and Na
are concerned.
The full range of the [O/Na] spectrum is covered by seven such bins,
with values of [O/Na] ranging from -1.4 to 0.4.
The average abundances of [O/Fe] and [Na/Fe] in the seven [O/Na] bins are
shown in Fig. 1.
[O/Na]=0.30, i.e. slightly larger than twice the average error on that ratio.
Provided the quoted error bars reflect statistical errors reliably,
it can be reasonably argued that stars found in different bins have a
truly different composition (in a statistically significant way), at least as far as O and Na
are concerned.
The full range of the [O/Na] spectrum is covered by seven such bins,
with values of [O/Na] ranging from -1.4 to 0.4.
The average abundances of [O/Fe] and [Na/Fe] in the seven [O/Na] bins are
shown in Fig. 1.
The resulting distribution histogram appears in
Fig. 2.
The number of stars in each [O/Na] bin has been multiplied by 100/91; i.e.
an overall normalization to 100 stars has been applied, allowing one to read
directly in the histogram percentages of the total.
Thus, 30% of the stars in the rightmost bin have on average
a composition of [O/Na] = 0.40, i.e. the highest
O/Na ratio, which presumably reflects the original composition of the cluster.
The remaining 70% of the stars have a composition modified to various degrees by the
nucleosynthesis products of stars that evolved on relatively short timescales (<108 yr),
i.e. stars with initial mass M>4  ,
according to the self-enrichment scenario
(e.g. Ventura et al. 2001).
,
according to the self-enrichment scenario
(e.g. Ventura et al. 2001).
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{5374fig2.eps}
\end{figure}](/articles/aa/full/2006/40/aa5374-06/Timg25.gif) |
Figure 2:
Distribution histogram of stars of NGC 2808 (in percentages
of total) as a function of [O/Na]; the distribution is
calculated from data obtained by Caretta et al. (2006) (Sect. 2).
Stars in the rightmost bin (30%) are presumably born with the original
(unprocessed) composition of the cluster ([O/Na]=0.40),
while the remaining 70% have a composition processed to various degrees through H-burning. |
| Open with DEXTER |
Usually, it is claimed that hot-bottom burning (HBB) in massive asymptotic giant branch
stars (AGBs) is responsible for the observed composition anomalies in GCs
(Cottrell & Da Costa 1981)![[*]](/icons/foot_motif.gif) .
Several custom-made detailed AGB models have recently been computed in order to test
the HBB hypothesis (Ventura et al. 2001, 2002; Denissenkov & Herwig 2003;
Karakas & Lattanzio 2003; Herwig 2004a,b; Ventura & D'Antona 2005a,b,c).
Most of these studies conclude that the AGB pollution scenario suffers from
severe drawbacks from the point of view of the nucleosynthesis
(e.g., Fenner et al. 2004; Charbonnel 2005).
These difficulties stem from the subtle competition between HBB and
third dredge-up, which contaminates the stellar envelope with the products of helium
burning. The problems can be summarized as follows:
(i) O is not depleted to the extent required by the observations, while Na
is over-produced or over-destroyed depending on the treatment of convection;
(ii) Mg is produced while it should be destroyed, and
the Mg isotopic ratio is in conflict with the (rare) available data;
(iii) C+N+O does not remain constant in AGB processed material, in contrast to
observations (Dickens et al. 1991; Smith et al. 1996; Smith et al. 2005;
Ivans et al. 1999).
Rotation-induced mixing makes the situation even worse (Decressin & Charbonnel 2005;
Decressin et al., in preparation) by strongly enriching the envelope of intermediate-mass
stars in O, already during the second dredge-up event.
Last but not least, it is sometimes claimed that massive AGB stars are not expected to
pollute the intracluster gas with s-process elements, in agreement with the observational
requirements obtained by James et al. (2004) and presented in Sect. 1; indeed, lower-mass
AGBs (1.5-3
.
Several custom-made detailed AGB models have recently been computed in order to test
the HBB hypothesis (Ventura et al. 2001, 2002; Denissenkov & Herwig 2003;
Karakas & Lattanzio 2003; Herwig 2004a,b; Ventura & D'Antona 2005a,b,c).
Most of these studies conclude that the AGB pollution scenario suffers from
severe drawbacks from the point of view of the nucleosynthesis
(e.g., Fenner et al. 2004; Charbonnel 2005).
These difficulties stem from the subtle competition between HBB and
third dredge-up, which contaminates the stellar envelope with the products of helium
burning. The problems can be summarized as follows:
(i) O is not depleted to the extent required by the observations, while Na
is over-produced or over-destroyed depending on the treatment of convection;
(ii) Mg is produced while it should be destroyed, and
the Mg isotopic ratio is in conflict with the (rare) available data;
(iii) C+N+O does not remain constant in AGB processed material, in contrast to
observations (Dickens et al. 1991; Smith et al. 1996; Smith et al. 2005;
Ivans et al. 1999).
Rotation-induced mixing makes the situation even worse (Decressin & Charbonnel 2005;
Decressin et al., in preparation) by strongly enriching the envelope of intermediate-mass
stars in O, already during the second dredge-up event.
Last but not least, it is sometimes claimed that massive AGB stars are not expected to
pollute the intracluster gas with s-process elements, in agreement with the observational
requirements obtained by James et al. (2004) and presented in Sect. 1; indeed, lower-mass
AGBs (1.5-3  )
are commonly considered to be the main source of s-elements in the Galaxy.
However, s-process nucleosynthesis (from neutrons released by 22Ne(
)
are commonly considered to be the main source of s-elements in the Galaxy.
However, s-process nucleosynthesis (from neutrons released by 22Ne(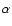 , n)) may
certainly occur if temperatures in the thermal pulses of massive AGB stars are
large enough (e.g. Goriely & Siess 2005, and references therein). Very few quantitative studies
have been devoted to that point, which clearly deserves additional investigation.
Until the question is settled, it should not be taken for granted that massive AGBs
do not produce s-elements at all; in our opinion, this constitutes another potential
problem with their role as polluters of GCs.
, n)) may
certainly occur if temperatures in the thermal pulses of massive AGB stars are
large enough (e.g. Goriely & Siess 2005, and references therein). Very few quantitative studies
have been devoted to that point, which clearly deserves additional investigation.
Until the question is settled, it should not be taken for granted that massive AGBs
do not produce s-elements at all; in our opinion, this constitutes another potential
problem with their role as polluters of GCs.
Although it is too early to discard the AGB hypothesis, we feel that hydrogen burning in rotating massive stars
may offer an interesting alternative (Decressin et al. 2006). In fact, as we argue in Sect. 4, this alternative
may be more attractive, as far as the constraints on the IMF are concerned; other advantages of that idea
are qualitatively discussed in Sect. 5. In the following, we explore both possibilities
for the mass range of the polluting stars, namely, we consider AGB stars of masses 4-9  and massive stars of mass >10
and massive stars of mass >10  .
.
We explore two scenarios of the self-enrichment, which differ by the degree of nuclear processing
in the ejecta of the polluters and thus by the nature of the gas
(i.e., pure stellar ejecta or mixture of ejecta with gas of original composition)
out of which the low-mass stars still surviving today were formed.
In this section we present the underlying assumptions in detail
and we evaluate the amount of ejecta vs. the amount of the long lived stars required in each
scenario. Then in Sect. 4 we derive the corresponding constraints on the IMF for each scenario,
in the cases where either intermediate or massive stars are the polluters.
The first scenario that we consider is the simpler one which assumes that:
- I-a)
- stars with masses between 0.1 and 100
 are formed from gas of "normal'' composition
(i.e. the same composition as the one of field halo stars at that time, meaning for instance
that [O/Na] = 0.4) and with an IMF that has to be determined;
are formed from gas of "normal'' composition
(i.e. the same composition as the one of field halo stars at that time, meaning for instance
that [O/Na] = 0.4) and with an IMF that has to be determined;
- I-b)
- the ejecta of some (rapidly evolving) sub-class of those stars are
polluted to various degrees by internal nucleosynthesis (i.e. the [O/Na] ratio in the ejecta varies between -1.4 and 0.25), with an abundance distribution
given by Fig. 2;
- I-c)
- the ejecta are retained fully in the cluster and form directly
a second generation of stars with mass 0.1-0.8
 (i.e., without being mixed with some original matter),
the same IMF as the one of the first generation low-mass stars, and with a composition
obviously different from the original one (as far as the H-burning products
are concerned);
(i.e., without being mixed with some original matter),
the same IMF as the one of the first generation low-mass stars, and with a composition
obviously different from the original one (as far as the H-burning products
are concerned);
- I-d)
- among the long-lived stars that we see today (with masses in the
0.1-0.8
 range) in NGC 2808, 30% are formed from the original gas and 70%
from the polluted ejecta.
range) in NGC 2808, 30% are formed from the original gas and 70%
from the polluted ejecta.
We shall see that this "Scenario I''
puts heavy constraints on the shape of the original IMF of the polluting stars,
requiring it to be much flatter than the one observed today in Galactic and extragalactic
stellar clusters. Indeed, it implies that the mass of the polluted ejecta should be about
2.3 times higher (70/30 = 2.33) than the total mass of the first generation stars that survive
today (mass between 0.1 and 0.8  ). Moreover, if AGBs are assumed to be the polluting
agents, we show that this scenario leads to the concomitant production of a large number
of stellar remnants (mostly white dwarfs), the mass of which should be higher than the stellar
mass of the cluster today. In contrast, if massive stars are assumed to be the polluting agents,
the mass of stellar remnants is found to be considerably reduced.
On the other hand, this scenario appears rather reasonable from the stellar nucleosynthesis
point of view, since it invokes ejecta contaminated to various degrees (including very small ones)
by the products of H-burning.
). Moreover, if AGBs are assumed to be the polluting
agents, we show that this scenario leads to the concomitant production of a large number
of stellar remnants (mostly white dwarfs), the mass of which should be higher than the stellar
mass of the cluster today. In contrast, if massive stars are assumed to be the polluting agents,
the mass of stellar remnants is found to be considerably reduced.
On the other hand, this scenario appears rather reasonable from the stellar nucleosynthesis
point of view, since it invokes ejecta contaminated to various degrees (including very small ones)
by the products of H-burning.
Our second scenario assumes that:
- II-a)
- stars with masses between 0.1 and 100
 are formed from gas of
"normal'' composition (i.e. the same composition as the one of field halo
stars at that time, meaning for instance that [O/Na] = 0.4) and with an IMF
that has to be determined (identical to I-a);
are formed from gas of
"normal'' composition (i.e. the same composition as the one of field halo
stars at that time, meaning for instance that [O/Na] = 0.4) and with an IMF
that has to be determined (identical to I-a);
- II-b)
- the ejecta of some (rapidly evolving) sub-class of those stars are
polluted to an extreme degree by internal nucleosynthesis
(i.e. the [O/Na] ratio in the ejecta is invariably -1.4);
- II-c)
- the timescale of the evolution of the polluters is shorter than the formation timescale of the low-mass stars (0.1-0.8
 ), i.e. shorter than about 100 Myr (Stahler & Palla 2005).
Then, the (extremely-processed) ejecta are mixed to various degrees with the gas of low-mass
protostars of original composition, which are still forming;
), i.e. shorter than about 100 Myr (Stahler & Palla 2005).
Then, the (extremely-processed) ejecta are mixed to various degrees with the gas of low-mass
protostars of original composition, which are still forming;
- II-d)
- among the long-lived stars that we see today (with masses in the
0.1-0.8
 range) in NGC 2808, 30% are formed from the original gas
(not contaminated at all by the ejecta) and 70% from
various mixtures of the extremely-processed ejecta with the original gas.
range) in NGC 2808, 30% are formed from the original gas
(not contaminated at all by the ejecta) and 70% from
various mixtures of the extremely-processed ejecta with the original gas.
Obviously, the starting and ending points of the two scenarios are identical (as they should
be since both must account for the observed abundance distribution in Fig. 2).
They differ in the intermediate steps. Scenario I involves two clearly distinct stellar generations, the second of which is exclusively made by the nuclearly processed ejecta of the first one.
Scenario II involves only one stellar generation, the low-mass stars of which
(0.1-0.8  )
are contaminated at formation and, to various degrees, by the
extremely-processed ejecta of their more massive and rapidly evolving sisters.
)
are contaminated at formation and, to various degrees, by the
extremely-processed ejecta of their more massive and rapidly evolving sisters.
The assumption of extreme processing of the ejecta in Scenario II is neither mandatory (ejecta
with various degrees of processing could also be assumed, as in Scenario I) nor easy to justify
on physical grounds, as we discuss in Sect. 5. However, it is made here for two reasons:
- a)
- combined with the abundance distribution diagram of NGC 2808
(top panel of Fig. 3), it allows one to evaluate the degree of mixing between
processed and original material in the various [O/Na] bins in a well-defined way
(see middle and bottom panels of Fig. 3 and the next paragraphs);
- b)
- precisely because the composition of the ejecta is so extreme,
less material of processed composition is required for the mixture.
Consequently, the constraints on the IMF (from the required ratio between
mass of ejecta and mass in low-mass stars of 0.1-0.8
 )
are less severe than
in Scenario I, as we show hereafter.
)
are less severe than
in Scenario I, as we show hereafter.
At this point, it should be stressed that our assumption that only stars of 0.1 to 0.8  are formed from the ejecta (points I-c and II-c) is also made only in order to minimize
the constraint on the IMF of the polluters (since their ejecta are used most efficiently,
by forming exclusively stars still visible today). If stars with M>0.8
are formed from the ejecta (points I-c and II-c) is also made only in order to minimize
the constraint on the IMF of the polluters (since their ejecta are used most efficiently,
by forming exclusively stars still visible today). If stars with M>0.8  are assumed
to also be formed from the ejecta, the required ejecta mass would still be larger, and the
corresponding IMF of the polluters even flatter, than the ones we derive in the next section.
are assumed
to also be formed from the ejecta, the required ejecta mass would still be larger, and the
corresponding IMF of the polluters even flatter, than the ones we derive in the next section.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{5374fig3.eps}
\end{figure}](/articles/aa/full/2006/40/aa5374-06/Timg26.gif) |
Figure 3:
Top: distribution histogram of stars of NGC 2808 (in percentages
of total) as a function of [O/Na] (same as in Fig. 2).
Stars in the rightmost bin (30%) are presumably born with the original
(unprocessed) composition of the cluster ([O/Na]=0.40),
while the remaining 70% have a
contaminated composition.
Scenario II (see text) assumes that the mixed composition is obtained by
mixing extremely-processed material (E-processed, with [O/Na]=-1.40, leftmost bin)
with an unprocessed one, to various degrees, as explained in
Sect. 3.2.
Middle:
open and filled circles indicate the amount of extremely-processed
(pi) and unprocessed (ui)
matter in each bin, respectively, while the histogram
is the same as in the top panel (but on a logarithmic scale).
Bottom: cumulative distributions of total ( squares),
extremely-processed ( open circles), and unprocessed matter
( filled circles), starting from the leftmost bin. Final values on the
right are P=35% for the extremely-processed and U=65% for the
unprocessed amounts of matter (see Sect. 3.2). |
| Open with DEXTER |
In order to evaluate the amount of ejecta with extremely-processed composition
in the framework of Scenario II, we proceed as follows: assuming a mixture of
unit mass of extremely-processed matter (mass fraction of a given element
 )
with f parts of original matter (mass fraction
)
with f parts of original matter (mass fraction
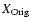 ),
the corresponding mass fraction
),
the corresponding mass fraction
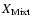 in the mixture will be:
in the mixture will be:
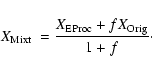 |
(1) |
For the ratio of two elements a and b one then has
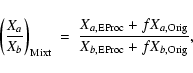 |
(2) |
from which one may recover the
dilution factor f as
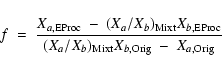 |
(3) |
as a function of the abundance ratio
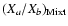 ,
provided the abundances of a and b in the original and the processed material are given.
,
provided the abundances of a and b in the original and the processed material are given.
In the framework of our Scenario II, we obtain the abundances of O and Na in the original
and processed material by finding the corresponding values in the rightmost and leftmost bins,
respectively, of the adopted [O/Na] distribution. These values appear in
Fig. 1, where the averages [O/Fe] and [Na/Fe] in each of
the adopted [O/Na] bins appear and are:
The metallicity of NGC 2808 is [Fe/H] = -1.1 (Carretta et al. 2006), which allows one
to find the absolute abundances of O and Na in the original and processed
material. Turning all abundances into mass fractions, one then may solve
Eq. (3) and find the dilution factor fi for each of the [O/Na] bins
(i=1,..., 7) in Fig. 3.
Obviously, in the leftmost bin (material of extremely-processed composition
exclusively) one has by definition f1=0, while in the rightmost bin
(material of original composition only) very high values are found for
f7 (
 ).
).
As mentioned in Sect. 2, the number of stars in each bin (ni) also represents the percentage
of material with (mixed) abundance ratio [O/Na], since the total has been
normalized to 100. The fraction
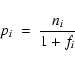 |
(4) |
then gives the amount of extremely-processed material (i.e. with [O/Na]=-1.4) in each bin, while
the remaining
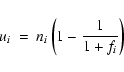 |
(5) |
represents the amount of unprocessed (original) material.
These amounts (also expressed as percentages of the total) appear in the middle panel of
Fig. 3.
Obviously, in the leftmost bin
(f1=0) one has p1=n1,
while in the rightmost bin
u7=n7. By summing the amounts of the processed and unprocessed material
over the seven bins, one then obtains the corresponding total amounts as
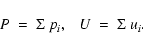 |
(6) |
Those quantities appear in the rightmost bin of the bottom panel of
Fig. 3. There is P=35% of material with extremely-processed
composition and U=65% with original composition in the surviving stars of
NGC 2808, in the framework of our Scenario II.
The two scenarios considered here are
sketched in Figs. 4 and 5.
The numbers appearing in those figures are percentages of the final total mass in low-mass
long-lived stars (0.1-0.8  ), as derived from our previous analysis (see also
Fig. 3). There is a big quantitative difference between the two scenarios,
concerning the ratio of the processed ejecta mass to the mass of stars with original composition
in the low-mass range. In Scenario I, this ratio is 2.33 (=70/30), whereas in Scenario II it is much lower, only
0.54 (=35/65). Of course, this difference stems from the
different assumptions on the composition of the ejecta: processed to various degrees
in Scenario I vs. extremely-processed in Scenario II.
), as derived from our previous analysis (see also
Fig. 3). There is a big quantitative difference between the two scenarios,
concerning the ratio of the processed ejecta mass to the mass of stars with original composition
in the low-mass range. In Scenario I, this ratio is 2.33 (=70/30), whereas in Scenario II it is much lower, only
0.54 (=35/65). Of course, this difference stems from the
different assumptions on the composition of the ejecta: processed to various degrees
in Scenario I vs. extremely-processed in Scenario II.
In this section we explore the constraints imposed on the stellar IMF
by the ratio mass(ejecta)/mass(low-mass stars) inferred
from our previous analysis.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{5374fig4.eps}
\end{figure}](/articles/aa/full/2006/40/aa5374-06/Timg42.gif) |
Figure 4:
Illustration of Scenario I
with numbers corresponding to the analysis performed in Sect. 3.1.
30% of the currently surviving low-mass stars of NGC 2808 are born
with the original composition. The heavier stars of that first generation
(either in the AGB stage, or through the winds of massive stars - WMS)
eject 2.33 times more mass of varied composition, from which only low-mass
stars (the remaining 70%) is formed. This scenario puts relatively mild
constraints on nucleosynthesis, but heavy ones on the
initial mass function of the first stellar generation. Percentages refer
to the total mass of low-mass stars of NGC 2808 (those still surviving today). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{5374fig5.eps}
\end{figure}](/articles/aa/full/2006/40/aa5374-06/Timg43.gif) |
Figure 5:
Illustration of Scenario II,
with numbers corresponding to the analysis performed in Sect. 3.2
and Fig. 3. 65% of the material of currently
surviving low-mass stars of NGC 2808 is of original composition ([O/Na]=0.40),
and 35% is of extremely-processed composition ([O/Na]=-1.40), ejected from
either AGB stars or
massive stars. The latter material is mixed with 35%
of the former to various degrees and forms low-mass stars (the currently surviving 70% stars
of mixed composition), while the remaining 30% of the unprocessed material
directly forms stars with the original composition. This scenario puts relatively
mild constraints on the initial mass function, but puts extreme ones on the
nucleosynthesis, since it requires all material ejected by the presumed
sources (AGB or massive stars) to have [O/Na]=-1.40. Percentages refer to the total mass
of the low-mass stars of NGC 2808 (those still surviving today). |
| Open with DEXTER |
Globular clusters provide, in principle, an ideal sample for accurately evaluating the
stellar IMF in the mass range
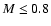
 and down to the
H-burning limit. Indeed, they are composed of stars with
the same age, well-determined distances, and small variations in chemical composition
(except for elements affected by H-burning) or in extinction within a cluster.
Moreover, the fraction of binary stars outside the cluster core is less than 15%
(e.g. Rubenstein & Bailyn 1999) and affects the determination of the luminosity
function very little. Once the luminosity function has been established, the existence of
accurate stellar evolutionary models (reproducing well the observed colour-magnitude diagrams
of clusters with metallicities [Fe/H] <-1, e.g. Pulone et al. 1998) allows one to derive
the IMF of low-mass stars straightforwardly.
and down to the
H-burning limit. Indeed, they are composed of stars with
the same age, well-determined distances, and small variations in chemical composition
(except for elements affected by H-burning) or in extinction within a cluster.
Moreover, the fraction of binary stars outside the cluster core is less than 15%
(e.g. Rubenstein & Bailyn 1999) and affects the determination of the luminosity
function very little. Once the luminosity function has been established, the existence of
accurate stellar evolutionary models (reproducing well the observed colour-magnitude diagrams
of clusters with metallicities [Fe/H] <-1, e.g. Pulone et al. 1998) allows one to derive
the IMF of low-mass stars straightforwardly.
The major potential problem in this enterprise is that what we are formally measuring is
the present-day mass function. This could differ from the IMF because of
the dynamical evolution of the cluster, which may have both internal and external origins:
internal, due to relaxation of the N-body system towards energy equipartition, by expelling
less massive bodies towards the periphery of the cluster and accumulating massive ones in the centre;
and external, due to tidal interactions with the Galactic potential (or molecular clouds,
other clusters etc.), which may result in the loss of the less massive bodies. Both effects lead to
the mass segregation of stars in space and time. Paresce & de Marchi (2000, hereafter PdM00)
find that the effects of mass segregation alter the stellar mass function both in the innermost
regions (making it flatter than the IMF) and in those outside the half-light radius (making it
steeper than the IMF); however, around the half-light radius, the effects of mass segregation
are insignificant (see Sect. 4 and Fig. 4 in PdM00).
By using HST measurements of the luminosity functions at (or just beyond) the half-light
radius of a dozen globular clusters, PdM00 find that the corresponding IMFs have the shape of
a lognormal distribution
characterized by a peak mass
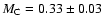
 and a standard deviation
and a standard deviation
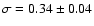
![[*]](/icons/foot_motif.gif) .
Their measurements cover the mass range 0.09-0.7
.
Their measurements cover the mass range 0.09-0.7  ,
but we
assume here that the derived IMF shape is valid up to the turn-off mass of
,
but we
assume here that the derived IMF shape is valid up to the turn-off mass of 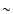 12 Gyr
globular clusters, i.e. up to
12 Gyr
globular clusters, i.e. up to  0.8
0.8  .
We then assume that in the mass range of
low-mass stars (0.1-0.8
.
We then assume that in the mass range of
low-mass stars (0.1-0.8  )
the IMF has the form
)
the IMF has the form
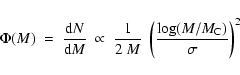 |
(7) |
with the values of 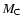 and
and 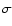 given in the previous paragraph.
The IMF of more massive stars (living less than
12 Gyr) is not observable in globular clusters, but it is measured
in young clusters, where it has been found that it can be approximated well
by a power-law of the form
given in the previous paragraph.
The IMF of more massive stars (living less than
12 Gyr) is not observable in globular clusters, but it is measured
in young clusters, where it has been found that it can be approximated well
by a power-law of the form
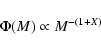 |
(8) |
with X=1.35 being the "classical'' Salpeter (1955) value. As discussed in Kroupa (2002,
and references therein), the Salpeter value fits the available data extremely well over
a wide range of cluster masses and in different galaxies and with a dispersion
of about 0.35, i.e.
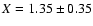 .
.
In this work we assume that the IMF of the globular clusters was a composite one, given by
Eqs. (7) and (8) for the mass ranges 0.1-0.8  and 0.8-100
and 0.8-100  ,
respectively.
We allow the value of X to vary in the range -0.25 to 1.35 and constrain it using the results
of the analysis in Sect. 3. All IMFs are normalized to
,
respectively.
We allow the value of X to vary in the range -0.25 to 1.35 and constrain it using the results
of the analysis in Sect. 3. All IMFs are normalized to
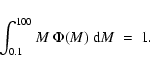 |
(9) |
Two of the adopted IMFs, with X=0.15 and 1.35, are shown in
Fig. 6 (denoted with letters A, and B respectively).
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{5374fig6.eps}
\end{figure}](/articles/aa/full/2006/40/aa5374-06/Timg55.gif) |
Figure 6:
Top:
examples of the stellar IMFs studied in this work. They are composed of (i) the Paresce & de Marchi
(2000, PdM) IMF of Eq. (7) in the range 0.1-0.8  ,
and (ii) of the power-law IMF of Eq. (8)
at M>0.8 ,
and (ii) of the power-law IMF of Eq. (8)
at M>0.8  ,
with slope X=0.15 and 1.35 for IMF A and B, respectively.
All IMFs are normalized to ,
with slope X=0.15 and 1.35 for IMF A and B, respectively.
All IMFs are normalized to
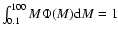 .
Middle: corresponding total masses of the IMFs
as a function of the lower integration limit M in the integral .
Middle: corresponding total masses of the IMFs
as a function of the lower integration limit M in the integral
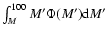 .
IMF A has more mass in heavy stars
(and, correspondingly, less in low-mass stars) than IMF B. Bottom:
corresponding ejecta mass fractions as a function of the lower integration
limit M in the integral .
IMF A has more mass in heavy stars
(and, correspondingly, less in low-mass stars) than IMF B. Bottom:
corresponding ejecta mass fractions as a function of the lower integration
limit M in the integral
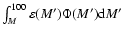 ,
where ,
where
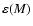 is the mass of the H-processed ejecta. Again, IMF A has a much higher
ejecta mass fraction in massive stars than IMF B.
is the mass of the H-processed ejecta. Again, IMF A has a much higher
ejecta mass fraction in massive stars than IMF B. |
| Open with DEXTER |
A couple of other interesting quantities appear in
Fig. 6. The mass fraction
in the form of stars heavier than a mass M is
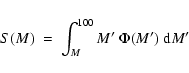 |
(10) |
where, by definition, S(0.1)=1. Flat IMFs have a higher fraction of their mass in
heavy stars and a correspondingly lower fraction in low-mass stars than IMFs with
a steep slope (see middle panel in
Fig. 6). We also present (bottom panel in Fig. 6)
the hereby defined ejecta mass fraction
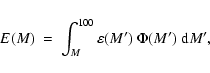 |
(11) |
where
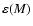 is defined as the part (in
is defined as the part (in  ) of the star that is processed
only through H-burning and is returned to the ISM. Even with the help of detailed stellar models
it is difficult to have precise values for
) of the star that is processed
only through H-burning and is returned to the ISM. Even with the help of detailed stellar models
it is difficult to have precise values for
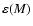 ,
since those values depend on
several at present poorly known ingredients, such as mixing criteria, mass-loss rates, etc.
In this work, we choose to deliberately maximize the amount of H-processed ejecta from each star,
in order to obtain upper limits to the slope of the corresponding IMF. For that purpose,
we adopt the following
,
since those values depend on
several at present poorly known ingredients, such as mixing criteria, mass-loss rates, etc.
In this work, we choose to deliberately maximize the amount of H-processed ejecta from each star,
in order to obtain upper limits to the slope of the corresponding IMF. For that purpose,
we adopt the following
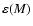 relations:
relations:
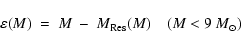 |
(12) |
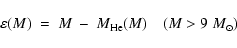 |
(13) |
where
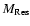 is the mass of the residue (white dwarf for M<9
is the mass of the residue (white dwarf for M<9  ,
neutron star or black hole otherwise) and
,
neutron star or black hole otherwise) and
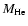 is the mass of the H-exhausted core of the star. This choice obviously maximizes the mass of the H-processed ejecta because it assumes that:
is the mass of the H-exhausted core of the star. This choice obviously maximizes the mass of the H-processed ejecta because it assumes that:
- in intermediate mass stars, all the mass outside the white dwarf remnant
is processed exclusively through H-burning: in reality, part of that mass
is processed in the He-burning shell, but we assume here that this is
negligible;
- in massive stars, all the mass outside the He-core is processed through
H-burning; in reality, part of that mass is not processed at all (i.e. it is
ejected with its original composition by the early stellar wind), while another
part (close to the He-core) is contaminated by He-burning products. Again, we
assume those parts to be negligible, in order to maximize the mass of the
H-processed ejecta.
In Fig. 7 we display the adopted
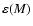 (from
Eqs. (12) and (13)), as well as
(from
Eqs. (12) and (13)), as well as
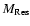 ,
which is given from the relations:
,
which is given from the relations:
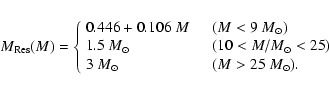 |
(14) |
The white dwarf vs. initial mass relation for M<9  is from Iben & Tutukov
(1984), which assumes that stars in the 10-25
is from Iben & Tutukov
(1984), which assumes that stars in the 10-25  range produce neutron
stars of 1.5
range produce neutron
stars of 1.5  ,
while more massive ones produce black holes
of 3
,
while more massive ones produce black holes
of 3  .
The mass of the neutron star or the black hole affects the
results discussed hereafter little, as far as it remains below the mass of the
He-core, which is a reasonable assumption.
.
The mass of the neutron star or the black hole affects the
results discussed hereafter little, as far as it remains below the mass of the
He-core, which is a reasonable assumption.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{5374fig7.eps}
\end{figure}](/articles/aa/full/2006/40/aa5374-06/Timg65.gif) |
Figure 7:
Mass of He-core ( dashed curve) for stars with
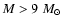 and mass of
stellar residues ( solid curve) as a function of initial
stellar mass. The dotted line indicates the initial stellar mass, while the areas
within thick curves represent the H-processed ejecta that may contribute to the self-enrichment
of globular clusters; the indicated amount is clearly an overestimation (see text).
and mass of
stellar residues ( solid curve) as a function of initial
stellar mass. The dotted line indicates the initial stellar mass, while the areas
within thick curves represent the H-processed ejecta that may contribute to the self-enrichment
of globular clusters; the indicated amount is clearly an overestimation (see text). |
| Open with DEXTER |
The ejecta mass fraction E(M) for the two IMFs A and B appear in the bottom panel of
Fig. 6. Flat IMFs
have higher ejecta mass fractions than IMFs with a steeper slope.
Finally, in a similar way, the mass fraction locked in residues is calculated as
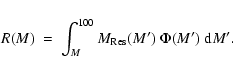 |
(15) |
From the defining Eqs. (9) to (15), one may calculate any quantity of interest for a given IMF;
e.g. the mass locked in low-mass stars (in the range 0.1-0.8  )
still surviving today is
)
still surviving today is
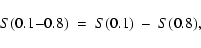 |
(16) |
while the ejecta mass fraction of stars in the 4 to 9  range is
range is
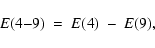 |
(17) |
and similar relations hold for e.g. the mass of residues.
Four quantities of interest, calculated along the previous lines for
all the IMFs studied here, are plotted in
Fig. 8 (top panel) as a function of the slope X of the M>0.8  part
of the IMF, which we wish to constrain. They are, respectively:
part
of the IMF, which we wish to constrain. They are, respectively:
- the ejecta mass fraction E from massive stars (10 to 100
 ).
It is assumed that the envelopes of those stars are processed through
H-burning at high enough temperatures and are ejected by gently blowing
stellar winds in the ISM, where they participate in the formation of new
stars;
).
It is assumed that the envelopes of those stars are processed through
H-burning at high enough temperatures and are ejected by gently blowing
stellar winds in the ISM, where they participate in the formation of new
stars;
- the ejecta mass fraction E from HBB in massive AGB stars (of 4-9
 );
these ejecta escape their stars at relatively low velocities and are trapped in the cluster
and form new stars. It is assumed here that the total envelope mass outside the
carbon-oxygen white dwarf is processed that way;
);
these ejecta escape their stars at relatively low velocities and are trapped in the cluster
and form new stars. It is assumed here that the total envelope mass outside the
carbon-oxygen white dwarf is processed that way;
- the mass fraction R in stellar residues (mostly white dwarfs) from all
stars present in the original IMF that evolved until today (i.e. stars in
the 0.8 to 100
 range);
range);
- the mass fraction S in long-lived stars (0.1-0.8
 ).
).
The first of these quantities increases when the slope of the high-mass part of
the IMF decreases (when the IMF becomes flatter), while the opposite happens with the last
quantity; the other two are relatively insensitive to the IMF slope.
Armed with these numbers, one may now explore the implications for NGC 2808 in the framework of the
self-enrichment scenario. In the middle panel of Fig. 8 the ratio of the H-processed
ejecta mass to the mass locked in low-mass stars of the original IMF (stars that still survive
today) is plotted vs the slope X.
Two cases are considered, namely, that the ejecta originate either in massive stars
(with mass 10-100  )
or in intermediate mass stars (AGBs of 4-9
)
or in intermediate mass stars (AGBs of 4-9  ).
Except for the steepest IMFs, the former ratio is always higher than the latter
(since the ejecta mass of 10-100
).
Except for the steepest IMFs, the former ratio is always higher than the latter
(since the ejecta mass of 10-100  is higher than the ejecta mass of 4-9
is higher than the ejecta mass of 4-9  ).
Of course, restraining the mass range of
massive stars that could contribute to the H-processed ejecta (assuming e.g.
that only stars in the 30-100
).
Of course, restraining the mass range of
massive stars that could contribute to the H-processed ejecta (assuming e.g.
that only stars in the 30-100  range develop sufficiently high
temperatures for
the operation of Ne-Na or Mg-Al cycles) or assuming a lower mass for the processed envelopes
of massive stars (instead of the Eq. (13) adopted here) would reduce the ejecta mass
fraction of massive stars accordingly and would bring down the corresponding curves in
Fig. 8 (top and middle panels). The same, of course, holds for the contribution
of AGBs, which could well be lower than assumed here
(for instance, if the mass of their H-processed ejecta is less than assumed in Eq. (12)).
Thus, the results presented in the middle panel of Fig. 8 should clearly be
considered only as upper limits to what AGBs or massive stars might do.
In reality, all curves involving ejecta E in the top and middle panels of
Fig. 8 should be shifted downwards.
range develop sufficiently high
temperatures for
the operation of Ne-Na or Mg-Al cycles) or assuming a lower mass for the processed envelopes
of massive stars (instead of the Eq. (13) adopted here) would reduce the ejecta mass
fraction of massive stars accordingly and would bring down the corresponding curves in
Fig. 8 (top and middle panels). The same, of course, holds for the contribution
of AGBs, which could well be lower than assumed here
(for instance, if the mass of their H-processed ejecta is less than assumed in Eq. (12)).
Thus, the results presented in the middle panel of Fig. 8 should clearly be
considered only as upper limits to what AGBs or massive stars might do.
In reality, all curves involving ejecta E in the top and middle panels of
Fig. 8 should be shifted downwards.
Those theoretical results are compared to the observationally inferred requirements
for NGC 2808 for both Scenarios I and II in
Fig. 8 (middle panel). As found in
Sect. 3, Scenario I requires a ratio of H-processed ejecta to mass in
low-mass stars with an original composition of
70/30=2.33, while Scenario II requires
a lower ratio, of
35/65=0.54. As can be seen from
Fig. 8 (middle panel), the requirement of Scenario I is
only satisfied for slopes X<0.8 in the case of massive stars and
X< 0.15 for the massive AGBs. The requirement of Scenario II is satisfied for
X< 1.25 in the former case and for X< 0.95 in the latter.
Those IMFs with the standard slope X=1.35 fail to satisfy observational
requirements by a factor of 2 in our Scenario II and by a factor of 10 in our Scenario I.
A diagram such as the one in the middle panel of Fig. 8 should offer
a way to determine the slope of the high-mass (>0.8  )
IMF of a globular cluster with
a measured abundance distribution such as NGC 2808. However, this determination is made in the
framework of models with extreme assumptions about both the polluter ejecta and their mixing
with the pristine gas. In Sect. 5 we discuss these assumptions and conclude that
the IMF should be much flatter (i.e. X should be much smaller) in a realistic scenario than
determined in the middle panel of Fig. 8. Still, it will be model-dependent
since the necessary ingredients (amount and composition of ejecta and degree of their mixing
with the ISM) cannot be constrained independently at present.
)
IMF of a globular cluster with
a measured abundance distribution such as NGC 2808. However, this determination is made in the
framework of models with extreme assumptions about both the polluter ejecta and their mixing
with the pristine gas. In Sect. 5 we discuss these assumptions and conclude that
the IMF should be much flatter (i.e. X should be much smaller) in a realistic scenario than
determined in the middle panel of Fig. 8. Still, it will be model-dependent
since the necessary ingredients (amount and composition of ejecta and degree of their mixing
with the ISM) cannot be constrained independently at present.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{5374fig8.eps}
\end{figure}](/articles/aa/full/2006/40/aa5374-06/Timg69.gif) |
Figure 8:
Top: mass fraction in low-mass stars surviviving today
(S(0.1-0.8  ), open squares),
mass fraction R(0.8-100 ), open squares),
mass fraction R(0.8-100  )
in stellar residues (i.e. white dwarfs, neutron stars, or black holes from stars
of initial mass M>0.8 )
in stellar residues (i.e. white dwarfs, neutron stars, or black holes from stars
of initial mass M>0.8  ,
open circles), and H-processed ejecta mass fractions Efrom stars in the 4-9 ,
open circles), and H-processed ejecta mass fractions Efrom stars in the 4-9  ( asterisks) and 10-100
( asterisks) and 10-100  ranges ( filled circles),
as a function of the slope X of the high-mass part of the IMF. For the low-mass part,
ranges ( filled circles),
as a function of the slope X of the high-mass part of the IMF. For the low-mass part,
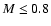  ,
the PdM00 IMF
of Eq. (7) is always assumed.
Letters A and B denote the results for the IMFs used in
Fig. 6.
Middle: ratio of ejecta mass (of either 4-9 ,
the PdM00 IMF
of Eq. (7) is always assumed.
Letters A and B denote the results for the IMFs used in
Fig. 6.
Middle: ratio of ejecta mass (of either 4-9  or 10-100
or 10-100  stars)
to the mass of low-mass stars
S(0.1-0.8) for each of the IMFs of our study. Note that
S represents stars (or material) of only original (unprocessed) composition. The two horizontal
lines correspond to the constraints imposed by the analysis of Sect. 2.2 and Figs. 2 and 3, according to
Scenarios I ( dashed) and II ( dotted), respectively.
Bottom: ratio of residue mass to the total mass of low-mass stars surviving
today, for each of the IMFs studied. The total mass is the sum of the stars formed from
original (unprocessed) material plus those formed from the ejecta of either AGBs (4-9
stars)
to the mass of low-mass stars
S(0.1-0.8) for each of the IMFs of our study. Note that
S represents stars (or material) of only original (unprocessed) composition. The two horizontal
lines correspond to the constraints imposed by the analysis of Sect. 2.2 and Figs. 2 and 3, according to
Scenarios I ( dashed) and II ( dotted), respectively.
Bottom: ratio of residue mass to the total mass of low-mass stars surviving
today, for each of the IMFs studied. The total mass is the sum of the stars formed from
original (unprocessed) material plus those formed from the ejecta of either AGBs (4-9  )
or
massive stars (10-100 )
or
massive stars (10-100  ). ). |
| Open with DEXTER |
At this point, it should be noted that
the IMF may critically affect the fate of a dense stellar cluster.
Simulations of the dynamical evolution of GCs, including the effects of tidal stripping
and of mass loss from stellar evolution, show indeed that a flat mass spectrum speeds
up the cluster disruption (e.g., Joshi et al. 2001; Giersz 2001).
This potential problem is alleviated in the present self-enrichment scenario, because the
mass lost by the polluters is assumed to be incorporated in the low-mass stars of the cluster.
Nevertheless, the self-enrichment scenario needs to be tested quantitatively
with realistic dynamical evolution models.
One way to further constrain the various scenarios is by searching for signatures left over
in the form of stellar residues.
In the bottom panel of Fig. 8 we explore the consequences of our different
assumptions for the mass of "dark objects'' in NGC 2808, namely residues of stars with
initial mass
M>0.8  .
Their mass (determined by the assumed IMF from Eq. (14) and given
in Fig. 8, top panel) is compared to the total mass of the long-lived stars
(
.
Their mass (determined by the assumed IMF from Eq. (14) and given
in Fig. 8, top panel) is compared to the total mass of the long-lived stars
(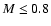
 )
of the cluster. The total mass is the sum of the original
(unpolluted) low-mass stars
S(0.1-0.8) plus the polluted ones. If the
polluted long-lived stars originate in the ejecta of 10-100
)
of the cluster. The total mass is the sum of the original
(unpolluted) low-mass stars
S(0.1-0.8) plus the polluted ones. If the
polluted long-lived stars originate in the ejecta of 10-100  stars
(mass
E(10-100)), the sum increases considerably at low X values, and
the ratio of residues to stars decreases in consequence. In contrast, if
the polluted long-lived stars originate in the ejecta of 4-9
stars
(mass
E(10-100)), the sum increases considerably at low X values, and
the ratio of residues to stars decreases in consequence. In contrast, if
the polluted long-lived stars originate in the ejecta of 4-9  stars
(mass E(4-9)), the sum decreases at low X and the mass of the residues
becomes comparable to the mass of active stars today, especially in case of
Scenario I. Thus, the mass ratio of residues to long-lived stars is
sensitive to the assumption made about the mass range of the polluters,
especially for flat IMFs (such as those required to explain the abundance
distribution of NGC 2808, and presumably of other clusters as well).
stars
(mass E(4-9)), the sum decreases at low X and the mass of the residues
becomes comparable to the mass of active stars today, especially in case of
Scenario I. Thus, the mass ratio of residues to long-lived stars is
sensitive to the assumption made about the mass range of the polluters,
especially for flat IMFs (such as those required to explain the abundance
distribution of NGC 2808, and presumably of other clusters as well).
Unfortunately, such a ratio has not been determined yet for the case of NGC 2808.
However, in the case of the cluster M 4
(another mildly metal-poor GC with [Fe/H
![$]\sim-1.08$](/articles/aa/full/2006/40/aa5374-06/img70.gif) ;
Ivans et al. 2001),
the number ratio of white dwarfs to long-lived
stars has been determined by Richer et al. (2002, hereafter RBF02). They used HST
observations of that cluster to probe its luminosity function (LF) down to the H-burning
limit (
;
Ivans et al. 2001),
the number ratio of white dwarfs to long-lived
stars has been determined by Richer et al. (2002, hereafter RBF02). They used HST
observations of that cluster to probe its luminosity function (LF) down to the H-burning
limit (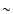 0.09
0.09  ).
Using stellar models of low-mass and low-metallicity stars (which still suffer from important
uncertainties), they transformed the LF into an MF and concluded that the latter can be fitted
by a power-law of slope
).
Using stellar models of low-mass and low-metallicity stars (which still suffer from important
uncertainties), they transformed the LF into an MF and concluded that the latter can be fitted
by a power-law of slope
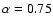 (or
(or
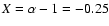 in the notation adopted here)
in the mass range 0.09-0.65
in the notation adopted here)
in the mass range 0.09-0.65  .
In a subsequent work, however, de Marchi et al. (2004) argue
that the use of more appropriate stellar models leads to a mass function similar to the one
that PdM00 had determined for 12 GCs (Eq. (7)). In the following we also adopt this low-mass MF
(the same used throughout our paper) for M 4.
.
In a subsequent work, however, de Marchi et al. (2004) argue
that the use of more appropriate stellar models leads to a mass function similar to the one
that PdM00 had determined for 12 GCs (Eq. (7)). In the following we also adopt this low-mass MF
(the same used throughout our paper) for M 4.
By applying substantial completeness corrections to their sample, RBF02 derive the number
of main sequence stars in the range 0.09 to 0.65  and the number of white dwarfs from progenitor stars in the range 0.8 to 8
and the number of white dwarfs from progenitor stars in the range 0.8 to 8  :
they are, respectively,
:
they are, respectively,
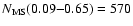 and
and
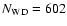 .
The number ratio of white dwarfs to long lived stars is thus
.
The number ratio of white dwarfs to long lived stars is thus 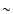 1.
It should be stressed that these numbers are determined essentially by the applied completeness corrections,
rather than by the observations (see Fig. 3, top panel, in RBF02).
1.
It should be stressed that these numbers are determined essentially by the applied completeness corrections,
rather than by the observations (see Fig. 3, top panel, in RBF02).
RBF02 find that a single-slope power-law IMF, with
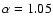 (or X=0.05), i.e. the
steepest slope compatible with their data, can accommodate this high ratio
of
(or X=0.05), i.e. the
steepest slope compatible with their data, can accommodate this high ratio
of
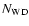 /
/
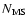 .
They assume, of course, that both the observed MS stars and the WDs
come from the original (first generation) IMF of the cluster; i.e., they do not consider
long-lived stars formed from the ejecta of the first generation. Since M 4 is a cluster with
observed O vs. Na anticorrelation (Ivans et al. 1999, 2001), their IMF determination has
meaning only under the assumption that the observed anticorrelation is due to internal
evolution and not to self-enrichment.
.
They assume, of course, that both the observed MS stars and the WDs
come from the original (first generation) IMF of the cluster; i.e., they do not consider
long-lived stars formed from the ejecta of the first generation. Since M 4 is a cluster with
observed O vs. Na anticorrelation (Ivans et al. 1999, 2001), their IMF determination has
meaning only under the assumption that the observed anticorrelation is due to internal
evolution and not to self-enrichment.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{5374fig9.eps}
\end{figure}](/articles/aa/full/2006/40/aa5374-06/Timg78.gif) |
Figure 9:
Top: number of stars per unit solar mass, as a function of the slope X
above the turn-off mass. The two curves corerspond to long-lived stars (0.1-0.8  )
and to stars leaving behind white dwarfs (0.8-9 )
and to stars leaving behind white dwarfs (0.8-9  initially).
Middle: number ratio of white dwarfs to long-lived stars for the various IMFs studied in this work.
The two solid curves correspond to the cases where the polluters are AGBs (asterisks) and WMS (filled circles),
as in the middle and bottom panels of Fig. 8.
The dotted curve is obtained by simply dividing the two curves of the top panel, i.e.
no creation of 0.1-0.8
initially).
Middle: number ratio of white dwarfs to long-lived stars for the various IMFs studied in this work.
The two solid curves correspond to the cases where the polluters are AGBs (asterisks) and WMS (filled circles),
as in the middle and bottom panels of Fig. 8.
The dotted curve is obtained by simply dividing the two curves of the top panel, i.e.
no creation of 0.1-0.8  stars by the ejecta of polluters (self-enrichment) is considered.
The horizontal dashed line represents the results of the study of Richer et al. (2002) for M 4.
Bottom: curves as in the middle panel, but for mass ratios instead of number ratios.
Also, the residues include not only white dwarfs (as in the middle panel)
but also neutron stars and black holes.
stars by the ejecta of polluters (self-enrichment) is considered.
The horizontal dashed line represents the results of the study of Richer et al. (2002) for M 4.
Bottom: curves as in the middle panel, but for mass ratios instead of number ratios.
Also, the residues include not only white dwarfs (as in the middle panel)
but also neutron stars and black holes. |
| Open with DEXTER |
For a composite IMF, kethe one adopted here (with PdM00 IMF below the turn-off mass of 0.8  and a power law above it), we find that a slope X=-0.3 above the turn-off mass is required
in the internal evolution scenario to reproduce the
derived
and a power law above it), we find that a slope X=-0.3 above the turn-off mass is required
in the internal evolution scenario to reproduce the
derived
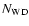 /
/
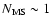 (middle panel of Fig. 9).
(middle panel of Fig. 9).
Somewhat surprisingly, in the self-enrichment scenario (middle and bottom
panels of Fig. 9), such a high
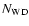 /
/
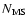 ratio is never obtained: values around 0.2 are
obtained if the polluters are assumed to be AGBs and much lower ones if the polluters are
massive stars. This may appear paradoxical, since at small IMF slopes and in the case of AGBs
as polluters, residues dominate long-lived stars by mass, as clearly seen in Fig. 9
(bottom panel). This apparent discrepancy is due to the fact that the ejecta mass of a e.g.
4
ratio is never obtained: values around 0.2 are
obtained if the polluters are assumed to be AGBs and much lower ones if the polluters are
massive stars. This may appear paradoxical, since at small IMF slopes and in the case of AGBs
as polluters, residues dominate long-lived stars by mass, as clearly seen in Fig. 9
(bottom panel). This apparent discrepancy is due to the fact that the ejecta mass of a e.g.
4  star can give rise to a dozen or so low-mass stars (
star can give rise to a dozen or so low-mass stars (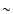 0.3
0.3  )
of 2nd generation;
thus, the resulting number ratio between WDs and long-lived stars is much lower than the
corresponding mass ratio between WDs and ejecta.
Interestingly, in the case of internal evolution (implicitly adopted in RBF02), the residues
should completely dominate the long lived stars by mass in M 4, by a factor of 10, as can be
seen in the bottom panel of Fig. 9 due to the fact that each residue (white dwarf, neutron star, or black hole)
is several times more massive than a typical low-mass star.
)
of 2nd generation;
thus, the resulting number ratio between WDs and long-lived stars is much lower than the
corresponding mass ratio between WDs and ejecta.
Interestingly, in the case of internal evolution (implicitly adopted in RBF02), the residues
should completely dominate the long lived stars by mass in M 4, by a factor of 10, as can be
seen in the bottom panel of Fig. 9 due to the fact that each residue (white dwarf, neutron star, or black hole)
is several times more massive than a typical low-mass star.
The low number ratio of white dwarfs over low-mass stars obtained in our self-enrichment
scenarios (lower than derived in M 4), does not necessarily point to a fatal flaw for those scenarios.
It may well be that the ejecta mass (and the resulting number of second generation stars) is lower than assumed here,
in which case a ratio closer to the observed one will be obtained. Such a reduced ejecta mass is, in fact,
quite plausible (see discussion in Sect. 5.1).
A determination of the polluter IMF on the basis of star counts has been also attempted
recently by D'Antona & Caloi (2004), who noted that AGB winds are helium-enriched
(mainly as a consequence of the second dredge-up; Ventura et al. 2001).
The second generation stars formed from AGB ejecta should then have a higher helium
content than the first generation stars, which were born with the primordial cluster
helium abundance. This difference in helium may substantially alter their advanced evolution.
D'Antona et al. (2002) evaluates the impact of a spread in helium within the low-mass
star population on a GC colour-magnitude diagram and discusses the evolutionary
properties of GC stars in which variations of the initial helium are allowed.
They show that within reasonable limits (Y varying between 0.24 for the proto-cluster
abundance and 0.28 for the most polluted stars), the impact on the main sequence,
turnoff, and RGB would be low and undetectable observationally. Also,
the horizontal branch luminosity appears to be only slightly affected.
As a consequence the age determination should only be modified in a limited way.
However, the differences in the morphology of the horizontal branch would be
noticeable; in particular, the He enrichment could play a role in the formation of blue tails.
Following this idea, D'Antona & Caloi (2004, hereafter DC04) studied
the morphology of the horizontal branch of NGC 2808 in detail. It is composed
of two well-separated regions: a red clump and an extended blue tail starting
from the blue side of the RR Lyrae gap and reaching below the cluster turn-off
(Bedin et al. 2000, and references therein).
DC04 shows that the dichotomy of the horizontal branch of NGC 2808 can be
reproduced by assuming different helium contents for the clump and blue HB stars
and argues that this unveils the signature of two separate star formation events
in the early cluster evolution. Within their self-enrichment framework
(similar, but not identical, to our Scenario I),
the red clump stars belong to the first stellar generation formed with the
original helium,
while second-generation stars born directly from the ejecta of AGB stars of various
masses (and thus with various He-enrichments) populate the blue part of the HB.
The lack of stars in the RR Lyrae region is attributed to the gap in helium
between the two stellar generations![[*]](/icons/foot_motif.gif) .
.
DC04 further explore the implications of their hypothesis by deriving the IMF
of the first stellar generation based on star counts along the HB of NGC 2808.
In order to explain the number of HB blue stars, they adopt a relation
between the progenitor AGB mass and the helium content of their ejecta (based on
stellar models) and derive a relatively flat IMF, with 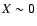 .
This value
is very close to the upper limit we derived in Sect. 4.3 for AGB stars being the polluters
within Scenario I.
.
This value
is very close to the upper limit we derived in Sect. 4.3 for AGB stars being the polluters
within Scenario I.
Helium enrichment is a natural outcome of AGB models.
However, the results of DC04 are extremely model-dependent;
they rely in particular on a simple linear relation between the average helium
content in the ejecta and the progenitor mass, require a fine-tuning of the
mass loss on the RGB, and depend on delicate transformations between the theoretical
and observational plane. Additionally, other phenomena may intervene in the
building of the colour-magnitude diagram morphology of a GC (mass-loss processes,
stellar multiplicity, stellar rotation, dynamical effects), which should be ultimately
taken into account in such an analysis (see e.g., Sosin et al. 1997; Castellani et al. 2006,
and references therein).
Claims of supporting evidence for the presence of helium-rich populations in GCs were recently
obtained through the detailed analysis of various colour-magnitude diagram features
(e.g., Lee et al. 2005, and references therein). This type of analysis newly supports
the self-enrichment hypothesis, but sheds no light on the nature of the polluters,
since both AGBs and WMS contribute a lot of He, as discussed in Sect. 5.
The results presented and discussed in this section illustrate how deep-counting observations of GC stars
may be used to constrain the massive star (=polluter) IMF of the GCs in the framework of the self-enrichment scenario.
It is true that the simplifying assumptions made in our work (upper mass limits for the IMFs
of the first - 100  - and second - 0.8
- and second - 0.8  - stellar generations; same form for the low mass part of the IMFs
in both stellar generations) are not unique, and a degenerate set of constraints would be obtained in a detailed analysis.
However, with larger observational data sets available for a given cluster (including e.g. abundance distributions
for several elements, number counts of white dwarfs and low mass stars - including those of the horizontal branch,
dynamical determination of the baryonic mass of the cluster etc.) and with improved theoretical understanding
of stellar nucleosynthesis issues (e.g. amount and composition of ejecta) this degeneracy will ultimately be lifted.
- stellar generations; same form for the low mass part of the IMFs
in both stellar generations) are not unique, and a degenerate set of constraints would be obtained in a detailed analysis.
However, with larger observational data sets available for a given cluster (including e.g. abundance distributions
for several elements, number counts of white dwarfs and low mass stars - including those of the horizontal branch,
dynamical determination of the baryonic mass of the cluster etc.) and with improved theoretical understanding
of stellar nucleosynthesis issues (e.g. amount and composition of ejecta) this degeneracy will ultimately be lifted.
Today, there is neither a unique, a well-defined, nor even a fully
self-consistent scenario for the self-enrichment of globular clusters.
The most commonly-invoked one assumes that the H-processed ejecta of massive
AGB stars of a first stellar generation (of unspecified, but presumably flatter-than-normal, IMF)
form a second stellar generation (of equally unspecified IMF)
and of appropriate chemical composition (i.e. in agreement with observed O/Fe
vs. Na/Fe ratios in GC stars). Most of the theoretical effort up to now has been
devoted to trying to reproduce the observed O vs. Na or Mg vs. Al relations
from the nucleosynthesis point of view (see references in Charbonnel 2005).
In this section, we discuss several aspects of the two self-enrichment
Scenarios (I and II), which are sketched in
Sect. 3 and which involve not only AGBs but also winds of
massive stars as alternative sources of the chemically polluted material.
We start by noting that any scenario of that kind necessarily involves assumptions about three quantities:
- a)
- the IMF (mass limits and shape) of the first stellar generation and, when it exists,
of the second one (there are two generations in our Scenario I but only one in our
Scenario II);
- b)
- the amount and composition of the stellar ejecta that contribute to the formation of the contaminated stars, as well as the mass range of the polluting stars;
- c)
- the amount of unprocessed gas, which is mixed to various degrees with the processed ejecta (equal to zero in our Scenario I).
From those quantities, only the second can be evaluated, in principle, from stellar nucleosynthesis calculations;
the other two can only be guessed at, or constrained, by a combination of theory and observations.
Since we lack the required input for item (b)![[*]](/icons/foot_motif.gif) at present we had to make some assumptions here. We assumed then that the
amount of H-processed ejecta is the maximum possible from both potential sources, AGBs or massive stars (Eqs. (12), (13) and
Fig. 7). Obviously, any other assumption reducing the amount
of the processed ejecta would result in IMFs that are even flatter than those found in
Sect. 4 (all other things being kept the same). As already discussed in Sect. 4.2, a smaller amount of H-processed
ejecta than assumed here is much more plausible physically for both AGB stars and massive stars.
at present we had to make some assumptions here. We assumed then that the
amount of H-processed ejecta is the maximum possible from both potential sources, AGBs or massive stars (Eqs. (12), (13) and
Fig. 7). Obviously, any other assumption reducing the amount
of the processed ejecta would result in IMFs that are even flatter than those found in
Sect. 4 (all other things being kept the same). As already discussed in Sect. 4.2, a smaller amount of H-processed
ejecta than assumed here is much more plausible physically for both AGB stars and massive stars.
We also made two different
assumptions about the composition of the ejecta, namely that they are processed to various degrees (Scenario I) or to an extreme degree
(Scenario II). Obviously, the latter assumption is utterly implausible, and it was used only to place absolute lower limits
to the slope of the polluter IMF. Indeed, it is hard to conceive that the whole envelope of all the polluters (AGBs or massive stars)
is processed to such an extreme degree ([O/Na]=-1.4); this may happen at some point of the evolution of some of the polluters, but it can
characterize neither the totality of the envelope evolution nor the whole mass range of the polluters.
Thus, the lower horizontal line of Scenario II (middle panel of Fig. 8)
is an extreme and unrealistic lower limit while the upper line
of Scenario I is more realistic in that respect. Still, observations suggest that it cannot be true, either.
Indeed, Pasquini et al. (2005) report the presence of Li in 9 turn-off stars of the
intermediate metallicity globular cluster NGC 6752 ([Fe/H]=-1.4), a cluster that displays
the anticorrelation of O vs. Na. The Li abundance in NGC 6752 correlates with the one
of O and anticorrelates with those of Na and N. The maximum Li abundance corresponds to stars
with [O/Fe![$]\sim0.4$](/articles/aa/full/2006/40/aa5374-06/img84.gif) ,
i.e. to stars formed from unprocessed material with a composition similar
to the one of field stars. It is no surprise then that the abundance of Li in those stars
(log(Li/H
,
i.e. to stars formed from unprocessed material with a composition similar
to the one of field stars. It is no surprise then that the abundance of Li in those stars
(log(Li/H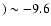 )
is at the level of the so-called "Spite plateau''
observed in field halo stars (e.g., Charbonnel & Primas 2005).
On the other hand, the lowest detected Li values are about 3 times lower and are found
in stars with very low [O/Na
)
is at the level of the so-called "Spite plateau''
observed in field halo stars (e.g., Charbonnel & Primas 2005).
On the other hand, the lowest detected Li values are about 3 times lower and are found
in stars with very low [O/Na
![$]\sim -1.1$](/articles/aa/full/2006/40/aa5374-06/img86.gif) in NGC 6752.
in NGC 6752.
The presence of so much Li (only within a factor of three below the
plateau level) in stars of modified composition in NGC 6752 clearly is at odds with our
Scenario I: if such stars are made exclusively from the H-processed ejecta of some class
of polluters (as assumed in our Scenario I), then no Li should be present there, in view
of the nuclear fragility of that element. And even if one assumes that some fresh Li can be
produced in H-burning (and ejected before subsequent destruction) through the
Cameron-Fowler (1971) mechanism, it is utterely implausible that the abundance of
this new Li is almost as high as the "Spite plateau''.
The most natural way to explain the presence of Li in the
O-depleted stars of NGC 6752 is to assume that those stars were formed from a mixture of
nuclearly processed material with material of normal composition, as in our Scenario II
(Prantzos & Charbonnel, in preparation).
Finally, in both Scenarios I and II we assumed that, while the original IMF contained stars
in the full mass range of 0.1 to 100  ,
the ejecta of the polluters
only formed stars in the 0.1-0.8
,
the ejecta of the polluters
only formed stars in the 0.1-0.8  range, i.e. still alive today. This assumption
has no physical justification and was only made in order to maximize the ratio of ejecta to live stars,
in the same spirit as the other assumptions discussed in this section. Assuming that the ejecta formed stars
in the full 0.1-100
range, i.e. still alive today. This assumption
has no physical justification and was only made in order to maximize the ratio of ejecta to live stars,
in the same spirit as the other assumptions discussed in this section. Assuming that the ejecta formed stars
in the full 0.1-100  range would obviously lead to flatter IMFs in order to satisfy the observational
requirements
range would obviously lead to flatter IMFs in order to satisfy the observational
requirements![[*]](/icons/foot_motif.gif) .
.
We conclude then that both our Scenarios I and II are grossly underestimating "reality''
in the framework of the self-enrichment hypothesis for globular clusters.
A realistic scenario should invoke both ejecta with varying composition (as in Scenario I,
more realistic on nucleosynthesis grounds) and mixture of those ejecta with pristine gas
(as in Scenario II, to account for Li observations). This implies that the horizontal
"observational'' lines in Fig. 8 (middle panel) should be replaced by a line lying above the
one of Scenario I. Also, a realistic scenario should
consider an amount of ejecta considerably lower than the
(deliberate) overestimate we made in Eqs. (12) and (13); consequently,
the curves of Fig. 8 (middle panel) should shift downwards,
as discussed in Sect. 4.3.
Overall the slope X of the polluter IMF in a realistic scenario should be much flatter
than derived in Sect. 4.3 and certainly much lower than 0 in case the polluters are AGB stars. In other terms, an extremely
flat IMF should be necessary to satisfy the constraints imposed by the abundance distribution
of Fig. 2.
In such a case, by extrapolating the trends obtained in the lower panel of
Fig. 8 (towards the left) one sees that:
- if the polluters are AGB stars, the mass of the cluster today should be completely dominated by residues (by a factor of several);
- in contrast, if the polluters are massive stars, the total mass of the residues today would be much lower than the mass of live stars in the cluster.
With these implications in mind, we now take a closer look at the self-enrichment scenario, for both invoked classes of polluters.
According to a commonly held idea, the peculiar chemical composition of GC stars stems
from pollution by the ejecta of AGB stars, massive enough (4-9  )
to develop HBB in their envelopes. Such stars evolve in time scales of
)
to develop HBB in their envelopes. Such stars evolve in time scales of  20 to 150 Myr and release
their ejecta at velocities v<30 km s-1 (e.g., Loup et al. 1993), lower than the escape
velocity from the cluster; the ejecta are trapped in the cluster and form new stars,
either directly (our Scenario I) or indirectly, after mixing with pristine material
to various degrees (our Scenario II, which accounts for the Li observations,
as argued in Sect. 5.1).
20 to 150 Myr and release
their ejecta at velocities v<30 km s-1 (e.g., Loup et al. 1993), lower than the escape
velocity from the cluster; the ejecta are trapped in the cluster and form new stars,
either directly (our Scenario I) or indirectly, after mixing with pristine material
to various degrees (our Scenario II, which accounts for the Li observations,
as argued in Sect. 5.1).
In our opinion, this idea suffers from several drawbacks
(in addition to the problematic nucleosynthesis predictions of the current models discussed
in Sect. 3). In particular, it gives no satisfactory answer to the roles of stars that are more
massive (M>9  )
and less massive (M<4
)
and less massive (M<4  )
than the presumed polluters.
)
than the presumed polluters.
1) Stars more massive than 9  evolve on time scales lower than 20 Myr and are quite
numerous (since a flat IMF is required in all cases to account for the observed abundance
distribution, as argued in this work). They release material processed through various
nuclear burning stages, both through their winds (slow in the main sequence,
quite fast in the Wolf-Rayet stage) and through the final stellar explosion as
supernovae.
A commonly given answer to the fate of their ejecta is that the fast-moving supernova
material (v>400 km s-1 even for the innermost SN regions) escapes the system and leaves
no trace behind. On its way, it sweeps up the previously released wind ejecta, but also any
ambient gas of pristine composition. Consequently, no original Li rich gas is left behind
to subsequently get mixed with the AGB ejecta. The second (polluted) stellar generation
should then be formed exclusively with AGB ejecta, which implies that AGBs should produce
their own Li at a level close to the Spite plateau. This is an extremely strong constraint
on the nucleosynthesis of AGB stars.
evolve on time scales lower than 20 Myr and are quite
numerous (since a flat IMF is required in all cases to account for the observed abundance
distribution, as argued in this work). They release material processed through various
nuclear burning stages, both through their winds (slow in the main sequence,
quite fast in the Wolf-Rayet stage) and through the final stellar explosion as
supernovae.
A commonly given answer to the fate of their ejecta is that the fast-moving supernova
material (v>400 km s-1 even for the innermost SN regions) escapes the system and leaves
no trace behind. On its way, it sweeps up the previously released wind ejecta, but also any
ambient gas of pristine composition. Consequently, no original Li rich gas is left behind
to subsequently get mixed with the AGB ejecta. The second (polluted) stellar generation
should then be formed exclusively with AGB ejecta, which implies that AGBs should produce
their own Li at a level close to the Spite plateau. This is an extremely strong constraint
on the nucleosynthesis of AGB stars.
Alternatively, one may argue that an insignificant amount of nuclearly processed ejecta
escapes the supernovae, the vast majority being trapped within a black hole. This is an
utterly implausible scenario, since neutron stars and pulsars are common in the Milky Way,
and there is no reason for massive stars in GCs not to produce such residues.
Finally, one might also invoke a peculiar IMF of the first stellar generation in GCs,
which lacks massive stars altogether. Such an ad hoc assumption, however, is not supported by
any theoretical arguments or numerical simulation results.
2) Stars in the mass range 2-4  evolve on timescales of 150 to 1000 Myr
and release
almost as much mass as those of 4-9
evolve on timescales of 150 to 1000 Myr
and release
almost as much mass as those of 4-9  (depending on the assumed IMF: for X=0.15we obtain
E(2-4)=0.35 E(4-9)). Even if they do not develop HBB in their envelopes,
they go through the third dredge-up phase, which brings He-burning products (in particular C)
and s-elements to the surface, slowly releasing them to the ISM. If new stars are formed
from these ejecta, C and s-element excesses should be observed in GC stars, which is not
the case. One then has to assume that the ejecta of 2 to 4
(depending on the assumed IMF: for X=0.15we obtain
E(2-4)=0.35 E(4-9)). Even if they do not develop HBB in their envelopes,
they go through the third dredge-up phase, which brings He-burning products (in particular C)
and s-elements to the surface, slowly releasing them to the ISM. If new stars are formed
from these ejecta, C and s-element excesses should be observed in GC stars, which is not
the case. One then has to assume that the ejecta of 2 to 4  form no new stars, why those
of their slightly more massive sisters manage to do it very efficiently. Perhaps, on time
scales >100 Myr, tidal interactions of the GCs with the Galactic potential are able to remove
most of the cluster gas (as well as part of its stars); still, some ejecta should be left
behind to form stars with C and s-elements excess. Until a consistent dynamical scenario is
developed to convincingly account for that point, we consider it to be one
of the drawbacks of the AGB scenario for the pollution of GCs.
form no new stars, why those
of their slightly more massive sisters manage to do it very efficiently. Perhaps, on time
scales >100 Myr, tidal interactions of the GCs with the Galactic potential are able to remove
most of the cluster gas (as well as part of its stars); still, some ejecta should be left
behind to form stars with C and s-elements excess. Until a consistent dynamical scenario is
developed to convincingly account for that point, we consider it to be one
of the drawbacks of the AGB scenario for the pollution of GCs.
The idea that WMS may be at the origin of some anomalies in the composition of GCs has been recently suggested
by Norris (2004) and Maeder & Meynet (2006), in order to explain the blue main sequence of the cluster  Centauri.
The high helium content of the stars of that sequence could originate in WMS, producing a large helium/metal ratio.
Omega Cen is, however, a peculiar case, showing a dispersion in its heavy metal content, unlike any other GC.
If the polluters of GCs are indeed the winds of massive stars, the scenario could run along the following lines.
Centauri.
The high helium content of the stars of that sequence could originate in WMS, producing a large helium/metal ratio.
Omega Cen is, however, a peculiar case, showing a dispersion in its heavy metal content, unlike any other GC.
If the polluters of GCs are indeed the winds of massive stars, the scenario could run along the following lines.
The winds of those stars, rich in H-burning products (especially if the stars are rotating),
are slowly released in the ambient ISM and they push it, opening circumstellar cavities.
They are finally mixed with pristine gas, still left over in the system after the formation of the first
stellar generation. By reaching the walls of these cavities, the shock waves of the subsequent SN explosions
induce the formation of new stars from this gas of mixed composition. The hot SN ejecta inside
the shock waves are expanding mainly along the cavities opened up previously by the massive star winds, and they
finally find their way out of the cluster, escaping the system altogether. Thus, the stars
we now observe in the cluster either have their original composition, or a composition resulting from
the mixture of pristine gas with WMS. On longer timescales (>20 Myr), the wind ejecta
of lower-mass stars (M<10  )
that do not explode are slowly released in the cluster. However, they never
form new stars, since there is no external agent to trigger condensation of that gas and to
induce star formation. As discussed before, tidal interactions ultimately strip that gas off the cluster.
)
that do not explode are slowly released in the cluster. However, they never
form new stars, since there is no external agent to trigger condensation of that gas and to
induce star formation. As discussed before, tidal interactions ultimately strip that gas off the cluster.
The advantages of the WMS scenario are that i) it may "naturally'' account for the
formation of the second stellar generation with mixed composition, which is triggered by
the SN shock waves; and ii) it may also explain why no trace of the He-burning products of the third dredge-up (which certainly occurs in
low-mass AGBs) is seen today in GC stars. These products, along with those of HBB in more massive AGBs, are
slowly released in a rarefied medium (since almost all of the gas of the system has been swept up or condensed
previously, after the passage of the shock waves); as a result, they
never condense to form new stars (for lack of triggering agent) and they are ultimately removed from
the cluster through tidal interactions.
Of course, this novel scenario also has its potential drawbacks. It assumes that WMS mix thoroughly with
pristine gas and that the subsequent shock wave triggers efficient star formation in the mixture, while
the SN ejecta escape the system. One may, in fact, imagine the opposite situation where the shock
waves disperse the gas or the SN ejecta mix with that gas (at least partially).
At the current stage of our knowledge, both alternatives are possible.
The WMS scenario sketched here is, admittedly, at a very qualitative level (but no more
than the scenario involving AGBs). It should be substantiated at least by nucleosynthesis
calculations demonstrating that WMS can indeed provide the chemical composition required
to explain the observations of abundances in GCs; such calculations have already been performed
and they will be presented elsewhere (Decressin et al. 2006).
We feel, however, that the WMS scenario opens very interesting perspectives for the
understanding of the self-enrichment of GCs.
In this work we have studied the constraints on the IMF of stars responsible for the observed
abundance anomalies in GCs, in the framework of the so-called self-enrichment scenario.
At present, there is neither a unique nor a well-defined, nor even a
self-consistent self-enrichment scenario for GCs. The parameter space is quite large and
involves (at least) the IMF (mass limits and shape) of the polluter stars, the amount
and composition of their ejecta, as well as the amount of unprocessed gas, which is mixed
to various degrees with these ejecta to form the observed contaminated low-mass stars.
In view of the many uncertainties related to the self-enrichment scenario, we explore
several possibilities in details, but our study is far from exhaustive in that respect
(Sect. 3). In particular, we explore two different types of self-enrichment scenarios, differing
in the composition of the polluter ejecta, i.e. the degree to which the ejecta are
contaminated by H-burning products.
In Scenario I, second generation stars are formed exclusively from ejecta processed
at various degrees, while in Scenario II they are formed
from extremely processed ejecta mixed to various degrees with pristine material.
Also, we explore two different possibilities for the polluters, namely AGB stars (4-9  )
and WMS (>10
)
and WMS (>10  ), since both of them can, in principle, release H-burning products
in the ISM at slow velocities. In each case we assume that the amount of ejecta is as large
as possible, in order to constrain the polluter IMF from one side.
), since both of them can, in principle, release H-burning products
in the ISM at slow velocities. In each case we assume that the amount of ejecta is as large
as possible, in order to constrain the polluter IMF from one side.
We adopt a composite IMF (Sect. 4.1) with an observationally-derived part in the mass range
0.1-0.8  (from PdM00) and a power-law for higher masses (i.e. for stars that are
extinguished today); our aim was to constrain the slope X of the power-law part of the IMF.
For a concrete illustration of our method, we chose NGC 2808, the GC for which the largest
sample of O and Na abundances is presently available. We derived the abundance distribution
of O/Na in that cluster (Sect. 2) and find that
(from PdM00) and a power-law for higher masses (i.e. for stars that are
extinguished today); our aim was to constrain the slope X of the power-law part of the IMF.
For a concrete illustration of our method, we chose NGC 2808, the GC for which the largest
sample of O and Na abundances is presently available. We derived the abundance distribution
of O/Na in that cluster (Sect. 2) and find that  30% of its stars have a pristine
composition, while the remaining 70% are contaminated to various degrees by H-burning products.
30% of its stars have a pristine
composition, while the remaining 70% are contaminated to various degrees by H-burning products.
We then show how this contamination can be obtained quantitatively in the framework of our
two self-enrichment scenarios and under the different assumptions made about the mass range
of the polluters (AGBs vs. WMS). We find that, in all cases, the IMF of the polluters has
to be flatter than the standard present-day IMF (i.e. with the Salpeter slope X=1.35).
The trend is more pronounced in Scenario I than in Scenario II, and also more pronounced in
the case of AGBs than in the case of WMS (Sect. 4.3). However, due the many uncertainties
involved, it is impossible to make a realistic quantitative prediction about the upper limit
of the slope X; in fact, we argue in Sect. 5.1 that a realistic scenario would lead to an even
much flatter IMF than those obtained in this work.
An IMF with X<-0.4 (i.e. much flatter than obtained here) was found in the
work of Smith & Norris (1982) for NGC 6752 and 47 Tuc,
in order to explain the observed C depletion in the framework of the self-enrichment scenario.
By using absolute abundances (and not only abundance ratios, as in our work)
they were also able to place an upper limit of 11  to the
IMF of the polluters. Clearly, such work should be repeated with updated stellar yields
and a wide basis of spectroscopic data on as many elements as possible, in order to constrain
the polluter IMF and even the validity of the various self-enrichment scenarios.
to the
IMF of the polluters. Clearly, such work should be repeated with updated stellar yields
and a wide basis of spectroscopic data on as many elements as possible, in order to constrain
the polluter IMF and even the validity of the various self-enrichment scenarios.
We find that the amount of stellar residues (both by mass and by number) present in the GC,
is sensite to the slope of the adopted IMF and to the mass range of the polluters, thereby
providing another potential discriminating test between the various possibilities.
We illustrate this (Sect. 4.4) by comparing our results to the number ratio ( 1)
of white dwarfs to low-mass stars
inferred in the cluster M 4.
We find that our results fall short of producing such a large ratio, the discrepancy being
more important in the case of WMS than in the case of AGBs. In fact, taken at face value,
our results might be interpreted as a complete failure of the self-enrichment scenario
(and as an argument for the internal evolution scenario).
We argue, however, that this "failure'' may be attributed to the extreme assumptions
adopted here and that more realistic assumptions would produce results closer to the
observations.
1)
of white dwarfs to low-mass stars
inferred in the cluster M 4.
We find that our results fall short of producing such a large ratio, the discrepancy being
more important in the case of WMS than in the case of AGBs. In fact, taken at face value,
our results might be interpreted as a complete failure of the self-enrichment scenario
(and as an argument for the internal evolution scenario).
We argue, however, that this "failure'' may be attributed to the extreme assumptions
adopted here and that more realistic assumptions would produce results closer to the
observations.
Finally, in Sect. 5 we discuss the various assumptions made in our study.
In particular, we comment on some problems associated (in our opinion) with AGBs,
the most frequently-invoked polluters of GCs (Sect. 5.2.1). We also develop for the first time
a possible scenario for the pollution of GCs by WMS in some detail,
and also invoke its own potential problems (Sect. 5.2.2). We conclude that WMS offer
an appealing alternative to AGBs as polluter candidates of GCs.
Overall, our study shows that the self-enrichment scenario of GCs can be quantitatively tested,
through progress in observations (abundance distributions for several elements, number
counts of white dwarfs and low mass stars, dynamical determination of the baryonic mass of
a given cluster), and theory (improved understanding of
the amount and composition of the ejecta of the various candidate polluters).
Acknowledgements
We are indebted to E. Carretta for providing us with the NGC 2808 data prior to publication.
We wish to warmly thank G. Meynet and G. Wallerstein for enlightening comments and a careful
reading of the manuscript, as well as T. Decressin, G. de Marchi, G. Meylan,
and P. Molaro for useful discussions. We thank the anonymous referee for constructive comments.
- Adams, F. C.,
& Fatuzzo, M. 1996, ApJ, 464, 256 [NASA ADS] [CrossRef]
- Armosky, B.
J., Sneden, C., Langer, G. E., & Kraft, R. P. 1994, AJ, 108,
1364 [NASA ADS] [CrossRef] (In the text)
- Bedin, L. R.,
Piotto, G., Zoccali, M., et al. 2000, A&A, 363, 159 [NASA ADS] (In the text)
- Brown, J. H.,
Burkert, A., & Truran, J. W. 1991, ApJ, 376, 115 [NASA ADS] [CrossRef] (In the text)
- Cameron, A.
G. W., & Fowler, W. A. 1971, ApJ, 164, 111 [NASA ADS] [CrossRef] (In the text)
- Carretta,
E., Bragaglia, A., Cacciari, C., & Rossetti, E. 2003, A&A,
410, 143 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Carretta,
E., Bragaglia, A., & Cacciari, C. 2004, ApJ, 610, L25 [NASA ADS] [CrossRef] (In the text)
- Carretta,
E. 2006, AJ, 131, 1766 [NASA ADS] [CrossRef] (In the text)
- Carretta,
E., Bragaglia, A., Gratton, R. G., et al. 2006, A&A, 450,
523 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
-
Castellani, V., Iannicola, G., Bono, G., et al. 2006, A&A, 446,
569 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Cayrel, R.
1986, A&A 168, 81
(In the text)
-
Charbonnel, C. 2005, From lithium to uranium: Element tracers of
early cosmic evolution (Cambridge Univ. Press), ed. V. Hill, P.
François, & F. Primas, IAU Symp., 228, 347
(In the text)
-
Charbonnel, C., & Primas, F. 2005, A&A, 442, 961 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Cohen, J. G.
1978, ApJ, 223, 487 [NASA ADS] [CrossRef]
- Cottrell,
P. L., & Da Costa, G. S. 1981, ApJ, 245, L79 [NASA ADS] [CrossRef] (In the text)
- D'Antona, F.,
Bellazzini, M., Caloi, V., et al. 2005, ApJ, 631, 868 [NASA ADS] [CrossRef]
- D'Antona, F.,
& Caloi, V. 2004, ApJ, 611, 871 [NASA ADS] [CrossRef] (In the text)
- D'Antona, F.,
Caloi, V., Montalban, J., Ventura, P., & Gratton, R. 2002,
A&A, 395, 69 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- D'Antona, F.,
Gratton, R., & Chieffi, A. 1983, Mem. Soc. Astron. It., 54,
173 [NASA ADS]
-
Decressin, T., & Charbonnel, C. 2005, From lithium to uranium:
Element tracers of early cosmic evolution (Cambridge Univ. Press),
ed. V. Hill, P. François, & F. Primas, IAU Symp., 228,
395
(In the text)
-
Decressin, T., Meynet, G., Charbonnel, C., Prantzos, N., &
Ekström, S. 2006, A&A, submitted
(In the text)
- De Marchi, G.,
Paresce, F., Straniero, O., & Prada Moroni, P. G. 2004,
A&A, 415, 971 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
-
Denissenkov, P. A., & Denissenkova, S. N. 1990, SvA Lett., 16,
275 [NASA ADS] (In the text)
-
Denissenkov, P. A., & Herwig, F. 2003, ApJ, 590, 99 [NASA ADS] [CrossRef] (In the text)
- Drake, J. J.,
Smith, V. V., & Suntzeff, N. B. 1992, ApJ, 395, L95 [NASA ADS] [CrossRef] (In the text)
- Dickens, R.
J., Croke, B. F. W., Cannon, R. D., & Bell, R. A. 1991, Nature,
351, 212 [NASA ADS] [CrossRef] (In the text)
-
Elmegreen, B. G. 1999, ApJ, 515, 323 [NASA ADS] [CrossRef]
- Fall, S. M., &
Rees, M. J. 1985, ApJ, 298, 18 [NASA ADS] [CrossRef] (In the text)
- Fenner, Y.,
Campbell, S., Karakas, A. I., Lattanzio, J. C., & Gibson, B. K.
2004, MNRAS, 353, 789 [NASA ADS] (In the text)
- Gratton, R.,
Bonifacio, P., Bragaglia, A., et al. 2001, A&A, 369, 87 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Giersz, M.
2001, MNRAS, 324, 218 [NASA ADS] (In the text)
- Goriely, S.,
& Siess, L. 2005, From lithium to uranium: Element tracers of
early cosmic evolution (Cambridge Univ. Press), ed. V. Hill, P.
François, & F. Primas, IAU Symp., 228, 451
(In the text)
- Gratton, R.,
Sneden, C., & Carretta, E. 2004, ARA&A, 42, 385 [NASA ADS] (In the text)
- Grundahl,
F., Briley, M., Nissen, P. E., & Feltzing, S. 2002, A&A,
385, L14 [NASA ADS] [CrossRef] [EDP Sciences]
- Harris, W. E.,
& Pudritz, R. E. 1994, ApJ, 429, 177 [NASA ADS] [CrossRef] (In the text)
- Herwig, F.
2004a, ApJ, 605, 425 [NASA ADS] [CrossRef] (In the text)
- Herwig, F.
2004b, ApJS, 155, 651 [NASA ADS] [CrossRef]
- Iben, I. 1976, ApJ,
208, 165 [NASA ADS] [CrossRef]
- Iben, I., &
Tutukov, A. 1984, ApJ, 284, 719 [NASA ADS] [CrossRef] (In the text)
- Ivans, I. I.,
Sneden, C., Kraft, R. P., et al. 1999, AJ, 118, 1273 [NASA ADS] [CrossRef] (In the text)
- Ivans, I. I.,
Kraft, R. P., Sneden, C., et al. 2001, AJ, 122, 1438 [NASA ADS] [CrossRef] (In the text)
- James, G.,
François, P., Bonifacio, P., et al. 2004a, A&A, 414,
1071 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- James, G.,
François, P., Bonifacio, P., et al. 2004b, A&A, 427,
825 [NASA ADS] [CrossRef] [EDP Sciences]
- Joshi, K. J.,
Nave, C. P., & Rasio, F. A. 2001, ApJ, 550, 691 [NASA ADS] [CrossRef] (In the text)
- Karakas, A.
I., & Lattanzio, J. C. 2003, PASA, 20, 279 [NASA ADS] (In the text)
- Kraft, R. P.
1994, PASP, 106, 553 [NASA ADS] [CrossRef]
- Kroupa, P.
2002, Science, 295, 82 [NASA ADS] [CrossRef] (In the text)
- Langer, G. E.,
Hoffman, R., & Sneden, C. 1993, PASP, 105, 301 [NASA ADS] [CrossRef] (In the text)
- Lee, Y. W., Joo, S.
J., Han, S. I., et al. 2005, ApJ, 621, L57 [NASA ADS] [CrossRef] (In the text)
- Loup, C.,
Forveille, T., Omont, A., & Paul, J. F. 1993, A&AS, 99,
291 [NASA ADS] (In the text)
- Maeder, A.,
& Meynet, G. 2006, A&A, 448, L37 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Michaud, G.,
Richard, O., & Richer, J. 2004, Mem.S.A.It., 75, 339 [NASA ADS] (In the text)
- Norris, J.
1981, ApJ, 612, L25 [NASA ADS] [CrossRef]
- Norris, J.
E., Cottrell, P. L., Freeman, K. C., & Da Costa, G. S. 1981,
ApJ, 244, 205 [NASA ADS] [CrossRef]
- Paresce, F.,
& De Marchi, G. 2000, ApJ, 534, 870 [NASA ADS] [CrossRef] (PdM00)
(In the text)
-
Parmentier, G. 2004, MNRAS, 351, 585 [NASA ADS] (In the text)
-
Parmentier, G., Jehin, E., Magain, P., et al. 1999, A&A, 352,
138 [NASA ADS] (In the text)
- Pasquini,
L., Bonifacio, P., Molaro, P., et al. 2005, A&A, 441, 549 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Peterson,
R. C. 1980, ApJ, 237, L87 [NASA ADS] [CrossRef]
- Pulone, L., De
Marchi, G., Paresce, F., & Allard, F. 1998, ApJ, 492, L41 [NASA ADS] [CrossRef] (In the text)
-
Pilachowski, C. A. 1989, in The abundance spread within globular
clusters, ed. G. Cayrel de Strobel, M. Spite, & T. L. Evans,
1
(In the text)
- Ramirez, S.
V., & Cohen, J. G. 2002, AJ, 123, 3277 [NASA ADS] [CrossRef] (In the text)
- Ramirez, S.
V., & Cohen, J. G. 2003, AJ, 125, 224 [NASA ADS] [CrossRef] (In the text)
- Richard, O.,
Michaud, G., Richer, J., et al. 2002, ApJ, 568, 979 [NASA ADS] [CrossRef] (In the text)
- Richer, H.,
Brewer, J., Fahlman, G., et al. 2002, ApJ, 574, L151 [NASA ADS] [CrossRef] (RBF02)
(In the text)
-
Rubenstein, E., & Bailyn, C. 1999, ApJ, 513, L33 [NASA ADS] [CrossRef] (In the text)
- Salpeter,
E. E. 1955, ApJ, 121, 161S [NASA ADS] [CrossRef] (In the text)
- Shetrone,
M. D. 1996, AJ, 112, 1517 [NASA ADS] [CrossRef] (In the text)
- Smith, G. H.,
& Norris, J. 1982, ApJ, 254, 594 [NASA ADS] [CrossRef] (In the text)
- Smith, G. H.,
Shetrone, M. D., Bell, R., Churchill, C. W., & Briley, M. M.
1996, AJ, 112, 1511 [NASA ADS] [CrossRef] (In the text)
- Smith, V. V.,
Cunha, K., Ivans, I. I., et al. 2005, ApJ, 633, 392 [NASA ADS] [CrossRef] (In the text)
- Sneden, C.
2005, From lithium to uranium: Element tracers of early cosmic
evolution (Cambridge Univ. Press), ed. V. Hill, P. François,
& F. Primas, IAU Symp., 228, 337
(In the text)
- Sneden, C.,
Gratton, R. G., & Crocker, D. A. 1991, A&A, 246, 354 [NASA ADS] (In the text)
- Sneden, C.,
Kraft, R. P., Guhathakurta, P., Peterson, R. C., & Fullbright,
J. P. 2004, AJ, 127, 2162 [NASA ADS] [CrossRef] (In the text)
- Sosin, C.,
Dorman, B., Djorgovski, G., et al. 1997, ApJ, 480, L35 [NASA ADS] [CrossRef] (In the text)
- Spite, M.,
Cayrel, R., & Plez, B. 2005, A&A, 430, 655 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Stahler, S.,
& Palla, F. 2005, The formation of stars (J. Wiley)
(In the text)
- Thoul, A.,
Jorissen, A., Goriely, S., et al. 2002, A&A, 383, 491 [NASA ADS] [CrossRef] [EDP Sciences]
- Truran, J.
1988, The Impact of Very High S/N Spectroscopy on Stellar Physics,
IAU Symp., 132, 577
(In the text)
- Truran, J. W.,
Brown, J., & Burkert, A. 1991, The formation and Evolution of
Star Clusters, ASP Conf. Ser., 13, 78
(In the text)
- Ventura,
P., & D'Antona, F. 2005a, A&A, 431, 279 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Ventura,
P., & D'Antona, F. 2005b, A&A, 439, 1075 [NASA ADS] [CrossRef] [EDP Sciences]
- Ventura,
P., & D'Antona, F. 2005c, ApJ, 635, L149 [NASA ADS] [CrossRef]
- Ventura, P.,
D'Antona, F., Mazzitelli, I., & Gratton, R. 2001, ApJ, 550,
L65 [NASA ADS] [CrossRef] (In the text)
- Ventura, P.,
D'Antona, F., & Mazzitelli, I. 2002, A&A, 393, 215 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
-
Zinnecker, H. 1984, MNRAS, 210, 43 [NASA ADS]
Copyright ESO 2006
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{5374fig1.eps}
\end{figure}](/articles/aa/full/2006/40/aa5374-06/Timg19.gif)
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{5374fig2.eps}
\end{figure}](/articles/aa/full/2006/40/aa5374-06/Timg25.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{5374fig3.eps}
\end{figure}](/articles/aa/full/2006/40/aa5374-06/Timg26.gif)
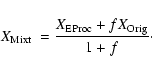
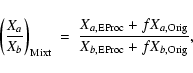
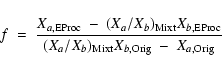
![\begin{displaymath}\rm [O/Fe]_{\rm Orig} =0.38,\end{displaymath}](/articles/aa/full/2006/40/aa5374-06/img34.gif)
![\begin{displaymath}\rm [Na/Fe]_{\rm Orig}=-0.03,\end{displaymath}](/articles/aa/full/2006/40/aa5374-06/img35.gif)
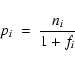
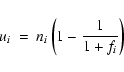
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{5374fig4.eps}
\end{figure}](/articles/aa/full/2006/40/aa5374-06/Timg42.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{5374fig5.eps}
\end{figure}](/articles/aa/full/2006/40/aa5374-06/Timg43.gif)
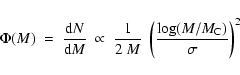
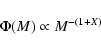
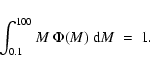
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{5374fig6.eps}
\end{figure}](/articles/aa/full/2006/40/aa5374-06/Timg55.gif)
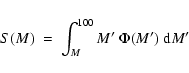
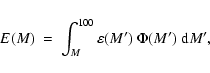
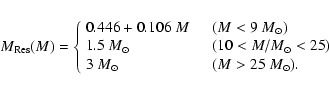
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{5374fig7.eps}
\end{figure}](/articles/aa/full/2006/40/aa5374-06/Timg65.gif)
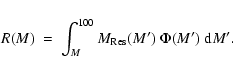
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{5374fig8.eps}
\end{figure}](/articles/aa/full/2006/40/aa5374-06/Timg69.gif)
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{5374fig9.eps}
\end{figure}](/articles/aa/full/2006/40/aa5374-06/Timg78.gif)