A&A 458, 245-257 (2006)
DOI: 10.1051/0004-6361:20065247
N. La Palombara1 - R. P. Mignani2 - E. Hatziminaoglou3 - M. Schirmer4 - G. F. Bignami5,6 - P. Caraveo1
1 - INAF - IASF Milano, Via E. Bassini 15, 20133 Milano, Italy
2 -
Mullard Space Science Laboratory, University College London, Holmbury St Mary,
Dorking, Surrey RH5 6NT, UK
3 -
Instituto de Astrofisica de Canarias, Via Lactea, 38200 La Laguna-Tenerife, Spain
4 -
Isaac Newton Group of Telescopes, Edificio Mayantigo, Calle Alvarez Abreu 68, 38700 Santa Cruz de la Palma, Spain
5 -
Centre d'Étude Spatiale des Rayonnements (CESR), CNRS-UPS, 9 Avenue du colonel Roche, 31028 Toulouse, France
6 -
Università di Pavia, Dipartimento di Fisica Teorica e Nucleare, via Ugo Bassi 6, 27100 Pavia, Italy
Received 22 March 2006 / Accepted 29 June 2006
Abstract
The limited angular resolution of ![]() -ray telescopes
prevents a direct identification of the majority of sources detected
so far. This is particularly true for the low latitude, probably
galactic, ones only 10% of which has been identified. Most
counterparts of the identified low-latitude
-ray telescopes
prevents a direct identification of the majority of sources detected
so far. This is particularly true for the low latitude, probably
galactic, ones only 10% of which has been identified. Most
counterparts of the identified low-latitude ![]() -ray sources are
Isolated Neutron Stars (INS), both radio-loud and radio-quiet (Geminga-like) objects, which are characterised by an
extremely high value of the X-ray-to-optical flux ratio
-ray sources are
Isolated Neutron Stars (INS), both radio-loud and radio-quiet (Geminga-like) objects, which are characterised by an
extremely high value of the X-ray-to-optical flux ratio
![]() .
Therefore, the systematic X-ray and optical
coverage of low-latitude unidentified
.
Therefore, the systematic X-ray and optical
coverage of low-latitude unidentified ![]() -ray sources aiming at
high
-ray sources aiming at
high
![]() sources seems one of the most promising
ways to spot INS candidate counterparts. Since low latitude sources
are heavily affected by the interstellar absorption at both X-ray and
optical wavelengths, we have focussed on two middle-latitude,
probably galactic, GRO/EGRET sources: 3EG J0616-3310 and 3EG J1249-8330. These two sources, which could belong to a local
galactic population, have been selected owing to their relatively good
positional accuracy, spectral shape and lack of candidate
extragalactic radio counterparts. Here we report on X-ray
observations of the two
sources seems one of the most promising
ways to spot INS candidate counterparts. Since low latitude sources
are heavily affected by the interstellar absorption at both X-ray and
optical wavelengths, we have focussed on two middle-latitude,
probably galactic, GRO/EGRET sources: 3EG J0616-3310 and 3EG J1249-8330. These two sources, which could belong to a local
galactic population, have been selected owing to their relatively good
positional accuracy, spectral shape and lack of candidate
extragalactic radio counterparts. Here we report on X-ray
observations of the two ![]() -ray error boxes performed with XMM-Newton and on their optical follow-up carried on with the Wide Field Imager at the ESO/MPG 2.2 m telescope. Less than half of
the
-ray error boxes performed with XMM-Newton and on their optical follow-up carried on with the Wide Field Imager at the ESO/MPG 2.2 m telescope. Less than half of
the ![]() 300 sources detected by the X-ray coverage have no optical
counterparts. Among those, we have selected few interesting sources
with
300 sources detected by the X-ray coverage have no optical
counterparts. Among those, we have selected few interesting sources
with
![]() ,
which we consider promising INS
candidates.
,
which we consider promising INS
candidates.
Key words: stars: neutron - gamma-rays: observations - X-rays: general
The nature of the Unidentified ![]() -ray Objects (UGOs) is one of
the main issues of the
-ray Objects (UGOs) is one of
the main issues of the ![]() -ray astronomy. The third Compton
Gamma Ray Observatory (CGRO) EGRET catalogue
(Hartman et al. 1999) contains 271 high-energy
-ray astronomy. The third Compton
Gamma Ray Observatory (CGRO) EGRET catalogue
(Hartman et al. 1999) contains 271 high-energy ![]() -ray sources
detected at energies above 0.1 GeV. The high-latitude ones
(
-ray sources
detected at energies above 0.1 GeV. The high-latitude ones
(
![]() )
are 191, and 93 of them have been identified with
blazars i.e. featureless flat spectrum radio-loud AGN and BL Lac objects (von Montigny et al. 1995), while 5 of the 80 sources at low
latitude have been identified with pulsating Isolated Neutron
Stars (INSs), both classical radio-pulsars and radio-quiet,
Geminga-like, objects (Thompson 2004; Caraveo 2002). In total, 170 EGRET sources, 74 of which at low latitudes, have no
counterpart at lower frequencies and remained unidentified. The
identification work had been hampered mainly by the poor localization
(about 1
)
are 191, and 93 of them have been identified with
blazars i.e. featureless flat spectrum radio-loud AGN and BL Lac objects (von Montigny et al. 1995), while 5 of the 80 sources at low
latitude have been identified with pulsating Isolated Neutron
Stars (INSs), both classical radio-pulsars and radio-quiet,
Geminga-like, objects (Thompson 2004; Caraveo 2002). In total, 170 EGRET sources, 74 of which at low latitudes, have no
counterpart at lower frequencies and remained unidentified. The
identification work had been hampered mainly by the poor localization
(about 1![]() in diameter at low-latitudes and up to 1.5
in diameter at low-latitudes and up to 1.5![]() at mid-latitudes) which frustrated the search for
counterparts at other wavelengths. Moreover, the limited
at mid-latitudes) which frustrated the search for
counterparts at other wavelengths. Moreover, the limited ![]() -ray
statistics made it impossible to perform "blind'' periodicity analysis
aimed at unveiling undiscovered INSs.
-ray
statistics made it impossible to perform "blind'' periodicity analysis
aimed at unveiling undiscovered INSs.
The latitude distribution analysis of the UGOs in the third EGRET catalogue (Fig. 1) shows that they can be grouped in at least
four different populations
(Romero et al. 2004; Grenier 2004,2001; Gehrels et al. 2000; Grenier 2000).
The presumably galactic UGOs (included those observed
at
![]() )
are equally distributed in 3 populations, with about 45 sources each. The GRP-I includes bright and relatively hard sources
near the galactic plane (
)
are equally distributed in 3 populations, with about 45 sources each. The GRP-I includes bright and relatively hard sources
near the galactic plane (
![]() ), with a concentration
towards the inner spiral arms (Bhattacharya et al. 2003) at distances of
a few kpc (Romero et al. 1999; Kanbach et al. 1996). Many of these sources are
well correlated with tracers of star formation, which means that their
age should be a few million years at most (Romero 2001; Grenier 2004).
The GRP-II includes variable sources at
), with a concentration
towards the inner spiral arms (Bhattacharya et al. 2003) at distances of
a few kpc (Romero et al. 1999; Kanbach et al. 1996). Many of these sources are
well correlated with tracers of star formation, which means that their
age should be a few million years at most (Romero 2001; Grenier 2004).
The GRP-II includes variable sources at
![]() which are
distributed in a sort of spherical halo around the Galactic Center
with a radial distribution equivalent to that of globular clusters
(Grenier 2004,2001). These sources are softer and
significantly more variable than GRP-I sources
(Nolan et al. 2003; Torres et al. 2001a,b); they are presumably older
(with an age of the order of a few Gyrs) and at distances between 2 and 8 kpc. The last group is the Local Gamma-Ray
Population (LGRP). It is composed by stable sources at
which are
distributed in a sort of spherical halo around the Galactic Center
with a radial distribution equivalent to that of globular clusters
(Grenier 2004,2001). These sources are softer and
significantly more variable than GRP-I sources
(Nolan et al. 2003; Torres et al. 2001a,b); they are presumably older
(with an age of the order of a few Gyrs) and at distances between 2 and 8 kpc. The last group is the Local Gamma-Ray
Population (LGRP). It is composed by stable sources at
![]() ,
which are fainter and softer than sources
located at lower Galactic latitude and have an evident asymmetric
distribution north of the Galactic center and south of the anticenter.
Gehrels et al. (2000) and Grenier (2000) suggested that these sources
might be associated with the Gould Belt, i.e. a 30 Myr old starburst
region, 300 pc in radius, composed by young massive and late type
stars, molecular clouds, and expanding interstellar medium.
Therefore, LGRP sources should be young (i.e. a few Myr old) nearby
(100-400 pc) and low luminosity (
,
which are fainter and softer than sources
located at lower Galactic latitude and have an evident asymmetric
distribution north of the Galactic center and south of the anticenter.
Gehrels et al. (2000) and Grenier (2000) suggested that these sources
might be associated with the Gould Belt, i.e. a 30 Myr old starburst
region, 300 pc in radius, composed by young massive and late type
stars, molecular clouds, and expanding interstellar medium.
Therefore, LGRP sources should be young (i.e. a few Myr old) nearby
(100-400 pc) and low luminosity (![]() 1032-33 erg s-1)
objects (Grenier 2004). But recently, using an improved interstellar emission model, Casandjian et al. (2005) have shown that most of these sources can correspond to the emission of clumpy dark clouds that surround all the molecolar clouds of the Gould Belt; therefore their existence is not confirmed. Finally, there is an isotropic population of extragalactic origin, which is characterized by a variety of spectra and variabilities and includes no more than 35 sources.
1032-33 erg s-1)
objects (Grenier 2004). But recently, using an improved interstellar emission model, Casandjian et al. (2005) have shown that most of these sources can correspond to the emission of clumpy dark clouds that surround all the molecolar clouds of the Gould Belt; therefore their existence is not confirmed. Finally, there is an isotropic population of extragalactic origin, which is characterized by a variety of spectra and variabilities and includes no more than 35 sources.
![\begin{figure}
\par\includegraphics[angle=+90,width=8cm,clip]{5247fig1.ps}
\end{figure}](/articles/aa/full/2006/40/aa5247-06/Timg20.gif) |
Figure 1:
Galactic distribution of the unidentified |
| Open with DEXTER | |
After the release of the third EGRET catalogue, only a few additional identifications have been obtained. From the extragalactic point of view, the multiwavelength approach has led to a blazar identification of 3EG J2016+3657 (Halpern et al. 2001b), 3EG J2006-2321 (Wallace et al. 2002) and 3EG J2027+3429 (Sguera et al. 2004), while for 3EG 1621+8203 (Mukherjee et al. 2002), 3EG J1735-1500 (Combi et al. 2003) and 3EG J0416+3650 (Sguera et al. 2005) a radio-galaxy has been proposed as counterpart. Within the Galaxy, 3EG J1824-1514 and 3EG J0241+6103 have been associated with the two well known microquasars LS 5039 (Paredes et al. 2000; Casares et al. 2005b) and LS I +61 303 (Kniffen et al. 1997; Massi et al. 2004; Casares et al. 2005a); Combi et al. (2004) suggested also the association between the microquasar candidate AX J1639-4642 and the UGO 3EG J1639-4702, but recently Bodaghee et al. (2006) have confirmed that it is an X-ray pulsar, thus excluding this possibility. In two cases a peculiar early-type binary system have been suggested as counterpart of an UGO, i.e. SAX J0635+0533 for 3EG J0634+0521 (Kaaret et al. 2000) and A0535+26 for 3EG J0542+2610 (Romero et al. 2001). Turning now to the INS family, the search for radio or X-ray pulsars has provided likely candidates for 3EG J0222+4253 (PSR J0218+4232, Kuiper et al. (2002)), 3EG J1048-5840 (PSR B1046-58, Kaspi et al. 2000), 3EG J2021+3716 (PSR J2021+3651, Roberts et al. 2002b) and 3EG J2227+6122 (RX/AX J2229.0+6114, Halpern et al. 2001a,c). Moreover, thanks to the Parkes Multi-beam pulsar Survey (PMS) of the galactic plane (Manchester et al. 2001), other promising pulsar candidates have been found for 3EG J1420-6038 and 3EG J1837-0606 (D'Amico et al. 2001) and for 3EG J1013-5915 (Camilo et al. 2001). However, none of the proposed identifications could be confirmed owing to the lack of contemporary radio data. Finally, various X-ray and radio studies have pointed to a close relationship between the pulsar wind nebulae (PWN) and the EGRET sources (Roberts 2005; Roberts et al. 2005,2001,2002a).
Apart from the cases of Cen A and of the LMC, all the EGRET sources identified so far fall either in the INS
or in the Blazar class. However, also in view of the High Energy
Stereoscopic System (HESS) results which are unveiling several
classes of very high energy ![]() -ray emitters
(Aharonian et al. 2005b,a,c; Brogan et al. 2005; Aharonian et al. 2005d), it is
hard to believe that these two classes exhaust all possible
-ray emitters
(Aharonian et al. 2005b,a,c; Brogan et al. 2005; Aharonian et al. 2005d), it is
hard to believe that these two classes exhaust all possible
![]() -ray source scenarios. Nevetheless, it has been argued that
rotation powered pulsars should dominate the Galactic
-ray source scenarios. Nevetheless, it has been argued that
rotation powered pulsars should dominate the Galactic ![]() -ray
source population (Yadigaroglu & Romani 1997) and that many of those
should be radio-quiet, since the
-ray
source population (Yadigaroglu & Romani 1997) and that many of those
should be radio-quiet, since the ![]() -ray beam is broader than the
radio one. The classic example of a radio-quiet pulsar is Geminga
(Caraveo et al. 1996), which offers an elusive template behaviour:
prominent in high energy
-ray beam is broader than the
radio one. The classic example of a radio-quiet pulsar is Geminga
(Caraveo et al. 1996), which offers an elusive template behaviour:
prominent in high energy ![]() -rays, easily detectable in X-rays
but downright faint in optical, with sporadic or no radio emission
(Bignami & Caraveo 1996). In the latest years, the idea that galactic
UGOs might be associated with Geminga-like objects has been
strengthened by the cases of three UGOs which were associated with radio-quiet INSs: 3EG J1835+5918, the brightest among
the unidentified UGOs and considered "the next Geminga''
(Halpern et al. 2002; Mirabal & Halpern 2001; Reimer et al. 2001), and the two sources 3EG J0010+7309 and 3EG J2020+4017, positionally coincident with the
supernova remnants CTA-1 (Brazier et al. 1998; Halpern et al. 2004) and
-rays, easily detectable in X-rays
but downright faint in optical, with sporadic or no radio emission
(Bignami & Caraveo 1996). In the latest years, the idea that galactic
UGOs might be associated with Geminga-like objects has been
strengthened by the cases of three UGOs which were associated with radio-quiet INSs: 3EG J1835+5918, the brightest among
the unidentified UGOs and considered "the next Geminga''
(Halpern et al. 2002; Mirabal & Halpern 2001; Reimer et al. 2001), and the two sources 3EG J0010+7309 and 3EG J2020+4017, positionally coincident with the
supernova remnants CTA-1 (Brazier et al. 1998; Halpern et al. 2004) and
![]() -Cygni (Brazier et al. 1996), respectively.
-Cygni (Brazier et al. 1996), respectively.
Table 1: Main characteristics of the eight EPIC observations of 3EG J0616-3310 (Field ID = 1-4) and 3EG J1249-8330 (Field ID = 5-8).
The energetic of the Geminga-like objects is not sufficient to account
for the very low latitude, presumably more distant, GRP-I sources but
could account for several middle latitude, rather nearby, objects of
the LGRP. Based on this rationale, we considered the case of two
middle latitude (see Fig. 1) UGOs:
3EG J0616-3310 and 3EG J1249-8330 (La Palombara et al. 2005, Paper I). Both
sources are characterized by a relatively good positional accuracy,
with a 95% confidence error circle radius
![]() ,
by a power law photon index
,
by a power law photon index
![]() and by a steady emission with fluxes above 0.1 GeV of
(
and by a steady emission with fluxes above 0.1 GeV of
(
![]() )
and (
)
and (
![]() photon cm-2 s-1, respectively (Hartman et al. 1999). In both cases, the lack of radio counterparts
down to a limit of a few tens of mJy
(Tornikoski et al. 2002; Sowards-Emmerd et al. 2004; Mattox et al. 2001) does not support an
extragalactic identification, while an association with the Gould Belt
appears more likely (their existence was confirmed also by Casandjian et al. 2005). Thus we have applied the multiwavelength approach
successfully used for the identification of Geminga as well as for
other UGOs associated with radio-quiet INS
(Mukherjee & Halpern 2004; Caraveo 2001). In the multiwavelength
approach, we start with the X-rays since they are the nearest
neighbours to
photon cm-2 s-1, respectively (Hartman et al. 1999). In both cases, the lack of radio counterparts
down to a limit of a few tens of mJy
(Tornikoski et al. 2002; Sowards-Emmerd et al. 2004; Mattox et al. 2001) does not support an
extragalactic identification, while an association with the Gould Belt
appears more likely (their existence was confirmed also by Casandjian et al. 2005). Thus we have applied the multiwavelength approach
successfully used for the identification of Geminga as well as for
other UGOs associated with radio-quiet INS
(Mukherjee & Halpern 2004; Caraveo 2001). In the multiwavelength
approach, we start with the X-rays since they are the nearest
neighbours to ![]() -rays and can be used to bridge the gap between
the poor resolution achievable in
-rays and can be used to bridge the gap between
the poor resolution achievable in ![]() -rays and the standards of
optical or radio astronomy. First, an X-ray image of the
-rays and the standards of
optical or radio astronomy. First, an X-ray image of the
![]() -ray error-box is taken and the detected X-ray sources are
cross-correlated with optical and radio catalogues, either available
in archives or produced from ad hoc observations. Next, potential INS candidates are singled out amongst X-ray sources
with an extremely high value of the X-ray-to-optical flux ratio
-ray error-box is taken and the detected X-ray sources are
cross-correlated with optical and radio catalogues, either available
in archives or produced from ad hoc observations. Next, potential INS candidates are singled out amongst X-ray sources
with an extremely high value of the X-ray-to-optical flux ratio
![]() .
This "top-down'' systematic strategy is
a time consuming exercise since it usually involves several
observing cycles with different instruments at different facilities,
both space and ground-based. Thus it can be pursued for a
large number of
.
This "top-down'' systematic strategy is
a time consuming exercise since it usually involves several
observing cycles with different instruments at different facilities,
both space and ground-based. Thus it can be pursued for a
large number of ![]() -ray sources only if a semi-automatic
procedure is set-up. Our work can be viewed as a preparatory step for
the massive identification work which will be needed in the coming
years, when AGILE (Tavani et al. 2003) and GLAST
(McEnery et al. 2004) will deliver hundreds of new
-ray sources only if a semi-automatic
procedure is set-up. Our work can be viewed as a preparatory step for
the massive identification work which will be needed in the coming
years, when AGILE (Tavani et al. 2003) and GLAST
(McEnery et al. 2004) will deliver hundreds of new ![]() -ray sources.
The improved angular resolution of these new
-ray sources.
The improved angular resolution of these new ![]() -ray telescopes will
provide arcmin positioning, thus easing considerably the identification
work. To this aim, a statistical approach will be necessary
(Torres & Reimer 2005).
-ray telescopes will
provide arcmin positioning, thus easing considerably the identification
work. To this aim, a statistical approach will be necessary
(Torres & Reimer 2005).
X-ray observations and data reduction techniques are presented in Sect. 2, while the X-ray source analysis is described in Sect. 3. The optical observations are described in Sect. 4, while the cross-correlations of the X-ray data with the optical and radio ones are described in Sect. 5. In Sect. 6 we discuss the source X-ray/optical analysis, while the most interesting sources are presented in Sect. 7. Finally, in Sect. 8 summary and conclusions are outlined.
Hot pixels, flickering pixels and bad columns, which produce spurious
source detections during an observation, are largely removed by the on
board data processing software while the remaining ones are masked by
the XMM/SAS. However, we found that several spurious events were
still present in the processed data. These have been localized using
the IRAF task cosmicrays and removed using the multipurpose XMM/SAS task evselect. We then filtered out time intervals
affected by high instrument background induced by soft proton flares
(energies less than a few hundred keV) hitting the detector surface.
To this aim, we accumulated the light curves of the events selected
close to the CCDs edges and with energies greater than 10 keV to avoid
contributions from real X-ray source variability. For the PN
data we considered only single pixels events (
![]() )
with energies
10-13 keV while for the MOS data we considered both single and
double pixels events (
)
with energies
10-13 keV while for the MOS data we considered both single and
double pixels events (
![]() )
with energies 10-12.4 keV in
CCDs 2-7. Then, we set a count rate threshold for good time
intervals at 0.15 and 0.35 cts s-1 for the MOS and the PN data, respectively. By selecting only events within the
"good'' time intervals we finally obtained three "clean'' event lists for
each observation, whose "effective'' exposure times are reported in
Table 1. As can be seen, the space weather was not
favourable during the observation of field 7 (which was so much
affected by the high particle background that we lost up to 80% of
the integration time) and, partly, for the observations of fields 3
and 4. An example of the processed EPIC/MOS image is shown in
Fig. 2, in the case of field 4.
)
with energies 10-12.4 keV in
CCDs 2-7. Then, we set a count rate threshold for good time
intervals at 0.15 and 0.35 cts s-1 for the MOS and the PN data, respectively. By selecting only events within the
"good'' time intervals we finally obtained three "clean'' event lists for
each observation, whose "effective'' exposure times are reported in
Table 1. As can be seen, the space weather was not
favourable during the observation of field 7 (which was so much
affected by the high particle background that we lost up to 80% of
the integration time) and, partly, for the observations of fields 3
and 4. An example of the processed EPIC/MOS image is shown in
Fig. 2, in the case of field 4.
In order to increase the signal to noise (S/N) ratio for the
detected sources and to reach fainter X-ray fluxes, for each observation we used the XMM/SAS task merge to merge the clean linearized event lists of
the 3 cameras. This was possible thanks to the
excellent relative astrometry between the MOS and the PN
(![]() 1'', a value much smaller than the FWHM of the PSF). In such a
way we obtained a "total'' event list, which was used to generate
images in 7 different energy ranges. Namely, we considered two standard coarse
soft/hard bands (0.5-2 and 2-10 keV) and a finer energy division
(0.3-0.5, 0.5-1, 1-2, 2-4.5, 4.5-10 keV). All images were built
with a spatial binning of 4
1'', a value much smaller than the FWHM of the PSF). In such a
way we obtained a "total'' event list, which was used to generate
images in 7 different energy ranges. Namely, we considered two standard coarse
soft/hard bands (0.5-2 and 2-10 keV) and a finer energy division
(0.3-0.5, 0.5-1, 1-2, 2-4.5, 4.5-10 keV). All images were built
with a spatial binning of 4
![]() 35 per pixel, roughly matching the
physical binning of the PN images (4''/pixel) and a factor
about four larger than the one of the MOS images
(1
35 per pixel, roughly matching the
physical binning of the PN images (4''/pixel) and a factor
about four larger than the one of the MOS images
(1
![]() 1/pixel). For each energy band, a corresponding set of
exposure maps (i.e. one for each of the three detectors) was
generated with the XMM/SAS task expmap, to account for
spatial quantum efficiency (QE), mirror vignetting and field of
view. Finally, the individual detector maps were merged in order to
obtain the "total'' exposure map for the relevant energy range. Both
images and exposure maps were used as a reference for the source
detection, which was performed in three steps:
1/pixel). For each energy band, a corresponding set of
exposure maps (i.e. one for each of the three detectors) was
generated with the XMM/SAS task expmap, to account for
spatial quantum efficiency (QE), mirror vignetting and field of
view. Finally, the individual detector maps were merged in order to
obtain the "total'' exposure map for the relevant energy range. Both
images and exposure maps were used as a reference for the source
detection, which was performed in three steps:
![\begin{figure}
\par\includegraphics[width=8cm,clip]{5247fig2.ps}
\end{figure}](/articles/aa/full/2006/40/aa5247-06/Timg32.gif) |
Figure 2: Processed XMM-Newton EPIC/MOS image of field 4 (see Table 1. Photons selected from three different energy bands are colour-coded: red (0.3-1 keV); green (1-3 keV); blue (3-10 keV). |
| Open with DEXTER | |
Table 2: X-ray sources detected in each energy range.
Unfortunately, even using the maximum number of spline nodes (20), the
fit performed in step 2 (see above) is not sufficiently flexible to
model the local variations of the background. Therefore, it was
necessary to correct each background map pixel by pixel,
measuring the counts both in the cheesed image and in the
background map itself applying the correction algorithm described in
Baldi et al. (2002). All sources in the master list were checked against
the corrected background maps and all their parameters calculated
again. Then, for all the selected energy bands, we applied a minimum
threshold of 8.5 on the corrected detection likelihoods ![]() ,
corresponding to a probability
,
corresponding to a probability
![]() that the source
count number in the energy band j originate from a background
fluctuation. This implies a contamination of at most 1 spurious source
per energy band. The revised source master list was then filtered to
include only sources with
that the source
count number in the energy band j originate from a background
fluctuation. This implies a contamination of at most 1 spurious source
per energy band. The revised source master list was then filtered to
include only sources with
![]() in at least one of the selected
energy bands and manually screened to reject residual false
detections. The final master lists contain a total of 146 and 148 sources for the 3EG J0616-3310 and in the 3EG J1249-8330 error box,
respectively.
in at least one of the selected
energy bands and manually screened to reject residual false
detections. The final master lists contain a total of 146 and 148 sources for the 3EG J0616-3310 and in the 3EG J1249-8330 error box,
respectively.
In order to perform a full statistical analysis, we computed the
number of detected sources
in each of the 7 energy ranges, i.e. those ones with
![]() in the energy
band j. Of course, most of the sources are detected in several bands: in
Table 2 we report, for each observation of both EGRET fields, the
number of detected sources in each energy range and its percentage over the total (that is
the total number of the sources which have been detected in at least one energy band).
in the energy
band j. Of course, most of the sources are detected in several bands: in
Table 2 we report, for each observation of both EGRET fields, the
number of detected sources in each energy range and its percentage over the total (that is
the total number of the sources which have been detected in at least one energy band).
We note that almost all sources are detected between 0.5 and 2 keV,
with half of them also detected between 1 and 2 keV, while only very
few sources are detected at very high or very low energies. The
number of sources detected in each energy band is, in absolute terms,
very different across the 8 pointings but, taking into account the
uneven effective exposure times (as it is evident in the case of the
observation of field 7, see Table 1), the relative
number is constant, especially for those pointings associated with the
same EGRET error box. However, we note that below 1 keV the
fraction of detected sources is indeed lower for the 3EG J1249-8330
error box than for the 3EG J0616-3310 one, probably because of the
difference in the neutral hydrogen column density, ![]() 1021 cm-2 and
1021 cm-2 and ![]()
![]() cm-2, respectively.
cm-2, respectively.
The histograms of the source count-rate (CR) distribution for the two
coarse soft (0.5-2 keV) and hard (2-10 keV) energy bands are shown
in Fig. 3, for the single pointings of the two EGRET error boxes. Since the number of sources per CR bin decreases
below the peak CR, we deduce that our sample becomes incomplete for
lower CR values (the same approach was used by
Zickgraf et al. 1997). Therefore, we assume the CR peak values as our
completeness limit. In all the pointings of the 3EG J0616-3310 error
box, the source count-rate distributions in the low (0.5-2 keV)
energy range are pretty similar, with peaks at
![]() ;
on the other hand, there are some differences among the distributions of 3EG J1249-8330. The marginal differences in the
count-rate distributions between the pointings of the two EGRET sources are an obvious effect of the larger
hydrogen column density. On the other hand, the count-rate
distributions in the high energy range (2-10 keV) are significantly
different, with peaks at
;
on the other hand, there are some differences among the distributions of 3EG J1249-8330. The marginal differences in the
count-rate distributions between the pointings of the two EGRET sources are an obvious effect of the larger
hydrogen column density. On the other hand, the count-rate
distributions in the high energy range (2-10 keV) are significantly
different, with peaks at
![]() .
.
![\begin{figure}
\par\includegraphics[angle=-90,width=6.3cm,clip]{5247f3a.ps}\hspace*{4mm}
\includegraphics[angle=-90,width=6.3cm,clip]{5247f3b.ps}
\end{figure}](/articles/aa/full/2006/40/aa5247-06/Timg42.gif) |
Figure 3:
Histograms of the source count-rate distributions for each
EPIC pointing of the error box of 3EG J0616-3310 (left, N1-N4)
and 3EG J1249-8330 (right, N5-N8), in the energy ranges 0.5-2 keV (red
line) and 2-10 keV (blue line). For observation 7 the distribution
peaks at higher count rate (
|
| Open with DEXTER | |
The histograms of the source signal-to-noise (S/N) distribution in the whole
energy range are reported in Fig. 4 for all the
pointings of the two EGRET error boxes. The two distributions peak
between 4.5 and 5.5, with only a few sources at
![]() .
.
Since the count statistics (usually a few tens of photons) of the
detected sources is too low to produce significant spectra, we have
performed a qualitative spectral analysis using the CR
measured in the seven energy ranges defined above to compute four
different Hardness Ratios (HRs):
![\begin{figure}
\par\includegraphics[angle=-90,width=6.3cm,clip]{5247f4a.ps}\hspace*{4mm}
\includegraphics[angle=-90,width=6.3cm,clip]{5247f4b.ps}
\end{figure}](/articles/aa/full/2006/40/aa5247-06/Timg50.gif) |
Figure 4: Histogram of the source S/N distribution for the 3EG J0616-3310 (left, N1-N4) and 3EG J1249-8330 (right, N5-N8) fields. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=6.3cm,clip]{5247f5a.ps}\hspace*{4mm}
\includegraphics[angle=-90,width=6.3cm,clip]{5247f5b.ps}
\end{figure}](/articles/aa/full/2006/40/aa5247-06/Timg51.gif) |
Figure 5:
Histograms of the HR distributions for sources in the 3EG J0616-3310 (left) and 3EG J1249-8330 (right) error boxes. Green bars
indicate the expected HRs computed for thermal bremsstrahlung
spectra with kT = 0.5, 1, 2 and 5 keV ( from left to right). Magenta bars
indicate the expected HRs computed for power-law spectra with
|
| Open with DEXTER | |
To obtain a further indication on
the sources spectra, we compared the measured HRs with the expected
ones computed for two different template spectral models
(Giacconi et al. 2001; Barcons et al. 2002), namely: a thermal bremsstrahlung,
with temperatures kT increasing from 0.5 (left) to 5 keV (right), and a power-law, with photon indexes ![]() increasing from 1 (right) to 2.5 (left). In such a way we could identify the spectral model
more appropriate for a given source and tentatively assign its most
likely spectral parameters. The values of the expected HRs are
overplotted as vertical bars in Fig. 5. As can be seen, the
distributions are compatible with a rather wide range of temperatures
and photon indexes, thus suggesting that we are indeed sampling
different types of sources. This conclusion is not surprising, since
the two areas are at medium galactic latitude and therefore are
expected to contain both galactic and extragalactic X-ray sources.
increasing from 1 (right) to 2.5 (left). In such a way we could identify the spectral model
more appropriate for a given source and tentatively assign its most
likely spectral parameters. The values of the expected HRs are
overplotted as vertical bars in Fig. 5. As can be seen, the
distributions are compatible with a rather wide range of temperatures
and photon indexes, thus suggesting that we are indeed sampling
different types of sources. This conclusion is not surprising, since
the two areas are at medium galactic latitude and therefore are
expected to contain both galactic and extragalactic X-ray sources.
In order to compute the source fluxes, we assumed a template power-law spectrum with average photon index
![]() .
For each
pointing, we estimated the hydrogen column density
.
For each
pointing, we estimated the hydrogen column density ![]() (see
Table 1) from the relation
(see
Table 1) from the relation
![]() cm-2 (Zombeck 1990) using the average
colour excess E(B-V) derived from the dust maps developed
by Schlegel et al. (1998). Following the procedure used by
Baldi et al. (2002), count-rate-to-flux convertion factors (CF) were computed for the PN and the MOS cameras
individually using their updated response matrices and then combined
with the effective exposure times of each pointing to derive the total conversion factor CF. For each pointing and for each
energy range we used the exposure maps of each camera and the
background map of the merged image to compute the flux limit
map, which gives, at each celestial coordinate, the minimum flux of a
source in order to be detected with a probability
cm-2 (Zombeck 1990) using the average
colour excess E(B-V) derived from the dust maps developed
by Schlegel et al. (1998). Following the procedure used by
Baldi et al. (2002), count-rate-to-flux convertion factors (CF) were computed for the PN and the MOS cameras
individually using their updated response matrices and then combined
with the effective exposure times of each pointing to derive the total conversion factor CF. For each pointing and for each
energy range we used the exposure maps of each camera and the
background map of the merged image to compute the flux limit
map, which gives, at each celestial coordinate, the minimum flux of a
source in order to be detected with a probability
![]() (Baldi et al. 2002). Then, we used the flux limit maps to derive the
total sky coverage of both EGRET error boxes. These are shown
in Fig. 6, in the two standard soft (0.5-2 keV) and hard (2-10 keV) energy bands.
(Baldi et al. 2002). Then, we used the flux limit maps to derive the
total sky coverage of both EGRET error boxes. These are shown
in Fig. 6, in the two standard soft (0.5-2 keV) and hard (2-10 keV) energy bands.
Figure 7 shows the cumulative log N-log S distributions of the sources detected in the two energy ranges 0.5-2 and 2-10 keV. For comparison, we overplotted the lower and upper limits of the same distributions as measured at high galactic latitude, where only extragalactic sources are expected to contribute (Baldi et al. 2002). In both cases our source density is above the upper limit of the high latitude distribution, expecially in the soft energy band and at low fluxes. This result points to a significant excess of galactic sources, whose fraction is larger at softer energies and lower fluxes.
![\begin{figure}
\par\includegraphics[angle=-90,width=6.1cm,clip]{5247f6a.ps}\hspace*{4mm}
\includegraphics[angle=-90,width=6.1cm,clip]{5247f6b.ps}\end{figure}](/articles/aa/full/2006/40/aa5247-06/Timg56.gif) |
Figure 6: The total sky coverage of the EPIC observations of the 3EG J0616-3310 (left) and 3EG J1249-8330 (right) error boxes, in the energy bands 0.5-2 keV (red line) and 2-10 keV (blue line). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=6.1cm,clip]{5247f7a.ps}\hspace*{4mm}
\includegraphics[angle=-90,width=6.1cm,clip]{5247f7b.ps}\end{figure}](/articles/aa/full/2006/40/aa5247-06/Timg57.gif) |
Figure 7: Cumulative log N-log S distribution of the sources detected in the EPIC observations of the 3EG J0616-3310 (left) and 3EG J1249-8330 (right) error boxes, in the energy bands 0.5-2 keV (red squares) and 2-10 keV (blue dots). For comparison, in both diagrams we also show the lower and upper limits of the high latitude log N-log S in the energy ranges 0.5-2 keV (red solid lines) and 2-10 keV (blue dashed lines). |
| Open with DEXTER | |
In order to search for the optical counterparts of our X-ray sources,
we used the Wide Field Imager
(WFI)![]() mounted
at the 2.2 m ESO/MPG telescope at La Silla (Chile), where we collected
data under programme ID 68.D-0478. The WFI is a wide field
mosaic camera, composed of eight
mounted
at the 2.2 m ESO/MPG telescope at La Silla (Chile), where we collected
data under programme ID 68.D-0478. The WFI is a wide field
mosaic camera, composed of eight
![]() pixel CCDs, with a
scale of
pixel CCDs, with a
scale of
![]() /pixel and a full field of view of
/pixel and a full field of view of
![]() .
As it matches very well the diameter of
XMM-Newton/EPIC field of view (
.
As it matches very well the diameter of
XMM-Newton/EPIC field of view (![]() 30 arcmin), WFI can
provide a complete coverage of the targets' area with a minimum number
of pointings. Observations in the filters U(877), B (842), V
(843),
R (844) and I
(845)
30 arcmin), WFI can
provide a complete coverage of the targets' area with a minimum number
of pointings. Observations in the filters U(877), B (842), V
(843),
R (844) and I
(845)![]() were requested in order to maximize the optical spectral coverage and
to optimise the objects classification in the colour space. To
compensate for the interchip gaps, for each passband the pointings
were split in sequences of five dithered exposures with shifts of 35'' and 21'' in RA and Dec, respectively. Observations were
performed in Service Mode between December 2001 and March 2002.
Unfortunately, bad weather conditions as well as scheduling problems
resulted in a highly incomplete and inhomogeneous dataset and in a
data quality in some cases far from optimal. In particular, only four
of the eight XMM-Newton fields were covered by the WFI,
i.e. fields 2, 3 and 4 of the 3EG J0616-3310 error box and field 8 of
the 3EG J1249-8330 error box (see Table 3 for a
summary of the observations).
were requested in order to maximize the optical spectral coverage and
to optimise the objects classification in the colour space. To
compensate for the interchip gaps, for each passband the pointings
were split in sequences of five dithered exposures with shifts of 35'' and 21'' in RA and Dec, respectively. Observations were
performed in Service Mode between December 2001 and March 2002.
Unfortunately, bad weather conditions as well as scheduling problems
resulted in a highly incomplete and inhomogeneous dataset and in a
data quality in some cases far from optimal. In particular, only four
of the eight XMM-Newton fields were covered by the WFI,
i.e. fields 2, 3 and 4 of the 3EG J0616-3310 error box and field 8 of
the 3EG J1249-8330 error box (see Table 3 for a
summary of the observations).
The data reduction was performed with a pre-release version of THELI, a fully automatic pipeline for the reduction of optical and near-IR imaging data obtained with single- or multi-chip cameras. A detailed description of this pipeline and the algorithms used can be found in Schirmer et al. (2003) and in Erben et al. (2005). Here we describe only the steps relevant for the the WFI multi-chip detector, such as astrometric and photometric calibration, image dedithering and coaddition. All pre-processing steps (debiasing, flat fielding, superflatting etc.) are similar to those performed with single chip cameras.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{5247fig8CMJN.eps}\end{figure}](/articles/aa/full/2006/40/aa5247-06/Timg61.gif) |
Figure 8: Composite BVR image (B = blue; V = green; R = red) of field 4 taken with WFI at the ESO/MPG 2.2 m telescope. |
| Open with DEXTER | |
The astrometric solution was performed in several steps. First, for
each CCD chip pre-processed image we run the
SExtractor object detection algorithm
(Bertin & Arnouts 1996) to generate a catalogue which contained high
S/N (DETECT_MINAREA = 10, DETECT_THRESH = 10) non saturated objects.
Objects classified as stars according to the SExtractor
parameters were then matched, using the crude WFI pointing
astrometric solution, with the USNO-A2 astrometric catalogue which
has a nominal intrinsic absolute astrometric accuracy of ![]()
![]()
![]() .
.
Thereafter, for each chip all the detected objects within the
overlapping regions of the dithering pattern were cross-matched and
the results were piped into two ![]() minimisation routines. The
first one fits two dimensional third order polynomials to the optical
distortion of each chip, whereas the second one determines the
relative photometric zeropoint with respect to all other chips. The
final image coaddition was performed chip by chip using as a reference
the computed chip distorsion maps and the relative chip flux
normalization.
minimisation routines. The
first one fits two dimensional third order polynomials to the optical
distortion of each chip, whereas the second one determines the
relative photometric zeropoint with respect to all other chips. The
final image coaddition was performed chip by chip using as a reference
the computed chip distorsion maps and the relative chip flux
normalization.
Before performing this step, individual weight maps were created for
each exposure, based on normalized skyflats. The detection of defect
pixels was performed on the individual chips by means of
SExtractor and Eye![]() .
Those pixels were then set to zero in the weight map. Thereafter, the
sky background was modelled and subtracted, and the chips were
resampled and coadded by means of the IRAF
EISdrizzle routine, using the weight maps created previously.
The registration of the individual chips was accurate within
.
Those pixels were then set to zero in the weight map. Thereafter, the
sky background was modelled and subtracted, and the chips were
resampled and coadded by means of the IRAF
EISdrizzle routine, using the weight maps created previously.
The registration of the individual chips was accurate within ![]() 1/10th of a pixel (
1/10th of a pixel (
![]() ), so that we did not introduce any
artificial decrease of the image quality. After mosaicing, the final
image was associated with its corresponding weight map, containing
information on how long each pixel has been exposed. This is
particular useful since, due to the dithering pattern and the gaps
between the CCDs, the total exposure time in the coadded image was
highly inhomogeneous. Using the method described above, we could
assign to the coadded mosaic a consistent global astrometric solution
accurate within
), so that we did not introduce any
artificial decrease of the image quality. After mosaicing, the final
image was associated with its corresponding weight map, containing
information on how long each pixel has been exposed. This is
particular useful since, due to the dithering pattern and the gaps
between the CCDs, the total exposure time in the coadded image was
highly inhomogeneous. Using the method described above, we could
assign to the coadded mosaic a consistent global astrometric solution
accurate within
![]() and a relative photometric zeropoint
costant within
and a relative photometric zeropoint
costant within ![]() 0.05 mag.
0.05 mag.
Figure 8 shows as example a composite WFI image of field 4 obtained after co-adding the single-passband BVR reduced images.
Table 3: Summary of the optical observations performed by the Wide Field Imager of the 2.2 m MPG/ESO telescope at La Silla.
Table 4:
Limiting magnitudes (3![]() )
of our multiband
optical-to-IR photometry.
)
of our multiband
optical-to-IR photometry. ![]() values are derived either from the
WFI observations or, when not available, from the
GSC-2.3 BJ,F,N equivalent (in italics). JHK values
are taken from 2MASS. An hyphen indicates that no measurements
are available. The last column lists the total number of
objects per pointing after matching over all the passbands.
values are derived either from the
WFI observations or, when not available, from the
GSC-2.3 BJ,F,N equivalent (in italics). JHK values
are taken from 2MASS. An hyphen indicates that no measurements
are available. The last column lists the total number of
objects per pointing after matching over all the passbands.
Source extraction was performed by SExtractor on the final co-added images using the previously created weight maps to properly account for the varying depths of the mosaics. Our parameter combination (DETECT_THRESH = 2.0 and DETECT_MINAREA = 8 pixels) turned out to be the optimal one as it maximizes the number of detections yielding little contamination by spurious objects, located around saturated stars. For uniformity reasons, we applied the same values for all catalogues. Even thought the detection threshhold is admittedly low, we decided to use this value in order to provide candidate optical counterparts for as many X-ray sources as possible. The extracted catalogues were overlayed on the images and the counterparts were visually inspected. The percentage of spurious objects at the images' borders was less than 1%.
Table 5: Results of the cross-correlations between the list of X-ray sources and the optical/IR master catalogues. For all fields, the total number of candidate counterparts is larger than those of the X-ray sources because of multiple matches.
Since a very high photometric accuracy is not critical for the
purpose of this work, default zeropoints provided by the WFI
science operation team![]() were used for the photometric calibration. The adopted zeropoints (in
the Vega magnitude system) are 21.96, 24.53, 24.12, 24.43 and 23.37
for the U, B, V, R, and I filters, respectively.
were used for the photometric calibration. The adopted zeropoints (in
the Vega magnitude system) are 21.96, 24.53, 24.12, 24.43 and 23.37
for the U, B, V, R, and I filters, respectively.
Since the optical coverage of the two fields performed with the WFI is not complete, both in terms of sky and passband (see Table 3), we have complemented our dataset using a, yet
unpublished, version of the Guide Star Catalogue 2 (GSC-2.3) which provides photometry in the BJ, F and Npassbands, overlapping the Johnson's B, R, and I![]() , down to 3
, down to 3![]() limiting magnitudes of
limiting magnitudes of
![]() ,
,
![]() and
and
![]() ,
with average errors of
,
with average errors of ![]() 0.25 (at
0.25 (at
![]() ). In addition, to extend our passband coverage
to the near-IR, we have used the Two Micron All Sky Survey
(2MASS) catalogue (Cutri et al. 2003), which provides photometry in the J (1.25
). In addition, to extend our passband coverage
to the near-IR, we have used the Two Micron All Sky Survey
(2MASS) catalogue (Cutri et al. 2003), which provides photometry in the J (1.25![]() ), H (1.65
), H (1.65![]() )
and K (2.65
)
and K (2.65![]() )
passbands down
to limiting magnitudes of 15.8, 15.1 and 14.3, respectively.
)
passbands down
to limiting magnitudes of 15.8, 15.1 and 14.3, respectively.
We then cross-correlated all the available catalogues (WFI, GSC-2.3 and 2MASS) to produce master optical-to-IR catalogues
for each of the eight fields. The four WFI catalogues (relative
to fields 2, 3, 4 and 8) were cross-correlated in turn with both the
2MASS Point Source and Extended Source Catalogues through the
Gator www
interface![]() .
Then, the two output catalogues were merged and cross-correlated with
the GSC-2.3. For the
remaining fields, we extracted the corresponding object catalogues
from the GSC-2.3 through the same interface and we
cross-correlated them with both the 2MASS Point Source and
Extended Source Catalogues using Gator. In all cases, we used a
fixed cross-correlation radius of 1 arcsec which largely accounts for
the uncertainty in the absolute astrometric calibrations of the WFI catalogues (
.
Then, the two output catalogues were merged and cross-correlated with
the GSC-2.3. For the
remaining fields, we extracted the corresponding object catalogues
from the GSC-2.3 through the same interface and we
cross-correlated them with both the 2MASS Point Source and
Extended Source Catalogues using Gator. In all cases, we used a
fixed cross-correlation radius of 1 arcsec which largely accounts for
the uncertainty in the absolute astrometric calibrations of the WFI catalogues (![]()
![]() ), of the GSC-2.3 (
), of the GSC-2.3 (![]()
![]()
![]() )
and 2MASS (
)
and 2MASS (![]()
![]()
![]() ).
The final colour coverage for each of the eight fields is summarized
in Table 4, together with the estimated limiting
magnitude in each passband and the total number of single objects
extracted from the optical-to-IR master catalogues. The same
catalogues are also used for a multi-colour analysis aimed at the
characterization of the stellar/galactic populations in the fields
(Hatziminaoglou et al., in preparation).
).
The final colour coverage for each of the eight fields is summarized
in Table 4, together with the estimated limiting
magnitude in each passband and the total number of single objects
extracted from the optical-to-IR master catalogues. The same
catalogues are also used for a multi-colour analysis aimed at the
characterization of the stellar/galactic populations in the fields
(Hatziminaoglou et al., in preparation).
Since the absolute coordinate accuracy
of XMM-Newton is ![]() 5'' (Kirsch et al. 2004), i.e. a factor 10 worse than the astrometric accuracy (
5'' (Kirsch et al. 2004), i.e. a factor 10 worse than the astrometric accuracy (![]()
![]() )
of our
optical/IR data, we first tried to
improve the accuracy of the X-ray coordinates.
After overlaying the X-ray positions on the Digital Sky Survey images, we found few X-ray sources which could
be confidently associated with a single bright optical object and we
assumed the optical positions as the true ones. Then, using the IRAF task geomap, we calculated the correction to be applied to
the X-ray coordinates (value always
)
of our
optical/IR data, we first tried to
improve the accuracy of the X-ray coordinates.
After overlaying the X-ray positions on the Digital Sky Survey images, we found few X-ray sources which could
be confidently associated with a single bright optical object and we
assumed the optical positions as the true ones. Then, using the IRAF task geomap, we calculated the correction to be applied to
the X-ray coordinates (value always ![]() 2'') and we applied it to
all the remaining X-ray sources using the IRAF task geoxytran. In the following, we decided to use a conservative value
of 5'' (i.e.
2'') and we applied it to
all the remaining X-ray sources using the IRAF task geoxytran. In the following, we decided to use a conservative value
of 5'' (i.e. ![]() 3 times our astrometric correction) for the
cross-correlation radius.
3 times our astrometric correction) for the
cross-correlation radius.
In Table 5 we report, for each XMM-Newton
field, the number of X-ray sources with and without candidate
optical/IR counterparts, as well as the total number of candidate
counterparts. It is evident that the results of the
cross-correlations are significantly different for the different
fields, depending on the varying limiting magnitude of the optical
coverage (see Table 4). For instance, for most X-ray
sources of fields 1 and 5-7 we found no candidate counterpart within 5'', owing to the limiting flux of GSC-2.3 which is, on average, a
factor 6 shallower in flux than the WFI catalogues. Indeed, the
fraction of X-ray sources without candidate counterparts decreases
drastically for fields 2-4. This is particularly true for field 4,
probably due to its short X-ray effective exposure time (see Table 1) which results in the detection of only relatively
bright X-ray sources, with presumably brighter optical counterparts.
Conversely, the longer X-ray effective exposure time of field 8 results in the detection of fainter
X-ray sources, presumably characterized by fainter optical
counterparts.
![\begin{figure}
\par\includegraphics[width=6.2cm,angle=-90,clip]{5247f9a.ps}\hspace*{4mm}
\includegraphics[width=6.2cm,angle=-90,clip]{5247f9b.ps}
\end{figure}](/articles/aa/full/2006/40/aa5247-06/Timg76.gif) |
Figure 9:
X-ray-to-optical flux ratios
|
| Open with DEXTER | |
The cross-correlation between X-ray and optical catalogues is
obviously affected by spurious matches. In order to estimate it, we
computed from the optical/IR master catalogues the total number of
objects within the areas encompassed by each XMM-Newton fields.
Then, we used the relation
![]() ,
where r is the
X-ray error circle radius (5'') and
,
where r is the
X-ray error circle radius (5'') and ![]() is the
surface density of the optical objects (per square degree), to obtain the chance coincidence
probability between an X-ray and an optical object
(Severgnini et al. 2005). By assuming an X-ray error circle of 5'',
for each observation we estimated the probability P to vary between 16 and 30% over all the eight fields (see Table 5),
which means that, at our limiting magnitudes, contamination effects
cannot be ignored in the evaluation of the candidate counterparts.
is the
surface density of the optical objects (per square degree), to obtain the chance coincidence
probability between an X-ray and an optical object
(Severgnini et al. 2005). By assuming an X-ray error circle of 5'',
for each observation we estimated the probability P to vary between 16 and 30% over all the eight fields (see Table 5),
which means that, at our limiting magnitudes, contamination effects
cannot be ignored in the evaluation of the candidate counterparts.
All X-ray sources were also cross-correlated with radio catalogues, namely:
Table 6:
Range of the expected
![]() flux ratios (min/max value in
logarithmic units) for the different object classes and EPIC fields. The X-ray fluxes
refer to the full XMM-Newton energy range (0.3-10 keV), while
the optical fluxes refer to the Johnson's B ( top) and V ( middle)
bands and to the Bj band ( bottom). For each source class the slight differences in the
flux ratios (min/max value in
logarithmic units) for the different object classes and EPIC fields. The X-ray fluxes
refer to the full XMM-Newton energy range (0.3-10 keV), while
the optical fluxes refer to the Johnson's B ( top) and V ( middle)
bands and to the Bj band ( bottom). For each source class the slight differences in the
![]() values are due to the different
values are due to the different ![]() of the various EPIC fields, which affects the count-rate-to-flux conversion factor.
of the various EPIC fields, which affects the count-rate-to-flux conversion factor.
Observations performed with several X-ray missions have shown that
different classes of X-ray emitters have different, rather narrow,
ranges of X-ray-to-optical flux ratios
![]() (Stocke et al. 1991; Krautter et al. 1999). In particular, such a ratio is very
high (i.e.
(Stocke et al. 1991; Krautter et al. 1999). In particular, such a ratio is very
high (i.e. ![]() 1000) for INSs while it is lower for all the other
classes of X-ray sources, with no, or small, overlapping between the
respective range of values. Therefore, we can use this parameter in
order to reject or retain an X-ray source as a candidate INS. For the
1000) for INSs while it is lower for all the other
classes of X-ray sources, with no, or small, overlapping between the
respective range of values. Therefore, we can use this parameter in
order to reject or retain an X-ray source as a candidate INS. For the
![]() values we considered the results of the Hamburg/ROSAT All Sky Survey (Zickgraf et al. 2003), which provides the
typical range of values for each class of celestial sources, as a
"reference'' classification scheme. We considered the same objects
classes, i.e. white dwarfs (WD), cataclysmic variables (CV), galaxies (G), cluster of galaxies (CG) and active galactic nuclei (AGN).
Moreover, we considered stars as a single class (S). In the Hamburg/RASS the X-ray flux is calculated in the ROSAT energy
range 0.1-2.4 keV, assuming a "typical'' spectral shape for each class
of sources, while the optical flux is based on their B magnitude.
values we considered the results of the Hamburg/ROSAT All Sky Survey (Zickgraf et al. 2003), which provides the
typical range of values for each class of celestial sources, as a
"reference'' classification scheme. We considered the same objects
classes, i.e. white dwarfs (WD), cataclysmic variables (CV), galaxies (G), cluster of galaxies (CG) and active galactic nuclei (AGN).
Moreover, we considered stars as a single class (S). In the Hamburg/RASS the X-ray flux is calculated in the ROSAT energy
range 0.1-2.4 keV, assuming a "typical'' spectral shape for each class
of sources, while the optical flux is based on their B magnitude.
In our case we calculated the source flux in the XMM-Newton
energy range 0.3-10 keV, and assumed a common emission model for all
sources (a power-law with photon index
![]() and galactic
column density). Moreover, as shown in the previous section, the
passband coverage of the WFI observations is incomplete, with
only V available in all fields (see Table 4) for 90 candidate counterparts (
and galactic
column density). Moreover, as shown in the previous section, the
passband coverage of the WFI observations is incomplete, with
only V available in all fields (see Table 4) for 90 candidate counterparts (![]() 70% of the total). However, for
fields 2 and 4 the B band limiting is deeper than the V band one
probably owing to the large QE of the detector. Therefore, to define
our classification scheme, we decided to compute the measured
70% of the total). However, for
fields 2 and 4 the B band limiting is deeper than the V band one
probably owing to the large QE of the detector. Therefore, to define
our classification scheme, we decided to compute the measured
![]() ratio for both the B and V bands, while, for
candidate counterparts with only GSC-2.3 photometry, the
ratio for both the B and V bands, while, for
candidate counterparts with only GSC-2.3 photometry, the
![]() ratio was computed from the BJ magnitude.
ratio was computed from the BJ magnitude.
Moreover, for each class of sources we had to correct the
![]() ratio found in the Hamburg/RASS by accounting for
the XMM-Newton detection band, the different assumed spectral
models and the different optical filter. To this aim, we have devised a
procedure which is described in the Appendix A. The computed
ratio found in the Hamburg/RASS by accounting for
the XMM-Newton detection band, the different assumed spectral
models and the different optical filter. To this aim, we have devised a
procedure which is described in the Appendix A. The computed
![]() ranges, relative to the B, Vand BJ passbands, for the different classes of X-ray sources are
listed in Table 6. The reported values are in rough agreement with the results obtained by Krautter et al. (1999) and by Zickgraf et al. (2003), except for the WD class. In this case, the discrepancy is due to the correction applied to the Hamburg-RASS flux ratio in order to obtain the corresponding XMM-Newton one. In
fact, in the first case a very soft blackbody spectrum (
T = 50 000 K) was
adopted, while we consider a rather hard (
ranges, relative to the B, Vand BJ passbands, for the different classes of X-ray sources are
listed in Table 6. The reported values are in rough agreement with the results obtained by Krautter et al. (1999) and by Zickgraf et al. (2003), except for the WD class. In this case, the discrepancy is due to the correction applied to the Hamburg-RASS flux ratio in order to obtain the corresponding XMM-Newton one. In
fact, in the first case a very soft blackbody spectrum (
T = 50 000 K) was
adopted, while we consider a rather hard (
![]() ), less realistic
power-law spectrum; moreover, the ROSAT energy range (0.1-2.4 keV) is
very suitable for the WD detection, which is not the case for the considered
XMM-Newton one (0.3-10 keV). Both the items imply that, if the count rate of a
WD is high enough to be detected by XMM-Newton, we would assign it an unrealistic
large flux.
), less realistic
power-law spectrum; moreover, the ROSAT energy range (0.1-2.4 keV) is
very suitable for the WD detection, which is not the case for the considered
XMM-Newton one (0.3-10 keV). Both the items imply that, if the count rate of a
WD is high enough to be detected by XMM-Newton, we would assign it an unrealistic
large flux.
Table 7:
Main characteristics of the X-ray sources with no candidate optical counterpart and
![]() .
.
The values of X-ray-to-optical flux ratios
![]() for
all X-ray sources are shown in Fig. 9 for all the
available optical passbands. When a single X-ray source has more than one candidate counterpart, we report the
for
all X-ray sources are shown in Fig. 9 for all the
available optical passbands. When a single X-ray source has more than one candidate counterpart, we report the
![]() value computed for each candidate counterpart. In the case of X-ray sources with no optical counterpart, we estimated the lower limits on the
value computed for each candidate counterpart. In the case of X-ray sources with no optical counterpart, we estimated the lower limits on the
![]() ratio from the limiting magnitudes of the different
fields (see Table 4). Thus, we assumed limiting
magnitudes V = 24.7 for fields 2-4 and V = 24.3 for field 8 while for
fields 1 and 5-7 we assumed a limiting magnitude of
BJ = 23.
ratio from the limiting magnitudes of the different
fields (see Table 4). Thus, we assumed limiting
magnitudes V = 24.7 for fields 2-4 and V = 24.3 for field 8 while for
fields 1 and 5-7 we assumed a limiting magnitude of
BJ = 23.
The systematic optical identification of all X-ray sources listed in
our catalogue will be presented in detail in a future paper (La
Palombara et al., in preparation). However, on the basis of our
X-ray-to-optical flux ratio classification scheme (see Table 6), it is very likely that sources with
![]() are stars. The
maximum value measured for
are stars. The
maximum value measured for
![]() is
is ![]() 1.9 for sources with a WFI candidate counterpart (fields 2-4 and 8) and
1.9 for sources with a WFI candidate counterpart (fields 2-4 and 8) and ![]() 1.2 for those with a candidate GSC
counterpart (pontings 1 and 5-7). These values are fully compatible
with those typical of various classes of X-ray sources,
especially the extragalactic ones (AGN or cluster of galaxies).
Therefore, if we assume that all the above X-ray sources are indeed
indentified with one of their putative optical counterparts, no matter
which one, none of them can be considered a likely INS. Of course, at this
stage we can not exclude a priori the possibility that
some of the candidate optical counterparts are
just unrelated field objects. In this case, the X-ray sources
would turn out to be unidentified and
their corresponding
1.2 for those with a candidate GSC
counterpart (pontings 1 and 5-7). These values are fully compatible
with those typical of various classes of X-ray sources,
especially the extragalactic ones (AGN or cluster of galaxies).
Therefore, if we assume that all the above X-ray sources are indeed
indentified with one of their putative optical counterparts, no matter
which one, none of them can be considered a likely INS. Of course, at this
stage we can not exclude a priori the possibility that
some of the candidate optical counterparts are
just unrelated field objects. In this case, the X-ray sources
would turn out to be unidentified and
their corresponding
![]() would increase,
moving nearer to INS values. Overlooked INS candidates will be
pinpointed after the systematic X-ray optical identification work, now
in progress (La Palombara et al., in preparation).
would increase,
moving nearer to INS values. Overlooked INS candidates will be
pinpointed after the systematic X-ray optical identification work, now
in progress (La Palombara et al., in preparation).
As a first step we decided to perform a selection within our sample by
considering only the 125 X-ray sources with no candidate optical
counterpart. To pinpoint more robust INS candidates we have to
select those sources which have the highest value of the
X-ray-to-optical flux ratio and, possibly, are characterized by a
soft X-ray spectrum, and thus might be associated to Geminga-like
neutron stars. According to Table 6, all the typical classes of X-ray sources are
characterized by
![]() ,
since only the brightest extragalactic sources can exceed this flux ratio level (due to the problems described in Sect. 6, we ignore the case of the WDs). Therefore,
we have decided to use
,
since only the brightest extragalactic sources can exceed this flux ratio level (due to the problems described in Sect. 6, we ignore the case of the WDs). Therefore,
we have decided to use
![]() as a threshold value and to select the sources whose flux ratio, taking into account also the relevant uncertainties, approaches to this value. In this way we can reject all the galactic sources, almost all the galaxies and clusters of galaxies and most of the AGNs. This selection limits our sample to 9 sources. For illustration purposes, Fig. 10 shows the
positions of these sources overlaied on the WFI V-band
images.
The main characteristics of these sources are summarized in
Table 7 where, for each source, we list the detection
energy bands, its flux and the corresponding X-ray-to-optical ratio
lower limit. We also report the more likely spectral parameters
derived by comparing the source HRs with different template
spectral models, namely: a thermal bremsstrahlung, with
temperatures
as a threshold value and to select the sources whose flux ratio, taking into account also the relevant uncertainties, approaches to this value. In this way we can reject all the galactic sources, almost all the galaxies and clusters of galaxies and most of the AGNs. This selection limits our sample to 9 sources. For illustration purposes, Fig. 10 shows the
positions of these sources overlaied on the WFI V-band
images.
The main characteristics of these sources are summarized in
Table 7 where, for each source, we list the detection
energy bands, its flux and the corresponding X-ray-to-optical ratio
lower limit. We also report the more likely spectral parameters
derived by comparing the source HRs with different template
spectral models, namely: a thermal bremsstrahlung, with
temperatures
![]() ,
1, 2 and 5 keV; a blackbody,
with temperatures
,
1, 2 and 5 keV; a blackbody,
with temperatures
![]() ,
0.1, 0.2 and 0.5 keV; a
power-law, with photon index
,
0.1, 0.2 and 0.5 keV; a
power-law, with photon index
![]() .
.
As it is seen from Table 7, we have singled out 8 INS
candidate counterparts associated to 3EG J0616-3310. While all of
them are potential candidates, XMMU J061807.6-331237 is certainly
more interesting as it meets both our selection criteria, since it is
characterized both by a relatively high X-ray-to-optical flux
ratio (>
![]() )
and by a soft emission spectrum (it is
detected only below 1 keV). Therefore this source appears a
promising candidates for a Geminga-like INS. On the other hand, XMMU J061429.8-333225 and XMMU J061450.2-331501, which are both detected
in EPIC field #3, stand out as the only sources with an
X-ray-to-optical flux ratio clearly greater than 2 (>
)
and by a soft emission spectrum (it is
detected only below 1 keV). Therefore this source appears a
promising candidates for a Geminga-like INS. On the other hand, XMMU J061429.8-333225 and XMMU J061450.2-331501, which are both detected
in EPIC field #3, stand out as the only sources with an
X-ray-to-optical flux ratio clearly greater than 2 (>
![]() and >
and >
![]() ,
respectively). However, both sources
are detected up to 2 keV while they are not seen below 0.5 keV. As a
result, their hardness ratios correspond to a thermal
blackbody temperature greater than 0.2 keV or to a
power-law photon index
,
respectively). However, both sources
are detected up to 2 keV while they are not seen below 0.5 keV. As a
result, their hardness ratios correspond to a thermal
blackbody temperature greater than 0.2 keV or to a
power-law photon index
![]() .
These values
would point towards younger objects than Geminga-like INSs. Indeed,
Becker & Trümper (1997) have shown that the power-law components of
X-ray detected INSs have average photon index of
.
These values
would point towards younger objects than Geminga-like INSs. Indeed,
Becker & Trümper (1997) have shown that the power-law components of
X-ray detected INSs have average photon index of ![]() 1.9,
compatible with those estimated for sources XMMU J061429.8-333225 and
XMMU J061450.2-331501. Thus, we consider XMMU J061807.6-331237, XMMU J061429.8-333225 and XMMU J061450.2-331501 our best INS candidate counterparts to 3EG J0616-3310. Owing to the shallower optical
coverage of the 3EG J1249-8330 error box (see Table 4), we could single out only one possible INS candidate
counterpart (XMMU J124642.5-832212). The X-ray spectral parameters of
this source are unconstrained but they suggest a rather hard thermal
spectrum which would not be compatible either with a Geminga-like or
with a young INSs. However, the X-ray-to-optical flux ratio of
this source (>
1.9,
compatible with those estimated for sources XMMU J061429.8-333225 and
XMMU J061450.2-331501. Thus, we consider XMMU J061807.6-331237, XMMU J061429.8-333225 and XMMU J061450.2-331501 our best INS candidate counterparts to 3EG J0616-3310. Owing to the shallower optical
coverage of the 3EG J1249-8330 error box (see Table 4), we could single out only one possible INS candidate
counterpart (XMMU J124642.5-832212). The X-ray spectral parameters of
this source are unconstrained but they suggest a rather hard thermal
spectrum which would not be compatible either with a Geminga-like or
with a young INSs. However, the X-ray-to-optical flux ratio of
this source (>
![]() ), similar to the one of XMMU J061807.6-331237, still makes it a possible INS candidate.
), similar to the one of XMMU J061807.6-331237, still makes it a possible INS candidate.
Identifying high-energy ![]() -ray sources is a difficult and
time-consuming task, owing primarily to the dimension of the error
boxes that have to be covered at different wavelengths. We have
developed a semiautomatic procedure, encompassing ad-hoc
X-ray space observations as well as optical ground based ones, aimed
at finding high
-ray sources is a difficult and
time-consuming task, owing primarily to the dimension of the error
boxes that have to be covered at different wavelengths. We have
developed a semiautomatic procedure, encompassing ad-hoc
X-ray space observations as well as optical ground based ones, aimed
at finding high
![]() candidate counterparts and we
have applied it to two middle latitude EGRET sources. We have
mapped the error boxes of 3EG J0616-3310 and 3EG J1249-8330 with
eight 10 ks XMM-Newton pointings and we have detected about 300 X-ray sources between 0.3 and 10 keV, down to flux limits of
candidate counterparts and we
have applied it to two middle latitude EGRET sources. We have
mapped the error boxes of 3EG J0616-3310 and 3EG J1249-8330 with
eight 10 ks XMM-Newton pointings and we have detected about 300 X-ray sources between 0.3 and 10 keV, down to flux limits of ![]()
![]() and
and ![]()
![]() erg cm-2 s-1in the energy ranges 0.5-2 and 2-10 keV, respectively. Four of the
eight XMM-Newton pointings have been covered in the optical
with the Wide Field Imager (WFI) at the 2.2 m MPG/ESO
telescope (La Silla) down to a limiting magnitude of
erg cm-2 s-1in the energy ranges 0.5-2 and 2-10 keV, respectively. Four of the
eight XMM-Newton pointings have been covered in the optical
with the Wide Field Imager (WFI) at the 2.2 m MPG/ESO
telescope (La Silla) down to a limiting magnitude of
![]() .
For the remaining fields, optical coverage down to
.
For the remaining fields, optical coverage down to
![]() has
been provided by the GSC-2.3. For all fields, the 2MASS
catalogue was also used to extend the available colour coverage in the
near IR in order not to miss possible very reddened counterparts. For
about 50% of the detected X-ray sources we found candidate
counterparts which yield X-ray-to-optical flux ratios comparable
with the typical range of values of the known X-ray source classes.
From the sample of the X-ray sources with no identification we have
selected 9 sources (8 associated to the 3EG J0616-3310 error box and 1 to the 3EG J1249-8330 one) characterized by X-ray-to-optical
flux ratios greater than 100. Although all the selected X-ray
sources can be considered viable candidate counterparts to the two
EGRET sources, we are not yet in the position to propose
robust INS identifications. However, we have singled out three
interesting sources (XMMU J061807.6-331237, XMMU J061429.8-333225 and
XMMU J061450.2-331501) which are particularly promising counterparts
to 3EG J0616-3310 and certainly worth further optical
investigations.
has
been provided by the GSC-2.3. For all fields, the 2MASS
catalogue was also used to extend the available colour coverage in the
near IR in order not to miss possible very reddened counterparts. For
about 50% of the detected X-ray sources we found candidate
counterparts which yield X-ray-to-optical flux ratios comparable
with the typical range of values of the known X-ray source classes.
From the sample of the X-ray sources with no identification we have
selected 9 sources (8 associated to the 3EG J0616-3310 error box and 1 to the 3EG J1249-8330 one) characterized by X-ray-to-optical
flux ratios greater than 100. Although all the selected X-ray
sources can be considered viable candidate counterparts to the two
EGRET sources, we are not yet in the position to propose
robust INS identifications. However, we have singled out three
interesting sources (XMMU J061807.6-331237, XMMU J061429.8-333225 and
XMMU J061450.2-331501) which are particularly promising counterparts
to 3EG J0616-3310 and certainly worth further optical
investigations.
While we shall pursue the study of our candidate counterparts, we note
that the need to characterize hundreds of X-ray and optical sources,
just to discard them, is an unavoidable bottleneck, limiting the
efficiency of any multiwavelength approach. Since the number of
serendipitous, unrelated sources is proportional to the surface
covered, a significant step forward will be possible only reducing the
dimension of the ![]() -ray error boxes. The next generation high
energy gamma ray telescopes, AGILE and GLAST,
promise to improve the source positioning, thus significantly reducing
the uncertainty region associated to each source. Smaller error boxes
can be covered with less X-ray and optical pointings, thus reducing
both the observing time and the number of sources in need of a
thorough characterization. Hopefully, this will mark a turning point
in the long straggle towards the identification of the UGOs both as
individual sources and as a population.
-ray error boxes. The next generation high
energy gamma ray telescopes, AGILE and GLAST,
promise to improve the source positioning, thus significantly reducing
the uncertainty region associated to each source. Smaller error boxes
can be covered with less X-ray and optical pointings, thus reducing
both the observing time and the number of sources in need of a
thorough characterization. Hopefully, this will mark a turning point
in the long straggle towards the identification of the UGOs both as
individual sources and as a population.
Acknowledgements
We wish to thank M. Chieregato, A. De Luca and S. Mereghetti for their useful comments and suggestions. We also thank S. Ghizzardi, M. Uslenghi and S. Vercellone for their technical support. The XMM-Newton data analysis is supported by the Italian Space Agency (ASI), through contract ASI/INAF I/023/05/0. The Guide Star Catalog used in this work was produced at the Space Telescope Science Institute under U.S. Government grant. These data are based on photographic data obtained using the Oschin Schmidt Telescope on Palomar Mountain and the UK Schmidt Telescope. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation.
![\begin{figure}
\includegraphics[width=18cm]{5247f10.ps}\end{figure}](/articles/aa/full/2006/40/aa5247-06/Timg103.gif) |
Figure 10: Finding charts of the X-ray sources listed in Table 7. For each source the 5'' radius error circle is superimposed on the corresponding V-band WFI image. |
| Open with DEXTER | |
Table A.1: Range of the applicable B-V colours for the selected classes of objects
According to Chieregato (2005), for each class of
sources the
![]() in the XMM-Newton is obtained from
the corresponding Hamburg/RASS one as follows:
in the XMM-Newton is obtained from
the corresponding Hamburg/RASS one as follows:
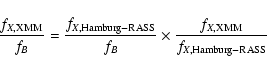 |
(A.1) |
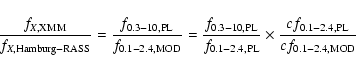 |
The
![]() values were
obtained from the
values were
obtained from the
![]() ones according to the
relation:
ones according to the
relation:
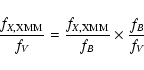 |
(A.2) |
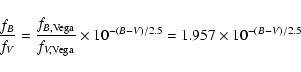 |
(A.3) |
For candidate counterparts with only GSC-2.3 photometry,
we considered the correction factor for the different
blue magnitude:
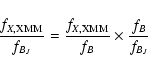 |
(A.4) |
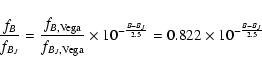 |
(A.5) |
We computed the
![]() ratios for all the candidate
counterparts. X-ray fluxes are the same determined in §3.4 while
optical fluxes were obtained from the measured WFI magnitudes
using the Pogson formula
ratios for all the candidate
counterparts. X-ray fluxes are the same determined in §3.4 while
optical fluxes were obtained from the measured WFI magnitudes
using the Pogson formula
![]() ,
assuming
fm=0 = 2.904, 6.478, 3.240, 3.828 and 1.997
,
assuming
fm=0 = 2.904, 6.478, 3.240, 3.828 and 1.997
![]() erg
cm-2 s-1 for
m = U, B, V, R and I passbands,
respectively (Zombeck 1990).
erg
cm-2 s-1 for
m = U, B, V, R and I passbands,
respectively (Zombeck 1990).
Since for the BJ band, there is no simple relation to obtain the
optical flux, we first estimated its Vega band flux. This is given by
the relation
![]() ,
where
,
where
![]() and
and
![]() are, respectively, the effective wavelength and width of
the filter, while
are, respectively, the effective wavelength and width of
the filter, while
![]() is the specific flux
calibration at
is the specific flux
calibration at
![]() for BJ=0. By referring
to the Asiago Database on Photometric Systems
(Moro & Munari 2000) we found
for BJ=0. By referring
to the Asiago Database on Photometric Systems
(Moro & Munari 2000) we found
![]() Å and
Å and
![]() Å. In order to obtain the specific flux
calibration f4731, we considered the spectral distribution of
Vega provided by Hayes (1985) and performed a linear interpolation
between 4725 and 4750 Å. In such a way we obtained
Å. In order to obtain the specific flux
calibration f4731, we considered the spectral distribution of
Vega provided by Hayes (1985) and performed a linear interpolation
between 4725 and 4750 Å. In such a way we obtained
![]() erg cm-2 s-1Å-1 and
erg cm-2 s-1Å-1 and
![]() erg
cm-2 s-1. Finally, we used the Pogson formula
erg
cm-2 s-1. Finally, we used the Pogson formula
![]() to obtain the optical
flux for a given magnitude BJ. In the case of the F band
magnitude, we applied the same procedure but assuming
to obtain the optical
flux for a given magnitude BJ. In the case of the F band
magnitude, we applied the same procedure but assuming
![]() = 6555 Å,
= 6555 Å,
![]() = 767 Å and
= 767 Å and
![]() erg cm-2 s-1 Å thus
obtaining
erg cm-2 s-1 Å thus
obtaining
![]() erg cm-2s-1.
erg cm-2s-1.