A&A 458, 79-88 (2006)
DOI: 10.1051/0004-6361:20065017
Globular cluster kinematics and X-ray emission in the early-type galaxy NGC 1399
S. Samurovic1,2,3 - I. J. Danziger2
1 - Dipartimento di Astronomia, Università di Trieste, via Tiepolo 11, 34131 Trieste, Italy
2 -
INAF, Osservatorio Astronomico di Trieste, via Tiepolo 11, 34131 Trieste, Italy
3 -
Astronomical Observatory, Volgina 7, 11160 Belgrade, Serbia and Montenegro
Received 13 February 2006 / Accepted 7 July 2006
Abstract
Context. Of the various observational methods used to address the question of dark matter in early-type galaxies there is the possibility of spatial overlap in using kinematics of stars, clusters and X-ray halos.
Aims. To investigate methods for the determination of velocity distribution profiles and deviations from a Gaussian distribution using globular clusters in early-type galaxies, and the implications for dark matter.
Methods. The maximum likelihood method together with standard statistical procedures were used to calculate the velocity dispersion. A new "tracer mass estimator'' was applied to obtain a mass estimate based on the globular clusters, which is then compared to the mass obtained using X-rays.
Results. In NGC 1399 the departures from a Gaussian distribution of the velocities at all radial distances are small. Our conclusion is that in spite of the observations that show that the velocity dispersion decreases between 4 and 10 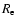 there is evidence that dark matter exists beyond
there is evidence that dark matter exists beyond
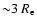 .
.
Key words: Galaxy: kinematics and dynamics - galaxies: elliptical
and lenticular, cD - galaxies: structure - dark matter - galaxies: individual: NGC 1399 - Galaxy: star clusters
The presence of dark matter in early-type galaxies continues to be one of the most important unsolved problems in extragalactic astrophysics. Although the currently popular theoretical models (such as cold dark matter models) predict huge amounts of dark matter in these galaxies, some recent observations fail to confirm this for particular galaxies (see, for example, Romanowsky et al. 2003; Peng et al. 2004; Samurovic & Danziger 2005) at least in regions interior to 3-5 effective radii (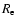 ).
Some other recent works claim to detect the presence of dark matter in ellipticals at smaller distances from the galactic center (see, for example, Thomas et al. 2005; Teodorescu et al. 2005; Cappellari et al. 2006; De Rijcke et al. 2006).
Of special importance are external regions of elliptical galaxies where dark matter might be expected to dominate luminous matter.
Studies that use integrated stellar light are limited to 3 to 4
).
Some other recent works claim to detect the presence of dark matter in ellipticals at smaller distances from the galactic center (see, for example, Thomas et al. 2005; Teodorescu et al. 2005; Cappellari et al. 2006; De Rijcke et al. 2006).
Of special importance are external regions of elliptical galaxies where dark matter might be expected to dominate luminous matter.
Studies that use integrated stellar light are limited to 3 to 4 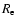 because of the low surface brightness beyond these regions.
If one wishes to study the mass distribution beyond
because of the low surface brightness beyond these regions.
If one wishes to study the mass distribution beyond
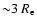 one
can use an X-ray methodology that analyzes hot gas at temperatures
one
can use an X-ray methodology that analyzes hot gas at temperatures
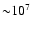 K.
Recently, Sivakoff et al. (2004) used the X-ray observations
by CHANDRA and assuming hydrostatic equilibrium found that for the X-ray bright galaxy NGC 1600 within
K.
Recently, Sivakoff et al. (2004) used the X-ray observations
by CHANDRA and assuming hydrostatic equilibrium found that for the X-ray bright galaxy NGC 1600 within
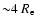 dark matter does not dominate.
However, two very recent studies by Humphrey et al. (2006) and Fukazawa et al. (2006) used X-ray data to demonstrate the existence of dark matter beyond
dark matter does not dominate.
However, two very recent studies by Humphrey et al. (2006) and Fukazawa et al. (2006) used X-ray data to demonstrate the existence of dark matter beyond
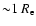 .
Some attempts to combine different observational techniques in order to determine the mass of early-type galaxies are given in Kronawitter et al. (2000), Saglia et al. (2000) and Samurovic & Danziger (2005).
.
Some attempts to combine different observational techniques in order to determine the mass of early-type galaxies are given in Kronawitter et al. (2000), Saglia et al. (2000) and Samurovic & Danziger (2005).
Fortunately, beyond
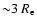 one can use other mass tracers such as globular clusters (GCs) and planetary nebulae (PNe) which can be observed at much larger radii. For example, Côté et al. (2003) recently studied NGC 4472 using 263 GCs out to
one can use other mass tracers such as globular clusters (GCs) and planetary nebulae (PNe) which can be observed at much larger radii. For example, Côté et al. (2003) recently studied NGC 4472 using 263 GCs out to
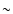 570 arcsec (
570 arcsec (
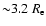 ,
but this should be
,
but this should be
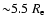 if they adopted the RC3 value) and found that the radial velocities and density profiles of globular clusters provide "unmistakable evidence'' for a massive dark halo. Peng et al. (2004) used PNe in NGC 5128 at distances out to 80 kpc (
if they adopted the RC3 value) and found that the radial velocities and density profiles of globular clusters provide "unmistakable evidence'' for a massive dark halo. Peng et al. (2004) used PNe in NGC 5128 at distances out to 80 kpc (
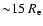 )
to conclude that dark matter is necessary to explain the observed kinematics, although their value of the mass-to-light ratio (in the B-band)
)
to conclude that dark matter is necessary to explain the observed kinematics, although their value of the mass-to-light ratio (in the B-band)
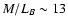 is much lower than that commonly thought for early-type galaxies at large radii (Bahcall et al. 1995).
is much lower than that commonly thought for early-type galaxies at large radii (Bahcall et al. 1995).
The most important quantity that is extracted from both GCs and PNe radial velocity observations is the velocity dispersion. Frequently authors do not explicitly state how they obtained their estimates of this quantity, so one is led to the conclusion that the adopted velocity distribution is purely Gaussian
or that the authors have used a simple statistical definition of the standard deviation to calculate it. In a recent series of papers Dirsch et al. (2003), Richtler et al. (2004) and Dirsch et al. (2004) analyzed the GC system of the galaxy NGC 1399, the central galaxy of the Fornax cluster. They used 468 radial velocities assuming a pure Gaussian distribution to conclude that the velocity dispersion of this galaxy remains approximately constant between 2 and 9 arcmin (corresponding to 12 kpc to 54 kpc, which corresponds to approximately 2.86 and 12.86 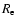 ,
under the assumption that one effective radius is 42 arcsec. This value of the effective radius comes from the RC3 catalog (de Vaucoulers et al. 1991) and we verified it using the growth curve of NGC 1399.
,
under the assumption that one effective radius is 42 arcsec. This value of the effective radius comes from the RC3 catalog (de Vaucoulers et al. 1991) and we verified it using the growth curve of NGC 1399.
In this paper we study the applicability of the assumption of a pure Gaussian distribution function for the GCs using the Dirsch et al. (2004) sample.
In Sect. 2 we outline some theoretical aspects relevant to the calculation of the velocity dispersion.
In Sect. 3 we present our results for the velocity dispersion
based on the sample of Dirsch et al. (2004). In Sect. 4 we compare these results with the results obtained using the X-ray methodology.
In Sect. 5 we present mass estimates of NGC 1399 based on globular clusters.
Our conclusions are presented in Sect. 6.
When dealing with the velocities related to the GCs and/or PNe one usually assumes a pure Gaussian velocity distribution: for example, Grillmair et al. (1994) analyzed 47 GCs within 9 arcmin in NGC 1399 using the methodology developed by Morrison et al. (1990) to calculate a velocity dispersion (
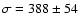
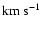 )
and a mass-to-light ratio in the B-band (
)
and a mass-to-light ratio in the B-band (
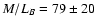 ,
interior to 9 arcmin). This technique uses a maximum likelihood approach and Morrison et al. state that since this technique is model-dependent, slightly non-Gaussian distributions can have significant effects on the performance of estimators. Richtler et al. (2004) used the maximum likelihood dispersion estimator given in Pryor & Meylan (1993). The Gaussian estimator can be expressed as:
,
interior to 9 arcmin). This technique uses a maximum likelihood approach and Morrison et al. state that since this technique is model-dependent, slightly non-Gaussian distributions can have significant effects on the performance of estimators. Richtler et al. (2004) used the maximum likelihood dispersion estimator given in Pryor & Meylan (1993). The Gaussian estimator can be expressed as:
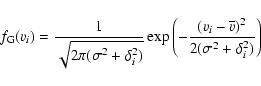 |
(1) |
where 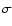 is the velocity dispersion, and it is assumed that each velocity vi (the GC velocity from which the systemic velocity,
is the velocity dispersion, and it is assumed that each velocity vi (the GC velocity from which the systemic velocity,
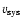 ,
is subtracted-in the case of NGC 1399
,
is subtracted-in the case of NGC 1399
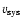 is fixed to 1441
is fixed to 1441
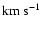 )
is drawn from a normal, Gaussian, distribution.
)
is drawn from a normal, Gaussian, distribution.
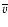 is the mean velocity and
is the mean velocity and 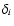 is a known measurement uncertainty of vi.
This equation is valid only if the distribution of errors is Gaussian.
is a known measurement uncertainty of vi.
This equation is valid only if the distribution of errors is Gaussian.
The maximum likelihood function is then given as
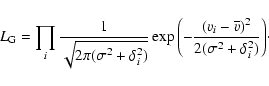 |
(2) |
Taking the logarithm of Eq. (2) and finding
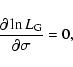 |
(3) |
one can calculate the velocity dispersion
using an iterative procedure as:
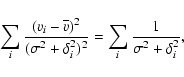 |
(4) |
where the sum includes all the velocities in a given bin. In all our calculations below we always set
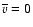 .
Using expressions given in Pryor & Meylan (1993) one can then calculate the uncertainty of the resulting velocity dispersion (these data were presented in Table 2 of Richtler et al. (2004) for different bins and different selections).
.
Using expressions given in Pryor & Meylan (1993) one can then calculate the uncertainty of the resulting velocity dispersion (these data were presented in Table 2 of Richtler et al. (2004) for different bins and different selections).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{5017fig1.eps}\end{figure}](/articles/aa/full/2006/40/aa5017-06/Timg34.gif) |
Figure 1:
Comparison between our calculation of the velocity dispersion of NGC 1399 (open circles) and calculations of Richtler et al. (2004) (filled circles), when a pure Gaussian distribution is assumed. Note that for the outermost point the two values overlap. |
| Open with DEXTER |
The globular cluster system of NGC 1399 was presented in Dirsch et al. (2003, wide-field photometry), Richtler et al. (2004, kinematics) and Dirsch et al. (2004, spectroscopy and database). In our analysis, we use the set of 445 GCs for which the estimated uncertainties are
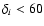
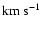 .
This selection enabled us to have a sufficiently large number of clusters in each chosen radial bin and it was also useful in the construction of the bins given in Table 2, which contain approximately 50 clusters each.
We took as a center of NGC 1399 the coordinates (J2000.0) given in the NED database:
.
This selection enabled us to have a sufficiently large number of clusters in each chosen radial bin and it was also useful in the construction of the bins given in Table 2, which contain approximately 50 clusters each.
We took as a center of NGC 1399 the coordinates (J2000.0) given in the NED database:
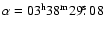 and
and
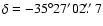 .
In Fig. 1 we present the comparison of our results (open circles) with those of Richtler et al. (2004)
(filled circles; the second column of their Table 2, no selection was performed). In this case a pure Gaussian distribution is assumed and the agreement is very good.
In Fig. 2 we present the comparison of our results (open symbols) with those of Richtler et al. (2004) (filled symbols) for red (C-R>1.6) and blue (C-R<1.6) clusters using the Richtler et al. bins (see also Table 1) (where the data for Washington C and Kron-Cousins R are taken from Dirsch et al. 2004).
Our total number of red and blue clusters
used in this comparison is 412: we have taken into account all the clusters for which we had colours and for which
.
In Fig. 1 we present the comparison of our results (open circles) with those of Richtler et al. (2004)
(filled circles; the second column of their Table 2, no selection was performed). In this case a pure Gaussian distribution is assumed and the agreement is very good.
In Fig. 2 we present the comparison of our results (open symbols) with those of Richtler et al. (2004) (filled symbols) for red (C-R>1.6) and blue (C-R<1.6) clusters using the Richtler et al. bins (see also Table 1) (where the data for Washington C and Kron-Cousins R are taken from Dirsch et al. 2004).
Our total number of red and blue clusters
used in this comparison is 412: we have taken into account all the clusters for which we had colours and for which
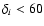
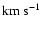 .
A pure Gaussian distribution is assumed.
If we place all GCs of a given colour in one bin our results are in very good agreement with those of Richtler et al.: for red GCs we found
.
A pure Gaussian distribution is assumed.
If we place all GCs of a given colour in one bin our results are in very good agreement with those of Richtler et al.: for red GCs we found
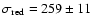
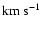 and they found
and they found
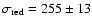
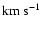 ,
and for blue GCs we found
,
and for blue GCs we found
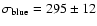
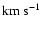 and they found
and they found
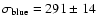
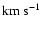 .
However, there are discrepancies related to the individual bins for the velocity dispersion values of Richtler et al. which we may attribute to our selection criterion: we took only GCs for which
.
However, there are discrepancies related to the individual bins for the velocity dispersion values of Richtler et al. which we may attribute to our selection criterion: we took only GCs for which
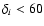
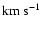 .
.
Table 1:
Projected velocity dispersion measurements of NGC 1399 for a Gaussian distribution (
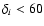
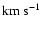 ).
).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{5017fig2.eps}\end{figure}](/articles/aa/full/2006/40/aa5017-06/Timg63.gif) |
Figure 2:
Comparison between our calculation of the velocity dispersion of NGC 1399 for red (open rectangles) and blue clusters (open triangles) and calculations of Richtler et al. (2004) for red (filled rectangles) and blue clusters (filled triangles). In all the cases we assumed a pure Gaussian distribution.
|
| Open with DEXTER |
In Table 1 we list our results for the projected velocity dispersion in the case of the pure Gaussian velocity distribution (with
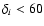
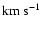 )
for the total sample of clusters. In this table we also give our results for blue and red clusters. We have used the bins defined in the Richtler et al. (2004) paper: as can be seen from Fig. 1 with these bins the velocity dispersion remains approximately constant throughout the galaxy.
Errors were calculated using the lengthy expressions of Pryor & Meylan (1993). With Richtler et al. binning of the data there exists a significant overlap of the bins: that is, there are many of the same clusters present in two different bins.
Therefore, we bin the data taking approximately 50 GCs in each separate bin (see Table 2):
using this approach and assuming a Gaussian distribution
)
for the total sample of clusters. In this table we also give our results for blue and red clusters. We have used the bins defined in the Richtler et al. (2004) paper: as can be seen from Fig. 1 with these bins the velocity dispersion remains approximately constant throughout the galaxy.
Errors were calculated using the lengthy expressions of Pryor & Meylan (1993). With Richtler et al. binning of the data there exists a significant overlap of the bins: that is, there are many of the same clusters present in two different bins.
Therefore, we bin the data taking approximately 50 GCs in each separate bin (see Table 2):
using this approach and assuming a Gaussian distribution![[*]](/icons/foot_motif.gif) , we see a decreasing trend in the velocity dispersion between
, we see a decreasing trend in the velocity dispersion between 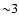 and
and 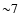 arcmin (see also Fig. 3; more details are given below in this section).
For example, using large (Richtler et al.) bins the last measured point was calculated for all GCs beyond 6.5 arcmin and some clusters (73 clusters between 6.5 and 7.5 arcmin) were already taken into account in a preceding bin.
For all the given bins we calculated the velocity dispersion and the skewness and kurtosis parameters, s3 and s4, using standard definitions and the NAG routine G01AAF
(see Table 2 in which we present the results based on the maximum likelihood function and, for comparison, the result obtained using the standard statistical definition). We are not trying to reconstruct the full line-of-sight velocity distribution, because it is known (see Merritt 1997) that for small samples such as ours which contain less than a few hundred objects per bin it is not possible - we simply calculate skewness and kurtosis parameters (we do not attribute much of significance to the numerical values of these parameters) in order to determine whether in some bin a significant departure from a Gaussian distribution exists. This is similar to the approach applied by Teodorescu et al. (2005) in their Fig. 18.
The results are graphically presented in Fig. 3 (left).
The results based on the maximum likelihood function and those based on the standard statistical method are in very good agreement.
In order to test whether differences in binning affect our calculations
we also performed the calculations using different binning with variable numbers of the GCs within a bin of fixed length (2 arcmin) without overlap of the bins.
In Tables 3 and 4 we present the results for the blue and red clusters, respectively.
Here we have used a bin width of 2 arcmin in order to include in each bin a statistically significant number of clusters.
In Tables 5 and 6 we present two different types of binnings for which the center of each bin is
placed on odd and even values of the radius, respectively (the obvious exceptions are the first and the last bin in Table 6).
Table 7 presents the results of one additional binning check
for which each bin contains approximately 75 clusters (instead of 50). The results for the blue, red and the total sample (which includes both blue and red clusters) given in Tables 3-7 were obtained using the same standard statistical procedure based on the same NAG routine; they are graphically presented in Figs. 3 (right)
and 4.
Although in Fig. 3 (left) we can see a declining trend in the velocity dispersion, the reduced
arcmin (see also Fig. 3; more details are given below in this section).
For example, using large (Richtler et al.) bins the last measured point was calculated for all GCs beyond 6.5 arcmin and some clusters (73 clusters between 6.5 and 7.5 arcmin) were already taken into account in a preceding bin.
For all the given bins we calculated the velocity dispersion and the skewness and kurtosis parameters, s3 and s4, using standard definitions and the NAG routine G01AAF
(see Table 2 in which we present the results based on the maximum likelihood function and, for comparison, the result obtained using the standard statistical definition). We are not trying to reconstruct the full line-of-sight velocity distribution, because it is known (see Merritt 1997) that for small samples such as ours which contain less than a few hundred objects per bin it is not possible - we simply calculate skewness and kurtosis parameters (we do not attribute much of significance to the numerical values of these parameters) in order to determine whether in some bin a significant departure from a Gaussian distribution exists. This is similar to the approach applied by Teodorescu et al. (2005) in their Fig. 18.
The results are graphically presented in Fig. 3 (left).
The results based on the maximum likelihood function and those based on the standard statistical method are in very good agreement.
In order to test whether differences in binning affect our calculations
we also performed the calculations using different binning with variable numbers of the GCs within a bin of fixed length (2 arcmin) without overlap of the bins.
In Tables 3 and 4 we present the results for the blue and red clusters, respectively.
Here we have used a bin width of 2 arcmin in order to include in each bin a statistically significant number of clusters.
In Tables 5 and 6 we present two different types of binnings for which the center of each bin is
placed on odd and even values of the radius, respectively (the obvious exceptions are the first and the last bin in Table 6).
Table 7 presents the results of one additional binning check
for which each bin contains approximately 75 clusters (instead of 50). The results for the blue, red and the total sample (which includes both blue and red clusters) given in Tables 3-7 were obtained using the same standard statistical procedure based on the same NAG routine; they are graphically presented in Figs. 3 (right)
and 4.
Although in Fig. 3 (left) we can see a declining trend in the velocity dispersion, the reduced 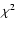 value is low for a constant velocity dispersion of 330
value is low for a constant velocity dispersion of 330
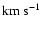 and is equal to 1.1 (the best fit case, when the first point is excluded). The
constant value of the velocity dispersion that ranges between 320 and 330
and is equal to 1.1 (the best fit case, when the first point is excluded). The
constant value of the velocity dispersion that ranges between 320 and 330
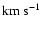 provides the best fit case when N=75 (the right hand panel of Fig. 3), but then
provides the best fit case when N=75 (the right hand panel of Fig. 3), but then
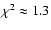 (all points are included in the fit).
(all points are included in the fit).
For the total sample of clusters (Fig. 3) we see a low velocity dispersion in the inner region (interior to 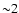 arcmin), a higher value of the velocity dispersion (beyond
arcmin), a higher value of the velocity dispersion (beyond 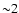 arcmin) and a decrease of the velocity dispersion between
arcmin) and a decrease of the velocity dispersion between 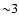 and
and 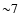 arcmin
(more evident in the left panel of Fig. 3, because of the binning applied).
arcmin
(more evident in the left panel of Fig. 3, because of the binning applied).
Table 2:
Projected velocity dispersion measurements of NGC 1399 for a Gaussian distribution with a fixed number of clusters per bin (
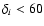
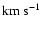 ,
,
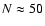 ).
).
Beyond 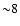 arcmin we notice an increase in the velocity dispersion.
We confirm the finding of Richtler et al. (2004) regarding the innermost point (<2 arcmin). Beyond
arcmin we notice an increase in the velocity dispersion.
We confirm the finding of Richtler et al. (2004) regarding the innermost point (<2 arcmin). Beyond 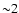 arcmin our results differ somewhat from
those by Richtler et al. because of the binning and selection criteria used.
arcmin our results differ somewhat from
those by Richtler et al. because of the binning and selection criteria used.
![\begin{figure}
\par\includegraphics[width=7.34cm,clip]{5017fig3.eps}\hspace*{2mm}
\includegraphics[width=7.34cm,clip]{5017fig4.eps}\end{figure}](/articles/aa/full/2006/40/aa5017-06/Timg84.gif) |
Figure 3:
Kinematics of NGC 1399 based on the total sample of red and blue GCs. Left: from top to bottom: radial velocity of the GCs in
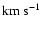 ,
velocity dispersion calculated in a given bin using a maximum likelihood method (open squares) and using standard statistical procedures (filled circles), s3 and s4 parameters.
In all the bins the total number of clusters per bin was approximately 50. Right:
the meaning of the data on the ordinate is the same as in the left panel.
It combines results for binning methods given as follows: filled circles represent the data in Table 5, open circles are for the data given in Table 6 and open triangles are for the data from Table 7. ,
velocity dispersion calculated in a given bin using a maximum likelihood method (open squares) and using standard statistical procedures (filled circles), s3 and s4 parameters.
In all the bins the total number of clusters per bin was approximately 50. Right:
the meaning of the data on the ordinate is the same as in the left panel.
It combines results for binning methods given as follows: filled circles represent the data in Table 5, open circles are for the data given in Table 6 and open triangles are for the data from Table 7. |
| Open with DEXTER |
The red clusters show a lower velocity dispersion than the blue clusters (see Fig. 4) and for a possible explanation we refer the reader to Sect. 4 of the paper by Richtler et al. (2004). Although both s3 and s4 parameters are small we see that while the calculated s3 parameters for blue clusters differ from those for red clusters, the s4 parameters for both classes are very similar. The binning in both cases was such that we kept the bin width constant and equal to 2 arcmin in order to have enough clusters per bin.
Table 3:
Kinematics data for NGC 1399 for the blue clusters.
Table 4:
Kinematics data for NGC 1399 for the red clusters.
Table 5:
Kinematics data for NGC 1399 for the total sample of blue and red clusters (part 1).
Forte et al. (2005) state there are indications (albeit not conclusive) that there could be an association between the red GCs and the stellar component and that blue GCs show a spatial distribution which is similar to that inferred for dark matter. However any attempt to draw conclusions from this is outside the province of this paper.
As an additional test we also calculated the velocity dispersion in the inner part of NGC 1399 (interior to 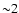 arcmin) in which we have 14 GCs (the innermost at
arcmin) in which we have 14 GCs (the innermost at
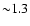 arcmin and the outermost at
arcmin and the outermost at 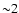 arcmin).
We calculated that for the total sample of blue and red clusters the velocity dispersion is
arcmin).
We calculated that for the total sample of blue and red clusters the velocity dispersion is 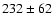
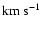 .
We note that this result is in agreement with the integrated stellar light observations thus giving credence to the feasibility of calculating galaxy kinematics even with the small number of mass tracers in a given bin.
.
We note that this result is in agreement with the integrated stellar light observations thus giving credence to the feasibility of calculating galaxy kinematics even with the small number of mass tracers in a given bin.
The X-ray methodology of studying mass in early-type galaxies is well known (see e.g. Mathews & Brighenti 2003; Samurovic & Danziger 2005). We assume that spherical symmetry in the galaxy holds, and that the condition of hydrostatic equilibrium is valid. For clarity we adopt the following 3 formulae from the referenced papers:
- 1)
- the total mass of the galaxy interior to the radius r is calculated using the following equation taken from Kim & Fabbiano (1995):
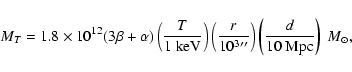 |
(5) |
where the exponent 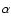 is related to the temperature (
is related to the temperature (
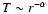 )
and in our calculations is taken to be zero, and
)
and in our calculations is taken to be zero, and 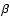 is the slope
used in the analytic King approximation model and is taken to be
is the slope
used in the analytic King approximation model and is taken to be
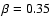 (Jones et al. 1997) and
(Jones et al. 1997) and
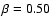 (interior to 50 arcsec, see Paolillo et al. 2002);
(interior to 50 arcsec, see Paolillo et al. 2002);
- 2)
- the mass-to-light ratio in the B-band is calculated
as a function of radius r:
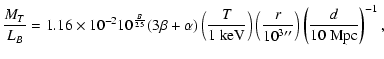 |
|
|
(6) |
where B is the B magnitude of the galaxy inside radius r (Kim & Fabbiano 1995);
- 3)
- the following simple formula taken from Mathews & Brighenti (2003) was used as an estimate of the temperature based on the stellar velocity dispersion assuming a virial condition:
![\begin{displaymath}kT_{\sigma {[\rm ~keV]}} = 6.367 \times 10^{-6} \sigma_{\rm [km~s^{-1}]} ^2
\end{displaymath}](/articles/aa/full/2006/40/aa5017-06/img108.gif) |
(7) |
where the temperature, 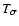 ,
is given in keV and the stellar velocity dispersion,
,
is given in keV and the stellar velocity dispersion, 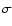 ,
is given in
,
is given in
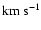 .
.
In Fig. 5 we show the mass-to-light ratio of the galaxy NGC 1399 in the B-band using Eq. (6). The parameter 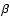 was taken to be 0.35 (dashed strip) and 0.50 (dotted strip) as given above. We present the estimates for the mass-to-light ratio beyond one effective radius; this limit is taken because we want to avoid the problems due to cooling flows in the central region and because we are interested in the comparison of different methodologies in the outer regions of the galaxies where dark matter is expected to play a significant role. For the discussion about the reliability of the X-ray mass estimates in the regions of the cooling flow and the problems related to the deviations from hydrostatic equilibrium see the paper by Ciotti & Pellegrini (2004). The sample of X-ray galaxies from O'Sullivan et al. (2003), which also includes NGC 1399, seems to show that beyond
was taken to be 0.35 (dashed strip) and 0.50 (dotted strip) as given above. We present the estimates for the mass-to-light ratio beyond one effective radius; this limit is taken because we want to avoid the problems due to cooling flows in the central region and because we are interested in the comparison of different methodologies in the outer regions of the galaxies where dark matter is expected to play a significant role. For the discussion about the reliability of the X-ray mass estimates in the regions of the cooling flow and the problems related to the deviations from hydrostatic equilibrium see the paper by Ciotti & Pellegrini (2004). The sample of X-ray galaxies from O'Sullivan et al. (2003), which also includes NGC 1399, seems to show that beyond
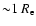 ,
for the set of galaxies with a cooling core (to which NGC 1399 belongs) there is not much cooling.
Since in our calculations we always assume a constant temperature in a given region, as stated above (
,
for the set of galaxies with a cooling core (to which NGC 1399 belongs) there is not much cooling.
Since in our calculations we always assume a constant temperature in a given region, as stated above (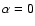 ), in Fig. 5 we present estimates of the mass-to-light ratio in three different regions characterized by different temperatures:
), in Fig. 5 we present estimates of the mass-to-light ratio in three different regions characterized by different temperatures:
- (i)
- interior to 100 arcsec we used
Eq. (7) and allowed the interval for the temperature between
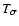 and
and
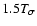 (virial assumption). The temperature was taken to be 0.61 keV as given in Brown & Bregman (1998) signifying that the value of the velocity dispersion taken was
(virial assumption). The temperature was taken to be 0.61 keV as given in Brown & Bregman (1998) signifying that the value of the velocity dispersion taken was 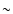 310
310
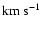 .
We see that within 100 arcsec (
.
We see that within 100 arcsec (
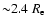 )
for
)
for
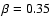 dark matter does not dominate, because the maximum value that the mass-to-light ratio can reach is
dark matter does not dominate, because the maximum value that the mass-to-light ratio can reach is 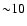 .
The same is true for the lower value of the temperature (T=0.61 keV) and
.
The same is true for the lower value of the temperature (T=0.61 keV) and
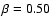 ,
whereas for the higher values of the temperature and
,
whereas for the higher values of the temperature and
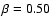 the mass-to-light ratio increases
suggesting the existence of dark matter (in this case the mass-to-light ratio can reach values of
the mass-to-light ratio increases
suggesting the existence of dark matter (in this case the mass-to-light ratio can reach values of 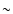 15.
The lack of dark matter within
15.
The lack of dark matter within
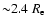 is consistent with our results for IC 1459, IC 3370 (Samurovic and Danziger 2005): for these two galaxies we did not find evidence for dominance of dark matter closer than
is consistent with our results for IC 1459, IC 3370 (Samurovic and Danziger 2005): for these two galaxies we did not find evidence for dominance of dark matter closer than
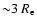 .
Saglia et al. (2000), using integrated stellar light, found that M/LB=10 (inside
.
Saglia et al. (2000), using integrated stellar light, found that M/LB=10 (inside
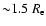 ,
for the distance of 17.6 Mpc; this scales to
,
for the distance of 17.6 Mpc; this scales to 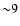 for the distance of 20.36 Mpc used in our paper) and at
for the distance of 20.36 Mpc used in our paper) and at
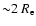 they found that
they found that
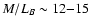 which scales to
which scales to
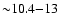 for our adopted distance.
It is also consistent with the results obtained by Méndez et al. (2001) who studied 535 PNe in the flattened elliptical galaxy NGC 4697 and found that, assuming isotropic velocity distribution, this galaxy does not show dark matter within
for our adopted distance.
It is also consistent with the results obtained by Méndez et al. (2001) who studied 535 PNe in the flattened elliptical galaxy NGC 4697 and found that, assuming isotropic velocity distribution, this galaxy does not show dark matter within
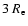 ;
;
- (ii)
- between 100 and 150 arcsec we used as a lower value
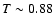 keV and as an upper value
keV and as an upper value 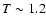 keV estimated from the paper of Jones et al. (1997) (their Fig. 3);
keV estimated from the paper of Jones et al. (1997) (their Fig. 3);
- (iii)
- beyond 150 arcsec we used
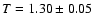 estimated by Jones et al. (1997).
estimated by Jones et al. (1997).
For comparison, in Fig. 5 we have also plotted the Grillmair et al. (1994) value which we transformed from the value of 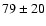 at 13.2 kpc to
at 13.2 kpc to 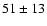 at the distance of 20.36 Mpc used in our paper
(see Fig. 3, left).
We will address this problem later in this section and also in the next section.
at the distance of 20.36 Mpc used in our paper
(see Fig. 3, left).
We will address this problem later in this section and also in the next section.
Although the X-ray data suggest that beyond
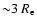 in NGC 1399 there should be a significant amount of dark matter, we note, however, that since NGC 1399 is a central galaxy of the Fornax cluster, the confinement of the hot gas may be
assisted by the external pressure of the intercluster medium (ICM) and is not wholly due to the gravitational field of NGC 1399 (Bertin 2000).
in NGC 1399 there should be a significant amount of dark matter, we note, however, that since NGC 1399 is a central galaxy of the Fornax cluster, the confinement of the hot gas may be
assisted by the external pressure of the intercluster medium (ICM) and is not wholly due to the gravitational field of NGC 1399 (Bertin 2000).
![\begin{figure}
\par\includegraphics[width=14.88cm,clip]{5017fig5.eps}\end{figure}](/articles/aa/full/2006/40/aa5017-06/Timg124.gif) |
Figure 4:
Kinematics of NGC 1399 based on the total sample of blue ( left) and red ( right) GCs.
From top to bottom: radial velocity of the GCs in
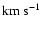 ,
velocity dispersion,
s3 and s4 parameters calculated in a given bin from Tables 3 and 4. ,
velocity dispersion,
s3 and s4 parameters calculated in a given bin from Tables 3 and 4. |
| Open with DEXTER |
Table 6:
Kinematics data for NGC 1399 for the total sample of blue and red clusters (part 2).
Table 7:
Kinematics data for NGC 1399 for the total sample of blue and red clusters (part 3).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{5017fig6.eps}\end{figure}](/articles/aa/full/2006/40/aa5017-06/Timg137.gif) |
Figure 5:
Estimates of the total mass-to-light ratio in the B-band in the solar units using X-rays assuming hydrostatic equilibrium and isotropic velocity distribution presented with three shaded regions. Three different
regions of the constant temperature were used beyond one effective radius:
region (1) is between 40 and 100 arcsec, region (2) is between 100 and 140 arcsec and the region (3) is between 140 and
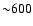 arcsec.
(1): the shaded regions interior to 100 arcsec cover the temperatures between 0.61 and 0.92 keV as estimated in Brown & Bregman (1998);
(2): shaded regions between 100 and 140 arcsec have for a lower value
arcsec.
(1): the shaded regions interior to 100 arcsec cover the temperatures between 0.61 and 0.92 keV as estimated in Brown & Bregman (1998);
(2): shaded regions between 100 and 140 arcsec have for a lower value
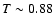 keV and for an upper value keV and for an upper value 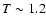 keV as estimated from the paper of Jones et al. (1997, their Fig. 3);
(3): beyond 140 arcsec keV as estimated from the paper of Jones et al. (1997, their Fig. 3);
(3): beyond 140 arcsec
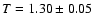 was used as estimated by Jones et al. (1997).
With a filled square we presented the mass-to-light ratio found by Grillmair et al. (1994,
was used as estimated by Jones et al. (1997).
With a filled square we presented the mass-to-light ratio found by Grillmair et al. (1994,
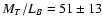 ).
Vertical dotted line is one effective radius. The regions shaded with dots are for the case for which ).
Vertical dotted line is one effective radius. The regions shaded with dots are for the case for which
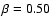 (Paolillo et al. 2002) and the regions shaded with lines are for the case for which (Paolillo et al. 2002) and the regions shaded with lines are for the case for which
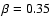 (Jones et al. 1997).
(Jones et al. 1997). |
| Open with DEXTER |
Recently Evans et al. (2003) introduced a new "tracer mass estimator'' which provides an estimate of the enclosed mass from the projected positions and line-of-sight velocities of a given tracer population (such as GCs and PNe). One can assume that the tracer population is spherically symmetric and has a number density that obeys a power law:
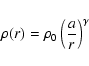 |
(8) |
where a is constant, and radius r ranges between
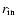 and
and
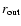 ,
inner and outer points of the given population, respectively.
The parameter
,
inner and outer points of the given population, respectively.
The parameter 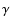 is determined using the surface density of the tracer population between
is determined using the surface density of the tracer population between
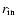 and
and
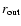 .
Evans et al. give the following formula for the mass enclosed within
.
Evans et al. give the following formula for the mass enclosed within
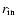 and
and
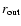 for the isotropic ("iso'' in the formulas below) case
("los'' stands for line-of-sight):
for the isotropic ("iso'' in the formulas below) case
("los'' stands for line-of-sight):
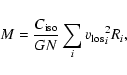 |
(9) |
where constant
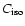 is given as:
is given as:
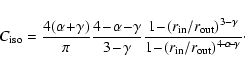 |
(10) |
The parameter 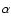 for an isothermal potential is equal to zero and this value was taken in all the calculations that we performed below. This is a reasonable assumption (see Evans et al. 2003, for details). We are aware of the initial assumptions about the isothermal potential which predicts a quasi-constant velocity dispersion profile but the calculated value of the mass is not much influenced by this. This assumption was used by Peng et al. (2004) in the calculation of the total mass of NGC 5128 for which there is a declining trend of the velocity dispersion.
for an isothermal potential is equal to zero and this value was taken in all the calculations that we performed below. This is a reasonable assumption (see Evans et al. 2003, for details). We are aware of the initial assumptions about the isothermal potential which predicts a quasi-constant velocity dispersion profile but the calculated value of the mass is not much influenced by this. This assumption was used by Peng et al. (2004) in the calculation of the total mass of NGC 5128 for which there is a declining trend of the velocity dispersion.
For the application of Eq. (10) we split the total sample of GCs into 5 bins:
each bin (except the first one which is 2 arcmin wide) contains the previous one in addition to a fixed width of 2 arcmin.
Our results (for mass and mass-to-light ratios) for the isotropic case are given in Table 8. In this table for comparison we also
provide estimates for mass and mass-to-light ratio obtained using X-ray methodology in the same bins. The errors for the estimates based on the X-rays
reflect uncertainty in the temperature.
In the calculation of the mass (and mass-to-light ratios) based on the GCs we used
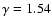 which was derived using a least-squares fit applied to the data published by Dirsch et al. (2003) for all the clusters in the sample. The outermost point at 10 arcmin was taken. The data from the Table 8 are graphically presented in Fig. 6. The large box contains estimates for the total mass-to-light ratio (open and filled triangles are for the determination based on the X-ray technique assuming hydrostatic equilibrium (open triangles are for
which was derived using a least-squares fit applied to the data published by Dirsch et al. (2003) for all the clusters in the sample. The outermost point at 10 arcmin was taken. The data from the Table 8 are graphically presented in Fig. 6. The large box contains estimates for the total mass-to-light ratio (open and filled triangles are for the determination based on the X-ray technique assuming hydrostatic equilibrium (open triangles are for
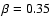 and filled triangles are for
and filled triangles are for
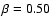 )
and open circles are for the estimate based on GCs assuming isotropy.
In the estimates of the mass-to-light ratio based on the X-rays we take T=1 keV in the first bin, and T=1.30 keV in all the other bins.
In a small inserted box we plot the estimates for the mass: the symbols have the same meaning as in the large box. In the inner regions (interior to
)
and open circles are for the estimate based on GCs assuming isotropy.
In the estimates of the mass-to-light ratio based on the X-rays we take T=1 keV in the first bin, and T=1.30 keV in all the other bins.
In a small inserted box we plot the estimates for the mass: the symbols have the same meaning as in the large box. In the inner regions (interior to 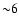 arcmin) of NGC 1399 we have good agreement between the two techniques. At
arcmin) of NGC 1399 we have good agreement between the two techniques. At 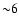 arcmin and beyond the estimate of the mass (and the mass-to-light ratio) based on
arcmin and beyond the estimate of the mass (and the mass-to-light ratio) based on
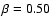 starts to diverge from the estimate based on the GCs, whereas the estimate based on
starts to diverge from the estimate based on the GCs, whereas the estimate based on
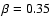 is consistent with it up to 8 arcmin. Note also that the estimate of Grillmair et al. (1994) is consistent with both results based on the GCs and X-rays (
is consistent with it up to 8 arcmin. Note also that the estimate of Grillmair et al. (1994) is consistent with both results based on the GCs and X-rays (
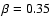 case).
case).
The only point for which there seems to be a discrepancy between the X-ray and the GC estimates is the one at 10 arcmin: the X-rays (with
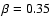 )
predict the mass-to-light ratio of
)
predict the mass-to-light ratio of 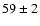 whereas the estimate based on the GCs gives
whereas the estimate based on the GCs gives 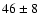 .
There may be two possible sources of this discrepancy:
(i) errors given in the X-ray case should be understood as minimal, because in these estimates we took into account only the uncertainty in temperature (
.
There may be two possible sources of this discrepancy:
(i) errors given in the X-ray case should be understood as minimal, because in these estimates we took into account only the uncertainty in temperature (
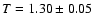 ). Note that Jones et al. (1997) at 10 arcmin calculated
). Note that Jones et al. (1997) at 10 arcmin calculated
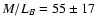 (scaled to the distance used in our paper; see their Fig. 7 - in our Fig. 6 we plotted the points at 3 and 10 arcmin based on their plot); note also that at
(scaled to the distance used in our paper; see their Fig. 7 - in our Fig. 6 we plotted the points at 3 and 10 arcmin based on their plot); note also that at 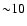 arcmin their best fit for the temperature is 1.22 keV which is somewhat lower than the value we took thus implying a lower mass-to-light ratio which is closer to that obtained using GC methodology;
(ii) the discrepancy between the two results may be real and might be attributed to the effect of a contribution to the X-ray gas pressure by the ICM referred to above. Peng et al. (2004) also used the Evans et al. (2003) "tracer mass estimator'' to calculate the mass-to-light ratio in NGC 5128. They found at 80 kpc (
arcmin their best fit for the temperature is 1.22 keV which is somewhat lower than the value we took thus implying a lower mass-to-light ratio which is closer to that obtained using GC methodology;
(ii) the discrepancy between the two results may be real and might be attributed to the effect of a contribution to the X-ray gas pressure by the ICM referred to above. Peng et al. (2004) also used the Evans et al. (2003) "tracer mass estimator'' to calculate the mass-to-light ratio in NGC 5128. They found at 80 kpc (
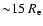 )
that
)
that
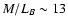 which suggests even smaller amounts of dark matter in the outer parts of this galaxy.
which suggests even smaller amounts of dark matter in the outer parts of this galaxy.
Different cosmological models and their predictions for the mass may in principle be tested. Richtler et al. (2004, references therein) tested among others, logarithmic potentials and Navarro et al. (1996, NFW) mass profiles. With the data which extend out to 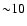 arcmin it is difficult to draw firm conclusions; the mass predicted by both NFW profile and the logarithmic potential is closer to the mass based on GCs and X-rays for which
arcmin it is difficult to draw firm conclusions; the mass predicted by both NFW profile and the logarithmic potential is closer to the mass based on GCs and X-rays for which
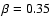 than to the X-rays for which
than to the X-rays for which
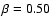 :
:
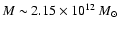 at
at 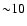 arcmin (scaled to the distance used in our paper; see the large open pentagon in the small inserted box of Fig. 6).
arcmin (scaled to the distance used in our paper; see the large open pentagon in the small inserted box of Fig. 6).
We see in Fig. 6 that there is agreement between the following four different estimates of the total mass-to-light ratio: (i) our estimate based on the GCs; (ii) our estimate based on the X-rays (the case with
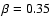 ); (iii) the estimate based on the Grillmair et al. (1994) paper based on the GCs; and (iv) the estimate based on the NFW approach (this last one is given only in the small inserted box of Fig. 6).
); (iii) the estimate based on the Grillmair et al. (1994) paper based on the GCs; and (iv) the estimate based on the NFW approach (this last one is given only in the small inserted box of Fig. 6).
In this paper we investigated the line-of-sight velocity distribution (LOSVD) calculated from the observations of GCs in the early-type galaxy NGC 1399. We have used recently published Dirsch et al. (2004) data from which we calculated velocity dispersions using both standard statistical procedures and the maximum likelihood approach.
![\begin{figure}
\par\includegraphics[width=13.2cm,clip]{5017fig7.eps}\end{figure}](/articles/aa/full/2006/40/aa5017-06/Timg152.gif) |
Figure 6:
Mass estimates using the GCs and X-ray methodology. Large box: estimates for the total mass-to-light ratio in the B-band in the solar units as a function of radius; the
triangles are for the determination based on the X-ray technique assuming hydrostatic equilibrium (the open triangles for
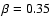 and the filled triangles for and the filled triangles for
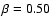 ), the open circles are for the estimate based on GCs assuming isotropy. The large open circle is the value obtained in the paper by Grillmair et al. (1994) scaled to the distance used in our paper (see text for details). The open square is the value obtained in the paper by Saglia et al. (2000) scaled to the distance used in our paper.
The filled square is the value obtained in the paper by Jones et al.
(1997) scaled to the distance used in our paper. The temperature is taken to be 1 keV in the first bin and 1.30 keV in all the other bins.
Small inserted box: estimates of the total mass in units of ), the open circles are for the estimate based on GCs assuming isotropy. The large open circle is the value obtained in the paper by Grillmair et al. (1994) scaled to the distance used in our paper (see text for details). The open square is the value obtained in the paper by Saglia et al. (2000) scaled to the distance used in our paper.
The filled square is the value obtained in the paper by Jones et al.
(1997) scaled to the distance used in our paper. The temperature is taken to be 1 keV in the first bin and 1.30 keV in all the other bins.
Small inserted box: estimates of the total mass in units of
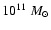 as a function of radius;
the symbols have the same meaning as in the large box. The large open pentagon in the small box is for the estimates of Richtler et al. (2004) for the mass based on the Navarro et al. profile and the logarithmic potential.
as a function of radius;
the symbols have the same meaning as in the large box. The large open pentagon in the small box is for the estimates of Richtler et al. (2004) for the mass based on the Navarro et al. profile and the logarithmic potential.
|
| Open with DEXTER |
Table 8:
Mass estimates of NGC 1399 using globular clusters and X-rays.
Our conclusions are as follows.
- (1)
- We show that the departures from the Gaussian distribution (given by the
skewness and kurtosis parameters, s3 and s4, estimated from the radial velocities) are not large and that the estimates of the velocity dispersion calculated using standard statistical procedures and the maximum likelihood approach do not differ much.
Using different binning we showed that slightly different trends in the velocity dispersion profile might be inferred.
- (2)
- We find that inside
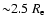 the mass is not dominated by dark matter (only for the case for which
the mass is not dominated by dark matter (only for the case for which
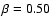 and
and
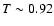 keV might one infer dark matter in this region). However, beyond
keV might one infer dark matter in this region). However, beyond
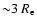 the high velocity dispersion and the X-rays indicate the presence of dark matter. This is not inconsistent with our previous results (Samurovic & Danziger 2005) for 2 early-type galaxies (IC 1459, IC 3370) for which dark matter interior to
the high velocity dispersion and the X-rays indicate the presence of dark matter. This is not inconsistent with our previous results (Samurovic & Danziger 2005) for 2 early-type galaxies (IC 1459, IC 3370) for which dark matter interior to
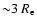 did not appear to dominate.
Our estimates of the total mass (and mass-to-light ratio) based on the X-ray and GC methodology imply
did not appear to dominate.
Our estimates of the total mass (and mass-to-light ratio) based on the X-ray and GC methodology imply
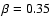 - this is in agreement with the value found in the paper by Jones et al. (1997).
Beyond 8 arcmin there seems to be a discrepancy between the two methodologies: the GC data imply a smaller total mass than that obtained using X-rays; it is not clear whether this discrepancy lies within the uncertainties or not.
- this is in agreement with the value found in the paper by Jones et al. (1997).
Beyond 8 arcmin there seems to be a discrepancy between the two methodologies: the GC data imply a smaller total mass than that obtained using X-rays; it is not clear whether this discrepancy lies within the uncertainties or not.
- (3)
- Using the new "tracer mass estimator'' of Evans et al. (2003) we find that the increase of the total mass of NGC 1399 beyond
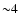 arcmin has a slow rise.
At
arcmin has a slow rise.
At 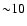 arcmin we calculated, for an isotropic case,
arcmin we calculated, for an isotropic case,
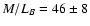 .
In spite of the hint of the decreasing velocity dispersion in NGC 1399 (between
.
In spite of the hint of the decreasing velocity dispersion in NGC 1399 (between 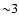 and
and 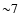 arcmin) the observations show evidence of dark matter in the outer parts of this galaxy.
The procedure outlined in our paper provides a means of comparison between different calculations of the total mass of an early-type galaxy without resorting to much more complex and computationally intensive superposition of orbits required in the Schwarzschild (1979) modelling.
arcmin) the observations show evidence of dark matter in the outer parts of this galaxy.
The procedure outlined in our paper provides a means of comparison between different calculations of the total mass of an early-type galaxy without resorting to much more complex and computationally intensive superposition of orbits required in the Schwarzschild (1979) modelling.
- (4)
- It is difficult to draw general conclusions regarding anisotropies in the outer parts of early-type galaxies at this point because the sample of galaxies is still too small and there are problems regarding the small number of observed clusters per galaxy. Judging from the sample of clusters used
in this paper we did not find large departures from a Gaussian distribution. In a previous work (Samurovic & Danziger 2005) in the case of IC 1459 (beyond
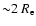 )
and NGC 3379 (beyond
)
and NGC 3379 (beyond
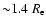 )
we found a hint of radial anisotropies. Dekel et al. (2005) using numerical simulations of disc-galaxy mergers recently found that for early-type galaxies the stellar orbits in their outer parts are very elongated.
Teodorescu et al. (2005) found that for PNe in the flattened early-type galaxy NGC 1344 the departures from a Gaussian distribution are small but they did not quantify them (see their Fig. 18).
)
we found a hint of radial anisotropies. Dekel et al. (2005) using numerical simulations of disc-galaxy mergers recently found that for early-type galaxies the stellar orbits in their outer parts are very elongated.
Teodorescu et al. (2005) found that for PNe in the flattened early-type galaxy NGC 1344 the departures from a Gaussian distribution are small but they did not quantify them (see their Fig. 18).
- (5)
- Given the fact that the full LOSVD profile of a given early-type galaxy obtained from integrated stellar light is typically based on the integrated spectra of several million stars andthe velocity dispersion based on GCs (and PNe) is based on at most several hundred objects, it is obvious that for more accurate kinematics of early-type galaxies at large radial distances an increased number of observed GCs (and PNe) is highly desirable.
Acknowledgements
We thank Francesca Matteucci for useful discussions.
This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
S.S. was supported with grants from MIUR COFIN 1998 Prot. No. 9802909231_001, the "Regione Friuli-Venezia-Giulia'' L.R. 3/98, CNAA Prot. No. 14/a and ASI Prot. No. I/R/043/02. S.S. expresses his gratitude to the TRIL (Training and Research in Italian Laboratories) programme of the Abdus Salam International Centre for Theoretical Physics. S.S. has been partially supported by
the Ministry of Science and Environmental Protection of the
Republic of Serbia through the project No. 1468, "Structure
Kinematics, and Dynamics of the Milky Way''. We thank the anonymous referee for the useful comments which helped to improve the manuscript.
- Bahcall, N. A., Lubin, L.
M., & Dorman, V. 1995, ApJ, 447, L81 [NASA ADS] (In the text)
- Bertin, G. 2000,
Dynamics of galaxies (Cambridge: Cambridge Univ. Press)
(In the text)
- Brown, B. A., & Bregman,
J. N. 1998, ApJ, 495, L75 [NASA ADS] [CrossRef] (In the text)
- Cappellari, M., Bacon, R.,
Bureau, M., et al. 2006, MNRAS, 360, 1126 [NASA ADS] (In the text)
- Ciotti, L., &
Pellegrini, S. 2004, MNRAS, 350, 609 [NASA ADS] (In the text)
- Côté, P.,
McLaughlin, D. E., Cohen, J. G., & Blakeslee, J. P. 2003, ApJ,
591, 850 [NASA ADS] [CrossRef] (In the text)
- De Rijcke, S., Prugniel,
P., Simien, F., & Dejonghe, H. 2006, MNRAS, accepted, preprint
[arXiv:astro-ph/0603700]
(In the text)
- Dekel, A., Stoehr, F.,
Mamon, G. A., Cox, T. J., & Primack, J. R. 2005, preprint
[arXiv:astro-ph/0501622]
(In the text)
- de Vaucouleurs, G.,
de Vaucouleurs, A., Corwin, H. G. Jr., et al., Third Reference
Catalogue of Bright Galaxies (New York: Springer-Verlag)
(In the text)
- Dirsch, B., Richtler, T.,
Geisler, D., et al. 2003, AJ, 125, 1908 [NASA ADS] [CrossRef] (In the text)
- Dirsch, B., Richtler, T.,
Geisler, D., et al. 2004, AJ, 127, 2114 [NASA ADS] [CrossRef] (In the text)
- Evans, N. W., Wilkinson,
M. I., Perrett, K. M., & Bridges, T. J. 2003, ApJ, 583,
752 [NASA ADS] [CrossRef] (In the text)
- Forte, J. C., Faifer, F.,
& Geisler, D. 2005, MNRAS, 357, 56 [NASA ADS] (In the text)
- Fukazawa, Y.,
Botoya-Nonesa, J. G., Pu, J., Ohto, A., & Kawano, N. 2006, ApJ,
636, 698 [NASA ADS] [CrossRef] (In the text)
- Grillmair, C. J.,
Freeman, K. C., Bicknell, G. V., et al. 1994, ApJ, 422, L9 [NASA ADS] [CrossRef] (In the text)
- Humphrey, P. J., Buote, D.
A., Gastaldello, F., et al. 2006, ApJ, submitted, preprint
[arXiv:astro-ph/0601301]
(In the text)
- Jones, C., Stern, C.,
Forman, W., et al. 1997, ApJ, 482, 143 [NASA ADS] [CrossRef] (In the text)
- Kim, D.-W., & Fabbiano,
G. 1995, ApJ, 441, 182 [NASA ADS] [CrossRef] (In the text)
- Kronawitter, A., Saglia,
R. P., Gerhard, O., & Bender, R. 2000, A&AS, 144, 53 [NASA ADS] (In the text)
- Mathews, W. G., &
Brighenti, F. 2003, ARA&A, 41, 191 [NASA ADS] (In the text)
- Méndez, R. H.,
Riffeser, A., Kudritzki, R.-P., et al. 2001, ApJ, 563, 135 [NASA ADS] [CrossRef] (In the text)
- Merritt, D. 1997, AJ, 114,
228 [NASA ADS] [CrossRef] (In the text)
- Morrison, H., Flynn, C.,
& Freeman, K. C. 1990, AJ, 100, 1191 [NASA ADS] [CrossRef] (In the text)
- Navarro, J. F., Frenk, C. S.,
& White, S. D. M. 1996, ApJ, 462, 563 [NASA ADS] [CrossRef] (In the text)
- O'Sullivan, E., Ponman,
T. J., & Collins, R. S. 2003, MNRAS, 340, 1375 [NASA ADS] (In the text)
- Paolillo, M., Fabbiano,
G., Peres, G., & Kim, D.-W. 2002, ApJ, 565, 883 [NASA ADS] [CrossRef] (In the text)
- Peng, E. W., Ford, H. C.,
& Freeman, K. C. 2004, ApJ, 602, 705 [NASA ADS] [CrossRef] (In the text)
- Pryor, C., & Meylan, G.
1993, in Structure and Dynamics of Globular Clusters, ed. S. G.
Djorgovski, & G. Meylan, ASP Conf. Ser., 50, 357
(In the text)
- Richtler, T., Dirsch, B.,
Gebhardt, K., et al. 2004, AJ, 127, 2094 [NASA ADS] [CrossRef] (In the text)
- Romanowsky, A. J.,
Douglas, N. G., Arnaboldi, M., et al. 2003, Science, 5640,
1696 [NASA ADS] [CrossRef] (In the text)
- Saglia, R. P.,
Kronawitter, A., Gerhard, O., & Bender, R. 2000, AJ, 119,
153 [NASA ADS] [CrossRef] (In the text)
- Samurovic, S., &
Danziger, I. J. 2005, MNRAS, 363, 769 [NASA ADS] (In the text)
- Schwarzschild, M. 1979,
ApJ, 232, 236 [NASA ADS] [CrossRef] (In the text)
- Sivakoff, G. R., Sarazin,
C. L., & Carlin, J. L. 2004, ApJ, 617, 262 [NASA ADS] [CrossRef] (In the text)
- Teodorescu, A. M.,
Méndez, R. H., Saglia, R. P., et al. 2005, ApJ, 635, 290 [NASA ADS] [CrossRef] (In the text)
- Thomas, J., Saglia, R. P.,
Bender, R., et al. 2005, MNRAS, 360, 1355 [NASA ADS] (In the text)
Copyright ESO 2006
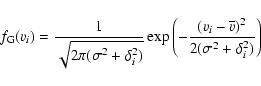
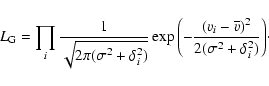
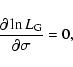
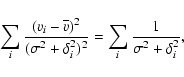
![\begin{figure}
\par\includegraphics[width=9cm,clip]{5017fig1.eps}\end{figure}](/articles/aa/full/2006/40/aa5017-06/Timg34.gif)
![\begin{figure}
\par\includegraphics[width=9cm,clip]{5017fig2.eps}\end{figure}](/articles/aa/full/2006/40/aa5017-06/Timg63.gif)
![\begin{figure}
\par\includegraphics[width=7.34cm,clip]{5017fig3.eps}\hspace*{2mm}
\includegraphics[width=7.34cm,clip]{5017fig4.eps}\end{figure}](/articles/aa/full/2006/40/aa5017-06/Timg84.gif)
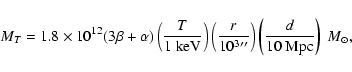
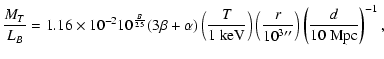
![\begin{displaymath}kT_{\sigma {[\rm ~keV]}} = 6.367 \times 10^{-6} \sigma_{\rm [km~s^{-1}]} ^2
\end{displaymath}](/articles/aa/full/2006/40/aa5017-06/img108.gif)
![\begin{figure}
\par\includegraphics[width=14.88cm,clip]{5017fig5.eps}\end{figure}](/articles/aa/full/2006/40/aa5017-06/Timg124.gif)
![\begin{figure}
\par\includegraphics[width=9cm,clip]{5017fig6.eps}\end{figure}](/articles/aa/full/2006/40/aa5017-06/Timg137.gif)
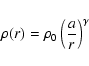
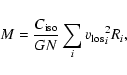
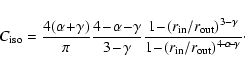
![\begin{figure}
\par\includegraphics[width=13.2cm,clip]{5017fig7.eps}\end{figure}](/articles/aa/full/2006/40/aa5017-06/Timg152.gif)