A&A 458, 69-78 (2006)
DOI: 10.1051/0004-6361:20064976

Internal kinematics of modelled interacting disc galaxies

T. Kronberger1,2 - W. Kapferer1 - S. Schindler1 - A. Böhm2,3 - E. Kutdemir2 - B. L. Ziegler2


1 - Institut für Astro- und Teilchenphysik, Universität Innsbruck, Technikerstr. 25, 6020 Innsbruck, Austria
2 - Institut für Astrophysik, Universität Göttingen, Friedrich-Hund-Platz 1, 37077 Göttingen, Germany
3 - Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany

Received 7 February 2006 / Accepted 19 June 2006

Abstract
We present an investigation of galaxy-galaxy interactions and their effects on the velocity fields of disc galaxies in combined N-body/hydrodynamic simulations, which include cooling, star formation with feedback, and galactic winds. Rotation curves (RCs) of the gas are extracted from these simulations in a way that follows the procedure applied to observations of distant, small, and faint galaxies as closely as possible. We show that galaxy-galaxy mergers and fly-bys disturb the velocity fields significantly and hence the RCs of the interacting galaxies, leading to asymmetries and distortions in the RCs. Typical features of disturbed kinematics are significantly rising or falling profiles in the direction of the companion galaxy and pronounced bumps in the RCs. In addition, tidal tails can leave strong imprints on the rotation curve. All these features are observable for intermediate redshift galaxies, on which we focus our investigations. We use a quantitative measure for the asymmetry of rotation curves to show that the appearance of these distortions strongly depends on the viewing angle. We also find in this way that the velocity fields settle back into relatively undisturbed equilibrium states after unequal mass mergers and fly-bys. About 1 Gyr after the first encounter, the RCs show no severe distortions anymore. These results are consistent with previous theoretical and observational studies. As an illustration of our results, we compare our simulated velocity fields and direct images with rotation curves from VLT/FORS spectroscopy and ACS images of a cluster at z=0.53 and find remarkable similarities.

Key words: galaxies: kinematics and dynamics - galaxies: interactions - methods: numerical - galaxies: structure

1 Introduction

The evolution of galaxies within the dense environment of a galaxy cluster is strongly influenced by various interaction phenomena. These environmental effects are superposed on the hierarchical growth predicted by cold dark matter (CDM) theories. Tidal interactions, for instance, have a higher probability in galaxy clusters and groups, due to the higher number density of galaxies. Going to higher redshifts, the merger frequency increases (Dressler et al. 1994), as galaxy clusters are assumed to assemble rather late in hierarchical CDM models. The relative velocities during encounters in galaxy clusters are higher than in the field and therefore reduce the probability for mergers.

In a recent paper we studied the influence of tidal interactions and mergers on the star formation rates of the involved galaxies using numerical simulations (Kapferer et al. 2005). However, not only is the star formation affected by galaxy-galaxy mergers, but also the internal kinematics of the gas. Most of the irregularities in the velocity field reflect disturbances in the gravitational potential of the galaxy. It is expected that kinematic disturbances fade within a few rotation cycles ($\le$1 Gyr) (e.g. Dale et al. 2001). Therefore, they can be used to trace the recent interaction history of a galaxy and give possible clues to the type of the respective interaction. In addition, identifying disturbances in the RCs is important for Tully-Fisher studies in order to accurately derive the maximum rotation velocity $V_{\rm max}$.

Observations by Rubin et al. (1999) have shown, for example, that rotation curves from several Virgo cluster galaxies exhibit clear kinematic disturbances. However, not all peculiarities are severe. Some rotation curves show only small asymmetries and others have no distortions at all. The authors did not find any strong correlations with Hubble type, local galaxy density, or HI deficiency. Many other studies have also relied on 1D information about the internal kinematics and used RCs to trace interactions in galaxy groups and clusters (e.g. Swaters et al. 1999; Dale et al. 2001; Conselice & Gallagher 1999; Mendes de Olivera et al. 2003). During the past few years it has become feasible to observe the full 2D velocity field of local galaxies. For example Chemin et al. (2006) investigated the H$\alpha$ line of 30 spiral and irregular galaxies in the Virgo cluster using Fabry-Perot interferometry (FPI). Their images show different signs of interactions in several objects. Likewise, the GHASP survey observed local field galaxies (Garrido et al. 2002) with FPI.

Almost all studies of distant, faint, and small galaxies are still based on slit spectroscopy (Vogt 2001; Böhm et al. 2004). Focussing on the environment of clusters, Ziegler et al. (2003) observed spirals in three intermediate redshift clusters ( z=0.3-0.6), using multi-object spectroscopy with VLT/FORS. In the same manner, Bamford et al. (2005) investigated five distant clusters. Using Subaru/FOCAS, Nakamura et al. (2006) examined four distant clusters. Finally, Metevier et al. (2006) studied a cluster at z=0.4 using Keck/LRIS. All these studies analysed the luminosity evolution of the galaxies via the Tully-Fisher relation. While Ziegler et al. (2003) and Nakamura et al. (2006) do not find significant differences between galaxies in clusters and in the field, Bamford et al. (2005) claim that cluster galaxies are on average brighter than their field counterparts. Part of this discrepancy may be attributed to the way distortions and irregularities in the RCs are accounted for.

Therefore, to systematically explore the influence of interactions on the velocity fields and hence the RCs, we present here a comprehensive analysis using numerical simulations. We present the results by closely mimicking the observations cited above. To this purpose we extract RCs that can be directly compared to the observed ones. Our N-body/SPH simulations have already been successfully applied to model RCs of isolated spiral galaxies (Kapferer et al. 2006). In that work we examined, for example, how observational constraints affect the quality of RCs. Here we go one step further to investigate the kinematics of tidally interacting and merging systems. Depending on the interaction geometry, galaxy mergers and fly-bys will cause distortions of different strengths in the velocity field of galaxies.

The main questions we will answer are what kind of distortions in the RCs can arise from tidal interactions? Are these peculiarities observable at intermediate and high redshifts? Are the features permanently visible or do they vanish within certain timescales? Some of the questions that we investigate in the present work were also addressed by Barton et al. (1999) and Heyl et al. (1996), who found qualitatively similar results to ours. However, as both groups used purely N-body models, they were not able to extract RCs as close to the observational procedure as we do (see Sect. 2.1). This is especially crucial in the treatment of high redshift galaxies, which we focus on in the present study. A very interesting work connecting observations and simulations was presented by Bournaud et al. (2004), who investigated tidal tails in interacting galaxies, also with respect to the signatures they leave in the position-velocity diagram of the galaxy. They found that, depending on the viewing angle, the sign of the velocity gradient can change in the presence of tidal tails.

This paper is organised as follows. In Sects. 2 and 3, we describe the simulations and the way we extract realistic rotation curves from the numerical data. Section 4 explains the interaction geometries used for the present work. In Sect. 5 the results for different interaction scenarios and their dependence on the viewing angle are presented, followed by a short discussion of some of the results' implications for observational properties of cluster galaxies in Sect. 6. We conclude with a summary of the main conclusions in Sect. 7.

2 Simulations

In this work we use some of the interacting systems presented in Kapferer et al. (2005). The simulations were carried out with the N-body/SPH code GADGET-2 developed by V. Springel (see Springel 2005 for details). In this code the gas of the galaxies is treated hydrodynamically, including cooling, star formation, stellar feedback, and galactic winds (Springel & Hernquist 2003). The collisionless dynamics of the dark matter and the stellar component is calculated using an N-body technique. The combined N-body/SPH simulation then calculates 5 Gyr of evolution. For every time step, we know the velocity of each particle and can extract realistic rotation curves. Other authors have used purely N-body techniques to investigate the kinematics of the modelled galaxies (e.g. Barton et al. 1999; Heyl et al. 1996). Although the overall kinematics of the disc is dominated by the darkmatter halo, disturbances of the gas have to be treated hydrodynamically, especially with respect to survival timescales of the distortions. The dynamics of the gas during an interaction is significantly different from the dynamics of the collisionless stellar component. Thus, a purely collisionless approach is insufficient for describing the kinematics of the gas in detail. Note that also the star formation rate of the interacting system is usually higher than that of the isolated system (Kapferer et al. 2005). Therefore, stronger galactic winds can occur, which will, in general, decrease the rotational velocities (see Paper I for a discussion of this effect). Nevertheless, the results obtained by the above-cited groups are very interesting and in several points similar to ours, so we will use them frequently as reference in subsequent sections. Iono et al. (2004) also used an N-body/SPH code to investigate position velocity diagrams of modelled galaxies, but focussed on signatures of radial gas flows.

In Kapferer et al. (2006, hereafter Paper I) we have shown that our models successfully reproduce rotation curves of isolated spiral galaxies. For completeness we repeat the initial conditions of our model galaxies in Table 1. These initial conditions were built according to Springel et al. (2005), which is based on the work of Mo et al. (1998). The two model galaxies were chosen such that they represent a Milky Way type and a small spiral galaxy, where the mass ratio of the two galaxies is 8:1.

Table 1: Properties of the initial conditions of the model galaxies.

Throughout the paper we adopt the standard $\Lambda$CDM cosmology with $\Omega_\Lambda=0.7$, $\Omega_{\rm m}=0.3$, and h=0.7.

2.1 Advanced rotation curve extraction

To follow the procedure applied in observations of distant, small, and faint galaxies as closely as possible we define as a first step a slit as shown in Fig. 1. Again, as in Paper I, we choose large relative slit widths as they are used in observations of intermediate and high redshift galaxies (e.g. Böhm et al. 2004; Nakamura et al. 2006). As a next step we project all stellar and gas particles of the N-body/SPH simulations onto a cartesian, uniform grid, with a spacing corresponding to typical spatial resolutions of the observations of intermediate redshift galaxies, for example, in the case of FORS1 the pixel scale of 0.2 $^{\prime\prime}$, which corresponds to $\sim $1.1 kpc for a redshift of z=0.4. Subsequently we derive a stellar blue band luminosity distribution I(x,z) (the coordinate system is chosen as indicated in Fig. 1) by assuming a stellar mass-to-light ratio of 1.2. This is the mean obtained using different star formation histories in the redshift range z=0.5-1.4 in Dickinson et al. (2003). Then we calculate a luminosity-weighted velocity field $V_{\rm {w}}$ as:

\begin{displaymath}V_{\rm {w}}(x,z)=V(x,z) \times I(x,z), \end{displaymath} (1)

where V(x,z) is the projected, 2D velocity field of the gas. This weighting assures that brighter regions contribute more to the velocity shift. To simulate seeing effects on our velocity-field measurements, a convolution with a Gaussian point spread function (PSF) was adopted on the luminosity-weighted velocity field with an FWHM according to typical observational conditions:

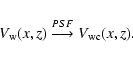\begin{displaymath}V_{\rm {w}}(x,z) \stackrel{PSF}{\longrightarrow} V_{\rm {wc}}(x,z). \end{displaymath} (2)

The FWHM of the seeing in observations is typically of the order of 0.5''-1.2'' (see e.g. Jäger et al. 2004). For our simulations we adopt a mean value of 0.8'' that corresponds, for example, to 4.3 kpc for a source at redshift z=0.4.

Finally, we compute the mean velocity at a certain galactocentric radius r, by averaging over all grid points within the slit perpendicular to the spatial axis. Hence, the velocity extracted for the RC at radius r reads:

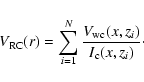\begin{displaymath}V_{\rm {RC}}(r) = \sum_{i=1}^N \frac{V_{\rm {wc}}(x,z_i)}{I_{\rm {c}}(x,z_i)}\cdot \end{displaymath} (3)

Here x=r is the apparent galactocentric radius along the spatial axis, and the sum runs over all grid points that lie within the defined slit. For all RCs presented in this work, we place the virtual slit along the major axis of the investigated galaxy. The normalisation with the convolved luminosity distribution $I_{\rm {c}}(x,z)$ is necessary to ensure that the rotational velocity V(r) of a constant velocity field would not be changed by the weighting and the seeing. This approach allows a direct comparison with 2D observations. In Fig. 2 we show the luminosity field derived from the stellar mass distribution, the unsmoothed and unweighted velocity field of the gas, and finally the extracted RC for one of our modelled galaxies in an early stage of an interaction (unequal mass merger).

We emphasise that the B-band mass-to-light ratio (M/L) is in general not constant for typical spiral galaxies but a complex function of radius (e.g. Verheijen et al. 2005). Therefore we extracted rotation curves by assuming different radial gradients in the mass-to-light ratio finding that the overall shape of the RC, which we investigate in this paper, is not sensitive to the specific choice of M/L. In Fig. 3 we show RCs extracted from one of our modelled systems using two different assumptions for the mass-to-light ratio. In one case we used a constant mass-to-light ratio while in the other case we extracted the RC using a linearly decreasing M/L with a slope of 0.1 kpc-1. Some quantitative differences are visible, but the shape of the RC is not affected.


  \begin{figure} \par\includegraphics[width=8.2cm,clip]{4976fig1.eps}\end{figure} Figure 1: Model galaxy A (gas (blue) and stars (yellow) are shown) and a virtual slit for extracting a rotation curve. The slit width d is indicated by the red lines. A coordinate system as used in the text (see Sect. 2.1) is shown.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.7cm,clip]{4976fig2.eps}\end{figure} Figure 2: Top left: luminosity field derived from the stellar-mass distribution; top right: the unsmoothed and unweighted velocity field of the gas. A virtual slit is indicated and a small part of the gaseous disc of the second galaxy is visible on the right hand side. Bottom left: the extracted RC for the modelled galaxy (dashed line) with 1$\sigma $ errors (solid lines). For this image series we use galaxy A in an early stage of an interaction (unequal mass merger).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.2cm,clip]{4976fig3.eps}\end{figure} Figure 3: Rotation curve extracted from one of our modelled systems along the major axis using two different assumptions for the mass-to-light ratio. The dashed line corresponds to a constant mass-to-light ratio, while the solid line was extracted using a linear decreasing M/L with a slope of 0.1 kpc-1.
Open with DEXTER

2.2 The spatial alignment and impact parameters

We follow the notation introduced by Duc et al. (2000) to describe the interaction geometry. Parameter b corresponds to the minimum separation of the galaxies' trajectories, as if they were point masses on Keplerian orbits (see Fig. 4). The two angles, $\Theta$ and $\Phi $, that define the spatial orientation of the disc are described in Fig. 4.


  \begin{figure} \par\includegraphics[width=17cm,clip]{4976fig4.eps}\end{figure} Figure 4: Sketch to illustrate the parameters used to define the interaction geometry. Figure from Kapferer et al. (2005). See also Duc et al. (2000) for further descriptions.
Open with DEXTER

For the complete sample, we selected the alignments in such a way as to cover as many geometries as possible, including minor and major mergers and fly-bys (achieved by increasing the minimum separation). The appearance of intrinsic RC distortions will of course not only depend on the interaction geometry but also on the angle under which the galaxy is observed (see Sect. 3.4). The interaction geometries we use for this work are listed in Table 2, which represents a small sub-sample of the large sample introduced by Kapferer et al. (2005).

Table 2: Interaction parameters for the simulations. C2: the two interacting model galaxies; C7: minimum separation [kpc]; C8: initial relative velocities of the two galaxies [km s-1].

3 Results

In the following subsections we study the kinematic distortions caused by unequal mass mergers, equal mass mergers, and fly-bys and investigate the dependence of their appearance on the viewing angle.

3.1 Rotation curve distortions caused by unequal mass mergers

To investigate the effects of unequal mass mergers on the RC of the massive partner in the interaction, we use simulation 1 (see Table 2), which is a co-rotating coplanar collision of model galaxy A with model galaxy B. Figure 5 shows the Gaussian smoothed images of the luminosity field of the galaxies, derived from the stellar mass distribution and with the assumption of a constant mass-to-light ratio (see Sect. 2.1). For the spatial resolution of the images, we chose 0.1''/pixel (0.54 kpc for z=0.4), which corresponds to the optical resolution FWHM of the ACS/WFC instrument on the Hubble Space Telescope (HST). It is obvious from these images that minor mergers are not always easy to detect in direct imaging, especially for intermediate and high redshift galaxies. In the early stages of an interaction, it is often possible to resolve the galaxy pairs, so the interaction is clearly visible. Later on it is more difficult to distinguish between an isolated galaxy and a late stage of interaction.

In Fig. 6 we show a sequence of images corresponding to different time steps in the merging process, where only the gas is shown. Note that the system is always viewed nearly face-on in this figure, while the RC is extracted from the system observed under an inclination angle of $i=80^\circ $ (edge-on is defined by $i=90^{\circ}$). Chart (a) represents 0.5 Gyr, (b) 0.6 Gyr, (c) 1 Gyr, and (d) 2 Gyr of evolution. In chart (a) in Fig. 6, the galaxy is shown shortly ($\sim $100 Myr) before the first encounter of the two gas discs, i.e. the moment, in which the two gas discs overlap completely for the first time. In the next chart (b) the two galaxies have their first encounter, whereas charts (c) and (d) show the galaxies 0.4 Gyr and 1.4 Gyr later, respectively. The massive partner (galaxy A) shows the typical features of merging events such as tidal tails and bridges. After 1.5 Gyr the perturbation in the gas distribution is still visible in a pronounced spiral arm, as shown in Fig. 6d on the right hand side.


  \begin{figure} \par\includegraphics[width=7.7cm,clip]{4976fig5.eps}\end{figure} Figure 5: Gaussian smoothed images of the luminosity field of the galaxies, derived from the stellar mass distribution and with the assumption of a constant mass-to-light ratio. The images a) to d) correspond to the images in Fig. 6 but observed under an inclination angle of 10$^\circ $. The sequence shows an unequal mass merger, where image a) represents 0.5 Gyr, b) 0.6 Gyr, c) 1 Gyr, and d) 2 Gyr of evolution. More details about the smoothing are listed in Sect. 2.1.
Open with DEXTER

In Fig. 7 the corresponding RCs are shown. The RCs were extracted as described in Sect. 2.1 for model galaxy A. Before the first encounter, the RC has an undisturbed shape. As galaxy B comes closer, galaxy A feels an acceleration towards the common centre of mass. This acceleration affects the velocity field in such a way that relative velocities with respect to the centre of galaxy A are enhanced towards the approaching galaxy B and weakened on the opposite side. In other words, the kinematic centre of the galaxy is shifted with respect to the geometrical centre of the gaseous disc. The RC of the merging-phase (b) shows strong signatures of the first encounter in its asymmetric shape. The incorporated galaxy B with its velocity component along the line of sight causes the acceleration on the left hand side of the RC. The right hand side of the RC is not affected yet. This part of the RC is not distorted and does resemble the "classical'' rotation curve shape rising in the inner part and turning over to a flat regime. The third RC corresponds to a later evolutionary step (400 Myr after RC (a)), where the less massive galaxy has passed galaxy A and left behind a disturbed velocity field. Although the RC has become almost symmetric again, it shows signs of interaction, especially the pronounced bumps in the outer parts ( ${\pm}{\sim} 10$ kpc). The last RC (d) shows the system 1.4 Gyr after the first encounter; note that galaxy B is no longer visible in the direct vicinity. Indeed the system has almost relaxed and nearly no signs of the interaction are left.


  \begin{figure} \par\includegraphics[width=7.6cm,clip]{4976fig6.eps}\end{figure} Figure 6: Sequence of images corresponding to different time steps in the merging process, with only the gas shown. The evolution of the system is calculated over 5 Gyr. Here a) represents 0.5 Gyr, b) 0.6 Gyr, c) 1 Gyr, and d) 2 Gyr of evolution.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8cm,clip]{4976fig7.eps}\end{figure} Figure 7: Rotation curves for an unequal mass merger (galaxies A and B) for different time steps, corresponding to the time series shown in Fig. 6 but observed under an inclination of $i=80^\circ $. The red lines always indicate the centre of galaxy A to highlight asymmetries in the RCs.
Open with DEXTER

In order to quantify the degree of asymmetry of the RC shape, we follow an approach used in Dale et al. (2001). We measure the area between the kinematically folded approaching and receding halves and divide it by the average area under the RC:

 
$\displaystyle \textrm{Asymmetry}=\sum \frac{\vert\vert V(r)\vert-\vert V(-r)\ve... ...t V(r)\vert+\vert V(-r)\vert}{\sqrt{\sigma^2(r)+\sigma^2(-r)}}\right]^{-1}\cdot$     (4)

Here $\sigma(r)$ is the uncertainty of the rotational velocity at position r. We adopted a value of 20 km s-1, which is typically the minimum uncertainty in observations of distant galaxies due to the limited spectral resolution. In Table 3 we list the asymmetry measure for different instances under different viewing angles for the unequal mass merger of simulation 1. The asymmetry of the RC increases with time as the two galaxies approach each other. After 0.5 Gyr a significant asymmetry is present along all lines-of-sight. The asymmetry reaches a maximum after 0.7 Gyr of evolution and subsequently falls to the value it had before the first encounter. The small drop in the asymmetry measure after 0.9 Gyr corresponds to the time between the first and second encounter. Note that the asymmetry strongly depends on the viewing angle at a certain instant. We will discuss this issue in Sect. 3.4. The small companion galaxy B, on the contrary, already loses most of its gas during the first pass through galaxy A and finally merges completely with the larger galaxy; hence, the distortions in the velocity field are so severe that we cannot make a more detailed investigation.

Table 3: Evolution of the asymmetry parameter1 for unequal mass mergers (simulations 1, 5, and 8) under different lines-of-sight (angle $\Phi $ is measured with respect to an arbitrarily chosen line-of-sight).

From both theoretical and observational studies, it is expected that kinematic disturbances fade within a few rotation cycles ($\le$1 Gyr) and therefore reflect the recent interaction history (e.g. Rubin et al. 1999; Dale et al. 2001). Our results from this and the subsequent sections confirm this statement numerically within the investigated interaction scenarios. The damping of the disturbances is listed quantitatively in Table 3. 1.4 Gyr after the first encounter, i.e. after 2 Gyr of evolution, the asymmetry measure reaches a value close to the one after 0.1 Gyr of evolution, i.e. before the first encounter.

In Fig. 8 the RC for model galaxy A 1.4 Gyr after the first encounter, i.e. after 2 Gyr of evolution is compared to the RC of the isolated model galaxy A after 2 Gyr of isolated evolution. The shape of the RC for model galaxy A resembles $\sim $1 Gyr after the first encounter the one of an isolated system, so the properties derived from it would not differ significantly within given errors. The only significant difference is the slope of the inner part of the RC. For intermediate and high-redshift galaxies, small bumps as in the right section of the red line would not be observable.

We study effects caused by collisions of counter-rotating discs using simulation 5 (see Table 2). The shape of the RCs do differ from those of the co-rotating case, as different velocity fields are superposed. However, there are also velocity components due to the movement of galaxy B on its orbit that is approaching galaxy A. These are the same for both configurations and are dominating for the unequal mass merger, which we investigate here. Connected to the relative trajectories of the galaxies is also a transfer of angular momentum, leading to increasing rotational velocities (Heyl et al. 1996); therefore, the shape of the RC of galaxy A during the interaction shows only a small dependence on the rotational direction of galaxy B.


  \begin{figure} \par\includegraphics[width=7.2cm,clip]{4976fig8.eps}\end{figure} Figure 8: Rotation curve of model galaxy A (blue, dashed line) 1.4 Gyr after the first encounter with model galaxy B, i.e. after 2 Gyr of evolution, as compared to the rotation curve of the isolated model galaxy A (red, solid line) after 2 Gyr of isolated evolution.
Open with DEXTER

  
3.2 Rotation curve distortions caused by equal mass mergers

In a next step we investigate the effects of equal mass mergers on the RCs of the interacting system. For this purpose we use simulation 2 (see Table 2), which is a co-rotating coplanar collision of two model galaxies B. Equal mass mergers massively disturb the velocity fields of the involved galaxies. Typically, the gaseous disc is almost completely destroyed in the merging process, and the orbits of the stars are randomized, leading to the formation of an elliptical galaxy. This result has been shown in many previous studies (e.g. Barnes & Hernquist 1991; Cretton et al. 2001; Naab & Burkert 2003; Bournaud et al. 2005). We also find this formation of an elliptical galaxy in our simulations; however, as this issue was investigated comprehensively by other authors, we do not discuss this in more detail in the present work. Instead, we chose two snapshots for which the gaseous disc is still observable and extracted the rotation curves for one of the interacting galaxies. The result is shown in Fig. 9 together with the corresponding interaction geometry. Note that in this figure the geometry is again illustrated as observed from nearly face-on, while the RC is extracted from the system observed under an inclination angle of $i=80^\circ $, as in the previous section. Panel (a) shows the system after 1.1 Gyr and panel (b) after 2 Gyr of evolution. The first encounter of the two gas discs happens after 1.2 Gyr of evolution, i.e. 0.1 Gyr after the snapshot shown in panel (a).


  \begin{figure} \par\includegraphics[width=7.5cm,clip]{4976fig9.eps}\end{figure} Figure 9: Rotation curves for an equal mass merger for different time steps corresponding to the interaction geometry illustrated in the lower panel. The galaxy from which the RC was extracted is highlighted. Here panel  a) shows the system after 1.1 Gyr and panel b) after 2 Gyr of evolution.
Open with DEXTER

Before the first encounter, the RC of the investigated galaxy is only slightly disturbed but shows an asymmetric shape. As in the previous section, the kinematic centre of the galaxy is shifted with respect to the geometrical centre, i.e. the maximum of the surface mass density of the gaseous disc, due to the influence of the approaching galaxy. As the two discs pass through each other, tidal tails and the bridges are formed. These features can be seen in panel (b), where the distribution of the gas is shown. An RC extracted from the highlighted galaxy does not show a symmetric shape either. Again the merging process introduces a strong acceleration on the right hand side in the galaxy, leading to the formation of a tidal tail. Therefore, the relative velocities on the right hand side decrease with respect to the centre, while the left hand side shows higher relative velocities, leading to the asymmetric shape. The decrease in the rotational velocities in the outermost parts on the right hand side of the RC emerges as gas from the tidal tail is covered by the slit. The gas and the stars of the tail falling back onto the rotating disc have a small radial velocity component at this projected position, as illustrated in Fig. 10. This possible change in the sign of the velocity gradients in the presence of tidal tails has already been found by Bournaud et al. (2004), who also points out the strong sensitivity of this result on the viewing angle. (We investigate this dependence on the viewing angle in Sect. 3.4.) A significant decrease in the outer parts of the RC (see Fig. 9) could indicate the presence of a massive tidal tail as consequence of a recent major merger event. However, this feature is not unique for tidal tails. As we will show in Sect. 3.4, the viewing angle of the observation also plays an important role (see also Bournaud et al. 2004).


  \begin{figure} \par\includegraphics[width=8cm,clip]{4976fig10.eps}\end{figure} Figure 10: Sketch to illustrate the decrease in the rotational velocities in the outer parts of the RCs that can be caused by gas from the tidal tail, which has small radial velocity components at this projected position and is covered by the slit.
Open with DEXTER

3.3 Rotation curve distortions caused by fly-bys

In order to estimate the influence of fly-bys on the shape of RCs, we use simulation 3 (see Table 2), which has a minimum separation of 50 kpc (at the first encounter). In Fig. 11 the RC of the highlighted galaxy for different snapshots is presented in the upper panel. In the lower panel the geometry corresponding to the different time steps of the interaction is shown. Panel (a) represents 0.5 Gyr, (b) 1.7 Gyr, (c) 2 Gyr, and (d) 3 Gyr of evolution. The change in the velocity field of the gaseous disc on short timescales is apparent in the right panel. The geometry (b) represents the nearest encounter, which is visible by a highly asymmetric shape. On the side pointing towards the companion, the RC does not flatten, due to the additional acceleration. On the opposite side, this feature is not present, instead the RC flattens. After 300 Myr (c), the velocity field does not show this asymmetry anymore, although the overall shape does not resemble an undisturbed RC. In the left panel we show the RC 0.5 Gyr after the beginning of the simulation (a) and after 2.5 Gyr of evolution (d). Note that the galaxies are spatially well-separated in both cases and that they would be therefore considered as isolated systems especially at high redshifts. The fly-by does not lead to persistent changes in the velocity field, and consequently the RCs do not show significant differences before and after the fly-by. The closest approach and the formation of observable distortions happens after $\sim $2 Gyr of evolution (panels (b) and (c)). After 3 Gyr of evolution, i.e. 1 Gyr after the appearance of the first distortions, the RC no longer shows signs of interaction. Thus, the velocity field again settles in this case to a relatively undisturbed equilibrium state after $\sim $1 Gyr.

Again we quantify the degree of asymmetry using Eq. (4) and present the results in Table 4. We find an increasing value for the asymmetry with time as the two galaxies approach each other. After $\sim $2 Gyr of evolution, the two galaxies come closest to each other. One Gyr later, the RC of the investigated galaxies shows a relatively undisturbed form again under most viewing angles, which again quantifies the settling time of $\sim $1 Gyr. In this interaction scenario we also find the strong dependence on the viewing angle in an interacting system.


  \begin{figure} \par\includegraphics[width=7.9cm,clip]{4976fig11.eps}\end{figure} Figure 11: Rotation curves for different snapshots of a fly-by of two model galaxies B. In the lower panel the alignment of the system and in the upper panel the corresponding rotation curves of the highlighted galaxy are shown. Here a) represents 0.5 Gyr, b) 1.7 Gyr, c) 2 Gyr, and d) 3 Gyr of evolution.
Open with DEXTER

Decreasing the minimum separation to 25 kpc as in simulation 4 (see Table 2) leads to slightly stronger distortions during the closest approach of the two galaxies, both in the mass distribution and in the kinematics. Nevertheless, the system settles back to an equilibrium state on approximately the same timescale as in the more distant fly-by discussed above ($\sim $1 Gyr). A fly-by of a less massive galaxy leads to lower asymmetries in the rotation curve (see simulation 7 in Table 4).

Table 4: Evolution of the asymmetry parameter1 for fly-bys (simulations 3, 4, and 7) under different lines-of-sight (angle $\Phi $ is measured with respect to an arbitrarily chosen line-of-sight).

  
3.4 Dependence of the results on the viewing angle

In an interacting system, two different velocity fields overlap. Therefore, the shape of the RC, which is a 1D representation of the full 3D velocity field, will significantly depend on the viewing angle. This fact is shown in Fig. 12 for the RCs extracted from the first encounter of model galaxies A and B seen nearly edge on from different viewing angles. The geometry is illustrated by the image series on the left hand side of the figure. Again this image series shows the system face-on, while the RCs are extracted from the galaxy observed under an inclination angle of $i=80^\circ $. We varied the azimuthal angle in steps of 45$^\circ $. The differences in the RCs are striking and are mainly caused by the velocity components of galaxy B on its trajectory and its projections.


  \begin{figure} \par\includegraphics[width=7.5cm,clip]{4976fig12.eps}\end{figure} Figure 12: Rotation curves for the first encounter of model galaxy A and B seen nearly edge on ( $i=80^\circ $) from different viewing angles. The geometry is illustrated by the image series on the left hand side. The snapshot corresponds to panel b) in Fig. 6 and therefore shows the system after 0.6 Gyr of evolution.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=6.5cm,clip]{4976fig13.eps}\end{figure} Figure 13: Rotation curves for model galaxy A after an equal mass merger from different viewing angles. The geometry is illustrated by the image series on the left hand side. The snapshot corresponds to panel b) in Fig. 9 and therefore shows the system after 2 Gyr of evolution. The change in the sign of the velocity gradient does not appear for all viewing angles.
Open with DEXTER

As we have shown in Sect. 3.2, the presence of a tidal tail can lead to a change in the sign of the velocity gradient, which was also described by Bournaud et al. (2004). However, this feature depends on the viewing angle, as in long-slit spectra (and also in position-velocity diagrams obtained from Fabry-Perot interferometry) we always look at only one (the line-of-sight) component of a 3D vector field. If this component is smaller at a certain position, because, for example, the gas there has been decoupled from the general rotation of the disc by tidal interaction, a decrease in the RC can be found. In Fig. 13 we show the interacting system with pronounced tidal tails from different lines-of-sight. Note that even a flat RC is possible in some configurations, although we found a change in the sign of the velocity gradient for most lines-of-sight. We also note that a prominent turn over in the RC is present in the third instance shown in Fig. 13. A part of the tidal tail is aligned with the line-of-sight. In their simulations for such configurations Bournaud et al. (2004) always found a change in the sign of the velocity gradient in their position-velocity diagrams, consistent with our results shown in Fig. 13. In addition to the line-of-sight, the time evolution of the tidal tail also plays an important role in the question of whether the turn over in the RC can be observed. Hibbard & Mihos (1995) showed that the kinematics of the tidal material depends on the radius, as well as on the time evolution. A decreasing outer part in the RC at a certain instant and under a certain line-of-sight can be interpreted, as pointed out in Fig. 10. However, this feature is not unique, as we mentioned before and a tidal tail is just one possible explanation.


  \begin{figure} \par\includegraphics[width=16.2cm,clip]{4976fig14.eps}\end{figure} Figure 14: ACS images taken in the F814 filter and rotation curves from the VLT/FORS spectroscopy of four galaxies in the distant cluster MS 0451.5-0305 at z=0.53. Tentatively, we find evidence for, e.g., tidal streams ( upper panel left, cf. Fig. 8) or a recent close fly-by/merger ( lower panel right, cf. Fig. 10). Note that the rotation curves give the observed values of the rotational velocity $V_{\rm rot}$; i.e. they are not corrected for inclination or offset angles ($\delta $) between the slit directions and the galaxies' major axes. The indicated rectangles correspond to the extensions of the derived RCs.
Open with DEXTER

As there is an infinite number of viewing angles to an infinite number of different interaction geometries, it is impossible to relate a specific observed RC distortion unambiguously to a certain interaction scenario without further information e.g. from high-resolution direct imaging. The specific shape of the RC will always depend on both the geometry of the interaction and the viewing angle. The situation is further complicated, as the dynamical evolution of the system is highly non-linear. However, these interaction-induced distortions have in common that the RCs become asymmetric, show significantly rising or falling profiles on the side pointing towards the other galaxy, and show pronounced bumps depending on the viewing angle (cf. Figs. 7 and 12). We found no observational biases for isolated galaxies that could produce such pronounced features (see Paper I for details). Most observational effects change the RC of a galaxy in a symmetric way (e.g. relative large slit widths, inclination). Spiral arms typically cause fluctuations of a few tens of km s-1that are superposed on the smooth rotation curve of the galaxy (see e.g. Sofue & Rubin 2001 and Paper I). Thus spiral arms can only account for smaller distortions but not for high asymmetries, as present in the present paper. Of course it is important to stress that galaxies in the universe are never isolated. The dynamical history of a galaxy will always influence the kinematics of the different components of galaxies. Not all asymmetries are caused by clearly observable mergers/interactions (Emergreen 2005 and references therein), although distinct asymmetries are often observed in interacting systems. Very recently disturbed isolated galaxies were investigated to search for indicators of interactions with dark galaxies, i.e. DM halos without any baryonic matter (Karachentsev et al. 2006).

4 Implications of the results for the observational properties of cluster galaxies

If the results, which were found in the previous sections for a restricted sample of interaction geometries, hold more generally, then they have an important implication for observational properties of cluster galaxy populations. First of all, stable regular discs show the classical RC, rising in the inner part and turning over to a flat regime. Interactions as mergers or fly-bys introduce instabilities to the gas, which lead to an enhanced star formation rate (e.g. Kapferer et al. 2005), provided the galaxy has not lost large fractions of its gas e.g. by ram-pressure stripping. As shown in the previous sections, these interactions also cause kinematic distortions. After the interaction, both the star formation and the kinematic distortions again settle back into a stable equilibrium state. Our results therefore suggest that enhanced star formation in apparently isolated galaxies can be triggered by non-equal mass mergers. In direct imaging, especially for high-redshift galaxies, those interactions are hardly visible. Additional investigation of the velocity field would help to reveal the dynamical state of the system. This implies that distortions in RCs can give evidence of the star formation of a galaxy and vice versa. As consequences of interactions being even longer observable in the velocity field than in direct imaging, these investigations can help to extract clues for the star formation history of a galaxy.

We now discuss briefly to what extent observations of distant cluster galaxies can be interpreted by simulations as presented here. To that purpose, we show thumbnails and rotation curves of four galaxies in Fig. 14 as examples. They are members of the cluster MS 0451.5-0305 at a mean redshift of z = 0.53, which was recently imaged by Ellis et al. using the ACS camera onboard HST in the F814W filter. The VLT/FORS spectra were obtained as part of a larger program to investigate galaxy transformations as described by Ziegler et al. (2003) (see also Jäger et al. 2004). Tilted MXU slitlets were placed along the photometric major axis as determined on groundbased images (VLT/FORS) since no full coverage of the cluster field by HST was available yet. The slitlets with 0.9 $^{\prime\prime}$ width are actually much longer than indicated on the thumbnails. The position-velocity diagrams (still unpublished) present the measured shifts of emission lines using the method introduced by Böhm et al. (2004) and Jäger et al. (2004) so that the displayed velocities are not corrected for the galaxy inclination and the effects caused by the observations. Note, however, that our $V_{\rm max}$ measurements fully accounted for geometrical (e.g. inclination) and observational effects (like seeing).

Two of the galaxies have rather regular structures and rotation curves, while the other two spirals are clearly distorted. They exhibit features that are very similar to what is seen in our simulations.

5 Summary and conclusions

In this work we have investigated the rotation curves of interacting spiral galaxies using N-body/SPH simulations with included prescriptions for cooling, star formation, and stellar feedback. We focussed on the questions of which distortions of the RCs can arise from mergers (in unequal mass mergers the mass ratio of our galaxies is 8:1) and fly-bys (25-50 kpc), how long these disturbances survive, and what is their dependence on the viewing angles. To summarise and conclude:

Acknowledgements
The authors would like to thank Volker Springel for providing them with GADGET2 and his initial-conditions generator. We are grateful to the anonymous referee for criticism that helped to improve the paper. The authors acknowledge the Austrian Science Foundation (FWF) through grant number P15868, the UniInfrastrukturprogramm 2004 des bm:bwk Forschungsprojekt Konsortium Hochleistungsrechnen, the German Science Foundation (DFG) through Grant number Zi 663/6-1, and the Volkswagen Foundation (I/76 520). In addition, the authors acknowledge the Deutsches Zentrum für Luft und Raumfahrt through grant 50 OR 0301, the ESO Mobilitätsstipendien des bm:bwk (Austria), and the Tiroler Wissenschaftsfonds (Gefördert aus Mitteln des vom Land Tirol eingerichteten Wissenschaftsfonds).

References

 
Copyright ESO 2006