A&A 457, 753-762 (2006)
DOI: 10.1051/0004-6361:20065240
N. Guessoum1 - P. Jean2 - N. Prantzos3
1 - American University of Sharjah, College of Arts & Sciences,
Physics Department, PO Box 26666, Sharjah, UAE
2 - CESR, CNRS/UPS, BP 4346, 31028 Toulouse Cedex 4, France
3 - Institut d'Astrophysique de Paris, 98bis Bd. Arago, 75104
Paris, France
Received 21 March 2006 / Accepted 28 June 2006
Abstract
We consider the production of positrons in microquasars, i.e. X-ray binary systems that exhibit jets frequently, but not continuously. We estimate the production rate of positrons in microquasars, both by simple energy considerations and in the framework of various proposed
models. We then evaluate the collective emissivity of the annihilation radiation produced by Galactic microquasars and we find that it might constitute a substantial contribution to the annihilation flux measured by INTEGRAL/SPI. We also discuss the possible spatial distribution of Galactic microquasars, on the basis of the (scarce) available data and the resulting morphology of the flux received on Earth. Finally, we consider nearby "misaligned'' microquasars, with jets occasionally hitting the atmosphere of the companion star; these would represent interesting point sources, for which we determine the annihilation flux and the corresponding light curve, as well as the line's spectral profile. We discuss the possibility of detection of such point sources by future instruments.
Key words: gamma rays: theory - line: formation - ISM: general - X-rays: binaries
Ever since the first detection of the gamma-ray signature (511 keV radiation) of the annihilating positrons in the Galaxy in 1970 (Johnson et al. 1972), the problem of the birth, propagation, interaction, and annihilation of the positrons has been a major topic of astrophysical investigation, both observationally and theoretically. Nonetheless, some of its fundamental issues, particularly the questions of positron origin and propagation, have remained mostly unsolved puzzles.
A series of observational campaigns, conducted by balloons![]() in the first two decades and
then by satellites
in the first two decades and
then by satellites![]() , have produced increasingly more precise, high-resolution spectra. Recent data have allowed a determination of
the physical conditions in the interstellar medium where the positrons annihilate (Guessoum et al. 2004; Churazov et al. 2005; Jean et al. 2006), based on an improved understanding of the various physical processes involved (Guessoum et al. 2005). In parallel, considerable progress has been made in mapping the Galaxy at 511 keV, first by CGRO-OSSE (Purcell et al. 1994; Cheng et al. 1997; Purcell et al. 1997; Milne et al. 2000; Milne et al. 2001) and, in particular, recently by INTEGRAL-SPI (Knödlseder et al. 2005).
, have produced increasingly more precise, high-resolution spectra. Recent data have allowed a determination of
the physical conditions in the interstellar medium where the positrons annihilate (Guessoum et al. 2004; Churazov et al. 2005; Jean et al. 2006), based on an improved understanding of the various physical processes involved (Guessoum et al. 2005). In parallel, considerable progress has been made in mapping the Galaxy at 511 keV, first by CGRO-OSSE (Purcell et al. 1994; Cheng et al. 1997; Purcell et al. 1997; Milne et al. 2000; Milne et al. 2001) and, in particular, recently by INTEGRAL-SPI (Knödlseder et al. 2005).
Despite that substantial progress, the origin of the huge amounts of positrons produced in the Galaxy (1043 e+ s-1) is still eluding us. A large number of potential sources has been proposed over the years: cosmic ray interactions with the interstellar medium (Ramaty et al. 1970), pulsars (Sturrock 1971), radioactive nuclei produced by explosive nucleosynthesis in supernovae (Clayton 1973) or novae (Clayton & Hoyle 1974), compact objects housing either neutron stars or black holes (Ramaty & Lingenfelter 1979), matter expelled by red giants (Norgaard 1980) and Wolf-Rayet stars (Dearborn & Blake 1985; Prantzos & Cassé 1986), gamma-ray bursts (Lingenfelter & Hueter 1984), (light) dark matter (Rudaz & Stecker 1988; Boehm et al. 2004), low-mass X-ray binaries (Prantzos 2004), hypernovae (Cassé et al. 2004), millisecond pulsars (Wang et al. 2006), and, most recently, pair production from the collision of gamma-ray photons from "SMall Mass Black Holes'' (SMMBHs) and X-ray photons from the Galactic Center black hole Sgr A* (Titarchuk & Chardonnet 2006).
The recent mapping of the Galaxy at 511 keV (Knödlseder et al. 2005), particularly the very large Bulge/Disc (B/D) ratio inferred, has placed rather severe constraints on the positron candidate sources. Of the aforementioned potential sources, Type Ia supernovae, low-mass X-ray binaries (LMXB's), and dark matter have emerged, for various reasons, as possible (or, rather, not impossible) candidates. However, each of these has its own difficulties:
In the case of LMXBs, positrons should be produced as e+-e- pairs in the inner regions of their accretion discs. Some of these would annihilate locally, but a non-negligible fraction would be channeled out by jets - when these exist. In general, positrons would reach the ISM relatively far from their source, and they would propagate and annihilate, contributing to the diffuse 511 keV emission. In special cases, when the jets are strongly inclined ("misaligned'') toward the plane of the binary system, positrons could periodically hit the atmosphere of the companion star where they would produce an annihilation signature, characterized, in particular, by its time variability and line profile.
In this paper we consider the possible fate of positrons ejected by microquasar jets. We first estimate the rate of positron production in jets, by reviewing estimates from other studies and by using simple energetics considerations; in that respect, we pay special attention to upper limits derived from the INTEGRAL-SPI measurements of positron annihilation fluxes from point sources in the Galaxy. We then consider two possible consequences: 1) the collective microquasar contribution to the flux of galactic annihilation radiation, which we find to be potentially substantial (especially from the central regions); and 2) the annihilation line signature of "misaligned'' microquasars. In the latter case, we study the fate of positrons in the companion's atmosphere in order to compute the photon emissivity, and determine the characteristic "light curve'' of such a source; we find that interesting observational signatures could be obtained from close enough and/or strongly active sources.
In Sect. 2 we present a brief overview of X-ray binaries, microquasars, and jets. In Sect. 3 we present our estimates of the rate of positrons produced by microquasar jets. In Sect. 4 we consider the overall contribution of microquasars to the global galactic annihilation flux. In Sect. 5 we consider the annihilation of positrons in misaligned microquasars. In Sect. 6 we summarize our conclusions.
X-ray binaries (XRB's) are systems containing a compact object
(either a neutron star or a stellar-mass black hole) accreting matter
from a companion star. A total of 280 galactic X-ray binaries are
currently known: 131 High Mass X-ray Binaries (HMXB's) (Liu et al. 2000), in which the companion star has a mass ![]() 5 solar masses (spectral type O or B) and where the mass
transfer usually takes place by way of the strong stellar wind; and
149 Low Mass X-ray Binaries (LMXB's) (Liu et al. 2001), in which the companion has a low mass (spectral type later than B), and the mass transfer is carried out by Roche lobe
overflow. Grimm et al. (2002) have shown that HMXB's tend to be distributed along the galactic plane, while LMXB's tend to be clustered in low Galactic longitudes. The number of XRB's brighter than
5 solar masses (spectral type O or B) and where the mass
transfer usually takes place by way of the strong stellar wind; and
149 Low Mass X-ray Binaries (LMXB's) (Liu et al. 2001), in which the companion has a low mass (spectral type later than B), and the mass transfer is carried out by Roche lobe
overflow. Grimm et al. (2002) have shown that HMXB's tend to be distributed along the galactic plane, while LMXB's tend to be clustered in low Galactic longitudes. The number of XRB's brighter than
![]() erg/s is estimated to
erg/s is estimated to ![]() 700 in the Galaxy (Grimm et al. 2002; Paredes 2005).
700 in the Galaxy (Grimm et al. 2002; Paredes 2005).
Among the detected XRB's, 43 have now been found to exhibit radio emission, which is interpreted as synchrotron radiation. It is generally believed that the radio emission is evidence of jets. Of the 43 objects, 35 are LMXB's and 8 are HMXB's. Moreover, of the 43 systems, 16 are confirmed cases with resolved jets (Ribó 2005; Paredes 2005; Chaty 2005). Such systems (a compact object accreting from a companion star and ejecting a stream of relativistic particles) are known as microquasars. It is likely that all 43 radio-emitting X-ray binaries (REXB) are microquasars. The population of microquasars in the Galaxy is estimated at about 100 (Paredes 2005), although only 16 are "officially'' known (or confirmed) at present. We note that Pandey et al. (2006a,b) have recently reported 4 new REX sources: IGR J17091-3624, IGR J17303-0601, IGR J17464-3213, and IGR J18406-0539; in addition, two sources, X Nor X-1 and IGR J17418-1212, have been presented as microquasars (Klein-Wolt et al. 2004; and Tsarevsky 2004, respectively). We refer to these six sources as "new tentative microquasars''. The catalog of microquasars is expected to grow rapidly with the array of instruments and studies now investigating these objects (from radio to gamma rays).
Although jets of such systems were first observed in 1979 (in the peculiar object SS 433), microquasars were identified and imaged in the Galaxy only in 1992 when Mirabel et al. (1992) performed high-resolution radio observations of the GC's "great annihilator'' 1E 1740.7-2942 and soon afterwards in GRS 1915+105 (Mirabel & Rodriguez 1994).
Recent studies (Falcke et al. 2004; Mirabel 2004; Fender et al. 2004, 2005a) considerably improved our understanding of the conditions that lead to the emergence of jets in XRBs. First and foremost, a connection has been established between X-ray flux and jet formation: jets seem to appear when the accretion disc X-ray luminosity is low. Jets are apparently produced when the inner disc is replenished; there is a clear general pattern of steady jets in the "low/hard state'' of the X-ray (microquasar) sources, while no jet is seen in "the high/soft state''.
A relatively elaborate model of this scenario has been proposed by Fender et al. (2004, 2005a). A relation between the power in the jet (when it exists) and the X-ray luminosity of a given source is derived:
![]() ,
with luminosities expressed in units of the corresponding Eddington luminosity. These authors argue that steady jets are produced when the X-ray spectrum of a source hardens beyond a certain value (which
may be universal or vary somewhat from one source to another). The spectrum softens when the X-ray luminosity increases above about 1% of the Eddington value; when this happens, the jet first increases in speed and then quickly gets suppressed and disappears.
,
with luminosities expressed in units of the corresponding Eddington luminosity. These authors argue that steady jets are produced when the X-ray spectrum of a source hardens beyond a certain value (which
may be universal or vary somewhat from one source to another). The spectrum softens when the X-ray luminosity increases above about 1% of the Eddington value; when this happens, the jet first increases in speed and then quickly gets suppressed and disappears.
There seems to be an agreement on the above relation between
![]() and
and
![]() ,
which is supposed to hold for sources
individually. On the other hand, there seems to be considerable
uncertainty over the value of
,
which is supposed to hold for sources
individually. On the other hand, there seems to be considerable
uncertainty over the value of
![]() (Fender et al. 2005b); indeed, using various sources (e.g. XTE J1118+480) for "calibration'', authors obtain values ranging from 0.006 as a
lower limit (Fender et al. 2005a) to 0.3 (Malzac et al. 2004), which Fender et al. (2005a) take as an upper limit. In the case of transient jets, Fender et al. (2005b) conclude that the value of
(Fender et al. 2005b); indeed, using various sources (e.g. XTE J1118+480) for "calibration'', authors obtain values ranging from 0.006 as a
lower limit (Fender et al. 2005a) to 0.3 (Malzac et al. 2004), which Fender et al. (2005a) take as an upper limit. In the case of transient jets, Fender et al. (2005b) conclude that the value of
![]() would range between 0.04 and 4.0, at least for black hole sources, which tend to exhibit jets that are about 10 times more powerful than those of neutron star jets, both in the steady and in the transient cases.
would range between 0.04 and 4.0, at least for black hole sources, which tend to exhibit jets that are about 10 times more powerful than those of neutron star jets, both in the steady and in the transient cases.
Secondly, a general correlation is also found between the velocity of the outflow and the X-ray luminosity of the accreting source: increases in X-ray luminosity tend to accelerate the jets as long as the source remains in the low/hard state. Fender et al. (2005a) further argue that the velocities of transient jets are significantly larger (
![]() c) than those of steady jets (
c) than those of steady jets (![]() 0.7 c). Jets with larger Lorentz factors have also been considered, but the standard cases are those presented by Fender et al. (2005a).
0.7 c). Jets with larger Lorentz factors have also been considered, but the standard cases are those presented by Fender et al. (2005a).
The particle content of the jets is among the major unresolved issues in the field of microquasars (e.g. Scheck et al. 2002). Observations of emission lines in the case of SS 433 (Marshall et al. 2002) suggest a substantial baryonic content of its jets. Several studies have considered the implications of a hadronic jet composition, either for the galactic cosmic ray content (Heinz & Sunyaev 2002; Fender et al. 2005b) or for the synthesis of Li on the surface of the companion star (Butt et al. 2003). Others have considered the gamma-ray and neutrino production at the surface of the companion by impinging high-energy protons (Romero & Orellana 2005). On the other hand, arguments for e+-e- pair-dominated jets have been put forward, especially in cases involving the extraction of the spin energy of the black hole (Celotti & Blandford 2001). A strong argument in favor of such a leptonic composition is the repeated observations of highly polarized jets. Several leptonic microquasar models have been proposed in recent times, e.g. Bosch-Ramon & Parades (2004a,b), Bosch-Ramon et al. (2005), Dermer & Böttcher (2006); see the review by Romero (2005). Some rather complex models have also been proposed, like "two-flow'' models (pair beam surrounded by a mildly relativistic e--p plasma) , or e--p jets that later get loaded with pairs by interactions with high-energy photons (e.g. Scheck et al. 2002, and references therein).
In this work we consider microquasar jets channeling positrons (or e+-e- pairs) from the inner regions of the source's accretion disc into the ISM or towards the companion star (if the jet is
"misaligned''). We also note that positrons can also be produced by hadrons from the jet colliding with nuclei (e.g. through p-p
![]() p + n +
p + n + ![]() ), but such processes would contribute
only negligible amounts of positrons due to the small numbers of high-energy hadrons as well as the low values of the relevant cross sections.
), but such processes would contribute
only negligible amounts of positrons due to the small numbers of high-energy hadrons as well as the low values of the relevant cross sections.
In order to estimate the flux of the resulting annihilation radiation, the rate of positron ejection by the jets must then be determined.
The high-temperature, high-density conditions in the inner regions of
the binary system's accretion disc produce electron-positron pairs
via
![]() reactions. A
fraction of them annihilate close to the compact object, but when
jets appear, they may channel out a significant number of pairs. A
few authors have attempted to model and estimate the production and
ejection of pairs in those conditions.
reactions. A
fraction of them annihilate close to the compact object, but when
jets appear, they may channel out a significant number of pairs. A
few authors have attempted to model and estimate the production and
ejection of pairs in those conditions.
According to Beloborodov (1999) the pairs are cooled to energies of 1-10 keV and blown away by soft radiation to form a semi-relativistic wind. Depending on the compactness of the source (
![]() ,
where L and R are the power and radius of the emitting region, and
,
where L and R are the power and radius of the emitting region, and
![]() is the Thomson cross section), the plasma will form an optically thin or thick atmosphere. The density of the outflow and the rate of ejection of electrons and
positrons depend on the rate of production of pairs (which, in turn, depend on the photon "seed'' spectrum and on the accretion disc model), the annihilation rate and the "escape efficiency'' of the pairs. Under the assumption of an optically thin pair wind, where the
pairs escape before they annihilate (
is the Thomson cross section), the plasma will form an optically thin or thick atmosphere. The density of the outflow and the rate of ejection of electrons and
positrons depend on the rate of production of pairs (which, in turn, depend on the photon "seed'' spectrum and on the accretion disc model), the annihilation rate and the "escape efficiency'' of the pairs. Under the assumption of an optically thin pair wind, where the
pairs escape before they annihilate (
![]() ,
with
,
with
![]() ,
where
,
where ![]() is the electron density), Beloborodov (1999) shows that the maximum pair luminosity is given by
is the electron density), Beloborodov (1999) shows that the maximum pair luminosity is given by
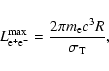 |
(1) |
Misra & Melia (1993) suggest that the intense radiation field is
responsible for the Compton acceleration of the pairs produced in the
inner regions of the accretion disc. They find that a large rate of
pairs (up to
![]() s-1) stream outwards from the
disc (at velocities of
s-1) stream outwards from the
disc (at velocities of ![]() 0.7 c), even after 90% have
annihilated near the base. One must note, however, that this large
rate is obtained with an accretion rate of
0.7 c), even after 90% have
annihilated near the base. One must note, however, that this large
rate is obtained with an accretion rate of ![]() 5
5
![]() yr-1, a rate that can normally be attained only in episodic outbursts. Indeed, the model of Misra & Melia (1993) was
mainly aiming to reproduce the 1E 1740.7-2942 "annihilation flare'' of 1991.
yr-1, a rate that can normally be attained only in episodic outbursts. Indeed, the model of Misra & Melia (1993) was
mainly aiming to reproduce the 1E 1740.7-2942 "annihilation flare'' of 1991.
Table 1: Limits on positron rates from SPI upper limits for XRB sources of interest. The positron rates were calculated assuming a positronium fraction of 95%. The bottom part of the table lists microquasar sources, the last two or three being misaligned ones.
Yamasaki et al. (1999) consider two-temperature
accretion discs by taking into account the formation of relativistic
pair outflows, in both AGN and microquasars. They show that in the
inner regions of the discs, when the mass accretion rate becomes
larger than about one tenth of the Eddington rate (
![]() g s-1 where M is the mass of the compact
object) or
g s-1 where M is the mass of the compact
object) or ![]()
![]() yr-1, most of the
viscously dissipated energy is converted into the thermal and kinetic
energy of the electron-positron pairs. They obtain a maximum power of
the pair outflow of 0.136
yr-1, most of the
viscously dissipated energy is converted into the thermal and kinetic
energy of the electron-positron pairs. They obtain a maximum power of
the pair outflow of 0.136
![]() for an accretion rate of 10
for an accretion rate of 10
![]() yr-1 (assuming
yr-1 (assuming
![]() and
and
![]() ), which translates into a pair ejection rate of
), which translates into a pair ejection rate of
![]() s-1, assuming the jet is leptonic.
s-1, assuming the jet is leptonic.
Considering the global energetics of microquasar jets in the Galaxy, one may note that
and
Finally, in attempting to fit the Nova Muscae 1991 "annihilation flare'', Kaiser & Hannikainen (2002) inferred a positron annihilation rate of
![]() s-1 in the atmosphere of the companion star (assuming a distance to Earth of
s-1 in the atmosphere of the companion star (assuming a distance to Earth of ![]() 5.5 kpc). They argued that such a high pair yield can be achieved when the plasma is "photon-starved'', that is when the number of high-energy photons in the disc strongly exceeds that of the soft seed photons (see Zdziarski et al. 1990).
5.5 kpc). They argued that such a high pair yield can be achieved when the plasma is "photon-starved'', that is when the number of high-energy photons in the disc strongly exceeds that of the soft seed photons (see Zdziarski et al. 1990).
Despite the wide range in the results obtained in the aforementioned studies, one concludes that a reasonable estimate for "steady-state'' production and ejection of pairs in normal conditions is ![]() 1041 s-1.
1041 s-1.
Taking a different, empirical approach, interesting upper-limit constraints to the microquasar positron emissivity may be established by way of the recent annihilation radiation measurements by
INTEGRAL-SPI. Knödleseder et al. (2005) have published 3-![]() flux upper limits for a dozen galactic microquasars/LMXB's/HMXB's; we have completed the data for other sources of interest to us here, particularly the "misaligned'' microquasars that we will consider in some detail in Sect. 5. Table 1 lists the sources we have considered, with the corresponding SPI upper-limits on their 511 keV emission flux (taking the sources to be point-like) and inferred rates of positron injection, assuming that positrons do not annihilate far from the source. The bottom part of the table lists microquasar sources, the last two or three being misaligned ones.
flux upper limits for a dozen galactic microquasars/LMXB's/HMXB's; we have completed the data for other sources of interest to us here, particularly the "misaligned'' microquasars that we will consider in some detail in Sect. 5. Table 1 lists the sources we have considered, with the corresponding SPI upper-limits on their 511 keV emission flux (taking the sources to be point-like) and inferred rates of positron injection, assuming that positrons do not annihilate far from the source. The bottom part of the table lists microquasar sources, the last two or three being misaligned ones.
It can be seen that the data of the Table imply that upper limits for the steady positron annihilation rate of individual sources are always >1041 e+ s-1 (albeit with large uncertainties, due in particular to uncertain distance estimates), so the upper-limit rates inferred from INTEGRAL data do not clash with the average value derived in the works cited above.
From the different considerations and estimates presented above, it
appears that a "canonical average'' rate of ![]() 1041 e+ s-1 ejected by the microquasar jets is not unreasonable. We will adopt this value for the determination of expected fluxes from individual sources (Sect. 5), but realizing the corresponding large
uncertainty, we will also consider lower (1040 e+ s-1) values for "weak-episode jets'' as well as larger (1042 e+ s-1) ones, in "strong flare'' cases. We immediately note
that should this average, "canonical value'' prove to be reasonably correct, the
1041 e+ s-1 ejected by the microquasar jets is not unreasonable. We will adopt this value for the determination of expected fluxes from individual sources (Sect. 5), but realizing the corresponding large
uncertainty, we will also consider lower (1040 e+ s-1) values for "weak-episode jets'' as well as larger (1042 e+ s-1) ones, in "strong flare'' cases. We immediately note
that should this average, "canonical value'' prove to be reasonably correct, the ![]() 100 microquasars that are believed to exist in the Galaxy (Paredes 2005) would produce a global annihilation emissivity near that measured by SPI (and previous instruments).
100 microquasars that are believed to exist in the Galaxy (Paredes 2005) would produce a global annihilation emissivity near that measured by SPI (and previous instruments).
Another upper limit on the collective emission by galactic microquasars may be derived by considering the global energetics. Indeed, (i) the total luminosity of LMXRBs in the Milky Way is 2-3
![]() erg s-1 (Grimm et al. 2002); while (ii) the luminosity of
erg s-1 (Grimm et al. 2002); while (ii) the luminosity of ![]() 1043 e+ s-1 observed by SPI/INTEGRAL is
1043 e+ s-1 observed by SPI/INTEGRAL is ![]() 1037 erg s-1, assuming the positronic jets are mildly relativistic (i.e. positrons have energies
<1 MeV). Of course, as Grimm et al. (2002) note, the Galactic LMXRB population is dominated by a dozen bright sources (of
1037 erg s-1, assuming the positronic jets are mildly relativistic (i.e. positrons have energies
<1 MeV). Of course, as Grimm et al. (2002) note, the Galactic LMXRB population is dominated by a dozen bright sources (of ![]() 1038 erg s-1 each) lying in the disk. But the
remaining fraction of
1038 erg s-1 each) lying in the disk. But the
remaining fraction of ![]() 90% is highly clustered towards the bulge (Fig. 1 in Grimm et al. 2002), as required by the SPI data and noted in Prantzos (2004), while their collective
luminosity is 2-3
90% is highly clustered towards the bulge (Fig. 1 in Grimm et al. 2002), as required by the SPI data and noted in Prantzos (2004), while their collective
luminosity is 2-3
![]() erg s-1, i.e. 20 times larger than required to explain the Galactic positron energetics. We note that those are precisely the low-luminosity (sub-Eddington) sources that may produce jets (see the discussion in Sect. 2). According to estimates by Paredes (2005), based on current microquasar statistics, there are about 100 microquasars in the Milky Way, which corresponds to about 1/3 of the
erg s-1, i.e. 20 times larger than required to explain the Galactic positron energetics. We note that those are precisely the low-luminosity (sub-Eddington) sources that may produce jets (see the discussion in Sect. 2). According to estimates by Paredes (2005), based on current microquasar statistics, there are about 100 microquasars in the Milky Way, which corresponds to about 1/3 of the ![]() 300 LMXRBs in our Galaxy as estimated by
Grimm et al. (2002). Applying this correction factor of 1/3 to the microquasar energetics, still leaves about 1038 erg s-1 available for positron production in their jets, i.e.
about 6 times more than required by SPI data. We note at this point that some of the currently observed microquasars result from HMXRBs, but their fraction is rather small (less than 20%) and does not affect the arguments presented here (see next section for a more detailed treatment). Moreover, we wish to stress the large (order-of-magnitude) uncertainty that exists in our current knowledge of the ratio between the energy that goes into positrons or into the
jet (as a whole) compared to the energy that is radiated, an issue that is further complicated by the unknown lepton-to-hadron content ratio of the jet.
300 LMXRBs in our Galaxy as estimated by
Grimm et al. (2002). Applying this correction factor of 1/3 to the microquasar energetics, still leaves about 1038 erg s-1 available for positron production in their jets, i.e.
about 6 times more than required by SPI data. We note at this point that some of the currently observed microquasars result from HMXRBs, but their fraction is rather small (less than 20%) and does not affect the arguments presented here (see next section for a more detailed treatment). Moreover, we wish to stress the large (order-of-magnitude) uncertainty that exists in our current knowledge of the ratio between the energy that goes into positrons or into the
jet (as a whole) compared to the energy that is radiated, an issue that is further complicated by the unknown lepton-to-hadron content ratio of the jet.
The simple estimate made in the previous paragraph implies that the ratio between the positron power and the X-ray luminosity of microquasars is, on average, about 16%. One must recall, however,
that there is a relation between the two quantities, namely
![]()
![]() (references given above), which leads to more realistic expectations.
(references given above), which leads to more realistic expectations.
Indeed, taking the derivative of the cumulative X-ray luminosity function given by Grimm et al. (2002) for LMXRB's (see Eq. (15) of Grimm et al. 2002) and assuming that 1/3 of LMXRBs are microquasars, one can derive a differential luminosity distribution function for
microquasars:
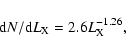 |
(2) |
Now if the total positron power in the Galaxy is required to be 1037 erg/s (i.e. 0.1 in Eddington units), and using the above equation (Eq. (2)) to integrate for the total power, one finds that for a = 0.5, B is between 0.9 and 1.6% depending on the assumption made on the maximum X-ray luminosity of the microquasar (1 or 0.1
![]() ,
respectively), which are very reasonable figures.
,
respectively), which are very reasonable figures.
Furthermore, having estimated B and thus obtained an analytic distribution function for the microquasars' positron emissivity, one can obtain the total rate of positrons emitted by all microquasars (of different luminosities) in the Galaxy by integrating dN/d![]() against the luminosities and the rate of positrons emitted by each source, as obtained by Yamasaki et al. (1999). Again, for the linear relation (a = 1) one obtains a total rate
against the luminosities and the rate of positrons emitted by each source, as obtained by Yamasaki et al. (1999). Again, for the linear relation (a = 1) one obtains a total rate
![]() between 0.3 and
between 0.3 and
![]() e+/s (depending on the maximum X-ray luminosity of a given microquasar, i.e. 0.1 or 1
e+/s (depending on the maximum X-ray luminosity of a given microquasar, i.e. 0.1 or 1
![]() ,
respectively); however, for the preferred non-linear relationship (a = 1/2), one obtains
,
respectively); however, for the preferred non-linear relationship (a = 1/2), one obtains
![]() between 1.8 and
between 1.8 and
![]() e+/s (microquasar X-ray luminosities of 0.1 and 1
e+/s (microquasar X-ray luminosities of 0.1 and 1
![]() ,
respectively), values that are very encouraging in considering microquasars as possible contributors to the overall positron annihilation flux from the central galactic regions.
,
respectively), values that are very encouraging in considering microquasars as possible contributors to the overall positron annihilation flux from the central galactic regions.
Assuming that ![]() 100 microquasars exist in the Galaxy (Paredes 2005), and noting from the locations plot of the 22 microquasars presently known/confirmed (Fig. 1) that about half of them are in the central regions, i.e.
100 microquasars exist in the Galaxy (Paredes 2005), and noting from the locations plot of the 22 microquasars presently known/confirmed (Fig. 1) that about half of them are in the central regions, i.e. ![]()
![]() degrees from the GC, we can estimate the flux of annihilation radiation that can be expected from such a population of sources with jets ejecting
degrees from the GC, we can estimate the flux of annihilation radiation that can be expected from such a population of sources with jets ejecting ![]() 1041 e+ s-1 on average and compare it to the global galactic centre annihilation flux reported by Knödlseder et al. (2005).
1041 e+ s-1 on average and compare it to the global galactic centre annihilation flux reported by Knödlseder et al. (2005).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{5240fig1.eps}\end{figure}](/articles/aa/full/2006/39/aa5240-06/Timg78.gif) |
Figure 1: Microquasars (position and type) in the Galaxy. |
| Open with DEXTER | |
The microquasars can have either ``misaligned'' (highly inclined with respect to the orbital plane) or "normal'' (low inclination) jets. The normal microquasars will pour out their positrons into the ISM, where the usual 2-3 photon production processes take place (see Guessoum et al. 2005).
In the case of misaligned microquasars (about 15-20% of the total) we assume, following Butt et al. (2003), that their jets hit the companion ![]() 10% of the time. Only 1 of the
10% of the time. Only 1 of the ![]() 2 annihilation photons will emerge then, the other being absorbed in the companion's atmosphere (see Sect. 5). The remaining 90% of the positrons are thrown into the ISM, where they
produce 2-3 photons each.
2 annihilation photons will emerge then, the other being absorbed in the companion's atmosphere (see Sect. 5). The remaining 90% of the positrons are thrown into the ISM, where they
produce 2-3 photons each.
The total flux of annihilating positrons coming from the inner Galaxy would be the sum of the flux contributed by the misaligned jets and the normal jets:
| (3) |
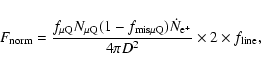 |
(4) |
![\begin{displaymath}F_{\rm mis} = { f_{\rm\mu Q} N_{\rm\mu Q} f_{{\rm mis}\rm\mu ...
...\rm jet-*} + 2\times (1 - f_{\rm jet-*})]\times f_{\rm line},
\end{displaymath}](/articles/aa/full/2006/39/aa5240-06/img81.gif) |
(5) |
With those parameter values, we obtain:
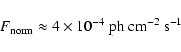 |
(6) |
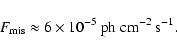 |
(7) |
As noted in Sect. 1, the spatial distribution of the 511 keV flux detected by SPI-INTEGRAL puts severe constraints on candidate sources of positrons. Although far from complete at present, the available sample of known/confirmed microquasars appears encouraging in that respect. Figure 1 displays the position and type (LMXB/HMXB) of the 22 currently known microquasars.
While fully aware that this list represents only about one fifth of the microquasars believed to exist in the Galaxy, we can still attempt to determine a Bulge-to-Disc (B/D) ratio of the annihilation produced by such sources and compare that with the limits obtained
from SPI data (Knödlseder et al. 2005), which inferred a rate of positron annihilation of
![]() e+ s-1 in the bulge and
e+ s-1 in the bulge and
![]() e+ s-1 in the disc.
e+ s-1 in the disc.
Referring to Table 1, which lists the types, positions and distances of these microquasars, we note that roughly 80% of them are LMXB's, about 15% of which are in the halo, 35% are in the disc, and about 50% are in the bulge, while 20% of the sources are HMXB's, ![]() 10% of which may be in the bulge and the rest in the disc. The canonical average rate of positron production has been taken to be about 1041 e+ s-1 by a typical jet from an LMXB microquasar, while for HMXB microquasars jets are ten times less powerful and thus about three times less productive in positrons (recall that
10% of which may be in the bulge and the rest in the disc. The canonical average rate of positron production has been taken to be about 1041 e+ s-1 by a typical jet from an LMXB microquasar, while for HMXB microquasars jets are ten times less powerful and thus about three times less productive in positrons (recall that
![]() ). One must then take into consideration the confinement probability of positrons ejected from these sources; we note that: i) according to Jean et al. (2006), positrons produced in the bulge do not escape, they end up
annihilating in the bulge if their energy is below
). One must then take into consideration the confinement probability of positrons ejected from these sources; we note that: i) according to Jean et al. (2006), positrons produced in the bulge do not escape, they end up
annihilating in the bulge if their energy is below ![]() 10 MeV, which is the case for positrons produced by microquasars, if one ignores (as in this basic treatment) internal acceleration
processes; ii) the scale height of LMXBs in the disk is
10 MeV, which is the case for positrons produced by microquasars, if one ignores (as in this basic treatment) internal acceleration
processes; ii) the scale height of LMXBs in the disk is ![]() 400 pc, while the gas has a scale height of
400 pc, while the gas has a scale height of ![]() 100 pc, so about 50% of positrons produced by LMXB's there are ejected toward the disk and annihilate, while the rest (50%) of the positrons are released in the halo and either contribute to a diffuse annihilation emission (unseen by spectrometers) or propagate following the galactic magnetic field lines toward the bulge (Prantzos 2006); iii) the escape fraction of positrons produced by HMXB's in the disk is unconstrained, and for simplicity we take it to be the same as that of positrons from disk LMXB's. With these fractions, the net rate of positrons annihilating in the bulge is found to be
100 pc, so about 50% of positrons produced by LMXB's there are ejected toward the disk and annihilate, while the rest (50%) of the positrons are released in the halo and either contribute to a diffuse annihilation emission (unseen by spectrometers) or propagate following the galactic magnetic field lines toward the bulge (Prantzos 2006); iii) the escape fraction of positrons produced by HMXB's in the disk is unconstrained, and for simplicity we take it to be the same as that of positrons from disk LMXB's. With these fractions, the net rate of positrons annihilating in the bulge is found to be ![]()
![]() e+ s-1 (about one third the SPI bulge rate), while the net rate of positrons annihilating in the disc is found to
be
e+ s-1 (about one third the SPI bulge rate), while the net rate of positrons annihilating in the disc is found to
be ![]()
![]() e+ s-1; this would give a B/D ratio of 2.4, which is somewhat smaller than the lower SPI limit (B/D)
e+ s-1; this would give a B/D ratio of 2.4, which is somewhat smaller than the lower SPI limit (B/D)
![]() ,
indicating that positrons produced in the disk are escaping in large(r) fractions than assumed here.
,
indicating that positrons produced in the disk are escaping in large(r) fractions than assumed here.
One can also turn these estimates around and set limits on positron production rates from microquasars, knowing that the net rates in the bulge and in the disc cannot exceed those set by SPI as mentioned above. (Note that since we are taking a canonical average value of positron production rate for all LMXB microquasars and assuming the HMXB microquasars to produce only one third as many positrons, for luminosity reasons as explained above, the B/D ratio is independent of the jet positron rate and cannot help set constraints on it, at least in our simple model.) Assuming the ratios of LMXB/HMXB microquasars and the escape fractions given in the previous paragraph, we find that the SPI limits would be violated if positrons are produced at steady rates greater than ![]()
![]() e+ s-1. Furthermore, we note that our model easily satisfies the Beacom & Yüksel (2005) constraint since our positrons have kinetic energies between 2.5 keV and 660 keV (jet speeds range from 0.1 c to 0.9 c), so their annihilation in flight does not produce continuum emission of photons at higher energies.
e+ s-1. Furthermore, we note that our model easily satisfies the Beacom & Yüksel (2005) constraint since our positrons have kinetic energies between 2.5 keV and 660 keV (jet speeds range from 0.1 c to 0.9 c), so their annihilation in flight does not produce continuum emission of photons at higher energies.
Finally, we note that the line profile that can be expected in this scenario is almost exactly the same as the one obtained by SPI and analysed recently (Churazov et al. 2005; Jean et al. 2006), since the positrons are here poured mostly into the ISM; the small fraction ejected from misaligned microquasars that annihilates on the companion star's surface will produce a line of similar profile, as the physical conditions (temperature and ionization) in the atmospheres of those stars are essentially identical (
![]() K, H/He composition, partially ionized) as those in the ISM phases where the positrons annihilate on large scales.
K, H/He composition, partially ionized) as those in the ISM phases where the positrons annihilate on large scales.
In this section we consider in some detail the fate of the jet positrons hitting the atmosphere of the companion star, in the case of misaligned microquasars. Although this happens in a small number
of cases (![]() 15-20% of all the microquasars, see Sect. 4) and for a small fraction of the XRB's period (
15-20% of all the microquasars, see Sect. 4) and for a small fraction of the XRB's period (![]() 10%) there are potentially interesting gamma ray signatures of such an interaction.
10%) there are potentially interesting gamma ray signatures of such an interaction.
Positrons arrive in the companion star with speeds ranging from 0.1 c to 0.9 c (canonical value
![]() c/2), i.e. kinetic energies of 2.5 keV to 660 keV. They lose energy in the stellar atmosphere which has a very sharp density profile (see Fig. 1 in Guessoum & Jean 2002). Using stellar atmosphere models presented in Guessoum & Jean (2002) we estimate the distance for the energetic positrons to slow down below 60 eV to be
c/2), i.e. kinetic energies of 2.5 keV to 660 keV. They lose energy in the stellar atmosphere which has a very sharp density profile (see Fig. 1 in Guessoum & Jean 2002). Using stellar atmosphere models presented in Guessoum & Jean (2002) we estimate the distance for the energetic positrons to slow down below 60 eV to be
![]() 0.1 g cm-2. At this
energy, positrons are able to form a positronium by charge exchange with H atoms. Low energy positrons that do not form a positronium quickly thermalize and annihilate in situ. The maximum atmospheric depth at which positrons annihilate (
0.1 g cm-2. At this
energy, positrons are able to form a positronium by charge exchange with H atoms. Low energy positrons that do not form a positronium quickly thermalize and annihilate in situ. The maximum atmospheric depth at which positrons annihilate (![]() )
is lower than the mean free path of 511 keV photons (
)
is lower than the mean free path of 511 keV photons (
![]() g cm-2) in the atmosphere. Then in these conditions, most (
g cm-2) in the atmosphere. Then in these conditions, most (![]() 0.95%) of the annihilation photons that are emitted upward do escape the atmosphere of the companion star.
0.95%) of the annihilation photons that are emitted upward do escape the atmosphere of the companion star.
This assumption can be considered valid as long as the jet impact
does not strongly deform the stellar atmosphere. It should be noted,
however, that the energy deposited by the jets into the star's
atmosphere (![]() 1036 erg s-1) is so large as to
substantially raise the surface temperature (the increase depending
on various thermodynamical effects) during the impact periods. While
this phenomenon has no bearing on the annihilation of our positrons,
it can still lead to some (transitory) observational effects, which
may be investigated. Indeed, the depth at which positrons
annihilate depends on the thermodynamic conditions of the gas
(density, temperature), and using the energy loss rate of positrons
in a totally ionized medium (see Eq. (3) of Murphy et al. 2005, and
additional references therein), we estimate that the depth at which
positrons with initial kinetic energy of 660 keV annihilate is
1036 erg s-1) is so large as to
substantially raise the surface temperature (the increase depending
on various thermodynamical effects) during the impact periods. While
this phenomenon has no bearing on the annihilation of our positrons,
it can still lead to some (transitory) observational effects, which
may be investigated. Indeed, the depth at which positrons
annihilate depends on the thermodynamic conditions of the gas
(density, temperature), and using the energy loss rate of positrons
in a totally ionized medium (see Eq. (3) of Murphy et al. 2005, and
additional references therein), we estimate that the depth at which
positrons with initial kinetic energy of 660 keV annihilate is
![]() 0.1 g cm-2 for a temperature of 104 K and
0.1 g cm-2 for a temperature of 104 K and ![]() 0.06 g cm-2 for a temperature of 106 K. Moreover, at this energy, the range of positron can vary also by a factor of
0.06 g cm-2 for a temperature of 106 K. Moreover, at this energy, the range of positron can vary also by a factor of ![]() 3.5 with the ionization fraction and the abundance (see Fig. 3 of Milne et al. 1999). In any case, the range of 660 keV positron is lower than the mean free path of 511 keV photons (
3.5 with the ionization fraction and the abundance (see Fig. 3 of Milne et al. 1999). In any case, the range of 660 keV positron is lower than the mean free path of 511 keV photons (![]() 6.6 g cm-2).
6.6 g cm-2).
Even if a deformation of the surface does occur, the positrons still annihilate at a depth ![]()
![]() and the upward 511 keV photons do escape the atmosphere. However, the impact of the jet produces a cavity which may reduce the escaping solid angle of the upward 511 keV photons. We take this effect into account in an approximate, geometric way.
and the upward 511 keV photons do escape the atmosphere. However, the impact of the jet produces a cavity which may reduce the escaping solid angle of the upward 511 keV photons. We take this effect into account in an approximate, geometric way.
The jet pressure on the stellar atmosphere is
![]() , where
, where
![]() is the power of the jet,
is the power of the jet,
![]() its velocity, and S is the impact surface on the secondary. As a first approximation, we consider that the jet
stops in the secondary star's atmosphere when the jet pressure is equal to the atmospheric gas pressure. At the impact, the jet compresses the atmosphere, producing a cavity with a depth that depends on the pressure profile of the secondary's atmosphere, the jet characteristics (power, velocity and opening angle) and the binary separation. For typical values of jet power
its velocity, and S is the impact surface on the secondary. As a first approximation, we consider that the jet
stops in the secondary star's atmosphere when the jet pressure is equal to the atmospheric gas pressure. At the impact, the jet compresses the atmosphere, producing a cavity with a depth that depends on the pressure profile of the secondary's atmosphere, the jet characteristics (power, velocity and opening angle) and the binary separation. For typical values of jet power
![]() erg s-1, velocity
erg s-1, velocity
![]() c/2 and opening angle
c/2 and opening angle
![]() 1
1![]() ,
we obtain
,
we obtain
![]() 105 erg cm-3, for a binary star separation of a = 2
105 erg cm-3, for a binary star separation of a = 2 ![]() and a secondary mass of 0.5
and a secondary mass of 0.5 ![]() .
Using the density and the temperature profile models of a 0.5
.
Using the density and the temperature profile models of a 0.5 ![]() secondary atmosphere (Guessoum & Jean 2002), we derived the atmospheric gas pressure as a function of the depth and estimated
cavity depths (below the photosphere) of
secondary atmosphere (Guessoum & Jean 2002), we derived the atmospheric gas pressure as a function of the depth and estimated
cavity depths (below the photosphere) of ![]() 107 cm.
107 cm.
The fraction of upward 511 keV photons that escape the cavity can be estimated by calculating the opening angle of the cavity (solid angle viewed from the center of the bottom of the cavity to
the edge of the top of the cavity). Using the same jet-binary parameters (the radius of a 0.5 ![]() is
is ![]() 0.7
0.7 ![]() )
and a jet impinging the surface perpendicularly, the radius of the jet impact on the secondary atmosphere is
)
and a jet impinging the surface perpendicularly, the radius of the jet impact on the secondary atmosphere is
![]() cm.
With a depth of 107 cm, the opening angle is then
cm.
With a depth of 107 cm, the opening angle is then ![]() 178
178![]() ,
yielding a solid angle of 6.2 sr, so the fraction of upward photons that escape the cavity is 98%. Considering the most pessimistic cases (small binary separation and jet impinging perpendicularly on
the surface, i.e. high jet pressure), the fraction of upward 511 keV photons escaping the cavity is always larger than 70% (e.g. with a separation of
,
yielding a solid angle of 6.2 sr, so the fraction of upward photons that escape the cavity is 98%. Considering the most pessimistic cases (small binary separation and jet impinging perpendicularly on
the surface, i.e. high jet pressure), the fraction of upward 511 keV photons escaping the cavity is always larger than 70% (e.g. with a separation of
![]() ,
the cavity depth is
,
the cavity depth is ![]() 108 cm and the escaping fraction is
108 cm and the escaping fraction is ![]() 77%). Therefore, we neglect this jet-pressure effect on the secondary atmosphere in the modeling of the 511 keV flux presented in the next paragraphs.
77%). Therefore, we neglect this jet-pressure effect on the secondary atmosphere in the modeling of the 511 keV flux presented in the next paragraphs.
We also checked that the magnetic field of the secondary does not
affect the jet: we compared the jet pressure with the magnetic
pressure
![]() ;
taking a most extreme value for the
stellar magnetic field
;
taking a most extreme value for the
stellar magnetic field
![]() G we obtain
G we obtain
![]() erg cm-3 which is lower than
erg cm-3 which is lower than
![]() .
.
The upward 511 keV photons that escape the atmosphere may enter the incoming jet. They traverse the jet if their mean free path is larger than the jet dimension. The minimum mean free path of 511 keV photons in the jet material is
![]() ,
with
,
with
![]() the electron plus positron density in the jet and
the electron plus positron density in the jet and
![]() the Thompson cross-section. At the secondary surface,
the Thompson cross-section. At the secondary surface, ![]() can be approximated by
can be approximated by
![]() .
Assuming a close binary system (e.g. a = 2
.
Assuming a close binary system (e.g. a = 2 ![]() and
R2 = 0.7
and
R2 = 0.7 ![]() )
to estimate the smallest impact area S and therefore the largest density
)
to estimate the smallest impact area S and therefore the largest density ![]() ,
we obtain
,
we obtain ![]() 6
6 ![]() (assuming
(assuming
![]() c/2 and
c/2 and
![]() 1
1![]() ). This lower limit is already larger than the size of the XRB separation. Consequently, the jet itself can be considered as quasi-transparent to those gamma photons and the general conclusion is that positrons annihilate near the surface, and about half the resulting 511 keV photons will be emitted upwards, towards the surface and the incoming jet.
). This lower limit is already larger than the size of the XRB separation. Consequently, the jet itself can be considered as quasi-transparent to those gamma photons and the general conclusion is that positrons annihilate near the surface, and about half the resulting 511 keV photons will be emitted upwards, towards the surface and the incoming jet.
The binary system rotates, and the secondary star periodically crosses the jet, which slowly precesses. Consequently, the 511 keV photon radiation flux received by an observer in a given direction is a function of time, and its intensity and time-variability
characteristics depend on the parameters of the XRB (period,
inclination, distance, separation and radius of the secondary star)
and of the jet (inclination with respect to the binary plane, opening
angle and precession period). The flux at 511 keV can be calculated
using the following expression:
![\begin{figure}
\par\includegraphics[width=9.0cm,clip]{5240fig2.eps}\end{figure}](/articles/aa/full/2006/39/aa5240-06/Timg137.gif) |
Figure 2: Schematic view of the irradiation of the secondary star by a jet. The binary system frame is represented by the dashed axes. |
| Open with DEXTER | |
To illustrate the temporal variations of the annihilation flux, we calculated the 511 keV light curve for the case of a "prototypical misaligned microquasar'', one that has similar
parameters (separation, inclination, primary and secondary masses...) as GRO J1655-40, which is one of two XRB's for which independent information is available on the jet orientation
(Narayan & McClintock 2005). However, we arbitrarily assumed a jet inclination of
![]() = 9
= 9![]() with respect to the binary plane. With such an inclination, the jets hit the companion star at about half of its upper hemisphere. We also assumed an opening angle
with respect to the binary plane. With such an inclination, the jets hit the companion star at about half of its upper hemisphere. We also assumed an opening angle
![]() = 1
= 1![]() and a precession period of 300 days which is the order of magnitude of the precession period of such an inclined jet (Kaufman Bernadó et al. 2002).
and a precession period of 300 days which is the order of magnitude of the precession period of such an inclined jet (Kaufman Bernadó et al. 2002).
Could there be some observational effects on the radio emission from the interaction of the jet with the surface of the star? In this regard, we first note that pairs in the jets will emit synchrotron
radiation for most (say 90%) of their transit (ejection) time, while the rest of the time they spend depositing their energies in the companion's atmosphere; this energy is lost first and foremost in the form of heat and then, at the end, as gamma rays, which get downgraded as X-rays and again as heat. It is thus not expected that much radio emission will come out of the jet's collision with the companion star's atmosphere, but this issue could be investigated further in the future.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{5240fig3.eps}\end{figure}](/articles/aa/full/2006/39/aa5240-06/Timg139.gif) |
Figure 3:
Instantaneous 511 keV photon flux induced by the jet (red curve) and the counterjet (blue curve) impacts on the secondary of a virtual XRB (see text). The jet inclination with respect to the binary plane is taken to be
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{5240fig4.eps}\end{figure}](/articles/aa/full/2006/39/aa5240-06/Timg140.gif) |
Figure 4: Details of the instantaneous 511 keV photon flux induced by the jet (red curve) and the counterjet (blue curve) impacts on the secondary of a virtual XRB (see caption of Fig. 3). a) The jet direction is parallel to the observer direction and only the hotspot induced by the first jet is visible; b) the jet direction is perpendicular to the observer direction and both hotspots induced by the jet and the counterjet are visible. The geometrical configurations of the jets and the binary system in these two cases are shown in Fig. 5. |
| Open with DEXTER | |
As for GRO J1655-40, this "prototypical'' microquasar was assumed to be at a distance of 3.2 kpc from Earth, to have a period of 2.62 days and to be composed of a compact object with a mass of 6.8 ![]() separated by 16.6
separated by 16.6 ![]() from a companion star with a radius of
5
from a companion star with a radius of
5 ![]() .
The inclination of the binary system is
.
The inclination of the binary system is
![]() .
Figure 3 shows the instantaneous 511 keV flux emitted by such a microquasar as a function of time. Details of this light curve are presented in Fig. 4 for two different dates: (a) when the direction of the jets lies approximately along the line of sight, and in (b) when the direction
of the jets is approximately perpendicular to the line of sight. The geometrical configurations of the jets and the binary system in these two cases are shown in Fig. 5.
.
Figure 3 shows the instantaneous 511 keV flux emitted by such a microquasar as a function of time. Details of this light curve are presented in Fig. 4 for two different dates: (a) when the direction of the jets lies approximately along the line of sight, and in (b) when the direction
of the jets is approximately perpendicular to the line of sight. The geometrical configurations of the jets and the binary system in these two cases are shown in Fig. 5.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{5240fig5.eps}\end{figure}](/articles/aa/full/2006/39/aa5240-06/Timg142.gif) |
Figure 5:
Schematic views of the jets (blue) arising from the compact object (black), the secondary star (red) presented at four positions in its orbit, and the annihilation hotspot (yellow) emitted from the secondary star atmosphere, presented at the dates |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{5240fig6.eps}\end{figure}](/articles/aa/full/2006/39/aa5240-06/Timg143.gif) |
Figure 6: Average 511 keV photon flux per XRB period, induced by the jet impacts on the secondary of an XRB. The parameters of the jets are identical to those of Figure. |
| Open with DEXTER | |
Figure 6 shows the time series of the 511 keV flux averaged per period of the XRB. The flux is minimum when the jet direction is perpendicular to the observer direction, as shown in
Figure 5b. In this configuration, the inclination ![]() of the direction of the photons emitted by the fraction of the hotspot that is visible can be close to 90
of the direction of the photons emitted by the fraction of the hotspot that is visible can be close to 90![]() during the crossing of the secondary. Consequently, a large fraction of these photons are absorbed in the atmosphere of the secondary (see Eq. (9) and Fig. 4b). Note that the average flux is
during the crossing of the secondary. Consequently, a large fraction of these photons are absorbed in the atmosphere of the secondary (see Eq. (9) and Fig. 4b). Note that the average flux is ![]() 10 times lower than the maximum of the instantaneous flux since the companion star crosses the jets during a fraction
10 times lower than the maximum of the instantaneous flux since the companion star crosses the jets during a fraction ![]() 10% of the period.
10% of the period.
The spectral shape of the annihilation radiation emitted by this virtual microquasar was calculated accordingly to the model of Guessoum et al. (2005), which provides annihilation spectra
as a function of the physical conditions of the gas in which the annihilation occurs. We assumed that positrons annihilate in a half-ionized and half-neutral plasma with a temperature of 8000 K.
The rotation of the binary system leads to a shift in the centroid of the 511 keV line. This Doppler shift is a function of time and depends on the observer direction. We calculated this spectral shift using the method described in Jean & Guessoum (2001). Figure 7 shows the spectra: integrated over the precession period (case 1); integrated over one XRB period at t = 100 days (case 2, see Fig. 3); integrated over one XRB period at t = 200 days (case 3). The line is blue-shifted by 0.3 keV in case 2 because most of the annihilation emission comes from the jet impact on the secondary which is moving toward the observer. In case 3, most of the annihilation emission comes from the jet impact on the secondary which is receding from the observer, thus
producing a line with a red-shift of 0.3 keV.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{5240fig7.eps}\end{figure}](/articles/aa/full/2006/39/aa5240-06/Timg144.gif) |
Figure 7: Spectra of the annihilation radiation emitted by GRO J1655-40. The parameters of the jets are identical to those of Fig. 3. We assumed that the 50% of positrons annihilates with the ionized component of the atmosphere and 50% with the neutral component. Case 1: total spectrum integrated over the precession period; case 2: spectrum integrated over one period at the date 100 days; case 3: spectrum integrated over one period at the date 200 days. |
| Open with DEXTER | |
The results presented in this section show that the measurements of the temporal and spectral profiles of the annihilation radiation emitted by microquasars with misaligned jets are useful to probe the characteristics of the jet. The maximum 511 keV instantaneous flux provides the rate of positrons in the jet (e.g. Fig. 3). The duration of the 511 keV emission in one XRB period allows one to estimate the opening angle of the jet (e.g. Fig. 4), while the long-term variation of the average flux allows for a determination of the precession period of the jet (e.g. Fig. 6). The spectral shape of the 511 keV line, do, in principle, allow one to infer the physical conditions of the plasma in which positrons annihilate, as Jean et al. (2006) demonstrated for the SPI data of positron annihilation in the ISM, although one must realize that in more complex situations a host of conditions and effects can render the extraction of physical information very complicated if not impossible.
Finally, in Table 2 we present our predicted maximum fluxes for the confirmed misaligned microquasars as well as for potential candidates, i.e. microquasars that may be at least occasionally misaligned and are not too far away for detection by future instruments. We must note that the values given in this table are for "average jets''; "strong-flare jets'' could be 10 times more powerful, thus producing 10 times more positrons and thus resulting in an annihilation flux 10 times higher (than what is given in the table); on the other hand, "weak episode jets'' would give positron rates and annihilation fluxes about 10 times lower. Indeed, the annihilation flux is directly proportional to the jet power.
Table 2: Predicted maximum 511 keV emission fluxes for confirmed or potentially misaligned nearby microquasars. Fluxes were calculated for "Average Jet'', that is using a positron rate of 1041 e+ s-1.
Among the rapidly growing body of data on microquasars, we present in Sect. 2 the main features, those of relevance to our study. The correlation between the power of the jet and the X-ray luminosity of the compact object is the most important of these features. We stress, in particular, that the ratio between the two, often assumed to be small, is highly uncertain; moreover, the content of the jets, leptonic or baryonic (i.e. electron-positron pairs vs. protons and pions), is unknown at present. Some of the implications of a baryonic content have been explored elsewhere (Butt et al. 2003; Romero & Orelana 2005); we explore here the consequences of a leptonic content.
In Sect. 3 we evaluate the rate of positron ejection by the microquasar jets, based on various models proposed in the literature, but also on simple energetic arguments relating the total power of the positrons in the jets to the estimated total X-ray luminosity of the "low luminosity - hard spectrum'' galactic LMXRBs. We find that a value of 1041 e+ s-1 could be considered as a "canonical average'', albeit with large (and difficult to evaluate) uncertainties.
In Sect. 4 we estimate the total positron production rate by the collective emission of Galactic microquasars and find it smaller (about one third) than what is inferred from SPI/INTEGRAL
observations of 511 keV radiation. The spatial morphology of the corresponding flux received on Earth depends on the assumed large scale distribution of Galactic microquasars, which is very poorly known at present; we find that the distribution of the currently available (incomplete) sample appears encouraging, in that respect. (We should also note that a large enough B/D ratio would be obtained with any source distributions that congregate in the bulge and/or suppress the annihilation of their positrons in the disk.) Finally, we constrain the rate of production of positrons by microquasars on the basis of the SPI flux results: we find that the SPI limits would be violated if positrons are produced at steady rates greater than ![]()
![]() e+ s-1.
e+ s-1.
Finally, in Sect. 5 we present an investigation of the physics of "misaligned'' microquasars, where the jet impinges on the companion star. We find that about half of the annihilation photons should, in general, escape the stellar atmosphere. We compute fluxes for a list of sources (see Tab. 2), a few of them known to be misaligned, and some of the others may turn out to be so as well. The expected annihilation fluxes are found to be low, however, and difficult to measure with the spectrometer SPI due to the distance of most of the "misaligned'' microquasars. Future instruments such as a gamma-ray lens (von Ballmoos et al. 2004) or a Compton telescope (Boggs & Jean 2001) would have the sensitivity required to measure these fluxes. Due to the rotation of the binary system, the secondary star periodically crosses the jet, leading to a "periodic'' and a Doppler-shifted annihilation emission. Due to the precession of the jet, we expect to observe a long-term modulation of the emission. A detection of a point source at 511 keV from a "misaligned'' microquasar, with such temporal and spectral signatures would confirm the presence of positrons in the jet. Moreover, such a measurement would allow for a determination of the rate of positrons channeled by the jet and the characteristics (opening angle, precession period) of the jet.
In summary, we have shown in this study that microquasar jets may constitute important sources of annihilation radiation, both diffuse (for most of them) or point sources (in the case of misaligned ones).
Acknowledgements
We wish to acknowledge helpful discussions with Didier Barret and Alexandre Marcowith. We are grateful to Mamta Pandey for bringing to our notice the four new microquasars that she and her collaborators have recently reported. And we thank the anonymous referee for several useful suggestions and requests for clarifications, which has led to a definite improvement of the paper.