A&A 457, 1071-1079 (2006)
DOI: 10.1051/0004-6361:20065227
M. Luna - J. Terradas - R. Oliver - J. L. Ballester
Departament de Física, Universitat de les Illes Balears, 07122 Palma de Mallorca, Spain
Received 17 March 2006 / Accepted 12 July 2006
Abstract
Aims. We study fast magnetohydrodynamic waves in a system of two coronal loops modeled as smoothed, dense plasma slabs in a uniform magnetic field. This allows us to analyse in a simple configuration the collective behaviour of the structure due to the interaction between the slabs.
Methods. We first calculate the normal modes of the system and find analytical expressions for the dispersion relation of the two-slab configuration. Next, we study the time-dependent problem of the excitation of slab oscillations by numerically solving the initial value problem. We investigate the behaviour of the system for several shapes of the initial disturbances.
Results. The symmetric mode respect to the centre of the structure is the only trapped mode for all distances between the slabs while the antisymmetric mode is leaky for small slab separations. Nevertheless, there is a wide range of slab separations for which the fundamental symmetric and antisymmetric trapped modes are allowed and have very close frequencies. These modes are excited according to the parity of the initial perturbation.
Conclusions. We find that for any initial disturbance the slabs oscillate with the normal modes of the coupled slab system, which are different from the modes of the individual slabs. We show that it is possible to excite the symmetric and antisymmetric trapped modes at the same time. This kind of excitation can produce the beating phenomenon, characterised by a continuous exchange of energy between the individual slabs.
Key words: Sun: corona - magnetohydrodynamics (MHD) - waves
Transversal coronal loop oscillations are routinely observed by the EUV telescope
on board ![]() .
Several oscillating loops have been studied in detail by
Aschwanden et al. (2002,1999); Verwichte et al. (2004); Schrijver et al. (2002). Information about the period, damping
time and amplitude of the oscillations has been derived. These kind of
oscillations have been interpreted as standing kink fast magnetohydrodynamic (MHD) waves since they produce displacements of the loop axis and the loop
footpoints seem to be anchored in the solar photosphere.
.
Several oscillating loops have been studied in detail by
Aschwanden et al. (2002,1999); Verwichte et al. (2004); Schrijver et al. (2002). Information about the period, damping
time and amplitude of the oscillations has been derived. These kind of
oscillations have been interpreted as standing kink fast magnetohydrodynamic (MHD) waves since they produce displacements of the loop axis and the loop
footpoints seem to be anchored in the solar photosphere.
In general, the observed oscillating loops belong to complex active regions and in most cases they cannot be considered as isolated magnetic tubes. A clear example of such configurations are coronal arcades, where loops are located forming ensembles of several magnetic flux tubes. There is also observational evidence of transversal loop oscillations in such complex structures. For example, Verwichte et al. (2004), have studied in detail the features of the oscillating loops forming an arcade which were presumably disturbed by a prominence eruption. In fact, these observations suggest that the loops do not oscillate independently and that different loops oscillate following an organised motion.
From the theoretical point of view the behaviour of isolated magnetic structures have been studied in several geometries by Díaz (2004); Cally (1986); Spruit (1981); Edwin & Roberts (1982,1983); Cally (2003), little work has yet been done on multi-structures. Berton & Heyvaerts (1987) studied the magnetohydrodynamic normal modes of a periodic magnetic medium while Bogdan & Fox (1991) and Keppens et al. (1993) analysed the scattering and absorption of acoustic waves by bundles of magnetic flux tubes with sunspot properties. Murawski & Roberts (1994); Murawski (1993) studied the propagation of fast waves in two slabs unbounded in the longitudinal direction. On the other hand, the collective nature of oscillations has been investigated in multifibril Cartesian systems (see Díaz et al. 2005) representing the oscillation of the fibril structure of prominences. These authors found that in a system of equal fibrils the only non-leaky mode is the symmetric one, which means that all the fibrils oscillate in spatial phase with the same frequency.
Here we consider a simple line-tied two-slab model without gravity and curvature; and solve the time-dependent problem of the excitation of coronal loop oscillations. In general, an initial disturbance is likely to deposit some energy in the trapped modes, while some energy will be emitted via the leaky waves. We concentrate on the conditions that lead to the excitation of trapped and leaky modes and analyse in detail the behaviour of the system when more than a single trapped mode is excited at the same time. We compare the results of the time-dependent simulations with the information provided by the normal modes. This allows us to study the interaction between the oscillating slabs which leads to a collective behaviour of the system.
This paper is organised as follows. In Sect. 2 the loop model and the basic MHD equations describing fast waves are presented. In Sect. 3 the features of trapped and leaky modes are analysed in detail. In Sect. 4 the time-dependent problem is considered and the resulting velocity profiles are studied for several initial perturbations. An analytical analysis of the beating is given in Sect. 5. Finally, in Sect. 6 the main conclusions are drawn.
We consider a system of two parallel loops modeled as dense plasma slabs of
half-width a and length L (Fig. 1). The distance between the
centres of the slabs is d, so the distance between their inner edges is d-2
a. The density profile is sharp and given by
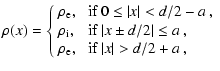 |
(1) |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{5227f1.eps}\end{figure}](/articles/aa/full/2006/39/aa5227-06/Timg19.gif) |
Figure 1: Sketch of the two-slab system. The shaded area represents the density enhancement of the two slabs while the hatched area represents the photospheric medium, that fixes the feet of the slabs and produces the line-tying effect. |
| Open with DEXTER | |
When considering perturbations about this equilibrium, we use the linearised
magnetohydrodynamic (MHD) equations in the low-![]() limit (
limit (![]() ). In
this limit the slow mode does not appear. To simplify the study of fast modes
it is also assumed that perturbations do not depend on y, hence the
Alfvén and fast modes are decoupled. Furthermore, we Fourier analyse in the
z-direction, i.e. we assume that perturbations are of the form
). In
this limit the slow mode does not appear. To simplify the study of fast modes
it is also assumed that perturbations do not depend on y, hence the
Alfvén and fast modes are decoupled. Furthermore, we Fourier analyse in the
z-direction, i.e. we assume that perturbations are of the form
![]() ,
which allows us to study the effect of photospheric line-tying by
selecting the appropriate value of kz (we concentrate on the fundamental
mode, with
,
which allows us to study the effect of photospheric line-tying by
selecting the appropriate value of kz (we concentrate on the fundamental
mode, with
![]() ). With the Fourier decomposition in z, the wave
equation for the fast modes is the Klein-Gordon equation
(Terradas et al. 2005a),
). With the Fourier decomposition in z, the wave
equation for the fast modes is the Klein-Gordon equation
(Terradas et al. 2005a),
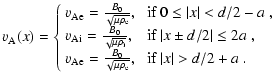 |
(3) |
Before considering the time-dependent problem of perturbations about the
equilibrium, we briefly describe the main oscillatory features of our two-slab
model, given by the normal mode analysis. Normal mode solutions of
Eq. (2) in a uniform medium have a dependence of the form
![]() with
with
![]() .
In the present
structure, the velocity of normal modes has the form
.
In the present
structure, the velocity of normal modes has the form
![]() ,
with
,
with
We then impose both boundary conditions on the four interfaces located at
![]() and
and
![]() ,
thus obtaining four equations for the
velocity and four equations for its x-derivative. These equations form a homogeneous linear system of eight equations with eight unknowns, i.e.
A,
B1, B2, C1, C2, D1, D2, E in Eq. (4).
For this system of equations to have a non-trivial solution, its determinant
must be zero. This gives the dispersion relation, which appears as a product of
two factors. One of these factors must vanish, which leaves us with the
following expressions,
,
thus obtaining four equations for the
velocity and four equations for its x-derivative. These equations form a homogeneous linear system of eight equations with eight unknowns, i.e.
A,
B1, B2, C1, C2, D1, D2, E in Eq. (4).
For this system of equations to have a non-trivial solution, its determinant
must be zero. This gives the dispersion relation, which appears as a product of
two factors. One of these factors must vanish, which leaves us with the
following expressions,
Equations (8) and (9) indicate that there are
two kinds of normal modes, whose spatial structure will be studied next.
Solutions to Eq. (8) are symmetric with
respect to x=0 and both slabs move in phase (see
Figs. 2a and b). On the other hand, solutions to
Eq. (9) are antisymmetric with
respect to x=0 and both slabs move in antiphase (see
Figs. 2c and d). In addition, Fig. 2 shows that normal modes can either be
trapped (as in panels a, b and d) or leaky (as in panel c). Trapped modes
attain their maximum amplitude in or near the slabs, but leaky modes present
oscillations growing in amplitude as
![]() .
.
![\begin{figure}
\par\mbox{\hspace{-0.cm}{\bf (a)}\hspace{4.25cm}{\bf (b)}\hspace{...
...7f4.eps}\hspace*{5mm}\includegraphics[width=4.25cm,clip]{5227f5.eps}\end{figure}](/articles/aa/full/2006/39/aa5227-06/Timg44.gif) |
Figure 2:
Velocity profile, vx(x), for the fundamental symmetric mode ( upper row) and
the fundamental antisymmetric mode ( lower row) for a slab half-width a=0.05 Land a density enhancement
|
| Open with DEXTER | |
We solve the transcendental Eqs. (8) and (9) and calculate ![]() for
different values of the slab separation, d, finding two types of curves
(Fig. 3). Figures 3a and b correspond to the real and imaginary
part of the frequency, that has been written as
for
different values of the slab separation, d, finding two types of curves
(Fig. 3). Figures 3a and b correspond to the real and imaginary
part of the frequency, that has been written as
![]() .
Here we only represent the fundamental and first harmonic of
the symmetric and antisymmetric modes. The frequency of trapped modes is real
and smaller than the external cut-off frequency,
.
Here we only represent the fundamental and first harmonic of
the symmetric and antisymmetric modes. The frequency of trapped modes is real
and smaller than the external cut-off frequency,
![]() .
Since
.
Since
![]() for trapped modes, these solutions correspond to standing
oscillations of the system. Leaky modes have complex frequency with
for trapped modes, these solutions correspond to standing
oscillations of the system. Leaky modes have complex frequency with
![]() ,
so that they represent damped oscillations, the origin of
the damping being that perturbations carry the energy away from the slabs.
Figure 3 shows that the fundamental symmetric mode (solid line) is
trapped for all distances. On the other hand, the fundamental antisymmetric mode
(dashed line) starts as leaky for small values of d/L and, as d/L is
increased, its curve crosses the external cut-off frequency, bifurcates and
gives rise to two branches. At the bifurcation point the imaginary part of the
frequency becomes zero (Fig. 3b) and the two branches have
,
so that they represent damped oscillations, the origin of
the damping being that perturbations carry the energy away from the slabs.
Figure 3 shows that the fundamental symmetric mode (solid line) is
trapped for all distances. On the other hand, the fundamental antisymmetric mode
(dashed line) starts as leaky for small values of d/L and, as d/L is
increased, its curve crosses the external cut-off frequency, bifurcates and
gives rise to two branches. At the bifurcation point the imaginary part of the
frequency becomes zero (Fig. 3b) and the two branches have
![]() .
Both branches are physically meaningless because they
have
.
Both branches are physically meaningless because they
have
![]() and
and ![]() is real and negative, which
implies an oscillatory solution in time with an exponential growth in space. For
even larger separations between the slabs (
is real and negative, which
implies an oscillatory solution in time with an exponential growth in space. For
even larger separations between the slabs (![]() )
the upper branch
reaches the external cut-off and the mode becomes trapped (thick dashed line),
becoming a physically relevant solution. All the harmonics (both symmetric and
antisymmetric) have the same behaviour as the fundamental antisymmetric mode,
although in the range of separations plotted in Fig. 3 they are leaky.
From Fig. 3b we see that the damping time,
)
the upper branch
reaches the external cut-off and the mode becomes trapped (thick dashed line),
becoming a physically relevant solution. All the harmonics (both symmetric and
antisymmetric) have the same behaviour as the fundamental antisymmetric mode,
although in the range of separations plotted in Fig. 3 they are leaky.
From Fig. 3b we see that the damping time,
![]() ,
increases with the separation d.
,
increases with the separation d.
![\begin{figure}
\par\hspace{-0.15cm}\includegraphics[width=5.05cm,clip]{5227f6.eps}\par\includegraphics[width=4.85cm,clip]{5227f7.eps}\end{figure}](/articles/aa/full/2006/39/aa5227-06/Timg51.gif) |
Figure 3:
a) Real part,
|
| Open with DEXTER | |
The behaviour of solutions for small and large separations between slabs can be
derived from Eqs. (8) and (9). For small separations, ![]() ,
we have
,
we have
![]() and from
Eq. (8) we recover the sausage mode
dispersion relation for one slab,
and from
Eq. (8) we recover the sausage mode
dispersion relation for one slab,
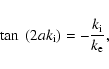 |
(10) |
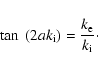 |
(11) |
For a very large separation between slabs,
![]() ,
both Eqs. (8) and (9) lead to
,
both Eqs. (8) and (9) lead to
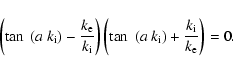 |
(12) |
![\begin{figure}
\par\mbox{\hspace{-0.cm}{\bf (a)}\hspace{4.25cm}{\bf (b)}\hspace{...
...10.eps}\hspace*{4mm}\includegraphics[width=4.35cm,clip]{5227f11.eps}\end{figure}](/articles/aa/full/2006/39/aa5227-06/Timg59.gif) |
Figure 4: Time-evolution of the velocity, vx, for a distance between slabs d=0.5 Land a symmetric initial impulse. |
| Open with DEXTER | |
Normal modes provide with information about the oscillatory state and parameters of the system, but coronal oscillations are often produced by an impulsive event and time dependent simulations are more appropriate to describe the evolution of the system. In the case of a single slab (Terradas et al. 2005b) an impulsive disturbance leads, after a time of the order of the Alfvén transit time across the slab, to a distribution of its energy into one or more normal modes. The question that arises is how this picture will be modified for a two-slab structure: after an impulsive event, does the system oscillate in a normal mode (or a sum of some normal modes) or do the modes of a single slab appear?
To study the effect of an arbitrary initial perturbation we consider the system
of two slabs with a typical density enhancement
(
![]() ), a typical slab half-width (a=0.05 L)
and we excite perturbations with different velocity profiles.
), a typical slab half-width (a=0.05 L)
and we excite perturbations with different velocity profiles.
To solve Eq. (2) numerically the code ![]() ,
(Sewell 2005),
based on finite elements, has been used. The code, which gives a numerical
approximation to vx (x,t), makes use of a second order implicit
Crank-Nicholson method with adaptive time step control. Since we consider a finite numerical domain, reflections at the domain boundaries may affect the
dynamics of the system of slabs. We have solved this problem by locating the
edges of the numerical domain far from the two slabs. Given that the size of
the domain is much larger than the loop thickness, a non-uniform grid with 4000 grid points in the full domain, 45 of them located inside each slab (
,
(Sewell 2005),
based on finite elements, has been used. The code, which gives a numerical
approximation to vx (x,t), makes use of a second order implicit
Crank-Nicholson method with adaptive time step control. Since we consider a finite numerical domain, reflections at the domain boundaries may affect the
dynamics of the system of slabs. We have solved this problem by locating the
edges of the numerical domain far from the two slabs. Given that the size of
the domain is much larger than the loop thickness, a non-uniform grid with 4000 grid points in the full domain, 45 of them located inside each slab (
![]() ), has been used. In addition, we have made sure that the artificial
diffusion introduced by the numerical scheme is small enough. This is a critical point since the artificial damping can be larger than the physical
damping, in our case arising from energy leakage, and may lead to the wrong
interpretation of the results. We have performed different simulations by
increasing the number of grid points and have found that the solutions
converge, which is an indication that numerical diffusion does not affect
considerably the results. In addition, we have checked that the same results
are obtained by solving the initial-value problem with a standard explicit
method based on finite differences.
), has been used. In addition, we have made sure that the artificial
diffusion introduced by the numerical scheme is small enough. This is a critical point since the artificial damping can be larger than the physical
damping, in our case arising from energy leakage, and may lead to the wrong
interpretation of the results. We have performed different simulations by
increasing the number of grid points and have found that the solutions
converge, which is an indication that numerical diffusion does not affect
considerably the results. In addition, we have checked that the same results
are obtained by solving the initial-value problem with a standard explicit
method based on finite differences.
![\begin{figure}
\par\includegraphics[width=5.15cm,clip]{5227f12.eps}\par\includegraphics[width=5.1cm,clip]{5227f13.eps}\end{figure}](/articles/aa/full/2006/39/aa5227-06/Timg62.gif) |
Figure 5:
a) Measured velocity at the centre of the right slab, x=d/2, for the
symmetric initial perturbation of Fig. 4. After a short
transient the system oscillates in a trapped mode, with period close to
|
| Open with DEXTER | |
The initial condition is the sum of two Gaussian profiles centred in
each of the slabs,
Let us start with the symmetric initial condition and a separation between
slabs d=0.5 L. To see which normal modes can be excited, we only need to
care about the symmetric ones, since the antisymmetric modes are not excited
because their symmetry is opposite to that of the initial perturbation. So we
inspect the dispersion diagram (Fig. 3) and see that for d=0.5 Lthere is only a symmetric trapped mode (the fundamental symmetric mode) and
infinite leaky symmetric modes (of which only one is shown in this plot). The
results of the simulation are displayed in Fig. 4, where we
have plotted the velocity, vx, as a function of x for different times
(t is given in units of the external Alfvén transit time,
![]() ). The initial perturbation produces
travelling disturbances to the left and right and these disturbances show some
dispersion as they propagate: short wavelengths are at the front and long
wavelengths at the back of the travelling disturbances
(Figs. 4c and d). A comparison of
Figs. 2a and 4d in the range
). The initial perturbation produces
travelling disturbances to the left and right and these disturbances show some
dispersion as they propagate: short wavelengths are at the front and long
wavelengths at the back of the travelling disturbances
(Figs. 4c and d). A comparison of
Figs. 2a and 4d in the range
![]() indicates that, for long times, the system settles down into
the trapped mode. To gain more insight into the time evolution we plot the
velocity at the centre of the right slab (at x=d/2) in
Fig. 5a. In this figure we see clearly two phases, a transient
(for
indicates that, for long times, the system settles down into
the trapped mode. To gain more insight into the time evolution we plot the
velocity at the centre of the right slab (at x=d/2) in
Fig. 5a. In this figure we see clearly two phases, a transient
(for
![]() )
and an oscillatory phase (for
)
and an oscillatory phase (for
![]() ). The transient is produced by two effects:
firstly, perturbations reflect and refract at the two slabs until the energy
contained in the initial impulse is transferred into the normal modes. This
phase has a duration, which we call the relaxation time, of the order of a few
times the Alfvén travel time between the two slabs, i.e. a few times
). The transient is produced by two effects:
firstly, perturbations reflect and refract at the two slabs until the energy
contained in the initial impulse is transferred into the normal modes. This
phase has a duration, which we call the relaxation time, of the order of a few
times the Alfvén travel time between the two slabs, i.e. a few times
![]() ;
secondly, the excited leaky modes carry their energy
towards
;
secondly, the excited leaky modes carry their energy
towards
![]() and so decay in a time of the order of
and so decay in a time of the order of
![]() .
In Terradas et al. (2005b) this phase was called the impulsive
leaky phase. From Fig. 3b we see that
.
In Terradas et al. (2005b) this phase was called the impulsive
leaky phase. From Fig. 3b we see that
![]() for the first leaky harmonic, which
means that this mode damps out in a time comparable to the relaxation time.
The very short duration of this and all other leaky modes makes them
practically undetectable in Fig. 5a. Further confirmation of
this interpretation of Fig. 5a is given in its power spectrum
(Fig. 5b), which displays a single power peak whose frequency
exactly matches that of the trapped symmetric mode, while the power at the
frequencies of leaky modes is negligible. As a conclusion, the trapped
fundamental symmetric mode is excited in this simulation and there is a good
agreement in the frequency and velocity profile with the normal mode results.
If leaky modes are excited, they cannot be detected because of their very
rapid damping.
for the first leaky harmonic, which
means that this mode damps out in a time comparable to the relaxation time.
The very short duration of this and all other leaky modes makes them
practically undetectable in Fig. 5a. Further confirmation of
this interpretation of Fig. 5a is given in its power spectrum
(Fig. 5b), which displays a single power peak whose frequency
exactly matches that of the trapped symmetric mode, while the power at the
frequencies of leaky modes is negligible. As a conclusion, the trapped
fundamental symmetric mode is excited in this simulation and there is a good
agreement in the frequency and velocity profile with the normal mode results.
If leaky modes are excited, they cannot be detected because of their very
rapid damping.
![\begin{figure}
\par\mbox{\hspace{-0.cm}{\bf (a)}\hspace{4.25cm}{\bf (b)}\hspace{...
...16.eps}\hspace*{4mm}\includegraphics[width=4.25cm,clip]{5227f17.eps}\end{figure}](/articles/aa/full/2006/39/aa5227-06/Timg74.gif) |
Figure 6: Time-evolution of the velocity, vx, for a distance between slabs d=0.5 Land an antisymmetric initial impulse. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5.15cm,clip]{5227f18.eps}\par\includegraphics[width=5.1cm,clip]{5227f19.eps}\end{figure}](/articles/aa/full/2006/39/aa5227-06/Timg75.gif) |
Figure 7: a) Measured velocity at the centre of the right slab, x=d/2, for the antisymmetric initial perturbation of Fig. 6. After a short transient the system oscillates in a leaky mode and so the perturbation attenuates exponentially. b) The periodogram of the signal in a) has a power peak whose period is in excellent agreement with that of the normal mode obtained from Eq. (9) (dotted line). The periodogram lacks other power peaks. |
| Open with DEXTER | |
Next, we perturb the same system with an antisymmetric initial condition, so
now the antisymmetric normal modes are excited. The results of the simulation,
which again show the propagation of perturbations in both directions along the
x-axis, are displayed in Fig. 6. In this case the
amplitude of the oscillations in both slabs decrease in time because all
antisymmetric modes are leaky for the selected separation between slabs
(d/L=0.5). In Fig. 7a the velocity measured in the centre of
the right slab, x=d/2, is plotted. After the relaxation time, which again is
of the order of
![]() ,
the signal is an attenuated oscillation,
as expected for leaky modes. In Fig. 7b we see the periodogram
of this signal, where the dashed line gives the theoretical frequency of the
fundamental leaky antisymmetric mode (from Fig. 3) and as in the
previous case coincides with the peak of the power spectrum. Nevertheless, now
the power peak is broad due to the exponential attenuation of the signal.
Regarding the spatial velocity profile, it is not easy to compare the results
of the simulation with those of the normal mode analysis, but still
Figs. 6c and d bear some resemblance with
Fig. 2c. We conclude that the considered
antisymmetric disturbance mostly excites the fundamental antisymmetric leaky
mode.
,
the signal is an attenuated oscillation,
as expected for leaky modes. In Fig. 7b we see the periodogram
of this signal, where the dashed line gives the theoretical frequency of the
fundamental leaky antisymmetric mode (from Fig. 3) and as in the
previous case coincides with the peak of the power spectrum. Nevertheless, now
the power peak is broad due to the exponential attenuation of the signal.
Regarding the spatial velocity profile, it is not easy to compare the results
of the simulation with those of the normal mode analysis, but still
Figs. 6c and d bear some resemblance with
Fig. 2c. We conclude that the considered
antisymmetric disturbance mostly excites the fundamental antisymmetric leaky
mode.
We next repeat this analysis for different slab separations and obtain an estimation of the real part of the frequency of the normal mode,
![]() ,
from the power spectrum of the simulations. With these
data we have superimposed in Fig. 3a, the value of
,
from the power spectrum of the simulations. With these
data we have superimposed in Fig. 3a, the value of
![]() calculated from the numerical simulations (see triangles and diamonds) on top
of the theoretical dispersion diagram. The agreement is outstanding for all
values of d/L, so we conclude that when the system is excited with a symmetric or antisymmetric initial condition, it later oscillates in a normal
mode predicted by the theory. As a corollary, the system acquires a collective
oscillation, given by a normal mode, and does not oscillate with the modes of
an individual slab.
calculated from the numerical simulations (see triangles and diamonds) on top
of the theoretical dispersion diagram. The agreement is outstanding for all
values of d/L, so we conclude that when the system is excited with a symmetric or antisymmetric initial condition, it later oscillates in a normal
mode predicted by the theory. As a corollary, the system acquires a collective
oscillation, given by a normal mode, and does not oscillate with the modes of
an individual slab.
Now, the system is excited using an initial condition with no particular symmetry about x=0. The initial condition that we consider is a Gaussian pulse centred in the right slab. This initial pulse is given by Eq. (13) with A=1, B=0 and, therefore, can be decomposed into the sum of a symmetric and an antisymmetric excitation. Since Eq. (2) is linear, we expect that this kind of initial disturbance will give rise to a superposition of the solutions arising from the corresponding symmetric and antisymmetric excitations. In this section we consider the slab separations d=0.5 L and d=2 L.
![\begin{figure}
\par\mbox{\hspace{-0.cm}{\bf (a)}\hspace{4.25cm}{\bf (b)}\hspace{...
...22.eps}\hspace*{4mm}\includegraphics[width=4.25cm,clip]{5227f23.eps}\end{figure}](/articles/aa/full/2006/39/aa5227-06/Timg77.gif) |
Figure 8: Time-evolution of vx for d=0.5 L and a non-symmetric initial excitation. |
| Open with DEXTER | |
Firstly, we consider the case d=0.5 L (Fig. 8), which
implies that the initial condition (Fig. 8a) is half the sum
of the symmetric and antisymmetric initial conditions of Sect. 4.1.
During the initial stages of the temporal evolution (Figs. 8b
and c) vx has no definite symmetry with respect to x=0 because the solution
is the sum of the symmetric and antisymmetric modes of Sect. 4.1.
Let us recall that these modes are the fundamental symmetric and the fundamental
antisymmetric, which are trapped and leaky, respectively. As a consequence,
after some time (Fig. 8d) the antisymmetric mode amplitude is
negligible in the vicinity of the slabs and the system oscillates in a symmetric
manner. In Fig. 9 the time dependence of the
velocity, vx, is plotted in both slab centres. Because of the superposition
of the antisymmetric leaky mode and the symmetric trapped mode both slabs
oscillate with different phases and amplitudes until
![]() .
Then, according to Fig. 7a, the antisymmetric
perturbation extinguishes and the two slabs oscillate in phase. The periodogram
of the two curves in this plot coincides with that Fig. 5b
because the leaky mode is a very short duration signal and so its contribution
to the periodogram is very small. In addition,
Fig. 9 gives us a way of recovering the signals in
Figs. 5a and 7a. By summing the signals in
Fig. 9 the contribution of the antisymmetric modes
vanishes because they have the same amplitude and opposite sign in the slab
centres, so we are left with the symmetric mode, i.e. with
Fig. 5a. In the same manner, the difference of the signals in
Fig. 9 leads to Fig. 7a. We thus
conclude that the initial condition excites the symmetric and antisymmetric
modes, as expected, and that the system oscillates in its collective modes and
not in the modes of a single slab.
.
Then, according to Fig. 7a, the antisymmetric
perturbation extinguishes and the two slabs oscillate in phase. The periodogram
of the two curves in this plot coincides with that Fig. 5b
because the leaky mode is a very short duration signal and so its contribution
to the periodogram is very small. In addition,
Fig. 9 gives us a way of recovering the signals in
Figs. 5a and 7a. By summing the signals in
Fig. 9 the contribution of the antisymmetric modes
vanishes because they have the same amplitude and opposite sign in the slab
centres, so we are left with the symmetric mode, i.e. with
Fig. 5a. In the same manner, the difference of the signals in
Fig. 9 leads to Fig. 7a. We thus
conclude that the initial condition excites the symmetric and antisymmetric
modes, as expected, and that the system oscillates in its collective modes and
not in the modes of a single slab.
| |
Figure 9: vx measured at the centres of the slabs for the simulation shown in Fig. 8. The solid and dashed lines correspond to the right and left slabs, respectively. |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\hspace{-0.cm}{\bf (a)}\hspace{4.25cm}{\bf (b)}\hspace{...
...27.eps}\hspace*{4mm}\includegraphics[width=4.25cm,clip]{5227f28.eps}\end{figure}](/articles/aa/full/2006/39/aa5227-06/Timg80.gif) |
Figure 10: Time evolution of vx for d=2L and a non-symmetric initial disturbance. Note the interchange of energy between the two slabs in the last two frames. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5.15cm,clip]{5227f29.eps}\par\includegraphics[width=5.2cm,clip]{5227f30.eps}\end{figure}](/articles/aa/full/2006/39/aa5227-06/Timg81.gif) |
Figure 11:
a) vx measured at the centre of the slabs for the simulation shown in
Fig. 10. The solid and dashed lines correspond to the right and
left slabs, respectively. b) Power spectrum of the previous signal (solid
line). The two vertical dashed lines indicate the periods of the fundamental
antisymmetric mode (at
|
| Open with DEXTER | |
Secondly, we perturb the system with the same initial condition but now the
distance between the slab centres is d=2 L. As can be appreciated in
Fig. 3, this choice of the slab separation results in the fundamental
antisymmetric mode becoming trapped. The evolution of the system is again
presented for different times (Fig. 10) and, although after some
time the two slabs seem to move in phase (Fig. 10b), in a later
stage the right slab has given all its energy to the left slab and so is
motionless (Fig. 10c). At an even later time
(Fig. 10d) the picture is just the opposite, with the left slab
fixed and the right slab in motion. Hence, the two slabs are continously
exchanging energy and the transition between the states depicted in
Figs. 10c and d takes place through a situation similar to that in
Fig. 10b, where both slabs are oscillating. This behaviour is
repeated periodically. This phenomenon is more clearly represented in
Fig. 11a, where the velocity, vx, is plotted at the centre
of both slabs. Contrary to the behaviour in the stationary regime for symmetric
or antisymmetric initial perturbations (Figs. 5a and 7a), the oscillations do not attain a constant amplitude, but
they instead display a sinusoidal modulation. This is a well known collective
beating phenomenon, like, for instance, that of two weakly coupled oscillators.
It is due to the simultaneous excitation of the symmetric and antisymmetric
modes with alike frequencies. These frequencies are recovered from the power
spectrum of the velocity at the centre of right slab
(Fig. 11b), which shows two power peaks with periods almost
identical to those of the fundamental antisymmetric mode (
![]() )
and the fundamental symmetric mode (
)
and the fundamental symmetric mode (
![]() ). This match between the frequency of the normal modes and the oscillations in the numerical simulation is also evident in Fig. 3a.
Both peaks in the power spectrum have similar height, which allows us to
conclude that the two normal modes have been excited with similar amplitude.
). This match between the frequency of the normal modes and the oscillations in the numerical simulation is also evident in Fig. 3a.
Both peaks in the power spectrum have similar height, which allows us to
conclude that the two normal modes have been excited with similar amplitude.
In fact, from Fig. 3 we see that there exists a range of slab
separations where both trapped modes, i.e. the fundamental symmetric and
antisymmetric, coexist and possess very close frequencies. In this range of
separations, which goes from
![]() to infinity, the beating
appears when non-symmetric initial disturbances are applied. Hereafter we refer
to this range of d as the band of beating and to the separation where the
band starts as the minimum distance of beating (
to infinity, the beating
appears when non-symmetric initial disturbances are applied. Hereafter we refer
to this range of d as the band of beating and to the separation where the
band starts as the minimum distance of beating (
![]() ). Then, our
analysis yields
). Then, our
analysis yields
![]() for a/L=0.05 and
for a/L=0.05 and
![]() .
In Sect. 5.1, we shall
study the beating properties for other density ratios and will show that this
band extends to smaller separations.
.
In Sect. 5.1, we shall
study the beating properties for other density ratios and will show that this
band extends to smaller separations.
For a slab separation in the beating band the system
oscillates in a superposition of the trapped symmetric and antisymmetric modes.
Then, in the stationary state, the system behaves as
| (14) |
We define
| (15) | |||
| (16) |
| (17) | |||
| (18) |
![\begin{figure}
\par\includegraphics[width=5.25cm,clip]{5227f31.eps}\par\includegraphics[width=5.25cm,clip]{5227f32.eps}\end{figure}](/articles/aa/full/2006/39/aa5227-06/Timg102.gif) |
Figure 12: The solid lines are a rescaled close-up view of Figs. 10d and c, respectively. The dashed lines correspond to f1(x) and f2(x), respectively. The analytical approximation then reproduces the velocity profile obtained in the time-dependent simulation when a substantial amount of energy is concentrated in a single slab. The difference among both curves to the right and left of the slabs arises from the system not having reached the stationary state. For greater times the difference becomes smaller. |
| Open with DEXTER | |
Given the spatial structure of vx 1 and vx 2, the velocity in the
centre of the right and left slabs obtained in the numerical simulations should
be similar to
vx 1(x=d/2,t) and
vx 2(x=-d/2,t), respectively, so we
have plotted these two functions together with their numerical counterparts
(Fig. 13). During the transient phase, the analytical approximation
differs from the time-dependent results, but once the stationary state is
reached (around
![]() )
the fitting is very good. The small
difference between the two solutions in the stationary phase is caused by the
slight amplitude difference of the two normal modes in the numerical simulation
(see Fig. 11b).
)
the fitting is very good. The small
difference between the two solutions in the stationary phase is caused by the
slight amplitude difference of the two normal modes in the numerical simulation
(see Fig. 11b).
![\begin{figure}
\par\includegraphics[width=5.15cm,clip]{5227f33.eps}\par\includegraphics[width=5.15cm,clip]{5227f34.eps}\end{figure}](/articles/aa/full/2006/39/aa5227-06/Timg104.gif) |
Figure 13: a) Superposition of vx measured at the centre of the right slab from the time-dependent numerical simulation (solid line) and the analytical approximation (dashed line). b) The same for the left slab. |
| Open with DEXTER | |
The beating oscillatory curve is a sinusoidal function multiplied by a sinusoidal envelope whose period (the beating period) is
![\begin{figure}
\par\mbox{\hspace{-0.02cm}{\bf (a)}\hspace{4.25cm}{\bf (b)}\hspac...
...39.eps}\hspace*{4mm}\includegraphics[width=4.28cm,clip]{5227f40.eps}\end{figure}](/articles/aa/full/2006/39/aa5227-06/Timg107.gif) |
Figure 14:
Plots of
|
| Open with DEXTER | |
In addition, it is useful to define the number of oscillations within a pulsation period, or
beating factor (![]() ),
),
We investigate the beating properties of two identical slabs with different
separations and density contrasts (the slabs width is held fixed and given by
a/L=0.05). In the previous section we have seen that the dispersion relation
allows us to extract information about the beating with the help of
Eqs. (23), (24) and (25). For this reason we start plotting the real and
imaginary parts of the frequency as functions of d for different values of
![]() (see Fig. 14). In these plots
we can appreciate that the minimum distance of beating (i.e. the slab
separation for which the fundamental antisymmetric mode transforms from leaky
into trapped) decreases as the density ratio increases. This means that denser
slabs can display beating for smaller separations. The oscillatory period
obtained from Eq. (24) is plotted in
Fig. 15a. For all the considered values of
(see Fig. 14). In these plots
we can appreciate that the minimum distance of beating (i.e. the slab
separation for which the fundamental antisymmetric mode transforms from leaky
into trapped) decreases as the density ratio increases. This means that denser
slabs can display beating for smaller separations. The oscillatory period
obtained from Eq. (24) is plotted in
Fig. 15a. For all the considered values of
![]() ,
the oscillatory period is more or less independent from the slab separation when this quantity is larger than the length of the loops. Nevertheless, for d<L (and for sufficiently high values
of the density contrast, like for example
,
the oscillatory period is more or less independent from the slab separation when this quantity is larger than the length of the loops. Nevertheless, for d<L (and for sufficiently high values
of the density contrast, like for example
![]() or 10) the oscillatory period decreases as the separation is reduced.
or 10) the oscillatory period decreases as the separation is reduced.
Two other parameters worth studying are the beating period,
![]() ,
and the beating factor,
,
and the beating factor, ![]() ,
extracted from the
dispersion relation data and Eqs. (23) and (25). These parameters are plotted in Figs. 15b and c, respectively. We see that the beating period grows to infinity with d/L which is the expected behaviour of two slabs
that tend to oscillate independently. On the other hand, we see that for small
slab separations
,
extracted from the
dispersion relation data and Eqs. (23) and (25). These parameters are plotted in Figs. 15b and c, respectively. We see that the beating period grows to infinity with d/L which is the expected behaviour of two slabs
that tend to oscillate independently. On the other hand, we see that for small
slab separations ![]() becomes rather small, implying that each beating
period contains only a few oscillatory periods. In particular, we find that
slabs with high density contrast can show strong beating for small distances in
comparison with slabs with small density contrasts.
becomes rather small, implying that each beating
period contains only a few oscillatory periods. In particular, we find that
slabs with high density contrast can show strong beating for small distances in
comparison with slabs with small density contrasts.
![\begin{figure}
\par\includegraphics[width=5cm,clip]{5227f41.eps}\par\includegrap...
...,clip]{5227f42.eps}\par\includegraphics[width=5cm,clip]{5227f43.eps}\end{figure}](/articles/aa/full/2006/39/aa5227-06/Timg112.gif) |
Figure 15:
a) Oscillatory period, b) beating period and c) beating factor, for the
density contrasts
|
| Open with DEXTER | |
We have studied the main features of a simple two-slab configuration (without gravity and curvature). Firstly, we have analysed in detail the normal modes of the system. We have derived analytical expressions for the dispersion relation and have found, in agreement with the results of Díaz et al. (2005), that the symmetric mode is the only trapped mode for any distance between the slabs. On the other hand, the antisymmetric mode is leaky for small slab separations, but there exists a wide range of slab separations (larger than the critical distance) where both trapped modes, i.e. the fundamental symmetric and antisymmetric, coexist and possess very close frequencies. Thus, trapped and/or leaky modes are excited according to the ratio d/L, but also according to the shape of the initial perturbation. It is then expected that initial disturbances with odd parity with respect to the centre of the system excite antisymmetric modes, whereas even disturbances lead to the excitation of symmetric modes.
Secondly, we have studied the temporal evolution of symmetric, antisymmetric
and arbitrary excitations for a typical coronal loop with a/L=0.05 and
![]() and different slab separations. We have
found that for symmetric disturbances and after a short transient all that
remains is the undamped trapped mode, with energy confined to both slabs. On
the other hand, since there are no trapped antisymmetric modes for slab
separations smaller that
and different slab separations. We have
found that for symmetric disturbances and after a short transient all that
remains is the undamped trapped mode, with energy confined to both slabs. On
the other hand, since there are no trapped antisymmetric modes for slab
separations smaller that
![]() ,
an antisymmetric-like initial
disturbance can only deposit energy in the leaky antisymmetric modes. The
excitation of the fundamental antisymmetrical trapped mode is only possible for
,
an antisymmetric-like initial
disturbance can only deposit energy in the leaky antisymmetric modes. The
excitation of the fundamental antisymmetrical trapped mode is only possible for
![]() .
.
An arbitrary excitation in the regime
![]() leads to the
simultaneous excitation of the symmetric and antisymmetric modes. Since their
frequencies are quite similar the oscillations do not attain a constant
amplitude and show a sinusoidal modulation. This is a well known collective
beating phenomenon which is completely equivalent to the behaviour of two weakly coupled oscillators. The frequency of oscillation of the system is
leads to the
simultaneous excitation of the symmetric and antisymmetric modes. Since their
frequencies are quite similar the oscillations do not attain a constant
amplitude and show a sinusoidal modulation. This is a well known collective
beating phenomenon which is completely equivalent to the behaviour of two weakly coupled oscillators. The frequency of oscillation of the system is
![]() with an envelope frequency or
beating frequency
with an envelope frequency or
beating frequency
![]() ,
where
,
where
![]() and
and
![]() are the antisymmetric and symmetric
normal mode frequencies, respectively. The beating is the result of the
continuous exchange of energy between the two slabs. We have also shown that
slabs with high density contrast can show strong beating for small distances
in comparison with slabs with small density contrasts.
are the antisymmetric and symmetric
normal mode frequencies, respectively. The beating is the result of the
continuous exchange of energy between the two slabs. We have also shown that
slabs with high density contrast can show strong beating for small distances
in comparison with slabs with small density contrasts.
It is important to remark that for moderate slab separations and any type of initial excitation, the system acquires a collectivemotion and does not oscillate with the modes of an individual slab. For this reason, and specially in coronal arcades, formed by ensembles of loops, it seems much more appropriate to describe the oscillations in terms of collective motions instead of individual loop oscillations. Nevertheless, since our model is too simple, it has no sense to perform a quantitative comparison with the observations of loop oscillations in coronal arcades. However, it is worth noticing that the most clear example of such kind of oscillations (see Verwichte et al. 2004) suggests that initially some loops of the arcade oscillate in phase while at later times the motions are in antiphase. This can be an indication of beating phenomenon as the result of the collective oscillation of some of the loops. Unfortunately, it is not possible to extract more conclusions since the amplitude of the oscillations is quickly damped and only a few periods are observed. Additional observations of oscillations in coronal arcades will be very useful.
Finally, in order to have a more realistic model additional effects such as gravity, gas pressure and curvature need to be included. However, one of the most significant improvements to the model is to consider two cylindrical loops instead of Cartesian slabs. Since the eigenfunction in cylindrical tubes are much more confined than in slabs, the interaction between the tubes will be in general smaller and the beating time will be much longer. In addition, instead of the two modes of the Cartesian slab (symmetric and antisymmetric), now the system will have four different modes of oscillation. Two of these modes will be symmetric while the other two will be antisymmetric in the xand y-directions. The normal mode analysis of this configuration will be the subject of a future work.
Acknowledgements
M. Luna thanks to Spanish Ministry of Education and Science for an FPI grant, which is partially supported by the European Social Fund. In addition, J. Terradas thanks the Spanish Ministry of Education and Science for the funding provided under a Juan de la Cierva fellowship. The authors acknowledge the Spanish Ministry of Science and Technology and the Conselleria d'Economia, Hisenda i Innovació of the Government of the Balearic Islands for the funding provided under grants AYA2003-00123 and PRIB-2004-10145, respectively.