A&A 457, 1003-1010 (2006)
DOI: 10.1051/0004-6361:20064935

Broad H$\alpha $ wings from the optically thin stellar wind of the hot components in symbiotic binaries

A. Skopal

Astronomical Institute, Slovak Academy of Sciences, 059 60 Tatranská Lomnica, Slovakia

Received 30 January 2006 / Accepted 10 July 2006

Abstract
Aims. To model broad H$\alpha $ wings observed in symbiotic binaries by an optically thin, bipolar stellar wind from their hot components as an alternative to that considering the Raman scattering of Ly$\beta $ photons on atomic hydrogen.
Methods. Profile-fitting analysis. Comparison of the observed broad H$\alpha $ wings and their luminosity with those predicted by the model.
Results. Synthetic H$\alpha $ profiles fit excellently the observed wings for $\vert\Delta v\vert \ga $ 200 km s-1 in our sample of 10 symbiotic stars during the quiescent as well as active phases. The wing profile formed in the stellar wind can be approximated by a function $f(\Delta v) \propto \Delta v^{-2}$, which is of the same type as that arising from the Raman scattering. Therefore it is not possible to distinguish between these two processes only by modeling the line profile. Some observational characteristics of the H$\alpha $-emission, its relationship with the emission measure of the symbiotic nebula and a steep radio spectrum at 1.4-15 GHz suggest the ionized stellar wind from the hot component to be the dominant source contributing to the H$\alpha $ wings during active phases. The model corresponding mass-loss rates from the hot components are of a few $\times 10^{-8}$  $M_{\odot}~{\rm yr}^{-1}$ and of a few $\times~(10^{-7} {-} 10^{-6})$  $M_{\odot}~{\rm yr}^{-1}$ during quiescent and active phases, respectively.

Key words: stars: binaries: symbiotics - stars: mass-loss - stars: winds, outflows

1 Introduction

Van Winckel et al. (1993) and Ivison et al. (1994) presented a large survey of high- and low-resolution H$\alpha $ line profiles of symbiotic stars. The profiles showed broad wings, in most cases extended well within the presented wavelength range of 6540-6580 Å. Their origin has been investigated by number of authors. A popular interpretation assumes Raman scattering of Ly$\beta $ photons on atomic hydrogen to be responsible for filling in the broad H$\alpha $ wings. This possibility was firstly pointed out by Nussbaumer et al. (1989) and the corresponding quantitative model was elaborated by Lee (2000) and Lee & Hyung (2000). Other possibilities for the H$\alpha $ wing formation mechanism - rotating disks, electron scattering, fast stellar wind and H$\alpha $ damping wings - were also discussed. Robinson et al. (1994) modeled the H$\alpha $ profiles on the assumption that they originate in an accretion disk. Acceptable fits were found only for CH Cyg, AG Dra and T CrB. Generally, the model wings were broader than the observed ones. The possibility of the electron scattering was analyzed by Arrieta & Torres-Peimbert (2003) for a representative case of M2-9. They found unrealistically high values of the electron temperature and concentration for the electron-scattering region. Concerning to the H$\alpha $ damping wings there is no elaborated application for symbiotic binaries. Lee (2000) only discussed briefly this possibility for the case of SY Mus (Schmutz et al. 1994). He came to conclusion that the wing emission arises in a much more extended region then that producing the line core. Skopal et al. (2002) modeled the extended H$\alpha $ wings from active phases of CH Cyg by a spherically symmetric and optically thin stellar wind. A comparison between the modeled and observed profiles was satisfactory and also the derived mass-loss rate was in agreement with that suggested by the radio observations. Therefore we propose the fast stellar wind from the hot component in symbiotic binaries to be the most promising alternative to that considering the Raman scattering process.

Accordingly, in Sect. 2 we introduce a model of a bipolar stellar wind at the optically thin limit to calculate the broad H$\alpha $ wings. In Sect. 3 we compare our model profiles with those observed during quiescent and active phases of selected symbiotic stars. In Sect. 4 we discuss observational characteristics of H$\alpha $  profiles connected with the hot star wind.

  \begin{figure} \par\includegraphics[width=6cm,clip]{4935f_1a.ps}\includegraphics[width=6cm,clip]{4935f_1b.ps} \end{figure} Figure 1: Geometry of the wind model we used to calculate the line profile of H$\alpha $ and its luminosity. The wind is produced by the central star (small circle at the mid of panels). A fraction of the wind is blocked by an optically thick disk/torus at the center that cut out a cone from the sphere with the opening angle $\pi - 2\theta _0$. By this way we simulate bipolar geometry of the stellar wind. The shadow belt on the side view ( left) and/or the annulus from the frontal view ( right) represents a part of the shell with the same radial velocity, $-v(r)\cos~(\theta)$. Radiation from the annulus, cut out by 4 $\tilde\theta$ radians, is blocked by the central disk (the darker part). The angle $\tilde\theta$ is counted in the plane containing the annulus.
Open with DEXTER

2 Model of the bipolar wind

2.1 Signatures of the mass outflow

Here we summarize main observational features of a mass outflow indicated for active symbiotic stars. They are: (i) broadening of emission line profiles and/or the P-Cygni type of profiles represent direct indications of a mass-flow from the star. Typical velocities are a few hundred of  km s-1 (e.g. Skopal et al. 1997; Fernández-Castro et al. 1995; Nussbaumer et al. 1995); (ii) a significant enhancement of the nebular emission in the continuum by a factor of $\approx$10 relatively to quiescent phases (Skopal 2005, Tables 3 and 4) can in part result from a supplement of new emitters into the particle bounded nebula, for example, due to an increase in the mass-loss rate from the active object; (iii) the radio light curves usually show a decline at beginnings of outbursts with an increase after the optical maximum (e.g. Fernández-Castro et al. 1995; Brocksopp et al. 2004). In some cases evolution from a point source to a spatial structure was observed (e.g. CH Cyg and Z And: Brocksopp et al. 2004; Kenny et al. 1996). This can be a result of a high-velocity mass-outflow, which gradually becomes optically thin at radio wavelengths. Velocities from a few hundred of  km s-1 to $1000\div 2000$  km s-1 can be derived from images (e.g. CH Cyg, Crocker et al. 2002,2001); (iv) the X-ray emission can be also explained by interaction of the outflowing material with surrounding nebular gas. The extended X-ray emission in the CH Cyg Chandra image was aligned with the optical and radio jets (Galloway & Sokoloski 2004). Thus the velocities connected with the X-ray emission can be similar to those derived from the radio. For Z And, Sokoloski et al. (2006) ascribed the X-ray emission from its major 2000-03 outburst to the shock-heated plasma as a consequence of the mass ejection from the white dwarf; (v) emission line profiles of forbidden lines from highly ionized atoms can be produced by the wind-wind collision zone in a binary system (e.g. Eriksson et al. 2004; Wallerstein et al. 1984). Aspects of the wind-dynamics including colliding winds in symbiotic binaries were reviewed by Walder & Folini (2000).

Finally, we note that different features of the outflowing material in the spectrum can reflect different driving mechanisms. For example, ejected rings or shells produce broad profiles with rather steep sides of all lines (FWHM  $\sim0.7\times$ FWZI). Classical novae 1494 Aql and V475 Sct demonstrate this case (Eyres et al. 2005; Chochol et al. 2005). For a star with a spherically symmetric and optically thin wind, the line emissivity is proportional to the square of the particle concentration, which is diluted with the radial distance r as 1/r2. In this case a strong line core, originating in the vicinity of the wind source, is accompanied with faint extended wings from large distances (FWHM $\ll$ FWZI). In the following model we consider this case.

Table 1: Parameters of H$\alpha $ models ($R_{\rm w}$, $\beta $, $v_{\infty }$), observed luminosities and corresponding mass-loss rates ($\dot M$) and emission measures ( $EM_{\rm w}$) of the hot star wind. $L_{\alpha }$(200) denotes the luminosity of the H$\alpha $ wings for $\vert\Delta v\vert \ge 200$  km s-1, while $L_{\alpha }(0)$ is the total line luminosity. Distances are from Skopal (2005).

2.2 Geometry of the wind

The geometry of our wind model is introduced in Fig. 1. The model assumes an optically thin stellar wind with a spherically symmetric structure and the origin at/around the central star. According to Skopal (2005) we put an optically thick disk/torus, characterized with the height H and radius $R_{\rm D}$, to the center of the hot object. We assume the disk to be seen edge-on due to a high orbital inclination. The outer rim of the disk cut out the angle 2 $\theta_0 = 2\tan^{-1}~(H/R_{\rm D})$ from a sphere with the center at the accretor, and by this way simulates bipolar shape of the stellar wind with the opening angle $\pi - 2\theta _0$ radians (Fig. 1 left). The wind with this geometry produces line profiles that are symmetrical with respect to the reference wavelength ($\lambda_0$). We assume that the particle concentration n(r) at any point in the wind is related to the mass loss rate $\dot M$ and the velocity v(r) via the mass continuity equation, i.e.

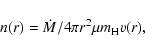\begin{displaymath}n(r) = \dot M/4\pi r^{2}\mu m_{\rm H} v(r), \end{displaymath} (1)

where $\mu$ is the mean molecular weight and $m_{\rm H}$ is the mass of the hydrogen atom. According to the Castor et al. (1975) model we approximate the velocity distribution in the hot star wind by

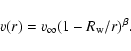\begin{displaymath}v(r) = v_{\infty}(1 - R_{\rm w}/r)^{\beta}. \end{displaymath} (2)

The velocity v(r) of the wind increases monotonically outward from its beginning at $R_{\rm w}$ and asymptotically approaches the terminal speed $v_{\infty }$. The distance r is counted from the center of the star and the parameter $\beta $ characterizes an acceleration of the wind, i.e. the "slope'' of v(r). A smaller $\beta $ corresponds to a faster transition to  $v_{\infty }$ (e.g. Bertout et al. 1985).

2.3 H$\alpha $ luminosity

In our simplified approach we assume that the wind is fully ionized and completely optically thin in H$\alpha $ with a steady mass-loss rate. The optically thin case is supported by the large velocity gradient in the stellar wind, because of its large terminal velocity ( $v_{\infty} \gg v_{\rm th}$, where  $v_{\rm th}$ is the thermal velocity). If a line photon, created by recombination in such a wind, has traveled a distance $l > 2 v_{\rm th}/({\rm d}v/{\rm d}l)$, it is Doppler shifted with respect to the surrounding gas by more than 2 $v_{\rm th}$ and thus cannot be absorbed any more in the same line transition (e.g. Lamers & Cassinelli 1999). Under such conditions the escape probability of the emitted photons will be close to 1. However the optically thin condition can be attained only at large distances from the source of the wind. A good agreement between the observed and modeled profiles for $\vert\Delta v\vert \ga $ 200  km s-1 (see below, Fig. 3) suggests the validity of the optically thin regime from about $1.2\div1.5$ $R_{\rm w}$ (Eq. (2) and parameters from Table 1).

The total line luminosity, $L(\rm H\alpha$), is related to the line emissivity of the wind, $\varepsilon_{\alpha} n_{\rm e}n^{+}$, by

\begin{displaymath}L({\rm H}\alpha) = 4\pi\varepsilon_{\alpha}\!\! \int_{r_{\rm i}}^{\infty}\!\! n_{\rm e}n^{+}(r)[1-w(r)]~r^2{\rm d}r, \end{displaymath} (3)

where $r_{\rm i}$ is a certain distance from the source of the wind where the integration starts from (its quantity is given by the model; $r_{\rm i} \ge H$, $R_{\rm w} < H$), $\varepsilon_{\alpha} = 3.56\times 10^{-25}~\rm erg~cm^{3}~s^{-1}$ is the volume emission coefficient in H$\alpha $ for $T_{\rm e} = 10^{4}$ K. We assume it to be constant throughout the wind. $n_{\rm e}$ and n+ are concentrations of electrons and ions (protons). We assume a completely ionized medium ( $n_{\rm e} \simeq n^{+}$) and radial distribution of particles as given by Eq. (1). The factor w(r) determines visibility of the wind for the outer observer. It can be expressed as
$\displaystyle w(r) = \sin\theta ~ = ~ H/r ~~~~~~ {\rm for}~~~ r < r_0,$      
$\displaystyle = \sin\theta_0 ~ = ~ H/r_0 ~~~ {\rm for}~~~ r > r_0 ,$     (4)

where $r_0^2 = R_{\rm D}^2 + H^2$ (Fig. 1). Therefore we have to integrate contributions from the shells between H and r0 and those above the r0 radius separately. Substitution of Eqs. (1), (2) and (4) into Eq. (3) and using dimensionless parameters $x=R_{\rm w}/r$, $\alpha = H/R_{\rm w}$ and $f=R_{\rm w}/r_0$ yields an expression for the H$\alpha $ luminosity as

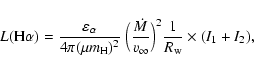\begin{displaymath}L({\rm H}\alpha) = \frac{\varepsilon_{\alpha}}{4\pi(\mu m_{\r... ...}{v_{\infty}}\Big)^{2}\frac{1}{R_{\rm w}} \times (I_1 + I_2), \end{displaymath} (5)

where
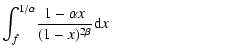                          I1 = $\displaystyle \int_{f}^{1/\alpha}\! \frac{1-\alpha x}{(1-x)^{2\beta}}{\rm d}x ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~$  
  = $\displaystyle \frac{\alpha}{2(\beta-1)}~\Big[\big(1-1/\alpha\big)^{2(1-\beta)} - \big(1-f\big)^{2(1-\beta)}\Big]$  
    $\displaystyle +~ \frac{1-\alpha}{2\beta-1}~\Big[\big(1-1/\alpha\big)^{1-2\beta} - \big(1-f\big)^{1-2\beta}\Big]$  
    $\displaystyle ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~{\rm for}~~ \beta \not= 0.5, 1,$  
  = $\displaystyle ~ \alpha\ln\frac{\alpha(1-f)}{\alpha-1}~- \frac{1-\alpha f}{1-f} ~~~~~~~~~{\rm for}~~ \beta = 1,$  
      = $\displaystyle (1- \alpha)\ln\frac{\alpha(1-f)}{\alpha-1} + 1 - \alpha f ~~{\rm for}~~ \beta = 0.5$ (6)

and

\begin{displaymath}I_2 = \int_{0}^{f}\! \frac{1-H/r_0}{(1-x)^{2\beta}}{\rm d}x ... ...ac{1-H/r_0}{(1-2\beta)}~\Big[1-\big(1-f\big)^{1-2\beta}\Big] . \end{displaymath} (7)

Analytical expression of the integral I2 was already introduced by Skopal et al. (2002). Thus comparing the H$\alpha $ luminosity from observations to that predicted by Eq. (5) allow us to estimate the mass-loss rate, $\dot M$. To determine theoretical values of $L({\rm H}\alpha)$ requires a knowledge of parameters characterizing the wind: $v_{\infty }$, $R_{\rm w}$, $\beta $ and $\theta_0$. To estimate their appropriate quantities we fit a synthetic-line profile to the observed one. This requires a different manner of integration of the wind's contributions. We introduce it in the following section.

Table 2: Emission measures and H$\alpha $ luminosities.

2.4 H$\alpha $ profile

To reconstruct the global line profile we redistribute the independent Doppler-shifted contributions from each volume element of the wind expanding material in the radial velocity co-ordinates. The profile thus represents a "broadening function'' resulting from a field of contributions which differ in emissivity and radial velocity. It can be compared only to high-velocity features in the profile produced by regions with $\tau({\rm H}\alpha) < 1$. A technique of integration can be understood with the help of Fig. 1. Volume elements of the same radial velocity, $RV = -v(r)\cos\theta$, are represented by annuli around the line of sight, and can be expressed as

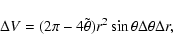\begin{displaymath}\Delta V = (2\pi - 4\tilde\theta) r^2 \sin\theta \Delta\theta \Delta r, \end{displaymath} (8)

where the angle 4 $\tilde\theta$ corresponds to a fraction of the annuli, which radiation is blocked by the central disk. The $\tilde\theta$ angle is counted in the plane containing the annulus of the radius $r \sin\theta$ and is related to H and $\theta$ as (Fig. 1 right)
$\displaystyle \sin\tilde\theta = \frac{H}{r \sin\theta}~~~~~~{\rm for}~~~ H < r < r_0,$      
$\displaystyle = \frac{\sin\theta_0}{\sin\theta}~~~~~~~{\rm for}~~~ r > r_0.$     (9)

In the sense of Eq. (3), radiative contributions of such cut-out annuli are $\Delta L({r},\theta) = \varepsilon_{\alpha} n({r})^2 \Delta V$. They correspond to a certain radial velocity $\Delta v$ (or $\Delta \lambda$) in the profile. With the aid of Eqs. (1) and (8) we can write them as

\begin{displaymath}\Delta L(r,\theta) = \xi \frac{(2\pi - 4\tilde\theta)\sin\th... ...r^2 {\rm v}(r)^2}\Delta\theta \Delta r ~~~ [{\rm erg~s^{-1}}], \end{displaymath} (10)

where ${v}(r) = v(r)/v_{\infty}$ and the factor

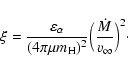\begin{displaymath}\xi = \frac{\varepsilon_{\alpha}}{(4\pi\mu m_{\rm H})^2} \Big(\frac{\dot M}{v_{\infty}}\Big)^2\cdot \end{displaymath} (11)

Redistributing all the visible emissions according to their radial velocities we obtain the resulting line profile. Integration of each shell begins from the direction at $\theta = \theta_1$ and ends at $\theta = \pi - \theta_1$. Their contributions are summarized from H to a distance at which the wind's emission can be neglected. Thus the line luminosity can be expressed as

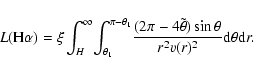\begin{displaymath}L({\rm H}\alpha) = \xi \int_{H}^{\infty}\! \int_{\theta_1}^{... ...lde\theta)\sin\theta} {r^2 {v}(r)^2} {\rm d}\theta{\rm d}r. \end{displaymath} (12)

According to the relation (9), integration has to be divided into two parts: for H < r < r0, $\theta_1 = \sin^{-1}~(H/r)$ and for r > r0, $\theta_1 = \theta_0$.
  \begin{figure} \par\includegraphics[angle=-90,width=12cm,clip]{4935f_2.eps} \end{figure} Figure 2: Luminosity of H$\alpha $ wings for $\vert\Delta v\vert \ge 200$ km s-1, $L_{\alpha }$(200), as a function of the mass-loss rate calculated according to Eq. (12) for parameters $R_{\rm w}$, $\beta $ and $v_{\infty }$ in Table 1. The observed quantities of $L_{\alpha }$(200) are denoted by filled diamonds (Table 1).
Open with DEXTER

Contributions from the nearest regions to the wind origin, $R_{\rm w}$, are characterized with $H < r \ll r_0$ and large values of $\theta_1$. According to relations (1) and (2) they are strong due to a high density of the wind and contribute mainly to the line center, because of a small radial velocity. However, their emission is reduced significantly by the large value of $\sin\tilde\theta$ in our model (Eq. (9)), i.e. a significant fraction of radiation is blocked by the torus. Integration ends at a finite limit of 200 $R_{\odot}$ (Fig. C1 in Skopal et al. 2002). After summing of all the contributions we scaled the synthetic profile to the maximum of the observed one. Examples are shown in Fig. 3. The input parameters, $v_{\infty }$ and $\theta_0$ can be inferred from observations, while the resulting parameters, $R_{\rm w}$, $\xi$ and $\beta $, are given by an appropriate fit to the observed profile (Sect. 3.2). If we rewrite the relation (12) in the form

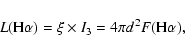\begin{displaymath}L({\rm H}\alpha) = \xi \times I_3 = 4\pi d^{2} F({\rm H}\alpha), \end{displaymath} (13)

we can express the ratio

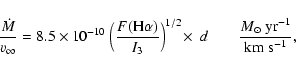\begin{displaymath}\frac{\dot M}{v_{\infty}} = 8.5 \times 10^{-10}~ \Big( \fra... ...s~d ~~~~~~~~ \frac{M_{\odot}~{\rm yr}^{-1}}{\rm km~s^{-1}} , \end{displaymath} (14)

where the distance d is in kpc and the observed bolometric flux $F({\rm H}\alpha)$ in $\rm erg~cm^{-2}~s^{-1}$. Following to Eq. (10) integral I3 is given by the geometry of the wind and is proportional to the sum of all its visible volume elements. For wing fluxes, e.g. $F_{\alpha}$(200) (see Sect. 3.3), the I3 integral includes contributions only with the radial velocity $\vert\Delta v\vert > $ 200  km s-1.

3 Comparison with observations

3.1 Data sources

In major part we used observations of H$\alpha $ profiles from the survey of van Winckel et al. (1993) and Ivison et al. (1994). Other sources are referred in Table 2. If possible, we selected objects that were observed during both quiescence and activity. We converted observed fluxes in relative units to fluxes in $\rm ~erg~cm^{-2}~s^{-1}~\AA^{-1}$ with the aid of simultaneous optical V and R photometry (Skopal et al. 2004, and references therein) and the model SED according to Skopal (2005). Approximate corrections for emission lines (Skopal 2003) were also included. To deredden the fluxes we used appropriate EB-V from Table 1 of Skopal (2005). For the purpose of Sect. 4 we also estimated emission measure, $EM_{\rm obs}$, of the symbiotic nebula at the dates of H$\alpha $  observations (Table 2). For the sake of simplicity and availability we used dereddened fluxes, FU, derived from U-magnitudes. Then according to Eq. (18) of Skopal (2005),

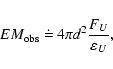\begin{displaymath}EM_{\rm obs}~\dot=~4\pi d^2 \frac{F_{U}}{\varepsilon_{U}}, \end{displaymath} (15)

where $\varepsilon_{U}$ is the volume emission coefficient per electron and per ion ( $\rm erg~cm^{3}~s^{-1}~\AA^{-1}$). We used the average value of $\varepsilon_{U}$ from both the sides of the Balmer jump corresponding to the electron temperature given by the SED (Skopal 2005).

3.2 Model parameters

Geometrical parameters of our wind model are described in Sect. 2.2. Some limits for parameters $R_{\rm D}$ and H can be estimated from the effective radius, $R_{\rm h}^{\rm eff}$, of the hot star. This parameter represents the radius of a sphere that produces the observed luminosity of the hot stellar source and can be derived from modeling the SED of the ultraviolet continuum (Skopal 2005). In our model $4\pi (R_{\rm h}^{\rm eff})^2 = 4\pi R_{\rm D} H$. During quiescent phases we observe $R_{\rm h}^{\rm eff} \approx 0.15~R_{\odot}$ (Skopal 2005, Table 3). Assuming the ratio $H/R_{\rm D} = 0.1$ then yields $R_{\rm D} = 0.5~R_{\odot}$ and $H = 0.05~R_{\odot}$. During active phases we assume flared disk with $H/R_{\rm D} = 0.3$. Then parameters H and $R_{\rm D}$ are adjusted to the corresponding $R_{\rm h}^{\rm eff}$ (a few of $R_{\odot}$) for objects we investigate here.

The origin of the wind, $R_{\rm w}$, and $\beta $ in the wind law are model parameters, while $v_{\infty }$ is given by the extension of the wings. Values of $R_{\rm w}$, and $\beta $ are critical for the synthetic profile. Generally, a larger value of $\beta $ corresponds to a slower and denser wind with a higher emissivity at a point r. Therefore the wind characterized with a larger value of $\beta $ produces a narrower profile. Regions close to the wind's origin ( $R_{\rm w} < H < r \ll r_0$) have the largest emissivity, because of high densities for small values of both r and v(r); they contribute mainly to the line core. However, a fraction of their radiation is blocked by the outer rim of the disk in our model. In addition, optical properties of these regions can deviate from the optically thin case. Therefore we do not aim to fit the core of the line by this procedure. At further distances ( $r \ga 1.2~R_{\rm w}$) the wind is accelerated to $v(r) \ga 200 {-} 250$  km s-1 (Eq. (2), $\beta\sim 1.7$). Contributions from these regions are more important to create the broad wings. A good agreement between the modeled and observed profiles for radial velocities $\vert\Delta v\vert \ga 200$  km s-1 (Fig. 3) is consistent with our assumption on the optically thin regime from this distance above the source of the wind.

3.3 Wing profiles, $\dot M$ and uncertainties

We reconstructed synthetic profiles according to Eqs. (10) and (12). To obtain an appropriate solution we calculated a grid of models for reasonable ranges of $R_{\rm w}$ and $\beta $. By this way we also estimated their uncertainties to $20\%$ and $10\%$, respectively. A comparison of resulting models with observations is shown in Fig. 3 and the corresponding parameters are introduced in Table 1. Models match perfectly the line profile for $\vert\Delta v\vert > 200$ km s-1. Therefore to determine the mass-loss rate from the hot star, $\dot M$, we compared the luminosity of wings for $\vert\Delta v\vert \ga 200$ km s-1 ( $L_{\alpha }$(200) in our notation) with that calculated according to Eq. (14) for the same radial velocity interval. Dependences of $L_{\alpha }$(200) on $\dot M$ for our models are plotted in Fig. 2. Uncertainties in the $\dot M$ values were determined from those of $F({\rm H\alpha}$), $\beta $ and $R_{\rm w}$. We estimated the uncertainty in the H$\alpha $ fluxes to $\sim$10%, which results mainly from determination of the level of the local continuum (Sect. 3.1). As $\dot M \propto \sqrt{L(\rm H\alpha)}$, the uncertainty in fluxes increases that of $\dot M$ with only square root. We estimated them to 8%-12%.

4 Discussion

We showed that the profiles from the ionized optically thin, bipolar stellar wind match well the observed H$\alpha $ wings for $\vert\Delta v\vert \ga 200$ km s-1. The curve fitting the profile is proportional to $\Delta v^{-2}$ (Eqs. (10) and (12)), which is of the same type as that including solely the Raman Ly $\beta \rightarrow {\rm H}\alpha$ scattering process (Lee 2000). From this point of view it is not possible to distinguish contributions from the ionized wind and the Raman scattering in the wing profile directly. However, both the processes take place in very different regions of the binary. The ionized stellar wind in our model is located around the hot star, while the Raman-scattered photons originate in the neutral part of the wind from the giant. Below we summarize observational characteristics of the H$\alpha $  emission that could help to identify main sources of radiation contributing to its broad wings.

  \begin{figure} \par {\hspace*{6.6cm}\sf Q U I E S C E N T ~ P H A S E S}\\ [-1mm... ...ngle=-90]{4935f_3k.eps} \includegraphics[angle=-90]{4935f_3l.eps}} \end{figure} Figure 3: Comparison of the modeled (M) and observed (O) H$\alpha $ line profiles for selected symbiotic stars during their quiescent phases ( top two raws of panels) and active phases ( the bottom raw of panels). The systemic velocity was subtracted. The model is described in Sect. 2.4 and the corresponding parameters are in Table 1. It fits the observed profiles for $\vert\Delta v\vert \protect\ga $ 200  km s-1. Fluxes are in 10-11 $\rm ~erg~cm^{-2}~s^{-1}~\AA^{-1}$.
Open with DEXTER

4.1 Observed properties of H$\alpha $ wings

(i) During eclipses of the hot component by the giant the H$\alpha $ emission in both the core and the wings decreased significantly. Examples here are AX Per (Skopal et al. 2001, Fig. 6), AR Pav (Quiroga et al. 2002, Fig. 2), FN Sgr (Brandi et al. 2005, Table 2, Fig. 4) and Z And (Skopal et al. 2006, Fig. 4). These observations suggest that a significant fraction of the broad H$\alpha $ wings is formed nearby the hot star.

(ii) Ikeda & Tamura (2000), Quiroga et al. (2002), Mikolajevska et al. (2003) and Brandi et al. (2005) revealed that the radial velocities from the wings of H$\alpha $ follow the orbital motion of the hot component in V1329 Cyg, AR Pav, AE Ara and FN Sgr, respectively. This implies that the region of the H$\alpha $ wings formation is connected with the hot star.

(iii) The wing profiles from our sample of objects are symmetrically placed around $\lambda_0$. In cases of CI Cyg (20/06/89, $\varphi = 0.85$) and AR Pav (17/07/88, $\varphi = 0.71$) we shifted the model by +12 and +15 km s-1, respectively, to match better observations. These shifts are consistent with the hot component orbital motion. Only in the case of Z And (22/09/88, $\varphi = 0.30$) the model was shifted by +10 km s-1, which is against the orbital motion. Nature of this difference is not clear.

(iv) In our sample of H$\alpha $ profiles we did not find systematic shifts, which could be associated with the Raman scattering. For example, the supposed blue-shifted component from the neutral wind at/around the binary axis that moves against the incident Ly$\beta $ photons (Schmid et al. 1999) and/or the redshift of the H$\alpha $ wing center as suggested by Jung & Lee (2004), were not indicated. From this point of view, a good agreement between systemic velocities determined independently from M-giant and H$\alpha $-wings radial velocities, respectively, for objects referred in the point (ii), is consistent with our finding.

  \begin{figure} \par\includegraphics[angle=-90,width=8.5cm,clip]{4935f_4.eps} \end{figure} Figure 4: Total H$\alpha $ line and wing luminosities, $L_{\alpha }$(0) and $L_{\alpha }$(200), respectively, as a function of the observed emission measure $EM_{\rm obs}$. The total line luminosities are divided by a factor of 5 for a better visual display. Corresponding quantities are from Table 2.
Open with DEXTER

4.2 H$\alpha $ luminosity as a function of the nebular emission

Here we investigate a relationship between the H$\alpha $ luminosities, $L_{\alpha }$(0), $L_{\alpha }$(200), and the emission measure of the symbiotic nebula, $EM_{\rm obs}$, which is due to photoionization. Relevant data are described in Sect. 3.1, summarized in Table 2 and plotted in Fig. 4.

During quiescent phases the nebular emission originates in the ionized part of the wind from the giant as given by the STB (Seaquist et al. 1984) model. This was independently supported by finding of Nussbaumer et al. (1988) that symbiotic objects fit well the CNO abundance ratios of normal red giants. Following analyses showed that the model is applicable for most of quiescent symbiotics (e.g. Mikolajewska et al. 2002; Seaquist et al. 1993). Within this model the ionized wind from the giant can contribute to only the H$\alpha $ core emission, because of its small radial velocity dispersion. The broad H$\alpha $ wings thus have to be of a different nature. Figure 4 plots the relevant quantities as a function of $\log~(EM_{\rm obs})$. The observed dependencies are in qualitative agreement with the model: The total H$\alpha $ emission, $L_{\alpha }(0)$, is a strong function of $EM_{\rm obs}$, whereas the wing emission, $L_{\alpha }$(200), shows only a faint dependence. Assuming that the wing emission originates in the hot stellar wind, the corresponding mass-loss rates are of a few $\times 10^{-8}$  $M_{\odot}~{\rm yr}^{-1}$ (Table 1, Fig. 2). However, such the wind can produce only very small nebular emission. According to Eqs. (3) and (5) its emission measure, $EM_{\rm w} = \int_{V}n_{\rm e}n^{+}[1-w(r)]~{\rm d}V$, can be expressed as

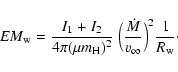\begin{displaymath}EM_{\rm w} = \frac{I_1 + I_2}{4\pi(\mu m_{\rm H})^2}~ \Big(\frac{\dot M}{v_{\infty}}\Big)^{2}\frac{1}{R_{\rm w}}\cdot \end{displaymath} (16)

Model parameters (Sect. 3.2 and Table 1) yield $EM_{\rm w} \approx 10^{58}$  cm-3. Thus during quiescent phases

\begin{displaymath}EM_{\rm w} \ll EM_{\rm obs}, \end{displaymath} (17)

because $EM_{\rm obs} \approx 10^{59}$  cm-3 (Table 2). Qualitatively, larger hot star luminosity gives rise to larger emission measure (Skopal 2005, Table 3) and probably drives a stronger hot star wind. This would explain the $L_{\alpha }$(200)/ $\log~(EM_{\rm obs})$ dependence. As $EM_{\rm w} \ll EM_{\rm obs}$, this dependence is faint and the wing emission cannot rival that from the ionized giant wind. Consequently, the radio emission satisfies that from the giant's wind (i.e. the STB model as mentioned above) without a detectable influence of the emission from the hot star wind.

During active phases the wing emission increases with $\log~(EM_{\rm obs})$ by a factor of $\sim$4.4 faster than during quiescence (Fig. 4). This supports the idea that the source of emission producing the broad H$\alpha $ wings is the ionized hydrogen. Our H$\alpha $-wing models then imply that its kinematics corresponds to a fast wind from the hot star at rates of a few $\times~(10^{-7} {-} 10^{-6})$  $M_{\odot}~{\rm yr}^{-1}$ (Table 1). The wind produces a large emission measure, because it increases with $\dot M^2$ (Eq. (16)). Our models yield $EM_{\rm w} \ga 10^{59}$  cm-3, which can rival the $EM_{\rm obs}$ (Tables 1 and 2). Thus during active phases

\begin{displaymath}EM_{\rm w} \la EM_{\rm obs}. \end{displaymath} (18)

Such a large emission also influences the radio spectrum. For example, during the active phase of Z And the steepness of the radio continuum between 1.4 and 15 GHz was a factor of $\sim$2 larger than during quiescence (Fig. 5), which implies optically thicker conditions. Therefore the cm radio emission from the activity could be attributed to optically thick f-f emission from the hot star wind (cf. Seaquist & Taylor 1992). However, we need more radio observations for active objects and to elaborate corresponding quantitative model taking into account their configuration, for example, that suggested by (Skopal 2005, Fig. 27).

Finally, we note that the presence of a strong hot star wind during active phases is consistent with the finding of Skopal (2005) that the low-temperature nebula (LTN) in active symbiotics has a high emissivity ( $N_{\rm e} \sim $ a few times 109 cm-3) and is located around the hot star, because it is subject to eclipses. Therefore the LTN in active symbiotics may be attributed to the emission of the wind from the hot component.

  \begin{figure} \par\includegraphics[angle=-90,width=8.2cm,clip]{4935f_5.eps} \end{figure} Figure 5: Radio observations of Z And at cm wavelengths during quiescence and the recent activity. Steeper continuum spectrum during activity suggests optically thicker conditions than during quiescence. The data are from Brocksopp et al. (2004).
Open with DEXTER

5 Concluding remarks

In this paper we introduced a model of the optically thin, bipolar stellar wind from the hot components in symbiotic binaries. We derived an expression, which relates the H$\alpha $ luminosity from the wind to the mass-loss rate (Eq. (5)) and calculated the corresponding line profile with the aid of Eq. (10). We applied the model to the observed H$\alpha $ profiles for 10 symbiotic stars during their quiescent and active phases. Synthetic profiles provide a good fit to wings for $\vert\Delta v\vert \ga 200$ km s-1 from the line center. According to Eq. (10) the wing profile can be approximated by the curve $f(\Delta v) \propto \Delta v^{-2}$, which is of the same type as that resulting from the Raman scattering process (Lee 2000). Therefore it is not possible to distinguish between contributions from the ionized hot stellar wind and that from the Raman scattering process by only modeling the line profile. To support the former possibility we investigated relationship between the emission from the H$\alpha $ wings and the emission measure of the symbiotic nebula.

We found that during quiescent phases the dependence $L_{\alpha }$(200)/ $\log~(EM_{\rm obs})$ is faint (cf. Fig. 4). The wing emission is relatively very small (Eq. (17)). If the wings originate in a fast hot star wind, the corresponding mass-loss rates are of a few $\times 10^{-8}$  $M_{\odot}~{\rm yr}^{-1}$ (Table 1). However, it is difficult to indicate their emission independently by other observations. Even in the radio the wing emission has no detectable effect - the radio spectra satisfy radiation of the ionized wind from the giant (the STB model).

During active phases the $L_{\alpha }$(200)/ $\log~(EM_{\rm obs})$ relation is a factor of $\sim$4.4 steeper than that from quiescence. In this case the wing emission can represent a significant fraction of the observed nebular emission (Eq. (18)) and thus can affect the radio spectrum. At cm wavelengths the steep continuum spectrum during the recent activity of Z And (Fig. 5) is consistent with an optically thick f-f emission from the hot star wind.

The $L_{\alpha }$(200)/ $\log~(EM_{\rm obs})$ relationship and other characteristics of the H$\alpha $ profiles (Sect. 4.1) suggest that the ionized hydrogen located around the hot star in the form of a fast stellar wind is the dominant source of the emission in the $\pm(200\div$2000) km s-1 broad H$\alpha $ wings during active phases. The corresponding mass-loss rates are of a few $\times~(10^{-7} {-} 10^{-6})$  $M_{\odot}~{\rm yr}^{-1}$ (Table 1). This finding allows us to attribute the LTN emission in active symbiotics to that from the hot star wind.

Acknowledgements
The author thanks the anonymous referee for inspiring comments. This research was in part supported by a grant of the Slovak Academy of Sciences No. 2/4014/04.

References

 
Copyright ESO 2006