A&A 457, 787-808 (2006)
DOI: 10.1051/0004-6361:20064842
P. Sánchez-Blázquez1,2 - J. Gorgas2 - N. Cardiel2,3 - J. J. González4
1 - Laboratoire d'Astrophysique, École Polytechnique Fédérale de Lausanne (EPFL),
Observatoire, 1290 Sauverny, Switzerland
2 -
Dpto. de Astrofísica, Fac. de Ciencias Físicas, Universidad
Complutense de Madrid, 28040 Madrid, Spain
3 -
Calar Alto Observatory, CAHA, Apartado 511, 04004 Almería, Spain
4 -
Instituto de Astronomía, Universidad Nacional Autónoma de
México, Apdo. Postal 70-264, México D.F., México
Received 11 January 2006 / Accepted 26 April 2006
Abstract
Aims. This paper commences a series devoted to the study of the stellar content of early-type galaxies. The goal of the series is to set constraints on the evolutionary status of these objects.
Methods. In this paper we describe the details of the galaxy sample, the observations, and the data reduction. Line-strength indices and velocity dispersions (![]() )
are measured in 98 early-type galaxies drawn from different environments, and the relation of the indices with the velocity dispersion analysed in detail.
)
are measured in 98 early-type galaxies drawn from different environments, and the relation of the indices with the velocity dispersion analysed in detail.
Results. The present sample indicates that some of the index-![]() relations depend on galaxy environment. In particular, the slope of the relation between Balmer lines and
relations depend on galaxy environment. In particular, the slope of the relation between Balmer lines and ![]() is steeper for galaxies in the Virgo cluster, small groups, and in the field than for galaxies in the Coma cluster. In several indices there is also a significant offset in the zero point between the relations defined by the different subsamples. The slopes of the index-
is steeper for galaxies in the Virgo cluster, small groups, and in the field than for galaxies in the Coma cluster. In several indices there is also a significant offset in the zero point between the relations defined by the different subsamples. The slopes of the index-![]() relation for the Virgo and low-density environment galaxies are explained by a variation of both age and metallicity, with velocity dispersion, as previously noted in other studies. For the galaxies in the Coma cluster, however, the relation of the indices with
relation for the Virgo and low-density environment galaxies are explained by a variation of both age and metallicity, with velocity dispersion, as previously noted in other studies. For the galaxies in the Coma cluster, however, the relation of the indices with ![]() only requires a variation of the abundance along the
only requires a variation of the abundance along the ![]() sequence. In agreement with other studies, we find that the models that better reproduce the slopes are those in which the
sequence. In agreement with other studies, we find that the models that better reproduce the slopes are those in which the ![]() elements vary more than the Fe-peak elements along the
elements vary more than the Fe-peak elements along the ![]() sequence, while, at a given
sequence, while, at a given ![]() ,
older galaxies show an higher
,
older galaxies show an higher ![]() /Fe ratio.
/Fe ratio.
Conclusions. The results can be explained assuming that galaxies in the Coma cluster have experienced a truncated star formation and chemical enrichment history compared to a more continuous time-extended history for their counterparts in lower density environments.
Key words: galaxies: evolution - galaxies: elliptical and lenticular, cD - galaxies: stellar content
A natural outcome of the hierarchical scenarios is that haloes in regions of the Universe that are destined to form a cluster collapse earlier and merge more rapidly (e.g., Kauffmann & Charlot 1998; de Lucia et al. 2006). Therefore, the study of the stellar content of early-type galaxies in different environments should allow us to test the hierarchical clustering scenarios of early-type galaxy formation.
Several works have analysed the differences in the evolution of cluster and field early-type galaxies through the study of the Fundamental Plane (FP), but the results remain controversial. In general, the evolution of the trends in cluster galaxies suggests an earlier formation for these systems when compared with their analogs in the field (Treu et al. 1999, 2001, 2002; van Dokkum & Ellis 2003; Gebhardt et al. 2003; Rusin et al. 2003; Bernardi et al. 2003; Yi et al. 2005), but the environmental dependencies do not appear to be as large (van Dokkum et al. 2001) as predicted by some interpretations of hierarchical models (e.g., Diaferio et al. 2001; de Lucia et al. 2004). However, the evolutionary trends in the FP can be hidden due to the age-metallicity degeneracy (Worthey 1994), if there is a relation between the age and the metallicity of the galaxies (Coles et al. 1999; Ferreras et al. 1999).
Another approach, in principle less affected by this problem, is to compare the absorption spectral features between galaxies in different environments.
Kuntschner & Davies (1998) studied a sample of galaxies in the Fornax cluster finding that they are mostly coeval, which contrasts with other studies in which intermediate-age or young populations have been found in a large fraction of non-cluster luminous elliptical galaxies (e.g., Rose 1985; G93; Forbes et al. 1998; Trager et al. 2000; Caldwell et al. 2003; Denicolo et al. 2005). However, whether such contrasting results are a product of differences in the environment is still an unanswered question. Some authors claim that other parameters such as the luminosity or the morphological type determine the star formation history (SFH) of early-type galaxies rather than environment. In this context, the differences between cluster and field galaxies found in several studies could be due to dissimilarities in the luminosity range of the different samples (see Poggianti et al. 2001b) and/or different proportions of S0 with respect to E galaxies. For example, Kuntschner & Davies (1998) found that, in the Fornax cluster, luminous elliptical galaxies are old and coeval, while (less luminous) S0 galaxies display a significant age spread. In accordance with this result, Smail et al. (2001) found, studying a sample of galaxies drawn from Abell 2218 at z=0.17, that elliptical at all magnitudes and luminous S0's are coeval, while the faintest S0's have younger luminosity-weighted ages (see also Treu et al. 2005).
Bernardi et al. (1998) found a small offset (
![]() mag) in the
Mg2-
mag) in the
Mg2-![]() relation between cluster and field galaxies, but the same
intrinsic scatter about the relation for both subsamples. They also concluded
that the differences are mainly driven by the faint objects. These authors
also studied the zero point of the Mg2-
relation between cluster and field galaxies, but the same
intrinsic scatter about the relation for both subsamples. They also concluded
that the differences are mainly driven by the faint objects. These authors
also studied the zero point of the Mg2-![]() relation among cluster
early-type galaxies and did not find any dependence of this value with
the cluster richness as measured by cluster X-ray luminosity, temperature of
the ICM, or velocity dispersion of member galaxies.
relation among cluster
early-type galaxies and did not find any dependence of this value with
the cluster richness as measured by cluster X-ray luminosity, temperature of
the ICM, or velocity dispersion of member galaxies.
More recently, Denicoló et al. (2005a) compared a sample of galaxies
in groups and in the field with the sample of Fornax
galaxies from Kuntschner (2000), finding that
the slopes of the index-![]() relations for ellipticals in low-density
regions are not significantly different from those
of cluster E/S0, although the scatter of the relations seems larger for group,
field, and isolated ellipticals than for cluster galaxies.
In the second paper of the series (Denicoló et al. 2005b), the authors calculate
ages and metallicities, finding that elliptical galaxies in low
density environments are, on average, 3-4 Gyr younger than their counterparts
in the Fornax cluster. The only caveat in this study is that both samples
only share one galaxy in common, and the differences can be due to systematic
offsets in the individual indices.
relations for ellipticals in low-density
regions are not significantly different from those
of cluster E/S0, although the scatter of the relations seems larger for group,
field, and isolated ellipticals than for cluster galaxies.
In the second paper of the series (Denicoló et al. 2005b), the authors calculate
ages and metallicities, finding that elliptical galaxies in low
density environments are, on average, 3-4 Gyr younger than their counterparts
in the Fornax cluster. The only caveat in this study is that both samples
only share one galaxy in common, and the differences can be due to systematic
offsets in the individual indices.
Thomas et al. (2005) also carried out an study of 124 early-type galaxies in high- and low-density environments.
They also found, in agreement with Denicoló, that massive early-type galaxies
in low density environments seem, on average, 2 Gyr younger and slightly (![]() 0.05-0.1 dex)
more metal rich than their counterparts in high-density environments, consisting
of galaxies drawed from the Coma and Virgo clusters.
Interestingly, these authors found very massive
(M>1011
0.05-0.1 dex)
more metal rich than their counterparts in high-density environments, consisting
of galaxies drawed from the Coma and Virgo clusters.
Interestingly, these authors found very massive
(M>1011 ![]() )
S0 galaxies showing low average ages between 2 and 5 Gyr, and very high metallicities
of [Z/H]
)
S0 galaxies showing low average ages between 2 and 5 Gyr, and very high metallicities
of [Z/H] ![]() 0.67 dex. These galaxies are only present in high density environments,
contrasting the above quoted result by Smail et al. (2001).
0.67 dex. These galaxies are only present in high density environments,
contrasting the above quoted result by Smail et al. (2001).
The lack of conclusive evidence for or against systematic differences between cluster and field galaxies has prompted us to carry out a systematic study analysing the stellar population of galaxies in different environments.
This paper starts a series devoted to the study of the stellar population in local early-type galaxies. The goal of the series is to shed light on the star formation history of these systems and the influence of the environment on their evolution. Although there have been several studies with larger samples that have studied the stellar population of the early-type galaxies in the Coma cluster and in the field, this is the first time that a large number of spectral features are analysed in a homogenous and high signal-to-noise ratio sample containing galaxies in both environments. Furthermore, these features are compared with the new stellar population synthesis models of Vazdekis et al. (2006, in preparation; hereafter V06), which themselves are an updated version of the Vazdekis et al. (2003) models with an improved stellar library, MILES (Sánchez-Blázquez et al. 2006). The new library contains 1003 stars covering the atmospheric parameter space in a homogenous way, reducing the uncertainties of the predictions at metallicities departing from solar. Although a more detailed description of these models and the derivation of age and metallicities procedures will be given in the Paper II of this series, we discuss here some of the results based on them. We refer the reader to Vazdekis et al. (2003) for details regarding the ingredients of the models.
The outline of the paper is as follows: Sect. 2 presents the sample description, observations, and data reduction. Section 3 presents the absorption-line measurements. Section 4 shows the relation of the absorption line indices with the velocity dispersion of the galaxies. Section 5 summarises our conclusions.
Table 1:
Sample of galaxies in the different observing runs. Type:
morphological type extracted from the NASA/IPAC Extragalactic Database; MB: absolute magnitude in the B-band, obtained
from the Lyon-Meudon Extragalactic Database; Env.: when
the galaxy is a member of a well-known cluster, the cluster name is indicated;
the label Pair indicates that the galaxy is a member of a pair of galaxies;
when the galaxies do not belong to a cluster, group, or pair of galaxies, it is
labeled as field galaxy; Run: observation run in which each galaxy was
observed;
![]() : exposure time (seconds); PA: position angle of the
major axis of the galaxy measured from north to east (degrees);
SA: orientation of the slit (degrees); Flag: environment assigned to each
galaxy (L: low-density environment: H: high-density environment);
Code: symbols used in Figure; Ref: reference used to assigned the environment Flag to each
galaxy (Gc93: García 1993; VCC85: Binggeli et al. 1985; GMP:
Godwin et al. 1983; CGCG: Zwicky et al. 1974). 6.
: exposure time (seconds); PA: position angle of the
major axis of the galaxy measured from north to east (degrees);
SA: orientation of the slit (degrees); Flag: environment assigned to each
galaxy (L: low-density environment: H: high-density environment);
Code: symbols used in Figure; Ref: reference used to assigned the environment Flag to each
galaxy (Gc93: García 1993; VCC85: Binggeli et al. 1985; GMP:
Godwin et al. 1983; CGCG: Zwicky et al. 1974). 6.
We analyse a sample of 98 early-type galaxies, which includes ellipticals (E) and S0 galaxies spanning a large range in velocity dispersion (from 40 km s-1 to 400 km s-1).
As one of the main goals of this work is to study the influence of the environment on the star formation history of early-type galaxies, the sample contains galaxies in the field, poor groups, and in the Virgo, Coma, and some Abell galaxy clusters. For the purpose of this series, we have divided the sample in two main groups that we call hereafter high density environment galaxies (HDEGs) and low density environment galaxies (LDEGs).
It is difficult to identify a single, optimal manner by which to separate a sample of galaxies to study the role of environment. In this series of papers, instead of using an indicator of the local density, we have chosen to separate and delineate galaxies by field, group, or cluster environments.
Therefore, in the first group we include galaxies residing in the central
regions
of the Coma cluster and one galaxy from the cluster Abell 2199 (NGC 6166).
We have assigned the galaxies in the
field, groups (including the groups Abell 569 and Abell 779 with very
low values of velocity dispersion and X-ray luminosity (see, e.g., Xian-Ping &
Yan-Jie 1999)), and in the Virgo cluster to the second group. This assignment of Virgo galaxies
to the LDEG group reflects that our classification should be taken in relative
terms, HDEG meaning, in fact the Coma-like rich clusters, while the rest the
of environments
are assigned to the LDEG group. The Virgo cluster contains significant substructure
(e.g., de Vaucouleurs 1961; Binggeli et al. 1985;
Binggeli et al. 1993; Gavazzi et al. 1999), being
an aggregation of sub-clumps that are very likely in the process of merging
(Binggeli 1997). The clump containing M 87 has an estimated mass from the
X-ray haloes of 1014 ![]() ,
but the other main sub-clumps, which include
M 86 and M 49, have masses one order of magnitude less (Bohringer et al. 1994), which is
the typical mass for a group of galaxies. All this suggests that Virgo can be considered
as a group of groups rather than as a normal cluster.
Furthermore,
and admittedly, this is an adhoc argument, as the
analysis of the stellar populations of Virgo early-type galaxies indicate
that they
are not dissimilar to those galaxies in poorer environments (field and small
groups) (e.g., Concannon 2003; Sánchez-Blázquez 2004),
while they are markedly different from our sample of ellipticals in the
Coma cluster (as it
will be shown throughout
this paper). We decided to group the Virgo galaxies together with the rest
of the galaxies in low-density environments to maximize the statistical
significance of the sample. Galaxies were considered to be in a group if they were
included in the
Lyon Group of Galaxies catalogue (García 1993). This catalogue
classifies galaxies in the Virgo cluster as belonging to the
groups LGG 289 and LGG 292. Galaxies were considered to be "Field''
galaxies if they were not listed as a member of a Lyon Galaxy Group
catalogue or as a member of a known cluster.
Coma clusters were selected from both the GMP catalogue
(Godwin et al. 1983) and the catalogue of galaxies
and clusters of galaxies (Zwicky et al. 1961). The last column
in Table 1 lists the catalogue reference giving the group
assigment.
Galaxies in both subsamples were selected to span a
wide range of luminosity and observational properties. Table 1
lists the whole sample together with their morphological type and absolute
magnitude. The distribution in velocity dispersion for LDEGs and HDEGs is
shown in Fig. 1. Although the
,
but the other main sub-clumps, which include
M 86 and M 49, have masses one order of magnitude less (Bohringer et al. 1994), which is
the typical mass for a group of galaxies. All this suggests that Virgo can be considered
as a group of groups rather than as a normal cluster.
Furthermore,
and admittedly, this is an adhoc argument, as the
analysis of the stellar populations of Virgo early-type galaxies indicate
that they
are not dissimilar to those galaxies in poorer environments (field and small
groups) (e.g., Concannon 2003; Sánchez-Blázquez 2004),
while they are markedly different from our sample of ellipticals in the
Coma cluster (as it
will be shown throughout
this paper). We decided to group the Virgo galaxies together with the rest
of the galaxies in low-density environments to maximize the statistical
significance of the sample. Galaxies were considered to be in a group if they were
included in the
Lyon Group of Galaxies catalogue (García 1993). This catalogue
classifies galaxies in the Virgo cluster as belonging to the
groups LGG 289 and LGG 292. Galaxies were considered to be "Field''
galaxies if they were not listed as a member of a Lyon Galaxy Group
catalogue or as a member of a known cluster.
Coma clusters were selected from both the GMP catalogue
(Godwin et al. 1983) and the catalogue of galaxies
and clusters of galaxies (Zwicky et al. 1961). The last column
in Table 1 lists the catalogue reference giving the group
assigment.
Galaxies in both subsamples were selected to span a
wide range of luminosity and observational properties. Table 1
lists the whole sample together with their morphological type and absolute
magnitude. The distribution in velocity dispersion for LDEGs and HDEGs is
shown in Fig. 1. Although the ![]() range covered by both
subsamples is similar, the LDEG sample is slightly skewed towards more massive
objects.
range covered by both
subsamples is similar, the LDEG sample is slightly skewed towards more massive
objects.
Long-slit spectroscopy was carried out in four observing runs using two
different telescopes. In Runs 1 and 3 (January 1998 and August 1999), we used
the Cassegrain Twin Spectrograph with a blue coated TEK CCD in the blue channel
on the 3.5 m telescope at the German-Spanish Astronomical Observatory at Calar
Alto (Almería, Spain). The observations in Runs 2 and 4 (March 1999 and
April 2001) were carried out with the ISIS double spectrograph mounted at the
f/11 Cassegrain focus on the William Herschel Telescope in the Roque de los
Muchachos Observatory (La Palma, Spain). Details of the observational
configurations for each run are given in Table 2.
As can be seen, the spectral resolution of Run 4
is very different from the rest of the runs. As the Lick indices depend on
the instrumental broadening (as well as velocity dispersion broadening),
special care has to be taken to degrade the spectra to the Lick resolution
to avoid systematic differences between observing Runs.
Typical exposure times varied from 1800 s for the brightest galaxies to 7200 s for the
faintest ones in the Coma cluster. Typical signal-to-noise ratios per Å,
measured in the range between 3500 and 6500 Å, are 110 and 50 for the LDEGs
and HDEGs galaxies, respectively. The wavelength coverage varies between
different runs, but all includes the range between 3500 and 5250 Å, which
allows us to the measure the D4000 break (Bruzual 1983) and 15 Lick/IDS indices
(from H![]() to Mgb; Trager et al. 1998, hereafter T98). When possible,
the slit was oriented along the major axis of the galaxies. The high quality of
the data allowed us to extract spatially resolved spectra and measured the
indices out to the effective radius with a high signal-to-noise ratio. In this
paper, we analyse only the central regions of the galaxies. The analysis of the
gradients will be the objective of Paper III in this series.
to Mgb; Trager et al. 1998, hereafter T98). When possible,
the slit was oriented along the major axis of the galaxies. The high quality of
the data allowed us to extract spatially resolved spectra and measured the
indices out to the effective radius with a high signal-to-noise ratio. In this
paper, we analyse only the central regions of the galaxies. The analysis of the
gradients will be the objective of Paper III in this series.
Table 1 lists the sample of galaxies together with additional information including total exposure times and position angles of the spectrograph slit. Additionally, we observed about 45 G-K stars to be used as templates for velocity dispersion measurements, as well as to transform our line-strength indices to the Lick system. Flux standards from Oke (1990) were observed to correct the continuum shape of the spectra. To check for the possibility of systematic effects between different runs, several galaxies were observed in more than one observing period.
The standard data reduction procedures (flat-fielding, cosmic ray removal, wavelength calibration, sky subtraction, and fluxing) were performed with RED uc m E (Cardiel 1999). This reduction package allows a parallel treatment of data and error frames and, therefore, produces an associated error spectrum for each individual data spectrum. We want to stress the importance of obtaining reliable errors on the measurements of individual features to analyse the effects of the correlated errors between the derived stellar population parameters. The use of this package allowed us to control errors more easily than what would have been possible with other available software packages.
Initial reduction of the CCD frames involved bias and dark current subtraction, the removal of pixel-to-pixel sensitivity variations (using flat-field exposures of a tungsten calibration lamp), and correction for two-dimensional low-frequency scale sensitivity variations (using twilight sky exposures).
The dichroics in Runs 2 and 4 produced an intermediate frequency pattern that varies with the position of the telescope. This pattern was removed during flat-fielding in the images of Run 4. Unfortunately, in Run 2 this was not possible as we did not acquire flat field exposures in all the galaxy positions. Fortunately, several galaxies from Run 2 were also observed in other runs. By dividing the spectra of these galaxies from Run 2 by the spectra acquired in other runs (previously resampled to the same instrumental resolution and dispersion), we obtained the shape of the oscillations in Run 2. The shape of this pattern turned out to be identical for all the galaxies with repeated observations, with the exception of small offsets between them. These offsets were quantified with respect to a galaxy of reference for all the galaxies of Run 2 (given the characteristic shape of the oscillation pattern, even for galaxies without repeated observations, it was straightforward to determine this offset using, for this purpose, similar spectra from other observing runs). Then, all the galaxies were divided by this reference pattern shifted to the previously calculated offset (for further details of the procedure, see Sánchez-Blázquez 2004). The uncertainty introduced by this correction was added to the final error budget, although it is not a dominant error source (see Table 4).
Prior to the wavelength calibration, arc frames were used to correct from C-distortion in the images. This rotation correction guaranteed alignment errors to be below 0.1 pixel. Spectra were converted to a linear wavelength scale using typically 120 arc lines fitted by 3th-5th order polynomials, with rms errors of 0.3-0.6 Å. In addition, all the spectra were corrected for S-distortion. This correction is performed with a routine that finds the maximum corresponding to the center of the galaxy as a function of wavelength and fits these positions with a low-order polynomial. Finally, the spectra were displaced with a technique that minimizes the errors due to the discretization of the signal. This technique does not assume that the signal is constant in a given pixel, but adopts a more realistic distribution by fitting a second order polynomial using the available information in the adjacent pixels. The S-distortion can change along the slit, but the correction only affect the measurements in the central parts, where the signal gradient is important. Therefore, we assume that the error of using the S-distortion pattern derived from the central galaxy region in the whole extent of the slit can be safely ignored.
Atmospheric extinction was calculated using the extinction curve of King (1985) for Runs 2 and 4, and the extinction curve of Calar Alto for Runs 1 and 3. To correct the effect of interstellar extinction, we used the curve of Savage & Mathis (1979). The reddenings were extracted from the RC3 catalogue of galaxies (de Vaucouleurs et al. 1991). Relative flux calibration of the spectra was achieved using exposures of standard stars (3, 4, 5, and 33 exposures were taken in Runs 1, 2, 3, and 4, respectively). All the calibration curves of each run were averaged and the flux calibration errors were estimated by the differences between the indices measured with different curves. To transform our indices into the spectrophotometric system of Lick/IDS, we measured line strengths in a sample of G-K giant stars in common with Worthey et al. (1994). The comparison is presented in Appendix A.
Since in the outer parts of some galaxies we measure indices in spectra
with light levels corresponding to only a few per cent of the sky signal (Paper
III), the sky subtraction is a critical step in our data reduction to
obtain reliable gradients. After correcting for both C- and S-distortion,
a sky image was generated for each galaxy observation. This was done by
fitting
a low-order polynomial (order zero or one) to regions selected at both sides of
the galaxy for each channel (pixel in the ![]() direction). A
possible systematic overestimation of the sky level could arise if the galaxy
contribution to the regions from where the sky is extracted was not negligible.
This overestimation of the sky level could increase the measured indices
dramatically in the outer regions. To explore this effect we have fitted de
Vaucouleurs profiles to the surface brightness profiles of our galaxies to
estimate the relative contribution of the galaxy. When necessary, the effect
has been taken into account, subtracting a scaled and
averaged galaxy spectrum from the sky spectra.
An underestimation of the sky level is very unlikely
because this would imply high systematic errors that should be clearly
detected such as unremoved sky lines (see Cardiel et al. 1995).
direction). A
possible systematic overestimation of the sky level could arise if the galaxy
contribution to the regions from where the sky is extracted was not negligible.
This overestimation of the sky level could increase the measured indices
dramatically in the outer regions. To explore this effect we have fitted de
Vaucouleurs profiles to the surface brightness profiles of our galaxies to
estimate the relative contribution of the galaxy. When necessary, the effect
has been taken into account, subtracting a scaled and
averaged galaxy spectrum from the sky spectra.
An underestimation of the sky level is very unlikely
because this would imply high systematic errors that should be clearly
detected such as unremoved sky lines (see Cardiel et al. 1995).
![\begin{figure}
\par\includegraphics[angle=-90,width=8.cm,clip]{4842fig1.ps}
\end{figure}](/articles/aa/full/2006/39/aa4842-06/Timg40.gif) |
Figure 1:
Distribution of central velocity dispersion in HDEGs (grey shaded
histogram) and LDEGs (empty histogram). The mean values of the distributions
are
|
| Open with DEXTER | |
Table 2: Observational configurations employed in the four different observing runs.
From each fully reduced galaxy frame, the spectra within an equivalent aperture
of 4
![]() at a redshift z=0.016 were co-added.
This corresponds to
a physical aperture size of 0.62 kpc assuming H0=70 km s-1 Mpc-1.
This aperture was
chosen as a compromise to obtain a fair number of co-added spectra for galaxies
in the Coma and in the Virgo clusters. This method does not fully extract
the same physical area for all galaxies, as the slit width was kept constant.
To quantify this second-order aperture effect, we also extracted spectra along
the slit, simulating equal-physical-area circular apertures (distance-weighted
co-added spectra), and found no significant differences. Therefore, we chose to
work with the first aperture (without correcting for second-order effects) so as
to maximize the S/N of our spectra.
at a redshift z=0.016 were co-added.
This corresponds to
a physical aperture size of 0.62 kpc assuming H0=70 km s-1 Mpc-1.
This aperture was
chosen as a compromise to obtain a fair number of co-added spectra for galaxies
in the Coma and in the Virgo clusters. This method does not fully extract
the same physical area for all galaxies, as the slit width was kept constant.
To quantify this second-order aperture effect, we also extracted spectra along
the slit, simulating equal-physical-area circular apertures (distance-weighted
co-added spectra), and found no significant differences. Therefore, we chose to
work with the first aperture (without correcting for second-order effects) so as
to maximize the S/N of our spectra.
Radial velocities and velocity dispersions for the galaxies were measured using
the MOVEL and OPTEMA algorithms described by G93. The MOVEL
algorithm is an iterative procedure based in the Fourier Quotient method
(Sargent et al. 1977) in which a galaxy model is processed in parallel to the
galaxy spectrum. The main improvement of the procedure is introduced through
the OPTEMA algorithm, which is able to overcome the typical template mismatch
problem by constructing an optimal template as a linear
combination of stellar spectra of different spectral types and luminosity
classes for each galaxy (see, for details, G93; Pedraz et al. 2002;
Sánchez-Blázquez 2004). To build the optimal template, we made use of 25,
40, 10, and 33 stars in Runs 1, 2, 3, and 4 respectively. To illustrate the
procedure, Fig. 2 shows a typical fit between the observed central
spectrum of a galaxy and the corresponding optimal template corrected with the
derived kinematic parameters. The errors in the radial velocity and velocity
dispersion (![]() )
were computed through numerical simulations. In each
simulation, a bootstrapped galaxy spectrum, obtained using the error spectrum
provided by the reduction with RED uc m E, is fed into the MOVEL and OPTEMA
algorithms (note that a different optimal template is computed in each
simulation). Errors in the parameters were then calculated as the unbiased
standard deviation of the different solutions. These final errors are expected
to be quite realistic, as they incorporate all the uncertainties of the whole
reduction process, from the first steps (e.g., flat-fielding) to the final
measurements of the parameters.
)
were computed through numerical simulations. In each
simulation, a bootstrapped galaxy spectrum, obtained using the error spectrum
provided by the reduction with RED uc m E, is fed into the MOVEL and OPTEMA
algorithms (note that a different optimal template is computed in each
simulation). Errors in the parameters were then calculated as the unbiased
standard deviation of the different solutions. These final errors are expected
to be quite realistic, as they incorporate all the uncertainties of the whole
reduction process, from the first steps (e.g., flat-fielding) to the final
measurements of the parameters.
To check the quality of the measured kinematics, we compared our
derived velocity dispersions with different data compiled from the literature.
We have chosen four different studies: G93, T98, Kuntschner et al. (2001), and
Moore et al. (2002), with 33, 52, 31,
and 12 galaxies in common with our sample, respectively.
Figure 3 shows the result of this comparison and, in
Table 3, we summarise the mean differences. As can be
seen, our velocity dispersions are, on average, ![]() 15 km s-1 larger
than those in other studies. In particular, the differences seem to be
larger as
15 km s-1 larger
than those in other studies. In particular, the differences seem to be
larger as ![]() increases. Using a linear fit to the data (represented
in
Fig. 3, we calculated that the maximum difference,
for a galaxy
with
increases. Using a linear fit to the data (represented
in
Fig. 3, we calculated that the maximum difference,
for a galaxy
with
![]() ,
is 17 km s-1. This difference in
,
is 17 km s-1. This difference in ![]() translates into errors in the indices of less than 0.1%.
This systematic effect can be the consequence of
template mismatches either in our study or in the others. Nevertheless, our
method makes use of several stars to calculate the optimal template, then
minimises the effect of a poor fit. Furthermore, the effect of mismatching
tend to underestimate the values of the velocity dispersion (Laird & Levison
1985; Bender 1990), instead of making them larger. It is not the purpose of
this section to investigate the real causes of the differences as this
systematic offset does not affect any of our conclusions.
translates into errors in the indices of less than 0.1%.
This systematic effect can be the consequence of
template mismatches either in our study or in the others. Nevertheless, our
method makes use of several stars to calculate the optimal template, then
minimises the effect of a poor fit. Furthermore, the effect of mismatching
tend to underestimate the values of the velocity dispersion (Laird & Levison
1985; Bender 1990), instead of making them larger. It is not the purpose of
this section to investigate the real causes of the differences as this
systematic offset does not affect any of our conclusions.
Table 3: Comparison of the velocity dispersions derived in this study and in previous works. The table columns are: Offset: mean offset between this study and the one in Col. 1; rms: dispersion among the mean value; Exp. rms: dispersion expected from the errors; z: result of a z-test to contrast the hypothesis of a null offset (a value higher than 1.96 allows us to reject the hypothesis with a significance level lower than 0.05); N: number of galaxies in each comparison. Units are km s-1.
![\begin{figure}
\par\includegraphics[angle=-90,width=9cm,clip]{4842fig2.ps}
\end{figure}](/articles/aa/full/2006/39/aa4842-06/Timg43.gif) |
Figure 2: Example of determination of kinematical parameters in the case of the galaxy NGC 3379. The upper panel shows the residuals of the optimal template fit, with the vertical dotted lines indicating the position of typical emission lines. In the lower panel, the thick and thin lines correspond to the galaxy and optimal template spectra, respectively. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.7cm,clip]{4842fig3.ps}
\end{figure}](/articles/aa/full/2006/39/aa4842-06/Timg44.gif) |
Figure 3: Comparison of the derived velocity dispersions calculated in this work with the data compiled from the literature. Different symbols represent different datasets, as indicated in the inset. The 1:1 relation and the linear fit to the data are drawn with dashed and solid lines, respectively. |
| Open with DEXTER | |
Line-strength indices in the Lick/IDS system (e.g., T98) and the D4000 defined by Bruzual (1983) were measured in these spectra. The errors were estimated from the uncertainties caused by photon noise, wavelength calibration, and flux calibration. We also added a residual error based on the comparison of galaxies observed in several runs and, in Run 2, the error due to the dichroic correction. Table 4 shows the typical values of the different sources of errors.
Table D.3 presents the fully corrected line-strength indices for our sample of galaxies.
Table 4: Typical values of the different considered error sources. Phot.: photonic noise; Flux: flux calibration; Wave.: wavelength calibration; Dichr.: typical error in the subtraction of the dichroic pattern (this error is only added in the measurements of Run 2). Res.: residual errors, based on repeated observations of 10 galaxies.
Table 5: Resolution at which Lick indices are measured.
The line-strength indices were transformed to the Lick system, taking into account three effects: (a) the differences in the spectral resolution between the Lick/IDS system and our setups, (b) the internal velocity broadening of the observed galaxies, and (c) small systematic offsets due to the continuum shape differences.
Finally, we calculated a residual error for each index based on repeated observations of galaxies in different runs. We have a total of 11 repeated observations of 10 different galaxies. The residual error was computed by comparing the rms dispersion with the estimated errors from known sources. The final residual errors are shown in the last column of Table 4.
Elliptical galaxies contain much less dust and ionised gas than spiral
galaxies and were regarded as dust- and gas-free objects for a long time.
However, surveys of large samples of early-type galaxies (Caldwel 1984;
Phillips et al. 1986; Goudfrooij et al. 1994) have revealed that 50-60 per
cent of these galaxies show weak optical emission lines. Some line-strength
indices are affected by these emission lines, in particular H![]() ,
Fe5015,
and Mgb. The effect of the emission on H
,
Fe5015,
and Mgb. The effect of the emission on H![]() is particularly important
because our estimation of ages (Paper II) relies on its strength. The
emission, when present, tends to fill the line, lowering the value of the index
and, hence, increasing the derived age.
To correct the H
is particularly important
because our estimation of ages (Paper II) relies on its strength. The
emission, when present, tends to fill the line, lowering the value of the index
and, hence, increasing the derived age.
To correct the H![]() index from this effect, we used the calibration of G93,
who showed that H
index from this effect, we used the calibration of G93,
who showed that H![]() is correlated with [O III] such that
EW(H
is correlated with [O III] such that
EW(H
![]() )/EW([O III]
)/EW([O III]![]() 5007)
5007) ![]() 0.7. Trager
et al. (2000a; hereafter T00a) carefully studied the accuracy of this
correction, finding a better value of 0.6 instead of 0.7. Whilst there is
evidence that this correction factor is uncertain for individual galaxies
(Mehlert et al. 2000), it is good enough in a statistical sense.
In any case, we have repeated the analysis eliminating all
the galaxies with [O III]
0.7. Trager
et al. (2000a; hereafter T00a) carefully studied the accuracy of this
correction, finding a better value of 0.6 instead of 0.7. Whilst there is
evidence that this correction factor is uncertain for individual galaxies
(Mehlert et al. 2000), it is good enough in a statistical sense.
In any case, we have repeated the analysis eliminating all
the galaxies with [O III]![]() 5007 > 0.4 Å and none
of the results presented in this work suffer variation.
To determine
the [O III] emission, we subtracted an emission-free template spectrum
from the galaxy spectrum and measured the residual equivalent width.
The zero-emission template was the one calculated during the determination of
the kinematics parameters, as described in Sect. 3.
An example of the process is shown in Fig. 4. The emission lines
[O III]
5007 > 0.4 Å and none
of the results presented in this work suffer variation.
To determine
the [O III] emission, we subtracted an emission-free template spectrum
from the galaxy spectrum and measured the residual equivalent width.
The zero-emission template was the one calculated during the determination of
the kinematics parameters, as described in Sect. 3.
An example of the process is shown in Fig. 4. The emission lines
[O III]
![]() and [N II]
and [N II]
![]() ,
which affect the
measurements of Fe5015 and Mgb, were replaced with the optimal template in
these regions.
A total of 37 galaxies (38% of our sample) were found to have evidence of
[O III]
,
which affect the
measurements of Fe5015 and Mgb, were replaced with the optimal template in
these regions.
A total of 37 galaxies (38% of our sample) were found to have evidence of
[O III]![]() 5007 emission (EW([O III]) > 0.2 Å). The
[O III] equivalent widths measured in the central spectra are presented
in the last column of Table D.3.
5007 emission (EW([O III]) > 0.2 Å). The
[O III] equivalent widths measured in the central spectra are presented
in the last column of Table D.3.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm,clip]{4842fig4.ps}
\end{figure}](/articles/aa/full/2006/39/aa4842-06/Timg53.gif) |
Figure 4:
Illustrative example of the procedure followed to measure
emission lines. The upper part of the figure shows the galaxy (NGC 4278; thin
line) and the template spectrum corrected for the kinematics parameters (thick
line). The difference between both spectra
(
|
| Open with DEXTER | |
To verify that our measurements have been properly transformed into the Lick system and that the errors have been properly estimated, we have compared our line strengths with data from 6 different works with galaxies in common: (i) G93, (ii) T98, (iii) Mehlert et al. (2000, hereafter M00), (iv) Kuntschner et al. (2001, hereafter K01), (v) Moore et al. (2002, hereafter M02), and (vi) Denicoló et al. (2005a, hereafter D05). Figure 5 shows this comparison and Table 6 summarises the mean offsets between different studies and the root mean square dispersions.
In general, our measurements agree with other studies fairly well, although we find significant offsets in the values of some indices. In particular, Mgb and C4668 seem to be depressed in our sample compared with the other studies. We will address throughout the paper the possible variation in our conclusions should an offset of -0.2 and -0.848 in Mgb and C4668 (corresponding to the mean difference in the comparison with other authors) be assumed.
We can obtain a good estimation of the quality of our errors comparing the dispersion along the 1:1 relation with the one expected from the errors. The last column of Table 6 shows the probability that the real scatter is larger than the one expected from the errors by chance. As can be seen, in most of the cases the observed scatter agrees with the one predicted from the errors, which indicates that the errors have been correctly estimated. However, this does not happen in the comparison with D05. As this is the only study in which the real scatter is significatively larger than the one expected by the errors, we think that these authors have underestimated the errors in their measurements.
![\begin{figure}
\par\mbox{\resizebox{4cm}{!}{\includegraphics[angle=-90]{4842fig5...
...}
\resizebox{4cm}{!}{\includegraphics[angle=-90]{4842fig5p.ps}} }\end{figure}](/articles/aa/full/2006/39/aa4842-06/Timg54.gif) |
Figure 5: Comparison between the Lick indices measured in this study with those in other works for the galaxies in common. Different symbols represent distinct references, as indicated in the insets. |
| Open with DEXTER | |
Furthermore, we have used the galaxies in common with other studies to double check the possibility of systematic differences between different observing runs confirming the absence of these differences. This comparison can be found in Appendix D, available in electronic form at http://www.edpsciences.org.
The relations between the central velocity dispersion and the strength of the
integrated stellar Mg and MgH features around 5100 Å have been studied in
numerous works (e.g., Terlevich et al. 1981; Gorgas et al. 1990; Guzmán et al. 1992; Bender et al. 1993; Jørgensen et al. 1996; Bender
et al. 1998; Bernardi et al. 1998; Colless et al. 1999;
Jørgensen 1999;
Concannon et al. 2000; Kuntschner 2000; Poggianti et al. 2001a;
Proctor & Sansom 2002; Worthey & Collobert 2003; Mehlert et al. 2003; Thomas
et al. 2004). Although, classically, the Mg2-![]() relation has been
interpreted as the interplay between mass and metallicity (Forbes et al. 1998;
Kobayashi & Arimoto 1999; Terlevich et al. 1999), nowadays there is still
much debate as to whether this relation reflects trends in stellar ages,
in metallicities, or in the relative abundance of different heavy elements
(e.g.,
T98; Jørgensen 1999; Trager et al. 2000b; K01;
Poggianti et al. 2001a; Mehlert et al. 2003; Caldwell et al. 2003; Thomas et al. 2005). The
problem is due to the well-known age-metallicity degeneracy, which makes very
difficult to separate both effects with the current stellar population models.
However, the use of a larger number of indices can help us to disentangle this
degeneracy, thanks to the different sensitivity of each index to variations of
these parameters.
relation has been
interpreted as the interplay between mass and metallicity (Forbes et al. 1998;
Kobayashi & Arimoto 1999; Terlevich et al. 1999), nowadays there is still
much debate as to whether this relation reflects trends in stellar ages,
in metallicities, or in the relative abundance of different heavy elements
(e.g.,
T98; Jørgensen 1999; Trager et al. 2000b; K01;
Poggianti et al. 2001a; Mehlert et al. 2003; Caldwell et al. 2003; Thomas et al. 2005). The
problem is due to the well-known age-metallicity degeneracy, which makes very
difficult to separate both effects with the current stellar population models.
However, the use of a larger number of indices can help us to disentangle this
degeneracy, thanks to the different sensitivity of each index to variations of
these parameters.
So far, most studies have concentrated on the relation of the Mg indices with
the velocity dispersion. In this section, we show the relation of 18 Lick
indices with ![]() .
Some of the relations have already been presented by
Sánchez-Blázquez et al. (2003), but they are shown here again for
completeness. Most of them, however, are new. We aim to answer two questions:
.
Some of the relations have already been presented by
Sánchez-Blázquez et al. (2003), but they are shown here again for
completeness. Most of them, however, are new. We aim to answer two questions:
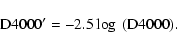 |
(2) |
Table 6:
Comparison of line strengths measured in this and other studies. Ref.:
reference of the comparison work (see description in the text); N: number of
galaxies in common; ![]() :
calculated offset between both studies (this work minus
other study);
:
calculated offset between both studies (this work minus
other study); ![]() :
rms dispersion;
:
rms dispersion;
![]() :
expected rms from the errors; t: t-parameter of the comparison of
means;
:
expected rms from the errors; t: t-parameter of the comparison of
means; ![]() :
probability that
:
probability that
![]() by chance.
by chance.
To study which parameters drive the relation of the indices with ![]() ,
we
have parameterised the models of V06 as a function of age and metallicity. The
relations are shown in Table 8b. In estimating these
expressions, we have restricted the age to the interval 4.7-17.78 Gyr, and the
metallicity range to -0.68<[M/H]<+0.2, which is the range covered
by the galaxies in our sample. To show that, we
have plotted, in Fig. 7, an index-index diagram
comparing the [MgFe]' (Thomas et al. 2003, TMB03
hereafter) and the H
,
we
have parameterised the models of V06 as a function of age and metallicity. The
relations are shown in Table 8b. In estimating these
expressions, we have restricted the age to the interval 4.7-17.78 Gyr, and the
metallicity range to -0.68<[M/H]<+0.2, which is the range covered
by the galaxies in our sample. To show that, we
have plotted, in Fig. 7, an index-index diagram
comparing the [MgFe]' (Thomas et al. 2003, TMB03
hereafter) and the H![]() indices, including
the LDEGs (open symbols) and HDEG (filled symbols). We have also over-plotted
the grid of models by V06. The caption of the figure indicates
the corresponding values of age and metallicity for each model.
The two last columns of Table 8b give,
for the LDEGs and HDEGs, respectively, the required
dependence of metallicity on (
indices, including
the LDEGs (open symbols) and HDEG (filled symbols). We have also over-plotted
the grid of models by V06. The caption of the figure indicates
the corresponding values of age and metallicity for each model.
The two last columns of Table 8b give,
for the LDEGs and HDEGs, respectively, the required
dependence of metallicity on (
![]() )
if the observed slope of the
particular index in the index-
)
if the observed slope of the
particular index in the index-
![]() diagram were to be driven
entirely by a metallicity dependence on
diagram were to be driven
entirely by a metallicity dependence on
![]() .
This is also illustrated in
Fig. 8 for both subsamples, LDEGs and HDEGs.
As can be seen
in Table 8b, the metallicity
dependence required to explain the slope of
the CN2, C4668, and Mgb indices with
.
This is also illustrated in
Fig. 8 for both subsamples, LDEGs and HDEGs.
As can be seen
in Table 8b, the metallicity
dependence required to explain the slope of
the CN2, C4668, and Mgb indices with ![]() is much larger than
that required to explain
the slope of the other indices.
Therefore, the metallicity cannot be the only parameter varying with the
velocity dispersion.
It does not seem probable, either, that a unique combination of age and
metallicity is responsible for the differences in the slope between indices,
since CN2, C4668, and Mgb are not especially sensitive to age variations
(e.g., Worthey 1994). A dependence of age on velocity dispersion in the
galaxies would produce steeper slopes in other indices, such as G4300
or Fe4531.
is much larger than
that required to explain
the slope of the other indices.
Therefore, the metallicity cannot be the only parameter varying with the
velocity dispersion.
It does not seem probable, either, that a unique combination of age and
metallicity is responsible for the differences in the slope between indices,
since CN2, C4668, and Mgb are not especially sensitive to age variations
(e.g., Worthey 1994). A dependence of age on velocity dispersion in the
galaxies would produce steeper slopes in other indices, such as G4300
or Fe4531.
The most plausible explanation is the existence of systematic changes
in the chemical
abundance ratios along the ![]() sequence. That is, not all the elements are
changing in lockstep with the velocity dispersion. As different indices have different
sensitivities to changes in the chemical composition, a variation of the latter
with
sequence. That is, not all the elements are
changing in lockstep with the velocity dispersion. As different indices have different
sensitivities to changes in the chemical composition, a variation of the latter
with ![]() would
produce differences in the slope of the relation. Although we do not have the tools to
derive detailed chemical abundances in early-type galaxies, we know that
the index CN2 is especially sensitive to variations of C and N, C4668 to variations
in the C abundance, while the Mgb index increases with the Mg abundance, and
it has an
inverse dependence with the C abundance
(Tripicco & Bell 1995, TB95 hereafter; Korn et al. 2005).
Therefore, the explanation of the differences in the slopes of these indices
with respect to the others would require, in principle, an increase of the
[Mg/Fe] (already noted by a number of authors, e.g., Worthey et al. 1992;
Greggio 1997; Jørgensen 1999;
Kuntschner 2000; Trager et al. 2000b; Thomas et al. 2002; M03; Thomas et al. 2005),
[C/Fe] and [N/Fe] (see Worthey 1998) ratios with
would
produce differences in the slope of the relation. Although we do not have the tools to
derive detailed chemical abundances in early-type galaxies, we know that
the index CN2 is especially sensitive to variations of C and N, C4668 to variations
in the C abundance, while the Mgb index increases with the Mg abundance, and
it has an
inverse dependence with the C abundance
(Tripicco & Bell 1995, TB95 hereafter; Korn et al. 2005).
Therefore, the explanation of the differences in the slopes of these indices
with respect to the others would require, in principle, an increase of the
[Mg/Fe] (already noted by a number of authors, e.g., Worthey et al. 1992;
Greggio 1997; Jørgensen 1999;
Kuntschner 2000; Trager et al. 2000b; Thomas et al. 2002; M03; Thomas et al. 2005),
[C/Fe] and [N/Fe] (see Worthey 1998) ratios with ![]() .
.
![\begin{figure}
\par\mbox{\resizebox{5.5cm}{!}{\includegraphics[angle=-90]{4842fi...
...\resizebox{5.5cm}{!}{\includegraphics[angle=-90]{4842fig6c.ps}} }
\end{figure}](/articles/aa/full/2006/39/aa4842-06/Timg60.gif) |
Figure 6:
Line-strength indices plotted against
|
| Open with DEXTER | |
Table 7:
a) Parameters of the linear fits
![]() .
First column:
y-intersect of the fit and its error; second column: slope, and corresponding
error, of the linear fit;
.
First column:
y-intersect of the fit and its error; second column: slope, and corresponding
error, of the linear fit; ![]() :
probability, given by a non-parametric
Spearman test, that the slope of the fit is significatively different from zero
by chance; N: number of galaxies used to make the fit; t: t parameter to
test the hypothesis b=0 (a t value higher than 1.9 indicates that
the slope
is significant different from zero with a significance level lower than
0.05);
:
probability, given by a non-parametric
Spearman test, that the slope of the fit is significatively different from zero
by chance; N: number of galaxies used to make the fit; t: t parameter to
test the hypothesis b=0 (a t value higher than 1.9 indicates that
the slope
is significant different from zero with a significance level lower than
0.05);
![]() :
standard deviation about the fit;
:
standard deviation about the fit;
![]() :
standard deviation expected from the errors;
:
standard deviation expected from the errors;
![]() :
standard
deviation not explained from the errors.
:
standard
deviation not explained from the errors.
Table 7:
b) Line-strength indices used in this work as a function of the logarithm
of age and metallicity using the models by V06. The last two columns express
the required variation in metallicity with velocity dispersion to explain the
slopes of the index-![]() relations, assuming that the slope is due to an
exclusive variation of this parameter with the velocity
dispersion.
relations, assuming that the slope is due to an
exclusive variation of this parameter with the velocity
dispersion.
However, there are other indices that also depend strongly on these elements
and, thus, before reaching the above conclusion, we should study whether the
variations in the relative abundance of these elements with ![]() are
compatible with the slopes obtained for the rest of the indices.
are
compatible with the slopes obtained for the rest of the indices.
Using a similar procedure to T00a, we have used the response functions of TB95 to calculate the variation of the Lick indices to changes in the abundances of different elements.
Instead of changing all the elements separately, we assume that some elements
are linked nucleosynthetically, so we vary them in lockstep. Following T00a, we
separate the elements into two different groups: (G1) Na, Si, Ca, O, and
Ti![]() ; (G2) Fe and Cr. In addition, we allow
the abundance of C, N, and Mg to vary independently. TB95 response functions are
for enhancement values corresponding to [X/H]=+0.3 dex. The fractional
response of an index I to other arbitrary values is (see T00a)
; (G2) Fe and Cr. In addition, we allow
the abundance of C, N, and Mg to vary independently. TB95 response functions are
for enhancement values corresponding to [X/H]=+0.3 dex. The fractional
response of an index I to other arbitrary values is (see T00a)
To compute the final index variations we have assumed the following composition: 53% of cool giants, 44% of turn off stars, and 3% of cool dwarfs stars, as in T00a.
We calculated the changes in the indices that are induced by changing the abundance ratio patterns according to the following four different prescriptions:
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm,clip]{4842fig7.ps}
\end{figure}](/articles/aa/full/2006/39/aa4842-06/Timg177.gif) |
Figure 7:
[MgFe]' versus H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.5cm,clip]{4842fig8.ps}
\end{figure}](/articles/aa/full/2006/39/aa4842-06/Timg178.gif) |
Figure 8:
Variation in metallicity required to explain the slope in the
index- |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{
\hspace*{4mm}\resizebox{3cm}{!}{\includegraphics[bb=94...
...{!}{\includegraphics[bb=94 149 529 641,angle=-90]{4842fig9d.ps}} }\end{figure}](/articles/aa/full/2006/39/aa4842-06/Timg179.gif) |
Figure 9:
Comparison of the observed slopes in the index- |
| Open with DEXTER | |
The first three models are simple variations of the different proposed
groups and are shown here to show the influence that the variation
of different groups of elements
have over the slopes of the indices with ![]() .
In the fourth
model, on the other hand, we have fixed the values for G1 and G2 as in model (iii),
which is the one with lower rms of the first three models, and we have
fitted the values of C, N, and Mg to reproduce the observed slopes in
CN2, C4668, and Mgb.
.
In the fourth
model, on the other hand, we have fixed the values for G1 and G2 as in model (iii),
which is the one with lower rms of the first three models, and we have
fitted the values of C, N, and Mg to reproduce the observed slopes in
CN2, C4668, and Mgb.
Figure 9 shows the comparison of the slopes with the variation
of the indices in the different proposed models. The rms of the dispersion
and the mean differences in the indices modeled by TB95 are summarised in Table 9. As it is apparent, the model that best reproduces the
observed slopes is model (iv), in which the Mg and the N change more than the
other ![]() -elements, while the C changes more than the Fe-peak elements, but
less than the
-elements, while the C changes more than the Fe-peak elements, but
less than the ![]() -elements. However, this variation of C gives slopes in
the G4300 index (also very C sensitive) steeper than observed. The observations
of this index do not fit well with the stellar atmosphere model of the coolest
giant star of TB95.
Therefore, the differences may also be due to a problem in the modeling. On the
other hand, there is a possibility that the C4668 index is not as sensitive to
variations in the C abundance as predicted by TB95 (Worthey 2004). Therefore,
we cannot make firm conclusions about the variation of the [C/Fe] abundance
with the velocity dispersion of the galaxies.
The reported values for the different models are only illustrative. We do not
pretend to quantify the real variations in the chemical abundance ratios with
the velocity dispersion, but only to obtain relative variation of some elements
with respect to the others.
To explain the differences in the slope of the relations of Mgb and
-elements. However, this variation of C gives slopes in
the G4300 index (also very C sensitive) steeper than observed. The observations
of this index do not fit well with the stellar atmosphere model of the coolest
giant star of TB95.
Therefore, the differences may also be due to a problem in the modeling. On the
other hand, there is a possibility that the C4668 index is not as sensitive to
variations in the C abundance as predicted by TB95 (Worthey 2004). Therefore,
we cannot make firm conclusions about the variation of the [C/Fe] abundance
with the velocity dispersion of the galaxies.
The reported values for the different models are only illustrative. We do not
pretend to quantify the real variations in the chemical abundance ratios with
the velocity dispersion, but only to obtain relative variation of some elements
with respect to the others.
To explain the differences in the slope of the relations of Mgb and
![]() Fe
Fe![]() with
with ![]() ,
some authors have already proposed the
existence of an increase in the Mg/Fe ratio with the velocity dispersion
(K01; Proctor & Sansom 2002; Mehlert et al. 2003; but,
for an opposing alternative, see Proctor et al. 2004). In this work, we propose
that, apart from the variation in this ratio, there is also a variation in the
[N/Fe] ratio with the velocity dispersion. On the other hand, although all the
,
some authors have already proposed the
existence of an increase in the Mg/Fe ratio with the velocity dispersion
(K01; Proctor & Sansom 2002; Mehlert et al. 2003; but,
for an opposing alternative, see Proctor et al. 2004). In this work, we propose
that, apart from the variation in this ratio, there is also a variation in the
[N/Fe] ratio with the velocity dispersion. On the other hand, although all the ![]() elements change along the
elements change along the ![]() sequence more than the Fe-peak elements,
the variation of the ratio [Mg/Fe] is larger than [X/Fe] for the rest of
sequence more than the Fe-peak elements,
the variation of the ratio [Mg/Fe] is larger than [X/Fe] for the rest of
![]() elements.
elements.
Although this experiment has been done using the calculated slopes for the
LDEG sample, the conclusions are the same for the HDEGs, as the slopes of the
metal-sensitive indices in both subsamples are very similar
(see Fig. 8).
This is not true, however, for the slopes of the age-sensitive indices.
In particular, the relation of H![]() with
with ![]() is much steeper for the first
subsample of galaxies (see Table 7a, and note the striking
difference for H
is much steeper for the first
subsample of galaxies (see Table 7a, and note the striking
difference for H![]() in Fig. 8). For LDEGs, these
indices are strongly correlated with
in Fig. 8). For LDEGs, these
indices are strongly correlated with ![]() ,
while for HDEGs the statistical
significance of the correlation is lower. There are
different points of views about the relation of the H
,
while for HDEGs the statistical
significance of the correlation is lower. There are
different points of views about the relation of the H![]() index with
velocity dispersion in the literature. While some authors report a strong correlation between
these two parameters (e.g., Jørgensen 1997; T98; Caldwell et al. 2003), others find
a weak or null correlation (e.g., Mehlert et al. 2003). These discrepancies
could be due to differences in the relation as a function of the environment.
In fact, the sample of T98 is composed mainly of field and
low density environment galaxies, while the sample of Mehlert et al. (2003)
consists of galaxies in the Coma cluster. Jørgensen's (1997) sample is more
heterogeneous, containing galaxies belonging to 11 different clusters of
variable density and field galaxies, while the Caldwell et al. (2003)
sample
consists of galaxies in the field and in the Virgo cluster, therefore, very
similar to our LDEG sample. In general, it seems that all the studies
analysing galaxies in low density environments find a correlation between
H
index with
velocity dispersion in the literature. While some authors report a strong correlation between
these two parameters (e.g., Jørgensen 1997; T98; Caldwell et al. 2003), others find
a weak or null correlation (e.g., Mehlert et al. 2003). These discrepancies
could be due to differences in the relation as a function of the environment.
In fact, the sample of T98 is composed mainly of field and
low density environment galaxies, while the sample of Mehlert et al. (2003)
consists of galaxies in the Coma cluster. Jørgensen's (1997) sample is more
heterogeneous, containing galaxies belonging to 11 different clusters of
variable density and field galaxies, while the Caldwell et al. (2003)
sample
consists of galaxies in the field and in the Virgo cluster, therefore, very
similar to our LDEG sample. In general, it seems that all the studies
analysing galaxies in low density environments find a correlation between
H![]() and
and ![]() ,
while those exclusively analysing galaxies in the Coma
cluster do not. However, Kuntschner (1998) finds a significant correlation
between H
,
while those exclusively analysing galaxies in the Coma
cluster do not. However, Kuntschner (1998) finds a significant correlation
between H![]() and
and ![]() in his sample of nearly coeval Fornax galaxies,
although he claims that the slope in this relation is driven mainly by
variations in metallicity, as the galaxies in the Fornax cluster span a very
broad metallicity range. To study the possibility of an age variation along
the
in his sample of nearly coeval Fornax galaxies,
although he claims that the slope in this relation is driven mainly by
variations in metallicity, as the galaxies in the Fornax cluster span a very
broad metallicity range. To study the possibility of an age variation along
the ![]() sequence, we have derived the change in age that would explain the
slope of the H
sequence, we have derived the change in age that would explain the
slope of the H![]() -
-![]() relation, assuming that the age is the only
parameter varying with
relation, assuming that the age is the only
parameter varying with ![]() .
For the LDEGs, this value is
.
For the LDEGs, this value is
![]() ,
while for HDEGs is only
,
while for HDEGs is only
![]() .
In fact, the metallicity
variation that explains the slope in the Fe4383-
.
In fact, the metallicity
variation that explains the slope in the Fe4383-![]() relation (
relation (
![]() )
can account for the slope of the
H
)
can account for the slope of the
H![]() -
-![]() relation obtained for HDEGs, without any further variation in
age. For the LDEGs an additional age variation of
relation obtained for HDEGs, without any further variation in
age. For the LDEGs an additional age variation of
![]() is, however, required.
is, however, required.
Summarising, we conclude that an increase of the overall
metallicity with the velocity dispersion for both HDEGs and LDEGs exists.
However, not
all the elements change in lockstep along the ![]() sequence. The models
that best reproduce the slopes in all the indices are those in which the
sequence. The models
that best reproduce the slopes in all the indices are those in which the ![]() elements change more than the Fe-peak elements and, furthermore, the
[Mg/Fe] and [N/Fe] ratios change more than the rest of the
elements change more than the Fe-peak elements and, furthermore, the
[Mg/Fe] and [N/Fe] ratios change more than the rest of the ![]() elements with the velocity dispersion of the galaxies. In the case of LDEGs,
the slopes of the index-
elements with the velocity dispersion of the galaxies. In the case of LDEGs,
the slopes of the index-![]() relations also reflect a trend in the mean age
of the galaxies in the sense that less massive galaxies are also younger. We
will analyse this relation in more detail in Paper II, where we derive ages
and metallicities for our sample of galaxies. None of these conclusions
would change if we increased the Mgb and C4668 indices by a constant value, as
all the results are based in the slope of the index-
relations also reflect a trend in the mean age
of the galaxies in the sense that less massive galaxies are also younger. We
will analyse this relation in more detail in Paper II, where we derive ages
and metallicities for our sample of galaxies. None of these conclusions
would change if we increased the Mgb and C4668 indices by a constant value, as
all the results are based in the slope of the index-![]() relations.
relations.
The low dispersion in the Mg2-![]() relation and the fact that it is
distance independent make it a powerful tool to constrain the models of
formation and evolution of galaxies. In fact, the low dispersion has been
used as an argument to give evidence that all ellipticals have nearly coeval stellar
populations (Bender et al. 1993; Bernardi et al. 1998) in clear
contradiction with other studies (G93; T98; Trager et al. 2001; Caldwell et al. 2003). Some authors
have studied this problem, concluding that the low scatter is due to a
conspiracy between the age and the metallicity, in the sense that younger
galaxies are also more metal rich, canceling the deviations with respect to the
mean relation (e.g., Worthey et al. 1995; Trager 1997; Pedraz et al. 1998; Jørgensen 1999; K01).
relation and the fact that it is
distance independent make it a powerful tool to constrain the models of
formation and evolution of galaxies. In fact, the low dispersion has been
used as an argument to give evidence that all ellipticals have nearly coeval stellar
populations (Bender et al. 1993; Bernardi et al. 1998) in clear
contradiction with other studies (G93; T98; Trager et al. 2001; Caldwell et al. 2003). Some authors
have studied this problem, concluding that the low scatter is due to a
conspiracy between the age and the metallicity, in the sense that younger
galaxies are also more metal rich, canceling the deviations with respect to the
mean relation (e.g., Worthey et al. 1995; Trager 1997; Pedraz et al. 1998; Jørgensen 1999; K01).
However, though small, an intrinsic dispersion does exists in the
Mg2-![]() relation. To understand the cause of this scatter, many
authors have tried to find correlations between the deviation from the relation
and other parameters. Bender et al. (1993) did not find any
correlation between the residuals of this relation and other structural
parameters of the galaxies such as effective radius, surface brightness, or
mass. Neither did they find any correlation between the residuals and the
position of the objects in the Fundamental Plane. On the other hand, Schweizer
et al. (1990) found a correlation between the deviation of the
Mg2-
relation. To understand the cause of this scatter, many
authors have tried to find correlations between the deviation from the relation
and other parameters. Bender et al. (1993) did not find any
correlation between the residuals of this relation and other structural
parameters of the galaxies such as effective radius, surface brightness, or
mass. Neither did they find any correlation between the residuals and the
position of the objects in the Fundamental Plane. On the other hand, Schweizer
et al. (1990) found a correlation between the deviation of the
Mg2-![]() relation and the fine structure parameter
relation and the fine structure parameter ![]() ,
which is an
indicator of recent interactions. González & Gorgas (1996, hereafter GG96)
found an anti-correlation between the residuals and the H
,
which is an
indicator of recent interactions. González & Gorgas (1996, hereafter GG96)
found an anti-correlation between the residuals and the H![]() index, and
concluded that recent episodes of star formation could explain, at least
partially, the present scatter in the relation (see also Worthey & Collobert
2003).
index, and
concluded that recent episodes of star formation could explain, at least
partially, the present scatter in the relation (see also Worthey & Collobert
2003).
In this section we investigate the scatter in the relations of the Lick indices
with the central velocity dispersion, trying to find which parameters are
varying between galaxies with the same velocity dispersion. As we said,
several studies suggest that the scatter in the Mg-![]() relations is due
to variations in the age of the galaxies at a given
relations is due
to variations in the age of the galaxies at a given ![]() through the
dilution of the metallic features in a young stellar population.
To explore this possibility, we have investigated, following the GG96 analysis,
the dependence of the residuals in the index-
through the
dilution of the metallic features in a young stellar population.
To explore this possibility, we have investigated, following the GG96 analysis,
the dependence of the residuals in the index-![]() relations on the
H
relations on the
H![]() index. We performed a t-test to study the degree of correlation
between them. Table 10 summarises the results. A correlation
is considered significant if the t value is higher than 1.96. As can be
seen in the table, we confirm the result obtained by GG96 concerning the
existence of an strong anti-correlation between the residuals of the
Mgb-
index. We performed a t-test to study the degree of correlation
between them. Table 10 summarises the results. A correlation
is considered significant if the t value is higher than 1.96. As can be
seen in the table, we confirm the result obtained by GG96 concerning the
existence of an strong anti-correlation between the residuals of the
Mgb-![]() relation and the H
relation and the H![]() index for the LDEGs, but, on the other
hand, we find a positive correlation between the residuals of the
Fe4383-
index for the LDEGs, but, on the other
hand, we find a positive correlation between the residuals of the
Fe4383-![]() relation and this index. This is illustrated in
Fig. 10. If the age were the main parameter responsible for
the scatter in the index-
relation and this index. This is illustrated in
Fig. 10. If the age were the main parameter responsible for
the scatter in the index-![]() relations, an anti-correlation of the
residuals in the Fe4383-
relations, an anti-correlation of the
residuals in the Fe4383-![]() with H
with H![]() should also be observed,
contrary to our findings. Therefore, our result excludes age as the only
parameter producing the dispersion in the index-
should also be observed,
contrary to our findings. Therefore, our result excludes age as the only
parameter producing the dispersion in the index-![]() relations. On the
other hand, if only variations of overall metallicity at a given
relations. On the
other hand, if only variations of overall metallicity at a given ![]() were
responsible for the dispersion, we would also expect the same behaviour in the
correlation of the residuals with H
were
responsible for the dispersion, we would also expect the same behaviour in the
correlation of the residuals with H![]() in both indices. Neither of these
two parameters can be entirely responsible for the residuals from the relations.
Interestingly, in the HDEG subsample, we do not find any correlation between
the residuals and the H
in both indices. Neither of these
two parameters can be entirely responsible for the residuals from the relations.
Interestingly, in the HDEG subsample, we do not find any correlation between
the residuals and the H![]() index (we only found a marginal correlation for
Fe5015 and Fe5335).
index (we only found a marginal correlation for
Fe5015 and Fe5335).
Table 8:
Difference between the slope of the index-![]() relation and the
expected index variation due to changes in the chemical composition.
relation and the
expected index variation due to changes in the chemical composition.
Discarding both age and metallicity as the only parameters responsible for
the departure of the galaxies from the index-![]() relations, we
investigate if a variation in the relative abundances between galaxies can help
to explain the observed scatter. Figure 11 shows the quotient
between the metallicities measured in the Mgb-H
relations, we
investigate if a variation in the relative abundances between galaxies can help
to explain the observed scatter. Figure 11 shows the quotient
between the metallicities measured in the Mgb-H![]() and Fe4383-H
and Fe4383-H![]() diagrams (see Paper II for details) as a function of velocity dispersion,
splitting the sample into galaxies older and younger than 7.5 Gyr (according to
their position in the H
diagrams (see Paper II for details) as a function of velocity dispersion,
splitting the sample into galaxies older and younger than 7.5 Gyr (according to
their position in the H![]() -[MgFe] plane, using V06 models). It is clear
from this figure that the [Mg/Fe] relation with
-[MgFe] plane, using V06 models). It is clear
from this figure that the [Mg/Fe] relation with ![]() depends on the
luminosity-weighted mean age of the galaxies and, therefore, on their
particular star formation history. In particular, older galaxies have, on
average, higher [Mg/Fe] than the younger ones. In the lower panel of
Fig. 11, we have added the galaxies from the Coma cluster. It can be
seen that they follow the trend of the older LDEGs, exhibiting, on average,
larger [Mg/Fe] ratios than younger LDEGs.
depends on the
luminosity-weighted mean age of the galaxies and, therefore, on their
particular star formation history. In particular, older galaxies have, on
average, higher [Mg/Fe] than the younger ones. In the lower panel of
Fig. 11, we have added the galaxies from the Coma cluster. It can be
seen that they follow the trend of the older LDEGs, exhibiting, on average,
larger [Mg/Fe] ratios than younger LDEGs.
These trends indicate that the scatter in the index-![]() relations is not
an exclusive effect of a dispersion in the age, but it is a consequence of the
variation of the element abundance ratios with this parameter. Furthermore, we
find a tendency for which older galaxies have, on average, higher [Mg/Fe]
ratios.
relations is not
an exclusive effect of a dispersion in the age, but it is a consequence of the
variation of the element abundance ratios with this parameter. Furthermore, we
find a tendency for which older galaxies have, on average, higher [Mg/Fe]
ratios.
Fisher et al. (1995) noted, studying a sample of 7 bright
early-type galaxies, a correlation between [Mg/Fe] and the age of the galaxies,
in the same way we did. These authors, however, did not find a
correlation between the residuals of the Mgb-![]() relation and the
H
relation and the
H![]() index. This could be due to the small sample analysed. Thomas et al. (2002)
also find a similar relation between the
index. This could be due to the small sample analysed. Thomas et al. (2002)
also find a similar relation between the
![]() Fe]
Fe]![]() ratio and the age, studying several
samples from the literature. Contrary to these findings, Trager et al. (2000b)
do not report any correlation between
ratio and the age, studying several
samples from the literature. Contrary to these findings, Trager et al. (2000b)
do not report any correlation between ![]() Fe]
Fe]![]() and the age of the galaxies. However these authors analysed the
relation between age, [Z/Fe], [E/Fe] and
and the age of the galaxies. However these authors analysed the
relation between age, [Z/Fe], [E/Fe] and ![]() ,
concluding that age cannot
be the only parameter responsible for the scatter in the Mg-
,
concluding that age cannot
be the only parameter responsible for the scatter in the Mg-![]() relation,
being necessary variations of [E/Fe] between galaxies with the same
relation,
being necessary variations of [E/Fe] between galaxies with the same
![]() ,
in agreement with our results.
,
in agreement with our results.
Since Mg is produced mainly in type II supernovae whilst the bulk of Fe is released by type I supernovae (e.g., Nomoto et al. 1984; Woosley & Weaver 1995; Thielemann et al. 1996), the existence of a trend between [Mg/Fe] and age favours the idea that the different element ratios are a consequence of different star formation histories (see, e.g., Greggio & Renzini 1983; Matteucci & Greggio 1986; Gibson 1997; Thomas et al. 1998), and that younger galaxies have suffered a more extended star formation history, incorporating the elements produced by low-mass stars (see, e.g., Worthey 1998). However, there are other possibilities that we explore later in Sect. 7. Again, in this section, none of the conclusions depends on the absolute values of the indices, therefore, they would not change if we add a constant offset to the C4668 and Mgb indices.
We want to finish this section justifying the use of the term [Mg/Fe] in our discussion when,
in reality, we are just comparing the metallicity measured in a Fe4383-H![]() diagram
with the one obtained using the Mgb-H
diagram
with the one obtained using the Mgb-H![]() combination. Figure 12
shows the values of Z(Fe4383)/Z(Mgb) compared with the parameter [
combination. Figure 12
shows the values of Z(Fe4383)/Z(Mgb) compared with the parameter [![]() /Fe] derived
from TMB03 models. To obtain these values, we used the indices Fe4383, H
/Fe] derived
from TMB03 models. To obtain these values, we used the indices Fe4383, H![]() ,
and Mgb, and followed an iterative process. We first measured age and metallicities
assuming [
,
and Mgb, and followed an iterative process. We first measured age and metallicities
assuming [![]() /Fe] = 0 and obtained a first guess of the age that we used to determine
[
/Fe] = 0 and obtained a first guess of the age that we used to determine
[![]() /Fe]. With this new value, we calculated, again, age and metallicity and so on,
until the derived parameters in two consecutive iterations were consistent within 5% accuracy.
As can be seen in Fig. 12, there is an excellent correspondence
between the values of [
/Fe]. With this new value, we calculated, again, age and metallicity and so on,
until the derived parameters in two consecutive iterations were consistent within 5% accuracy.
As can be seen in Fig. 12, there is an excellent correspondence
between the values of [![]() /Fe] derived with TMB03 models and the
ratio of metallicities
measured using Fe4383 and Mgb with the V06 models. We could have used a transformation
to derive [
/Fe] derived with TMB03 models and the
ratio of metallicities
measured using Fe4383 and Mgb with the V06 models. We could have used a transformation
to derive [![]() /Fe] values from Z(Fe4383)/Z(Mgb) values, but several
aspects of the models need to be understood before
deriving any meaningful number. In any case, we are not making any conclusion
based on the absolute value of [Mg/Fe]. We prefer to use the term [Mg/Fe]
instead of the most general [
/Fe] values from Z(Fe4383)/Z(Mgb) values, but several
aspects of the models need to be understood before
deriving any meaningful number. In any case, we are not making any conclusion
based on the absolute value of [Mg/Fe]. We prefer to use the term [Mg/Fe]
instead of the most general [![]() /Fe] since different
/Fe] since different ![]() -elements may have different
behaviours in spheroidal systems, as seems to be the case in the bulge
stars of our Galaxy (see, e.g., Fulbright et al. 2005).
-elements may have different
behaviours in spheroidal systems, as seems to be the case in the bulge
stars of our Galaxy (see, e.g., Fulbright et al. 2005).
Table 9:
Statistical analysis of the correlations between the residuals of the
index-![]() relation and the H
relation and the H![]() index. For a significance level lower
than
index. For a significance level lower
than
![]() ,
a value of t higher than 1.96 confirms the existence of
correlation.
,
a value of t higher than 1.96 confirms the existence of
correlation.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.3cm,clip]{4842fig10a.ps}\par\includegraphics[angle=-90,width=8.3cm,clip]{4842fig10b.ps}
\end{figure}](/articles/aa/full/2006/39/aa4842-06/Timg190.gif) |
Figure 10:
H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{4842fig11a.ps}\par\includegraphics[angle=-90,width=8.8cm,clip]{4842fig11b.ps}
\end{figure}](/articles/aa/full/2006/39/aa4842-06/Timg191.gif) |
Figure 11:
Ratio of the metallicities calculated in the Mgb-H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{4842fig12.ps}
\end{figure}](/articles/aa/full/2006/39/aa4842-06/Timg192.gif) |
Figure 12:
Comparison of Z(Fe4383)/Z(Mgb) with the values of [ |
| Open with DEXTER | |
Some studies have analysed the possible differences between the line-strength
indices of galaxies in different environments.
Guzmán et al. (1992) found systematic variations in the zero-point of the
Mg2-![]() relation for a sample of Coma galaxies as a function of their
distance to the cluster centre. Jørgensen et al. (1996, 1997), examining a
sample of eleven clusters, detected a weak correlation between the intensity of
the Mg line and the local density within the clusters, in agreement with the
Guzmán et al. result. Similar differences have been found by several other
authors (e.g., de Carvalho & Djorgovski 1992), while others (e.g., Bernardi
et al. 1998) do not find evidence of an environmental influence on the
zero point of the relation of the indices with the velocity dispersion of the
galaxies. The dependence of the absorption features on the environment has been
studied, almost exclusively, with just two indices, Mg2 and Mgb.
relation for a sample of Coma galaxies as a function of their
distance to the cluster centre. Jørgensen et al. (1996, 1997), examining a
sample of eleven clusters, detected a weak correlation between the intensity of
the Mg line and the local density within the clusters, in agreement with the
Guzmán et al. result. Similar differences have been found by several other
authors (e.g., de Carvalho & Djorgovski 1992), while others (e.g., Bernardi
et al. 1998) do not find evidence of an environmental influence on the
zero point of the relation of the indices with the velocity dispersion of the
galaxies. The dependence of the absorption features on the environment has been
studied, almost exclusively, with just two indices, Mg2 and Mgb.
In this section, we study the differences on 17 Lick indices, at a given
![]() ,
between LDEGs and HDEGs.
To quantify possible systematic differences, we have performed a linear
least-squares fit to the index-
,
between LDEGs and HDEGs.
To quantify possible systematic differences, we have performed a linear
least-squares fit to the index-![]() relations of the LDEGs subsample (see
Sect. 5) and have measured the mean offsets (weighting
with errors) of the HDEGs from the fits. Table 11 shows
these mean offsets (d) with their errors (
relations of the LDEGs subsample (see
Sect. 5) and have measured the mean offsets (weighting
with errors) of the HDEGs from the fits. Table 11 shows
these mean offsets (d) with their errors (
![]() ,
where s is the standard deviation and
,
where s is the standard deviation and
![]() the effective number of points).
We find significant differences in the following indices: H
the effective number of points).
We find significant differences in the following indices: H![]() ,
H
,
H![]() ,
Ca4455, Fe4531, Fe5015, and also in the indices CN2 and C4668,
whose differences have been previously reported by Sánchez-Blázquez et al. (2003). On the other hand, in agreement with other studies (e.g.,
Bernardi et al. 1998), we do not find any significant difference in the Mgb
index of both subsamples at a given velocity dispersion. In the next section,
we discuss the possible causes of these differences.
,
Ca4455, Fe4531, Fe5015, and also in the indices CN2 and C4668,
whose differences have been previously reported by Sánchez-Blázquez et al. (2003). On the other hand, in agreement with other studies (e.g.,
Bernardi et al. 1998), we do not find any significant difference in the Mgb
index of both subsamples at a given velocity dispersion. In the next section,
we discuss the possible causes of these differences.
Table 10:
Mean differences in the Lick indices at a given ![]() between
galaxies in different environments. For each index, we list the mean offset
d and its error
between
galaxies in different environments. For each index, we list the mean offset
d and its error ![]() and the t-parameter (of the statistical test
and the t-parameter (of the statistical test
![]() ).
).
In Sánchez-Blázquez et al. (2003), we briefly discussed possible mechanisms that would produce differences in the CN and C4668 between galaxies in different environments. In this section, we extend this discussion to include the rest of the indices analysed.
If we assume than the differences in CN2, C4668, Fe5015, and Fe4531 between
HDEGs and LDEGs are due to variations in some chemical species with respect to
Fe, the existence of differences in C, N and Ti abundances
between both subsamples would be required. This is a very qualitative statement. To check if a
variation of these chemical species is compatible with the calculated offsets
for all the indices, we follow a similar approach to that in
Sect. 5.1. In this case, instead of comparing the variation of the
indices with the velocity dispersion, we compare the offsets between galaxies
in different environments and try to reproduce these differences by varying the
abundances of different chemical species. We separated the elements into 6 different groups: (i) ![]() elements: Ne, Na, Mg, Si, S, and O; (ii) C;
(iii) N; (iv) Ti; (v) Ca; and (vi) Fe-peak elements (Fe and Cr). We have built
4 different models. In building the models, we have not tried to fit all the
indices by varying the ratios of different elements arbitrarily, but we have
proposed 4 simple permutations that can give a rough idea of the differences in the chemical
composition between galaxies in different environments. This rough idea, though,
can give us important clues to understand the differences in the star
formation history of galaxies between LDEG and HDEG.
The models can be described as follows:
elements: Ne, Na, Mg, Si, S, and O; (ii) C;
(iii) N; (iv) Ti; (v) Ca; and (vi) Fe-peak elements (Fe and Cr). We have built
4 different models. In building the models, we have not tried to fit all the
indices by varying the ratios of different elements arbitrarily, but we have
proposed 4 simple permutations that can give a rough idea of the differences in the chemical
composition between galaxies in different environments. This rough idea, though,
can give us important clues to understand the differences in the star
formation history of galaxies between LDEG and HDEG.
The models can be described as follows:
![\begin{displaymath}\begin{tabular}{@{}l@{}c@{$\;$}l@{}}
\raisebox{0ex}[3ex]{\mb...
... 0.05~dex and the
N abundance by 0.15~dex.}
\end{tabular}\\
\end{displaymath}](/articles/aa/full/2006/39/aa4842-06/img196.gif)
Figure 13 shows the comparison of the observed offsets between galaxies in different environments and the ones obtained from the different models. The lines in the figures indicate the 1:1 relation (the last column of Table 12 indicates the rms of the dispersion around this relation). From the analysis of the figure and the rms of the residuals, we can conclude the following:
Table 11: Differences in the abundances of the distinct chemical species used to build the 4 models described in the text. The last column shows the dispersion around the 1:1 relation when comparing the offsets in the indices between galaxies in different environments and the offsets in the indices due to the changes in the chemical species of each model.
![\begin{figure}
\par\resizebox{4.2cm}{!}{\includegraphics[bb=88 145 578 630,angle...
...m}{!}{\includegraphics[bb=88 145 578 630,angle=-90]{4842fig13d.ps}}
\end{figure}](/articles/aa/full/2006/39/aa4842-06/Timg198.gif) |
Figure 13: Comparison of the offsets between HDEGs and LDEGs with the differences in the indices obtained in different models in which we have calculated the variation in the Lick indices due to variations on the ratio of different chemical elements (see text for a more detailed description). The error bars indicate the errors in the offsets. |
| Open with DEXTER | |
In summary, to reproduce the observed differences between the indices of LDEGs and HDEGs through variations in the abundances of different elements, we have to assume a variation in all the chemical species, in the sense that LDEGs are, on average, more metal rich than HDEGs. The relative changes in all the chemical species, however, are not the same. In particular, the models that best explain the differences are those that assume a higher variation in N, Ti, Ca, and probably C, between galaxies in different environments.
Ti and Ca are elements that are very difficult to interpret. Ca is an
![]() -element, but in early-type galaxies seems to track Fe-peak elements
(Worthey 1998; TMB03; Cenarro et al. 2004). Ti is a
poorly understood element. Nucleosynthesis theories predict that this element is
produced in type II supernovae and that its abundance is similar to that of Fe.
However, in galactic bulge stars, this element is found in higher proportions
than in the solar partition, even for stars of solar metallicity (McWillian &
Rich 1994, 2004), which has not been reproduced by any nucleosynthesis model.
This element can also be overabundant with respect to Fe in massive ellipticals
(Worthey 1998). So, we do not try to discuss the origin of the differences in
these two elements between galaxies in different environments. The conclusions
of this section would not change if we were to add a constant offset to the
indices C4668 and Mgb, as the conclusions
are based upon differences between galaxies in
different environments, not on the absolute values of these indices.
-element, but in early-type galaxies seems to track Fe-peak elements
(Worthey 1998; TMB03; Cenarro et al. 2004). Ti is a
poorly understood element. Nucleosynthesis theories predict that this element is
produced in type II supernovae and that its abundance is similar to that of Fe.
However, in galactic bulge stars, this element is found in higher proportions
than in the solar partition, even for stars of solar metallicity (McWillian &
Rich 1994, 2004), which has not been reproduced by any nucleosynthesis model.
This element can also be overabundant with respect to Fe in massive ellipticals
(Worthey 1998). So, we do not try to discuss the origin of the differences in
these two elements between galaxies in different environments. The conclusions
of this section would not change if we were to add a constant offset to the
indices C4668 and Mgb, as the conclusions
are based upon differences between galaxies in
different environments, not on the absolute values of these indices.
In the following subsection, we extend the discussion already presented in Sánchez-Blázquez et al. (2003) about the possible mechanisms that can lead to a difference in the [C/Fe] and [N/Fe] ratios between low- and high-density environment galaxies.
C is produced predominantly by the triple-alpha reaction of He, while N is
produced in the conversion of C and O during the CNO cycles. The problem is to
determine the evolutionary phases in which these elements are predominantly
produced. Several studies seem to favour intermediate-mass stars (between 5 and
8 ![]() )
as the main contributors to N (Renzini & Voli 1981; Henry et al. 2000; Chiappini et al. 2003), although it
is also predicted to be produced in massive stars (Meynet & Maeder 2002).
There is still more controversy over the location of the C production.
Some authors claim that this occurs in low- and intermediate-mass stars
(Renzini & Voli 1981; Chiappini et al. 2003a) based on the variation of
[C/Fe] with metallicity in the stars of the galactic disk. This ratio remains
constant from
)
as the main contributors to N (Renzini & Voli 1981; Henry et al. 2000; Chiappini et al. 2003), although it
is also predicted to be produced in massive stars (Meynet & Maeder 2002).
There is still more controversy over the location of the C production.
Some authors claim that this occurs in low- and intermediate-mass stars
(Renzini & Voli 1981; Chiappini et al. 2003a) based on the variation of
[C/Fe] with metallicity in the stars of the galactic disk. This ratio remains
constant from
![]() to solar metallicities, as would be expected if
it were produced in non-massive stars. On the other hand, recent measurements
of the C/O abundances among halo and disk stars show a discontinuity around
to solar metallicities, as would be expected if
it were produced in non-massive stars. On the other hand, recent measurements
of the C/O abundances among halo and disk stars show a discontinuity around
![]() O/H
O/H![]() .
Oxygen is mainly created in massive stars; therefore, if
the main contributors to the C abundance were also these stars, we would not
expect to find this discontinuity. However, other authors affirm that, to
explain the abundances of the observed C in stars in the galactic disk, most of the
C has to be produced in massive stars (Carigi 2000; Henry et al. 2000). The
conclusions of the different authors are very dependent on the adopted yields.
The works that favour massive stars as the main contributors to the C abundance
in the interstellar medium are based in the Maeder (1992) yields, which predict
a strong dependence of the C yields in massive stars on the metallicity.
However, this work has been improved in the new models of Meynet & Maeder
(2002), which have taken into account the effects due to the stellar rotation.
Using these models, Chiappini et al. (2003) showed that,
considering massive stars as the main producers of C, it is not possible to
explain the solar C/O ratio. In this work we consider that C is produced mainly
in low- and intermediate-mass stars (1
.
Oxygen is mainly created in massive stars; therefore, if
the main contributors to the C abundance were also these stars, we would not
expect to find this discontinuity. However, other authors affirm that, to
explain the abundances of the observed C in stars in the galactic disk, most of the
C has to be produced in massive stars (Carigi 2000; Henry et al. 2000). The
conclusions of the different authors are very dependent on the adopted yields.
The works that favour massive stars as the main contributors to the C abundance
in the interstellar medium are based in the Maeder (1992) yields, which predict
a strong dependence of the C yields in massive stars on the metallicity.
However, this work has been improved in the new models of Meynet & Maeder
(2002), which have taken into account the effects due to the stellar rotation.
Using these models, Chiappini et al. (2003) showed that,
considering massive stars as the main producers of C, it is not possible to
explain the solar C/O ratio. In this work we consider that C is produced mainly
in low- and intermediate-mass stars (1 ![]()
![]() ), while N is
mainly produced in intermediate mass stars (5
), while N is
mainly produced in intermediate mass stars (5![]() /
/
![]() ).
During the AGB, these stars eject significant amounts of 4He, 12C,
13C, and 14N into the interestellar
medium.
Of course, the interpretation is subject to change if new results in stellar
nucleosynthesis report that these stars are not the main contributors to these
elements.
).
During the AGB, these stars eject significant amounts of 4He, 12C,
13C, and 14N into the interestellar
medium.
Of course, the interpretation is subject to change if new results in stellar
nucleosynthesis report that these stars are not the main contributors to these
elements.
A difference in the relative abundance of C and N between LDEGs and HDEGs may be due to:
The second mechanism that could produce variations in the chemical abundances
of C and N between galaxies in different environments is a difference in their
star formation history. In particular, if we assumed that the main contributors
to the C and N are the intermediate- and low-mass stars, the timescale for the
release of these elements into the interstellar medium would be ![]()
![]() years (this is, approximately, the lifetime of an
8
years (this is, approximately, the lifetime of an
8 ![]() star). Therefore, if star formation in the HDEGs was shorter than
this, the stars would not incorporate those elements. However, if the
timescale of the star formation in LDEGs were long enough for stars between 3
and 8
star). Therefore, if star formation in the HDEGs was shorter than
this, the stars would not incorporate those elements. However, if the
timescale of the star formation in LDEGs were long enough for stars between 3
and 8 ![]() to complete their evolution until the AGB, and to release
the products of their nucleosynthesis into the interstellar medium, the next
generation of stars would incorporate those elements, which would produce the
observed differences between both subsamples (LDEGs and HDEGs). These
differences in the star formation timescales were proposed in
Sect. 5.2 to explain the trends between Z(Mgb)/Z(Fe4383) and
age. Note that the ages and metallicities that we are measuring are mean values
weighted with the luminosity of the stars. Therefore, it is not required that
all the stars of the LDEGs are formed more recently, since the differences
could be produced by a small percentage of stars formed in later bursts (see
Trager et al. 2000b).
to complete their evolution until the AGB, and to release
the products of their nucleosynthesis into the interstellar medium, the next
generation of stars would incorporate those elements, which would produce the
observed differences between both subsamples (LDEGs and HDEGs). These
differences in the star formation timescales were proposed in
Sect. 5.2 to explain the trends between Z(Mgb)/Z(Fe4383) and
age. Note that the ages and metallicities that we are measuring are mean values
weighted with the luminosity of the stars. Therefore, it is not required that
all the stars of the LDEGs are formed more recently, since the differences
could be produced by a small percentage of stars formed in later bursts (see
Trager et al. 2000b).
In Sect. 5.2 we showed that the [Mg/Fe] ratio is related to the age in such a way that older galaxies exhibit, on average, larger [Mg/Fe] ratios than the younger ones.
Several different mechanisms have been proposed to explain the existence, in giant elliptical galaxies, of an overabundance of [Mg/Fe] (see, for example, Worthey et al. 1992). All are based on the assumption that this parameter quantifies the relative importance of the chemical enrichment from type II versus the delayed type Ia supernovae. We assess whether these proposed mechanisms can explain the relation between the age and the relative abundance of Mg with respect to Fe.
To explore the possibility of a variation of the IMF slope with ![]() ,
we
made use of the Vazdekis et al. (2003) stellar population models. In these
models, a new calibration of the CaT index in the near-infrared derived from a
new stellar library (Cenarro et al. 2002) was presented. These authors found
that this index has a high sensitivity to the slope of the IMF. They also
analysed a sample of galaxies with high quality observed spectra (Cenarro
et al. 2003), proposing the existence of a variation of the IMF with metallicity,
in the sense that the larger the metallicity, the larger the IMF slope.
,
we
made use of the Vazdekis et al. (2003) stellar population models. In these
models, a new calibration of the CaT index in the near-infrared derived from a
new stellar library (Cenarro et al. 2002) was presented. These authors found
that this index has a high sensitivity to the slope of the IMF. They also
analysed a sample of galaxies with high quality observed spectra (Cenarro
et al. 2003), proposing the existence of a variation of the IMF with metallicity,
in the sense that the larger the metallicity, the larger the IMF slope.
This dependence of the IMF on metallicity would give rise to the observed tendency of [Mg/Fe] with age, if there were a relation between age and metallicity, i.e., younger galaxies were also more metal rich. This relation has been observed in several studies (Trager et al. 2000b; K01 among others), although it is difficult to separate the real trend from the one caused by the correlated errors in both parameters (see, e.g., K01). A discussion of this relation is presented in Paper II.
Figure 14 shows the relation between the slope of the IMF derived
from the relation given in Cenarro et al. (2003) to the Z(Mgb)/Z(Fe4383)
ratio (the quotient between the metallicity measured separately with both Mgb
and Fe4383 combined with H![]() ,
which can be used as an estimation of behaviour
(not the numerical value) of the [Mg/Fe] ratio (see Sect. 5.2).
As can be seen, the slope of the IMF
obtained in this way is higher for galaxies with larger [Mg/Fe] ratios, which
is the opposite of the expected trend. Therefore, although we do not discard
the possibility of differences in the IMF between galaxies, they cannot be the
responsible for the relation between [Mg/Fe] abundance and age.
,
which can be used as an estimation of behaviour
(not the numerical value) of the [Mg/Fe] ratio (see Sect. 5.2).
As can be seen, the slope of the IMF
obtained in this way is higher for galaxies with larger [Mg/Fe] ratios, which
is the opposite of the expected trend. Therefore, although we do not discard
the possibility of differences in the IMF between galaxies, they cannot be the
responsible for the relation between [Mg/Fe] abundance and age.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.4cm,clip]{4842fig14.ps}
\end{figure}](/articles/aa/full/2006/39/aa4842-06/Timg207.gif) |
Figure 14:
Slope of the IMF ( |
| Open with DEXTER | |
In this paper we have investigated the relations between line-strength indices and velocity dispersion with the aim of understanding their origin, the causes of the scatter, and the influence of environment. The main results can be summarised as follows:
Acknowledgements
We would like to thank Brad Gibson, Daisuke Kawata and Christopher Thom for their careful reading of the manuscript and for their useful comments. We are also grateful to Javier Cenarro, Reynier Peletier, and Alexandre Vazdekis for fruitful discussions. We are very grateful to the referee, Jim Rose, for his very constructive report and many useful suggestions. The WHT is operated on the island of La Palma by the Royal Greenwich Observatory at the Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias. The Calar Alto Observatory is operated jointly by the Max-Planck Institute für Astronomie, Heidelberg, and the Spanish Instituto de Astrofísica de Andalucía (CSIC). This research has made use of the SIMBAD database operated at CDS, Strasbourg, France. This work was supported by the Spanish research project AYA 2003-01840, the European Community through its NOVA fellowship program, and the Australian Research Council. We are grateful to the CATs for generous allocation of telescope time.
Figure A.1 shows, for the stars observed in the different runs, the comparison between the original Lick/IDS index measurements and the indices determined from our data. Table A.1 shows the offsets obtained in the different observing periods and the final offset adopted in this paper.
Table A.1: Final Lick/IDS offsets (Lick/IDS - This work).
Table B.1:
Mean offset, rms (![]() ), and rms expected by
the errors (
), and rms expected by
the errors (![]() (exp)) in the comparison between stars observed
in Run 4 and in the other runs. The last column shows the z parameter,
which indicates the significance of the mean offset. A z-value higher
than 1.96 indicates that the offsets are significant with a significance
level lower than 0.05.
(exp)) in the comparison between stars observed
in Run 4 and in the other runs. The last column shows the z parameter,
which indicates the significance of the mean offset. A z-value higher
than 1.96 indicates that the offsets are significant with a significance
level lower than 0.05.
![\begin{figure}
\mbox{\resizebox{4.2cm}{!}{\includegraphics[angle=-90]{4842fig16a...
...resizebox{4.2cm}{!}{\includegraphics[angle=-90]{4842fig16o.ps}} }\end{figure}](/articles/aa/full/2006/39/aa4842-06/Timg230.gif) |
Figure B.1: Comparison of the indices measured in the common stars between Run 4 and the other runs. |
The observed spectrum of a galaxy is the convolution of the integrated spectrum of its stellar population with the instrumental broadening and the distribution of line-of-sight velocities of the stars. The broadening of the spectra causes the indices to appear weaker than they intrinsically are. To compare line-strength indices among different galaxies, it is necessary to correct for the velocity dispersion and instrumental resolution broadening effects. This was done by using the optimal template obtained in the calculation of the velocity dispersion and radial velocity. This reference spectrum is the composition of the template stellar spectra that best matches the spectrum of each galaxy, corrected for differences in the intensities of the spectral lines. We used these composite templates instead of individual spectra because the variation of the indices with the broadening varies with their intensity (see Kuntschner 2000).
The templates were first broadened to the Lick resolution (which varies with
wavelength) and then convolved with a Gaussian function of widths ranging from 0 to 450 km s-1 (in steps of 20 km s-1) to simulate the velocity
dispersion broadening within a galaxy. Index strengths were measured for each
spectrum and a correction factor was calculated as
| (C.1) |
Table C.1:
Average polynomial coefficients for each line index correction
function, where
![]() .
The last column shows the
maximum error due to this correction for a galaxy of
.
The last column shows the
maximum error due to this correction for a galaxy of
![]() km s-1.
km s-1.
Although we have checked the possible existence of offsets between different observing runs by comparing galaxies observed more than once, the number of available galaxies to make this comparison was admittedly sparse. Therefore, in this appendix, we repeat the comparison with other authors subdividing the galaxies in different observing runs. Table D.1 shows this comparison.
To check if the offsets with other authors were different in the
different observing runs,
we have performed a t-test comparing the offsets of Runs 2, 3, and 4 with
the offsets obtained in Run 1.
The results are shown in Table D.2.
A value of t larger than 1.96 indicates that the offset in the corresponding
run is significatively different than the offset obtained in Run 1 (with a
significance level lower than
![]() ), and it would
suggest the existence of offsets between runs. The only two cases in which that
happens are in the comparison of H
), and it would
suggest the existence of offsets between runs. The only two cases in which that
happens are in the comparison of H![]() with the data of D05 (the offset
in Run 2
is significatively larger than the one obtained in Run 1), and in the
comparison of Fe4383 with the same reference, D05 (the offset in Run 3 is
larger as well, but negative, than in the comparison with Run 1).
In the first case, the number of galaxies in common between D05 and Run 2 is
only 3, which makes the result very uncertain.
In the later case, we do not obtain significant differences in the
offsets of Fe4383 between Run 3 and other runs when we compare them with
other references (different than D05).
We conclude, therefore, that the measurements obtained in different
observing runs do not present any systematic difference.
with the data of D05 (the offset
in Run 2
is significatively larger than the one obtained in Run 1), and in the
comparison of Fe4383 with the same reference, D05 (the offset in Run 3 is
larger as well, but negative, than in the comparison with Run 1).
In the first case, the number of galaxies in common between D05 and Run 2 is
only 3, which makes the result very uncertain.
In the later case, we do not obtain significant differences in the
offsets of Fe4383 between Run 3 and other runs when we compare them with
other references (different than D05).
We conclude, therefore, that the measurements obtained in different
observing runs do not present any systematic difference.
Table D.1:
Comparison of line strengths measured in this and other studies. Ref.:
reference of the comparison work (see description in the text); N: number of
galaxies in common; ![]() :
calculated offset between both studies (other
studies minus this work);
:
calculated offset between both studies (other
studies minus this work); ![]() :
rms dispersion;
:
rms dispersion;
![]() :
expected rms from the errors; t: t-parameter of the comparison of
means.
:
expected rms from the errors; t: t-parameter of the comparison of
means.
Table D.2: t-parameter in the comparison of the offsets between different observing runs and other authors. A t-value higher than 1.96 indicates that the offsets are significant different, which would suggest the existence of systematic differences between observing runs.
Table D.3:
Fully corrected line-strength indices in the central
2
![]() aperture, where eqap represents
4
aperture, where eqap represents
4
![]() at redshift z=0.016.
at redshift z=0.016.