A&A 457, 385-391 (2006)
DOI: 10.1051/0004-6361:20065581
High order correction terms for the peak-peak correlation function in nearly-Gaussian models
A. P. A. Andrade1,2 - A. L. B. Ribeiro1 - C. A. Wuensche2
1 - Laboratório de Astrofísica Teórica e Observacional,
Universidade Estadual de Santa Cruz, Brazil
2 - Divisão de Atrofísica, Instituto Nacional de Pesquisas
Espaciais, Brazil
Received 10 May 2006 / Accepted 9 June 2006
Abstract
Context. One possible way to investigate the nature of the primordial power spectrum fluctuations is by investigating the statistical properties of the local maximum in the density fluctuation fields.
Aims. In this work we present a study of the mean correlation function, 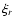 ,
and the correlation function for high-amplitude fluctuations (peak-peak correlation) in a slighlty non-Gaussian context.
,
and the correlation function for high-amplitude fluctuations (peak-peak correlation) in a slighlty non-Gaussian context.
Methods. From the definition of the correlation excess, we computed the Gaussian two-point correlation function and, using an expansion in generalized Hermite polynomials, we estimated the correlation of high-density peaks in a non-Gaussian field with a generic distribution and power spectrum. We also applied the results to a scale-mixed distribution model, which corresponds to a nearly Gaussian model.
Results. The results reveal that, even for a small deviation from Gaussianity, we can expect high-density peaks to be much more correlated than in a Gaussian field with the same power spectrum. In addition, the calculations reveal how the amplitude of the peaks in the fluctuation field is related to the existing correlations.
Conclusions. Our results may be used as an additional tool for investigating the behavior of the N-point correlation function, to understand how non-Gaussian correlations affect the peak-peak statistics, and extract more information about the statistics of the density field.
Key words: methods: statistical - large-scale structure of Universe
Investigation of the statistical properties of
cosmological density fluctuations is a very useful tool for understanding
the origin of the cosmic structure. Cosmological models to describe
primordial fluctuations can be roughly divided into two classes: Gaussian and non-Gaussian.
The most accepted model for structure formation assumes initial quantum
fluctuations created during inflation and amplified by gravitational effects.
The standard inflationary models predict an uncorrelated random field, with a scale-invariant power spectrum, which follows a nearly-Gaussian distribution
(Guth & Pi 1982; Gangui et al. 1994). However, non-Gaussian fluctuations are also allowed in a wide class
of alternative models, such as: the multiple interactive fields (Allen et al. 1987; Salopek et al. 1989),
the cosmic defects models (Kibble 1976), and the hybrid models (Magueijo & Brandenbergher 2000; Battye & Weller 2000).
By discriminating between different classes of models, the statistical properties
of the fluctuations field can be used to investigate the nature of cosmic structure.
However, non-Gaussian models include an infinite range of possible statistics.
As a consequence, performing statistical tests of this kind is not a straightforward
task, since there is no adequate general test for every kind of model. To attack this
problem, any effort to better understand how the statistical properties of the density
fluctuation field affect the observed Universe is welcome, since it may bring extra pieces
of information to the investigation of cosmic structure.
Due to the importance of characterizing non-Gaussian signatures, many statistical
approaches have been used to study the distribution of fluctuations in the cosmic
microwave background radiation (CMBR) (Chiang et al. 2003; Bond & Efstathiou 1987; Eriksen et al. 2005; Cabella et al. 2004; Komatsu et al. 2003) and the large-scale structure (LSS) (Frith et al. 2005; Takada & Jain 2003; Verde et al. 2001; Fry 1985). One possible way to investigate the nature of the primordial
power spectrum fluctuations is by investigating the statistical properties of the local
maximum in the density fluctuation fields. Since some of the peak properties, such as number, frequency, correlation, height, and extrema, are highly dependent upon the statistics of the fluctuation
field, we can gather information about the statistical distribution function by studying
the morphological properties of the fluctuations fields (Bardeen et al. 1986; Novikov et al. 1999; Larson & Wandelt 2005). Other useful
statistical estimators applied to investigate density fluctuations are
the wavelets tools (McEwen et al. 2004; Mukherjee & Wang 2004; Vielva et al. 2004), the phase correlations (Coles et al. 2004; Naselsky et al. 2005), and the most widely used estimator: the N-point correlations in phase (Lewin et al. 1999; Verde & Heavens 2001; Komatsu et al. 2005) or density spaces (Takada & Jain 2005; Coles & Jones 1991; Heavens & Sketh 1999; Heavens & Gupta 2001; Peebles 2001; Eriksen et al. 2004).
The extensive use of the two-point correlation function to characterize the statistical
properties of the fluctuations field is justified by the mathematical simplicity in the
Gaussian condition, since the mean correlation function can be obtained analytically, and
it specifies a Gaussian distribution completely (as well as its power spectrum). However,
this assumption is not true for a non-Gaussian case, where higher
order correlations may make a significant contribution, despite the great effort demanded to compute a wide range of
correlations. However, it is possible to detect primordial non-Gaussianity with a non-zero
measure of the N-point correlation
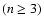 .
In order to achieve a good
description of non-Gaussian signatures in cosmic structure, many works have been done to
estimate the three-point correlation function and the related bi or tri-spectrum for a few
classes of non-Gaussian models (Verde & Heavens 2001; Komatsu et al. 2003; Eriksen et al. 2005; Komatsu et al. 2005; Gaztanaga & Wagg 2004; Hansen et al. 2004; Creminelli et al. 2005; De Troia et al. 2003). It is believed that,
with the advent of the CMBR experiments and the high quality surveys in cosmology, the
N-point correlation function will be the main statistical descriptor for the cosmic structure.
.
In order to achieve a good
description of non-Gaussian signatures in cosmic structure, many works have been done to
estimate the three-point correlation function and the related bi or tri-spectrum for a few
classes of non-Gaussian models (Verde & Heavens 2001; Komatsu et al. 2003; Eriksen et al. 2005; Komatsu et al. 2005; Gaztanaga & Wagg 2004; Hansen et al. 2004; Creminelli et al. 2005; De Troia et al. 2003). It is believed that,
with the advent of the CMBR experiments and the high quality surveys in cosmology, the
N-point correlation function will be the main statistical descriptor for the cosmic structure.
In this work we present a technique for extracting non-Gaussian components from a two-point
correlation function. In the presence of a non-Gaussian component, and
even between two points, it is possible to estimate the influence of higher order correlations
for models with different statistical descriptions. By performing the calculation of the
high-order correction terms for the peak-peak correlation function, we show how the
amplitude of peaks is dependent on the correlations involved. We point out that for a non-Gaussian statistics the higher order correlations impose some
restrictions for the amplitude of high-density peaks.
This paper is divided as follows. In Sect. 2 we give a general description of a random
variable field and estimate the peak-peak correlation function for a Gaussian field. In
Sect. 3 we describe the general treatment to obtain the peak-peak non-Gaussian correlation
function. In Sect. 4 we apply the calculations for a slightly non-Gaussian model in two steps: first we consider an approximated solution for a non-Gaussian
model with null high-order correlations and finally we estimate the complete solution for a slightly non-Gaussian field. In Sect. 5, we summarize our results and discuss the
possibilities for using the
peak-peak correlation function as a statistical descriptor of the density fluctuation field.
Most of the models for the early universe (i.e. inflation) actually
predict that the fluctuation field is random. This requires that
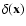 be treated as a random variable in
the 3D-space and assumes that the universe is a random realization of a statistical
ensemble of possible universes.
be treated as a random variable in
the 3D-space and assumes that the universe is a random realization of a statistical
ensemble of possible universes.
We define a random variable,
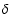 ,
using the fact that, instead of knowing its
exact value, we only know how to measure various values of
,
using the fact that, instead of knowing its
exact value, we only know how to measure various values of
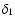 ,
,
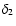 ,
...
,
...
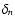 ,
which define a random variable field
under certain experimental conditions. Therefore, a random variable can only be characterized
by a certain statistical ensemble of realizations. When we say that a random variable is known,
it means that we only know the statistical sample that characterizes it. To completely describe
the statistical properties of a random variable,
,
which define a random variable field
under certain experimental conditions. Therefore, a random variable can only be characterized
by a certain statistical ensemble of realizations. When we say that a random variable is known,
it means that we only know the statistical sample that characterizes it. To completely describe
the statistical properties of a random variable,
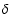 ,
we define the probability
density function,
,
we define the probability
density function, ![$P[\delta]$](/articles/aa/full/2006/38/aa5581-06/img27.gif) ,
which can be obtained from the Fourier transform of the
characteristic distribution function,
,
which can be obtained from the Fourier transform of the
characteristic distribution function,
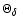 (Gnedenko & Kolmogorov 1968):
(Gnedenko & Kolmogorov 1968):
![\begin{displaymath}%
P[\delta]=\frac{1}{2\pi}\int_{-\infty}^{\infty}{\rm e}^{-{\rm i}u\delta}\Theta_{\delta}(u){\rm d}u.
\end{displaymath}](/articles/aa/full/2006/38/aa5581-06/img29.gif) |
(1) |
The characteristic function,
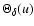 ,
can be obtained by the McLaurin series for the moments, m:
,
can be obtained by the McLaurin series for the moments, m:
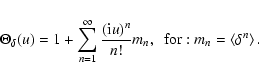 |
(2) |
Another possibility for obtaining the characteristic function of a random variable
is to use the distribution in series of cumulants:
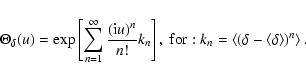 |
(3) |
Since the physical importance of the cumulants kn in Eq. (3) decreases as n increases, it is usual to confine the statistical calculations
of random variables to the first few terms of the cumulant distribution series and,
for convenience, set the higher order terms to zero. However, the calculations presented
in the next sections show that, even if the cumulant terms are very small, they can
significantly contribute to the statistical description of non-Gaussian fields.
The main numerical indication of the correlation degree between random variables
are the N-order correlation functions. The autocorrelation (or double correlation)
for a random variable 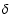 is defined by:
is defined by:
![\begin{displaymath}%
K_2[\delta_1\delta_2]=\left<\delta_1\delta_2\right>-\left<\delta_1\right>\left<\delta_2\right>.
\end{displaymath}](/articles/aa/full/2006/38/aa5581-06/img34.gif) |
(4) |
The triple correlation is similarly defined in terms of all possible
combinations between the three variables, as:
![$\displaystyle %
K_3[\delta_1\delta_2\delta_3] = \left<\delta_1\delta_2\delta_3\...
...\delta_1\delta_2]-\left<\delta1\right>\left<\delta2\right>\left<\delta3\right>.$](/articles/aa/full/2006/38/aa5581-06/img35.gif) |
|
|
(5) |
Note that, in the case where we have the same three variables (
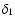 =
=
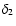 =
=
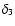 ), the three-point correlation
function is similar to the third cumulant of the distribution. Higher
order correlations between several variables can be defined, in a similar
way, by the difference between all the possible correlations involved.
), the three-point correlation
function is similar to the third cumulant of the distribution. Higher
order correlations between several variables can be defined, in a similar
way, by the difference between all the possible correlations involved.
For a statistical process where the correlation functions of order greater
than one are null, we set the variable described by this correlation function as
not random, or deterministic. In the case where the correlation functions of order
greater than two are null, we have a Gaussian variable. For the case of correlation
functions of order greater than two and not completely null, the variable is considered
to be non-Gaussian. In this sense, we can say that a Gaussian random field is a simplified version of a general random field.
Usually, the cosmological density fluctuation field is statistically described by
the mean correlation function,
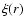 ,
applied to a galaxy or a cluster distribution,
with two-point mean separation defined by r (Peebles 1980). For an isotropic and homogenous field, the correlation function is defined as the
excess of probability for a density field described by a Poisson distribution. Therefore, the probability of finding two points in a volume
,
applied to a galaxy or a cluster distribution,
with two-point mean separation defined by r (Peebles 1980). For an isotropic and homogenous field, the correlation function is defined as the
excess of probability for a density field described by a Poisson distribution. Therefore, the probability of finding two points in a volume
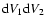 ,
separated
by a distance r12 is given by:
,
separated
by a distance r12 is given by:
![\begin{displaymath}%
{\rm d}P = n^2{\rm d}V_1{\rm d}V_2\left[1 + \xi(r_{12})\right].
\end{displaymath}](/articles/aa/full/2006/38/aa5581-06/img39.gif) |
(6) |
Describing the fluctuation field in Fourier modes, we have:
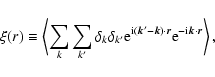 |
(7) |
which is equivalent, in a continuous space, to:
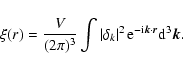 |
(8) |
For a Gaussian random field, the n-dimensional probability density function can
be estimated from the Fourier transform of the characteristic function
(Eqs. (1) and (2)) defined for the moment distribution of s
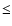 2:
2:
![$\displaystyle P^G[\delta_1,\delta_2 ... \delta_n]
=\frac{1}{(2\pi)^n} \int_{0}^...
...ft[-{\rm i}\displaystyle
\sum_{\alpha=1}^{n} u_{\alpha}\delta_{\alpha}\right]}.$](/articles/aa/full/2006/38/aa5581-06/img43.gif) |
|
|
(9) |
The expression above can be reduced to:
![$\displaystyle P^G[\delta_1,\delta_2 ... \delta_n]~~=~~\frac{1}{(2\pi)^{\frac{n}...
...elta_{\alpha})\right]
\left[ \delta_{\beta}-K_1(\delta_{\beta})\right] \right],$](/articles/aa/full/2006/38/aa5581-06/img44.gif) |
|
|
(10) |
where
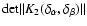 and
and
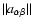 are the determinant and the inverse of the
correlation matrix respectively.
are the determinant and the inverse of the
correlation matrix respectively.
For a bidimensional Gaussian fluctuation field with zero mean, the correlation matrix can
be obtained and inverted, resulting in:
![\begin{displaymath}%
P^G[\delta_1,\delta_2] = \frac{1}{2\pi\sigma^2}\left(\frac{1}{1-A^2}\right)^\frac{1}{2}{\rm e}^{-Q[\delta_1,\delta_2]},
\end{displaymath}](/articles/aa/full/2006/38/aa5581-06/img47.gif) |
(11) |
where
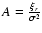 ,
for:
,
for:
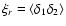 ,
,
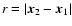 ,
,
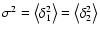 ,
and:
,
and:
![\begin{displaymath}%
Q= \frac{1}{2} \left(
\frac{1}{1-A^2}\right)\frac{1}{\sigma^2}\left[\delta_1^2+\delta_2^2-2A\delta_1\delta_2 \right],
\end{displaymath}](/articles/aa/full/2006/38/aa5581-06/img52.gif) |
(12) |
where 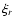 is equal to
is equal to
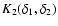 ,
the mean correlation function for a Gaussian field.
,
the mean correlation function for a Gaussian field.
To find the correlation function between high density peaks, we calculate the probability of
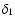 and
and
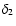 exhibiting density
values that are higher than the variance field
exhibiting density
values that are higher than the variance field
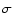 ,
by a factor
,
by a factor
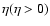 .
For a Gaussian field, this probability is given by the integral (Padmanabhan 1999):
.
For a Gaussian field, this probability is given by the integral (Padmanabhan 1999):
![\begin{displaymath}%
P^G[\delta_1 >\eta\sigma, \delta_2 >\eta\sigma] =
\int_{\e...
..._{\eta\sigma}^{\infty}{\rm d}\delta_2P^{G}[\delta_1,\delta_2].
\end{displaymath}](/articles/aa/full/2006/38/aa5581-06/img56.gif) |
(13) |
The integral above can be obtained by substituting Eqs. (9) into (13). For a weakly correlated field, where
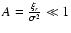 ,
and high density peaks,
,
and high density peaks,
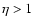 ,
the integral above will be
,
the integral above will be
![$\displaystyle P^G[\delta_1 >\eta\sigma, \delta_2 >\eta\sigma]=
\int_{\eta\sigma...
...ma}\right)F^{p+1}\left(\frac{\delta_2}{\sigma}\right)
\right]\frac{(2A)^p}{p!},$](/articles/aa/full/2006/38/aa5581-06/img59.gif) |
|
|
(14) |
where F is the Err function (erf):
![\begin{displaymath}%
F^{p+1}(Z)= \frac{(-{\rm i})^p}{2\pi}
\int_{-\infty}^{\inft...
...ft[ -{\rm i} \lambda z -\frac{z^2}{2} \right]} {\rm d}\lambda.
\end{displaymath}](/articles/aa/full/2006/38/aa5581-06/img60.gif) |
(15) |
The final result is
![\begin{displaymath}%
P^G[\delta_1 >\eta\sigma, \delta_2 >\eta\sigma] =
\left[\fr...
...c{1}{\eta} {\rm e}^{-\frac{\eta^2}{2}}\right]^2 (1 +2A\eta^2).
\end{displaymath}](/articles/aa/full/2006/38/aa5581-06/img61.gif) |
(16) |
Redefining expression 16, the probability of finding peaks 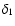 and
and 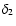 with density
with density 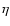 times the variance,
times the variance, 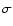 ,
is
,
is
![\begin{displaymath}%
P^G[\delta_1 >\eta\sigma, \delta_2 >\eta\sigma] \equiv
[P^G(\delta>\eta\sigma)]^2 [1 + \xi_{\eta}^G(r)],
\end{displaymath}](/articles/aa/full/2006/38/aa5581-06/img66.gif) |
(17) |
where
![$[P^G[\delta>\eta\sigma)]]^2$](/articles/aa/full/2006/38/aa5581-06/img67.gif) is the mean probability of finding high density peaks in a bi-dimensional random field, and
is the mean probability of finding high density peaks in a bi-dimensional random field, and
![$[1 + \xi_{\eta}^G(r)]$](/articles/aa/full/2006/38/aa5581-06/img68.gif) is the probability excess expressed in terms of the mean correlation function,
is the probability excess expressed in terms of the mean correlation function, 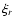 .
Then, for weakly correlated fields:
.
Then, for weakly correlated fields:
![\begin{displaymath}%
\xi_\eta^G(r) \equiv 2A\eta^2 \approx {\rm e}^{2A\eta^2}-1 = \exp\left[2\left(\frac{\eta}{\sigma}
\right)^2\xi_r\right]-1.
\end{displaymath}](/articles/aa/full/2006/38/aa5581-06/img69.gif) |
(18) |
The correlation function of high density peaks in a non-Gaussian field can also be computed
using Eq. (13), except that we have to consider the non-Gaussian probability of finding
both peaks 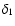 and
and 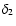 ,
the
,
the
![$P^{\rm NG}[\delta_1,\delta_2]$](/articles/aa/full/2006/38/aa5581-06/img70.gif) .
This probability can be
estimated using Eq. (9), performing the sum over terms of order higher than 2. Since the
summation is also computed for additional terms, the result can be synthesized by:
.
This probability can be
estimated using Eq. (9), performing the sum over terms of order higher than 2. Since the
summation is also computed for additional terms, the result can be synthesized by:
![\begin{displaymath}%
P^{\rm NG}[\delta_1 >\eta\sigma, \delta_2 >\eta\sigma]\! = ...
...
\left[1 \!+\! \xi_{\eta}^G(r)\!+\! C_{\eta}^{\rm NG}\right],
\end{displaymath}](/articles/aa/full/2006/38/aa5581-06/img71.gif) |
(19) |
which results in:
![\begin{displaymath}%
P^{\rm NG}[\delta_1 >\eta\sigma, \delta_2 >\eta\sigma] =
\...
...^{-\frac{\eta^2}{2}}\right]^2 (1 +2A\eta^2+C_{\eta}^{\rm NG}),
\end{displaymath}](/articles/aa/full/2006/38/aa5581-06/img72.gif) |
(20) |
where the factor
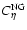 carries the corrections terms of higher order (s
carries the corrections terms of higher order (s
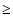 3).
3).
One intriguing question we could ask is how important the high-order residual terms for
slightly non-Gaussian statistics are. First, we could consider the approximated case
in which the extra calculation in Eq. (9) was avoided, so correlation terms of order (s
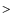 2) could be neglected (
2) could be neglected (
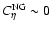 )
and the non-Gaussian
peak-peak correlation function would be reduced to:
)
and the non-Gaussian
peak-peak correlation function would be reduced to:
![\begin{displaymath}%
\xi_\eta^{\rm NG}(r) \approx \exp \left[2\left(\frac{\eta}{\sigma}\right)^2\xi_r^{\rm NG}\right]-1.
\end{displaymath}](/articles/aa/full/2006/38/aa5581-06/img76.gif) |
(21) |
This solution is similar to the calculation for a Gaussian random field, except that we were considering a non-Gaussian mean correlation function.
At this point we want to assess the robustness of the assumption
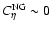 ,
stated in the previous paragraph. For this purpose, we compute the higher order correction terms
considering a slightly non-Gaussian component, which means a very small contribution to
correlations of order greater than two. However, the non-Gaussian probability described in
Eq. (9) cannot be calculated using the Fourier transform of the characteristic function, since there is no analytical
solution for that expression. One possible way to obtain
,
stated in the previous paragraph. For this purpose, we compute the higher order correction terms
considering a slightly non-Gaussian component, which means a very small contribution to
correlations of order greater than two. However, the non-Gaussian probability described in
Eq. (9) cannot be calculated using the Fourier transform of the characteristic function, since there is no analytical
solution for that expression. One possible way to obtain
![$P^{\rm NG}[\delta_1,\delta_2]$](/articles/aa/full/2006/38/aa5581-06/img70.gif) ,
as
suggested by Gnedenko & Kolmogorov (1968), is to expand it in a series of generalized Hermite polynomials, H:
,
as
suggested by Gnedenko & Kolmogorov (1968), is to expand it in a series of generalized Hermite polynomials, H:
![$\displaystyle P^{\rm NG}[\delta_1,\delta_2 ...\delta_n]= P^G[\delta_1,\delta_2....
...\omega)H_{\alpha,\beta...\omega}\left[\delta -\kappa_1 (\delta) \right]\right],$](/articles/aa/full/2006/38/aa5581-06/img77.gif) |
|
|
(22) |
where bs is the quasi-moment function and
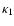 the first
cumulant of the distribution. The definitions of bs and H are given in Appendix A.
By Eq. (22), the non-Gaussian probability is expressed in terms of a Gaussian
probability added to higher order
the first
cumulant of the distribution. The definitions of bs and H are given in Appendix A.
By Eq. (22), the non-Gaussian probability is expressed in terms of a Gaussian
probability added to higher order 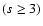 correction terms, which are related to the
deviation from Gaussianity. Combining Eqs. (13), (19), and (22), we can estimate the higher-order correction term for a bi-dimensional using the following:
correction terms, which are related to the
deviation from Gaussianity. Combining Eqs. (13), (19), and (22), we can estimate the higher-order correction term for a bi-dimensional using the following:
![$\displaystyle C^{\rm NG}_{\eta}~~=~~\int_{\eta\sigma}^{\infty} \int_{\eta\sigma...
...a,\delta_\beta)H_{\alpha,\beta}\left[\delta
-\kappa_1 (\delta) \right] \right].$](/articles/aa/full/2006/38/aa5581-06/img80.gif) |
|
|
(23) |
Note that the calculation of
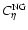 starts at s
starts at s
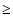 3, ensuring that the terms used in the expansion are related to the non-Gaussian contributions.
Details of the calculation involved in these higher order terms are also presented in Appendix A.
3, ensuring that the terms used in the expansion are related to the non-Gaussian contributions.
Details of the calculation involved in these higher order terms are also presented in Appendix A.
In order to estimate how the high-order terms affect the correlation between high-density
peaks, we estimated the
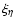 for a Gaussian and a slightly non-Gaussian field, computing
the approximated solutions (Eq. (21)) and the full calculation of the expansion (Eq. (22)) until
for a Gaussian and a slightly non-Gaussian field, computing
the approximated solutions (Eq. (21)) and the full calculation of the expansion (Eq. (22)) until 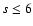 order. For this comparison, we have considered a mixed probability distribution, as proposed by Ribeiro et al. (2001), hereafter (RWL).
order. For this comparison, we have considered a mixed probability distribution, as proposed by Ribeiro et al. (2001), hereafter (RWL).
The general procedure to create a wide class of non-Gaussian models is to admit the
existence of an operator that transforms Gaussianity into non-Gaussianity according to
a specific rule. An alternative approach for studing non-Gaussian fields
was proposed by
RWL, in which the PDF is treated as a mixture:
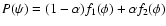 ,
where
,
where 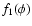 is a (dominant) Gaussian PDF and
is a (dominant) Gaussian PDF and 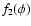 is a second distribution,
with
is a second distribution,
with
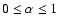 .
The
.
The 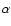 parameter gives the absolute level of Gaussian deviation,
while
parameter gives the absolute level of Gaussian deviation,
while 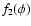 modulates the shape of the resultanting non-Gaussian distribution. RWL used this
mixed scenario to probe the evolution of galaxy cluster abundance in the universe and found
that even at a level of non-Gaussianity
modulates the shape of the resultanting non-Gaussian distribution. RWL used this
mixed scenario to probe the evolution of galaxy cluster abundance in the universe and found
that even at a level of non-Gaussianity
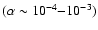 the mixed
field can introduce significant changes in the cluster abundance rate.
the mixed
field can introduce significant changes in the cluster abundance rate.
The effects of such mixed models in the CMBR power spectrum, combining a Gaussian adiabatic
field with a second non-Gaussian isocurvature fluctuation field to produce a positive skewness density field, was discussed by Andrade et al. (2004) (hereafter AWR04). In this
approach, they adopted a scale-dependent mixture parameter and a power-law
initial spectrum to simulate the CMBR temperature and polarization power spectra for a flat
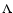 -CDM model, generating a large grid of cosmological-parameter
combination. The choice of a scale-dependent mixture is not unjustified, since it could
fit both CMB and high-z galaxy clustering in the Universe (e.g. AWR04; Avelino & Liddle 2004; Mathis et al. 2004). At the same time, in a mixed scenario, the scale-dependence acts in order to keep a continuously mixed field inside the Hubble horizon. Simulation results show how the shape and amplitude of the fluctuations in CMBR depend
upon such mixed fields and how a standard adiabatic Gaussian field can be distinguished
from a mixed non-Gaussian one. They also allow one to quantify the contribution of the
second component. By applying a
-CDM model, generating a large grid of cosmological-parameter
combination. The choice of a scale-dependent mixture is not unjustified, since it could
fit both CMB and high-z galaxy clustering in the Universe (e.g. AWR04; Avelino & Liddle 2004; Mathis et al. 2004). At the same time, in a mixed scenario, the scale-dependence acts in order to keep a continuously mixed field inside the Hubble horizon. Simulation results show how the shape and amplitude of the fluctuations in CMBR depend
upon such mixed fields and how a standard adiabatic Gaussian field can be distinguished
from a mixed non-Gaussian one. They also allow one to quantify the contribution of the
second component. By applying a 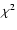 test to recent CMBR observations, the contribution
of the isocurvature field was estimated by Andrade et al. (2005) (hereafter AWR05) as
test to recent CMBR observations, the contribution
of the isocurvature field was estimated by Andrade et al. (2005) (hereafter AWR05) as
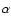 0 = 0.0004
0 = 0.0004
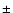 0.00030 with a 68% confidence limit. In the present work, we also investigate
the predictions of scale-dependent mixed non-Gaussian cosmological density fields for the
peak-peak correlation function.
0.00030 with a 68% confidence limit. In the present work, we also investigate
the predictions of scale-dependent mixed non-Gaussian cosmological density fields for the
peak-peak correlation function.
To obtain the mean correlation function, 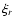 ,
we have computed the Fourier transform
of the power spectrum related to a pure Gaussian field and a mixed non-Gaussian PDF.
In this sense, we rewrite Eq. (8), which is equivalent to:
,
we have computed the Fourier transform
of the power spectrum related to a pure Gaussian field and a mixed non-Gaussian PDF.
In this sense, we rewrite Eq. (8), which is equivalent to:
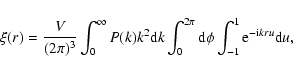 |
(24) |
where
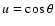 .
For an isotropic field, we have:
.
For an isotropic field, we have:
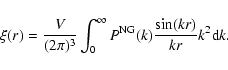 |
(25) |
For the mixture correlation function, we consider a mixed-scale power spectrum described as:
![\begin{displaymath}%
P^{Mix}(k)=A_{n}P(k)[1+M(\alpha_0)k] = \beta k^n[1+M(\alpha_0)k].
\end{displaymath}](/articles/aa/full/2006/38/aa5581-06/img97.gif) |
(26) |
This power spectrum was estimated by the correlated mixed-model that considers a possible
mixture, inside the horizon, between fluctuations of an adiabatic Gaussian field and an isocurvature non-Gaussian one (AWR04). In this model, 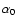 is the mixture parameter
that modulates the contribution of the isocurvature field (
is the mixture parameter
that modulates the contribution of the isocurvature field (
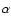
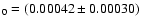 )
as estimated from recent CMB observations.
For a null
)
as estimated from recent CMB observations.
For a null 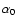 ,
the field is purely Gaussian with a simple
power- law spectrum, and An is the normalization constant of the primordial power spectrum, estimated as
,
the field is purely Gaussian with a simple
power- law spectrum, and An is the normalization constant of the primordial power spectrum, estimated as 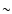 1.3
1.3 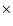 10-11 for recent CMBR observations (AWR05).
10-11 for recent CMBR observations (AWR05).
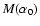 is the mixed term, which accounts for the statistical effects of the second component in the power spectrum,
expressed as a functional of both distributions,
is the mixed term, which accounts for the statistical effects of the second component in the power spectrum,
expressed as a functional of both distributions,
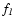 and
and
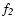 :
:
![\begin{displaymath}%
M^{\rm mix}(\alpha_0,k)\equiv\int_\nu[(1-\alpha_0k)f_1(\nu)+\alpha_0kf_2(\nu)]\nu^2\; {\rm d}\nu.
\end{displaymath}](/articles/aa/full/2006/38/aa5581-06/img104.gif) |
(27) |
Evaluating the integral in Eq. (25) for a mixed power spectrum, we find an expression
for the mean correlation function:
![\begin{displaymath}%
\xi^{\rm Mix}(R)=A_{n}\left[\frac{1.76\times 10^{-2}}{3\pi
...
...0^{-4}M(\alpha_0)}{3\pi \left(\frac{R}{R_0}\right)^2} \right],
\end{displaymath}](/articles/aa/full/2006/38/aa5581-06/img105.gif) |
(28) |
where R0 is about 25 Mpc, the mean correlation width for galaxy clusters.
In Fig. 1, we show the mean correlation function estimated for (i) a purely Gaussian field,
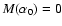 ,
(ii) for a mixed PDF,
,
(ii) for a mixed PDF,
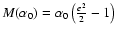 ,
and also (iii) the individual contribution of the non-Gaussian field for
,
and also (iii) the individual contribution of the non-Gaussian field for
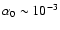 .
In this plot, it is possible to observe the importance of even a small contribution of the second component to the mean correlation function. For
.
In this plot, it is possible to observe the importance of even a small contribution of the second component to the mean correlation function. For
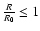
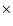 10-3
the non-Gaussian component dominates the correlation function. This behavior illustrates
the excess of power on small scales, as observed on the CMB angular
power spectrum in the mixed context (AWR04).
10-3
the non-Gaussian component dominates the correlation function. This behavior illustrates
the excess of power on small scales, as observed on the CMB angular
power spectrum in the mixed context (AWR04).
![\begin{figure}
\par\includegraphics[height=5.55cm,width=7.5cm,clip]{5581fig1.eps}\end{figure}](/articles/aa/full/2006/38/aa5581-06/Timg109.gif) |
Figure 1:
The mean two-point correlation function estimated for
non-correlated or weakly correlated fields: pure Gaussian, pure log-normal and, mixed field with
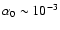 . . |
| Open with DEXTER |
Inserting the mean correlation function described in Eq. (28)
into the approximated expression of the correlation function for high
density peaks (Eq. (21)) for a few classes of PDFs, we estimate
the functions 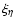 plotted in Fig. 2. In this plot,
we show that the effect of the second component is still observed and
that the correlation function for high density peaks is also sensitive
for different non-Gaussian distributions. Comparing Figs. 1 and 2,
we see how the high density peaks can be much more correlated than the
mean field for a non-Gaussian case, especially on small scales,
plotted in Fig. 2. In this plot,
we show that the effect of the second component is still observed and
that the correlation function for high density peaks is also sensitive
for different non-Gaussian distributions. Comparing Figs. 1 and 2,
we see how the high density peaks can be much more correlated than the
mean field for a non-Gaussian case, especially on small scales,
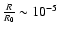 ,
where
,
where
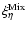 is nearly two orders of magnitude greater than the mean correlation.
is nearly two orders of magnitude greater than the mean correlation.
![\begin{figure}
\par\includegraphics[height=5.55cm,width=7.5cm,clip]{5581fig2.eps}\end{figure}](/articles/aa/full/2006/38/aa5581-06/Timg113.gif) |
Figure 2:
The two-point correlation function computed for 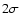 density peaks
in both a pure Gaussian and mixed context ( density peaks
in both a pure Gaussian and mixed context (
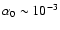 ). For this estimation,
we used: ). For this estimation,
we used:
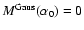 ; ;
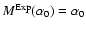 ; ;
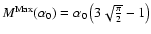 ; ;
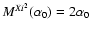 and
and
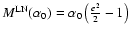 . . |
| Open with DEXTER |
With the help of a program that performs algebraic and numerical calculations, we actually computed
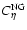 ,
as indicated in Eq. (23), for correlations
up to the 6-th order (
,
as indicated in Eq. (23), for correlations
up to the 6-th order (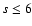 ). This limit was set in order to keep a meaningful
non-Gaussian distortion, avoiding more time-consuming calculations. We
do not present the full computed expression in this
section since it contains hundreds of non-linear terms in the
mean correlation function
). This limit was set in order to keep a meaningful
non-Gaussian distortion, avoiding more time-consuming calculations. We
do not present the full computed expression in this
section since it contains hundreds of non-linear terms in the
mean correlation function 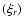 and
and 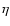 ,
where the coefficients are
the high-order correlations (or cumulants). In fact, the
,
where the coefficients are
the high-order correlations (or cumulants). In fact, the
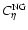 is
more accurately described as
is
more accurately described as
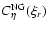 .
In Appendix A, we
show the steps in calculating the quasi-moment function, blm, and
the Hermite polynomials, Hlm.
.
In Appendix A, we
show the steps in calculating the quasi-moment function, blm, and
the Hermite polynomials, Hlm.
![\begin{figure}
\par\includegraphics[height=5.45cm,width=7.55cm,clip]{5581fig3a.e...
...mm}
\includegraphics[height=5.45cm,width=7.55cm,clip]{5581fig3b.eps}\end{figure}](/articles/aa/full/2006/38/aa5581-06/Timg117.gif) |
Figure 3:
The behavior of the higher order factor,
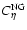 ,
for
a fixed mean correlation ( ,
for
a fixed mean correlation (
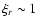 ). The curves in A) show the factor
estimated for third-order correlation, ). The curves in A) show the factor
estimated for third-order correlation,
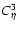 ,
fourth, ,
fourth,
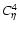 ,
and fifth, ,
and fifth,
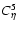 .
In B) the sixth-order factor, .
In B) the sixth-order factor,
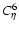 ,
is also plotted. ,
is also plotted. |
| Open with DEXTER |
In general, correlations of a very high order tend to zero (Gnedenko & Kolmogorov 1968), the most extreme case being the normal distribution, where all cumulants of 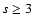 are null. Deviations from Gaussianity are set by the increment of non-vanishing cumulants in the expansion of
are null. Deviations from Gaussianity are set by the increment of non-vanishing cumulants in the expansion of
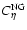 .
A possible question that may be raised is related to the convergence and normalization of the expansion in Eq. (23) in which some terms are set as non-vanishing. However, investigation
of general nearly Gaussian deviations have already been performed by the use of the Edgeworth
expansion in one-dimension by setting the function to zero in higher-order terms
and normalizing it appropriately (Martinez-Gonzalez et al. 2002). Following these authors, we have considered the following behavior as a working
hypothesis for such coefficients: we set the terms
.
A possible question that may be raised is related to the convergence and normalization of the expansion in Eq. (23) in which some terms are set as non-vanishing. However, investigation
of general nearly Gaussian deviations have already been performed by the use of the Edgeworth
expansion in one-dimension by setting the function to zero in higher-order terms
and normalizing it appropriately (Martinez-Gonzalez et al. 2002). Following these authors, we have considered the following behavior as a working
hypothesis for such coefficients: we set the terms 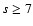 to zero and the cumulants involved in the quasi moment function to 10-3 for
to zero and the cumulants involved in the quasi moment function to 10-3 for
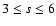 .
.
One very interesting result is summarized in Fig. 3. In order to follow the absolute behavior of the corrections terms in the nearly Gaussian field, we set the normalization value of the mean correlation function to one,
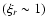 and explore the
and explore the 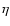 dependence of
dependence of
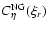 with the purpose of understanding
how the amplitude of the fluctuations is related to the high-order correlations.
While computing only third-order terms, the
with the purpose of understanding
how the amplitude of the fluctuations is related to the high-order correlations.
While computing only third-order terms, the
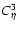 describes a gradual enhancement
in the correlation function. For fourth and sixth-order terms, the
describes a gradual enhancement
in the correlation function. For fourth and sixth-order terms, the
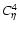 and
and
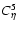 ,
what is observed, in the case of small
Gaussian deviationis, is that the
,
what is observed, in the case of small
Gaussian deviationis, is that the
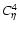 and
and
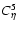 just overlap each other, meaning that the fifth-order correlations do not contribute significantly.
However, the fourth-order correlation describes peaks of maximum density allowed by a weakly
correlated field at about
just overlap each other, meaning that the fifth-order correlations do not contribute significantly.
However, the fourth-order correlation describes peaks of maximum density allowed by a weakly
correlated field at about
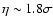 .
For higher order correlations, the
.
For higher order correlations, the
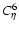 shows a very large increment in the two-point correlation
for densities of about
shows a very large increment in the two-point correlation
for densities of about 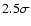 and a nearly null contribution to peaks with amplitudes (
and a nearly null contribution to peaks with amplitudes (
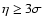 ).
).
We conclude that one should not expect very high density peaks for the specified,
slightly non-Gaussian, correlated field. However, factors of order
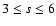 ,
are quite significant for peaks with amplitude up to
,
are quite significant for peaks with amplitude up to 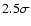 and are too far from a null correction, even if we consider weakly correlated fields.
Then, we cannot consider the simplified solution in Eq. (21) as a good
description of the two-point correlation function for high density
peaks despite our choice of considering only a small deviation from Gaussianity.
It is important to note that this result is independent of the power spectrum or the mean
correlation function. It only shows the influence of higher order
correlations in the amplitude of the field of fluctuations.
and are too far from a null correction, even if we consider weakly correlated fields.
Then, we cannot consider the simplified solution in Eq. (21) as a good
description of the two-point correlation function for high density
peaks despite our choice of considering only a small deviation from Gaussianity.
It is important to note that this result is independent of the power spectrum or the mean
correlation function. It only shows the influence of higher order
correlations in the amplitude of the field of fluctuations.
Analyzing the relation between 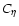 and
and 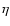 ,
we gain
some insight into the amplitude of such high-order terms, since
,
we gain
some insight into the amplitude of such high-order terms, since
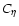 controls the amplitude of the permitted peaks in the fluctuations
field. Increasing values of correlations with s > 6 imply a high
probability of very high-amplitude (very rare) peaks, which contradict the observations of large-scale structures. However,
when we impose correlation levels of the order 10-3 up to sixth order, we
favor the existence of peaks up to
controls the amplitude of the permitted peaks in the fluctuations
field. Increasing values of correlations with s > 6 imply a high
probability of very high-amplitude (very rare) peaks, which contradict the observations of large-scale structures. However,
when we impose correlation levels of the order 10-3 up to sixth order, we
favor the existence of peaks up to 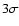 ,
which is very reasonable for a nearly Gaussian field.
,
which is very reasonable for a nearly Gaussian field.
In Fig. 4 we show the behavior of the two-point correlation
function estimated for a Gaussian,
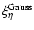 ;
for a mixed approximated
solution,
;
for a mixed approximated
solution,
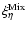 ,
and for the non-Gaussian complete
solution,
,
and for the non-Gaussian complete
solution,
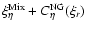 . In this plot, we set the amplitude threshold of
. In this plot, we set the amplitude threshold of
 and test the dependence
on
and test the dependence
on  .
The observed effect of
.
The observed effect of
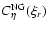 is to
amplify the correlations between high density peaks. This result is
valid for the case of an increasing mean correlation function and does
not depend on the mixed model. While non-Gaussian deviation tends
to add non-vanish high-order correlations, we conclude that we can
expect high-density peaks to be much more correlated even in a slightly non-Gaussian model.
is to
amplify the correlations between high density peaks. This result is
valid for the case of an increasing mean correlation function and does
not depend on the mixed model. While non-Gaussian deviation tends
to add non-vanish high-order correlations, we conclude that we can
expect high-density peaks to be much more correlated even in a slightly non-Gaussian model.
![\begin{figure}
\par\includegraphics[height=5.45cm,width=7.1cm,clip]{5581fig4.eps}\end{figure}](/articles/aa/full/2006/38/aa5581-06/Timg128.gif) |
Figure 4:
The behavior of the two-point correlation
function is shown for three estimated cases: a pure Gaussian,
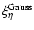 (lower curve); a mixed approximated solution,
(lower curve); a mixed approximated solution,
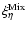 with
with
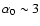 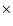 10-3 (mid curve); and for the complete non-Gaussian solution,
10-3 (mid curve); and for the complete non-Gaussian solution,
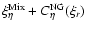 ,
estimated for a PDF of the type: (Gauss + Exp) with ,
estimated for a PDF of the type: (Gauss + Exp) with
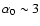 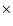 10-3 10-3 |
| Open with DEXTER |
In this work, we have estimated the two-point mean correlation function
and the peak-peak correlation function for the density field.
In the Gaussian case, the calculations are simplified,
since the Fourier transform of the power spectrum describes
the random variable completely. However, for a non-Gaussian field, the
calculations are much more complicated, since high-order correlations
between these two-points may not vanish and strongly contribute to the final
function, even in a small deviation from the Gaussian case.
In this work, we showed that, when considering a mixed model, both the mean correlation and
the peak-peak correlation functions are much more intense on small scales than in the Gaussian case. This result can be particularly relevant since it is generally accepted that galaxies form in high-density regions. In addition, we conclude that the peak-peak correlation function is quite sensitive to the PDF of the fluctuations field, especially for a mixed model. This result suggests that it is possible to use the
peak-peak correlation function as a test of the nature of cosmic structures.
Nevertheless, we have to be careful when approximating terms for
high-order correlations, since the peak-peak correlation function is
very sensitive to the correction terms. We also point out that
correlations of order
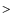 2 can be a very important tool
for characterizing non-Gaussian fields, and they definitely deserve deeper
investigation. Estimating high order correlations allows us to investigate the behavior of the N-point correlation function, as well as gather more information about the amplitude of the expected high-density fluctuation
field. As seen in Fig. 3, correlations may restrict the amplitude of the density peaks. Furthermore, from the amplitude of the peaks found in the density field (in CMB or LSS fluctuations), we are able to extract more information about the statistics of the density field. It is also
good to remember that the presence of correlations of order
2 can be a very important tool
for characterizing non-Gaussian fields, and they definitely deserve deeper
investigation. Estimating high order correlations allows us to investigate the behavior of the N-point correlation function, as well as gather more information about the amplitude of the expected high-density fluctuation
field. As seen in Fig. 3, correlations may restrict the amplitude of the density peaks. Furthermore, from the amplitude of the peaks found in the density field (in CMB or LSS fluctuations), we are able to extract more information about the statistics of the density field. It is also
good to remember that the presence of correlations of order 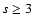 lead to formation of structures in earlier times than would be expected for a model with the same power spectrum but with weaker spatial correlations. The results
presented in this paper may be used to set new constraints in structure formation models.
lead to formation of structures in earlier times than would be expected for a model with the same power spectrum but with weaker spatial correlations. The results
presented in this paper may be used to set new constraints in structure formation models.
One possible application of this method in investigations of primordial
non-Gaussianity could be implemented in the search for maximum-amplitude
fluctuations of the full sky CMB temperature maps, such those derived from WMAP (Spergel et al. 1989) and the future Planck mission (Wright 2000). However, variations in the
number of density peaks and their correlation could as well be related to
non-Gaussian Galactic foregrounds or other contaminants. Once such a non-Gaussian trace has detected, we have to be very careful before assigning it a primordial origin. To avoid misunderstanding, the investigation of the peak statistics in CMB datasets should be realized over
several datasets and different frequencies. Indeed, one possible manner to
minimize the foregrounds effects is to analyze the most sensitive and
cleaned map, such as the WMAP three-year di-biased internal linear combination,
WMAP-DILC map, or the WMAP coadded map, with the combination of Q+V+W frequencies.
This analysis will be the next test applied to the non-Gaussian mixed model.
Acknowledgements
APAA thanks FAPESB and CNPq for the financial support under grant 1431030005400. ALBR thanks CNPq for the financial support under grants 470185/2003-1 and 306843/2004-8.
CAW was partially supported by the CNPq grant 307433/2004-8.
To obtain the non-Gaussian probability for a multi-dimensional case, we have to
perform the calculation in Eq. (22) by expanding the Hermite polynomials and
the quasi-moment function. One possible way to obtain the quasi-moment functions,
bs, is by relating to the correlation function, since:
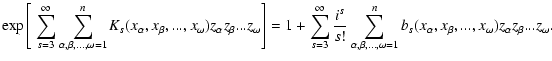 |
|
|
(A.1) |
The generalized Hermite polynomials can be obtained by the definition
![$\displaystyle %
H_{\alpha\beta...\omega}[x]= {\rm e}^{\phi[x]}\left(
-\frac{\pa...
...right)...\left(
-\frac{\partial}{\partial x_{\omega}}\right){\rm e}^{-\phi[x]},$](/articles/aa/full/2006/38/aa5581-06/img130.gif) |
|
|
(A.2) |
where:
![$\phi[x]=\frac{1}{2}\sum_{\alpha,\beta=1}^{n}a_{\alpha\beta}x_{\alpha}x_{\beta}$](/articles/aa/full/2006/38/aa5581-06/img131.gif) ,
with
,
with
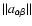 the elements of the inverse correlation matrix
the elements of the inverse correlation matrix
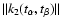 .
The unidimensional case of Eq. (24) is known as
the Edgeworth series, while the bidimensional case corresponds to:
.
The unidimensional case of Eq. (24) is known as
the Edgeworth series, while the bidimensional case corresponds to:
![$\displaystyle P^{NG}[\delta_1,\delta_2]=
\left[1+ \displaystyle \sum_{s=3}^{\in...
...a-\kappa_1\left(\delta\right)\right]\right]P^{G}\left[\delta_1,\delta_2\right],$](/articles/aa/full/2006/38/aa5581-06/img134.gif) |
|
|
(A.3) |
where
![$b_{lm}= b_{l+m}[\underbrace {\delta_1 \cdots
\delta_1}_{l \ \textrm{times} }; \underbrace {\delta_2 \cdots \delta_2}_{m \
\textrm {times}}]$](/articles/aa/full/2006/38/aa5581-06/img135.gif) ,
,
and
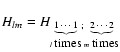 .
.
Performing the calculations for the quasi-moment function, we have
Note that the first five terms of bs are equivalent to the correlation function,
only the sixth term has additional terms. As an example, for s = 3, we obtain four different
forms of b3:
Proceeding in a similar manner, we find five terms for b4, six for b5,
and seven terms for b6.
The best way to find the Hermite polynomials is using expression (Gnedenko & Kolmogorov 1968)
![\begin{displaymath}%
y_\alpha=y_\alpha[x]=\frac{\partial \phi[x]}{\partial
x_\alpha}=\sum_{\beta=1}^{n}a_{\alpha\beta}x_\beta, %
\end{displaymath}](/articles/aa/full/2006/38/aa5581-06/img145.gif) |
(A.4) |
where:
where we used the notation
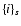 to indicate a simetrization set.
to indicate a simetrization set.
To perform the calculation above for blm and Hlm up to (l+m = 6)and perform the integration in 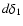 and
and 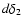 ,
we used a software for
algebraic and numerical calculations.
,
we used a software for
algebraic and numerical calculations.
- Allen, T. J. Grinstein, B.,
& Wise, M. B. 1987, Phys. Lett. B, 197, 66 [NASA ADS] (In the text)
- Andrade, A. P. A., Wuensche, C.
A., & Ribeiro, A. L. B. 2004, ApJ, 602, 555 [NASA ADS] [CrossRef] (In the text)
- Andrade, A. P. A., Wuensche, C.
A., & Ribeiro, A. L. B. 2005, PRD, 71, 043501 [NASA ADS] (In the text)
- Avelino, P. P., & Liddle,
A. R. 2004, MNRAS, 348, 105 [NASA ADS] [CrossRef] (In the text)
- Bardeen, J. M., Bond, J. R.,
Kaiser, N., & Szalay, A. S. 1986, ApJ, 304, 15 [NASA ADS] [CrossRef] (In the text)
- Battye, R. A., & Weller,
J. 2000, PRD, 61, 043501 [NASA ADS] (In the text)
- Bond, J. R., &
Efstathiou, G. 1987, MNRAS, 226, 655 [NASA ADS] (In the text)
- Cabella, P., et al. 2004,
Phys. Rev. D, 69, 063007 [NASA ADS] [CrossRef] (In the text)
- Chiang, L., Naselsky, P. D.,
Verkhodanov, O. V., & Way, M. J. 2003, ApJ, 590, L65 [NASA ADS] [CrossRef] (In the text)
- Coles, P., Dineen, P., Earl,
J., & Wright, D. 2004, MNRAS, 350, 989 [NASA ADS] [CrossRef] (In the text)
- Coles, P., & Jones, B.
1991, MNRAS, 248, 1 [NASA ADS] (In the text)
- Creminelli, P., et al. 2005
[arXiv:astro-ph/059029]
(In the text)
- De Troia, G., Ade, P. A. R.,
Bock, J. J., et al. 2003, MNRAS, 343, 284 [NASA ADS] [CrossRef] (In the text)
- Eriksen, H. K., Banday, A.
J., Górski, K. M., & Lilje, P. B. 2005, ApJ, 622, 58 [NASA ADS] [CrossRef] (In the text)
- Eriksen, H. K., Banday, A.
J., & Gorski, K. M. 2002, A&A, 395, 409 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Frith, W. J., Outram, P. J.,
& Shanks, T. 2005, MNRAS [arXiv:astro-ph/0507704]
(In the text)
- Fry, J. N. 1985, ApJ, 289,
10 [NASA ADS] [CrossRef] (In the text)
- Gangui, A., Lucchin, F.,
Matarrese, S., & Mollerach, S. 1994, ApJ, 430, 447 [NASA ADS] [CrossRef] (In the text)
- Gaztanaga, E., & Wagg, J.
2004, Phys. Rev. D, 68, 021302 [NASA ADS] [CrossRef] (In the text)
- Gnedenko, B. V., &
Kolmogorov, A. N. 1968, Limit Distributions for Sums of Independent
random variables, Addison-Wesley
(In the text)
- Guth, A. H., & Pi, S. Y.
1982, PRL, 49, 1110 [NASA ADS] [CrossRef] (In the text)
- Hanses, F. K., Cabella, P.,
Marinucci, D., & Vittorio, N. 2004, ApJ, 607, L67 [NASA ADS] [CrossRef] (In the text)
- Heavens, A. F., & Sketh,
R. K. 1999, MNRAS, 310, 1062 [NASA ADS] [CrossRef] (In the text)
- Heavens, A. F., & Gupta,
S. 2001, MNRAS, 324, 960 [NASA ADS] [CrossRef] (In the text)
- Kibble, T. W. B. 1976, J.
Physics A, 9, 1387 [NASA ADS] (In the text)
- Komatsu, E., et al. 2003,
ApJ, 148, 119 [NASA ADS] [CrossRef] (In the text)
- Komatsu, E., Spergel, D. N.,
& Wandelt, B. D. 2005, ApJ, 634, 14 [NASA ADS] [CrossRef] (In the text)
- Larson, D. L., & Wandelt,
B. D. 2005 [arXiv:astro-ph/0505046]
(In the text)
- Lewin, A., Albrecht, A.,
& Magueijo, J. 1999, MNRAS, 302, 131 [NASA ADS] [CrossRef] (In the text)
- Magueijo, J., &
Brandenbergher, R. 2000, in Lecture notes of the International
School on Cosmology, Kish Island, Iran, to be publ. in Large Scale
Structure Formation, ed. R. Mansouri, & R. Brandenberger
(Kluwer). Also [arXiv:astro-ph/0002030]
(In the text)
- Mathis, H., Diego, J. M.,
& Silk, J. 2004, MNRAS, 353, 681 [NASA ADS] [CrossRef] (In the text)
- Martinez-Gonzalez 2002,
MNRAS, 336, 22 [NASA ADS] [CrossRef] (In the text)
- McEwen, J. D. 2004, MNRAS,
359, 1583 [NASA ADS] [CrossRef]
- Mukherjee, P., & Wang, Y.
2004, ApJ, 613, 51 [NASA ADS] [CrossRef] (In the text)
- Naselsky, P., et al. 2005,
PRD [arXiv:astro-ph/0505011]
(In the text)
- Novikov, D., Feldman, H. A.,
& Shandarin, S. F. 1999, Int. J. Mod. Phys. D, 8, 291 [NASA ADS] (In the text)
- Padmanabhan, T. 1999, in
Lectures notes of the International School on Cosmology, Kish
Island, to be publ. in Large Scale Structure Formation, ed. R.
Mansouri, & R. Brandenberger (Kluwer). Also
[arXiv:astro-ph/9911374]
(In the text)
- Peebles, P. J. E. 1980, The
Large Scale Structure of the Universe
(In the text)
- Peebles, P. J. E. 2001
[arXiv:astro-ph/0103040]
(In the text)
- Ribeiro, A. L. B., Wuensche, C.
A., & Letelier, P. S. 2000, ApJ, 539, 1 [NASA ADS] [CrossRef] (In the text)
- Salopek, D. S., Bond, J. R.,
& Bardeen, J. M. 1989, PRD, 40, 1753 [NASA ADS] (In the text)
- Spergel, et al. 2006, ApJ
[arXiv:astro-ph/0603449]
(In the text)
- Takada, M., & Jain, B.
2003, MNRAS, 340, 580 [NASA ADS] [CrossRef] (In the text)
- Tojeiro, R., et al. 2005, MNRAS
[arXiv:astro-ph/0507096]
(In the text)
- Verde, L., & Heavens, A. F.
2001, ApJ, 553, 14 [NASA ADS] [CrossRef] (In the text)
- Verde, L., Jimenez, R.,
Kamionkowski, M., & Matarrese, S. 2001, MNRAS, 325, 412 [NASA ADS] [CrossRef] (In the text)
- Vielva, P., et al. 2004, ApJ,
609, 22 [NASA ADS] [CrossRef] (In the text)
- Wright, E. L. 2000, IAU Symp.
204, Manchester, England
(In the text)
Copyright ESO 2006
![\begin{displaymath}%
P[\delta]=\frac{1}{2\pi}\int_{-\infty}^{\infty}{\rm e}^{-{\rm i}u\delta}\Theta_{\delta}(u){\rm d}u.
\end{displaymath}](/articles/aa/full/2006/38/aa5581-06/img29.gif)
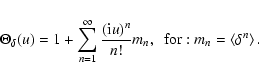
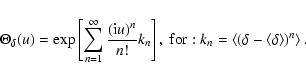
![\begin{displaymath}%
{\rm d}P = n^2{\rm d}V_1{\rm d}V_2\left[1 + \xi(r_{12})\right].
\end{displaymath}](/articles/aa/full/2006/38/aa5581-06/img39.gif)
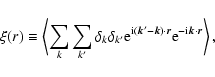
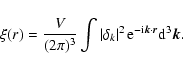
![$\displaystyle P^G[\delta_1,\delta_2 ... \delta_n]
=\frac{1}{(2\pi)^n} \int_{0}^...
...ft[-{\rm i}\displaystyle
\sum_{\alpha=1}^{n} u_{\alpha}\delta_{\alpha}\right]}.$](/articles/aa/full/2006/38/aa5581-06/img43.gif)
![$\displaystyle P^G[\delta_1,\delta_2 ... \delta_n]~~=~~\frac{1}{(2\pi)^{\frac{n}...
...elta_{\alpha})\right]
\left[ \delta_{\beta}-K_1(\delta_{\beta})\right] \right],$](/articles/aa/full/2006/38/aa5581-06/img44.gif)
![\begin{displaymath}%
P^G[\delta_1,\delta_2] = \frac{1}{2\pi\sigma^2}\left(\frac{1}{1-A^2}\right)^\frac{1}{2}{\rm e}^{-Q[\delta_1,\delta_2]},
\end{displaymath}](/articles/aa/full/2006/38/aa5581-06/img47.gif)
![\begin{displaymath}%
Q= \frac{1}{2} \left(
\frac{1}{1-A^2}\right)\frac{1}{\sigma^2}\left[\delta_1^2+\delta_2^2-2A\delta_1\delta_2 \right],
\end{displaymath}](/articles/aa/full/2006/38/aa5581-06/img52.gif)
![\begin{displaymath}%
P^G[\delta_1 >\eta\sigma, \delta_2 >\eta\sigma] =
\int_{\e...
..._{\eta\sigma}^{\infty}{\rm d}\delta_2P^{G}[\delta_1,\delta_2].
\end{displaymath}](/articles/aa/full/2006/38/aa5581-06/img56.gif)
![$\displaystyle P^G[\delta_1 >\eta\sigma, \delta_2 >\eta\sigma]=
\int_{\eta\sigma...
...ma}\right)F^{p+1}\left(\frac{\delta_2}{\sigma}\right)
\right]\frac{(2A)^p}{p!},$](/articles/aa/full/2006/38/aa5581-06/img59.gif)
![\begin{displaymath}%
F^{p+1}(Z)= \frac{(-{\rm i})^p}{2\pi}
\int_{-\infty}^{\inft...
...ft[ -{\rm i} \lambda z -\frac{z^2}{2} \right]} {\rm d}\lambda.
\end{displaymath}](/articles/aa/full/2006/38/aa5581-06/img60.gif)
![\begin{displaymath}%
P^G[\delta_1 >\eta\sigma, \delta_2 >\eta\sigma] =
\left[\fr...
...c{1}{\eta} {\rm e}^{-\frac{\eta^2}{2}}\right]^2 (1 +2A\eta^2).
\end{displaymath}](/articles/aa/full/2006/38/aa5581-06/img61.gif)
![\begin{displaymath}%
P^G[\delta_1 >\eta\sigma, \delta_2 >\eta\sigma] \equiv
[P^G(\delta>\eta\sigma)]^2 [1 + \xi_{\eta}^G(r)],
\end{displaymath}](/articles/aa/full/2006/38/aa5581-06/img66.gif)
![\begin{displaymath}%
\xi_\eta^G(r) \equiv 2A\eta^2 \approx {\rm e}^{2A\eta^2}-1 = \exp\left[2\left(\frac{\eta}{\sigma}
\right)^2\xi_r\right]-1.
\end{displaymath}](/articles/aa/full/2006/38/aa5581-06/img69.gif)
![\begin{displaymath}%
P^{\rm NG}[\delta_1 >\eta\sigma, \delta_2 >\eta\sigma]\! = ...
...
\left[1 \!+\! \xi_{\eta}^G(r)\!+\! C_{\eta}^{\rm NG}\right],
\end{displaymath}](/articles/aa/full/2006/38/aa5581-06/img71.gif)
![\begin{displaymath}%
P^{\rm NG}[\delta_1 >\eta\sigma, \delta_2 >\eta\sigma] =
\...
...^{-\frac{\eta^2}{2}}\right]^2 (1 +2A\eta^2+C_{\eta}^{\rm NG}),
\end{displaymath}](/articles/aa/full/2006/38/aa5581-06/img72.gif)
![\begin{displaymath}%
\xi_\eta^{\rm NG}(r) \approx \exp \left[2\left(\frac{\eta}{\sigma}\right)^2\xi_r^{\rm NG}\right]-1.
\end{displaymath}](/articles/aa/full/2006/38/aa5581-06/img76.gif)
![$\displaystyle P^{\rm NG}[\delta_1,\delta_2 ...\delta_n]= P^G[\delta_1,\delta_2....
...\omega)H_{\alpha,\beta...\omega}\left[\delta -\kappa_1 (\delta) \right]\right],$](/articles/aa/full/2006/38/aa5581-06/img77.gif)
![$\displaystyle C^{\rm NG}_{\eta}~~=~~\int_{\eta\sigma}^{\infty} \int_{\eta\sigma...
...a,\delta_\beta)H_{\alpha,\beta}\left[\delta
-\kappa_1 (\delta) \right] \right].$](/articles/aa/full/2006/38/aa5581-06/img80.gif)
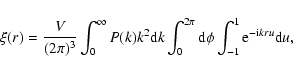
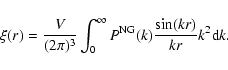
![\begin{displaymath}%
P^{Mix}(k)=A_{n}P(k)[1+M(\alpha_0)k] = \beta k^n[1+M(\alpha_0)k].
\end{displaymath}](/articles/aa/full/2006/38/aa5581-06/img97.gif)
![\begin{displaymath}%
M^{\rm mix}(\alpha_0,k)\equiv\int_\nu[(1-\alpha_0k)f_1(\nu)+\alpha_0kf_2(\nu)]\nu^2\; {\rm d}\nu.
\end{displaymath}](/articles/aa/full/2006/38/aa5581-06/img104.gif)
![\begin{displaymath}%
\xi^{\rm Mix}(R)=A_{n}\left[\frac{1.76\times 10^{-2}}{3\pi
...
...0^{-4}M(\alpha_0)}{3\pi \left(\frac{R}{R_0}\right)^2} \right],
\end{displaymath}](/articles/aa/full/2006/38/aa5581-06/img105.gif)
![\begin{figure}
\par\includegraphics[height=5.55cm,width=7.5cm,clip]{5581fig1.eps}\end{figure}](/articles/aa/full/2006/38/aa5581-06/Timg109.gif)
![\begin{figure}
\par\includegraphics[height=5.55cm,width=7.5cm,clip]{5581fig2.eps}\end{figure}](/articles/aa/full/2006/38/aa5581-06/Timg113.gif)
![\begin{figure}
\par\includegraphics[height=5.45cm,width=7.55cm,clip]{5581fig3a.e...
...mm}
\includegraphics[height=5.45cm,width=7.55cm,clip]{5581fig3b.eps}\end{figure}](/articles/aa/full/2006/38/aa5581-06/Timg117.gif)
![\begin{figure}
\par\includegraphics[height=5.45cm,width=7.1cm,clip]{5581fig4.eps}\end{figure}](/articles/aa/full/2006/38/aa5581-06/Timg128.gif)
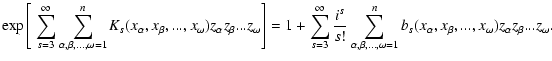
![$\displaystyle %
H_{\alpha\beta...\omega}[x]= {\rm e}^{\phi[x]}\left(
-\frac{\pa...
...right)...\left(
-\frac{\partial}{\partial x_{\omega}}\right){\rm e}^{-\phi[x]},$](/articles/aa/full/2006/38/aa5581-06/img130.gif)
![$\displaystyle P^{NG}[\delta_1,\delta_2]=
\left[1+ \displaystyle \sum_{s=3}^{\in...
...a-\kappa_1\left(\delta\right)\right]\right]P^{G}\left[\delta_1,\delta_2\right],$](/articles/aa/full/2006/38/aa5581-06/img134.gif)
![$b_{lm}= b_{l+m}[\underbrace {\delta_1 \cdots
\delta_1}_{l \ \textrm{times} }; \underbrace {\delta_2 \cdots \delta_2}_{m \
\textrm {times}}]$](/articles/aa/full/2006/38/aa5581-06/img135.gif) ,
,
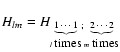 .
.![\begin{displaymath}%
y_\alpha=y_\alpha[x]=\frac{\partial \phi[x]}{\partial
x_\alpha}=\sum_{\beta=1}^{n}a_{\alpha\beta}x_\beta, %
\end{displaymath}](/articles/aa/full/2006/38/aa5581-06/img145.gif)