A&A 457, 707-715 (2006)
DOI: 10.1051/0004-6361:20065524

Effect of coronal structure on loop oscillations

G. R. Donnelly - A. J. Díaz - B. Roberts

Mathematical Institute, University of St Andrews, St Andrews KY16 9SS, Scotland, UK

Received 28 April 2006 / Accepted 3 July 2006

Abstract
Aims. We investigate the influence of longitudinal structuring of the surrounding corona on the modes of oscillation of a coronal magnetic flux tube.
Methods. A partial differential equation is derived for the total pressure perturbation of the fast modes and it is solved analytically in terms of Bessel functions, obtaining a dispersion relation.
Results. The introduction of coronal structuring changes the cutoff frequency, enhancing coronal leakage, so even the fundamental kink mode may become leaky. Structure also modifies the loop's oscillatory frequencies and may result in higher harmonics being trapped.
Conclusions. Depending on the structuring, two competing effects take place: environmental structuring enhances leakage, while loop structuring helps confine the modes. This has important consequences for coronal seismology, leading to the absence of trapped modes for certain parameters and shifts in frequencies.

Key words: Sun: oscillations - Sun: magnetic fields - Sun: corona

1 Introduction

An important feature of the solar corona is the wide variety of structures which occur as a result of the Sun's complex magnetic field. Many of these structures share the feature that they have a density enhancement (high plasma density compared with the surrounding plasma), allowing them to act as an MHD wave guide. They may also have temperature or magnetic field enhancements or depletions, but in the low-$\beta$ corona it is density (and through this the Alfvén speed) that plays the major role.

The excellent observational ability of spacecrafts such as TRACE and SOHO has provided us with an array of detections of both standing (Aschwanden et al. 2002; Ofman & Wang 2002; Nakariakov et al. 1999; Aschwanden et al. 1999; Wang et al. 2002c,2003,2002b,a; Schrijver et al. 2002; Schrijver & Brown 2000) and propagating (De Moortel et al. 2002b; Williams et al. 2001; Robbrecht et al. 2000; De Moortel et al. 2002c; Williams et al. 2002; Berghmans & Clette 1999; De Moortel et al. 2000) waves occurring in coronal loops. Despite these capabilities it is still difficult to make direct observations of fundamental quantities such as the magnetic field strength. However, the technique of coronal seismology (McEwan et al. 2006; Nakariakov et al. 1999; Andries et al. 2005a; De Moortel et al. 2002a; Roberts et al. 1984; Andries et al. 2005b; Roberts 1986; Nakariakov & Ofman 2001) allows information carried by MHD waves to be extracted from observations of oscillatory events and the results interpreted using theoretical models.

There have been several theoretical models of coronal loops. The first models considered only the simplest aspects of magnetic structuring, using a Cartesian slab (e.g. Roberts 1981; Edwin & Roberts 1982) or a cylindrical tube (e.g. Edwin & Roberts 1983; Spruit 1982). In cylindrical models the coronal loop is represented by an infinitely long and straight uniform magnetic flux tube. The loop has a plasma density enhancement compared with its environment, and the magnetic field is directed along the loop. This configuration produces a rich array of wave behaviour and is widely used in coronal seismology. From this model several features may be added, such as the presence of magnetic twist (Sakai et al. 2000; Bennett et al. 1999), or field-aligned flows (Nakariakov & Roberts 1995; Terra-Homem et al. 2003; Somasundaram et al. 1999), the role of line-tying effects (Díaz et al. 2004), longitudinal stratification (Roberts 2006; Mendoza-Briceño et al. 2004; Andries et al. 2005b; James 2003; Nakariakov & Ofman 2001; Nakariakov et al. 2000), curvature (Verwichte et al. 2006; Díaz 2006; Smith et al. 1997; Selwa et al. 2005; Van Doorsselaere et al. 2004; Díaz et al. 2006b; Brady & Arber 2005), coronal leakage (Cally 2003; Díaz et al. 2004; Cally 1986; Brady & Arber 2005), magnetic shells (Mikhalyaev & Solov'ev 2005; Erdelyi & Carter 2006), loops of elliptical cross-section (Ruderman 2003) or multithreaded loops (Oliver et al. 2006; Gruszecki et al. 2006). Extensive reviews can be found in (Nakariakov & Verwichte 2005; Aschwanden 2004).

Despite extensive work there are still many aspects of coronal loop oscillations and coronal seismology to be explored. Here we consider the role of footpoint structuring in the loop and the coronal environment. We consider a uniform line-tied loop with longitudinal structuring in the loop's environment by incorporating a dense chromospheric layer. The chromospheric layer modifies the properties of the modes (Díaz et al. 2004), but its inclusion in the surrounding medium has other consequences which are explored in this paper. In an unbounded homogeneous loop of radius a, the fundamental kink mode propagates as a trapped mode for all wavenumbers k, with a phase speed equal to the kink speed ck in the thin tube ($k a\ll 1$) limit (Edwin & Roberts 1983; Spruit 1982). However, for a suitable depth of chromospheric layer, we find that the kink mode no longer propagates as a trapped mode. Also, in the case where it is trapped in the thin tube limit, it now propagates with a kink speed that is modified by the presence of the chromospheric layer.

Many results of coronal seismology, such as the deduction of the coronal magnetic field strength from the TRACE loop oscillations (Nakariakov & Ofman 2001), use the fact that the fundamental kink mode is trapped in the thin tube limit and is propagating at the kink speed. The result that the fundamental kink mode may not be trapped in the thin tube limit may thus have important implications for coronal seismology.

2 Equilibrium model and wave equations

We consider a spatially structured static equilibrium of a cylindrically symmetric line-tied coronal loop or magnetic flux tube (lying parallel to the z axis) of length 2 L and radius a. The magnetic field $\vec{B}_0 = B_0 \vec{e}_z$ is assumed to be uniform throughout the medium and aligned with the loop. The equilibrium density  $\rho_0(r,z)$ is structured in both the radial and longitudinal directions. Gravitational effects are ignored.

Small amplitude oscillations about this equilibrium are introduced. The ideal adiabatic MHD equations (neglecting gravitational effects) reduce to the following system of coupled partial differential equations (see, for example, Díaz et al. 2002; Roberts 1991)

 \begin{displaymath}\frac{\partialP_{{\rm T}}}{\partial t}=\rho_0 v_{\rm A}^2(z) ... ...al v_z}{\partial z}-\rho_0 c_{\rm f}^2(z)\nabla \cdot \vec{v}, \end{displaymath} (1)
 \begin{displaymath}\rho_0\left[\frac{\partial^2}{\partial t^2}-v_{\rm A}^2(z) \f... ...a_\perp}\left[\frac{\partial P_{{\rm T}}}{\partial t}\right] , \end{displaymath} (2)
 \begin{displaymath}\rho_0\left[\frac{\partial^2}{\partial t^2}-c_{\rm T}^2(z) \f... ...f}^2(z)}\frac{\partial^2 P_{{\rm T}}}{\partial z \partial t} , \end{displaymath} (3)

where $v_{\rm A}(z)=B_0 / \sqrt{\mu \rho_0(z)}$ and $c_0(z)=\sqrt{\gamma P_0 / \rho_0(z)}$ are the Alfvén and sound speeds, $c_{\rm T}^{-2}=v_{\rm A}^{-2}+c_0^{-2}$ determines the tube speed $c_{\rm T}$, and $c_{\rm f}^2=v_{\rm A}^2+c_0^2$. The subscript "$\perp$'' denotes components perpendicular to the equilibrium magnetic field, so the perturbed flow is $\vec{v}=\vec{v}_\perp +v_z\vec{e}_z$, with $\vec{v}_\perp = v_r\vec{e}_r + v_\theta \vec{e}_\theta$ in cylindrical coordinates. The perturbed total pressure is  $P_{{\rm T}}$. Equations (1)-(3) apply in each region (coronal and chromospheric) of the flux tube and its environment.

The low $\beta$ or cold plasma approximation ($\beta=0$) is now taken, in which we neglect the effect of plasma pressure; this is a good approximation in the corona where the plasma beta is small. Consequently, the slow mode is removed from the system, since Eq. (3) becomes decoupled and gives vz=0. Some care should be taken in making this approximation to other regions of the solar atmosphere, such as the chromosphere or photosphere, as pressure effects and gravitational stratification play a greater role in these layers (see Roberts 2004, for a recent discussion). The implication of the $\beta \rightarrow 0$ limit on the speeds of the system are that $c_0 \rightarrow 0$, $c_{\rm T} \rightarrow 0$ and $c_{\rm f} \rightarrow v_{\rm A}$ so acoustic aspects are lost and the fast modes are decoupled from the Alfvén waves; hence the zero-$\beta$ assumption allows a study of fast modes to be undertaken.

We allow for a general longitudinal and transverse structuring in the form of step functions, the equilibrium plasma density profile taking the form

 \begin{displaymath}\rho_0(r,z)=\left\{ \begin{array}{ll} \rho_{\rm i}(z) , \qquad r < a\\ \rho_{\rm e}(z) , \qquad r > a\\ \end{array}\right. \end{displaymath} (4)

where we denote internal and external equilibrium values by a subscript "i'' and "e'' respectively. Making these steps, Eqs. (1) and (2) lead to the wave equation for $P_{{\rm T}}$ (Díaz et al. 2002, 2004)

 \begin{displaymath}\left[\frac{\partial^2}{\partial t^2}-v_{\rm A}^2(z) \nabla^2 \right]P_{{\rm T}}=0 , \end{displaymath} (5)

and Eq. (2) is retained in the same form, with appropriate density and Alfvén profiles depending on whether it is being applied internally or externally to the tube.

We consider trapped modes for which there is no propagation of energy towards or away from the loop. This is achieved by imposing $\vec{v}_\perp \rightarrow 0$ and $P_{{\rm T}}\rightarrow 0$ as $r \rightarrow \infty$. The loop is line-tied with the footpoints fixed in the dense photosphere, where it is expected that coronal perturbations carry such small energy that they are incapable of perturbing the dense photospheric plasma; this leads to the line-tying boundary condition $\vec{v}_\perp(z=\pm L)=0$. In this model we have interfaces over which the equilibrium plasma properties jump discontinuously so we must know how the perturbations behave across such surfaces. There are two types of interface: those parallel to the applied equilibrium magnetic field and those which are not parallel to the equilibrium magnetic field. In the case where the interface is parallel to the equilibrium field, the boundary conditions are (Goedbloed 1983; Díaz et al. 2001; Díaz 2004)

 \begin{displaymath}\vec{\hat{n}}\cdot [\vec{v}]=\vec{\hat{n}}\cdot [\vec{B}]=0 , \quad [P_{{\rm T}}]=0~. \end{displaymath} (6)

Thus, the perturbed pressure $P_{{\rm T}}$ and the components of the perturbed velocity and magnetic field perpendicular to the interface are required to be continuous.

For interfaces which are not parallel to the equilibrium magnetic field, the boundary conditions are

 \begin{displaymath}[\vec{v}]=[\vec{B}]=[P_{{\rm T}}]=0 ; \end{displaymath} (7)

in this case all components of the velocity and the magnetic field, as well as the total pressure, must be continuous at the interface.

3 Analytical solution

We study oscillatory solutions to Eq. (5) in cylindrical coordinates. Following Díaz et al. (2002), we assume a solution which is separable in space and Fourier analysing in time, writing $P_{{\rm T}}$ in the form

 \begin{displaymath}P_{{\rm T}}(r,\theta,z,t)=u(r) \; \Phi(\theta) \; h(z) \; \exp({\rm i}\omega t) , \end{displaymath} (8)

with $\omega$ the frequency. This form for the total pressure perturbations $P_{{\rm T}}$ produces a set of ordinary differential equations:

 \begin{displaymath}\frac{{\rm d}^2 u}{{\rm d} r^2}+\frac{1}{r}\frac{{\rm d} u}{{\rm d} r}-\left(\lambda^2+\frac{m^2}{r^2}\right)u=0 , \end{displaymath} (9)


 \begin{displaymath}\frac{{\rm d}^2 \Phi}{{\rm d} \theta^2}+m^2 \Phi =0 , \end{displaymath} (10)

and

 \begin{displaymath}\frac{{\rm d}^2 h}{{\rm d} z^2}+\left(\frac{\omega^2}{v_{\rm ... ...(z)}+\lambda^2\right)h=0~, \qquad j=i \quad {\rm or} \quad e , \end{displaymath} (11)

where m2 and $\lambda^2$ are the separation constants.

Solving Eq. (10) for $\Phi$ gives

 \begin{displaymath}\Phi(\theta)=\Phi(0)\exp ({\rm i} m \theta) . \end{displaymath} (12)

This solution applies in both the tube interior and the exterior, since the total pressure must be continuous across the tube boundary. The periodicity in the $\theta$-direction implies that m must be an integer, the same for both the interior and exterior regions.

Equation (9) for u(r) inside the loop has the form of a Bessel (or modified Bessel) equation of order m for $(\lambda^{\rm i})^2 > 0$ (or $(\lambda^{\rm i})^2 < 0$); we write

 \begin{displaymath}u^{\rm i}(r)=A\left\{ \begin{array}{ll} I_m(\lambda^{\rm i} r... ...}\}^\star)^2=-(\lambda^{\rm i})^2 > 0 . \\ \end{array}\right. \end{displaymath} (13)

We have required the solution to be finite in the region r < a.

In the environment of the tube the equation for u(r) takes the form of a modified Bessel equation; since we consider trapped modes, it is required that all perturbations decline to zero as $r \rightarrow \infty$, with the implication that $(\lambda^{\rm e})^2 > 0$ and then

 \begin{displaymath}u^{\rm e}(r)=C K_m(\lambda^{\rm e} r) , \qquad (\lambda^{\rm e})^2 > 0 . \end{displaymath} (14)

The fact that $(\lambda^{\rm e})^2 > 0$ for trapped modes is significant; the frequency, $\omega_{\rm cut}$, at which $(\lambda^{\rm e})^2$ changes sign defines the cutoff frequency, marking the transition between trapped and leaky behaviour. For a homogeneous loop embedded in a homogeneous environment, the resultant cutoff frequency for the first family of even modes is

 \begin{displaymath}\omega_{\rm cut}=\pi v_{\rm Ae}/2 L . \end{displaymath} (15)

Finally, we consider the equation for h(z), which defines the longitudinal structuring. We can proceed generally, without specifying the equilibrium density profile, by noting that for certain choices of Alfvén profile the differential operator

 \begin{displaymath}\frac{{\rm d}^2}{{\rm d}z^2}+\frac{\omega^2}{v_{\rm A}^2(z)}+\lambda^2 \end{displaymath} (16)

is self-adjoint. If this is the case and $h(z= \pm L)=0$, which is equivalent to the line-tying condition $\vec{v}_\perp(z=\pm L)=0$, then the Sturm-Liouville theorem can be applied with the implication that the set of solutions to Eq. (11) form a complete set on $-L \le z \le L$. Hence, there exists an infinite set of solutions to Eq. (11), and accordingly we label h(z) and u(r) by a subscript n. This gives an orthonormal set for $h_n^{\rm i}(z)$. The function $h_1^{\rm i}(z)$ is the solution of Eq. (11) when n=1 and $\lambda^2=\lambda_1^2$. This allows the external solutions $h_n^{\rm e}(z)$ to be expanded in terms of the complete set of internal solutions $h_m^{\rm i}(z)$:

 \begin{displaymath}h_n^{\rm e}(z)=\sum_{m=1}^\infty H_{nm} h_m^{\rm i}(z) , \end{displaymath} (17)

where the coefficients Hnm are given by

 \begin{displaymath}H_{nm}=\int_{-L}^{L} h_n^{\rm e}(z) h_m^{\rm i}(z) {\rm d}z . \end{displaymath} (18)

In order to satisfy the continuity of $P_{{\rm T}}$ and vr on the tube interface r=a, we write the solution for $P_{{\rm T}}$ as a linear combination of all solutions (Díaz et al. 2001):

 \begin{displaymath}P_{{\rm T}}(r,\theta,z)=\Phi(\theta)\left\{ \begin{array}{ll}... ...{\rm e}(r) h_n^{\rm e}(z) , \quad r > a.\\ \end{array}\right. \end{displaymath} (19)

Assuming that the radial component of the perpendicular perturbed velocity vr has the same separable form as $P_{{\rm T}}$, we find from Eq. (2)

 \begin{displaymath}v_r(r,\theta,z)= \Phi(\theta)\left\{ \begin{array}{ll} \sum\l... ...\rm d} r} h_n^{\rm e}(z) , \quad r > a. \\ \end{array}\right. \end{displaymath} (20)

From the continuity of $P_{{\rm T}}$ and vr we can derive the set of linear equations for the amplitude coefficients Cs present in solution (14):
 
$\displaystyle \sum\limits_{s=1}^\infty H_{sn} \left[\frac{1}{\lambda_n^{\rm i}}... ...^{\rm e}} I_m(\lambda_n^{\rm i} a) K_m^\prime(\lambda_s^{\rm e} a) \right]C_s=0$     (21)

for $(\lambda_n^{\rm i})^2>0$, and
 
$\displaystyle \sum\limits_{s=1}^\infty H_{sn} \left[\frac{1}{\{\lambda_n^{\rm i... ...J_m(\{\lambda_n^{\rm i}\}^\star a) K_m^\prime(\lambda_s^{\rm e} a) \right]C_s=0$     (22)

in the case of $(\lambda_n^{\rm i})^2<0$. These two sets of equations are written as separate summations though the terms in them may in fact be mixed as $(\lambda_n^{\rm i})^2$ could change in sign after a finite number of terms. If such a change of sign occurs after l terms, then the appropriate summation would be
 
    $\displaystyle \sum\limits_{s=1}^l H_{sn} \left[\frac{1}{\lambda_n^{\rm i}} I_m^... ..._s^{\rm e}} I_m(\lambda_n^{\rm i} a) K_m^\prime(\lambda_s^{\rm e} a) \right]C_s$  
    $\displaystyle +\sum\limits_{s=l+1}^\infty H_{sn} \left[\frac{1}{\{\lambda_n^{\r... ...m(\{\lambda_n^{\rm i}\}^\star a) K_m^\prime(\lambda_s^{\rm e} a) \right]C_s=0 .$ (23)

The dispersion relation for the trapped modes of oscillation of a line-tied coronal loop with arbitrary longitudinal environmental structuring and step functions in the radial coordinate is satisfied when the determinant of the system of Eq. (23) vanishes. This condition describes the sausage (m=0), kink (m=1) and fluting ($m \ge 2$) modes. An interesting aspect of the dispersion relation is that, due to the summation over all harmonics, each mode is in general a combination of both surface and body modes, whereas in homogeneous tubes these may be considered separately.

4 Results for a uniform loop


  \begin{figure} \par\includegraphics[width=5.6cm,clip]{5524f1.eps} \end{figure} Figure 1: A sketch of the equilibrium configuration showing a slice (in r and z) of a cylindrically symmetric uniform coronal loop, of length 2L and radius a. The plasma density in the tube interior is $\rho _{\rm i}$ and the coronal region is of density $\rho _{\rm e}$. In the chromospheric layers (of depth L-W), the density is $\rho _{\rm che}$ in the external chromosphere and $\rho _{\rm chi}$ in the internal chromosphere. The magnetic field is everywhere uniform and directed parallel to the loop. The footpoints of the loop are fixed at the chromospheric/photospheric base ($z = \pm L$).The configuration is cylindrically symmetric.
Open with DEXTER

In order to investigate the effect of chromospheric layers on the oscillations of a coronal loop we consider first the special case of an entirely uniform loop surrounded by a coronal environment with chromospheric layers. This allows a more straightforward discussion of the new effects. Later, we return to the more realistic model in which the chromospheric layers occur both inside and outside the loop. Consider, then, the equilibrium configuration of Fig. 1, but here assuming an entirely uniform loop profile, of density $\rho_{\rm i}=\rho_{\rm chi}$. The chromospheric inhomogeneity is then confined entirely to the loop's environment, so that for r > a the density profile is

 \begin{displaymath}\rho_{\rm e}(z)=\left\{ \begin{array}{ll} \rho_{\rm che} , \q... ...o_{\rm e} , \qquad \vert z\vert \le W , \\ \end{array}\right. \end{displaymath} (24)

where $\rho _{\rm che}$ and $\rho _{\rm e}$ are the densities in the chromospheric and coronal regions. The symmetry of the equilibrium means that waves can be split into odd (having a node at the loop apex z=0) or even (with an anti-node at the loop apex) modes. Hence the solution to Eq. (11) for the loop interior (for r < a) is

 \begin{displaymath}h_n^{\rm i}(z)=\frac{1}{L^{1/2}}\left\{ \begin{array}{ll} \co... ...sin(M_n^{\rm i} z) , \qquad {\rm odd} . \\ \end{array}\right. \end{displaymath} (25)

In the exterior (for r > a), the equivalent solution for the even modes is

 \begin{displaymath}h_n^{\rm e}(z)=\Lambda_{ev}\left\{ \begin{array}{ll} \cos(M_n... ...\qquad \qquad \qquad \qquad W < z < L . \\ \end{array}\right. \end{displaymath} (26)

The multiplicative factors $\frac{1}{L^{1/2}}$ and $\Lambda_{ev}$ have been chosen to normalise the functions $h_n^{\rm i}(z)$ and $h_n^{\rm e}(z)$ to satisfy

\begin{displaymath}\int_{-L}^L\left[ h_n^{\rm i}(z)\right]^2 {\rm d}z=\int_{-L}^L\left[ h_n^{\rm e}(z)\right]^2 {\rm d}z=1 . \end{displaymath} (27)

This leads to
 
    $\displaystyle \Lambda_{ev}^{-2}=(L-W)\cos^2(M_n^{\rm che}W)+W\sin^2[M_n^{\rm e}(L-W)]$  
    $\displaystyle \hspace{0.5in}- \frac{1}{2 M_n^{\rm e}}\cos^2(M_n^{\rm che} W)\sin[2 M_n^{\rm e}(L-W)]$  
    $\displaystyle \hspace{0.5in} +\frac{1}{2 M_n^{\rm che}}\sin(2M_n^{\rm che} W)\sin[ M_n^{\rm e}(L-W)]$ (28)

with an equivalent expression for the odd multiplicative factor, $\Lambda_{\rm od}$. The terms $M_n^{\rm i}$, $M_n^{\rm che}$ and $M_n^{\rm e}$ are defined by

 \begin{displaymath}\begin{array}{ll} (M_n^{\rm i})^2=(\lambda_n^{\rm i})^2+\frac... ...lambda_n^{\rm e})^2+\frac{\omega^2}{v_{\rm Ae}^2} , \end{array}\end{displaymath} (29)

where $\lambda_n^{\rm i}$ and $\lambda_n^{\rm e}$ are the separation constants for the interior and exterior regions, respectively.

The line tying condition $h_n(z=\pm L)=0$ is automatically satisfied by our choice of solution (26) in the loop environment, but $M_n^{\rm i}$ is restricted to be

 \begin{displaymath}M_n^{\rm i} = \frac{n \pi}{2 L} ; \end{displaymath} (30)

if the integer n is odd then this is an even mode, and if n is even then this is an odd mode. There are an infinite set of solutions to Eqs. (9) and (10) and therefore the systems of Eqs. (21) and (22) are infinite sets. For the environment region we must apply the boundary conditions for an interface perpendicular to the equilibrium magnetic field at $z = \pm W$(Eq. (7)), which require the total pressure, magnetic field and velocity to be continuous across this boundary. This leads to the conditions (via the ideal induction equation) that  $h_n^{\rm e}(z)$ and $\frac{{\rm d} h_n^{\rm e}}{{\rm d} z}$ be continuous across this surface. The result is the transcendental equation

 \begin{displaymath}M_n^{\rm che}\cot\left[M_n^{\rm che}(L-W)\right]=M_n^{\rm e}\tan\left[M_n^{\rm e}W\right] \end{displaymath} (31)

for the even modes, and

 \begin{displaymath}M_n^{\rm che}\cot\left[M_n^{\rm che}(L-W)\right]=-M_n^{\rm e}\cot\left[M_n^{\rm e}W\right] \end{displaymath} (32)

for the odd modes. It has been assumed that $\frac{\omega^2}{v_{\rm Ache}^2}+(\lambda_n^{\rm e})^2 >0$ and $\frac{\omega^2}{v_{\rm Ae}^2}+(\lambda_n^{\rm e})^2 >0$. There are equivalent forms for the case of one or both of $\frac{\omega^2}{v_{\rm Ache}^2}+(\lambda_n^{\rm e})^2$ and $\frac{\omega^2}{v_{\rm Ae}^2}+(\lambda_n^{\rm e})^2$ being negative; these can be obtained simply by observing that $\sin ({\rm i} x)=-{\rm i} \sinh (x)$ and $\cos ({\rm i}x) = \cosh (x)$. Equations (31) and (32) have an infinite number of solutions for the exterior, and Eq. (30) another infinite set of solutions for the interior.

The final coefficient we require, in order to evaluate the determinant of the system of Eqs. (23) and obtain our dispersion relation, are the values of Hnm. For the even modes, the coefficients Hnm are evaluated using Eq. (18), giving

 
                          H2n-1,2m-1 = $\displaystyle \Lambda_{ev} L^{-0.5} \left[\sin[M^{\rm che}(L-W)] \left\{\frac{\sin[(M^{\rm i}-M^{\rm e})W]}{[M^{\rm i}-M^{\rm e}]}\right. \right.$  
    $\displaystyle \left. + \frac{\sin[(M^{\rm i}+M^{\rm e})W]}{[M^{\rm i}+M^{\rm e}]}\right\}$  
       
    $\displaystyle -\cos[M^{\rm e} W] \left\{ \frac{\cos[M^{\rm i} W+ M^{\rm che}(W-L)]}{M^{\rm i}+M^{\rm che}}\right.$  
       
    $\displaystyle \left. \left.+\frac{\cos[M^{\rm i} W+ M^{\rm che}(L-W)]}{M^{\rm che}-M^{\rm i}}\right\} \right]\cdot$ (33)

Again, in writing (33) it has been assumed that $[M^{\rm i}]^2$, $[M^{\rm che}]^2$ and $[M^{\rm e}]^2$ are all positive but equivalent forms can be obtained when this is not the case.

There is a similar form for the Hnm coefficient in the case of the odd modes.


  \begin{figure} \par\mbox{\subfigure[]{\includegraphics[width=6cm,clip]{5524f2a.e... ...{4mm} \subfigure[]{\includegraphics[width=6cm,clip]{5524f2b.ps} } } \end{figure} Figure 2: a) Dispersion diagram for $v_{\rm Ae}=2.5 v_{\rm Ai}$, $v_{\rm Ache}=0.25 v_{\rm Ai}$ and W / L =0.8, showing the dimensionless frequency $\omega L / v_{\rm Ai}$ as a function of a/ L. The solid and dashed curves are kink and sausage modes respectively. Case b) shows the results of a) but scaling the frequency against the tube radius a and plotting logarithmically as a function of L/a. The cutoff curve is displayed in a) and b) by the dotted line.
Open with DEXTER

4.1 Dependence on loop radius a

We first study the dispersive nature of the modes as the ratio a/L of the loop radius to the loop half-length varies. Figure 2a shows the dispersion diagram for the even modes, for appropriate coronal parameters. The dispersion diagram displays a band of dispersive fast modes, similar in behaviour to those of Edwin & Roberts (1983). There is only one mode propagating in the thin tube limit $a/L \ll 1$, which is the fundamental kink mode with frequency $\omega L / v_{\rm Ai}=1.84$. This differs from the frequency of the fundamental kink mode in a homogeneous environment, which gives $\omega L / v_{\rm Ai}=2.06$ for these parameters. The sausage modes and the higher harmonics of the kink modes all have cutoff frequencies, so none propagate in the thin tube limit. Figure 2b shows the same plot of the dispersion diagram displayed in Fig. 2a but here with lengths normalised against the loop radius a. This plot is useful for coronal seismology, since it relates the frequency of the mode with the loop length, which can be deduced in many of the observations. In accordance with Edwin & Roberts (1983), the frequency for the fundamental kink mode is almost insensitive to the loop radius for realistic values of L / a ($\approx$ 101-104). This is a useful property for coronal seismology, since errors due to inaccuracy in determining the loop radius are minimal if the mode observed is the fundamental kink mode.

The cutoff curve is marked by a dotted line showing the cutoff frequency $\omega=\omega_{\rm cut}$, with $\omega_{\rm cut} L / v_{\rm Ai} =1.87$ in Fig. 2. Therefore, we observe an immediate consequence of the chromospheric layer, which causes the cutoff frequency to shift from its value $\frac{\omega_{\rm cut} L }{ v_{\rm Ai}} =\frac{\pi v_{\rm Ae}}{2 v_{\rm Ai}} \approx 3.92$ in a homogeneous environment (Eq. (15)), independently of the internal structure of the loop.

4.2 Dependence on chromospheric depth

The parameter W/L provides a measure of the extent of the chromosphere. This parameter leads to two limiting cases, $W / L \rightarrow 0$ and $W / L \rightarrow 1$, in which the longitudinal structuring is eliminated and the loop's environment becomes uniform. In both cases we expect a structure similar to that found in Edwin & Roberts (1983). The first case, $W / L \rightarrow 0$, consists of a uniform loop embedded in a dense chromospheric plasma. The loop has an enhancement in Alfvén speed over its environment and so is incapable of supporting trapped modes of oscillation. The second case, of $W / L \rightarrow 1$, consists of a loop embedded in low density coronal material. In this case the loop has a depression in Alfvén speed compared with its environment, which is exactly the structure Edwin & Roberts (1983) found to support trapped modes of oscillation.

It is interesting to examine the effect of letting $W / L \rightarrow 1$, on the system in Eq. (23). The first thing to note is that the solutions to Eq. (9) inside and outside the loop become identical for n=m, and hence these solutions are orthogonal; therefore,

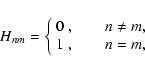\begin{displaymath}H_{nm}=\left\{ \begin{array}{ll} 0~, \qquad n \ne m , \\ 1~, \qquad n = m , \\ \end{array}\right. \end{displaymath} (34)

so the system in Eq. (23) becomes diagonal. The diagonal terms are equivalent to the dispersion relation for the trapped modes of oscillation of a magnetic tube with magnetic environment (in the zero-$\beta$ limit) when line-tying is imposed, so a longitudinal dependence of the form of Eq. (24) is assumed. Then the nth term on the diagonal represents the dispersion relation for modes of oscillation with n extrema in the longitudinal direction (Díaz et al. 2004). Hence, each diagonal term represents a family of modes with a particular longitudinal wavenumber and each family has its own cutoff frequency $\omega_{\rm cut}=\pi n v_{\rm Ae}/ 2L$. These families are decoupled from each other. When longitudinal structure is incorporated the modes of oscillation become a superposition of these different families, and so have varying longitudinal wavenumbers.

Figure 3 displays the dimensionless frequency against W / L for a thin tube, a/ L=0.1, so essentially plots the variation of the modified kink speed, ck, as a function of W/L. We see that in the limit $W / L \rightarrow 1$ only the fundamental kink mode is trapped; this is similar to the case in Fig. 2. The most striking difference between Fig. 3 and those against a/L is that the cutoff curve exhibits a non-uniform variation, varying from $\omega_{\rm cut}=\pi v_{\rm Ache} /2L$ as $W / L \rightarrow 0$ to $\omega_{\rm cut}=\pi v_{\rm Ae} / 2L$ as $W / L \rightarrow 1$. This variability in the cutoff frequency is perhaps expected from the presence of the parameter Win Eqs. (31) and (32) and is independent of a/L. As a result of the non-uniform cutoff curve, each mode has a cutoff frequency and value of W / L for which the mode becomes leaky and this is specific to that mode; this is in contrast to the uniform tube, where all cutoff frequencies are the same.

For values of a/ L larger than one there are many trapped sausage and kink modes present for a relatively small range of chromospheric depths ( $W / L \approx 0.8{-}1.0$), as would be expected from Fig. 2 for a large value of a/ L. The frequencies are almost independent of chromospheric depth, provided they lie below the cutoff curve. However, even the fundamental kink mode also has a cutoff frequency for small W / L. For further details in this range see Donnelly (2006).


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{5524f3.ps} \end{figure} Figure 3: Plot of the dimensionless frequency $\omega L / v_{\rm Ai}$ as a function of W/L for $v_{\rm Ae}=2.5 v_{\rm Ai}$, $v_{\rm Ache}=0.25 v_{\rm Ai}$ and a loop radius a=0.1 L. The solid line represents the fundamental kink mode, which is the only one mode trapped for these parameters. The dotted curve shows the dimensionless cutoff frequency as a function of W/L. Only the fundamental kink mode is below the cutoff for this value of a/L, as we can check in Fig. 2a.
Open with DEXTER

To investigate the effect of the chromospheric layers on the nature of the fundamental kink mode we plot in Fig. 4 a superposition of the dispersion curves and cutoff curves on a single diagram. Three cases are displayed: $v_{\rm Ache}=0.125v_{\rm Ae}$ for which $\rho_{\rm che}=64 \rho_{\rm e}$; $v_{\rm Ache}=0.25v_{\rm Ae}$ for which $\rho_{\rm che}=16 \rho_{\rm e}$; and $v_{\rm Ache}=0.5v_{\rm Ae}$ for which $\rho_{\rm che}=4 \rho_{\rm e}$. Thus, we evolve the diagram from the case of the chromosphere being 64 times denser than the coronal region to the case of a nearly uniform environment (low-density chromosphere). The cutoff curves evolve from one of steep gradients to a flat curve (which would be a straight line in the case $v_{\rm Ache}=v_{\rm Ae}$, no chromosphere). Also, the range of W /Lallowing the loop to trap the fundamental kink mode increases from the relatively small range of $W / L \approx 0.8{-}1.0$ when $v_{\rm Ache}=0.125v_{\rm Ae}$ to being trapped for all values of W / L in the final case, when $v_{\rm Ache}=0.5v_{\rm Ae}$. The dispersion becomes less pronounced as the curves move towards a uniform environment model.


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{5524f4.ps} \end{figure} Figure 4: Superposition of plots of dimensionless frequency $\omega L / v_{\rm Ai}$ against W/L with $v_{\rm Ae}=2 v_{\rm Ai}$ and a=0.1 L, for $v_{\rm Ache}=0.125v_{\rm Ae}$(solid), $v_{\rm Ache}=0.25v_{\rm Ae}$ (dashed) and $v_{\rm Ache}=0.5v_{\rm Ae}$ (dash-dotted). The cutoff lines for each of these cases have been overplotted as dotted lines and labelled "1'', "2'' and "3'', respectively.
Open with DEXTER

Previous work has shown that in a cylindrical geometry the eigenfunctions of such trapped modes do not penetrate deeply into the environment of the loop (Díaz et al. 2001,2004) and so would have no strong interaction with neighbouring structures, although as the mode propagates close to its cutoff frequency its eigenfunctions are expected to penetrate further into the environment. However, this is not the behaviour here. Figure 5 gives the evolution of the dimensionless total pressure perturbation at the loop apex (z=0) as a function of radial coordinate (panel a) and at the loop boundary (r=a) as a function of the longitudinal coordinate (panel b), along the dispersion curve displayed in Fig. 3. There is little difference in the penetrations of the eigenfunctions between a point close to the cutoff frequency (Fig. 5a, solid line) and a point far from it (Fig. 5a, dashed line). This suggests that the interaction between neighbouring loops is weak, unless the loops are in a tightly packed group. Figure 5b shows that the structure of the eigenfunction evolves along the dispersion curve. At W/L=0.99, $P_{{\rm T}}$ behaves much as expected for the fundamental kink mode, having one extremum in both the radial and longitudinal directions. However, for W/L=0.79 the eigenfunction has developed three extrema in the longitudinal direction, although it retains the single extrema in the radial direction.

  \begin{figure} \par\mbox{\subfigure[]{\includegraphics[width=6cm,clip]{5524f5a.p... ...4mm} \subfigure[]{\includegraphics[width=6cm,clip]{5524f5b.ps} }}\end{figure} Figure 5: Plots of $P_{{\rm T}}/ \rho _{\rm i} v_{\rm Ai}^2$ as a function of a) the radial coordinate r/a for the loop apex z/L=0, and b) of the longitudinal coordinate z/L for r=a. Here we fix $v_{\rm Ae}=2.5 v_{\rm Ai}$, $v_{\rm Ache}=0.25 v_{\rm Ai}$ and a=0.1 L. The following parameters were used: W/L=0.79 (solid line), W/L=0.89 (dotted line), and W/L=0.99 (dashed line).
Open with DEXTER


  \begin{figure} \par\mbox{\subfigure[]{\includegraphics[width=6cm,clip]{5524f6a.p... ...e{4mm} \subfigure[]{\includegraphics[width=6cm,clip]{5524f6b.ps} }} \end{figure} Figure 6: Plots showing $\omega L / v_{\rm Ai}$ as a function of W / L for structured loops surrounded by structured media. The solid curve is the fundamental kink mode and the dotted curve shows the dimensionless cutoff frequency as a function of W/Lwith $v_{\rm Ae}=2.5 v_{\rm Ai}$ and a/L =0.1. The following parameters were used: a) $v_{\rm Achi}=0.25 v_{\rm Ai}$ and $v_{\rm Ache}=0.35 v_{\rm Ai}$, b) $v_{\rm Achi}=0.35 v_{\rm Ai}$ and $v_{\rm Ache}=0.25 v_{\rm Ai}$.
Open with DEXTER

5 Results for a non-uniform loop

In the previous section we discussed the simplified case of a uniform loop lying within an environment structured by the presence of chromospheric layers. We now turn to the more realistic case in which chromospheric layers arise both inside and outside the loop (Fig. 1).

We consider a longitudinally structured loop of length 2L and radius a. The structuring in the environment region is the same as discussed previously. The loop has a uniform coronal region of extent 2W and a uniform chromospheric region of depth (L-W) at either end of the loop. These four regions are denoted by subscripts "e'', "che'', "i'' and "chi'', respectively. The same general procedure is followed as previously, resulting in a solution $h_n^{\rm i}(z)$ in the region r < a which is of the same form as $h_n^{\rm e}(z)$ discussed earlier. Note that the sign of $[\lambda_n^{\rm i}]^2$ is unrestricted as we may consider both body and surface modes; this results in hyperbolic, rather than trigonometric, behaviour. The solutions $h_n^{\rm e}(z)$ in the environment (r > a) remain as before. The same boundary conditions are applied at each interface, with the addition of the interface perpendicular to the magnetic field inside the loop. We make use of the Sturm-Liouville theorem (Arfken 1985) which states that the solutions of an eigenvalue equation such as (11) in self-adjoint form with boundary conditions $h_m(z = \pm L)=0$ form a complete set on the region $-L \le z \le L$. The Sturm-Liouville theorem guarantees that the the eigenvalues of this equation are ordered, countable and form a complete basis. Therefore, we may apply the Sturm-Liouville theorem to expand the external solution $h_n^{\rm e}(z)$ in terms of the internal solutions $h_m^{\rm i}(z)$(Díaz et al. 2004).

These steps lead to a dispersion relation taking an identical form to Eqs. (23) from the previous case. However, the modification of $h_n^{\rm i}(z)$ due to the internal structure of the loop results in changes to the set of $\lambda_n^{\rm i}$, which are solutions of

 \begin{displaymath}M_n^{\rm chi}\cot\left[M_n^{\rm chi}(L-W)\right]=M_n^{\rm i}\tan\left[M_n^{\rm i}W\right] \end{displaymath} (35)

for the even modes, and

 \begin{displaymath}M_n^{\rm chi}\cot\left[M_n^{\rm chi}(L-W)\right]=-M_n^{\rm i}\cot\left[M_n^{\rm i}W\right] \end{displaymath} (36)

for the odd modes; here

 \begin{displaymath}[M_n^{\rm chi}]^2=\frac{\omega^2}{v_{\rm Achi}^2}+(\lambda_n^... ...\rm i}]^2=\frac{\omega^2}{v_{\rm Ai}^2}+(\lambda_n^{\rm i})^2. \end{displaymath} (37)

The coefficients Hnm arising in the solution depend on  $h_m^{\rm i}(z)$and  $h_n^{\rm e}(z)$, being evaluated using Eq. (18), so are different from the case of a uniform tube.

5.1 Dispersion diagrams

There are two main cases of interest: the case where the loop footpoint is denser than the surrounding chromosphere (resulting in the footpoint having a depression in Alfvén speed compared with its surroundings), so $v_{\rm Achi} < v_{\rm Ache}$; and the case when the loop footpoint is less dense than the surrounding chromosphere (giving a footpoint with an enhancement in Alfvén speed compared with its surroundings), so $v_{\rm Achi} > v_{\rm Ache}$. If $v_{\rm Achi} < v_{\rm Ache}$, we expect trapped modes to propagate in the limit $W / L \rightarrow 0$ since the loop still has a density enhancement over its surroundings and so may act as a waveguide. This is illustrated by Fig. 6a, showing the dispersion diagram for $v_{\rm Ae}=2.5 v_{\rm Ai}$, $v_{\rm Achi}=0.25 v_{\rm Ai}$ and $v_{\rm Ache}=0.35 v_{\rm Ai}$, with a/L =0.1. The dispersion curve shown is the fundamental kink mode. The kink mode now propagates as a trapped mode for all W / L. Also in Fig. 6a we can see the cutoff frequency which varies with W / L and is the same as in Fig. 3; as expected, the cutoff frequency is independent of the internal structure of the loop.

The second case of interest is when $v_{\rm Achi} > v_{\rm Ache}$, so that the loop footpoint is less dense than the surrounding chromosphere and in the limit of $W / L \rightarrow 0$ we expect leaky modes. Figure 6b shows the dispersion diagram for the case $v_{\rm Ae}=2.5 v_{\rm Ai}$, $v_{\rm Achi}=0.35 v_{\rm Ai}$, and $v_{\rm Ache}=0.25 v_{\rm Ai}$, with a/L =0.1. The dispersion curve shown is the fundamental kink mode, which behaves similarly to the case of a uniform loop discussed earlier. The cutoff curve, shown as a dotted curve, is unchanged from Fig. 3, despite the different internal structure of the loop.

5.2 Eigenfunctions

To understand a mode of oscillation it is important to examine the perturbations it causes to the plasma through which it propagates. Here we consider the eigenfunctions associated with the fundamental kink mode shown in Fig. 6a for different values of W / L. Figure 7a shows the total pressure perturbation and Fig. 7b the radial velocity, both in the loop surface (r=a). For W / L =0.99, the total pressure perturbation has one extremum. However, as W / L is reduced additional extrema in the total pressure perturbation arise in the dense zones near the footpoints (case W/L= 0.9 in Fig. 6a), and then these additional extrema become wider as W/L is further decreased (cases W/L= 0.75 to W/L= 0.25) until the structure returns to one extremum as $W / L \rightarrow 0$.

Regarding the radial velocity component, vrhas little variation with r inside the loop ($r \le a$) and decreases exponentially for r>a with a very similar rate for all values of W/L. This is in accordance with Andries et al. (2005a) and Díaz et al. (2006a), who also remark that vr is less sensitive to longitudinal structure.


  \begin{figure} \par\mbox{\subfigure[]{\includegraphics[width=6cm,clip]{5524f7a.p... ...{4mm} \subfigure[]{\includegraphics[width=6cm,clip]{5524f7b.ps} }}\end{figure} Figure 7: Plots of a) $P_{{\rm T}}/ \rho _{\rm i} v_{\rm Ai}^2$ and b) $v_r/v_{\rm Ai}$ as a function of the longitudinal coordinate z/L along the loop boundary (r=a). The following parameters were used: W/L=0.25 (dotted line), W/L=0.5 (dashed line), W/L=0.75 (dot-dashed line), W/L=0.9 (long-dashed line), W/L=0.99 (solid line), with $v_{\rm Ae}=2.5 v_{\rm Ai}$, $v_{\rm Achi}=0.25 v_{\rm Ai}$, $v_{\rm Ache}=0.35 v_{\rm Ai}$ and a/L =0.1. The normalization has been chosen so that the slope of $P_{{\rm T}}$ at the footpoint z=L is the same for each W/L.
Open with DEXTER

Another property of interest is the penetration of an eigenfunction into the environment, which can give a indication of the importance of interaction with neighbouring loops. Figure 8 shows cuts of $P_{{\rm T}}$ as a function of r / a, with z /L =0. From these plots of $P_{{\rm T}}$ at the loop apex, it is clear that penetration is greater for smaller values of W/L. However, for the realistic range $W/L \approx 0.8{-}0.9$, interaction between neighbouring loops is weak unless closely packed.


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{5524f8.ps} \end{figure} Figure 8: Plots of $P_{{\rm T}}/ \rho _{\rm i} v_{\rm Ai}^2$ as a function of the radial coordinate r/a, for the loop apex z/L=0. The following parameters were used: W/L=0.1 (solid line), W/L=0.5 (dotted line), and W/L=0.99(dashed line), with $v_{\rm Ae}=2.5 v_{\rm Ai}$, $v_{\rm Achi}=0.25 v_{\rm Ai}$, $v_{\rm Ache}=0.35 v_{\rm Ai}$ and a/L =0.1.
Open with DEXTER

We now discuss the evolution of the eigenfunctions associated with the dispersion diagram shown in Fig. 6b, that is $v_{\rm Ache} < v_{\rm Achi}$. Similar to Fig. 5b, the total pressure perturbation shows the expected structure for the fundamental kink mode with one extremum when $W/L \approx 1$, but as W / L is reduced structures in the form of depressions are produced in the footpoints, with their magnitude increasing as W/L is reduced. Hence, for smaller values of W/L the oscillation power in the loop footpoint is greater, possibly making detection in this region more likely. The difference with Fig. 6 is that this transition appears as the frequency becomes closer to the cutoff, which now happens for realistic values of W / L. The total pressure eigenfunction does not penetrate more deeply into the loop's environment, even as the cutoff frequency is approached. The structure of vr is unchanged along the dispersion curve, although its maximum amplitude again shows an increase as W/L decreases (see also Andries et al. 2005b; and Díaz & Roberts 2006). Since a/L is small, vr is almost constant across the loop.

6 Discussion and conclusions

We have discussed the trapped oscillations of a coronal loop with a complex footpoint structure. The loop has been modelled as a cylindrically symmetric magnetic flux tube with a uniform or non-uniform structured density profile embedded in a longitudinally structured environment. The zero-$\beta$approximation has been employed. We have derived the dispersion relation for a generally structured profile and studied the effect of uniform dense chromospheric layers, firstly in the environment and then both inside and outside the loop; the interior and exterior structures are different.

It is found that the introduction of internal loop structuring results in a modification to the oscillatory frequency of the modes, which can lead to the loop supporting trapped modes (in accordance with Díaz et al. 2004). However, the inclusion of structuring in the loop environment results in a change in the cutoff frequency but only a slight alteration to the oscillatory frequency compared with that produced by the internal structuring, except in the region where the frequency of the mode approaches the cutoff frequency and is shifted in keeping with the cutoff frequency. These two effects appear to be universal across all density profiles.

We have found that the cutoff frequency depends upon the parameters of these chromospheric layer but is independent of the loop interior; the cutoff curve is the same for both uniform and structured loops, provided the environmental structuring is unchanged. This effect is more important for shorter loops where (L-W)/L is smaller, as a larger modification to the cutoff frequency is produced in such cases. The modification to the cutoff frequency as a result of the chromospheric layers may result in an enhancement in coronal leakage. In the case of a thin chromospheric layer, there is a single trapped kink mode with all higher harmonics and sausage modes possessing the same cutoff frequency. However, for certain parameters both the fundamental and first harmonic kink mode can be trapped. Importantly, no sausage modes lie under the cutoff for the thin tube, for any case examined, suggesting that the standing sausage mode is always leaky in the thin tube limit.

The evolution of $P_{{\rm T}}$ along the dispersion curve of the fundamental kink mode shows the development of structure in the loop's dense footpoints, and also a greater amplitude of oscillation in these regions for both the uniform and structured loop cases. Hence, these modes may be more readily detected in the footpoint regions of coronal loops.

All previous models have had a uniform cutoff curve, so all modes have the same cutoff frequency. The introduction of the dispersive effect produced by the chromospheric layers yields a non-uniform cutoff curve: no two modes possess the same cutoff frequency. As a result of the non-uniform cutoff, it is found that the fundamental kink mode of a uniform loop does not propagate as a trapped mode in the thin tube limit for certain chromospheric depths (typically W/L < 0.7; see Fig. 6b). This also happens in the case of a structured loop, if the footpoint is denser than the surrounding chromosphere. The observation that the fundamental kink mode is no longer trapped in the thin tube limit could have important consequences for coronal seismology. However, this result is lost in the structured loop if the chromospheric region is denser than the footpoint. It is possible that modes may propagate close to their cutoff frequency in this model with a substantial shift in their frequency, but penetration of the eigenfunctions into the loop's environment is no greater here than any other point on the dispersion curve; this indicates that the interaction between neighbouring loops is not significant for the case where the fundamental kink mode has a cutoff frequency. If the fundamental kink mode propagates as a trapped mode for small W/L, we find that the total pressure penetrates more deeply into the environment. But in the realistic range of $W/L \approx 0.8{-}0.9$ penetration is low, indicating interaction between neighbouring loops is not as strong as in Cartesian slabs (Oliver et al. 2006; Gruszecki et al. 2006; Díaz 2004).

The introduction of uniform chromospheric layers with sharp interfaces marking the boundaries between the chromosphere and the corona or the upper section of the loop can be regarded as a first step towards understanding the role of coronal structuring in more complex loop models.

Acknowledgements
G.R.D. acknowledges financial support from the Particle Physics and Astronomy Research Council. A.J.D. acknowledges financial support from PPARC on the St Andrews Solar Theory Rolling Grant.

References

 
Copyright ESO 2006