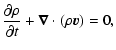 |
(1) | ||
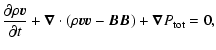 |
(2) | ||
![$\displaystyle \frac{\partial E}{\partial t} + \vec{\nabla}\cdot \left[ (E+P_{\rm tot})\vec{v}-\vec{B}(\vec{B} \cdot \vec{v}) \right] =0 ,$](/articles/aa/full/2006/38/aa5371-06/img10.gif) |
(3) | ||
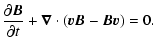 |
(4) |
A&A 457, 371-384 (2006)
DOI: 10.1051/0004-6361:20065371
S. Fromang1,2 - P. Hennebelle3 - R. Teyssier4
1 - Department of Applied Mathematics
and Theoretical Physics, University of Cambridge, Centre for
Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
2 -
Astronomy Unit, Queen Mary, University of London,
Mile End Road, London E1 4NS, UK
3 - Laboratoire de radioastronomie
millimétrique, UMR 8112 du CNRS,
École normale supérieure et Observatoire de Paris, 24 rue Lhomond,
75231 Paris Cedex 05, France
4 - Service d'Astrophysique,
CEA/DSM/DAPNIA/SAp, Centre d'Études de Saclay, L'orme des Merisiers,
91191 Gif-sur-Yvette Cedex, France
Received 5 April 2006 / Accepted 30 June 2006
Abstract
Aims. In this paper, we present a new method to perform numerical simulations of astrophysical MHD flows using the Adaptive Mesh Refinement framework and Constrained Transport.
Methods. The algorithm is based on a previous work in which the MUSCL-Hancock scheme was used to evolve the induction equation. In this paper, we detail the extension of this scheme to the full MHD equations and discuss its properties.
Results. Through a series of test problems, we illustrate the performances of this new code using two different MHD Riemann solvers (Lax-Friedrich and Roe) and the need of the Adaptive Mesh Refinement capabilities in some cases. Finally, we show its versatility by applying it to two completely different astrophysical situations well studied in the past years: the growth of the magnetorotational instability in the shearing box and the collapse of magnetized cloud cores.
Conclusions. We have implemented a new Godunov scheme to solve the ideal MHD equations in the AMR code RAMSES. We have shown that it results in a powerful tool that can be applied to a great variety of astrophysical problems, ranging from galaxies formation in the early universe to high resolution studies of molecular cloud collapse in our galaxy.
Key words: magnetohydrodynamics (MHD) - methods: numerical
Developing efficient numerical algorithms for the equations of magnetohydrodynamics (MHD) is of great astrophysical interest. Magnetic fields are ubiquitous in a great variety of environments. They are important components of the dynamics in such places as the early universe, the interstellar and intergalactic medium, the environment and interior of stars and the accretion flow around young stellar objects.
In the last few decades, finite differences methods have been widely used in investigations of a number of astrophysical situations in which the magnetic field is important with such codes as ZEUS (Stone & Norman 1992a,b), NIRVANA (Ziegler & Yorke 1997) or the Pencil Code (Brandenburg & Dobler 2002) for example. Even though, as expected, the numerical method breaks down in some circumstances (Falle 2002), a considerable amount of progress have been made in our understanding of MHD in astrophysics. A few attempts have also been made to try to extend the Smoothed Particle Hydrodynamics (SPH) method to MHD (,,). At the moment, it is not clear, however, how efficient the resulting codes will prove to be in the future.
In the last few years, several attempts have been made to try to extend the standard Godunov approach (Toro 1997), initially designed to solve the Euler equations, to MHD. In addition to the accurate description of new waves that are peculiar to MHD (Alfvén waves, the slow and fast modes), one of the most dramatic challenge in the development of such schemes comes from the solenoidality constraint, which states that the divergence of the magnetic field has to vanish everywhere at all times. The first algorithms that attempted to solve this problem kept the cell centering strategy of the standard Godunov approach. They used either a "divergence cleaning'' step (see for example Brackbill & Barnes 1980; or Ryu et al. 1998), or various reformulations of the MHD equations including additional divergence-waves (Powell et al. 1999) or divergence-damping terms (Dedner et al. 2002) to enforce the solenoidality constraint. A novel cell-centered MHD scheme has been recently developed by Crockett et al. (2005) that combines most of these ideas into one single algorithm. Alternative approach used the "staggered'' discretisation of the grid commonly used in "ZEUS-like'' codes along with the more geometrical Constrained Transport (CT) algorithm (Evans & Hawley 1988). This is for example the case of Balsara & Spicer (1999), Tóth (2000) and Londrillo & Del Zanna (2000, 2004). Gardiner & Stone (2005a) also explored the possibility of combining the CT algorithm with the PPM scheme in the new code ATHENA.
Recently, we proposed to extend the well-known MUSCL-Hancock algorithm originally designed for the Euler equation to the induction equation (Teyssier et al. 2006). We showed that three variants of our scheme have good performances. Two are compatible with the Adaptive Mesh Refinement (AMR) algorithm implemented in RAMSES (Teyssier 2002). This first part was limited to the induction equation, and could only be applied to situations where the magnetic field does not affect the flow. This is enough, however, to capture the physics of fast dynamos, especially with the help of the AMR. Here we extend our approach to the full set of MHD equations and implement it in RAMSES.
The plan of the paper is as follows: in Sect. 2, we present the details of the numerical algorithm. The discussion is based on our earlier work (Teyssier et al. 2006), where the technical details of the scheme are presented. In Sects. 3 and 4, we illustrate the properties of the code on standard 1D and 2D test problems. In Sect. 5, it is used to study a few 3D flows of astrophysical significance: the growth of the magnetorotational instability in accretion disks and the collapse of magnetized cloud cores. Finally, we summarise the properties of the code and highlight future possible developments in Sect. 6.
The equations we seek to solve are the usual MHD equations. When
written in conservative form, they read:
As discussed in the introduction, this set of equations has to be
completed by the solenoidal constraint, to be satisfied at all times:
| (7) |
In the followings, we describe our scheme using 3 dimensional
coordinates x, y and z. The physical variables are discretized
on a standard 3D Cartesian grid. The center of each cell is located
at the position
(xi,yj,zk). In a given cell, faces normal to the
x-direction have coordinates
![]() and cover a surface
element defined by
yj-1/2<y<yj+1/2 and
zk-1/2<z<zk+1/2. The coordinates of the other faces, normal to
the y and z direction, can be similarly defined.
and cover a surface
element defined by
yj-1/2<y<yj+1/2 and
zk-1/2<z<zk+1/2. The coordinates of the other faces, normal to
the y and z direction, can be similarly defined.
As for the Euler equations, the hydrodynamical variables (density,
momentum, energy) are volume-averaged over a cell and the
discretized values are defined at the cell center. For example:
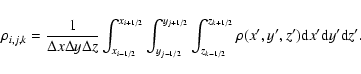 |
(9) |
 |
(10) |
As outlined in Londrillo & Del Zanna (2000), the system of MHD
equations written in Sect. 2.1 can be broken in two
sub-systems. The first involved the time evolution of the
cell-centered, volume-averaged variables and is reminiscent of the
standard Euler equations, which includes mass, momentum
and energy conservation. This set of equations, quite
naturally called the "Euler system'', can be written in vectorial
form
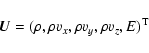 |
(12) |
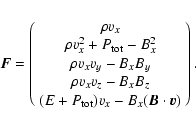 |
(13) |
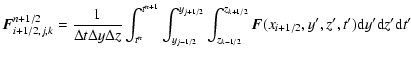 |
(15) |
In this paper, we intend to extend the well-known MUSCL-Hancock
scheme (van Leer 1977; Toro 1997) to the equations of ideal MHD. When
applied to the Euler equations, this method performs the conservative
update of the volume-average variables ![]() in two steps: a
predictor step and a corrector step. In the former, the vector
in two steps: a
predictor step and a corrector step. In the former, the vector
![]() is computed at the half time step
is computed at the half time step
![]() using a Taylor expansion of the underlying hyperbolic system. It
is also spatially reconstructed from the cell center to the cell faces
using a piecewise linear reconstruction based on TVD slope limiters.
In the predictor step, the fluxes appearing in
Eq. (14) are evaluated by solving a 1D
Riemann problem between the two (left and right) reconstructed states
at each cell interface.
using a Taylor expansion of the underlying hyperbolic system. It
is also spatially reconstructed from the cell center to the cell faces
using a piecewise linear reconstruction based on TVD slope limiters.
In the predictor step, the fluxes appearing in
Eq. (14) are evaluated by solving a 1D
Riemann problem between the two (left and right) reconstructed states
at each cell interface.
The first step in the MUSCL approach is the computation of
finite-difference approximation of the spatial derivatives of all
cell-centered quantities. As usually done in higher order finite
volume schemes, spatial derivatives are approximated using slope
limiters, in order to obtain positivity preserving, non oscillatory
solutions. Except for the final conservative update, we always use
the primitive variables
![]() in all
intermediate calculations. In addition to these 5 cell-centered
variables, we need to define volume-averaged magnetic field
components. We use for that purpose the average of their
corresponding face-centered components
in all
intermediate calculations. In addition to these 5 cell-centered
variables, we need to define volume-averaged magnetic field
components. We use for that purpose the average of their
corresponding face-centered components
The standard MUSCL methodology can be applied to the Euler sub-system,
using the previously defined cell-centered vector ![]() .
The
solution is advanced in time up to tn+1/2 using a Taylor
expansion of the Euler system in non-conservative form based on
the previously computed TVD slopes
.
The
solution is advanced in time up to tn+1/2 using a Taylor
expansion of the Euler system in non-conservative form based on
the previously computed TVD slopes
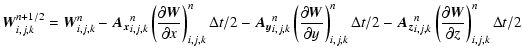 |
(17) |
Using the TVD slopes computed at time tn, we reconstruct
the primitive variables at each cell-interface, except for the
longitudinal magnetic field component, since its predicted value has
been already computed at the correct location (see
Sect. 2.4). For example, at the two interfaces
perpendicular to the x-axis, we obtain the two following
reconstructed states
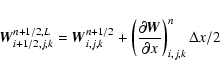 |
(18) |
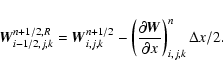 |
(19) |
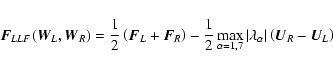 |
(20) |
To form the full set of MHD equations, Eq. (11)
has to be completed by the induction equation, called here the
induction sub-system. As for the Euler system, the induction equation
can be written in conservative form by a straightforward integration in
space-time
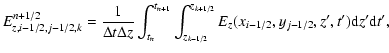 |
(23) |
In order to obtain a second-order accurate and non-oscillatory
solution, we need to use spatial reconstruction of the magnetic field
components based on TVD slope limiters. The main difference arises
because of the finite-surface representation of the magnetic field.
Indeed, we need a piecewise linear representation of Bx within the
y-z plane. For that purpose, we use the same TVD slopes (MinMod and
MonCen) as above, using the face-averaged value of the 3 magnetic
field components at time tn. For Bx, we need to compute only the
2 transverse slopes
![]() and
and
![]() .
A similar property holds for By and Bz.
.
A similar property holds for By and Bz.
Various methods to perform the predictor step for the induction system
were recently explored by Teyssier et al. (2006) for the kinematic
case. These methods were referred to as Runge-Kutta, U-MUSCL and
C-MUSCL. The extension of the first two to the full set of MHD equations, while possible, is computationally expensive because they
require to solve one (U-MUSCL) or two (Runge-Kutta) Riemann problems
in the predictive step. Moreover, the large stencil of the
Runge-Kutta scheme is not compatible with the compact stencil
required by our tree-based AMR implementation. For these various
reasons, we decide to use only the C-MUSCL scheme in our current MHD application. It combines the nice properties of being
computationnally efficient and compatible with the AMR requirements.
The price to pay is a reduced stability range for the time step, since
the Courant factor has to be less than
![]() ,
instead of 1 for the other schemes (see Teyssier et al.
2006, for details).
,
instead of 1 for the other schemes (see Teyssier et al.
2006, for details).
The purpose of the predictive step is to advance the solution between tn and tn+1/2 using the CT algorithm. For that, EMF need to be
spatially interpolated on cell edges at time tn. The idea of
C-MUSCL is to do it by simple arithmetic averages of the magnetic
field and velocity components. For example, the EMF
Ez,i-1/2,j-1/2,kn is calculated by:
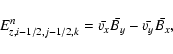 |
(24) |
| |
= | (25) | |
| = | (26) | ||
| = | (27) | ||
| = | (28) |
As described above, after the predictor step, we have obtained the 5 cell-centered Euler variables
![]() and the 3 face-centered magnetic field components
Bxn+1/2,
Byn+1/2 and
Bzn+1/2. Using
Eq. (16) at time tn+1/2, we have also obtained
the 3 predicted cell-centered components of the magnetic field. We
finally augment the vector
and the 3 face-centered magnetic field components
Bxn+1/2,
Byn+1/2 and
Bzn+1/2. Using
Eq. (16) at time tn+1/2, we have also obtained
the 3 predicted cell-centered components of the magnetic field. We
finally augment the vector
![]() with these
3 new cell-centered predicted variables.
with these
3 new cell-centered predicted variables.
Following again the MUSCL methodology, we now need to reconstruct complete MHD states at each cell-edge, in order to compute the EMF for the final conservative update of the magnetic field components. This reconstruction will produce 4 different states in the 4 cells adjacent to the edge. For obvious reasons, these 4 states, separated by 4 boundaries (labelled N for North, S for South, W for West and E for East) will be labelled in clockwise order by NE, SE, SW and NW.
We first reconstruct the cell-centered state to the cell edges using
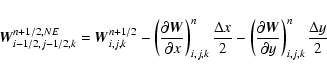 |
(29) |
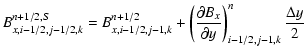 |
(30) | ||
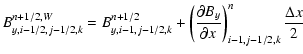 |
(31) |
| = | |||
| + | |||
| + | (32) |
| = | |||
| + | |||
| (33) |
The AMR algorithm used in RAMSES is described in details in
Teyssier (2002) and its extension to MHD in Teyssier et al. (2006).
We briefly recall the main features here. It is a tree-based AMR code
originally designed for cosmological applications. The data structure
is a "Fully Threaded Tree'' (Khokhlov 1998). The grid is divided
into groups of 8 cells, called "octs'', that share the same parent
cell. Each oct has access to its parent cell address in memory, but
also to neighboring parent cells. When a cell is refined, it is
called a "split'' cell, while in the opposite case, it is called a
"leaf'' cell. The computational domain is always defined as the unit
cube, which corresponds in our terminology to the first level of
refinement in the hierarchy ![]() .
The grid is then recursively
refined up to the minimum level of refinement
.
The grid is then recursively
refined up to the minimum level of refinement
![]() ,
in order
to build the coarse grid. This coarse grid is the base Cartesian
grid, covering the whole computational domain, from which adaptive
refinement can proceed. This base grid is eventually refined further
up to some maximum level of refinement
,
in order
to build the coarse grid. This coarse grid is the base Cartesian
grid, covering the whole computational domain, from which adaptive
refinement can proceed. This base grid is eventually refined further
up to some maximum level of refinement
![]() ,
according to some
user defined refinement criterion. When
,
according to some
user defined refinement criterion. When
![]() ,
the
computational grid is a traditional Cartesian grid, for which the
previous scheme apply without any modification. When refined cells
are created, however, some issues specific to AMR must be addressed.
,
the
computational grid is a traditional Cartesian grid, for which the
previous scheme apply without any modification. When refined cells
are created, however, some issues specific to AMR must be addressed.
When a cell is refined, eight new cells (i.e. a new "oct'') are
created for which new cell-centered variables and new magnetic field
components are needed. This operation is usually referred to as the
"prolongation operator''. The traditional approach relies on a
conservative interpolation of the 5 cell-centered conservative
variables
![]() .
For the
face-centered variables, each of the six faces of the parent cell are
split into 4 new fine faces. Three new faces, at the center of the
parent cell, are also split into four new children faces. The
resulting magnetic field components, fine or coarse, need to satisfy
the divergence-free constraint in integral form.
.
For the
face-centered variables, each of the six faces of the parent cell are
split into 4 new fine faces. Three new faces, at the center of the
parent cell, are also split into four new children faces. The
resulting magnetic field components, fine or coarse, need to satisfy
the divergence-free constraint in integral form.
This critical step has been solved by Balsara (2001) and Tóth & Roe (2002) in the CT framework. We recommend both of these articles for a detailed description of the method. The idea is to used slope limiters to interpolate the magnetic field component inside each parent face, in a flux-conserving way, and then to use a 3D reconstruction, which is divergence-free in a local sense inside the whole cell volume, in order to compute the new magnetic field components for each central children faces. In our case, the same slope limiters as in the Godunov scheme (MinMod or MonCen) can be used.
This prolongation operator is used to estimate the magnetic field in newly refined cells, but also to define a temporary "buffer zone'', two "ghost cells'' wide, that set the proper boundary for fine cells at a coarse-fine level boundary. This is the main reason why compact stencils are needed for the underlying Godunov scheme.
The other important step is to define the reverse operation, when a split cell is de-refined, and becomes a leaf cell again. This operation is usually called the Restriction Operator in the multigrid terminology. The solenoidality constraint needs again to be satisfied, which translates into conserving the magnetic flux. The magnetic field component in the coarse face is just the arithmetic average of the 4 fine face values. This is reminiscent of the "flux correction step'' for the Euler system (Teyssier 2002; Berger & Oliger 1984; Berger & Colella 1989).
The "EMF correction step'' is more specific to the induction equation. For a coarse face which is adjacent, in any direction, to a refined face, the coarse EMF in the conservative update of the solution needs to be replaced by the arithmetic average of the two fine EMF vectors. This guarantees that the magnetic field remains divergence-free, even at coarse-fine boundaries.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{5371f1.ps}
\end{figure}](/articles/aa/full/2006/38/aa5371-06/Timg106.gif) |
Figure 1: Amplitude ( upper panel) and phase velocity ( lower panel) of the circularly polarized Alfvén wave as a function of time. The full lines display result using a Roe solver whereas the dotted lines show results obtained with a Lax-Friedrich solver. The resolutions are from top to bottom, 100, 30 and 10 grid points per wavelength. |
| Open with DEXTER | |
The first test we present is the propagation of non-linear circularly
polarised Alfvén waves. Such waves, which are exact solution of the
MHD equations, propagate in a gas of uniform density, ![]() and
along a uniform magnetic field, B0z. They are given by:
and
along a uniform magnetic field, B0z. They are given by:
![]() ,
,
![]() ,
,
![]() ,
,
![]() where
where
![]() and
and
![]() .
.
We have simulated the propagation of these waves on a uniform grid,
for
![]() ,
,
![]() ,
and k=0.1. This
leads to a wave period equal to 0.1. The agreement between the
analytical and numerical solutions depends on the numerical
resolution. Figure 1 displays the wave amplitude ( upper panel) and phase velocity (lower panel) as a function
of time for the Roe and Lax-Friedrich solvers and different
resolutions, namely 10, 30 and 100 points per wavelength. With 10 grid points per wavelength, the amplitude quickly decays
because of
numerical dissipation and in about 5 wave periods, the amplitude of
the waves is only 40
,
and k=0.1. This
leads to a wave period equal to 0.1. The agreement between the
analytical and numerical solutions depends on the numerical
resolution. Figure 1 displays the wave amplitude ( upper panel) and phase velocity (lower panel) as a function
of time for the Roe and Lax-Friedrich solvers and different
resolutions, namely 10, 30 and 100 points per wavelength. With 10 grid points per wavelength, the amplitude quickly decays
because of
numerical dissipation and in about 5 wave periods, the amplitude of
the waves is only 40![]() of its initial value. With 30 and 100 grid
points
per wavelength the agreement is much better and almost no decay has
occurred even after 50 wave periods in the latter case. In the
lower panel, the wave velocity is also seen to agree better and better
with its theoretical value, vw=1, as the resolution is increased (note
that for 100 grid points, the wave velocity obtained with the Roe solver is
not represented as it is indistinguishable from the Lax-Friedrich
results). As expected the Roe solver leads to slightly better results
in both cases than the Lax-Friedrich solver.
of its initial value. With 30 and 100 grid
points
per wavelength the agreement is much better and almost no decay has
occurred even after 50 wave periods in the latter case. In the
lower panel, the wave velocity is also seen to agree better and better
with its theoretical value, vw=1, as the resolution is increased (note
that for 100 grid points, the wave velocity obtained with the Roe solver is
not represented as it is indistinguishable from the Lax-Friedrich
results). As expected the Roe solver leads to slightly better results
in both cases than the Lax-Friedrich solver.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{5371f2.ps}
\end{figure}](/articles/aa/full/2006/38/aa5371-06/Timg117.gif) |
Figure 2:
Solution to the MHD shock tube showing the density as a
function of x, obtained with RAMSES when
|
| Open with DEXTER | |
| |
= | (34) | |
| = | (35) |
Here, we use RAMSES to illustrate how the AMR scheme can help to solve
this problem. Figure 2 shows the density vs.
position when
![]() at time t=0.4. The grid is composed of 400 cells evenly distributed between -1 and 1.5. The AMR is
switched off in this first run. The compound wave is clearly visible
at
at time t=0.4. The grid is composed of 400 cells evenly distributed between -1 and 1.5. The AMR is
switched off in this first run. The compound wave is clearly visible
at
![]() .
The whole solution looks identical to previous
results published in the literature with similar codes
(Ryu & Jones 1995; Londrillo & Del Zanna 2000; Cargo & Gallice 1997).
.
The whole solution looks identical to previous
results published in the literature with similar codes
(Ryu & Jones 1995; Londrillo & Del Zanna 2000; Cargo & Gallice 1997).
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{5371f3.ps}
\end{figure}](/articles/aa/full/2006/38/aa5371-06/Timg126.gif) |
Figure 3:
Zoom on the region in which the compound wave develops when
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{5371f4.ps}
\end{figure}](/articles/aa/full/2006/38/aa5371-06/Timg127.gif) |
Figure 4:
Complete solution of the MHD shock tube when |
| Open with DEXTER | |
Taking now ![]() and computing the solution of the MHD shock tube
on a uniform grid, we also found that the compound wave remains for
low resolution as described by Torrilhon (2004). This is
illustrated in Fig. 3, which is a zoom on the
structure of the solution in the neighbourhood of the compound
wave. The black lines are computed on a uniform grid and correspond to
increasing resolution. Namely, from top to bottom (at
and computing the solution of the MHD shock tube
on a uniform grid, we also found that the compound wave remains for
low resolution as described by Torrilhon (2004). This is
illustrated in Fig. 3, which is a zoom on the
structure of the solution in the neighbourhood of the compound
wave. The black lines are computed on a uniform grid and correspond to
increasing resolution. Namely, from top to bottom (at
![]() ),
the number of cells are 800, 1200, 1600, 2000, 3000, 5000,
10 000 and 20 000. The red line shows the result of the same model
computed using the AMR scheme with a refinement strategy based on the
magnitude of the gradient of all 7 flow variables. The finest
resolution in this run is equivalent to having 106 cells on a
uniform grid. We found the result of this model to be almost
indistinguishable from the regular solution (remember that this is the
ONLY physical solution to this problem). Interestingly, this is not
the case for the uniform runs. Even though the compound wave is seen
to gradually disappear as the resolution is increased, features
departing from the correct solution are still observed even when
20 000 grid zones are used. This illustrates the extremely large
resolution needed to accurately calculate the solution of this problem
and shows the interest of using AMR. Indeed, the AMR run used only
10 000 cells for the same equivalent resolution as 106 grid cells,
which corresponds to a gain of about 2500 in CPU time.
),
the number of cells are 800, 1200, 1600, 2000, 3000, 5000,
10 000 and 20 000. The red line shows the result of the same model
computed using the AMR scheme with a refinement strategy based on the
magnitude of the gradient of all 7 flow variables. The finest
resolution in this run is equivalent to having 106 cells on a
uniform grid. We found the result of this model to be almost
indistinguishable from the regular solution (remember that this is the
ONLY physical solution to this problem). Interestingly, this is not
the case for the uniform runs. Even though the compound wave is seen
to gradually disappear as the resolution is increased, features
departing from the correct solution are still observed even when
20 000 grid zones are used. This illustrates the extremely large
resolution needed to accurately calculate the solution of this problem
and shows the interest of using AMR. Indeed, the AMR run used only
10 000 cells for the same equivalent resolution as 106 grid cells,
which corresponds to a gain of about 2500 in CPU time.
The complete solution of the AMR model is shown in Fig. 4. As is Fig. 2, the solid line represents the density as a function of position. The dashed line shows the corresponding refinement level. It scale is indicated on the right axis. As expected, the grid is highly refined at the location of the shocks and contact discontinuities. It is important to understand that the AMR is not just a fancy tool for this test, but is actually essential to solve it properly. One might indeed think that increasing the order of the numerical scheme would help to converge to the regular solution at lower resolution. Torrilhon & Balsara (2004) actually showed that the improvement when using third or fourth order WENO schemes is small. This is because the accuracy of any such schemes breaks down to first order close to discontinuities, which is precisely where the compound wave lies.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{5371f5.ps}
\end{figure}](/articles/aa/full/2006/38/aa5371-06/Timg128.gif) |
Figure 5: Time history of the magnetic energy in the magnetic loop advection test. The different curves are obtained using the Roe Riemann solver ( solid line) and the Lax-Friedrich solver ( dashed line). |
| Open with DEXTER | |
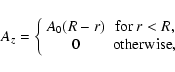 |
(36) |
A simple way to evaluate the efficiency of the scheme is to compare the time history of the magnetic energy Em. This is done in Fig. 5, where Em is represented as a function of time for the Roe solver (solid line) and for the Lax-Friedrich solver (dashed line). We first note that the results are very similar to those published by Gardiner & Stone (2005a). This demonstrates that, using only TVD linear reconstruction, our scheme provides comparable accuracy to the piecewise parabolic scheme of Gardiner & Stone (2005a). As expected, the Lax-Friedrich solver is more dissipative, while the results obtained using the Roe solver exactly reproduce the results obtained in the pure advection case (Teyssier et al. 2006), to which we refer the reader for more details, especially regarding the AMR scheme.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{5371f6.ps}
\end{figure}](/articles/aa/full/2006/38/aa5371-06/Timg133.gif) |
Figure 6: Snapshot of the density at time t=0.5 resulting from the Orszag-Tang test. The grid is uniform and composed of 5122 cells. The result is computed using the Roe Riemann solver and the C-MUSCL predictive step. |
| Open with DEXTER | |
One of the most well-known 2D MHD test is the Orszag-Tang test. The initial condition of the flow create a vortex that is unstable and quickly breaks down into turbulence. Although no analytical solution is known for this test, it has been so widely documented in the literature that it is now very useful as a first 2D benchmark for a code.
The initial state is defined as
| |
= | (37) | |
| = | (38) | ||
| = | (39) |
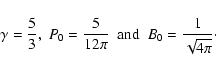
![\begin{figure}
\par\includegraphics[width=4.2cm,clip]{5371f7.ps}\hspace*{3mm}
\i...
...f14.ps}\hspace*{3mm}
\includegraphics[width=4.2cm,clip]{5371f15.ps}
\end{figure}](/articles/aa/full/2006/38/aa5371-06/Timg141.gif) |
Figure 7: Time evolution of the magnetic field lines during the current sheet test. The calculation was performed on a uniform grid composed of 2562 cells, using the Roe solver and the MonCen slope limiter. From top left to bottom right, the snapshots corresponds successively to times t=0,0.5,1,1.5,2,2.5,3, 3.5 and 4. The entire figure can be compared to Fig. 12 of Gardiner & Stone (2005a). |
| Open with DEXTER | |
Gardiner & Stone (2005a) recently described a 2D test that follows the time evolution of a current sheet created by a magnetic field discontinuity. Reconnection occurs at the location of the discontinuity. Because no explicit dissipation is included in the code, the entire evolution is driven by the numerical resisitivity of the scheme, and, as such, is sensitive to every details of the algorithm. The initial setup is described in the followings.
![\begin{figure}
\par\includegraphics[width=10cm,clip]{5371f16.ps}
\end{figure}](/articles/aa/full/2006/38/aa5371-06/Timg142.gif) |
Figure 8:
This figure compares the magnetic field lines obtained at
time t=2 for high-resolution runs ( bottom) and low-resolution runs
( top), as well as for the Roe solver ( right) and the local
Lax-Friedrich solver ( left). Both low and high-resolution runs
were performed using the AMR scheme:
|
| Open with DEXTER | |
The computational domain lies in the domain
![]() and
and
![]() and is divided in 256 uniform cells in each
directions. At time t=0, density and pressure are uniform:
and is divided in 256 uniform cells in each
directions. At time t=0, density and pressure are uniform: ![]() and P=0.1. The magnetic field components vanish in the x and z direction and By is defined by
and P=0.1. The magnetic field components vanish in the x and z direction and By is defined by
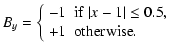 |
(40) |
![\begin{figure}
\par\includegraphics[width=15.4cm,clip]{5371f17.ps}
\end{figure}](/articles/aa/full/2006/38/aa5371-06/Timg148.gif) |
Figure 9: This figure shows a zoom on the bottom left magnetic island for the high-resolution run with the Roe solver at time t=3. On the left, only octs boundaries are plotted to clarify the visualization of the AMR grid. On the right, a grey scale image of the thermal pressure is shown, with strong transverse shock-waves clearly visible as sharp discontinuities. |
| Open with DEXTER | |
We first present our numerical results using the Roe solver with the MonCen slope limiter. They are represented in Fig. 7. The magnetic field lines are plotted at times t=0, 0.5, 1, 1.5, 2, 2.5, 3, 3.5and 4. As reported by Gardiner & Stone (2005a), magnetic islands form, grow and eventually merge with each other. At the end of the simulation, four islands are clearly visible at the location of each discontinuity. A direct comparison between our results and Fig. 12of Gardiner & Stone (2005a) shows that both codes agree almost perfectly up to time t=2.5. On the other hand, at later time, no strong evolution is observed in our case, while for the ATHENA code, the flow symmetry is broken and the two islands merge into a single large one (Gardiner & Stone 2005a). As discussed above, this difference is an indication that both codes, although very similar, have different dissipative properties.
The next step is to test our AMR scheme in 2D: we perform the same
exact simulation, except that now we use a base grid of
nx=ny=32,
which corresponds to
![]() ,
with 3 additional levels of
refinement, so that
,
with 3 additional levels of
refinement, so that
![]() .
The formal resolution is thus
equivalent to the first test with a regular Cartesian grid. We use a
refinement strategy based on the gradient of the thermal pressure:
.
The formal resolution is thus
equivalent to the first test with a regular Cartesian grid. We use a
refinement strategy based on the gradient of the thermal pressure:
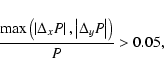 |
(41) |
In order to study the convergence of each solution, we take
advantage of the
speed-up provided by the AMR grid to perform additional
high-resolution simulation. Using the same refinement strategy, we
now set
![]() ,
so that the formal resolution is now
nx=ny=1024. We present in Fig. 9 the resulting
AMR grid, together with a grey-scale image of the thermal pressure.
We see that AMR cells are optimally distributed in order to properly
sample the current sheet, as well as sharp MHD waves propagating
perpendicular to the current sheet. The results obtained at t=2using both Riemann solvers are shown at the bottom plots of
Fig. 8. The Roe solution has not changed when
compared to its low-resolution counterpart. This demonstrates that
the lower numerical dissipation of the Roe solver allows a faster
convergence of the numerical solution. Interestingly, the
Lax-Friedrich high-resolution solution has also converged toward the
same solution, except for the static magnetic island at the flow
stagnation point. This demonstrates that using AMR can provide fast
convergence towards the true solution, even with a rather dissipative
scheme. On the other hand, the static island in the center of the flow
seems to be highly sensitive to the details of the scheme. As opposed
to Lax-Friedrich, the Roe solver has the interesting property that
for a static velocity field, the numerical dissipation vanishes
exactly. The difference between the 2 solvers is therefore maximized
at the stagnation point, where both schemes are converging towards 2 different solutions, even at our highest resolution. This peculiar
behavior is due to the fact that this reconnection problem is
performed without any physical resistivity. It should be therefore
considered only as an interesting numerical test, rather than a true
physical application.
,
so that the formal resolution is now
nx=ny=1024. We present in Fig. 9 the resulting
AMR grid, together with a grey-scale image of the thermal pressure.
We see that AMR cells are optimally distributed in order to properly
sample the current sheet, as well as sharp MHD waves propagating
perpendicular to the current sheet. The results obtained at t=2using both Riemann solvers are shown at the bottom plots of
Fig. 8. The Roe solution has not changed when
compared to its low-resolution counterpart. This demonstrates that
the lower numerical dissipation of the Roe solver allows a faster
convergence of the numerical solution. Interestingly, the
Lax-Friedrich high-resolution solution has also converged toward the
same solution, except for the static magnetic island at the flow
stagnation point. This demonstrates that using AMR can provide fast
convergence towards the true solution, even with a rather dissipative
scheme. On the other hand, the static island in the center of the flow
seems to be highly sensitive to the details of the scheme. As opposed
to Lax-Friedrich, the Roe solver has the interesting property that
for a static velocity field, the numerical dissipation vanishes
exactly. The difference between the 2 solvers is therefore maximized
at the stagnation point, where both schemes are converging towards 2 different solutions, even at our highest resolution. This peculiar
behavior is due to the fact that this reconnection problem is
performed without any physical resistivity. It should be therefore
considered only as an interesting numerical test, rather than a true
physical application.
To illustrate the possibilities of RAMSES, we present in this section two 3D tests of astrophysical significance: the development of Magneto-Rotational Instability (MRI) and the formation of a magnetized molecular core.
The development of MHD turbulence resulting from the growth of the MRI is likely to be at the origin of an efficient radial transport in accretion disks. This instability has been extensively studied using finite difference codes like ZEUS (Hawley et al. 1995); our goal is here to compare the results of RAMSES with those obtained in earlier studies during the last decade.
The MRI is a linear instability that was first discovered in the 60s (Velikhov 1959; Chandrasekhar 1961) before being applied to accretion disks theory by Balbus & Hawley (1991). It operates in rotating flows threaded by a weak magnetic field when the angular velocity decreases outward. Numerical simulations applied to accretion disks have shown that the linear growth of the instability is followed by MHD turbulence that transports angular momentum outward in the disk, thereby solving a long standing issue in accretion disk theory (see Balbus & Hawley 1998, for a review). One subclass of these simulations has been realised using the so-called shearing box approximation. It is a local expansion of the dynamical equation in a Cartesian box around a particular radius of the accretion disk (Goldreich & Lynden-Bell 1965). The interest of this local approach is that it is able to capture the dynamics of the accretion disk and enables large resolution to be achieved at the same time. With such a model, the properties of the MHD turbulence can be rather well studied.
So far, most of the shearing box simulations have been done using artificial viscosity codes, like ZEUS (Hawley et al. 1995), NIRVANA (Papaloizou et al. 2004) or the Pencil Code (Brandenburg et al. 1995). Recently, Gardiner & Stone (2005b) applied the ATHENA code to the same problem. They found that using a Riemann solver make little difference.
We have implemented the shearing box model in RAMSES. To do so, two
main modifications have to be made. First, the inertial terms
appearing in the equations are treated as source terms. Second, the
boundary conditions need to be adapted to the model. They are
periodic in y and z, which respectively correspond to the ![]() and z coordinates of the standard cylindrical coordinates. The
boundary conditions in x (the equivalent of R in cylindrical
coordinates) are the so-called shearing boundary conditions widely
discussed in the literature (Gardiner & Stone 2005b; Hawley et al. 1995).
and z coordinates of the standard cylindrical coordinates. The
boundary conditions in x (the equivalent of R in cylindrical
coordinates) are the so-called shearing boundary conditions widely
discussed in the literature (Gardiner & Stone 2005b; Hawley et al. 1995).
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{5371f18.ps}
\end{figure}](/articles/aa/full/2006/38/aa5371-06/Timg154.gif) |
Figure 10: Structure of the flow in the (x,z) plane after 60 orbits. The arrows shows the poloidal velocity field overplotted on gray scale contours of the y-component of the magnetic field. Because of the growth of the MRI, the entire flow has become turbulent. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{5371f19.ps}
\end{figure}](/articles/aa/full/2006/38/aa5371-06/Timg155.gif) |
Figure 11: Time history of the volume averaged Maxwell stress tensor normalized by pressure, obtained in the shearing box model. The solid line was computed using RAMSES and the dashed line was calculated using ZEUS. Both models use exactly the same set of parameters. Both shows sustained MHD turbulence and a similar amount of angular momentum transport. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{5371f20.ps}\par\vspace*{2mm}...
...1.ps}\par\vspace*{2mm}
\includegraphics[width=7cm,clip]{5371f22.ps}
\end{figure}](/articles/aa/full/2006/38/aa5371-06/Timg156.gif) |
Figure 12: Three timesteps illustrating the hydrodynamical collapse. |
| Open with DEXTER | |
The initial conditions of our runs are those of the standard shearing
box model. The initial density is uniform and equal to unity
everywhere. The velocity is such that
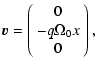 |
(42) |
| (43) |
![\begin{figure}
\par\mbox{\includegraphics[width=7cm,clip]{5371f23.ps}\hspace{4mm...
...1f25.ps}\hspace{4mm}
\includegraphics[width=7cm,clip]{5371f26.ps} }
\end{figure}](/articles/aa/full/2006/38/aa5371-06/Timg165.gif) |
Figure 13: Two timesteps illustrating the magnetized collapse. The upper panels display the equatorial density and velocity field whereas bottom panels displays the density in x-z plane. The calculation is performed with the Lax-Friedrich solver. |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[width=7cm,clip]{5371f27.ps}\hspace{4mm...
...f29.ps}\hspace{4mm}
\includegraphics[width=7cm,clip]{5371f30.ps} }\end{figure}](/articles/aa/full/2006/38/aa5371-06/Timg171.gif) |
Figure 14: Same as Fig. 13 except that the calculation has been carried out with the Roe solver. |
| Open with DEXTER | |
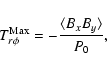 |
(44) |
Such calculations in the hydrodynamical case have been performed by several authors using either SPH methods (e.g. Hennebelle et al. 2004) or grid based method (e.g. Matsumoto & Hanawa 2003). In the magnetized case, much fewer 3D calculations have been carried out using SPH (Hosking & Whitworth 2004), nested grid (Machida et al. 2005a,b; Banerjee & Pudritz 2006) or an AMR implementation (Ziegler 2005).
In order to do a precise comparison, we adopt the same initial conditions
as Hosking & Whitworth (2005) and Ziegler (2005).
The cloud has initially a uniform density of
![]() g cm-3, a temperature of 10 K and a radius of
g cm-3, a temperature of 10 K and a radius of
![]() pc.
The total mass is equal to one solar mass and the initial ratio
of thermal to gravitational energy is about 0.35.
The cloud is initially in solid body rotation with angular
velocity
pc.
The total mass is equal to one solar mass and the initial ratio
of thermal to gravitational energy is about 0.35.
The cloud is initially in solid body rotation with angular
velocity
![]() s-1 leading to an
initial ratio of rotational to gravitational energy of about 0.45.
To induce fragmentation, an m=2 perturbation on the density field
with an amplitude of 10
s-1 leading to an
initial ratio of rotational to gravitational energy of about 0.45.
To induce fragmentation, an m=2 perturbation on the density field
with an amplitude of 10![]() has been setup initially.
The magnetic field is initially uniform and parallel to the rotation axis.
We use the same barotropic equation of state as Hosking & Whitworth (2005),
namely
has been setup initially.
The magnetic field is initially uniform and parallel to the rotation axis.
We use the same barotropic equation of state as Hosking & Whitworth (2005),
namely
![]() with
with
![]() g cm-3. All calculations have
initially 643 cells and uses 8 additional AMR levels. The
refinement criteria
is based on the Jeans length which is numerically described by at
least 10 cells.
g cm-3. All calculations have
initially 643 cells and uses 8 additional AMR levels. The
refinement criteria
is based on the Jeans length which is numerically described by at
least 10 cells.
Figure 12 displays three snapshots of the
hydrodynamical case performed with the Lax-Friedrich solver. The equatorial
density field is displayed and the arrows show the velocity field.
The top panel is very similar to the second panel of Fig. 8 of Ziegler (2005).
Both spiral patterns have approximately the same size and the same
orientation.
Timing is also very similar (agreement within about 5![]() of accuracy).
The result compares well to the SPH calculation of Hosking & Whitworth (2005) shown in their Fig. 2 (bottom-right panel).
The second panel of Fig. 12 appears to be similar to
the bottom-left panel of Fig. 3 of Hosking & Whitworth (2005).
In both cases about 5 fragments have formed located approximately at the same
position in both simulations. The third panel shows the density field 0.01 Myr after the time of the second panel which is comparable to the
timeshift between left-bottom and right-bottom of Fig. 3 of
Hosking & Whitworth (2005). The agreement is less good than
for earlier time. Our results remain symmetric
which is not the case for the Hosking & Whitworth's results.
of accuracy).
The result compares well to the SPH calculation of Hosking & Whitworth (2005) shown in their Fig. 2 (bottom-right panel).
The second panel of Fig. 12 appears to be similar to
the bottom-left panel of Fig. 3 of Hosking & Whitworth (2005).
In both cases about 5 fragments have formed located approximately at the same
position in both simulations. The third panel shows the density field 0.01 Myr after the time of the second panel which is comparable to the
timeshift between left-bottom and right-bottom of Fig. 3 of
Hosking & Whitworth (2005). The agreement is less good than
for earlier time. Our results remain symmetric
which is not the case for the Hosking & Whitworth's results.
In this section we present results for the MHD collapse. The intensity of the magnetic field is such that the cloud mass-to-flux ratio is twice the critical mass-to-flux ratio. This corresponds to the first MHD case studied by Ziegler (2005).
Figure 13 shows results for a calculation performed with the Lax-Friedrich solver whereas Fig. 14 shows results obtained with the Roe solver. Upper panels of Figs. 13 and 14 display the equatorial density field whereas bottom panels display the density in the x-z plane. Left panels display results at a time close to the first panel of Fig. 10 of Ziegler (2005). Right panels display results about 0.01 Myr later.
In his simulation, Ziegler reports the formation of a binary having a
separation at time
![]() of about 0.06
of about 0.06 ![]() where
where
![]() is the freefall time.
As shown in Fig. 13, there are no binaries with the Lax-Friedrich
solver. There is also a shift in time (of about
is the freefall time.
As shown in Fig. 13, there are no binaries with the Lax-Friedrich
solver. There is also a shift in time (of about ![]() )
since the collapse
occurs slightly later than
)
since the collapse
occurs slightly later than
![]() .
On the contrary, as shown
in Fig. 14, in the simulation performed with the Roe solver,
a binary forms at time
.
On the contrary, as shown
in Fig. 14, in the simulation performed with the Roe solver,
a binary forms at time
![]() although we find a separation
of 0.03
although we find a separation
of 0.03 ![]() instead of 0.06
instead of 0.06 ![]() .
Ziegler reports also another case with
stronger magnetic field for which the mass-to-flux ratio is 1.2 times
the critical mass-to-flux ratio. In this case he finds no binary. We have
also performed this simulation (not displayed here for conciseness)
and we confirm the absence of binary. Although the formation of the binary
appears to be a good numerical test, it should be said that it is somehow
physically artificial since it relies on initial conditions for which
the density field is perturbed but not the magnetic field. As a
result, the magnetic Jeans mass at the density maximum is lowered,
thus making the perturbation very unstable. Indeed we have performed a
simulation in which the m=2 perturbation has been applied to the
magnetic field as well. In this case, instead of a binary, we find two very shallow local maxima.
.
Ziegler reports also another case with
stronger magnetic field for which the mass-to-flux ratio is 1.2 times
the critical mass-to-flux ratio. In this case he finds no binary. We have
also performed this simulation (not displayed here for conciseness)
and we confirm the absence of binary. Although the formation of the binary
appears to be a good numerical test, it should be said that it is somehow
physically artificial since it relies on initial conditions for which
the density field is perturbed but not the magnetic field. As a
result, the magnetic Jeans mass at the density maximum is lowered,
thus making the perturbation very unstable. Indeed we have performed a
simulation in which the m=2 perturbation has been applied to the
magnetic field as well. In this case, instead of a binary, we find two very shallow local maxima.
Right panels of Fig. 14 show that the two fragments have merged leaving a single central fragment. This is an important difference with the hydrodynamical case in which five fragments have been found (although further evolution reveals that two of these fragments merge with the central one). Another important departure from the hydrodynamical case is the presence of strong outflows (right-bottom panel). There are very similar to the outflows shown in Machida et al. (2005b). Outflows are also obtained with the Lax-friedrich solver (right-botton panel of Fig. 13) although the flow structure is slightly different. With the Roe solver, the velocity field along the z-axis vanishes whereas this is not the case with the Lax-Friedrich solver. The disk appears to be thicker with the Lax-Friedrich solver than with the Roe solver.
We conclude that RAMSES-MHD is able to reproduce quantitatively results obtained by various authors including fragmentation and outflows. Significant differences appear between results obtained with the Lax-Friedrich and the Roe solvers although the former is able to reproduce the main features of the flow.
In this paper, we have presented an extension of RAMSES to MHD. The algorithm is based on the MUSCL-Hancock approach already used in the hydrodynamic version of RAMSES (Teyssier 2002). The induction equation is evolved in time using the standard CT scheme (Evans & Hawley 1988). To do so, time averaged EMFs are computed on cell edges by solving a 2D Riemann problem, as described in Londrillo & Del Zanna (2000). Several tests are presented that illustrate the properties and robustness of the code. In particular, we show that the AMR scheme implemented in RAMSES can be crucial to describe accurately the propagation of some unusual waves peculiar to MHD like the compound waves.
We also demonstrate the versatility of RAMSES by studying two problems of astrophysical significance: the development of MHD turbulence in accretion disk and the collapse of dense core in the interstellar medium. In both cases, we report results that are consistent with previous studies published in the literature. These two applications show that RAMSES is well suited to study a wide variety of problems involving MHD in astrophysics.
In future studies, several improvements will now be investigated. It will be particularly useful, for example, to develop a proper 2D Riemann solver to calculate the time averaged EMFs, instead of making linear combination of 1D solvers as it is done now. Nonlinear Riemann solvers could also be implemented, like HLLC (Miyoshi & Kusano 2005) for example. Obviously, an extension to curvilinear coordinates would also be very interesting, particularly for applications involving accretion disks or galaxies. Finally, it will be necessary in some cases to go beyond the ideal MHD framework and to implement new physics like ohmic dissipation or ambipolar diffusion.
Acknowledgements
The authors thank Emmanuel Dormy and Stéphane Colombi for useful discussions. Some of the simulations presented in this paper were performed on the QMUL High Performance Computing Facility purchased under the SRIF initiative and at CCRT, the CEA supercomputing center.