We have considered two parallel propagating kinetic Alfvén waves (KAW) propagating in a plasma with
A&A 457, 675-680 (2006)
DOI: 10.1051/0004-6361:20054715
R. P. Sharma - M. Malik
Center for Energy Studies, Indian Institute of Technology, Delhi 110016, India
Received 19 December 2005 / Accepted 16 May 2005
Abstract
We have considered two parallel propagating kinetic Alfvén waves (KAW) propagating in a plasma with ![]() in the limit
(
in the limit
(
![]() ). The spatial amplification and
ultimately filamentation of a perturbation present on one of the KAW has
been studied, especially in the presence of second KAW. Nonlinear evolution
of the perturbation, present on the main KAW, into the filamentary
structures and its dependence on various parameters of the second KAW has
been investigated in detail for solar wind parameters. These filamentary
structures can act as a source for the particle acceleration by wave
particle interaction because the KAW are mixed modes and Landau damping is
possible. The relevance of this work to the solar wind turbulence spectrum
and the energization of heliosphere particles by the solar wind is
discussed.
). The spatial amplification and
ultimately filamentation of a perturbation present on one of the KAW has
been studied, especially in the presence of second KAW. Nonlinear evolution
of the perturbation, present on the main KAW, into the filamentary
structures and its dependence on various parameters of the second KAW has
been investigated in detail for solar wind parameters. These filamentary
structures can act as a source for the particle acceleration by wave
particle interaction because the KAW are mixed modes and Landau damping is
possible. The relevance of this work to the solar wind turbulence spectrum
and the energization of heliosphere particles by the solar wind is
discussed.
Key words: plasmas - Sun: solar wind
The solar wind is formed by the gas-dynamic expansion of the solar corona.
In situ observations have revealed that the solar wind exists in two
distinct states: the fast stream (>700 km s-1) and the slow
(![]() 400 km s-1) stream. The low speed streams originate in the open fields above
active regions of the solar corona. The high speed streams originate over
coronal holes The predominance of nearly incompressible Alfvén waves in
the solar wind stream has also been confirmed by Daily (1973), Parker
(1980a,b) and Bavassano et al. (1982). Hollweg et al. (1982) analyzed
data from the Helios 2 satellite and found Alfvén waves making a
significant contribution to the high speed streams. A detailed discussion of
Alfvén wave domination in the solar wind is given by Denskat & Burlaga
(1977). The Alfvén waves observed in situ in the solar wind provide a
clue that dissipation of Alfvén waves in the solar corona could provide
the heat input and wave pressure gradient (wave ponderomotive force)
necessary to heat and accelerate the high speed solar wind (Parker 1991).
Alfvén waves can be dissipated in the solar corona by magnetic
reconnection, current cascade, MHD turbulence, Alfvén resonance,
resonance absorption or phase mixing. A number of authors have investigated
the heating and acceleration of the solar wind.
400 km s-1) stream. The low speed streams originate in the open fields above
active regions of the solar corona. The high speed streams originate over
coronal holes The predominance of nearly incompressible Alfvén waves in
the solar wind stream has also been confirmed by Daily (1973), Parker
(1980a,b) and Bavassano et al. (1982). Hollweg et al. (1982) analyzed
data from the Helios 2 satellite and found Alfvén waves making a
significant contribution to the high speed streams. A detailed discussion of
Alfvén wave domination in the solar wind is given by Denskat & Burlaga
(1977). The Alfvén waves observed in situ in the solar wind provide a
clue that dissipation of Alfvén waves in the solar corona could provide
the heat input and wave pressure gradient (wave ponderomotive force)
necessary to heat and accelerate the high speed solar wind (Parker 1991).
Alfvén waves can be dissipated in the solar corona by magnetic
reconnection, current cascade, MHD turbulence, Alfvén resonance,
resonance absorption or phase mixing. A number of authors have investigated
the heating and acceleration of the solar wind.
Ulysses and Helios observations have shown that in the high speed streams,
the minor (heavy) ions flow faster than the protons by about the local
Alfvén speed along the magnetic field and that they are hotter than the
protons roughly in proportion to their masses. Remote observations by UVCS
on SOHO indicate that in the vicinity of 3 ![]() ,
the O5+ ions have a perpendicular temperature
,
the O5+ ions have a perpendicular temperature
![]() K, while the protons have
K, while the protons have
![]() K. Also the bulk flow speeds of O5+ are faster than the proton speeds
where
K. Also the bulk flow speeds of O5+ are faster than the proton speeds
where
![]() .
The heavy ions are strongly anisotropic in
temperature. (See Hollweg & Isenberg 2002, and references therein for a
thorough review.) A number of authors have investigated the heating of the
solar wind ions due to wave-particle interactions (e.g. Hollweg & Turner
1978; Dusenbery & Hollweg 1981; Marsch et al. 1982; Isenberg 1984; Leer
et al. 1992; Hu et al. 1997; Czechowski et al. 1998; Cranmer et al. 1999).
.
The heavy ions are strongly anisotropic in
temperature. (See Hollweg & Isenberg 2002, and references therein for a
thorough review.) A number of authors have investigated the heating of the
solar wind ions due to wave-particle interactions (e.g. Hollweg & Turner
1978; Dusenbery & Hollweg 1981; Marsch et al. 1982; Isenberg 1984; Leer
et al. 1992; Hu et al. 1997; Czechowski et al. 1998; Cranmer et al. 1999).
A number of mechanisms for the acceleration of the solar wind have been investigated and are also able to explain many observations, but a mechanism that can explain all the observations is still lacking. The filamentation process (hot spot formation) may provide a clue to the dissipation problem, as it is a fast way to transport energy at small scales.
The Kinetic Alfvén wave (KAW) is the shear Alfvén wave modified by
short wavelength effects, and it can be produced when an obliquely
propagating shear Alfvén wave is affected by the electron temperature
and inertia such that a non-zero parallel electric field arises within the
wave itself due to the local charge separation (Lysak & Lotko 1996; Wu
2003). The parallel component of the perturbed electric field can play an
important role in accelerating and heating plasma particles. KAW has been
discussed extensively in the fields of laboratory, space, and astrophysical
plasmas since the pioneering theoretical work of Hasegawa & Chen (1975).
The importance of KAWs in explaining the physics of small scale auroral arcs
has been widely accepted. Indeed, localized waveforms with scales of the
order of ![]()
![]() /
/![]()
![]() or
or ![]()
![]() (
(![]()
![]() is the electron gyrofrequency, and
is the electron gyrofrequency, and
![]() and
and ![]()
![]() are the
Alfvén speed and ion Larmor radius, respectively.
are the
Alfvén speed and ion Larmor radius, respectively. ![]()
![]() = c
= c![]() /
/![]()
![]() ,
with c
,
with c![]() and
and ![]()
![]() being the ion
sound speed and gyrofrequency) accompanied by features of plasma
energization were observed on the auroral and cusp field lines (see, e.g.,
Stasiewicz et al. 2000, and references therein). These structures were
referred to as solitary KAWs because of their large amplitude and
localization (Louarn et al. 1994; Wahlund et al. 1994).
being the ion
sound speed and gyrofrequency) accompanied by features of plasma
energization were observed on the auroral and cusp field lines (see, e.g.,
Stasiewicz et al. 2000, and references therein). These structures were
referred to as solitary KAWs because of their large amplitude and
localization (Louarn et al. 1994; Wahlund et al. 1994).
Most of the work related to filamentation is done in the framework of the
Hall MHD (Champeaux et al. 1997, 1998). However, not much of the
analytical or numerical work has been done on the KAW filamentation. In this
paper we have studied the filamentation of a perturbation present on a KAW
(we term it the main KAW) in the presence of the second KAW. The paper is
organized as follows. In Sect. 2, the beam width parameter of the main KAW
as well as that of perturbation is derived in the presence of the second KAW
in the intermediate ![]() regime (
regime (![]() /
/
![]() ). The threshold (critical) field values of the main KAW and the
perturbation present on it are also obtained. This work has been applied to
the solar wind. The third section provides discussion and conclusion.
). The threshold (critical) field values of the main KAW and the
perturbation present on it are also obtained. This work has been applied to
the solar wind. The third section provides discussion and conclusion.
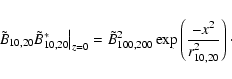 |
(1) |
The dynamical equation governing the propagation of the KAW in the x-z plane
can be obtained by using the standard method (Bellan et al. 1998; Shukla
& Stenflu 1999, 2000; Shukla & Sharma 2002; Shukla & Sharma et al. 2004) and can be written as

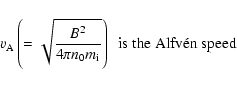
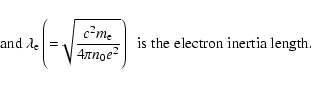
Also,
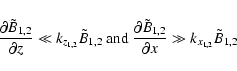
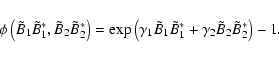
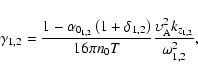
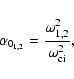
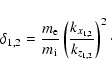
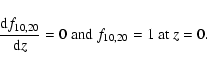
![$\displaystyle \phi _{\rm eff} =\phi \left( {\tilde {B}_1 \tilde {B}_1 ^\ast ,\t...
..._{10} \tilde {B}_{10}
^\ast ,\tilde {B}_2 \tilde {B}_2 ^\ast } \right)} \right]$](/articles/aa/full/2006/38/aa4715-05/img75.gif) |
![$\displaystyle \frac{\partial \tilde {A}_{11}^2 }{\partial z}-\frac{1}{\upsilon ...
...gamma _2 \tilde {B}_2 \tilde {B}_2^\ast } \right)} \right]\tilde
{A}_{11}^2 =0.$](/articles/aa/full/2006/38/aa4715-05/img76.gif) |
(14b) |
Here,
![]() (
S11-S10).
(
S11-S10). ![]()
![]() represents the modification in dimensionless density when the non-linear
interaction between the main KAW and the perturbation present on it has been
taken in to account.
represents the modification in dimensionless density when the non-linear
interaction between the main KAW and the perturbation present on it has been
taken in to account.
![]() is the measure of the change in the angle between the
magnetic field of the main wave and that of the perturbation. This angle
changes with the distance of propagation because of the nonlinear effects.
The value of
is the measure of the change in the angle between the
magnetic field of the main wave and that of the perturbation. This angle
changes with the distance of propagation because of the nonlinear effects.
The value of
![]() depends on the phase angle between the main
KAW field and that of the perturbation field at z=0 and the phase shift
introduced in the perturbation field due to the nonlinearity in the medium.
depends on the phase angle between the main
KAW field and that of the perturbation field at z=0 and the phase shift
introduced in the perturbation field due to the nonlinearity in the medium.
In writing Eq. (14b) the nonlinear part has been expanded as
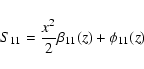 |
(17) |
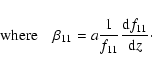 |
(18) |
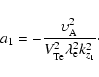 |
(20) |
The typical solar wind parameters (Jokipii 1973; Dendy 1995) for
![]() are as given below (around 1 AU).
are as given below (around 1 AU).
![]() K;
K;
![]() K;
K;
![]() G;
G;
![]() Hz;
number of protons = 5 protons/c.c.
Hz;
number of protons = 5 protons/c.c.
We find that
![]() Hz;
Hz;
![]() cm;
cm;
![]() cm/s;
cm/s;
![]() cm/s.
cm/s.
For ![]() 1=0.04 Hz and
1=0.04 Hz and
![]() ;
we get
;
we get
![]() cm-1;
cm-1;
![]() cm-1.
cm-1.
For ![]() 2=0.06 Hz and kx2
2=0.06 Hz and kx2
![]() ;
we get
;
we get
![]() cm-1;
cm-1;
![]() cm-1 .
cm-1 .
Here
![]() is the ion cyclotron frequency and
is the ion cyclotron frequency and
![]() is the electron
plasma frequency.
is the electron
plasma frequency.
For these typical parameters, the critical value of the magnetic field as
given by Eq. (12) is
![]() G
(
G
(
![]() for
for ![]() 2=0) for
2=0) for
![]() km and
km and
![]() G (
G (![]()
![]() for
for
![]() 1= 0) for
1= 0) for
![]() km
(here
km
(here
![]() ).
).
The critical magnetic field value of the perturbation as given by Eq. (23) is
![]() G, for the main kinetic Alfvén wave
field
G, for the main kinetic Alfvén wave
field
![]() G,
G,
![]() km and the
other KAW field
km and the
other KAW field
![]() G,
G,
![]() km and
km and
![]() km.
km.
![\begin{figure}
\par\subfigure[]{\includegraphics[width=9cm,clip]{aa4715f1aCMJN.e...
...\subfigure[]{\includegraphics[width=9cm,clip]{aa4715f1bCMJN.eps} }\end{figure}](/articles/aa/full/2006/38/aa4715-05/Timg125.gif) |
Figure 1:
a) The variation of the magnetic field intensity of the Main
KAW for
f1= 0.04 Hz,
f2 = 0.06 Hz,
B100 (z=0, x=0) =
|
| Open with DEXTER | |
![\begin{figure}
\par\subfigure[]{\includegraphics[width=9cm,clip]{aa4715f2aCMJN.e...
...subfigure[]{\includegraphics[width=9cm,clip]{aa4715f2bCMJN.eps} }
\end{figure}](/articles/aa/full/2006/38/aa4715-05/Timg127.gif) |
Figure 2:
a) The variation of the magnetic field intensity of the Main
KAW for
f1 = 0.04 Hz,
f2= 0.02 Hz,
B100 (z=0, x=0) =
|
| Open with DEXTER | |
![\begin{figure}
\par\subfigure[]{\includegraphics[width=9cm,clip]{aa4715f3aCMJN.e...
...subfigure[]{\includegraphics[width=9cm,clip]{aa4715f3bCMJN.eps} }
\end{figure}](/articles/aa/full/2006/38/aa4715-05/Timg129.gif) |
Figure 3:
a) The magnetic field intensity of the perturbation present
on the main KAW for
f1= 0.04 Hz,
f2= 0.02 Hz,
B100 (z=0, x=0) =
|
| Open with DEXTER | |
![\begin{figure}
\par\subfigure[]{\includegraphics[width=9cm,clip]{aa4715f4aCMJN.e...
...subfigure[]{\includegraphics[width=9cm,clip]{aa4715f4aCMJN.eps} }
\end{figure}](/articles/aa/full/2006/38/aa4715-05/Timg130.gif) |
Figure 4:
a) The magnetic field intensity of the perturbation present
on the main KAW for
f1= 0.04 Hz,
f2= 0.06 Hz,
B100 (z=0, x=0) =
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{aa4715f5CMJN.eps}
\end{figure}](/articles/aa/full/2006/38/aa4715-05/Timg131.gif) |
Figure 5: |Bk|2 against k at x=0 in the presence of second KAW. |
| Open with DEXTER | |
Figures 1a,b depict the intensity distribution of the main KAW in the solar wind at different distances along the direction of propagation but at different x values. The filamentary structures are seen at different locations. This can be explained using Eq. (11). When the initial magnetic field (maximum field at z = 0) of the KAW is more than its critical magnetic field, the non-linear term (second term in the right hand side of Eq. (11)) dominates and the value of f10 decreases with the distance of propagation. But when f10 becomes very small, the diffraction term (first term in the right hand side of the Eq. (11)) starts to dominate. Therefore, f10 increases with the distance of the propagation until f10 become so large that the diffraction term becomes smaller compared to the nonlinear term. f10 further decreases due to the nonlinear effects, until it becomes so small that the diffraction term again dominates and f10 start to diverge and this process repeats. Hence, the main KAW attains a certain minimum beam width parameter (f10), and the intensity of the main KAW in these small size structures becomes very high.
Figures 1a and b display the variation of the intensity of the main KAW for different values of the initial magnetic field strength of the second KAW in the solar wind. In the presence of the second KAW, the intensity profile of the filaments are greatly modified. This is because the additional term arising due to the presence of the second KAW in the nonlinear term of Eq. (11) will change the rate of change of the non-linear term with z and hence the balance of the nonlinear term and the diffraction term takes place at a lower value of f. This effect is equivalent to the case if we increase the intensity of the main (first) KAW.
Next we studied the effect of changing the frequency of the second KAW on the filament formation of the main KAW. Figures 2a,b display the intensity profile of the filaments of the main KAW for different frequencies. When we increase the frequency of the second KAW, the intensity of the filaments of the main KAW decreases and the spacing between them increases. This happens because of the complex nonlinear dynamics of the beam width of the main beam field on the frequency
Next we have studied the effect of the presence of the second KAW on a perturbation present on the main KAW. First we studied the dependence of the filamentation of the perturbation by changing the frequency of the second KAW. Figures 3a,b show the intensity of the perturbation for different frequencies of the second KAW. The increases in the frequency of the second KAW result in decrease in magnetic field intensity of the filaments of the perturbation and the spacing between the primary filaments increases.
Figures 4a,b illustrates the dependence of the intensity of the perturbation on the magnetic field intensity of the second wave. The increases in the magnetic field intensity of the second KAW results in the increase in the magnetic field intensity of the filaments of the perturbation. The abovementioned process, filamentation, is very important in transferring the energy of KAWs from large scale (smaller frequency) to small scale (higher frequency) so that Landau damping is possible. Because of the filamentation, higher modes appear and the energy that was localized in the lower modes will be redistributed in the higher modes. This will change the spectrum of the Alfvénic turbulence in the solar wind. Due to this, the spectral index is also expected to change. The presence of secondary filaments in the intensity profile of the perturbation present on the main KAW will further affect the spectral transfer of the energy from larger scale to smaller scale. The relevance of this to heating and acceleration of the solar wind, coronal heating and the auroral formation can also be extended. The heating rate can be estimated by using the velocity space diffusion coefficient and the Fokker Planck equation or from more rigorous models. In order to study these effects we need to study the effect of filament formation on the wavenumber spectrum. In Fig. 5 we have presented these studies in one typical case when the filaments are formed by the nonlinear interaction of two KAWs without perturbation.
We studied the Fourier components
![]() for the main KAW
against k at a fixed x value in Fig. 5. Figure 5 is obtained from
Fig. 1b of the filamentary structures. The data set was obtained at x=0
and the FFT was taken and
for the main KAW
against k at a fixed x value in Fig. 5. Figure 5 is obtained from
Fig. 1b of the filamentary structures. The data set was obtained at x=0
and the FFT was taken and
![]() against
kz was
plotted. This figure depicts the power spectra
against
kz was
plotted. This figure depicts the power spectra
![]() against k at fixed x value (here x = 0 is chosen). It appears that with
increasing values of the k, the scaling of the spectra changes from the
k-1 towards Kolmogorov scaling k-5/3.
against k at fixed x value (here x = 0 is chosen). It appears that with
increasing values of the k, the scaling of the spectra changes from the
k-1 towards Kolmogorov scaling k-5/3.
Acknowledgements
This work is partially supported by DST (India). M. Malik is very grateful to CSIR for providing financial assistance for the present work.