A&A 457, L9-L12 (2006)
DOI: 10.1051/0004-6361:20065917
LETTER TO THE EDITOR
Accurate stellar masses in the multiple system T Tauri
G. Duchêne1 -
H. Beust1 -
F. Adjali1 -
Q. M. Konopacky2 -
A. M. Ghez2
1 - Laboratoire d'Astrophysique de Grenoble, BP 53, 38041
Grenoble Cedex 9, France
2 -
Department of Physics and Astronomy, UCLA, Los Angeles,
CA 90095-1562, USA
Received 27 June 2006 / Accepted 26 July 2006
Abstract
Aims. We obtain accurate estimates for the individual masses of the components of the tight binary system T Tau S to settle the ongoing debate on the nature of T Tau Sa, a so-called infrared companion.
Methods. We take advantage of the fact that T Tau S belongs to a triple system composed of two hierarchical orbits to simultaneously analyze the motion of T Tau Sb in the rest frames of T Tau Sa and T Tau N. With this method, it is possible to pinpoint the location of the center of mass of T Tau S and, thereby, to determine individual masses for T Tau Sa and T Tau Sb with no prior assumption about the mass/flux ratio of the system. This improvement over previous studies of the system results in much better constraints on orbital parameters.
Results. We find individual masses of
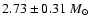 for T Tau Sa and of
for T Tau Sa and of
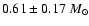 for T Tau Sb (in agreement with its early-M spectral type), including the uncertainty on the distance to the system. These are among the most precise estimates of the mass of any Pre-Main Sequence star, a remarkable result since this is the first system in which individual masses of T Tauri stars can be determined from astrometry only. This model-independent analysis confirms that T Tau Sa is an intermediate-mass star, presumably a very young Herbig Ae star, that may possess an almost edge-on disk.
for T Tau Sb (in agreement with its early-M spectral type), including the uncertainty on the distance to the system. These are among the most precise estimates of the mass of any Pre-Main Sequence star, a remarkable result since this is the first system in which individual masses of T Tauri stars can be determined from astrometry only. This model-independent analysis confirms that T Tau Sa is an intermediate-mass star, presumably a very young Herbig Ae star, that may possess an almost edge-on disk.
Key words: stars: individual: T Tau - stars: pre-main sequence -
binaries: close - astrometry
The most robust method to determine the mass of stars is to
monitor the Keplerian orbital motion of multiple systems. This
method is particularly valuable for contracting Pre-Main Sequence
(PMS) stars, such as T Tauri stars (TTS), for which mass estimates
from evolutionary models can differ by factors as large as 2 (e.g.,
Baraffe et al. 2002). However, there are only about 20 individual TTS with well-determined masses, all of them having radial
velocity curves or a Keplerian circumstellar disk (see Hillenbrand & White 2004 for a recent review).
The triple system T Tauri is among the best-studied PMS multiple
systems (see, e.g., Beck et al. 2004). The optically bright T Tau N, a
 ,
,
 1 Myr-old star, is associated with the
infrared(IR)-bright T Tau S tight binary system, which was resolved
less than a decade ago (Koresko 2000). The latter consists of
T Tau Sb, a deeply embedded, early M-type TTS, and of T Tau Sa, an
extremely red and highly variable object (Ghez et al. 1991) that has
been classified as an infrared companion (IRC). Despite two decades of
steady observations, the nature of that third component remains
largely unknown. It shares many spectral properties with heavily
embedded, Class I protostars, but its physical association with two
normal TTS seems to contradict this hypothesis if the system is coeval
(Koresko et al. 1997). Alternatively, Ghez et al. (1991) proposed that
T Tau Sa, which underwent a strong outburst, is a low-mass FU Ori
object. More recently, it has been suggested that T Tau Sa is an
intermediate-mass PMS star surrounded by an opaque edge-on
circumstellar disk (Duchêne et al. 2005).
1 Myr-old star, is associated with the
infrared(IR)-bright T Tau S tight binary system, which was resolved
less than a decade ago (Koresko 2000). The latter consists of
T Tau Sb, a deeply embedded, early M-type TTS, and of T Tau Sa, an
extremely red and highly variable object (Ghez et al. 1991) that has
been classified as an infrared companion (IRC). Despite two decades of
steady observations, the nature of that third component remains
largely unknown. It shares many spectral properties with heavily
embedded, Class I protostars, but its physical association with two
normal TTS seems to contradict this hypothesis if the system is coeval
(Koresko et al. 1997). Alternatively, Ghez et al. (1991) proposed that
T Tau Sa, which underwent a strong outburst, is a low-mass FU Ori
object. More recently, it has been suggested that T Tau Sa is an
intermediate-mass PMS star surrounded by an opaque edge-on
circumstellar disk (Duchêne et al. 2005).
Determining the mass of T Tau Sa from its orbital motion within this
triple system would help our understanding of its exact nature. While
it has been suggested that this system may be on an unbound orbit
(Loinard et al. 2003), other studies have found possible closed orbits
and derived a total mass of 2-6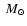 for T Tau S (Johnston et al. 2003; Beck et al. 2004). Using a refined method, Johnston et al. (2004a,b) attempted for the first time to determine
the individual masses of T Tau Sa and Sb. All of these studies
suggested that the IRC is the most massive component of the
system. However, they were based on simplifying (and sometimes
invalid) assumptions regarding the flux ratio and/or mass ratio of the
T Tau S system, resulting in additional sources of uncertainty.
for T Tau S (Johnston et al. 2003; Beck et al. 2004). Using a refined method, Johnston et al. (2004a,b) attempted for the first time to determine
the individual masses of T Tau Sa and Sb. All of these studies
suggested that the IRC is the most massive component of the
system. However, they were based on simplifying (and sometimes
invalid) assumptions regarding the flux ratio and/or mass ratio of the
T Tau S system, resulting in additional sources of uncertainty.
Here, the combined orbital motion of the triple system is revisited
using an almost assumption-free, generic approach, in order to obtain a
precise estimate of the individual stellar masses within the
T Tau S tight system. This Letter is composed as follows: the
fitting method and the observations used in this analysis are
presented in Sect. 2; the results and
implications are discussed in Sect. 3.
2 Approach and astrometric dataset
Two types of astrometric data are available for the T Tau multiple
system. The first type is high-resolution IR data, which resolves all
three components in data obtained since 1997. The second type is radio
data, which detected only two of the components for over two decades,
T Tau N and a southern source. Although this southern source is
shown by Loinard et al. (2003) to be physically associated with
T Tau Sb, Smith et al. (2003) and Johnston et al. (2004a) argue that
it might be offset from it by up to 0
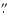 01-0
01-0
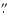 03. In our
analysis, we assume that the radio and IR source are indeed the same
object. Only a much longer IR follow-up of the system would allow one
to determine whether this assumption is valid.
03. In our
analysis, we assume that the radio and IR source are indeed the same
object. Only a much longer IR follow-up of the system would allow one
to determine whether this assumption is valid.
2.1 Fitting method
Two general approaches have been used in previous attempts to fit the
orbital motion of the T Tau Sa-Sb tight binary system. First, it is
possible to consider in the fit only the IR datasets, which provide
the location of both components. In this case, however, the short
timespan probed since 1997 poorly constrains the orbit and a wide
range of total system masses is allowed (Beck et al. 2004). Including
our most recent IR measurements (see Sect. 2.2) only
slightly improves this conclusion.
In a second approach, the separation between T Tau N and T Tau Sb,
estimated from the much longer radio observations, is transformed into
a T Tau Sa-Sb separation prior to fitting the orbital motion. In
this case, one has to make some assumptions regarding the unknown
location of T Tau Sa with respect to T Tau N. In the past, two
main categories of assumptions were made. First, some authors
considered that T Tau Sa follows a constant linear motion with
respect to T Tau N (Loinard et al. 2003; Johnston et al. 2003),
implicitly assuming that it is coincident with the center of mass of
T Tau S. However, while T Tau Sa is indeed more massive than its
companion, the mass of the latter is not negligible (see
Sect. 3). Second, it was assumed that the
historical location of the photocenter of T Tau S, which has been
observed for over 15 years, can be used to trace the location of
T Tau Sa prior to 1997 (Johnston et al. 2004a,b). This requires one
to assume that the IR flux ratio within the T Tau S system remains
constant. Evidence for large variability in at least one of the two
components of the system is growing, however (Ghez et al. 1991; Beck
et al. 2004).
To limit as much as possible the number of assumptions in the
analysis, we decided to fit simultaneously two types of data, namely
the location of T Tau Sb in two rest frames: with respect to
T Tau Sa and to T Tau N. We did not use the separation between
T Tau N and T Tau Sa because it would not be independent of the
other two types of measurements.
We assume that T Tau Sb follows a bound Keplerian orbit around
T Tau Sa and use the
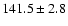 pc distance to the system
estimated by Loinard et al. (2005). We further assume that the motion
of the center of mass of T Tau S, which is a Keplerian orbit around
T Tau N, can be approximated by a parabolic motion over the 20
years of observations probed here. This is justified as the period of
this outer orbit is at least 400 years (Johnston et al. 2004a,b). Fitting the motion of T Tau Sb in both rest frames
simultaneously allows us to determine individual masses from
astrometry only, as the ratio of the amplitude of the motion of
T Tau Sb in both frames is a direct measurement of the mass ratio.
pc distance to the system
estimated by Loinard et al. (2005). We further assume that the motion
of the center of mass of T Tau S, which is a Keplerian orbit around
T Tau N, can be approximated by a parabolic motion over the 20
years of observations probed here. This is justified as the period of
this outer orbit is at least 400 years (Johnston et al. 2004a,b). Fitting the motion of T Tau Sb in both rest frames
simultaneously allows us to determine individual masses from
astrometry only, as the ratio of the amplitude of the motion of
T Tau Sb in both frames is a direct measurement of the mass ratio.
We use a Levenberg-Marquardt 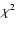 minimization routine (Press et al. 1992) that simultaneously fits for 14 independent parameters. The
T Tau Sa-Sb orbit is described by 7 parameters: semi-major axis
(a), eccentricity (e), inclination with respect to the plane of
the sky (i), position angle of ascending node (
minimization routine (Press et al. 1992) that simultaneously fits for 14 independent parameters. The
T Tau Sa-Sb orbit is described by 7 parameters: semi-major axis
(a), eccentricity (e), inclination with respect to the plane of
the sky (i), position angle of ascending node (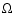 ,
measured
Eastward from North), azimuth of periastron (
,
measured
Eastward from North), azimuth of periastron (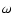 ), time of
periastron passage (
), time of
periastron passage (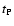 )
and orbital period (P). The
parabolic motion of the center of mass of T Tau S with respect to
T Tau N is described by 6 parameters defined by its right ascension
)
and orbital period (P). The
parabolic motion of the center of mass of T Tau S with respect to
T Tau N is described by 6 parameters defined by its right ascension
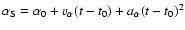 and a corresponding equation for its declination, with
t0=2000.0. Finally, the last parameter describes the mass ratio in
the system:
and a corresponding equation for its declination, with
t0=2000.0. Finally, the last parameter describes the mass ratio in
the system:
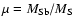 ,
where
,
where
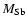 and
and 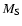 are the mass of T Tau Sb and of
the whole T Tau S system, respectively. Kepler's third law is used
to determine
are the mass of T Tau Sb and of
the whole T Tau S system, respectively. Kepler's third law is used
to determine 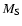 from the values of a and P; the
individual stellar masses
from the values of a and P; the
individual stellar masses
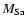 and
and
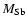 are
derived from the values of
are
derived from the values of 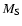 and
and 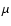 .
The minimization
routine was run with several tens of thousand initial guesses spanning
wide ranges for all fit parameters to ensure convergence on the
absolute minimum of the
.
The minimization
routine was run with several tens of thousand initial guesses spanning
wide ranges for all fit parameters to ensure convergence on the
absolute minimum of the 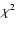 function.
function.
The uncertainties on the fit parameters are estimated using a
bootstrap method, a robust method when performing a fit with many
(correlated) parameters. We created 10 000 artificial datasets
containing as many points as the observed dataset, in which each point
is randomly drawn from a Gaussian distribution centered on the actual
measurement and whose width is given by the associated astrometric
uncertainty, and run the 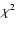 minimization routine for each
realization. The resulting distribution of values for each fit
parameter is characterized by a mean value equal to that of the best
fit and by a standard deviation that we consider as the estimate of
the uncertainty on the fit parameter.
minimization routine for each
realization. The resulting distribution of values for each fit
parameter is characterized by a mean value equal to that of the best
fit and by a standard deviation that we consider as the estimate of
the uncertainty on the fit parameter.
Because this fitting method is based on a fit of all available
measurements without further transformation, and because no parameter
is set to an ad hoc fixed value, it is very robust and essentially
assumption-free.
![\begin{figure}\par\includegraphics[width=15.2cm,clip]{5917fig1.eps}
\end{figure}](/articles/aa/full/2006/37/aa5917-06/Timg18.gif) |
Figure 1:
Observed motion of T Tau Sb in the
reference frame of T Tau Sa ( left) and T Tau N ( right). The dotted
curves represent our best combined fit; each observation is
connected to its modeled counterpart by a straight line. In the
left-hand panel, the square indicates the fixed location of
T Tau Sa and the dashed line connects it to the periastron. In the
right-hand panel, filled diamonds represent the VLA measurements;
the open diamonds indicate the 1998 VLA measurement excluded from
the final fit and its fitted counterpart. In this panel, the dashed
curve represents the motion of T Tau Sa. |
| Open with DEXTER |
2.2 IR astrometric dataset
A dozen high spatial resolution IR observations of the T Tau triple
system have been published; they usually simultaneously provide the
position of T Tau Sb with respect to both other stars. All
astrometric measurements listed in Beck et al. (2004) and Duchêne et al. (2005) are included in our fit![[*]](/icons/foot_motif.gif) . Two
additional observations of the system were recently published by
Mayama et al. (2006). However, they are significantly offset
(
. Two
additional observations of the system were recently published by
Mayama et al. (2006). However, they are significantly offset
(
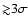 )
from all other quasi-contemporaneous measurements;
these measurements are likely biased or suffer from underestimated
uncertainties and they have been discarded from the analysis.
)
from all other quasi-contemporaneous measurements;
these measurements are likely biased or suffer from underestimated
uncertainties and they have been discarded from the analysis.
In addition to these measurements, we present new K-band speckle
interferometric datasets obtained on the 10 m Keck I telescope in 1997,
2004 and 2005. For the last two epochs, the T Tau Sa-Sb system is
sufficiently well-resolved that the relative astrometry of all
components could be determined from shift-and-add images. On the other
hand, in 1997, the system was close to the diffraction limit (
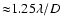 )
and traditional speckle analysis was conducted. The
usual basic reduction techniques were first applied to all datasets
(see Ghez et al. 1993 for more details). Because T Tau is a
hierarchical triple system, a 2-step method identical to that
described in Duchêne et al. (2003) was used to extract its
properties. The new astrometric and photometric data are presented in
Table 1.
)
and traditional speckle analysis was conducted. The
usual basic reduction techniques were first applied to all datasets
(see Ghez et al. 1993 for more details). Because T Tau is a
hierarchical triple system, a 2-step method identical to that
described in Duchêne et al. (2003) was used to extract its
properties. The new astrometric and photometric data are presented in
Table 1.
Loinard et al. (2003) and Johnston et al. (2003, 2004b) have published
a series of VLA centimeter observations of T Tau spanning 20 years,
from 1983 to 2003. Both groups independently analyzed the 1983, 1988,
1992, 1995 and 2001 datasets, and obtained very similar results. We
found that using either sets of results for these epochs yields very
similar fits![[*]](/icons/foot_motif.gif) . In the following, we use the 2 cm astrometric results
from Johnston et al. (2003, 2004b) in order to ensure a maximum
uniformity among the radio datasets and their analysis, as well as the
1998 3.7 cm measurement from Loinard et al. (2003), since no 2 cm
observations were conducted at that epoch.
. In the following, we use the 2 cm astrometric results
from Johnston et al. (2003, 2004b) in order to ensure a maximum
uniformity among the radio datasets and their analysis, as well as the
1998 3.7 cm measurement from Loinard et al. (2003), since no 2 cm
observations were conducted at that epoch.
Table 1:
New astrometric and photometric data for
the T Tau system.
3 Results and implications
Overall, we considered in our fit a total of 11 astrometric
measurements of the T Tau Sa-Sb system and 16 measurements of the
T Tau N-Sb system. This is the most extensive dataset fitted to
date on this system, considering that we did not try to fit the
historical location of the photocenter of T Tau S (but see
Sect. 3.1).
3.1 Individual masses within T Tau S
Fitting all measurements described in Sect. 2, a
best fit solution with
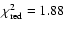 is obtained, a
slightly large value considering that there are 40 degrees of
freedom. In fact, the 1998 VLA measurement reported by Loinard et al. (2003) is 4.1
is obtained, a
slightly large value considering that there are 40 degrees of
freedom. In fact, the 1998 VLA measurement reported by Loinard et al. (2003) is 4.1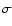 away from the fitted value and contributes a
large amount to the total
away from the fitted value and contributes a
large amount to the total 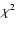 .
All other measurements are within
3
.
All other measurements are within
3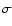 of the fit, and all but three less than 2
of the fit, and all but three less than 2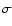 away from
it, as expected from a Gaussian distribution of the astrometric
uncertainties. This particular VLA measurement is the only one
included in our fit that was obtained at 3.7 cm. Substantial
differences were noted in the past between 2 cm and 3.7 cm VLA
measurements for this source (Johnston et al. 2003, 2004b), and we
therefore consider this point as suspicious.
away from
it, as expected from a Gaussian distribution of the astrometric
uncertainties. This particular VLA measurement is the only one
included in our fit that was obtained at 3.7 cm. Substantial
differences were noted in the past between 2 cm and 3.7 cm VLA
measurements for this source (Johnston et al. 2003, 2004b), and we
therefore consider this point as suspicious.
Excluding the 1998 VLA measurement, a best fit solution which is less
than 2.7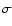 away from all remaining measurements and that has a
much more acceptable
away from all remaining measurements and that has a
much more acceptable
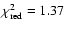 is obtained with 38
degrees of freedom. No fit parameter is different by more than
1.4
is obtained with 38
degrees of freedom. No fit parameter is different by more than
1.4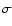 from the previous solution, and we consider this new
solution as our best fit in the following. The best fit parameters are
listed in Table 2 and the solution is illustrated in
Fig. 1. Note that it is not possible to distinguish
the ascending and descending nodes of the orbit from astrometry only:
an identical projected orbit could be described with
from the previous solution, and we consider this new
solution as our best fit in the following. The best fit parameters are
listed in Table 2 and the solution is illustrated in
Fig. 1. Note that it is not possible to distinguish
the ascending and descending nodes of the orbit from astrometry only:
an identical projected orbit could be described with
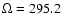
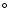 and
and
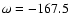
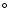 .
.
Table 2:
Parameters of the best orbital solution.
We then performed a consistency check regarding the historical
measurements of the IR photocenter of the T Tau S binary. While
strong variability prevents using these measurements in the fit, it
must be verified that the photocenter is located along the line
joining the fitted location of T Tau Sa and T Tau Sb at all
epochs. The photocenter lies within 2.4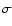 of the predicted line
connecting the two components for all measurements listed in Ghez et al. (1995) and Roddier et al. (2000), giving more confidence to the
validity of the fit.
of the predicted line
connecting the two components for all measurements listed in Ghez et al. (1995) and Roddier et al. (2000), giving more confidence to the
validity of the fit.
Including the uncertainty induced by the distance estimate, the total
relative uncertainty on
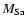 is about 11%, among the
most accurate individual mass estimates for a TTS that does not belong
to an eclipsing binary system (Hillenbrand & White 2004). The
uncertainty on
is about 11%, among the
most accurate individual mass estimates for a TTS that does not belong
to an eclipsing binary system (Hillenbrand & White 2004). The
uncertainty on
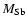 is about 28%, still a remarkably
accurate estimate for a TTS, considering that only astrometric
measurements were taken into account in this analysis.
is about 28%, still a remarkably
accurate estimate for a TTS, considering that only astrometric
measurements were taken into account in this analysis.
The results obtained here are in good agreement with those presented
by Johnston et al. (2004a,b), although with uncertainties that are at
least half for all parameters: the best estimate for
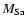 to date was
to date was
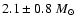 (Johnston et al. 2004b). This
significant improvement is due to a combination of factors: the
increased time coverage of high-resolution IR datasets, a simpler
characterization of the T Tau N-S orbit (parabolic motion instead
of a Keplerian orbit with several parameters fixed to ad hoc values),
the improved distance estimate obtained by Loinard et al. (2005), and
the smaller number of assumptions used in our analysis. In this work,
the only assumptions that could be disputed are the parabolic
approximation of the orbital motion of T Tau S around T Tau N over
20 years and the match between the radio and IR location of
T Tau Sb. The fact that a very satisfying fit was obtained appears
to validate these hypotheses.
(Johnston et al. 2004b). This
significant improvement is due to a combination of factors: the
increased time coverage of high-resolution IR datasets, a simpler
characterization of the T Tau N-S orbit (parabolic motion instead
of a Keplerian orbit with several parameters fixed to ad hoc values),
the improved distance estimate obtained by Loinard et al. (2005), and
the smaller number of assumptions used in our analysis. In this work,
the only assumptions that could be disputed are the parabolic
approximation of the orbital motion of T Tau S around T Tau N over
20 years and the match between the radio and IR location of
T Tau Sb. The fact that a very satisfying fit was obtained appears
to validate these hypotheses.
The mass derived for T Tau Sb is in excellent agreement with its
known, early-M spectral type (Duchêne et al. 2002), as already
discussed by Johnston et al. (2004a,b). For the first time, however,
an accurate estimate of the mass of T Tau Sa is obtained, leaving
little doubt that it is somewhat more massive than T Tau N itself
and suggesting that T Tau Sa is a young embedded Herbig Ae
star. This is the first time that this is determined with such
certainty for an IRC. As discussed in Duchêne et al. (2005), it is
likely that T Tau Sa is surrounded by a compact and partially opaque
circumstellar disk that accounts for the apparent faintness of this
intrinsically bright object. Given the orbital parameters of the
T Tau Sa-Sb system, the radius of this disk must be
 3 AU, i.e., half the periastron distance. This disk must be
very inclined with respect to the orbital plane (
3 AU, i.e., half the periastron distance. This disk must be
very inclined with respect to the orbital plane (
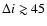
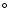 ), raising the possibility of gravitational instabilities.
), raising the possibility of gravitational instabilities.
Within about 10 years, spatially-resolved IR observations of the
T Tau triple system will allow the derivation of accurate orbital
parameters for T Tau S without making use of radio datasets. With
such an analysis, it will be possible to determine whether the
southern radio component of T Tau arises from the chromosphere of
T Tau Sb or whether it is a separate object that is simply
associated with this object.
In the shorter term, the dynamical stability of the T Tau system must
be studied in more detail: the system contains three stars within
100 AU of each other, each of them possessing a circumstellar
disk. The overall velocity of T Tau S with respect to T Tau N is
of the order of 6 km s-1, very similar to the velocity of a
100 AU-radius circular orbit for a 5 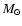 system (assuming
system (assuming
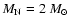 ). This suggests that the outer orbit is seen
close to face-on and has a low eccentricity. If this is indeed
the case, the application of the stability criterion proposed by
Eggleton & Kiseleva (1995) suggests that the system could be
marginally stable. Moreover, the stability of the circumstellardisks
is not necessarily ensured in such a tight system. This motivates a
follow-up dynamical study similar to that performed for the quadruple
system GG Tau (Beust & Dutrey 2005, 2006) to determine the possible
solutions for the outer orbit that preserve the three components and
their disks for at least 1 Myr, i.e., the age of the system. A
preliminary analysis, which will be presented in a forthcoming paper,
suggests that the three-body system is stable over a few Myrs, whereas
the fate of the circumstellar disks is not yet established.
). This suggests that the outer orbit is seen
close to face-on and has a low eccentricity. If this is indeed
the case, the application of the stability criterion proposed by
Eggleton & Kiseleva (1995) suggests that the system could be
marginally stable. Moreover, the stability of the circumstellardisks
is not necessarily ensured in such a tight system. This motivates a
follow-up dynamical study similar to that performed for the quadruple
system GG Tau (Beust & Dutrey 2005, 2006) to determine the possible
solutions for the outer orbit that preserve the three components and
their disks for at least 1 Myr, i.e., the age of the system. A
preliminary analysis, which will be presented in a forthcoming paper,
suggests that the three-body system is stable over a few Myrs, whereas
the fate of the circumstellar disks is not yet established.
Acknowledgements
We acknowledge our referee, Mike Simon, for his insightful
remarks. We thank J. Lu for her help in calibrating the NIRC
camera, L. Saugé and X. Delfosse for clarifying discussions on
the methods to derive uncertainties, and L. Loinard for
providing his radio measurements. This work was funded in part
by the NASA Astrobiology Institute and the NSF Science &
Technology Center for AO, managed by UCSC (AST-9876783). The
data presented herein were obtained at the W.M. Keck
Observatory, which is operated as a scientific partnership among
the California Institute of Technology, the University of
California and the National Aeronautics and Space
Administration. The Observatory was made possible by the
generous financial support of the W.M. Keck Foundation.
- Baraffe, I.,
Chabrier, G., Allard, F., & Hauschildt 2002, A&A, 382,
563 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Beck, T. L., Schaefer,
G. H., Simon, M., et al. 2004, ApJ, 614, 235 [NASA ADS] [CrossRef] (In the text)
- Beust, H., &
Dutrey, A. 2005, A&A, 439, 585 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Beust, H., &
Dutrey, A. 2006, A&A, 446, 137 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Duchene, G., Ghez, A.
M., & McCabe, C. 2002, ApJ, 568, 771 [NASA ADS] [CrossRef] (In the text)
- Duchene, G., Ghez, A.
M., McCabe, C., & Weinberger, A. J. 2003, ApJ, 592, 288 [NASA ADS] [CrossRef] (In the text)
- Duchene, G., Ghez, A.
M., McCabe, C., & Ceccarelli, C. 2005, ApJ, 628, 832 [NASA ADS] [CrossRef] (In the text)
- Eggleton, P.,
& Kiseleva, L. 1995, ApJ, 455, 640 [NASA ADS] [CrossRef] (In the text)
- Ghez, A. M.,
Neugebauer, G., Gorham, P. W., et al. 1991, AJ, 102, 2066 [NASA ADS] [CrossRef] (In the text)
- Ghez, A. M.,
Neugebauer, G., & Matthews, K. 1993, AJ, 106, 2005 [NASA ADS] [CrossRef] (In the text)
- Ghez, A. M.,
Weinberger, A. J., Neugebauer, G., et al. 1995, AJ, 110, 753 [NASA ADS] [CrossRef] (In the text)
-
Hillenbrand, L. A., & White, R. J. 2004, ApJ, 604, 741 [NASA ADS] [CrossRef] (In the text)
- Johnston, K.
J., Gaume, R. A., Fey, A. L., et al. 2003, AJ, 125, 858 [NASA ADS] [CrossRef] (In the text)
- Johnston, K.
J., Fey, A. L., Gaume, R. A., et al. 2004a, ApJ, 604, L65 [NASA ADS] [CrossRef] (In the text)
- Johnston, K.
J., Fey, A. L., Gaume, R. A., et al. 2004b, AJ, 128, 822 [NASA ADS] [CrossRef] (In the text)
- Koresko, C. D.
2000, ApJ, 531, L147 [NASA ADS] [CrossRef] (In the text)
- Koresko, C. D.,
Herbst, T. M., & Leinert, Ch. 1997, ApJ, 480, 741 [NASA ADS] [CrossRef] (In the text)
- Loinard, L.,
Rodríguez, L. F., & Rodríguez, M. I. 2003, ApJ, 587,
L47 [NASA ADS] [CrossRef] (In the text)
- Loinard, L.,
Mioduszewski, A. J., Rodríguez, L. F., et al. 2005, ApJ, 619,
L179 [NASA ADS] [CrossRef] (In the text)
- Mayama, S., Tamura,
M., Hayashi, M., et al. 2006, PASJ, 58, 375 [NASA ADS] (In the text)
- Press, W. H.,
Flannery, B. P., Teulosly, S. A., & Vetterling, W. T. 1992,
Numerical Recipes in FORTRAN (Cambridge Univ. Press)
(In the text)
- Roddier, F.,
Roddier, C., Brandner, W., et al. 2000, in Birth and evolution of
binary stars, ed. B. Reipurth, & H. Zinnecker, 60
(In the text)
- Smith, K.,
Pestalozzi, M., Güdel, M., et al. 2003, A&A, 406, 957 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Tamazian, V. S.
2004, AJ, 127, 2378 [NASA ADS] [CrossRef]
Copyright ESO 2006
![\begin{figure}\par\includegraphics[width=15.2cm,clip]{5917fig1.eps}
\end{figure}](/articles/aa/full/2006/37/aa5917-06/Timg18.gif)