A&A 456, 1109-1120 (2006)
DOI: 10.1051/0004-6361:20065141

Elemental abundances in the atmosphere of clump giants[*],[*]

T. V. Mishenina1 - O. Bienaymé2 - T. I. Gorbaneva1 - C. Charbonnel3,4 - C. Soubiran5 - S. A. Korotin1 - V. V. Kovtyukh1


1 - Astronomical Observatory of Odessa National University and Isaac Newton Institute of Chile, Odessa Branch, Shevchenko Park, 65014 Odessa, Ukraine
2 - Observatoire Astronomique de l'Université Louis Pasteur, 11 rue de l'Université, 67000 Strasbourg, France
3 - Geneva Observatory, 1290 Sauverny, Switzerland
4 - LATT CNRS UMR 5572, 14 Av. E. Belin, 31400 Toulouse, France
5 - Observatoire Aquitain des Sciences de l'Univers, CNRS UMR 5804, BP 89, 33270 Floirac, France

Received 4 March 2006 / Accepted 24 May 2006

Abstract
Aims. The aim of this paper is to provide the fundamental parameters and abundances for a large sample of local clump giants with a high accuracy. This study is a part of a big project, in which the vertical distribution of the stars in the Galactic disc and the chemical and dynamical evolution of the Galaxy are being investigated.
Methods. The selection of clump stars for the sample group was made applying a colour-absolute magnitude window to nearby Hipparcos stars. The effective temperatures were estimated by the line depth ratio method. The surface gravities ($\log~{g}$) were determined by two methods (the first one was the method based on the ionization balance of iron and the second one was the method based on fitting of the wings of the Ca I 6162.17 Å line). The abundances of carbon and nitrogen were obtained from the molecular synthetic spectrum, and the Mg and Na abundances were derived using the non-LTE approximation. The "classical" models of stellar evolution without atomic diffusion and rotation-induced mixing were employed.
Results. The atmospheric parameters ( $T_{{\rm eff}}$, $\log~{g}$, [Fe/H], Vt) and Li, C, N, O, Na, Mg, Si, Ca, and Ni abundances in 177 clump giants of the Galactic disc were determined. The underabundance of carbon, overabundance of nitrogen, and "normal'' abundance of oxygen were detected. A small sodium overabundance was found. A possibility of a selection of the clump giants based on their chemical composition and the evolutionary tracks was explored.
Conclusions. The theoretical predictions based on the classical stellar evolution models are in good agreement with the observed surface variations of the carbon and nitrogen just after the first dredge-up episode. The giants show the same behaviour of the dependencies of O, Mg, Ca, and Si ($\alpha $-elements) and Ni (iron-peak element) abundances vs. [Fe/H] as dwarfs do. This allows us to use such abundance ratios to study the chemical and dynamical evolution of the Galaxy.

Key words: stars: abundances

1 Introduction

Low-mass stars (i.e., below $\sim$2.3 $M_{\odot }$) climb the red giant branch (hereafter RGB) with a degenerate He core whose mass increases until it reaches a critical value of about 0.45 $M_{\odot }$at the top of the RGB. At this point, helium ignites in a series of flashes removing this degeneracy. The star then becomes a "clump'' giant, which undergoes the central He burning. All the low-mass stars have similar core masses at the beginning of He burning, and hence similar luminosities. Due to this fact, the red giants at this evolutionary stage exhibit a specific feature in the colour-magnitude diagram (CMD), called the "clump''. According to evolutionary tracks and in agreement with the observation of open clusters, all giants older than about 1 Gyr fall in the clump (Girardi 1999).

Clump giants are especially interesting in two aspects. Their intrinsic brightness combined with the numerous and sharp features of their spectra make them good tracers for Galactic kinematics and chemistry. They are also very useful in clarifying the advanced evolutionary stages of the low mass stars. Until now, the comprehensive investigation of a large sample of these stars has not yet been carried out.

This work is a part of our study of the Galactic disc surface mass density (Siebert et al. 2003; Bienaymé et al. 2006) of the properties of both thin and thick discs, and the abundance trends in the solar neighbourhood (Soubiran et al. 2003; Mishenina et al. 2004; Soubiran & Girard 2005). In this part of the project, the local clump giants observed with high spectral resolution and high signal-to-noise ratios (S/N) serve as reference stars. Here we take the opportunity to provide strong observational constraints for the theory of stellar evolution. As a matter of fact, the chemical composition of the clump giant atmospheres reflects both the chemical composition of the prestellar matter and nucleosynthesis and mixing processes inside the stars. Therefore, for successful Galactic studies we need to know the abundances of which chemical elements are not affected by the mixing processes. On the other hand, we can use the elements with abundances affected by the mixing processes to distinguish different stages of the stellar evolution, in particular the clump phase.

While investigating the clump giants, we faced the problem of their selection, since this region of the CMD is also occupied by the stars of the ascending giant branch. The differentiation between the first-ascending RGB stars and the "clump'' stars is rather complicated. Even for open cluster stars, it is very difficult to establish, with a good level of certainty, which stars from the group under investigation are the real clump ones (Pasquini et al. 2004). We can solve the problem of the correct selection using the extended observational data on the clump giants, selected with photometric criteria. However, is it possible to identify the clump giants based on additional criteria, including the data about their chemical composition?

When the star moves towards the RGB, the superficial convection zone deepens and the nuclearly processed material penetrates into the atmosphere, changing its chemical composition. During this so-called first dredge-up phase, the surface abundances of Li, C, N, and Na, together with the 12C/13C ratio, are being altered. The effect depends both on the stellar mass and metallicity (see Charbonnel 1994). Typically, the surface abundance of carbon decreases by $\sim$0.1-0.2 dex, and that of nitrogen increases by 0.3 dex or more (Iben 1991).

Despite a large dispersion, the abundances of CNO elements and their isotopes observed previously in the giants of the solar metallicity (Lambert & Ries 1981; Kjrgaard et al. 1982) were found to be in a good agreement with theoretical predictions (Iben 1991). We reinvestigate this problem with a larger sample of stars that have been observed with higher quality.

For the giants and supergiants of solar metallicity, the sodium overabundance has been found in many studies (Cayrel de Strobel et al. 1970; Korotin & Mishenina 1999; Boyarchuk et al. 2001; Andrievsky et al. 2002). As has been shown in some papers (Mashonkina et al. 1993; Korotin & Mishenina 1999), the Na overabundance cannot only be explained by deviations from LTE. In this paper, we look into this problem using recent theoretical considerations and track calculations. The aim of this paper is to provide the fundamental parameters and abundances for a large sample of local clump giants, determined with a high accuracy, and to use these data to 1) probe the vertical distribution of the stars in the Galactic disc; 2) investigate the Galactic chemical evolution; and 3) explore the possibility of selecting the clump giants based on their elemental abundances.

In Sect. 2, we described the photometric selection criteria for the clump giants and the detail of our spectroscopic observations. In Sect. 3, the determination of the atmospheric parameters is presented. In Sect. 4, the chemical abundances are determined. In Sect. 5, we discussed the behaviour of each element in our sample with metallicity. In Sect. 6, we provided the analysis of the signs of the first dredge-up in stars under current study.

2 Selection of the stars and observations

The clump stars analysed in this paper were selected using a colour-absolute magnitude window applied to nearby Hipparcos stars. Stars were selected from the Hipparcos catalogue according to the following criteria:

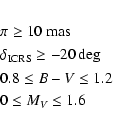
\begin{eqnarray*}&&\pi \ge 10~\rm {mas}\\ &&\delta_{\rm { ICRS}} \ge -20\deg\\ &&0.8 \le B-V \le 1.2\\ && 0 \le M_{V} \le 1.6 \end{eqnarray*}


where $\pi$ is the Hipparcos parallax and $ \delta_{\rm {ICRS}}$[*] the declination. The Johnson B-V colour was transformed from the $\it Tycho$2 $B_{\rm T}-V_{\rm T}$ colour, applying Eq. (1.3.20) from ESA (1997):

\begin{displaymath}B-V = 0.850 ~(B_{\rm T}-V{\rm _T}).\end{displaymath}

The absolute magnitude MV was computed using the V magnitude transformed from the Hipparcos $H_{\rm p}$ magnitude to the Johnson system with the equation calibrated by Harmanec (1998).

Among the nearly 400 giants selected, about a half of them were observed: the first priority group contained stars, for which radial velocities were not determined, and their [Fe/H] were not accurate or were old. The known spectroscopic binaries were excluded.

The list was completed with a few clump stars having distances in the range of 100-200 pc, for which we were expecting the low metallicity. Most of the clump stars with B-V between 0.75 and 0.8, even lacking previously published metallicities, were also included in the list and observed. Finally, we have included six $\it Tycho$-2 stars that are distant clump stars located at about 500 pc from the Galactic plane toward the North Galactic Pole. They were previously identified from the low S/N spectra (Bienaymé et al. 2006).

The spectra of the studied stars were obtained using the facilities of the 1.93 m telescope of the Haute-Provence Observatoire (France) equipped with the échelle spectrograph ELODIE. The resolving power was 42 000, the region of the wavelengths was 4400-6800 Å, and the signal-to-noise ratio was about 130-230 (at 5500 Å). The initial processing of the spectra (image extraction, cosmic particles removal, flatfielding, etc.) was carried out following Katz et al. (1998). Further processing of the spectra (continuum level location, measurement of the equivalent widths, etc.) was performed using the software package DECH20 (Galazutdinov 1992). The equivalent widths were measured using the Gaussian fitting.

In Fig. 1 we have shown the comparison of our EWs measured in the spectrum of HD 180711 with those reported by Boyarchuk et al. (1996). In Boyarchuk et al. (1996), the spectra of program stars were obtained using the 2.6 m telescope at the Crimean Astrophysical Observatory (Ukraine) with a coudé échelle spectrograph. The reciprocal dispersion of those spectra was 3 Å/mm. An agreement between two independent EW systems appears to be good, as one can see in Fig. 1. $\Delta{\it EW} = {\it EW}($our $){-}{\it EW}($Boyarchuk $) = 0.23\pm4.5$ mÅ.


  \begin{figure} \par\includegraphics[width=6.3cm,clip]{5141fig1.eps}\end{figure} Figure 1: Comparison between EWs measured from the spectrum of HD 180711 and those from Boyarchuk et al. (1996). Upper panel: EWs from Boyarchuk et al. (1996); lower panel: our determinations.
Open with DEXTER

The basic characteristics of studied stars are given in Table A.1. The spectral classes Sp, magnitudes V(Simbad) were taken from the SIMBAD database, the magnitude V(Hipparcos) was transformed from the Hipparcos Hp to the Johnson system, the parallaxes $\pi$ were taken from the Hipparcos catalogue (ESA 1997), and the MV were calculated. The 6 fainter stars of the sample are not part of the Hipparcos catalogue. Their spectral type come from SIMBAD. The V magnitudes were extracted from the General Catalogue of Photometric Data by Mermilliod et al. (1997). Absolute magnitudes Mv have been estimated from the TGMET software.

3 Atmospheric parameters

3.1 Effective temperature $T_{{\rm eff}}$

The temperatures were determined with the very high level of accuracy ( $\sigma = 10{-}15$ K) using the line depth ratios. The spectral lines of high and low excitation potentials respond differently to the change in effective temperature ( $T_{{\rm eff}}$). Therefore, the ratio of their depths (or equivalent widths) is a very sensitive temperature indicator. This technique allows one to determine $T_{{\rm eff}}$  with an exceptional level of accuracy. The method used is based on the ratio of the central depths of two lines having very different functional $T_{{\rm eff}}$ dependences. This method is independent of the interstellar reddening and only marginally dependent on individual characteristics of the stars, such as rotation, microturbulence, and metallicity. NLTE effects will most likely affect ratios of high- and low-excitation line strengths, and ratios between different chemical elements. Perhaps these effects and also those of varying individual stellar chemical abundance can be reduced by the statistics of a large number of different line ratios. The zeropoint is well established and is based on a large number of independent measurements from the literature; it would be unlikely that the error on the zeropoint is larger than 20-50 K.

We used a set of 100 line ratio - $T_{{\rm eff}}$  relations obtained in Kovtyukh et al. (2006), with the mean random error of a single calibration being 65-95 K (45-50 K in most cases and 90-95 K in the least accurate cases). The use of $\sim$70-100 calibrations per spectrum reduces the uncertainty to 5-25 (1$\sigma$) K. This precision indicates that these 100 calibrations are weakly sensitive to non-LTE effects, metallicity, surface gravity, micro- and macroturbulence, rotation, and other individual stellar parameters. These relations have been calibrated with the reference stars in common with Gray & Brown (2001) - 21 stars, $\sigma=27$ K; Blackwell & Lynas-Gray (1998) - 18 stars, $\sigma= 81$ K; Alonso et al. (1999) - 14 stars, $\sigma=47$ K; Strassmeier & Schordan (2000) - 20 stars, $\sigma=71$ K; and Soubiran et al. (1998) - 103 stars, $\sigma=106$ K (see Fig. 2). For the majority of stars, we obtained an internal error smaller than 20 K.


  \begin{figure} \par\includegraphics[width=6cm,clip]{5141fig2.eps}\end{figure} Figure 2: Comparison between the temperatures derived in the present work and those derived by Gray & Brown (2001) - open squares, Blackwell & Lynas-Gray (1998) - solid circles, Alonso et al. (1999) - solid triangles, Strassmeier & Schordan (2000) - open circles, and Soubiran et al. (1998) - solid squares.
Open with DEXTER

After the accurate effective temperatures have been determined, the other atmospheric parameters were found iteratively.

3.2 Surface gravity ${\log}$ g, microturbulent velocity Vt, and metallicity [Fe/H]

Because clump giants have similar luminosity, but different initial masses, their gravities cannot be correctly determined using their parallaxes and mass data. These $\log~{g}$ values are affected by $\pm$0.3 dex, if the stellar mass is based on an assumption of mass of 2.2 $~M_{\odot}$. We used the two following methods of spectroscopic determination of the gravity $\log~{g}$: 1) using the iron ionization equilibrium assumption, where the average iron abundance determined from Fe I lines and Fe II lines must be identical, and 2) from the wing fitting of the Ca I 6162 Å  line. For the method of the ionization equilibrium, we used iron lines with ${\it EW} < 120$ mÅ; the wing profiles for such lines practically do not depend on damping constants, but they are sensitive to microturbulent velocity Vt  and metallicity [Fe/H]. Therefore, we take adopted $T_{{\rm eff}}$, and then we obtain the parameters ($\log~{g}$, Vt, and [Fe/H]) iteratively. Two or three steps were enough to get a good convergence.

The second method is motivated by the fact that the Ca I line is strong in giants, and therefore its wing profile is sensitive to the gas pressure in a stellar atmosphere, and to the surface gravity. The use of the Ca I triplet lines (6102, 6122, 6162 Å) as indicators of surface gravity was proposed for dwarfs and subgiants by Edvardsson (1988), and analysed by Cayrel et al. (1996). Cayrel et al. (1996) explored the possible influence of errors on the profiles of these lines. They found that a change of 10$\%$ of the damping constants has a negligible influence, a change of 15$\%$ becomes more or less detectable. The effective temperatures were also varied by 100 K, and no alteration of profiles was detected. NLTE effects are important in the core of the line, but negligible in the wings. Recently, Affer et al. (2005) used this method for K dwarfs and subgiants. We applied this method to giants to assess our gravity determination in case of iron ionization equilibrium. The Ca I 6162 Å  line, which was recommended by Katz et al. (2003) as a best luminosity indicator among the triplet lines, was used. We estimated the influence of atmospheric parameter uncertainties on accuracy of the gravity determination. The Ca I wings are not sensitive to the microturbulent velocity Vt. A change by 30 K in $T_{{\rm eff}}$  brings the errors in $\log~{g}$ about 0.05-0.10 (for $T_{{\rm eff}}$ = 5000 K and 4500 K, respectively). To determine the calcium abundance value, we used weaker Ca I lines, which are presumed to be less affected by the damping and the microturbulent velocity.

The departures from LTE in the computation of the wing profiles for these lines are negligible for dwarfs and subgiants (Cayrel et al. 1996), but in the case of giants it may elevate the level of uncertainty in $\log~{g}$ up to 0.2 dex. The total error of the $\log~{g}$ determination for giants is about 0.2-0.3 dex. An example of the line wing fitting for HD 180711 is given in Fig. 3. The values of $\log~{g}$, obtained by two methods, are given in Table A.2. The mean difference $\Delta $ ($\log~{g}$(Ca) - $\log~{g}$(IE)) is -0.01 $\sigma= \pm 0.09$The results of these two methods applications are in good agreement. The value of surface gravity for each star was obtained by keeping the condition of the ionization equilibrium between the Fe I and Fe II species, and these values were used for abundance determination.

The value of the microturbulent velocity Vt is determined by the standard method from a condition of independence of the iron abundances determined from the given line of Fe I upon its equivalent width EW. The accuracy of Vt determination is $\Delta $ Vt = $\pm$0.2 km s-1.

The [Fe/H] metallicity is obtained from the abundance determined from Fe I lines. (In this paper we use the customary spectroscopic notation  $[X/Y]=\log_{10}~(N_X/N_Y)_{\rm star}$ - log $_{10}~(N_{X}/N_{Y})_{\odot}$).

In Table A.2 we give the mean $T_{{\rm eff}}$, the number of calibrations used (N), the errors of the mean $\sigma$, $\log~{g}$, Vt, and metallicities [Fe/H]$_{\rm I}$ and [Fe/H]$_{\rm II}$, which were determined from Fe I and Fe II lines, respectively.


  \begin{figure} \par\includegraphics[width=6.5cm,clip]{5141fig3.eps}\end{figure} Figure 3: Derivation of $\log~{g}$ from the Ca I 6162 Å  profile for HD 180711.
Open with DEXTER

4 Determination of chemical abundances

We employ the grid of stellar atmospheres from Kurucz (1993) to compute abundances of Li, C, N, O, Na, Mg, Si, Ca, and Ni. The choice of the model was made using the standard interpolation on $T_{{\rm eff}}$  and $\log~{g}$. The abundance analysis of Si, Ca, Ni, and Fe has been done in the LTE approximation (Kurucz's WIDTH9 code) using the measured equivalent widths of these elements' lines and the solar oscillator strengths (Kovtyukh & Andrievsky 1999). Abundances of Fe, Si, Ca, Ni were derived from a differential analysis relatively to the Sun's data (see discussion in Mishenina et al. 2004). In Table A.3, the relative-to-solar Fe, Si, Ca, and Ni abundances and individual errors are given.

4.1 The Li abundance

The Li abundances in program stars were obtained by fitting synthetic spectra to the observational profiles. We used the STARSP LTE spectral synthesis code developed by Tsymbal (1996). Considering a wide range of temperatures and metallicities of our sample stars, a special effort was put into a compilation of a full list of atomic and molecular lines close to the 7Li 6707 Å line (Mishenina & Tsymbal 1997). In Fig. 4, the comparison was made of the observed and the calculated spectra of HD 90633 for different lithium abundances log A(Li) = 1.0, 1.85, and 2.1, where log A(X $) = 12 + \log~(N_{X}/N_{H}$). The derived values of log A(Li)> 0.5 dex are given for 24 stars in Table A.4. We consider the lithium abundance of about 0.5 dex as a lower limit of the reliable determination. The comparison of our results with values found in the literature (Brown et al. 1989) shows a good agreement $\Delta $ log  $A{\rm (Li)Brown}~ -~ \log~A($Li)our =  $-0.01 \pm 0.13~$ (for 8 common stars).

4.2 CNO abundances

The abundances of carbon, nitrogen, and oxygen are determined by the method of synthetic spectrum using the STARSP code (Tsymbal 1996). The spectrum of a molecule C2 at 5630 Å (head of a band C2 (0,1) of the Svan system d $^{3}\Pi_{g} - {\rm a}^{3}\Pi_{u}$) was used to derive the carbon abundance. The nitrogen abundance was determined from the spectrum of a molecule CN at 6330 Å  and 6470 Å  (red system ${\rm A}^{2}\Pi - {\rm X}^{2}\Sigma$, heads of bands CN (5,1) and (6,2)). The wavelengths and parameters of molecular lines (including $\log~gf$) were taken from Kurucz (1993), and they were corrected using the technique proposed by Kuznetsova & Shavrina (1996). For these spectral regions, the contribution from blended lines of other systems of a molecule C2, molecule CN, and (NH, OH, CH, MgH, and SiH) was estimated. The lines from our list were compared to the lines from the solar spectrum, using the atmosphere model from the Kurucz grid. The contribution from the blended lines in the solar spectrum appears to be insignificant (except for lines of a molecule CN in the regions of a molecule C2 and line [OI] 6300.3 Å). For the regions of a molecule C2 and [OI] 6300.3 Å  line, the CN lines were included in the final line list. The calculation was carried out with the dissociation potentials D0 (C 2) = 6.15 eV and D0 (CN) = 7.76 eV. In Fig. 5, a comparison between the synthetic spectrum and the observed one near 5630 Å  is shown. In Table A.4, the abundances of carbon, nitrogen, and oxygen are given with the scale $\log{A({\rm H})} = 12$. Below, we use the values relative to solar and iron abundances ([C, N, O/Fe]). The solar C, N, O abundances are determined by fitting the synthetic and solar spectra. As solar spectra, we used those of the Moon and asteroids that were obtained with the spectrograph ELODIE. The adopted solar values of log log A(C), log A(N), and log A(O) are the following: 8.55, 7.97, and 8.70, respectively.


  \begin{figure} \par\includegraphics[width=6.5cm,clip]{5141fig4.eps}\end{figure} Figure 4: Comparison between the observed spectrum for HD 90633 and the synthetic one with the Li abundances log A(Li) = 1.0, 1.85, and 2.1.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=6.5cm,clip]{5141fig5.eps}\end{figure} Figure 5: Comparison between the observed spectrum for HD 94084 and the synthetic one with the C abundances log A(C) = 8.36, 8.46, and 8.56.
Open with DEXTER

4.3 NLTE abundances of magnesium and sodium

In the spectra of cool giants, the lines of sodium and magnesium are strong enough ( ${\it EW}> 200$ mÅ), therefore one can expect a significant deviation from LTE. For determination of the abundances of Na and Mg, we used an NLTE approximation. Four lines of Na I and 9 lines of Mg I were considered.

NLTE abundances of Mg and Na were determined with the help of a modified version of the MULTI code (Carlsson 1986) described in Korotin et al. (1999a,b). In such a modified version, in particular, additional opacity sources from the ATLAS9 code (Kurucz 1993) were included. This was done to calculate the continuum opacity more precisely, and to take into account the absorption by a great number of spectral lines (especially within the region of the near UV). This allowed us to more accurately calculate the intensity distribution in the region 900-1500 Å. In turn, this significantly affects the determination of the radiative rates of bound - free transitions. A simultaneous solution of the radiative transfer and statistical equilibrium equations has been performed in the approximation of a complete frequency redistribution for all the lines. All the NLTE calculations were also based on the Kurucz grid of atmospheric models.

4.4 Parameters of sodium and magnesium atoms

The model of the sodium atom described by Sakhibullin (1987) has been modified (see Korotin & Mishenina 1999). It consists of 27 levels of Na I and the ground level of Na II. We considered the radiative transitions between the first 20 levels of Na I and the ground level of Na II. Transitions between the remaining levels were only used in the equations of particle number conservation. Finally, 46 $\it bound-bound$ and 20  $\it bound-free$ transitions were included in the linearization procedure. For 34 transitions the radiative rates were fixed.

We employed the model of the magnesium atom consisting of 97 levels: 84 levels of Mg I, 12 levels of Mg II, and a ground state of Mg III. Within the described system of the magnesium atom levels, we considered the radiative transitions between the first 59 levels of Mg I and the ground level of Mg II. Transitions between the rest levels were not taken into account, and they were used only in the equations of particle number conservation. For detail see Mishenina et al. (2004).

The difference between synthetic and observed spectra becomes visible if the sodium and magnesium abundances are changed by about 0.05 dex. The difference between sodium and magnesium abundances derived under the LTE assumption and for the NLTE case is within an interval of 0.10-0.15 dex. As an example, for better comparison we have shown the LTE line profile in Figs. 6-9.

In Table A.4, NLTE abundances of Na and Mg are given in the scale where $\log~A ($H) = 12.

4.5 Abundance determination errors


  \begin{figure} \par\includegraphics[width=6.5cm,clip]{5141fig6.eps} \end{figure} Figure 6: NLTE profile fitting for HD 162076 (for the line Na I 5683 Å) and the LTE profile (dashed line).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=6.5cm,clip]{5141fig7.eps} \end{figure} Figure 7: Same as Fig. 6, but for the lines Na I 6164, 6160.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=6.5cm,clip]{5141fig8.eps} \end{figure} Figure 8: Same as Fig. 6, but for the lines Mg I 4703.
Open with DEXTER

The metallicities [Fe/H] for the giants have been determined. These determinations were based on the iron abundance values derived from Fe I lines. For this purpose, we used from 100 to 170 lines, depending on the temperature of the star: for the cooler stars, the number of iron lines was lower. The typical line-to-line scatter for Fe I is 0.11 dex s.d. The abundances of silicon, calcium, and nickel have been determined from 12 to 22 lines of Si I, 8 to 10 lines of Ca I, and 15 to 20 lines of Ni I. Typical standard deviations of the abundances derived from a single line of these elements are 0.12, 0.14, and 0.10, respectively.

Several factors may influence the abundance determination. Among them are: 1) the accuracy of the model parameters; 2) the equivalent width measurements; 3) the quality of the synthetic spectrum adjustment; and 4) internal errors of the method used. Concerning the last factor, one can notice that somewhat different abundance results can be obtained if one uses the LTE or NLTE approximations, 1D-, 2D-, or 3D atmosphere models. There are also uncertainties in atomic constants. The use of the differential method minimizes these determination errors. Uncertainties that are attributed to observed spectrum are the following. A change in equivalent width of 2 mÅ corresponds to a change in abundance of about 0.03-0.06 dex for Fe I, Si I, Ca I, and Ni I. The fitting procedure between synthetic and observed spectra in the case of C2 lines produces uncertainty of about 0.02 dex. In other cases (N, Na, Mg), it is about 0.05 dex. The value of total uncertainty due to the choice of the stellar parameters is shown in Table 1. The atmospheric parameters were changed by  $\Delta T_{\rm eff} = +100$ K, $\Delta $ $\log~{g}$ = +0.2, $\Delta ~[{\rm Fe/H}] = -0.25$ for [Fe/H] < 0 and $\Delta~[$Fe/H] = +0.1 for [Fe/H]>0, $\Delta~V_{t}= +0.2$ km s-1.


  \begin{figure} \par\includegraphics[width=6.5cm,clip]{5141fig9.eps} \end{figure} Figure 9: Same as Fig. 6, but for the lines Mg I 5173, 5184.
Open with DEXTER

As one can see from Table 1, the total uncertainty reaches 0.18-0.24 dex for iron abundance determined from Fe II species, and 0.10-0.12 dex in the case of the Fe I species. For C, N, and O abundances, such uncertainties are: 0.13-0.23, 0.09-0.13, and 0.09-0.21, respectively. In the case of carbon, the maximal error takes place for the cooler stars. For oxygen, the uncertainty is caused by the choice of the model metallicity for metal-deficient stars. For Na, Mg, and Si abundances, the total error is about 0.08-0.11, and for Ca and Ni it is about 0.11-0.16. The microturbulence uncertainty supplies the largest uncertainty to the Fe I iron abundance.

Table 1: Abundance determination errors. Parameter variation and corresponding uncertainty in abundance determination ( $\Delta~T_{\rm eff} = +100$ K, $\Delta $ $\log~{g}$ = +0.2, $\Delta~[$Fe/H] = -0.25 for [Fe/H] < 0 and $\Delta~[$Fe/H] = +0.1 for [Fe/H]>0, $\Delta~V_{t}= +0.2$ km s-1).

5 Abundance trends with metallicity

5.1 The C, N, O abundance

The abundance ratios [C/Fe], [N/Fe], and [O/Fe] for each star in our set are plotted against [Fe/H] in Figs. 10, 11, and 13. For the whole sample of giants, the average values of the abundances of these elements are the following: $\langle[{\rm C/Fe}]\rangle=-0.23\pm0.08$, $\langle[{\rm O/Fe }]\rangle= 0.08\pm0.16$, and $\langle[{\rm N/Fe }]\rangle=0.25\pm0.09$. For the stars of metallicity [Fe/H]> -0.3 they are: $\langle[{\rm C/Fe}]\rangle=-0.24\pm0.07$, $\langle[{\rm O/Fe }]\rangle= 0.04\pm0.12$, and $\langle[{\rm N/Fe }]\rangle=0.24\pm0.08$. For stars near the solar metallicity $--0.01 < [{\rm Fe/H}] < 0.01$, they are: $\langle[{\rm C/Fe}]\rangle=-0.28\pm0.05$, $\langle[{\rm O/Fe }]\rangle= 0.02\pm0.08$, and $\langle[{\rm N/Fe }]\rangle=0.21\pm0.07$. These averaged abundance ratios agree well with evolutionary model predictions of Iben (1991), who showed that stars should have decreased carbon and increased nitrogen abundances in their atmospheres.


  \begin{figure} \par\includegraphics[width=6.5cm,clip]{5141fi10.eps} \end{figure} Figure 10: Carbon abundance [C/Fe] vs. [Fe/H].
Open with DEXTER

Thus, our data (see Fig. 10) exhibit a clear anticorrelation between [C/Fe] and [Fe/H]. In Fig. 12, we compare our determinations (open circles) of the carbon abundance with those of Lambert & Ries (1981), Kjrgaard & Gustafsson (1982) for all stars. The mean values obtained in these works are: $\langle[{\rm C/Fe}]\rangle=-0.22\pm0.21$(Lambert & Ries 1981) and $\langle[{\rm C/Fe}]\rangle=-0.31\pm0.30$(Kjrgaard & Gustafsson 1982). They are within the error limits of determinations with our value $\langle[{\rm C/Fe}]\rangle=-0.23\pm0.08$, but in our case we have smaller scatter. The dependence of [C/Fe] on [Fe/H] (see Fig. 12) is clearly observed only for our clump giant sample; however, it is probably not a feature of the clump stars. The same behaviour of [C/Fe] versus [Fe/H] was discovered in the disc dwarfs (Bensby & Feltzing 2006; Reddy et al. 2006), but the average values of [C/Fe] are different for dwarfs and for giants. Therefore, we can conclude that the observed trend is not a peculiar feature of the clump giants, since it reflects the general tendency of the C abundance decreasing with [Fe/H] increasing. We have detected it because our [C/Fe] are obtained with a smaller scatter, compared to other similar works.

We have found some (not distinctive) dependence between [N/Fe] and [Fe/H] (see Fig. 11), but quite large scatter for our nitrogen data prevents us from making a definitive conclusion. An analysis of the C and N abundances within the frameworks of the evolutionary models is presented in Sect. 6.

The abundance of oxygen increases with the metallicity decrease (see Fig. 13). This behaviour is similar to $\alpha $-element behaviour in the dwarf stars. This confirms the well-known fact that the relative-to-iron abundance of the $\alpha $-elements decreases when the metallicity increases. This is connected with the growing contribution from the SNe I stars to the iron enrichment. Obviously, the determined oxygen abundance in giants can be used in an investigation of Galactic evolution.


  \begin{figure} \par\includegraphics[width=6.5cm,clip]{5141fi11.eps}\end{figure} Figure 11: Nitrogen abundance [N/Fe] vs. [Fe/H].
Open with DEXTER


  \begin{figure} \par\includegraphics[width=6.5cm,clip]{5141fi12.eps}\end{figure} Figure 12: Comparison of our carbon abundances (open circles) and those of Kjrgaard et al. (1982) (asterisks) and Lambert & Ries (1981) (filled circles).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=6.5cm,clip]{5141fi13.eps}\end{figure} Figure 13: Oxygen abundance [O/Fe] vs. [Fe/H].
Open with DEXTER

5.2 The Na abundance


  \begin{figure} \par\includegraphics[width=6.5cm,clip]{5141fi14.eps}\end{figure} Figure 14: Sodium abundance [Na/Fe] vs. [Fe/H].
Open with DEXTER


  \begin{figure} \par\includegraphics[width=6.5cm,clip]{5141fi15.eps}\end{figure} Figure 15: Sodium abundance [Na/Fe] vs. $\log~{g}$.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=6.5cm,clip]{5141fi16.eps} \end{figure} Figure 16: Sodium abundance [Na/Fe] vs. nitrogen abundance [N/Fe].
Open with DEXTER

We found a small Na overabundance of about 0.1 dex (see Fig. 14), and we also established that there is no visible dependence of [Na/Fe] upon $\log~{g}$  (see Fig. 15). Some overabundance of sodium can be the sign of the NeNa cycle operation. Nevertheless, an absence of any dependence between [Na/Fe] and $\log~{g}$  does not support this supposition. On the other hand, this can be the result of a restricted region of the $\log~{g}$  we considered. Additionally, there is a correlation between [Na/Fe] and [N/Fe] (see Fig. 16). We notice that the behaviour of [Na/Fe] vs. [Fe/H] is not similar for giants and for dwarfs (Soubiran & Girard 2005). We will consider the sodium abundance below in Sect. 6.

5.3 The $\alpha $-element and Ni abundances

The behaviour of Mg, Ca, and Si ($\alpha $-elements) and Ni (iron-peak element) (see Figs. 17-20) abundances vs. [Fe/H] in giants is the same as in dwarfs (Soubiran & Girard 2005). This allows us to use abundances of these elements to study the chemical and dynamical evolution of the Galaxy.


  \begin{figure} \par\includegraphics[width=6.5cm,clip]{5141fi17.eps} \end{figure} Figure 17: Magnesium abundance [Mg/Fe] vs. [Fe/H].
Open with DEXTER


  \begin{figure} \par\includegraphics[width=6.5cm,clip]{5141fi18.eps}\end{figure} Figure 18: Calcium abundance [Ca/Fe] vs. [Fe/H].
Open with DEXTER

6 Abundance variations due to the first dredge-up

Due to surface abundance modifications during the first dredge-up episode, clump giants do not exhibit the chemical pattern that they inherited at their birth. In this section, we compare our data with first dredge-up theoretical predictions.

6.1 Stellar models

We computed evolution models from the pre-main sequence up to the AGB phase for stars with initial masses of 1.0, 1.5, 2.0, 2.5, and 3.0 $M_{\odot }$, and for three values of [Fe/H], i.e., -0.293, 0, and +0.252, using the code STAREVOL (i.e., Siess et al. 2000; Palacios et al. 2006). These are "classical'' models, i.e., they do not take into account atomic diffusion and rotation-induced mixing. The nuclear reaction rates are those of NACRE (Angulo et al. 1999). For the radiative opacities, we use the OPAL tables above 8000 K (Iglesias & Rogers 1996), and at lower temperatures, the atomic and molecular opacities of Alexander & Fergusson (1994). The conductive opacities are computed from a modified version of the Iben (1975) fit to the Hubbard & Lampe (1969) tables for non-relativistic electrons, and from Itoh et al. (1983) and Mitake et al. (1984) for relativistic electrons. The equation of state is described in detail in Siess et al. (2000) and accounts for the non-ideal effects due to Coulomb interactions and pressure ionization. The standard mixing length theory is used to model the convection $\alpha_{\rm MLT} = 1.75$ calibrated for the solar case. Neither overshooting, nor undershooting is considered for convection. The atmosphere is treated in the gray approximation and integrated up to an optical depth $\tau \simeq 5\times10^{-3}$. Mass loss is considered during the whole evolution and follows the Reimer (1975) empirical relation.


  \begin{figure} \par\includegraphics[width=6.5cm,clip]{5141fi19.eps}\end{figure} Figure 19: Silicon abundance [Si/Fe] vs. [Fe/H].
Open with DEXTER


  \begin{figure} \par\includegraphics[width=6.5cm,clip]{5141fi20.eps}\end{figure} Figure 20: Nickel abundance [Ni/Fe] vs. [Fe/H].
Open with DEXTER

6.2 Comparison with theoretical predictions

In Figs. 21-23 we show the corresponding evolutionary tracks together with the positions of the sample stars in the HR diagram. As expected, the objects appear to be slightly more massive, on average, when one moves to higher metallicity.


  \begin{figure} \par\includegraphics[width=12cm,clip]{5141fi21.eps} \end{figure} Figure 21: Comparison of the theoretical tracks and predictions for surface abundance variations with observations. Position of our target stars with [Fe/H]<-0.15 in the H-R diagram.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=12cm,clip]{5141fi22.eps}\end{figure} Figure 22: Same as Fig. 21 for [Fe/H]=0. Top right panel: the solid lines are those assuming an initial [C/Fe] equal to solar, while the dotted lines are obtained by simply shifting the previous ones by -0.15.
Open with DEXTER

Also shown in these figures are the predictions for the surface abundance variations of C, N, and Na as a function of effective temperatures along the RGB, together with the corresponding observational data. Stars with [Fe/H] below -0.15 are compared with the [Fe/H]=-0.293 tracks, those with [Fe/H] between -0.15 and +0.12 are compared with the [Fe/H]=0tracks, and the more metallic ones with the [Fe/H]=+0.252 tracks. As can be seen, the region of the clump in the evolutionary tracks overlaps the region where the first dredge-up ceases.

Our finding about the nitrogen abundance is in good agreement with the prediction of the canonical theory of evolution for first dredge-up phase.


  \begin{figure} \par\includegraphics[width=12cm,clip]{5141fi23.eps}\end{figure} Figure 23: Same as Fig. 22 for [Fe/H]=0.252 and [C/Fe]=-0.20.
Open with DEXTER

In the case of carbon, we show two sets of tracks for the two more metallic subsamples: one assuming an initial [C/Fe] equal to solar, while the other is obtained by simply shifting the previous ones by -0.15 and -0.20 dex, respectively. These quantities correspond to the values of the upper envelope of [C/Fe] at the corresponding [Fe/H] (see Fig. 10). Again, the models explain the observational pattern well.

Regarding sodium, the observed dispersion is higher than the theoretical one. Numerous overabundances are observed, especially for the more metal-rich subsample. This cannot be attributed to an extra-mixing process because any additional processing of the envelope of the giant would also lead to further changes in the C and N abundances, which are not observed in our sample. One possibility to remove part of the discrepancy could lie in the rates that intervene in the NeNa cycle. For the reaction that forms sodium, 22Ne(p, $\gamma )^{23}$Na, the new rate calculated by Hale et al. (2001), is slightly smaller (for the central temperature of the models on the main sequence, i.e., below $\sim$20 million degrees) than the NACRE prescription used in the present computations. Thus it would, not favour a stronger dredge-up of sodium. On the other hand, the present uncertainty of the 23Na(p, $\gamma )^{24}$Mg and 23Na(p, $\alpha)^{20}$Ne reactions is still large (Hale et al. 2004). The possibility that the initial sodium abundance was higher for some stars also exists. The disc dwarfs show some dispersion of the Na abundance, and this is confirmed, for example, by Mishenina et al. (2003) and Edvardsson et al. (1993) (especially for [Fe/H]> 0).


  \begin{figure} \par\includegraphics[width=6.5cm,clip]{5141fi24.eps}\end{figure} Figure 24: Predictions for surface abundance variations of O during the first dredge-up for the [Fe/H]=0 models, and comparison with the observations.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=6.5cm,clip]{5141fi25.eps}\end{figure} Figure 25: Li abundance log A(Li) vs. $T_{{\rm eff}}$  for our sample stars compared with the theoretical predictions for the tracks at [Fe/H]=0. The line with the strongest Li depletion corresponds to the 1.0 $M_{\odot }$model.
Open with DEXTER

In the central regions of the main sequence stars, 16O is partially converted into 14N. However, the convective envelope hardly reaches the O-depleted region during the first dredge-up for the mass range considered here (see, for example, Fig. 1 of Charbonnel 1994). As a consequence, surface O variations are not expected in our sample stars (Fig. 24). In our sample of giants, we observe an O/Fe versus Fe/H variation (Fig. 13) similar to the variation observed with dwarfs (see Figs. 4 and 10 in Soubiran & Girard 2005).

6.3 The Li abundance

According to the theory, the surface Li abundance decreases with respect to its value at the end of the main sequence (MS) by a factor of 30 to 60, depending on the stellar mass and metallicity (Iben 1991). Starting from the present interstellar medium abundance of log N(Li) = 3.3, we thus expect the Li values that lie around 1.5 after the first dredge-up, as shown in Fig. 25. Let us insist on the fact that these are "classical'' predictions that do not take the effect of non-standard transport processes such as those induced by rotation into account, and that are thus not able to explain the Li patterns observed in low-mass main sequence stars (Charbonnel & Talon 2005; see the review by Deliyannis et al. 2000). As such, we have the right to expect lower values of lithium for our giants, as proves to be true by observation (Brown et al. 1989; Mallik 1999).

The observed Li abundances versus the effective temperatures for the giants studied here are depicted in Fig. 25.

In the case of low-mass stars ( $M_{\rm star}<2.2{-}2.5~M_{\odot}$, HD 8733, 15453, 42341, 46374, 90633, 117304, 136138, 139254, 148604, 171994, and 192836) that undergo some extramixing at the RGB bump (Charbonnel et al. 1998; Charbonnel & Balachandran 2000), the fact that we see some Li certainly indicates that these objects are RGB stars that have not yet reached the bump. Otherwise, their Li would have been destroyed.

In the case of more massive stars that do not undergo this extramixing because they do not go through the bump, Li should be consistent with the standard post dredge-up values predicted by the models.

It is most likely that the Li abundance cannot be used as the criterion to segregate the clump giants from RGB giants.

6.4 Determination of the evolutionary status

The stars considered in this study have been selected as clump stars according to photometric criteria. Nevertheless, our sample could be contaminated by ascending giant branch stars that cohabit with clump stars in the considered region of the CMD (see Figs. 21-23). It would thus be interesting to perform a more subtle separation of the clump giants from the whole sample of the stars.

We aimed to do this selection by comparing the abundances of individual stars with theoretical predictions of stellar evolution models. This is, however, a very difficult task since the clump overlaps the region where the first dredge-up ceases in the evolutionary tracks. Despite this difficulty, we checked the status of each sample star individually following the procedure described below.

We first attributed a mass and evolutionary status to each object by comparing its position in the HRD with the theoretical tracks. The values of obtained masses for our target stars are given in Table A1. Again, the stars with [Fe/H] below -0.15 are compared with the [Fe/H]=-0.293models, those with [Fe/H] between -0.15 and +0.12 are compared with the [Fe/H]=0 models, and the more metallic ones with the [Fe/H]=+0.252 ones. From this first iteration, 125 of our sample stars were identified as possible RHB or clump stars, 4 as subgiants, 38 as probable RGBs, and 2 as probable AGB stars.

Then, for each star, we checked whether its nitrogen abundance was compatible with the model predictions for the corresponding stellar mass previously attributed. The carbon abundance was used only as a cross-check because of the variation it presents as a function of metallicity (see Sect. 5.1). Among the 125 possible RGB/clump stars, 15 objects have no N determination and 32 objects appear to still be undergoing the first dredge-up dilution, as indicated by their [N/Fe] and effective temperature. For the others, we made the following distinctions: (i) 38 stars are found to have completed their first dredge-up, but present slightly lower (by 0.05 to 0.2 dex) N abundances than predicted values for the corresponding stellar mass. 3 stars have N overabundances by $\sim$0.2 dex. We consider, however, that these slight discrepancies are not significant because of the observational error bars on the effective temperature and on the abundance determination. Moreover, part of the small discrepancy can be accounted for by the fact that not all the stars have the exact metallicity of the theoretical tracks they are compared with. (ii) 16 giants have a N abundance in good agreement with the post-dredge predictions for the given stellar mass. Both the (i) and (ii) stars would be preferentially identified as RGB stars according to their effective temperature, although they are still good clump candidates. (iii) 21 stars could be selected as clump giants according to both their N abundance in good agreement with the post-dredge predictions and their effective temperature.

We have thus reliably selected 21 clump giants, plus 54 clump candidates and about 100 usual giants that show all the signs of first dredge-up. Unfortunately, we have to state that some uncertainty exists in the separation of the clump giants, if we rely only on the evolutionary tracks and elemental abundances that are sensitive to the stellar evolution.

An important conclusion of the present study is that the theoretical predictions of the classical models do account well for the observed surface variations of both carbon and nitrogen during the first dredge-up episode.

However, it should be noted that the considered analysis and the results depend on the accuracy of the determination of the chemical composition and the theoretical preconditions used.

7 Conclusions

We have performed the detailed analysis of the atmospheric parameters and the abundances of some elements in 177 giant stars.

The stars analysed in this study have been selected as clump stars according to the photometric criteria. We have estimated the possibility of defining the evolutionary status of these giants on the basis of evolutionary tracks and their measured element abundances that are modified during stellar evolution. We reliably selected 21 clump giants, about 54 clump candidates, and about 100 usual giants that show all the signs of a first dredge-up.

The determined C, N, and Na abundances in our program stars reflect the CNO- and NaNe cycle operation in the giant stars.

The O, Mg, Ca, and Si ($\alpha $-elements) and Ni (iron-peak element) abundances in giants show trends similar to those observed in dwarfs which allows us to use these abundances to study the chemical and dynamical evolution of the Galaxy.

Acknowledgements
T.M. and V.K. thank the Observatoire Astronomique de l'Université Louis Pasteur de Strasbourg for its kind hospitality. The authors also thank the referee, Prof. B. Edvardsson, for very useful and fruitful comments and suggestions on the manuscript. The work was made within the framework of the French-Ukrainian project "Dnipro''-"Egide''.

References

 

  
Online Material

Appendix A

Table A.1: The basic characteristics of studied stars.

Table A.2: Parameters of atmospheres of studied stars.

Table A.3: Si, Ca, and Ni abundances.

Table A.4: The abundances of lithium, carbon, nitrogen, oxygen, sodium, and magnesium in atmospheres of studied stars.


Copyright ESO 2006