A&A 456, 235-244 (2006)
DOI: 10.1051/0004-6361:20064991
B. Mookerjea![]() - C. Kramer
- M. Röllig
- M. Masur
- C. Kramer
- M. Röllig
- M. Masur
KOSMA, I. Physikalisches Institut, Universität zu Köln, Zülpicher Strasse 77, 50937 Köln, Germany
Received 9 February 2006 / Accepted 9 June 2006
Abstract
Aims. The aim of the paper is to understand the emission from the photon dominated regions in Cepheus B, estimate the column densities of neutral carbon in bulk of the gas in Cepheus B and to derive constraints on the factors which determine the abundance of neutral carbon relative to CO.
Methods. This paper presents
![]() fully sampled maps of [C I] at 492 GHz and 12CO 4-3 observed with KOSMA at 1
fully sampled maps of [C I] at 492 GHz and 12CO 4-3 observed with KOSMA at 1![]() resolution. The new observations have been combined with the FCRAO 12CO 1-0, IRAM-30 m 13CO 2-1 and C18O 1-0 data, and far-infrared continuum data from HIRES/IRAS. The KOSMA-
resolution. The new observations have been combined with the FCRAO 12CO 1-0, IRAM-30 m 13CO 2-1 and C18O 1-0 data, and far-infrared continuum data from HIRES/IRAS. The KOSMA-![]() spherical PDR model has been used to understand the [C I] and CO emission from the PDRs in Cepheus B and to explain the observed variation of the relative abundances of both C0 and CO.
spherical PDR model has been used to understand the [C I] and CO emission from the PDRs in Cepheus B and to explain the observed variation of the relative abundances of both C0 and CO.
Results. The emission from the PDR associated with Cepheus B is primarily at
![]() between -14 and -11 km s-1. We estimate about 23% of the observed [C II] emission from the molecular hotspot is due to the ionized gas in the H II region. Over bulk of the material the C0 column density does not change significantly,
between -14 and -11 km s-1. We estimate about 23% of the observed [C II] emission from the molecular hotspot is due to the ionized gas in the H II region. Over bulk of the material the C0 column density does not change significantly,
![]() cm-2, although the CO column density changes by an order of magnitude. The observed C/CO abundance ratio varies between 0.06 and 4 in Cepheus B. We find an anti-correlation of the observed C/CO abundance ratio with the observed hydrogen column density, which holds even when all previous observations providing C/CO ratios are included. Here we show that this observed variation of C/CO abundance with total column density can be explained only by clumpy PDRs consisting of an ensemble of clumps. At high H2 column densities high mass clumps, which exhibit low C/CO abundance, dominate, while at low column densities, low mass clumps with high C/CO abundance dominate.
cm-2, although the CO column density changes by an order of magnitude. The observed C/CO abundance ratio varies between 0.06 and 4 in Cepheus B. We find an anti-correlation of the observed C/CO abundance ratio with the observed hydrogen column density, which holds even when all previous observations providing C/CO ratios are included. Here we show that this observed variation of C/CO abundance with total column density can be explained only by clumpy PDRs consisting of an ensemble of clumps. At high H2 column densities high mass clumps, which exhibit low C/CO abundance, dominate, while at low column densities, low mass clumps with high C/CO abundance dominate.
Key words: ISM: clouds - ISM: dust, extinction - ISM: H II regions - ISM: structure
Photon Dominated Regions (PDRs) are predominantly neutral, atomic and
molecular regions where the physical and chemical processes are
dominated by Far Ultraviolet (FUV) radiation (cf.
Sternberg & Dalgarno 1995; Hollenbach & Tielens 1997) and the major carbon-bearing
species changes from C+ through C0 to CO. While FUV photons (
![]() eV) are primarily responsible for the heating of the
cloud surfaces via photoelectric effect on dust grains, at larger depths
of about 10 mag into the clouds cosmic ray induced heating dominates.
Owing to the clumpy nature of the molecular clouds, contrary to the
initial ideas, PDRs are not strictly confined to the surface of the
molecular clouds. Rather the extended [C II] and [C I] emission observed
from allover the molecular clouds suggest formation of PDRs deep inside
the molecular clouds, at the surfaces of clumps inundated with
FUV photons escaping into the cloud. Further, the chemical abundances
of several key species like e.g., CN and HCN depend to a large extent on
the abundances of C0 and C+ in the gas phase (Boger & Sternberg 2005).
PDRs may therefore be seen as the most ubiquitous phase of the ISM,
observations of which together with proper modeling provide insight
into the physical conditions within the molecular clouds. On a more
global scale, PDRs provide direct insight into the chemical evolution
of the ISM deluged with FUV photons and PDR models suggest
radiation-induced feedback mechanisms that may regulate star formation
rates and the column density of gas through giant molecular clouds.
eV) are primarily responsible for the heating of the
cloud surfaces via photoelectric effect on dust grains, at larger depths
of about 10 mag into the clouds cosmic ray induced heating dominates.
Owing to the clumpy nature of the molecular clouds, contrary to the
initial ideas, PDRs are not strictly confined to the surface of the
molecular clouds. Rather the extended [C II] and [C I] emission observed
from allover the molecular clouds suggest formation of PDRs deep inside
the molecular clouds, at the surfaces of clumps inundated with
FUV photons escaping into the cloud. Further, the chemical abundances
of several key species like e.g., CN and HCN depend to a large extent on
the abundances of C0 and C+ in the gas phase (Boger & Sternberg 2005).
PDRs may therefore be seen as the most ubiquitous phase of the ISM,
observations of which together with proper modeling provide insight
into the physical conditions within the molecular clouds. On a more
global scale, PDRs provide direct insight into the chemical evolution
of the ISM deluged with FUV photons and PDR models suggest
radiation-induced feedback mechanisms that may regulate star formation
rates and the column density of gas through giant molecular clouds.
To the south of the Cepheus OB3 association of early-type stars lies the
giant Cepheus molecular cloud, at a distance of about 730 pc
(Blaauw 1964). Cepheus B, with a size of 4 pc, is the hottest
12CO component (Sargent 1977,1979) and is located near the
northwestern edge of the cloud, adjacent to the H II region S155
(Sharpless 1959). The interface between the molecular cloud and the
OB stars, is delineated by the optically visible H II region S155,
whose very sharp edges clearly indicate the presence of ionization
fronts bounding the dust/molecular cloud. The OB association itself
consists of two subgroups of different ages, with the youngest lying
closer to the molecular cloud (Sargent 1979). Felli et al. (1978)
presented radio continuum observations which confirmed that the
molecular cloud Cepheus B is surrounded by an ionization front driven by
the radiation field of the bright stars that are part of the youngest
generation of the Cepheus B OB3 association. The structure of the
diffuse ionized gas and its energy balance can be accounted for by the
UV radiation coming from the brightest members of the OB3 association
(viz., HD 217086 and 217061). The physical association between the
Cepheus B molecular cloud and the S155 H II region was also confirmed
by the H2CO and recombination line observations of
Panagia & Thum (1981). Minchin et al. (1992) used a combination of low-J CO
and far-infrared (FIR) continuum observations to show that the
Cepheus B molecular cloud terminates at its north-west edge with a
hotspot. The hotspot lies 1![]() to the east of the peak in CO
column density. The high temperature of the hotspot and the associated
FIR emission cannot be explained by only considering the stars in the
OB3 association. It was further proposed by Minchin et al. (1992) and
later confirmed using radio and near-infrared (NIR) continuum
observations by Testi et al. (1995) that the hotspot is indeed energized
by a highly reddened main sequence star (NIR-A) of spectral type
B1-B0.5, together with a small cluster of young stars.
to the east of the peak in CO
column density. The high temperature of the hotspot and the associated
FIR emission cannot be explained by only considering the stars in the
OB3 association. It was further proposed by Minchin et al. (1992) and
later confirmed using radio and near-infrared (NIR) continuum
observations by Testi et al. (1995) that the hotspot is indeed energized
by a highly reddened main sequence star (NIR-A) of spectral type
B1-B0.5, together with a small cluster of young stars.
In a first study with the KOSMA 3 m telescope, Beuther et al. (2000)
mapped the Cepheus B cloud in 2-1 and 3-2 transitions of 12CO,
13CO, and C18O at 2![]() resolution and used PDR models of
Störzer et al. (2000) to interpret the emission at four selected
positions. The hotspot emission indicated the presence of shocks.
Based on the derived local volume densities of
resolution and used PDR models of
Störzer et al. (2000) to interpret the emission at four selected
positions. The hotspot emission indicated the presence of shocks.
Based on the derived local volume densities of ![]()
![]() cm-3,
and average volume density less than 103 cm-3,
Beuther et al. (2000) concluded that Cepheus B is highly clumped with
clumps filling only 2% to 4% by volume of the cloud. In this
work [C I] at 492 GHz was detected from two selected positions and
detection of [C I] emission from deep inside the cloud was also put
forward as an additional evidence for the clumpiness of Cepheus B.
cm-3,
and average volume density less than 103 cm-3,
Beuther et al. (2000) concluded that Cepheus B is highly clumped with
clumps filling only 2% to 4% by volume of the cloud. In this
work [C I] at 492 GHz was detected from two selected positions and
detection of [C I] emission from deep inside the cloud was also put
forward as an additional evidence for the clumpiness of Cepheus B.
In clumpy or homogeneous PDR scenario both [C I] and 12CO 4-3 emission arise from regions closer to the surfaces of the FUV
irradiated clumps or molecular cloud surfaces respectively. Thus the
[C I] and 12CO 4-3 emission trace similar regions. While [C I] emission necessarily implies photodissociation of molecular CO, the
higher kinetic temperature (the upper energy level being 56 K) required
to excite the 12CO 4-3 line suggest origin of this emission from
the outer surfaces of dense (since the critical density of the 12CO 4-3 transition for collisions with H2 is ![]() 105 cm-3)
clumps embedded in a UV radiation field. Thus in order to trace the
PDR we have observed largescale (
105 cm-3)
clumps embedded in a UV radiation field. Thus in order to trace the
PDR we have observed largescale (
![]() )
fully-sampled maps of
the [C I] and 12CO 4-3 emission from the Cepheus B molecular cloud.
At a common resolution of 1
)
fully-sampled maps of
the [C I] and 12CO 4-3 emission from the Cepheus B molecular cloud.
At a common resolution of 1![]() ,
this dataset has been combined
with FCRAO 12CO 1-0, IRAM-30 m 13CO 2-1 and C18O 1-0 data, and
FIR continuum data from HIRES/IRAS. This allows for a
detailed analysis of the PDRs in Cepheus B, since observed
transitions span a substantial range of critical densities and
temperatures (Table 1).
,
this dataset has been combined
with FCRAO 12CO 1-0, IRAM-30 m 13CO 2-1 and C18O 1-0 data, and
FIR continuum data from HIRES/IRAS. This allows for a
detailed analysis of the PDRs in Cepheus B, since observed
transitions span a substantial range of critical densities and
temperatures (Table 1).
Table 1: Parameters of the observed transitions used to study the PDRs in Cepheus B.
![\begin{figure}
\par\includegraphics[angle=0,width=16.0cm,angle=0]{4991fig1.eps}
\end{figure}](/articles/aa/full/2006/34/aa4991-06/Timg28.gif) |
Figure 1:
Velocity-integrated intensity maps of [C I] 3P1-3P0 emission
( color) overlayed with contours of a) 12CO 4-3, b) 13CO 2-1, c) 12CO 1-0 and d) C18O 1-0 intensities. All maps are integrated over the range
|
| Open with DEXTER | |
We have used the KOSMA 3 m submillimeter telescope on Gornergrat,
Switzerland (Kramer et al. 1998; Winnewisser et al. 1986) to observe the emission
of fine-structure line of neutral carbon at 492 GHz (609 ![]() m,
3P1-3P0; hereafter [C I]) and J = 4-3 transition of 12CO
emission at 461 GHz from the PDRs associated with Cepheus B.
We used the Submillimeter Array Receiver for Two frequencies (SMART)
(Graf et al. 2002) on KOSMA for these observations. SMART is a
dual-frequency eight-pixel SIS-heterodyne receiver capable of observing
simultaneously in the two atmospheric windows centered around
650
m,
3P1-3P0; hereafter [C I]) and J = 4-3 transition of 12CO
emission at 461 GHz from the PDRs associated with Cepheus B.
We used the Submillimeter Array Receiver for Two frequencies (SMART)
(Graf et al. 2002) on KOSMA for these observations. SMART is a
dual-frequency eight-pixel SIS-heterodyne receiver capable of observing
simultaneously in the two atmospheric windows centered around
650 ![]() m and 350
m and 350 ![]() m. The IF signals were analyzed with
array-acousto-optical spectrometers with a spectral resolution of
1.5 MHz (Horn et al. 1999).
m. The IF signals were analyzed with
array-acousto-optical spectrometers with a spectral resolution of
1.5 MHz (Horn et al. 1999).
The observations were performed in the position-switched On-The-Fly mode
between November 2004 and March 2005. The HPBW of the [C I] and 12CO 4-3 observations are 60
![]() with a beam efficiency of
with a beam efficiency of
![]() %. Atmospheric calibration was done by measuring the
atmospheric emission at the OFF-position to derive the opacity
(Hiyama 1998). Sideband imbalances were corrected using standard
atmospheric models (Cernicharo 1985). All data presented in this
paper are in units of main beam temperature (
%. Atmospheric calibration was done by measuring the
atmospheric emission at the OFF-position to derive the opacity
(Hiyama 1998). Sideband imbalances were corrected using standard
atmospheric models (Cernicharo 1985). All data presented in this
paper are in units of main beam temperature (
![]() ), calculated
from the observed calibrated antenna temperature (
), calculated
from the observed calibrated antenna temperature (
![]() )
using the
derived beam efficiencies (
)
using the
derived beam efficiencies (
![]() )
for the relevant telescope,
)
for the relevant telescope,
![]() =
=
![]() .
From observations of reference
sources we estimate the relative calibration accuracy to be
.
From observations of reference
sources we estimate the relative calibration accuracy to be ![]() 15%.
Data was reduced using the GILDAS
15%.
Data was reduced using the GILDAS![]() astronomical data reduction package.
astronomical data reduction package.
We have complemented the [C I] and 12CO 4-3 datasets for Cepheus B
with low-J CO observations available in literature. We have obtained the
12CO 1-0 dataset from the FCRAO outer Galaxy survey (Heyer et al. 1998)
and 13CO 2-1 and C18O 1-0 datasets observed with the IRAM 30 m by
Ungerechts et al. (2000) in 1995. The beam efficiency,
![]() (defined as
(defined as
![]() /
/
![]() )
used to derive the
)
used to derive the
![]() scale are 0.45, 0.48 and 0.75 for the 12CO 1-0, 13CO 2-1 and C18O 1-0
lines respectively (Heyer et al. 1998; Kramer & Wild 1994). All datasets have been smoothed to a resolution of 1
scale are 0.45, 0.48 and 0.75 for the 12CO 1-0, 13CO 2-1 and C18O 1-0
lines respectively (Heyer et al. 1998; Kramer & Wild 1994). All datasets have been smoothed to a resolution of 1![]() for comparison with our
observations. These CO datasets provide deeper insight into the
physical conditions of the regions emitting [C I] and 12CO 4-3
emission. 12CO 1-0 being optically thick, is most likely to be
arising from closer to the PDR surface. The 13CO 2-1 and C18O 1-0
on the other hand are most likely to be optically thin and hence arise
from deeper inside the clumps, and hence are crucial for ascertaining
the physical parameters (like the optical extinction) characterizing
the emitting regions.
for comparison with our
observations. These CO datasets provide deeper insight into the
physical conditions of the regions emitting [C I] and 12CO 4-3
emission. 12CO 1-0 being optically thick, is most likely to be
arising from closer to the PDR surface. The 13CO 2-1 and C18O 1-0
on the other hand are most likely to be optically thin and hence arise
from deeper inside the clumps, and hence are crucial for ascertaining
the physical parameters (like the optical extinction) characterizing
the emitting regions.
Dust continuum emission accounts for about 98% of the cooling of the
molecular clouds. Here we have used FIR continuum maps to
estimate the intensity of the FUV radiation field crucial for the
chemical and physical structure of the PDRs. We have obtained
HIRES-processed (Aumann et al. 1990) IRAS maps of Cepheus B at 60 and
100 ![]() m from the Infrared Processing and Analysis Center,
Caltech. These dust continuum maps have angular resolutions
(1
m from the Infrared Processing and Analysis Center,
Caltech. These dust continuum maps have angular resolutions
(1
![]() 5) comparable to our sub-millimeter datasets.
5) comparable to our sub-millimeter datasets.
Figure 1a shows the integrated intensity maps of [C I] and 12CO 4-3 emission from Cepheus B. The maps are centered at
![]() 57
57![]() 25
25
![]() 7
7
![]()
![]() 34
34![]() 40
40
![]() 7
(J2000). The 12CO 4-3 emission peaks at the position of the hotspot,
and drops off significantly towards the south-east, and does not show
much substructures. The [C I] emission in contrast though rather weak at
the position of the hotspot, has almost uniform intensity over the
ridge extended along the east-west direction with an isolated peak to
the south-west (below the hotspot) and an extended high intensity peak
deep into the molecular cloud to the east of the map. The somewhat
different distribution of 12CO 4-3 and [C I] emission suggest that
while the 12CO 4-3 emission traces higher temperature and densities
as in the hotspot, the [C I] emission being optically thin traces the
embedded PDR surfaces of the molecular material with higher column
density better. The features seen in the 12CO 4-3 map agree
reasonably well with the features seen in the 12CO 3-2 map by
Beuther et al. (2000).
7
(J2000). The 12CO 4-3 emission peaks at the position of the hotspot,
and drops off significantly towards the south-east, and does not show
much substructures. The [C I] emission in contrast though rather weak at
the position of the hotspot, has almost uniform intensity over the
ridge extended along the east-west direction with an isolated peak to
the south-west (below the hotspot) and an extended high intensity peak
deep into the molecular cloud to the east of the map. The somewhat
different distribution of 12CO 4-3 and [C I] emission suggest that
while the 12CO 4-3 emission traces higher temperature and densities
as in the hotspot, the [C I] emission being optically thin traces the
embedded PDR surfaces of the molecular material with higher column
density better. The features seen in the 12CO 4-3 map agree
reasonably well with the features seen in the 12CO 3-2 map by
Beuther et al. (2000).
Figures 1b, c and d show overlays of the observed [C I] emission with the 13CO 2-1, 12CO 1-0 and C18O 1-0 intensities respectively. The [C I] and 13CO 2-1 appear to be almost concomitant tracing similar features in the Cepheus B cloud. To the west of the map the 12CO 1-0 emission is similar in parts with the [C I] emission. However the 12CO 1-0 intensities drop off more drastically towards the east, which is similar to the features seen in the 12CO 4-3 map. This is probably due to the higher column densities to the east, as manifested by the peaks in the 13CO and C18O maps. The lower 12CO 4-3 emission to the east, stem from a combination of lower densities and kinetic temperatures. The C18O 1-0 emission, tracing higher column densities, looks markedly different from the 12CO 4-3 emission and almost similar to the [C I] emission except for the region close to the hotspot where, the C18O emission is almost absent. The faint 13CO 2-1 emission and almost no C18O 1-0 emission from the hotspot is consistent with the results of Minchin et al. (1992), who found a distinct lack of 13CO emission at the position of the hotspot.
Previous low-J CO observations showed that the Cepheus B emission
consists of two major velocity components: one, the north-western part
of the cloud closer to the hot spot emits at ![]() -15 km s-1,
confirming the association of the hot spot with S155 having the same
system velocity and second, the south-eastern part emitting at
-15 km s-1,
confirming the association of the hot spot with S155 having the same
system velocity and second, the south-eastern part emitting at ![]() -12 km s-1 (Minchin et al. 1992; Beuther et al. 2000).
-12 km s-1 (Minchin et al. 1992; Beuther et al. 2000).
![\begin{figure}
\par\includegraphics[angle=0,width=9.0cm,angle=0]{4991fig2.eps}
\end{figure}](/articles/aa/full/2006/34/aa4991-06/Timg44.gif) |
Figure 2: Overlay of [C I] (color) and 12CO 4-3 (contours) velocity channel maps of Cepheus B. The colorscale ranges between 1 and 11.6 K km s-1 and the 12CO 4-3 contours are between 5 and 120 K km s-1 in steps of 15 K km s-1. |
| Open with DEXTER | |
An overlay of the [C I] and 12CO 4-3 channel maps (Fig. 2) shows that bulk of the cloud emits between -14and -11 km s-1, although substructures contributing to the 12CO 4-3 emission change from the hotspot to the clump to the south-west of the map. The emission from the hotspot is slightly blue-shifted, between -16and -14 km s-1. At -15.5 km s-1, we detect in [C I] a clump to the extreme north of the map. At -10.5 km s-1 the 12CO 4-3 emission from the cloud is too low and the [C I] emission is restricted mainly to the east of the ridge. It is interesting to note that at -11.5 km s-1 the [C I] and 12CO 4-3 emission from the south-western clump are exactly concomitant.
![\begin{figure}
\par\includegraphics[angle=0,width=7.0cm,angle=0]{4991fig3.eps}
\end{figure}](/articles/aa/full/2006/34/aa4991-06/Timg45.gif) |
Figure 3:
Observed CI, 12CO 4-3, 12CO 1-0, 13CO 2-1 and [C II] spectra
at the position of the molecular hotspot in
Cepheus B. The [C II] spectrum is adopted from Boreiko et al. (1990). The ratio
of integrated intensities 12CO 4-3/12CO 1-0
at this position is 1.9. All data are shown at a common resolution of
1 |
| Open with DEXTER | |
Table 2: Velocity components derived from Gaussian fitting of spectra at the position of the hotspot in Cepheus B.
Figure 3 shows the [C I], CO and [C II] 158 ![]() m spectra
observed at the position of the hotspot. The [C II] spectrum was observed
by Boreiko et al. (1990) using the Kuiper Airborne Observatory with a
resolution of 43
m spectra
observed at the position of the hotspot. The [C II] spectrum was observed
by Boreiko et al. (1990) using the Kuiper Airborne Observatory with a
resolution of 43
![]() ,
similar to the resolution of the other spectra
(60
,
similar to the resolution of the other spectra
(60
![]() ). The velocity resolution is 0.8 km s-1. It is one of the very
few heterodyne spectra of the [C II] line taken so far. These spectra
show that at the position of the hotspot the PDR emission is dominated
by the velocity component at
). The velocity resolution is 0.8 km s-1. It is one of the very
few heterodyne spectra of the [C II] line taken so far. These spectra
show that at the position of the hotspot the PDR emission is dominated
by the velocity component at
![]() of -13.8 km s-1 and the
lineshapes with the exception of [C II]are all primarily Gaussian. The
[C II] line at the hotspot position appears to be the broadest, with
traces of an extended blue wing. Boreiko et al. (1990) have explained the
[C II] emission from the hotspot position to be from two velocity
components, the main narrow component is centered at -13.6 km s-1 with a
width of 3.8 km s-1, while the blue component is centered at -16.8 km s-1 and has a width of 6.0 km s-1. Table 2 presents results
of fitting Gaussian profiles to the different spectral lines observed at
the hotspot. Broadly we find that both [C I] and CO emission arise around
of -13.8 km s-1 and the
lineshapes with the exception of [C II]are all primarily Gaussian. The
[C II] line at the hotspot position appears to be the broadest, with
traces of an extended blue wing. Boreiko et al. (1990) have explained the
[C II] emission from the hotspot position to be from two velocity
components, the main narrow component is centered at -13.6 km s-1 with a
width of 3.8 km s-1, while the blue component is centered at -16.8 km s-1 and has a width of 6.0 km s-1. Table 2 presents results
of fitting Gaussian profiles to the different spectral lines observed at
the hotspot. Broadly we find that both [C I] and CO emission arise around
![]() of -13.8 km s-1 and have linewidths
of -13.8 km s-1 and have linewidths ![]() 2.2 km s-1. We
have reproduced the Gaussian fits to the [C II] spectra obtained by
Boreiko et al. (1990) using the same parameters. The broader blue
component at -16.5 km s-1 does not appear to be associated with the
emission from the PDR/molecular cloud at all, rather the velocity
matches the
2.2 km s-1. We
have reproduced the Gaussian fits to the [C II] spectra obtained by
Boreiko et al. (1990) using the same parameters. The broader blue
component at -16.5 km s-1 does not appear to be associated with the
emission from the PDR/molecular cloud at all, rather the velocity
matches the
![]() shown by H
shown by H![]() emission from the H
II region S155 (Boreiko et al. 1990). Based on the Gaussian fit to the
[C II] spectrum, we estimate
emission from the H
II region S155 (Boreiko et al. 1990). Based on the Gaussian fit to the
[C II] spectrum, we estimate ![]() 77% of the measured [C II] emission
arises from the PDR and the remaining from the ionized gas. The
estimated relative contribution of PDRs to [C II] emission from nearby
galaxies using the [N II] 122
77% of the measured [C II] emission
arises from the PDR and the remaining from the ionized gas. The
estimated relative contribution of PDRs to [C II] emission from nearby
galaxies using the [N II] 122 ![]() m is
m is ![]() 70-85%
(Malhotra et al. 2001; Kramer et al. 2005), roughly consistent with the above
result for Cepheus B.
70-85%
(Malhotra et al. 2001; Kramer et al. 2005), roughly consistent with the above
result for Cepheus B.
![\begin{figure}
\par\includegraphics[angle=0,width=8.0cm,angle=0]{4991fig4a.eps}\includegraphics[angle=0,width=8.0cm,angle=0]{4991fig4b.eps}
\end{figure}](/articles/aa/full/2006/34/aa4991-06/Timg47.gif) |
Figure 4:
a) Distribution of observed 12CO 4-3/12CO 1-0 ratio
in Cepheus B. b) Distribution of excitation temperatures
|
| Open with DEXTER | |
Figure 4a shows a map of the ratio of the 12CO 4-3/12CO 1-0 intensities integrated over the velocity range between -20 and -5 km s-1 for the region in Cepheus B. It shows a smooth gradient between ratios of 0.3-0.6 in the south-east and ratios of 1.5-2.2 to the north-west of the mapped region.
Ratios of ![]() ,
as seen towards the bulk of the molecular
ridge, suggest that both transitions are thermalized and can be
explained in terms of LTE and optically thick emission.
Neglecting the Rayleigh-Jeans correction, the ratio is expected to be
1.0 in this case.
The calibration uncertainty of line ratios is
,
as seen towards the bulk of the molecular
ridge, suggest that both transitions are thermalized and can be
explained in terms of LTE and optically thick emission.
Neglecting the Rayleigh-Jeans correction, the ratio is expected to be
1.0 in this case.
The calibration uncertainty of line ratios is ![]() 20%. The
4-3/1-0 ratio is sensitive to excitation temperatures only
upto 50 K, beyond that the ratio remains almost constant with increasing
20%. The
4-3/1-0 ratio is sensitive to excitation temperatures only
upto 50 K, beyond that the ratio remains almost constant with increasing
![]() .
.
While ratios less than 0.8 suggest sub-thermal excitation of 12CO 4-3,
ratios above 1.2 are inconsistent with above assumptions. At the
position of the hotspot for which the spectra are shown in
Fig. 3
the integrated intensity ratio 4-3/1-0 has a value of 1.9. Similar
to this position, at all other positions with high 4-3/1-0 ratios, we
do not see any evidence of self absorption of either line by cold
foreground gas. Within the framework of single
![]() and LTE,
differences in optical thickness and volume filling factors of the
emitting regions of the two lines could still partially explain the
observed high 4-3/1-0 ratios. However we consider strong outwardly
increasing temperature gradients to be the more plausible explanation.
Such a gradient results in an inconsistency in deriving a single
and LTE,
differences in optical thickness and volume filling factors of the
emitting regions of the two lines could still partially explain the
observed high 4-3/1-0 ratios. However we consider strong outwardly
increasing temperature gradients to be the more plausible explanation.
Such a gradient results in an inconsistency in deriving a single
![]() from this ratio, since the 4-3 transition will predominantly trace the
warm, still dense, outer regions, while the 1-0 traces the somewhat
inner, colder regions. Such high 12CO ratios are typically found in
the surface regions of molecular clouds subject to strong UV fields
(Kramer et al. 2004; Beuther et al. 2000; Kramer et al. 1996; Castets et al. 1990).
from this ratio, since the 4-3 transition will predominantly trace the
warm, still dense, outer regions, while the 1-0 traces the somewhat
inner, colder regions. Such high 12CO ratios are typically found in
the surface regions of molecular clouds subject to strong UV fields
(Kramer et al. 2004; Beuther et al. 2000; Kramer et al. 1996; Castets et al. 1990).
Excitation temperatures derived from the 4-3/1-0 line ratios vary
smoothly between ![]() 8 K in the south-east of the mapped region and
more than 50 K in the north-west near the position of the hot core and
at the western edge of the molecular cloud (Fig. 4b).
In the following discussion, we have assumed a constant
excitation temperature of 50 K for 4-3/1-0>0.9.
8 K in the south-east of the mapped region and
more than 50 K in the north-west near the position of the hot core and
at the western edge of the molecular cloud (Fig. 4b).
In the following discussion, we have assumed a constant
excitation temperature of 50 K for 4-3/1-0>0.9.
![\begin{figure}
\par\includegraphics[angle=0,width=7.5cm,angle=0]{4991fig5a.eps}\includegraphics[angle=0,width=8.5cm,angle=0]{4991fig5b.eps}
\end{figure}](/articles/aa/full/2006/34/aa4991-06/Timg49.gif) |
Figure 5:
a) N(C) vs. N(CO) for independent positions
(positions separated by 1 |
| Open with DEXTER | |
We have estimated the C0 and CO column densities based on LTE
approximation. For these calculations we have used the observed [C I] and
C18O 1-0 line intensities, the
![]() estimated from the
12CO 4-3/12CO 1-0 ratios and a relative abundance ratio [CO]/[C18O]
of 500 (Wilson & Rood 1994). Further we have assumed both [C I] and C18O 1-0 to be optically thin. The more detailed PDR analysis presented in
Sect. 6, strongly supports this latter assumption.
estimated from the
12CO 4-3/12CO 1-0 ratios and a relative abundance ratio [CO]/[C18O]
of 500 (Wilson & Rood 1994). Further we have assumed both [C I] and C18O 1-0 to be optically thin. The more detailed PDR analysis presented in
Sect. 6, strongly supports this latter assumption.
Assuming LTE N(CO) depends linearly on
![]() above 20 K, while in
contrast, N(C) is rather independent of the assumed
above 20 K, while in
contrast, N(C) is rather independent of the assumed
![]() to within
20% between 20 and 150 K. However, in between 10 and 20 K, N(C)
drops by more than a factor of 2, while N(CO) remains constant within
30%.
to within
20% between 20 and 150 K. However, in between 10 and 20 K, N(C)
drops by more than a factor of 2, while N(CO) remains constant within
30%.
Figure 5a shows a scatterplot of the the C0 column
densities, N(C) versus the CO column densities, N(CO). CO column
densities vary by more than one order of magnitude between 1017and
![]() cm-2, corresponding to optical extinctions
between
cm-2, corresponding to optical extinctions
between ![]() 1 mag and 30 mag. Although the range of values
of N(C) at different positions appear to be similar to the range
shown by N(CO), a histogram of N(C) shows that for most positions N(C)
does not show much variation, staying almost constant at a mean value of
1 mag and 30 mag. Although the range of values
of N(C) at different positions appear to be similar to the range
shown by N(CO), a histogram of N(C) shows that for most positions N(C)
does not show much variation, staying almost constant at a mean value of
![]() cm-2 with an rms of
cm-2 with an rms of
![]() cm-2.
cm-2.
Figure 5b shows a map of the N(C)/N(CO) (C/CO hereafter)
overlayed with contours of integrated intensities of C18O.
This plot shows that regions of higher C18O 1-0 intensities, presumably tracing high H2 column densities, show
rather low values of C/CO, in contrast to the outskirts. The ridge
and the south-western core show low values of C/CO (![]() 0.1),
while the ratio rises gradually to values up to 4 outside these regions
where the CO emission is more diffuse.
0.1),
while the ratio rises gradually to values up to 4 outside these regions
where the CO emission is more diffuse.
The constancy of C0 column densities is also reflected in
Fig. 6 showing a scatterplot of the C/CO abundance ratio
versus H2 column densities or optical extinctions derived from
N(CO) assuming a CO/H2 abundance of
![]() (Blake et al. 1987). The C/CO ratio is
(Blake et al. 1987). The C/CO ratio is ![]() 1 for 2 mag and drops to 0.1 for 20 mag.
A linear fit to the data results in
1 for 2 mag and drops to 0.1 for 20 mag.
A linear fit to the data results in
![\begin{displaymath}\log\left[N({\rm C^0})/N({\rm CO})\right] = (-1.01\pm0.03) N({\rm
H}_2) + (21.5\pm0.72)
\end{displaymath}](/articles/aa/full/2006/34/aa4991-06/img54.gif) |
(1) |
Figure 6 also shows the C/CO abundances derived in other
Galactic star forming regions and diffuse clouds. These studies cover a
range of optical extinctions between 0.3 mag and ![]() 100 mag with
C/CO abundances varying by more than two orders of magnitude between
100 mag with
C/CO abundances varying by more than two orders of magnitude between
![]() 4 and
4 and ![]() 10-2, approximately following the slope we find in
Cepheus B.
10-2, approximately following the slope we find in
Cepheus B.
Clearly, the [C I] 1-0 line is not a straightforward tracer of optical extinctions or total H2 column densities and total masses.
The scatter of C/CO abundance varies with ![]() .
For
.
For ![]() 's upto
20 mag the scatter decreases from being almost comparable to the mean
C/CO itself to about 50% of the mean. At
's upto
20 mag the scatter decreases from being almost comparable to the mean
C/CO itself to about 50% of the mean. At ![]() 20 mag the scatter
is the smallest, with the C/CO abundance from five different data
sets agreeing to a value of 0.1 with a scatter of 0.05. Note that
several studies which cover only a small range of extinctions find
rather constant C/CO abundances.
20 mag the scatter
is the smallest, with the C/CO abundance from five different data
sets agreeing to a value of 0.1 with a scatter of 0.05. Note that
several studies which cover only a small range of extinctions find
rather constant C/CO abundances.
In Sect. 6 we show that clumpy PDR models naturally explain the observed variation of the C/CO abundance.
![\begin{figure}
\par\includegraphics[angle=0,width=8.0cm,angle=0]{4991fig6.eps}
\end{figure}](/articles/aa/full/2006/34/aa4991-06/Timg56.gif) |
Figure 6:
Column density ratio of C to CO in Cepheus B.
Plotted as in Fig. 5 are independent positions,
which are separated by 1 |
| Open with DEXTER | |
The spectral lines observed in Cepheus B which are used here are not sensitive to the FUV radiation field, and there are no largescale [C II] observations available in the literature for this region. We thus estimate the FUV radiation field from the observed FIR continuum. Because dust grains absorb most of the FUV photons incident on the cloud and most of that energy is reemitted in the form of FIR continuum, and other heating mechanisms like cosmic ray heating can be neglected, the intensity of the FUV radiation can be inferred from the FIR continuum. This estimate is valid even if a fraction of FUV photons escape without impinging the cloud.
We have estimated the FIR intensity of the mapped region using the
HIRES processed 60 and 100 ![]() m IRAS fluxes following the relationship
(Nakagawa et al. 1998):
m IRAS fluxes following the relationship
(Nakagawa et al. 1998):
![\begin{displaymath}I_{\rm FIR} = 3.25 \times 10^{-11} \!\left[ \frac{f_\nu(60~\m...
...ac{f_\nu(100~\mbox{$\mu$ m})}{\rm Jy~sr^{-1}}\right] \!\cdot~
\end{displaymath}](/articles/aa/full/2006/34/aa4991-06/img57.gif) |
(2) |
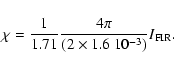 |
(3) |
![\begin{figure}
\par\includegraphics[angle=0,width=8.0cm,angle=0]{4991fig7.eps}
\end{figure}](/articles/aa/full/2006/34/aa4991-06/Timg60.gif) |
Figure 7: FUV intensity distribution (red contours) in Cepheus B estimated from the FIR fluxes measured by IRAS, overlayed with [C I] integrated intensities (in color). Contour levels of the FUV intensity are indicated at the top left corner. The intensity scale for the [C I] map are the same as in Fig. 1. White stars denote HD 217086 (north) and HD 217061, Crosses denote the NIR sources A-NIR (south) and B-NIR and the filled triangle denotes the location of the hot spot. |
| Open with DEXTER | |
Figure 7 shows the distribution of FUV intensity
calculated as above, overlayed with the observed [C I] emission.
Within the region mapped, the FUV field varies smoothly between
![]() 25 in the south-east and 1500 times Draine field, in the
north-west near the hot spot. This variation of
25 in the south-east and 1500 times Draine field, in the
north-west near the hot spot. This variation of ![]() correlates well
with the corresponding variation of excitation temperatures derived
from the 12CO line ratios (Fig. 5b).
correlates well
with the corresponding variation of excitation temperatures derived
from the 12CO line ratios (Fig. 5b).
In Fig. 7 we have marked the positions of the nearest O and
B stars, HD 217086 (north-west), HD 217061 (west) and the embedded NIR
sources A and B (cf. Testi et al. 1995).
NIR-A, which does not have any infrared excess and which is deemed to be
a highly reddened main sequence star of spectral type B1-B0.5, is
responsible for the excitation of the associated blister H II region
(the radio continuum source A). The FUV intensity distribution
calculated as above is consistent with the results of Testi et al. (1995)
and suggest that the star A-NIR is mostly responsible for the FIR
emission from the region. The total estimated FIR luminosity from the
IRAS fluxes and for the assumed distance of 730 pc for Cepheus B is
![]() 104
104
![]() and this is consistent with the luminosity due to a
B1 type star as well.
and this is consistent with the luminosity due to a
B1 type star as well.
We interpret here the observed anti-correlation of the C/CO abundance
ratio with the hydrogen column density (N(H2)) in terms of PDRs
created due to the FUV irradiation of molecular material. For this we
have used the KOSMA-![]() PDR model (Störzer et al. 1996; Röllig et al. 2006).
This model considers spherical clouds illuminated by an isotropic FUV
radiation field and cosmic rays, calculates the resulting chemical and
temperature structure of the cloud. This is followed by radiation
transfer calculations to estimate the emission of different species.
The KOSMA-
PDR model (Störzer et al. 1996; Röllig et al. 2006).
This model considers spherical clouds illuminated by an isotropic FUV
radiation field and cosmic rays, calculates the resulting chemical and
temperature structure of the cloud. This is followed by radiation
transfer calculations to estimate the emission of different species.
The KOSMA-![]() model has 13CO chemistry included in its network.
The emission from the models are calculated as a function of the
hydrogen volume density, FUV radiation field and mass of the spherical
clump. The KOSMA-
model has 13CO chemistry included in its network.
The emission from the models are calculated as a function of the
hydrogen volume density, FUV radiation field and mass of the spherical
clump. The KOSMA-![]() model assumes that a clump has a power-law
density profile of
model assumes that a clump has a power-law
density profile of
![]() for
for
![]() and
n(r) = const. for
and
n(r) = const. for
![]() .
The surface density
.
The surface density
![]() is about half the average clump density.
is about half the average clump density.
![\begin{figure}
\par\includegraphics[angle=0,width=9.0cm,angle=0]{4991fig8.eps}
\end{figure}](/articles/aa/full/2006/34/aa4991-06/Timg67.gif) |
Figure 8:
Results from the PDR models for external FUV fields of
|
| Open with DEXTER | |
First, we have used PDR models to derive the range of allowed hydrogen
volume densities based on the observed CI/13CO 2-1 and CI/12CO 4-3 intensity ratios. At all the positions for which we have
calculated C/CO abundance ratio the CI/13CO 2-1 ratio varies
between 0.3 and 0.7, while the CI/12CO 4-3 ratio varies between 0.2
and 0.6. Based on FIR maps the FUV field in the mapped region varies
between 50 and 103 Draine units. Figure 8 shows the
contours bracketing the observed two line ratios for constant FUV
field and different PDR clump densities and masses. These two line
ratios do not allow to discriminate between different clump masses.
The best fitting clump densities lie between
![]() and
and
![]() cm-3, for clump masses between 10-2 and 10
cm-3, for clump masses between 10-2 and 10
![]() .
This range of densities is rather independent of the FUV field.
We note that the clump masses are not very well constrained, however the
intersection of the two ratio contours in Fig. 8
provide physically reasonable limits on clump masses, which have been
loosely used in our subsequent analysis, but do not have any
significant impact on our final results. The observed 12CO 4-3/1-0 line
ratios are consistent with this interpretation.
.
This range of densities is rather independent of the FUV field.
We note that the clump masses are not very well constrained, however the
intersection of the two ratio contours in Fig. 8
provide physically reasonable limits on clump masses, which have been
loosely used in our subsequent analysis, but do not have any
significant impact on our final results. The observed 12CO 4-3/1-0 line
ratios are consistent with this interpretation.
![\begin{figure}
\par\includegraphics[angle=0,width=9.0cm,angle=0]{4991fig9.eps}
\end{figure}](/articles/aa/full/2006/34/aa4991-06/Timg69.gif) |
Figure 9:
Abundance profiles of C0 and CO calculated by the KOSMA- |
| Open with DEXTER | |
We first explore the single spherical PDR models described above, in
order to derive the observed C/CO vs. N(H2) anti-correlation. As shown
above, clumps with masses between 10-2 and 10
![]() with
densities
with
densities ![]() 105 cm-3 reproduce the range of [C I]/13CO2-1
and [C I]/12CO4-3 intensity ratios observed in Cepheus B. In
Fig. 9, we present the calculated radial variation of
the C and CO abundances for two PDR clumps with masses of 10-3 and
1
105 cm-3 reproduce the range of [C I]/13CO2-1
and [C I]/12CO4-3 intensity ratios observed in Cepheus B. In
Fig. 9, we present the calculated radial variation of
the C and CO abundances for two PDR clumps with masses of 10-3 and
1
![]() .
The surface density is fixed at 105 cm-3 and the FUV
field is fixed at 102 (in Draine units), the average value
derived from the HIRES data in Sect. 5.
.
The surface density is fixed at 105 cm-3 and the FUV
field is fixed at 102 (in Draine units), the average value
derived from the HIRES data in Sect. 5.
At the surface of the PDRs carbon is fully ionized by the incident FUV
radiation. Increasing depth leads to increased absorption of the FUV
radiation by both gas and dust. This allows C+ to recombine with
electrons to form C0. At even larger depths CO starts to form because
the photodissociating FUV photons are attenuated sufficiently leading to
a chemical stratification typical of PDR models, C+/C0/CO. The
absolute depth where this transition occurs depends on the gas density
n and the FUV intensity ![]() .
In spherical models it also depends on
the size
.
In spherical models it also depends on
the size
![]() of the cloud since the local mean intensity
of the cloud since the local mean intensity
![]() at a certain
depth is larger for a small clump compared to a bigger one. Accordingly
a clump with
at a certain
depth is larger for a small clump compared to a bigger one. Accordingly
a clump with
![]()
![]() consists of a much larger CO core
than a clump with
consists of a much larger CO core
than a clump with
![]()
![]() .
The average CO column
density increases with mass. The dependence of N(C) on the mass is
weaker. Once the clump becomes massive enough to significantly shield
the photodissociating FUV photons a further increase in mass does not
lead to larger C0 columns but larger CO column densities. This
behavior is illustrated in Fig. 9 with the abundance of CO
at the inner core (with relative
.
The average CO column
density increases with mass. The dependence of N(C) on the mass is
weaker. Once the clump becomes massive enough to significantly shield
the photodissociating FUV photons a further increase in mass does not
lead to larger C0 columns but larger CO column densities. This
behavior is illustrated in Fig. 9 with the abundance of CO
at the inner core (with relative
![]() )
of the clumps being identical
in both cases. Thus the 1
)
of the clumps being identical
in both cases. Thus the 1
![]() clump has a much higher total fraction
of CO and lower C/CO than the lower mass clump. This indicates that
the lines of sight having high C/CO abundance ratios are dominated by
clumps of smaller sizes.
clump has a much higher total fraction
of CO and lower C/CO than the lower mass clump. This indicates that
the lines of sight having high C/CO abundance ratios are dominated by
clumps of smaller sizes.
Table 3:
KOSMA-![]() calculations of H2, C and CO column
densities of spherical clumps with n=105 cm-3 and
calculations of H2, C and CO column
densities of spherical clumps with n=105 cm-3 and
![]() (Draine units). The column densities are for individual clumps, and
not the column densities observed per beam.
(Draine units). The column densities are for individual clumps, and
not the column densities observed per beam.
Table 3 lists the clump-averaged C, CO and H2 column
densities of the KOSMA-![]() PDR model, considering a single
spherical clump. We note here that the column densities in
Table 3 correspond to those calculated by the PDR model
for a single clump and do not corroborate with the observed column
densities per beam, as plotted in Fig. 6. The C/CO ratios
calculated by the PDR model is correlated with the mass of the clump.
We have checked the peak optical depths of the [C I] line emission in a pencil
beam centered on the clump and for the line center position.
For all clumps studied here, these peak opacities are less than 0.5.
The clump and line averaged opacities of the [C I] line are much less.
This justifies our previous assumption, used in the LTE analysis,
that the [C I] line is optically thin. Similarly, the modelled 13CO peak
opacities indicate that the C18O line is optically thin.
PDR model, considering a single
spherical clump. We note here that the column densities in
Table 3 correspond to those calculated by the PDR model
for a single clump and do not corroborate with the observed column
densities per beam, as plotted in Fig. 6. The C/CO ratios
calculated by the PDR model is correlated with the mass of the clump.
We have checked the peak optical depths of the [C I] line emission in a pencil
beam centered on the clump and for the line center position.
For all clumps studied here, these peak opacities are less than 0.5.
The clump and line averaged opacities of the [C I] line are much less.
This justifies our previous assumption, used in the LTE analysis,
that the [C I] line is optically thin. Similarly, the modelled 13CO peak
opacities indicate that the C18O line is optically thin.
PDR models with n=105 cm-3 have clump sizes ranging between
0.004 pc (for
![]()
![]() )
and 0.08 pc (for
)
and 0.08 pc (for
![]()
![]() ). In comparison, a beam of 60
). In comparison, a beam of 60
![]() corresponds to a diameter of 0.21 pc at the distance of Cepheus B. It
is thus not possible to compare the observed C/CO vs. N(H2) per
60
corresponds to a diameter of 0.21 pc at the distance of Cepheus B. It
is thus not possible to compare the observed C/CO vs. N(H2) per
60
![]() beam correlation directly with the N(H2) per clump
(N(H2)
beam correlation directly with the N(H2) per clump
(N(H2)![]() in Table 3) obtained from the single
spherical PDR clumps.
in Table 3) obtained from the single
spherical PDR clumps.
The observed uniformity of the [C I] intensity distribution throughout the PDR (Fig. 1) and the failure to interpret the C/CO vs. N(H2) using single spherical PDR model leaves open two possible physical scenarios: (i) clumpiness of the medium, i.e., either there are multiple plane-parallel slabs stacked or there is an ensemble of clumps along the line of sight, and (ii) a single, homogeneous plane-parallel PDR slab inclined relative to the major sources of UV radiation HD 217086 and HD 217061.
![\begin{figure}
\par\includegraphics[angle=0,width=8.0cm,angle=0]{4991fig10.eps}
\end{figure}](/articles/aa/full/2006/34/aa4991-06/Timg80.gif) |
Figure 10:
KOSMA- |
| Open with DEXTER | |
We first consider the simplified clumpy PDR interpretation using
ensemble of clumps having the same mass and density at each position.
Figure 10 shows that the observed C/CO abundances and
total H2 column densities of Cepheus B can be reproduced with
clumpy PDR models. It shows results based on the ensemble
interpretation using the spherical PDR models with n=105 cm-3,
![]() and 102 and n=104 cm-3and
and 102 and n=104 cm-3and
![]() .
The drawn lines correspond to model calculations. We
consider an ensemble of clumps with mass
.
The drawn lines correspond to model calculations. We
consider an ensemble of clumps with mass
![]() (also marked in
Fig. 10) contributing to a total mass of
(also marked in
Fig. 10) contributing to a total mass of
![]() in
a 60
in
a 60
![]() beam. The total number of clumps in the beam is given by
beam. The total number of clumps in the beam is given by
![]() /
/
![]() .
Table 4
summarizes the defining parameters of the clump ensembles for which
the C/CO abundance ratios are shown in Fig. 10. We find
that the observed C/CO anti-correlation depends primarily on the
characteristic mass of individual clump along a particular line of
sight and does not have a strong dependence on the assumed FUV field.
For clumps with densities of 104 cm-3, masses below 0.1
.
Table 4
summarizes the defining parameters of the clump ensembles for which
the C/CO abundance ratios are shown in Fig. 10. We find
that the observed C/CO anti-correlation depends primarily on the
characteristic mass of individual clump along a particular line of
sight and does not have a strong dependence on the assumed FUV field.
For clumps with densities of 104 cm-3, masses below 0.1
![]() result in much higher values of C/CO ratios than observed.
The area filling factors (
result in much higher values of C/CO ratios than observed.
The area filling factors (
![]() )
of the ensemble vary between
1.6 and 3.3 (Table 4), from the higher to the lower values
of clump masses considered in our calculations. This indicates that
the clumps fill the beam and in most cases partially overlap.
)
of the ensemble vary between
1.6 and 3.3 (Table 4), from the higher to the lower values
of clump masses considered in our calculations. This indicates that
the clumps fill the beam and in most cases partially overlap.
Table 4:
Results of PDR model calculations for ensembles of clumps having
same mass and density.
![]() is the area filling factor of the
clumps.
is the area filling factor of the
clumps.
For the sake of completeness we also explored the second possible
physical scenario, an inclined plane-parallel PDR, which might
produce the observed uniform PDR emission apparently deep into the cloud
and the observed C/CO and N(H2) anti-correlation. For this
purpose we have used the plane-parallel PDR models illuminated from
one side by Koester et al. (1994) in order to explicitly calculate the
C/CO ratios and N(H2) for selected values of volume densities and
UV-field. We have explored several values of n, slab-size (N(H2))
and ![]() and have found consistently that for face-on PDRs the
calculated C/CO ratio drops much faster with N(H2) as compared to
the observations. Figure 10 shows the results of
calculation for a plane-parallel model with
and have found consistently that for face-on PDRs the
calculated C/CO ratio drops much faster with N(H2) as compared to
the observations. Figure 10 shows the results of
calculation for a plane-parallel model with
![]() cm-3 and
cm-3 and
![]() ,
for different slab-sizes or total N(H2). Changing the
inclination of the PDR has the same effect on both N(C) and N(CO), and
thus the C/CO ratio remains unaltered, though N(H2) changes as
the reciprocal of the sinus of the inclination angle. For this
particular set of models we find that at N(H2) =
,
for different slab-sizes or total N(H2). Changing the
inclination of the PDR has the same effect on both N(C) and N(CO), and
thus the C/CO ratio remains unaltered, though N(H2) changes as
the reciprocal of the sinus of the inclination angle. For this
particular set of models we find that at N(H2) =
![]() cm-2 the calculated C/CO ratio is 0.08. In contrast, observationally we
find the C/CO ratio to be 0.08 at N(H2)
cm-2 the calculated C/CO ratio is 0.08. In contrast, observationally we
find the C/CO ratio to be 0.08 at N(H2)
![]() cm-2.
There is a discrepancy by a factor of 10 in N(H2), which can be
explained by an inclination angle of 6
cm-2.
There is a discrepancy by a factor of 10 in N(H2), which can be
explained by an inclination angle of 6![]() .
Similarly, different
inclination angles are required to bring the different plane-parallel
models to conform to the observed slope of the anti-correlation.
Hence, though it might be possible to explain individual positions by
making suitable choice of inclination angles, it is not possible to
reproduce the observed anti-correlation at all positions in Cepheus B
using a single inclination angle. Further, the anti-correlation as
has been shown in Fig. 6 holds for a wide range of
sources so it is rather unlikely that all of them would either have
the same inclination angle or have different inclination angles and
still conform to the same anti-correlation. The plane-parallel
models thus fail to reproduce the slope of the C/CO vs. N(H2) anti-correlation entirely which extends over two orders of magnitude
in N(H2). Intuitively, both uniformity of [C I] emission over the
entire ridge of Cepheus B and the C/CO vs. N(H2) anti-correlation
seen in most PDRs appear to be obvious outcomes of homogeneous
plane-parallel models which are inclined. However, explicit
calculations suggest that although the homogeneous plane parallel
models predict almost constant N(C) with changing N(H2), they do not
reproduce the observed global C/CO vs. N(H2) anti-correlation even
when inclined.
.
Similarly, different
inclination angles are required to bring the different plane-parallel
models to conform to the observed slope of the anti-correlation.
Hence, though it might be possible to explain individual positions by
making suitable choice of inclination angles, it is not possible to
reproduce the observed anti-correlation at all positions in Cepheus B
using a single inclination angle. Further, the anti-correlation as
has been shown in Fig. 6 holds for a wide range of
sources so it is rather unlikely that all of them would either have
the same inclination angle or have different inclination angles and
still conform to the same anti-correlation. The plane-parallel
models thus fail to reproduce the slope of the C/CO vs. N(H2) anti-correlation entirely which extends over two orders of magnitude
in N(H2). Intuitively, both uniformity of [C I] emission over the
entire ridge of Cepheus B and the C/CO vs. N(H2) anti-correlation
seen in most PDRs appear to be obvious outcomes of homogeneous
plane-parallel models which are inclined. However, explicit
calculations suggest that although the homogeneous plane parallel
models predict almost constant N(C) with changing N(H2), they do not
reproduce the observed global C/CO vs. N(H2) anti-correlation even
when inclined.
We conclude that the spherical clumpy PDR model reproduces the frequently observed global C/CO vs. N(H2) anti-correlation over the entire range of observed N(H2). These clumpy PDR models can thus be used to understand the typical density and size (hence mass) of the regions that dominate the observed emission. This does not imply the absence of clumps of sizes smaller or larger than those reproducing the observed C/CO ratios. However the emission cannot be dominated by such clumps if the intensity and abundance ratios of these clumps differ significantly from the observed numbers. Hence the low observed relative abundance ratio C/CO originate from positions of high column density where the emission is dominated by a few more massive clumps, while high ratios originate at positions covered by many small clumps, having a low line of sight column density.
The calculations presented here are meant to be of qualitative nature in order to derive insight into the clump parameters which determine the observed C/CO ratio.
Figure 5 shows that the C/CO ratio is higher towards the south-eastern part of the ridge further away from the sources of FUV radiation. This together with the results of clumpy PDR models which find that higher C/CO ratios are associated with clumps of smaller mass present an interesting situation. In Cepheus B towards the north-western edge there are evidences of embedded sources while there are none to the south-east. Thus, using the clumpy PDR models we see that regions with embedded sources correspond to lines of sight with higher mass clumps.
We have presented the first largescale fully-sampled maps of [C I] (492 GHz) and 12CO 4-3, of the edge-on PDR, Cepheus B. The [C I] emission does not delineate the PDR clearly, rather it traces the bulk emission of the more quiescent part of the molecular ridge extending to the east. Bulk of the PDR gas emits at velocities between -14 and -11 km s-1. The 12CO 4-3 emission is strongly dominated by the hotspot present toward the north-western tip of the molecular cloud. We observed 12CO 4-3/1-0 intensity ratios in excess of 1.5 towards the north-western edge of the cloud. Such ratios can only be explained in terms of temperature gradients along the line of sight. Excitation temperature, derived from the observed 12CO 4-3/1-0 ratio, varies between 20 K (in the quiescent parts of the cloud) to 50 K (close to the hotspot). We conclude that [C I] primarily traces the higher column density regions while 12CO 4-3 traces the higher temperature and density regions.
In Cepheus B we find that N(C) remains nearly constant although N(CO) varies over one order of magnitude. The observed C/CO ratio varies between 0.06 and 4.0 and shows a direct anti-correlation with the hydrogen column density N(H2).
As estimated from the FIR continuum emission, the FUV radiation field
in Cepheus B varies between 25 and 1500 in Draine units, with an
average value of 100 over most of the [C I] emitting region. We
have used the KOSMA-![]() PDR model to explain the observed intensity
ratios and the observed C/CO vs. N(H2) anti-correlation. These
PDR model calculations show that for
PDR model to explain the observed intensity
ratios and the observed C/CO vs. N(H2) anti-correlation. These
PDR model calculations show that for
![]() ,
the observed
CI/13CO 2-1 and CI/12CO 4-3 ratios indicate local hydrogen densities
between 104-105 cm-3 with even higher values at a few
positions. The 12CO 4-3/1-0 ratio can be reproduced by the PDR
models and the modelled clumps indeed exhibit outwardly increasing
temperature gradients, as predicted from LTE analysis.
,
the observed
CI/13CO 2-1 and CI/12CO 4-3 ratios indicate local hydrogen densities
between 104-105 cm-3 with even higher values at a few
positions. The 12CO 4-3/1-0 ratio can be reproduced by the PDR
models and the modelled clumps indeed exhibit outwardly increasing
temperature gradients, as predicted from LTE analysis.
The observed global C/CO vs. N(H2) anti-correlation and its slope cannot be reproduced by single spherical PDR models or by plane-parallel homogeneous slabs with or without inclination. We were able to explain the observed anti-correlation between C/CO and N(H2) considering an ensemble of clumps of the same mass and density (n=105 cm-3) for each observed position. We find that (i) the C/CO ratio is characteristic of the dominant mass in the ensemble, clumps of smaller mass have higher C/CO ratio and (ii) clumps of larger mass have to necessarily dominate emission along lines of sight with higher column density in order to reproduce the observed lower C/CO ratio.
Acknowledgements
We thank Hans Ungerechts for allowing the use of the datasets from the Cepheus B on-the-fly project at the IRAM 30 m telescope. This material is based upon work supported by the Deutsche Forschungs Gemeinschaft (DFG) via grant SFB494 and the National Science Foundation under Grant No. AST-0228974. This research has made use of NASA's Astrophysics Data System.