A&A 456, 359-365 (2006)
DOI: 10.1051/0004-6361:20054624

Effects of $\alpha$ particles on the angular momentum loss from the Sun[*]

B. Li - X. Li

Institute of Mathematical and Physical Sciences, University of Wales Aberystwyth, SY23 3BZ, UK

Received 1 December 2005 / Accepted 31 May 2006

Abstract
Aims. The classic Weber-Davis model of the solar wind is reconsidered by incorporating alpha particles and by allowing the solar wind to flow out of the equatorial plane in an axisymmetrical configuration.
Methods. In the ion momentum equations of the solar wind, the ion gyro-frequency is many orders of magnitude higher than any other frequency. This requires that the difference between proton and alpha velocity vectors be aligned with the background magnetic field. With the aid of this alignment condition, the governing equations of the multi-fluid solar wind are derived from the standard transport equations. The governing equations are numerically solved along a prescribed meridional magnetic field line located at colatitude $70^\circ$ at 1 AU and a steady state fast solar wind solution is found.
Results. A general analysis concludes, in agreement with the Weber-Davis model, that the magnetic field helps the coronal plasma to achieve an effective corotation out to the Alfvénic radius, where the poloidal Alfvénic Mach number MT equals unity (MT is defined by Eq. (20)). The model computations show that, magnetic stresses predominate the angular momentum loss of the Sun. For the fast wind considered, the proton contribution to the angular momentum loss, which can be larger than the magnetic one, is almost completely canceled by the alpha particles that develop an azimuthal speed in the direction opposite to the solar rotation. The Poynting flux associated with the azimuthal components is negligible in the energy budget. However, the solar rotation can play some role in reducing the relative speed between alpha particles and protons for low latitude fast solar wind streams in interplanetary space.

Key words: Sun: solar wind - Sun: magnetic fields - stars: winds, outflows

1 Introduction

The solar angular momentum loss rate ${\cal L}$ consists of the particle contribution ${\cal L}_{\rm P}$ and that contained in magnetic stresses ${\cal L}_{\rm M}$. The comparison of measurements of these quantities with models, the Weber-Davis analysis (1967) in particular, has yielded divergent results. Missions before Helios measured a total angular momentum flux ${\cal L}$ consistent with the Weber-Davis model (about 1030 dyne cm sr-1), but the measured azimuthal angle of the bulk flow was generally greater than $1^\circ$ at 1 AU (or equivalently 7 km s-1 for an average slow wind of 400 km s-1) (see Pizzo et al. 1983, and references therein). Such a large azimuthal flow speed implies that particles play a far more important role than magnetic stresses in reducing the angular momentum of the Sun. However, in the Weber-Davis model, 3/4 of the angular momentum flux at 1 AU is due to magnetic stresses. The Helios data show that ${\cal L}$ is $0.2{-}0.3 \times 10^{30}$ dyne cm sr-1, in which ${\cal L}_{\rm M}$ is about $0.15{-}0.2\times 10^{30}$ dyne cm sr-1 (Pizzo et al. 1983). Although the measured magnitude of ${\cal L}$ is smaller than that computed in the Weber-Davis model, the distribution of angular momentum flux between particles and magnetic stresses is largely compatible with their prediction. An equally important finding concerns further distribution of ${\cal L}_{\rm P}$ between two major ion species in the solar wind, namely, protons and alpha particles. Alpha particles are found to carry an angular momentum flux in the direction of counter-rotation with the Sun. This flux is substantial enough to offset the proton contribution which could be comparable to the magnetic one. This finding cannot be addressed by the Weber-Davis model where the solar wind was treated as a bulk flow and only protons were considered.

Apart from being essential in the problem of solar angular momentum loss, the azimuthal ion motions may also provide a possible means to resolve a long standing observational puzzle, namely that alpha particles are observed to flow faster than protons in the fast solar wind. The differential streaming in the fast wind could be as pronounced as 150 km s-1 at 0.3 AU before decreasing to about 40 km s-1 at 1 AU (Marsch et al. 1982). Such a behavior has yet to be understood. One possible mechanism is the coupling between the azimuthal and meridional motions, facilitated by the strong magnetic field (McKenzie et al. 1979; Hollweg & Isenberg 1981). Although the Poynting flux may still be negligible (cf. Acuna & Whang  1976; Alexander & de La Torre 1995; Hu et al. 2003), the proposed coupling is expected to limit, at least to a non-trivial extent, the ion differential streaming. As pointed out by Hollweg & Isenberg (1983), one shortcoming of the formulation of McKenzie et al. (1979) is that protons are privileged over alphas: the azimuthal magnetic field is assumed to be determined entirely by the protons whose azimuthal flow is neglected. Hence the formulation cannot properly account for the azimuthal dynamics of protons or alphas. In addition, the formulae are applicable only to the equatorial plane where the slow solar wind prevails at solar minimum.

The goal of this paper is to extend the Weber-Davis model by including alpha particles self-consistently. This approach allows us to assess the individual contributions of ion flows and magnetic stresses to the angular momentum loss of the Sun. The effect of the coupling between azimuthal and meridional motions in limiting the proton-alpha differential streaming will also be explored quantitatively. Given that the differential streaming is more prominent in the fast wind, which in general flows out of the equatorial plane, it is necessary to formulate the model such that it treats both protons and alphas on an equal footing, and allows the solar wind to flow outside the equatorial plane. In this sense, this paper also extends the model of McKenzie et al. (1979).

The paper is organized as follows. The derivation of the governing equations is given in the appendix. Section 2 details the physical model and also describes the assumptions on the background poloidal magnetic field and the ion heating mechanism. A general analysis is then given in Sect. 3. Section 4 presents the numerical results and the effect of the solar rotation. In Sect. 5, the main results are summarized.

  
2 Model

The solar wind is assumed to consist of electrons (e), protons (p) and alpha particles ($\alpha$). Since the role of alpha particles is not necessarily minor, their contribution has to be self-consistently taken into account (Li et al. 1997). This is done by rewriting the momentum equations (Schunk 1977) in the flux tube frame, instead of the standard spherical coordinate system ( $r, \theta, \phi$). Central to the derivation is that the ion-cyclotron frequency $\Omega_k = Z_k e B_l/m_k c$ is many orders of magnitude higher than any other frequency present in the ion momentum equations (McKenzie et al. 1979). Here mk is the mass of ion species k ( $k=\rm p, \alpha$), Zk is the charge of species k in units of the electron charge e, Bl denotes the meridional magnetic field strength, and c is the speed of light. The derivation is provided in the appendix, the resulting governing equations are quoted here to save space.

   
2.1 Governing equations

As described in Appendix A, in addition to the impicit assumptions in deriving the five-moment transport equations (Schunk 1977), we make the following assumptions:
1.
axial symmetry is assumed ( $\partial/\partial\phi\equiv 0$);
2.
the electron inertia is neglected in the electron momentum equation;
3.
quasi-neutrality is assumed;
4.
both viscosity and resistivity are neglected;
5.
quasi-zero current is assumed, the only exception to this occurs when ion momentum equations are derived;
6.
the electric field in the magnetic induction law is convected by electrons, i.e., contributions like Hall effects are neglected;
7.
the Spitzer law is used for the field-aligned electron heat flux, and the ion heat fluxes are neglected;
8.
we are only interested in steady state solutions. However, time-dependent equations are solved to yield steady state solutions.

Given these assumptions, the governing equations take the form

       
                                     $\displaystyle \frac{\partial n_k}{\partial t} +\frac{1}{a}\frac{\partial}{\partial l} \left(n_k v_{k l} a\right) =0,$ (1)
    $\displaystyle \frac{\partial v_{k l}}{\partial t} + v_{k l}\frac{\partial v_{k ... ..._k}{\partial l} +\frac{Z_k}{n_{\rm e} m_k}\frac{\partial p_{\rm e}}{\partial l}$  
    $\displaystyle \qquad+ \frac{G M_\odot}{r} \frac{\partial}{\partial l}\ln r -\fr... ...delta t} +\frac{Z_k n_k}{n_{\rm e}}\frac{\delta M_{{\rm e} l}}{\delta t}\right)$  
    $\displaystyle \qquad- v_{k\phi}^2\frac{\partial }{\partial l}\ln r\sin\theta$  
    $\displaystyle \qquad+ \tan\Phi\left[ v_{k l}\left(\frac{\partial}{\partial l} v_{k\phi} +v_{k\phi}\frac{\partial}{\partial l}\ln r\sin\theta \right)\right.$  
    $\displaystyle \qquad- \left. \frac{1}{n_k m_k}\left(\frac{\delta M_{k\phi}}{\de... ...frac{Z_k n_k}{n_{\rm e}}\frac{\delta M_{\rm e\phi}}{\delta t}\right)\right] =0,$ (2)
    $\displaystyle \frac{\partial T_{\rm e}}{\partial t} +v_{{\rm e} l}\frac{\partia... ... e} l}a) -\frac{\gamma-1}{n_{\rm e} k_{\rm B}}\frac{\delta E_{\rm e}}{\delta t}$  
    $\displaystyle \qquad-\frac{\gamma-1}{n_{\rm e} k_{\rm B} a} \frac{\partial}{\pa... ...m e} T_{\rm e}^{5/2} \frac{\partial T_{\rm e}}{\partial l}\cos^2\Phi\right) =0,$ (3)
    $\displaystyle \frac{\partial T_k}{\partial t} + v_{k l}\frac{\partial T_k}{\par... ...partial l}(v_{k l}a) -\frac{\gamma-1}{n_k k_{\rm B}}\frac{\delta E_k}{\delta t}$  
    $\displaystyle \qquad-\frac{\gamma-1}{n_k k_{\rm B}} Q_k =0,$ (4)
    $\displaystyle \frac{\partial}{\partial t}v_{p \phi} + v_{{\rm p} l} \left(\frac... ...} v_{\rm p\phi} +v_{\rm p\phi}\frac{\partial}{\partial l}\ln r\sin\theta\right)$  
    $\displaystyle \qquad+ \frac{n_\alpha m_\alpha}{n_{\rm p} m_{\rm p}} v_{\alpha l... ...v_{\alpha\phi} +v_{\alpha\phi}\frac{\partial}{\partial l}\ln r\sin\theta\right)$  
    $\displaystyle \qquad-\frac{B_l}{4\pi n_{\rm p} m_{\rm p}}\left(\frac{\partial}{\partial l} B_\phi +B_\phi \frac{\partial}{\partial l}\ln r\sin\theta\right) =0,$ (5)
    $\displaystyle \frac{\partial}{\partial t}B_{\phi} + \frac{r\sin\theta}{a}\frac{... ...ac{a}{r\sin\theta}\left(B_\phi v_{{\rm e} l}-v_{\rm e\phi}B_l\right)\right] =0,$ (6)
    $\displaystyle (v_{\alpha \phi}-v_{\rm p\phi})=\frac{B_\phi}{B_l}(v_{\alpha l}-v_{{\rm p} l}),$ (7)

where $n_{\sf s}$, $\vec{v}_{\sf s}$ and $T_{\sf s}$ denote the number density, velocity and temperature of species ${\sf s}$ ( ${\sf s}=\rm e,p,\alpha$), respectively. The species pressure is $p_{\sf s}= n_{\sf s} k_{\rm B} T_{\sf s}$, where $k_{\rm B}$ is the Boltzmann constant. By assuming quasi-neutrality and quasi-zero current, we have $n_{\rm e}=\sum_{k}Z_k n_k$ and $\vec{v}_{\rm e}= \sum_{k}Z_k n_k \vec{v}_k/ n_{\rm e}$ ( $k = p, \alpha$). G is the gravitational constant, $M_\odot$ is the solar mass, and $\gamma=5/3$ is the adiabatic index. Coordinate l measures the arclength of the poloidal magnetic field line from the footpoint at the coronal base. Both the heliocentric distance r and colatitude $\theta$ are evaluated along the poloidal magnetic field. The cross-sectional area of the flux tube, a, scales as $a \propto 1/B_l$. $\Phi $ is the magnetic azimuthal angle, defined by $\tan\Phi=B_\phi/B_l$. The poloidal magnetic field Bl and the heat deposition to ion species k, denoted by Qk, will be specified in Sects. 2.2 and 2.3, respectively.
  \begin{figure} \par\includegraphics[width=16.2cm,clip]{4624fig1.eps} \end{figure} Figure 1: a) The poloidal magnetic field configuration given as contours of the magnetic flux function. The equator points upward. The line of force on which the model equations are solved is displayed by the thick contour. This field line is located at $\theta =70^\circ $ at 1 AU and originates from $31.5^\circ $ on the Sun. b) Radial distribution of the poloidal magnetic field strength Bl along the designated field line. At 1 AU, Bl is $3.3\gamma $.
Open with DEXTER

The energy and momentum exchange rates $\delta E_{\sf s} /\delta t$ and $\delta \vec {M}_{\sf s}/\delta t$ are due to Coulomb collisions of species ${\sf s}$ with all the remaining ones (Schunk 1977),

  
                             $\displaystyle \frac{\delta \vec{M}_{\sf s}}{\delta t}$ = $\displaystyle \sum_{\sf t} n_{\sf s} m_{\sf s}\nu_{\sf st}\Phi_{\sf st} \left(\vec{v}_{\sf t}-\vec{v}_{\sf s}\right),$ (8)
$\displaystyle \frac{\delta E_{\sf s}}{\delta t}$ = $\displaystyle \sum_{\sf t} \frac{n_{\sf s} m_{\sf s} \nu_{\sf st}}{m_{\sf s}+m_... ...si_{\sf st} +m_{\sf t}(\vec{v}_{\sf t}-\vec{v}_{\sf s})^2\Phi_{\sf st}\right] .$ (9)

Expressions for the collision frequency $\nu_{\sf st}$ as well as correction factors $\Phi_{\sf st}$ and $\Psi_{\sf st}$ have been given by, e.g., Li et al. (1997) and will not be repeated here. In the computation, the Coulomb logarithm $\ln\Lambda$ is taken to be 21. The electron thermal conductivity  $\kappa_{\rm e}$ in Eq. (3) is $7.8\times 10^{-7}$ erg K-7/2 cm-1 s-1 (Spitzer 1962).

   
2.2 Background poloidal magnetic field

To avoid complications associated with the cross-field force balance, we choose to prescribe the background poloidal magnetic field by adopting an analytical model given in Banaszkiewicz et al. (1998). In the present implementation, the model magnetic field consists of dipole and current-sheet components only. A set of parameters M=3.6222, Q=0, K=1.0534 and a1=2.5 are chosen such that the last open magnetic field line is anchored at $\theta=40^\circ$ on the Sun, and the poloidal magnetic field strength is 3.3$\gamma$ at $\theta =70^\circ $ at 1 AU, compatible with Ulysses measurements (Smith & Balogh 1995).

Figure 1a shows the magnetic field configuration in the meridional plane. The thick solid line represents the field line along which we will find solar wind solutions. This field line is rooted at colatitude  $31.5^\circ $ on the Sun, and reaches $70^\circ$ at 1 AU, which corresponds to the edge of the fast stream observed by Ulysses (McComas et al. 2000). Plotted in Fig. 1b is the radial profile of the poloidal magnetic field strength Bl along the designated field line.

   
2.3 Ion heating

To produce fast solar wind solutions, an empirical energy flux, launched from the Sun and in the direction of $\vec{B}$, is assumed to heat ions only. This energy flux is assumed to dissipate at a rate Q with a characteristic length $l_{\rm d}$, i.e.,

 \begin{displaymath}Q=F_{\rm E} \frac{B_l}{B_{l \rm E} l_{\rm d}}\exp\left(-\frac{l}{l_{\rm d}}\right), \end{displaymath} (10)

where $F_{\rm E}$ is the input empirical flux scaled to the orbit of the Earth, $R_{\rm E} = 215$ $R_\odot$, $R_\odot$ being the solar radius. Moreover, $B_{l\rm E}$ is the poloidal magnetic field strength at $R_{\rm E}$. Q is then assumed to be apportioned between protons and alpha particles by
 
$\displaystyle Q_{\alpha}= \frac{\Delta}{1+\Delta}, Q_{\rm p}= \frac{1}{1+\Delta}, % \Delta=\frac{\rho_{\alpha}}{\rho_{\rm p}} \chi ,$     (11)

where $\rho_k = n_k m_k$ ( $k=\rm p, \alpha$) is the ion mass density, and $\chi$ is a parameter indicating the degree by which the alpha particles are preferentially heated, with $\chi\equiv 1$ standing for the neutral heating: heating rate per ion is proportional to its mass.

In the computations, the following parameters

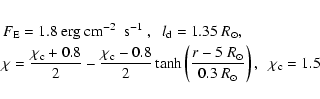
\begin{eqnarray*}&&F_{\rm E} = \mbox{1.8~erg~cm$^{-2}$ ~s$^{-1}$ }, \hskip 0.2cm... ...-5~R_\odot}{0.3 ~R_\odot}\right), \hskip 0.2cm \chi_{\rm c}=1.5 \end{eqnarray*}


are chosen to yield a fast solar wind solution. As can be seen, $\chi$ varies smoothly from $\chi_{\rm c}$ in the inner corona to 0.8 far from the Sun with a rather steep transition occurring at 5 $R_\odot$. A preferential heating that favors alpha particles in the inner corona ( $\chi_{\rm c}>1$) is necessary to produce a positive relative speed $v_{\alpha l}-v_{{\rm p} l}$.

   
3 General analysis

Before solving Eqs. (1) to (7) to find solar wind solutions, one can conduct an analysis to reach some general conclusions.

   
3.1 Alignment conditions

Equation (6) derives from the $\phi$ component of the magnetic induction law. For a steady state, it can be integrated to yield
 
$\displaystyle v_{\rm e\phi} -\Omega r\sin\theta=\frac{B_\phi}{B_l} v_{{\rm e} l}.$     (12)

The constant of integration $\Omega$ can be identified as the angular rotation rate of the flux tube. Combining Eqs. (7) and (12), one finds
 
$\displaystyle v_{\rm p\phi} -\Omega r\sin\theta=\frac{B_\phi}{B_l} v_{{\rm p} l... ...space{1cm} v_{\alpha\phi} -\Omega r\sin\theta=\frac{B_\phi}{B_l} v_{\alpha l} .$     (13)

That is, in the frame strictly corotating with the Sun, all species (electrons, protons and alpha particles) flow along the magnetic field. The alignment conditions were first recognized by Parker (1958), and have been extended to general axisymmetrical MHD flows by, e.g., Low & Tsinganos (1986) and Hu et al. (2003).

   
3.2 Angular momentum conservation law

In a steady state, Eq. (5) leads to
 
$\displaystyle r\sin\theta\left[v_{\rm p\phi}+\frac{\rho_\alpha v_{\alpha l}}{\r... ... v_{\alpha\phi} -\frac{B_\phi B_l}{4\pi\rho_{\rm p} v_{{\rm p} l}} \right] = L,$     (14)

where the tube invariant L comes from the integration. The physical meaning of L can be better seen by noting that the constant
 
$\displaystyle {\cal L} = \rho_{\rm p} v_{{\rm p} l} L \frac{a}{a_{\rm E}} R_{\rm E}^2 = {\cal L}_p + {\cal L}_\alpha +{\cal L}_{\rm M}$     (15)

is the angular momentum loss per solid angle, where
 
$\displaystyle {\cal L}_k = r\sin\theta \rho_k v_{k l} v_{k\phi} \frac{a}{a_{\rm... ...\cal L}_M = -r\sin\theta\frac{B_\phi B_l}{4\pi} \frac{a}{a_{\rm E}}R_{\rm E}^2,$     (16)

with $k=\rm p, \alpha$. Subscript E denotes values evaluated at $R_{\rm E}=1$ AU. Obviously, both outflowing particles and magnetic stresses contribute to the angular momentum flux.

The conservation law for the angular momentum, Eq. (14), is valid for an arbitrary flux tube in an azimuthally symmetric solar wind. The single-fluid version (or equivalently the two-fluid one) of this conservation law has already been obtained by, e.g., Low & Tsinganos (1986) and Hu et al. (2003).

   
3.3 Expressions for ${v}_{{\rm p} \phi }$, ${v}_{\alpha \phi }$ and B$_\phi $

The alignment condition, Eq. (13), together with Eq. (14) leads to
   
                           $\displaystyle v_{\rm p\phi}$ = $\displaystyle \frac{\Omega r\sin\theta}{M_T^2-1} \left[M_{\rm p}^2\frac{L}{\Ome... ...^2\theta}-1 + M_\alpha^2\frac{v_{\alpha l}-v_{{\rm p} l}}{v_{\alpha l}}\right],$ (17)
$\displaystyle v_{\alpha\phi}$ = $\displaystyle \frac{\Omega r\sin\theta}{M_T^2-1} \left[M_{\rm p}^2\frac{L}{\Omega r^2\sin^2\theta}-1 \right.$  
    $\displaystyle +\left. M_{\rm p}^2\frac{v_{\alpha l}-v_{{\rm p} l}}{v_{{\rm p} l}} \left(\frac{L}{\Omega r^2\sin^2\theta}-1\right)\right],$ (18)
$\displaystyle B_{\phi}$ = $\displaystyle \frac{4\pi\rho_{\rm p} v_{{\rm p} l}}{B_l r\sin\theta} \frac{L-\l... ...\alpha l}}{\rho_{\rm p} v_{{\rm p} l}}\right) \Omega r^2\sin^2\theta}{M_T^2-1},$ (19)

where MT, $M_{\rm p}$ and $M_\alpha$ are defined as
 
$\displaystyle M_T^2 = M_{\rm p}^2+M_\alpha^2, \hskip 0.2cm M_k^2=\frac{v_{k l}^2}{B_l^2/4\pi\rho_k},$     (20)

with $k=\rm p, \alpha$. The poloidal Alfvénic Mach number MT is thus comprised of both $M_{\rm p}$ and $M_\alpha$.

For the solar wind, $M_T \ll 1$ is valid near 1 $R_\odot$, but $M_T \gg 1$ holds at 1 AU. Hence, there must exist a point between 1 $R_\odot$ and 1 AU where MT=1. At this location, which will be termed the Alfvénic point, $B_\phi$ is singular unless the numerator in Eq. (19) vanishes,

 
$\displaystyle L = \left(1+\frac{\rho_\alpha v_{\alpha l}}{\rho_{\rm p} v_{{\rm p} l}}\right) \Omega r_{\rm a}^2\sin^2\theta_{\rm a},$     (21)

where subscript a denotes values at the Alfvénic point. We have employed the fact that the ion mass flux ratio $\rho_\alpha v_{\alpha l}/\rho_{\rm p} v_{{\rm p} l}$ is a constant. The angular momentum loss per solid angle then becomes
$\displaystyle {\cal L} = \dot{M} \Omega r_{\rm a}^2 \sin^2\theta_{\rm a},$     (22)

where

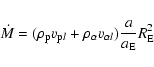
\begin{eqnarray*}\dot{M} = (\rho_{\rm p} v_{{\rm p} l}+\rho_\alpha v_{\alpha l})\frac{a}{a_{\rm E}}R_{\rm E}^2 \end{eqnarray*}


is the mass loss rate per solid angle of the solar wind.

Hence the conclusion of Weber & Davis (1967) still holds: the magnetic field helps the coronal plasma to achieve an effective corotation to the Alfvénic point, as long as the poloidal Alfvénic Mach number MT is defined by Eq. (20).


  \begin{figure} \par\includegraphics[width=16.4cm,clip]{4624fig2.eps} \end{figure} Figure 2: Results derived from a 1.5D 3-fluid solar wind model which incorporates the azimuthal components self-consistently. The radial distribution of a) the densities of protons $n_{\rm p}$ and alpha particles $n_\alpha $ (solid lines), as well as electrons $n_{\rm e}$ (dashed line), b) the poloidal flow speeds of protons ( $v_{{\rm p}l}$) and alphas ( $v_{\alpha l}$), and c) the temperatures of electrons ($T_{\rm e}$), protons ($T_{\rm p}$) and alpha particles ($T_\alpha $). The error bars in a) are the upper and lower limits for the electron density derived by Fisher & Guhathakurta (1995). The error bars in c) represent the uncertainties of UVCS measurements for the effective proton temperature reported by Kohl et al. (1998). Please note that both measurements are made for polar coronal holes.
Open with DEXTER

   
3.4 Energy conservation law

Combining the governing equations in the steady state, one can derive an energy conservation law,

 
                               $\displaystyle \frac{a}{a_{\rm E}}\left[\rho_{\rm p} v_{{\rm p} l}\frac{v_{{\rm ... ...}{2} +\rho_\alpha v_{\alpha l}\frac{v_{\alpha l}^2+v_{\alpha\phi}^2}{2} \right]$  
    $\displaystyle \qquad+ \left(\rho_{\rm p} v_{{\rm p} l}+\rho_\alpha v_{\alpha l}\right)\frac{a}{a_{\rm E}} {G M_\odot}\left(\frac{1}{R_\odot}-\frac{1}{r}\right)$  
    $\displaystyle \qquad+ \frac{a}{a_{\rm E}} \frac{B_\phi}{4\pi}\left(v_{{\rm e} l}B_\phi-v_{\rm e\phi}B_l\right)$  
    $\displaystyle \qquad+ \frac{a}{a_{\rm E}}\frac{\gamma}{\gamma-1} \left(p_{\rm e} v_{{\rm e} l} + p_{\rm p} v_{{\rm p} l} +p_\alpha v_{\alpha l}\right)$  
    $\displaystyle \qquad- \frac{a}{a_{\rm E}}\kappa_{\rm e} T_{\rm e}^{5/2}\frac{\partial T_{\rm e}}{\partial l}\cos^2\Phi$  
    $\displaystyle \qquad+ \int_{r}^{R_{\rm E}}\frac{a}{a_{\rm E}} (Q_{\rm p}+Q_\alpha) {\rm d} l = {\cal F},$ (23)

where the constant ${\cal F}$ is the total energy flux scaled to $R_{\rm E}$. The terms on the left hand side of Eq. (23) correspond, respectively, to the kinetic and potential energy fluxes, the Poynting flux, the enthalpy flux, the electron conductive flux, and the source term due to the heat deposition. The ratio of the Poynting flux to ${\cal F}$ will be used to assess the relative importance of the Poynting flux in the energy budget.

   
4 Numerical results

Equations (1) to (7) are solved by using a fully implicit numerical scheme (Hu et al. 1997). From an arbitrary initial guess, the equations are advanced in time until a steady state is achieved. The computational domain extends from 1 $R_\odot$ to 1.2 AU. At 1 $R_\odot$, ion densities as well as species temperatures are fixed,

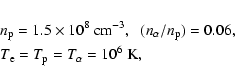
\begin{eqnarray*}&& n_{\rm p}=1.5\times 10^8~ \mbox{cm}^{-3}, \hskip 0.2cm (n_... ... T_{\rm e}=T_{\rm p} = T_{\alpha} = 10^6~\mbox{K}, \hskip 0.2cm \end{eqnarray*}


while $v_{{\rm p}l}$ and $v_{\alpha l}$ are specified to ensure mass conservation. ${v}_{{\rm p} \phi }$ and $B_\phi$ are evaluated in accordance with Eqs. (17) and (19), where L is computed at the grid point immediately adjacent to the base. At the outer boundary (1.2 AU), all dependent variables are linearly extrapolated for simplicity. We also take $\Omega=2.865\times 10^{-6}$ rad s-1. For the steady state solutions presented in this paper, the maximum relative errors in the conserved quantities are smaller than $1\%$.

Figure 2 displays the radial distribution of (a) the species densities $n_{\rm e}$, $n_{\rm p}$ and $n_\alpha $, (b) poloidal flow speeds $v_{{\rm p}l}$ and $v_{\alpha l}$, and (c) species temperatures $T_{\rm e}$, $T_{\rm p}$ and $T_\alpha $. The model yields the following parameters at 1 AU,

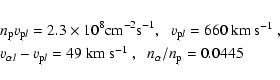
\begin{eqnarray*}&& n_{\rm p} v_{{\rm p} l} = 2.3 \times 10^8 \mbox{cm}^{-2} \mb... ...49\mbox{~km~s$^{-1}$ },\hskip 0.2cm n_\alpha/n_{\rm p} = 0.0445 \end{eqnarray*}


which agree well with the Ulysses observations of the fast wind (McComas et al. 2000). In addition, the modeled electron density fits observations reasonably well in the inner corona (Fig. 2a). However, without considering the non-thermal contribution, the modeled proton temperature is higher than that inferred from UVCS measurements (Fig. 2c). Moreover, $T_{\rm p}$ and $T_\alpha $ at 1 AU are much smaller than values given by in situ measurements (McComas et al. 2000). The poor match is due to the oversimplified heating function. As for the poloidal flow speeds, the alphas initially fall behind the protons below 2 $R_\odot$ beyond which a positive $\Delta v_l =v_{\alpha l}-v_{{\rm p} l}$ develops. $v_{\alpha l}$ reaches a maximum around 66 $R_\odot$, and starts to decrease thereafter.

To examine the differential streaming further, $\Delta v_l =v_{\alpha l}-v_{{\rm p} l}$ is plotted in Fig. 3a. The poloidal flow speeds of protons ( $v_{{\rm p}l}$) and alpha particles ( $v_{\alpha l}$) are replotted in Fig. 3b (a different scale is used, see Fig. 2b). In addition, model results from the corresponding computation that neglects the solar rotation (i.e., $\Omega\equiv 0$) are plotted as dotted lines for comparison. For the ease of description, we shall call the model with (without) azimuthal components the 1.5D (1D) model. It is found that the effect of the azimuthal components on the poloidal dynamics can be adequately represented by the flow speed profiles. Below the local maximum of 78.6 km s-1 at 7.28 $R_\odot$, Fig. 3a shows no difference in the $\Delta v_l$ profile between 1D and 1.5D models. The differential streaming, $\Delta v_l$, for both models plummets from nearly zero at the coronal base to about -44.6 km s-1 at 1.44 $R_\odot$, and rises thereafter to the local maximum. Interestingly, in the 1D model, beyond the local maximum $\Delta v_l$ undergoes only a modest decrease to 66.3 km s-1 at 1 AU, while in the 1.5D model $\Delta v_l$ is 48.7 km s-1 at 1 AU. This further reduction in the differential streaming is achieved through a slight rise in the $v_{{\rm p}l}$ profile accompanied by a modest deceleration of alpha particles (Fig. 3b).

This behavior is not surprising since in the poloidal momentum equation (Eq. (2)),

 
$\displaystyle v_{k l} \frac{\partial v_{k l}}{\partial l} -v_{k\phi}^2 \frac{\p... ...sec^2\Phi\right) -\frac{\partial}{\partial l}\frac{\Omega^2 r^2\sin^2\theta}{2}$     (24)

can be obtained when the alignment condition, Eq. (13), is used. When viewed in the frame corotating with the Sun ( $v_{k l} \sec\Phi$ is the ion speed seen in that frame), the solar rotation ensures that all particles move in the same centrifugal potential ( $\Omega^2 r^2\sin^2\theta/2$). Neglecting all other contributions, and taking the difference of the proton and alpha version of Eq. (24), one arrives at

\begin{eqnarray*}\frac{\partial}{\partial l}\left[\left(v_{\alpha l}^2 -v_{{\rm p} l}^2\right)\sec^2\Phi\right] = 0 , \end{eqnarray*}


or
$\displaystyle \left(v_{\alpha l}^2-v_{{\rm p} l}^2\right) \propto \cos^2\Phi.$     (25)

With the development of the magnetic azimuthal angle, $\cos^2\Phi$ decreases monotonically with increasing distance (cf. Fig. 4a). As a consequence, the differential streaming  $\Delta v_l$ decreases. Figure 3 can be seen as a direct illustration of the effect of solar rotation in limiting the ion differential streaming, predicted by McKenzie et al. (1979) and Hollweg & Isenberg (1981).

Figure 4 displays the radial profiles of (a) $-\tan\Phi=-B_\phi/B_l$, (b) the azimuthal speeds of protons ( ${v}_{{\rm p} \phi }$), alpha particles ( ${v}_{\alpha \phi }$) and electrons ( $v_{\rm e\phi }$), and (c) the specific contribution of protons ( $\xi _{\rm p} = {\cal L}_{\rm p}/{\cal L}$), alpha particles ( $\xi _\alpha = {\cal L}_\alpha /{\cal L}$) and the magnetic stresses ( $\xi _{\rm M} = {\cal L}_{\rm M}/{\cal L}$) to the angular momentum flux (cf. Eq. (15)). In addition, the sum $\xi_{\rm p} +\xi_\alpha$, which gives the overall particle contribution $\xi_{\rm P}$, is also plotted. Given in dotted line is $\zeta $, the ratio of the Poynting flux to the total energy flux (cf. Eq. (23)). In Fig. 4c, the dashed line is used to plot negative values. The asterisks in Fig. 4b denote the Alfvénic point, which is located at $r_{\rm a}=11.8~ R_\odot$.

  \begin{figure} \par\includegraphics[width=12cm,clip]{4624fig3.eps} \end{figure} Figure 3: Radial distributions of a) the differential streaming, $v_{\alpha l}-v_{{\rm p} l}$, and b) the poloidal flow speeds of protons ( $v_{{\rm p}l}$) and alpha particles ( $v_{\alpha l}$). Solid lines are used to plot the 1.5D model, whereas dotted lines are used for the corresponding 1D model which neglects the solar rotation.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=17cm,clip]{4624fig4.eps} \end{figure} Figure 4: Radial distributions of a) $-\tan\Phi=-B_\phi/B_l$ where $\Phi $ is the magnetic azimuthal angle, b) the azimuthal speeds of protons ${v}_{{\rm p} \phi }$, alpha particles ${v}_{\alpha \phi }$ as well as electrons $v_{\rm e\phi }$, c) the relative importance of the proton fluid $\xi _{\rm p} = {\cal L}_{\rm p}/{\cal L}$, the alpha fluid $\xi _\alpha = {\cal L}_\alpha /{\cal L}$, the sum of the two $\xi _{\rm P} = \xi _{\rm p}+\xi _\alpha $, and the magnetic stresses $\xi _{\rm M} = {\cal L}_{\rm M}/{\cal L}$ in the total angular momentum loss of the Sun (please see Eq. (16) in text). In addition, the ratio of the Poynting flux to the total energy flux, $\zeta $, is plotted as dotted line. The dashed line represents negative values. In panel b), the asterisks denote the Alfvénic point, where the poloidal Alfvénic Mach number (defined by Eq. (20)) equals unity.
Open with DEXTER

From Fig. 4a, it is obvious that only beyond, say 10 $R_\odot$, does a spiral angle $\Phi $ develop. This can be explained in view of Eqs. (12), (13): within 10 $R_\odot$ the left hand side is much smaller than the poloidal flow speed on the right hand side for any species. On the other hand, in interplanetary space, the species azimuthal speed is much smaller than $\Omega r\sin\theta$, the Parker theory for the spiral magnetic field is recovered, i.e., $\tan\Phi =B_\phi/B_l \approx -\Omega r\sin\theta/v_l$, where vl can be taken as the poloidal speed of any species.

In the inner corona, both protons and alpha particles tend to corotate with the Sun: ${v}_{{\rm p} \phi }$ and ${v}_{\alpha \phi }$ are positive (Fig. 4b). The azimuthal speed of the alpha particles is slightly larger than that of the protons below 2 $R_\odot$, and from there on, the alpha particles are gradually turned opposite to the solar rotation. ${v}_{\alpha \phi }$ becomes negative beyond 5.71 $R_\odot$, eventually ${v}_{\alpha \phi }$ reaches -24.7 km s-1 at 1 AU. On the other hand, the proton azimuthal speed ${v}_{{\rm p} \phi }$ increases from a local minimum of 0.78 km s-1 at 12.5 $R_\odot$ monotonically to 4.8 km s-1 at 1 AU.

The behavior of the azimuthal flow speeds can be explained by Eqs. (17) and (18). Near the coronal base, both $M_{\rm p}^2$ and $M_\alpha^2$ are far from unity. It then follows from Eqs. (17) and (18) that

 
$\displaystyle v_{\rm p\phi}\approx \Omega r\sin\theta, \hskip 0.2cm v_{\alpha\phi}\approx \Omega r\sin\theta .$     (26)

At $r \le 2\mbox{~}R_\odot$, a negative $\Delta v_l$ makes ${v}_{\alpha \phi }$ slightly larger than ${v}_{{\rm p} \phi }$. For $r > r_{\rm a}$, the solar wind expands almost radially. As a result, $M_k^2/v_{k l} = (4\pi \rho_k v_{k l}/B_l)/B_l \propto r^2$ ( $k=\rm p, \alpha$) holds fairly accurately. The variation of $v_{{\rm p}l}$ beyond $r_{\rm a}$ is very modest. We therefore have $M_{\rm p}^2\gg 1$ for $r\gg r_{\rm a}$. From the identity $M_\alpha^2/M_{\rm p}^2=\eta v_{\alpha l}/v_{{\rm p} l} $, it follows that $M_\alpha^2$ is a substantial fraction of $M_{\rm p}^2$ given that the ion mass flux ratio $\eta=\rho_\alpha v_{\alpha l}/\rho_{\rm p} v_{{\rm p} l}$ is 0.19 in this solution. Hence close to 1 AU, the azimuthal speeds of both protons and alphas are determined by the terms associated with the differential streaming in Eqs. (17) and (18), namely, for $r\gg r_{\rm a}$,
    $\displaystyle v_{\rm p\phi}\approx \Omega r\sin\theta \frac{\eta}{1+\eta {v_{\alpha l}/v_{{\rm p} l}}}\frac{v_{\alpha l}-v_{{\rm p} l}}{v_{{\rm p} l}},$  
    $\displaystyle v_{\alpha\phi}\approx -\Omega r\sin\theta \frac{1}{1+\eta {v_{\alpha l}/v_{{\rm p} l}}}\frac{v_{\alpha l}-v_{{\rm p} l}}{v_{{\rm p} l}}\cdot$ (27)

As a result, $v_{\rm p\phi}/v_{\alpha\phi}\approx -\eta$ holds. However, this asymptotic behavior of the ion azimuthal speeds for $r\gg r_{\rm a}$ does not hold in general. If the alpha abundance is far from unity, the azimuthal magnetic field will be solely determined by protons, and ${v}_{{\rm p} \phi }$ should behave like $v_{\rm p\phi}\propto r^{-1}$ for $r\gg r_{\rm a}$ when the differential streaming term in Eq. (17) is neglected.

Now let us move on to Fig. 4c. It can be seen that, from the coronal base to 1 AU, magnetic stresses play a dominant role in the total angular momentum budget, the particle contribution $\xi_{\rm P}$ is no more than $2.6\%$. However, the individual angular momentum flux carried by protons or alpha particles is not necessarily small in magnitude. As a matter of fact, protons contribute more to the total angular momentum flux than magnetic stresses do beyond 101 $R_\odot$. However the proton contribution is virtually canceled by the alpha particles that counter-rotate with the Sun. This can be understood in light of Eqs. (17) and (18). As has been described, far away from the Alfvénic point, $r\gg r_{\rm a}$, both ${v}_{{\rm p} \phi }$ and ${v}_{\alpha \phi }$ are mainly determined by the terms associated with the differential streaming. From the identity $\rho_\alpha v_{\alpha l} M_{\rm p}^2/v_{{\rm p} l}\equiv \rho_{\rm p} v_{{\rm p} l} M_\alpha^2/v_{\alpha l}$, one can see that for $r\gg r_{\rm a}$, $\xi_\alpha$ and $\xi_{\rm p}$ tend to have the same magnitude but opposite sign. At this point, we can also see from the dotted line in Fig. 4c that although the solar rotation introduces appreciable difference in the meridional dynamics, the Poynting flux never exceeds $0.12\%$ of the total energy budget. Needless to say, its contribution to the solar wind acceleration is in fact determined by its difference between 1 $R_\odot$ and 1 AU.

At 1 AU, the model yields a total angular momentum loss of ${\cal L} =0.17\times 10^{30}$ dyne cm sr-1, in which the magnetic part is ${\cal L}_{\rm M}= 0.165 \times 10^{30}$ dyne cm sr-1, consistent with measurements (Pizzo et al. 1983; Marsch & Richter 1984). However, the absolute azimuthal speed ${v}_{{\rm p} \phi }$ or ${v}_{\alpha \phi }$ is larger than the measured values (although these quantities can only be determined with a modest precision). Moreover, $\xi_{\rm P}$ never turns negative, in this sense at variance with the measurements: Pizzo et al. (1983) and Marsch & Richter (1984) showed that particles in the fast wind tend to carry a negative angular momentum flux. Pizzo et al. (1983) suggested that the discrepancies between the model and measurements may be removed by including the stream interaction in the super-Alfvénic region. This is however beyond the scope of this paper.

  
5 Concluding remarks

The main aim of this paper is to extend the Weber-Davis analysis (Weber & Davis 1967) on the transport of the angular momentum from the Sun by including alpha particles and by allowing the solar wind to flow out of the equatorial plane in an axisymmetrical configuration. Following McKenzie et al. (1979), we exploit the fact that the gyro-frequency of ions is many orders of magnitude higher than any other frequency in ion momentum equations. From this it follows that the difference between proton and alpha velocities must be in the direction of the magnetic field. Using this alignment condition, the governing equations are then derived from the standard five-moment transport equations.

The model equations also enable us to examine quantitatively the effect of azimuthal components in limiting the proton-alpha differential streaming in the fast wind. For simplicity, we choose to solve the governing equations on a prescribed poloidal magnetic field line located at a colatitude of $70^\circ$ at 1 AU, corresponding to the edge of the fast stream observed by Ulysses at solar minimum conditions (McComas et al. 2000). The effects of the azimuthal components on the meridional dynamics, if any, are optimal in this regard. These effects are directly shown by a comparison of two models with and without azimuthal components.

The main results can be summarized as follows:

1.
The general analysis concludes that, in agreement with the Weber-Davis model, the magnetic field helps the coronal plasma to achieve an effective corotation from the coronal base to the Alfvénic radius, where the poloidal Alfvénic Mach number MT=1. MT has to include the contribution from alpha particles (Eq. (20)).

2.
In the low latitude fast solar wind, the angular momentum loss from the Sun is almost entirely due to magnetic stresses. The proton contribution, which can be as important as the magnetic one in interplanetary space, is offset by alpha particles that develop an azimuthal speed in the direction of counter-rotation with the Sun.
3.
The Poynting flux associated with the azimuthal components is negligible. Nevertheless, the solar rotation has an appreciable effect in limiting the proton-alpha differential streaming in fast solar wind streams at low latitudes in interplanetary space.
Although the fast solar wind solution is largely compatible with in situ measurements in terms of the ion mass fluxes and terminal speeds, it fails in a detailed fashion. For instance, the model is not able to predict a proton temperature profile consistent withUVCS measurements in the inner corona, nor does it predict an ion differential speed as large as 150 km s-1 at 0.3 AU to be comparable with the Helios observation (Marsch et al. 1982). Hence, including the azimuthal components cannot solely account for the deceleration of alphas relative to protons in interplanetary space. More sophisticated mechanisms, the ion-cyclotron resonance for instance, are expected to alleviate the discrepancies (e.g., Li 2003), but can hardly help achieve a satisfactory match (e.g., Hu & Habbal 1999). Nevertheless, such a direction is for sure worth pursuing and is left for a future study.

The model also suffers from the inconsistency that the force balance in the direction perpendicular to the poloidal magnetic field is replaced by prescribing a background magnetic field. In a more rigorous treatment, the poloidal magnetic field should be derived self-consistently. In principle, such a task can be accomplished by adopting an iterative approach: the parallel and perpendicular force balance are solved alternately until a convergence is met (Pneuman & Kopp 1971; Sakurai 1985). By doing so, the angular momentum loss from the Sun can be obtained self-consistently for all poloidal flux tubes. An accurate estimate of the duration over which the angular momentum of the Sun is completely removed is then possible (see Hu et al. 2003).

The present paper is aimed at presenting a rather general analysis of the angular momentum loss from a magnetized rotating object for flows assuming axial symmetry and incorporating two major ion species. Although for the present Sun, the centrifugal and magnetic forces are so weak that they have little impact on the meridional dynamics (especially below the Alfvénic point), a similar study as presented in the text can be carried out for stars that rotate at a faster rate or have a stronger magnetic field than the Sun.

Acknowledgements
This research is supported by a PPARC rolling grant to the University of Wales Aberystwyth. We thank Shadia Rifai Habbal for her input. We thank the anonymous referee for his/her comments which helped to improve this paper.

References

 

  
Online Material

Appendix A: Derivation of the governing equations

In this appendix, it is shown how the 5-moment transport equations are reduced to the governing equations in Sect. 2.1. The approach adopted here closely follows that by McKenzie et al. (1979; see also Hollweg & Isenberg 1981). The original derivation of McKenzie et al. (1979) is restricted to the equatorial flow, and ions other than protons are treated as test particles. Employing the same spirit, we extend their derivation to general flows assuming axial symmetry. In addition, all ion species are treated on an equal footing, which is particularly important for the solar wind since alpha particles can not be seen as test particles. The central point is that, due to the presence of a strong magnetic field (in the sense that the ion gyro-frequency is many orders of magnitude higher than any other frequency in the momentum equations), the difference vector between proton and alpha velocities must be aligned with the magnetic field.

A.1 General momentum equation

First of all, let us examine the momentum equation for species ${\sf s}$ (Schunk 1977),

 
$\displaystyle n_{\sf s} m_{\sf s} \left[ \frac{\partial \vec{v}_{\sf s}}{\parti... ...\vec{v}_{\sf s}\times\vec{B}\right) -\frac{\delta\vec{M}_{\sf s}}{\delta t} =0.$     (A.1)

As usual, species ${\sf s}$ is characterized by its density $n_{\sf s}$, velocity  $\vec{v}_{\sf s}$, mass $m_{\sf s}$, electric charge $e_{\sf s}$ and pressure $p_{\sf s}$. $e_{\sf s}$ can also be measured in units of electron charge e, i.e., $e_{\sf s} = Z_{\sf s} e$ with $Z_e \equiv -1$ by definition. The momentum exchange rate $\delta \vec {M}_{\sf s}/\delta t$ is due to the Coulomb frictions. It is customary to neglect the electron inertia ( $m_{\rm e} = 0$). As a result, the electrostatic field $\vec{E}$ can be expressed as
 
$\displaystyle \vec{E}=-\frac{1}{c}\vec{v}_{\rm e}\times\vec{B} -\frac{\nabla p_... ...n_{\rm e} e}+\frac{1}{n_{\rm e} e}\frac{\delta \vec{M}_{\rm e}}{\delta t} \cdot$     (A.2)

Substituting the expression for $\vec{E}$ into the magnetic induction law

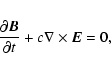
\begin{eqnarray*}\frac{\partial \vec{B}}{\partial t} +c\nabla\times\vec{E} =0 , \end{eqnarray*}


one then arrives at
 
$\displaystyle \frac{\partial \vec{B}}{\partial t}- \nabla\times\left(\vec{v}_{\rm e} \times \vec{B}\right) = 0,$     (A.3)

where $\vec{B}$ is the magnetic field. The terms in Eq. (A.2) other than the motional electric field $-\vec{v}_{\rm e}\times\vec{B}/c$ are many orders of magnitude smaller and thus have been neglected. All terms have to be kept when $\vec{E}$ is substituted into the ion momentum equation however.

The plasma in question consists of two ion species, protons (p) and an additional one (i). (Subscript i is used here to indicate that in principle the equations to be developed are also applicable if other ion species than alpha particles is considered.) As the frequency in question is well below the electron plasma frequency, the expression for $n_{\rm e}$ follows from quasi-neutrality,

$\displaystyle n_{\rm e} = n_{\rm p} + Z_{\rm i} n_{\rm i} .$     (A.4)

Neglecting the displacement current in the Ampere's law, one finds the expression for  $\vec{v}_{\rm e}$
 
$\displaystyle \vec{v}_{\rm e} = \frac{n_{\rm p}\vec{v}_{\rm p}+ Z_{\rm i} n_{\rm i}\vec{v}_{\rm i}}{n_{\rm e}} -\frac{\vec{j}}{n_{\rm e} e}, \hspace{0.5cm}$     (A.5)

where $\vec{j}=c\nabla\times\vec{B}/4\pi$ is the electric current density.

Substitution of Eq. (A.2) into Eq. (A.1) for ion species k ($k=\rm p,i$) then leads to

 
                              $\displaystyle \frac{\partial \vec{v}_k}{\partial t}+ \vec{v}_k\cdot\nabla\vec{v}_k +\frac{\nabla p_k}{n_k m_k} +\frac{Z_k\nabla p_{\rm e}}{n_{\rm e} m_k}$  
    $\displaystyle \qquad+\frac{GM_S}{r^2}\hat{r} -\frac{Z_k}{4\pi n_{\rm e} m_k}\left(\nabla\times\vec{B}\right)\times\vec{B}$  
    $\displaystyle \qquad-\frac{1}{n_k m_k}\left[\frac{\delta\vec{M}_k}{\delta t} +\frac{Z_k n_k}{n_{\rm e}}\frac{\delta\vec{M}_{\rm e}}{\delta t} \right]$  
    $\displaystyle \qquad+\frac{Z_k e}{m_k c} \frac{n_j Z_j}{n_{\rm e}} \left(\vec{v}_j-\vec{v}_k\right)\times\vec{B} =0 ,$ (A.6)

where subscript j stands for ion species other than k, namely, $j=\rm p$ for $k=\rm i$ and vice versa. Note that, when deriving Eq. (A.6), we have used Eq. (A.5) to evaluate the electron velocity $\vec{v}_{\rm e}$ in the expression for $\vec{E}$. The electric current $\vec{j}$ can be dropped when $\vec{v}_{\rm e}$ is evaluated elsewhere. This is because, in the context of the solar wind, $\vec{j}$ is the large-scale electric current and is negligible since the spatial scale at which the magnetic field evolves is well beyond the proton inertial length.

A.2 Alignment conditions for electrons

Now it becomes necessary to separate explicitly the poloidal and azimuthal components of the magnetic field and species velocities, namely,

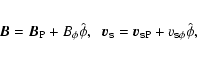
\begin{eqnarray*}\vec{B}=\vec{B}_{\rm P} + B_\phi \hat{\phi}, \hspace{0.2cm} \ve... ..._{\sf s}=\vec{v}_{{\sf s} \rm P} + v_{{\sf s} \phi} \hat{\phi}, \end{eqnarray*}


where subscript P stands for the poloidal component. The assumption of azimuthal symmetry ( $\partial/\partial\phi=0$) allows ${\vec B}_{\rm P}$ to be expressed in terms of the magnetic flux function $\psi(r, \theta; t)$, i.e.,

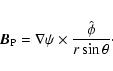
\begin{eqnarray*}\vec{B}_{\rm P}=\nabla\psi\times\frac{\hat{\phi}}{r\sin\theta}\cdot \end{eqnarray*}


The magnetic induction law, Eq. (A.3), can then be rewritten as
  
    $\displaystyle \frac{\partial{\psi}}{\partial t} + \vec{v}_{\rm eP}\cdot\nabla\psi=0,$ (A.7)
    $\displaystyle \frac{\partial B_\phi}{\partial t} + r\sin\theta\nabla\cdot\left[... ... \left(B_\phi \vec{v}_{\rm eP}-v_{\rm e\phi} \vec{B}_{\rm P}\right)\right] =0 .$ (A.8)

For a steady state, from Eq. (A.7) follows $\vec{v}_{\rm eP}\cdot\nabla\psi=0$, which is equivalent to
 
$\displaystyle \vec{v}_{\rm eP}\times\vec{B}_{\rm P} =0.$     (A.9)

In other words, the poloidal components of the electron velocity and magnetic field are strictly parallel. In light of this alignment condition, Eq. (A.8) can be shown to reduce to Eq. (6) in the text.

A.3 Equations cast in the flux tube frame

It proves useful to work in the flux tube frame, whose base vectors are

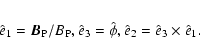
\begin{eqnarray*}\hat{e}_1=\vec{B}_{\rm P}/B_{\rm P}, \hat{e}_3=\hat{\phi}, \hat{e}_2=\hat{e}_3\times\hat{e}_1. \end{eqnarray*}


By definition, the magnetic field has only two components, i.e.,

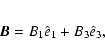
\begin{eqnarray*}\vec{B} = B_1 \hat{e}_1 +B_3 \hat{e}_3, \end{eqnarray*}


We restrict ourselves to time-independent axisymmetrical flows only. Taking the dot product of $\hat{e}_1$ with Eq. (A.6), one arrives at
 
                                         $\displaystyle v_{k1}\partial_1 v_{k1} - v_{k3}^2\partial_1\ln r\sin\theta$  
    $\displaystyle \qquad +{v_{k2}^2} \hat{e}_1\cdot(\hat{e}_2\cdot\nabla\hat{e}_2) ... ...k2}\partial_2 v_{k1} +v_{k1}v_{k2}\hat{e}_1\cdot(\hat{e}_1\cdot\nabla\hat{e}_2)$  
    $\displaystyle \qquad +\frac{1}{n_k m_k} \partial_1 p_k +\frac{Z_k}{n_{\rm e} m_k}\partial_1 p_{\rm e} +\frac{G M_\odot}{r}\partial_1\ln r$  
    $\displaystyle \qquad +\frac{Z_k}{4\pi n_{\rm e} m_k} B_3 \left(\partial_1 B_3 +B_3\partial_1 \ln r\sin\theta\right)$  
    $\displaystyle \qquad -\frac{n_j}{A_k n_{\rm e}} c_0 (v_{j1}-v_{k1}) +\Omega_{k1}\frac{B_3}{B_1}\frac{Z_j n_j}{n_{\rm e}}(v_{j2}-v_{k2}) =0.$ (A.10)

Similarly, taking the dot product of Eq. (A.6) with $\hat{e}_2$ and $\hat{e}_3$ results in, respectively,
 
                                         $\displaystyle \frac{v_{k1}^2}{\cal{R}} -v_{k3}^2\partial_2\ln r\sin\theta$  
    $\displaystyle \qquad+ v_{k2}\partial_2 v_{k2} + v_{k1}\partial_1 v_{k2} + v_{k1}v_{k2}\hat{e}_2\cdot(\hat{e}_2\cdot\nabla\hat{e}_1)$  
    $\displaystyle \qquad +\frac{1}{n_k m_k} \partial_2 p_k +\frac{Z_k}{n_{\rm e} m_k}\partial_2 p_{\rm e} +\frac{G M_\odot}{r} \partial_2\ln r$  
    $\displaystyle \qquad -\frac{Z_k}{4\pi n_{\rm e} m_k} \left[\frac{B_1^2}{\cal{R}... ...t(\partial_2\frac{B_1^2+B_3^2}{2} +B_3^2\partial_2\ln r\sin\theta\right)\right]$  
    $\displaystyle \qquad -\frac{n_j}{A_k n_{\rm e}} c_0 (v_{j2}-v_{k2})$  
    $\displaystyle \qquad +\Omega_{k1}\frac{Z_j n_j}{n_{\rm e}} \left[(v_{j3}-v_{k3})-(v_{j1}-v_{k1})\frac{B_3}{B_1}\right] =0,$ (A.11)

and
 
                                  $\displaystyle v_{k1}\left(\partial_1 v_{k3}+v_{k3}\partial_1\ln r\sin\theta \right)$  
    $\displaystyle \qquad+v_{k2}\left(\partial_2 v_{k3}+v_{k3}\partial_2\ln r\sin\theta \right)$  
    $\displaystyle \qquad-\frac{Z_k}{4\pi n_{\rm e} m_k} B_1\left(\partial_1 B_3 + B_3\partial_1\ln r\sin\theta\right)$  
    $\displaystyle \qquad-\frac{n_j}{A_k n_{\rm e}} c_0 (v_{j3}-v_{k3})$  
    $\displaystyle \qquad -\Omega_{k1}\frac{Z_j n_j}{n_{\rm e}}(v_{j2}-v_{k2}) =0,$ (A.12)

where

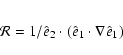
\begin{eqnarray*}{\cal R}=1 /\hat{e}_2\cdot(\hat{e}_1\cdot\nabla\hat{e}_1) \end{eqnarray*}


is the (signed) curvature radius of the poloidal magnetic field line, while

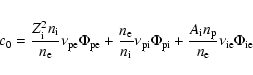
\begin{eqnarray*}c_0 = \frac{Z_{\rm i}^2 n_{\rm i}}{n_{\rm e}}\nu_{\rm pe} \Phi_... ...+\frac{A_{\rm i} n_{\rm p}}{n_{\rm e}}\nu_{\rm ie}\Phi_{\rm ie} \end{eqnarray*}


is a coefficient associated with Coulomb frictions. Here $A_{\rm i} = m_{\rm i}/m_{\rm p}$ is the mass number of species i. In addition, $\Omega_{k1}=Z_k e B_1/m_k c$ is the gyro-frequency for species k. $\partial_n = \hat{e}_n\cdot\nabla$ is the directional derivative operator along $\hat{e}_n$ (n=1,2,3).

The ion gyro-frequency is many orders of magnitude higher than any other frequency in the momentum equation. This has two consequences. First, from Eq. (A.12), vj2-vk2 is far smaller than vk3 from an order-of-magnitude estimate. Since $v_{\rm e2}=0$ (see Eq. (A.9)), both $v_{\rm p2}$ and $v_{\rm i2}$ should be very small and can be safely neglected unless they appear alongside the ion-cyclotron frequency. Second, Eq. (A.11) leads to

$\displaystyle v_{\rm i3}-v_{\rm p3}=\frac{B_3}{B_1}\left(v_{\rm i1}-v_{\rm p1}\right) .$     (A.13)

In other words, the ion velocity difference is aligned with the magnetic field. This is Eq. (7).

Solving Eq. (A.12) for vj2-vk2 and then substituting it into Eq. (A.10), one arrives at the poloidal momentum equation (Eq. (2)). It is interesting to note that the magnetic field does not appear explicitly in this equation (except for the term $\tan\Phi$), although it plays an essential role in coupling the azimuthal and meridional motions. Combining Eq. (A.12) for p and i, one can obtain Eq. (5). The partial differentiation with respect to time t in the equation is merely for numerical purpose.

In closing, we note that the p and i versions of Eq. (A.11) can be combined to yield a force balance condition in the $\hat{e}_2$ direction,

 
                                     $\displaystyle \frac{\rho_{\rm p} v_{\rm p1}^2}{\cal{R}} -\rho_{\rm p} v_{\rm p3}^2\partial_2\ln r\sin\theta$  
    $\displaystyle \qquad+\frac{\rho_{\rm i} v_{\rm i1}^2}{\cal{R}} -\rho_{\rm i} v_{\rm i3}^2\partial_2\ln r\sin\theta$  
    $\displaystyle \qquad+ \partial_2 p_{\rm p} + \partial_2 p_{\rm i} +\partial_2 p_{\rm e} +(\rho_{\rm p}+\rho_{\rm i})\frac{G M_\odot}{r} \partial_2\ln r$  
    $\displaystyle \qquad- \frac{1}{4\pi} \left[\frac{B_1^2}{\cal{R}}- \left(\partial_2\frac{B_1^2+B_3^2}{2} +B_3^2\partial_2\ln r\sin\theta\right)\right] =0.$ (A.14)

If further expressing the geometrical coefficient ${\cal R}$, the differentiation $\partial_2$ and the Lorentz force in terms of the magnetic flux function $\psi$, one can eventually derive a second-order quasi-linear partial differential equation (PDE) for $\psi$. This PDE can then be solved by using the approaches proposed by Pneuman & Kopp (1971) or Sakurai (1985).


Copyright ESO 2006